Чему равно cp – § 11. Физические основы термодинамики Основные формулы

Определение отношения cp/cv для воздуха методом клемана-дезорма

Цель работы: изучение различных изопроцессов, протекающих в газах, экспериментальное определение CP/CV для воздуха.

Приборы и принадлежности: прибор Клемана-Дезорма, манометр, насос, секундомер.

Элементы теории и метод эксперимента

Теплоемкостью CM какого-либо тела называется величина, численно равная количеству теплоты dQ, которое нужно сообщить этому телу, чтобы повысить его температуру на один кельвин:

. (1)

Теплоемкость единицы массы вещества C называется удельной теплоемкостью, теплоемкость единицы количества вещества (одного моля) C называется молярной теплоемкостью. Удельная и молярная теплоемкости связаны соотношением

, (2)

Где M – молярная масса.

Теплоемкость зависит от условий, при которых происходит нагревание тела. В частности, когда нагревание происходит при постоянном объеме, мы имеем дело с теплоемкостью при постоянном объеме (обычно обозначается как

CV). Аналогично в случае нагревания при постоянном давлении имеем дело с теплоемкостью при постоянном давлении CP.

Выведем выражения для СV и CP для одного моля идеального газа.

Изохорный процесс. Выражение для Cv

В соответствии с первым началом термодинамики количество теплоты dQ, переданное системе (например, газу), расходуется на приращение внутренней энергии DU системы и совершение системой работы dA над внешними телами

. (3)

Если нагревание происходит при постоянном объеме, то газ не совершает работы (dA=0) и вся теплота, подводимая к нему, идет на увеличение его внутренней энергии. Тогда на основе (3) и исходя из определения теплоемкости (1) можно записать, что

, (4)

Где DU – изменение внутренней энергии одного моля газа. Выражение (4) определяет молярную теплоемкость газа при постоянном объеме.

Изобарный процесс. Выражение для Cp

Если нагревание проводится при постоянном давлении P, то совершенная системой элементарная работа над внешними телами может быть определена как dA=PdV, где DV – изменение объема одного моля газа. Тогда на основе (1) и (3) можем записать, что

. (5)

Из уравнения Менделеева-Клапейрона, записанного для одного моля газа PV=RT, следует, что

.

Так как P=Const, то Dp=0 и, следовательно, PdV=RdT. Подставляя полученное выражение в (5) и учитывая (4), получаем выражение для молярной теплоемкости газа при постоянном давлении

. (6)

Из (4) и (6) следует, что всегда СP > CV.

Число степеней свободы I и его связь с теплоемкостями Cp и СV

Важным параметром идеального газа является число степеней свободы его молекулы –

I, определяющее минимальное количество координат, с помощью которых можно однозначно задать положение молекулы в пространстве. Экспериментально установлено, что при определении числа степеней свободы молекул атомы нужно рассматривать как материальные точки. Для одноатомных газов, например He, положение молекулы (а точнее, атома) в пространстве может быть задано тремя координатами: x, y,z. Соответственно и число степеней свободы молекулы такого газа I=3. Двухатомные газы, такие как N2, O2 и другие, имеют I=5. Действительно, если рассматривать молекулы таких газов как два жестко связанных атома, то для полного определения положения молекулы в пространстве необходимо помимо трех координат, определяющих положение ее центра масс, задать также два угла (j и q), определяющих ориентацию молекулы в пространстве. Степени свободы в такой молекуле можно разделить на поступательные (x, y,z) и вращательные (j и q). Вообще, число степеней свободы молекулы определяется формулой

I=νПост+νВращ+2·νКолеб,

Где VПост – число поступательных степеней свободы, νВращ – число вращательных степеней свободы, νКолеб – число колебательных степеней свободы.

Молекулярно-кинетическая теория позволяет установить связь между числом степеней свободы молекулы газа I и его теплоемкостями CP и CV. Согласно закону равнораспределения На каждую степень свободы (поступательную, вращательную и колебательную) в среднем приходится одинаковая кинетическая энергия, равная. Таким образом, энергия одной молекулы может быть записана в виде

. (7)

Внутренняя энергия одного моля идеального газа соответственно равна

. (8)

Тогда из (4) и (6) получим, что

, . (9)

Адиабатический процесс.

Уравнение Пуассона. Постоянная адиабаты γ

Процесс, протекающий без теплообмена с внешней средой, называется адиабатическим. Для вывода уравнения адиабаты идеального газа, то есть уравнения, связывающего параметры состояния идеального газа при адиабатическом процессе, воспользуемся уравнением (3) первого начала термодинамики, записывая при этом элементарную работу d

A в виде PdV и элементарное изменение внутренней энергии DU в виде , где M – масса газа. Получим

. (10)

При адиабатическом процессе DQ = 0 и выражение (10) приводится к виду

. (11)

Для дальнейшего вывода возьмем дифференциал от обеих частей уравнения Менделеева-Клапейрона

. (12)

Уравнения (11) и (12) можно привести к виду

, (13)

Где .

Левую часть этого уравнения можно представить в виде D(ln(PVγ)), откуда следует, что

PVγ=Const. (14)

Полученное уравнение адиабаты идеального газа в переменных P, V называют уравнением Пуассона.

Описание экспериментального макета.

Методика определения постоянной адиабаты γ

Экспериментальная установка состоит из баллона Б (см. рис. 1) емкостью 25 л, к которому через резиновую пробку подсоединены последовательно U-образный манометр М, краны коммутации газовых потоков К1 и К2 и насос Н, включаемый в сеть ~220 В. Положения кранов на различных этапах проведения эксперимента приведены в табл. 1.

Принцип определения постоянной адиабаты состоит в следующем. В баллон насосом нагнетается воздух до давления немного больше атмосферного (разность давлений контролируется манометром M). Затем производится выдержка воздуха в баллоне в течение некоторого промежутка времени (2…3 минуты).

При этом температура воздуха в баллоне за счет теплообмена становится равной температуре окружающей среды.

Таблица 1

№	Насос	Операция	Положение кранов К2 К1
1	Включен	Накачка воздуха В баллон
2	Выключен	Выдержка 2-3 минуты
3	Выключен	Сброс давления В баллоне. Выдержка 4, 8, 12, 16 c
4	Выключен	Изолирование баллона От атмосферы. Выдержка 2-3 минуты

Поскольку масса газа в ходе эксперимента меняется, то расчеты удобно вести для одного моля газа.

После выравнивания температур молярный объем газа будет V1, давление P1 и температура T1 (точка 1 на рис. 2).

Сообщим на короткое время полость баллона с атмосферой, установив соответствующим образом краны К1 и К2. Как только давление в баллоне станет равным атмосферному (уровни воды в коленах манометра выровняются), закроем краны, прерывая сообщение полости баллона с атмосферой. Молярный объем теперь станет равным

V2, а температура T2, что соответствует точке 2 на рис. 2. Поскольку процесс 1-2 протекает в течение короткого промежутка времени, можно пренебречь потерями теплоты за счет теплообмена через стенку баллона. Тогда переход газа из состояния 1 в состояние 2 происходит адиабатически и на участке 1-2 справедливо уравнение Пуассона

P1V1γ = P2V2γ. (15)

После 2-3 минут выдержки при закрытых кранах воздух в баллоне изохорно нагревается до первоначальной температуры T1. Давление при этом повысится вследствие нагрева до величины P3, что соответствует точке 3 на рис. 2. Кривая 1-3, таким образом, является изотермой, и для нее справедлив закон Бойля-Мариотта

P1V1=P3V2. (16)

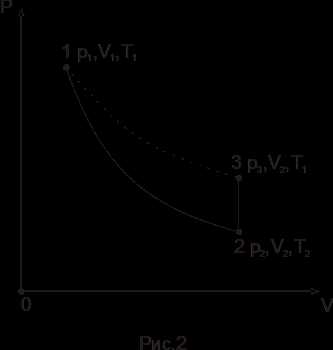
Из (15) и (16) следует, что . Логарифмируя это выражение, найдем, что

. (17)

В условиях эксперимента давление P2 равно атмосферному. Давление P1 может быть определено по формуле

P1=P2+ρGH,

Где ρ – плотность жидкости в манометре, H – разность уровней жидкости в манометре при давлении P1, G – ускорение свободного падения. Аналогично можно определить и давление P3 по формуле P3=P2+ρGh, где H – разность уровней жидкости в трубках манометра при измерении P3. Так как давления P1, P3 мало отличаются от атмосферного P2, то формулу (17) можно упростить, используя приближенное равенство ln(1+x)≈x, выполняющееся для всех x<<1. Тогда

. (18)

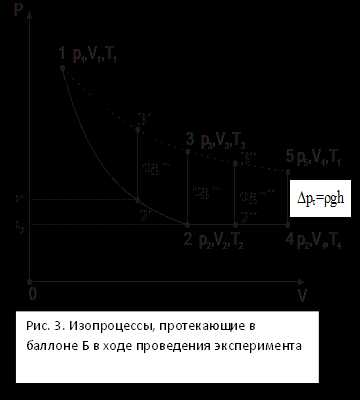Величина H в выражении (18) получена в предположении, что краны К1 и К2 закрываются в момент окончания адиабатического процесса 1-2 (рис. 2).

В случае если краны были закрыты до окончания процесса 1-2, давление в баллоне снизится до величины p2′ (см. рис. 3). При этом разность уровней жидкости в коленах манометра после расширения и затем изохорного нагревания H′ окажется завышенной. Значение γ, определенное по (18), окажется больше истинного.

Если кран закрыть спустя некоторое время после завершения адиабатного процесса 1-2, то за это время температура воздуха в баллоне за счет теплообмена с окружающей средой немного повысится (процесс 2-2′′ на рис. 3). Соответствующая разность уровней H″ окажется заниженной, что приведет к уменьшению γ.

Закрыть краны точно в момент, когда газ находится в состоянии 2, на практике не представляется возможным. Поэтому определять H приходится косвенным путем.

Рассмотрим процесс адиабатного расширения 1-2 при открытом кране с учетом теплообмена с окружающей средой во время протекания процесса 2-4 (рис. 3). Допустим, что газ находится в состоянии 1. Откроем краны и произведем сообщение полости баллона с атмосферой. По окончании адиабатического процесса 1-2 температура воздуха в баллоне станет равной

T2 и будет меньше комнатной, давление станет равным атмосферному P2.

Если теперь оставить краны открытыми на время τ, то температура воздуха в баллоне вследствие теплообмена возрастет до величины T4 (изобарный процесс 2-4). Закроем после этого краны и оставим их в таком положении до тех пор, пока температура внутри баллона не станет равной температуре окружающей среды T1 (изохорный процесс 4-5). При этом давление газа в сосуде повысится на некоторую величину DPτ, определяемую по соответствующей разности уровней жидкости в коленах манометра M. При уменьшении времени выдержки τ величина Hτ возрастает и при τ→ 0 приближается к истинному значению H. Таким образом, величину H можно определить, имея график зависимости Hτ=F(τ), полученный в ходе эксперимента. Можно показать, что в условиях нашего опыта имеет место соотношение

Ln(Hτ)=ln(H)-aτ, (19)

Где a – некоторая константа. Получив на опыте ряд значений ln(Hτ), соответствующих различным длительностям расширения τ, и построив график зависимости ln(Hτ)=F(τ), можно, продлив полученную прямую до пересечения с осю ln(Hτ), получить логарифм искомой величины H (рис. 4).

Порядок выполнения работы

1. Перед началом работы проверить наличие жидкости в манометре. В случае недостаточного уровня сообщить об этом преподавателю или лаборанту. При наличии разности уровней в коленах манометра установить краны в положение 3, сбросив лишнее давление в баллоне. Перевести краны К1 и К2 в положение 1 (см. таблицу приложения).

2. Включить насос (при этом давление в баллоне начнет увеличиваться) и добиться разности уровней в коленах манометра H2-H1=20-25 см. Занести показания манометра H=H2-H1 в таблицу.

При проведении последующих серий измерений придерживаться выбранного значения H.

3. Установить краны в положение 2 и выключить насос.

4. Выдержать воздух в баллоне в течение не менее 2-3 минут.

5. Установить кран К2, а затем К1 в положение 3 и сбросить давление в баллоне до атмосферного (при этом разность уровней в коленах манометра станет равной нулю).

6. Выдержать в таком положении баллон в течение времени τ=16 с.

7. Перевести краны в положение 4, изолировав таким образом баллон от атмосферы, и выждать не менее 2-3 минут, после чего вновь измерить разность уровней в коленах манометра Hτ и занести показания в таблицу.

8. Повторить пункты 1-7 не менее трех раз.

9. Повторить измерения по пунктам 1-8, устанавливая время выдержки τ по пункту 6 сначала 12, затем 8 и 4 с. Данные занести в таблицу.

10. Используя методику, описанную в методических указаниях получить значение ln(H), рассчитать значение H, по формуле (18) рассчитать γ.

11. Рассчитать погрешность результата измерений Dγ, принимая точность шкалы манометра DH=1мм. Погрешность ln(H) следует взять соответствующей 1 мм на графике. Сравнить полученное значение γ с теоретическим, считая воздух смесью двухатомных газов.

Вопросы и задания для самоконтроля

1. Дайте определение теплоемкости тела (удельной, молярной). От чего она зависит?

2. Перечислите виды изопроцессов в газе. Сформулируйте условия их протекания.

3. Сформулируйте первое начало термодинамики. Примените его к различным изопроцессам.

4. Дайте определение адиабатного процесса. Выведите уравнение Пуассона. Запишите его в переменных V, T и P, T.

5. Дайте определение числа степеней свободы. Как распределяется энергия молекулы по степеням свободы?

6. Покажите связь теплоемкости газа с числом степеней свободы его молекулы.

7. Запишите выражения для работы в изохорном, изобарном процессах. Выведите выражение для работы газа в изотермическом процессе.

8. Выведите выражение для работы газа в адиабатном процессе.

Таблица экспериментальных данных

Н=…мм DН=…мм DH=…мм

T, с	Значение Hτ, мм	<Hτ>, мм	Ln<Hτ>
1	2	3
16
12
8
4

Формулы для расчета погрешности

, P=0,95, TСт=1,96 .

, , , .

Записи по теме

naparah.com

Число степеней свободы различных молекул. Методические материалы

Цифровой ресурс может использоваться для обучения в рамках программы средней школы (профильного и углубленного уровней).

Компьютерная модель иллюстрирует особенности движения молекул. Рассматриваются одноатомная, двухатомная и трехатомная молекулы, вводится понятие «степени свободы».

Краткая теория

Числом степеней свободы материального объекта называют число независимых координат, которые необходимо задать, чтобы однозначно определить положение этого объекта относительно рассматриваемой системы отсчета.

Например, положение материальной точки в пространстве определяется тремя координатами x, y, z, следовательно, материальная точка обладает тремя степенями свободы.

Две материальные точки, находящиеся на неизменном расстоянии друг от друга (например, модель двухатомной молекулы с жесткой связью между атомами), имеют пять степеней свободы – три поступательные и две вращательные. Таким образом, двухатомная молекула может совершать пять независимых движений: три поступательных движения вдоль осей X, Y, Z и два вращения относительно осей X и Y (рис. 1). Опыт показывает, что вращение относительно оси Z, на которой лежат центры обоих атомов, может быть возбуждено только при очень высоких температурах. При обычных температурах вращение около оси Z не происходит, так же как не вращается одноатомная молекула.

Рис. 1.

Каждое независимое движение называется степенью свободы. Таким образом, одноатомная молекула имеет 3 поступательные степени свободы, «жесткая» двухатомная молекула имеет 5 степеней (3 поступательные и 2 вращательные), а многоатомная молекула – 6 степеней свободы (3 поступательные и 3 вращательные).

При достаточно высоких температурах в многоатомных молекулах возбуждаются дополнительные – колебательные степени свободы, связанные с изменением расстояний между атомами. Например, в двухатомной молекуле при данных условиях насчитывается 6 стпеней свободы (3 поступательные, 2 вращательные и 1 колебательная).

В классической статистической физике доказывается так называемая теорема о равномерном распределении энергии по степеням свободы:

Если система молекул находится в тепловом равновесии при температуре T, то средняя кинетическая энергия равномерно распределена между всеми степенями свободы и для каждой поступательной и вращательной степени свободы молекулы она равна:

Если рассматриваются и колебательные степени свободы, то для каждой колебательной степени свободы молекулы средняя кинетическая энергия равна kT, так как колебательное движение связано с наличием не только кинетической, но и потенциальной энергии, причем для малых (гармонических) колебаний среднее значение потенциальной энергии равно среднему значению кинетической. Поэтому на каждую колебательную степень свободы приходится:

Работа с моделью

Модель может быть использована в режиме ручного переключения кадров и в режиме автоматической демонстрации ().

Рекомендации по применению модели

Данная модель может быть применена в качестве иллюстрации на уроках изучения нового материала, повторения в 10 классе по теме «Основное уравнение молекулярно-кинетической теории».

Понятие «степень свободы» довольно трудное для восприятия учащимися средней школы. Модель позволяет продемонстрировать характер движения различных молекул.

Пример планирования урока с использованием модели

Тема «Основное уравнение молекулярно-кинетической теории»

Цель урока: вывести и проанализировать основное уравнение МКТ.

№ п/п Этапы урока Время, мин Приемы и методы 1 Организационный момент 2 2 Проверка домашнего задания по теме «Средняя квадратичная скорость движения молекул» 5 Индивидуальный опрос 3 Объяснение нового материала по теме «Основное уравнение молекулярно-кинетической теории» 30 Объяснение нового материала с использованием модели «Число степеней свободы различных молекул» 4 Анализ полученной формулы 5 Фронтальная работа 5 Объяснение домашнего задания 3

Таблица 1.

Примеры вопросов и заданий

 

1.	Чему равна молярная теплоемкость гелия при постоянном объеме?
2.	Чему равна молярная теплоемкость аргона при постоянном давлении?
3.	Чему равно отношение Cp / CV для азота?

files.school-collection.edu.ru

Электронные таблицы. Функции.: Электронные таблицы в ЕГЭ

В ЕГЭ представлено несколько типов заданий, имеющих отношение к текущей теме (функции в электронных таблицах).

Чаще всего в качестве используемых в задании функций используются СУММ и СРЗНАЧ.
При решении подобных задач рекомендуется рисовать таблицу.

A7. Ад­ре­са­ция в элек­трон­ных таблицах

Пример1:
 В элек­трон­ной таб­ли­це зна­че­ние фор­му­лы =CPЗHAЧ(A3:D4) равно 5. Чему равно зна­че­ние фор­му­лы =СРЗНАЧ(АЗ:С4), если зна­че­ние фор­му­лы =CУMM(D3:D4) равно 4?

Решение:

Функ­ция СУММ(D3:D4) счи­та­ет сумму зна­че­ний ячеек D3 и D4: D3 + D4 = 4.

 Функ­ция СРЗНАЧ(A3:D4) счи­та­ет сред­нее ариф­ме­ти­че­ское диа­па­зо­на A3:D4, т. е. сумму зна­че­ний вось­ми ячеек A3, B3, C3, D3, A4, B4, C4, D4, делённую на их ко­ли­че­ство. Умно­жим сред­нее зна­че­ние на 8 и найдём сумм­му зна­че­ний этих ячеек: СУММ(A3:D4) = 5 * 8 = 40.

Вы­чтем из по­лу­чен­ной суммы СУММ(A3:D4) зна­че­ние суммы D3 + D4 и найдём зна­че­ние суммы СУММ(A3:C4): оно равно 40 — 4 = 36.

Те­перь раз­де­лим по­лу­чен­ный ре­зль­тат на ко­ли­че­ство ячеек дан­ной суммы (их здесь 6) и найдём ис­ко­мую ве­ли­чи­ну: СРЗНАЧ(АЗ:С4) = 36 / 6 = 6.

Пример 2(обратный вариант)
В элек­трон­ной таб­ли­це зна­че­ние фор­му­лы =CУMM(B2:D2) равно 15. Чему равно зна­че­ние ячей­ки А2, если зна­че­ние фор­му­лы =CP3HAЧ(A2:D2) равно 4?

Решение:

Функ­ция СРЗНАЧ(A2:D2) счи­та­ет сред­нее ариф­ме­ти­че­ское диа­па­зо­на A2:D2, т. е. сумму зна­че­ний четырёх ячеек A2, B2, C2, D2, делённую на 4. Умно­жим сред­нее знач­ние на число ячеек и по­лу­чим сумму зна­че­ний ячеек A2 + B2 + C2 + D2 = 4 * 4 = 16.

Те­перь, вы­чтем из по­лу­чен­ной сумы зна­че­ние =CУMM(B2:D2) и найдём A2: A2 = 16 — 15 = 1.

Проверочный тест

Пройдите пробный тест, составленный из 5 заданий (А7). Два из них на работу с функциями, описание выше. Три остальных — на адресацию в ячейках, хоть и не используют функции, но хороши для общего повторения.

Внимание!

 Дополнительно посмотреть варианты заданий A7 можно на сайте Решу ЕГЭ
Там же можно пройти тестирование по данному (и другим) типу задания.

prosmotrf.blogspot.com

No related posts.