19.Частная производная
Определение 1.11 Пусть задана функция двух переменных z=z(x,y), (x,y)D. ТочкаM0(x0;y0) — внутренняя точка области D.
Если в D присутствует такая окрестность UM0 точки M0, что для всех точек
то точка M0 называется точкой локального максимума. А само значение z(M0) — локальным максимумом.
А если же для всех точек
то точка M0 называется точкой локального минимума функции
Локальный максимум и локальный минимум называются локальными экстремумами функции z(x,y). На рис. 1.4 поясняется геометрический смысл локального максимума: M0 — точка максимума, так как на поверхности z =z (x,y) соответствующая ей точка C0 находится выше любой соседней точки C (в этом локальность максимума).

Заметим, что на поверхности в целом есть точки (например, В), которые находятся выше C0, но эти точки (например, В) не являются «соседними» с точкой C0.
В частности, точке В соответствует понятие глобального максимума:
Аналогично определяется и глобальный минимум:
Нахождение глобальных максимумов и минимумов будет рассмотрено в п.1.10.
Теорема 1.3 (необходимые условия экстремума).
Пусть задана функция z =z (x,y), (x,y)D. Точка M0(x0;y0D — точка локального экстремума.
Если в этой точке существуют z’
Геометрическое доказательство «очевидно». Если в точке C0 на (рис.1.4) провести касательную плоскость, то она «естественно» пройдет горизонтально, т. е. под углом 0° к оси Ох и к оси Оу.
Тогда в соответствии с геометрическим смыслом частных производных (рис.1.3):
что и требовалось доказать.
Определение 1.12.
Если в точке M0 выполняются условия (1.41), то она называется стационарной точкой функции z (x,y).
Теорема 1.4 (достаточные условия экстремума).
Пусть задана z =z (x,y), (x,y)D, которая имеет частные производные второго порядка в некоторой окрестности точки M0(x0,y0)D. Причем M0 — стационарная точка (т. е. необходимые условия (1.41) выполнены). Вычислим:
Если:
Доказательство теоремы использует темы (формула Тейлора функции нескольких переменных и теория квадратичных форм), которые в этом пособии не рассматриваются.
Пример 1.13.
Исследовать на экстремум:
Решение
то есть найдены четыре стационарные точки. 2.
по теореме 1.4 в точке – минимум. Причём
по теореме 1.4 в точке
— максимум. Причём
studfiles.net
В чём смысл частных производных? — Мегаобучалка
По своей сути частные производные 1-го порядка напоминают «обычную» производную:
– это функции, которые характеризуют скорость изменения функции в направлении осей и соответственно. Так, например, функция характеризует крутизну «подъёмов» и «склонов» поверхности в направлении оси абсцисс, а функция сообщает нам о «рельефе» этой же поверхности в направлении оси ординат.
! Примечание: здесь подразумеваются направления, которые параллельны координатным осям
.В целях лучшего понимания рассмотрим конкретную точку плоскости и вычислим в ней значение функции («высоту»):
– а теперь представьте, что вы здесь находитесь (НА САМОЙ поверхности).
Вычислим частную производную по «икс» в данной точке:
Отрицательный знак «иксовой» производной сообщает нам об убывании функции в точке по направлению оси абсцисс. Иными словами, если мы сделаем маленький-маленький (бесконечно малый) шажок в сторону острия оси (параллельно данной оси), то спустимся вниз по склону поверхности.
Теперь узнаем характер «местности» по направлению оси ординат:
Производная по «игрек» положительна, следовательно, в точке по направлению оси функция возрастает. Если совсем просто, то здесь нас поджидает подъём в гору.
Кроме того, частная производная в точке характеризует скорость изменения функции по соответствующему направлению. Чем полученное значение больше
Но то были два частных пути. Совершенно понятно, что из точки, в которой мы находимся, (и вообще из любой точки данной поверхности) мы можем сдвинуться и в каком-нибудь другом направлении. Таким образом, возникает интерес составить общую «навигационную карту», которая сообщала бы нам о «ландшафте» поверхности по возможностив каждой точке области определения данной функции по всем доступным путям.
Систематизируем элементарные прикладные правила:
1) Когда мы дифференцируем по , то переменная считается константой.
2) Когда же дифференцирование осуществляется по , то константой считается .
3) Правила и таблица производных элементарных функций справедливы и применимы для любой переменной ( , либо какой-нибудь другой), по которой ведется дифференцирование.
Шаг второй. Находим частные производные второго порядка. Их четыре.
Обозначения:
или – вторая производная по «икс»
или – вторая производная по «игрек»
или – смешанная производная «икс по игрек»
или – смешанная производная «игрек по икс»
Со второй производной нет никаких проблем. Говоря простым языком, вторая производная – это производная от первой производной.
Для удобства я перепишу уже найденные частные производные первого порядка:
Сначала найдем смешанные производные:
Как видите, всё просто: берем частную производную и дифференцируем ее еще раз, но в данном случае – уже по «игрек».
Аналогично:
В практических примерах можно ориентироваться на следующее равенство:
Таким образом, через смешанные производные второго порядка очень удобно проверить, а правильно ли мы нашли частные производные первого порядка.
Находим вторую производную по «икс».
Никаких изобретений, берем и дифференцируем её по «икс» еще раз:
Аналогично:
Следует отметить, что при нахождении , нужно проявить повышенное внимание, так как никаких чудесных равенств для их проверки не существует.
Вторые производные также находят широкое практическое применение, в частности, они используются в задаче отыскания экстремумов функции двух переменных.
Пример 2
Вычислить частные производные первого порядка функции в точке . Найти производные второго порядка.
Пример 3
Найти частные производные первого порядка функции . Проверить, что . Записать полный дифференциал первого порядка .
Решение: Находим частные производные первого порядка:
Обратите внимание на подстрочный индекс: , рядом с «иксом» не возбраняется в скобках записывать, что – константа. Данная пометка может быть очень полезна для начинающих, чтобы легче было ориентироваться в решении.
Дальнейшие комментарии:
(1) Выносим все константы за знак производной. В данном случае и , а, значит, и их произведение считается постоянным числом.
(2) Не забываем, как правильно дифференцировать корни.
(1) Выносим все константы за знак производной, в данной случае константой является .
(2) Под штрихом у нас осталось произведение двух функций, следовательно, нужно использовать правило дифференцирования произведения .
(3) Не забываем, что – это сложная функция (хотя и простейшая из сложных). Используем соответствующее правило: .
Теперь находим смешанные производные второго порядка:

, значит, все вычисления выполнены верно.
Запишем полный дифференциал . В контексте рассматриваемого задания не имеет смысла рассказывать, что такое полный дифференциал функции двух переменных. Важно, что этот самый дифференциал очень часто требуется записать в практических задачах.
Полный дифференциал первого порядка функции двух переменных имеет вид:
В данном случае:
То есть, в формулу нужно тупо просто подставить уже найденные частные производные первого порядка. Значки дифференциалов и в этой и похожих ситуациях по возможности лучше записывать в числителях:
Пример 4
Найти частные производные первого порядка функции . Проверить, что . Записать полный дифференциал первого порядка .
Рассмотрим серию примеров, включающих в себя сложные функции.
Пример 5
Найти частные производные первого порядка функции .
Записать полный дифференциал .
Решение:
(1) Применяем правило дифференцирования сложной функции .
Следует помнить очень важный момент: когда мы по таблице превращаем синус (внешнюю функцию) в косинус, то вложение (внутренняя функция) у нас не меняется.
(2) Здесь используем свойство корней: , выносим константу за знак производной, а корень представляем в нужном для дифференцирования виде.
Аналогично:
Запишем полный дифференциал первого порядка:
Пример 6
Найти частные производные первого порядка функции .
Записать полный дифференциал .
Это пример для самостоятельного решения (ответ в конце урока). Полное решение не привожу, так как оно достаточно простое
Довольно часто все вышерассмотренные правила применяются в комбинации.
Пример 7
Найти частные производные первого порядка функции .
(1) Используем правило дифференцирования суммы
(2) Первое слагаемое в данном случае считается константой, поскольку в выражении нет ничего, зависящего от «икс» – только «игреки». Всегда приятно, когда дробь удается превратить в ноль.
Для второго слагаемого применяем правило дифференцирования произведения. Кстати, в этом смысле ничего бы не изменилось, если бы вместо была дана функция – важно, что здесь произведение двух функций, КАЖДАЯ из которых зависит от «икс», а поэтому, нужно использовать правило дифференцирования произведения. Для третьего слагаемого применяем правило дифференцирования сложной функции.
(1) В первом слагаемом и в числителе и в знаменателе содержится «игрек», следовательно, нужно использовать правило дифференцирования частного: . Второе слагаемое зависит ТОЛЬКО от «икс», значит, считается константой и превращается в ноль. Для третьего слагаемого используем правило дифференцирования сложной функции.
Мехматовский анекдот для разрядки:
Однажды в пространстве функций появилась злобная производная и как пошла всех дифференцировать. Все функции разбегаются кто куда, никому не хочется превращаться! И только одна функция никуда не убегает. Подходит к ней производная и спрашивает:
– А почему это ты от меня никуда не убегаешь?
– Ха. А мне всё равно, ведь я «е в степени икс», и ты со мной ничего не сделаешь!
На что злобная производная с коварной улыбкой отвечает:
– Вот здесь ты ошибаешься, я тебя продифференцирую по «игрек», так что быть тебе нулем.
Кто понял анекдот, тот освоил производные, минимум, на «тройку».
Пример 8
Найти частные производные первого порядка функции .
Это пример для самостоятельного решения.
Пример 9
Дана функция двух переменных . Найти все частные производные первого и второго порядков.
Это пример для самостоятельного решения. Полное решение и образец оформления где-то рядом.
Что дальше? Дальше знакомимся с родственной темой – частными производными функции трёх переменных. После этого я рекомендую ДОБРОСОВЕСТНО (жить будет легче 😉 отработать технику дифференцирования.
Примеры: , , , ,
, , .
, ,
megaobuchalka.ru
Особенности вычисления частных производных — Мегаобучалка
Подведем итог, чем же отличается нахождение частных производных от нахождения «обычных» производных функции одной переменной:
1) Когда мы находим частную производную , то переменнаясчитается константой.
2) Когда мы находим частную производную , то переменнаясчитается константой.
3) Правила и таблица производных элементарных функций справедливы и применимы для любой переменной (, либо какой-нибудь другой), по которой ведется дифференцирование.
Шаг второй. Находим частные производные второго порядка. Их четыре.
Обозначения:
или – вторая производная по «икс»
или – вторая производная по «игрек»
или – смешанная производная «по икс игрек»
или – смешанная производная «по игрек икс»
В понятии второй производной нет ничего сложного. Говоря простым языком, вторая производная – это производная от первой производной.
Для наглядности я перепишу уже найденные частные производные первого порядка:
Сначала найдем смешанные производные:
Как видите, всё просто: берем частную производную и дифференцируем ее еще раз, но в данном случае – уже по «игрек».
Аналогично:
Для практических примеров, когда все частные производные непрерывны, справедливо следующее равенство:
Таким образом, через смешанные производные второго порядка очень удобно проверить, а правильно ли мы нашли частные производные первого порядка.
Находим вторую производную по «икс».
Никаких изобретений, берем и дифференцируем её по «икс» еще раз:
Аналогично:
Следует отметить, что при нахождении , нужно проявить повышенное внимание, так как никаких чудесных равенств для проверки не существует.
Пример 2
Найти частные производные первого и второго порядка функции
Это пример для самостоятельного решения (ответ в конце урока).
При определенном опыте частные производные из примеров №№1,2 будут решаться Вами устно.
Переходим к более сложным примерам.
Пример 3
Найти частные производные первого порядка функции . Проверить, что . Записать полный дифференциал первого порядка .
Решение: Находим частные производные первого порядка:
Обратите внимание на подстрочный индекс: , рядом с «иксом» не возбраняется в скобках записывать, что – константа. Данная пометка может быть очень полезна для начинающих, чтобы легче было ориентироваться в решении.
Дальнейшие комментарии:
(1) Выносим все константы за знак производной. В данном случае и , а, значит, и их произведение считается постоянным числом.
(2) Не забываем, как правильно дифференцировать корни.
(1) Выносим все константы за знак производной, в данной случае константой является .
(2) Под штрихом у нас осталось произведение двух функций, следовательно, нужно использовать правило дифференцирования произведения .
(3) Не забываем, что – это сложная функция (хотя и простейшая из сложных). Используем соответствующее правило: .
Теперь находим смешанные производные второго порядка:
, значит, все вычисления выполнены верно.
Запишем полный дифференциал . В контексте рассматриваемого задания не имеет смысла рассказывать, что такое полный дифференциал функции двух переменных. Важно, что этот самый дифференциал очень часто требуется записать в практических задачах.
Полный дифференциал первого порядка функции двух переменных имеет вид:
.
В данном случае:
То есть, в формулу нужно просто подставить уже найденные частные производные первого порядка. Значки дифференциалов и в этой и похожих ситуациях по возможности лучше записывать в числителях:
Пример 4
Найти частные производные первого порядка функции . Проверить, что . Записать полный дифференциал первого порядка .
Это пример для самостоятельного решения. Полное решение и образец оформления задачи – в конце урока.
Рассмотрим серию примеров, включающих в себя сложные функции.
Пример 5
Найти частные производные первого порядка функции .
Записать полный дифференциал .
Решение:
(1) Применяем правило дифференцирования сложной функции . С урока Производная сложной функцииследует помнить очень важный момент: когда мы по таблице превращаем синус (внешнюю функцию) в косинус, то вложение (внутренняя функция) у нас не меняется.
(2) Здесь используем свойство корней: , выносим константу за знак производной, а корень представляем в нужном для дифференцирования виде.
Аналогично:
Запишем полный дифференциал первого порядка:
Пример 6
Найти частные производные первого порядка функции .
Записать полный дифференциал .
Это пример для самостоятельного решения (ответ в конце урока). Полное решение не привожу, так как оно достаточно простое
Довольно часто все вышерассмотренные правила применяются в комбинации.
Пример 7
Найти частные производные первого порядка функции .
(1) Используем правило дифференцирования суммы.
(2) Первое слагаемое в данном случае считается константой, поскольку в выражении нет ничего, зависящего от «икс» – только «игреки».
(Знаете, всегда приятно, когда дробь удается превратить в ноль).
Для второго слагаемого применяем правило дифференцирования произведения. Кстати, в алгоритме ничего бы не изменилось, если бы вместо была дана функция – важно, что здесь мы имеем произведение двух функций, КАЖДАЯ из которых зависит от «икс», поэтому нужно использовать правило дифференцирования произведения. Для третьего слагаемого применяем правило дифференцирования сложной функции.
Найдем теперь частную производную по y:
(1) В первом слагаемом и в числителе и в знаменателе содержится «игрек», следовательно, нужно использовать правило дифференцирования частного: . Второе слагаемое зависит ТОЛЬКО от «икс», значит, считается константой и превращается в ноль. Для третьего слагаемого используем правило дифференцирования сложной функции.
Для тех читателей, которые мужественно добрались почти до конца урока, расскажу старый мехматовский анекдот для разрядки.
Однажды в пространстве функций появилась злобная производная и как пошла всех дифференцировать. Все функции разбегаются кто куда, никому не хочется превращаться! И только одна функция никуда не убегает. Подходит к ней производная и спрашивает:
– А почему это ты от меня никуда не убегаешь?
– Ха. А мне всё равно, ведь я «е в степени икс», и ты со мной ничего не сделаешь!
На что злобная производная с коварной улыбкой отвечает:
– Вот здесь ты ошибаешься, я тебя продифференцирую по «игрек», так что быть тебе нулем.
(Кто понял анекдот, тот освоил производные, минимум, на «тройку»).
Пример 8
Найти частные производные первого порядка функции .
Это пример для самостоятельного решения. Полное решение и образец оформления задачи – в конце урока.
Пример 9
Дана функция двух переменных . Найти все частные производные первого и второго порядков.
Это пример для самостоятельного решения. Полное решение и образец оформления где-то рядом.
Решения и ответы:
Пример 2:
, , ,
Пример 4: Ссылка для просмотра ниже.
Пример 6:
, ,
megaobuchalka.ru
12. Частные производные высших порядков
Пусть функция
имеет в некоторой областиD частную производную по одной из
переменных (она называется также частной производной
первого порядка). Тогда эта производная,
сама являясь функцией тех же переменных,
может иметь в некоторой точке
(она называется также частной производной
первого порядка). Тогда эта производная,
сама являясь функцией тех же переменных,
может иметь в некоторой точке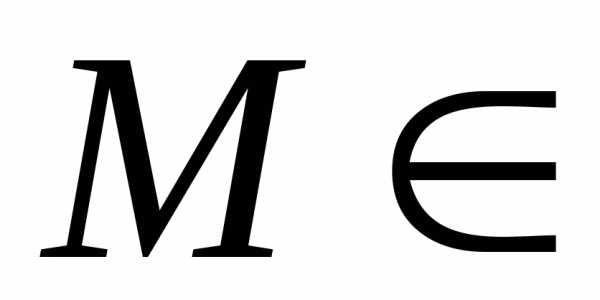 Dчастные производные
по той же
Dчастные производные
по той же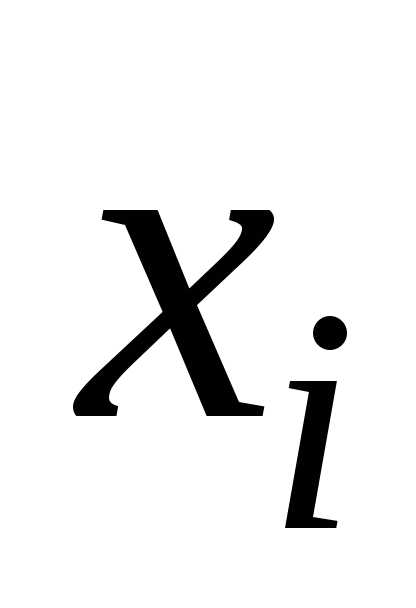 или по любой другой переменной
или по любой другой переменной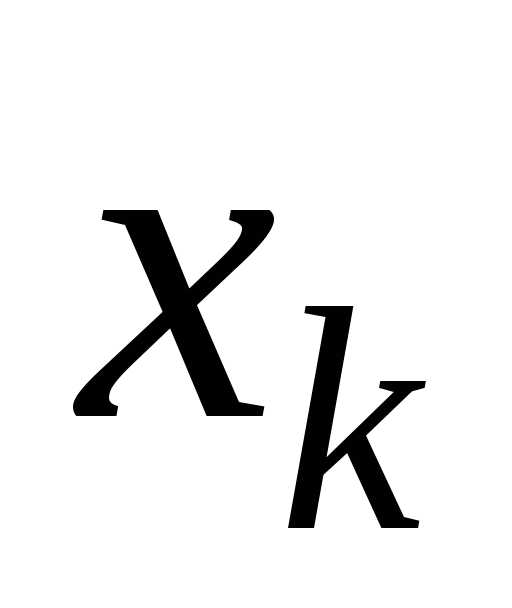 .
Для исходной функцииэти производные будут ужепроизводными
второго порядка (иливторыми частными производными). Производнаявторого
порядка функции по аргументам
.
Для исходной функцииэти производные будут ужепроизводными
второго порядка (иливторыми частными производными). Производнаявторого
порядка функции по аргументам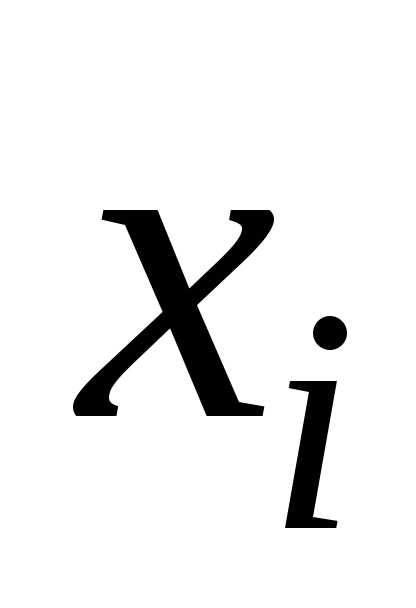 и
и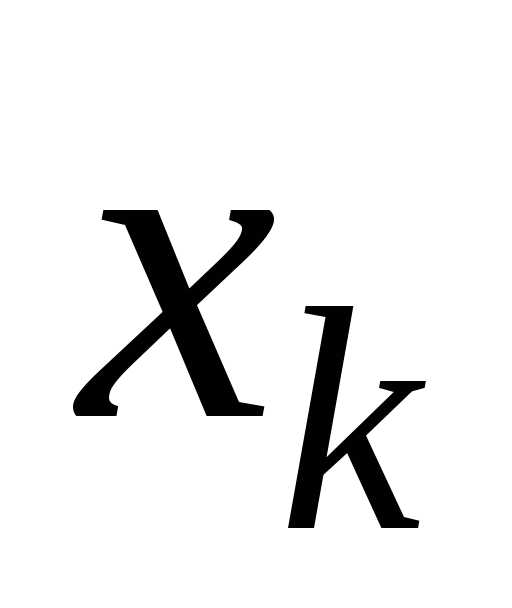 в точке
в точке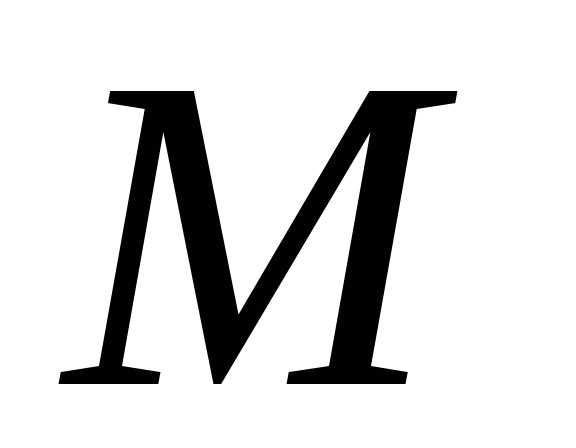 обозначается одним из следующих
символов:
обозначается одним из следующих
символов:
Если 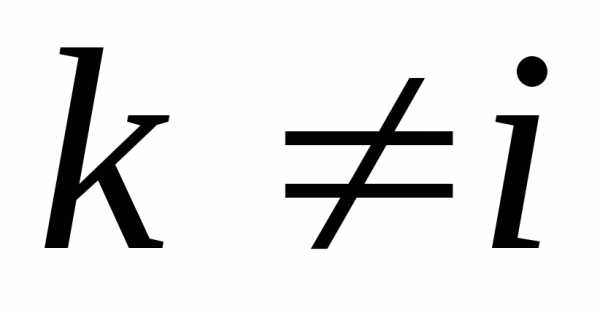 ,
точастная
производная второго порядка называется смешанной.
Если
,
точастная
производная второго порядка называется смешанной.
Если 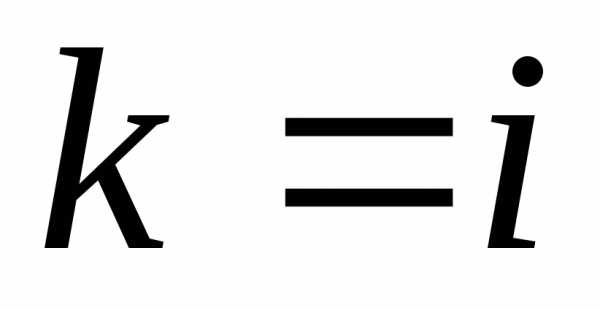 ,
то частная производная второго порядка
обозначается
,
то частная производная второго порядка
обозначается
Частные производные третьего порядка определяются как частные производные от частных производных второго порядка и т.д.
Следует отметить свойство смешанных частных производных:
Теорема. Если в точке Dсмешанные частные
производные
Dсмешанные частные
производные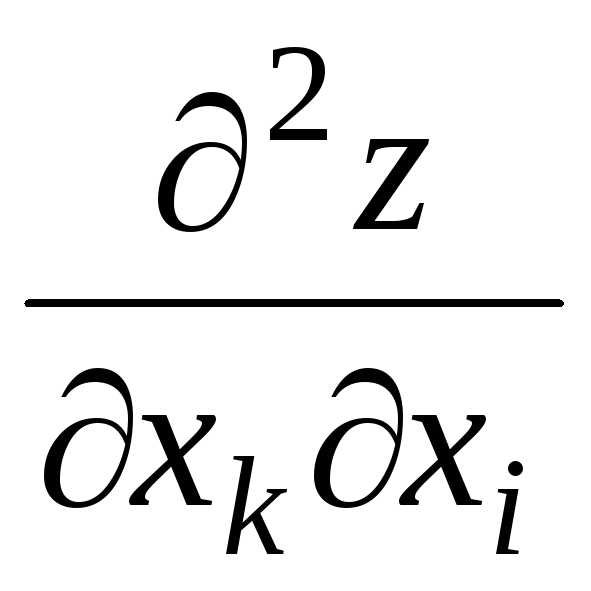 и
и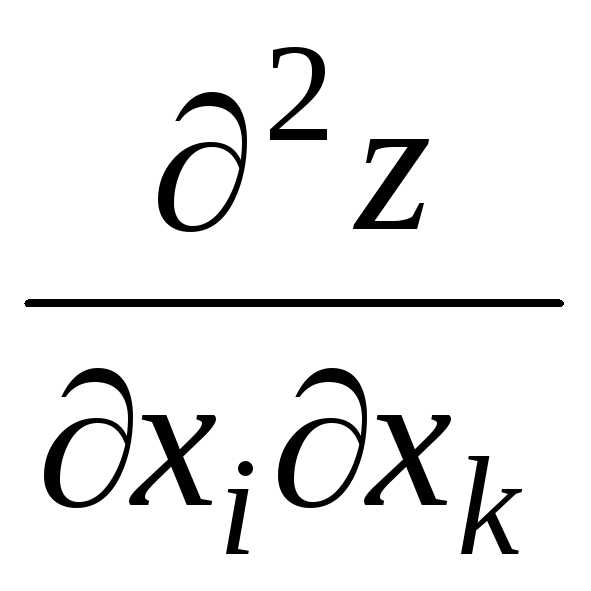 непрерывны, то они равны между собой в
этой точке, т.е.
непрерывны, то они равны между собой в
этой точке, т.е.
,
или значение смешанной производной не зависит от того порядка, в котором производится дифференцирование.
Это свойство верно и для смешанных производных любого порядка.
Теорема. Если функция
определена в некоторой областиDи имеет в этой
области всевозможные частные производные
до 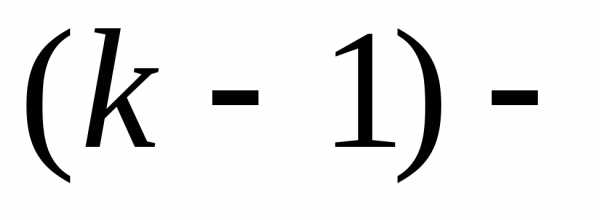 го
порядка включительно инепрерывные
в Dсмешанные
производные
го
порядка включительно инепрерывные
в Dсмешанные
производные  го
порядка, то значение любой
го
порядка, то значение любой 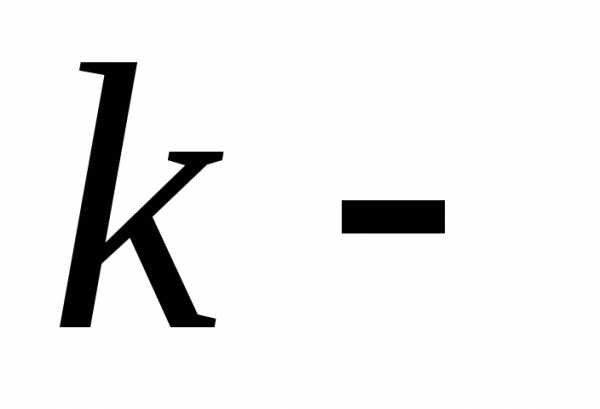 той
смешанной производной не зависит от
того порядка, в котором производятся
последовательные дифференцирования.
той
смешанной производной не зависит от
того порядка, в котором производятся
последовательные дифференцирования.
Пример
5. Найти
частные производные второго порядка
функции 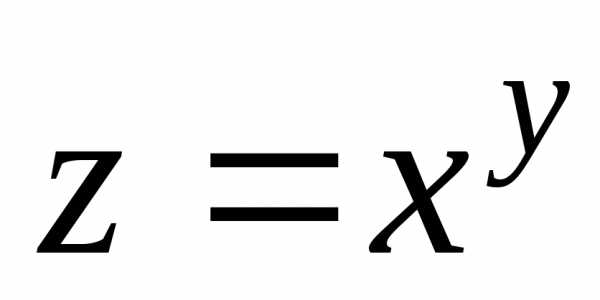 .
.
Решение. Частные производные первого порядка для этой функции мы нашли раньше, рассматривая пример 1:
Найдем теперь частные производные от частных производных первого порядка, получим тем самым частные производные второго порядка заданной функции:
На примере убеждаемся, что смешанные частные производные не зависят от порядка дифференцирования, поэтому в дальнейшем будем находить только одну из них.
13. Дифференциалы высших порядков
Пусть функция
определена в некоторой областиD и имеет в этой области непрерывные
частные производные первого порядка.
Тогда она имеет и полный дифференциал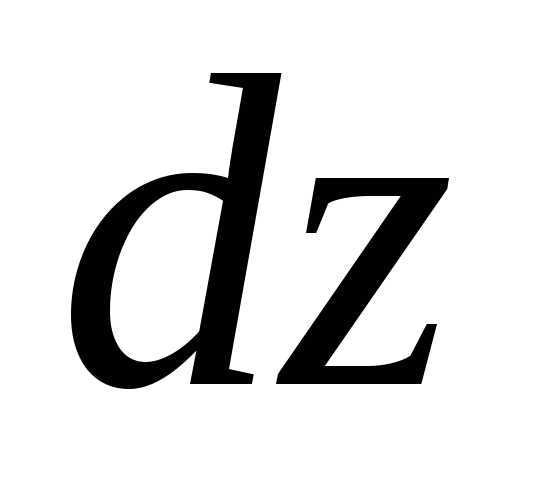 :
:
,
который,
в свою очередь, является некоторой
функцией от тех же переменных. Если
предположить существование непрерывных
частных производных второго порядка
для функции  ,
то в этом случае функция
,
то в этом случае функция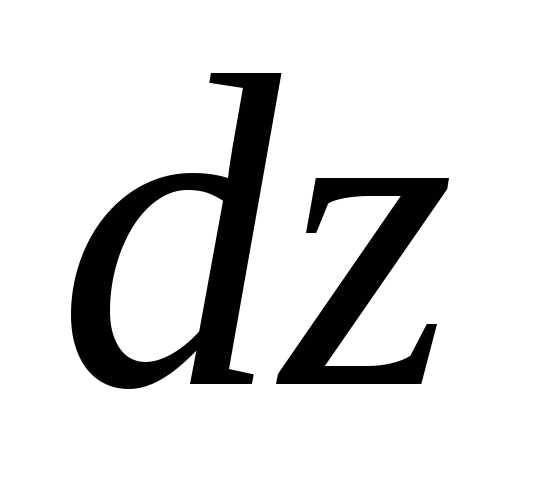 будет иметь непрерывные частные
производные первого порядка, и можно
будет говорить о дифференциале от этого
дифференциала:
будет иметь непрерывные частные
производные первого порядка, и можно
будет говорить о дифференциале от этого
дифференциала: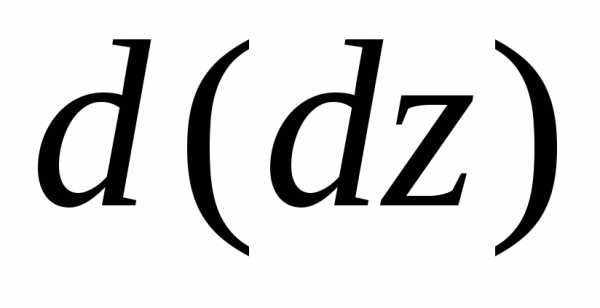 ,
который называетсядифференциалом
второго порядка (или вторым
дифференциалом)
функции
и обозначается.
,
который называетсядифференциалом
второго порядка (или вторым
дифференциалом)
функции
и обозначается.
Замечание. Приращения при этом рассматриваются какпостоянные и остаются одними и теми же при переходе от одного дифференциала к следующему. Следовательно, дифференциалы любого порядка выше первого от независимых переменных равны нулю, т.е.
, .
(7)
.
(7)
Поэтому, применяя правила дифференцирования и помня о равенстве смешанных производных по одному и тому же набору переменных, получим:
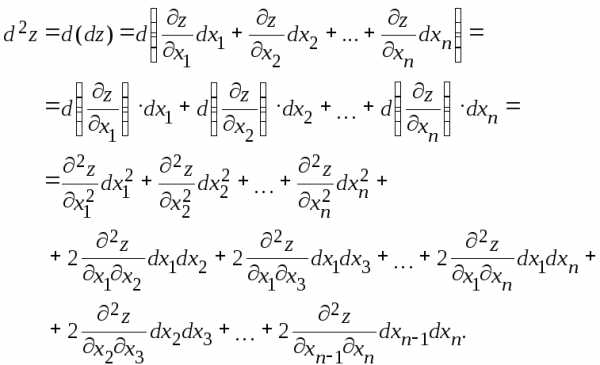
Здесь
и далее
,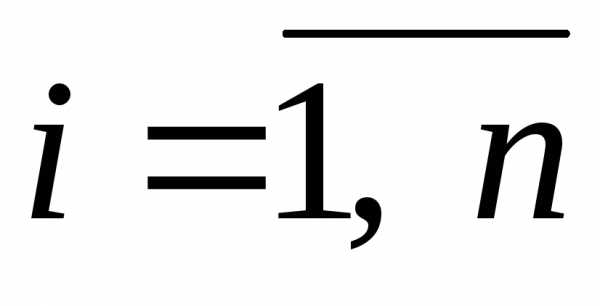 .
.
Аналогично
определяются дифференциалы
третьего 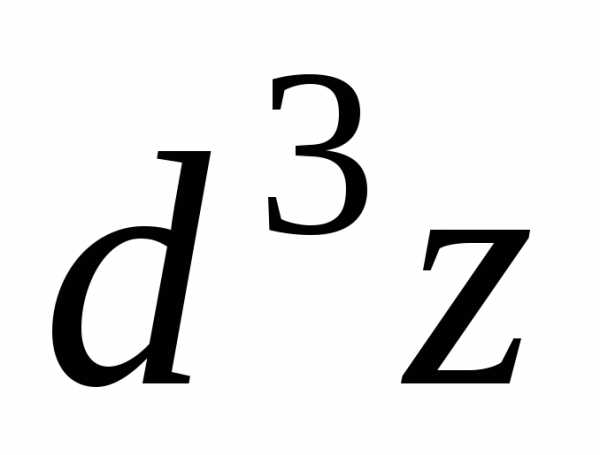 ,четвертого
,четвертого 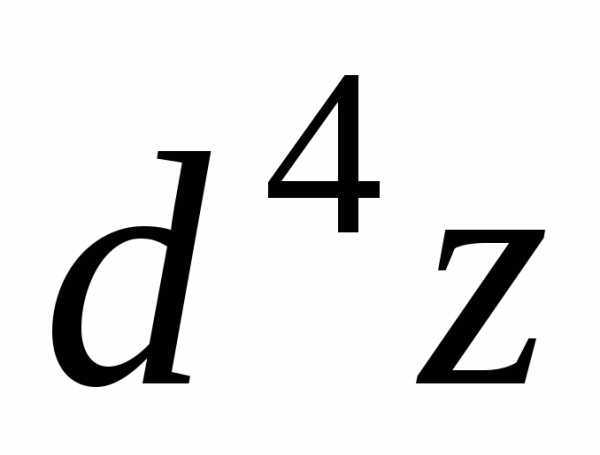 и т.д.порядков. Если определен
дифференциал
и т.д.порядков. Если определен
дифференциал 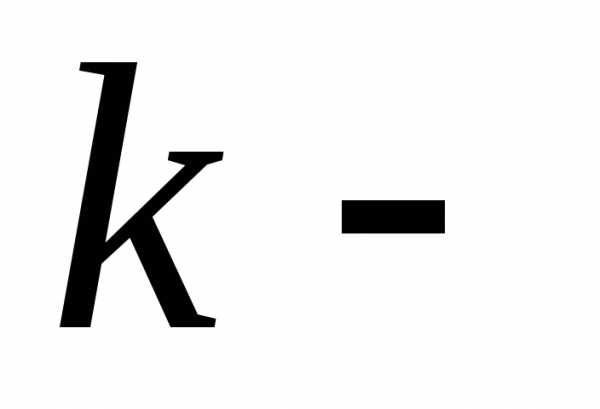 го
порядка
го
порядка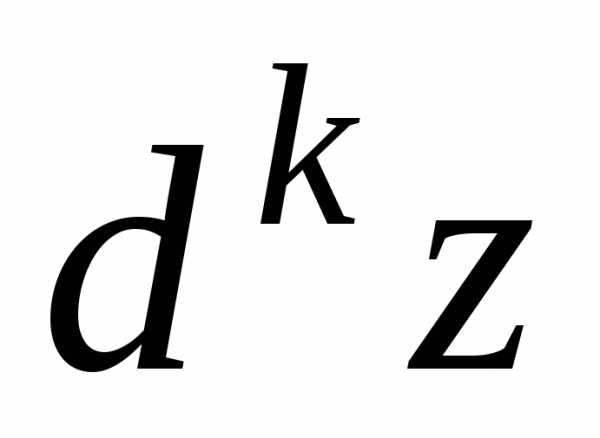 ,
то дифференциал
,
то дифференциал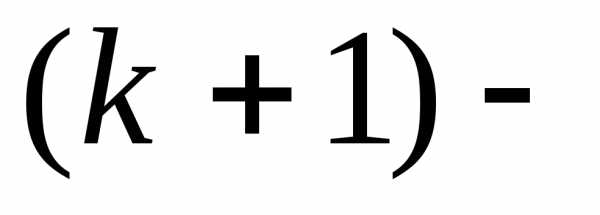 го
порядка определяется как полный
дифференциал от дифференциала
го
порядка определяется как полный
дифференциал от дифференциала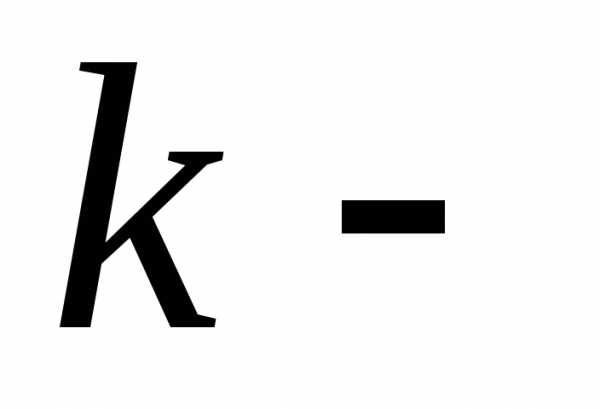 го
порядка:
го
порядка:
.
Сложность выражения для дифференциала зависит как от количества переменных, так и от его порядка. Поэтому проще запомнить символическое равенство
,
которое
нужно понимать следующим образом:
сначала многочлен, стоящий в скобках, формальнопо правилам алгебры
возводится в степень, затем все полученные
члены «умножаются» на ,
т.е.
,
т.е. дописывается в числителе каждой дроби
при
дописывается в числителе каждой дроби
при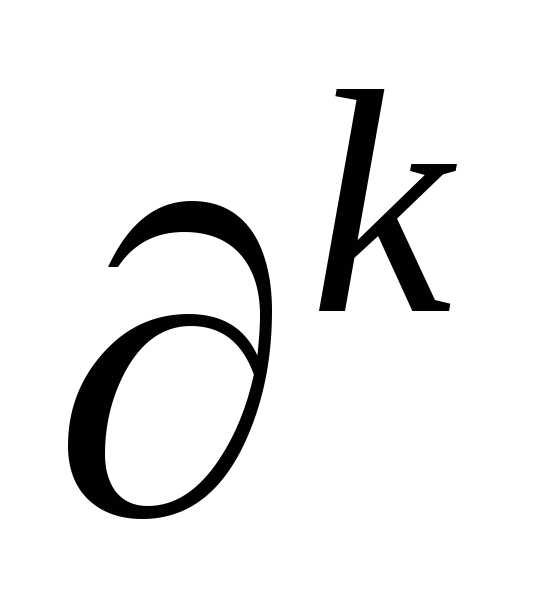 ,
а после этого всем символам возвращается
их значение производных и дифференциалов.
,
а после этого всем символам возвращается
их значение производных и дифференциалов.
Например, если , то
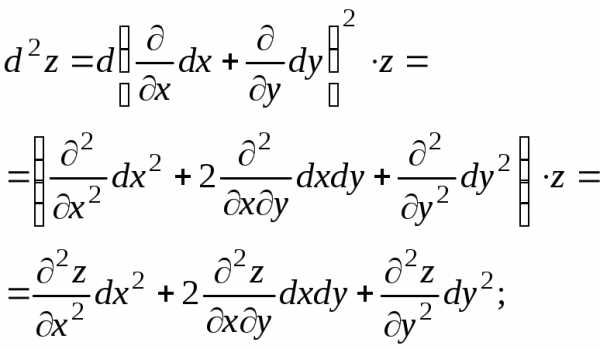
т.е.
(8)

таким образом,
(9)
и т.д.
Пример 6. Найти дифференциалы до третьего порядка включительно функции .
Решение. Для нахождения дифференциалов функции воспользуемся свойствами дифференциала, выраженными формулами (6) (дифференциал суммы, разности, произведения двух функций и т.д.) и определением дифференциала второго, третьего и т.д. порядков:
Теперь дифференцируем полученное выражение, помня, что дифференциалы независимых переменных есть константы, т.е. дифференциалы любого порядка выше первого от независимых переменных равны нулю (см. формулу (7)):
Дифференцируя третий раз, применяя те же правила, получим:
Здесь
.
Для дифференциалов второго и третьего порядка данной функции мы получили бы те же самые выражения, если бы воспользовались для их нахождения формулами (8) и (9), т.е. если бы сначала нашли все частные производные нужных порядков, а потом подставили их в эти формулы. Проверьте и сравните.
Из полученных выражений для дифференциалов заданной функции мы можем теперь записать выражения для частных производных этой функции любого порядка, по любым независимым переменным, сопоставляя полученное с формулами (8) и (9), например:
 ,
, 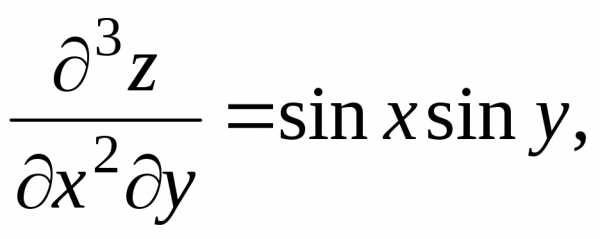
 ,
.
,
.
Пример 7. Найти дифференциалы до третьего порядка включительно функции .
Решение. Так как все частные
производные данной функции по переменной ,
начиная со второй, равны нулю, то здесь
легко сразу воспользоваться формулами
(3) и (4):
,
начиная со второй, равны нулю, то здесь
легко сразу воспользоваться формулами
(3) и (4):
.
studfiles.net
