Таблица косинусов синусов пи: Таблица значений тригонометрических функций

Содержание

Чиcло пи. π, 2π, 1/π, π/2, π/3, π/4, π/180, (π/180)2, π2, π3, π4 и др.

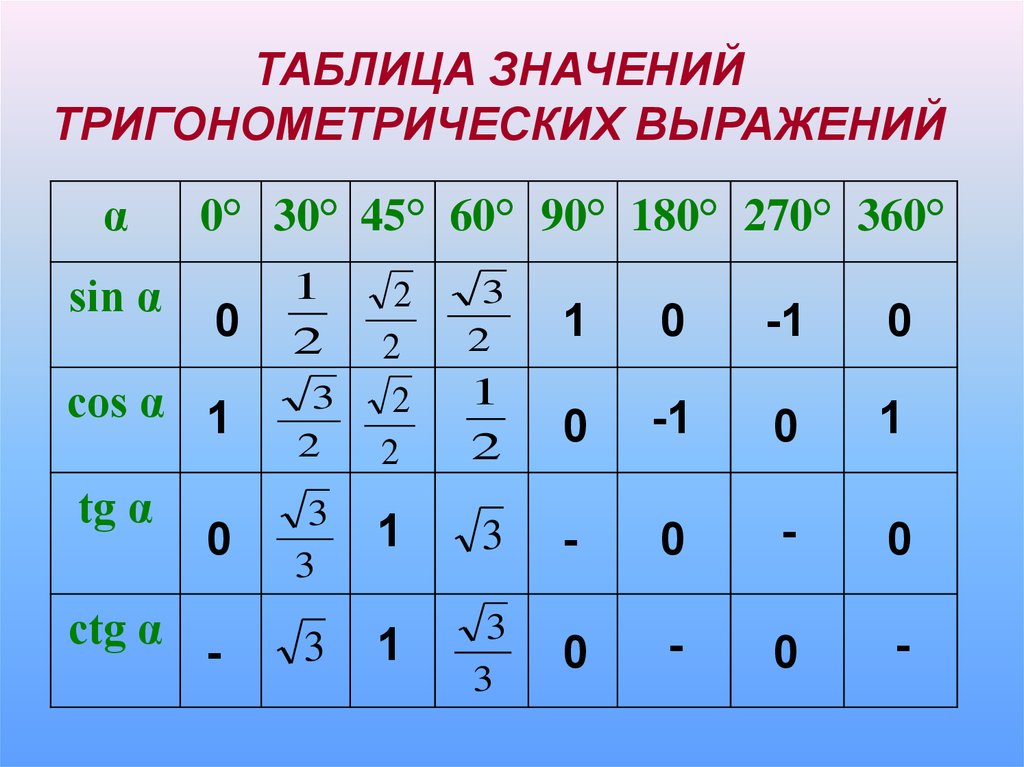
Раздел недели: Плоские фигуры. Свойства, стороны, углы, признаки, периметры, равенства, подобия, хорды, секторы, площади и т.д.

Поиск на сайте DPVA

Поставщики оборудования

Полезные ссылки

О проекте

Обратная связь

Ответы на вопросы.

Оглавление

Таблицы DPVA.ru — Инженерный Справочник

Адрес этой страницы (вложенность) в справочнике dpva.ru: главная страница / / Техническая информация/ / Математический справочник / / Таблицы численных значений. (Таблица квадратов, кубов, синусов ….) + Таблицы Брадиса / / Чиcло пи. π, 2π, 1/π, π/2, π/3, π/4, π/180, (π/180)², π², π³, π⁴ и др.

Чиcло пи. π, 2π, 1/π, π/2, π/3, π/4, π/180, (π/180)

², π², π³, π², корень квадратный из π, ln π, lg π, π^e, e^π, e^-π, e^1/(2π), iⁱ , e^-1/(2π) и др.

3.14159 26535 89793 23846 26433 83279 50288 41971 69399 37510 58209 74944 59230 78164 06286 20899 86280 34825 34211 70679… (100 знаков после запятой)

π^e =	22.4592 =	22.45915 77183 61045 47342 71522…
e^π =	23.1407 =	23.14069 26327 79269 00572 90864…
e^-π =	0.0432 =	0. 04321 39182 63772 24977 44177…
e^1/(2π) =	4.8105 =	4.81047 73809 65351 65547 30357…
iⁱ =e^-1/(2π) =	0.2079 =	0.20787 95763 50761 90854 69556…
log _e π = ln π =	1.1447 =	1.14472 98858 49400 17414 34273 51353 05871 16472 94812 91531…
log ₁₀ π = lg π =	0.4971 =	0.49714 98726 94133 85435 12682 88290 89887 36516 78324 38044…
log ₁₀ = lg =	0.3991 =	0.39908 99341 79057 52478 25035 91507 69595 02099 34102 92128

Поиск в инженерном справочнике DPVA.

Введите свой запрос:

Дополнительная информация от Инженерного cправочника DPVA, а именно — другие подразделы данного раздела:

Поиск в инженерном справочнике DPVA. Введите свой запрос:

Если Вы не обнаружили себя в списке поставщиков, заметили ошибку, или у Вас есть дополнительные численные данные для коллег по теме, сообщите , пожалуйста.
Вложите в письмо ссылку на страницу с ошибкой, пожалуйста.

Коды баннеров проекта DPVA.ru
Начинка: KJR Publisiers

Консультации и техническая
поддержка сайта: Zavarka Team

Проект является некоммерческим. Информация, представленная на сайте, не является официальной и предоставлена только в целях ознакомления. Владельцы сайта www.dpva.ru не несут никакой ответственности за риски, связанные с использованием информации, полученной с этого интернет-ресурса.

Free xml sitemap generator

Mathway | Популярные задачи

1	Найти точное значение	sin(30)
2	Найти точное значение	sin(45)
3	Найти точное значение	sin(30 град. )
4	Найти точное значение	sin(60 град. )
5	Найти точное значение	tan(30 град. )
6	Найти точное значение	arcsin(-1)
7	Найти точное значение	sin(pi/6)
8	Найти точное значение	cos(pi/4)
9	Найти точное значение	sin(45 град. )
10	Найти точное значение	sin(pi/3)
11	Найти точное значение	arctan(-1)
12	Найти точное значение	cos(45 град. )
13	Найти точное значение	cos(30 град. )
14	Найти точное значение	tan(60)
15	Найти точное значение	csc(45 град. )
16	Найти точное значение	tan(60 град. )
17	Найти точное значение	sec(30 град. )
18	Найти точное значение	cos(60 град. )
19	Найти точное значение	cos(150)
20	Найти точное значение	sin(60)
21	Найти точное значение	cos(pi/2)
22	Найти точное значение	tan(45 град. )
23	Найти точное значение	arctan(- квадратный корень из 3)
24	Найти точное значение	csc(60 град. )
25	Найти точное значение	sec(45 град. )
26	Найти точное значение	csc(30 град. )
27	Найти точное значение	sin(0)
28	Найти точное значение	sin(120)
29	Найти точное значение	cos(90)
30	Преобразовать из радианов в градусы	pi/3
31	Найти точное значение	tan(30)
32	Преобразовать из градусов в радианы	45
33	Найти точное значение	cos(45)
34	Упростить	sin(theta)^2+cos(theta)^2
35	Преобразовать из радианов в градусы	pi/6
36	Найти точное значение	cot(30 град. )
37	Найти точное значение	arccos(-1)
38	Найти точное значение	arctan(0)
39	Найти точное значение	cot(60 град. )
40	Преобразовать из градусов в радианы	30
41	Преобразовать из радианов в градусы	(2pi)/3
42	Найти точное значение	sin((5pi)/3)
43	Найти точное значение	sin((3pi)/4)
44	Найти точное значение	tan(pi/2)
45	Найти точное значение	sin(300)
46	Найти точное значение	cos(30)
47	Найти точное значение	cos(60)
48	Найти точное значение	cos(0)
49	Найти точное значение	cos(135)
50	Найти точное значение	cos((5pi)/3)
51	Найти точное значение	cos(210)
52	Найти точное значение	sec(60 град. )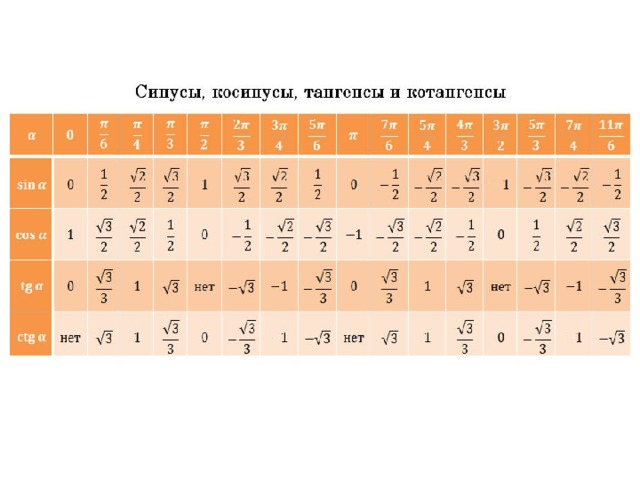
53	Найти точное значение	sin(300 град. )
54	Преобразовать из градусов в радианы	135
55	Преобразовать из градусов в радианы	150
56	Преобразовать из радианов в градусы	(5pi)/6
57	Преобразовать из радианов в градусы	(5pi)/3
58	Преобразовать из градусов в радианы	89 град.
59	Преобразовать из градусов в радианы	60
60	Найти точное значение	sin(135 град. )
61	Найти точное значение	sin(150)
62	Найти точное значение	sin(240 град. )
63	Найти точное значение	cot(45 град. )
64	Преобразовать из радианов в градусы	(5pi)/4
65	Найти точное значение	sin(225)
66	Найти точное значение	sin(240)
67	Найти точное значение	cos(150 град. )
68	Найти точное значение	tan(45)
69	Вычислить	sin(30 град. )
70	Найти точное значение	sec(0)
71	Найти точное значение	cos((5pi)/6)
72	Найти точное значение	csc(30)
73	Найти точное значение	arcsin(( квадратный корень из 2)/2)
74	Найти точное значение	tan((5pi)/3)
75	Найти точное значение	tan(0)
76	Вычислить	sin(60 град. )
77	Найти точное значение	arctan(-( квадратный корень из 3)/3)
78	Преобразовать из радианов в градусы	(3pi)/4
79	Найти точное значение	sin((7pi)/4)
80	Найти точное значение	arcsin(-1/2)
81	Найти точное значение	sin((4pi)/3)
82	Найти точное значение	csc(45)
83	Упростить	arctan( квадратный корень из 3)
84	Найти точное значение	sin(135)
85	Найти точное значение	sin(105)
86	Найти точное значение	sin(150 град. )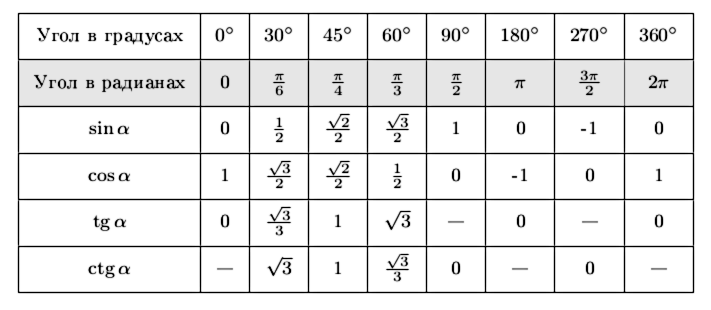
87	Найти точное значение	sin((2pi)/3)
88	Найти точное значение	tan((2pi)/3)
89	Преобразовать из радианов в градусы	pi/4
90	Найти точное значение	sin(pi/2)
91	Найти точное значение	sec(45)
92	Найти точное значение	cos((5pi)/4)
93	Найти точное значение	cos((7pi)/6)
94	Найти точное значение	arcsin(0)
95	Найти точное значение	sin(120 град. )
96	Найти точное значение	tan((7pi)/6)
97	Найти точное значение	cos(270)
98	Найти точное значение	sin((7pi)/6)
99	Найти точное значение	arcsin(-( квадратный корень из 2)/2)
100	Преобразовать из градусов в радианы	88 град.

Интерполяция синусов и косинусов

В предыдущем посте показано, как можно использовать линейную интерполяцию для заполнения пробелов в таблице логарифмов. Вы можете сделать то же самое для таблицы синусов и косинусов, но есть способ получше.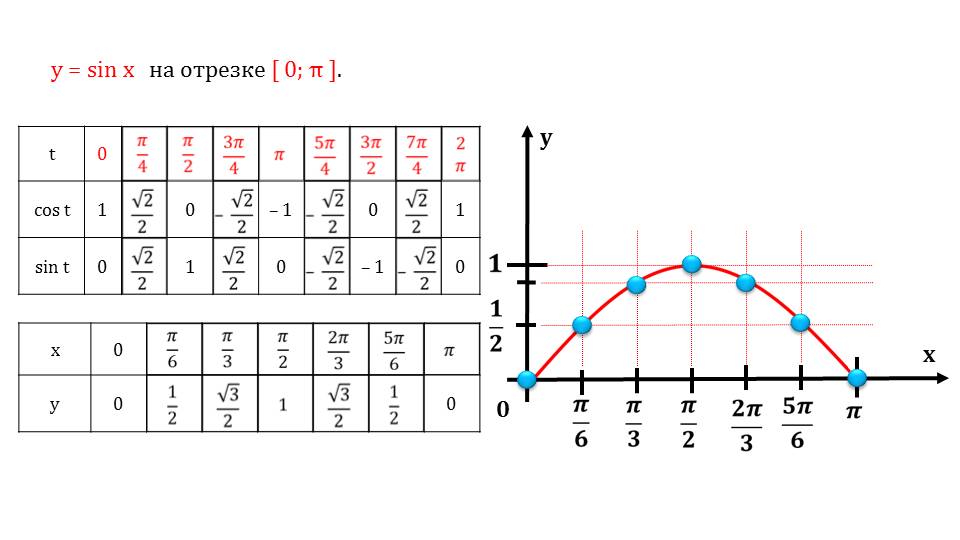 Как и прежде, мы предполагаем, что вы работаете вручную, используя только карандаш, бумагу и справочник таблиц.

Линейная интерполяция

Предположим, вы хотите найти синус 12,3456° и у вас есть таблица синусов для углов с шагом 0,1°. В Таблице 4.10 A&S мы находим

SIN 12,3 ° = 0,21303 03862 74977
SIN 12,4 ° = 0,21473 53271 67063

Если бы мы использовали линейную интерполяцию, мы оценили

SIN 12,3456 ° = SIN 12,3 ° + 0,456 (SIN 12,4 ° SIN 12,4 °. ) = 0,21380 78393 21768

с точностью до шести знаков после запятой.

Лучший подход

Другим подходом может быть использование тождества

sin(θ + φ) = sin θ cos φ + cos θ sin φ

вместо линейной интерполяции, установив θ = 12,3° и φ = 0,0456°. Мы можем найти синус и косинус θ в нашей таблице, но как нам найти синус и косинус φ?

Косинус вычислить легко: установите его равным 1. Для небольшого угла x (в радианах) косинус x приблизительно равен 1 с погрешностью менее x ²/2. В радианах

φ = 0,0456 π/180 = 0,00079 58701 38909

, поэтому ошибка усечения при аппроксимации cos φ с 1 составляет около 3×10 ^-7 .

Вычислить синус φ несложно, но для этого нужно преобразовать φ в радианы. Вы, вероятно, могли бы найти коэффициент преобразования в своем справочнике, например. в Таблице 1.1 A&S.

0,0456° = 0,0456 × 0,01745 32925 19943

Когда φ выражено в радианах, sin φ = φ с погрешностью менее φ³/6 (см. здесь).

Соединяя части вместе, мы получаем

sin(θ + φ) = sin 12,3° × 1 + cos 12,3° × φ

, что, используя приведенные выше числа, дает нам 0,213807852476, что примерно на 6×10 ^-8 .

Больше точности

Если мы хотим еще больше точности, нам нужно найти самое слабое звено в наших расчетах. Ошибка аппроксимации sin φ как φ порядка φ³, а ошибка аппроксимации cos φ как 1 порядка φ², поэтому последний является самым большим источником ошибки.

Если мы аппроксимируем cos φ как 1 – φ²/2, ошибка будет порядка φ ⁴ , а самым слабым звеном будет синусоидальная аппроксимация с ошибкой порядка φ³, которая все еще довольно мала. Общая ошибка при вычислении sin 12,3456° будет меньше 10 ^-10, если мы используем это приближение более высокого порядка для косинуса φ.

Сравните и сопоставьте

Вернемся к аппроксимации косинуса малого угла на 1 и сравним два приведенных выше подхода аппроксимации.

Линейная интерполяция:

sin 12,3456° = sin 12,3° + 0,456(sin 12,4° – sin 12,3°)

Формула сложения:

sin 12,3456° = sin 12,3° + 0,01801 (π2/s 0,01801) )

Вторые члены в двух подходах равны

0,0456(sin 12,4° – sin 12,3°)/0,1

0,0456 (π/180) (cos 12,3°).

Эти два числа похожи, потому что

(sin 12,4° – sin 12,3°)/0,1 ≈ (π/180) (cos 12,3°).

Член слева представляет собой разностный коэффициент для синуса при 12,3° с шагом ч = 0,1, а член справа представляет собой производную синуса при 12,3°.

Подожди, а производная от синуса не просто косинус? Это когда вы работаете в радианах , поэтому в исчислении почти всегда используются радианы, но когда вы работаете в градусах, производная синуса равна π/180, умноженной на косинус.

Это показывает, что если вы аппроксимируете косинусы малых углов как 1, формула суммы сводится к одночленной аппроксимации Тейлора.

КриссТал : Тригонометрические уравнения

[Домашняя страница]
[Страница математики]

[Введение в числа]
[Введение в алгебру]
[Треугольник Паскаля]
[Тригонометрия]
[Рассмотрение логарифмов]
[Графики]
[Тригонометрические уравнения]
[Исчисление: дифференцирование]
[Сферическая тригонометрия9] 900 ]
[Веселье с формулами]

[Отзывы читателей (математика)]

[Язык]
[Путешествия]
[Затмения]
[Лондон]
[Астрономия]
[Математика]
[Физика]
[Химия]
[Биология]
[Футбол]
[Телевидение]
9 [Другое]
9 Рекламная ссылка
Чтобы разместить здесь ссылку, свяжитесь с веб-мастером.

В алгебре мы рассмотрели решение простых уравнений, таких как 5X — 2 = 0 и квадратные уравнения типа X ² — 3X + 1 = 0 . В тригонометрии мы ввели тригонометрические функции (синусы, косинусы и тангенсы).

В этом эссе мы объединим тригонометрическую функцию в уравнения, которые можно решить.

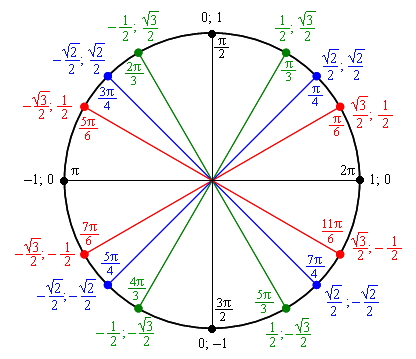
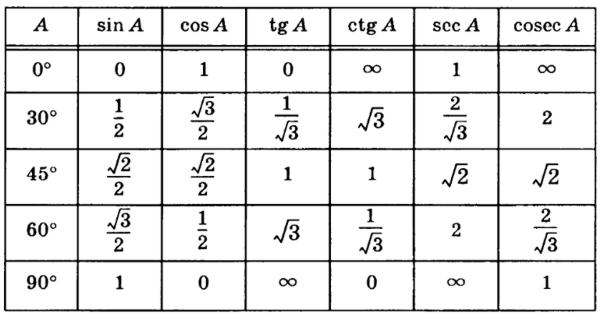
Начнем с того, что вспомним тригонометрические соотношения: Sin X / Cos X = Тан Х Sin ² X + Cos ² X = 1 Кроме того, существуют отношения, называемые двойными углами : Sin 2X = 2 Sin X Cos X Cos 2X = Cos ² X — Sin ² X Поскольку Sin ² X + Cos ² X = 1, это последнее соотношение можно также записать как: Cos 2X = 1 — 2 Sin ² X Кос 2X = 2 Кос ² Х — 1

Прежде чем мы сможем решить сложные тригонометрические уравнения, мы должны посмотреть, как изменяются синусы и косинусы.

Ниже приведен график Y = Sin X. X измеряется в радианах. Синусы периодические. Они колеблются между 1 и -1 в течение 360 ^o (2 π радиан), начиная и заканчивая 0,

. Ниже приведен график Y = Cos X. Он аналогичен, но в другой фазе.

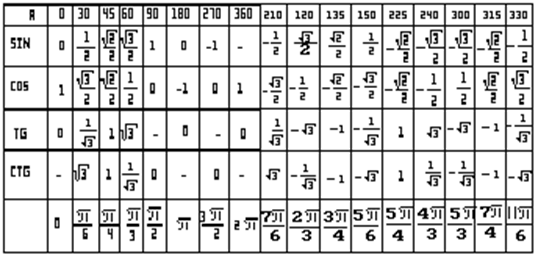
Косинусы также колеблются между 1 и -1 в течение 360 ^o (2 π радиан), начиная и заканчивая 1.

В приведенной ниже таблице обобщена информация как для синусов, так и для косинусов между 0 ^o и 360 ^o (от 0 до 2 π радиан). Эта информация будет использоваться при решении тригонометрических уравнений.

Уголок (^или)	Угол (рад)	Синус	Косинус
0	0	0	1
30	№/6	1 / 2	√3 / 2
45	№/4	1 / √2	1 / √2
60	№/3	√3 / 2	1 / 2
90	№/2	1	0
120	2π / 3	√3 / 2	-1 / 2
135	3π / 4	1 / √2	-1 / √2
150	5π / 6	1 / 2	-√3 / 2
180	№	0	-1
210	7π / 6	-1 / 2	-√3 / 2
225	5π / 4	-1 / √2	-1 / √2
240	4π / 3	-√3 / 2	-1 / 2
270	3π / 2	-1	0
300	5π / 3	-√3 / 2	1 / 2
315	7π / 4	-1 / √2	1 / √2
330	11π / 6	-1 / 2	√3 / 2
360	2π	0	1

Используя приведенную выше таблицу или графики и немного алгебры, решите следующие уравнения для значений между 0 ^o и 360 ^o .

Sin X = 1/2

Используя таблицу, легко увидеть, что X имеет два значения в требуемом диапазоне. Их:

X = 30 ^o и X = 150 ^o .

Cos X + 1 / 2 = 0

Преобразование уравнения (чтобы получить Cos X с одной стороны и числа с другой стороны) дает:

Cos X = -1 / 2

Используя таблицу, мы видим, что X имеет два значения в требуемом диапазоне. Это:

X = 120 ^o и X = 240 ^o .

Cos X Tan X = 1 / √2

Использование идентификатора для замены Tan X дает:

Cos X (Sin X / Cos X) = 1 / √2

Косинусы сокращаются, чтобы дать:

Sin X = 1 / √2

Это дает два значения X:

X = 45 ^o и X = 135 ^o .

2 Кос 2Х + 1 = 0

Переставьте уравнение:

Cos 2X = — 1/2

Следовательно, 2X = 120 ^o и 240 ^o, что дает:

X = 60 ^o и X = 120 ^o.

Sin X — Cos 2X = 0

Используя тождество двойного угла, замените Cos 2X на (1 — 2 Sin ² X):

Грех X — (1 — 2 Sin ² X) = 0

Sin X — 1 + 2 Sin ² X = 0

которое преобразуется в квадратное уравнение в Sin ² X:

2 Sin ² X + Sin X — 1 = 0

Это можно решить, разложив на множители:

(2 Sin X — 1) (Sin X + 1) = 0

Это уравнение дает 0, если либо 2 Sin X — 1 = 0, либо Sin X + 1 = 0. Другими словами:

Sin X = 1/2 или Sin X = -1

Первое уравнение дает два значения (X = 30 ^o , X = 150 ^o ), второе уравнение дает одно значение (270 ^o ). Таким образом, решение исходного уравнения:

X = 30 ^o , X = 150 ^o и X = 270 ^o .