Аналитическое вычисление производной функции на языке Scala / Хабр
Введение
Данный алгоритм реализован на языке Scala, характерной особенностью которого является использование case-классов, так удачно подходящих для написания алгоритма дифференцирования. В этой статье планируется описать лишь часть программы, содержащей алгоритм нахождения производной, поскольку разработка парсера для математических выражений это другая большая тема,
заслуживающая отдельной статьи
Подготовка
Сначала опишем структуру данных, в которой будет храниться исходная математическая функция. Опишем трейт MathAST:
sealed trait MathAST
И его наследников:
sealed trait SingleToken extends MathAST{
val a: MathAST
}
sealed trait DoubleToken extends MathAST{
val a: MathAST
val b: MathAST
}
sealed trait LeafToken extends MathAST
SingleToken будет реализовывать case-классы унарных операторов, таких как sin(a), -a, ln(a) и т.
LeafToken — «листья» дерева, т.е. константы, переменные и зарезервированные имена констант (число Пи и экспонента).
Опишем классы/объекты операторов и токенов:
case object Pi extends LeafToken case object Exponenta extends LeafToken case class Sin(override val a: MathAST) extends SingleToken case class Cos(override val a: MathAST) extends SingleToken … case class Mul(override val a: MathAST, override val b: MathAST) extends DoubleToken case class Add(override val a: MathAST, override val b: MathAST) extends DoubleToken … case class Differentiate(f: MathAST, dx: Variable) extends MathAST case class Variable(name: String) extends LeafToken case class Constant(value: BigDecimal) extends LeafToken
Обратите внимание на класс Differentiate, он имеет особую сигнатуру: f – исходная функция, dx – переменная, по которой происходит дифференцирование.
Теперь есть все, чтобы представить математическую функцию в виде дерева вычислений, для примера возьмем функцию: , которая примет вид:Mul(Constant(BigDecimal(2)), Pow(x, Constant(BigDecimal(2)))
Конечно, чтобы получить дерево-выражение из обычной строки, введенной пользователем, нужно написать парсер, но, как было упомянуто выше, это уже другая тема.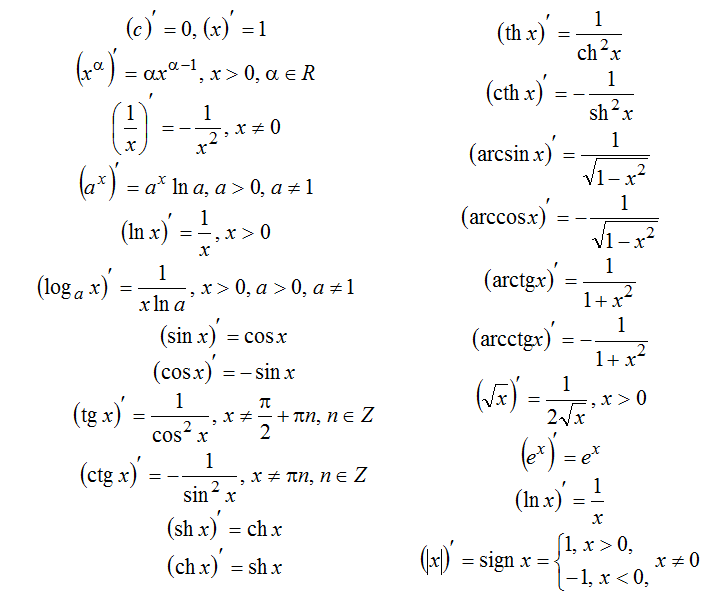 Скажу лишь что в программе используется самодельный парсер, наследующий трейт Parsers из пакета scala.util.parsing.combinator.
Скажу лишь что в программе используется самодельный парсер, наследующий трейт Parsers из пакета scala.util.parsing.combinator.
Алгоритм нахождения производной
В основе которого лежат правила дифференцирования и таблица производных.
Опишем рекурсивную функцию, которая и будет преобразовывать исходную математическую функцию в результирующую функцию-производную:
def differentiate(f: MathAST)(implicit dx: String): MathAST
Аргумент dx, содержащий имя переменной (по которой происходит дифференцирование) помечен как неявный (
На вход рекурсивной функции подается выражение — исходная функция f(x) (в формате MathAST), возвращаемое значение — функция-производная в том же формате.
Примечание 1: Выражение может быть бинарным, унарным или токеном.
Примечание 2: Оператором может быть один из: «+», «-», «^», «*», «/», «abs», «sin», «cos», «tg», «ctg», «ln», «arcsin», «arccos», «arctg», «arcctg», «(», «)».
Примечание 3: Входные и выходные данные представлены в формате MathAST — дерево-выражение.
Общий алгоритм
В общем виде алгоритм слишком абстрактный, поэтому дальше разберем его подробнее.
- Рекурсивная функция получает на вход данные и используя сопоставление с образцом (pattern-matching) выполняет необходимые действия, в зависимости от типа данных.
- Функция высчитывает производную для входного выражения и возвращает выражение-результат. Может получиться, что аргументы a и/или b оказались не константой и не переменной, а сложной функцией u(x),
тогда понадобится рекурсивно посчитать еще и производную u’(x), т.е. вернуть [ differentiate(u(x)) ] — перейти к шагу 1 с новыми данными — u(x). - Если данные не корректны вернуть сообщение об ошибке.
Детали принципа работы и связь с математическими абстракциями
Функция приняла на вход данные — выражение-функцию, которую следует обработать в соответствии с правилами дифференцирования
Если бинарное выражение
Бинарные выражения помечены трейтом DoubleToken. »):
»):
case Add(a, b) => Add(differentiate(a), differentiate(b)) case Sub(a, b) => Sub(differentiate(a), differentiate(b)) …
- Если оператор «+»: вернуть [ differentiate(a) + differentiate(b) ].
- Если оператор «-»: вернуть [ differentiate(a) — differentiate(b) ].
- Если оператор «*»: Умножение представляет из себя более сложный случай, операнды a и b могут быть константами или переменными (всего 4 комбинации: u(x)*c, u(x)*v(x), c*c, c*u(x)).
Функция анализирует какой из 4 вариантов попался и возвращает выражение используя правило дифференцирования № 1, № 3, и №5,
если один из операндов – сложная функция. Например: если a = u(x), а b = v(x), то вернуть [ differentiate(a) * b + a * differentiate(b)) ].
Приватный метод isDependsOnVar проверяет, зависит ли подвыражение от переменной, по которой производится дифференцирование. c, c=const
Constant(BigDecimal(0))
}else Add(Mul(differentiate(a), b), Mul(a, differentiate(b)))
}
c, c=const
Constant(BigDecimal(0))
}else Add(Mul(differentiate(a), b), Mul(a, differentiate(b)))
}Если унарное выражение
Классы SingleToken обрабатываются следующим образом:
case e: SingleToken => val d = e match { case Sin(x) => Cos(x) case Cos(x) => Usub(Sin(x)) case Tg(x) => Div(Constant(BigDecimal(1)), Pow(Cos(x), Constant(BigDecimal(2)))) … } if (isLeaf(e.a)) d else Mul(d, differentiate(e.a))Оператор проверяется на соответствие одному из доступных операторов («sin», «-», «cos», …)
Для примера, оператор «sin»: вернуть [ cos(a) ], если a = x, если же a — сложная функция u(x), то вернуть [ cos(a) * differentiate(a) ].С остальными операторами происходят аналогичные действия, используя правило дифференцирования сложной функции и табличные правила взятия производной.
Отдельно следует рассмотреть оператор abs — модуль, поскольку его нет в таблице.

Приватный метод isLeaf выясняет сложная функция или нет, в первом случае нужно вернуть текущий результат умноженный на производную вложенной функции, а во втором просто вернуть текущий результат.
Если один токен
Речь идет о переменной или константе
case Variable(a) => if (a == dx) Constant(BigDecimal(1)) else Constant(BigDecimal(0)) case Constant(a) => Constant(BigDecimal(0)) case Pi | Exponenta => Constant(BigDecimal(0)) case _ => throw new AbstractEvaluateException("Differentiate: Wrong input data")- Введены некорректные данные, вывести сообщение об ошибке и завершить работу.
- Если переменная (по которой осуществляется дифференцирование, например x), вернуть [ 1 ].
- Если константа, вернуть [ 0 ].
Напоследок добавим строку:
case Differentiate(_f, _dx) => differentiate(_f)(_dx.name)
Это на случай, если внутри функции есть вложенная производная, т.
 c, c=const
Constant(BigDecimal(0))
}else Add(Mul(differentiate(a), b), Mul(a, differentiate(b)))
}
case e: SingleToken =>
val d = e match {
case Sin(x) => Cos(x)
case Cos(x) => Usub(Sin(x))
case Tg(x) => Div(Constant(BigDecimal(1)), Pow(Cos(x), Constant(BigDecimal(2))))
case Ctg(x) => Usub(Div(Constant(BigDecimal(1)), Pow(Sin(x), Constant(BigDecimal(2)))))
case Abs(x) => Div(x, Abs(x))
case Ln(x) => Div(Constant(BigDecimal(1)), x)
case Sqrt(x) => Div(Constant(BigDecimal(1)), Mul(Constant(BigDecimal(2)), Sqrt(x)))
case Usub(x) => Usub(differentiate(x))
case Arcsin(x) => Div(Constant(BigDecimal(1)), Sqrt(Sub(Constant(BigDecimal(1)), Pow(x, Constant(BigDecimal(2))))))
case Arccos(x) => Usub(Div(Constant(BigDecimal(1)), Sqrt(Sub(Constant(BigDecimal(1)), Pow(x, Constant(BigDecimal(2)))))))
case Arctg(x) => Div(Constant(BigDecimal(1)), Sub(Constant(BigDecimal(1)), Pow(x, Constant(BigDecimal(2)))))
case Arcctg(x) => Usub(Div(Constant(BigDecimal(1)), Sub(Constant(BigDecimal(1)), Pow(x, Constant(BigDecimal(2))))))
case _ => throw new AbstractEvaluateException(«Differentiate: Unknown unary operator»)
}
if (isLeaf(e.
c, c=const
Constant(BigDecimal(0))
}else Add(Mul(differentiate(a), b), Mul(a, differentiate(b)))
}
case e: SingleToken =>
val d = e match {
case Sin(x) => Cos(x)
case Cos(x) => Usub(Sin(x))
case Tg(x) => Div(Constant(BigDecimal(1)), Pow(Cos(x), Constant(BigDecimal(2))))
case Ctg(x) => Usub(Div(Constant(BigDecimal(1)), Pow(Sin(x), Constant(BigDecimal(2)))))
case Abs(x) => Div(x, Abs(x))
case Ln(x) => Div(Constant(BigDecimal(1)), x)
case Sqrt(x) => Div(Constant(BigDecimal(1)), Mul(Constant(BigDecimal(2)), Sqrt(x)))
case Usub(x) => Usub(differentiate(x))
case Arcsin(x) => Div(Constant(BigDecimal(1)), Sqrt(Sub(Constant(BigDecimal(1)), Pow(x, Constant(BigDecimal(2))))))
case Arccos(x) => Usub(Div(Constant(BigDecimal(1)), Sqrt(Sub(Constant(BigDecimal(1)), Pow(x, Constant(BigDecimal(2)))))))
case Arctg(x) => Div(Constant(BigDecimal(1)), Sub(Constant(BigDecimal(1)), Pow(x, Constant(BigDecimal(2)))))
case Arcctg(x) => Usub(Div(Constant(BigDecimal(1)), Sub(Constant(BigDecimal(1)), Pow(x, Constant(BigDecimal(2))))))
case _ => throw new AbstractEvaluateException(«Differentiate: Unknown unary operator»)
}
if (isLeaf(e.
Заключение
Весь код исходников можно скачать на github’е, протестировать программу онлайн можно на сайте Калькулятор производных онлайн, приложение выполнено в виде REST сервиса и дополнено модулями упрощения выражений.

Список литературы
- Математический портал «mathprofi.ru» mathprofi.ru/slozhnye_proizvodnye_logarifmicheskaja_proizvodnaja.html
- Odersky M. «Programming in Scala (second edition)»
- Хостманн К. «Scala для нетерпеливых»
Логарифмическая производная — примеры вычисления
Метод решения
Пусть
(1)
есть дифференцируемая функция от переменной x. В начале мы рассмотрим ее на множестве значений x, для которых y принимает положительные значения: . В дальнейшем мы покажем, что все полученные результаты применимы и для отрицательных значений .В некоторых случаях, чтобы найти производную функции (1), ее удобно предварительно прологарифмировать
,
а затем вычислить производную. Тогда по правилу дифференцирования сложной функции,
.
Отсюда
(2) .Производная от логарифма функции называется логарифмической производной:
.- Логарифмическая производная функции y = f(x)
- – это производная натурального логарифма этой функции: (ln f(x) )′.

Случай отрицательных значений y
Теперь рассмотрим случай, когда переменная может принимать как положительные, так и отрицательные значения. В этом случае возьмем логарифм от модуля и найдем его производную:
.
Отсюда
(3) .
То есть, в общем случае, нужно найти производную от логарифма модуля функции .Сравнивая (2) и (3) мы имеем:
.
То есть формальный результат вычисления логарифмической производной не зависит от того, взяли мы по модулю или нет. Поэтому, при вычислении логарифмической производной, мы можем не беспокоится о том, какой знак имеет функция .Прояснить такую ситуацию можно с помощью комплексных чисел. Пусть, при некоторых значениях x, отрицательна: . Если мы рассматриваем только действительные числа, то функция не определена. Однако, если ввести в рассмотрение комплексные числа, то получим следующее:
.
То есть функции и отличаются на комплексную постоянную :
.
Поскольку производная от постоянной равна нулю, то
.
Свойство логарифмической производной
Из подобного рассмотрения следует, что логарифмическая производная не изменится, если умножить функцию на произвольную постоянную :
.
Действительно, применяя свойства логарифма, формулы производной суммы и производной постоянной, имеем:.
Примеры применений логарифмической производной
Все примеры
Применять логарифмическую производную удобно в тех случаях, когда исходная функция состоит из произведения степенных или показательных функций. В этом случае операция логарифмирования превращает произведение функций в их сумму. Это упрощает вычисление производной.
Далее мы приводим примеры вычисления производных для следующих функций:
Пример 1
Все примеры
Найти производную функции:
.Решение
Логарифмируем исходную функцию:
.Дифференцируем по переменной x.
В таблице производных находим:
.
Применяем правило дифференцирования сложной функции.
;
;
;
;
(П1.1) .
Умножим на :.
Итак, мы нашли логарифмическую производную:
.
Отсюда находим производную исходной функции:
.Примечание
Если мы хотим использовать только действительные числа, то следует брать логарифм от модуля исходной функции:
.
Тогда
;
.
И мы получили формулу (П1.1). Поэтому результат не изменился.Ответ
Пример 2
Все примеры
С помощью логарифмической производной, найдите производную функции
.Решение
Логарифмируем:
(П2.1) .
Дифференцируем по переменной x:
;
;;
;
;
.Умножим на :
.
Отсюда мы получаем логарифмическую производную:
.Производная исходной функции:
.Примечание
Здесь исходная функция неотрицательная: . Она определена при . Если не предполагать, что логарифм может быть определен для отрицательных значений аргумента, то формулу (П2.
 1) следует записать так:
1) следует записать так:
.
Посколькуи
,
то это не повлияет на окончательный результат.Ответ
.
Пример 3
Все примеры
Найдите производную
.Решение
Дифференцирование выполняем с помощью логарифмической производной. Логарифмируем, учитывая что :
(П3.1) .Дифференцируя, получаем логарифмическую производную.
;
;
;
(П3.2) .Поскольку , то
.
Примечание
Проделаем вычисления без предположения, что логарифм может быть определен для отрицательных значений аргумента. Для этого возьмем логарифм от модуля исходной функции:
.
Тогда вместо (П3.1) имеем:
;.
Сравнивая с (П3.2) мы видим, что результат не изменился.Ответ
.
Калькулятор ряда Тейлора+ онлайн-решатель с бесплатными шагами
Онлайн-калькулятор ряда Тейлора поможет вам найти разложение и сформировать ряд Тейлора для заданной функции.
 С помощью этого калькулятора вы можете найти пошаговое решение для любой заданной функции.
С помощью этого калькулятора вы можете найти пошаговое решение для любой заданной функции.Ряд Тейлора — это функция, которую мы получаем суммированием бесконечных членов. Эти члены являются производными данных функций только в одной точке.
Этот калькулятор также поможет вам найти Maclaurin серии функций. Ряд Маклорена можно найти, положив точку равной нулю.
Что такое калькулятор ряда Тейлора?
Калькулятор ряда Тейлора — это онлайн-калькулятор, который дает разложение функции в одной точке.
Это удобный инструмент для определения бесконечных сумм и частичных сумм функций, расширяющий идею линеаризации.
Процесс поиска решения или расширения является длительным и сложным, но это ядро 9{3} + . . . \]
Приведенное выше выражение является общей формой ряда Тейлора для функции f(x) . В этом уравнении f’(a) , f’’(a) представляет производную функции в конкретной точке a .
 Чтобы определить Maclaurin Series , просто замените точку ‘ a’ на ноль.
Чтобы определить Maclaurin Series , просто замените точку ‘ a’ на ноль.Как пользоваться калькулятором ряда Тейлора?
Вы можете использовать калькулятор серии Taylor , введя функцию, переменную и точку в соответствующих полях.
Процедура использования калькулятора ряда Тейлора сделана удобной для пользователя. Вам просто нужно выполнить простые шаги, указанные ниже.
Шаг 1
Введите функцию , чей ряд Тейлора вы хотите найти. Например, это может быть любая тригонометрическая функция, такая как sin(x) , или алгебраическая функция, такая как многочлен. Функция представлена как f(x) .
Шаг 2
Введите имя вашей переменной . Выражение, введенное на предыдущем шаге, должно быть функцией этой переменной. Кроме того, ряд Тейлора рассчитывается с использованием этой переменной.
Шаг 3
Установите желаемую точку .
 Эта точка может варьироваться от одной проблемы к другой.
Эта точка может варьироваться от одной проблемы к другой.Шаг 4
Теперь вставьте порядок вашего уравнения в указанное последнее место.
Результат
Нажмите ‘ отправить 9n) \]
Как работает калькулятор ряда Тейлора?
Этот калькулятор работает, находя производные терминов и упрощая их. Прежде чем мы продолжим, мы должны знать о некоторых основных терминах, таких как производные, порядок многочлена, факториал и т. д.
Что такое производные?
Производные просто мгновенная скорость изменения любой величины. Производная функции представляет собой наклон линии, касательной к кривой при любом значении переменной.
Например, если скорость изменения переменной y находится относительно переменной x . Тогда производная обозначается термином ‘dy/dx’ и общая формула для вычисления производной:
\[ \frac{dy}{dx} = \lim_{a \to 0} \frac{f (x + a) – f(x)}{a} \]
Что такое факториал?
Факториал является произведением любого целого числа на все целые числа до 1.
 Например, факториал 5 будет 5.4.3.2.1, что равно 120. Он представлен как 5!
Например, факториал 5 будет 5.4.3.2.1, что равно 120. Он представлен как 5!Каков порядок уравнения?
Наивысший порядок членов уравнения известен как порядок уравнения. Например, если старший порядок члена равен 2, то порядок уравнения будет 2, и оно будет называться уравнением второго порядка .
Что такое суммирование?
Суммирование — это операция сложения нескольких терминов вместе. Знак Sigma ($\sum$) используется для обозначения суммирования. Обычно он используется для добавления компонентов дискретных сигналов. 9{4} + … \]
Метод расчета
Калькулятор просит пользователя ввести данные, которые были объяснены в предыдущем разделе. После нажатия кнопки отправки он через несколько секунд показывает результат с подробными инструкциями.
Вот упрощенные шаги, которые используются для получения окончательных результатов.
Нахождение производных
Нахождение производных функций является первым шагом.
 Калькулятор находит производные от членов в соответствии с их порядком. Вроде вначале вычисляет производную первого порядка, потом вторую и так далее в зависимости от порядка уравнения.
Калькулятор находит производные от членов в соответствии с их порядком. Вроде вначале вычисляет производную первого порядка, потом вторую и так далее в зависимости от порядка уравнения.Ввод значений
На этом шаге переменная заменяется точкой, в которой требуется значение. Это простой шаг, на котором функция выражается через значение точки.
Упрощение
Теперь калькулятор помещает результаты предыдущего шага в общую формулу ряда Тейлора. На этом этапе после ввода значений выражение упрощается с помощью простых математических шагов, таких как факториал и т. д.
Суммирование
Наконец, калькулятор добавляет знак суммирования и выдает результат. Суммирование полезно, если мы хотим определить интервал сходимости или некоторые конкретные значения переменной, на которых сходится ряд Тейлора.
Построение графиков
Рисовать график вручную сложно и сложно. Но этот калькулятор показывает приблизительный график для данной переменной до 3-го порядка.
 .
.Краткая история серии Тейлора
Тейлор — имя ученого, который представил эту серию в 1715 году. Его полное имя — Брук Тейлор.
В середине 1700-х годов другой ученый Колин Маклорен широко использовал ряд Тейлора в особом случае, когда нуль берется в качестве точки производных. Это известно по его имени как серия Маклорена.
Применение ряда Тейлора
- Помогает вычислять определенные интегралы , так как некоторые функции могут не иметь первообразных.
- Ряды Тейлора могут помочь понять поведение функции в ее конкретной области.
- Рост функций также можно понять с помощью ряда Тейлора.
- Ряды Тейлора и ряды Маклорена используются для нахождения приблизительного значения фактора Лоренца в специальной теории относительности.
- Основы движения маятника также выводятся из ряда Тейлора.
Ограничения ряда Тейлора
- Наиболее распространенное ограничение ряда Тейлора заключается в том, что по мере того, как мы продвигаемся к дальнейшим шагам, с ним становится все сложнее справиться.

- Существует два типа ошибок, которые могут повлиять на все расчеты: ошибка округления и ошибка усечения . Вдали от точки расширения ошибка усечения быстро растет.
- Расчеты занимают много времени и времени, если мы делаем их вручную. 9{3} \]
График
Серию можно визуализировать на следующем графике на рисунке ниже.
Рисунок 2
Все математические изображения/графики созданы с помощью GeoGebra.
Калькулятор дифференциального уравнения второго порядка
< Список математических калькуляторов > Калькулятор суммы РиманаПроизводная функции абсолютного значения
Пусть |f(x)| быть функцией абсолютного значения.
Тогда формула для нахождения производной |f(x)| приведен ниже.
По приведенной формуле найдем производную от |x|.
|х|’ = [х/|х|](х)’
|х|’ = [х/|х|](1)
|х|’ = х/|х|
Следовательно, производная от |x| равно х/|х|.
Пусть y = |x|’.

Тогда имеем y = x/|x|.
В y = x/|x|, если мы подставим x = 0, знаменатель станет равным нулю.
Поскольку знаменатель становится равным нулю, y становится неопределенным при x = 0
Подставим некоторые случайные значения вместо x в y.
, когда x = -3,
y = -3/|-3| = -3/3 = -1
при x = -2,
y = -2/|-2| = -2/2 = -1
при x = -1,
y = -1/|-1| = -1/1 = -1
при x = 0,
y = 0/|0| = 0/0 = не определено
, когда x = 1,
y = 1/|1| = 1/1 = 1
при x = 2,
y = 2/|2| = 2/2 = 1
при x = 3,
y = 3/|3| = 3/3 = 1
Сведем приведенный выше расчет в табл.
Теперь, основываясь на приведенной выше таблице, мы можем получить график производной от |x|.
Найдите производную каждой из следующих функций абсолютного значения.
Пример 1 :
|2x + 1|
Решение:
|2x + 1|’ = [(2x + 1)/|2x + 1|](2x + 1)’
= [(2x + 1)/|2x + 1|](2)
= 2(2x + 1)/| 2x + 1|
Пример 2 :
Решение:
|x 3 + 1|’ = [(х 3 + 1)/|х 3 + 1|](х 3 + 1)’
= [(х 3 + 1)/|x 3 + 1|](3x 2 )
= 3x 2 (x 3 + 1)/|x 3 904|
Пример 3 :
|x| 3
Решение:
В заданной функции |x| 3 , используя цепное правило, сначала мы должны найти производную для показателя степени 3, а затем для |x|.


 c, c=const
Constant(BigDecimal(0))
}else Add(Mul(differentiate(a), b), Mul(a, differentiate(b)))
}
c, c=const
Constant(BigDecimal(0))
}else Add(Mul(differentiate(a), b), Mul(a, differentiate(b)))
}
 c, c=const
Constant(BigDecimal(0))
}else Add(Mul(differentiate(a), b), Mul(a, differentiate(b)))
}
case e: SingleToken =>
val d = e match {
case Sin(x) => Cos(x)
case Cos(x) => Usub(Sin(x))
case Tg(x) => Div(Constant(BigDecimal(1)), Pow(Cos(x), Constant(BigDecimal(2))))
case Ctg(x) => Usub(Div(Constant(BigDecimal(1)), Pow(Sin(x), Constant(BigDecimal(2)))))
case Abs(x) => Div(x, Abs(x))
case Ln(x) => Div(Constant(BigDecimal(1)), x)
case Sqrt(x) => Div(Constant(BigDecimal(1)), Mul(Constant(BigDecimal(2)), Sqrt(x)))
case Usub(x) => Usub(differentiate(x))
case Arcsin(x) => Div(Constant(BigDecimal(1)), Sqrt(Sub(Constant(BigDecimal(1)), Pow(x, Constant(BigDecimal(2))))))
case Arccos(x) => Usub(Div(Constant(BigDecimal(1)), Sqrt(Sub(Constant(BigDecimal(1)), Pow(x, Constant(BigDecimal(2)))))))
case Arctg(x) => Div(Constant(BigDecimal(1)), Sub(Constant(BigDecimal(1)), Pow(x, Constant(BigDecimal(2)))))
case Arcctg(x) => Usub(Div(Constant(BigDecimal(1)), Sub(Constant(BigDecimal(1)), Pow(x, Constant(BigDecimal(2))))))
case _ => throw new AbstractEvaluateException(«Differentiate: Unknown unary operator»)
}
if (isLeaf(e.
c, c=const
Constant(BigDecimal(0))
}else Add(Mul(differentiate(a), b), Mul(a, differentiate(b)))
}
case e: SingleToken =>
val d = e match {
case Sin(x) => Cos(x)
case Cos(x) => Usub(Sin(x))
case Tg(x) => Div(Constant(BigDecimal(1)), Pow(Cos(x), Constant(BigDecimal(2))))
case Ctg(x) => Usub(Div(Constant(BigDecimal(1)), Pow(Sin(x), Constant(BigDecimal(2)))))
case Abs(x) => Div(x, Abs(x))
case Ln(x) => Div(Constant(BigDecimal(1)), x)
case Sqrt(x) => Div(Constant(BigDecimal(1)), Mul(Constant(BigDecimal(2)), Sqrt(x)))
case Usub(x) => Usub(differentiate(x))
case Arcsin(x) => Div(Constant(BigDecimal(1)), Sqrt(Sub(Constant(BigDecimal(1)), Pow(x, Constant(BigDecimal(2))))))
case Arccos(x) => Usub(Div(Constant(BigDecimal(1)), Sqrt(Sub(Constant(BigDecimal(1)), Pow(x, Constant(BigDecimal(2)))))))
case Arctg(x) => Div(Constant(BigDecimal(1)), Sub(Constant(BigDecimal(1)), Pow(x, Constant(BigDecimal(2)))))
case Arcctg(x) => Usub(Div(Constant(BigDecimal(1)), Sub(Constant(BigDecimal(1)), Pow(x, Constant(BigDecimal(2))))))
case _ => throw new AbstractEvaluateException(«Differentiate: Unknown unary operator»)
}
if (isLeaf(e.




 1) следует записать так:
1) следует записать так: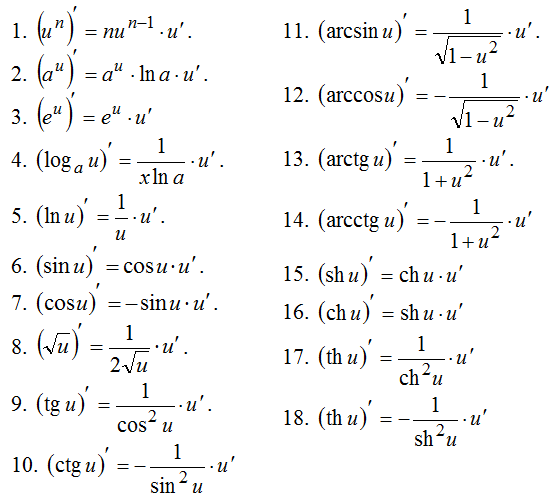 С помощью этого калькулятора вы можете найти пошаговое решение для любой заданной функции.
С помощью этого калькулятора вы можете найти пошаговое решение для любой заданной функции. Чтобы определить Maclaurin Series , просто замените точку ‘ a’ на ноль.
Чтобы определить Maclaurin Series , просто замените точку ‘ a’ на ноль. Эта точка может варьироваться от одной проблемы к другой.
Эта точка может варьироваться от одной проблемы к другой. Например, факториал 5 будет 5.4.3.2.1, что равно 120. Он представлен как 5!
Например, факториал 5 будет 5.4.3.2.1, что равно 120. Он представлен как 5! Калькулятор находит производные от членов в соответствии с их порядком. Вроде вначале вычисляет производную первого порядка, потом вторую и так далее в зависимости от порядка уравнения.
Калькулятор находит производные от членов в соответствии с их порядком. Вроде вначале вычисляет производную первого порядка, потом вторую и так далее в зависимости от порядка уравнения. .
.

