Тригонометрические свойства. Основные формулы тригонометрии
В этой статье собраны таблицы синусов, косинусов, тангенсов и котангенсов . Сначала мы приведем таблицу основных значений тригонометрических функций, то есть, таблицу синусов, косинусов, тангенсов и котангенсов углов 0, 30, 45, 60, 90, …, 360 градусов (0, π/6, π/4, π/3, π/2, …, 2π радиан). После этого мы дадим таблицу синусов и косинусов, а также таблицу тангенсов и котангенсов В. М. Брадиса, и покажем, как использовать эти таблицы при нахождении значений тригонометрических функций.
Навигация по странице.
Таблица синусов, косинусов, тангенсов и котангенсов для углов 0, 30, 45, 60, 90, … градусов
Список литературы.
- Алгебра: Учеб. для 9 кл. сред. шк./Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова; Под ред. С. А. Теляковского.- М.: Просвещение, 1990.- 272 с.: ил.- ISBN 5-09-002727-7
- Башмаков М. И. Алгебра и начала анализа: Учеб. для 10-11 кл.
 сред. шк. — 3-е изд. — М.: Просвещение, 1993. — 351 с.: ил. — ISBN 5-09-004617-4.
сред. шк. — 3-е изд. — М.: Просвещение, 1993. — 351 с.: ил. — ISBN 5-09-004617-4. - Алгебра и начала анализа: Учеб. для 10-11 кл. общеобразоват. учреждений / А. Н. Колмогоров, А. М. Абрамов, Ю. П. Дудницын и др.; Под ред. А. Н. Колмогорова.- 14-е изд.- М.: Просвещение, 2004.- 384 с.: ил.- ISBN 5-09-013651-3.
- Гусев В. А., Мордкович А. Г. Математика (пособие для поступающих в техникумы): Учеб. пособие.- М.; Высш. шк., 1984.-351 с., ил.
- Брадис В. М. Четырехзначные математические таблицы: Для общеобразоват. учеб. заведений. — 2-е изд. — М.: Дрофа, 1999.- 96 с.: ил. ISBN 5-7107-2667-2
Позволяют установить ряд характерных результатов – свойств синуса, косинуса, тангенса и котангенса . В этой статье мы рассмотрим три основных свойства. Первое из них указывает знаки синуса, косинуса, тангенса и котангенса угла α
в зависимости от того, углом какой координатной четверти является α
. Дальше мы рассмотрим свойство периодичности, устанавливающее неизменность значений синуса, косинуса, тангенса и котангенса угла α
при изменении этого угла на целое число оборотов.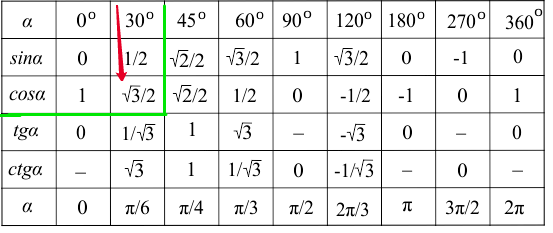
Если же Вас интересуют свойства функций синуса, косинуса, тангенса и котангенса, то их можно изучить в соответствующем разделе статьи .
Навигация по странице.
Знаки синуса, косинуса, тангенса и котангенса по четвертям
Ниже в этом пункте будет встречаться фраза «угол I , II , III и IV координатной четверти». Объясним, что же это за углы.
Возьмем единичную окружность , отметим на ней начальную точку А(1, 0) , и повернем ее вокруг точки O на угол α , при этом будем считать, что мы попадем в точку A 1 (x, y) .
Говорят, что угол α является углом I , II , III , IV координатной четверти , если точка А 1 лежит в I , II , III , IV четверти соответственно; если же угол α таков, что точка A 1 лежит на любой из координатных прямых Ox или Oy , то этот угол не принадлежит ни одной из четырех четвертей.
Для наглядности приведем графическую иллюстрацию. На чертежах ниже изображены углы поворота 30
, −210
, 585
и −45
градусов, которые являются углами I
, II
, III
и IV
координатных четвертей соответственно.
На чертежах ниже изображены углы поворота 30
, −210
, 585
и −45
градусов, которые являются углами I
, II
, III
и IV
координатных четвертей соответственно.
Углы 0, ±90, ±180, ±270, ±360, … градусов не принадлежат ни одной из координатных четвертей.
Теперь разберемся, какие знаки имеют значения синуса, косинуса, тангенса и котангенса угла поворота α в зависимости от того, углом какой четверти является α .
Для синуса и косинуса это сделать просто.
По определению синус угла α — это ордината точки А 1 . Очевидно, что в I и II координатных четвертях она положительна, а в III и IV четвертях – отрицательна. Таким образом, синус угла α имеет знак плюс в I и II четвертях, а знак минус – в III и VI четвертях.
В свою очередь косинус угла α
— это абсцисса точки A 1
. В I
и IV
четвертях она положительна, а во II
и III
четвертях – отрицательна. Следовательно, значения косинуса угла α
в I
и IV
четвертях положительны, а во II
и III
четвертях – отрицательны.
Чтобы определить знаки по четвертям тангенса и котангенса нужно вспомнить их определения: тангенс – это отношение ординаты точки A 1 к абсциссе, а котангенс – отношение абсциссы точки A 1 к ординате. Тогда из правил деления чисел с одинаковыми и разными знаками следует, что тангенс и котангенс имеют знак плюс, когда знаки абсциссы и ординаты точки A 1 одинаковые, и имеют знак минус – когда знаки абсциссы и ординаты точки A 1 различны. Следовательно, тангенс и котангенс угла имеют знак + в I и III координатных четвертях, и знак минус – во II и IV четвертях.
Действительно, например, в первой четверти и абсцисса x , и ордината y точки A 1 положительны, тогда и частное x/y , и частное y/x – положительно, следовательно, тангенс и котангенс имеют знаки + . А во второй четверти абсцисса x – отрицательна, а ордината y – положительна, поэтому и x/y , и y/x – отрицательны, откуда тангенс и котангенс имеют знак минус.
Переходим к следующему свойству синуса, косинуса, тангенса и котангенса.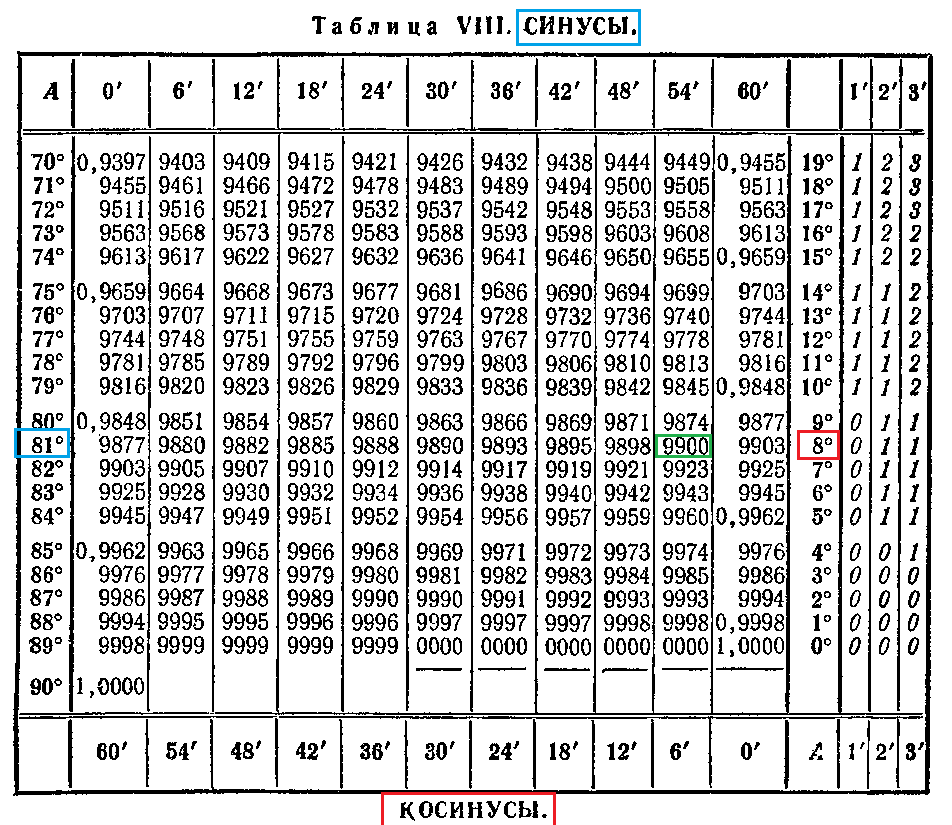
Свойство периодичности
Сейчас мы разберем, пожалуй, самое очевидное свойство синуса, косинуса, тангенса и котангенса угла. Оно состоит в следующем: при изменении угла на целое число полных оборотов значения синуса, косинуса, тангенса и котангенса этого угла не изменяются.
Это и понятно: при изменении угла на целое число оборотов мы из начальной точки А всегда будем попадать в точку А 1 на единичной окружности, следовательно, значения синуса, косинуса, тангенса и котангенса остаются неизменными, так как неизменны координаты точки A 1 .
С помощью формул рассматриваемое свойство синуса, косинуса, тангенса и котангенса можно записать так: sin(α+2·π·z)=sinα , cos(α+2·π·z)=cosα , tg(α+2·π·z)=tgα , ctg(α+2·π·z)=ctgα , где α — угол поворота в радианах, z – любое , абсолютная величина которого указывает количество полных оборотов, на которые изменяется угол α , а знак числа z указывает направление поворота.
Если же угол поворота α
задан в градусах, то указанные формулы перепишутся в виде sin(α+360°·z)=sinα
, cos(α+360°·z)=cosα
, tg(α+360°·z)=tgα
, ctg(α+360°·z)=ctgα
.
Приведем примеры использования этого свойства. Например, , так как , а . Вот еще пример: или .
Это свойство вместе с формулами приведения очень часто используется при вычислении значений синуса, косинуса, тангенса и котангенса «больших» углов.
Рассмотренное свойство синуса, косинуса, тангенса и котангенса иногда называют свойством периодичности.
Свойства синусов, косинусов, тангенсов и котангенсов противоположных углов
Пусть А 1 – точка, полученная в результате поворота начальной точки А(1, 0) вокруг точки O на угол α , а точка А 2 – это результат поворота точки А на угол −α , противоположный углу α .
Свойство синусов, косинусов, тангенсов и котангенсов противоположных углов базируется на достаточно очевидном факте: упомянутые выше точки А 1
и А 2
либо совпадают (при ), либо располагаются симметрично относительно оси Ox
. То есть, если точка A 1
имеет координаты (x, y)
, то точка А 2
будет иметь координаты (x, −y)
. Отсюда по определениям синуса, косинуса, тангенса и котангенса записываем равенства и .
Сопоставляя их, приходим к соотношениям между синусами, косинусами, тангенсами и котангенсами противоположных углов α
и −α
вида .
Это и есть рассматриваемое свойство в виде формул.
Приведем примеры использования этого свойства. Например, справедливы равенства и .
Остается лишь заметить, что свойство синусов, косинусов, тангенсов и котангенсов противоположных углов, как и предыдущее свойство, часто используется при вычислении значений синуса, косинуса, тангенса и котангенса, и позволяет полностью уйти от отрицательных углов.
Список литературы.
- Алгебра: Учеб. для 9 кл. сред. шк./Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова; Под ред. С. А. Теляковского.- М.: Просвещение, 1990.- 272 с.: ил.- ISBN 5-09-002727-7
- Алгебра и начала анализа: Учеб. для 10-11 кл. общеобразоват. учреждений / А. Н. Колмогоров, А. М. Абрамов, Ю. П. Дудницын и др.; Под ред. А. Н. Колмогорова.- 14-е изд.- М.: Просвещение, 2004.- 384 с.: ил.
 — ISBN 5-09-013651-3.
— ISBN 5-09-013651-3. - Башмаков М. И. Алгебра и начала анализа: Учеб. для 10-11 кл. сред. шк. — 3-е изд. — М.: Просвещение, 1993. — 351 с.: ил. — ISBN 5-09-004617-4.
- Гусев В. А., Мордкович А. Г. Математика (пособие для поступающих в техникумы): Учеб. пособие.- М.; Высш. шк., 1984.-351 с., ил.
Тригонометрия — раздел математической науки, в котором изучаются тригонометрические функции и их использование в геометрии. Развитие тригонометрии началось еще во времена античной Греции. Во времена средневековья важный вклад в развитие этой науки внесли ученые Ближнего Востока и Индии.
Данная статья посвящена базовым понятиям и дефинициям тригонометрии. В ней рассмотрены определения основных тригонометрических функций: синуса, косинуса, тангенса и котангенса. Разъяснен и проиллюстрирован их смысл в контексте геометрии.
Yandex.RTB R-A-339285-1
Изначально определения тригонометрических функций, аргументом которых является угол, выражались через соотношения сторон прямоугольного треугольника.
Определения тригонометрических функций
Синус угла (sin α) — отношение противолежащего этому углу катета к гипотенузе.
Косинус угла (cos α) — отношение прилежащего катета к гипотенузе.
Тангенс угла (t g α) — отношение противолежащего катета к прилежащему.
Котангенс угла (c t g α) — отношение прилежащего катета к противолежащему.
Данные определения даны для острого угла прямоугольного треугольника!
Приведем иллюстрацию.
В треугольнике ABC с прямым углом С синус угла А равен отношению катета BC к гипотенузе AB.
Определения синуса, косинуса, тангенса и котангенса позволяют вычислять значения этих функций по известным длинам сторон треугольника.
Важно помнить!
Область значений синуса и косинуса: от -1 до 1. Иными словами синус и косинус принимают значения от -1 до 1. Область значений тангенса и котангенса — вся числовая прямая, то есть эти функции могут принимать любые значения.
Определения, данные выше, относятся к острым углам. В тригонометрии вводится понятие угла поворота, величина которого, в отличие от острого угла, не ограничена рамками от 0 до 90 градусов.Угол поворота в градусах или радианах выражается любым действительным числом от — ∞ до + ∞ .
В тригонометрии вводится понятие угла поворота, величина которого, в отличие от острого угла, не ограничена рамками от 0 до 90 градусов.Угол поворота в градусах или радианах выражается любым действительным числом от — ∞ до + ∞ .
В данном контексте можно дать определение синуса, косинуса, тангенса и котангенса угла произвольной величины. Представим единичную окружность с центром в начале декартовой системы координат.
Начальная точка A с координатами (1 , 0) поворачивается вокруг центра единичной окружности на некоторый угол α и переходит в точку A 1 . Определение дается через координаты точки A 1 (x , y).
Синус (sin) угла поворота
Синус угла поворота α — это ордината точки A 1 (x , y). sin α = y
Косинус (cos) угла поворота
Косинус угла поворота α — это абсцисса точки A 1 (x , y). cos α = х
Тангенс (tg) угла поворота
Тангенс угла поворота α — это отношение ординаты точки A 1 (x , y) к ее абсциссе. t g α = y x
Котангенс (ctg) угла поворота
Котангенс угла поворота α — это отношение абсциссы точки A 1 (x , y) к ее ординате. c t g α = x y
c t g α = x y
Синус и косинус определены для любого угла поворота. Это логично, ведь абсциссу и ординату точки после поворота можно определить при любом угле. Иначе обстоит дело с тангенсом и котангенсом. Тангенс не определен, когда точка после поворота переходит в точку с нулевой абсциссой (0 , 1) и (0 , — 1). В таких случаях выражение для тангенса t g α = y x просто не имеет смысла, так как в нем присутствует деление на ноль. Аналогично ситуация с котангенсом. Отличием состоит в том, что котангенс не определен в тех случаях, когда в ноль обращается ордината точки.
Важно помнить!
Синус и косинус определены для любых углов α .
Тангенс определен для всех углов, кроме α = 90 ° + 180 ° · k , k ∈ Z (α = π 2 + π · k , k ∈ Z)
Котангенс определен для всех углов, кроме α = 180 ° · k , k ∈ Z (α = π · k , k ∈ Z)
При решении практических примеров не говорят «синус угла поворота α «. Слова «угол поворота» просто опускают, подразумевая, что из контекста и так понятно, о чем идет речь.
Числа
Как быть с определением синуса, косинуса, тангенса и котангенса числа, а не угла поворота?
Синус, косинус, тангенс, котангенс числа
Синусом, косинусом, тангенсом и котангенсом числа t называется число, которое соответственно равно синусу, косинусу, тангенсу и котангенсу в t радиан.
Например, синус числа 10 π равен синусу угла поворота величиной 10 π рад.
Существует и другой подход к определению синуса, косинуса, тангенса и котангенса числа. Рассмотрим его подробнее.
Любому действительному числу t ставится в соответствие точка на единичной окружности с центром в начале прямоугольной декартовой системы координат. Синус, косинус, тангенс и котангенс определяются через координаты этой точки.
Начальная точка на окружности — точка A c координатами (1 , 0).
Положительному числу t
Отрицательному числу t соответствует точка, в которую перейдет начальная точка, если будет двигаться по окружности против часовой стрелки и пройдет путь t .
Теперь, когда связь числа и точки на окружности установлена, переходим к определению синуса, косинуса, тангенса и котангенса.
Синус (sin) числа t
Синус числа t — ордината точки единичной окружности, соответствующей числу t. sin t = y
Косинус (cos) числа t
Косинус числа t — абсцисса точки единичной окружности, соответствующей числу t. cos t = x
Тангенс (tg) числа t
Тангенс числа t — отношение ординаты к абсциссе точки единичной окружности, соответствующей числу t. t g t = y x = sin t cos t
Последние определения находятся в соответствии и не противоречат определению, данному в начале это пункта. Точка на окружности, соответствующая числу t , совпадает с точкой, в которую переходит начальная точка после поворота на угол t радиан.
Тригонометрические функции углового и числового аргумента
Каждому значению угла α соответствует определенное значение синуса и косинуса этого угла. Также, как всем углам α , отличным от α = 90 ° + 180 ° · k , k ∈ Z (α = π 2 + π · k , k ∈ Z) соответствует определенное значение тангенса. Котангенс, как сказано выше, определен для всех α , кроме α = 180 ° · k , k ∈ Z (α = π · k , k ∈ Z).
Также, как всем углам α , отличным от α = 90 ° + 180 ° · k , k ∈ Z (α = π 2 + π · k , k ∈ Z) соответствует определенное значение тангенса. Котангенс, как сказано выше, определен для всех α , кроме α = 180 ° · k , k ∈ Z (α = π · k , k ∈ Z).
Можно сказать, что sin α , cos α , t g α , c t g α — это функции угла альфа, или функции углового аргумента.
Аналогично можно говорить о синусе, косинусе, тангенсе и котангенсе, как о функциях числового аргумента. Каждому действительному числу t соответствует определенное значение синуса или косинуса числа t . Всем числам, отличным от π 2 + π · k , k ∈ Z соответствует значение тангенса. Котангенс, аналогично, определен для всех чисел, кроме π · k , k ∈ Z.
Основные функции тригонометрии
Синус, косинус, тангенс и котангенс — основные тригонометрические функции.
Из контекста обычно понятно, с каким аргументом тригонометрической функции (угловой аргумент или числовой аргумент) мы имеем дело.
Вернемся к данным в самом начале определениям и углу альфа, лежащему в пределах от 0 до 90 градусов. Тригонометрические определения синуса, косинуса, тангенса и котангенса полностью согласуются с геометрическими определениями, данными с помощью соотношений сторон прямоугольного треугольника. Покажем это.
Тригонометрические определения синуса, косинуса, тангенса и котангенса полностью согласуются с геометрическими определениями, данными с помощью соотношений сторон прямоугольного треугольника. Покажем это.
Возьмем единичную окружность с центром в прямоугольной декартовой системе координат. Повернем начальную точку A (1 , 0) на угол величиной до 90 градусов и проведем из полученной точки A 1 (x , y) перпендикуляр к оси абсцисс. В полученном прямоугольном треугольнике угол A 1 O H равен углу поворота α , длина катета O H равна абсциссе точки A 1 (x , y) . Длина катета, противолежащего углу, равна ординате точки A 1 (x , y) , а длина гипотенузы равна единице, так как она является радиусом единичной окружности.
В соответствии с определением из геометрии, синус угла α равен отношению противолежащего катета к гипотенузе.
sin α = A 1 H O A 1 = y 1 = y
Значит, определение синуса острого угла в прямоугольном треугольнике через соотношение сторон эквивалентно определению синуса угла поворота α , при альфа лежащем в пределах от 0 до 90 градусов.
Аналогично соответствие определений можно показать для косинуса, тангенса и котангенса.
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
С центром в точке A .
α — угол, выраженный в радианах.
Определение
Синус (sin α) — это тригонометрическая функция, зависящая от угла α между гипотенузой и катетом прямоугольного треугольника, равная отношению длины противолежащего катета |BC| к длине гипотенузы |AC|.
Косинус (cos α) — это тригонометрическая функция, зависящая от угла α между гипотенузой и катетом прямоугольного треугольника, равная отношению длины прилежащего катета |AB| к длине гипотенузы |AC|.
Принятые обозначения
;
;
.
;
;
.
График функции синус, y = sin x
График функции косинус, y = cos x
Свойства синуса и косинуса
Периодичность
Функции y = sin x и y = cos x периодичны с периодом 2 π .
Четность
Функция синус — нечетная.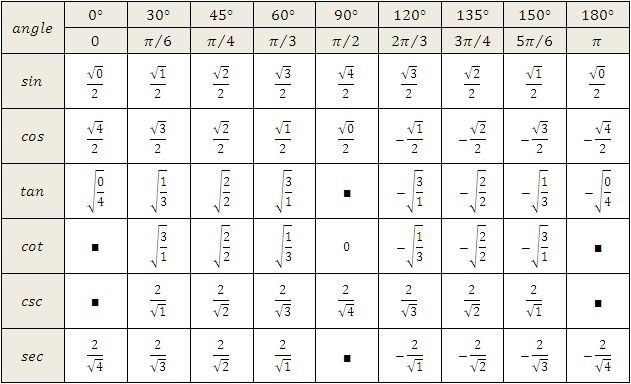 Функция косинус — четная.
Функция косинус — четная.
Область определения и значений, экстремумы, возрастание, убывание
Функции синус и косинус непрерывны на своей области определения, то есть для всех x (см. доказательство непрерывности). Их основные свойства представлены в таблице (n — целое).
| y = sin x | y = cos x | |
| Область определения и непрерывность | — ∞ | — ∞ |
| Область значений | -1 ≤ y ≤ 1 | -1 ≤ y ≤ 1 |
| Возрастание | ||
| Убывание | ||
| Максимумы, y = 1 | ||
| Минимумы, y = -1 | ||
| Нули, y = 0 | ||
| Точки пересечения с осью ординат, x = 0 | y = 0 | y = 1 |
Основные формулы
Сумма квадратов синуса и косинуса
Формулы синуса и косинуса от суммы и разности
;
;
Формулы произведения синусов и косинусов
Формулы суммы и разности
Выражение синуса через косинус
;
;
;
.
Выражение косинуса через синус
;
;
;
.
Выражение через тангенс
; .
При ,
имеем:
;
.
При :
;
.
Таблица синусов и косинусов, тангенсов и котангенсов
В данной таблице представлены значения синусов и косинусов при некоторых значениях аргумента.
Выражения через комплексные переменные
;
Формула Эйлера
Выражения через гиперболические функции
;
;
Производные
; . Вывод формул > > >
Производные n-го порядка:
{ -∞
Секанс, косеканс
Обратные функции
Обратными функциями к синусу и косинусу являются арксинус и арккосинус , соответственно.
Арксинус, arcsin
Арккосинус, arccos
Использованная литература:
И.Н. Бронштейн, К.А. Семендяев, Справочник по математике для инженеров и учащихся втузов, «Лань», 2009.
Изначально синус и косинус возникли из-за необходимости рассчитывать величины в прямоугольных треугольниках.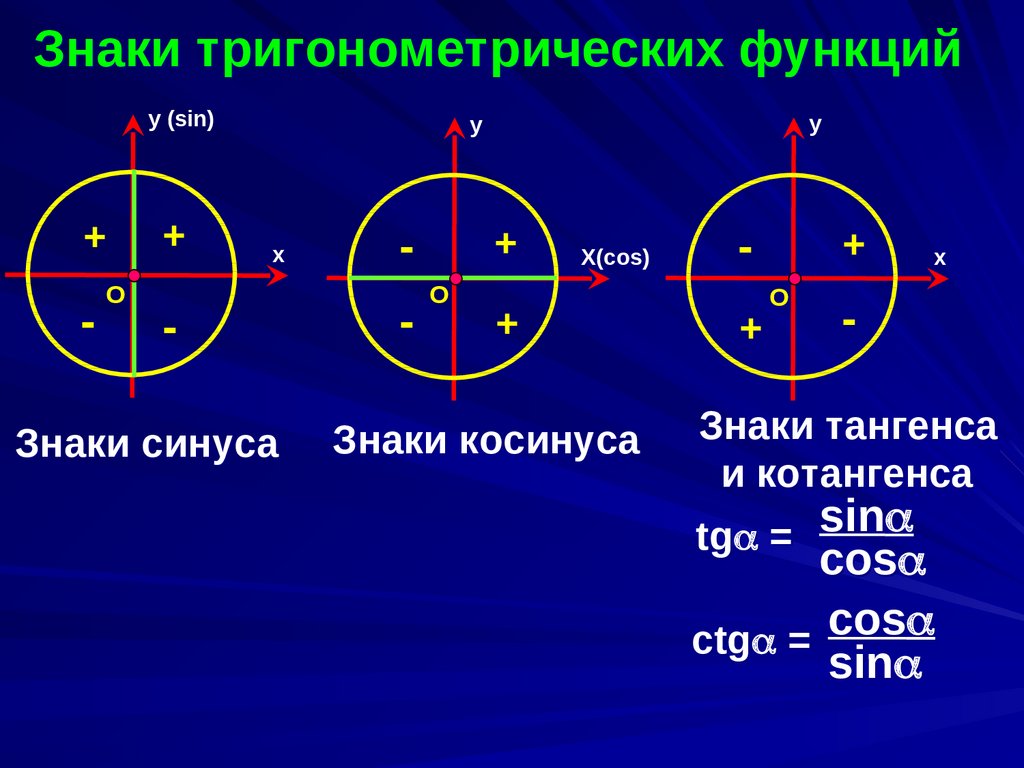 Было замечено, что если значение градусной меры углов в прямоугольном треугольнике не менять, то соотношение сторон, насколько бы эти стороны ни изменялись в длине, остается всегда одинаковым.
Было замечено, что если значение градусной меры углов в прямоугольном треугольнике не менять, то соотношение сторон, насколько бы эти стороны ни изменялись в длине, остается всегда одинаковым.
Именно так и были введены понятия синуса и косинуса. Синус острого угла в прямоугольном треугольнике – это отношение противолежащего катета к гипотенузе, а косинус – прилежащего к гипотенузе.
Теоремы косинусов и синусов
Но косинусы и синусы могут применяться не только в прямоугольных треугольниках. Чтобы найти значение тупого или острого угла, стороны любого треугольника, достаточно применить теорему косинусов и синусов.
Теорема косинусов довольно проста: «Квадрат стороны треугольника равен сумме квадратов двух других сторон за вычетом удвоенного произведения этих сторон на косинус угла между ними».
Существует две трактовки теоремы синусов: малая и расширенная. Согласно малой: «В треугольнике углы пропорциональны противолежащим сторонам». Данную теорему часто расширяют за счет свойства описанной около треугольника окружности: «В треугольнике углы пропорциональны противолежащим сторонам, а их отношение равно диаметру описанной окружности».
Производные
Производная — математический инструмент, показывающий, как быстро меняется функция относительно изменения ее аргумента. Производные используются , геометрии, и , ряде технических дисциплин.
При решении задач требуется знать табличные значения производных тригонометрических функций: синуса и косинуса. Производной синуса является косинус, а косинуса — синус, но со знаком «минус».
Применение в математике
Особенно часто синусы и косинусы используются при решении прямоугольных треугольников и задач, связанных с ними.
Удобство синусов и косинусов нашло свое отражение и в технике. Углы и стороны было просто оценивать по теоремам косинусов и синусов, разбивая сложные фигуры и объекты на «простые» треугольники. Инженеры и , часто имеющие дело с расчетами соотношения сторон и градусных мер, тратили немало времени и усилий для вычисления косинусов и синусов не табличных углов.
Тогда «на подмогу» пришли таблицы Брадиса, содержащие тысячи значений синусов, косинусов, тангенсов и котангенсов разных углов.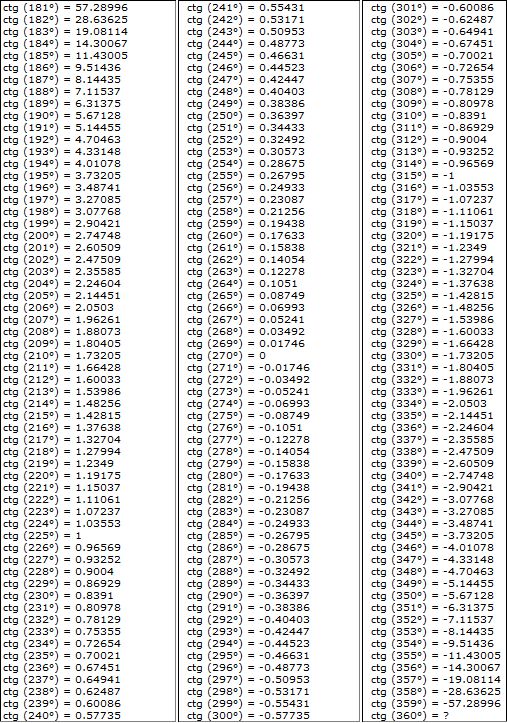 В советское время некоторые преподаватели заставляли своих подопечных страницы таблиц Брадиса наизусть.
В советское время некоторые преподаватели заставляли своих подопечных страницы таблиц Брадиса наизусть.
Радиан — угловая величина дуги, по длине равной радиусу или 57,295779513° градусов.
Градус (в геометрии) — 1/360-я часть окружности или 1/90-я часть прямого угла.
π = 3.141592653589793238462… (приблизительное значение числа Пи).
Таблица косинусов для углов: 0°, 30°, 45°, 60°, 90°, 120°, 135°, 150°, 180°, 210°, 225°, 240°, 270°, 300°, 315°, 330°, 360°.
| Угол х (в градусах) | 0° | 30° | 45° | 60° | 90° | 120° | 135° | 150° | 180° | 210° | 225° | 240° | 270° | 300° | 315° | 330° | 360° |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Угол х (в радианах) | 0 | π/6 | π/4 | π/3 | π/2 | 2 x π/3 | 3 x π/4 | 5 x π/6 | π | 7 x π/6 | 5 x π/4 | 4 x π/3 | 3 x π/2 | 5 x π/3 | 7 x π/4 | 11 x π/6 | 2 x π |
| cos x | 1 | √3/2 (0,8660) | √2/2 (0,7071) | 1/2 (0,5) | 0 | -1/2 (-0,5) | -√2/2 (-0,7071) | -√3/2 (-0,8660) | -1 | -√3/2 (-0,8660) | -√2/2 (-0,7071) | -1/2 (-0,5) | 0 | 1/2 (0,5) | √2/2 (0,7071) | √3/2 (0,8660) | 1 |
Таблица тригонометрических функций.
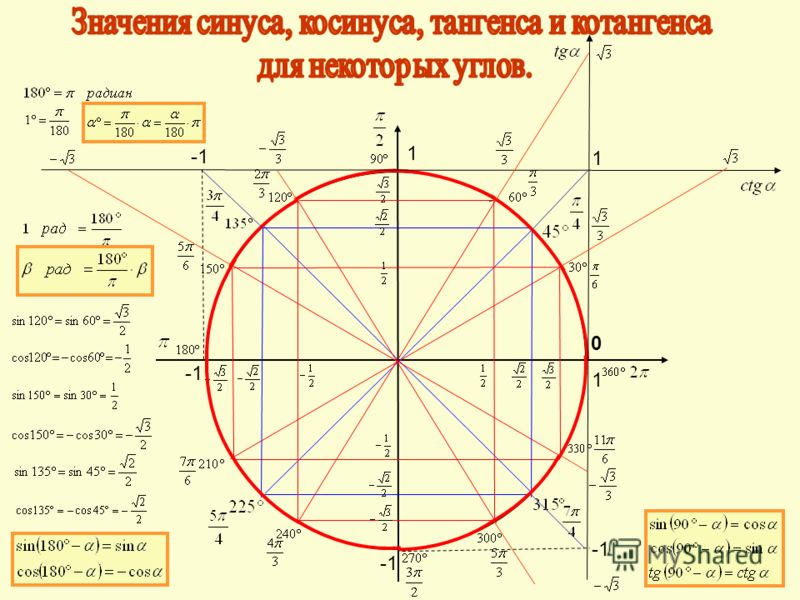
Таблица тригонометрических функций — это записанные в таблицу посчитанные значения синусов, косинусов, тангенсов и котангенсов углов от 0° до 360°. Используя таблицу тригонометрических функций Вы сможете провести расчеты даже если под руками не окажется инженерного калькулятора. Чтобы узнать значение тригонометрических функций от нужного Вам угла достаточно найти их в таблице.
Таблица тригонометрических функций углов от 0° до 90°
| α | sin α | cos α | tg α | ctg α |
| 0° | 0 | 1 | 0 | ∞ |
| 1° | 0.017452 | 0.999848 | 0.017455 | 57.289962 |
| 2° | 0.034899 | 0.999391 | 034921″>0.034921 | 28.636253 |
| 3° | 0.052336 | 0.99863 | 0.052408 | 19.081137 |
| 4° | 0.069756 | 0.997564 | 0.069927 | 14.300666 |
| 5° | 0.087156 | 0.996195 | 0.087489 | 11.430052 |
| 6° | 0.104528 | 0.994522 | 0.105104 | 9.514364 |
| 7° | 0.121869 | 0.992546 | 0.122785 | 144346″>8.144346 |
| 8° | 0.139173 | 0.990268 | 0.140541 | 7.11537 |
| 9° | 0.156434 | 0.987688 | 0.158384 | 6.313752 |
| 10° | 0.173648 | 0.984808 | 0.176327 | 5.671282 |
| 11° | 0.190809 | 0.981627 | 0.19438 | 5.144554 |
| 12° | 0.207912 | 0.978148 | 0.212557 | 4.70463 |
| 13° | 224951″>0.224951 | 0.97437 | 0.230868 | 4.331476 |
| 14° | 0.241922 | 0.970296 | 0.249328 | 4.010781 |
| 15° | 0.258819 | 0.965926 | 0.267949 | 3.732051 |
| 16° | 0.275637 | 0.961262 | 0.286745 | 3.487414 |
| 17° | 0.292372 | 0.956305 | 0.305731 | 3.270853 |
| 18° | 0. 309017 309017 | 0.951057 | 0.32492 | 3.077684 |
| 19° | 0.325568 | 0.945519 | 0.344328 | 2.904211 |
| 20° | 0.34202 | 0.939693 | 0.36397 | 2.747477 |
| 21° | 0.358368 | 0.93358 | 0.383864 | 2.605089 |
| 22° | 0.374607 | 0.927184 | 0.404026 | 2.475087 |
| 23° | 0.390731 | 920505″>0.920505 | 0.424475 | 2.355852 |
| 24° | 0.406737 | 0.913545 | 0.445229 | 2.246037 |
| 25° | 0.422618 | 0.906308 | 0.466308 | 2.144507 |
| 26° | 0.438371 | 0.898794 | 0.487733 | 2.050304 |
| 27° | 0.45399 | 0.891007 | 0.509525 | 1.962611 |
| 28° | 0.469472 | 0.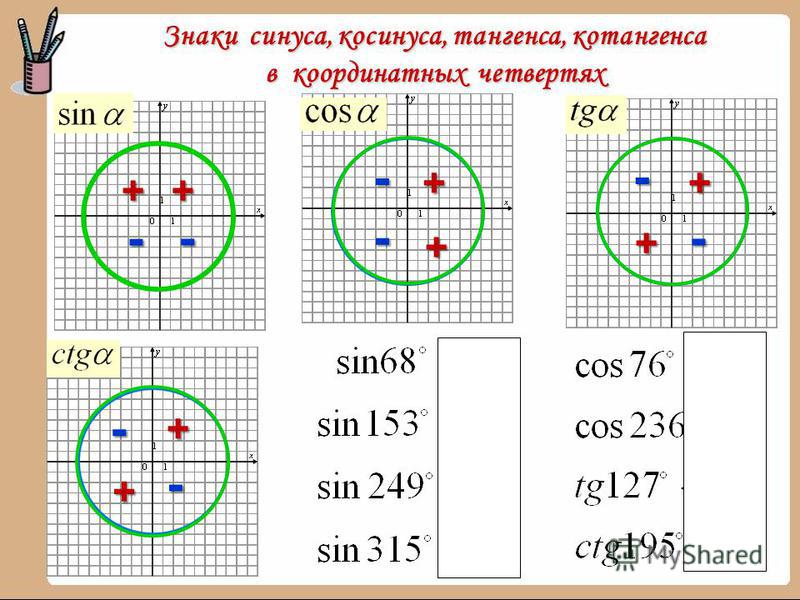 882948 882948 | 0.531709 | 1.880726 |
| 29° | 0.48481 | 0.87462 | 0.554309 | 1.804048 |
| 30° | 0.5 | 0.866025 | 0.57735 | 1.732051 |
| 31° | 0.515038 | 0.857167 | 0.600861 | 1.664279 |
| 32° | 0.529919 | 0.848048 | 0.624869 | 1.600335 |
| 33° | 0.544639 | 0.838671 | 649408″>0.649408 | 1.539865 |
| 34° | 0.559193 | 0.829038 | 0.674509 | 1.482561 |
| 35° | 0.573576 | 0.819152 | 0.700208 | 1.428148 |
| 36° | 0.587785 | 0.809017 | 0.726543 | 1.376382 |
| 37° | 0.601815 | 0.798636 | 0.753554 | 1.327045 |
| 38° | 0.615661 | 0.788011 | 0. 781286 781286 | 1.279942 |
| 39° | 0.62932 | 0.777146 | 0.809784 | 1.234897 |
| 40° | 0.642788 | 0.766044 | 0.8391 | 1.191754 |
| 41° | 0.656059 | 0.75471 | 0.869287 | 1.150368 |
| 42° | 0.669131 | 0.743145 | 0.900404 | 1.110613 |
| 43° | 0.681998 | 0.731354 | 0.932515 | 072369″>1.072369 |
| 44° | 0.694658 | 0.71934 | 0.965689 | 1.03553 |
| 45° | 0.707107 | 0.707107 | 1 | 1 |
| 46° | 0.71934 | 0.694658 | 1.03553 | 0.965689 |
| 47° | 0.731354 | 0.681998 | 1.072369 | 0.932515 |
| 48° | 0.743145 | 0.669131 | 1.110613 | 0.900404 |
| 49° | 75471″>0.75471 | 0.656059 | 1.150368 | 0.869287 |
| 50° | 0.766044 | 0.642788 | 1.191754 | 0.8391 |
| 51° | 0.777146 | 0.62932 | 1.234897 | 0.809784 |
| 52° | 0.788011 | 0.615661 | 1.279942 | 0.781286 |
| 53° | 0.798636 | 0.601815 | 1.327045 | 0.753554 |
| 54° | 0.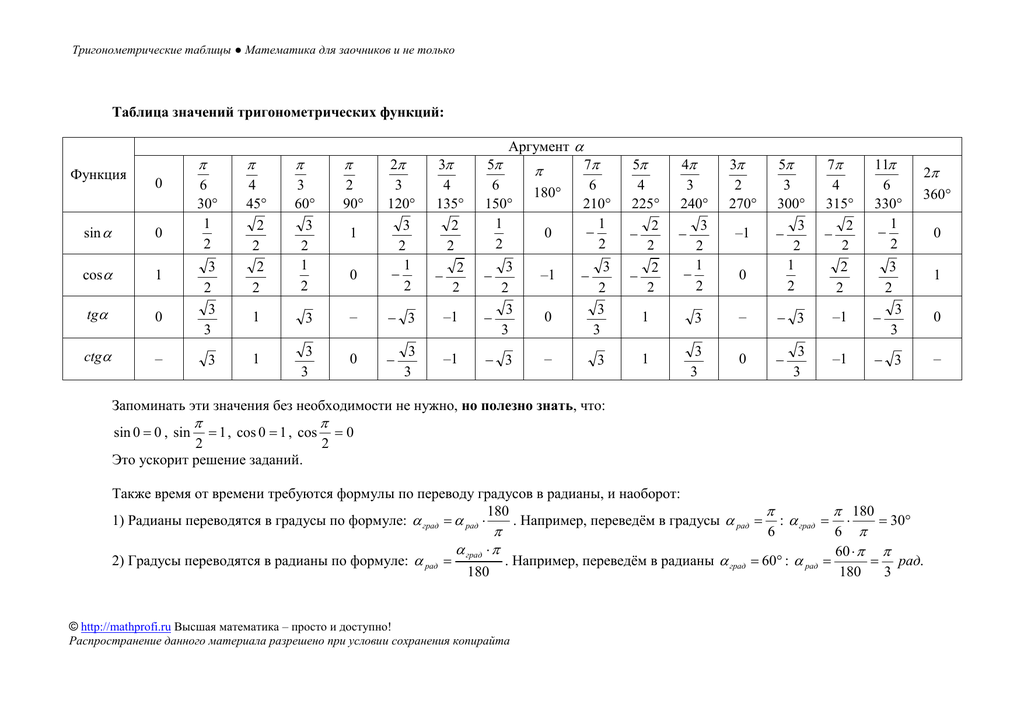 809017 809017 | 0.587785 | 1.376382 | 0.726543 |
| 55° | 0.819152 | 0.573576 | 1.428148 | 0.700208 |
| 56° | 0.829038 | 0.559193 | 1.482561 | 0.674509 |
| 57° | 0.838671 | 0.544639 | 1.539865 | 0.649408 |
| 58° | 0.848048 | 0.529919 | 1.600335 | 0.624869 |
| 59° | 0.857167 | 515038″>0.515038 | 1.664279 | 0.600861 |
| 60° | 0.866025 | 0.5 | 1.732051 | 0.57735 |
| 61° | 0.87462 | 0.48481 | 1.804048 | 0.554309 |
| 62° | 0.882948 | 0.469472 | 1.880726 | 0.531709 |
| 63° | 0.891007 | 0.45399 | 1.962611 | 0.509525 |
| 64° | 0.898794 | 0.438371 | 050304″>2.050304 | 0.487733 |
| 65° | 0.906308 | 0.422618 | 2.144507 | 0.466308 |
| 66° | 0.913545 | 0.406737 | 2.246037 | 0.445229 |
| 67° | 0.920505 | 0.390731 | 2.355852 | 0.424475 |
| 68° | 0.927184 | 0.374607 | 2.475087 | 0.404026 |
| 69° | 0.93358 | 0.358368 | 2. 605089 605089 | 0.383864 |
| 70° | 0.939693 | 0.34202 | 2.747477 | 0.36397 |
| 71° | 0.945519 | 0.325568 | 2.904211 | 0.344328 |
| 72° | 0.951057 | 0.309017 | 3.077684 | 0.32492 |
| 73° | 0.956305 | 0.292372 | 3.270853 | 0.305731 |
| 74° | 0.961262 | 0.275637 | 3.487414 | 286745″>0.286745 |
| 75° | 0.965926 | 0.258819 | 3.732051 | 0.267949 |
| 76° | 0.970296 | 0.241922 | 4.010781 | 0.249328 |
| 77° | 0.97437 | 0.224951 | 4.331476 | 0.230868 |
| 78° | 0.978148 | 0.207912 | 4.70463 | 0.212557 |
| 79° | 0.981627 | 0.190809 | 5.144554 | 0. 19438 19438 |
| 80° | 0.984808 | 0.173648 | 5.671282 | 0.176327 |
| 81° | 0.987688 | 0.156434 | 6.313752 | 0.158384 |
| 82° | 0.990268 | 0.139173 | 7.11537 | 0.140541 |
| 83° | 0.992546 | 0.121869 | 8.144346 | 0.122785 |
| 84° | 0.994522 | 0.104528 | 9.514364 | 0.105104 |
| 85° | 996195″>0.996195 | 0.087156 | 11.430052 | 0.087489 |
| 86° | 0.997564 | 0.069756 | 14.300666 | 0.069927 |
| 87° | 0.99863 | 0.052336 | 19.081137 | 0.052408 |
| 88° | 0.999391 | 0.034899 | 28.636253 | 0.034921 |
| 89° | 0.999848 | 0.017452 | 57.289962 | 0.017455 |
| 90° | 1 | 0 | ∞ | 0 |
Таблица тригонометрических функций углов от 91° до 180°
| α | sin α | cos α | tg α | ctg α |
| 91° | 999848″>0.999848 | -0.017452 | -57.289962 | -0.017455 |
| 92° | 0.999391 | -0.034899 | -28.636253 | -0.034921 |
| 93° | 0.99863 | -0.052336 | -19.081137 | -0.052408 |
| 94° | 0.997564 | -0.069756 | -14.300666 | -0.069927 |
| 95° | 0.996195 | -0.087156 | -11.430052 | -0.087489 |
| 96° | 994522″>0.994522 | -0.104528 | -9.514364 | -0.105104 |
| 97° | 0.992546 | -0.121869 | -8.144346 | -0.122785 |
| 98° | 0.990268 | -0.139173 | -7.11537 | -0.140541 |
| 99° | 0.987688 | -0.156434 | -6.313752 | -0.158384 |
| 100° | 0.984808 | -0.173648 | -5.671282 | -0.176327 |
| 101° | 981627″>0.981627 | -0.190809 | -5.144554 | -0.19438 |
| 102° | 0.978148 | -0.207912 | -4.70463 | -0.212557 |
| 103° | 0.97437 | -0.224951 | -4.331476 | -0.230868 |
| 104° | 0.970296 | -0.241922 | -4.010781 | -0.249328 |
| 105° | 0.965926 | -0.258819 | -3.732051 | -0.267949 |
| 106° | 961262″>0.961262 | -0.275637 | -3.487414 | -0.286745 |
| 107° | 0.956305 | -0.292372 | -3.270853 | -0.305731 |
| 108° | 0.951057 | -0.309017 | -3.077684 | -0.32492 |
| 109° | 0.945519 | -0.325568 | -2.904211 | -0.344328 |
| 110° | 0.939693 | -0.34202 | -2.747477 | -0.36397 |
| 111° | 93358″>0.93358 | -0.358368 | -2.605089 | -0.383864 |
| 112° | 0.927184 | -0.374607 | -2.475087 | -0.404026 |
| 113° | 0.920505 | -0.390731 | -2.355852 | -0.424475 |
| 114° | 0.913545 | -0.406737 | -2.246037 | -0.445229 |
| 115° | 0.906308 | -0.422618 | -2.144507 | -0.466308 |
| 116° | 898794″>0.898794 | -0.438371 | -2.050304 | -0.487733 |
| 117° | 0.891007 | -0.45399 | -1.962611 | -0.509525 |
| 118° | 0.882948 | -0.469472 | -1.880726 | -0.531709 |
| 119° | 0.87462 | -0.48481 | -1.804048 | -0.554309 |
| 120° | 0.866025 | -0.5 | -1.732051 | -0.57735 |
| 121° | 857167″>0.857167 | -0.515038 | -1.664279 | -0.600861 |
| 122° | 0.848048 | -0.529919 | -1.600335 | -0.624869 |
| 123° | 0.838671 | -0.544639 | -1.539865 | -0.649408 |
| 124° | 0.829038 | -0.559193 | -1.482561 | -0.674509 |
| 125° | 0.819152 | -0.573576 | -1.428148 | -0.700208 |
| 126° | 809017″>0.809017 | -0.587785 | -1.376382 | -0.726543 |
| 127° | 0.798636 | -0.601815 | -1.327045 | -0.753554 |
| 128° | 0.788011 | -0.615661 | -1.279942 | -0.781286 |
| 129° | 0.777146 | -0.62932 | -1.234897 | -0.809784 |
| 130° | 0.766044 | -0.642788 | -1.191754 | -0.8391 |
| 131° | 75471″>0.75471 | -0.656059 | -1.150368 | -0.869287 |
| 132° | 0.743145 | -0.669131 | -1.110613 | -0.900404 |
| 133° | 0.731354 | -0.681998 | -1.072369 | -0.932515 |
| 134° | 0.71934 | -0.694658 | -1.03553 | -0.965689 |
| 135° | 0.707107 | -0.707107 | -1 | -1 |
| 136° | 694658″>0.694658 | -0.71934 | -0.965689 | -1.03553 |
| 137° | 0.681998 | -0.731354 | -0.932515 | -1.072369 |
| 138° | 0.669131 | -0.743145 | -0.900404 | -1.110613 |
| 139° | 0.656059 | -0.75471 | -0.869287 | -1.150368 |
| 140° | 0.642788 | -0.766044 | -0.8391 | -1.191754 |
| 141° | 62932″>0.62932 | -0.777146 | -0.809784 | -1.234897 |
| 142° | 0.615661 | -0.788011 | -0.781286 | -1.279942 |
| 143° | 0.601815 | -0.798636 | -0.753554 | -1.327045 |
| 144° | 0.587785 | -0.809017 | -0.726543 | -1.376382 |
| 145° | 0.573576 | -0.819152 | -0.700208 | -1.428148 |
| 146° | 559193″>0.559193 | -0.829038 | -0.674509 | -1.482561 |
| 147° | 0.544639 | -0.838671 | -0.649408 | -1.539865 |
| 148° | 0.529919 | -0.848048 | -0.624869 | -1.600335 |
| 149° | 0.515038 | -0.857167 | -0.600861 | -1.664279 |
| 150° | 0.5 | -0.866025 | -0.57735 | -1.732051 |
| 151° | 48481″>0.48481 | -0.87462 | -0.554309 | -1.804048 |
| 152° | 0.469472 | -0.882948 | -0.531709 | -1.880726 |
| 153° | 0.45399 | -0.891007 | -0.509525 | -1.962611 |
| 154° | 0.438371 | -0.898794 | -0.487733 | -2.050304 |
| 155° | 0.422618 | -0.906308 | -0.466308 | -2.144507 |
| 156° | 406737″>0.406737 | -0.913545 | -0.445229 | -2.246037 |
| 157° | 0.390731 | -0.920505 | -0.424475 | -2.355852 |
| 158° | 0.374607 | -0.927184 | -0.404026 | -2.475087 |
| 159° | 0.358368 | -0.93358 | -0.383864 | -2.605089 |
| 160° | 0.34202 | -0.939693 | -0.36397 | -2.747477 |
| 161° | 325568″>0.325568 | -0.945519 | -0.344328 | -2.904211 |
| 162° | 0.309017 | -0.951057 | -0.32492 | -3.077684 |
| 163° | 0.292372 | -0.956305 | -0.305731 | -3.270853 |
| 164° | 0.275637 | -0.961262 | -0.286745 | -3.487414 |
| 165° | 0.258819 | -0.965926 | -0.267949 | -3.732051 |
| 166° | 241922″>0.241922 | -0.970296 | -0.249328 | -4.010781 |
| 167° | 0.224951 | -0.97437 | -0.230868 | -4.331476 |
| 168° | 0.207912 | -0.978148 | -0.212557 | -4.70463 |
| 169° | 0.190809 | -0.981627 | -0.19438 | -5.144554 |
| 170° | 0.173648 | -0.984808 | -0.176327 | -5.671282 |
| 171° | 156434″>0.156434 | -0.987688 | -0.158384 | -6.313752 |
| 172° | 0.139173 | -0.990268 | -0.140541 | -7.11537 |
| 173° | 0.121869 | -0.992546 | -0.122785 | -8.144346 |
| 174° | 0.104528 | -0.994522 | -0.105104 | -9.514364 |
| 175° | 0.087156 | -0.996195 | -0.087489 | -11.430052 |
| 176° | 069756″>0.069756 | -0.997564 | -0.069927 | -14.300666 |
| 177° | 0.052336 | -0.99863 | -0.052408 | -19.081137 |
| 178° | 0.034899 | -0.999391 | -0.034921 | -28.636253 |
| 179° | 0.017452 | -0.999848 | -0.017455 | -57.289962 |
| 180° | 0 | -1 | 0 | ∞ |
Таблица тригонометрических функций углов от 181° до 270°
| α | sin α | cos α | tg α | ctg α |
| 181° | 017452″>-0.017452 | -0.999848 | 0.017455 | 57.289962 |
| 182° | -0.034899 | -0.999391 | 0.034921 | 28.636253 |
| 183° | -0.052336 | -0.99863 | 0.052408 | 19.081137 |
| 184° | -0.069756 | -0.997564 | 0.069927 | 14.300666 |
| 185° | -0.087156 | -0.996195 | 0.087489 | 11.430052 |
| 186° | 104528″>-0.104528 | -0.994522 | 0.105104 | 9.514364 |
| 187° | -0.121869 | -0.992546 | 0.122785 | 8.144346 |
| 188° | -0.139173 | -0.990268 | 0.140541 | 7.11537 |
| 189° | -0.156434 | -0.987688 | 0.158384 | 6.313752 |
| 190° | -0.173648 | -0.984808 | 0.176327 | 5.671282 |
| 191° | 190809″>-0.190809 | -0.981627 | 0.19438 | 5.144554 |
| 192° | -0.207912 | -0.978148 | 0.212557 | 4.70463 |
| 193° | -0.224951 | -0.97437 | 0.230868 | 4.331476 |
| 194° | -0.241922 | -0.970296 | 0.249328 | 4.010781 |
| 195° | -0.258819 | -0.965926 | 0.267949 | 3.732051 |
| 196° | 275637″>-0.275637 | -0.961262 | 0.286745 | 3.487414 |
| 197° | -0.292372 | -0.956305 | 0.305731 | 3.270853 |
| 198° | -0.309017 | -0.951057 | 0.32492 | 3.077684 |
| 199° | -0.325568 | -0.945519 | 0.344328 | 2.904211 |
| 200° | -0.34202 | -0.939693 | 0.36397 | 2.747477 |
| 201° | 358368″>-0.358368 | -0.93358 | 0.383864 | 2.605089 |
| 202° | -0.374607 | -0.927184 | 0.404026 | 2.475087 |
| 203° | -0.390731 | -0.920505 | 0.424475 | 2.355852 |
| 204° | -0.406737 | -0.913545 | 0.445229 | 2.246037 |
| 205° | -0.422618 | -0.906308 | 0.466308 | 2.144507 |
| 206° | 438371″>-0.438371 | -0.898794 | 0.487733 | 2.050304 |
| 207° | -0.45399 | -0.891007 | 0.509525 | 1.962611 |
| 208° | -0.469472 | -0.882948 | 0.531709 | 1.880726 |
| 209° | -0.48481 | -0.87462 | 0.554309 | 1.804048 |
| 210° | -0.5 | -0.866025 | 0.57735 | 1.732051 |
| 211° | 515038″>-0.515038 | -0.857167 | 0.600861 | 1.664279 |
| 212° | -0.529919 | -0.848048 | 0.624869 | 1.600335 |
| 213° | -0.544639 | -0.838671 | 0.649408 | 1.539865 |
| 214° | -0.559193 | -0.829038 | 0.674509 | 1.482561 |
| 215° | -0.573576 | -0.819152 | 0.700208 | 1.428148 |
| 216° | 587785″>-0.587785 | -0.809017 | 0.726543 | 1.376382 |
| 217° | -0.601815 | -0.798636 | 0.753554 | 1.327045 |
| 218° | -0.615661 | -0.788011 | 0.781286 | 1.279942 |
| 219° | -0.62932 | -0.777146 | 0.809784 | 1.234897 |
| 220° | -0.642788 | -0.766044 | 0.8391 | 1.191754 |
| 221° | 656059″>-0.656059 | -0.75471 | 0.869287 | 1.150368 |
| 222° | -0.669131 | -0.743145 | 0.900404 | 1.110613 |
| 223° | -0.681998 | -0.731354 | 0.932515 | 1.072369 |
| 224° | -0.694658 | -0.71934 | 0.965689 | 1.03553 |
| 225° | -0.707107 | -0.707107 | 1 | 1 |
| 226° | 71934″>-0.71934 | -0.694658 | 1.03553 | 0.965689 |
| 227° | -0.731354 | -0.681998 | 1.072369 | 0.932515 |
| 228° | -0.743145 | -0.669131 | 1.110613 | 0.900404 |
| 229° | -0.75471 | -0.656059 | 1.150368 | 0.869287 |
| 230° | -0.766044 | -0.642788 | 1.191754 | 0.8391 |
| 231° | 777146″>-0.777146 | -0.62932 | 1.234897 | 0.809784 |
| 232° | -0.788011 | -0.615661 | 1.279942 | 0.781286 |
| 233° | -0.798636 | -0.601815 | 1.327045 | 0.753554 |
| 234° | -0.809017 | -0.587785 | 1.376382 | 0.726543 |
| 235° | -0.819152 | -0.573576 | 1.428148 | 0.700208 |
| 236° | 829038″>-0.829038 | -0.559193 | 1.482561 | 0.674509 |
| 237° | -0.838671 | -0.544639 | 1.539865 | 0.649408 |
| 238° | -0.848048 | -0.529919 | 1.600335 | 0.624869 |
| 239° | -0.857167 | -0.515038 | 1.664279 | 0.600861 |
| 240° | -0.866025 | -0.5 | 1.732051 | 0.57735 |
| 241° | 87462″>-0.87462 | -0.48481 | 1.804048 | 0.554309 |
| 242° | -0.882948 | -0.469472 | 1.880726 | 0.531709 |
| 243° | -0.891007 | -0.45399 | 1.962611 | 0.509525 |
| 244° | -0.898794 | -0.438371 | 2.050304 | 0.487733 |
| 245° | -0.906308 | -0.422618 | 2.144507 | 0.466308 |
| 246° | 913545″>-0.913545 | -0.406737 | 2.246037 | 0.445229 |
| 247° | -0.920505 | -0.390731 | 2.355852 | 0.424475 |
| 248° | -0.927184 | -0.374607 | 2.475087 | 0.404026 |
| 249° | -0.93358 | -0.358368 | 2.605089 | 0.383864 |
| 250° | -0.939693 | -0.34202 | 2.747477 | 0.36397 |
| 251° | 945519″>-0.945519 | -0.325568 | 2.904211 | 0.344328 |
| 252° | -0.951057 | -0.309017 | 3.077684 | 0.32492 |
| 253° | -0.956305 | -0.292372 | 3.270853 | 0.305731 |
| 254° | -0.961262 | -0.275637 | 3.487414 | 0.286745 |
| 255° | -0.965926 | -0.258819 | 3.732051 | 0.267949 |
| 256° | 970296″>-0.970296 | -0.241922 | 4.010781 | 0.249328 |
| 257° | -0.97437 | -0.224951 | 4.331476 | 0.230868 |
| 258° | -0.978148 | -0.207912 | 4.70463 | 0.212557 |
| 259° | -0.981627 | -0.190809 | 5.144554 | 0.19438 |
| 260° | -0.984808 | -0.173648 | 5.671282 | 0.176327 |
| 261° | 987688″>-0.987688 | -0.156434 | 6.313752 | 0.158384 |
| 262° | -0.990268 | -0.139173 | 7.11537 | 0.140541 |
| 263° | -0.992546 | -0.121869 | 8.144346 | 0.122785 |
| 264° | -0.994522 | -0.104528 | 9.514364 | 0.105104 |
| 265° | -0.996195 | -0.087156 | 11.430052 | 0.087489 |
| 266° | 997564″>-0.997564 | -0.069756 | 14.300666 | 0.069927 |
| 267° | -0.99863 | -0.052336 | 19.081137 | 0.052408 |
| 268° | -0.999391 | -0.034899 | 28.636253 | 0.034921 |
| 269° | -0.999848 | -0.017452 | 57.289962 | 0.017455 |
| 270° | -1 | 0 | ∞ | 0 |
Таблица тригонометрических функций углов от 271° до 360°
| α | sin α | cos α | tg α | ctg α |
| 271° | 999848″>-0.999848 | 0.017452 | -57.289962 | -0.017455 |
| 272° | -0.999391 | 0.034899 | -28.636253 | -0.034921 |
| 273° | -0.99863 | 0.052336 | -19.081137 | -0.052408 |
| 274° | -0.997564 | 0.069756 | -14.300666 | -0.069927 |
| 275° | -0.996195 | 0.087156 | -11.430052 | -0. 087489 087489 |
| 276° | -0.994522 | 0.104528 | -9.514364 | -0.105104 |
| 277° | -0.992546 | 0.121869 | -8.144346 | -0.122785 |
| 278° | -0.990268 | 0.139173 | -7.11537 | -0.140541 |
| 279° | -0.987688 | 0.156434 | -6.313752 | -0.158384 |
| 280° | -0.984808 | 0.173648 | -5. 671282 671282 | -0.176327 |
| 281° | -0.981627 | 0.190809 | -5.144554 | -0.19438 |
| 282° | -0.978148 | 0.207912 | -4.70463 | -0.212557 |
| 283° | -0.97437 | 0.224951 | -4.331476 | -0.230868 |
| 284° | -0.970296 | 0.241922 | -4.010781 | -0.249328 |
| 285° | -0.965926 | 0. 258819 258819 | -3.732051 | -0.267949 |
| 286° | -0.961262 | 0.275637 | -3.487414 | -0.286745 |
| 287° | -0.956305 | 0.292372 | -3.270853 | -0.305731 |
| 288° | -0.951057 | 0.309017 | -3.077684 | -0.32492 |
| 289° | -0.945519 | 0.325568 | -2.904211 | -0.344328 |
| 290° | -0. 939693 939693 | 0.34202 | -2.747477 | -0.36397 |
| 291° | -0.93358 | 0.358368 | -2.605089 | -0.383864 |
| 292° | -0.927184 | 0.374607 | -2.475087 | -0.404026 |
| 293° | -0.920505 | 0.390731 | -2.355852 | -0.424475 |
| 294° | -0.913545 | 0.406737 | -2.246037 | -0.445229 |
| 295° | 906308″>-0.906308 | 0.422618 | -2.144507 | -0.466308 |
| 296° | -0.898794 | 0.438371 | -2.050304 | -0.487733 |
| 297° | -0.891007 | 0.45399 | -1.962611 | -0.509525 |
| 298° | -0.882948 | 0.469472 | -1.880726 | -0.531709 |
| 299° | -0.87462 | 0.48481 | -1.804048 | -0.554309 |
| 300° | 866025″>-0.866025 | 0.5 | -1.732051 | -0.57735 |
| 301° | -0.857167 | 0.515038 | -1.664279 | -0.600861 |
| 302° | -0.848048 | 0.529919 | -1.600335 | -0.624869 |
| 303° | -0.838671 | 0.544639 | -1.539865 | -0.649408 |
| 304° | -0.829038 | 0.559193 | -1.482561 | -0.674509 |
| 305° | 819152″>-0.819152 | 0.573576 | -1.428148 | -0.700208 |
| 306° | -0.809017 | 0.587785 | -1.376382 | -0.726543 |
| 307° | -0.798636 | 0.601815 | -1.327045 | -0.753554 |
| 308° | -0.788011 | 0.615661 | -1.279942 | -0.781286 |
| 309° | -0.777146 | 0.62932 | -1.234897 | -0.809784 |
| 310° | 766044″>-0.766044 | 0.642788 | -1.191754 | -0.8391 |
| 311° | -0.75471 | 0.656059 | -1.150368 | -0.869287 |
| 312° | -0.743145 | 0.669131 | -1.110613 | -0.900404 |
| 313° | -0.731354 | 0.681998 | -1.072369 | -0.932515 |
| 314° | -0.71934 | 0.694658 | -1.03553 | -0.965689 |
| 315° | 707107″>-0.707107 | 0.707107 | -1 | -1 |
| 316° | -0.694658 | 0.71934 | -0.965689 | -1.03553 |
| 317° | -0.681998 | 0.731354 | -0.932515 | -1.072369 |
| 318° | -0.669131 | 0.743145 | -0.900404 | -1.110613 |
| 319° | -0.656059 | 0.75471 | -0.869287 | -1.150368 |
| 320° | 642788″>-0.642788 | 0.766044 | -0.8391 | -1.191754 |
| 321° | -0.62932 | 0.777146 | -0.809784 | -1.234897 |
| 322° | -0.615661 | 0.788011 | -0.781286 | -1.279942 |
| 323° | -0.601815 | 0.798636 | -0.753554 | -1.327045 |
| 324° | -0.587785 | 0.809017 | -0.726543 | -1.376382 |
| 325° | 573576″>-0.573576 | 0.819152 | -0.700208 | -1.428148 |
| 326° | -0.559193 | 0.829038 | -0.674509 | -1.482561 |
| 327° | -0.544639 | 0.838671 | -0.649408 | -1.539865 |
| 328° | -0.529919 | 0.848048 | -0.624869 | -1.600335 |
| 329° | -0.515038 | 0.857167 | -0.600861 | -1.664279 |
| 330° | 5″>-0.5 | 0.866025 | -0.57735 | -1.732051 |
| 331° | -0.48481 | 0.87462 | -0.554309 | -1.804048 |
| 332° | -0.469472 | 0.882948 | -0.531709 | -1.880726 |
| 333° | -0.45399 | 0.891007 | -0.509525 | -1.962611 |
| 334° | -0.438371 | 0.898794 | -0.487733 | -2.050304 |
| 335° | 422618″>-0.422618 | 0.906308 | -0.466308 | -2.144507 |
| 336° | -0.406737 | 0.913545 | -0.445229 | -2.246037 |
| 337° | -0.390731 | 0.920505 | -0.424475 | -2.355852 |
| 338° | -0.374607 | 0.927184 | -0.404026 | -2.475087 |
| 339° | -0.358368 | 0.93358 | -0.383864 | -2.605089 |
| 340° | 34202″>-0.34202 | 0.939693 | -0.36397 | -2.747477 |
| 341° | -0.325568 | 0.945519 | -0.344328 | -2.904211 |
| 342° | -0.309017 | 0.951057 | -0.32492 | -3.077684 |
| 343° | -0.292372 | 0.956305 | -0.305731 | -3.270853 |
| 344° | -0.275637 | 0.961262 | -0.286745 | -3.487414 |
| 345° | 258819″>-0.258819 | 0.965926 | -0.267949 | -3.732051 |
| 346° | -0.241922 | 0.970296 | -0.249328 | -4.010781 |
| 347° | -0.224951 | 0.97437 | -0.230868 | -4.331476 |
| 348° | -0.207912 | 0.978148 | -0.212557 | -4.70463 |
| 349° | -0.190809 | 0.981627 | -0.19438 | -5.144554 |
| 350° | 173648″>-0.173648 | 0.984808 | -0.176327 | -5.671282 |
| 351° | -0.156434 | 0.987688 | -0.158384 | -6.313752 |
| 352° | -0.139173 | 0.990268 | -0.140541 | -7.11537 |
| 353° | -0.121869 | 0.992546 | -0.122785 | -8.144346 |
| 354° | -0.104528 | 0.994522 | -0.105104 | -9.514364 |
| 355° | 087156″>-0.087156 | 0.996195 | -0.087489 | -11.430052 |
| 356° | -0.069756 | 0.997564 | -0.069927 | -14.300666 |
| 357° | -0.052336 | 0.99863 | -0.052408 | -19.081137 |
| 358° | -0.034899 | 0.999391 | -0.034921 | -28.636253 |
| 359° | -0.017452 | 0.999848 | -0.017455 | -57. 289962 289962 |
| 360° | 0 | 1 | 0 | ∞ |
Таблицы значений тригонометрических функций Таблицу синусов Таблица косинусов Таблица тангенсов Таблица котангенсов
Тригонометрические формулы
Все таблицы и формулы
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 Все представленные здесь значения обладают точностью до четвертого знака после запятой. Промежуточные значения углов, которых нет в данной таблице находятся методом поправок.
Все представленные здесь значения обладают точностью до четвертого знака после запятой. Промежуточные значения углов, которых нет в данной таблице находятся методом поправок.
|
Как пользоватся таблицей Брадиса ⇒
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
синусы, косинусы, тангенсы и котангенсы
Таблица Брадиса — это таблица, которая поможет вычислить значения синусов, косинусов, тангенсов и котангенсов углов с точностью до одной минуты без калькулятора.
Как пользоваться таблицей Брадиса?
Таблицы Брадиса имеют одинаковую для всех функций структуру. Значения аргументов находятся в левом столбце и в верхней колонке. Соответствующее значение функции расположено в клетке, находящейся на пересечении столбца и колонки, которые задают значение аргумента.
Таблица БрадисаВозьмем для примера таблицу синусов. Допустим, следует определить, чему равно значение синуса для угла 10 градусов и 30 минут. Находим в левом столбце значение 10 градусов (11-я строка), а в верхней колонке – 30 минут (6-й столбец). На пересечении 11 строки и 6-го столбца, находим значение функции, 0.1822. Три последних столбца предназначены для уточнения значений минут. Дело в том, что в верхней колонке значения представлены только значения минут, кратные 6.
Если необходимо найти значения синуса, косинуса, тангенса или котангенса угла, который отсутствует в таблице Брадиса, следует выбирать наиболее близкое к нему значение. И прибавить или вычесть поправку соответствующую разнице, которая может быть равна 1′, 2′, 3′.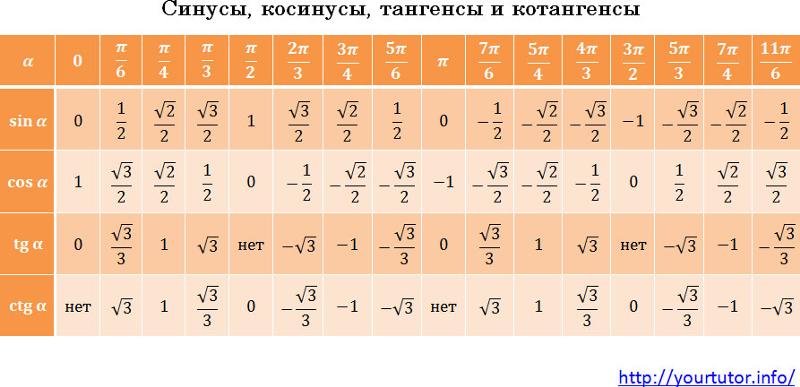 Например, для угла 10 градусов и 32 минуты к уже найденному значению 0.1822 следует прибавить поправку из второго столбика, 6. Итак, синус 10 градусов 32 минут будет равен 0.1822+0.0006=0.1828.
Например, для угла 10 градусов и 32 минуты к уже найденному значению 0.1822 следует прибавить поправку из второго столбика, 6. Итак, синус 10 градусов 32 минут будет равен 0.1822+0.0006=0.1828.
Рассмотрим ещё примеры:
sin(15°25′) = sin(15°24′)+поправка 1′ = 0.2656+0.0003 = 0.2659
sin(15°28′) = sin(15°30′)-поправка 2′ = 0.2672-0.0006 = 0.2666
При вычислении значений синуса поправка имеет положительный знак, для косинуса поправку необходимо брать с отрицательным знаком:
cos(15°25′) = sin(15°24′)+поправка 1′ = 0.9641-0.0001 = 0.9640
cos(15°28′) = sin(15°30′)-поправка 2′ = 0.9636+0.0002 = 0.9638
Поскольку синус и косинус, тангенс и котангенс для данного угла взаимосвязаны, по таблице синусов можно определять и значения косинусов, а по таблице тангенсов – значения котангенсов. Но аргумент для косинуса и для котангенса следует искать в правом столбце (четвертом справа) и в нижней строке.
Аргументы тригонометрических функций в таблицах Брадиса заданы в градусах. Для перевода градусов в радианы значение угла следует умножить на 180 и разделить на 3.1415926.
Для перевода градусов в радианы значение угла следует умножить на 180 и разделить на 3.1415926.
Как видим, таблицы В.М.Брадиса позволяют определять четыре значащих цифры любой функции. Поэтому они называются «четырехзначными». Такой точности расчетов заведомо хватает для 90% инженерных расчетов.
В настоящее время, когда калькуляторы есть и в часах, и в мобильных телефонах, расчеты функций по таблицам Брадиса можно считать «пережитком прошлого». Но, скажем честно, славного прошлого. Большое ведь видится на расстоянии. И ракеты тогда все-таки взлетали…
Таблицы имеют горизонтальную прокрутку. Для прокрутки на десктопной версии сайта: скролл внизу таблицы или стрелками на клавиатуре, на мобильной версии — свайп таблицы влево)
Таблица Брадиса для синуса и косинуса
| sin | 0′ | 6′ | 12′ | 18′ | 24′ | 30′ | 36′ | 42′ | 48′ | 54′ | 60′ | cos | 1′ | 2′ | 3′ |
0. 0000 0000 | 90° | ||||||||||||||
| 0° | 0.0000 | 0017 | 0035 | 0052 | 0070 | 0087 | 0105 | 0122 | 0140 | 0157 | 0175 | 89° | 3 | 6 | 9 |
| 1° | 0175 | 0192 | 0209 | 0227 | 0244 | 0262 | 0279 | 0297 | 0314 | 0332 | 0349 | 88° | 3 | 6 | 9 |
| 2° | 0349 | 0366 | 0384 | 0401 | 0419 | 0436 | 0454 | 0471 | 0488 | 0506 | 0523 | 87° | 3 | 6 | 9 |
| 3° | 0523 | 0541 | 0558 | 0576 | 0593 | 0610 | 0628 | 0645 | 0663 | 0680 | 0698 | 86° | 3 | 6 | 9 |
| 4° | 0698 | 0715 | 0732 | 0750 | 0767 | 0785 | 0802 | 0819 | 0837 | 0854 | 0. 0872 0872 | 85° | 3 | 6 | 9 |
| 5° | 0.0872 | 0889 | 0906 | 0924 | 0941 | 0958 | 0976 | 0993 | 1011 | 1028 | 1045 | 84° | 3 | 6 | 9 |
| 6° | 1045 | 1063 | 1080 | 1097 | 1115 | 1132 | 1149 | 1167 | 1184 | 1201 | 1219 | 83° | 3 | 6 | 9 |
| 7° | 1219 | 1236 | 1253 | 1271 | 1288 | 1305 | 1323 | 1340 | 1357 | 1374 | 1392 | 82° | 3 | 6 | 9 |
| 8° | 1392 | 1409 | 1426 | 1444 | 1461 | 1478 | 1495 | 1513 | 1530 | 1547 | 1564 | 81° | 3 | 6 | 9 |
| 9° | 1564 | 1582 | 1599 | 1616 | 1633 | 1650 | 1668 | 1685 | 1702 | 1719 | 0.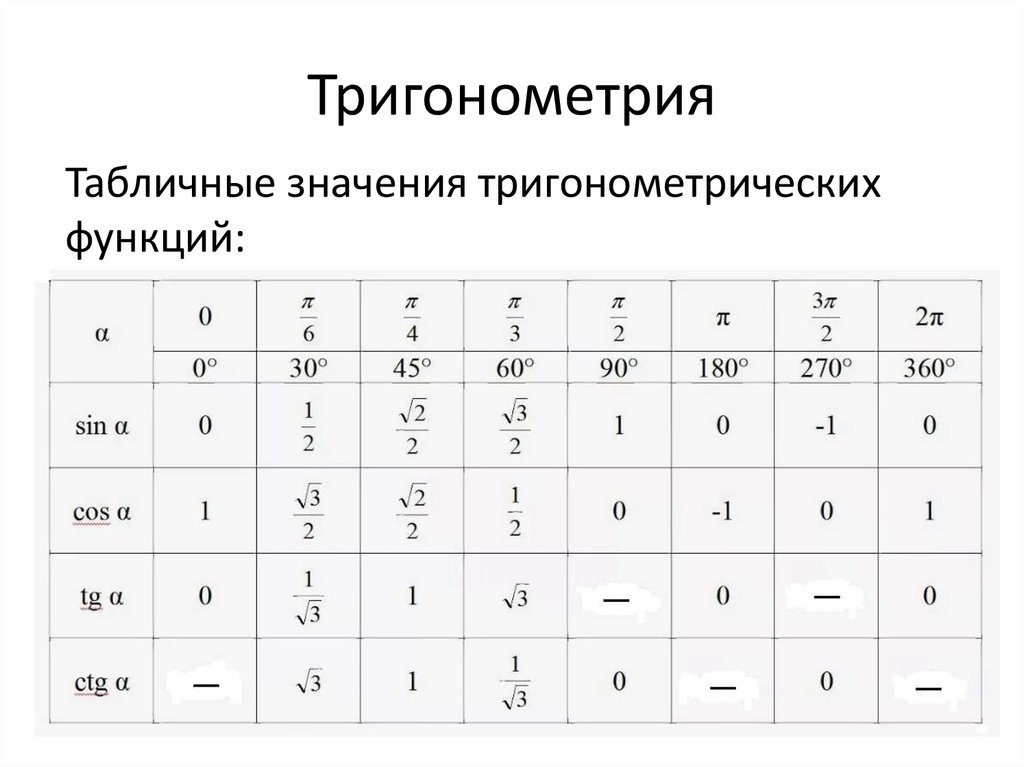 1736 1736 | 80° | 3 | 6 | 9 |
| 10° | 0.1736 | 1754 | 1771 | 1788 | 1805 | 1822 | 1840 | 1857 | 1874 | 1891 | 1908 | 79° | 3 | 6 | 9 |
| 11° | 1908 | 1925 | 1942 | 1959 | 1977 | 1994 | 2011 | 2028 | 2045 | 2062 | 2079 | 78° | 3 | 6 | 9 |
| 12° | 2079 | 2096 | 2113 | 2130 | 2147 | 2164 | 2181 | 2198 | 2215 | 2233 | 2250 | 77° | 3 | 6 | 9 |
| 13° | 2250 | 2267 | 2284 | 2300 | 2317 | 2334 | 2351 | 2368 | 2385 | 2402 | 2419 | 76° | 3 | 6 | 8 |
| 14° | 2419 | 2436 | 2453 | 2470 | 2487 | 2504 | 2521 | 2538 | 2554 | 2571 | 0. 2588 2588 | 75° | 3 | 6 | 8 |
| 15° | 0.2588 | 2605 | 2622 | 2639 | 2656 | 2672 | 2689 | 2706 | 2723 | 2740 | 2756 | 74° | 3 | 6 | 8 |
| 16° | 2756 | 2773 | 2790 | 2807 | 2823 | 2840 | 2857 | 2874 | 2890 | 2907 | 2924 | 73° | 3 | 6 | 8 |
| 17° | 2924 | 2940 | 2957 | 2974 | 2990 | 3007 | 3024 | 3040 | 3057 | 3074 | 3090 | 72° | 3 | 6 | 8 |
| 18° | 3090 | 3107 | 3123 | 3140 | 3156 | 3173 | 3190 | 3206 | 3223 | 3239 | 3256 | 71° | 3 | 6 | 8 |
| 19° | 3256 | 3272 | 3289 | 3305 | 3322 | 3338 | 3355 | 3371 | 3387 | 3404 | 0.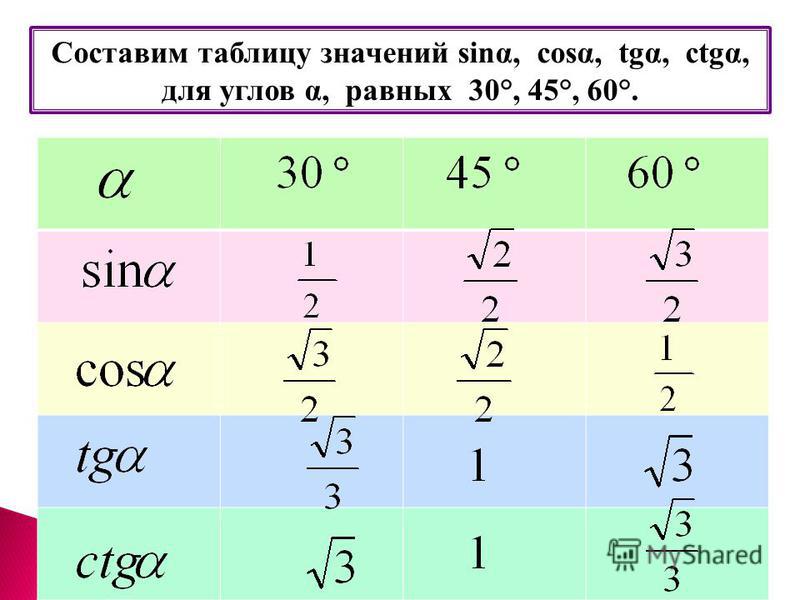 3420 3420 | 70° | 3 | 5 | 8 |
| 20° | 0.3420 | 3437 | 3453 | 3469 | 3486 | 3502 | 3518 | 3535 | 3551 | 3567 | 3584 | 69° | 3 | 5 | 8 |
| 21° | 3584 | 3600 | 3616 | 3633 | 3649 | 3665 | 3681 | 3697 | 3714 | 3730 | 3746 | 68° | 3 | 5 | 8 |
| 22° | 3746 | 3762 | 3778 | 3795 | 3811 | 3827 | 3843 | 3859 | 3875 | 3891 | 3907 | 67° | 3 | 5 | 8 |
| 23° | 3907 | 3923 | 3939 | 3955 | 3971 | 3987 | 4003 | 4019 | 4035 | 4051 | 4067 | 66° | 3 | 5 | 8 |
| 24° | 4067 | 4083 | 4099 | 4115 | 4131 | 4147 | 4163 | 4179 | 4195 | 4210 | 0.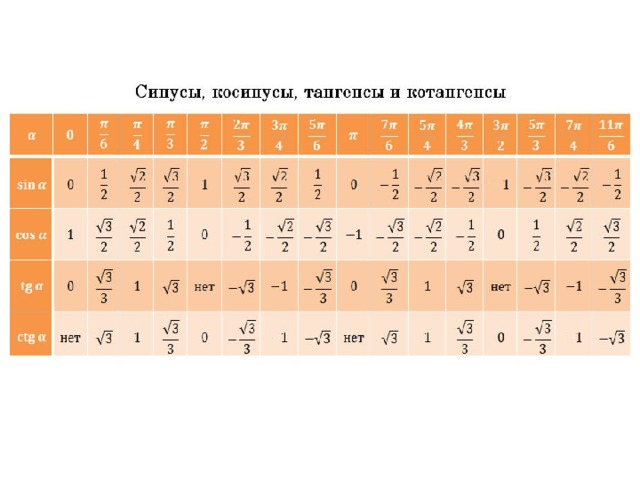 4226 4226 | 65° | 3 | 5 | 8 |
| 25° | 0.4226 | 4242 | 4258 | 4274 | 4289 | 4305 | 4321 | 4337 | 4352 | 4368 | 4384 | 64° | 3 | 5 | 8 |
| 26° | 4384 | 4399 | 4415 | 4431 | 4446 | 4462 | 4478 | 4493 | 4509 | 4524 | 4540 | 63° | 3 | 5 | 8 |
| 27° | 4540 | 4555 | 4571 | 4586 | 4602 | 4617 | 4633 | 4648 | 4664 | 4679 | 4695 | 62° | 3 | 5 | 8 |
| 28° | 4695 | 4710 | 4726 | 4741 | 4756 | 4772 | 4787 | 4802 | 4818 | 4833 | 4848 | 61° | 3 | 5 | 8 |
| 29° | 4848 | 4863 | 4879 | 4894 | 4909 | 4924 | 4939 | 4955 | 4970 | 4985 | 0.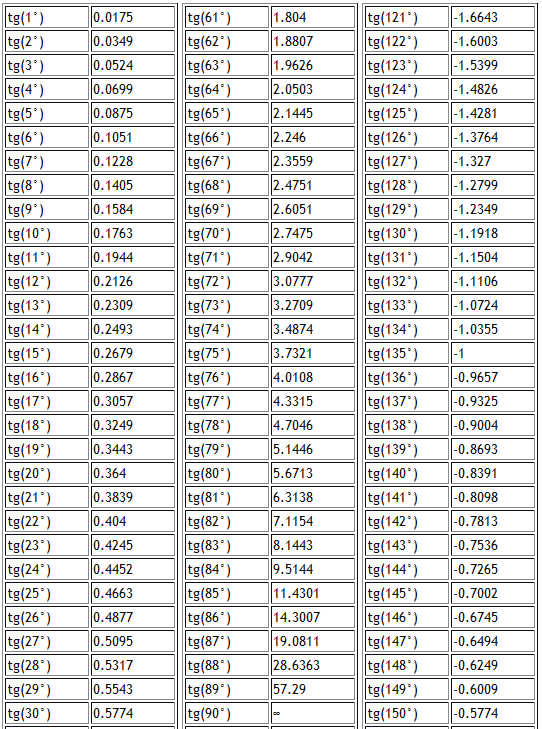 5000 5000 | 60° | 3 | 5 | 8 |
| 30° | 0.5000 | 5015 | 5030 | 5045 | 5060 | 5075 | 5090 | 5105 | 5120 | 5135 | 5150 | 59° | 3 | 5 | 8 |
| 31° | 5150 | 5165 | 5180 | 5195 | 5210 | 5225 | 5240 | 5255 | 5270 | 5284 | 5299 | 58° | 2 | 5 | 7 |
| 32° | 5299 | 5314 | 5329 | 5344 | 5358 | 5373 | 5388 | 5402 | 5417 | 5432 | 5446 | 57° | 2 | 5 | 7 |
| 33° | 5446 | 5461 | 5476 | 5490 | 5505 | 5519 | 5534 | 5548 | 5563 | 5577 | 5592 | 56° | 2 | 5 | 7 |
| 34° | 5592 | 5606 | 5621 | 5635 | 5650 | 5664 | 5678 | 5693 | 5707 | 5721 | 0. 5736 5736 | 55° | 2 | 5 | 7 |
| 35° | 0.5736 | 5750 | 5764 | 5779 | 5793 | 5807 | 5821 | 5835 | 5850 | 5864 | 0.5878 | 54° | 2 | 5 | 7 |
| 36° | 5878 | 5892 | 5906 | 5920 | 5934 | 5948 | 5962 | 5976 | 5990 | 6004 | 6018 | 53° | 2 | 5 | 7 |
| 37° | 6018 | 6032 | 6046 | 6060 | 6074 | 6088 | 6101 | 6115 | 6129 | 6143 | 6157 | 52° | 2 | 5 | 7 |
| 38° | 6157 | 6170 | 6184 | 6198 | 6211 | 6225 | 6239 | 6252 | 6266 | 6280 | 6293 | 51° | 2 | 5 | 7 |
| 39° | 6293 | 6307 | 6320 | 6334 | 6347 | 6361 | 6374 | 6388 | 6401 | 6414 | 0. 6428 6428 | 50° | 2 | 4 | 7 |
| 40° | 0.6428 | 6441 | 6455 | 6468 | 6481 | 6494 | 6508 | 6521 | 6534 | 6547 | 6561 | 49° | 2 | 4 | 7 |
| 41° | 6561 | 6574 | 6587 | 6600 | 6613 | 6626 | 6639 | 6652 | 6665 | 6678 | 6691 | 48° | 2 | 4 | 7 |
| 42° | 6691 | 6704 | 6717 | 6730 | 6743 | 6756 | 6769 | 6782 | 6794 | 6807 | 6820 | 47° | 2 | 4 | 6 |
| 43° | 6820 | 6833 | 6845 | 6858 | 6871 | 6884 | 6896 | 8909 | 6921 | 6934 | 6947 | 46° | 2 | 4 | 6 |
| 44° | 6947 | 6959 | 6972 | 6984 | 6997 | 7009 | 7022 | 7034 | 7046 | 7059 | 0.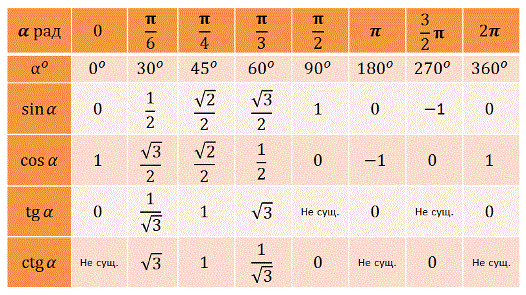 7071 7071 | 45° | 2 | 4 | 6 |
| 45° | 0.7071 | 7083 | 7096 | 7108 | 7120 | 7133 | 7145 | 7157 | 7169 | 7181 | 7193 | 44° | 2 | 4 | 6 |
| 46° | 7193 | 7206 | 7218 | 7230 | 7242 | 7254 | 7266 | 7278 | 7290 | 7302 | 7314 | 43° | 2 | 4 | 6 |
| 47° | 7314 | 7325 | 7337 | 7349 | 7361 | 7373 | 7385 | 7396 | 7408 | 7420 | 7431 | 42° | 2 | 4 | 6 |
| 48° | 7431 | 7443 | 7455 | 7466 | 7478 | 7490 | 7501 | 7513 | 7524 | 7536 | 7547 | 41° | 2 | 4 | 6 |
| 49° | 7547 | 7559 | 7570 | 7581 | 7593 | 7604 | 7615 | 7627 | 7638 | 7649 | 0.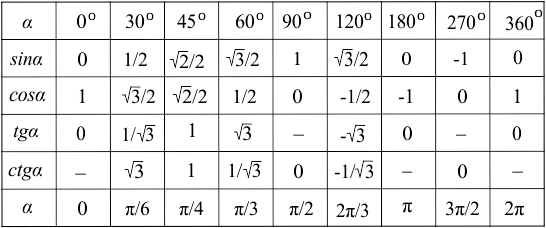 7660 7660 | 40° | 2 | 4 | 6 |
| 50° | 0.7660 | 7672 | 7683 | 7694 | 7705 | 7716 | 7727 | 7738 | 7749 | 7760 | 7771 | 39° | 2 | 4 | 6 |
| 51° | 7771 | 7782 | 7793 | 7804 | 7815 | 7826 | 7837 | 7848 | 7859 | 7869 | 7880 | 38° | 2 | 4 | 5 |
| 52° | 7880 | 7891 | 7902 | 7912 | 7923 | 7934 | 7944 | 7955 | 7965 | 7976 | 7986 | 37° | 2 | 4 | 5 |
| 53° | 7986 | 7997 | 8007 | 8018 | 8028 | 8039 | 8049 | 8059 | 8070 | 8080 | 8090 | 36° | 2 | 3 | 5 |
| 54° | 8090 | 8100 | 8111 | 8121 | 8131 | 8141 | 8151 | 8161 | 8171 | 8181 | 0.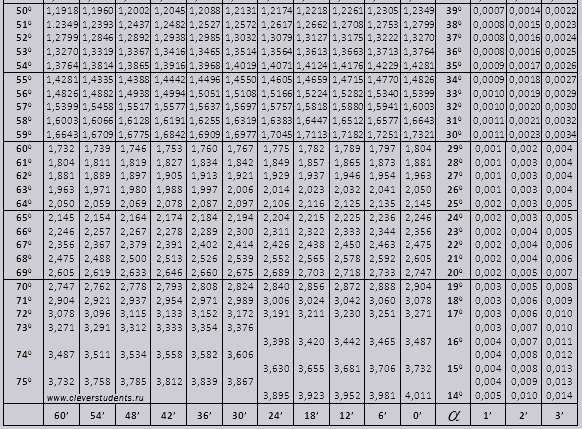 8192 8192 | 35° | 2 | 3 | 5 |
| 55° | 0.8192 | 8202 | 8211 | 8221 | 8231 | 8241 | 8251 | 8261 | 8271 | 8281 | 8290 | 34° | 2 | 3 | 5 |
| 56° | 8290 | 8300 | 8310 | 8320 | 8329 | 8339 | 8348 | 8358 | 8368 | 8377 | 8387 | 33° | 2 | 3 | 5 |
| 57° | 8387 | 8396 | 8406 | 8415 | 8425 | 8434 | 8443 | 8453 | 8462 | 8471 | 8480 | 32° | 2 | 3 | 5 |
| 58° | 8480 | 8490 | 8499 | 8508 | 8517 | 8526 | 8536 | 8545 | 8554 | 8563 | 8572 | 31° | 2 | 3 | 5 |
| 59° | 8572 | 8581 | 8590 | 8599 | 8607 | 8616 | 8625 | 8634 | 8643 | 8652 | 0.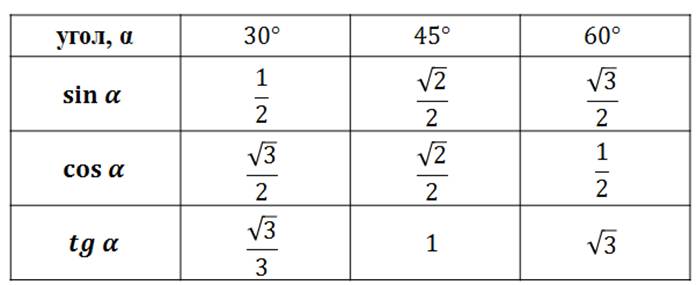 8660 8660 | 30° | 1 | 3 | 4 |
| 60° | 0.8660 | 8669 | 8678 | 8686 | 8695 | 8704 | 8712 | 8721 | 8729 | 8738 | 8746 | 29° | 1 | 3 | 4 |
| 61° | 8746 | 8755 | 8763 | 8771 | 8780 | 8788 | 8796 | 8805 | 8813 | 8821 | 8829 | 28° | 1 | 3 | 4 |
| 62° | 8829 | 8838 | 8846 | 8854 | 8862 | 8870 | 8878 | 8886 | 8894 | 8902 | 8910 | 27° | 1 | 3 | 4 |
| 63° | 8910 | 8918 | 8926 | 8934 | 8942 | 8949 | 8957 | 8965 | 8973 | 8980 | 8988 | 26° | 1 | 3 | 4 |
| 64° | 8988 | 8996 | 9003 | 9011 | 9018 | 9026 | 9033 | 9041 | 9048 | 9056 | 0. 9063 9063 | 25° | 1 | 3 | 4 |
| 65° | 0.9063 | 9070 | 9078 | 9085 | 9092 | 9100 | 9107 | 9114 | 9121 | 9128 | 9135 | 24° | 1 | 2 | 4 |
| 66° | 9135 | 9143 | 9150 | 9157 | 9164 | 9171 | 9178 | 9184 | 9191 | 9198 | 9205 | 23° | 1 | 2 | 3 |
| 67° | 9205 | 9212 | 9219 | 9225 | 9232 | 9239 | 9245 | 9252 | 9259 | 9256 | 9272 | 22° | 1 | 2 | 3 |
| 68° | 9272 | 9278 | 9285 | 9291 | 9298 | 9304 | 9311 | 9317 | 9323 | 9330 | 9336 | 21° | 1 | 2 | 3 |
| 69° | 9336 | 9342 | 9348 | 9354 | 9361 | 9367 | 9373 | 9379 | 9383 | 9391 | 0.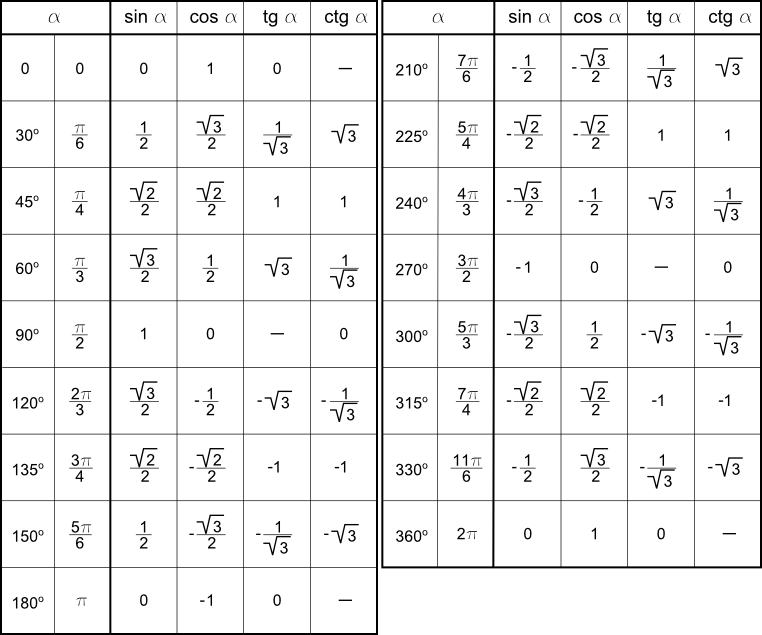 9397 9397 | 20° | 1 | 2 | 3 |
| 70° | 9397 | 9403 | 9409 | 9415 | 9421 | 9426 | 9432 | 9438 | 9444 | 9449 | 0.9455 | 19° | 1 | 2 | 3 |
| 71° | 9455 | 9461 | 9466 | 9472 | 9478 | 9483 | 9489 | 9494 | 9500 | 9505 | 9511 | 18° | 1 | 2 | 3 |
| 72° | 9511 | 9516 | 9521 | 9527 | 9532 | 9537 | 9542 | 9548 | 9553 | 9558 | 9563 | 17° | 1 | 2 | 3 |
| 73° | 9563 | 9568 | 9573 | 9578 | 9583 | 9588 | 9593 | 9598 | 9603 | 9608 | 9613 | 16° | 1 | 2 | 2 |
| 74° | 9613 | 9617 | 9622 | 9627 | 9632 | 9636 | 9641 | 9646 | 9650 | 9655 | 0.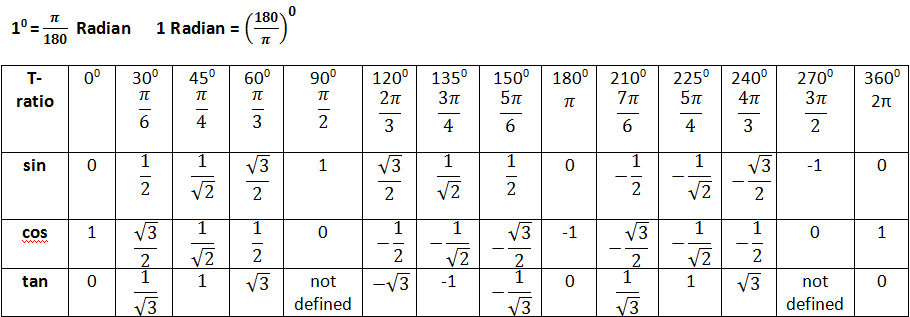 9659 9659 | 15° | 1 | 2 | 2 |
| 75° | 9659 | 9664 | 9668 | 9673 | 9677 | 9681 | 9686 | 9690 | 9694 | 9699 | 9703 | 14° | 1 | 1 | 2 |
| 76° | 9703 | 9707 | 9711 | 9715 | 9720 | 9724 | 9728 | 9732 | 9736 | 9740 | 9744 | 13° | 1 | 1 | 2 |
| 77° | 9744 | 9748 | 9751 | 9755 | 9759 | 9763 | 9767 | 9770 | 9774 | 9778 | 9781 | 12° | 1 | 1 | 2 |
| 78° | 9781 | 9785 | 9789 | 9792 | 9796 | 9799 | 9803 | 9806 | 9810 | 9813 | 9816 | 11° | 1 | 1 | 2 |
| 79° | 9816 | 9820 | 9823 | 9826 | 9829 | 9833 | 9836 | 9839 | 9842 | 9845 | 0.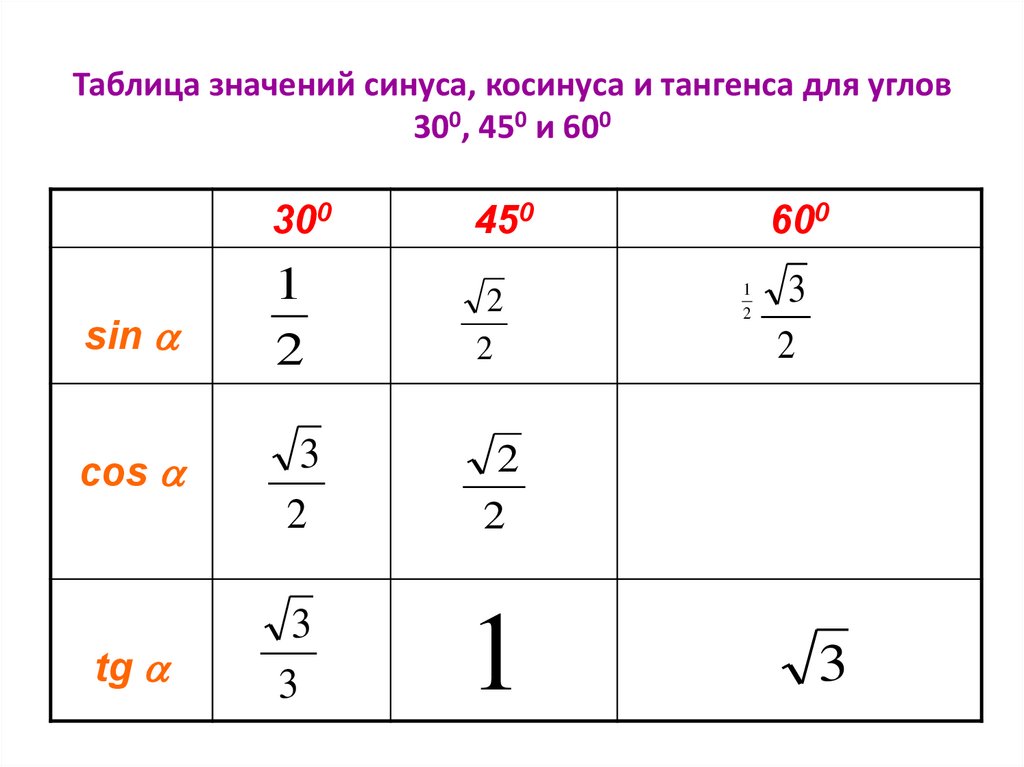 9848 9848 | 10° | 1 | 1 | 2 |
| 80° | 0.9848 | 9851 | 9854 | 9857 | 9860 | 9863 | 9866 | 9869 | 9871 | 9874 | 9877 | 9° | 0 | 1 | 1 |
| 81° | 9877 | 9880 | 9882 | 9885 | 9888 | 9890 | 9893 | 9895 | 9898 | 9900 | 9903 | 8° | 0 | 1 | 1 |
| 82° | 9903 | 9905 | 9907 | 9910 | 9912 | 9914 | 9917 | 9919 | 9921 | 9923 | 9925 | 7° | 0 | 1 | 1 |
| 83° | 9925 | 9928 | 9930 | 9932 | 9934 | 9936 | 9938 | 9940 | 9942 | 9943 | 9945 | 6° | 0 | 1 | 1 |
| 84° | 9945 | 9947 | 9949 | 9951 | 9952 | 9954 | 9956 | 9957 | 9959 | 9960 | 9962 | 5° | 0 | 1 | 1 |
| 85° | 9962 | 9963 | 9965 | 9966 | 9968 | 9969 | 9971 | 9972 | 9973 | 9974 | 9976 | 4° | 0 | 0 | 1 |
| 86° | 9976 | 9977 | 9978 | 9979 | 9980 | 9981 | 9982 | 9983 | 9984 | 9985 | 9986 | 3° | 0 | 0 | 0 |
| 87° | 9986 | 9987 | 9988 | 9989 | 9990 | 9990 | 9991 | 9992 | 9993 | 9993 | 9994 | 2° | 0 | 0 | 0 |
| 88° | 9994 | 9995 | 9995 | 9996 | 9996 | 9997 | 9997 | 9997 | 9998 | 9998 | 0.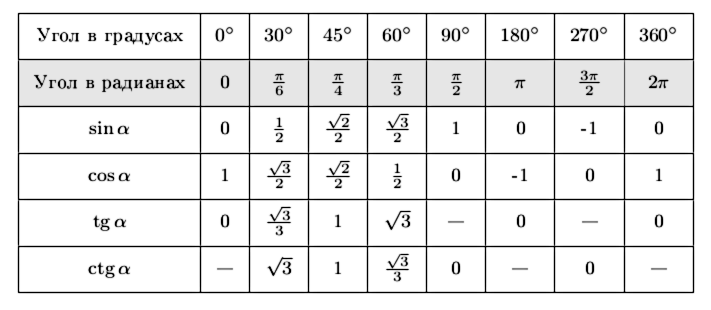 9998 9998 | 1° | 0 | 0 | 0 |
| 89° | 9998 | 9999 | 9999 | 9999 | 9999 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 0° | 0 | 0 | 0 |
| 90° | 1.0000 | ||||||||||||||
| sin | 60′ | 54′ | 48′ | 42′ | 36′ | 30′ | 24′ | 18′ | 12′ | 6′ | 0′ | cos | 1′ | 2′ | 3 |
Таблица Брадиса для тангенса и котангенса
| tg | 0′ | 6′ | 12′ | 18′ | 24′ | 30′ | 36′ | 42′ | 48′ | 54′ | 60′ | ctg | 1′ | 2′ | 3′ |
| 0 | 90° | ||||||||||||||
| 0° | 0,000 | 0017 | 0035 | 0052 | 0070 | 0087 | 0105 | 0122 | 0140 | 0157 | 0175 | 89° | 3 | 6 | 9 |
| 1° | 0175 | 0192 | 0209 | 0227 | 0244 | 0262 | 0279 | 0297 | 0314 | 0332 | 0349 | 88° | 3 | 6 | 9 |
| 2° | 0349 | 0367 | 0384 | 0402 | 0419 | 0437 | 0454 | 0472 | 0489 | 0507 | 0524 | 87° | 3 | 6 | 9 |
| 3° | 0524 | 0542 | 0559 | 0577 | 0594 | 0612 | 0629 | 0647 | 0664 | 0682 | 0699 | 86° | 3 | 6 | 9 |
| 4° | 0699 | 0717 | 0734 | 0752 | 0769 | 0787 | 0805 | 0822 | 0840 | 0857 | 0,0875 | 85° | 3 | 6 | 9 |
| 5° | 0,0875 | 0892 | 0910 | 0928 | 0945 | 0963 | 0981 | 0998 | 1016 | 1033 | 1051 | 84° | 3 | 6 | 9 |
| 6° | 1051 | 1069 | 1086 | 1104 | 1122 | 1139 | 1157 | 1175 | 1192 | 1210 | 1228 | 83° | 3 | 6 | 9 |
| 7° | 1228 | 1246 | 1263 | 1281 | 1299 | 1317 | 1334 | 1352 | 1370 | 1388 | 1405 | 82° | 3 | 6 | 9 |
| 8° | 1405 | 1423 | 1441 | 1459 | 1477 | 1495 | 1512 | 1530 | 1548 | 1566 | 1584 | 81° | 3 | 6 | 9 |
| 9° | 1584 | 1602 | 1620 | 1638 | 1655 | 1673 | 1691 | 1709 | 1727 | 1745 | 0,1763 | 80° | 3 | 6 | 9 |
| 10° | 0,1763 | 1781 | 1799 | 1817 | 1835 | 1853 | 1871 | 1890 | 1908 | 1926 | 1944 | 79° | 3 | 6 | 9 |
| 11° | 1944 | 1962 | 1980 | 1998 | 2016 | 2035 | 2053 | 2071 | 2089 | 2107 | 2126 | 78° | 3 | 6 | 9 |
| 12° | 2126 | 2144 | 2162 | 2180 | 2199 | 2217 | 2235 | 2254 | 2272 | 2290 | 2309 | 77° | 3 | 6 | 9 |
| 13° | 2309 | 2327 | 2345 | 2364 | 2382 | 2401 | 2419 | 2438 | 2456 | 2475 | 2493 | 76° | 3 | 6 | 9 |
| 14° | 2493 | 2512 | 2530 | 2549 | 2568 | 2586 | 2605 | 2623 | 2642 | 2661 | 0,2679 | 75° | 3 | 6 | 9 |
| 15° | 0,2679 | 2698 | 2717 | 2736 | 2754 | 2773 | 2792 | 2811 | 2830 | 2849 | 2867 | 74° | 3 | 6 | 9 |
| 16° | 2867 | 2886 | 2905 | 2924 | 2943 | 2962 | 2981 | 3000 | 3019 | 3038 | 3057 | 73° | 3 | 6 | 9 |
| 17° | 3057 | 3076 | 3096 | 3115 | 3134 | 3153 | 3172 | 3191 | 3211 | 3230 | 3249 | 72° | 3 | 6 | 10 |
| 18° | 3249 | 3269 | 3288 | 3307 | 3327 | 3346 | 3365 | 3385 | 3404 | 3424 | 3443 | 71° | 3 | 6 | 10 |
| 19° | 3443 | 3463 | 3482 | 3502 | 3522 | 3541 | 3561 | 3581 | 3600 | 3620 | 0,3640 | 70° | 3 | 7 | 10 |
| 20° | 0,3640 | 3659 | 3679 | 3699 | 3719 | 3739 | 3759 | 3779 | 3799 | 3819 | 3839 | 69° | 3 | 7 | 10 |
| 21° | 3839 | 3859 | 3879 | 3899 | 3919 | 3939 | 3959 | 3979 | 4000 | 4020 | 4040 | 68° | 3 | 7 | 10 |
| 22° | 4040 | 4061 | 4081 | 4101 | 4122 | 4142 | 4163 | 4183 | 4204 | 4224 | 4245 | 67° | 3 | 7 | 10 |
| 23° | 4245 | 4265 | 4286 | 4307 | 4327 | 4348 | 4369 | 4390 | 4411 | 4431 | 4452 | 66° | 3 | 7 | 10 |
| 24° | 4452 | 4473 | 4494 | 4515 | 4536 | 4557 | 4578 | 4599 | 4621 | 4642 | 0,4663 | 65° | 4 | 7 | 11 |
| 25° | 0,4663 | 4684 | 4706 | 4727 | 4748 | 4770 | 4791 | 4813 | 4834 | 4856 | 4877 | 64° | 4 | 7 | 11 |
| 26° | 4877 | 4899 | 4921 | 4942 | 4964 | 4986 | 5008 | 5029 | 5051 | 5073 | 5095 | 63° | 4 | 7 | 11 |
| 27° | 5095 | 5117 | 5139 | 5161 | 5184 | 5206 | 5228 | 5250 | 5272 | 5295 | 5317 | 62° | 4 | 7 | 11 |
| 28° | 5317 | 5340 | 5362 | 5384 | 5407 | 5430 | 5452 | 5475 | 5498 | 5520 | 5543 | 61° | 4 | 8 | 11 |
| 29° | 5543 | 5566 | 5589 | 5612 | 5635 | 5658 | 5681 | 5704 | 5727 | 5750 | 0,5774 | 60° | 4 | 8 | 12 |
| 30° | 0,5774 | 5797 | 5820 | 5844 | 5867 | 5890 | 5914 | 5938 | 5961 | 5985 | 6009 | 59° | 4 | 8 | 12 |
| 31° | 6009 | 6032 | 6056 | 6080 | 6104 | 6128 | 6152 | 6176 | 6200 | 6224 | 6249 | 58° | 4 | 8 | 12 |
| 32° | 6249 | 6273 | 6297 | 6322 | 6346 | 6371 | 6395 | 6420 | 6445 | 6469 | 6494 | 57° | 4 | 8 | 12 |
| 33° | 6494 | 6519 | 6544 | 6569 | 6594 | 6619 | 6644 | 6669 | 6694 | 6720 | 6745 | 56° | 4 | 8 | 13 |
| 34° | 6745 | 6771 | 6796 | 6822 | 6847 | 6873 | 6899 | 6924 | 6950 | 6976 | 0,7002 | 55° | 4 | 9 | 13 |
| 35° | 0,7002 | 7028 | 7054 | 7080 | 7107 | 7133 | 7159 | 7186 | 7212 | 7239 | 7265 | 54° | 4 | 8 | 13 |
| 36° | 7265 | 7292 | 7319 | 7346 | 7373 | 7400 | 7427 | 7454 | 7481 | 7508 | 7536 | 53° | 5 | 9 | 14° |
| 37° | 7536 | 7563 | 7590 | 7618 | 7646 | 7673 | 7701 | 7729 | 7757 | 7785 | 7813 | 52° | 5 | 9 | 14 |
| 38° | 7813 | 7841 | 7869 | 7898 | 7926 | 7954 | 7983 | 8012 | 8040 | 8069 | 8098 | 51° | 5 | 9 | 14 |
| 39° | 8098 | 8127 | 8156 | 8185 | 8214 | 8243 | 8273 | 8302 | 8332 | 8361 | 0,8391 | 50° | 5 | 10 | 15 |
| 40° | 0,8391 | 8421 | 8451 | 8481 | 8511 | 8541 | 8571 | 8601 | 8632 | 8662 | 0,8693 | 49° | 5 | 10 | 15 |
| 41° | 8693 | 8724 | 8754 | 8785 | 8816 | 8847 | 8878 | 8910 | 8941 | 8972 | 9004 | 48° | 5 | 10 | 16 |
| 42° | 9004 | 9036 | 9067 | 9099 | 9131 | 9163 | 9195 | 9228 | 9260 | 9293 | 9325 | 47° | 6 | 11 | 16 |
| 43° | 9325 | 9358 | 9391 | 9424 | 9457 | 9490 | 9523 | 9556 | 9590 | 9623 | 0,9657 | 46° | 6 | 11 | 17 |
| 44° | 9657 | 9691 | 9725 | 9759 | 9793 | 9827 | 9861 | 9896 | 9930 | 9965 | 1,0000 | 45° | 6 | 11 | 17 |
| 45° | 1,0000 | 0035 | 0070 | 0105 | 0141 | 0176 | 0212 | 0247 | 0283 | 0319 | 0355 | 44° | 6 | 12 | 18 |
| 46° | 0355 | 0392 | 0428 | 0464 | 0501 | 0538 | 0575 | 0612 | 0649 | 0686 | 0724 | 43° | 6 | 12 | 18 |
| 47° | 0724 | 0761 | 0799 | 0837 | 0875 | 0913 | 0951 | 0990 | 1028 | 1067 | 1106 | 42° | 6 | 13 | 19 |
| 48° | 1106 | 1145 | 1184 | 1224 | 1263 | 1303 | 1343 | 1383 | 1423 | 1463 | 1504 | 41° | 7 | 13 | 20 |
| 49° | 1504 | 1544 | 1585 | 1626 | 1667 | 1708 | 1750 | 1792 | 1833 | 1875 | 1,1918 | 40° | 7 | 14 | 21 |
| 50° | 1,1918 | 1960 | 2002 | 2045 | 2088 | 2131 | 2174 | 2218 | 2261 | 2305 | 2349 | 39° | 7 | 14 | 22 |
| 51° | 2349 | 2393 | 2437 | 2482 | 2527 | 2572 | 2617 | 2662 | 2708 | 2753 | 2799 | 38° | 8 | 15 | 23 |
| 52° | 2799 | 2846 | 2892 | 2938 | 2985 | 3032 | 3079 | 3127 | 3175 | 3222 | 3270 | 37° | 8 | 16 | 24 |
| 53° | 3270 | 3319 | 3367 | 3416 | 3465 | 3514 | 3564 | 3613 | 3663 | 3713 | 3764 | 36° | 8 | 16 | 25 |
| 54° | 3764 | 3814 | 3865 | 3916 | 3968 | 4019 | 4071 | 4124 | 4176 | 4229 | 1,4281 | 35° | 9 | 17 | 26 |
| 55° | 1,4281 | 4335 | 4388 | 4442 | 4496 | 4550 | 4605 | 4659 | 4715 | 4770 | 4826 | 34° | 9 | 18 | 27 |
| 56° | 4826 | 4882 | 4938 | 4994 | 5051 | 5108 | 5166 | 5224 | 5282 | 5340 | 5399 | 33° | 10 | 19 | 29 |
| 57° | 5399 | 5458 | 5517 | 5577 | 5637 | 5697 | 5757 | 5818 | 5880 | 5941 | 6003 | 32° | 10 | 20 | 30 |
| 58° | 6003 | 6066 | 6128 | 6191 | 6255 | 6319 | 6383 | 6447 | 6512 | 6577 | 6643 | 31° | 11 | 21 | 32 |
| 59° | 6643 | 6709 | 6775 | 6842 | 6909 | 6977 | 7045 | 7113 | 7182 | 7251 | 1,7321 | 30° | 11 | 23 | 34 |
| 60° | 1,732 | 1,739 | 1,746 | 1,753 | 1,760 | 1,767 | 1,775 | 1,782 | 1,789 | 1,797 | 1,804 | 29° | 1 | 2 | 4 |
| 61° | 1,804 | 1,811 | 1,819 | 1,827 | 1,834 | 1,842 | 1,849 | 1,857 | 1,865 | 1,873 | 1,881 | 28° | 1 | 3 | 4 |
| 62° | 1,881 | 1,889 | 1,897 | 1,905 | 1,913 | 1,921 | 1,929 | 1,937 | 1,946 | 1,954 | 1,963 | 27° | 1 | 3 | 4 |
| 63° | 1,963 | 1,971 | 1,980 | 1,988 | 1,997 | 2,006 | 2,014 | 2,023 | 2,032 | 2,041 | 2,05 | 26° | 1 | 3 | 4 |
| 64° | 2,050 | 2,059 | 2,069 | 2,078 | 2,087 | 2,097 | 2,106 | 2,116 | 2,125 | 2,135 | 2,145 | 25° | 2 | 3 | 5 |
| 65° | 2,145 | 2,154 | 2,164 | 2,174 | 2,184 | 2,194 | 2,204 | 2,215 | 2,225 | 2,236 | 2,246 | 24° | 2 | 3 | 5 |
| 66° | 2,246 | 2,257 | 2,267 | 2,278 | 2,289 | 2,3 | 2,311 | 2,322 | 2,333 | 2,344 | 2,356 | 23° | 2 | 4 | 5 |
| 67° | 2,356 | 2,367 | 2,379 | 2,391 | 2,402 | 2,414 | 2,426 | 2,438 | 2,450 | 2,463 | 2,475 | 22° | 2 | 4 | 6 |
| 68° | 2,475 | 2,488 | 2,5 | 2,513 | 2,526 | 2,539 | 2,552 | 2,565 | 2,578 | 2,592 | 2,605 | 21° | 2 | 4 | 6 |
| 69° | 2,605 | 2,619 | 2,633 | 2,646 | 2,66 | 2,675 | 2,689 | 2,703 | 2,718 | 2,733 | 2,747 | 20° | 2 | 5 | 7 |
| 70° | 2,747 | 2,762 | 2,778 | 2,793 | 2,808 | 2,824 | 2,840 | 2,856 | 2,872 | 2,888 | 2,904 | 19° | 3 | 5 | 8 |
| 71° | 2,904 | 2,921 | 2,937 | 2,954 | 2,971 | 2,989 | 3,006 | 3,024 | 3,042 | 3,06 | 3,078 | 18° | 3 | 6 | 9 |
| 72° | 3,078 | 3,096 | 3,115 | 3,133 | 3,152 | 3,172 | 3,191 | 3,211 | 3,230 | 3,251 | 3,271 | 17° | 3 | 6 | 10 |
| 73° | 3,271 | 3,291 | 3,312 | 3,333 | 3,354 | 3,376 | 3 | 7 | 10 | ||||||
| 3,398 | 3,42 | 3,442 | 3,465 | 3,487 | 16° | 4 | 7 | 11 | |||||||
| 74° | 3,487 | 3,511 | 3,534 | 3,558 | 3,582 | 3,606 | 4 | 8 | 12 | ||||||
| 3,630 | 3,655 | 3,681 | 3,706 | 3,732 | 15° | 4 | 8 | 13 | |||||||
| 75° | 3,732 | 3,758 | 3,785 | 3,812 | 3,839 | 3,867 | 4 | 9 | 13 | ||||||
| 3,895 | 3,923 | 3,952 | 3,981 | 4,011 | 14° | 5 | 10 | 14 | |||||||
| tg | 60′ | 54′ | 48′ | 42′ | 36′ | 30′ | 24′ | 18′ | 12′ | 6′ | 0′ | ctg | 1′ | 2′ | 3′ |
Полезен ли материал?
Таблица значений син кос
В этой статье собраны таблицы синусов, косинусов, тангенсов и котангенсов. Сначала мы приведем таблицу основных значений тригонометрических функций, то есть, таблицу синусов, косинусов, тангенсов и котангенсов углов 0, 30, 45, 60, 90, …, 360 градусов ( 0, π/6, π/4, π/3, π/2, …, 2π радиан). После этого мы дадим таблицу синусов и косинусов, а также таблицу тангенсов и котангенсов В. М. Брадиса, и покажем, как использовать эти таблицы при нахождении значений тригонометрических функций.
Сначала мы приведем таблицу основных значений тригонометрических функций, то есть, таблицу синусов, косинусов, тангенсов и котангенсов углов 0, 30, 45, 60, 90, …, 360 градусов ( 0, π/6, π/4, π/3, π/2, …, 2π радиан). После этого мы дадим таблицу синусов и косинусов, а также таблицу тангенсов и котангенсов В. М. Брадиса, и покажем, как использовать эти таблицы при нахождении значений тригонометрических функций.
Навигация по странице.
Таблица синусов, косинусов, тангенсов и котангенсов для углов 0, 30, 45, 60, 90, … градусов
Тригонометрические определения синуса, косинуса, тангенса и котангенса позволяют указать значения тригонометрических функций для углов 0 и 90 градусов:
, а котангенс нуля градусов не определен, и
, а тангенс 90 градусов не определен.
В курсе геометрии из прямоугольных треугольников с углами 30 , 60 и 90 градусов, а также 45 , 45 и 90 градусов находятся значения синуса, косинуса, тангенса и котангенса углов 30, 45 и 60 градусов:
,
и
.
Занесем указанные значения тригонометрических функций для углов 0 , 30 , 45 , 60 и 90 градусов ( 0 , π/6 , π/4 , π/3 , π/2 радиан) в таблицу, назовем ее таблицей основных значений синуса, косинуса, тангенса и котангенса.
Используя формулы приведения, только что составленную таблицу синусов, косинусов, тангенсов и котангенсов можно расширить, дополнив значениями тригонометрических функций для углов 120 , 135 , 150 , 180 , 210 , 225 , 240 , 270 , 300 , 315 , 330 и 360 градусов ( 0, π/6, π/4, π/3, π/2, …, 2π радиан). При этом она принимает следующий вид.
Опираясь на свойство периодичности синуса, косинуса, тангенса и котангенса, таблицу основных значений тригонометрических функций можно расширить еще, заменив углы 0, 30, 45, 60, 90, …, 360 градусов соответственно на , где z – любое целое число. Из такой таблицы можно найти значения для всех углов, которым соответствуют точки единичной окружности, указанные на чертеже ниже.
Основные значения тригонометрических функций, собранные в заполненной выше таблице, желательно знать наизусть, так как они очень часто используются при решении задач.
Как пользоваться таблицей синусов, косинусов, тангенсов и котангенсов?
Использовать таблицу синусов, косинусов, тангенсов и котангенсов основных углов 0, 30, 45, 60, 90, …, 360 градусов очень просто – она дает непосредственные значения тригонометрических функций, находящиеся на пересечении соответствующей строки, указывающей название тригонометрической функции, и столбца, указывающего данное значение угла.
Например, значение косинуса угла 60 градусов находится на пересечении строки, в крайней левой ячейке которой находится запись cos , и столбца, в верхней ячейке которого записан угол 60 градусов. Так из таблицы находим, что значение косинуса 60 градусов равно одной второй. Для разъяснения приведем графическую иллюстрацию.
Расширенная таблица основных значений тригонометрических функций используется аналогично. С помощью расширенной таблицы основных значений синуса, косинуса, тангенса и котангенса можно сразу указать, например, чему равен тангенс угла 1 020 градусов. Он равен минус корню из трех, так как . Проиллюстрируем это.
Он равен минус корню из трех, так как . Проиллюстрируем это.
Таблицы синусов и косинусов, тангенсов и котангенсов Брадиса
Таблицы синусов, косинусов, тангенсов и котангенсов Брадиса разделены на таблицу синусов и косинусов, а также на таблицу тангенсов и котангенсов. Причем таблица тангенсов и котангенсов состоит из двух частей — тангенсы углов, близких к 90 градусов, и котангенсы малых углов вынесены в отдельную таблицу.
В таблицах Брадиса с точностью до четырех знаков после десятичной запятой приведены приближенные значения синусов и косинусов, а также четыре цифры приближенных значений тангенсов и котангенсов острых углов, содержащих целое число градусов и целое число минут.
Сначала дадим таблицу Брадиса, имеющую название таблица Брадиса: синусы и косинусы.
Теперь приведем таблицу тангенсов углов от 0 до 76 градусов и котангенсов углов от 14 до 90 градусов.
Наконец, осталось заполнить таблицу Брадиса тангенсов углов, близких к 90 градусам, и котангенсов малых углов. Она содержит непосредственные приближенные значения тангенсов углов от 76 до 90 градусов и котангенсов углов от 0 до 14 градусов.
Она содержит непосредственные приближенные значения тангенсов углов от 76 до 90 градусов и котангенсов углов от 0 до 14 градусов.
Как пользоваться таблицами синусов и косинусов, тангенсов и котангенсов Брадиса?
Осталось разобраться, как пользоваться таблицей синусов и косинусов, а также таблицами тангенсов и котангенсов Брадиса.
Значение синуса угла находится в таблице синусов на пересечении строки, содержащей в крайней левой ячейке нужное число градусов, и столбца, содержащего в верхней ячейке нужное число минут. Например, из таблицы синусов Брадиса можно определить, что синус 17 градусов 42 минут приближенно равен 0,3040 , вот иллюстрация тому, как это значение было найдено.
Несложно заметить, что в верхней строке минуты идут по порядку через шесть. А как определять значения, если количество минут имеет промежуточное значение, например 44 ? Для этого нужно внести соответствующую поправку, которую дают три крайних правых столбца таблицы. Например, синус 17 градусов 44 минут равен 0,3046 , так как синус 17 градусов 42 минут равен 0,3040 , и требуется еще поправка на 2 минуты в плюс, равна 0,0006 . Поправки содержатся в трех крайних правых столбцах таблицы синусов и косинусов Брадиса.
Поправки содержатся в трех крайних правых столбцах таблицы синусов и косинусов Брадиса.
Если бы нам нужно было найти синус 17 градусов 47 минут, то от значения синуса 17 градусов 48 минут 0,3057 мы бы отняли поправку на 1 минуту, равную 0,0003 . В итоге мы получим искомое значение, равное 0,3054 .
Для нахождения значений косинусов используется та же таблица синусов и косинусов Брадиса. Однако следует ориентироваться на нижнюю строку при выборе соответствующего значения градуса и на четвертую справа строку при выборе нужного числа минут.
Например, косинус 20 градусов равен 0,9397 .
Другой пример: значение косинуса 20 градусов 2 минут равно 0,9397−0,0002=0,9395 , а значение косинуса 20 градусов 5 минут равно 0,9391+0,0001=0,9392 (обратите внимание: что нужно быть внимательным со знаками поправок, нужно помнить, что при возрастании острого угла его косинус убывает).
Таблица тангенсов и котангенсов Брадиса углов от 0 до 76 градусов и котангенсов углов от 14 до 90 градусов используется абсолютно аналогично таблице синусов и косинусов.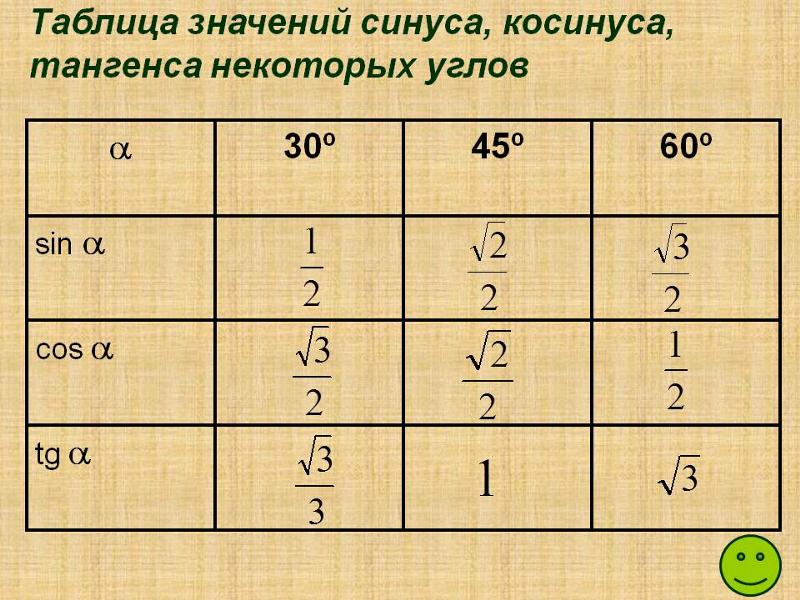
К примеру, тангенс 75 градусов 44 минут равен 3,923+0,010=3,933 , а котангенс 32 градусов 50 минут равен 1,5517−0,0020=1,5497 . Вот тому графические иллюстрации.
Таблица тангенсов углов, близких к 90 градусов, и котангенсов малых углов содержит значения тангенсов и котангенсов, не нуждающиеся в поправках. Для примера найдем значение тангенса угла 78 градусов 37 минут, оно равно 4,967 .
А котангенс угла 2 градуса 13 минут равен 25,83 .
Если угол выходит за пределы от 0 до 90 градусов, то сначала следует использовать формулы приведения и перейти к вычислению значения тригонометрической функции, аргумент которой заключен между 0 и 90 градусами. А если угол выражен в радианах, то прежде чем использовать таблицы Брадиса для нахождения синуса, косинуса, тангенса или котангенса данного угла, его нужно перевести в градусы (этому вопросу посвящен материал статьи перевод градусов в радианы и обратно).
В статье, мы полностью разберемся, как выглядит таблица тригонометрических значений, синуса, косинуса, тангенса и котангенса .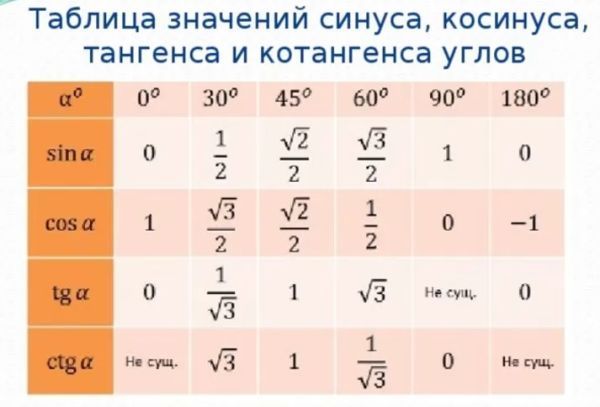 Рассмотрим основное значение тригонометрических функций, от угла в 0,30,45,60,90. 360 градусов. И посмотрим как пользоваться данными таблицами в вычислении значения тригонометрических функций.
Рассмотрим основное значение тригонометрических функций, от угла в 0,30,45,60,90. 360 градусов. И посмотрим как пользоваться данными таблицами в вычислении значения тригонометрических функций.
Первой рассмотрим таблицу косинуса, синуса, тангенса и котангенса от угла в 0, 30, 45, 60, 90. градусов. Определение данных величин дают определить значение функций углов в 0 и 90 градусов:
sin 0 0 =0, cos 0 0 = 1. tg 0 0 = 0, котангенс от 0 0 будет неопределенным
sin 90 0 = 1, cos 90 0 =0, ctg90 0 = 0,тангенс от 90 0 будет неопределенным
Если взять прямоугольные треугольники углы которых от 30 до 90 градусов. Получим:
sin 30 0 = 1/2, cos 30 0 = √3/2, tg 30 0 = √3/3, ctg 30 0 = √3
sin 45 0 = √2/2, cos 45 0 = √2/2, tg 45 0 = 1, ctg 45 0 = 1
sin 60 0 = √3/2, cos 60 0 = 1/2, tg 60 0 =√3 , ctg 60 0 = √3/3
Изобразим все полученные значения в виде тригонометрической таблицы:
Таблица синусов, косинусов, тангенсов и котангенсов!
Если использовать формулу приведения, наша таблица увеличится, добавятся значения для углов до 360 градусов. Выглядеть она будет как:
Выглядеть она будет как:
Так же исходя из свойств периодичности таблицу можно увеличить, если заменим углы на 0 0 +360 0 *z . 330 0 +360 0 *z, в котором z является целым числом. В данной таблице возможно вычислить значение всех углов, соответствующими точками в единой окружности.
Разберем наглядно как использовать таблицу в решении.
Все очень прост. Так как нужное нам значение лежит в точке пересечения нужных нам ячеек. К примеру возьмем cos угла 60 градусов, в таблице это будет выглядеть как:
В итоговой таблице основных значений тригонометрических функций, действуем так же. Но в данной таблице возможно узнать сколько составит тангенс от угла в 1020 градусов, он = -√3 Проверим 1020 0 = 300 0 +360 0 *2. Найдем по таблице.
Для более поиска тригонометрических значений углов с точностью до минут используются таблицы Брадиса. Подробная инструкция как ими пользоваться на странице по ссылке.
Таблица Брадиса. Для синуса, косинуса, тангенса и котангенса.
Таблицы Брадиса поделены на несколько частей, состоят из таблиц косинуса и синуса, тангенса и котангенса — которая поделена на две части (tg угла до 90 градусов и ctg малых углов).
Синус и косинус
tg угла начиная с 0 0 заканчивая 76 0 , ctg угла начиная с 14 0 заканчивая 90 0 .
tg до 90 0 и ctg малых углов.
Разберемся как пользоваться таблицами Брадиса в решении задач.
Найдем обозначение sin (обозначение в столбце с левого края) 42 минут (обозначение находится на верхней строчке). Путем пересечения ищем обозначение, оно = 0,3040.
Величины минут указаны с промежутком в шесть минут, как быть если нужное нам значение попадет именно в этот промежуток. Возьмем 44 минуты, а в таблице есть только 42. Берем за основу 42 и воспользуемся добавочными столбцами в правой стороне, берем 2 поправку и добавляем к 0,3040 + 0,0006 получаем 0,3046.
При sin 47 мин, берем за основу 48 мин и отнимаем от нее 1 поправку, т. е 0,3057 — 0,0003 = 0,3054
е 0,3057 — 0,0003 = 0,3054
При вычислении cos работаем аналогично sin только за основу берем нижнюю строку таблицы. К примеру cos 20 0 = 0.9397
Значения tg угла до 90 0 и cot малого угла, верны и поправок в них нет. К примеру, найти tg 78 0 37мин = 4,967
а ctg 20 0 13мин = 25,83
Ну вот мы и рассмотрели основные тригонометрические таблицы. Надеемся это информация была для вас крайне полезной. Свои вопросы по таблицам, если они появились, обязательно пишите в комментариях!
Если материал был полезен, вы можете отправить донат или поделиться данным материалом в социальных сетях:
Калькулятор поможет рассчитать точные значения тригонометрических функций sin, cos, tg и ctg для различных значений углов в градусах или радианах.
На данной странице таблица Брадиса, которая дает значение sin, cos, tg, ctg любого острого угла, содержащего целое число градусов и десятых долей градуса. Для нахождения значения угла берется число на пересечении строки, которое соответствует числу градусов и столбца, которое соответствует числу минут. Например, sin 70°30′ = 0.9426.
Например, sin 70°30′ = 0.9426.
что такое? Как найти синус, косинус и тангенс
В этой статье собраны таблицы синусов, косинусов, тангенсов и котангенсов . Сначала мы приведем таблицу основных значений тригонометрических функций, то есть, таблицу синусов, косинусов, тангенсов и котангенсов углов 0, 30, 45, 60, 90, …, 360 градусов (0, π/6, π/4, π/3, π/2, …, 2π радиан). После этого мы дадим таблицу синусов и косинусов, а также таблицу тангенсов и котангенсов В. М. Брадиса, и покажем, как использовать эти таблицы при нахождении значений тригонометрических функций.
Навигация по странице.
Таблица синусов, косинусов, тангенсов и котангенсов для углов 0, 30, 45, 60, 90, … градусов
Список литературы.
- Алгебра: Учеб. для 9 кл. сред. шк./Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова; Под ред. С. А. Теляковского.- М.: Просвещение, 1990.- 272 с.: ил.- ISBN 5-09-002727-7
- Башмаков М. И. Алгебра и начала анализа: Учеб.
 для 10-11 кл. сред. шк. — 3-е изд. — М.: Просвещение, 1993. — 351 с.: ил. — ISBN 5-09-004617-4.
для 10-11 кл. сред. шк. — 3-е изд. — М.: Просвещение, 1993. — 351 с.: ил. — ISBN 5-09-004617-4. - Алгебра и начала анализа: Учеб. для 10-11 кл. общеобразоват. учреждений / А. Н. Колмогоров, А. М. Абрамов, Ю. П. Дудницын и др.; Под ред. А. Н. Колмогорова.- 14-е изд.- М.: Просвещение, 2004.- 384 с.: ил.- ISBN 5-09-013651-3.
- Гусев В. А., Мордкович А. Г. Математика (пособие для поступающих в техникумы): Учеб. пособие.- М.; Высш. шк., 1984.-351 с., ил.
- Брадис В. М. Четырехзначные математические таблицы: Для общеобразоват. учеб. заведений. — 2-е изд. — М.: Дрофа, 1999.- 96 с.: ил. ISBN 5-7107-2667-2
Соотношения между основными тригонометрическими функциями – синусом, косинусом, тангенсом и котангенсом — задаются тригонометрическими формулами . А так как связей между тригонометрическими функциями достаточно много, то этим объясняется и обилие тригонометрических формул. Одни формулы связывают тригонометрические функции одинакового угла, другие – функции кратного угла, третьи – позволяют понизить степень, четвертые – выразить все функции через тангенс половинного угла, и т. д.
д.
В этой статье мы по порядку перечислим все основные тригонометрические формулы, которых достаточно для решения подавляющего большинства задач тригонометрии. Для удобства запоминания и использования будем группировать их по назначению, и заносить в таблицы.
Навигация по странице.
Основные тригонометрические тождества
Основные тригонометрические тождества задают связь между синусом, косинусом, тангенсом и котангенсом одного угла. Они вытекают из определения синуса, косинуса, тангенса и котангенса, а также понятия единичной окружности . Они позволяют выразить одну тригонометрическую функцию через любую другую.
Подробное описание этих формул тригонометрии, их вывод и примеры применения смотрите в статье .
Формулы приведения
Формулы приведения следуют из свойств синуса, косинуса, тангенса и котангенса , то есть, они отражают свойство периодичности тригонометрических функций, свойство симметричности, а также свойство сдвига на данный угол. Эти тригонометрические формулы позволяют от работы с произвольными углами переходить к работе с углами в пределах от нуля до 90
градусов.
Эти тригонометрические формулы позволяют от работы с произвольными углами переходить к работе с углами в пределах от нуля до 90
градусов.
Обоснование этих формул, мнемоническое правило для их запоминания и примеры их применения можно изучить в статье .
Формулы сложения
Тригонометрические формулы сложения показывают, как тригонометрические функции суммы или разности двух углов выражаются через тригонометрические функции этих углов. Эти формулы служат базой для вывода следующих ниже тригонометрических формул.
Формулы двойного, тройного и т.д. угла
Формулы двойного, тройного и т.д. угла (их еще называют формулами кратного угла) показывают, как тригонометрические функции двойных, тройных и т.д. углов () выражаются через тригонометрические функции одинарного угла . Их вывод базируется на формулах сложения.
Более детальная информация собрана в статье формулы двойного, тройного и т.д. угла .
Формулы половинного угла
Формулы половинного угла показывают, как тригонометрические функции половинного угла выражаются через косинус целого угла . Эти тригонометрические формулы следуют из формул двойного угла.
Эти тригонометрические формулы следуют из формул двойного угла.
Их вывод и примеры применения можно посмотреть в статье .
Формулы понижения степени
Тригонометрические формулы понижения степени призваны содействовать переходу от натуральных степеней тригонометрических функций к синусам и косинусам в первой степени, но кратных углов. Иными словами, они позволяют понижать степени тригонометрических функций до первой.
Формулы суммы и разности тригонометрических функций
Основное предназначение формул суммы и разности тригонометрических функций заключается в переходе к произведению функций, что очень полезно при упрощении тригонометрических выражений. Указанные формулы также широко используются при решении тригонометрических уравнений, так как позволяют раскладывать на множители сумму и разность синусов и косинусов.
Формулы произведения синусов, косинусов и синуса на косинус
Переход от произведения тригонометрических функций к сумме или разности осуществляется посредством формул произведения синусов, косинусов и синуса на косинус .
Copyright by cleverstudents
Все права защищены.
Охраняется законом об авторском праве. Ни одну часть сайта www.сайт, включая внутренние материалы и внешнее оформление, нельзя воспроизводить в какой-либо форме или использовать без предварительного письменного разрешения правообладателя.
Тригонометрические тождества — это равенства, которые устанавливают связь между синусом, косинусом, тангенсом и котангенсом одного угла, которая позволяет находить любую из данных функций при условии, что будет известна какая-либо другая.
tg \alpha = \frac{\sin \alpha}{\cos \alpha}, \enspace ctg \alpha = \frac{\cos \alpha}{\sin \alpha}
tg \alpha \cdot ctg \alpha = 1
Данное тождество говорит о том, что сумма квадрата синуса одного угла и квадрата косинуса одного угла равна единице, что на практике дает возможность вычислить синус одного угла, когда известен его косинус и наоборот.
При преобразовании тригонометрических выражений очень часто используют данное тождество, которое позволяет заменять единицей сумму квадратов косинуса и синуса одного угла и также производить операцию замены в обратном порядке.
Нахождение тангенса и котангенса через синус и косинус
tg \alpha = \frac{\sin \alpha}{\cos \alpha},\enspace
Данные тождества образуются из определений синуса, косинуса, тангенса и котангенса. Ведь если разобраться, то по определению ординатой y
является синус, а абсциссой x
— косинус. Тогда тангенс будет равен отношению \frac{y}{x}=\frac{\sin \alpha}{\cos \alpha}
, а отношение \frac{x}{y}=\frac{\cos \alpha}{\sin \alpha}
— будет являться котангенсом.
Добавим, что только для таких углов \alpha , при которых входящие в них тригонометрические функции имеют смысл, будут иметь место тождества , ctg \alpha=\frac{\cos \alpha}{\sin \alpha} .
Например: tg \alpha = \frac{\sin \alpha}{\cos \alpha} является справедливой для углов \alpha , которые отличны от \frac{\pi}{2}+\pi z , а ctg \alpha=\frac{\cos \alpha}{\sin \alpha} — для угла \alpha , отличного от \pi z , z — является целым числом.
Зависимость между тангенсом и котангенсом
tg \alpha \cdot ctg \alpha=1
Данное тождество справедливо только для таких углов \alpha , которые отличны от \frac{\pi}{2} z . Иначе или котангенс или тангенс не будут определены.
Опираясь на вышеизложенные пункты, получаем, что tg \alpha = \frac{y}{x} , а ctg \alpha=\frac{x}{y} . Отсюда следует, что tg \alpha \cdot ctg \alpha = \frac{y}{x} \cdot \frac{x}{y}=1 . Таким образом, тангенс и котангенс одного угла, при котором они имеют смысл, являются взаимно обратными числами.
Зависимости между тангенсом и косинусом, котангенсом и синусом
tg^{2} \alpha + 1=\frac{1}{\cos^{2} \alpha}
— сумма квадрата тангенса угла \alpha
и 1
, равна обратному квадрату косинуса этого угла. {2} \alpha = 1
. Это уравнение имеет два решения \cos \alpha = \pm \sqrt{1-\frac34}=\pm\sqrt\frac14
.
{2} \alpha = 1
. Это уравнение имеет два решения \cos \alpha = \pm \sqrt{1-\frac34}=\pm\sqrt\frac14
.
По условию \frac{\pi}{2}
Для того, чтобы найти ctg \alpha , воспользуемся формулой ctg \alpha = \frac{\cos \alpha}{\sin \alpha} . Соответствующие величины нам известны.
ctg \alpha = -\frac12: \frac{\sqrt3}{2} = -\frac{1}{\sqrt 3} .
В этой статье будут рассмотрены три основных свойства тригонометрических функций: синуса, косинуса, тангенса и котангенса.
Первое свойство — знак функции в зависимости от того, какой четверти единичной окружности приналдежит угол α . Второе свойство — периодичность. Согласно этому свойству, тигонометрическая функция не меняет значения при изменении угла на целое число оборотов. Третье свойсто определяет, как меняются значения функций sin, cos, tg, ctg при противоположных углах α и — α .
Yandex.RTB R-A-339285-1
Часто в математическом тексте или в контексте задачи можно встретить фразу: «угол первой, второй, третьей или четвертой координатной четверти». Что это такое?
Что это такое?
Обратимся к единичной окружности. Она разделена на четыре четверти. Отметим на окружности начальную точку A 0 (1 , 0) и, поворачивая ее вокруг точки O на угол α , попадем в точку A 1 (x , y) . В зависимости от того, в какой четверти будет лежать точка A 1 (x , y) , угол α будет называться углом первой, второй, третьей и четвертой четвети соответственно.
Для наглядности приведем иллюстрацию.
Угол α = 30 ° лежит в первой четверти. Угол — 210 ° является углом второй четверти. Угол 585 ° — угол третьей четверти. Угол — 45 ° — это угол четвертой четверти.
При этом углы ± 90 ° , ± 180 ° , ± 270 ° , ± 360 ° не принадлежат ни одной четверти, так как лежат на координатных осях.
Теперь рассмотрим знаки, которые принимают синус, косинус, тангенс и котангенс в зависимости от того, в какой четверти лежит угол.
Чтобы определить знаки синуса по четвертям, вспомним опредение. Синус — это ордината точки A 1 (x , y) . Из рисунка видно, что в первой и второй четвертях она положительна, а в третьей и четверной — отрицательна.
Косинус — это абсцисса точки A 1 (x , y) . В соответсии с этим, определяем знаки косинуса на окружности. Косинус положителен в первой и четвертой четвертях, а отрицателен во второй и третьей четверти.
Для определения знаков тангенса и котангенса по четвертям также вспоминаем определения этих тригонометрических функций. Тангенс — отношение ординаты точки к абсциссе. Значит, по правилу деления чисел с разными знаками, когда ордината и абсцисса имеют одинаковые знаки, знак тангенса на окружности будет положительным, а когда ордината и абсцисса имеют разные знаки — отрицательным. Аналогично определяются знаки котангенса по четвертям.
Важно помнить!
- Синус угла α имеет знак плюс в 1 и 2 четвертях, знак минус — в 3 и 4 четвертях.
- Косинус угла α имеет знак плюс в 1 и 4 четвертях, знак минус — в 2 и 3 четвертях.
- Тангенс угла α имеет знак плюс в 1 и 3 четвертях, знак минус — в 2 и 4 четвертях.
- Котангенс угла α имеет знак плюс в 1 и 3 четвертях, знак минус — в 2 и 4 четвертях.

Свойство периодичности
Свойство периодичности — одно из самых очевидных свойств тригонометрических функций.
Свойство периодичности
При изменении угла на целое число полных оборотов значения синуса, косинуса, тангенса и котангенса данного угла остаются неизменными.
Действительно, при изменении угла на целое число оборотов мы всегда будем попадать из начальной точки A на единичной окружности в точку A 1 с одними и теми же координатами. Соответственно, не будут меняться и значения синуса, косинуса, тангенса и котангенса.
Математически данное свойство записывается так:
sin α + 2 π · z = sin α cos α + 2 π · z = cos α t g α + 2 π · z = t g α c t g α + 2 π · z = c t g α
Какое применение на практике находит это свойство? Свойство периодичности, как и формулы приведения, часто используется для вычисления значений синусов, косинусов, тангенсов и котангенсов больших углов.
Приведем примеры.
sin 13 π 5 = sin 3 π 5 + 2 π = sin 3 π 5
t g (- 689 °) = t g (31 ° + 360 ° · (- 2)) = t g 31 ° t g (- 689 °) = t g (- 329 ° + 360 ° · (- 1)) = t g (- 329 °)
Вновь обратимся к единичной окружности.
Точка A 1 (x , y) — результат поворота начальной точки A 0 (1 , 0) вокруг центра окружности на угол α . Точка A 2 (x , — y) — результат поворота начальной точки на угол — α .
Точки A 1 и A 2 симметричны относительно оси абсцисс. В случае, когда α = 0 ° , ± 180 ° , ± 360 ° точки A 1 и A 2 совпадают. Пусть одна точка имеет координаты (x , y) , а вторая — (x , — y) . Вспомним определения синуса, косинуса, тангенса, котангенса и запишем:
sin α = y , cos α = x , t g α = y x , c t g α = x y sin — α = — y , cos — α = x , t g — α = — y x , c t g — α = x — y
Отсюда следует свойство синусов, косинусов, тангенсов и котангенсов противоположных углов.
Свойство синусов, косинусов, тангенсов и котангенсов противоположных углов
sin — α = — sin α cos — α = cos α t g — α = — t g α c t g — α = — c t g α
Согласно этому свойству, справедливы равенства
sin — 48 ° = — sin 48 ° , c t g π 9 = — c t g — π 9 , cos 18 ° = cos — 18 °
Рассмотренное свойство часто используется при решении практических задач в случаях, когда нужно избавиться от отрицательных знаков углов в агрументах тригонометрических функций.
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
Отношение противолежащего катета к гипотенузе называют синусом острого угла прямоугольного треугольника.
\sin \alpha = \frac{a}{c}
Косинус острого угла прямоугольного треугольника
Отношение близлежащего катета к гипотенузе называют косинусом острого угла прямоугольного треугольника.
\cos \alpha = \frac{b}{c}
Тангенс острого угла прямоугольного треугольника
Отношение противолежащего катета к близлежащему катету называют тангенсом острого угла прямоугольного треугольника.
tg \alpha = \frac{a}{b}
Котангенс острого угла прямоугольного треугольника
Отношение близлежащего катета к противолежащему катету называют котангенсом острого угла прямоугольного треугольника.
ctg \alpha = \frac{b}{a}
Синус произвольного угла
Ордината точки на единичной окружности , которой соответствует угол \alpha
называют синусом произвольного угла поворота \alpha
.
\sin \alpha=y
Косинус произвольного угла
Абсцисса точки на единичной окружности, которой соответствует угол \alpha называют косинусом произвольного угла поворота \alpha .
\cos \alpha=x
Тангенс произвольного угла
Отношение синуса произвольного угла поворота \alpha к его косинусу называют тангенсом произвольного угла поворота \alpha .
tg \alpha = y_{A}
tg \alpha = \frac{\sin \alpha}{\cos \alpha}
Котангенс произвольного угла
Отношение косинуса произвольного угла поворота \alpha к его синусу называют котангенсом произвольного угла поворота \alpha .
ctg \alpha =x_{A}
ctg \alpha = \frac{\cos \alpha}{\sin \alpha}
Пример нахождения произвольного угла
Если \alpha — некоторый угол AOM , где M — точка единичной окружности, то
\sin \alpha=y_{M} , \cos \alpha=x_{M} , tg \alpha=\frac{y_{M}}{x_{M}} , ctg \alpha=\frac{x_{M}}{y_{M}} .
Например, если \angle AOM = -\frac{\pi}{4} , то: ордината точки M равна -\frac{\sqrt{2}}{2} , абсцисса равна \frac{\sqrt{2}}{2} и потому
\sin \left (-\frac{\pi}{4} \right)=-\frac{\sqrt{2}}{2} ;
\cos \left (\frac{\pi}{4} \right)=\frac{\sqrt{2}}{2} ;
tg ;
ctg
\left (-\frac{\pi}{4} \right)=-1
. {\circ}\left(2\pi\right)
{\circ}\left(2\pi\right)
5.3 Другие тригонометрические функции. Предварительное исчисление 2e
Цели обучения
В этом разделе вы:
- Найдите точные значения тригонометрических функций секанса, косеканса, тангенса и котангенса числа π3, π3, π4, π4 и π6.π6.
- Используйте опорные углы для вычисления тригонометрических функций секанса, косеканса, тангенса и котангенса.

- Использовать свойства четных и нечетных тригонометрических функций.
- Распознавать и использовать основные тождества.
- Вычисление тригонометрических функций с помощью калькулятора.
Пандус для инвалидных колясок, соответствующий стандартам Закона об американцах-инвалидах, должен образовывать с землей угол, касательная которого составляет 112112 или меньше, независимо от его длины. Тангенс представляет собой отношение, поэтому это означает, что на каждый 1 дюйм подъема рампа должна иметь 12 дюймов пробега. Тригонометрические функции позволяют нам задавать формы и пропорции объектов независимо от точных размеров. Мы уже определили функции синуса и косинуса угла. Хотя синус и косинус являются наиболее часто используемыми тригонометрическими функциями, есть еще четыре. Вместе они составляют набор из шести тригонометрических функций. В этом разделе мы исследуем остальные функции.
Нахождение точных значений тригонометрических функций секанс, косеканс, тангенс и котангенс
Чтобы определить оставшиеся функции, мы еще раз нарисуем единичный круг с точкой (x,y)(x,y), соответствующей углу t,t, как показано на рисунке 1. Как и в случае с синусом и косинусом, мы можем использовать координаты (x, y) (x, y), чтобы найти другие функции.
Как и в случае с синусом и косинусом, мы можем использовать координаты (x, y) (x, y), чтобы найти другие функции.
Рисунок 1
Первая функция, которую мы определим, это тангенс. Тангенс угла равен отношению y -значение x -значение соответствующей точки на единичной окружности. На рисунке 1 тангенс угла tt равен yx,x≠0.yx,x≠0. Поскольку значение y равно синусу t,t, а значение x равно косинусу t,t, тангенс угла tt также может быть определен как sintcost,cost≠0. sintcost,стоимость≠0. Функция тангенса обозначается аббревиатурой tan.tan. Остальные три функции могут быть выражены как обратные функции, которые мы уже определили.
- Функция секанса является обратной функцией косинуса. На рисунке 1 секанс угла tt равен 1cost=1x,x≠0,1cost=1x,x≠0. Функция секущей обозначается как sec.sec.
- Функция котангенса является обратной величиной функции тангенса.
 На рисунке 1 котангенс угла tt равен costint=xy,y≠0.costsint=xy,y≠0. Функция котангенса сокращенно обозначается как cot.cot.
На рисунке 1 котангенс угла tt равен costint=xy,y≠0.costsint=xy,y≠0. Функция котангенса сокращенно обозначается как cot.cot. - Функция косеканса является обратной величиной функции синуса. На рисунке 1 косеканс угла tt равен 1sint=1y,y≠0,1sint=1y,y≠0. Функция косеканса обозначается аббревиатурой csc.csc.
Функции тангенса, секанса, косеканса и котангенса
Если tt — действительное число и (x,y)(x,y) — точка, в которой конечная сторона угла в tt радиан пересекает единичную окружность, то
tant=yx,x≠0sect=1x, x≠0csct=1y,y≠0cott=xy,y≠0tant=yx,x≠0sect=1x,x≠0csct=1y,y≠0cott=xy,y≠0
Пример 1
Нахождение тригонометрических функций из точки на единичной окружности
Точка (−32,12)(−32,12) находится на единичной окружности, как показано на рис. 2. Найти sint,cost,tant,sect,csct ,sint,cost,tant,sect,csct и cott.cott.
Рисунок 2
Решение
Поскольку нам известны (x,y)(x,y) координаты точки на единичной окружности, обозначенной углом t,t, мы можем использовать эти координаты для нахождения шести функций:
sint=y=12cost=x =-32tant=yx=12-32=12(-23)=-13=-33sect=1x=1-32=-23=-233csct=1y=112=2cott=xy=-3212=-32(21) =−3sint=y=12cost=x=−32tant=yx=12−32=12(−23)=−13=−33sect=1x=1−32=−23=−233csct=1y=112=2cott=xy =−3212=−32(21)=−3
Попытайся #1
Точка (22,−22)(22,−22) находится на единичной окружности, как показано на рис. 3. Найдите sint,cost,tant,sect,csct,sint,cost,tant,sect,csct и котт.котт.
3. Найдите sint,cost,tant,sect,csct,sint,cost,tant,sect,csct и котт.котт.
Рисунок 3
Пример 2
Нахождение тригонометрических функций угла
Найти sint,cost,tant,sect,csct,sint,cost,tant,sect,csct и cottcott при t=π6.t=π6.
Решение
Ранее мы использовали свойства равносторонних треугольников, чтобы показать, что sinπ6=12sinπ6=12 и cosπ6=32.cosπ6=32. Мы можем использовать эти значения и определения тангенса, секанса, косеканса и котангенса как функции синуса и косинуса, чтобы найти остальные значения функции.
tanπ6 = sinπ6cosπ6 = 1232 = 13 = 33tanπ6 = sinπ6cosπ6 = 1232 = 13 = 33
secπ6 = 1cosπ6 = 132 = 23 = 233Seec 6 = 1cosπ6 = 132 = 23 = 233
CSC 6 = 1SIINπ6 = 232 = 233
. =112=2
cotπ6=cosπ6sinπ6=3212=3cotπ6=cosπ6sinπ6=3212=3
Попытайся #2
Найдите sint,cost,tant,sect,csct,sint,cost,tant,sect,csct и cottcott при t=π3. t=π3.
t=π3.
Поскольку мы знаем значения синуса и косинуса для обычных углов первого квадранта, мы можем также найти значения других функций для этих углов, установив xx равным косинусу, а yy равным синусу, а затем используя определения тангенса, секанс, косеканс и котангенс. Результаты представлены в таблице 1.
| Угол | 00 | π6, или 30°π6, или 30° | π4, или 45°π4, или 45° | π3, или 60°π3, или 60° | π2, или 90°π2, или 90° |
| Косинус | 1 | 3232 | 2222 | 1212 | 0 |
| Синус | 0 | 1212 | 2222 | 3232 | 1 |
| Тангенс | 0 | 3333 | 1 | 33 | Не определено |
| Секущая | 1 | 233233 | 22 | 2 | Не определено |
| Косеканс | Не определено | 2 | 22 | 233233 | 1 |
| Котангенс | Не определено | 33 | 1 | 3333 | 0 |
Стол 1
Использование опорных углов для вычисления тангенса, секанса, косеканса и котангенса
Мы можем вычислять тригонометрические функции углов за пределами первого квадранта, используя эталонные углы, как мы уже сделали с функциями синуса и косинуса. Процедура та же: найдите опорный угол, образованный конечной стороной данного угла с горизонтальной осью. Значения тригонометрической функции для исходного угла будут такими же, как и для исходного угла, за исключением положительного или отрицательного знака, который определяется как x — и y -значения в исходном квадранте. На рис. 4 показано, какие функции в каком квадранте положительны.
Процедура та же: найдите опорный угол, образованный конечной стороной данного угла с горизонтальной осью. Значения тригонометрической функции для исходного угла будут такими же, как и для исходного угла, за исключением положительного или отрицательного знака, который определяется как x — и y -значения в исходном квадранте. На рис. 4 показано, какие функции в каком квадранте положительны.
Чтобы помочь нам вспомнить, какие из шести тригонометрических функций положительны в каждом квадранте, мы можем использовать мнемоническую фразу «Умный класс триггеров». Каждое из четырех слов во фразе соответствует одному из четырех квадрантов, начиная с квадранта I и вращаясь против часовой стрелки. В квадранте I, то есть « А », а 11 из шести тригонометрических функций положительны. В квадранте II « S mart», только s ine и его обратная функция, косеканс, положительны. В квадранте III, « T rig», только t тангенс и его обратная функция, котангенс, положительны. Наконец, в квадранте IV « C девушка» только c озин и его обратная функция, секанс, положительны.
В квадранте III, « T rig», только t тангенс и его обратная функция, котангенс, положительны. Наконец, в квадранте IV « C девушка» только c озин и его обратная функция, секанс, положительны.
Рисунок 4
Как
Учитывая угол не в первом квадранте, используйте опорные углы, чтобы найти все шесть тригонометрических функций.
- Измерьте угол, образованный конечной стороной заданного угла и горизонтальной осью. Это опорный угол.
- Оцените функцию при эталонном угле.
- Обратите внимание на квадрант, в котором находится конечная сторона исходного угла. На основе квадранта определите, является ли выход положительным или отрицательным.
Пример 3
Использование опорных углов для нахождения тригонометрических функций
Используйте опорные углы, чтобы найти все шесть тригонометрических функций от −5π6. −5π6.
−5π6.
Решение
Угол между конечной стороной этого угла и осью x равен π6, π6, так что это опорный угол. Поскольку −5π6−5π6 находится в третьем квадранте, где xx и yy отрицательны, косинус, синус, секанс и косеканс будут отрицательными, а тангенс и котангенс будут положительными.
cos(-5π6)=-32,sin(-5π6)=-12,tan(-5π6)=33sec(-5π6)=-233,csc(-5π6)=-2,cot(-5π6)= 3cos(-5π6)=-32,sin(-5π6)=-12,tan(-5π6)=33sec(-5π6)=-233,csc(-5π6)=-2,cot(-5π6)=3
Попытайся #3
Используйте опорные углы, чтобы найти все шесть тригонометрических функций от −7π4.−7π4.
Использование четных и нечетных тригонометрических функций
Чтобы иметь возможность свободно использовать наши шесть тригонометрических функций как с положительными, так и с отрицательными входными значениями угла, мы должны изучить, как каждая функция обрабатывает отрицательные входные данные. Как оказалось, между функциями в этом отношении есть важное различие.
Как оказалось, между функциями в этом отношении есть важное различие.
Рассмотрим функцию f(x)=x2,f(x)=x2, показанную на рисунке 5. График функции симметричен относительно и -ось. На протяжении всей кривой любые две точки с противоположными значениями x имеют одинаковое значение функции. Это соответствует результату расчета: (4)2=(−4)2,(4)2=(−4)2,(−5)2=(5)2,(−5)2=(5)2 , и так далее. Таким образом, f(x)=x2f(x)=x2 — четная функция, такая, что два противоположных входа имеют одинаковый выход. Это означает, что f(−x)=f(x).f(−x)=f(x).
Рисунок 5 Функция f(x)=x2f(x)=x2 является четной функцией.
Теперь рассмотрим функцию f(x)=x3,f(x)=x3, показанную на рисунке 6. График несимметричен относительно и -ось. На всем протяжении графика любые две точки с противоположными значениями x также имеют противоположные значения y . Итак, f(x)=x3f(x)=x3 — нечетная функция, такая, что два противоположных входа имеют противоположные выходы. Это означает, что f(−x)=−f(x).f(−x)=−f(x).
Итак, f(x)=x3f(x)=x3 — нечетная функция, такая, что два противоположных входа имеют противоположные выходы. Это означает, что f(−x)=−f(x).f(−x)=−f(x).
Рисунок 6 Функция f(x)=x3f(x)=x3 является нечетной функцией.
Мы можем проверить, является ли тригонометрическая функция четной или нечетной, нарисовав единичный круг с положительным и отрицательным углами, как показано на рисунке 7. Синус положительного угла равен y.y. Синус отрицательного угла равен − и . Таким образом, функция синуса является нечетной функцией. Таким образом мы можем проверить каждую из шести тригонометрических функций. Результаты представлены в таблице 2.
Рисунок 7
| sint=ysin(-t)=-ysint≠sin(-t)sint=ysin(-t)=-ysint≠sin(-t) | стоимость=xcos(-t)=xcost=cos(-t)cost=xcos(-t)=xcost=cos(-t) | tan(t)=yxtan(-t)=-yxtant≠tan(-t)tan(t)=yxtan(-t)=-yxtant≠tan(-t) |
| сек=1xсек(-t)=1xсек=сек(-t)сек=1xсек(-t)=1xсек=сек(-t) | csct=1ycsc(-t)=1-ycsct≠csc(-t)csct=1ycsc(-t)=1-ycsct≠csc(-t) | cott=xycott(-t)=x-ycott≠cot(-t)cott=xycott(-t)=x-ycott≠cot(-t) |
Стол 2
Четные и нечетные тригонометрические функции.

Четная функция — это функция, в которой f(−x)=f(x).f(−x)=f(x).
Нечетная функция — это функция, в которой f(−x)=−f(x).f(−x)=−f(x).
Косинус и секанс четны:
cos(-t)=costsec(-t)=sectcos(-t)=costsec(-t)=sect
Синус, тангенс, косеканс и котангенс нечетны:
sin(-t)=-sinttan(-t)=-tantcsc(-t)=-csctcot(-t)=-cottsin(-t)=- sinttan(-t)=-tantcsc(-t)=-csctcot(-t)=-cott
Пример 4
Использование четных и нечетных свойств тригонометрических функций
Если секанс угла tt равен 2, чему равен секанс −t?−t?
Решение
Секанс — четная функция. Сеанс угла равен секансу противоположного ему угла. Итак, если секанс угла t равно 2, секанс −t−t также равен 2.
Попытайся #4
Если котангенс угла tt равен 3,3, чему равен котангенс угла −t?−t?
Распознавание и использование фундаментальных идентичностей
Мы исследовали ряд свойств тригонометрических функций. Теперь мы можем пойти дальше и вывести некоторые фундаментальные тождества. Идентичности — это утверждения, истинные для всех значений входных данных, для которых они определены. Обычно тождества можно вывести из уже известных нам определений и отношений. Например, тождество Пифагора, которое мы узнали ранее, было получено из теоремы Пифагора и определений синуса и косинуса.
Теперь мы можем пойти дальше и вывести некоторые фундаментальные тождества. Идентичности — это утверждения, истинные для всех значений входных данных, для которых они определены. Обычно тождества можно вывести из уже известных нам определений и отношений. Например, тождество Пифагора, которое мы узнали ранее, было получено из теоремы Пифагора и определений синуса и косинуса.
Фундаментальные тождества
Мы можем вывести некоторые полезные тождества из шести тригонометрических функций. Остальные четыре тригонометрические функции можно связать обратно с функциями синуса и косинуса, используя следующие основные соотношения: =costsint
Пример 5
Использование тождеств для вычисления тригонометрических функций
- ⓐ Учитывая sin(45°)=22,cos(45°)=22,sin(45°)=22,cos(45°)=22, вычислить tan(45°).tan(45°).
- ⓑ Даны sin(5π6)=12,cos(5π6)=−32,оценитьsec(5π6).sin(5π6)=12,cos(5π6)=−32,оценитьsec(5π6).

Решение
Поскольку мы знаем значения синуса и косинуса для этих углов, мы можем использовать тождества для вычисления других функций.
ⓐ
tan(45°)=sin(45°)cos(45°)=2222=1tan(45°)=sin(45°)cos(45°)=2222=1
ⓑ
сек(5π6 )=1cos(5π6)=1−32=−23=−233сек(5π6)=1cos(5π6)=1−32=−23=−233
Попытайся #5
Вычислить csc(7π6).csc(7π6).
Пример 6
Использование тождеств для упрощения тригонометрических выражений
Simplify secttant.secttant.
Решение
Мы можем упростить это, переписав обе функции в терминах синуса и косинуса.
secttant = 1costsintcostto Разделим функции, мы умножаем на взаимную. = 1costcostsintDivide из косинусов. = 1SintSimplify и используем идентичность. = Csctsectant = 1costsintcostto делятся на функции, мы умножаем. и используйте идентификатор.=csct
и используйте идентификатор.=csct
Показав, что secttantsecttant можно упростить до csct,csct, мы фактически установили новую идентичность.
сектант=csctsecttant=csct
Попытайся #6
Упрощение (tant)(стоимость).(tant)(стоимость).
Альтернативные формы пифагорейской идентичности
Мы можем использовать эти фундаментальные тождества для получения альтернативных форм пифагорейского тождества, cos2t+sin2t=1.cos2t+sin2t=1. Одна форма получается делением обеих частей на cos2t:cos2t:
cos2tcos2t+sin2tcos2t=1cos2t1+tan2t=sec2tcos2tcos2t+sin2tcos2t=1cos2t1+tan2t=sec2t
Другая форма получается делением обеих частей на sin2t:sin2t:
cos2tsin2t+sin2tsin2t=1sin2tcot2t+1=csc2tcos2tsin2t+sin2tsin2t=1sin2tcot2t+1=csc2t
Альтернативные формы пифагорейской идентичности
1+tan2t=sec2t1+tan2t=sec2t
cot2t+1=csc2tcot2t+1=csc2t
Пример 7
Использование тождеств для связи тригонометрических функций
Если cos(t)=1213cos(t)=1213 и tt находится в квадранте IV, как показано на рисунке 8, найдите значения остальных пяти тригонометрических функций.
Рисунок 8
Решение
Мы можем найти синус, используя тождество Пифагора, cos2t+sin2t=1,cos2t+sin2t=1, и остальные функции, связав их с синусом и косинусом.
(1213) 2+sin2t = 1 sin2t = 1– (1213) 2 sin2t = 1-144169 sin2t = 25169 sint = ± 25169 Sint = ± 25169sint = ± 513 (1213) 2+sin2t = 1 sin2t = 1– (1213) 2 sin2t = 1-144169 sin2t = 25169 sint = ± 25169 sint = ± 25169 sint = ± 513
y -значения в квадранте, где находится угол. Поскольку угол находится в квадранте IV, где значения y отрицательные, его синус отрицательный, -513.-513.
Остальные функции можно вычислить, используя тождества, связывающие их с синусом и косинусом.
tant=sintcost=-5131213=-512sect=1cost=11213=1312csct=1sint=1-513=-135cott=1tant=1-512=-125tant=sintcost=-5131213=-512sect=1cost=11213=1312csct= 1sint=1−513=−135cott=1tant=1−512=−125
Попытайся #7
Если sec(t)=−178sec(t)=−178 и 0
Как мы обсуждали в начале главы, функция, которая повторяет свои значения через равные промежутки времени, называется периодической функцией. Тригонометрические функции являются периодическими. Для четырех тригонометрических функций, синуса, косинуса, косеканса и секанса, оборот одного круга или 2π, 2π, приведет к одинаковым результатам для этих функций. А для тангенса и котангенса только половина оборота даст одинаковые результаты.
Другие функции также могут быть периодическими. Например, длина месяцев повторяется каждые четыре года. Если xx представляет продолжительность времени, измеряемую в годах, а f(x)f(x) представляет количество дней в феврале, то f(x+4)=f(x).f(x+4)=f( Икс).
Этот шаблон повторяется снова и снова во времени. Другими словами, каждые четыре года в феврале гарантированно будет такое же количество дней, как и четыре года назад. Положительное число 4 является наименьшим положительным числом, удовлетворяющим этому условию, и называется периодом. А период — это кратчайший интервал, за который функция завершает один полный цикл — в этом примере период равен 4 и представляет собой время, которое требуется нам, чтобы убедиться, что в феврале одинаковое количество дней.
А период — это кратчайший интервал, за который функция завершает один полный цикл — в этом примере период равен 4 и представляет собой время, которое требуется нам, чтобы убедиться, что в феврале одинаковое количество дней.
Период функции
Период PP повторяющейся функции ff — это число, представляющее интервал, такой что f(x+P)=f(x)f(x+P)=f(x) для любого значения x.x.
Период функций косинуса, синуса, секанса и косеканса равен 2π,2π.
Период функций тангенса и котангенса равен π.π.
Пример 8
Нахождение значений тригонометрических функций
Нахождение значений шести тригонометрических функций угла tt на основе рисунка 9 .
Рисунок 9
Решение
sint=y=-32cost=x=-12tant=sintcost=-32-12=3sect=1cost=1-12=-2csct=1sint=1-32=-233cott=1tant=13=33sint=y=-32cost =x=−12tant=sintcost=−32−12=3sect=1cost=1−12=−2csct=1sint=1−32=−233cott=1tant=13=33
Попытайся #8
Найдите значения шести тригонометрических функций угла tt
на основе рисунка 10 .
Рисунок 10
Пример 9
Нахождение значения тригонометрических функций
Если sin(t)=-32sin(t)=-32 и cos(t)=12,cos(t)=12, найти sec(t),csc(t), tan(t), cot(t).sec(t),csc(t),tan(t), cot(t).
Решение
sect=1cost=112=2csct=1sint=1−32−233tant=sintcost=−3212=−3cott=1tant=1−3=−33sect=1cost=112=2csct=1sint=1−32−233tant=sintcost= −3212=−3cott=1tant=1−3=−33
Попытайся #9
Если sin(t)=22sin(t)=22 и cos(t)=22,cos(t)=22, найти sec(t),csc(t),tan(t) и cot(t).sec(t),csc(t),tan(t ) и кроватка(т).
Вычисление тригонометрических функций с помощью калькулятора
Мы научились вычислять шесть тригонометрических функций для обычных углов первого квадранта и использовать их в качестве справочных углов для углов в других квадрантах. Чтобы оценить тригонометрические функции других углов, мы используем научный или графический калькулятор или компьютерную программу. Если калькулятор имеет режим градусов и режим радиан, убедитесь, что выбран правильный режим, прежде чем выполнять вычисления.
Если калькулятор имеет режим градусов и режим радиан, убедитесь, что выбран правильный режим, прежде чем выполнять вычисления.
Вычисление функции тангенса с помощью научного калькулятора, в отличие от графического калькулятора или системы компьютерной алгебры, похоже на вычисление синуса или косинуса: введите значение и нажмите клавишу TAN. Для взаимных функций может не быть специальных клавиш с надписью CSC, SEC или COT. В этом случае функция должна оцениваться как обратная величина синуса, косинуса или тангенса.
Если нам нужно работать с градусами, а наш калькулятор или программное обеспечение не имеет режима градусов, мы можем ввести градусы, умноженные на коэффициент преобразования π180π180, чтобы преобразовать градусы в радианы. Чтобы найти секанс 30°, 30°, мы могли бы нажать
(для научного калькулятора): 130×π180COS(для научного калькулятора): 130×π180COS
или
(для графического калькулятора): 1cos(30π180)(для графического калькулятора): 1cos(30π180)
Как
Для измерения угла в радианах используйте научный калькулятор, чтобы найти косеканс.
- Если в калькуляторе есть режимы в градусах и в радианах, установите его в режим в радианах.
- Введите: 1 /1 /
- Введите значение угла в скобках.
- Нажмите клавишу SIN.
- Нажмите клавишу =.
Как
Для измерения угла в радианах используйте графическую утилиту/калькулятор, чтобы найти косеканс.
- Если графическая утилита имеет режим градусов и режим радиан, установите ее в режим радиан.
- Введите: 1 /1 /
- Нажмите клавишу SIN.
- Введите значение угла в скобках.
- Нажмите клавишу ВВОД.
Пример 10
Вычисление косеканса с помощью технологии
Вычисление косеканса числа 5π7,5π7.
Решение
Для инженерного калькулятора введите следующую информацию:
1 / ( 5 ×π / 7 ) SIN =1 / ( 5 ×π / 7 ) SIN =
csc(5π7)≈1,279csc(5π7)≈1,279
Попытайся #10
Вычислите котангенс числа −π8. −π8.
−π8.
5.3 Секционные упражнения
Устный
1.
Могут ли на интервале [0,2π),[0,2π) быть одинаковыми значения синуса и косинуса радианной меры? Если да, то где?
2.
Как бы вы оценили косинус ππ градусов? Объясните свои рассуждения.
3.
Для любого угла в квадранте II, если бы вы знали синус угла, как бы вы могли определить косинус угла?
4.
Описать секущую.
5.
Тангенс и котангенс имеют период π.π. Что это говорит нам о выводе этих функций?
Алгебраический
В следующих упражнениях найдите точное значение каждого выражения.
6.
tanπ6tanπ6
7.
секπ6секπ6
8.
cscπ6cscπ6
9.
детская кроватка π6 кроватка π6
10.
tanπ4tanπ4
11.
секπ4секπ4
12.
cscπ4cscπ4
13.
кроватка 4 кроватка 4
14.
tanπ3tanπ3
15.
секπ3секπ3
16.
cscπ3cscπ3
17.
кроватка 3 кроватка 3
В следующих упражнениях используйте опорные углы для вычисления выражения.
18.
тан5π6tan5π6
19.
сек7π6сек7π6
20.
csc11π6csc11π6
21.
кроватка13π6кроватка13π6
22.
tan7π4tan7π4
23.
сек3π4сек3π4
24.
csc5π4csc5π4
25.
кроватка11π4кроватка11π4
26.
tan8π3tan8π3
27.
сек4π3сек4π3
28.
csc2π3csc2π3
29.
кроватка5π3cot5π3
30.
загар225°загар225°
31.
сек300°сек300°
32.
csc150°csc150°
33.
раскладушка240°раскладушка240°
34.
tan330°tan330°
35.
сек120°сек120°
36.
csc210°csc210°
37.
кроватка315°кроватка315°
38.
Если sint=34,sint=34 и tt находится в квадранте II, найти costcost, sectsect, csctcsct, tanttant,cott.cott.
39.
Если cost=−13,cost=−13 и tt находится в квадранте III, найдите sint,sect,csct,tant,cott.sint,sect,csct,tant,cott.
40.
Если tant=125,tant=125 и 0≤t<π2,0≤t<π2, найти sint,cost,sect,csct,sint,cost,sect,csct и cott.cott.
41.
Если sint=32sint=32 и cost=12,cost=12, найти sect,csct,tant,sect,csct,tant и cott.cott.
42.
Если sin40°≈0,643sin40°≈0,643 а также cos40°≈0,766cos40°≈0,766 найти sec40°,csc40°,tan40°,sec40°,csc40°,tan40°, а также cotи40°.cotи40°.
43.
Если sint=22,sint=22, каково значение sin(−t)?sin(−t)?
44.
Если стоимость = 12, стоимость = 12, каково значение cos(−t)?cos(−t)?
45.
Если sect=3.1,sect=3.1, какова сек(-t)?сек(-t)?
46.
Если csct=0,34,csct=0,34, каково значение csc(−t)?csc(−t)?
47.
Если tant=-1,4, tant=-1,4, чему равен тангенс(-t)?тангенс(-t)?
48.
Если cott=9,23,cott=9,23, чему равно cot(-t)?cot(-t)?
Графический
В следующих упражнениях используйте угол в единичной окружности, чтобы найти значение каждой из шести тригонометрических функций.
49.
50.
51.
Технология
Для оценки следующих упражнений используйте графический калькулятор.
52.
csc5π9csc5π9
53.
кроватка4π7cot4π7
54.
секπ10секπ10
55.
tan5π8tan5π8
56.
сек3π4сек3π4
57.
cscπ4cscπ4
58.
tan98°tan98°
59.
раскладушка33°раскладушка33°
60.
кроватка140°кроватка140°
61.
сек310°сек310°
Расширения
В следующих упражнениях используйте тождества для вычисления выражения.
62.
Если tan(t)≈2,7,tan(t)≈2,7 и sin(t)≈0,94,sin(t)≈0,94, найти cos(t).cos(t).
63.
Если tan(t)≈1,3,tan(t)≈1,3 и cos(t)≈0,61, cos(t)≈0,61, найти sin(t).sin(t).
64.
Если csc(t)≈3,2, csc(t)≈3,2 и cos(t)≈0,95, cos(t)≈0,95, найти tan(t).tan(t).
65.
Если cot(t)≈0,58,cot(t)≈0,58 и cos(t)≈0,5, cos(t)≈0,5, найти csc(t).csc(t).
66.
Определите, является ли функция f(x)=2sinxcosxf(x)=2sinxcosx четной, нечетной или ни той, ни другой.
67.
Определите, является ли функция f(x)=3sin2xcosx+secxf(x)=3sin2xcosx+secx четной, нечетной или ни той, ни другой.
68.
Определите, является ли функция f(x)=sinx-2cos2xf(x)=sinx-2cos2x четной, нечетной или ни той, ни другой.
69.
Определите, является ли функция f(x)=csc2x+secxf(x)=csc2x+secx четной, нечетной или ни одной из них.
В следующих упражнениях используйте тождества для упрощения выражения.
70.
cscttantcscttant
71.
sectcsctsectcsct
Реальные приложения
72.
Количество солнечного света в определенном городе можно смоделировать с помощью функции h=15cos(1600d),h=15cos(1600d), где hh представляет количество часов солнечного света, а dd — день в году. Используйте уравнение, чтобы найти, сколько часов солнечного света будет 11 февраля, 42 и день года. Укажите период функции.
Укажите период функции.
73.
Количество солнечного света в определенном городе можно смоделировать функцией h=16cos(1500d),h=16cos(1500d), где hh представляет часы солнечного света, а dd это день года. Используйте уравнение, чтобы найти, сколько часов солнечного света будет 24 сентября, 267 -й -й день года. Укажите период функции.
74.
Уравнение P=20sin(2πt)+100P=20sin(2πt)+100 моделирует кровяное давление, P,P, где tt представляет время в секундах. а) Найдите артериальное давление через 15 секунд. б) Каковы максимальное и минимальное артериальное давление?
75.
Высота поршня, h,h, в дюймах, может быть смоделирована уравнением y=2cosx+6,y=2cosx+6, где xx представляет собой угол поворота коленчатого вала. Найдите высоту поршня, когда угол поворота коленчатого вала составляет 55°,55°.
76.
Высота поршня, h,h, в дюймах, может быть смоделирована уравнением y=2cosx+5,y=2cosx+5, где xx представляет собой угол поворота коленчатого вала. Найдите высоту поршня, когда угол поворота коленчатого вала составляет 55°,55°.
Таблица Брадиса косинусов, закона синусов, тангенсов, котангенсов
Таблица Брадиса — представляет собой таблицу, которая помогает вычислить значение синусов, косинусов, тангенсов и котангенсов углов с точностью до одной минуты без калькулятора.
Таблица, которая поможет с расчетами при решении задач в школе (математика, алгебра, геометрия и физика в старших классах) и вузах. На этой странице четырехзначные онлайн математические знаки для синусов, косинусов, тангенсов и котангенсов. Пользоваться таблицами просто.
Как бы ни совершенствовалась вычислительная техника, определение синусов, косинусов, тангенсов и котангенсов с помощью таблицы Bradis всегда будет актуальным.
Таблица Брадиса создана выдающимся учителем-математиком Владимиром Модестовичем Брадисом. Чтобы научиться пользоваться таблицами Bradis, представленными ниже, мы предлагаем вам сначала ознакомиться с инструкцией.
Как пользоваться столом Брадис?
Пример: Найти синус девяносто градусов. Все что относится к синусу вверху и слева к косинусам внизу и справа. Слева найдите угол 90 градусов. И смотрим результат: 1. Те числа, что вверху и внизу таблицы (со штрихами: ‘) это минуты .
В таблице Брадиса указаны значения углов, кратные 6 минутам. Если вы хотите найти значения синуса, косинуса, тангенса или котангенса угла, которого нет в таблице Брадиса, вам следует выбрать наиболее близкое к нему значение. И добавить (вычесть) поправку к проекту, соответствующую разнице, которая может быть равна 1′, 2′, 3′.
Пример:
Таблица Брадиса для синуса и косинуса
| sin | 0′ | 6′ | 12′ | 18′ | 24′ | 30′ | 36′ | 42′ | 48′ | 54′ | 60′ | потому что | 1′ | 2′ | 3′ |
| 0,0000 | 90° | ||||||||||||||
| 0° | 0,0000 | 0017 | 0035 | 0052 | 0070 | 0087 | 0105 | 0122 | 0140 | 0157 | 0175 | 89° | 3 | 6 | 9 |
| 1° | 0175 | 0192 | 0209 | 0227 | 0244 | 0262 | 0279 | 0297 | 0314 | 0332 | 0349 | 88° | 3 | 6 | 9 |
| 2° | 0349 | 0366 | 0384 | 0401 | 0419 | Номер 0436 | 0454 | 0471 | 0488 | 0506 | 0523 | 87° | 3 | 6 | 9 |
| 3° | 0523 | 0541 | 0558 | 0576 | 0593 | 0610 | 0628 | 0645 | 0663 | 0680 | 0698 | 86° | 3 | 6 | 9 |
| 4° | 0698 | 0715 | 0732 | 0750 | 0767 | 0785 | 0802 | 0819 | 0837 | 0854 | 0,0872 | 85° | 3 | 6 | 9 |
| 5° | 0,0872 | 0889 | 0906 | 0924 | 0941 | 0958 | 0976 | 0993 | 1011 | 1028 | 1045 | 84° | 3 | 6 | 9 |
| 6° | 1045 | 1063 | 1080 | 1097 | 1115 | 1132 | 1149 | 1167 | 1184 | 1201 | 1219 | 83° | 3 | 6 | 9 |
| 7° | 1219 | 1236 | 1253 | 1271 | 1288 | 1305 | 1323 | 1340 | 1357 | 1374 | 1392 | 82° | 3 | 6 | 9 |
| 8° | 1392 | 1409 | 1426 | 1444 | 1461 | 1478 | 1495 | 1513 | 1530 | 1547 | 1564 | 81° | 3 | 6 | 9 |
| 9° | 1564 | 1582 | 1599 | 1616 | 1633 | 1650 | 1668 | 1685 | 1702 | 1719 | 0,1736 | 80° | 3 | 6 | 9 |
| 10° | 0,1736 | 1754 | 1771 | 1788 | 1805 | 1822 | 1840 | 1857 | 1874 | 1891 | 1908 | 79° | 3 | 6 | 9 |
| 11° | 1908 | 1925 | 1942 | 1959 | 1977 | 1994 | 2011 | 2028 | 2045 | 2062 | 2079 | 78° | 3 | 6 | 9 |
| 12° | 2079 | 2096 | 2113 | 2130 | 2147 | 2164 | 2181 | 2198 | 2215 | 2233 | 2250 | 77° | 3 | 6 | 9 |
| 13° | 2250 | 2267 | 2284 | 2300 | 2317 | 2334 | 2351 | 2368 | 2385 | 2402 | 2419 | 76° | 3 | 6 | 8 |
| 14° | 2419 | 2436 | 2453 | 2470 | 2487 | 2504 | 2521 | 2538 | 2554 | 2571 | 0,2588 | 75° | 3 | 6 | 8 |
| 15° | 0,2588 | 2605 | 2622 | 2639 | 2656 | 2672 | 2689 | 2706 | 2723 | 2740 | 2756 | 74° | 3 | 6 | 8 |
| 16° | 2756 | 2773 | 2790 | 2807 | 2823 | 2840 | 2857 | 2874 | 2890 | 2907 | 2924 | 73° | 3 | 6 | 8 |
| 17° | 2924 | 2940 | 2957 | 2974 | 2990 | 3007 | 3024 | 3040 | 3057 | 3074 | 3090 | 72° | 3 | 6 | 8 |
| 18° | 3090 | 3107 | 3123 | 3140 | 3156 | 3173 | 3190 | 3206 | 3223 | 3239 | 3256 | 71° | 3 | 6 | 8 |
| 19° | 3256 | 3272 | 3289 | 3305 | 3322 | 3338 | 3355 | 3371 | 3387 | 3404 | 0,3420 | 70° | 3 | 5 | 8 |
| 20° | 0,3420 | 3437 | 3453 | 3469 | 3486 | 3502 | 3518 | 3535 | 3551 | 3567 | 3584 | 69° | 3 | 5 | 8 |
| 21° | 3584 | 3600 | 3616 | 3633 | 3649 | 3665 | 3681 | 3697 | 3714 | 3730 | 3746 | 68° | 3 | 5 | 8 |
| 22° | 3746 | 3762 | 3778 | 3795 | 3811 | 3827 | 3843 | 3859 | 3875 | 3891 | 3907 | 67° | 3 | 5 | 8 |
| 23° | 3907 | 3923 | 3939 | 3955 | 3971 | 3987 | 4003 | 4019 | 4035 | 4051 | 4067 | 66° | 3 | 5 | 8 |
| 24° | 4067 | 4083 | 4099 | 4115 | 4131 | 4147 | 4163 | 4179 | 4195 | 4210 | 0,4226 | 65° | 3 | 5 | 8 |
| 25° | 0,4226 | 4242 | 4258 | 4274 | 4289 | 4305 | 4321 | 4337 | 4352 | 4368 | 4384 | 64° | 3 | 5 | 8 |
| 26° | 4384 | 4399 | 4415 | 4431 | 4446 | 4462 | 4478 | 4493 | 4509 | 4524 | 4540 | 63° | 3 | 5 | 8 |
| 27° | 4540 | 4555 | 4571 | 4586 | 4602 | 4617 | 4633 | 4648 | 4664 | 4679 | 4695 | 62° | 3 | 5 | 8 |
| 28° | 4695 | 4710 | 4726 | 4741 | 4756 | 4772 | 4787 | 4802 | 4818 | 4833 | 4848 | 61° | 3 | 5 | 8 |
| 29° | 4848 | 4863 | 4879 | 4894 | 4909 | 4924 | 4939 | 4955 | 4970 | 4985 | 0,5000 | 60° | 3 | 5 | 8 |
| 30° | 0,5000 | 5015 | 5030 | 5045 | 5060 | 5075 | 5090 | 5105 | 5120 | 5135 | 5150 | 59° | 3 | 5 | 8 |
| 31° | 5150 | 5165 | 5180 | 5195 | 5210 | 5225 | 5240 | 5255 | 5270 | 5284 | 5299 | 58° | 2 | 5 | 7 |
| 32° | 5299 | 5314 | 5329 | 5344 | 5358 | 5373 | 5388 | 5402 | 5417 | 5432 | 5446 | 57° | 2 | 5 | 7 |
| 33° | 5446 | 5461 | 5476 | 5490 | 5505 | 5519 | 5534 | 5548 | 5563 | 5577 | 5592 | 56° | 2 | 5 | 7 |
| 34° | 5592 | 5606 | 5621 | 5635 | 5650 | 5664 | 5678 | 5693 | 5707 | 5721 | 0,5736 | 55° | 2 | 5 | 7 |
| 35° | 0,5736 | 5750 | 5764 | 5779 | 5793 | 5807 | 5821 | 5835 | 5850 | 5864 | 0,5878 | 54° | 2 | 5 | 7 |
| 36° | 5878 | 5892 | 5906 | 5920 | 5934 | 5948 | 5962 | 5976 | 5990 | 6004 | 6018 | 53° | 2 | 5 | 7 |
| 37° | 6018 | 6032 | 6046 | 6060 | 6074 | 6088 | 6101 | 6115 | 6129 | 6143 | 6157 | 52° | 2 | 5 | 7 |
| 38° | 6157 | 6170 | 6184 | 6198 | 6211 | 6225 | 6239 | 6252 | 6266 | 6280 | 6293 | 51° | 2 | 5 | 7 |
| 39° | 6293 | 6307 | 6320 | 6334 | 6347 | 6361 | 6374 | 6388 | 6401 | 6414 | 0,6428 | 50° | 2 | 4 | 7 |
| 40° | 0,6428 | 6441 | 6455 | 6468 | 6481 | 6494 | 6508 | 6521 | 6534 | 6547 | 6561 | 49° | 2 | 4 | 7 |
| 41° | 6561 | 6574 | 6587 | 6600 | 6613 | 6626 | 6639 | 6652 | 6665 | 6678 | 6691 | 48° | 2 | 4 | 7 |
| 42° | 6691 | 6704 | 6717 | 6730 | 6743 | 6756 | 6769 | 6782 | 6794 | 6807 | 6820 | 47° | 2 | 4 | 6 |
| 43° | 6820 | 6833 | 6845 | 6858 | 6871 | 6884 | 6896 | 8909 | 6921 | 6934 | 6947 | 46° | 2 | 4 | 6 |
| 44° | 6947 | 6959 | 6972 | 6984 | 6997 | 7009 | 7022 | 7034 | 7046 | 7059 | 0,7071 | 45° | 2 | 4 | 6 |
| 45° | 0,7071 | 7083 | 7096 | 7108 | 7120 | 7133 | 7145 | 7157 | 7169 | 7181 | 7193 | 44° | 2 | 4 | 6 |
| 46° | 7193 | 7206 | 7218 | 7230 | 7242 | 7254 | 7266 | 7278 | 7290 | 7302 | 7314 | 43° | 2 | 4 | 6 |
| 47° | 7314 | 7325 | 7337 | 7349 | 7361 | 7373 | 7385 | 7396 | 7408 | 7420 | 7431 | 42° | 2 | 4 | 6 |
| 48° | 7431 | 7443 | 7455 | 7466 | 7478 | 7490 | 7501 | 7513 | 7524 | 7536 | 7547 | 41° | 2 | 4 | 6 |
| 49° | 7547 | 7559 | 7570 | 7581 | 7593 | 7604 | 7615 | 7627 | 7638 | 7649 | 0,7660 | 40° | 2 | 4 | 6 |
| 50° | 0,7660 | 7672 | 7683 | 7694 | 7705 | 7716 | 7727 | 7738 | 7749 | 7760 | 7771 | 39° | 2 | 4 | 6 |
| 51° | 7771 | 7782 | 7793 | 7804 | 7815 | 7826 | 7837 | 7848 | 7859 | 7869 | 7880 | 38° | 2 | 4 | 5 |
| 52° | 7880 | 7891 | 7902 | 7912 | 7923 | 7934 | 7944 | 7955 | 7965 | 7976 | 7986 | 37° | 2 | 4 | 5 |
| 53° | 7986 | 7997 | 8007 | 8018 | 8028 | 8039 | 8049 | 8059 | 8070 | 8080 | 8090 | 36° | 2 | 3 | 5 |
| 54° | 8090 | 8100 | 8111 | 8121 | 8131 | 8141 | 8151 | 8161 | 8171 | 8181 | 0,8192 | 35° | 2 | 3 | 5 |
| 55° | 0,8192 | 8202 | 8211 | 8221 | 8231 | 8241 | 8251 | 8261 | 8271 | 8281 | 8290 | 34° | 2 | 3 | 5 |
| 56° | 8290 | 8300 | 8310 | 8320 | 8329 | 8339 | 8348 | 8358 | 8368 | 8377 | 8387 | 33° | 2 | 3 | 5 |
| 57° | 8387 | 8396 | 8406 | 8415 | 8425 | 8434 | 8443 | 8453 | 8462 | 8471 | 8480 | 32° | 2 | 3 | 5 |
| 58° | 8480 | 8490 | 8499 | 8508 | 8517 | 8526 | 8536 | 8545 | 8554 | 8563 | 8572 | 31° | 2 | 3 | 5 |
| 59° | 8572 | 8581 | 8590 | 8599 | 8607 | 8616 | 8625 | 8634 | 8643 | 8652 | 0,8660 | 30° | 1 | 3 | 4 |
| 60° | 0,8660 | 8669 | 8678 | 8686 | 8695 | 8704 | 8712 | 8721 | 8729 | 8738 | 8746 | 29° | 1 | 3 | 4 |
| 61° | 8746 | 8755 | 8763 | 8771 | 8780 | 8788 | 8796 | 8805 | 8813 | 8821 | 8829 | 28° | 1 | 3 | 4 |
| 62° | 8829 | 8838 | 8846 | 8854 | 8862 | 8870 | 8878 | 8886 | 8894 | 8902 | 8910 | 27° | 1 | 3 | 4 |
| 63° | 8910 | 8918 | 8926 | 8934 | 8942 | 8949 | 8957 | 8965 | 8973 | 8980 | 8988 | 26° | 1 | 3 | 4 |
| 64° | 8988 | 8996 | 9003 | 9011 | 9018 | 9026 | 9033 | 9041 | 9048 | 9056 | 0,9063 | 25° | 1 | 3 | 4 |
| 65° | 0,9063 | 9070 | 9078 | 9085 | 9092 | 9100 | 9107 | 9114 | 9121 | 9128 | 9135 | 24° | 1 | 2 | 4 |
| 66° | 9135 | 9143 | 9150 | 9157 | 9164 | 9171 | 9178 | 9184 | 9191 | 9198 | 9205 | 23° | 1 | 2 | 3 |
| 67° | 9205 | 9212 | 9219 | 9225 | 9232 | 9239 | 9245 | 9252 | 9259 | 9256 | 9272 | 22° | 1 | 2 | 3 |
| 68° | 9272 | 9278 | 9285 | 9291 | 9298 | 9304 | 9311 | 9317 | 9323 | 9330 | 9336 | 21° | 1 | 2 | 3 |
| 69° | 9336 | 9342 | 9348 | 9354 | 9361 | 9367 | 9373 | 9379 | 9383 | 9391 | 0,9397 | 20° | 1 | 2 | 3 |
| 70° | 9397 | 9403 | 9409 | 9415 | 9421 | 9426 | 9432 | 9438 | 9444 | 9449 | 0,9455 | 19° | 1 | 2 | 3 |
| 71° | 9455 | 9461 | 9466 | 9472 | 9478 | 9483 | 9489 | 9494 | 9500 | 9505 | 9511 | 18° | 1 | 2 | 3 |
| 72° | 9511 | 9516 | 9521 | 9527 | 9532 | 9537 | 9542 | 9548 | 9553 | 9558 | 9563 | 17° | 1 | 2 | 3 |
| 73° | 9563 | 9568 | 9573 | 9578 | 9583 | 9588 | 9593 | 9598 | 9603 | 9608 | 9613 | 16° | 1 | 2 | 2 |
| 74° | 9613 | 9617 | 9622 | 9627 | 9632 | 9636 | 9641 | 9646 | 9650 | 9655 | 0,9659 | 15° | 1 | 2 | 2 |
| 75° | 9659 | 9664 | 9668 | 9673 | 9677 | 9681 | 9686 | 9690 | 9694 | 9699 | 9703 | 14° | 1 | 1 | 2 |
| 76° | 9703 | 9707 | 9711 | 9715 | 9720 | 9724 | 9728 | 9732 | 9736 | 9740 | 9744 | 13° | 1 | 1 | 2 |
| 77° | 9744 | 9748 | 9751 | 9755 | 9759 | 9763 | 9767 | 9770 | 9774 | 9778 | 9781 | 12° | 1 | 1 | 2 |
| 78° | 9781 | 9785 | 9789 | 9792 | 9796 | 9799 | 9803 | 9806 | 9810 | 9813 | 9816 | 11° | 1 | 1 | 2 |
| 79° | 9816 | 9820 | 9823 | 9826 | 9829 | 9833 | 9836 | 9839 | 9842 | 9845 | 0,9848 | 10° | 1 | 1 | 2 |
| 80° | 0,9848 | 9851 | 9854 | 9857 | 9860 | 9863 | 9866 | 9869 | 9871 | 9874 | 9877 | 9° | 0 | 1 | 1 |
| 81° | 9877 | 9880 | 9882 | 9885 | 9888 | 9890 | 9893 | 9895 | 9898 | 9900 | 9903 | 8° | 0 | 1 | 1 |
| 82° | 9903 | 9905 | 9907 | 9910 | 9912 | 9914 | 9917 | 9919 | 9921 | 9923 | 9925 | 7° | 0 | 1 | 1 |
| 83° | 9925 | 9928 | 9930 | 9932 | 9934 | 9936 | 9938 | 9940 | 9942 | 9943 | 9945 | 6° | 0 | 1 | 1 |
| 84° | 9945 | 9947 | 9949 | 9951 | 9952 | 9954 | 9956 | 9957 | 9959 | 9960 | 9962 | 5° | 0 | 1 | 1 |
| 85° | 9962 | 9963 | 9965 | 9966 | 9968 | 9969 | 9971 | 9972 | 9973 | 9974 | 9976 | 4° | 0 | 0 | 1 |
| 86° | 9976 | 9977 | 9978 | 9979 | 9980 | 9981 | 9982 | 9983 | 9984 | 9985 | 9986 | 3° | 0 | 0 | 0 |
| 87° | 9986 | 9987 | 9988 | 9989 | 9990 | 9990 | 9991 | 9992 | 9993 | 9993 | 9994 | 2° | 0 | 0 | 0 |
| 88° | 9994 | 9995 | 9995 | 9996 | 9996 | 9997 | 9997 | 9997 | 9998 | 9998 | 0,9998 | 1° | 0 | 0 | 0 |
| 89° | 9998 | 9999 | 9999 | 9999 | 9999 | 1. 0000 0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 0° | 0 | 0 | 0 |
| 90° | 1.0000 | ||||||||||||||
| грех | 60′ | 54′ | 48′ | 42′ | 36′ | 30′ | 24′ | 18′ | 12′ | 6′ | 0′ | потому что | 1′ | 2′ | 3′ |
Таблица Брадиса для тангенсов и котангенсов
Тангенс угла x — отношение противолежащего катета к прилежащему:
Котангенс угла х — отношение прилежащего катета к противолежащему:
Тангенс угла — отношение дальний угол к середине. Котангенс угла равен противному.
| тг | 0′ | 6′ | 12′ | 18′ | 24′ | 30′ | 36′ | 42′ | 48′ | 54′ | 60′ | КТГ | 1′ | 2′ | 3′ |
| 0 | 90° | ||||||||||||||
| 0° | 0,000 | 0017 | 0035 | 0052 | 0070 | 0087 | 0105 | 0122 | 0140 | 0157 | 0175 | 89° | 3 | 6 | 9 |
| 1° | 0175 | 0192 | 0209 | 0227 | 0244 | 0262 | 0279 | 0297 | 0314 | 0332 | 0349 | 88° | 3 | 6 | 9 |
| 2° | 0349 | 0367 | 0384 | 0402 | 0419 | 0437 | 0454 | 0472 | 0489 | 0507 | 0524 | 87° | 3 | 6 | 9 |
| 3° | 0524 | 0542 | 0559 | 0577 | 0594 | 0612 | 0629 | 0647 | 0664 | 0682 | 0699 | 86° | 3 | 6 | 9 |
| 4° | 0699 | 0717 | 0734 | 0752 | 0769 | 0787 | 0805 | 0822 | 0840 | 0857 | 0,0875 | 85° | 3 | 6 | 9 |
| 5° | 0,0875 | 0892 | 0910 | 0928 | 0945 | 0963 | 0981 | 0998 | 1016 | 1033 | 1051 | 84° | 3 | 6 | 9 |
| 6° | 1051 | 1069 | 1086 | 1104 | 1122 | 1139 | 1157 | 1175 | 1192 | 1210 | 1228 | 83° | 3 | 6 | 9 |
| 7° | 1228 | 1246 | 1263 | 1281 | 1299 | 1317 | 1334 | 1352 | 1370 | 1388 | 1405 | 82° | 3 | 6 | 9 |
| 8° | 1405 | 1423 | 1441 | 1459 | 1477 | 1495 | 1512 | 1530 | 1548 | 1566 | 1584 | 81° | 3 | 6 | 9 |
| 9° | 1584 | 1602 | 1620 | 1638 | 1655 | 1673 | 1691 | 1709 | 1727 | 1745 | 0,1763 | 80° | 3 | 6 | 9 |
| 10° | 0,1763 | 1781 | 1799 | 1817 | 1835 | 1853 | 1871 | 1890 | 1908 | 1926 | 1944 | 79° | 3 | 6 | 9 |
| 11° | 1944 | 1962 | 1980 | 1998 | 2016 | 2035 | 2053 | 2071 | 2089 | 2107 | 2126 | 78° | 3 | 6 | 9 |
| 12° | 2126 | 2144 | 2162 | 2180 | 2199 | 2217 | 2235 | 2254 | 2272 | 2290 | 2309 | 77° | 3 | 6 | 9 |
| 13° | 2309 | 2327 | 2345 | 2364 | 2382 | 2401 | 2419 | 2438 | 2456 | 2475 | 2493 | 76° | 3 | 6 | 9 |
| 14° | 2493 | 2512 | 2530 | 2549 | 2568 | 2586 | 2605 | 2623 | 2642 | 2661 | 0,2679 | 75° | 3 | 6 | 9 |
| 15° | 0,2679 | 2698 | 2717 | 2736 | 2754 | 2773 | 2792 | 2811 | 2830 | 2849 | 2867 | 74° | 3 | 6 | 9 |
| 16° | 2867 | 2886 | 2905 | 2924 | 2943 | 2962 | 2981 | 3000 | 3019 | 3038 | 3057 | 73° | 3 | 6 | 9 |
| 17° | 3057 | 3076 | 3096 | 3115 | 3134 | 3153 | 3172 | 3191 | 3211 | 3230 | 3249 | 72° | 3 | 6 | 10 |
| 18° | 3249 | 3269 | 3288 | 3307 | 3327 | 3346 | 3365 | 3385 | 3404 | 3424 | 3443 | 71° | 3 | 6 | 10 |
| 19° | 3443 | 3463 | 3482 | 3502 | 3522 | 3541 | 3561 | 3581 | 3600 | 3620 | 0,3640 | 70° | 3 | 7 | 10 |
| 20° | 0,3640 | 3659 | 3679 | 3699 | 3719 | 3739 | 3759 | 3779 | 3799 | 3819 | 3839 | 69° | 3 | 7 | 10 |
| 21° | 3839 | 3859 | 3879 | 3899 | 3919 | 3939 | 3959 | 3979 | 4000 | 4020 | 4040 | 68° | 3 | 7 | 10 |
| 22° | 4040 | 4061 | 4081 | 4101 | 4122 | 4142 | 4163 | 4183 | 4204 | 4224 | 4245 | 67° | 3 | 7 | 10 |
| 23° | 4245 | 4265 | 4286 | 4307 | 4327 | 4348 | 4369 | 4390 | 4411 | 4431 | 4452 | 66° | 3 | 7 | 10 |
| 24° | 4452 | 4473 | 4494 | 4515 | 4536 | 4557 | 4578 | 4599 | 4621 | 4642 | 0,4663 | 65° | 4 | 7 | 11 |
| 25° | 0,4663 | 4684 | 4706 | 4727 | 4748 | 4770 | 4791 | 4813 | 4834 | 4856 | 4877 | 64° | 4 | 7 | 11 |
| 26° | 4877 | 4899 | 4921 | 4942 | 4964 | 4986 | 5008 | 5029 | 5051 | 5073 | 5095 | 63° | 4 | 7 | 11 |
| 27° | 5095 | 5117 | 5139 | 5161 | 5184 | 5206 | 5228 | 5250 | 5272 | 5295 | 5317 | 62° | 4 | 7 | 11 |
| 28° | 5317 | 5340 | 5362 | 5384 | 5407 | 5430 | 5452 | 5475 | 5498 | 5520 | 5543 | 61° | 4 | 8 | 11 |
| 29° | 5543 | 5566 | 5589 | 5612 | 5635 | 5658 | 5681 | 5704 | 5727 | 5750 | 0,5774 | 60° | 4 | 8 | 12 |
| 30° | 0,5774 | 5797 | 5820 | 5844 | 5867 | 5890 | 5914 | 5938 | 5961 | 5985 | 6009 | 59° | 4 | 8 | 12 |
| 31° | 6009 | 6032 | 6056 | 6080 | 6104 | 6128 | 6152 | 6176 | 6200 | 6224 | 6249 | 58° | 4 | 8 | 12 |
| 32° | 6249 | 6273 | 6297 | 6322 | 6346 | 6371 | 6395 | 6420 | 6445 | 6469 | 6494 | 57° | 4 | 8 | 12 |
| 33° | 6494 | 6519 | 6544 | 6569 | 6594 | 6619 | 6644 | 6669 | 6694 | 6720 | 6745 | 56° | 4 | 8 | 13 |
| 34° | 6745 | 6771 | 6796 | 6822 | 6847 | 6873 | 6899 | 6924 | 6950 | 6976 | 0,7002 | 55° | 4 | 9 | 13 |
| 35° | 0,7002 | 7028 | 7054 | 7080 | 7107 | 7133 | 7159 | 7186 | 7212 | 7239 | 7265 | 54° | 4 | 8 | 13 |
| 36° | 7265 | 7292 | 7319 | 7346 | 7373 | 7400 | 7427 | 7454 | 7481 | 7508 | 7536 | 53° | 5 | 9 | 14° |
| 37° | 7536 | 7563 | 7590 | 7618 | 7646 | 7673 | 7701 | 7729 | 7757 | 7785 | 7813 | 52° | 5 | 9 | 14 |
| 38° | 7813 | 7841 | 7869 | 7898 | 7926 | 7954 | Из 7983 | 8012 | 8040 | 8069 | 8098 | 51° | 5 | 9 | 14 |
| 39° | 8098 | 8127 | 8156 | 8185 | 8214 | 8243 | 8273 | 8302 | 8332 | 8361 | 0,8391 | 50° | 5 | 10 | 15 |
| 40° | 0,8391 | 8421 | 8451 | 8481 | 8511 | 8541 | 8571 | 8601 | 8632 | 8662 | 0,8693 | 49° | 5 | 10 | 15 |
| 41° | 8693 | 8724 | 8754 | 8785 | 8816 | 8847 | 8878 | 8910 | 8941 | 8972 | 9004 | 48° | 5 | 10 | 16 |
| 42° | 9004 | 9036 | 9067 | 9099 | 9131 | 9163 | 9195 | 9228 | 9260 | 9293 | 9325 | 47° | 6 | 11 | 16 |
| 43° | 9325 | 9358 | 9391 | 9424 | 9457 | 9490 | 9523 | 9556 | 9590 | 9623 | 0,9657 | 46° | 6 | 11 | 17 |
| 44° | 9657 | 9691 | 9725 | 9759 | 9793 | 9827 | 9861 | 9896 | 9930 | 9965 | 10000 | 45° | 6 | 11 | 17 |
| 45° | 10000 | 0035 | 0070 | 0105 | 0141 | 0176 | 0212 | 0247 | 0283 | 0319 | 0355 | 44° | 6 | 12 | 18 |
| 46° | 0355 | 0392 | 0428 | 0464 | 0501 | 0538 | 0575 | 0612 | 0649 | 0686 | 0724 | 43° | 6 | 12 | 18 |
| 47° | 0724 | 0761 | 0799 | 0837 | 0875 | 0913 | 0951 | 0990 | 1028 | 1067 | 1106 | 42° | 6 | 13 | 19 |
| 48° | 1106 | 1145 | 1184 | 1224 | 1263 | 1303 | 1343 | 1383 | 1423 | 1463 | 1504 | 41° | 7 | 13 | 20 |
| 49° | 1504 | 1544 | 1585 | 1626 | 1667 | 1708 | 1750 | 1792 | 1833 | 1875 | 1,1918 | 40° | 7 | 14 | 21 |
| 50° | 1,1918 | 1960 | 2002 | 2045 | 2088 | 2131 | 2174 | 2218 | 2261 | 2305 | 2349 | 39° | 7 | 14 | 22 |
| 51° | 2349 | 2393 | 2437 | 2482 | 2527 | 2572 | 2617 | 2662 | 2708 | 2753 | 2799 | 38° | 8 | 15 | 23 |
| 52° | 2799 | 2846 | 2892 | 2938 | 2985 | 3032 | 3079 | 3127 | 3175 | 3222 | 3270 | 37° | 8 | 16 | 24 |
| 53° | 3270 | 3319 | 3367 | 3416 | 3465 | 3514 | 3564 | 3613 | 3663 | 3713 | 3764 | 36° | 8 | 16 | 25 |
| 54° | 3764 | 3814 | 3865 | 3916 | 3968 | 4019 | 4071 | 4124 | 4176 | 4229 | 1,4281 | 35° | 9 | 17 | 26 |
| 55° | 1,4281 | 4335 | 4388 | 4442 | 4496 | 4550 | 4605 | 4659 | 4715 | 4770 | 4826 | 34° | 9 | 18 | 27 |
| 56° | 4826 | 4882 | 4938 | 4994 | 5051 | 5108 | 5166 | 5224 | Уже 5282 | 5340 | 5399 | 33° | 10 | 19 | 29 |
| 57° | 5399 | 5458 | 5517 | 5577 | 5637 | 5697 | 5757 | 5818 | 5880 | 5941 | 6003 | 32° | 10 | 20 | 30 |
| 58° | 6003 | 6066 | 6128 | 6191 | 6255 | 6319 | 6383 | 6447 | 6512 | 6577 | 6643 | 31° | 11 | 21 | 32 |
| 59° | 6643 | 6709 | 6775 | 6842 | 6909 | 6977 | 7045 | 7113 | 7182 | 7251 | 1,7321 | 30° | 11 | 23 | 34 |
| 60° | 1 732 | 1 739 | 1 746 | 1 753 | 1 760 | 1 767 | 1 775 | 1 782 | 1 789 | 1 797 | 1 804 | 29° | 1 | 2 | 4 |
| 61° | 1 804 | 1 811 | 1 819 | 1 827 | 1 834 | 1 842 | 1 849 | 1 857 | 1 865 | 1 873 | 1 881 | 28° | 1 | 3 | 4 |
| 62° | 1 881 | 1 889 | 1 897 | 1 905 | Б/у 1 913 | 1 921 | 1 929 | 1 937 | 1 946 | 1 954 | 1 963 | 27° | 1 | 3 | 4 |
| 63° | 1 963 | 1 971 | 1 980 | 1 988 | 1 997 | 2 006 | 2 014 | 2 023 | 2 032 | 2 041 | Из 2. 05 05 | 26° | 1 | 3 | 4 |
| 64° | 2 050 | 2 059 | 2069 | 2 078 | 2 087 | 2 097 | 2 106 | 2 116 | 2 125 | 2 135 | 2 145 | 25° | 2 | 3 | 5 |
| 65° | 2 145 | 2 154 | 2 164 | 2 174 | 2 184 | 2 194 | 2 204 | 2 215 | 2 225 | 2 236 | 2 246 | 24° | 2 | 3 | 5 |
| 66° | 2 246 | 2 257 | 2 267 | 2 278 | 2 289 | 2,3 | 2 311 | 2 322 | 2 333 | 2 344 | 2 356 | 23° | 2 | 4 | 5 |
| 67° | 2 356 | 2 367 | 2 379 | 2 391 | 2 402 | 2 414 | 2 426 | 2 438 | 2 450 | 2 463 | 2 475 | 22° | 2 | 4 | 6 |
| 68° | 2 475 | 2 488 | 2,5 | 2 513 | 2 526 | 2 539 | 2 552 | 2 565 | 2 578 | 2,592 | 2 605 | 21° | 2 | 4 | 6 |
| 69° | 2 605 | 2 619 | 2 633 | 2 646 | Из 2,66 | 2 675 | 2 689 | 2 703 | 2 718 | 2 733 | 2 747 | 20° | 2 | 5 | 7 |
| 70° | 2 747 | 2 762 | 2 778 | 2 793 | 2 808 | 2 824 | 2 840 | 2 856 | 2 872 | 2 888 | 2 904 | 19° | 3 | 5 | 8 |
| 71° | 2 904 | 2 921 | 2 937 | 2 954 | 2 971 | 2 989 | 3 006 | 3 024 | 3 042 | 3,06 | 3 078 | 18° | 3 | 6 | 9 |
| 72° | 3 078 | 3 096 | 3 115 | 3 133 | 3 152 | 3 172 | 3 191 | 3 211 | 3 230 | 3 251 | 3 271 | 17° | 3 | 6 | 10 |
| 73° | 3 271 | 3 291 | 3 312 | 3 333 | 3 354 | 3 376 | 3 398 | 3. 42 42 | 3 442 | 3 465 | 3 487 | 16° | 4 | 7 | 11 |
| 74° | 3 487 | 3 511 | 3 534 | 3 558 | 3 582 | До 3.606 | 3 630 | 3 655 | 3 681 | 3 706 | 3 732 | 15° | 4 | 8 | 13 |
| 75° | 3 732 | 3 758 | 3 785 | 3 812 | 3 839 | 3 867 | 3 895 | 3 923 | 3 952 | 3 981 | 4 011 | 14° | 5 | 10 | 14 |
| тг | 60′ | 54′ | 48′ | 42′ | 36′ | 30′ | 24′ | 18′ | 12′ | 6′ | 0′ | КТГ | 1′ | 2′ | 3′ |
Краткий курс Дейва по тригонометрии
Краткий курс Дэйва по тригонометрииСодержание
- Кому следует пройти этот курс?
- Тригонометрия для вас
- Ваш фон
- Как выучить тригонометрию
- Применение тригонометрии
- Астрономия и география
- Инженерия и физика
- Математика и ее приложения
- Что такое тригонометрия?
- Тригонометрия как вычислительная геометрия
- Угловые измерения и таблицы
- Измерение угла
- Понятие угла
- Радианы и длина дуги
- Упражнения, советы и ответы
- О разрядах точности
- Аккорды
- Что такое аккорд?
- Тригонометрия началась с аккордов
- Синус
- Связь между синусом и хордой
- Слово «синус»
- Синусы и прямоугольные треугольники
- Стандартное обозначение прямоугольного треугольника
- Упражнения, советы и ответы
- Косинусы
- Определение косинуса
- Прямоугольные треугольники и косинусы
- Тождество Пифагора для синусов и косинусов
- Синусы и косинусы для особых общих углов
- Упражнения, советы и ответы
- Касательные и наклон
- Определение касательной
- Тангенс относительно синуса и косинуса
- Касательные и прямоугольные треугольники
- уклоны линий
- Углы возвышения и депрессии
- Опять общие углы
- Упражнения, советы и ответы
- Тригонометрия прямоугольных треугольников
- Решение прямоугольных треугольников
- Обратные триггерные функции: арксинус, арккосинус и арктангенс
- Остальные три тригонометрические функции: котангенс, секанс и косеканс
- Упражнения, советы и ответы
- Пифагоровы тройки
- Тригонометрические функции и их обратные
- Произвольные углы и единичная окружность
- Синусы и косинусы произвольных углов
- Свойства синусов и косинусов, следующие из определения
- Графики функций синуса и косинуса
- Графики функций тангенса и котангенса
- Графики функций секанса и косеканса
- Тригонометрия косоугольных треугольников
- Решение косоугольных треугольников
- Закон косинусов
- Закон синусов
- Упражнения, советы и ответы
- Резюме тригонометрических тождеств
- Более важные личности
- Менее важные личности
- Действительно неясные личности
Примечание. Если ваш браузер поддерживает Java, вы можете перетаскивать точки на диаграммах, и диаграмма настраивается сама собой.
Свободные точки, окрашенные в красный цвет, можно свободно перетаскивать, и по мере их перемещения остальная часть диаграммы (кроме других свободных точек)
подстроится соответствующим образом. Скользящие точки, окрашенные в оранжевый цвет, можно перетаскивать
примерно как свободные точки, за исключением того, что их движение ограничено либо прямой
линия или круг, в зависимости от точки.
Если вы перетащите точку поворота, окрашенную в зеленый цвет,
вся диаграмма будет переведена вместе с ней.
Другие точки также можно перетаскивать, если отображается точка поворота, и
диаграмма будет повернута и расширена вокруг точки поворота.
Кроме того, если вы наберете r или клавишу пробела , пока курсор находится над диаграммой, тогда диаграмма будет сброшена к исходной конфигурации. Если вы наберете u или вернете , цифра будет поднята со страницы в отдельное окно.
Если ваш браузер поддерживает Java, вы можете перетаскивать точки на диаграммах, и диаграмма настраивается сама собой.
Свободные точки, окрашенные в красный цвет, можно свободно перетаскивать, и по мере их перемещения остальная часть диаграммы (кроме других свободных точек)
подстроится соответствующим образом. Скользящие точки, окрашенные в оранжевый цвет, можно перетаскивать
примерно как свободные точки, за исключением того, что их движение ограничено либо прямой
линия или круг, в зависимости от точки.
Если вы перетащите точку поворота, окрашенную в зеленый цвет,
вся диаграмма будет переведена вместе с ней.
Другие точки также можно перетаскивать, если отображается точка поворота, и
диаграмма будет повернута и расширена вокруг точки поворота.
Кроме того, если вы наберете r или клавишу пробела , пока курсор находится над диаграммой, тогда диаграмма будет сброшена к исходной конфигурации. Если вы наберете u или вернете , цифра будет поднята со страницы в отдельное окно. Ввод d или возврат , когда курсор находится над окном, вернет диаграмму на страницу. Обратите внимание, что вы можете изменить размер плавающего окна, чтобы сделать диаграмму больше.
Ввод d или возврат , когда курсор находится над окном, вернет диаграмму на страницу. Обратите внимание, что вы можете изменить размер плавающего окна, чтобы сделать диаграмму больше.
Здесь используются специальные символы. : Некоторые старые веб-браузеры не отображают математические символы. В следующей таблице показаны математические символы, используемые здесь. Если в первом столбце есть какие-либо записи, которые кажутся пустыми или отображаются в виде вопросительных знаков, тогда ваш веб-браузер не будет отображать эти символы, и вам нужно будет использовать другой веб-браузер, чтобы увидеть все символы.
| Символ | Описание | Пример |
|---|---|---|
| минус | x y | |
| ± | plus or minus sign | x ± y |
| ° | degree sign | 45° |
| √ | square root sign | √2 |
| 3 √ | cube root sign | 3 √5 |
| ≠ | not equal to | x ≠ y |
| ≤ | less than or equal to | x ≤ y |
| ≥ | greater than or equal to | x ≥ y |
Начат в июле 1996 г. Авторские права © 1996, 1997.
Авторские права © 1996, 1997.
Дэвид Э. Джойс
Кафедра математики и информатики
Университет Кларка
Вустер, Массачусетс, 01610
Электронная почта: [email protected]
Краткий триггерный курс Дэйва находится по адресу http://aleph0.clarku.edu/~djoyce/java/trig.
Тригонометрические функции
Тригонометрические функции — это функции, связанные с углом. Существует шесть тригонометрических функций: синус, косинус, тангенс и их обратные косеканс, секанс и котангенс соответственно. Синус, косинус и тангенс являются наиболее широко используемыми тригонометрическими функциями. Их обратные числа, хотя и используются, менее распространены в современной математике. Тригонометрические функции также называют круговыми функциями.
Обычно тригонометрические функции обсуждаются двумя основными способами: в терминах прямоугольных треугольников и в терминах единичной окружности. Чаще всего вводится определение тригонометрических функций в виде прямоугольного треугольника, за которым следуют их определения в терминах единичной окружности.
Определение прямоугольного треугольника
Выход тригонометрической функции представляет собой отношение длин двух сторон прямоугольного треугольника. Рассмотрим угол θ как один из углов прямоугольного треугольника. Ниже приведены определения тригонометрических функций. Эти функции часто записываются в сокращенной форме.
| sine: | |
| cosine: | |
| tangent: |
| cosecant: | |
| secant: | |
| cotangent: |
Термины, используемые для описания сторон прямоугольного треугольника, — это гипотенуза, прилежащая сторона и противоположная сторона, как показано на рисунке выше.
- Смежный: сторона рядом с θ, которая не является гипотенузой
- Напротив: сторона, противоположная θ.

- Гипотенуза: самая длинная сторона треугольника, лежащая напротив прямого угла.
Обычный метод запоминания вышеупомянутых взаимосвязей — использование мнемонического выражения «soh cah toa». Буквы s, c и t обозначают синус, косинус и тангенс, а o, a и h обозначают противоположное, смежное и гипотенузу.
Косеканс, секанс и котангенс являются величинами, обратными синусу, косинусу и тангенсу соответственно. Таким образом, пока мы помним определения синуса, косинуса и тангенса, мы можем взять их обратные значения, чтобы определить определения косеканса, секанса и котангенса.
Пример:
Найдите значения шести тригонометрических величин по прямоугольному треугольнику ниже.
Гипотенуза треугольника равна 10, а прилежащая сторона имеет длину 5. Используя теорему Пифагора, находим длину третьей, противоположной, стороны:
5 2 + b 2 = 10 2
25 + b 2 = 100
b 2 = 75
Теперь, когда мы знаем все стороны треугольника, подставим 60° к углу треугольника. их в тригонометрические функции, как определено выше:
их в тригонометрические функции, как определено выше:
Определение единичной окружности
Тригонометрические функции также могут быть определены как значения координат на единичной окружности. Единичная окружность — это окружность радиусом 1 с центром в начале координат. Определение тригонометрических функций в виде прямоугольного треугольника допускает углы от 0 ° до 90 ° (0 и в радианах). Использование определений единичного круга позволяет нам расширить область применения тригонометрических функций на все действительные числа. См. рисунок ниже.
Имея точку (x, y) на единичной окружности, мы можем сформировать прямоугольный треугольник, как показано на рисунке. В таком треугольнике гипотенуза — это радиус единичной окружности, или 1. θ — это угол, образованный между начальной стороной угла вдоль оси x и конечной стороной угла, образованного вращением луча по часовой стрелке или против часовой стрелки. Конечная сторона угла является гипотенузой прямоугольного треугольника и является радиусом единичной окружности. Поэтому его длина всегда равна 1. Точка, в которой конечная сторона угла пересекает единичную окружность, имеет значение x, равное cos(θ), и значение y, равное sin(θ).
Поэтому его длина всегда равна 1. Точка, в которой конечная сторона угла пересекает единичную окружность, имеет значение x, равное cos(θ), и значение y, равное sin(θ).
Таким образом, на единичной окружности косинус и синус можно определить как:
синуса, косинуса и тангенса соответственно и определяются как:
Значения тригонометрических функций также могут быть представлены длинами отрезков прямых в координатной плоскости с единичным кругом, как показано на рис. диаграмма ниже.
Значения тригонометрических функций для специальных углов
Значения тригонометрических функций можно найти через значения координат пересечений на единичной окружности. Хотя мы можем найти значение любой тригонометрической функции для любого значения θ, есть некоторые углы, которые чаще используются в тригонометрии и их стоит запомнить. Ниже приведен список значений функций синуса, косинуса и тангенса специальных углов в первом квадранте.
Опорный угол
Острые углы в первом квадранте можно использовать для определения значений тригонометрических функций углов в других квадрантах. Эти углы называются опорными углами, поскольку мы будем ссылаться на их значения для определения других значений. Это всегда наименьший угол (относительно оси абсцисс), который можно составить из конечной стороны угла. На рисунках ниже показан угол θ и его исходный угол θ’ в квадранте, отличном от первого квадранта.
| Квадрант II | Квадрант III | Квадрант IV |
|---|---|---|
| θ’= 180° — θ | θ’= θ — 180° | θ’= 360° — θ |
Если один угол является опорным углом другого, то тригонометрические функции этих двух углов имеют одинаковые значения по модулю, и нам нужно только обратить внимание на их знаки исходя из квадранта, в котором лежит крайняя сторона угла , Например, 30° — это опорный угол 210° со значениями синусов sin(30°)= и sin(210°)=. Мы можем видеть, что значения синуса обоих имеют величину , хотя и имеют разные знаки.
Мы можем видеть, что значения синуса обоих имеют величину , хотя и имеют разные знаки.
Ниже приведена таблица, показывающая знаки 6 тригонометрических функций в каждом квадранте.
| Sin | Cos | Tan | Csc | Sec | Cot | |
| Quadrant I | + | + | + | + | + | + |
| Квадрант II | + | — | — | + | — | — |
| Quadrant III | — | — | + | — | — | + |
| Quadrant IV | — | + | — | — | + | — |
Как только мы определили опорный угол, мы можем определить значение тригонометрических функций в любом из других квадрантов, применяя соответствующий знак к их значению для опорного угла.
Пример:
Используйте эталонные углы, чтобы найти значения cos(150°) и sin(315°).
Поскольку 150° находится в квадранте II, исходный угол для 150° равен 180°-150°=30°, где cos(30°)=. Кроме того, поскольку 150 ° находится в квадранте II, косинус отрицателен, тогда cos (150 °) =.
Поскольку 315° находится в квадранте IV, исходный угол для 315° равен 360°-315°=45°, где sin(45)°=. Кроме того, поскольку 315 ° находится в квадранте IV, синус отрицательный, тогда sin (315 °) =.
Тригонометрические функции являются периодическими функциями
Периодическая функция – это функция f, в которой существует некоторое положительное значение p, такое что
f(x+p) = f(x)
для всех x в области f, p является наименьшим положительным число, для которого f является периодическим, и называется периодом f.
Все 6 тригонометрических функций являются периодическими функциями. Независимо от того, с какой точки мы начинаем на единичной окружности, если мы пройдем расстояние 2π (360 °) по единичной окружности от этой точки, мы вернемся в нашу начальную точку, что указывает на то, что тригонометрическая функция имеет то же значение под углом. Это означает, что тригонометрические функции повторяют свои значения.
Это означает, что тригонометрические функции повторяют свои значения.
Функции синуса, косинуса, косеканса и секанса имеют период 2π. Функции тангенса и котангенса имеют период π.
sin(θ+2π) = sin(θ)
cos(θ+2π) = cos (θ)
csc(θ+2π) = csc (θ)
sec(θ+2π) = sec ( θ)
tan(θ+π) = tan (θ)
cot(θ+π) = cot (θ)
Пример:
Найдите cos() и tan(), используя их периоды.
Тригонометрические функции четные или нечетные
Нечетная функция — это функция, в которой -f(x)=f(-x). Он имеет симметрию относительно начала координат. Четная функция — это функция, в которой f(x)=f(-x), что означает, что отображение графика по оси Y даст тот же график. Из 6 тригонометрических функций синус, тангенс, косеканс и котангенс являются нечетными функциями. Косинус и секанс — четные функции. Поэтому:
| Четные функции | Нечетные функции |
|---|---|
| cos(-θ) = cos(θ) сек(-θ) = сек(θ) | sin(-θ) = -sin(θ) tan(-θ) = -tan(θ) csc(-θ) = -csc(θ) кроватка(-θ) = -кроватка (θ) |
Обратные тригонометрические функции
Обратные тригонометрические функции являются обратными функциями тригонометрических функций. В частности, это арксинус, арккосинус, арктангенс, арккосеканс, арксеканс и арктангенс. Входом обратных тригонометрических функций являются тригонометрические отношения угла, а выходом — угол:
В частности, это арксинус, арккосинус, арктангенс, арккосеканс, арксеканс и арктангенс. Входом обратных тригонометрических функций являются тригонометрические отношения угла, а выходом — угол:
θ = arcsin(x), где –1≤x≤1 θ = arccos(x), где –1≤x≤1 θ = арктангенс (х) θ = arccsc(x), где x≤-1 или 1≤x θ = угловая секунда(x), где x≤-1 или 1≤x θ = арктангенс(x) |
Обратные тригонометрические функции также записываются как sin -1 (x), cos -1 (x), tan -1 (x), csc -1 (x) ), сек -1 (x) и раскладушка -1 (x).
Пример:
Учитывая sin(30°) = 0,5, что такое arcsin(0,5)?
arcsin(0.5) = 30°
Примечание: это дает результат только в первом квадранте. Если рассматривать другие квадранты, arcsin(0.5) также равен 150°. Кроме того, поскольку арксинус является периодической функцией, для учета всех возможных значений арксинуса нам необходимо учитывать его периодичность. Таким образом, решение равно
Таким образом, решение равно
30°+n×360° или 150°+n×360°
, где n — целое число. При использовании других обратных тригонометрических функций также необходимо учитывать их периодичность для определения всех решений.
Графики тригонометрических функций
На рисунке ниже показаны графики нескольких периодов шести тригонометрических функций. Обратитесь к страницам синуса, косинуса и тангенса для подробного объяснения того, как построить график тригонометрических функций, подвергшихся определенным преобразованиям (те же объяснения применимы к косекансу, секансу и котангенсу с небольшими отличиями).
Функция котангенса
Функция котангенса — это тригонометрическая функция, одна из трех обратных функций , которые мы рассматриваем на этих страницах, две другие — это функция косеканса и функция секанса . Обратная функция — это функция, которая является обратной (или мультипликативной обратной ) другой функции (см. ниже). Функция котангенса (обычно сокращенно cot ) является обратной функцией функции тангенса . Как и в случае с другими тригонометрическими функциями, используемыми в современном мире, функция котангенса, безусловно, была известна арабским ученым, а таблицы значений котангенса, как известно, существовали к десятому веку нашей эры. Чтобы точно понять, как связаны функция котангенса и функция тангенса, рассмотрим приведенную ниже диаграмму.
ниже). Функция котангенса (обычно сокращенно cot ) является обратной функцией функции тангенса . Как и в случае с другими тригонометрическими функциями, используемыми в современном мире, функция котангенса, безусловно, была известна арабским ученым, а таблицы значений котангенса, как известно, существовали к десятому веку нашей эры. Чтобы точно понять, как связаны функция котангенса и функция тангенса, рассмотрим приведенную ниже диаграмму.
Котангенс как отрезок единичной окружности
Как и другие тригонометрические функции, котангенс может быть представлен в виде отрезка, связанного с единичной окружностью . На диаграмме показан котангенс угла поворота θ от сорока пяти градусов (измерено против часовой стрелки от положительной оси x ). Отрезок AF (показан красным) является котангенсом и лежит на прямой, касательной к окружности в точке 9. 0943 А . Отрезок PF является продолжением отрезка OP (и, кстати, также является секущей ). Помните, что точка P — это точка на окружности единичного круга, чьи координаты x и y представляют значения cos ( θ ) и sin ( θ ) соответственно (отрезки прямой, представляющие синус и косинус также показаны). Помните, что одно из определений функции тангенса — это частное функции синуса и косинуса . Щелкните здесь , чтобы увидеть интерактивную демонстрацию, в которой используется единичный круг, чтобы показать, как функции синуса, косинуса и котангенса соотносятся друг с другом (примечание: чтобы интерактивная страница работала, ваш браузер должен поддерживать Java).
0943 А . Отрезок PF является продолжением отрезка OP (и, кстати, также является секущей ). Помните, что точка P — это точка на окружности единичного круга, чьи координаты x и y представляют значения cos ( θ ) и sin ( θ ) соответственно (отрезки прямой, представляющие синус и косинус также показаны). Помните, что одно из определений функции тангенса — это частное функции синуса и косинуса . Щелкните здесь , чтобы увидеть интерактивную демонстрацию, в которой используется единичный круг, чтобы показать, как функции синуса, косинуса и котангенса соотносятся друг с другом (примечание: чтобы интерактивная страница работала, ваш браузер должен поддерживать Java).
Помните, что функция тангенса может быть определена либо как частное противоположной и смежной, либо как частное функций синуса и косинуса. Если вы еще не вывели этот факт из диаграммы, вы увидите в интерактивной демонстрации, что значение sin ( θ ) приближается к единице , а значение cos ( θ ) приближается к нулю , значение cot ( θ ) также стремится к нулю. Однако при приближении значения sin ( θ ) к нулю и значения cos ( θ ) к единице значение cot ( θ ) стремится к бесконечности. Таким образом, значение кроватки ( θ ), когда cos ( θ ) равно единице, равно undefined . Как упоминалось, тангенс 9Функция 0028 представляет собой частное функций синуса и косинуса. Поскольку функция котангенса является обратной величиной функции тангенса, мы также можем выразить функцию котангенса через функции синуса и косинуса:
Однако при приближении значения sin ( θ ) к нулю и значения cos ( θ ) к единице значение cot ( θ ) стремится к бесконечности. Таким образом, значение кроватки ( θ ), когда cos ( θ ) равно единице, равно undefined . Как упоминалось, тангенс 9Функция 0028 представляет собой частное функций синуса и косинуса. Поскольку функция котангенса является обратной величиной функции тангенса, мы также можем выразить функцию котангенса через функции синуса и косинуса:
| COT ( θ ) = | COS ( θ ) | ||||||||||||||||||||||||||||||||||||||||||||||
| SIN ( θ ) |
| детская кроватка ( θ ) = | 1 | ||||||||||||||||||||||||||||||||||||||||||||||
| желтовато-коричневый ( θ ) | 2
И, наконец, поскольку функции косинуса и синуса представлены координатами x и y соответственно точки P (то есть точки, в которой конечная сторона угла θ пересекает окружность единичной окружности), мы можем также сделать вывод, что:
Мы также можем определить функцию котангенса в терминах прямоугольного треугольника. В треугольнике ABC раскладушка ( θ ) = б / а В прямоугольном треугольнике ABC тангенс угла θ является частным противоположных и смежных (то есть сторон, обозначенных a и b соответственно). Поскольку функция котангенса есть , обратная функции тангенса, то котангенс угла θ будет частным смежных и напротив . Это дает нам:
Для тех, кто интересуется такими вещами, мы использовали Microsoft Excel для создания собственной таблицы значений котангенса для углов в диапазоне от ноль градусов (0°) до триста шестьдесят градусов (360°) с шагом в одну десятую градуса. Если вы изучите таблицу, то увидите, что существует значительный диапазон углов, сосредоточенных вокруг девяносто градусов (90°) и двести семьдесят градусов (270°), для которых значение, возвращаемое функцией котангенса, довольно невелика и изменяется относительно медленно. Для углов близких к ноль градусов (0°), сто восемьдесят градусов (180°) или триста шестьдесят градусов (360°) однако значение, возвращаемое функцией секанса, быстро увеличивается. Этого следовало ожидать, так как значение тангенса ( θ ) очень мало для этих углов, поэтому его обратное будет соответственно большим. На самом деле значение, возвращаемое функцией котангенса для угла в ноль градусов, сто восемьдесят градусов или триста шестьдесят градусов, считается равным 9.0943 undefined , так как уравнение кроватка ( θ ) = 1 / тангенс ( θ ) будет включать деление на ноль. График функции котангенса для углов в диапазоне от 0° до 720° Как и функция тангенса, значения функции котангенса будут варьироваться от нуля до бесконечности (или, точнее, от нуля до очень большого неопределенного значения). Поскольку функция котангенса является обратной функцией тангенса, значение котангенса будет неопределенным, если значение тангенса равно нулю, и нулем, если значение тангенса не определено. Как видно из таблицы значений котангенса и графика функции котангенса, значение котангенса отрицательно для всех углов, для которых синус и косинус имеют разный знак (т.е. в квадранте II и квадранте IV ), и положительный для всех углов, для которых синус и косинус имеют один и тот же знак (т. Если вы читали страницы о тангенсах, косекансах и секансах (или, возможно, даже если не читали), вы знаете, что вертикальные красные линии на графике — это асимптоты . Асимптота кривой представляет собой линию, которая по мере того, как расстояние между кривой и линией приближается к нулю, когда значение кривой приближается к бесконечности. В этом случае асимптотами можно считать «пробелы» в графике, где значение ctg ( θ ) не определено. Обратите также внимание на то, что по мере того, как график пересекает асимптоту, значение cot ( θ ) переходит от своего максимального положительного значения к максимальному отрицательному значению (или наоборот). Вы также можете увидеть, как различаются значения по обе стороны от асимптоты, изучив таблицу значений котангенса. График функции котангенса может включать несколько очень больших положительных и отрицательных пиков, так как значение тангенса ( θ ) стремится к нулю. Как и в случае с другими тригонометрическими функциями, которые мы рассмотрели, нам не нужно использовать таблицы для нахождения котангенса угла (или угла, соответствующего заданному значению котангенса), так как любой современный научный калькулятор может сделать это за нас, даже хотя в большинстве калькуляторов нет специальной кнопки для функции котангенса. Введите эти нажатия клавиш, чтобы найти котангенс угла 48°. Поскольку функция котангенса является обратной функцией тангенса, все, что мы здесь сделали, это использовали кнопку функции тангенса на калькуляторе, а затем применили встроенную кнопку функции обратной функции калькулятора (обычно помеченную 9). Калькулятор отображает значение раскладушки (48°) Все идет нормально. Теперь давайте предположим, что вы хотите найти размер острого угла в прямоугольном треугольнике, сначала найдя частное смежного и противоположного (т.е. котангенс угла). Если у вас есть значения длин сторон треугольника, вы можете достаточно легко найти значение котангенса угла. Нахождение угла не так просто, как для трех основных тригонометрических функций, поскольку в большинстве калькуляторов нет специальной кнопки для функция арккотангенса (обратная функция котангенса). К счастью, есть относительно простой способ обойти это. Найдем значение угла θ для прямоугольного треугольника, показанного ниже. Мы хотим найти величину угла θ Для угла θ стороны b и a являются смежными и противоположными соответственно. На самом деле мы можем найти размер угла за одну операцию на калькуляторе Windows. Мы делаем это, используя скобки во введенной последовательности клавиш, чтобы заставить калькулятор сначала найти обратное значение частного соседнего и противоположного (т.е. котангенс угла). Затем мы применяем арктангенс функция к результату. Вот последовательность клавиш для использования: Введите эти нажатия клавиш, чтобы найти размер угла θ Возможно, вы уже поняли, что здесь мы находили тангенс угла, взяв , обратную котангенса . Затем мы просто применили к результату функцию арктангенс . Если вы правильно ввели нажатия клавиш, вы должны увидеть экран, подобный показанному ниже. Калькулятор отображает значение угла θ Функция котангенса вместе с другими тригонометрическими функциями может быть представлена в виде бесконечного ряда . Значение, возвращаемое тригонометрической функцией для заданного угла, не может быть вычислено с помощью простой алгебраической формулы. Для большинства углов точное значение можно получить только как сумму бесконечного числа слагаемых, чего, очевидно, достичь невозможно.
History of Trigonometry — Part 3
Это третья из трех статей по истории тригонометрии.
Часть 2 (разделы 5–7) можно найти здесь. Часть 1 (разделы 1-4) можно найти здесь. 8. Арабы собирают знания из известного мира Арабская цивилизация традиционно отмечает свое начало с 622 года н.э., когда Мухаммед, которому угрожали убийством, бежал из Мекки в Медину, где Мухаммед и его последователи нашли безопасность и уважение. Спустя столетие арабы зарекомендовали себя как мощная объединенная сила на обширных территориях Ближнего Востока и Ближнего Востока.0943 Абу
Джафар Аль-Мансур переехал из Дамаска, чтобы основать город Багдад в период с 762 по 766 год. Аль-Мансур послал своих эмиссаров для поиска и сбора знаний. В Китае они научились производить бумагу и, используя этот новый навык, начали программу перевода текстов по математике, астрономии, естественным наукам и философии на арабский язык. Эту работу продолжили его преемники,
Халифы Мохаммад Аль-Махди и Харун Аль-Рашид . Стремление к знаниям стало прочной и важной частью арабской культуры.
Аль-Мансур основал научную академию, которая стала называться «Дом Мудрости». Эта академия привлекала в Багдад ученых из разных стран и религий для совместной работы и установления традиций арабской науки, которые должны были продолжаться и в средние века. Некоторые из этих работ были позднее переведены средневековыми учеными на латынь и переданы в Европу. господство Багдада и влияние арабского мира продлится следующие 500 лет.
Ученые Дома Мудрости представляли многие культуры и переводили работы египетских, вавилонских, греческих, индийских и китайских астрономов и математиков. Математический трактат Птолемея был одним из первых, переведенных с греческого на арабский г. Исхаком бен Хунайном г. (830-910). Он вызывал восхищение своим обширным содержанием и стал известен
по-арабски Аль-Мегисте (Великая Книга). Название « Альмагест » сохранилось и по сей день, и оно признано как великим синтезом, так и кульминацией математической астрономии древнегреческого мира.
9. Индия: синус, косинус и версинусГреческая астрономия стала известна в Индии в период 300-400 гг. н.э. Однако индийские астрономы уже давно использовали планетарные данные и методы расчета от вавилонян, и хотя это было намного позже того, как Птолемей написал Альмагест, индийские астрономы 4-го века не полностью переняли греческую планетарную теорию. Древние работы, такие как «Панча-сиддхантика » (теперь утеряны), которые были переданы через версию Врахамихиры [см. Часть 1, раздел 3] и 9 Арьябхаты.0943 г. Арьябхатия г. (499 г. н.э.) продемонстрировал, что у индийских ученых были свои собственные способы решения астрономических проблем и что они обладали большими навыками в [См. примечание 1 ниже]
Даже в самых старых индийских текстах аккорд [чтобы напомнить себе об аккордах, см. раздел о Клавдии Птолемее в предыдущей статье] не используется, и вместо этого появляются некоторые очень ранние версии тригонометрических таблиц с помощью синусов.
На этой диаграмме $SB$ — это дуга угла $\theta$, а $AS$ — это джия . Таким образом, отношение между джия и нашим синусом таково: $$ джия (\тета)=R\sin\тета$$ , где $R$ — радиус окружности.
Во многих индийских синусоидальных таблицах используется $R = 3438$, что является результатом, если длина окружности равна 360 $ х 60 $ или 21 600 $ минут. [См. примечание 2 ниже]
К V веку были определены и использованы еще две функции. Длина $EA$ называлась котиджйа (наш косинус), а АБ назывался уткрама-джйа (наш версинус). Иногда это называлось sama , что означает «стрела», или sagitta на латыни
Функция версинуса для радиуса окружности $R$: $\mbox{vers }\theta = R — \cos\ theta $ [см. Примечание 3 ниже]
В работе Арьябхаты он использует $R = 3438$ и взял это значение для расчета своей таблицы синусов. Это стало стандартом для более поздних работ. 10. Тригонометрия в арабской цивилизацииВведение и развитие тригонометрии в самостоятельную науку в арабской цивилизации заняло в общей сложности около 400 лет. В начале 770-х годов индийские астрономические работы достигли C aliph Al-Mansur в Багдаде и были переведены как Zij al-Sindhind , и это ввело индийские методы расчета в Ислам.
Известный своей книгой по алгебре, Абу Джафар Мухаммад ибн Муса аль-Хорезми (см. «Развитие алгебры, часть 1») также написал книгу об индийских методах расчета ( al-hisab al-hindi ) и выпустил улучшенную версию Zij.
аль-Синдхинд . Версия Аль-Хорезми Zij использовала синусы и версины и разработала процедуры для тангенсов и котангенсов для решения астрономических задач.
Многие работы на греческом, санскрите и сирийском языках были принесены учеными в Дом Мудрости Аль-Мансура и переведены. Среди них были работы Евклида, Архимеда Аполлония и, конечно же, Птолемея. Теперь у арабов было две конкурирующие версии астрономии, и вскоре победил Альмагест.
Индийское использование синуса и связанных с ним функций было намного проще применять в расчетах, и шестидесятеричная система счисления от вавилонян продолжала использоваться, поэтому, за исключением этих двух изменений, ранние арабские версии Альмагеста остались верны к Птолемею. [См. примечание 5 ниже]
Абу аль-Вафа аль-Бузджани (Абул Вафа 940-998) внес важный вклад как в геометрию, так и в арифметику и был первым, кто систематически изучал тригонометрические тождества. Изучение тождеств было важно, поскольку установление соотношений между суммами и разностями, а также дробями и кратными углами сделало астрономические вычисления более эффективными.
Синус, версинус и косинус были разработаны в контексте астрономических задач, тогда как тангенс и котангенс были разработаны на основе изучения теней гномона. В своем Альмагесте Абул Вафа объединил их и впервые установил отношения между шестью фундаментальными тригонометрическими функциями. Он также использовал $R = 1$ для радиус основной окружности.
Из этих соотношений Абул Вафа смог продемонстрировать ряд новых тождеств, используя эти новые функции: 92 \theta$$
Абул Вафа также разработал методы расчета тригонометрических таблиц с помощью усовершенствованной техники разности для получения значений с точностью до $5$ шестидесятеричных ($8$ десятичных) разрядов.
Греческие астрономы уже давно представили модель Вселенной со звездами внутри огромной сферы. Они также работали со сферическими треугольниками, но Абул Вафа был первым арабским астрономом, который разработал способы измерения расстояния между звездами, используя свою новую систему тригонометрических функций, включая версину.
На диаграмме выше синий треугольник со сторонами $a$, $b$ и $c$ представляет расстояния между звездами внутри сферы. Вершина, где отмечены три угла $\alpha$, $\beta$ и $\gamma$, является положением наблюдателя. Синие кривые — это большие круги на сфере, и, измеряя углы, находя более точные значения их функций и принимая значение для $R$ радиус сферы, стало возможным найти расстояния по большому кругу между звездами. Гениальным применением теоремы Менелая [см. Историю тригонометрии, часть 2] с использованием особых случаев больших кругов с двумя прямыми углами Абул Вафа показал, как теорему можно применить к сферическим треугольникам. Это был значительный прогресс в сферической тригонометрии, позволивший рассчитать правильное направление для молитвы. (кибла) и должен был иметь важные применения в навигации и картографии. Лунный кратер Абул-Вафа назван в честь его работы в области астрономии.
Из диаграммы $O$ — центр полукруга, а $AED$ — прямоугольный треугольник с перпендикуляром из $E$ в $C$. Следовательно, треугольники $AEC$ и $EDC$ подобны. Угол $EOD$ в два раза больше угла $EAD$, а углы $EAC$ и $DEC$ равны. Если радиус окружности $R =1$, то $EC = \sin\theta$ и $OC = \cos\theta$ $$\mbox{So }\tan\left(\frac{\ theta}{2}\right)=\frac{EC}{AC}=\frac{\sin\theta}{1+\cos\theta} \mbox{ . . . а также . . . } \tan\left(\frac{\theta}{2}\right)=\frac{DC}{EC}=\frac{1-\cos\theta}{\sin\theta}$$ Отсюда он вывел формулы половинного угла и кратного угла.
В то время как открывались многие новые аспекты тригонометрии, хорда, синус, версинус и косинус были разработаны при исследовании астрономических задач и воспринимались как свойства углов в центре небесного тела. сфера. Напротив, свойства тангенса и котангенса были получены из измерения теней гномона и проблем определения времени.
В своей демаркации координат городов он использовал сферические треугольники для нахождения координат городов и других мест, чтобы установить местный меридиан ( кибла ) и таким образом найти правильное направление Мекки и в своем Исчерпывающем трактате о тенях он показал, как использовать gnomons [см. Краткую историю измерения времени] для определения времени суток.
Абу Мухаммад Джабир ибн Афлах (Джабир ибн Афла ок. 1100–1160), вероятно, работал в Севилье в первой половине 12 века. Его работа считается важной в передаче знаний в Европу.
Результатом этого проекта стало создание гораздо более точных астрономических таблиц для расчета положения Солнца, Луны и планет относительно неподвижных звезд, называемых Альфонсовыми таблицами, сделанными в Толедо где-то между 1252 и 1270 годами. были таблицами, которые Колумб использовал для плавания в Новый Свет, и они оставались самыми точными таблицами до 16 века. К концу 10 века тригонометрия заняла важное место в астрономических текстах с главами, посвященными синусам и хордам, теням (тангенсам и котангенсам) и формулам для сферических вычислений. Был также значительный интерес к разрешению плоских треугольников.
Это была коллекция и значительное улучшение предыдущих знаний. Книги I, II и IV содержат части «Начал», «Альмагеста» и ряда других греческих источников. Книга III посвящена основам геометрии сферических треугольников и разрешению плоских треугольников с помощью теоремы синусов:
$$\frac{a}{\sin A}=\frac{b}{\sin B}=\ frac{c}{\sin C}$$ Книга V содержит основные главы по тригонометрии, посвященные прямоугольным треугольникам и шести фундаментальным соотношениям, эквивалентным тем, которые мы используем сегодня; синус, косинус, тангенс, котангенс, секанс и косеканс.
Quadripartitum был, вероятно, первым всеобъемлющим средневековым трактатом по тригонометрии, написанным в Европе, по крайней мере, за пределами Испании и ислама. Когда Ричард был аббатом Сент-Олбанса, он пересмотрел работу, приняв во внимание Флореса года Джабира ибн Афла года.
В период с 1326 по 1327 год Ричард также разработал вычислительное устройство, названное экваториальным , сложной зубчатой астролябией с четырьмя гранями.
Георг фон Пейербах (1423-1461) Работа Пейербаха помогла проложить путь коперниканской концепции миросистемы; он создал новую теорию планет, сделал более точные расчеты затмений и движений планет и ввел использование синуса в свою тригонометрию.
Theoricae Novae Planetarum Пейербаха (Новые теории планет) была составлена около 1454 г. и опубликована в 1473 г. типографией Региомонтана в Нюрнберге. В то время как книга была связана с попыткой технического решения теорий Евдокса и Птолемея, Пейербах утверждал, что движение планет определяется Солнцем, и это рассматривается как шаг к теории Коперника. Эту книгу читали Коперник, Галилей и Кеплер, и она стала стандартным астрономическим текстом вплоть до семнадцатого века.
В 1460 году он начал работу над новым переводом Альмагеста Птолемея, но до своей смерти в 1461 году он закончил только шесть из запланированных тринадцати книг.
Понимая, что существует необходимость в систематическом изложении тригонометрии, Региомонтан начал свою основную работу, De Triangulis Omnimodis (О треугольниках всех видов) 1464. В своем предисловии к «Чтецу» он говорит: «Ибо никто не может обойти науку о треугольниках и достичь удовлетворительного знания о звездах . Первая книга дает основные определения количества, отношения, равенства, окружности, дуги, хорды и функции синуса. Далее идет список аксиом, которые он примет, а затем $33$ теорем для прямоугольных, равнобедренных и разносторонних треугольников. Дана формула площади треугольника, а затем правило синусов с примерами его применения. Книги с III по V охватывают важнейшую теорию сферических тригонометрия. Вся книга организована в стиле Евклида с утверждениями и теоремами, изложенными в логической иерархии. Эта работа, опубликованная в 1533 году, имела для Коперника большую ценность. Региомонтан также построил первую астрономическую обсерваторию в Германии в Нюрнберге с мастерской, где он изготавливал астрономические инструменты. Региомонтан умер во время вспышки чумы в Риме в 1476 году. 12. Заключительная глава: Тригонометрия меняет мировую системуНиколай Коперник (1473 — 1543)Коперник написал краткий план предложенной им системы под названием Commentariolus , который он разослал друзьям где-то между 1510 и 1514 годами. К этому времени он использовал наблюдения за планетой Меркурий и таблицы Альфонсов, чтобы убедить себя, что он может объяснить движение Земли как одной из планет. В рукописи произведения Коперника есть выжил, и считается, что к 1530-м годам большая часть его работы была завершена, но он отложил публикацию книги. Его ученик Ретикус прочитал рукопись, сделал краткое изложение теории Коперника и опубликовал его как Narratio Prima (Первое сообщение) в 1540 году. Георг Иоахим фон Лаухен по прозвищу Ретикус (1514-1574)
Варфоломей Питискус (1561 — 1613)
|

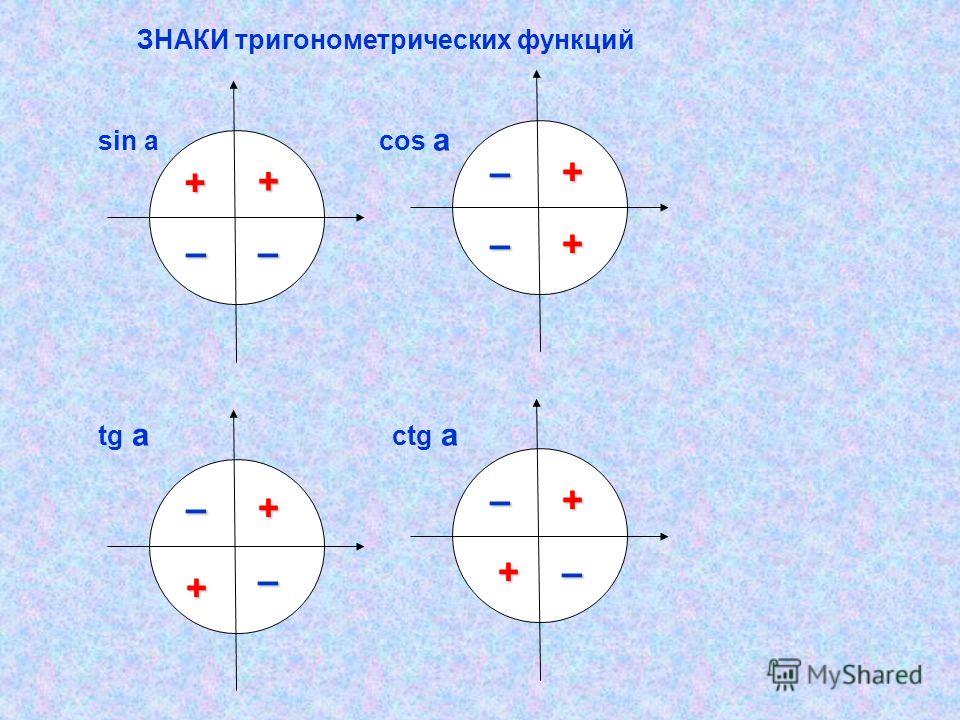 — ISBN 5-09-013651-3.
— ISBN 5-09-013651-3. для 10-11 кл. сред. шк. — 3-е изд. — М.: Просвещение, 1993. — 351 с.: ил. — ISBN 5-09-004617-4.
для 10-11 кл. сред. шк. — 3-е изд. — М.: Просвещение, 1993. — 351 с.: ил. — ISBN 5-09-004617-4.