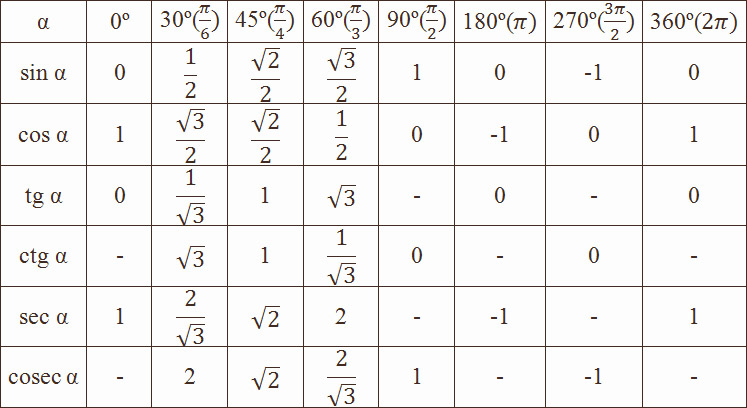
в радианах, от 0° до 360°, как пользоваться
Содержание:
- Таблица косинусов в радианах
- Таблица косинусов от 0° до 180°
- Таблица косинусов от 181° до 360°
- Как пользоваться таблицей
Содержание
- Таблица косинусов в радианах
- Таблица косинусов от 0° до 180°
- Таблица косинусов от 181° до 360°
Таблица косинусов в радианах
Радиан представляет собой угол, который соответствует дуге с длиной, определяемой радиусом.
В радианах принято измерять плоские углы.
Радианная мера является угловой мерой, измеряемой в радианах, определяется, как отношение рассматриваемого угла к радиану.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Проанализируем данное определение. Заметим, что справедливым является вывод о величине в 2 \(\pi\) радиан, характерной для полного угла.
При решении задач по тригонометрии и геометрии часто приходится иметь дело с углами, измеряемыми в радианах. Упростить вычисление величин можно, если воспользоваться таблицей косинусов углов, для которых известна радианная мера. Кроме того, радианы нередко присутствуют в заданиях по различным темам математического анализа.
Источник: ru.onlinemschool.comТаблица косинусов от 0° до 180°
Градусы, минуты и секунды являются общеизвестными измерительными единицами, предусмотренными для плоских углов.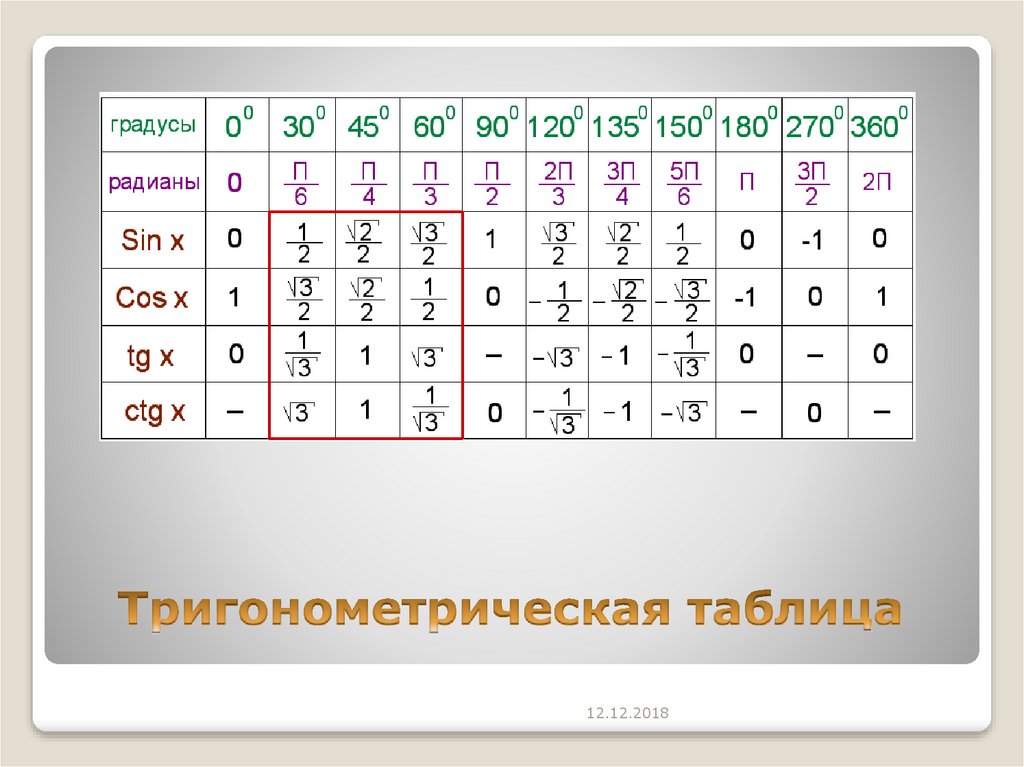
{\circ }}}}{\displaystyle \approx 0{,}0174532925}\)
Таблица косинусов от 181° до 360°
Косинус представляет собой вид тригонометрической функции, демонстрирующей отношение прилегающего катета к гипотенузе.
В геометрических задачах принято вычислять тригонометрические функции, характерные для острого угла, по соотношениям сторон, которыми обладает прямоугольный треугольник. Предположим, что имеется некий треугольник АОВ с прямым углом. Обозначим в нем за гипотенузу сторону ОВ, а для острого угла запишем следующее равенство:
\(\angle AOB=\alpha\)
При таких исходных данных косинус можно вычислить по формуле:
\(\cos \alpha ={\frac {OA}{OB}}\)
Однако не во всех случаях вышеуказанное соотношение подходит для проведения вычислений. Значительно упростить решение тригонометрических задач можно, если воспользоваться таблицей косинусов:
Источник: ru.onlinemschool.comКак пользоваться таблицей
Таблица, в которой собраны значения косинусов для углов от 0° до 360°, либо углов, выраженных в радианной мере, является информационным материалом, который используют математики и физики.
С помощью данного справочного пособия удается упростить и сократить решения разных задач по алгебре, геометрии, физике, математическому анализу, тригонометрии и другим дисциплинам, где приходится часто сталкиваться с массивными вычислениями.
Пользоваться рассматриваемой таблицей достаточно просто. Стандартный алгоритм действий ее применения в решении примеров состоит в выполнении нескольких ключевых операций:
- выявить тригонометрическую функцию в математическом соотношении;
- при необходимости требуется привести функцию к табличной форме;
- найти по таблице значение косинуса;
- путем подстановки известной величины продолжить математические преобразования и вычисления.
Насколько полезной была для вас статья?
У этой статьи пока нет оценок.
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Поиск по содержимому
Получение косинуса 109° в таблице косинусов таблицы тригонометрических функций
Косинус
11 ноября 2022 г.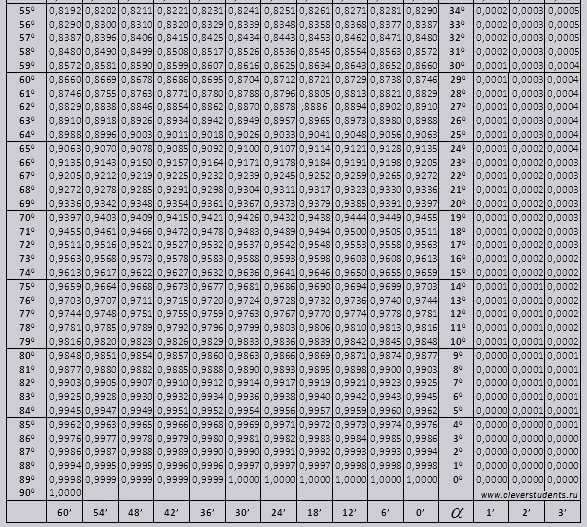
В этой статье мы разъясним метод обработки для расчета cos 109° = -0,325569….
Ориентируясь на таблицу косинусов (cos) в таблице тригонометрических функций, объясним, как вычислить значение.
Такой таблицей является таблица косинусов.
| 角度 | значение | 角度 | value |
|---|---|---|---|
| COS1 ° | 0.999847 | COS2 ° | 0.99939 |
| COS3 ° | 0.998629 | COS4 ° | 0.997564 |
| · · · | · · · | ||
| COS30 ° | $\displaystyle \frac{\sqrt{3}}{2}$ | COS45 ° | $\displaystyle \frac{1}{\sqrt{2}}$ |
| COS60 ° | $\displaystyle \frac{1}{2}$ | COS90 ° | 0 |
Как вы рассчитали таблицу тригонометрических функций (таблицу косинусов) в конце математического объяснения?
Это объяснение объясняет, как вычислить cos109°.
$$\cos 109°=-0,325569…$$
Этот сайт создан доктором Томсоном tom lab Он работает под именем
оглавление
Подтвердить 109 цифр cos 10°
Как можно скорее выразим cos 109° в 10 цифрах! $$\cos 109° = -0,3255681545 \cdots$$.
Найдем это значение в таблице косинусов.
Также проверьте cos110° = -0,3421
Вычислите значение cos109°
Существует три метода вычисления значения cos109° без проверки тригонометрической таблицы, за исключением очень сложного.
- С помощью транспортира составьте из бумаги прямоугольный треугольник с углом 109°.
- Формула полуширины, формула двойного угла.0102
- Решите с помощью разложения Маклорена
Поскольку в методе 1 используется линейка, точное значение вычислить невозможно, и полученное значение является приблизительным.
Метод 2 не рекомендуется, так как вывод становится очень сложным и появляются даже мнимые числа.
Поэтому на этот раз я объясню третий метод, используя разложение Маклорена.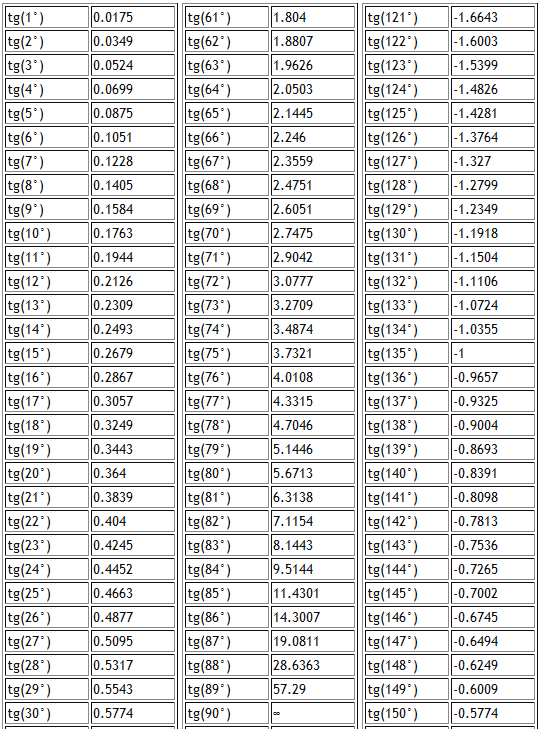
Получите cos109° с помощью разложения Маклорена
Разложение Маклорена можно использовать для решения \(\cos x\) по следующей формуле. 97}{7!}\ cdots\\$$
Проще говоря, вы можете использовать \(x\) из \(\cos x\) для вычисления значения \(\cos x\).
Даже если вы не знаете разложения Маклорена, ничего страшного, если вы знаете формулу.
использовать метод радианов для x
Однако обратите внимание, что метод \(x\) должен быть заменен.
$$radical=\displaystyle \frac{\pi}{180}\times 109°$$
Вычисление этой формулы дает 9@`,
Следовательно, смежный = 0,7071 метра
Пример 3
Если длина гипотенузы 1 метр, а длина прилежащего катета 0,8 метра, чему равен угол `тета`?
Посмотрите на таблицу/диаграмму косинуса (угла) для 0,8 метра и найдите угол.
Уголок | Смежное расстояние (или косинус) | |
? | `0,8 метра` |
Ближайшее = 36° = 0,809 метра
Но на калькуляторе, если вы подставите 0,8 и нажмете арккосинус (cos -1 ), это даст вам 36,87° (что более точно).