| ГОСТы, СНиПы Карта сайта TehTab.ru Поиск по сайту TehTab.ru | Навигация по справочнику TehTab.ru: главная страница / / Техническая информация/ / Математический справочник/ / Теория вероятностей и статистика / / Таблица. Функция распределения вероятностей стандартного нормального закона. Таблица квантилей стандартного нормального закона распределения.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Нашли ошибку? Есть дополнения? Напишите нам об этом, указав ссылку на страницу. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
TehTab.ru Реклама, сотрудничество: [email protected] | Обращаем ваше внимание на то, что данный интернет-сайт носит исключительно информационный характер. Информация, представленная на сайте, не является официальной и предоставлена только в целях ознакомления. Все риски за использование информаци с сайта посетители берут на себя. Проект TehTab.ru является некоммерческим, не поддерживается никакими политическими партиями и иностранными организациями. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Раздел недели: Плоские фигуры. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Поиск на сайте DPVA Поставщики оборудования Полезные ссылки О проекте Обратная связь Ответы на вопросы. Оглавление Таблицы DPVA.ru — Инженерный Справочник | Адрес этой страницы (вложенность) в справочнике dpva.ru: главная страница / / Техническая информация/ / Математический справочник / / Теория вероятностей. Математическая статистика. Комбинаторика. / / Таблица. Функция распределения вероятностей стандартного нормального закона. Таблица квантилей стандартного нормального закона распределения. Поделиться:
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Если Вы не обнаружили себя в списке поставщиков, заметили ошибку, или у Вас есть дополнительные численные данные для коллег по теме, сообщите , пожалуйста. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Коды баннеров проекта DPVA.ru Консультации и техническая | Проект является некоммерческим. Информация, представленная на сайте, не является официальной и предоставлена только в целях ознакомления. Владельцы сайта www.dpva.ru не несут никакой ответственности за риски, связанные с использованием информации, полученной с этого интернет-ресурса. Free xml sitemap generator Free xml sitemap generator | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Z TABLE — Z TABLE
Таблица отрицательных показателей Z
Используйте приведенную ниже таблицу отрицательных показателей Z, чтобы найти значения слева от среднего, как показано на графике рядом. Соответствующие значения, которые меньше среднего, отмечены отрицательным баллом в таблице z и представляют собой площадь под кривой нормального распределения слева от z.
1.1 – Отрицательная Z-таблицаПоложительная Z-оценочная таблица
Используйте положительную Z-оценочную таблицу ниже, чтобы найти значения справа от среднего, как показано на графике рядом. Соответствующие значения, которые превышают среднее значение, отмечены положительной оценкой в z-таблице и представляют площадь под кривой нормального распределения слева от z.
1.2 — Положительная таблица Z Примечание. Не стесняйтесь использовать и делиться приведенными выше изображениями, если вы указываете авторство нашего сайта, указывая ссылку на https://www.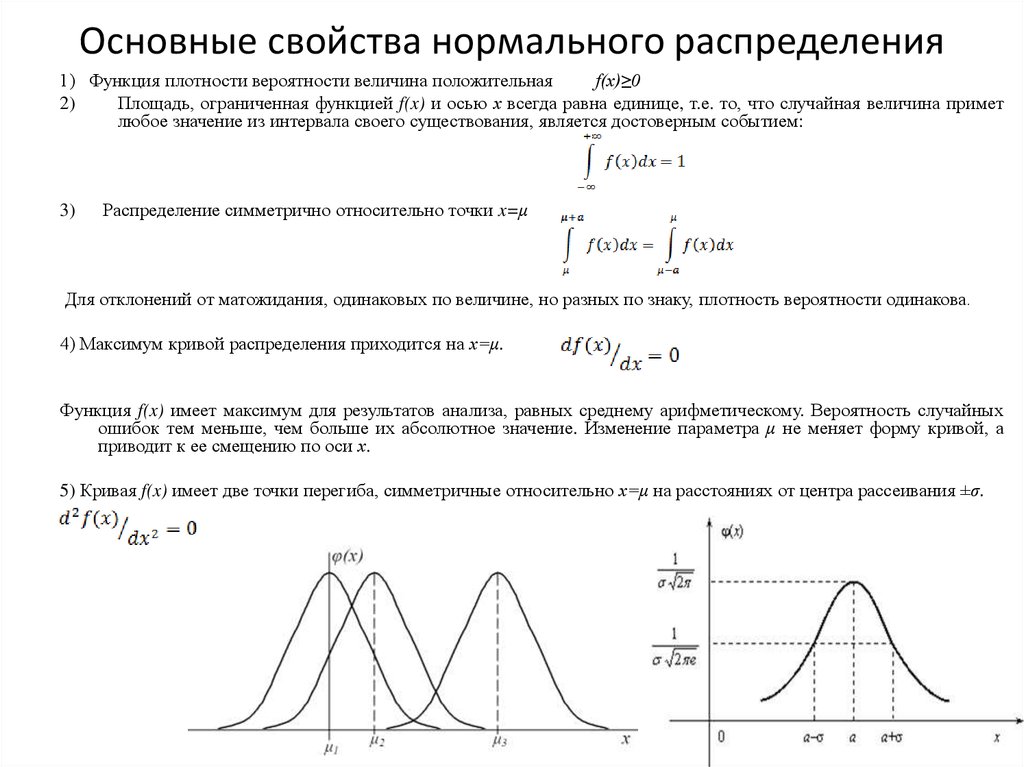 ztable.net
ztable.net
Как использовать формулу Z Score.
Однако, чтобы использовать Z-Tables, вам нужно знать кое-что, что называется Z-Score. Это Z-оценка, которая отображается в Z-таблице и обычно либо заранее предоставляется, либо должна быть получена с использованием формулы Z-оценки. Но прежде чем мы взглянем на формулу, давайте разберемся, что такое Z Score 9.0005
Что такое показатель Z?Показатель A Z, также называемый стандартным показателем, представляет собой измерение того, на сколько стандартных отклонений ниже или выше генеральной совокупности означает необработанный показатель. Проще говоря, именно Z Score дает вам представление об отношении значения к среднему и о том, насколько далеко от среднего находится точка данных.
A Z Score измеряется стандартными отклонениями от среднего значения. Это означает, что если Z Score = 1, то это значение равно одному стандартному отклонению от среднего. Тогда как, если Z Score = 0, это означает, что значение идентично среднему.
Оценка Z может быть как положительной, так и отрицательной в зависимости от того, находится ли оценка выше среднего (в этом случае она положительна) или ниже среднего (в этом случае она отрицательна)
Оценка Z помогает нам сравнить результаты с нормой население или среднее значение
Формула Z-показателяФормула Z-показателя или стандартная формула для расчета задается как
Если у нас нет предварительно предоставленного нам Z-показателя, мы будем использовать приведенную выше формулу для расчета Z-оценка с использованием других доступных данных, таких как наблюдаемое значение, среднее значение выборки и стандартное отклонение. Точно так же, если у нас есть стандартная оценка и отсутствует любое из трех других значений, мы можем подставить их в приведенную выше формулу, чтобы получить отсутствующее значение.
Понимание того, как использовать формулу Z-оценки на примере
Давайте разберемся, как рассчитать Z-оценку, формулу Z-оценки и использовать Z-таблицу на простом примере из реальной жизни.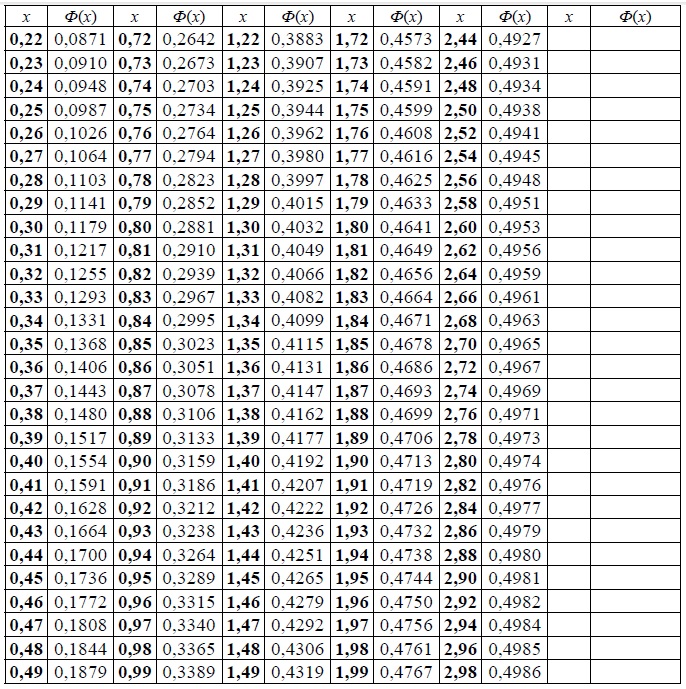
В: В конце семестра подсчитываются 300 экзаменационных баллов студентов колледжа. Эрик набрал в общей сложности 800 баллов (X) из 1000. Средний балл для партии составил 700 (µ), а стандартное отклонение — 180 (σ). Давайте узнаем, насколько хорошо Эрик набрал по сравнению со своими товарищами по группе.
Используя приведенные выше данные, нам нужно сначала стандартизировать его оценку и использовать соответствующую z-таблицу, прежде чем мы определим, насколько хорошо он работал по сравнению с его товарищами по группе.
Чтобы узнать Z-показатель, мы используем формулу
Z-показатель = (наблюдаемое значение – среднее значение выборки)/стандартное отклонение Показатель Z = (800-700) / 180
Показатель Z = 0,56
Когда у нас есть показатель Z, который был получен с помощью формулы показателя Z, мы можем теперь перейти к следующей части, которая посвящена пониманию того, как читать таблицу Z и сопоставлять значение полученного нами показателя Z, используя его.
Как читать Z-таблицу
Само собой разумеется, что для сопоставления Z-оценки с Z-таблицей первое, что вам нужно, это сама Z-оценка. В приведенном выше примере мы получаем, что Z-показатель Эрика равен 0,56.
Когда у вас есть Z-счет, следующим шагом будет выбор между двумя таблицами. Это выбор между использованием отрицательной Z-таблицы и положительной Z-таблицы в зависимости от того, является ли значение вашего Z-показателя положительным или отрицательным.
Что мы в основном устанавливаем с положительным или отрицательным показателем Z, так это то, лежат ли ваши значения слева от среднего или справа от среднего. Чтобы найти область слева от среднего значения, у вас будет отрицательный Z-показатель и вы будете использовать отрицательную Z-таблицу. Точно так же, чтобы найти область справа от среднего, у вас будет положительная оценка Z и используйте положительную таблицу Z.
Теперь, когда у нас есть Z-показатель Эрика, который, как мы знаем, является положительным 0,56, и мы знаем, какую соответствующую таблицу выбрать для него, мы воспользуемся положительной Z-таблицей (таблица 1.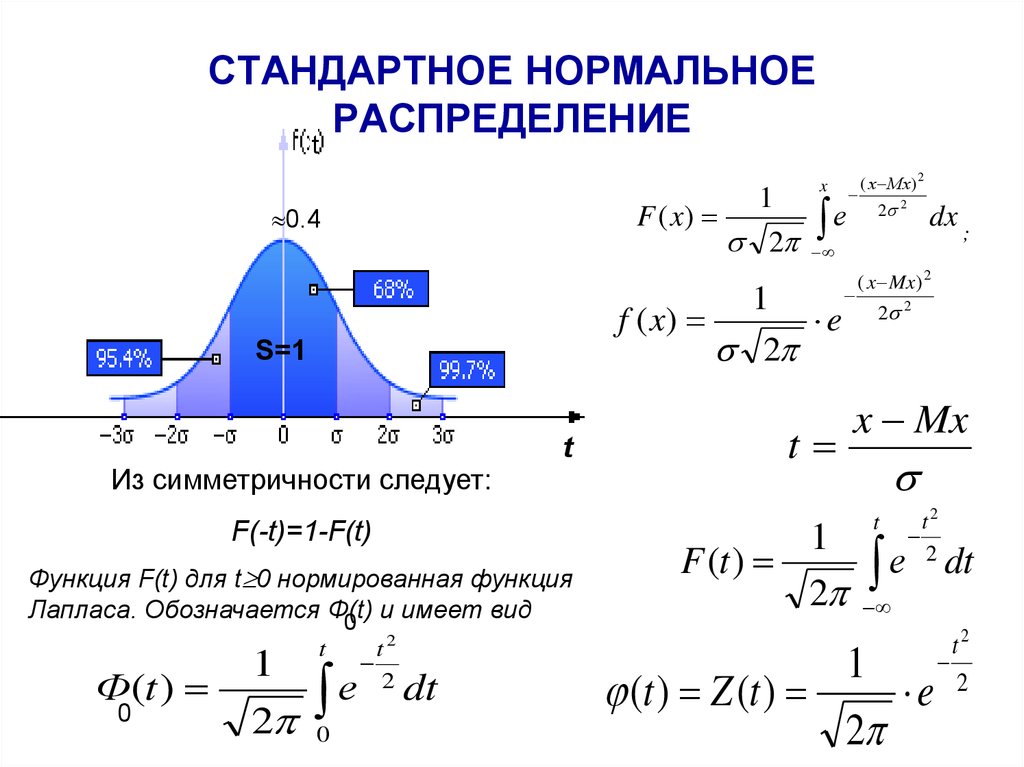 2), чтобы предсказать, насколько хорошо или плохо выступил Эрик по сравнению с своим товарищам по партии.
2), чтобы предсказать, насколько хорошо или плохо выступил Эрик по сравнению с своим товарищам по партии.
Теперь, когда мы выбрали подходящую таблицу для поиска, на следующем этапе процесса мы узнаем, как отобразить значение Z-показателя в соответствующей таблице. Давайте разберемся на примере, который мы выбрали с показателем Z Эрика, равным 0,56. счет).
Получив это, пройдите вдоль оси X в самой верхней строке, чтобы найти значение цифр во втором десятичном разряде (0,06 на основе Z-показателя Эрика)
После сопоставления этих двух значений найдите в таблице пересечение строки первых двух цифр и столбца второго десятичного значения. Пересечение этих двух и есть ответ, который мы ищем.
В нашем примере мы получаем пересечение со значением 0,71226 (~ 0,7123)
Чтобы получить это в процентах, мы умножаем это число на 100. Таким образом, 0,7123 x 100 = 71,23%. Отсюда мы узнаем, что Эрик справился лучше, чем 71,23% студентов.
Возьмем еще один пример, но на этот раз для отрицательного показателя z и отрицательной таблицы z.
Давайте рассмотрим нашу Z-оценку = -1,35
На основании того, что мы обсуждали ранее, поскольку z-оценка отрицательна, мы будем использовать отрицательную таблицу z (таблица 1.1)
Сначала пройдем горизонтально вниз по Ось Y в крайнем левом столбце, чтобы найти значение первых двух цифр, равное -1,3
Получив это, мы пройдем по оси X в самой верхней строке, чтобы отобразить второе десятичное число (0,05 в случае) и найдите для него соответствующий столбец.
Пересечение строки первых двух цифр и столбца второго десятичного значения в приведенной выше таблице Z является искомым ответом, который в нашем примере равен 0,08851 или 8,85%
(обратите внимание, что этот метод отображения значение Z-оценки одинаково как для положительной, так и для отрицательной Z-оценки. Это потому, что для стандартной таблицы нормального распределения обе половины кривых по обе стороны от среднего идентичны. Таким образом, это зависит только от независимо от того, является ли значение Z Score положительным или отрицательным, или мы ищем область слева от среднего или справа от среднего, когда дело доходит до выбора соответствующей таблицы)
Почему две таблицы Z? Есть две таблицы Z, чтобы упростить задачу.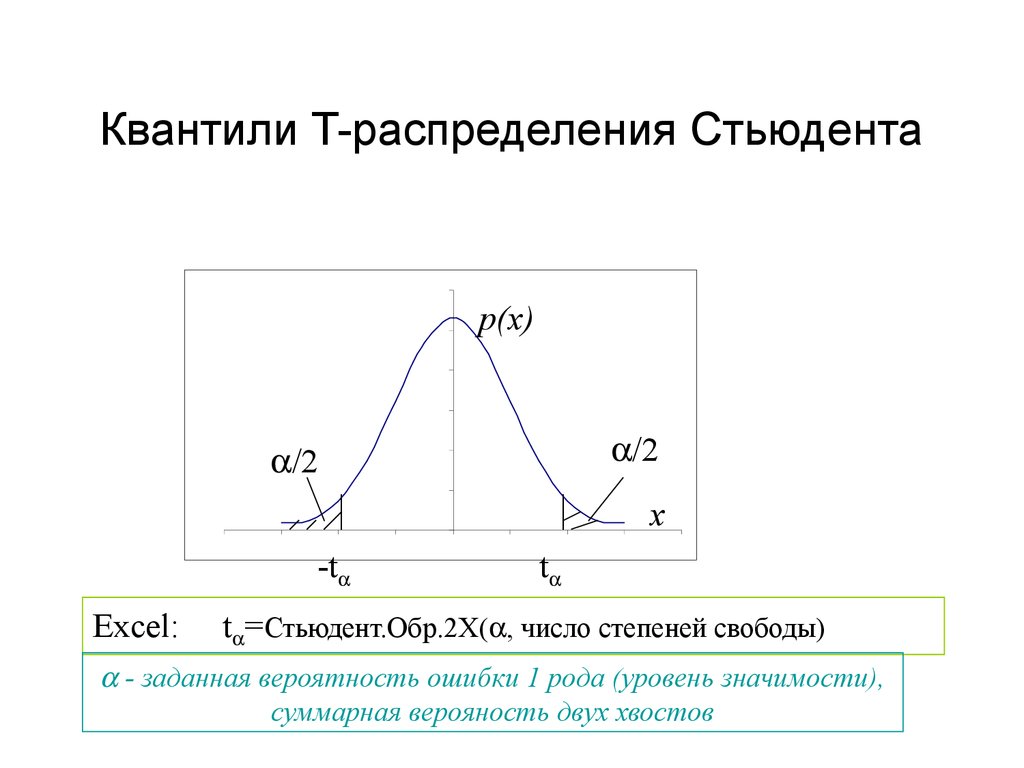 Конечно, его можно объединить в одну большую Z-таблицу, но это может быть немного сложным для многих новичков, а также увеличивает вероятность человеческих ошибок во время вычислений. Использование двух таблиц Z упрощает жизнь, так что в зависимости от того, хотите ли вы узнать площадь от среднего значения для положительного или отрицательного значения, вы можете использовать соответствующую таблицу Z-оценки.
Конечно, его можно объединить в одну большую Z-таблицу, но это может быть немного сложным для многих новичков, а также увеличивает вероятность человеческих ошибок во время вычислений. Использование двух таблиц Z упрощает жизнь, так что в зависимости от того, хотите ли вы узнать площадь от среднего значения для положительного или отрицательного значения, вы можете использовать соответствующую таблицу Z-оценки.
Если вы хотите узнать площадь между средним и отрицательным значением, вы будете использовать первую таблицу (1.1), показанную выше, которая является левой/отрицательной Z-таблицей. Если вы хотите узнать площадь между средним и положительным значением, вам понадобится вторая таблица (1.2), над которой находится правая/положительная Z-таблица.
Что такое стандартное отклонение? (σ) Стандартное отклонение, обозначаемое символом (σ) , греческой буквой сигмы, представляет собой не что иное, как квадратный корень из дисперсии. Принимая во внимание, что дисперсия – это среднее квадратов отличий от среднего значения.
1. Что такое P (Z ≥ 1,20)
Ответ: 0,11507
Чтобы найти ответ, используя приведенную выше Z-таблицу, мы сначала посмотрим на соответствующее значение для первые две цифры по оси Y, которые равны 1,2, а затем перейдите к оси X, чтобы найти значение для второго десятичного знака, равное 0,00. Следовательно, мы получаем оценку как 0,11507
2. Чему равно P (Z ≤ 1,20)
(То же самое, что и выше, используя другую таблицу. Попробуйте решить это самостоятельно для практики)
Ответ: 0,88493
Таблица истории стандартного нормального распределения
Заслуга в открытии, происхождении и составлении стандартного нормального распределения принадлежит французскому математику XVI века Абрахаму де Муавру (26 мая 1667 г. – 27 ноября 1754 г.). который хорошо известен своей «формулой де Муавра», которая связывает комплексные числа и тригонометрию.
Де Муавр создал нормальное распределение благодаря своему научному и математическому подходу к азартным играм. Он пытался придумать математическое выражение для нахождения вероятности подбрасывания монеты и различных интересных аспектов азартных игр.
Он пытался придумать математическое выражение для нахождения вероятности подбрасывания монеты и различных интересных аспектов азартных игр.
Он обнаружил, что, хотя наборы данных могут иметь широкий диапазон значений, мы можем «стандартизировать» их, используя кривую распределения в форме колокола, которая упрощает анализ данных, установив для нее среднее значение, равное нулю, и стандартное отклонение, равное единице. Открытая им колоколообразная кривая распределения стала известна как нормальная кривая.
Это открытие было чрезвычайно полезным, и в последующие годы его использовали другие математики. Стало понятно, что нормальное распределение применимо к большому количеству математических явлений и явлений из реальной жизни. Например, бельгийский астроном Ламбер Кетле (22 nd февраля 1796 г. по 17 th февраля 1874 г.) обнаружил, что, несмотря на рост, вес и силу людей, представлен большой диапазон данных с ростом людей от 3 до 8 футов и весом от нескольких фунтов до нескольких сотен фунтов. была прочная связь между ростом, весом и силой людей в соответствии со стандартной кривой нормального распределения.
была прочная связь между ростом, весом и силой людей в соответствии со стандартной кривой нормального распределения.
Нормальная кривая использовалась не только для стандартизации наборов данных, но и для анализа ошибок и моделей распределения ошибок. Например, нормальная кривая использовалась для анализа ошибок в измерениях астрономических наблюдений. Галилей обнаружил, что ошибки симметричны по своей природе, а в девятнадцатом веке стало понятно, что даже ошибки имеют закономерность нормального распределения.
Такое же распределение было открыто в конце 18 -го века известным французским математиком Лапласом (Пьер-Симон, маркиз де Лаплас; с 23 по марта 1749 года по 5 -е марта 1827 года). Центральная предельная теорема Лапласа утверждает, что распределение выборочных средних соответствует стандартному нормальному распределению и что чем больше набор данных, тем больше распределение отклоняется от нормального распределения.
Принимая во внимание, что в теории вероятностей частный случай центральной предельной теоремы, известной как теорема де Муавра-Лапласа, утверждает, что нормальное распределение может использоваться как приближение к биномиальному распределению при определенных условиях.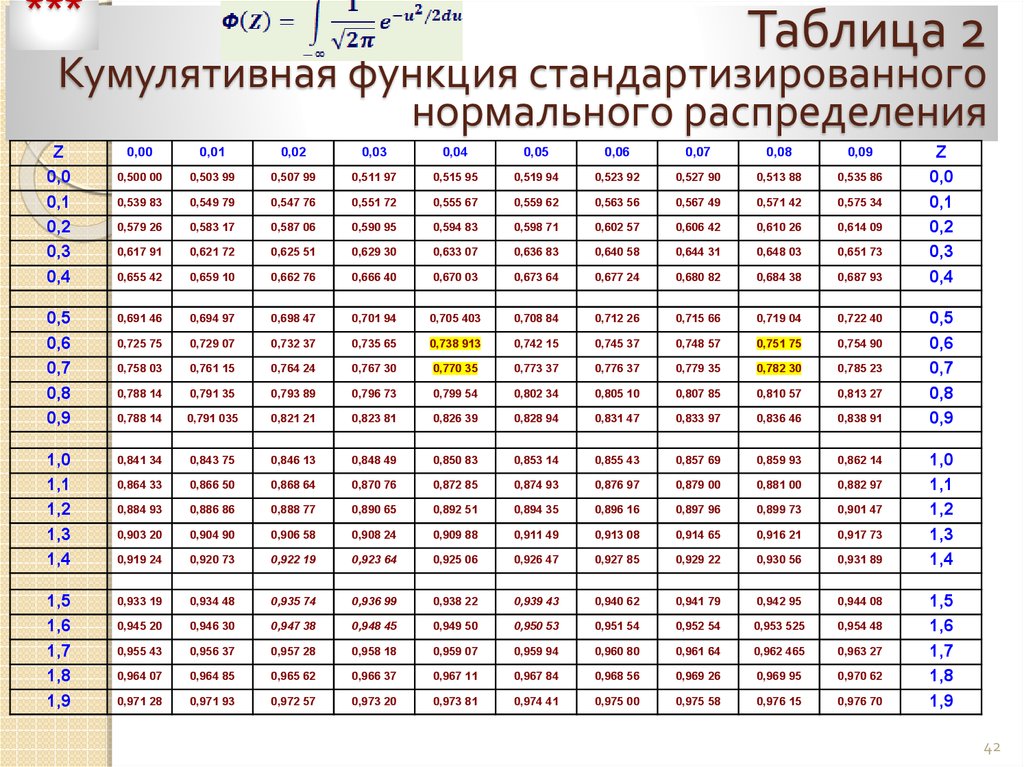 Эта теорема появляется во втором издании книги Абрахама де Муавра, изданной в 1738 году, под названием «Доктрина случайностей».
Эта теорема появляется во втором издании книги Абрахама де Муавра, изданной в 1738 году, под названием «Доктрина случайностей».
Теги: таблица z, таблица z-оценки, таблица нормального распределения, стандартная таблица нормального распределения, таблица стандартного нормального распределения, z-таблица, таблица z-оценки, таблица преобразования z, ztable, таблица норм, таблица значений z, таблица распределения z, таблицы z, таблицы z оценок, таблица zscore, нормальное распределение таблицы z, таблица стандартных отклонений, статистика таблицы z, диаграмма таблицы z, таблица стандартного распределения, диаграмма z оценок, диаграмма z-оценок. сообщите об этом объявлении
Раздел 7.2: Приложения нормального распределения
Цели
К концу этого урока вы сможете…
- найти и интерпретировать площадь под кривой нормали
- найти значение нормальной случайной величины
Чтобы получить краткий обзор этого раздела, посмотрите этот краткий видеообзор. (Обратите внимание, что это то же самое видео для раздела 7.1, если вы уже смотрели его.)
(Обратите внимание, что это то же самое видео для раздела 7.1, если вы уже смотрели его.)
Поиск площадей с помощью таблицы как найти площадь под кривой. Мы будем учиться двумя разными способами — с помощью таблицы и с помощью технологии.
Поскольку каждая нормально распределенная случайная величина имеет несколько иную форму распределения, единственный способ найти площади с помощью таблицы — это стандартизировать переменную — преобразовать нашу переменную так, чтобы ее среднее значение равнялось 0, а стандартное отклонение — 1. Как мы делаем это? Используйте z-счет!
| Z = | х — мк |
| о |
Как мы отмечали в разделе 7. 1, если случайная величина X имеет среднее значение μ и стандартное отклонение σ, тогда преобразование X с использованием z-оценки создает случайную величину со средним значением 0 и стандартным отклонением 1! Имея это в виду, нам просто нужно научиться находить области под стандартной нормальной кривой , которую затем можно применить к любой нормально распределенной случайной величине.
1, если случайная величина X имеет среднее значение μ и стандартное отклонение σ, тогда преобразование X с использованием z-оценки создает случайную величину со средним значением 0 и стандартным отклонением 1! Имея это в виду, нам просто нужно научиться находить области под стандартной нормальной кривой , которую затем можно применить к любой нормально распределенной случайной величине.
Поиск площади под стандартной кривой нормали слева
Прежде чем мы рассмотрим несколько примеров, нам нужно сначала увидеть, как работает таблица. Прежде чем мы начнем раздел, вам нужна копия таблицы. Вы можете скачать распечатанную копию этой таблицы или использовать таблицу в конце учебника. Это должно выглядеть примерно так:
Сначала это довольно ошеломляюще, но если вы посмотрите на картинку вверху (найдите минутку и проверьте ее), вы увидите, что она указывает на область слева. Это ключ — значения в середине представляют области слева от соответствующего значения z. Чтобы определить, к какому z-значению оно относится, мы смотрим влево, чтобы получить первые две цифры, и выше к столбцам, чтобы получить значение сотых. (Значения Z с большей точностью необходимо округлить до сотых, чтобы использовать эту таблицу.)
Чтобы определить, к какому z-значению оно относится, мы смотрим влево, чтобы получить первые две цифры, и выше к столбцам, чтобы получить значение сотых. (Значения Z с большей точностью необходимо округлить до сотых, чтобы использовать эту таблицу.)
Скажем, мы ищем область слева от -2,84. Для этого мы начнем со строки -2,8 и пройдемся, пока не дойдем до столбца 0,04. (См. рисунок.)
Из рисунка видно, что площадь слева от -2,84 равна 0,0023.
Поиск областей с помощью StatCrunch
Щелкните Стат. > Калькуляторы > Обычный Введите среднее значение, стандартное отклонение, x и направление неравенства. Затем нажмите Вычислить. На изображении ниже показано P (Z < 1,23). |
Давайте попробуем несколько примеров.
Пример 1
а. Найдите площадь слева от Z = -0,72
[раскрыть ответ]
Площадь слева от -0,72 примерно равна 0,2358 .
б. Найдите площадь слева от Z = 1,90
[указать ответ]
Площадь слева от 1,90 примерно равна 0,9713 .
Нахождение площади под стандартной нормальной кривой вправо
Чтобы найти области справа, нам нужно помнить правило дополнения. Уделите минутку и вернитесь к правилу из Раздела 5.2.
Поскольку мы знаем, что вся площадь равна 1,
(Площадь справа от z 0 ) = 1 — (Площадь слева от z 0 )
Пример 2
a. Найдите площадь справа от Z = -0,72
[раскрыть ответ]
| площадь справа от -0,72 | = | 1 — (область слева от -0,72) |
| = | 1 — 0,2358 | |
| = | 0,7642 |
б. Найдите площадь справа от Z = 2,68
Найдите площадь справа от Z = 2,68
[укажите ответ]
| площадь справа 2,68 | = | 1 — (площадь слева от 2,68) |
| = | 1 — 0,9963 | |
| = | 0,0037 |
Альтернативная идея заключается в использовании свойства симметрии нормальной кривой. Вместо того, чтобы смотреть вправо от Z=2,68 в примере 2 выше, мы могли бы посмотреть на область слева от -2,68 . Поскольку кривая симметрична, эти области одинаковы.
Нахождение площади под стандартной нормальной кривой между двумя значениями
Чтобы найти площадь между двумя значениями, мы разделяем ее на две части. Предположим, мы хотим найти площадь между Z = -2,43 и Z = 1,81.
Вместо этого мы найдем площадь, оставшуюся от 1,81, а затем вычтем площадь, оставшуюся от -2,43. Вот так:
Вот так:
Таким образом, площадь между -2,43 и 1,81 = 0,9649 — 0,0075 = 0,9574
Примечание: StatCrunch может рассчитать «между» вероятностями, так что вы не будете необходимо выполнить приведенный выше расчет, если вы используете StatCrunch.
Пример 3
а. Найдите площадь между Z = 0,23 и Z = 1,64. б. Найдите площадь между Z = -3,5 и Z = -3,0.
[раскрыть ответ]
область между -3,5 и -3,0 = 0,0013 — 0,0002 = 0,0011
Поиск площадей под нормальной кривой с помощью таблицы
- Нарисуйте эскиз нормальной кривой и заштрихуйте нужную область.
- Подсчитайте соответствующие Z-показатели.
- Найдите соответствующую площадь под стандартной кривой нормали.
Если вы помните, это именно то, что мы видели на демонстрации в области нормального распределения. Перейдите по ссылке и снова изучите взаимосвязь между площадью под стандартной нормальной кривой и нестандартной нормальной кривой.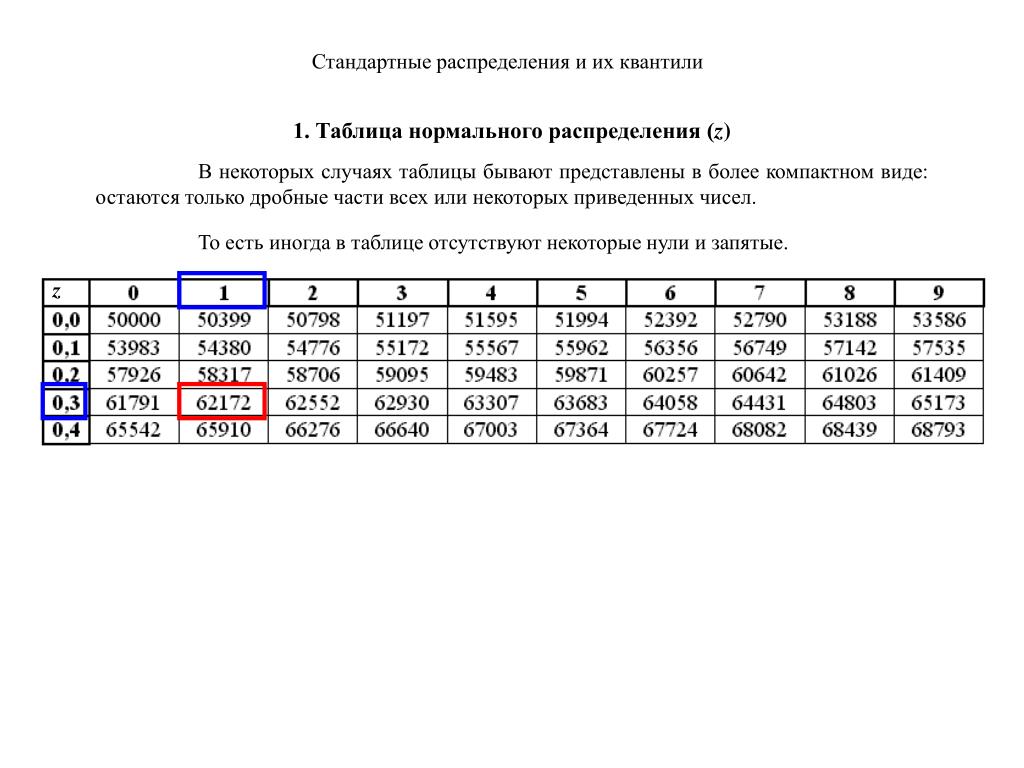
Поиск областей под кривой нормали с помощью StatCrunch
Несмотря на то, что здесь нет «стандарта» в заголовке, направления на самом деле точно такие же, как и выше!
Щелкните Стат. > Калькуляторы > Обычный Введите среднее значение, стандартное отклонение, x и направление неравенства. Затем нажмите Вычислить. На изображении ниже показано P (Z < 1,23). |
Теперь мы, наконец, добрались до настоящей причины, по которой мы изучаем нормальное распределение. Мы хотим иметь возможность отвечать на вопросы о переменных, которые имеют нормальное распределение. Вопросы типа…
- Какая доля людей являются гениями?
- Является ли систолическое артериальное давление 110 необычным?
- Какой процент лампочек определенной марки излучает от 300 до 400 люмен?
- Каков 90-й процентиль веса годовалых мальчиков?
На все эти вопросы можно ответить, используя нормальное распределение!
Пример 4
Давайте снова рассмотрим распределение IQ, которое мы рассматривали в примере 1 в разделе 7. 1.
1.
В этом примере мы видели, что тесты на коэффициент интеллекта (IQ) человека предназначены для нормального распределения со средним значением 100 и стандартным отклонением 15.
Мы также видели, что в 1916 января психолог Льюис М. Турман установил ориентир в 140 баллов (в сегодняшних тестах он был увеличен до 136) для «потенциального гения».
Используя эту информацию, какой процент людей являются «потенциальными гениями»?
Решение:
- Нарисуйте набросок кривой нормали и заштрихуйте нужную область.
- Подсчитайте соответствующие Z-показатели.
Z = Х — мк = 136 — 100 = 2,4 о 15 - Найдите соответствующую площадь под стандартной кривой нормали.

P(Z>2,4) = P(Z<-2,4) = 0,0082.
Исходя из этого, получается, что около 0,82% людей могут быть охарактеризованы как «потенциальные гении» по критериям доктора Турмана.
Пример 5
Источник: stock.xchng
В примере 2 в разделе 7.1 нам сказали, что вес годовалых мальчиков распределен приблизительно нормально, со средним значением 22,8 фунта и стандартным отклонением около 2,15. (Источник: About.com)
Если мы случайным образом выберем годовалого мальчика, какова вероятность того, что он будет весить не менее 20 фунтов?
Решение:
Давайте сделаем это с помощью технологий. Начать все же следует с наброска:
Используя StatCrunch, мы получаем следующий результат:
Согласно этим результатам вероятность того, что случайно выбранный годовалый мальчик будет весить более 20 фунтов, составляет около 0,9036.
Почему бы тебе не попробовать парочку?
Пример 6
Фото: A Syed
Предположим, что объем краски в 1-галлонных банках с краской производства Acme Paint Company приблизительно нормально распределен со средним значением 1,04 галлона и стандартным отклонением 0,023 галлона.
Какова вероятность того, что случайно выбранная 1-галлонная банка на самом деле будет содержать по крайней мере 1 галлон краски?
[ раскрыть ответ ]
В этом случае мы хотим P(X ≥ 1). Снова воспользовавшись StatCrunch, получаем следующий результат:
Согласно расчетам вероятность того, что в случайно выбранной банке окажется больше 1 галлона, составляет примерно 0,9590.
Пример 7
Предположим, что количество света (в люменах), излучаемого 40-ваттными лампами определенной марки, нормально распределено со средним значением 450 люмен и стандартным отклонением 20 люмен.
Какой процент ламп излучает от 425 до 475 люмен?
[ раскрыть ответ ]
Чтобы ответить на этот вопрос, нам нужно знать:
P(425 < X < 475)
Чтобы использовать StatCrunch, нам нужно найти вероятность быть меньше 425, а затем вычесть это из вероятности быть меньше 475:
P(X<425) :
P(X<475):
Итак, P(425 < X < 475) = 0,8944 - 0,1056 = 0,7888
Таким образом, процент излучения от 425 до 475 люмен составляет около 79%.
Поиск значений
Следующий тип вопросов исходит из другого направления. Вместо того, чтобы давать значения и спрашивать вероятность, мы теперь будем рассматривать задачи, где вероятность известна, а значения нет. Например, такие вопросы:
- Каков 90-й процентиль веса годовалых мальчиков?
- Какой показатель IQ ниже 80% всех показателей IQ?
- Какой вес должен быть у годовалого мальчика, чтобы все, кроме 5% годовалых мальчиков, весили меньше, чем он?
Как и в предыдущих типах задач, мы научимся делать это, используя как таблицу, так и технологию. Убедитесь, что вы знаете оба метода — они оба используются во многих областях науки!
Убедитесь, что вы знаете оба метода — они оба используются во многих областях науки!
Нахождение Z-показателей с помощью таблицы
Идея здесь в том, что значения в таблице представляют площадь слева, поэтому, если нас попросят найти значение с площадью 0,02 слева, мы ищем 0,02 на внутри таблицы и найдите соответствующий Z-счет.
Поскольку у нас нет площади ровно 0,02, нам нужно немного подумать. У нас есть два варианта: (1) взять ближайшую область или (2) усреднить два значения, если они равноудалены от двух областей.
В данном случае они почти равноудалены, поэтому мы возьмем среднее значение и скажем, что Z-значение, соответствующее этой области, равно среднему значению -2,05 и -2,06, поэтому -2,055 .
Определение Z-показателей с помощью StatCrunch
Щелкните Стат. > Калькуляторы > Обычный Введите среднее значение, стандартное отклонение, направление неравенства и вероятность (оставьте X пустым). |
Давайте попробуем несколько!
Пример 8
а. Найдите Z-показатель с площадью 0,9.0 влево.
[ раскрыть ответ ]
Используя обычный калькулятор в StatCrunch, мы получаем следующий результат:
Таким образом, Z-показатель с площадью 0,90 слева равен 1,28 . (Обычно мы округляем Z-значения до сотых.)
b. Найдите Z-показатель с площадью 0,10 вправо.
[ раскрыть ответ ]
Фактически это то же значение, что и в примере 7 выше! Площадь 0,10 вправо означает, что она должна иметь площадь 0,90 влево, поэтому ответ снова 1,28 .
в. Найдите такой Z-показатель, что P(Z < z 0 ) = 0,025.
[ раскрыть ответ ]
Используя StatCrunch, мы получаем следующий результат:
Таким образом, Z-счет равен -1,96 .
Итак, мы поговорили о том, как найти z-показатель по площади. Если вы помните, в технологических инструкциях не указывалось, что дистрибутив должен быть стандартным , нормальным — мы на самом деле находим значения в любое нормальное распределение , которое соответствует заданной области/вероятности с использованием тех же методов.
Пример 9
Снова обратимся к показателям IQ со средним значением 100 и стандартным отклонением 15. Найдите 90-й процентиль для показателей IQ.
Решение:
Во-первых, нам нужно перевести проблему в область или вероятность. В разделе 3.4 мы сказали, что k -й процентиль набора данных делит нижние k % набора данных из верхнего (100- к )%. Таким образом, 90-й процентиль делит нижние 90% от верхних 10%, то есть примерно 90% ниже и около 10% выше.
Используя StatCrunch, мы получаем следующий результат:
Следовательно, 90-й процентиль для показателей IQ составляет около 119.
Пример 10
Фото: A Syed
Предположим, что объем краски в 1-галлонных банках с краской производства Acme Paint Company приблизительно нормально распределен со средним значением 1,04 галлона и стандартным отклонением 0,023 галлона.
Какой объем, по словам компании Acme Paint Company, превышает 95% их банок?
[ раскрыть ответ ]
Это значение всего на 5% меньше указанного. Используя StatCrunch, мы получили следующий результат:
На основании этого расчета компания Acme Paint Company может сказать, что 95% ее банок содержат не менее 1,002 галлона краски.
Пример 11
Снова обратимся к весу годовалых мальчиков. (Вес годовалых мальчиков распределен примерно нормально, в среднем 22,8 фунта и стандартное отклонение около 2,15.)
Какой вес должен быть у годовалого мальчика, чтобы все, кроме 5% годовалых мальчиков, весили меньше, чем он?
[ раскрыть ответ ]
Снова используя StatCrunch, мы находим значение с площадью 0,95 слева:
Таким образом, годовалый мальчик должен весить около 26,3 фунтов. для всех, кроме 5% всех годовалых мальчиков, вес меньше, чем он.
для всех, кроме 5% всех годовалых мальчиков, вес меньше, чем он.
Находка z
αОбозначение z α («z-альфа») представляет собой Z-оценку с площадью α справа.
Концепция z α широко используется на протяжении оставшейся части курса, поэтому важно один, чтобы быть удобным с. Приложения не будут сразу очевидны, но суть в том, что мы будем искать события маловероятные — а так имеют очень маленькую вероятность в «хвост».
Давайте попробуем несколько примеров.
Пример 12
а. Найти z 0,01
[открыть ответ]
С помощью StatCrunch получаем следующий результат:
Следовательно, z 0,01 = 2,33
б. Найти z 0,05
[ выявить ответ]
Используя StatCrunch, мы получаем следующий результат:
Следовательно, z 0,05 = 1,64 (или 1,645)
c.

 5120
5120 4
4 7794
7794 8665
8665 9319
9319 9664
9664 2
2 9948
9948
 9995
9995 50
50 645
645 ru:
ru: Свойства, стороны, углы, признаки, периметры, равенства, подобия, хорды, секторы, площади и т.д.
Свойства, стороны, углы, признаки, периметры, равенства, подобия, хорды, секторы, площади и т.д.
 07
07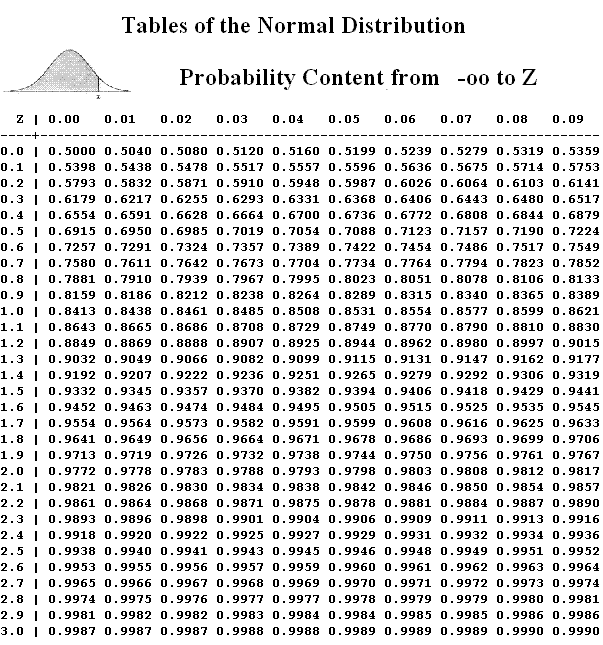 6064
6064 6
6 8212
8212 8944
8944 9429
9429 9
9 9868
9868 9946
9946 9980
9980 2
2 751
751 Введите свой запрос:
Введите свой запрос: