Таблица с косинусами и синусами: Таблицы значений основных тригонометрических функций: синуса, косинуса, тангенса, котангенса

Чётность, нечётность, периодичность тригонометрических функций

Четность, нечетность, периодичность тригонометрических функций

План урока

• Четность, нечетность тригонометрических функций;
• Исследование тригонометрических функций на четность, нечетность;
• Периодичность тригонометрических функций;
• Определение периода тригонометрических функций.

Цели урока

• Знать определение четности, нечетности, периодичности функций, в том числе тригонометрических функций;
• Уметь исследовать функцию на четность, нечетность, находить период тригонометрических функций.

Разминка

1. Найти область определения функций y=4cosx-π3; y=tg x+2π7.
2. Найти множество значений функции y=cos x-sin x2.
3. Назовите формулы синуса, косинуса, тангенса, котангенса отрицательных аргументов.
4. Что такое четная функция? Нечетная функция?

Четность, нечетность тригонометрических функций

 

В курсе основной школы были изучены такие понятия, как четность, нечетность функций.

Напомним их.

---

Функция y=f(x) называется  четной , если для каждого значения x из ее области определения выполняется равенство f(-x)=f(x).

 

Функция y=f(x) называется  нечетной , если для каждого значения x из ее области определения выполняется равенство f(-x)=-f(x).

---

Областью определения функций y=sin x, y=cos x является множество R всех действительных чисел и кроме того для любого значения x справедливы равенства sin(-x)=-sin x, cos(-x)=cos x. Тогда функция y=sin x – нечетная функция, а y=cos x – четная. Областью определения функции y=tg x является множество всех действительных чисел, кроме x=π2+πn, n∈Z и в каждой точке области определения верно равенство tg(-x)=-tg x. Тогда функция y=tg x – нечетная. Аналогично рассуждая, получим, что на множестве R за исключением чисел x=πn, n∈Z функция y=ctg x – нечетная.

---

Пример 1

Выяснить, является ли четной, нечетной или не является ни четной, ни нечетной функция:

 

1) f(x)=3×4+3cos x;

2) f(x)=2sin x1+cos x.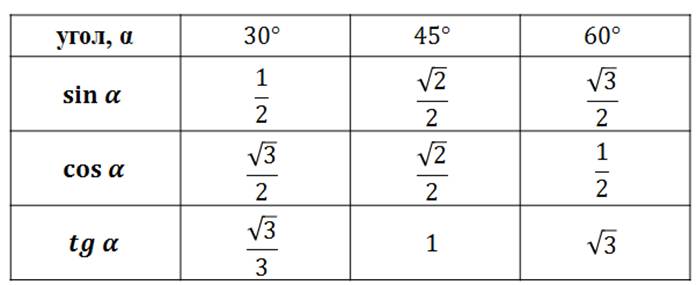

---

Решение

 

1) Функция определена на множестве всех действительных чисел. Найдем f(-x) и сравним с f(x).

f-x=3-x4+3cos-x=3×4+3cos x=f(x).

Значит, данная функция является четной.

 

2) Область определения функции Df:1+cos x≠0, откуда x≠π+2πn, n∈Z.

f-x=2 sin-x1+cos-x=-2sin x1+cos x=-2 sin x1+cos x=-fx.

Функция f(x)=2sin x1+cos x – нечетная.

 

Ответ: 1) четная; 2) нечетная.

---

Упражнение 1

Выяснить, является ли четной, нечетной или не является ни четной, ни четной функция:

 

1) y=51-2sin x;

2) y=3+sin x-cos x.

---

Известно, что для любого действительного x справедливы равенства sinx+2π=sin x, cosx+2π=cos x, т.е. если периодически изменять аргумент на 2π, то значения синуса и косинуса будут повторяться. Такие функции называются периодическими с периодом 2π.

---

Функция f(x) называется периодической, если существует такое ненулевое число T, что для любого x из области определения этой функции выполняется равенство fx-T=fx=fx+T. Число T называется периодом функции f(x).

---

Из определения следует, что если x принадлежит области определения fx, то и числа x-T, x+T (а вообще говоря, числа x+Tn, n∈Z) также принадлежат области определения этой периодической функции, fx+Tn=fx, n∈Z.

Функции y=tg x, y=ctg x являются периодическими с периодом T=π.

---

Пример 2

Докажите, что функция является периодической с периодом T.

 

1) f(x)=sin x2, T=4π;

2) f(x)=sin 2x+cosx, T=π.

---

Решение

 

1) Функция определена на всей числовой оси. Докажем, что для любого действительного числа x выполняется равенство fx+T=fx.

fx+4π=sinx+4π2=sinx2+2π=sin x2=fx.

 

Итак, равенство  f(x+T)=f(x) выполняется для любого x из области определения. Аналогично f(x-T)=f(x). Значит, T=4π — период данной функции.

 

2) Для преобразования формулы, задающей функцию, воспользуемся формулой синуса двойного аргумента и вынесем общий множитель за скобки.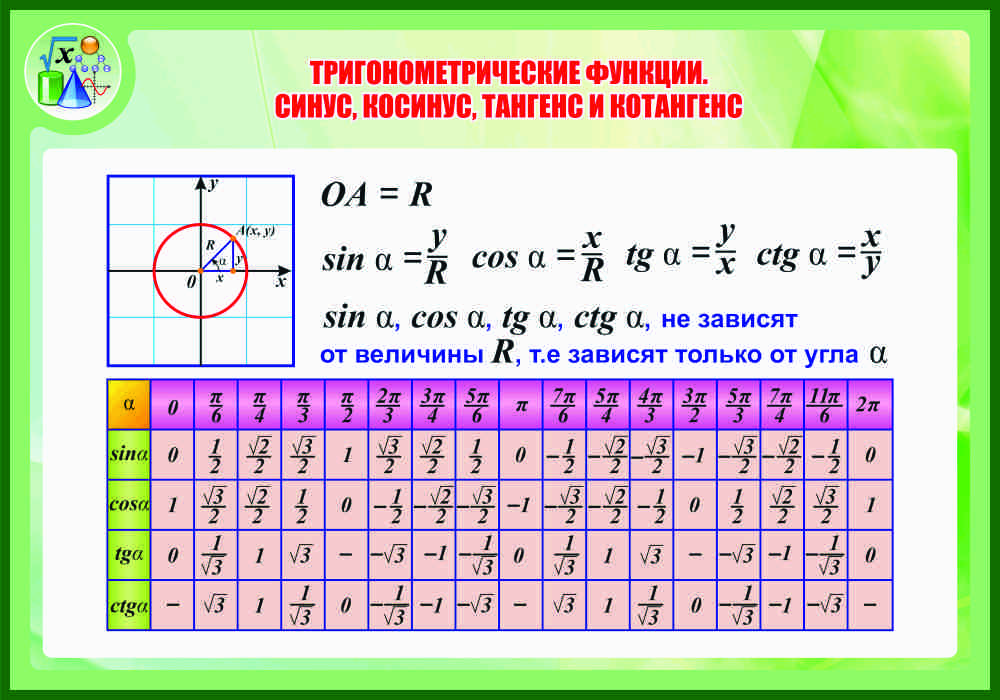

f(x)=cos x 2sin x+1.

 

Функция определена на всей числовой оси. Докажем выполнение равенства f(x+T)=f(x) для каждой точки области определения.

fx+π=cos x+π2 sinx+π+1=

=-cos x -2 sin x+1=cos x 2 sin x+1=f(x) .

 

Равенство fx+T=f(x) выполняется для любого x из области определения. Аналогично, f(x-T)=f(x), т.е. T=π – период данной функции.

---

Пример 3

Найти наименьший положительный период функции fx=sin 23 x.

---

Решение

 

Функция определена на всей числовой оси. Так как она периодическая, то для каждой точки области определения выполняется равенство fx+T=fx, т.е. sin23x+T=sin23x,

sin23x+23T=sin23x, отсюда 23T=2π, T=3π.

 

Ответ: 3π.

---

Чтобы лучше запомнить, какая из тригонометрических функций будет четной, какая – нечетной, а также наименьший положительный период, заполним следующую таблицу.

 

Таблица четности, нечетности, периодичности тригонометрических функций

 

Функция	Четность, нечетность	Наименьший  положительный период
y=sinx	Нечетная
y=cosx	Четная
	Нечетная
y=ctgx	Нечетная

---

Упражнение 2

1. Доказать, что функция является периодической с периодом T.

 

1) y=sin34x, T=8π3;

2) y=sin 5x-cos 5x, T=2π5;

3) y=tg 3x-2π3, T=π3;

4) y=tg x, T=π.

 

2. Найти наименьший положительный период функций: 

 

1) y=6-sin x;

2) y=cos 4x.

---

Контрольные вопросы

 

1. Какие из тригонометрических функций являются четными? Нечетными?
2. Назовите наименьший положительный период каждой тригонометрической функции.

---

Ответы

Упражнение 1

 

1. ни четная, ни нечетная;

2. ни четная, ни нечетная.

 

Упражнение 2

 

2.  1) 2π; 2) π2.

таблиц синус-косинусоидальных триггеров

таблиц синус-косинусоидальных триггеров

Таблицы синуса и косинуса

для углов в градусах

Для синуса прочтите первые 6 столбцов.
Для косинуса прочтите последние 6 столбцов.

6

6

1 5 0,004000110 0,14610 0,14100010 0.15300 14 9 300100011 0,3778000114 0.00110 9.0011 3100111 0.00117 0.00110 9.0011205 5

0011

7 0,

011

angle	angle + .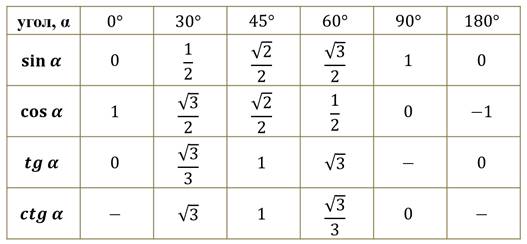 0	angle +.2	angle +.4	angle +.6	angle + .8	angle +1.0
0	0.0000	0.0035	0.0070	0.0105	0.0140	0.0175	89
1	0.0175	0.0209	0.0244	0.0279	0.0314	0.0349	88
2	0,0349	0,0384	0,0419	0,0454	0,0488	0,0523	87
3	0.0523	0.0558	0.0593	0.0628	0.0663	0.0698	86
4	0.0698	0.0732	0.0767	0.0802	0.0837	0.0872	85
5	0,0872	0,0906	0,0941	0,0976	0,1011	84
6	0. 1045	0.1080	0.1115	0.1149	0.1184	0.1219	83
7	0.1219	0.1253	0.1288	0.1323	0.1357	0,1392	82
8	0,1392	0,1426	0,1461	0.1564	81
9	0.1564	0.1599	0.1633	0.1668	0.1702	0.1736	80
10	0.1736	0.1771	0.1805	0,1840	0,1874	0,1908	79
11	0,1908	0,19142	0.1977	0.2011	0.2045	0.2079	78
12	0. 2079	0.2113	0.2147	0.2181	0.2215	0.2250	77
13	0.2250	0,2284	0,2317	0,2351	0,2385	0,2419	76
0.2419	0.2453	0.2487	0.2521	0.2554	0.2588	75
15	0.2588	0.2622	0.2656	0.2689	0.2723	0.2756	74
16	0,2756	0,2790	0,2823	0,2857	0,2890	0,2924
17	0.2924	0.2957	0.2990	0.3024	0.3057	0.3090	72
18	0.3090	0. 3123	0.3156	0.3190	0.3223	0.3256	71
19	0,3256	0,3289	0,3322	0,3355	7 0.0011	0.3420	70
20	0.3420	0.3453	0.3486	0.3518	0.3551	0.3584	69
21	0.3584	0.3616	0.3649	0.3681	0,3714	0,3746	68
22	0,3746	0,3778	0.0011	0.3843	0.3875	0.3907	67
23	0.3907	0.3939	0.3971	0.4003	0.4035	0.4067	66
24	0.4067	0. 4099	0,4131	0,4163	0,4195	0,4226	65
25	26 0.0011	0.4258	0.4289	0.4321	0.4352	0.4384	64
26	0.4384	0.4415	0.4446	0.4478	0.4509	0.4540	63
27	0,4540	0,4571	0,4602	0,4633	0,4664	0,4695	161200009	28	0.4695	0.4726	0.4756	0.4787	0.4818	0.4848	61
29	0.4848	0.4879	0.4909	0.4939	0.4970	0.5000	60
30	0,5000	0,5030	0,5060	0,5090	0,5110	0	59
31	0. 5150	0.5180	0.5210	0.5240	0.5270	0.5299	58
32	0.5299	0.5329	0.5358	0.5388	0.5417	0,5446	57
33	0,5446	0,5476	0,5505	0.5563	0.5592	56
34	0.5592	0.5621	0.5650	0.5678	0.5707	0.5736	55
35	0.5736	0.5764	0.5793	0,5821	0,5850	0,5878	54
36	0,5878	0.5934	0.5962	0.5990	0.6018	53
37	0.6018	0.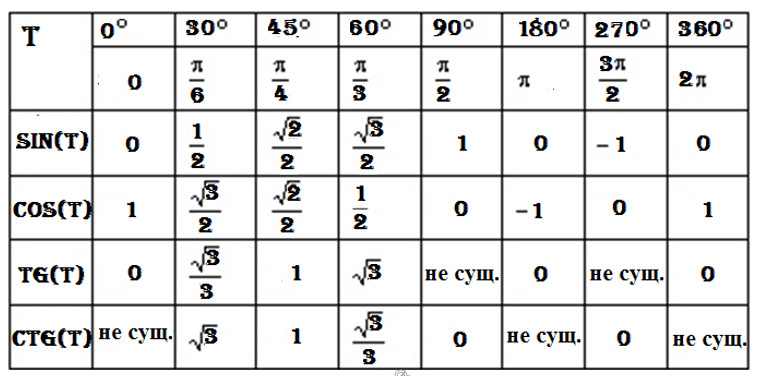 6046	0.6074	0.6101	0.6129	0.6157	52
38	0.6157	0,6184	0,6211	0,6239	0,6266	0,6293	51
011	0.6293	0.6320	0.6347	0.6374	0.6401	0.6428	50
40	0.6428	0.6455	0.6481	0.6508	0.6534	0.6561	49
41	0,6561	0,6587	0,6613	0,6639	0,6665	0,6691	0010 48
42	0.6691	0.6717	0.6743	0.6769	0.6794	0.6820	47
43	0.6820	0.6845	0. 6871	0.6896	0.6921	0,6947	46
44	0,6947	0,6972	0,6997	0,7012	0.7046	0.7071	45
45	0.7071	0.7096	0.7120	0.7145	0.7169	0.7193	44
46	0.7193	0.7218	0.7242	0,7266	0,7290	0,7314	43
47	0,7314	0,70137	0.7361	0.7385	0.7408	0.7431	42
48	0.7431	0.7455	0.7478	0.7501	0.7524	0.7547	41
49	0.7547	0,7570	0,7593	0,7615	0,7638	0,7660	40
150 9	0. 7660	0.7683	0.7705	0.7727	0.7749	0.7771	39
51	0.7771	0.7793	0.7815	0.7837	0.7859	0.7880	38
52	0,7880	0,7902	0,7923	0,7944	0,7965	0,7986
53	0.7986	0.8007	0.8028	0.8049	0.8070	0.8090	36
54	0.8090	0.8111	0.8131	0.8151	0.8171	0.8192	35
55	0,8192	0,8211	0,8231	0,8251
0.8290	34
56	0.8290	0. 8310	0.8329	0.8348	0.8368	0.8387	33
57	0.8387	0.8406	0.8425	0.8443	0,8462	0,8480	32
58	0,8480	0,8499	0.8536	0.8554	0.8572	31
59	0.8572	0.8590	0.8607	0.8625	0.8643	0.8660	30
60	0.8660	0.8678	0,8695	0,8712	0,8729	0,8746	29
61	0.8763	0.8780	0.8796	0.8813	0.8829	28
62	0.8829	0.8846	0. 8862	0.8878	0.8894	0.8910	27
63	0,8910	0,8926	0,8942	0,8957	0,8973	0,8988	26	26	0009	64	0.8988	0.9003	0.9018	0.9033	0.9048	0.9063	25
65	0.9063	0.9078	0.9092	0.9107	0.9121	0.9135	24
66	0,9135	0,9150	0,9164	0,9178	0,	23
67	0.9205	0.9219	0.9232	0.9245	0.9259	0.9272	22
68	0.9272	0.9285	0.9298	0. 9311	0.9323	0,9336	21
69	0,9336	0,9348	0,9361	9,0373	0.9385	0.9397	20
70	0.9397	0.9409	0.9421	0.9432	0.9444	0.9455	19
71	0.9455	0.9466	0.9478	0,9489	0,9500	0,9511	18
72	0,9511	9,0011521	0.9532	0.9542	0.9553	0.9563	17
73	0.9563	0.9573	0.9583	0.9593	0.9603	0.9613	16
74	0.9613	0,9622	0,9632	0,9641	0,9650	0,9659	7	0. 9659	0.9668	0.9677	0.9686	0.9694	0.9703	14
76	0.9703	0.9711	0.9720	0.9728	0.9736	0.9744	13
77	0,9744	0,9751	0,9759 ​​	0,9767	0,9774	0,9781	0010 12
78	0.9781	0.9789	0.9796	0.9803	0.9810	0.9816	11
79	0.9816	0.9823	0.9829	0.9836	0.9842	0,9848	10
80	0,9848	0,9854	0,9860	0,	0.9871	0.9877	9
81	0.9877	0.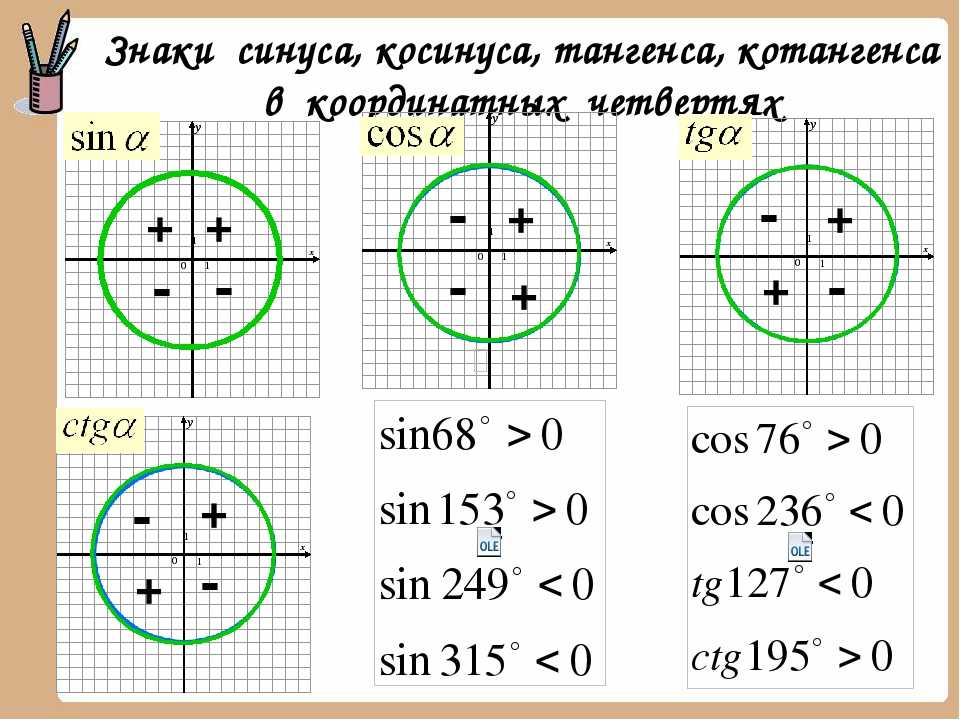 9882	0.9888	0.9893	0.9898	0.9903	8
82	0.9903	0.9907	0.9912	0,9917	0,9921	0,9925	7
83	0,9925		0,			0.9938	0.9942	0.9945	6
84	0.9945	0.9949	0.9952	0.9956	0.9959	0.9962	5
85	0.9962	0.9965	0,9968	0,9971	0,9973	0,9976	4
86	0.9978	0.9980	0.9982	0.9984	0.9986	3
87	0.9986	0.9988	0.9990	0. No related posts. Добавить комментарий Отменить ответ Ваш адрес email не будет опубликован. Обязательные поля помечены * Комментарий * Имя * Email * Сайт