Тригонометрические формулы. Таблица углов. Формулы приведения
Факт 1.
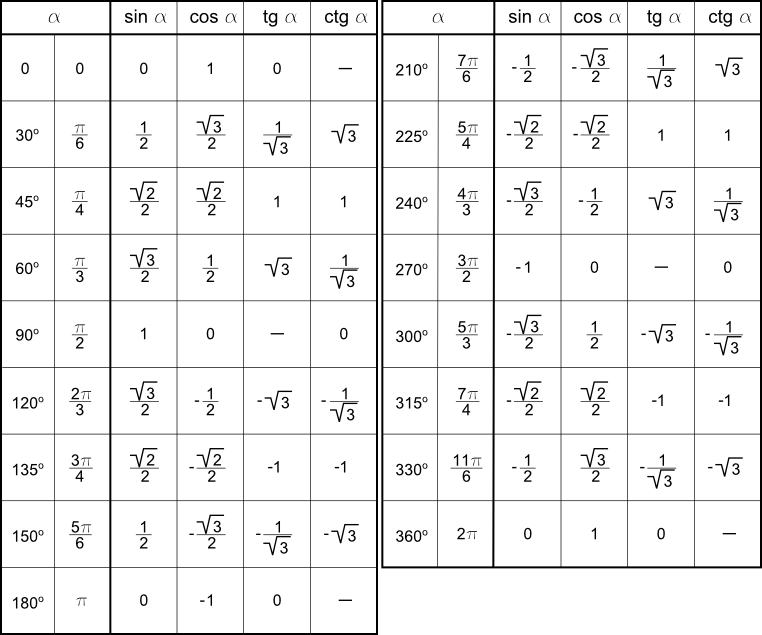
\(\bullet\) Таблица синусов, косинусов, тангенсов и котангенсов углов из первой четверти:
Факт 2.
\(\bullet\) Знаки синуса, косинуса:
Так как \(\mathrm{tg}\,\alpha=\dfrac{\sin\alpha}{\cos\alpha}\) и \(\mathrm{ctg}\,\alpha=\dfrac{\cos\alpha}{\sin\alpha}\), то тангенс и котангенс положительны в \(I\) и \(III\) четвертях и отрицательны во \(II\) и \(IV\) четвертях.
Факт 3.
Формулы приведения.
\(\bullet\) Случай 1. Если угол можно представить в виде \(n\cdot \pi\pm \alpha\), где \(n\in\mathbb{N}\), то \[\sin(n\cdot \pi\pm
\alpha)=\bigodot \sin\alpha\] где на месте \(\bigodot\) стоит знак синуса угла \(n\cdot \pi\pm \alpha\). \[\cos(n\cdot \pi\pm
\alpha)=\bigodot \cos\alpha\] где на месте \(\bigodot\) стоит знак косинуса угла \(n\cdot \pi\pm \alpha\).
Знак угла можно найти, определив, в какой четверти он находится.
Знак определяется таким же образом, как и в случае \(1\).
Заметим, что в первом случае функция остается неизменной, а во втором случае — меняется (говорят, что функция меняется на кофункцию).
Алгоритм применения формул приведения для тангенса и котангенса полностью аналогичен.
Пример 1. Найти \(\cos \dfrac{13\pi}{3}\).
Преобразуем угол: \(\dfrac{13\pi}{3}=\dfrac{12\pi+\pi}{3}=4\pi+\dfrac{\pi}3\), следовательно, \(\cos \dfrac{13\pi}{3}=\cos \left(4\pi+\dfrac{\pi}3\right)=\cos\dfrac{\pi}3=\dfrac12\)
Пример 2.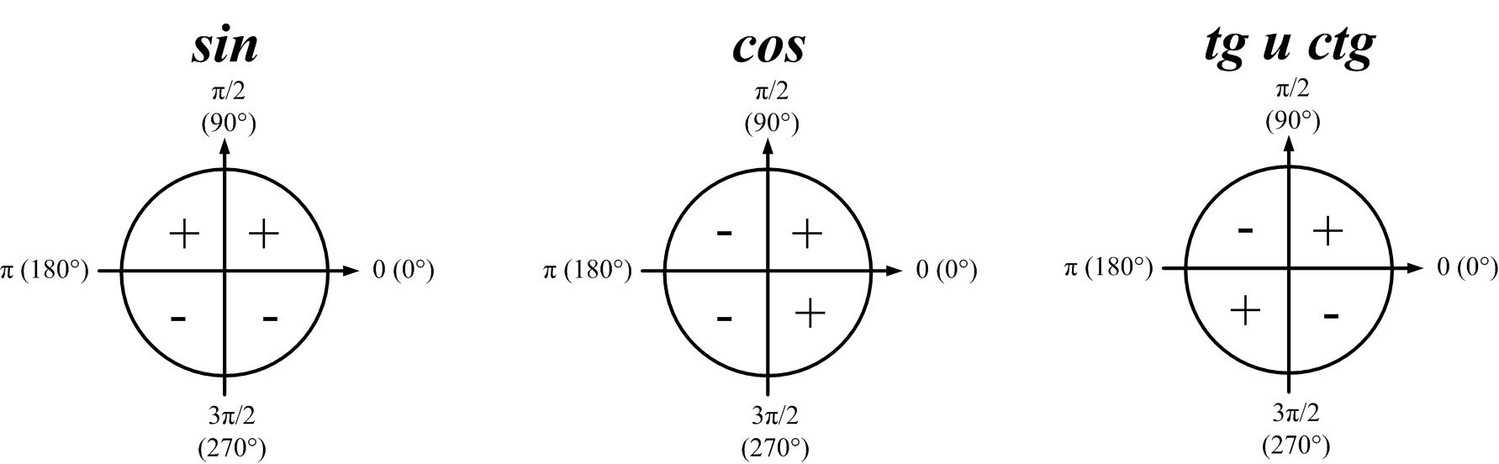
Найти \(\sin \dfrac{17\pi}{6}\).
Преобразуем угол: \(\dfrac{17\pi}{6}=\dfrac{18\pi-\pi}{6}=3\pi-\dfrac{\pi}6\), следовательно, \(\sin \dfrac{17\pi}{6}=\sin \left(3\pi-\dfrac{\pi}6\right)=\sin\dfrac{\pi}6=\dfrac12\)
Пример 3. Найти \(\mathrm{tg}\,\dfrac{15\pi}4\).
Преобразуем угол: \(\dfrac{15\pi}4=\dfrac{16\pi-\pi}4=4\pi-\dfrac{\pi}4\), следовательно, \(\mathrm{tg}\,\dfrac{15\pi}4=\mathrm{tg}\left(4\pi-\dfrac{\pi}4\right)= -\mathrm{tg}\,\dfrac{\pi}4=-1\)
Пример 4. Найти \(\mathrm{ctg}\,\dfrac{19\pi}3\).
Преобразуем угол: \(\dfrac{19\pi}3=\dfrac{18\pi+\pi}3=6\pi+\dfrac{\pi}3\), следовательно, \(\mathrm{ctg}\,\dfrac{19\pi}3=\mathrm{ctg}\left(6\pi+\dfrac{\pi}3\right)= \mathrm{ctg}\,\dfrac{\pi}3=\dfrac{\sqrt3}3\)
столбцов | Японская математика периода Эдо
Тригонометрические функции происходят из тригонометрии , которая имеет дело с отношениями между шестью типами отношений, мыслимых для прямоугольного треугольника, и включает шесть типов функций, которые связывают значения таких отношений с угол.
Термин тригонометрия означает съемку треугольника. Предшественник тригонометрических функций уже можно было увидеть в Древнем Египте 4000 лет назад, а их концепцию можно было также увидеть в астрономии Вавилона и Греции.
Книга под названием Арьябхатия , написанная в Индии в шестом веке, описывает метод вычисления значений синусов различных углов и ясно признает это понятие типом тригонометрической функции. Считается, что тригонометрические функции Индии были переданы в Европу через Аравию и что используемые сегодня обозначения sin, cos и tan были изобретены в Европе.
Они были переданы в Японию через книги по математике и астрономии, написанные на голландском языке, и через китайские переводы европейской математики и астрономии, переданные в Китай (в таких книгах, как Чунчжэн лишу ). Они в основном использовались в астрономических расчетах, геодезии и навигации и часто появлялись в книгах по физике в Европе. Поскольку тригонометрические функции представляют собой соответствие между углами и числами, они не могли бы родиться без понятия угла.
Однако Васану не хватало концепции угла. Направления указывались путем соотнесения их с двенадцатью хорарными знаками, но, поскольку они не были определены количественно, промежуточные направления не могли быть точно выражены. Углы использовались только в области астрономии, геодезии и навигации.
Тригонометрические таблицы — это таблицы, в которых перечислены значения синуса (sin), косинуса (cos) и тангенса (tan) для заданного угла. Птолемей ( c .85- c .165) в Древней Греции перечислил значения синусов в Альмагесте . Более точно, эта таблица называется таблицей хорд , в которой перечислены хорды, умноженные на две длины стороны, противоположной углу (центральному углу), удвоенной заданному углу прямоугольного треугольника (окружности), гипотенуза (радиус ) имеет длину 60,
Рисунок, показывающий отношения между таблицей хорд и тригонометрическими функциями
В таблице хорд Птолемея (Птолемея) указана Crdθ, длина хорды AB, которая соответствует ∠AOB, и она рассчитана в предположении, что OA=OB=60.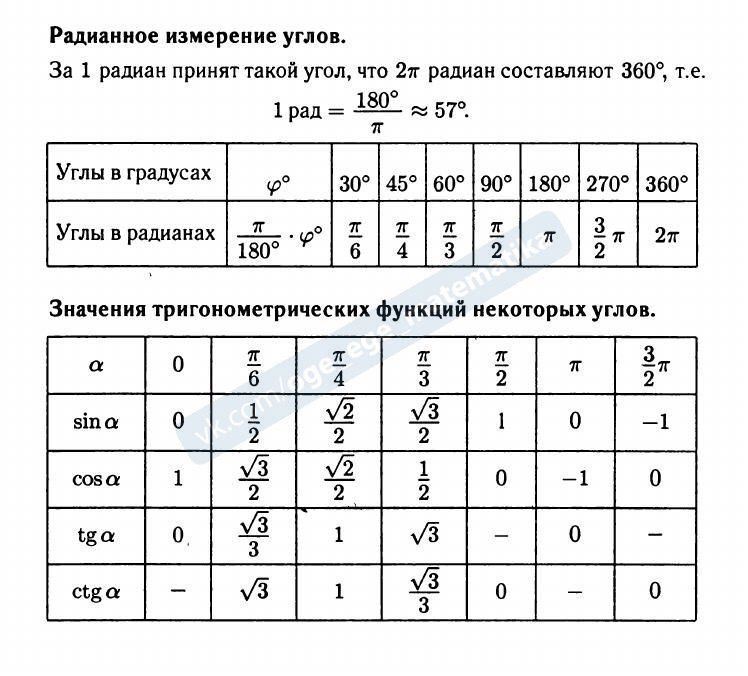
Например, мы видим такие значения, как
в таблице.
С другой стороны, поскольку sin x определяется как sin∠AOM=AM, когда OA=1, существует соотношение Crd θ=2×60 sin θ/2. Из Crd 60°=60 следует, что 120 sin 30°=60 или
,
Мы могли бы получить текущую таблицу синусов, разделив каждый угол пополам и разделив длину каждой хорды на 120 в таблице. Птолемей также описал метод расчета, использованный для создания таблицы в Almagest , и начал с таких углов, как 30°, 45° и 60°, которые было легко вычислить, и вычислил значения как длины сторон правильного пятиугольник и правильный десятиугольник для 36° и 72°. Кроме того, он вывел формулу, с помощью которой можно вычислить длины хорд для суммы и остатка двух углов, используя теорему, называемую Теорема Птолемея и формула для вычисления длины хорды для угла, который составляет половину заданного угла (длины хорды для суммы и остатка углов).
Затем можно вычислить значения синуса для 12°, 6°, 3°, 1,5° и т. д. Затем он показал, что значение синуса для 0,5° больше, чем в 2/3 раза, чем для 0,75°, и меньше, чем в 4/3 раза, чем для 0,375°, и доказал, что эти два значения совпадают расчетным путем. Таким образом, Птолемей перечислил длину каждой хорды для центральных углов от 0° до 180° в единицах 0,5° (следовательно, значения синусов для 0° до 9°0° с шагом 0,25°).
Глядя на значение для центрального угла 120°, например, в этой таблице, он описывает интерполяцию, что длина хорды для центрального угла 120° составляет 103;55,23 и увеличивается с приращением ;0,31,18 по мере увеличения угла с приращением . Здесь интересно то, что дробная часть длины представлена в шестидесятеричной системе , и причина, по которой радиус установлен равным 60, заключается в том, что вычисления могут быть упрощены при интерполяции. Для справки, первый десятичный знак назывался partes minutae primae , а второе десятичное место называлось partes minutae secundae
в средневековой Европе.
Minutus — прилагательное, означающее «дробный». Именно поэтому первое подразделение времени и углов называется «минутой», а второе подразделение называется «секундой». Затем давайте вычислим sin 60° с помощью этой таблицы. Так как sin 60° это половина длины хорды для центрального угла 120° окружности с радиусом 1, при делении длины хорды
на 120 получаем
и находим, что оно идентично .
В Индии сторона, противоположная углу (половина хорды), называлась « джйа », а в арабском мире она транскрибировалась и называлась « джаиб ». Поскольку этот звук означает «залив» на арабском языке, латинское слово « sinus » для «залива» использовалось, когда это слово было переведено на латынь в двенадцатом веке. Так в Европе начались исследования по тригонометрии, в которых правильную хорду называли синусом или синусом. Среди прочих, астрономы усердно изучали тригонометрию, и Иоганнес Мюллер (1436-1476), известный как Региомонтан, написал первый учебник по тригонометрии
) и опубликовал первые тригонометрические таблицы Tabula directionum (1490 г.). Opus palatinum Г. Ретикуса (1514-1576), опубликованный в 1596 году, представлял собой сборник тригонометрических и тригонометрических таблиц объемом более 1400 страниц. Говорят, что Коперник и Кеплер создали революционные теории в астрономии, используя тригонометрические таблицы. Считается, что первыми тригонометрическими таблицами в Японии были Санреки закко от Такебе Катахиро (1664-1739). Такебе Катахиро, известный вычислением числа Пи, создал таблицу полуаккордов, полученную путем вычисления значений греха x в единицах 1 градуса с точностью до одиннадцати знаков после запятой, используя значение числа Пи. Такебе назвал один градус один gen , и, поскольку он вычислил значения, используя круг диаметром 1, длина полухорды была sin x shaku . Такебе создал таблицу, как показано на рисунке, основанную на вычислении длины дуги, сагитты и полухорды в единицах 1 9.
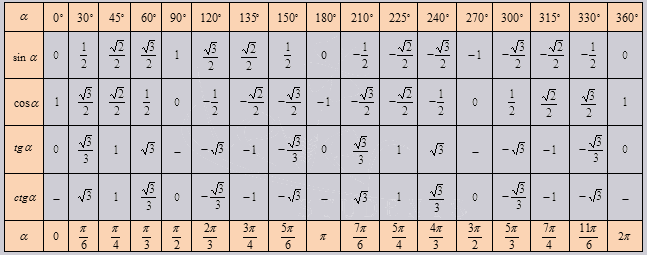0007 ген . Эта книга была воспроизведена в Takebe Katahiro’s Sanreki zakko (1995) Сато Кеничи.Фигурка для дуги, сагитты и полуаккорда от Takebe
Такебе открыл формулу, которая находит половину дуги ( hanse ) из диаметра d и сагитты c , формулу, которая находит стрелу из половины дуги и диаметра d, и другие. Он также вычислил, что АМ или длина полухорды для угла 1° составляет 0,0087262032187, а для угла 2° — 0,0161679.…, …, что для 30° было 0,25, что для 45° было 0,35355339…, что для 60° было 0,433012701…, и так далее, в предположении, что длина дуги для угла 1° была 0,00872664626 в окружности с диаметр 1
Поскольку это длины полухорд для диаметра 1, полная хорда (синус) в 2 раза больше этих значений.
Тригонометрические таблицы, фактически используемые в нашей стране, были китайскими переводами тригонометрических таблиц, используемых в Европе и называемых Катсуен Хассен Хё .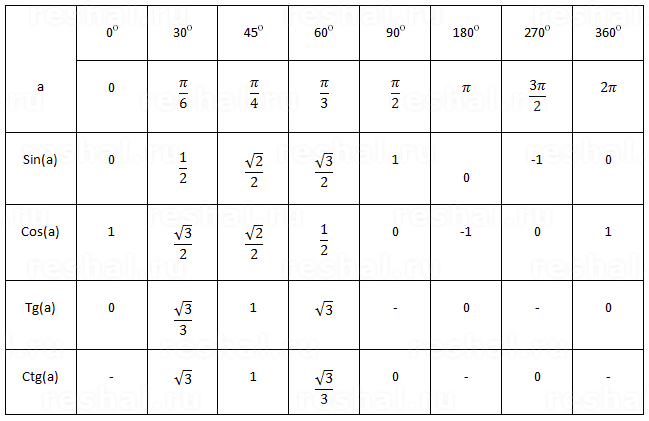
Hassen означает восемь типов значений, показанных на рисунке, и совокупный термин синуса (sin x ), косинуса (cos x ), , , , , версинуса (1-cos x ) и закрытого синус (1-sin x ).
Хассен
На рисунке предполагается, что OA=OP=OB=radius=1,
определено следующее обозначение:
Seigen (синус) = PR = sin x , Yogen (косинус) = DP = cos x
Seisetsu (тангенс)=AT=tan x ,
Seiya (стих)=RA=1-cos x , Yoya (покрытый синус)=QP=1-sin x .
Тогда по теореме Пифагора получаем sin 2 x +cos 2 x =1.
Здесь есть два типа таблиц, в которых предполагается, что прямой угол равен 90 градусам: одна таблица использует одну минуту, полученную путем деления одного градуса на 60, а другая использует одну минуту, полученную путем деления одного градуса на 100. Katsuen hyo (1857) Мори Масакадо, как показано на рисунке, принимает один градус за 60 минут, а Shinporekisho zokuhen (1846) Сибукавы Кагесуке (1787-1856) принимает один градус за 100 минут.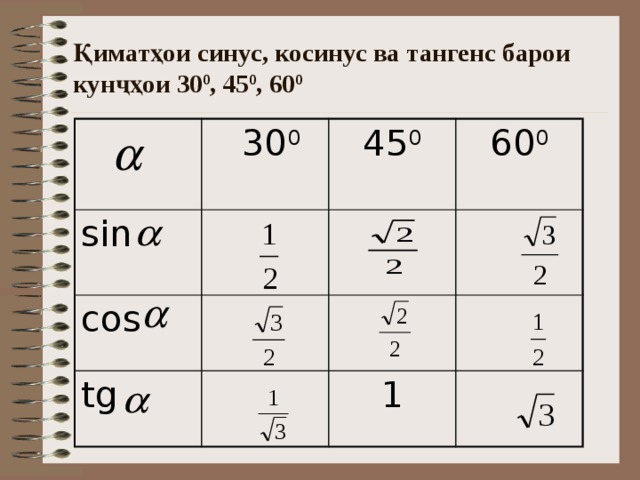
Katsuen hassen hyo знаменит тем, что Ино Тадатака (1745-1818), хорошо известный нам своей картографией Японии, возил его при межевании земли. Информацию об использовании тригонометрических таблиц в геодезии и картографии можно найти в колонке «Методы съемки».
Поскольку в астрономии используется сферическая тригонометрия, мы находим множество умножений тригонометрических функций. Была создана таблица логарифмов для тригонометрических функций, которая использовалась для преобразования умножений в сложения, и эта таблица также была импортирована и представлена в Японии. Тригонометрические таблицы необходимы при решении трансцендентных уравнений типа sin x = x + b , которое появляется при нахождении длины хорды, делящей окружность на три равные части. Поскольку тригонометрические таблицы теперь встроены в электронные таблицы, с их помощью можно просто решить задачу о делении круга на три равные части.
Синус, косинус и измерение Земли
Метки:
Аль-Баттани — Астрономия — Махбуб Гани — Математики — Математика — Насир ад-Дин ат-Туси — Тригонометрия — Математика долгое время была областью знаний мусульманских математиков.
В этой статье рассматривается вклад Ат-Туси, Аль-Баттани и других в тригонометрию, с акцентом на прогресс, представленный их открытиями, по сравнению с древней традицией, отраженной в Альмагесте Птолемея.
Махбуб Гани*
Рисунок 1: Страница книги Османского альманаха времен правления Баязида II. Библиотека-музей дворца Топкапы, R 1711. |
Именно в школе большинство из нас впервые заигрывали с тригонометрией, попутно впервые получив в руки научный калькулятор для определения синусов, косинусов и тангенсов углов. Для некоторых из нас — может быть, правильнее сказать, лишь для некоторых — эти странные функции были встречены с восторгом и ликованием, представляя собой первую настоящую встречу с нетривиальной математикой. В большинстве случаев изложение тригонометрии проводится в контексте задач на треугольники, которые довольно быстро становятся повторяющимися и скучными.
Следовательно, многие студенты не осознают решающей актуальности и важности тригонометрии в решении более интересных и сложных задач, взятых из астрономии, картографии и навигации, если назвать несколько областей. Более того, весело определяя неизвестные углы и стороны треугольников с полной зависимостью от калькулятора, мы не перестаем задаваться вопросом, как, скажем, синус того или иного угла можно было вычислить без вычислительной машины, полагаясь на ручку, бумагу и человеческую смекалку. один.
Рождение тригонометрии связано с астрономией, одной из наиболее активно изучаемых мусульманами наук, в частности из-за ее важности для определения точного времени ритуальных молитв. Но еще до мусульман греческие астрономы вычисляли неизвестные стороны и углы определенных треугольников, зная значения остальных сторон или углов, чтобы понять движение солнца, луны и пяти известных тогда планет.
Вдохновленные такими вопросами, как положение солнца, луны и планет, греки составляли таблицы и правила, которые позволяли решать задачи геометрического характера.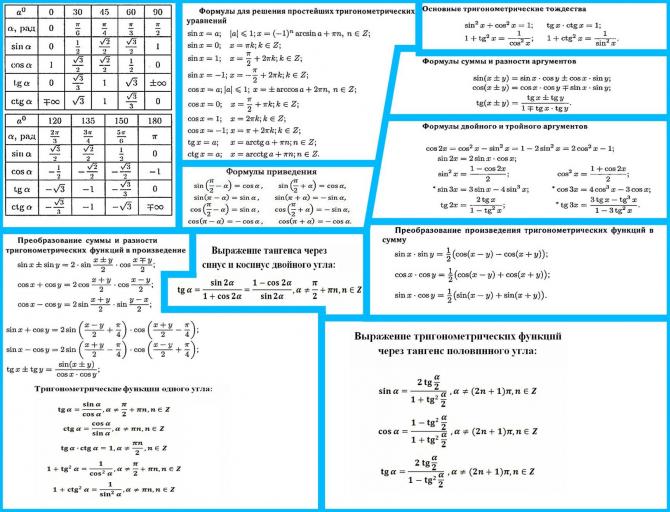
Наиболее полное изложение предмета можно найти в Альмагест Птолемея, астронома, работавшего в Александрии в начале второго века н.э. Трактат Птолемея попал к европейским ученым через мусульман, которые передали оригинальное греческое название (что означало Великое устройство ) в более кратких и превосходных терминах с помощью комбинации транслитерации и предваряющих слов, чтобы получить Al-Majest , просто означающее The Greatest , таким образом, отражая почетное положение, которое эта работа занимала в мусульманских научных кругах. Астрономы-эллинисты в основном опирались на таблицу, найденную в Книге I из Альмагест , который был обозначен как «Таблица аккордов в круге», для решения всех их плоских тригонометрических задач. Для дуг при углах с шагом от полградуса до 180 градусов в таблице приведены длины хорд, стягивающих углы в окружности радиусом 60 единиц. В своей работе The Transversal Figure мусульманский астроном тринадцатого века Насир ад-Дин ат-Туси объясняет, как эта таблица длин хорд используется для решения задач, связанных с прямоугольными треугольниками.
Ат-Туси делает важное наблюдение, устанавливающее связь между треугольниками и дугами окружностей: любой треугольник можно вписать в окружность, и поэтому его стороны можно рассматривать как хорды, стягивающие дуги, противоположные углам треугольника. Недостаток такой зависимости от этих таблиц был двояким. Во-первых, потребовались значительные манипуляции с таблицей и промежуточные шаги, чтобы решить все вариации, которые могли возникнуть при решении неизвестных длин или углов прямоугольного треугольника. Это контрастирует с использованием шести знакомых тригонометрических функций — синуса, косинуса и тангенса и их обратных величин, секанса, косеканса и котангенса — характерных для современных методов, которые впервые были разработаны и систематизированы мусульманскими математиками. Второе неудобство таблиц длин хорд заключается в том, что они часто требовали удвоения углов для расчета длины дуги.
Рисунок 2: Миниатюрные изображения Саур (Телец) и Джауза (Близнецы). |
Мирзазаде Салим Эфенди. Икд аль-Джуман фи тарих ахль аз-заман . Библиотека Стамбульского университета, T 5393.На самом деле, цепь мусульманских ученых еще до 10 -го -го века уже заложила основы тригонометрии, проложив путь Насиру ад-Дину ат-Туси к сбору, систематизации и разработке вкладов. Это был Мухаммед ибн Джабир ибн Синан Абу Абдулла, известный как Аль-Баттани, поскольку он родился в Баттане, Месопотамия, и он является одной из самых влиятельных фигур в тригонометрии. Он считается одним из величайших мусульманских астрономов и математиков, в конце концов умер в Дамаске в 9 г.29 г. н.э. Его мотивацией для первопроходцев в изучении тригонометрии были его наблюдения за движением планет:
» … после того, как я долго занимался изучением этой науки, я заметил, что работы по движению планет постоянно отличались друг от друга. другое, и что многие авторы допустили ошибки в способах проведения своих наблюдений и установления своих правил.
Я также заметил, что со временем положение планет менялось в соответствии с недавними и более ранними наблюдениями; изменения, вызванные наклоном эклиптики, влияющие на исчисление лет и затмений. Постоянное внимание к этим вещам привело меня к совершенствованию и подтверждению такой науки. »
Что еще более важно, аль-Баттани объяснил свои математические операции и призвал других «продолжать наблюдения и поиски» , чтобы усовершенствовать и расширить его работу. Так же как Аль-Баттани, Абу аль-Вафа, Ибн Юнус и Ибн аль-Хайсам разработали сферическую тригонометрию и применили ее для решения астрономических задач.
Аль-Баттани был первым, кто использовал выражения «синус» и «косинус», определив их как длины, а не отношения, как мы знаем их сегодня; исходное определение синуса легко получить из современной версии, умножив его на гипотенузу рассматриваемого треугольника. Тангенс упоминается Аль-Баттани как «растянутая тень», тень воображаемого горизонтального стержня, закрепленного на стене.
Аль-Бируни (973-1048 гг. н.э.) определил тригонометрические функции тангенса и котангенса, которые в предварительной форме были унаследованы от индейцев. Аль-Бируни был среди тех, кто заложил основы современной тригонометрии; Мохаммед ибн Муса аль-Хорезми, родившийся в 780 г. н.э., разработал таблицы синуса, косинуса и тригонометрии, которые позже были переведены на Запад. Однако прошло еще 500 лет, прежде чем современная математика открыла тригонометрию касательных, а затем еще 100 лет, прежде чем Коперник узнал об этом.
В заключение стоит упомянуть некоторые другие важные достижения мусульман в области тригонометрии, а также замечательное применение Аль-Бируни в измерении окружности Земли. Непременный закон синусов был сформулирован и доказан Насир ад-Дином ат-Туси путем извлечения и искусного использования элементарных идей геометрии. Затем он приступил к применению закона для систематического решения всевозможных проблем. Абу аль-Вафа доказал известную теорему сложения для синусов, которая намного эффективнее и элегантнее по сравнению с исходным утверждением в 9.
0170 Альмагест с длинами хорд. До появления компьютеров было важно построить точные таблицы ключевых функций для регулярных значений аргумента функции. Это была кропотливая и трудоемкая процедура; в случае с тригонометрическими таблицами требовалось, во-первых, очень точный способ вычисления синуса 1 степени, а во-вторых, набор правил интерполяции на основе таблиц. Оба эти вопроса были предметом критического исследования ряда мусульманских ученых, таких как Аль-Бируни, Ибн Юнус и Аль-Каши. Для достижения аппроксимации синуса в 1 градус Аль-Каши использует процедуру, которая в современном языке называется итерационным методом.
Рис. 3: Художественное изображение Аль-Бируни на египетской марке. |
Греки любили проводить геодезические исследования для определения различных фундаментальных расстояний, связанных с землей, таких как ее окружность. Один из таких методов описан Птолемеем в его Географии .
Аль-Бируни был известен своим характерным сухим юмором и в полной мере использовал его, чтобы представить свой метод вычисления окружности земли: « Вот еще один метод определения окружности Земли. Он не требует прогулок по пустыням. «Эксперимент был проведен, когда он путешествовал с королем Махмудом из Газны в то, что мы сейчас знаем как северо-западную Индию. Свой оперативный отчет он записал в Об определении координат городов . Этот метод осуществляется с вершины горы и требует знания ее высоты, поэтому Аль-Бируни сначала излагает метод, которым определяется эта величина. Как пишет Аль-Бируни, он применил этот метод на горе близ Нанданы в Индии: « Когда мне довелось жить в форте Нандана на земле Индии, я заметил с соседней высокой горы, стоящей к западу от форта, большой план, лежащий к югу от горы. Мне пришло в голову, что я должен изучить этот метод там. »
Окончательное значение длины окружности оказалось соответствующим значению, определенному более сложной процедурой, включающей геодезическую съемку.