Математика. Значения тригонометрических функций некоторых углов.
Синус пи, косинус пи, тангенс пи и других углов в радианах
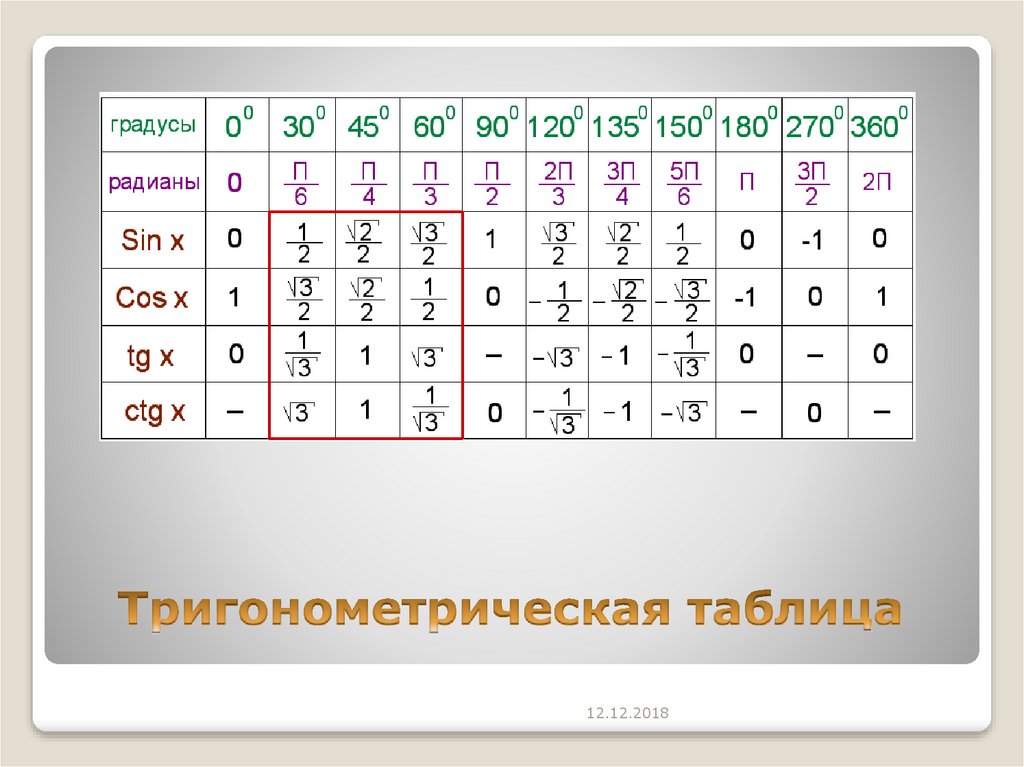
Приведенная ниже таблица косинусов, синусов и тангенсов также подходит для нахождения значения тригонометрических функций, аргумент которых задан в радианах. Для этого воспользуйтесь второй колонкой значений угла. Благодаря этому можно перевести значение популярных углов из градусов в радианы. Например, найдем угол 60 градусов в первой строке и под ним прочитаем его значение в радианах. 60 градусов равно π/3 радиан.
Число пи однозначно выражает зависимость длины окружности от градусной меры угла. Таким образом, пи радиан равны 180 градусам.
Любое число, выраженное через пи (радиан) можно легко перевести в градусную меру, заменив число пи (π) на 180.
Примеры:
1. Синус пи.
sin π = sin 180 = 0
таким образом, синус пи — это тоже самое, что синус 180 градусов и он равен нулю.
2. Косинус пи
3. Тангенс пи tg π = tg 180 = 0 таким образом, тангенс пи — это тоже самое, что тангенс 180 градусов и он равен нулю.
Таблица значений синуса, косинуса, тангенса для углов 0 — 360 градусов (часто встречающиеся значения)
| значение угла α (градусов) | значение угла α в радианах (через число пи) | sin (синус) | cos (косинус) | tg (тангенс) | ctg (котангенс) | sec (секанс) | cosec (косеканс) |
| 0 | 0 | 0 | 1 | 0 | — | 1 | — |
| 15 | π/12 | 2 — √3 | 2 + √3 | ||||
| 30 | π/6 | 1/2 | √3/2 | 1/√3 | √3 | 2/√3 | 2 |
| 45 | π/4 | √2/2 | √2/2 | 1 | 1 | √2 | √2 |
| 60 | π/3 | √3/2 | 1/2 | √3 | 1/√3 | 2 | 2/√3 |
| 75 | 5π/12 | 2 + √3 | 2 — √3 | ||||
| 90 | π/2 | 1 | 0 | — | 0 | — | 1 |
| 105 | 7π/12 | — | — 2 — √3 | √3 — 2 | |||
| 120 | 2π/3 | √3/2 | -1/2 | -√3 | -√3/3 | ||
| 135 | 3π/4 | √2/2 | -√2/2 | -1 | -1 | -√2 | √2 |
| 150 | 5π/6 | 1/2 | -√3/2 | -√3/3 | -√3 | ||
| 180 | π | 0 | -1 | 0 | — | -1 | — |
| 210 | 7π/6 | -1/2 | -√3/2 | √3/3 | √3 | ||
| 240 | 4π/3 | -√3/2 | -1/2 | √3 | √3/3 | ||
| 270 | 3π/2 | -1 | 0 | — | 0 | — | -1 |
| 360 | 2π | 0 | 1 | 0 | — | 1 | — |
Если в таблице значений тригонометрических функций вместо значения функции указан прочерк (тангенс (tg) 90 градусов, котангенс (ctg) 180 градусов) значит при данном значении градусной меры угла функция не имеет определенного значения.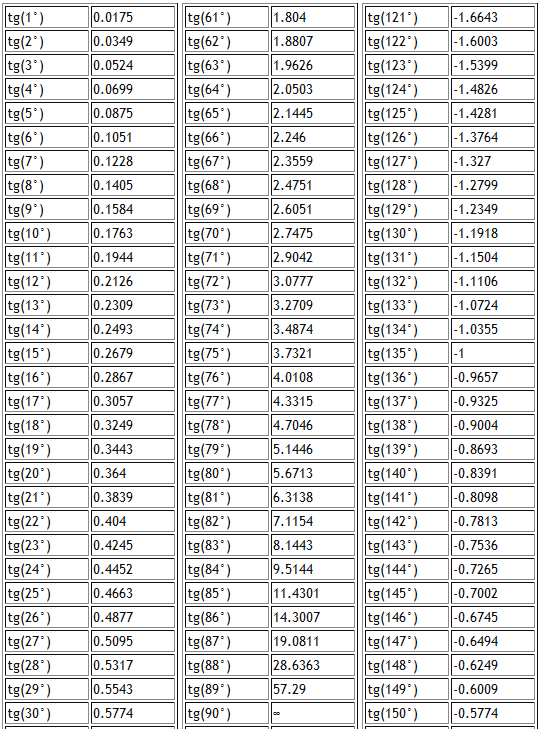 Если же прочерка нет — клетка пуста, значит мы еще не внесли нужное значение. Мы интересуемся, по каким запросам к нам приходят пользователи и дополняем таблицу новыми значениями, несмотря на то, что текущих данных о значениях косинусов, синусов и тангенсов самых часто встречающихся значений углов вполне достаточно для решения большинства задач.
Если же прочерка нет — клетка пуста, значит мы еще не внесли нужное значение. Мы интересуемся, по каким запросам к нам приходят пользователи и дополняем таблицу новыми значениями, несмотря на то, что текущих данных о значениях косинусов, синусов и тангенсов самых часто встречающихся значений углов вполне достаточно для решения большинства задач.
Таблица значений тригонометрических функций sin, cos, tg для наиболее популярных углов 0, 15, 30, 45, 60, 90 … 360 градусов (цифровые значения «как по таблицам Брадиса»)
| значение угла α (градусов) | значение угла α в радианах | sin (синус) | cos (косинус) | tg (тангенс) | ctg (котангенс) |
|---|---|---|---|---|---|
| 0 | 0 | 0 | 1 | 0 | — |
| 15 | π/12 | 0,2588 | 0,9659 | 0,2679 | 3,7321 |
| 30 | π/6 | 0,5000 | 0,8660 | 0,5774 | 1,7321 |
| 45 | π/4 | 0,7071 | 0,7071 | 1 | 1 |
50 | 5π/18 | 0,7660 | 0,6428 | 1. | 0,8391 |
| 60 | π/3 | 0,8660 | 0,5000 | 1,7321 | 0,5774 |
65
| 13π/36 | 0,4226 | 2,1445 | 0,4663 | |
70
| 7π/18 | 0,9397 | 0,3420 | 2,7475 | 0,3640 |
| 75 | 5π/12 | 0,9659 | 0,2588 | 3,7321 | 0,2679 |
| 90 | π/2 | 1 | 0 | — | 0 |
105
| 5π/12 | 0,9659 | -0,2588 | -3,7321 | -0,2679 |
| 120 | 2π/3 | 0,8660 | -0,5000 | -1,7321 | -0,5774 |
| 135 | 3π/4 | 0,7071 | -0,7071 | -1 | -1 |
140 | 7π/9 | 0,6428 | -0,7660 | -0,8391 | -1,1918 |
| 150 | 5π/6 | 0,5000 | -0,8660 | -0,5774 | -1,7321 |
| 180 | π | 0 | -1 | 0 | — |
| 270 | 3π/2 | -1 | 0 | — | 0 |
| 360 | 2π | 0 | 1 | 0 | — |
Определение триггерных функций — макеты
Каждый треугольник состоит из шести частей: трех сторон и трех углов. Если вы измерите стороны, а затем соедините эти измерения в пары (сняв по две за раз), у вас получится три разных пары. Решайте задачи на деление с парами — меняйте порядок в каждой паре — и у вас будет шесть разных ответов. Эти шесть разных ответов представляют собой шесть триггерных функций.
Если вы измерите стороны, а затем соедините эти измерения в пары (сняв по две за раз), у вас получится три разных пары. Решайте задачи на деление с парами — меняйте порядок в каждой паре — и у вас будет шесть разных ответов. Эти шесть разных ответов представляют собой шесть триггерных функций.
Например, если стороны треугольника равны 3, 4 и 5, то шесть делений будут 3/4, 4/3, 3/5, 5/3, 4/5 и 5/4.
Шесть триггерных функций называются синус, косинус, тангенс, котангенс, секанс, и косеканс. Многие люди путают произносимое слово sine с знаком — вы не сможете увидеть разницу, когда услышите это, если не будете осторожны с контекстом. Вы можете «уйти по касательной» в некоторых личных отношениях, но эта фраза имеет совершенно другое значение в триггере.
Триг тоже не имеет в виду совместное подписание займа. Остальные три коэффициента специфичны для триггерного разговора — их ни с чем не спутаешь.
Интерпретация триггерных сокращений
Несмотря на то, что слово sine не такое уж длинное, у вас есть трехбуквенное сокращение для этой триггерной функции и всех остальных.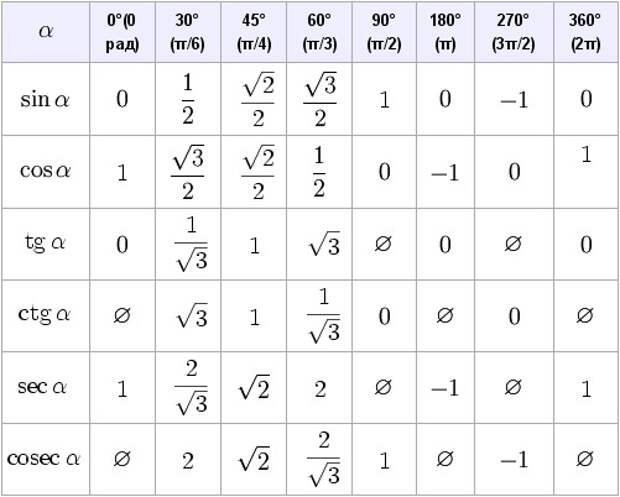 Математикам проще использовать аббревиатуры, и эти версии лучше подходят для клавиш калькулятора. Функции и их сокращения:
Математикам проще использовать аббревиатуры, и эти версии лучше подходят для клавиш калькулятора. Функции и их сокращения:
Как видите, первые три буквы в полном имени составляют аббревиатуру, кроме косеканса.
Обозначение
Чаще всего для обозначения углов используются буквы α (альфа), β (бета), γ (гамма) и θ (тета). Кроме того, во многих уравнениях используется переменная x для представления меры угла.
Алгебра имеет обычные обозначения, включающие надстрочные индексы, такие как 2 в x 2 . В тригонометрии верхние индексы имеют те же правила и характеристики, что и в другой математике. Но верхние индексы триггеров часто выглядят совсем по-другому. На следующем рисунке показано, как вы используете верхние индексы в триггере.
Но верхние индексы триггеров часто выглядят совсем по-другому. На следующем рисунке показано, как вы используете верхние индексы в триггере.
Первая запись показывает, как можно избежать необходимости писать круглые скобки каждый раз, когда вы хотите возвести триггерную функцию в степень. Эта нотация удобна и эффективна, но может сбивать с толку, если вы не знаете «кода».
Вторая запись показывает, как написать обратную функцию триггера. Это означает, что вы должны взять значение функции и разделить его на число 1. Последняя запись показывает, как вы пишете функцию обратного синуса . Использование верхнего индекса –1 между синусом и углом означает, что вы говорите об обратном синусе (или arcsin ), а не обратная функция.
Работа с уголками
Функции в алгебре используют множество операций и символов, которые отличаются от обычных знаков сложения, вычитания, умножения и деления в арифметике. Например, взгляните на операцию извлечения квадратного корня:
.
Подстановка 25 под корнем (символ квадратного корня) дает ответ 5. Другие операции в алгебре, такие как абсолютное значение, факториал и ступенчатая функция, также используются в тригонометрии. Но мир триггеров расширяет горизонты, представляя еще более увлекательные процессы.
При работе с триггерными функциями у вас есть совершенно новый набор значений, которые нужно изучить или найти. Например, подстановка 25 в синусоидальную функцию выглядит так: sin 25. Ответ, который появляется, — либо 0,423, либо –0,132, в зависимости от того, используете ли вы градусы или радианы.
Обычно вы не можете определить или запомнить все значения, которые вы получаете, помещая меры угла в триггерные функции. Итак, вам нужны тригонометрические таблицы значений или научные калькуляторы для изучения тригонометрии.
В общем, когда вы применяете триггерную функцию к измерению угла, вы получаете некоторое действительное число (если этот угол находится в его области определения).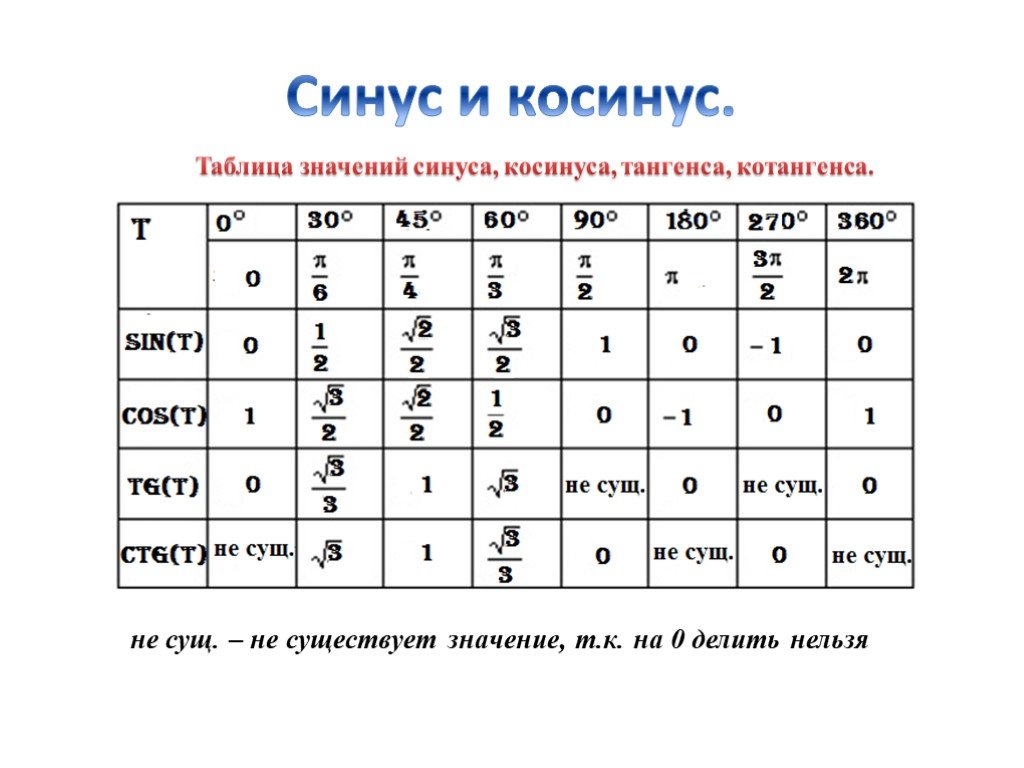 Некоторые функции углов и триггеров имеют хорошие значения, но большинство — нет. На следующем рисунке показаны триггерные функции для угла 30 градусов.
Некоторые функции углов и триггеров имеют хорошие значения, но большинство — нет. На следующем рисунке показаны триггерные функции для угла 30 градусов.
Некоторые характеристики, которые подтверждают записи, заключаются в том, что функции синуса и косинуса всегда имеют значения, которые находятся между –1 и 1 включительно. Кроме того, функции секанса и косеканса всегда имеют значения, которые равны или больше 1 или равны или меньше чем –1. 9{-ix}}{2}.\]
Обратные тригонометрические функции многозначны,
таким образом, требуя разрезания ветвей, и обычно имеют действительные значения
только на части реальной линии. Определения и разрезы ветвей
приведены в документации каждой функции.
Соглашения об отсечении ветвей, используемые mpmath, по существу
такие же, как и в большинстве стандартных математических программ,
такие как Mathematica и собственная библиотека Python cmath (начиная с Python 2.6;
более ранние версии Python реализуют некоторые функции
ошибочно).
Преобразование градусов в радианы
градусы() -
мпмат.градусов( x ) Преобразует угол в радианах \(x\) в угол в градусах:
>>> из импорта mpmath * >>> мп.дпс = 15; mp.pretty = Истина >>> градусы (пи/3) 60,0
радианы() -
мпмат.радиан( x ) Преобразует градусный угол \(x\) в радианы:
>>> из импорта mpmath * >>> мп.дпс = 15; mp.pretty = Истина >>> радианы(60) 1.0471975511966
Тригонометрические функции
cos() -
мпмат.cos( x , **kwargs ) Вычисляет косинус \(x\), \(\cos(x)\).
>>> из импорта mpmath * >>> мп.дпс = 25; mp.pretty = Истина >>> cos(pi/3) 0,5 >>> cos(100000001) -0,9802850113244713353133243 >>> cos(2+3j) (-4,189625690968807230132555 - 9,109227893755336597979197j) >>> cos(inf) нан >>> nprint(chop(taylor(cos, 0, 6))) [1,0, 0,0, -0,5, 0,0, 0,0416667, 0,0, -0,00138889]
Интервалы поддерживаются через
mpmath.: iv.cos()
iv.cos() >>> iv.dps = 25; iv.pretty = Истина >>> iv.cos([0,1]) [0,540302305868139717400936602301, 1,0] >>> iv.cos([0,2]) [-0.41614683654714238699756823214, 1.0]
грех() -
мпмат.грех( x , **kwargs ) Вычисляет синус \(x\), \(\sin(x)\).
>>> из импорта mpmath * >>> мп.дпс = 25; mp.pretty = Истина >>> грех(пи/3) 0,8660254037844386467637232 >>> грех(100000001) 0,1975887055794968911438743 >>> грех(2+3j) (9,1544991469114295734673 - 4,168906959966564350754813j) >>> грех(инф) нан >>> nprint(chop(taylor(sin, 0, 6))) [0,0, 1,0, 0,0, -0,166667, 0,0, 0,00833333, 0,0]
Интервалы поддерживаются через
mpmath.iv.sin():>>> iv.dps = 25; iv.pretty = Истина >>> iv.sin([0,1]) [0,0, 0,841470984807896506652502331201] >>> iv.sin([0,2]) [0,0, 1,0]
загар() -
мпмат.
коричневый( x , **kwargs ) Вычисляет тангенс \(x\), \(\tan(x) = \frac{\sin(x)}{\cos(x)}\). Касательная функция сингулярна в точке \(x = (n+1/2)\pi\), но
tan(x)всегда возвращает конечный результат, так как \((n+1/2)\pi\) не может быть точно представлено с помощью арифметики с плавающей запятой.>>> из импорта mpmath * >>> мп.дпс = 25; mp.pretty = Истина >>> загар(пи/3) 1.732050807568877293527446 >>> загар(100000001) -0,2015625081449864533091058 >>> загар(2+3j) (-0,003764025641504248292751221 + 1,003238627353609801446359j) >>> загар(инф) нан >>> nprint(chop(taylor(tan, 0, 6))) [0,0, 1,0, 0,0, 0,333333, 0,0, 0,133333, 0,0]
Интервалы поддерживаются через
mpmath.iv.tan():>>> iv.dps = 25; iv.pretty = Истина >>> iv.tan([0,1]) [0,0, 1,557407724654050697482944] >>> iv.tan([0,2]) # Интервал включает особенность [-инф, +инф]
сек() -
мпмат.
сек( x ) Вычисляет секанс \(x\), \(\mathrm{sec}(x) = \frac{1}{\cos(x)}\). Функция секущей сингулярна в точке \(x = (n+1/2)\pi\), но
sec(x)всегда возвращает конечный результат, так как \((n+1/2)\pi\) не может быть точно представлено с помощью арифметики с плавающей запятой.>>> из импорта mpmath * >>> мп.дпс = 25; mp.pretty = Истина >>> сек(пи/3) 2.0 >>> сек(10000001) -1,184723164360392819100265 >>> сек(2+3к) (-0,04167496441114427004834991 + 0,0906111371962375965296612j) >>> сек(инф) нан >>> nprint(chop(taylor(sec, 0, 6))) [1,0, 0,0, 0,5, 0,0, 0,208333, 0,0, 0,0847222]
Интервалы поддерживаются через
mpmath.iv.sec():>>> iv.dps = 25; iv.pretty = Истина >>> IV.сек([0,1]) [1.0, 1.85081571768092561791175326276] >>> iv.sec([0,2]) # Интервал включает особенность [-инф, +инф]
csc() -
мпмат.csc( x ) Вычисляет косеканс \(x\), \(\mathrm{csc}(x) = \frac{1}{\sin(x)}\).
 Эта функция косеканса сингулярна в точке \(x = n \pi\), но с
исключение точки \(x = 0\),
Эта функция косеканса сингулярна в точке \(x = n \pi\), но с
исключение точки \(x = 0\), csc(x)возвращает конечный результат поскольку \(n \pi\) не может быть точно представлено с использованием чисел с плавающей запятой арифметика.>>> из импорта mpmath * >>> мп.дпс = 25; mp.pretty = Истина >>> csc(pi/3) 1.15470053837925152
98 >>> csc(10000001) -1,864910497503629858938891 >>> csc(2+3j) (0,020975320743980579048 + 0,04120098628857412646300981j) >>> csc(inf) нанИнтервалы поддерживаются через
mpmath.iv.csc():>>> iv.dps = 25; iv.pretty = Истина >>> iv.csc([0,1]) # Интервал включает особенность [1.18839510577812121626159943988, +inf] >>> iv.csc([0,2]) [1.0, +инф]
детская кроватка() -
мпмат.детская кроватка( x ) Вычисляет котангенс \(x\), \(\ mathrm{cot}(x) = \frac{1}{\tan(x)} = \frac{\cos(x)}{\sin(x)}\).
 Эта функция котангенса сингулярна в точке \(x = n \pi\), но с
исключение точки \(x = 0\),
Эта функция котангенса сингулярна в точке \(x = n \pi\), но с
исключение точки \(x = 0\), кроватка(х)возвращает конечный результат поскольку \(n \pi\) не может быть точно представлено с использованием чисел с плавающей запятой арифметика.>>> из импорта mpmath * >>> мп.дпс = 25; mp.pretty = Истина >>> раскладушка(пи/3) 0,5773502691896257645091488 >>> детская кроватка(10000001) 1,574131876209625656003562 >>> детская кроватка(2+3j) (-0,003739710376336956660117409 - 0,9967577965693583104609688j) >>> детская кроватка(инф) нан
Интервалы поддерживаются через
mpmath.iv.cot():>>> iv.dps = 25; iv.pretty = Истина >>> iv.cot([0,1]) # Интервал включает сингулярность [0.642092615934330703006419974862, +inf] >>> IV.кот([1,2]) [-инф, +инф]
Тригонометрические функции с измененным аргументом
cospi() -
мпмат.cospi( x , **kwargs ) Вычисляет
x
sinpi() 9{-1}(х)\). Поскольку \(-1 \le \cos(x) \le 1\) для действительного \(x\), обратная
косинус имеет действительное значение только для \(-1 \le x \le 1\). На этом интервале
Поскольку \(-1 \le \cos(x) \le 1\) для действительного \(x\), обратная
косинус имеет действительное значение только для \(-1 \le x \le 1\). На этом интервале acos() определяется как монотонно убывающая
функция, принимающая значения между \(+\pi\) и \(0\). Основные значения:
>>> из импорта mpmath *
>>> мп.дпс = 25; mp.pretty = Истина
>>> acos(-1)
3.141592653589793238462643
>>> acos(0)
1,570796326794896619231322
>>> акос(1)
0,0
>>> nprint(chop(taylor(acos, 0, 6)))
[1,5708, -1,0, 0,0, -0,166667, 0,0, -0,075, 0,0]
9{-1}(\cos(x)) = x\) только для \(0 \le \Re[x] < \pi\):
>>> для x в [1, 10, -1, 2+3j, 10+3j]:
... print("%s %s" % (cos(acos(x)), acos(cos(x))))
...
1,0 1,0
(10,0 + 0,0j) 2,566370614359172953850574
-1,0 1,0
(2,0 + 3,0 Дж) (2,0 + 3,0 Дж)
(10,0 + 3,0 дж) (2,566370614359172953850574 - 3,0 дж)
Арккосинус имеет две точки ветвления: \(x = \pm 1\). акос() размещает разрезы ветвей вдоль отрезков линии \((-\infty, -1)\) и
\((+1, +\infty)\). В общем 9{-1}(х)\).
Поскольку \(-1 \le \sin(x) \le 1\) для действительного \(x\), обратная
синус имеет действительное значение только для \(-1 \le x \le 1\).
На этом интервале он определяется как монотонно возрастающая
функция, принимающая значения между \(-\pi/2\) и \(\pi/2\).
В общем 9{-1}(х)\).
Поскольку \(-1 \le \sin(x) \le 1\) для действительного \(x\), обратная
синус имеет действительное значение только для \(-1 \le x \le 1\).
На этом интервале он определяется как монотонно возрастающая
функция, принимающая значения между \(-\pi/2\) и \(\pi/2\).
Основные значения:
>>> из импорта mpmath *
>>> мп.дпс = 25; mp.pretty = Истина
>>> как(-1)
-1,570796326794896619231322
>>> как(0)
0,0
>>> асин(1)
1,570796326794896619231322
>>> nprint(chop(taylor(asin, 0, 6)))
[0,0, 1,0, 0,0, 0,166667, 0,0, 0,075, 0,0]
9{-1}(\sin(x)) = x\) только для \(-\pi/2 < \Re[x] < \pi/2\):
>>> для x в [1, 10, -1, 1+3j, -2+3j]:
... print("%s %s" % (chop(sin(asin(x))), asin(sin(x))))
...
1,0 1,0
10,0 -0,5752220392306202846120698
-1,0 -1,0
(1,0 + 3,0к) (1,0 + 3,0к)
(-2,0 + 3,0j) (-1,141592653589793238462643 - 3,0j)
Обратный синус имеет две точки ветвления: \(x = \pm 1\). asin() размещает разрезы ветвей вдоль отрезков линии \((-\infty, -1)\) и
\((+1, +\infty)\). В общем 9{-1}(х)\).
Это функция с действительным знаком для всех действительных \(x\) с диапазоном
\((-\пи/2, \пи/2)\).
В общем 9{-1}(х)\).
Это функция с действительным знаком для всех действительных \(x\) с диапазоном
\((-\пи/2, \пи/2)\).
Основные значения:
>>> из импорта mpmath *
>>> мп.дпс = 25; mp.pretty = Истина
>>> атан(-инф)
-1,570796326794896619231322
>>> атан(-1)
-0,7853981633974483096156609
>>> атан(0)
0,0
>>> атан(1)
0,7853981633974483096156609
>>> атан(инф)
1,570796326794896619231322
>>> nprint(chop(taylor(atan, 0, 6)))
[0,0, 1,0, 0,0, -0,333333, 0,0, 0,2, 0,0]
9{-1}(\tan(x)) = x\) только для \(-\pi/2 < \Re[x] < \pi/2\):
>>> MP.dps = 25
>>> для x в [1, 10, -1, 1+3j, -2+3j]:
... print("%s %s" % (загар(атан(х)), атан(загар(х))))
...
1,0 1,0
10,0 0,5752220392306202846120698
-1,0 -1,0
(1,0 + 3,0j) (1,0000000000000000000000001 + 3,0j)
(-2,0 + 3,0j) (1,141592653589793238462644 + 3,0j)
Арктангенс имеет две точки ветвления: \(x = \pm i\). атан() размещает разрезы ветвей вдоль отрезков линии \((-i \infty, -i)\) и
\((+i, +i \infty)\). В общем 9{-1}(1/х)\).
Функция sinc
sinc() -
мпмат. Синк ( x ) sinc(x) вычисляет ненормализованную функцию sinc, определенную как
\[\begin{split}\mathrm{sinc}(x) = \begin{case}
\sin(x)/x, & \mbox{if } x \ne 0 \\
1, & \mbox{если } х = 0.
\end{case}\end{split}\]
См. sincpi() для получения информации о нормализованной функции sinc.
Простые значения и пределы включают:
>>> из импорта mpmath *
>>> мп.дпс = 15; mp.pretty = Истина
>>> синк(0)
1,0
>>> синк(1)
0,841470984807897
>>> синк(инф)
0,0
Интеграл функции sinc является синусоидальным интегралом Si:
>>> quad(sinc, [0, 1])
0,946083070367183
>>> си(1)
0,946083070367183
sincpi() -
мпмат. СинкПи ( х ) sincpi(x) вычисляет нормализованную функцию sinc, определенную как
\[\begin{split}\mathrm{sinc}_{\pi}(x) = \begin{case}
\sin(\pi x)/(\pi x), & \mbox{if } x \ne 0 \\
1, & \mbox{если } х = 0.

 1918
1918 iv.cos()
iv.cos() 

 Эта функция косеканса сингулярна в точке \(x = n \pi\), но с
исключение точки \(x = 0\),
Эта функция косеканса сингулярна в точке \(x = n \pi\), но с
исключение точки \(x = 0\), 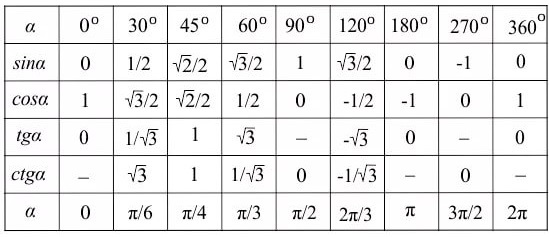 Эта функция котангенса сингулярна в точке \(x = n \pi\), но с
исключение точки \(x = 0\),
Эта функция котангенса сингулярна в точке \(x = n \pi\), но с
исключение точки \(x = 0\),  Поскольку \(-1 \le \cos(x) \le 1\) для действительного \(x\), обратная
косинус имеет действительное значение только для \(-1 \le x \le 1\). На этом интервале
Поскольку \(-1 \le \cos(x) \le 1\) для действительного \(x\), обратная
косинус имеет действительное значение только для \(-1 \le x \le 1\). На этом интервале  В общем 9{-1}(х)\).
Поскольку \(-1 \le \sin(x) \le 1\) для действительного \(x\), обратная
синус имеет действительное значение только для \(-1 \le x \le 1\).
На этом интервале он определяется как монотонно возрастающая
функция, принимающая значения между \(-\pi/2\) и \(\pi/2\).
В общем 9{-1}(х)\).
Поскольку \(-1 \le \sin(x) \le 1\) для действительного \(x\), обратная
синус имеет действительное значение только для \(-1 \le x \le 1\).
На этом интервале он определяется как монотонно возрастающая
функция, принимающая значения между \(-\pi/2\) и \(\pi/2\).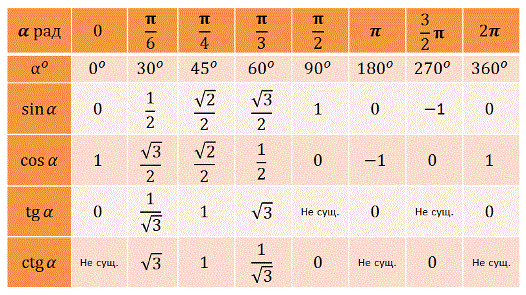 В общем 9{-1}(х)\).
Это функция с действительным знаком для всех действительных \(x\) с диапазоном
\((-\пи/2, \пи/2)\).
В общем 9{-1}(х)\).
Это функция с действительным знаком для всех действительных \(x\) с диапазоном
\((-\пи/2, \пи/2)\).
