Таблица точки окружности: Числовая окружность в координатной плоскости — урок. Алгебра, 10 класс.

Содержание

Задачи для самостоятельного решения — Студопедия

Поделись

Определение числовой окружности на координатной плоскости

Расположим числовую окружность в координатной плоскости так, чтобы центр окружности совместился с началом координат, а её радиус принимаем за единичный отрезок. Начальная точка числовой окружности A совмещена с точкой (1;0).

Каждая точка числовой окружности имеет в координатной плоскости свои координаты х и у, причем:
1) при x>0, у>0 – в первой четверти;
2) при х<0, у>0 – во второй четверти;
3) при х<0, у<0 – в третьей четверти;
4) при х>0, у<0 – в четвертой четверти.

Для любой точки М(х;у) числовой окружности выполняются неравенства: −1<x<1; −1<у<1.

Запомните уравнение числовой окружности: x2+y2=1.

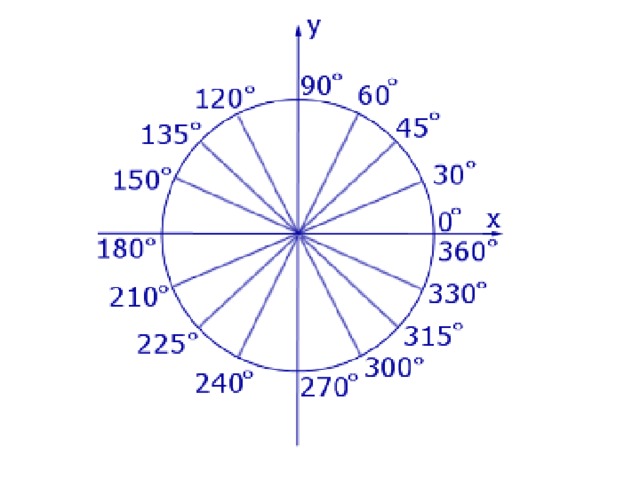
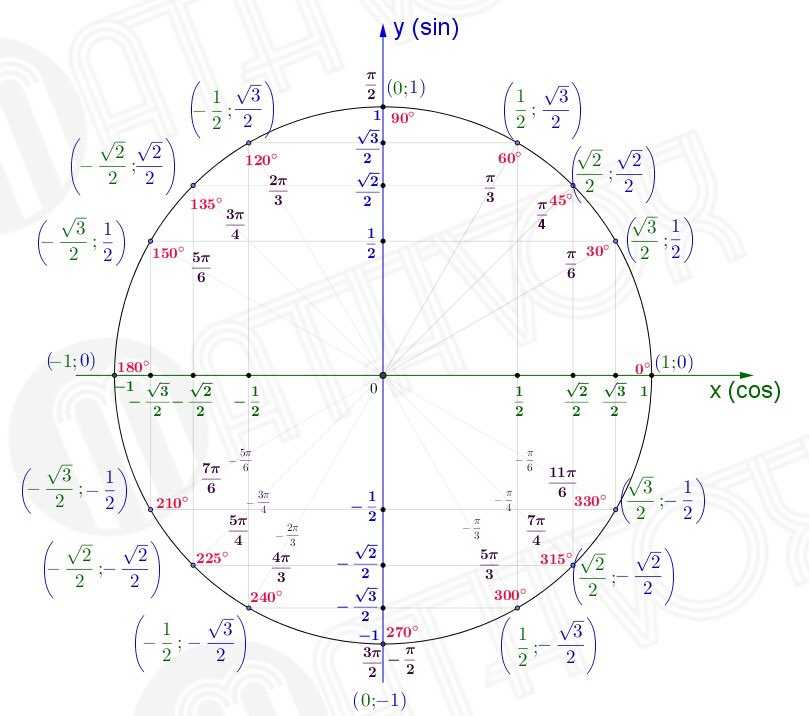
Нам важно научиться находить координаты точек числовой окружности, представленных на рисунке.

Найдем координату точки π4

Точка М(π4) – середина первой четверти.

Опустим из точки М перпендикуляр МР на прямую ОА и рассмотрим треугольник OMP.Так как дуга АМ составляет половину дуги АВ, то ∠MOP=45°.
Значит, треугольник OMP – равнобедренный прямоугольный треугольник и OP=MP, т.е. у точки M абсцисса и ордината равны: x=y.
Так как координаты точки M(х;y) удовлетворяют уравнению числовой окружности, то для их нахождения нужно решить систему уравнений:
{x2+y2=1,x=y.
Решив данную систему, получаем: y=x=√22.
Значит, координаты точки M, соответствующей числу π4, будут M(π4)=M(√22;√22).
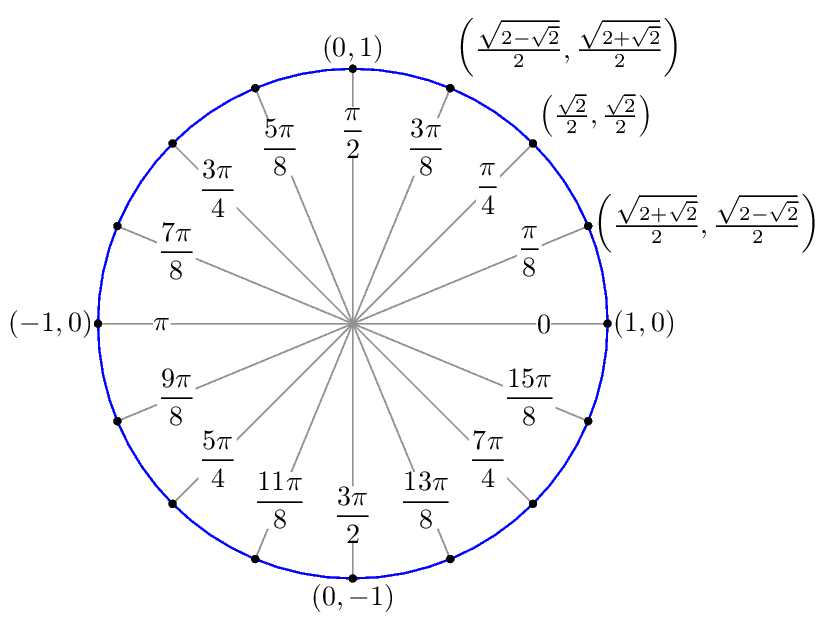
Аналогичным образом рассчитываются координаты точек, представленных на предыдущем рисунке.

Координаты точек числовой окружности

Рассмотрим примеры

Пример 1.
Найти координату точки числовой окружности: Р(45π4).

Решение:
Т.к. числам t и t+2π∗k, где k-целое число, соответствует одна и та же точка числовой окружности то:

45π4=(10+54)∗π=10π+5π4=5π4+2π∗5.
Значит, числу 45π4 соответствует та же точка числовой окружности, что и числу 5π4.

Посмотрев значение точки 5π4 в таблице, получаем: P(45π4)=P(−√22;−√22).

Пример 2.
Найти координату точки числовой окружности: Р(−37π3).

Решение:

Т.к. числам t и t+2π∗k, где k-целое число, соответствует одна и та же точка числовой окружности то:
−37π3=−(12+13)∗π=−12π–π3=−π3+2π∗(−6).
Значит, числу −37π3 соответствует та же точка числовой окружности, что и числу –π3, а числу –π3 соответствует та же точка, что и 5π3. Посмотрев значение точки 5π3 в таблице, получаем:
P(−37π3)=P(12;−√32).

Пример 3.
Найти на числовой окружности точки с ординатой у=12 и записать, каким числам t они соответствуют?

Решение:
Прямая у=12 пересекает числовую окружность в точках М и Р. Точка М соответствует числу π6 (из данных таблицы). Значит, и любому числу вида: π6+2π∗k. Точка Р соответствует числу 5π6, а значит, и любому числу вида 5π6+2π∗k.

Получили, как часто говорят в таких случаях, две серии значений:
π6+2π∗k и 5π6+2π∗k.
Ответ : t=π6+2π∗k и t=5π6+2π∗k.

Пример 4.
Найти на числовой окружности точки с абсциссой x≥−√22 и записать, каким числам t они соответствуют.

Решение:

Прямая x=−√22 пересекает числовую окружность в точках М и Р. Неравенству x≥−√22 соответствуют точки дуги РМ. Точка М соответствует числу

3π4 (из данных таблицы). Значит, и любому числу вида −3π4+2π∗k. Точка Р соответствует числу −3π4, а значит, и любому числу вида −3π4+2π∗k.

Тогда получим −3π4+2π∗k≤t≤3π4+2πk.

Ответ : −3π4+2π∗k≤t≤3π4+2πk.

Задачи для самостоятельного решения

1) Найти координату точки числовой окружности: Р(61π6).
2) Найти координату точки числовой окружности: Р(−52π3).

3) Найти на числовой окружности точки с ординатой у=−12 и записать, каким числам t они соответствуют.
4) Найти на числовой окружности точки с ординатой у≥−12 и записать, каким числам t они соответствуют.
5) Найти на числовой окружности точки с абсциссой x≥−√32 и записать, каким числам t они соответствуют.

Ответы можете присылать мне в личных сообщениях в вК или на электронную почту [email protected],

Подписывайте номер группы и свою фамилию и имя

Понравилась статья? Добавь ее в закладку (CTRL+D) и не забудь поделиться с друзьями:

числовая окружность, числовая окружность на координатной плоскости

1. Введение числовой окружности

Изучение тригонометрии вызывает у учащихся очень большие трудности по ряду причин:

1). В тригонометрии изучается новая геометрическая модель множества действительных чисел – числовая окружность.

2). Необычны обозначения действий: sin, cos, tg, ctg.

3). Очень много формул.

А.Г. Мордкович считает, что сначала необходимо внимательно изучить числовую окружность, — это снимает частично первую трудность. В изучении числовой окружности он выделяет 3 этапа.

Мотивация: рассматриваются примеры из реальной действительности, описывающиеся тригонометрическими функциями, например, движения Земли вокруг Солнца, вокруг своей оси, фазы Луны, приливы и отливы, качание маятника и др. процессы периодичности.

— Все такие процессы описываются функциями особого вида – тригонометрическими, но прежде чем изучить эти функции следует ознакомиться с некоторыми понятиями, на основе которых они получаются.

Этапы изучения числовой окружности:

1 этап. Понятие единичной окружности. Делается заголовок: «Некоторые вспомогательные геометрические примеры».

Пусть дана окружность (O,R). Длинна окружности измеряется по формуле l = 2πR.

— Если считать R = 1, то l = 2π и будем называть такую окружность единичной. Проведем два взаимно перпендикулярных диаметра: AC- горизонтальный, BD – вертикальный. Выясним, чему равна длина частей окружности: например, дуга AC= π, как половина длины окружности; дуга AB малая = π/2, как четверть; дуга AB большая = 3π/2, и т.д. Нумеруются четверти. Пусть М – середина дуги АВ малой. Точки Р и К делят дугу АВ на три равные части. Найдём длины других дуг: АМ малой (π/4), АК малой (π/6), АР = π/3 и т.д.

С концами А и В на окружности две дуги. Договоримся о том, как эти дуги различать: выберем направление движения по окружности против хода часовой

стрелки, тогда дуга АВ – малая, ВА –большая.

Далее рассматриваются примеры на нахождение длин других дуг (при этом точки берутся из других четвертей). В конце рассматриваются дуги длина, которых равна 1 единица, 2 ед ,…, 6 ед. (с помощью прикидки π/4<1< π/3). На окружности нет дуги равней 7 единиц, т.к. 7>2 π.

2 этап. Числовая окружность. Повторяется понятие числовой прямой, решаются две задачи: 1). по заданному числу построить точку на числовой прямой и 2) указать число, которое соответствует данной точке.

— Двигаться можно не только по прямой, но и, например, по замкнутой линии – окружности. На соревнованиях дорожка имеет форму близкую к окружности. Каждому расстоянию, т.е. каждому положительному числу на беговой дорожке, можно сопоставить определённую точку (рисунок).

Можно и каждому отрицательному числу сопоставить некоторую точку – точку, полученную движением в обратном направлении. Тогда беговую дорожку можно рассматривать как числовую окружность. Удобнее в качестве числовой окружности рассматривать единичную, т.к. при работе с ней длины дуг выражаются без использования радиуса. Дается определение (описание) понятия.

Определение. Дана единичная окр-ть, на кот. отмечено начало- точка А (правый конец горизонтального диаметра). Поставим в соответствие каждой точке t∈ℝ точку окружности по следующему правилу:

1). если t>0, то двигаясь из точки А в направлении против хода часовой стрелки (положительное направление обхода окружности) опишем по окружности путь АМ длины t. Точка М и будет искомой точкой М(t).

2). если t<0, то двигаясь от точки А в направлении по ходу часовой стрелки (отрицательное направление обхода окружности) опишем на окружности путь АМ длины t. Точка М – искомая точка М(t).

3). если t=0, то поставим в соответствие этому числу точку А. (А(0)).

Единичную окружность с указанным соответствием между действительными числами и точками окружности будем называть числовой окружностью.

— Как вы помните, на числовой прямой решаются две задачи – по заданному числу построить точку и обратная, аналогичные задачи нужно научиться решать и на числовой окружности.

Далее решаются задачи: 1). По заданному числу построить точку: .

Так как числа указанного вида будут в дальнейшем часто использоваться, то целесообразно постепенно получить 2 макета.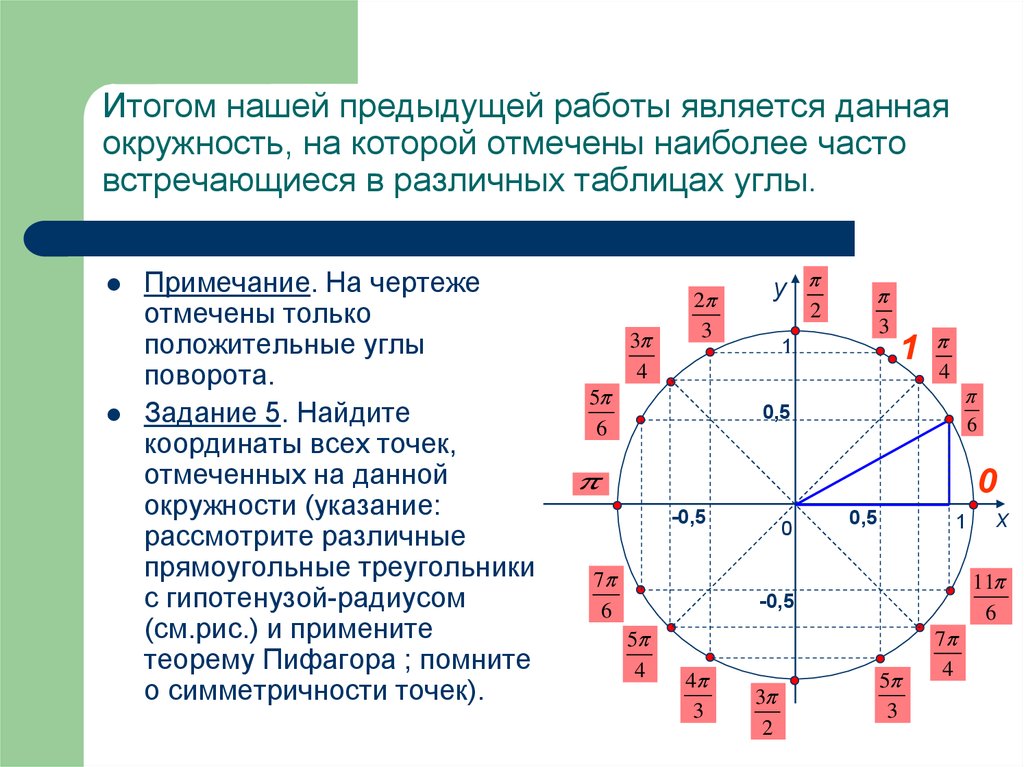

Далее рассматриваются числа, не выражающиеся через π: +/- 1, +/-2 (с помощью прикидки).

Делается вывод: на числовой окружности, как и на числовой прямой, каждому числу соответствует единственная точка окружности.

2).Указать число соответствующее данной точке.

Вывод: одной и той же точке числовой окружности соответствует бесконечно много чисел (т.е. если точке М числовой окружности соответствует число t, то этой же точке соответствуют все числа вида t+2πk, k∈Ζ; M(t)+M(t+2πk), k∈Ζ). В этом отличие числовой окружности от числовой прямой.

В результате у одной и той же точки окружности бесконечно много «имен». Например, М(π/4)=М(-7π/4)=…, но имя π/4 будем называть «главным именем», т.к. оно принадлежит промежутку [0;2π).

Далее решаются упражнения: дано большое число 23π/4, постройте точку; дана точка укажите главное имя и все числа соответствующие этой точке.

Далее А. Г. Мордкович вводит форму аналитической записи дуги числовой окружности. Например, дуги АВ: — ядро дуги (границы – числа по модулю минимальные и взяты из промежутка [0; 2π).

Другая второстепенная запись той же дуги: .

В итоге, множество промежутков данного вида записывается следующим образом: – аналитическая запись дуги АВ. Рассматриваются и другие пример: дуга ВА: . C помощью таких упражнений идёт подготовка к решению простейших тригонометрических неравенств.

3 этап. Числовая окружность на координатной плоскости.

Поместим числовую окружность в прямоугольную систему координат следующим образом: центр окружности – начало координат; диаметр АС попадет на Ох, BD на Оу.

Угол МОН = 45⁰. Треугольник М₁ОН – прямоугольный и равнобедренный.

х² + у² = 1,

Тогда каждая точка числовой окружности будет меть как криволинейную координату по окружности, так и декартовы координаты на плоскости.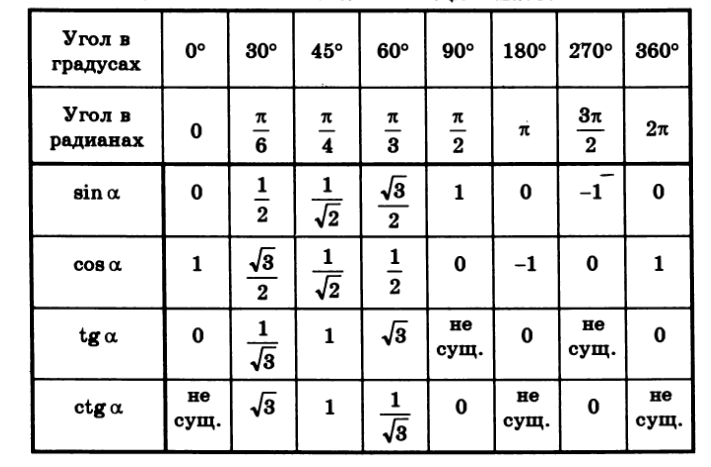 M(t) = M(x;y).

З адача заключается в том, что бы установить связь между этими координатами. При этом должны учитываться следующие условия:

1). если точка М принадлежит 1 четверти, то х>0, y>0; 2 четверти: x<0,y>0;…

2). |x|≤1, |y|≤1

3). x²+y²=1 – уравнение числовой окр в декартовой системе координат.

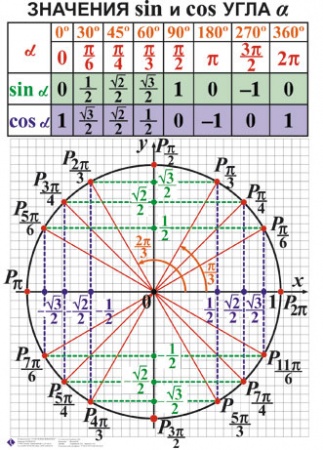
Далее устанавливается зависимость между координатами основных точек: А, В, С, D, точек М(п/4), М₁(3п/4),…, N(п/6), N₁(5п/6), …, K(п/3), K₁(2п/3),…

В результате заполняются таблицы вида:

Точка окр-ти	0		…
Абсцисса х	1	0	…
Ордината у	0	1	…

Таблица 2.

Точка окр-ти	0		…
Абсцисса х	1	0	…
Ордината у	0	1	…

Далее выполняются упражнения:

1. Найти координаты х и у точек числовой окружности. Р₁(45п/4), Р₂(-37п/3)…

Используется ранее полученное утверждение: числам t и t + 2пk соответствует одна и та же точка числовой окружности.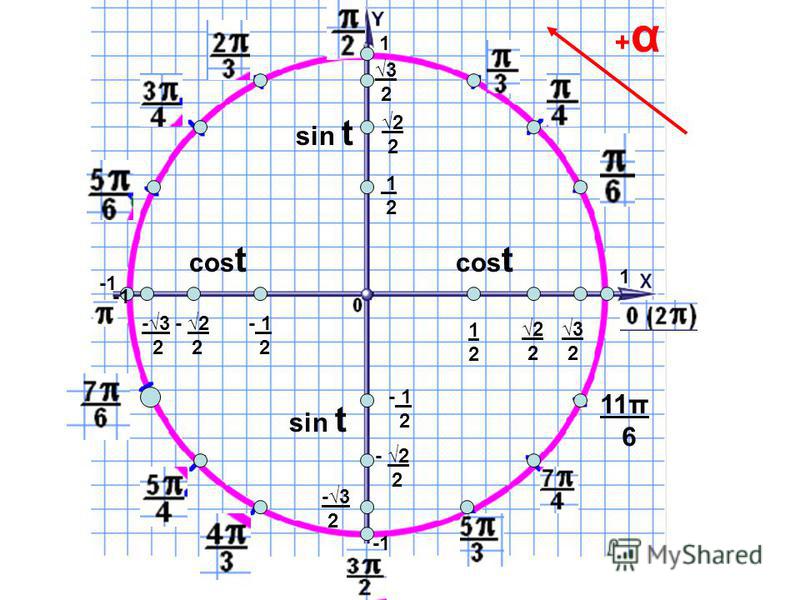

2. Найти на числовой окружности точку с заданной абсциссой (ординатой) и

написать каким числам t они соответствуют. Таким образом идёт подготовка к решению простейших тригонометрических уравнений.

3. Найти на числовой окружности точки с абсциссой (ординатой) большей или меньшей заданного числа и записать каким значениям t они соответствуют. (идет подготовка к решению простейших тригонометрических неравенств)