Брошюра, Тригонометрические таблицы и эвольвентные функции
Применяются условия использования
Загрузки- Описание
- В середине двадцатого века американские производители инструментов иногда распространяли тригонометрические таблицы с рекламой своей продукции. Эта небольшая бумажная брошюра содержит определения синуса, косинуса, тангенса, котангенса, секанса и косеканса, а также формулы для нахождения длины сторон прямоугольного и косоугольного треугольников, когда известны различные углы и стороны. Затем он дает таблицы пяти разрядов значений шести упомянутых тригонометрических функций, а также таблицу десятичных эквивалентов. В дополнение к этому материалу в брошюре есть раздел об эвольвентной функции, который включает таблицы и формулы для прямозубых и косозубых колес.
- Также показаны прецизионные металлорежущие инструменты производства Illinois Tool Works, которая позиционирует себя как «штаб-квартира инженерных режущих инструментов».
- Брошюра принадлежала машинисту и специалисту по музеям Джорджу А. Нортону. Дата авторского права — 1954 год.
- Сравните 1986.3078.01.
- Местоположение
- В настоящее время не просматривается
- Имя объекта
- Брошюра
- дата изготовления
- 1954
- производитель
- Иллинойс Инструмент Воркс Инк.
- место изготовления
- США: Иллинойс, Чикаго
- Физическое описание
- бумага (общий материал)
- Измерения
- общий: 0,5 см х 7,8 см х 16,5 см; 3/16 дюйма x 3 1/16 дюйма x 6 1/2 дюйма
- Идентификационный номер
- недоступный номер
- 1986.3078
- каталожный номер
- 1986. 3078.02
3078.02- Кредитная линия
- Дар Джорджа А. Нортона
- предмет
- Математика
- Больше товаров в
- Медицина и наука: Математика
- Тригонометрия
- Наука и математика
- Источник данных
- Национальный музей американской истории
Номинировать этот объект для фотографирования.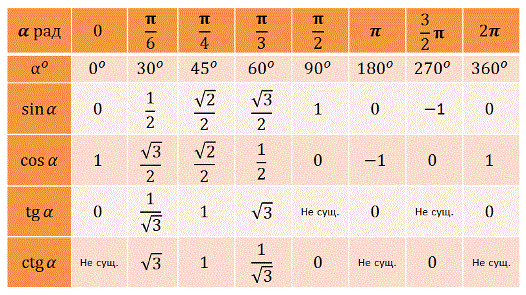
Наша база данных коллекций находится в стадии разработки. Мы можем обновить эту запись на основе дальнейших исследований и обзоров. Узнайте больше о нашем подходе к публикации нашей коллекции в Интернете.
Если вы хотите узнать, как вы можете использовать контент на этой странице, ознакомьтесь с Условиями использования Смитсоновского института. Если вам нужно запросить изображение для публикации или другого использования, посетите страницу Права и репродукции.
Примечание. Отправка комментариев временно недоступна, пока мы работаем над улучшением сайта. Приносим извинения за прерывание. Если у вас есть вопрос, касающийся коллекций музея, сначала ознакомьтесь с часто задаваемыми вопросами о коллекциях. Если вам нужен личный ответ, воспользуйтесь нашей контактной страницей.
Тригонометрическая таблица соотношений | Таблица тригонометрических функций
Тригонометрическая формула, соотношение и таблица углов
Тригонометрическая функция — это математическая функция, которая связывает один угол в треугольнике с длинами его сторон.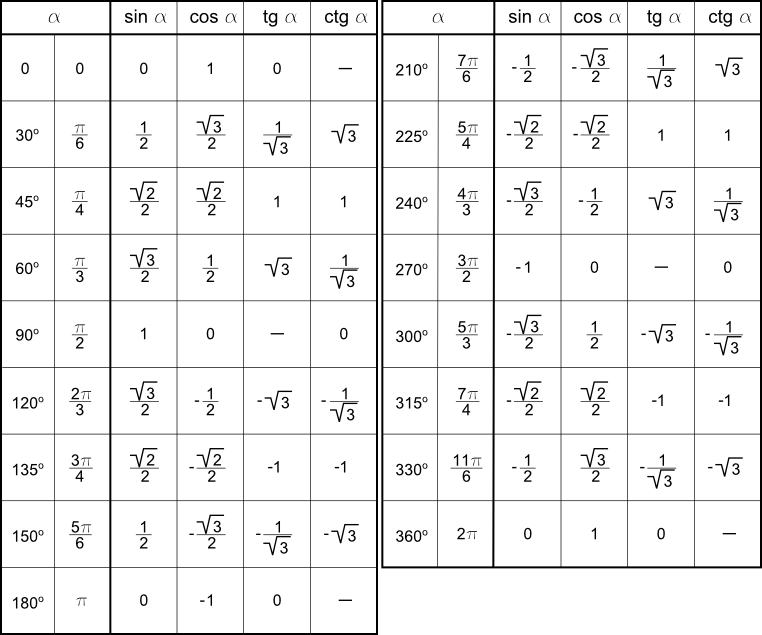
Существует шесть основных тригонометрических функций: синус, косинус, тангенс, котангенс, секанс и косеканс.
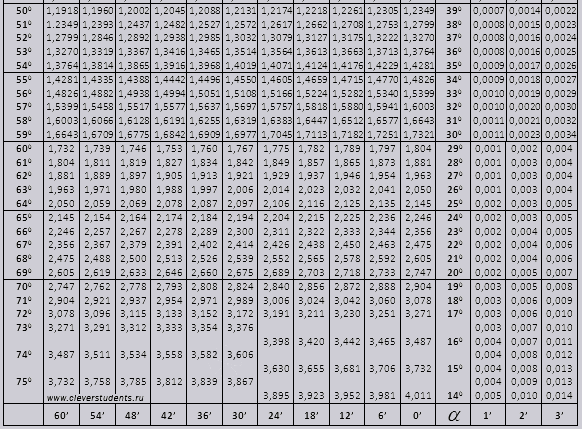
Тригонометрическая функция данного угла определяется его отношением к длине гипотенузы треугольника. В таблице ниже показаны тригонометрические функции для выбранных углов в градусах.
Зарегистрируйтесь, чтобы получить бесплатный пробный тест и учебные материалы
+91
Подтвердите OTP-код (обязательно)
Я согласен с условиями и политикой конфиденциальности.
Тригонометрическая функция угла 0° sin(0) = 0 cos(0) = 1 tan(0) = 0 1° sin(1) = 0,0174532925 cos(1) = 0,9851063801 tan(1) = 0,0174532925 2° sin(2) = 0,0349065804 cos(2) = 0,9899
В таблице перечислены тригонометрическая функция, угол в радианах и значение функции.Тригонометрические отношения
Тригонометрическая функция — это математическая функция, описывающая отношение между двумя углами в прямоугольном треугольнике. Наиболее известными тригонометрическими функциями являются синус, косинус и тангенс.
- Тригонометрические уравнения
- Тригонометрические тождества
Тригонометрические функции дополнительных углов
Когда два угла являются дополнительными, сумма их углов равна 90°. Тригонометрические функции дополнительных углов легко вычислить, потому что они просто обратны тригонометрическим функциям самих углов.
Например, если мы это знаем, то мы знаем и это. А если мы это знаем, то мы и это знаем.
В следующей таблице приведены тригонометрические функции дополнительных углов.
- Angle
- sin
- cos
- tan
- cot
- 90°
- 100
- 1
- 45°
- 0.
