Таблица умножения (примеры на умножение и деление)
60,00 ₽
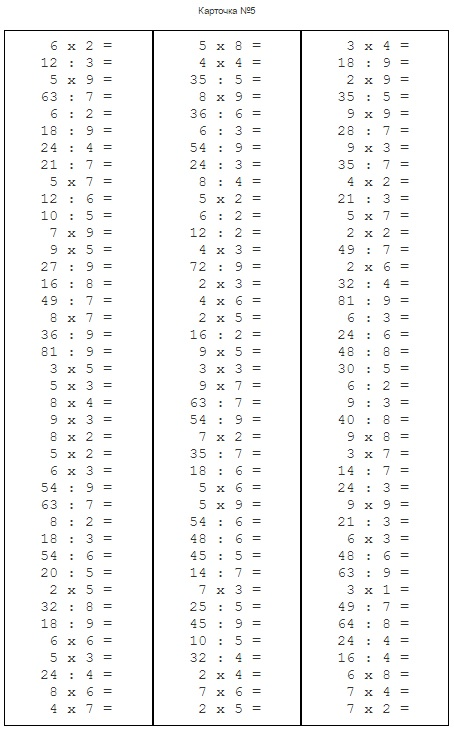
Примеры на умножение и деление вразброс. Можно сформировать карточки только на умножение, деление или смешанные примеры. Для детей, которые уже знают таблицу умножения. Без ответов. Для печати А4.
Артикул: i-1443 Категория: Для учебы Метки: Таблица умножения, 2 класс
- Описание
- Детали
- Отзывы (0)
Описание
Таблица умножения (примеры на умножение и деление) — программа, которая представляет собой тренажер для счета. С помощью генератора примеров можно создать и распечатать готовые примеры на умножение и деление вразброс для детей 1-2 класса. Причем, в зависимости от потребности, можно сформировать карточки только на умножение, деление или смешанные примеры.
Программа написана в Excel с помощью макросов. Формируется примеры: 6 столбиков по 40 примеров на листе формата А4. Примеры генерируются случайным образом, количество генераций не ограничено.
Генератор примеров по математике будет очень удобен как для родителей, так и для учителей. Не нужно заранее покупать задачники и пособия по математике с примерами. Можно скачать файл и сгенерировать карточки в любое время независимо от подключения к интернету и распечатать.
Для ознакомления с программой можно бесплатно скачать примеры, которые получаются при использовании программы. Для получения новой карточки примеров достаточно скачать, нажать на кнопку генерации и распечатать.
Чтобы выучить таблицу умножения, можно скачать карточку с примерами для заучивания и проверки своих знаний
Данную программу также можно скачать в составе сборника заданий для 2 класса.
Для того, чтобы выучить таблицу умножения на каждое число в отдельности, скачайте программу «Таблица умножения для изучения (умножение и деление на каждое число и вразброс)«.
Для того, чтобы решать примеры в excel (без печати) с автоматической проверкой ответов, скачайте программы «Тренажер на таблицу умножения» или «Таблица умножения для изучения (с автопроверкой)«.
Другие программы, которые помогут закрепить навыки счета:
- Таблица умножения — карточки
- Игра «Крестики-нолики» на таблицу умножения
- Игра «Найди примеры» на таблицу умножения
- Математический лабиринт (таблица умножения)
- Умножение и деление по типам (табличное, внетабличное, круглых чисел)
- Головоломка «Квадрат множителей»
Также есть программы, в которых можно выбрать уровень сложности. В них можно начать с решения легких примеров, а затем перейти к более сложным.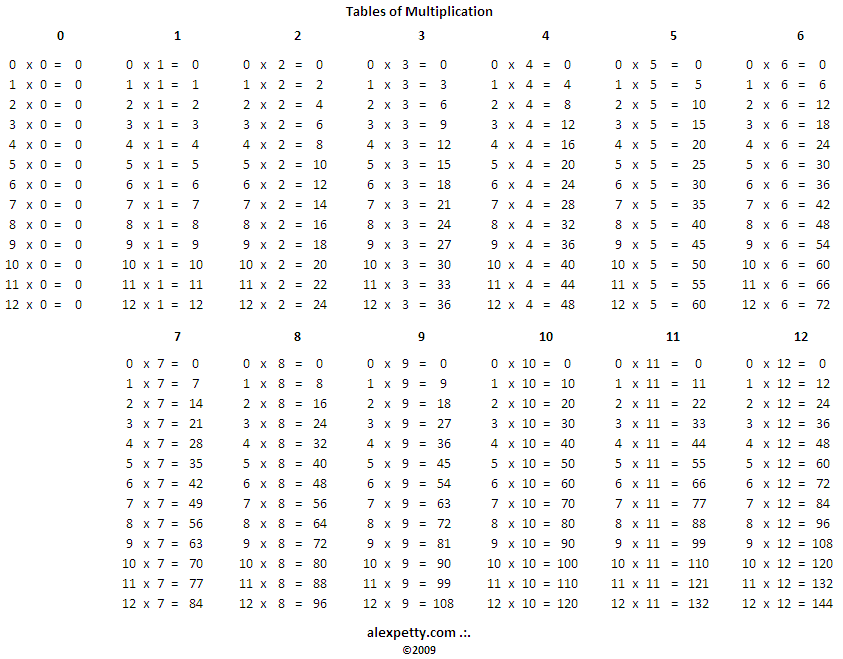
На сайте представлен каталог программ, в котором все программы распределены по группам. С помощью каталога Вы можете выбрать те программы, которые подходят именно Вам.
Вам также будет интересно…
Таблица умножения для изучения (умножение и деление на каждое число и вразброс)
Оценка 5.00 из 5
75,00 ₽В корзинуИгра «Найди примеры на таблицу умножения»
65,00 ₽В корзинуИгра «Крестики-нолики» (таблица умножения)
65,00 ₽В корзинуКвадрат множителей
Оценка 5.00 из 5
70,00 ₽В корзинуТаблица умножения для изучения (с автопроверкой)
100,00 ₽В корзинуМатематический кроссворд 2 (все действия)
90,00 ₽В корзинуТренажер на таблицу умножения
60,00 ₽В корзинуУмножение и деление по типам (табличное, внетабличное, круглых чисел)
100,00 ₽В корзинуГоловоломка «Математический лабиринт (таблица умножения)»
95,00 ₽В корзину
Примеры на деление и умножение
Примеры на деление и умножение — для распечатки и интерактивного решения
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| www.L1158.ru | www.1158.su L1158@inbox. 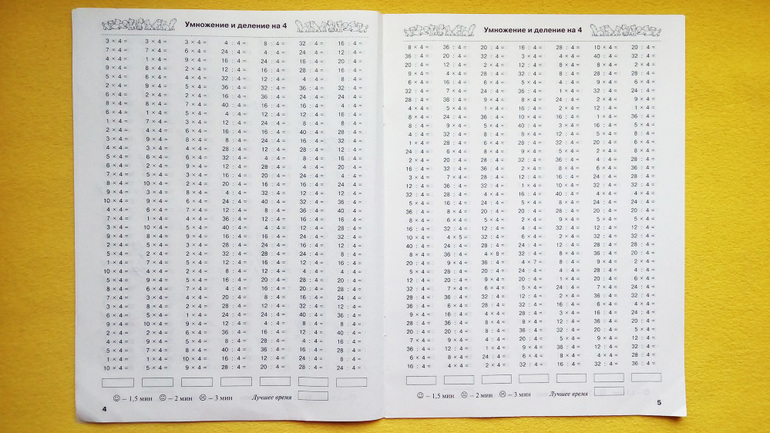 ru ru |
Бесплатные печатные таблицы умножения и таблицы умножения
Обеспечение академического роста
Быть ребенком нелегко. В их списке так много дел и так мало времени, чтобы выполнить все это. Они должны помнить время своих любимых шоу и пытаться закончить свою зелень. А озорство — это деятельность, которая требует тщательного планирования с их стороны, чтобы шалости были достаточно забавными, чтобы рассмешить кого-то, но не настолько глупыми, чтобы их можно было оправдать.
Вот что приходит на ум, когда мы видим детей, занимающихся этими видами деятельности. Мы не задумываемся о том, какой до- или посткризисный анализ они проведут по своему окружению, прежде чем придумывать свои шалости. Мы можем аплодировать их памяти, когда видим, как они декламируют диалоги из своих любимых шоу, но редко обращаем внимание на их наблюдательность, когда видим, как они подражают животным. Итак, почему мы становимся критичными и озабоченными, когда дело доходит до их академического мастерства?
Та часть, где мы хотим, чтобы они учились и росли в учебе, — это то, где мы должны быть наиболее любезными из способности понимания нашего ребенка. Именно здесь мы должны поощрять их следовать своим инстинктам и подвергать сомнению свою точку зрения. Мы должны помочь им решать проблемы по-своему, проявляя смекалку и попадая в яблочко, а не пуская стрелы в темноте.
Именно здесь мы должны поощрять их следовать своим инстинктам и подвергать сомнению свою точку зрения. Мы должны помочь им решать проблемы по-своему, проявляя смекалку и попадая в яблочко, а не пуская стрелы в темноте.
Мы уделяем большое внимание занятиям по математике, потому что это заставляет наших детей критически относиться к окружающему миру и важно для их академического пути. Но следим ли мы за тем, чтобы они практиковали применение понятий, а не просто запоминали теории?
Действительно, такие понятия, как сложение и вычитание, можно сделать на пальцах, но как насчет умножения и деления? Достаточно ли легко они укореняются в сознании ребенка? Или нам нужен более накопительный и увлекательный подход, чтобы научить наших детей тому, что это не так сложно, как кажется?
Читайте дальше, чтобы успешно ответить на приведенные выше вопросы и помочь своим детям полюбить все тонкости умножения.
СОДЕРЖАНИЕ:
- Умножение: глупый друг дополнения
- Как начать обучение умножению: визуальный подход — Группы
- Повторное дополнение к умножению выражений
- Стратегии умножения
- .
 Свойство
Свойство - Установка диаграмм умножения
- Советы для мастерства Таблицы
- Ресурсы умножения (бесплатные печатные изделия)
Умножение: Дополнительное место. в дополнение к обучению. Они видят задачу, говорящую 2 + 1, представляют два объекта, вызывают в воображении еще один такого же типа, считают их все и вуаля! 2 + 1 = 3.
Но им трудно представить объекты подобным образом, когда они видят выражение, в котором вместо плюса стоит крестик.
2 ✕ 3 . . .
Источник
Так что теперь?
Развлекаемся с умножением!
Мы научились умножать с помощью традиционного, более привычного и скучного подхода, называемого механическим заучиванием. Мы просто запоминаем факты 2, отвечаем на вопрос и идем дальше, думая, что полностью поняли концепцию. Но это становится проблемой, когда мы сталкиваемся с понятием в более поздних классах, где умножение — это не просто независимая задача, которую нужно решить.
В таких случаях понятия умножения связаны с понятиями деления. А деление связано с дробями, которые, в свою очередь, связаны с десятичными знаками. Существует целая династия понятий, где дети не могут избежать умножения, потому что у него есть свои приложения, такие как оценка, оценка количества денег, порядок операций, вычисление расстояний и даже задачи на прошедшее время.
Так как же сделать умножение более доступным для детей, а не просто зубрежкой?
Ответ заключается в том, как мы обучаем этому на начальном уровне. Простой термин под названием Groups и простой подход под названием Repeated Addition — отличные места для начала!
Связанное чтение: Новые математические советы и стратегии для улучшения навыков решения задач у детей к детям правильно. Переход от сложения к умножению можно облегчить с помощью «Групп».Скажем так: использование Групп похоже на умножение в сахарной оболочке, потому что такой подход помогает детям понять его легче.
Обучение умножению с помощью группВозможно, тогда они не будут так бояться этого.
Изображение выше можно легко описать как «5 групп по 2 самолета в каждой».
А как узнать общее количество самолетов? Прибавив «2» пять раз, т. е.
2 + 2 + 2 + 2 + 2 и получится 10.Источник
Легкий!Чтобы помочь вашим детям научиться составлять повторяющиеся выражения сложения; Вы можете попробовать эту игру на SplashLearn!
Повторное сложение в выражениях умноженияПосле того, как ваши маленькие ученики освоят написание повторяющихся предложений на сложение, следующим шагом будет научить их выражениям умножения. Рассмотрим следующий пример:
4 группы по 5 черепах
Повторное добавление предложения:
5 + 5 + 5 + 5
Теперь, когда ваш ребенок устанет писать выражения сложения, вы можете познакомить его с простым способом написания этих выражений короче и лаконичнее.
Нетрудно будет показать вашему малышу, что мы только что написали цифру «5» четыре раза. Следовательно, мы также можем записать это как:
4 раза 5
И это становится выражением умножения:
4 ✕ 5
Но этот шаг становится решающим, поскольку именно здесь мы подсознательно совершаем ошибку. . Мы начинаем учить их решать эти выражения и забываем о том, что этот шаг тоже нужно больше практиковать.
Support Is Key
Прежде чем приступить к подсчету пропусков, необходимо ознакомиться с выражениями умножения.Дети должны уметь находить произведение, не зная правил умножения. Мы можем сделать это, поощряя учащихся связывать выражения с ситуациями, давая им случайные выражения умножения и прося их представить, что могло привести к этому выражению.
Позвольте их творчеству стать частью их обучения. Когда все это будет сделано и ваши дети перестанут рисовать свои символы умножения, такие как буква «Х» в алфавите (да, разница есть), вы поймете, что они готовы!
Попробуйте эту игру и помогите своему ребенку стать экспертом в преобразовании повторяющихся выражений сложения в выражения умножения, прежде чем мы перейдем к обучению их решению выражений.

Стратегии умножения 101:Умножение с помощью пальцев Источник
Да, вы правильно прочитали!
Обычно мы просто складываем с помощью пальцев, потому что это кажется довольно простым и понятным, но мы также можем умножать с помощью пальцев.
Попробуем решить это выражение:
4 ✕ 5
Эта стратегия позволяет легко найти ответ на выражение умножения с меньшими числами.
PS: Не волнуйтесь, мы вас прикроем! Следующая часть посвящена стратегии умножения больших чисел.Умножение с помощью пальцев
Шаг 1 : Поднимите столько пальцев, сколько второе число, которое в этом выражении является числом 5.Шаг 2 : Пропустить счет до первой цифры (в данном случае «4» ) столько раз, сколько пальцев вы подняли.
Умножение на пальцахВот так и получается ответ на заданное выражение.

4 ✕ 5 = 20
Распределительное свойство
Дети очень легко осваивают факты умножения 2, 3, 4, 5, и мы можем использовать это с пользой, обучая их распределительному свойству. окончательная стратегия умножения.
Попробуем решить это выражение:
3 ✕ 9
Шаг 1: Запишем большее число как сумму 5 и другого числа:
✕ 3 +3 90 ( 4)
Шаг 2: Разделите это выражение в виде суммы двух меньших выражений, например,:
3 ✕ 9 = (3 ✕ 5) + (3 ✕ 4)
Шаг 3: Решите эти меньшие выражения и сложите результаты, чтобы найти окончательный ответ.
3 ✕ 9 = 15 + 12 = 27
Вуаля!
Три простых шага, и наши юные ученики больше не будут болтать об умножении.
Умножение в повседневной жизни
Стратегии умножения больше похожи на простые ритуалы, помогающие детям решать проблемы.
Но это все равно не даст им представления о том, насколько это важно в реальном мире.
Мы можем помочь нашим начинающим математикам связать умножение с реальной жизнью, попросив их проверить следующий счет за продукты, который они принесли домой, или спросив их о количестве саженцев/цветов на клумбе, когда они идут в сад. Подсчитывая суммы денег, стоя в очереди у кассы в магазине, где есть ситуация «купи или пока», умножение может быть их спасением в реальном смысле!
Процесс подготовки детей к старшим классам начинается, когда они понимают, что такое умножение. Для этой цели существует очень полезный инструмент, который называется Таблица умножения.
Давайте посмотрим, как это работает.
Таблица умноженияБазовая таблица умножения содержит сведения об умножении чисел от 1 до 10, и использовать таблицу умножения так же просто, как приготовить бутерброд. Это может быть даже проще, чем это.
Попробуем решить это выражение с помощью таблицы умножения:
Уравнение: 7 ✕ 9
Шаг 1: Найдите 7-ю строку и 9-й столбец.
Шаг 1 – Поиск строк и столбцов
Шаг 2 – Поиск перекрывающихся строк и столбцов
Шаг 2: Найдите прямоугольник, в котором строка номер 7 пересекается со столбцом номер 9.
И вот, ответ на наше выражение:
7 ✕ 9 = 63
Чтобы упростить задачу, вы можете обратиться к таблице умножения, которую можно бесплатно распечатать в конце этого блога. Мы также включили пустую таблицу умножения, чтобы вы могли создавать свои собственные игры, такие как бинго с умножением!
Переместительное свойство
Таблица умножения для коммутативного свойства
Прежде чем вы спросите, таблицы умножения работают и в обратном порядке. Вы можете поискать столбец, в котором показаны факты о 7, и строку, в которой показаны факты о 9, и ответ останется тем же.
Этот факт называется коммутативным свойством умножения, т.е. Это просто игра на перспективу!
Взгляните,
ИллюстрацияНа этом рисунке показаны 3 группы по 6 мячей в каждой, поэтому выражение умножения для этого будет:
3 ✕ 6Но если мы посмотрим на картинку по-другому,
Иллюстрация
Теперь это 6 групп по 3 мяча в каждой, поэтому выражение умножения будет таким:
6 ✕ 3Поскольку общее количество мячей в любом случае одинаково, оба приведенных выше выражения будут иметь одинаковый результат.

Итак,
3 ✕ 6 = 6 ✕ 3
Дети могут использовать этот аварийный люк, когда они застряли в таблице умножения большего числа, и могут легко найти ответ, вспомнив соответствующий факт умножения меньшего числа. количество.
Актуальность таблиц умноженияТаблицы умножения важны, потому что они помогают учащимся ознакомиться с фактами различных чисел. Таким образом, когда наши юные ученики переходят к изучению своей таблицы умножения, это будет не просто механическое заучивание. Вместо этого они напрягали бы свои мозги, чтобы использовать коммутативные свойства, если они когда-нибудь где-нибудь застряли, или они могли бы также использовать распределительное свойство для получения факта умножения.
ИсточникИспользование таблицы умножения является ступенькой к изучению процесса многозначного умножения. По мере того, как дети переходят в разные классы, умножение становится важным и основным навыком для сложных аспектов математики, которые им предстоит пройти.

Таким образом, детям необходимо иметь возможность опираться на то, что они уже знают, и таблица умножения может помочь им освоиться.
Таблицы умножения — это вспомогательные методы, которые могут помочь им лучше учиться. Но настоящее испытание — это когда дети начинают учить свою таблицу умножения, и мы здесь, чтобы помочь с этим!
Таблица умножения
Таблица умножения несомненно возвращает нас в самые тревожные дни нашего детства. Дети прочно закрепятся в мире математики, как только поймут, что таблицы умножения на 7 и 8 нельзя воспринимать легкомысленно.
Источник Двойки, пятерки и десятки называются братством (или сестричеством) умножения, поскольку они никогда не предают нас. Эти числа могут помочь детям запомнить и другие таблицы умножения.
Терпение — главная добродетель для занятий с маленькими детьми. Если вы показываете им образец в чем-то, они с готовностью принимают это знание, потому что это удобно. Показ им цепочки цифр и просьба запечатлеть ее в памяти не поможет им в долгосрочной перспективе.

Выучить таблицу умножения нельзя, просто повторяя ее 3 раза в день в течение 3 дней. Это больше похоже на рецепт от врача, чем на стратегию, чтобы хорошо чему-то научиться. Тем не менее, вот несколько советов, которые помогут нашим учащимся с таблицей умножения.
Похожие чтения: Лучшие математические приложения для детейСоветы по работе с таблицами умножения
Таблица умножения 1Этой таблицы умножения нечего бояться. Какое бы число вы ни умножали на 1, результатом будет само число.
Таблица умножения 1 Таблица умножения 2Число 2 — это то, что мы называем «удвоить или ничего!»
Любое число, которое вы умножите на 2, удвоится или просто сложится само с собой.
Таблица умножения на 2 Таблица умножения на 3Таблица умножения 3
Вот самый простой способ попрактиковаться в таблице умножения на 3.Если вы хотите умножить число на 3, сначала умножьте его на 2, а затем прибавьте то же самое. номер к нему.
Давайте посмотрим на этот пример:
Если вы хотите найти 3 ✕ 6 , вернитесь к своим двойкам и проверьте 2 ✕ 6 и , добавьте к нему 6 .
Итак – 3 ✕ 6 = (2 ✕ 6) + 6 = 12 + 6 = 18
добавьте к нему 8 .
Итак – 3 ✕ 8 = (2 ✕ 8 ) + 8 = 16 + 8 = 24
Таблица умножения 4Время для удвоения числа. Из этого нет простого выхода. Если вы хотите умножить число на 4, удвойте его один раз, а затем удвойте то, что получится!
Таблица умножения 4 Таблица умножения 5Второе в любимом братстве, это число даже не нуждается в подвохе, но если ваш ребенок все же застрянет с этим.
Вот что вы можете сделать:
Любое число, на которое вы хотите умножить 5, прибавьте к его концу 0, а затем половину числа!
Таблица умножения 5Например,
Если вы хотите найти 5 ✕ 7 , прикрепите 0 в конце 7 ,
Итак, теперь это 70 . А половина 70 это 35 .
Итак, 5 ✕ 7 = 35
Таблица умножения 6Эта таблица работает так же, как таблица 3. Если вы хотите найти произведение числа с 6, вернитесь к 5s, умножьте это число на 5, а затем прибавьте то же число.
Таблица умножения 6Итак, если вы хотите найти 6 ✕ 8 , сделайте 5 ✕ 8 вместо этого, а затем добавьте к нему 8 .
SO 6 ✕ 8 = (5 ✕ 8 ) + 8 = 40 + 8 = 48.
.этот, убедитесь, что они знают свои предыдущие таблицы, чтобы этот не казался таким сложным. Таблица умножения на 7
Давайте посмотрим, как мы можем подойти к этому.
До 7 раз 6, трюк состоит в том, чтобы использовать коммутативное свойство, то есть
7 ✕ 2 = 2 ✕ 7 = 147 ✕ 3 = 3 ✕ 7
7 ✕ 4 = 4 ✕ 7 = 28
7 ✕ 5 = 5 ✕ 7 = 35
7 ✕ 6 = 6 ✕ 7 = 42
799999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999997. 6. остальные числа, самый простой трюк — не забывать добавлять группу из 7.
7 ✕ 7 будет еще одна группа из 7, чем 7 ✕ 6,
SO 7 ✕ 7 = 42 + 7 = 49
7 ✕ 8 будут на одну еще Группа
7 ✕ 8 .
из 7, чем 7 ✕ 7,
SO 7 ✕ 8 = 49 + 7 = 56
и 7 ✕
Итак, 7 ✕ 9 = 56 + 7 = 63.Тада! Мы освоили и таблицу 7.
Таблица умножения 8
Самый простой способ выучить таблицу умножения 8 — использовать свойство коммутативности для первых нескольких шагов, а затем добавить группу «8» для оставшихся кратных, точно так же, как в вашей таблице умножения на 7.Для практики вы можете скачать карточки для таблицы умножения на 8, прикрепленные в конце.
Таблица умножения 8 Таблица умножения 9Простой способ запомнить эту таблицу умножения — использовать факты 10.
Чтобы умножить число на 9, добавьте ноль в конце числа, а затем вычтите то же число.
Таблица умножения 9Например,
Чтобы найти 9 ✕ 8 ,
Присоедините 0 в конце числа 8 и вычтите из него 8 ;
Таблица умножения на 10
То есть 9 ✕ 8 = 80 – 8 = 72Самые старшие и самые легкие дети могут написать эту таблицу умножения с закрытыми глазами и не сделать ошибок.

Просто добавьте ноль в конце любого числа, которое вы умножаете на 10, и вы получите ответ.10 ✕ 7 = 70
Таблица умножения на 1010 ✕ 10 = 100.
Время похлопать себя по спине!
Теперь у вас есть несколько проверенных приемов, которые помогут вашим детям справиться с этими предвестниками беспокойства!
Прежде чем вы научите своего бесстрашного ученика всему умножению, у нас есть некоторые ресурсы, которые, как мы думаем, будут очень полезны, когда ваш ребенок начнет это новое приключение в понимании умножения и его тайн.
Ресурсы по умножению (бесплатные печатные формы)
Чтобы лучше попрактиковаться и освежить в памяти все концепции умножения, попробуйте эти рабочие листы по умножению на SplashLearn.
Вы также можете щелкнуть любую из приведенных ниже ссылок, чтобы напрямую загрузить эти ресурсы с помощью SplashLearn.
Читайте также: Как помочь детям с математикой: 6 инновационных подходовТаблица умножения
Таблица умножения с ответами
Flash Card of 2
Flash Card of 3
Flash Card of 4
Flash Card of 5
Flash Card of 6
Flash Card of 7
Flash Card of 8
Flash Card of 9
Таблицы умножения до 10
Присоединяйтесь к нашему сообществу из 40 миллионов бесстрашных учащихся
Родители, зарегистрируйтесь бесплатно!
Q1.
Как я могу запоминать вещи быстрее?
Повторно практикуя , мы можем легко выработать рефлекторные реакции памяти. Например, запоминание 6 ✕ 7 = 42 можно облегчить, если попрактиковаться в предложении «шесть семерок — сорок два».
Q2. Что такое настольные игры?
Отличная игра с таблицами умножения «Угадай выражения» , где организатор называет число, а вы записываете как можно больше выражений за ограниченное время. Произведение этих выражений должно быть указанным числом. Побеждает тот, кто даст больше всего правильных ответов.
Q3. Как вы учите умножению отстающих учеников?
Используйте метод пропуска счета или используйте пальцы для умножения . Позвольте учащемуся попрактиковаться в многократном сложении, рисуя модели групп или массивов, прежде чем они начнут изучать свою таблицу умножения. Изучение коммутативных и дистрибутивных свойств числа
может оказаться дополнительной помощью. Q4. Полезны ли таблицы умножения?
Важно, чтобы учащиеся освоились с концепцией, прежде чем они начнут практиковать ее самостоятельно. Таблицы умножения могут быть хорошим справочным инструментом для отработки фактов перед началом процесса запоминания таблицы умножения.
Q5. Как проще всего научиться умножению?
То, как мы знакомим учащихся с концепцией, зависит от того, как они строят ее основу. Попросить учеников вычислить двойное или тройное число может быть забавно, и это хорошая отправная точка. Затем мы можем постепенно вводить понятие групп или таблицы умножения, когда учащиеся освоятся с этим понятием.
Рабочие листыДобро пожаловать на страницу рабочих листов дивизиона на Math-Drills.com! Пожалуйста, уделите нам все свое внимание, пока мы представляем эту страницу. Наши рабочие листы для деления помогут вам научить студентов очень важному понятию деления. Если учащиеся хорошо помнят факты умножения, преподавание фактов деления должно быть легким делом.
Если вы хотите, чтобы ваши ученики добились успеха в изучении деления, пожалуйста, убедитесь, что они знают свои факты умножения до 81, как умножать на 0 и как умножать на 10. Если они не знают этих вещей, это займет много времени. намного дольше.
На этой странице вы найдете множество рабочих листов деления, включая факты деления и деление в длинное деление с остатком и без него. Мы начнем с некоторых фактов деления, которые, как вы знаете, являются просто фактами умножения, выраженными другим способом. Основное отличие состоит в том, что вы не можете разделить на 0 и получить действительное число. Если вы действительно хотите, чтобы ваши ученики произвели впечатление, скажем, за обеденным столом, когда их родители спрашивают их, что они узнали сегодня, вы можете научить их тому, что деление на ноль не определено.
Оставшаяся часть страницы посвящена длинному делению, которое почему-то не нравится некоторым представителям населения. Длинное деление является наиболее сложным, когда учащиеся не знают свои факты умножения, поэтому сначала убедитесь, что они знают их.
О, мы это уже говорили. А как насчет алгоритма длинного деления... может быть, того, который вы, или ваши родители, или ваши дедушки и бабушки выучили? Мы с уверенностью говорим: да! Причина, по которой вы и ваши предки использовали его, заключается в том, что это эффективный и красивый алгоритм, который позволит вам решить некоторые из самых сложных задач на деление, с которыми не справятся даже блоки с основанием 10. Он работает одинаково хорошо для десятичных и целых чисел. Длинное деление на самом деле не так сложно.
Самые популярные рабочие листы деления на этой неделе
Длинное деление - однозначный делитель и двузначное частное без остатка ( 3490 просмотров на этой неделе )3-значное на 2-значное длинное деление с остатками и шагами, показанными в ключе ответа ( 1881 просмотров на этой неделе )3-значное деление на 1-значное длинное деление с остатками с поддержкой сетки и подсказками ( 1857 просмотров на этой неделе )4-значное деление на 2-значное длинное деление с остатками и шагами, показанными в ключе ответа ( 1335 просмотров на этой неделе )Деление на 9 с коэффициентами от 1 до 9 ( 1252 просмотров на этой неделе )Рабочие листы с фактами о делениях
Рабочие листы с фактами о делениях, включая таблицы делений, факты о делениях и рабочие листы с фактами об отдельных делениях.
Таблицы фактов отдела
Таблицы фактов о подразделениях в Серые от 1 до 12 Таблицы фактов о подразделениях в Серые от 1 до 12 (Ответы пропущены) Таблицы фактов о подразделениях в цветах от 1 до 12 Таблицы фактов о разделах в наборе Монтессори-цвета от 1 до 12 Выделенные факты
Факты о горизонтальном делении рабочих листовМанипуляторы могут помочь учащимся «усвоить» концепцию деления. Например, учащиеся могут перегруппировать блоки с основанием десять в блоки, а затем разделить блоки на стопки. Например, 81 ÷ 9 в конечном итоге будет 9 стопками по 9 единиц.
Подразделение, по сути, задает вопрос: «Сколько _____ в _____?» На вопрос 81 ÷ 9, подсказка будет звучать так: «Сколько девяток в числе 81?» Эта подсказка пригодится учащимся при изучении математики на более поздних этапах, когда будут возникать более сложные понятия, такие как деление десятичных дробей или дробей.
«Сколько третей в четырех?» или еще лучше, Сколько третьих чашек в четырех чашках?» При необходимости достаньте мерные чашки.
Факты горизонтального подразделения с дивидендами на 25 Факты горизонтального подразделения с дивидендами на 36 Факты о горизонтальном делении с дивидендами до 49 Факты горизонтального подразделения с дивидендами на 64 Факты горизонтального подразделения с дивидендами на 81 Факты горизонтального подразделения с дивидендами на 100 Факты горизонтального подразделения с дивидендами на 121 Факты горизонтального подразделения с дивидендами на 144 Факты горизонтального подразделения с дивидендами на 169 Факты горизонтального подразделения с дивидендами на 196 Факты о горизонтальном делении с дивидендами до 225
Факты вертикального деления рабочих листовФакты о вертикальном делении Дивиденды до 25 Со знаком деления Факты о вертикальном делении Дивиденды до 36 Со знаком деления Факты о вертикальном делении Дивиденды до 49 со знаком деления Факты о вертикальном делении Дивиденды до 64 Со знаком деления Факты о вертикальном делении Дивиденды на 81 со знаком деления Факты о вертикальном делении крупным шрифтом Дивиденды до 81 Со знаком деления Факты о вертикальном делении Дивиденды до 100 Со знаком деления Факты о вертикальном делении Дивиденды до 121 со знаком деления Факты о вертикальном делении Дивиденды до 144 со знаком деления Факты о вертикальном делении Дивиденды до 169 со знаком деления Факты о вертикальном делении Дивиденды до 196 со знаком деления Факты вертикального подразделения Дивиденды до 225 Со знаком разделения Факты о вертикальном делении Дивиденды до 25 с символом длинного деления (50 на странице) Факты о вертикальном делении Дивиденды до 36 с символом длинного деления (50 на странице) Факты о вертикальном делении Дивиденды до 49 с символом длинного деления (50 на странице) Факты о вертикальном делении Дивиденды до 64 с символом длинного деления (50 на странице) Факты о вертикальном делении Дивиденды до 81 с символом длинного деления (50 на странице) Факты о вертикальном разделении Дивиденды до 100 С символом длинного деления (50 на странице) Факты о вертикальном делении Дивиденды до 121 с символом длинного деления (50 на странице) Факты о вертикальном делении Дивиденды до 144 с символом длинного деления (50 на странице) Факты о вертикальном делении Дивиденды до 169 с символом длинного деления (50 на странице) Факты о вертикальном делении Дивиденды до 196 с символом длинного деления (50 на странице) Факты о вертикальном разделении Дивиденды до 225 С символом длинного деления (50 на странице)
Факты о горизонтальном делении рабочих листов с номерами фокусаФакты деления с делителем числа 1 (частное 1-9) Факты деления с делителем от 2 (частное 1-9) Факты деления с делителем от 3 (частное 1-9) Факты деления с делителем от 4 (частное 1-9) Факты о дивизионе с Делитель 5 (Частное 1-9) Факты деления с делителем от 6 (частное 1-9) Факты деления с делителем числа 7 (частное 1-9) Факты деления с делителем числа 8 (частное 1-9) Факты деления с делителем числа (частное 1-9) Факты деления с делителем числа 1 (частное 1-12 ) Факты деления с делителем на 2 (частное 1-12 ) Факты о дивизионе с Делитель 3 (Частное 1-12 ) Факты деления с делителем на 4 (частное 1-12 ) Факты деления с делителем числа 5 (частное 1-12 ) Факты деления с делителем на 6 (частное 1-12 ) Факты деления с делителем числа 7 (частное 1-12 ) Факты деления с делителем числа 8 (частное 1-12 ) Факты о дивизионе с Делитель 9 (Частное 1-12 ) Факты деления с делителем числа 10 (частное 1-12 ) Факты деления с делителем числа 11 (частное 1-12 ) Факты деления с делителем числа 12 (частное 1-12 )
Факты о делении рабочих листов с комбинациями фокусных чиселДеление на 1, 2, 5 и 10 (Частное 1-12) Деление на 1, 2, 5 и 10 (Частное 1-12) (Горизонтальное) Деление на 3, 4 и 6 (Частное 1-12) Деление на 7, 8 и 9(Коэффициент 1-12) Деление на 11 и 12 (Частное 1-12)
Рабочие листы на длинное деление
Рабочие листы на длинное деление для отработки различных стратегий деления на длинное, включая вопросы без остатков, остатков и десятичных частных.
Полное деление рабочих листов с без остаткаНужен более простой способ деления больших чисел? Попробуйте этот метод, используя степени десяти. Чтобы успешно использовать этот метод, учащиеся должны уметь умножать на десять и вычитать. Студенты вычитают делимое, умноженное на убывающие степени десяти, пока не получат ноль или остаток. Пример: 1458 ÷ 54. Примечание 54 × 1 = 54, 54 × 10 = 540 (больше не нужно). 1458 - 540 - 540 = 378. Обратите внимание, что 540 было вычтено дважды, так что количество раз, когда 54 «входит» в 1458, составляет 20 раз. Продолжая, 378 - 54 - 54 - 54 - 54 - 54 - 54 - 54 = 0. Поскольку 54 было вычтено семь раз, частное увеличивается на семь и в сумме получается 27. Другими словами, 54 "входит" в 1458, 27. раз.
Мы могли бы также упомянуть, что этот метод может быть еще более сложным, если использовать степени, кратные десяти. В приведенном выше примере использование 54 × 5 = 270 помогло бы быстрее получить частное.
Делитель десяти; 2-значный коэффициент 1-значный делитель; 1-значный коэффициент 1-значный делитель; 2-значный коэффициент 1-значный делитель; 3-значный коэффициент 2-значный делитель; 2-значный коэффициент 2-значный делитель; 3-значный коэффициент 2-значный делитель; 4-значный коэффициент 3-значный делитель; 3-значный коэффициент 3-значный делитель; 4-значный коэффициент 3-значный делитель; 5-значный коэффициент
Европейское длинное деление рабочих листов без остатка1-значный делитель; 1-значный коэффициент (европейский) 1-значный делитель; 2-значный коэффициент (европейский) 1-значный делитель; 3-значный коэффициент (европейский) 2-значный делитель; 2-значный коэффициент (европейский) 2-значный делитель; 3-значный коэффициент (европейский) 2-значный делитель; 4-значный коэффициент (европейский) 3-значный делитель; 2-значный коэффициент (европейский) 3-значный делитель; 3-значный коэффициент (европейский) 3-значный делитель; 4-значный коэффициент (европейский)
Полное деление рабочих листов с остаткамиВы когда-нибудь думали, что можете помочь ученику лучше понять вещи и получить более точный ответ, используя при этом остатки? Это довольно легко на самом деле.
Остатки обычно даются вне контекста, в том числе в приведенных ниже ключах ответов. Остаток на самом деле является числителем дробного частного. Например, 19 ÷ 3 равно 6 с остатком 1, что точнее 6 1/3. Использование дробных частных означает, что ваши ученики всегда найдут точный ответ на все вопросы о делении на длинное деление, и во многих случаях ответ будет более точным (например, сравните 6 1/3 с 6,3333....).
Делитель десяти; 2-значный коэффициент 1-значный делитель; Двузначный дивиденд 1-значный делитель; 3-значный дивиденд 1-значный делитель; 4-значный дивиденд 2-значный делитель; 3-значный дивиденд 2-значный делитель; 4-значный дивиденд 2-значный делитель; 5-значный дивиденд 3-значный делитель; 4-значный дивиденд 3-значный делитель; 5-значный дивиденд 3-значный делитель; 6-значный дивиденд
Полное деление рабочих листов с десятичными дробями1-значный делитель; Двузначный дивиденд 1-значный делитель; 3-значный дивиденд 1-значный делитель; 4-значный дивиденд 2-значный делитель; 3-значный дивиденд 2-значный делитель; 4-значный дивиденд 2-значный делитель; 5-значный дивиденд 3-значный делитель; 4-значный дивиденд 3-значный делитель; 5-значный дивиденд 3-значный делитель; 6-значный дивиденд
Европейское длинное деление рабочих листов с остатками1-значный делитель; Двузначный дивиденд (европейский) 1-значный делитель; 3-значный дивиденд (европейский) 1-значный делитель; 4-значный дивиденд (европейский) 2-значный делитель; 3-значный дивиденд (европейский) 2-значный делитель; 4-значный дивиденд (европейский) 2-значный делитель; 5-значный дивиденд (европейский) 3-значный делитель; 4-значный дивиденд (европейский) 3-значный делитель; 5-значный дивиденд (европейский) 3-значный делитель; 6-значный дивиденд (европейский)
Европейское длинное деление рабочие листы с десятичными частными1-значный делитель; Двузначный дивиденд (европейский) 1-значный делитель; 3-значный дивиденд (европейский) 2-значный делитель; Двузначный дивиденд (европейский) 2-значный делитель; 3-значный дивиденд (европейский) 2-значный делитель; 4-значный дивиденд (европейский) 3-значный делитель; 3-значный дивиденд (европейский) 3-значный делитель; 4-значный дивиденд (европейский) 3-значный делитель; 5-значный дивиденд (европейский)
Полное деление
с остатками рабочих листов с шагами, показанными в ключе ответаМы подумали, что было бы полезно включить несколько рабочих листов с длинным делением с показанными шагами.
В ключах ответов для этих рабочих листов для разделения используется стандартный алгоритм, который вы могли бы изучить, если бы вы ходили в англоязычную школу. Изучение этого алгоритма само по себе иногда недостаточно, поскольку оно может не привести к хорошему концептуальному пониманию. Одним из инструментов, который помогает учащимся изучить стандартный алгоритм и развить понимание деления, является набор десятичных блоков. Обучая студентов сначала делению на блоки с основанием десять, а затем переходя к стандартному алгоритму, учащиеся получат концептуальное понимание, а также смогут использовать эффективный алгоритм для деления в длинное число. Студенты, обладающие обоими этими качествами, естественно, добьются больших успехов в своих будущих математических исследованиях.
2-значный на 1-значный Длинное деление с остатком с шагами, показанными в ключе ответа 3-значный на 1-значный Длинное деление с остатком с шагами, показанными в ключе ответа 4-значный на 1-значный Длинное деление с остатком с шагами, показанными в ключе ответа 5-значный на 1-значный Длинное деление с остатком с шагами, показанными в ключе ответа 6-значный на 1-значный Длинное деление с остатком с шагами, показанными в ключе ответа 3-значный на 2-значный Длинное деление с остатками с шагами, указанными в ключе ответа 4-значный на 2-значный Длинное деление с остатком с шагами, указанными в ключе ответа 5-значный на 2-значный Длинное деление с остатком с шагами, показанными в ключе ответа 6-значный на 2-значный Длинное деление с остатком с шагами, показанными в ключе ответа 4-значный на 3-значный Длинное деление с остатком с шагами, указанными в ключе ответа 5-значный на 3-значный Длинное деление с остатками с шагами, показанными в ключе ответа 6-значный на 3-значный Длинное деление с остатком с шагами, показанными в ключе ответа
Длинное деление на сетке
Длинное деление с помощью сетки
и БЕЗ остатка Рабочие листыНекоторым учащимся трудно выстроить все в ряд при выполнении алгоритма деления в длину, поэтому эти рабочие листы содержат сетку и более широкое расстояние между цифрами, чтобы помочь учащимся правильно расположить числа.
Ключи к ответам включают типичные шаги, которые учащиеся записывают при решении каждой задачи; однако возможны небольшие вариации в реализации. Например, некоторые люди не обращают внимания на знаки вычитания, некоторые могут показывать шаги вычитания нуля и т. д.
2-значный на 1-значный Длинное деление с Помощью в работе с сетью и подсказками и БЕЗ остатка 3-значный на 1-значный Длинное деление с помощью Grid Assistance и подсказками и БЕЗ остатка 3-значный на 2-значный Длинное деление с помощью Grid Assistance и подсказками и БЕЗ остатка 4-значный на 1-значный Длинное деление с помощью Grid Assistance и подсказками и БЕЗ остатка 4-значный на 2-значный Длинное деление с помощью Grid Assistance и подсказками и БЕЗ остатка 5-значный на 1-значный Длинное деление с помощью Grid Assistance и подсказками и БЕЗ остатка 5-значный на 2-значный Длинное деление с помощью Grid Assistance и подсказками и БЕЗ остатка 6-значный на 1-значный Длинное деление с помощью Grid Assistance и подсказками и БЕЗ остатка 6-значный на 2-значный Длинное деление с Поддержка сетки и подсказки и НЕТ остатка 3-значный на 1-значный Длинное деление с помощью Grid Assistance и БЕЗ остатка 3-значный на 2-значный Длинное деление с помощью Grid Assistance и БЕЗ остатка 4-значный на 1-значный Длинное деление с помощью Grid Assistance и БЕЗ остатка 4-значный на 2-значный Длинное деление с помощью Grid Assistance и БЕЗ остатка 5-значный на 1-значный Long Division с Grid Assistance и БЕЗ остатка 5-значный на 2-значный Длинное деление с помощью Grid Assistance и БЕЗ остатка 6-значный на 1-значный Длинное деление с помощью Grid Assistance и БЕЗ остатка 6-значный на 2-значный Длинное деление с помощью Grid Assistance и БЕЗ остатка
Длинное деление с помощью сетки
и НЕКОТОРЫЕ остатки листов2-значный на 1-значный Длинное деление с помощью Grid Assistance и подсказками и некоторыми остатками 3-значный на 1-значный Длинное деление с помощью Grid Assistance и подсказками и некоторыми остатками 3-значный на 2-значный Длинное деление с помощью Grid Assistance и подсказками и некоторыми остатками 4-значный за 1-значный Длинное деление с помощью Grid Assistance и подсказками и некоторые остатки 4-значный на 2-значный Длинное деление с помощью Grid Assistance и подсказками и некоторыми остатками 5-значный на 1-значный Длинное деление с помощью Grid Assistance и подсказками и некоторыми остатками 5-значный на 2-значный Длинное деление с помощью Сетка и подсказки и некоторые остатки 6-значный на 1-значный Длинное деление с помощью Grid Assistance и подсказками и некоторыми остатками 6-значный на 2-значный Длинное деление с помощью Сетка и подсказки и некоторые остатки 3-значный на 1-значный Длинное деление с помощью Grid Assistance и некоторые остатки 3-значный на 2-значный Длинное деление с помощью Grid Assistance и некоторые остатки 4-значный на 1-значный Длинное деление с помощью Grid Assistance и некоторые остатки 4-значный на 2-значный Длинное деление с помощью Grid Assistance и некоторые остатки 5-значный на 1-значный Длинное деление с помощью Grid Assistance и некоторые остатки 5-значный на 2-значный Длинное деление с помощью Grid Assistance и некоторые остатки 6-значный на 1-значный Длинное деление с помощью Grid Assistance и некоторые остатки 6-значный на 2-значный Длинное деление с помощью Grid Assistance и некоторые остатки
Правила делимости
Рабочие листы для отработки правил делимости, включая различные малые и большие числа и сосредоточение внимания на различных делителях.
Правила делимостиПризнак делимости на 2, 5 и 10
Число делится на 2, если последняя цифра (цифра в разряде единиц) четная. Следовательно, числа, оканчивающиеся на 0, 2, 4, 6 или 8, делятся на 2. Число делится на 5, если его последняя цифра — 0 или 5. Число делится на 10, если последняя цифра — 0.
Делимость на 3, 6 и 9
Число делится на 3, если сумма его цифр делится на 3. Например, 285 делится на 3, потому что 2 + 8 + 5 = 15 делится на 3. A число делится на 6, если оно делится и на 3, и на 2 (см. правила выше). Число делится на 9, если сумма его цифр делится на 9. Например, 285 не делится на 9, потому что 2 + 8 + 5 = 15 не делится на 9.
Делимость на 4, 7 и 8
Число делится на 4, если две последние цифры числа делятся на 4. Для числа 7 можно использовать несколько стратегий. Дополнительную информацию см. в разделе «Трюки с делимостью для изучения математики». Число делится на 8, если последние три цифры делятся на 8.
Это стандартное правило, которое может быть немного поверхностным для больших чисел, например, кто знает, делится ли 680 на 8? По этой причине мы предлагаем наше решение Math-Drills.com, которое требует немного арифметических действий, но может быть довольно легко выполнено с небольшой практикой. Как вы знаете, 8 равно 2 в третьей степени, поэтому мы подумали, что если бы вы могли разделить последние три цифры числа на 2 три раза, то оно будет делиться на 8. 680 ÷ 2 ÷ 2 ÷ 2 = 340 ÷ 2 ÷ 2 = 170 ÷ 2 = 85. У нас есть победитель! 680 действительно делится на 8.
Делимость на 2, 5 и 10 (2 цифры) Делимость на 3, 6 и 9 (двухзначное) Делимость на 4, 7 и 8 (2 цифры) Делимость чисел от 2 до 10 (2-значные) Делимость на 2, 5 и 10 (3 цифры) Делимость 3, 6 и 9 (3-значный) Делимость на 4, 7 и 8 (3 цифры) Делимость чисел от 2 до 10 (3-значные) Делимость на 2, 5 и 10 (4 цифры) Делимость на 3, 6 и 9 (4 цифры) Делимость на 4, 7 и 8 (4 цифры) Делимость чисел от 2 до 10 (4-значные)
Деление в других основных системах счисления
Деление чисел в системах счисления, отличных от десятичных, включая двоичные, четверичные, восьмеричные, двенадцатеричные и шестнадцатеричные числа.


 Свойство
Свойство Возможно, тогда они не будут так бояться этого.
Возможно, тогда они не будут так бояться этого.  Нетрудно будет показать вашему малышу, что мы только что написали цифру «5» четыре раза. Следовательно, мы также можем записать это как:
Нетрудно будет показать вашему малышу, что мы только что написали цифру «5» четыре раза. Следовательно, мы также можем записать это как: 

 Но это все равно не даст им представления о том, насколько это важно в реальном мире.
Но это все равно не даст им представления о том, насколько это важно в реальном мире. 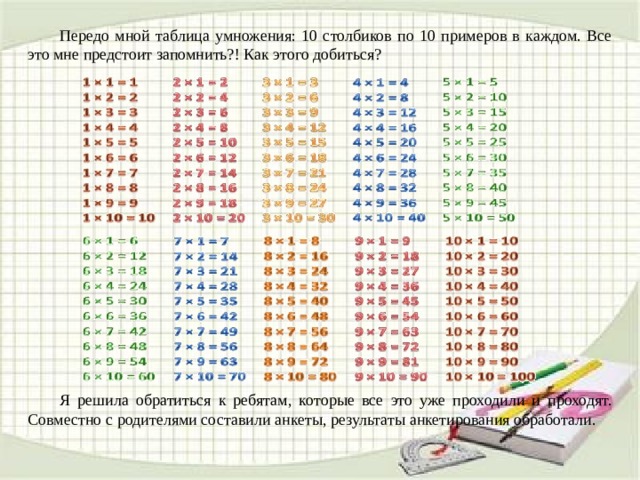


 Если вы хотите умножить число на 3, сначала умножьте его на 2, а затем прибавьте то же самое. номер к нему.
Если вы хотите умножить число на 3, сначала умножьте его на 2, а затем прибавьте то же самое. номер к нему.  Вот что вы можете сделать:
Вот что вы можете сделать: этот, убедитесь, что они знают свои предыдущие таблицы, чтобы этот не казался таким сложным. Таблица умножения на 7
этот, убедитесь, что они знают свои предыдущие таблицы, чтобы этот не казался таким сложным. Таблица умножения на 7

 Как я могу запоминать вещи быстрее?
Как я могу запоминать вещи быстрее?
 Если вы хотите, чтобы ваши ученики добились успеха в изучении деления, пожалуйста, убедитесь, что они знают свои факты умножения до 81, как умножать на 0 и как умножать на 10. Если они не знают этих вещей, это займет много времени. намного дольше.
Если вы хотите, чтобы ваши ученики добились успеха в изучении деления, пожалуйста, убедитесь, что они знают свои факты умножения до 81, как умножать на 0 и как умножать на 10. Если они не знают этих вещей, это займет много времени. намного дольше. О, мы это уже говорили. А как насчет алгоритма длинного деления... может быть, того, который вы, или ваши родители, или ваши дедушки и бабушки выучили? Мы с уверенностью говорим: да! Причина, по которой вы и ваши предки использовали его, заключается в том, что это эффективный и красивый алгоритм, который позволит вам решить некоторые из самых сложных задач на деление, с которыми не справятся даже блоки с основанием 10. Он работает одинаково хорошо для десятичных и целых чисел. Длинное деление на самом деле не так сложно.
О, мы это уже говорили. А как насчет алгоритма длинного деления... может быть, того, который вы, или ваши родители, или ваши дедушки и бабушки выучили? Мы с уверенностью говорим: да! Причина, по которой вы и ваши предки использовали его, заключается в том, что это эффективный и красивый алгоритм, который позволит вам решить некоторые из самых сложных задач на деление, с которыми не справятся даже блоки с основанием 10. Он работает одинаково хорошо для десятичных и целых чисел. Длинное деление на самом деле не так сложно.
 «Сколько третей в четырех?» или еще лучше, Сколько третьих чашек в четырех чашках?» При необходимости достаньте мерные чашки.
«Сколько третей в четырех?» или еще лучше, Сколько третьих чашек в четырех чашках?» При необходимости достаньте мерные чашки.
 Остатки обычно даются вне контекста, в том числе в приведенных ниже ключах ответов. Остаток на самом деле является числителем дробного частного. Например, 19 ÷ 3 равно 6 с остатком 1, что точнее 6 1/3. Использование дробных частных означает, что ваши ученики всегда найдут точный ответ на все вопросы о делении на длинное деление, и во многих случаях ответ будет более точным (например, сравните 6 1/3 с 6,3333....).
Остатки обычно даются вне контекста, в том числе в приведенных ниже ключах ответов. Остаток на самом деле является числителем дробного частного. Например, 19 ÷ 3 равно 6 с остатком 1, что точнее 6 1/3. Использование дробных частных означает, что ваши ученики всегда найдут точный ответ на все вопросы о делении на длинное деление, и во многих случаях ответ будет более точным (например, сравните 6 1/3 с 6,3333....).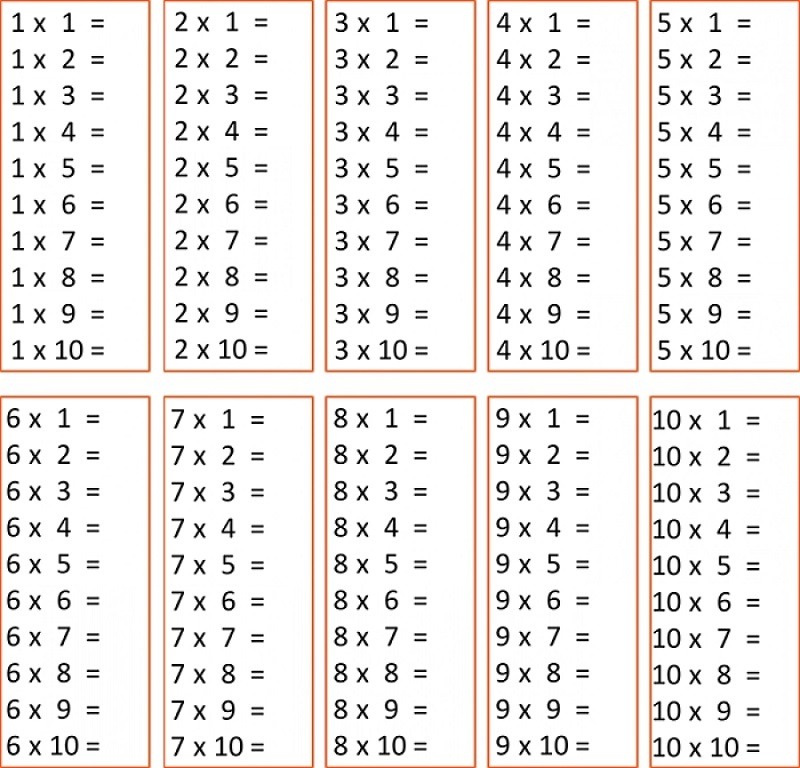 В ключах ответов для этих рабочих листов для разделения используется стандартный алгоритм, который вы могли бы изучить, если бы вы ходили в англоязычную школу. Изучение этого алгоритма само по себе иногда недостаточно, поскольку оно может не привести к хорошему концептуальному пониманию. Одним из инструментов, который помогает учащимся изучить стандартный алгоритм и развить понимание деления, является набор десятичных блоков. Обучая студентов сначала делению на блоки с основанием десять, а затем переходя к стандартному алгоритму, учащиеся получат концептуальное понимание, а также смогут использовать эффективный алгоритм для деления в длинное число. Студенты, обладающие обоими этими качествами, естественно, добьются больших успехов в своих будущих математических исследованиях.
В ключах ответов для этих рабочих листов для разделения используется стандартный алгоритм, который вы могли бы изучить, если бы вы ходили в англоязычную школу. Изучение этого алгоритма само по себе иногда недостаточно, поскольку оно может не привести к хорошему концептуальному пониманию. Одним из инструментов, который помогает учащимся изучить стандартный алгоритм и развить понимание деления, является набор десятичных блоков. Обучая студентов сначала делению на блоки с основанием десять, а затем переходя к стандартному алгоритму, учащиеся получат концептуальное понимание, а также смогут использовать эффективный алгоритм для деления в длинное число. Студенты, обладающие обоими этими качествами, естественно, добьются больших успехов в своих будущих математических исследованиях. Ключи к ответам включают типичные шаги, которые учащиеся записывают при решении каждой задачи; однако возможны небольшие вариации в реализации. Например, некоторые люди не обращают внимания на знаки вычитания, некоторые могут показывать шаги вычитания нуля и т. д.
Ключи к ответам включают типичные шаги, которые учащиеся записывают при решении каждой задачи; однако возможны небольшие вариации в реализации. Например, некоторые люди не обращают внимания на знаки вычитания, некоторые могут показывать шаги вычитания нуля и т. д.
 Это стандартное правило, которое может быть немного поверхностным для больших чисел, например, кто знает, делится ли 680 на 8? По этой причине мы предлагаем наше решение Math-Drills.com, которое требует немного арифметических действий, но может быть довольно легко выполнено с небольшой практикой. Как вы знаете, 8 равно 2 в третьей степени, поэтому мы подумали, что если бы вы могли разделить последние три цифры числа на 2 три раза, то оно будет делиться на 8. 680 ÷ 2 ÷ 2 ÷ 2 = 340 ÷ 2 ÷ 2 = 170 ÷ 2 = 85. У нас есть победитель! 680 действительно делится на 8.
Это стандартное правило, которое может быть немного поверхностным для больших чисел, например, кто знает, делится ли 680 на 8? По этой причине мы предлагаем наше решение Math-Drills.com, которое требует немного арифметических действий, но может быть довольно легко выполнено с небольшой практикой. Как вы знаете, 8 равно 2 в третьей степени, поэтому мы подумали, что если бы вы могли разделить последние три цифры числа на 2 три раза, то оно будет делиться на 8. 680 ÷ 2 ÷ 2 ÷ 2 = 340 ÷ 2 ÷ 2 = 170 ÷ 2 = 85. У нас есть победитель! 680 действительно делится на 8.