Правильная таблица умножения — это просто!)
Ни о каком абстрактном мышлении здесь не может быть и речи — отвлекает всё, надо напрягаться даже чтобы просто прочитать. Но не будем сурово осуждать всех творцов, они хотели как лучше, а получилось как всегда.
Вместо злобствования попробуем немного поколдовать над всем известным, казалось бы простейшим предметом и последовательно очистить зерна истины от плевел маразма улучшательства.
Для начала убираем лишние краски, картинки, искажения и получаем обычные колонки примеров умножения:
Затем по принципу соблюдения необходимых и достаточных условий, отсекаем лишнее как скульпторы: все примеры умножения на 1 и 10 как элементарные и все повторы. Последнее очень важно, ведь при механическом запоминании следует бойкий ответ 6х8=48, а вот 8х6= уже вызывает заминку либо ошибку. При исключении повторов такое нереально, поскольку уже сама система подачи материала заставляет понять что это одно и то же. Кроме того, психологически облегчает учёбу не только снижение числа примеров со 100 до 36, но и последовательное уменьшение их количества в колонках:
Именно такой, сокращенный вариант (правда с колонкой 1 х . ..= ) можно было увидеть на обложках школьных тетрадей до 1970-х гг. Несомненно, можно остановиться на этом для удобства механического запоминания, но понимания математики оно не добавит. Поэтому двигаемся дальше.
..= ) можно было увидеть на обложках школьных тетрадей до 1970-х гг. Несомненно, можно остановиться на этом для удобства механического запоминания, но понимания математики оно не добавит. Поэтому двигаемся дальше.
Внимательный читатель наверное заметил, что до сих пор мы говорили о ПРИМЕРАХ умножения, а не о ТАБЛИЦЕ умножения.
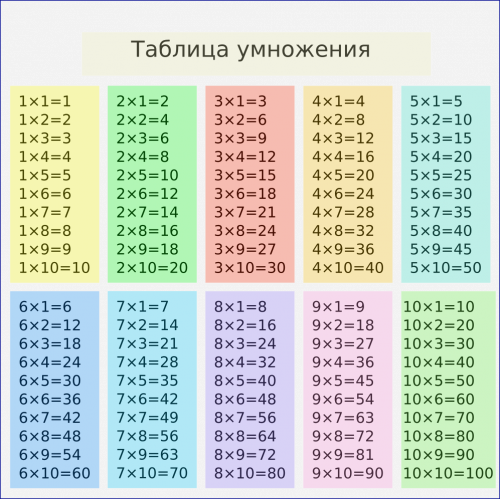
Смотрим как выглядит настоящая, легкая, удобная для запоминания таблица умножения с полным и правильным названием: таблица умножения И ДЕЛЕНИЯ, поскольку множители одновременно являются и делителями. Хорошо заметна симметрия таблицы из-за выделения идущих по диагонали квадратов чисел:
историческое название «таблица Пифагора»
а так выглядела в древности таблица умножения у шумеров:
Делаем последнюю концептуальную трансформацию — начинаем таблицу умножения не сверху, а снизу. Почему? Во-первых, это интуитивно понятнее: ниже — меньше, выше — больше, а направление слева направо сохраняется как совпадающее с направлением письма слева — меньше, затем направо — больше. Во-вторых … расскажем чуть позднее.
Во-вторых … расскажем чуть позднее.
Правильную таблицу умножения можно дать ученику и в готовом виде, но лучше всего если он сам её составит. Да-да. Это вполне доступно даже первокласснику!
Рисуем сетку и нумеруем ряды и столбцы с 1 до 9 — это соответствует примерам умножения на 1, они же будут выполнять функции сомножителя/кратности/во сколько раз.
Затем учеником заполняются ряд и столбец с 2 путем прибавления числа 2 для каждой последующей клеточки, затем ряд и столбец с 3 и так далее, получается простая таблица умножения:
Что это даёт?
Уже с начальной школы ученик привыкает к табличной форме, с которой ему потом придется часто встречаться, интуитивно понимает, что таблицы создаются как удобный и концентрированный справочный материал, часть из которого надо знать наизусть для удобства применения.
Поначалу для удобства пользования таблицей лучше пользоваться «уголком» для выделения строк и столбцов — вырезаем квадрат с одного угла чистого тетрадного листа. Привычка координатного поиска образуется достаточно быстро.
Привычка координатного поиска образуется достаточно быстро.
При таком подходе не нужно тупо механически запоминать колонки примеров умножения, а сразу можно дать пользоваться всей таблицей. Пусть она лежит перед глазами в помощь решению примеров и через некоторое время тренировок запоминание придет само, в неё ученик будет заглядывать все реже и реже.
Таблица должна стать тем же, чем она была изначально — помощью в работе. Упор всегда и везде должен быть не на запоминание, а на понимание и знание где можно найти справочный материал и как им пользоваться.
При самостоятельном заполнении таблицы умножения построчно сразу становится очевидным что умножение — это всего лишь многоКРАТНОЕ сложение, и соответственно деление — это многоКРАТНОЕ вычитание, поэтому легко приходит понимание принципиальной разницы выражений «на сколько больше/меньше» и во сколько раз больше/меньше». Это очень важно для последующего составления уравнений по условиям задач.
Выделение штриховкой или цветом диагонали (квадратов чисел) ясно показывает симметричность таблицы, т.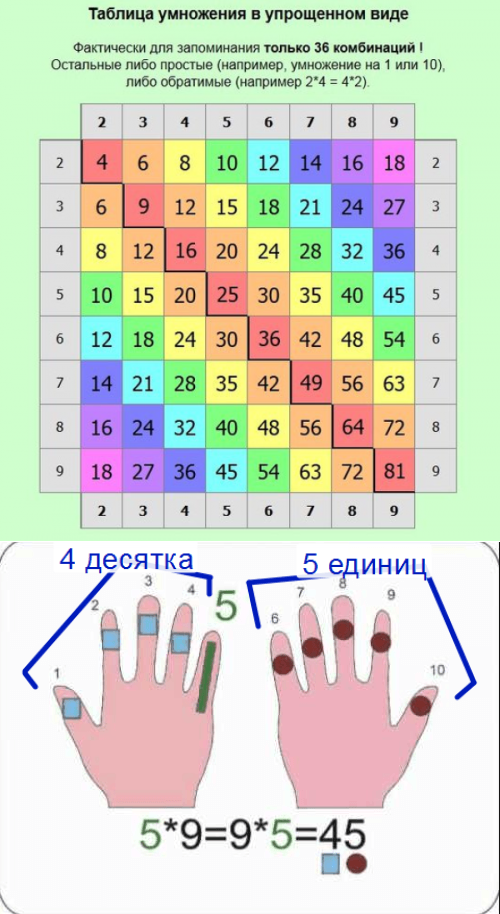 е. равнозначность последовательности сомножителей и здесь избыточность материала играет в сторону закрепления его (повторение — мать учения) и самостоятельного выявления такой закономерности.
е. равнозначность последовательности сомножителей и здесь избыточность материала играет в сторону закрепления его (повторение — мать учения) и самостоятельного выявления такой закономерности.
Уже потом, когда потребуется в процессе обучения, дети узнАют сколько полезного и интересного связано со знакомой с первого класса простенькой табличкой. Подобно Журдену из «Мещанина во дворянстве» Ж.Б. Мольера, который с удивлением узнал что он говорит прозой, детям надо будет только добавить новую терминологию и новые выводы.
Например, им будут говорить уже не просто о втором сомножителе или кратности сложения, а назовут его коэффициентом.
Каждая строка и столбец таблицы представляют из себя арифметическую прогрессию, от которой легко переходим уже к геометрической прогрессии, факториалам и прочим будто бы сложностям.
Если выделить любой прямоугольник на такой таблице, то в правом верхнем углу его будет указана площадь (чудо!), т.е. таким образом демонстрируется что алгебра и геометрия — это всего лишь разные способы отображения общих закономерностей единой науки математики. Другими словами, наглядно показывается что произведение чисел соответствует площади прямоугольника, а квадрат числа — это действительно квадрат (соответственно для куба надо рисовать третью координату). А отсюда легко переходим к решению геометрических задач алгебраическими способами и наоборот — смотря что удобнее.
Другими словами, наглядно показывается что произведение чисел соответствует площади прямоугольника, а квадрат числа — это действительно квадрат (соответственно для куба надо рисовать третью координату). А отсюда легко переходим к решению геометрических задач алгебраическими способами и наоборот — смотря что удобнее.
Понимание графиков с осями Х и Y, названиями «абсцисса» и «ордината» уже не вызовет затруднений — это будет привычная с начальных классов форма представления материала, надо только дорисовать стрелочки. И… объяснить чем отличаются кардинальные числа от ординальных (они же количественные и порядковые соответственно).
В конце-концов и понимание интеграла как суммы бесконечно малых величин исходит именно из понимания сути умножения натуральных чисел (и опять геометрические аналоги — площадь на криволинейной трапеции на графике функции), иначе интегрирование будет тупо восприниматься как заученные механические действия при обнаружении хитрой закорючки в виде длинной буквы S.
Так что большинство проблем из-за НЕПОНИМАНИЯ ОСНОВ.
источник: http://igor-grek.ucoz.ru/news/tablica/2011-06-16-119
Правильная таблица умножения — Ясная Академия :: Ясная практика жизни — ЖЖ
Для многих математика в школе была непонятным и нелюбимым предметом. В большинстве случаев ученики не виноваты, просто их изначально неправильно учили и чем дальше, тем хуже учат. Рассмотрим ситуацию на примере всем известной «таблицы умножения». Есть такой старый анекдот: «Женщина возмущается что очень удобно 5х5=25, 6х6=36, а вот почему 7х7=49, неужели было трудно 47 сделать?» Очень практичный подход — сделать как ей удобно, а не как правильно. В начальной школе у всех нас «учительница первая моя», которая крайне редко идет против стандарта, действует «как учили», «по учебнику» и в соответствии с «методическими планами». Творчество и новаторство в этой области выражается в «женских» подходах — с со стихами и песнями, танцами и бубнами, зверушками и финтифлюшками от всей души с наивным желанием сделать привлекательнее и «красивше», с твердой уверенностью в том что «дэти, эта нелза понят, эта нужьна проста запомнит»:
Ни о каком абстрактном мышлении здесь не может быть и речи — отвлекает всё, надо напрягаться даже чтобы просто прочитать. Но не будем сурово осуждать всех творцов, они хотели как лучше, а получилось как всегда.
Но не будем сурово осуждать всех творцов, они хотели как лучше, а получилось как всегда.
Вместо злобствования попробуем немного поколдовать над всем известным, казалось бы простейшим предметом и последовательно очистить зерна истины от плевел маразма улучшательства.
Для начала убираем лишние краски, картинки, искажения и получаем обычные колонки примеров умножения:
Затем по принципу соблюдения необходимых и достаточных условий, отсекаем лишнее как скульптор: все примеры умножения на 1 и 10 как элементарные и все повторы. Последнее очень важно, ведь при механическом запоминании следует бойкий ответ 6х8=48, а вот 8х6= уже вызывает заминку либо ошибку. При исключении повторов такое нереально, поскольку уже сама система подачи материала заставляет понять что это одно и то же. Кроме того, психологически облегчает учёбу не только снижение числа примеров со 100 до 36, но и последовательное уменьшение их количества в колонках:
Именно такой, сокращенный вариант (правда с колонкой 1 х . ..= ) можно было увидеть на обложках школьных тетрадей до 1970-х гг. Несомненно, можно остановиться на этом для удобства механического запоминания, но понимания математики оно не добавит. Поэтому двигаемся дальше.
..= ) можно было увидеть на обложках школьных тетрадей до 1970-х гг. Несомненно, можно остановиться на этом для удобства механического запоминания, но понимания математики оно не добавит. Поэтому двигаемся дальше.
Внимательный читатель наверное заметил, что до сих пор мы говорили о ПРИМЕРАХ умножения, а не о ТАБЛИЦЕ умножения.
Смотрим как выглядит настоящая, легкая, удобная для запоминания таблица умножения с полным и правильным названием: таблица умножения И ДЕЛЕНИЯ, поскольку множители одновременно являются и делителями. Хорошо заметна симметрия таблицы из-за выделения идущих по диагонали квадратов чисел:
историческое название «таблица Пифагора»
а так выглядела в древности таблица умножения у шумеров:
Делаем последнюю концептуальную трансформацию — начинаем таблицу умножения не сверху, а снизу. Почему? Во-первых, это интуитивно понятнее: ниже — меньше, выше — больше, а направление слева направо сохраняется как совпадающее с направлением письма слева — меньше, затем направо — больше. Во-вторых … расскажем чуть позднее.
Во-вторых … расскажем чуть позднее.
Правильную таблицу умножения можно дать ученику и в готовом виде, но лучше всего если он сам её составит. Да-да. Это вполне доступно даже первокласснику!
Рисуем сетку и нумеруем ряды и столбцы с 1 до 9 — это соответствует примерам умножения на 1, они же будут выполнять функции сомножителя/кратности/во сколько раз.
Затем учеником заполняются ряд и столбец с 2 путем прибавления числа 2 для каждой последующей клеточки, затем ряд и столбец с 3 и так далее, получается простая таблица умножения:
Что это даёт?
Уже с начальной школы ученик привыкает к табличной форме, с которой ему потом придется часто встречаться, интуитивно понимает, что таблицы создаются как удобный и концентрированный справочный материал, часть из которого надо знать наизусть для удобства применения.
Поначалу для удобства пользования таблицей лучше пользоваться «уголком» для выделения строк и столбцов — вырезаем квадрат с одного угла чистого тетрадного листа. Привычка координатного поиска образуется достаточно быстро.
Привычка координатного поиска образуется достаточно быстро.
При таком подходе не нужно тупо механически запоминать колонки примеров умножения, а сразу можно дать пользоваться всей таблицей. Пусть она лежит перед глазами в помощь решению примеров и через некоторое время тренировок запоминание придет само, в неё ученик будет заглядывать все реже и реже.
Таблица должна стать тем же, чем она была изначально — помощью в работе. Упор всегда и везде должен быть не на запоминание, а на понимание и знание где можно найти справочный материал и как им пользоваться.
При самостоятельном заполнении таблицы умножения построчно сразу становится очевидным что умножение — это всего лишь многоКРАТНОЕ сложение, и соответственно деление — это многоКРАТНОЕ вычитание, поэтому легко приходит понимание принципиальной разницы выражений «на сколько больше/меньше» и во сколько раз больше/меньше». Это очень важно для последующего составления уравнений по условиям задач.
Выделение штриховкой или цветом диагонали (квадратов чисел) ясно показывает симметричность таблицы, т.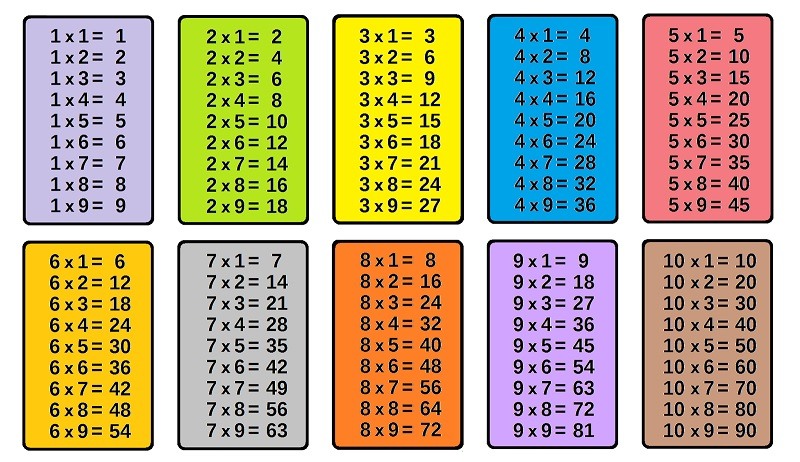 е. равнозначность последовательности сомножителей и здесь избыточность материала играет в сторону закрепления его (повторение — мать учения) и самостоятельного выявления такой закономерности.
е. равнозначность последовательности сомножителей и здесь избыточность материала играет в сторону закрепления его (повторение — мать учения) и самостоятельного выявления такой закономерности.
Уже потом, когда потребуется в процессе обучения, дети узнАют сколько полезного и интересного связано со знакомой с первого класса простенькой табличкой. Подобно Журдену из «Мещанина во дворянстве» Ж.Б. Мольера, который с удивлением узнал что он говорит прозой, детям надо будет только добавить новую терминологию и новые выводы.
Например, им будут говорить уже не просто о втором сомножителе или кратности сложения, а назовут его коэффициентом.
Каждая строка и столбец таблицы представляют из себя арифметическую прогрессию, от которой легко переходим уже к геометрической прогрессии, факториалам и прочим будто бы сложностям.
Если выделить любой прямоугольник на такой таблице, то в правом верхнем углу его будет указана площадь (чудо!), т.е. таким образом демонстрируется что алгебра и геометрия — это всего лишь разные способы отображения общих закономерностей единой науки математики. Другими словами, наглядно показывается что произведение чисел соответствует площади прямоугольника, а квадрат числа — это действительно квадрат (соответственно для куба надо рисовать третью координату). А отсюда легко переходим к решению геометрических задач алгебраическими способами и наоборот — смотря что удобнее.
Другими словами, наглядно показывается что произведение чисел соответствует площади прямоугольника, а квадрат числа — это действительно квадрат (соответственно для куба надо рисовать третью координату). А отсюда легко переходим к решению геометрических задач алгебраическими способами и наоборот — смотря что удобнее.
Понимание графиков с осями Х и Y, названиями «абсцисса» и «ордината» уже не вызовет затруднений — это будет привычная с начальных классов форма представления материала, надо только дорисовать стрелочки. И… объяснить чем отличаются кардинальные числа от ординальных (они же количественные и порядковые соответственно).
В конце-концов и понимание интеграла как суммы бесконечно малых величин исходит именно из понимания сути умножения натуральных чисел (и опять геометрические аналоги — площадь на криволинейной трапеции на графике функции), иначе интегрирование будет тупо восприниматься как заученные механические действия при обнаружении хитрой закорючки в виде длинной буквы S.
Так что большинство проблем из-за НЕПОНИМАНИЯ ОСНОВ.
Отсюда
Метки: Демид, детишки, математика
Что означает МУЛЬТ?
Аббревиатура » Термин
Термин » Аббревиатура
Слово в термине
#ABCDEFGHIJKLMNOPQRSTUVWXYZ НОВЫЙ
Сокр. » Срок
Срок » Сокр.
Слово в термине
Фильтровать по: Выбрать категорию из списка…──────────ВсеМатематика (1)Символы NASDAQ (1)ИТ (1)НАСА (2)Автомобили (1) Сортировать по: ПопулярностьПо алфавитуКатегория
| Term | Definition | Rating |
|---|---|---|
| MULT | Multi Solutions, Inc. Business » NASDAQ Symbols | Rate it: |
| MULT | Multiply Правительственный » NASA | Оцените: |
| MULT | Multiple Правительственный » NASA | Оцените: | 0037
Multi Trailer Miscellaneous » Automotive | Rate it: | |
| MULT | Multiplication Table Computing » IT | Rate it: |
| MULT | Множитель Академия и наука » Математика | Оцените: |
Что означает
МУЛЬТ ?- Mult
- Движение объединения и борьбы Trique (исп.
 Movimiento de Unificación y Lucha Triqui) — одна из старейших и сильнейших левых организаций в штате Оахака в Мексике. MULT работает с коренными жителями Оахаки.
Движение объединения и борьбы Trique установило более тесные связи с EZLN из Чьяпаса.
Movimiento de Unificación y Lucha Triqui) — одна из старейших и сильнейших левых организаций в штате Оахака в Мексике. MULT работает с коренными жителями Оахаки.
Движение объединения и борьбы Trique установило более тесные связи с EZLN из Чьяпаса.
подробнее »
Знаете что такое
MULT ? Есть еще одно хорошее объяснение для MULT ? Не держите это в себе! Все еще не можете найти искомое определение аббревиатуры? Используйте нашу технологию Power Search , чтобы искать более уникальные определения в Интернете!Цитата
Используйте приведенные ниже параметры цитирования, чтобы добавить эти сокращения в свою библиографию.
Самый большой ресурс в Интернете для
Акронимы и сокращения
Участник сети STANDS4
Просмотреть Abbreviations.com
#ABCDEFGHIJKLMNOPQRSTUVWXYZ
Бесплатно, регистрация не требуется:
Добавить в Chrome
Получите мгновенное объяснение любой аббревиатуры или аббревиатуры, которая попадется вам в любом месте в Интернете!
Бесплатно, регистрация не требуется:
Добавить в Firefox
Получите мгновенное объяснение любой аббревиатуры или аббревиатуры, которая попадется вам в любом месте в Интернете!
Викторина
Окончательный тест аббревиатуры
»
Сделай сам
A.
 Повредите сами
Повредите самиB. Выпей сам
C. Не навреди себе
D. Сделай сам
Вставить
Поделись изображением МУЛЬТ
»Нажмите, чтобы просмотреть:
Символы единиц измерения
Если у вас есть современный компьютер и быстрое подключение к Интернету, это сообщение вскоре должно быть заменено веб-страницей, которую вы хотите просмотреть. Если это сообщение отображается в течение длительного периода времени, это может быть связано со следующими причинами:
Символы единиц СИ представляют собой сокращенные версии полного названия единицы измерения. Существуют строгие правила в отношении написания, использования заглавных букв, пунктуация, шрифт и стиль шрифта для символов.
Символы единиц СИ обычно представляют собой сокращенные версии названия единиц. Например,
основные единицы секунд, метров, килограммов, ампер, кельвинов, молей и кандел имеют
символы единиц с, м, кг, А, К, моль и
CD.
Например,
основные единицы секунд, метров, килограммов, ампер, кельвинов, молей и кандел имеют
символы единиц с, м, кг, А, К, моль и
CD.
Названия единиц могут быть расширены путем добавления префикса, указывающего на степень десяти. Пока базовой единицей длины является метр, также можно использовать единицы измерения километры, мегаметры, сантиметры, миллиметров и др. Они имеют символы единиц км, мм, см и мм.
Некоторые символы единиц СИ представляют собой один символ, например с, символ секунд.
Некоторые символы единиц СИ состоят из нескольких символов, например моль, символ родинок, и км на километры.
Пробелы появляются в некоторых символах единиц измерения, таких как «Н·м», символ ньютон-метров.
Ограниченное количество математических символов может отображаться в символах единиц измерения. Например
м 2 — условное обозначение квадратных метров,
км/ч» — это обозначение километров в час,
и
${\rm{nV/}}\sqrt {{\rm{Гц}}} $ — единица
используется для описания интенсивности случайного шума.
Символы единиц СИ аналогичны, но отличаются от аббревиатуры, инициализмы и акронимы. Поскольку все эти могут появляться в технических и научных документах, они кратко изложены ниже.
Руководства по стилю обычно позволяют сокращать документы на замена общеизвестных слов и фраз несколькими символами, известна как аббревиатура. Например, латинская фраза «и так далее» обычно появляется как и т. д., в то время как термин «против» заменяется на «в.» или «против». Аббревиатуры иногда применяется к единицам СИ, с сек. замена секунд и темп. использовал вместо температуры.
При чтении текста вслух сокращения обычно преобразуются вернуться к полному слову. Если табличка на чьем-то столе показывает Доктор Нет, мы приветствуем человека как доктор Нет. Мы не пытаемся произнести аббревиатуру как двухсимвольное слово dr, и мы не прочитать отдельные буквы ди-а.
Хотя символы единиц СИ не являются аббревиатурами, они читаются одинаково
как сокращения. Когда мы видим символ Па
мы произносим слово паскаль, а не буквы горо-ай или
неофициальный термин для человека, который породил нас, наш папа.
Как правило, следует избегать сокращения названий единиц СИ. Используйте полное название единицы СИ, например секунды и килограммы, или используйте символы единиц измерения, такие как песок кг. Не используйте сокращения, такие как сек. за секунду и килограмм за килограмм.
| Приемлемо? | Примеры сокращений |
|---|---|
| № | Карточный домик рухнул, когда выпало 20 на него упал килограммовый груз. |
| Да | Карточный домик рухнул, когда выпало 20 килограммовая масса упала на него. |
| Да | Карточный домик рухнул, когда выпало 20. на него упала масса кг. |
Многие сокращения имеют точку как неотъемлемую часть выражения. Аббревиатура и т. д. всегда имеет точку в конце, даже если она стоит в середине предложения. Напротив, точка никогда не используется в символе единицы СИ, если только символ появляется в конце предложения.
| Приемлемо? | Пунктуация с символами единиц |
|---|---|
| Да | Карточный домик рухнул, когда
20
кг
на него упала масса. |
| № | Карточный домик рухнул, когда 20 кг. на него упала масса. |
| Да | Тяжело, похоже 20 кг. |
Когда группа слов заменяется набором (обычно) их первого буквы, это известно как инициализм. Условия RSVP, PS, QED, CEO, UK, UN, FBI и SI — все инициализмы. При чтении вслух мы обычно произносим каждое отдельное слово письмо, как будто нас просят произнести его по буквам. Например, мы произносим SI как ess-eye. Мы не пытаемся произнесите это как двухбуквенное испанское слово, означающее «да», и мы не заменяем его именем, которое оно представляет — Международная система единиц.
В нетехнической связи некоторые названия единиц заменяются на
инициализмы. Это особенно часто встречается, когда слово «за» является частью
имени подразделения. Километры в час часто выражаются в км/ч,
мили в час как mph, а частей на миллион как ppm. В качестве примечания, SI
система не позволяет даже прописанные названия миль в час и частей
за миллион, который будет использован.
В технических и научных сообщениях не используйте инициализм названий единиц СИ. Допускаются инициализмы других фраз, но не для названий единиц СИ.
| Приемлемо? | Пример использования инициализма |
|---|---|
| Да | Десять самых популярных автомобилей, продаваемых в США имеют среднюю максимальную скорость 200 километров в час. |
| Да | Десять самых популярных автомобилей, продаваемых в США, имеют среднюю максимальную скорость 200 км/ч. |
| № | Десять самых популярных автомобилей, продаваемых в США, имеют среднюю максимальную скорость 200 км/ч. |
| № | Десять самых популярных автомобилей, продаваемых в США, имеют среднюю максимальную скорость 200 км/ч. |
Иногда список символов, представляющих фразу, произносится как слово. Например, NASA, NATO, AWOL, SWAT, NASDAQ, FIFO и LIFO — все они сокращения.
Правила использования заглавных букв и пунктуации в аббревиатурах часто неясны и со временем меняются. Они могут начинаться с заглавных букв, иногда разделенных точками.
Если название относится к организации, оно, как правило, сохраняет все заглавные буквы.
формат. Но если аббревиатура относится к приему или фразе, которые становятся общепринятыми
используется, то аббревиатура в конечном итоге повышается до статуса слова. Радар, сонар, акваланг,
Laser и snafu изначально были аббревиатурами, но сегодня считаются словами.
Они могут начинаться с заглавных букв, иногда разделенных точками.
Если название относится к организации, оно, как правило, сохраняет все заглавные буквы.
формат. Но если аббревиатура относится к приему или фразе, которые становятся общепринятыми
используется, то аббревиатура в конечном итоге повышается до статуса слова. Радар, сонар, акваланг,
Laser и snafu изначально были аббревиатурами, но сегодня считаются словами.
Иногда говорящий сам решает, нужно ли что-то говорить. рассматривается как аббревиатура, инициализм или акроним. Термин ASAP может произноситься как можно скорее, или да-эс-да-горох, или да-сок.
| Срок | Предпочтительный Символ единицы измерения | Приемлемо Символ единицы измерения | Не использовать как символ или в тексте |
|---|---|---|---|
| секунд (время) | с | сек. | |
| минут (время) | мин | мин. | |
| час | ч | час.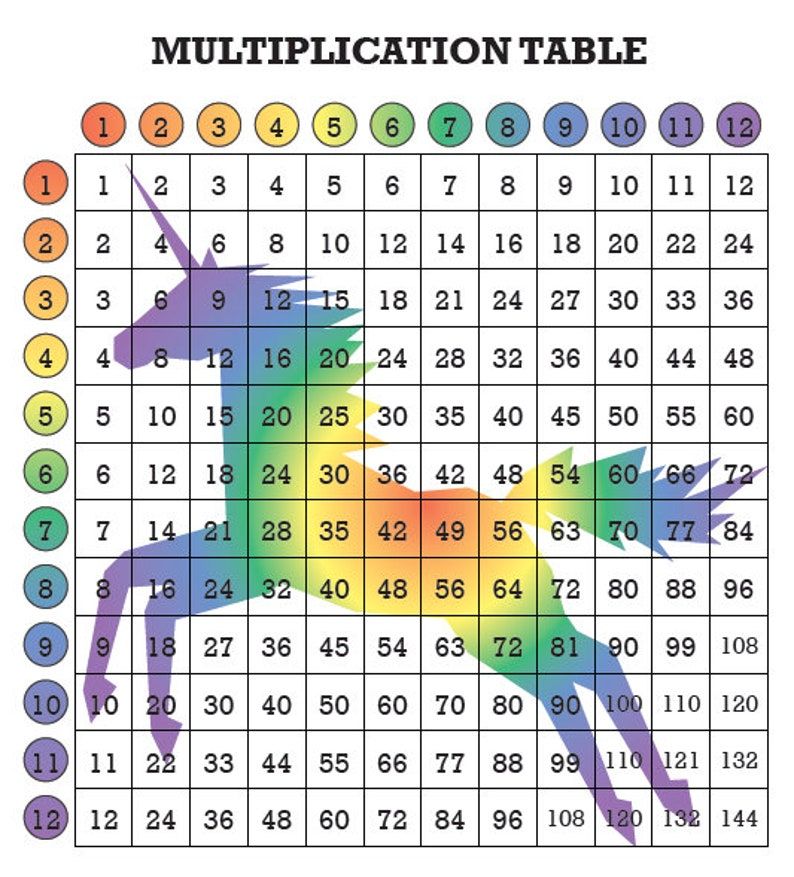 | |
| секунд (время) | ▮″ | сек | |
| минута (угол) | ▮′ | мин | |
| градус (угол) | ▮° | град | |
| градус Цельсия | ℃ | С | по Цельсию |
| метр в секунду | м/с | м/с, м/с | |
| килограмм | кг | кг | |
| километр в час | км/ч | км/ч, км/ч | |
| миль в час | Нет | миль в час, миль в час | |
| кубический сантиметр | см 3 | куб.см, куб.см. | |
| квадратных метров | м 2 | кв.м. | |
| Ом | Ом | Ом | Р |
| милли | м | мил. | |
| микро | μ | у | |
| часть на сотню | % | процентов | |
| тысячная часть | Нет | пт, ‰ | |
| часть на десять тысяч | Нет | ‱ | |
| часть на миллион | частей на миллион | ||
| частей на миллиард | Нет | частей на миллион | |
| частей на триллион | Нет | п. п. п. |
Если вы собираетесь создавать документы, содержащие символы SI, вам потребуется доступ как к прописным, так и к строчным буквам в Латинский и греческий алфавиты. Латинский алфавит это \[\начать{массив}{с} {\ rm {abcdefghijklmnopqrstuvwxyz}} \\ {\rm{ABCDEFGHIJKLMNOPQRSTUVWXYZ}} \конец{массив}\] и греческий алфавит \[\начать{массив}{с} \альфа\бета\гамма\дельта\варепсилон\дзета\эта\тета\йота\каппа\лямбда\мю\ню\ксио\пи\ро\сигма\тау\ипсилон\варфи\хи\пси\омега\\ {\ rm A} {\ rm B} \ Gamma \ Delta {\ rm E} {\ rm Z} {\ rm H} \ Theta {\ rm I} {\ rm K} \ Lambda {\ rm M} {\ rm N} \ Xi {\ rm O} \ Pi {\ rm P} \ Sigma {\ rm T} \ Upsilon \ Phi {\ rm X} \ Psi \ Omega \конец{массив}\]
Система СИ крайне требовательна к шрифту и стилю шрифта
для символов единиц. Все символы единиц СИ должны быть написаны латинскими буквами.
шрифт и обычный вес. Они никогда не могут быть написаны на
курсивный шрифт. Они никогда не могут быть написаны жирным шрифтом.
У них может никогда не быть индексов.
Они никогда не могут быть украшены полосами, штрихами, знаками ударения и т. д.
Все символы единиц СИ должны быть написаны латинскими буквами.
шрифт и обычный вес. Они никогда не могут быть написаны на
курсивный шрифт. Они никогда не могут быть написаны жирным шрифтом.
У них может никогда не быть индексов.
Они никогда не могут быть украшены полосами, штрихами, знаками ударения и т. д.
Правила, перечисленные выше, применяются каждый раз, когда символ единицы СИ появляется, даже если находится в предложении, окруженном текстом другой шрифт или стиль шрифта.
| Приемлемо? | Примеры шрифта символа единицы СИ и стиля шрифта |
|---|---|
| № | Несмотря на занос 80 м, водитель сказал:» Я только ехал 50 км/ч офицер. » |
| Да | Несмотря на занос 80 м, водитель сказал: Я только собирался 50 км/ч офицер.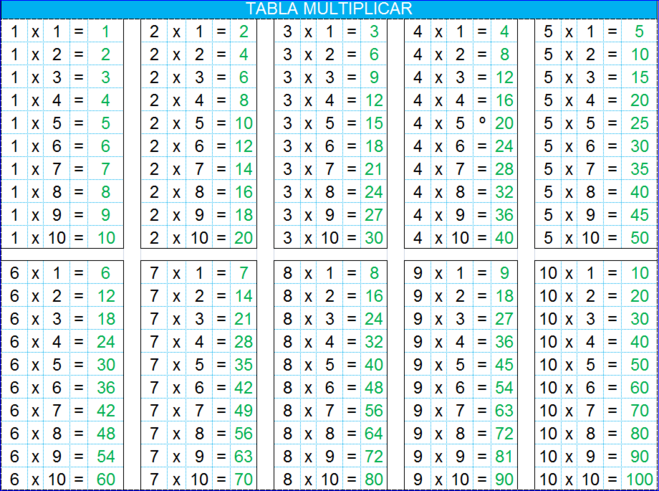 » » |
Символы единиц СИ определяются с использованием заглавных букв. на каждом персонаже. Вы никогда не должны изменять эту заглавную букву, так как это может существенно изменить значение символа. Например, строчный символ s представляет собой базовую единицу времени, секунды — в то время как символ верхнего регистра S представляет собой базу единица электропроводности Сименс.
Некоторые заголовки пишутся заглавными буквами. Это допустимо иметь символ единицы СИ в таком названии, но он должен сохранить свой правильный регистр, даже если он в нижнем регистре.
Никогда не начинайте предложение с символа единицы СИ. Грамматическое правило которые требуют, чтобы первая буква предложения была заглавной, может быть несовместимым с правилами SI о капитализации.
| Приемлемо? | Примеры использования заглавных букв в символах единиц СИ |
|---|---|
| Да | Котел взорвался, когда давление достигло
100 МПа. . . |
| Да | ВЛИЯНИЕ ДАВЛЕНИЙ БОЛЕЕ 100 МПа В НЕАРМИРОВАННЫХ КОТЛАХ. |
| № | ВЛИЯНИЕ ДАВЛЕНИЙ СВЫШЕ 100 МПа В НЕАРМИРОВАННЫХ КОТЛАХ. |
Первый символ символа единицы СИ пишется с большой буквы только тогда, когда название подразделения чествует человека. Сюда входят единицы, соответствующие написание имени лауреата в ваттах, ньютонах и герцах. Это также включает такие единицы, как фарад и бел, где единица написана иначе, чем имя лауреата (в данном случае Фарадей и Белл).
Единственным исключением из правила предыдущего абзаца является литр. Он не назван в честь человека, поэтому изначально использовался символ нижнего регистра. л. Это можно легко спутать с цифрой один, 1. Из-за этого заглавный символ L теперь является приемлемым символом единицы для литров. Строчная версия по-прежнему считается приемлемой. символ, если вы предпочитаете использовать его.
Электрическая единица сопротивления, ом, названа в честь Георга Ома. Нахождение
разумный символ единицы сложен, как заглавная буква
О может быть трудно различить
от числительного для числа ноль, 0. Использование двух букв не так много
лучше, так как О может ошибаться
для английского слова, о. Есть два решения этой проблемы.
Наиболее распространенным является использование греческого алфавита для символа единицы,
используя заглавную букву омега,
Ом. Если
Греческий алфавит недоступен, тогда Ом
считается приемлемым символом единицы для ома. Обратите внимание на первую букву
полное имя — строчная буква «о», а первая буква символа — буква «о».
заглавная О.
Нахождение
разумный символ единицы сложен, как заглавная буква
О может быть трудно различить
от числительного для числа ноль, 0. Использование двух букв не так много
лучше, так как О может ошибаться
для английского слова, о. Есть два решения этой проблемы.
Наиболее распространенным является использование греческого алфавита для символа единицы,
используя заглавную букву омега,
Ом. Если
Греческий алфавит недоступен, тогда Ом
считается приемлемым символом единицы для ома. Обратите внимание на первую букву
полное имя — строчная буква «о», а первая буква символа — буква «о».
заглавная О.
Имя единицы измерения, например метр, может быть указано во множественном числе. символ единицы, такие как m, никогда не может быть сделано множественное число.
Помните, что s в нижнем регистре — это символ единицы СИ для секунд.
Добавление s в конец другого символа единицы измерения может сделать его похожим на
вы умножаете на время, или меняете саму единицу.
| Приемлемо? | Примеры множественного числа |
|---|---|
| Под вопросом | Таблица двойная метр длинный. |
| Да | Таблица двойная метров длинный. |
| Да | Таблица 2 м длинный. |
| № | Таблица 2 мс длинный. |
| № | Таблица 2 м длинный. |
Вам никогда не разрешается изменять символ единицы СИ, добавление индекса. Вы можете определить символы количества SI с помощью индексов.
| Приемлемо? | Примеры символов и индексов единиц СИ |
|---|---|
| Да | Среднеквадратичное давление оказалось равным ${P_{{\rm{rms}}}} = 6\;{\rm{кПа}}$ . |
| № | Среднеквадратичное давление оказалось равным $P = 6\;{\rm{kP}}{{\rm{a}}_{{\rm{rms}}}}$ . |
| № | Среднеквадратичное давление оказалось равным ${P_{{\rm{rms}}}} = 6\;{\rm{kP}}{{\rm{a}}_{{\rm{rms}}}}$
. |
Между числом и символом единицы измерения должен быть один условный пробел. Не пропускайте этот пробел и не используйте для его заполнения дефис, точку, знак умножения или любой другой символ. Не допускайте перевода строки или разрыва страницы между числом и символом единицы измерения.
| Приемлемо? | Примеры символа единицы измерения Пробел |
|---|---|
| Да | Таблица 2 м длинный. |
| № | Таблица 2м длинный. |
| № | Таблица 2-м длинный. |
| № | Таблица 2‧м длинный. |
| № | Таблица 2×м длинный. |
| № | Стол 2 м длинный. |
Единицами можно управлять с помощью умножения, деления и возведения в степень
операции, но вообще не сложение, вычитание и другие математические
операции. Эти операции могут быть показаны с помощью символов, перечисленных ниже.
Эти операции могут быть показаны с помощью символов, перечисленных ниже.
Любой символ единицы может быть умножен на другой символ единицы. Эти умножение обычно изображается точкой в центре или обычной космос. Центрированная точка предпочтительнее, когда есть вероятность, что единицу можно спутать с другой единицей.
| Приемлемо? | Примеры символа единицы, умноженного на символ единицы |
|---|---|
| Да | Н·м или Н м |
| Под вопросом | Два метра-секунды 2 м с а две миллисекунды — это 2 мс. |
| Да | Два метра-секунды 2 м·с а две миллисекунды — это 2 мс. |
| № | Нм или Н-м или Н×м или Н*м |
| Да — исключения из обычного правила | Втч, кВтч, ВА, кВА |
Любой символ единицы может быть разделен любым другим символом единицы. Есть
три способа показать это: с косой чертой (технически называемой солидусом),
с отрицательным показателем или со знаком горизонтального деления. Эти
те же параметры доступны для символов количества и чисел.
Эти
те же параметры доступны для символов количества и чисел.
За косой чертой может следовать только один символ единицы измерения, если не используются круглые скобки чтобы смысл был ясен.
Слово per может использоваться с названиями единиц для обозначения деления, например, в километрах в час. Однако буква p не может использоваться для обозначения деления, как в kph.
| Приемлемо? | Примеры символа единицы, разделенного символом единицы |
|---|---|
| Да | м/с или Н·м -1 или $\frac{{\rm{m}}}{{\rm{s}}}$ или кг· м/с 2 или кг·м×с -2 или ${\rm{nV/}}\sqrt {{\rm{Гц}}} $ или кг/(с 2 · А) |
| № | Н÷м или кг/с 2 × A или кг/с 2 /А |
Допустимо возводить символы единиц в степени. Показатели могут
быть либо положительным, либо отрицательным. Хотя обычно это целые числа,
приложения, в которых имеет смысл говорить о нецелочисленных степенях. Экспоненты
нуля не используются, потому что это можно сделать, опустив единицу
символ целиком. Показатель степени +1 обычно не записывается, так как предполагается, что
ни один показатель степени не совпадает с показателем степени +1. Знаки плюс обычно
опущены в показателях, как они предполагаются.
Хотя обычно это целые числа,
приложения, в которых имеет смысл говорить о нецелочисленных степенях. Экспоненты
нуля не используются, потому что это можно сделать, опустив единицу
символ целиком. Показатель степени +1 обычно не записывается, так как предполагается, что
ни один показатель степени не совпадает с показателем степени +1. Знаки плюс обычно
опущены в показателях, как они предполагаются.
Никогда не помещайте имя устройства в то же выражение, что и символ устройства. Используйте либо все имена, либо все символы, а не их сочетание.
Слово «за» используется вместо «разделено на» в именах единиц измерения. Не используйте слово «за» с символами единиц измерения.
Названия единиц измерения могут использоваться без чисел, с числами, выраженными словами, или с числами, написанными цифрами.
Символы единиц измерения всегда должны иметь связанный с ними номер, и этот номер должен быть выражен цифрами (а не словами).

 Movimiento de Unificación y Lucha Triqui) — одна из старейших и сильнейших левых организаций в штате Оахака в Мексике. MULT работает с коренными жителями Оахаки.
Движение объединения и борьбы Trique установило более тесные связи с EZLN из Чьяпаса.
Movimiento de Unificación y Lucha Triqui) — одна из старейших и сильнейших левых организаций в штате Оахака в Мексике. MULT работает с коренными жителями Оахаки.
Движение объединения и борьбы Trique установило более тесные связи с EZLN из Чьяпаса. Повредите сами
Повредите сами