Таблица всех синусов углов: Таблица синусов и косинусов

Содержание

Таблица синусов углов, вычислить синус угла

Главная
Справочник
Таблицы
Таблицы по геометрии
Таблица синусов

Рассчитать синус угла
Таблица синусов 1° — 180°
Таблица синусов 180° — 360°

Как известно, прямоугольный треугольник имеет три угла, два катета и гипотенузу. Отношения сторон выражаются некоторыми числами. Отношение величины противолежащего от острого угла катета к величине гипотенузы называется синусом угла.

\[ sin (\alpha) = \frac{a}{c} \]

где
а — противолежащий катет;
с — гипотенуза;

Для того, чтобы найти синус заданного угла, достаточно просто воспользоваться таблицей тригонометрических функций. В данной таблице помещены величины синусов всех углов, начиная с 0° до 360°. При решении многих задач требуется найти величину стороны треугольника, если известны противолежащий угол и гипотенуза. Воспользовавшись таблицей, находим синус угла, а потом требуемую сторону.

Онлайн калькулятор вам поможет быстро и правильно совершить необходимые расчеты. Для этого вам потребуется лишь внести исходные данные.

Таблица синусов 1° — 180°

Таблица синусов 180° — 360°

В вашем браузере отключен Javascript.
Чтобы произвести расчеты, необходимо разрешить элементы ActiveX!

Таблицы по геометрии Калькулятор Расчёт Преобразовать Углы 4096

Если материал понравился Вам и оказался для Вас полезным, поделитесь им со своими друзьями!

Таблица косинусов
Таблицы по геометрии Калькулятор Расчёт Конвертер Преобразовать Углы
Таблица тангенсов
Таблицы по геометрии Калькулятор Расчёт Преобразовать Углы
Таблица котангенсов
Таблицы по геометрии Калькулятор Расчёт Преобразовать Углы
Таблица Брадиса: синусы, косинусы, тангенсы и котангенсы
Таблицы по геометрии Расчёт Математика Тригонометрия Таблицы Формулы

Декодирование URL адресов
Работа с текстом Калькулятор Расчёт Конвертер Преобразовать Текст
Что такое Ватт
1 ватт определяется как мощность, при которой за 1 секунду времени совершается работа в 1 джоуль.
Электротехника Формулы Физика Теория Электричество
Что такое лошадиная сила
Лошадиная сила — единица мощности. Она примерно равна значению в 75 кгс/м/с., что соответствует усилию, которое необходимо затратить для подъёма груза в 75 кг. на высоту одно метра за одну секунду.
Разное Мощность Сила Единицы измерения Деньги Справочник
Калькулятор размеров колец на пальцы
Выбор обручальных колец — один из самых волнующих моментов для молодоженов. Изготовленные из белого, красного или желтого золота, простые или с гравировкой — все в обручальных кольцах имеет свой вес и важность. Не менее важно выбрать правильный размер. Как это сделать, чтобы не пришлось бороться с тугим или слишком свободным брачным кольцом на пальце?

Калькуляторы размеров одежды Калькулятор Расчёт Конвертер Преобразовать Размеры
Закон Кулона
Сила взаимодействия двух неподвижных точечных электрических зарядов в вакууме прямо пропорциональна произведению их модулей и обратно пропорциональна квадрату расстояния между ними.
Законы Формулы Физика Теория Электричество Закон
1 mBTC это сколько BTC ? Чему равен 1 сатоши ? Что такое сатоши ?
Bitcoin, Биткойн, часто Биткоин (от англ. bit — единица информации «бит», англ. coin — «монета») — пиринговая (как торрент или e-mule) электронная платёжная система, использующая одноимённую виртуальную валюту.
Разное Единицы измерения Деньги Справочник
Сколько весят животные?
Обзор веса нескольких животных
Масса и вес Масса Теория Единицы измерения
Сколько в ампере ватт, как перевести амперы в ватты и киловатты
Мощность – это скорость расходования энергии, выраженная в отношении энергии ко времени: 1 Вт = 1 Дж/1 с. Один ватт равен отношению одного джоуля (единице измерения работы) к одной секунде.
Электротехника Формулы Физика Теория Электричество

Теория и практика по треугольникам (Часть Ⅱ)

Площадь треугольников.

Свойства треугольников.

Тригонометрия в прямоугольных треугольниках.

Что такое синус/косинус.

Таблицы Брадиса. Как пользоваться.

Теорема синусов и косинусов.

Геометрия — это искусство хорошо рассуждать на плохо выполненных чертежах.

Г. Абель

С основными свойствами разобрались, теперь рассмотрим формулы и их приминение.

Площадь произвольного треугольника

Нет, это не кривая пентаграмма, нужны на этом рисунке только обозначения. Рассмотрим формулы школьной программы.

Высоту умножаем на ту сторону, на которую приходит высота:
В эту формулу подставляем угол между сторонами a и b:

Удобно использовать эту формулу, когда известны все стороны треугольника, p — полупериметр (половина суммы длин всех сторон):

Данная формула отлично помогает найти радиус вписанной окружности для любого треугольника, если известна площадь:

А эта формула помогает найти радиус описанной окружности для любого треугольника:

А зачем такое количество формул? К каждой задаче будут предоставлять разное дано, удобно знать и применять все формулы, чтобы максимально быстро решать задачи.

Полезные формулы для прямоугольного и равностороннего треугольника:

В данном случае получается, что один катет «b» — высота треугольника, а катет «а» — основание.

Эту формулу можно вывести большим количеством способов, самый простой через формулу №2

Задача №1. Дано на рисунке:

Оттолкнемся от вопроса: нужно найти площадь. Помимо 5 формул для произвольного треугольника, нам подойдет формула нахождения площади через полупроизведение катетов.

Вариантов здесь много (можно через т. Пифагора), но самый быстрый — найти ∠А = 180°− 90° − 60° = 30°, тогда площадь найдем по (2) формуле: S = ½absinα

Ответ: 60

Задача №2. Дано на рисунке:

Снова оттолкнемся от вопроса: нужно найти площадь. Дан обычный треугольник, значит, наш выбор ограничен первыми 5−ью формулами. В первой нужна высота, во второй угол, а в третьей полупериметр, но мы же знаем все стороны! Для начала найдем периметр и полупериметр:

Теперь можно подставить все числа в формулу площади:

Главное — правильно определиться с формулой.

Ответ: 84

Задача №3. Дано на рисунке:

В ΔABH: ∠A = 180°− 90° − 45° = 45°, значит, ∠A = ∠B => BH = AH = 12.

Тогда площадь можно найти по формуле (1) S=½bh. Высота AH = 12, основание AC = 16+12 = 28. => S = ½×12×28 = 168

Ответ: 168.

Задача №4. Дано на рисунке:

Оттолкнемся от отношения, которое нам дано. Мы знаем, что сумма данных углов равна 90°, если ∠ACM = х и ∠ВCM = 2х, тогда 2х+х = 90°

∠ACM = х = 30° => ∠ВCM = 60°. А что у нас равно 4-ем? Да, медиана! А медиана, проведенная из прямого угла, равна половине гипотенузы (2−ое свойство). Тогда отметим равные углы:

В ΔBCM получается ∠ВCM = ∠СВM = 60°, тогда ∠СМВ = 60° и ΔBCM — правильный:

Площадь найдем по (2) формуле: S = ½absinα:

Ответ: 8√3

Задача №5. Дано на рисунке:

В дано есть только стороны, а найти нужно угол. Как это сделать? Вот стороны 14,2 и 7,1 во сколько раз отличаются? Да, в 2 раза, а значит угол ∠BAL = 30° (против угла в 30° лежит катет, который в два раза меньше гипотенузы).

Значит, ∠A = 60° => ∠ACB = 180° − 90° − 60° = 30°, а ∠ACB — смежный с ∠ACV => ∠ACV = 180° − 30° = 150°.

Что касается LC: внимательно рассмотрим ΔALC, можно даже лупой воспользоваться. Что видишь? ∠LAC = ∠ACL = 30° => ΔALC — равнобедренный, LC = AL = 14,2.

Ответ: 14,2 и 150°

Тригонометрия в прямоугольных треугольниках

В прямоугольном треугольнике три стороны: 2 катета и гипотенуза.

Катеты меньшие стороны треугольника. Гипотенуза большая сторона, которая лежит напротив угла в 90°.

Относительно угла α:

Катет, который составляет угол, называют прилежащим. Катет, который находится напротив угла, называют противолежащим. Логично? Замечательно!

Тригонометрические функции (синус, косинус…) задают связь между углом и длинами сторон.

Но хорошо бы знать какие-то значения тригонометрических функций при определенных углах. Все значения вместе образуют таблицу Брадиса. С ее помощью можно вычислить почти любое значение тригонометрической функции при заданом угле. Но как с ней работать?

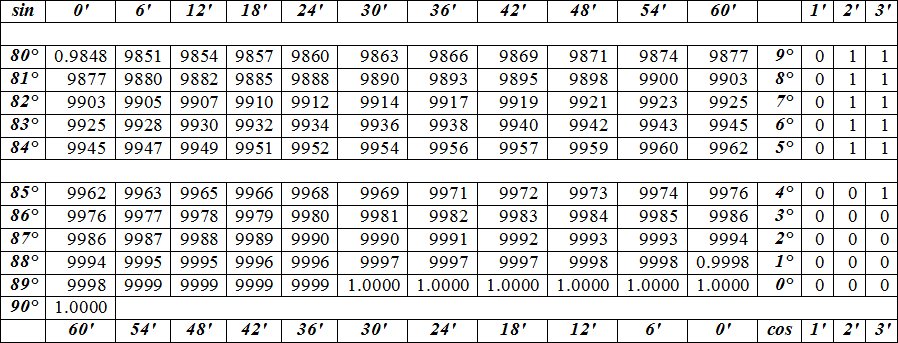
Найдем sin(10°). Для этого выберем столбец sin и в нем найдем 10°. Ближайшее значение — это то, что нам нужно — 0,1736.

А что за столбец 0′; 6′; 12′ и т.д. Это минуты! Не те, которых мы ждем в конце урока, а градусные минуты.

Из общего: и те, и другие минуты измеряются в промежутке от 0 до 60.

Градусные минуты делят один градус на 60 минут (1°=60′), нужны они для большей точности задания угла.

p.s. Есть еще и градусные секунды, и в одной градусной минуте 60 градусных секунд, знакомо? 1° = 60′ = 3600».

Найдем cos(77,7°)

Семь десятых градуса нужно перевести в минуты. Можно через пропорцию:

Теперь в таблице нужно найти 77°42′ для косинуса. Для синуса минуты прописаны, а для косинуса нет. Но мы же люди не гордые, сами напишем, но в обратном порядке. На пересечении 77° и 42′ получаем наше значение:

Но чтобы не загромождать таблицу 0, его в начале пишут только в первых строчках, поэтому ответ cos(77,7°) = 0,213.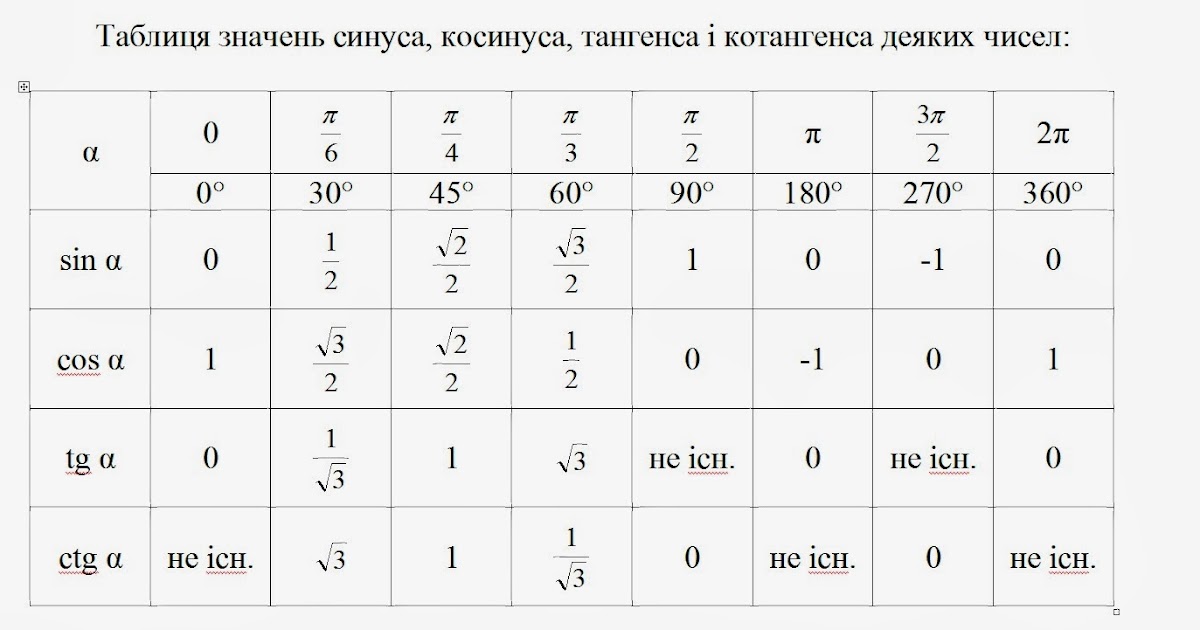

В задачах же таким обилием углов похвастаться нельзя, достаточно знать значения для 30°; 45°; 60°; 90°.

Искусство решать геометрические задачи чем-то напоминает трюки иллюзионистов — иногда,

даже зная решение задачи, трудно понять, как можно было до него додуматься.

И.Д. Новиков

Задача №6. Дано на рисунке:

В этой задаче известен противолежащий катет относительно угла в 45°, а найти нужно гипотенузу. Смотрим, где у нас есть противполежащий катет и гипотенуза? Это синус!

Смотрим в таблице, чему равен синус 45°, и подставляем в отношение:

Ответ: 16√2

Задача №7. Дано на рисунке:

Мы разобрались с тригонометрическими функциями в прямоугольных треугольниках, значит, и в этой задаче нужно перейти к прямоугольному треугольнику.

В ΔLTK — равнобедренный : ∠L = ∠LKT = (180° − 120°)/2 = 30°

Отлично, в прямоугольном ΔLVK: ∠L = 30° и известна гипотенуза, а нам нужно найти противолежащий катет, чем воспользуемся? Опять синусом!

Ответ: 15

Теорема синусов и теорема косинусов

Сразу возникает вопрос, а теорема тангенсов тоже есть? Конечно, есть, но она очень редко используется.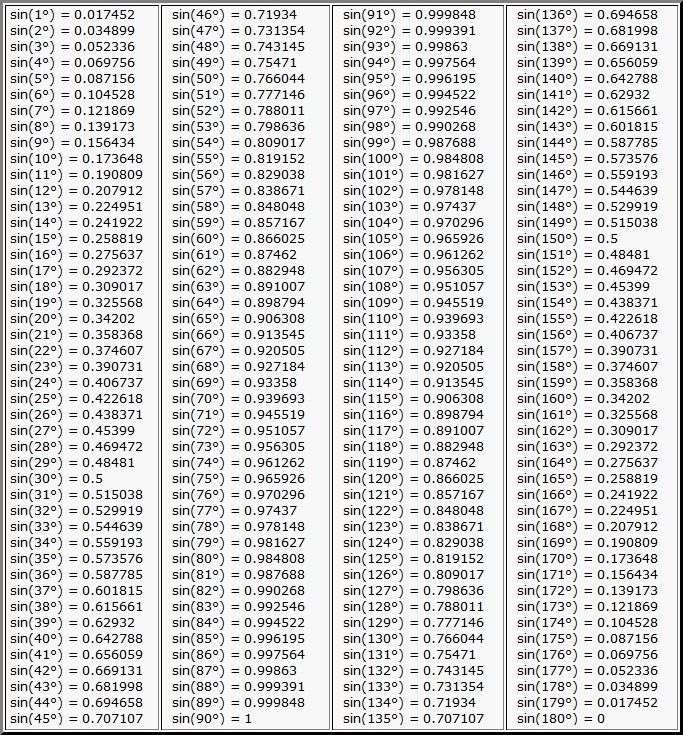

Для любого треугольника можно записать такое соотношение, это будет теорема синусов:

Запомни, что сторона относится к синусу противолежащего угла.

Следствие из теорма синусов гласит, что любое соотношение равно двум радиусам описанной окружности:

Для любого треугольника можно записать такое соотношение, это будет теорема косинусов:

А что будет, если α = 90°, а cos(90) = 0? Получится:

Теорема Пифагора, вот так просто можно запомнить теорему косинусов. Начать как теорему Пифагора, а затем вычесть удвоенное произведение на косинус угла между ними.

Можно записать и для других сторон в этом же треугольнике:

Задача №8. Дано на рисунке:

Запишем теорему синусов для двух отношений:

Выразим отсюда KT:

∠K = 180° − 60° − 45° = 75°. Чтобы найти синус угла 75°, советую посмотреть эту статью, нужно воспользовать формулой суммы синусов:

Тогда представим 75° в виде двух табличных значений:

Аналогично выразим LT:

Ответ: 16,3 и 22,3

Задача №9.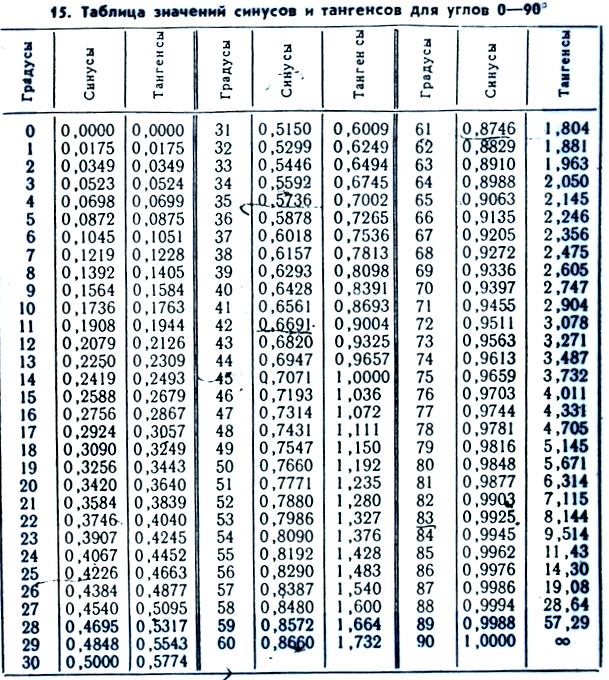 Дано на рисунке:

Найти нужно x и y. Запишем теорему косинусов для этого треугольника:

Икс выразим через игрек:

Ответ: 48; 18

Отлично, поздравляю тебя с Elementary по геометрии!

Что нужно знать:

Вертикальные, смежные, соответственные, накрест лежащие углы.
Равенство и подобие треугольников.
Что такое медиана, биссектриса, высота.
Свойства треугольников.
Площадь треугольников.
Синус/косинус в треугольнике.
Теорему синусов и косинусов.

Задачи для закрепления по треугольникам

Нашел опечатку, или что-то непонятно — напиши.

Группа с полезной информацией и легким математическим юмором.

Используя тригонометрическую таблицу, найдите меру угла A при sin A 01822…

Перейти к

Тригонометрические таблицы. Упражнение 19.

налог на товары и услуги
Банковское дело
Акции и дивиденды
Квадратные уравнения с одной переменной
Факторизация
Соотношение и пропорция
Матрицы
Арифметика и геометрическая прогрессия
Отражение
Формула раздела
Уравнение прямой линии
Сходство
Локус
Круги
Конструкции
Измерение
Тригонометрические тождества
Тригонометрические таблицы
Высоты и расстояния

Главная > ML Aggarwal Solutions Класс 10 Математика > Глава 19.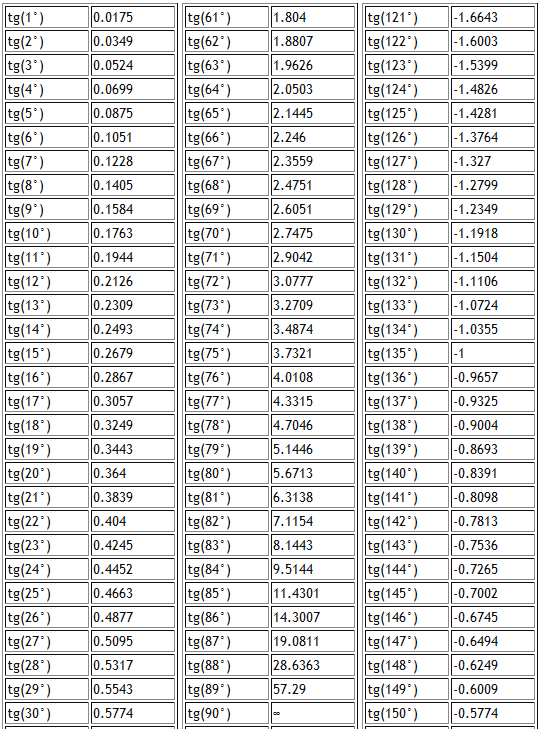

Тригонометрические таблицы > Тригонометрические таблицы. Упражнение 19.> Вопрос 24

Вопрос 24 Тригонометрические таблицы Упражнение 19

Используя тригонометрическую таблицу, найдите величину угла A, когда sin A = 0,1822.

Ответ:

Решение:-

Таблицы натуральных синусов можно использовать для получения приблизительных значений синуса с точностью до четырех знаков после запятой для любых углов от 0 до 90 градусов.

Найдите в таблице натуральных синусов значение (≤ 0,1822), достаточно близкое к 0,1822.

Мы находим значение 0,1822 в горизонтальной строке, начинающейся с 10 ^o, и в столбце, возглавляемом цифрой 30’.

Получаем, что A = 10 ^o 30’.

Связанные вопросы

Найдите значение следующего выражения: cos 62

o 27′

Найдите значение следующего выражения: sin 65^o 20′

Найдите значение следующего выражения: sin 35^o 22′

Найдите значение следующего выражения: sin 23^o 56′

Найдите значение следующего выражения: cos 3^o 11′

Используйте таблицы, чтобы найти острый угол θ, учитывая, что: sin θ = 0,2357

Фейсбук WhatsApp

Копировать ссылку

Было ли это полезно?

Упражнения

Тригонометрические таблицы Упражнение 19

Главы

GST

Банковское дело

Акции и дивиденды

Квадратные уравнения с одной переменной

Factorization

Ratio and Proportion

Matrices

Arithmetic and Geometric Progression

Reflection

Section Formula

Equation of Straight Line

Similarity

Locus

Circles

Constructions

Mensuration

Trigonometric Identities

Тригонометрические таблицы

Высоты и расстояния

Курсы

Быстрые ссылки

Условия и политика

Все права защищены. Он предается изучению углов и длины треугольника. Тригонометрическая таблица широко используется при решении геометрических вычислений. Значения стандартных тригонометрических углов, таких как 0°, 30°, 45°, 60° и 90°, можно получить с помощью тригонометрических таблиц.

Некоторые тригонометрические соотношения: синус, косинус, тангенс, косеканс, секанс и котангенс. При решении тригонометрических задач большую роль играют значения тригонометрических отношений стандартных углов. Изучение тригонометрических таблиц упрощает понимание и применение этой концепции. Изучение формул тригонометрии может облегчить процесс решения тригонометрических задач.

Знакомство с площадью четырехугольника

Это площадь, ограниченная сторонами четырехугольника. Многоугольник, состоящий из четырех сторон, можно назвать «четырехугольником». Некоторыми примерами четырехугольника являются трапеция, параллелограмм, ромб, воздушный змей, прямоугольник, квадрат и так далее. площадь четырехугольника — это общее пространство, занимаемое внутри четырехугольника. Четырехугольник можно получить, соединив только четыре точки, состоящие из трех точек, лежащих на одной прямой. Эта двумерная фигура состоит из четырех вершин, четырех углов и четырех сторон, а стороны четырехугольника не всегда равны. Площадь четырехугольника зависит от формы.

Некоторые важные свойства четырехугольника

Смежные углы в двух парах четырехугольника могут составлять 180 градусов.
Все четырехугольники имеют четыре угла, четыре вершины и четыре стороны.
Сумма внутренних углов четырехугольника равна 360 градусов.
Четырехугольник состоит из двух диагоналей.

Различные типы четырехугольников перечислены ниже

Параллелограмм: этот тип четырехугольника состоит из двух пар параллельных сторон, причем противоположные стороны всегда параллельны и равны по длине, но противоположные углы равны по размеру.
Ромб: это параллелограмм, у которого четыре равные стороны. Ромб похож на квадрат. Диагонали ромба пересекаются посередине под углом 90 градусов и делят друг друга пополам. Сумма только двух смежных углов равна 180°. Одним из ярких примеров ромба является форма ромба.
Трапеция: Четырехугольник, у которого пара противоположных сторон параллельны, называется трапецией. Ноги трапеции относятся к сторонам, которые не параллельны друг другу. А основания трапеции — это стороны, которые параллельны друг другу.
Прямоугольник: прямоугольник, у которого противоположные стороны равны и параллельны, а количество внутренних углов равно прямому углу. В прямоугольнике диагонали делят друг друга пополам. Не все параллелограммы являются прямоугольниками, но все прямоугольники являются параллелограммами.
Воздушный змей: Воздушный змей состоит из двух пар смежных сторон и пары равных противоположных углов. А перпендикулярно диагонали воздушного змея пересекают

Некоторые советы и рекомендации по эффективному изучению тригонометрических таблиц

Сосредоточьтесь на изучении формул синуса, косинуса и тангенса.
No related posts.