Вертикальные и смежные углы равны. Смежные и вертикальные углы
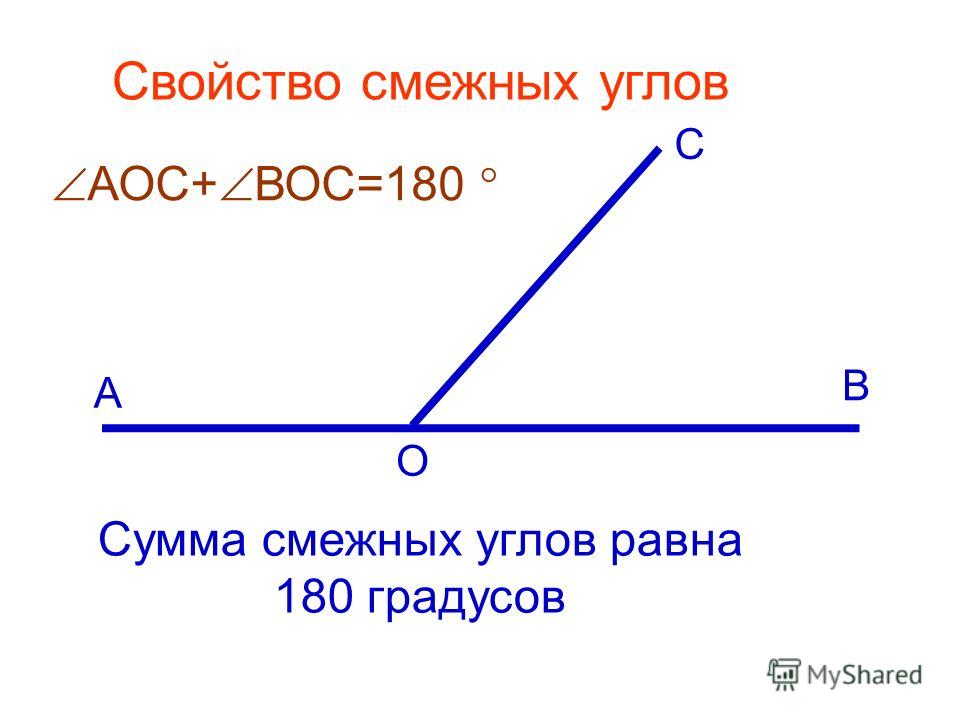
Два угла называются смежными, если у них одна сторона общая, а другие стороны этих углов являются дополнительными лучами. На рисунке 20 углы АОВ и ВОС смежные.
Сумма смежных углов равна 180°
Теорема 1. Сумма смежных углов равна 180°.
Доказательство. Луч ОВ (см. рис.1) проходит между сторонами развернутого угла. Поэтому ∠ АОВ + ∠ ВОС = 180° .
Из теоремы 1 следует, что если два угла равны, то смежные с ними углы равны.
Вертикальные углы равны
Два угла называются вертикальными, если стороны одного угла являются дополнительными лучами сторон другого. Углы АОВ и COD, BOD и АОС, образованные при пересечении двух прямых, являются вертикальными (рис. 2).
Теорема 2. Вертикальные углы равны.
Доказательство. Рассмотрим вертикальные углы АОВ и COD (см. рис. 2). Угол BOD является смежным для каждого из углов АОВ и COD. По теореме 1
∠ АОВ + ∠ BOD = 180°, ∠ COD + ∠ BOD = 180°.
Отсюда заключаем, что ∠ АОВ = ∠ COD.
Следствие 1. Угол, смежный с прямым углом, есть прямой угол.
Рассмотрим две пересекающиеся прямые АС и BD (рис.3). Они образуют четыре угла. Если один из них прямой (угол 1 на рис.3), то остальные углы также прямые (углы 1 и 2, 1 и 4 — смежные, углы 1 и 3 — вертикальные). В этом случае говорят, что эти прямые пересекаются под прямым углом и называются перпендикулярными (или взаимно перпендикулярными). Перпендикулярность прямых АС и BD обозначается так: AC ⊥ BD.
Серединным перпендикуляром к отрезку называется прямая, перпендикулярная к этому отрезку и проходящая через его середину.
АН — перпендикуляр к прямой
Рассмотрим прямую а и точку А, не лежащую на ней (рис.4). Соединим точку А отрезком с точкой Н прямой а. Отрезок АН называется перпендикуляром, проведенным из точки А к прямой а, если прямые АН и а перпендикулярны. Точка Н называется основанием перпендикуляра.
Чертежный угольник
Справедлива следующая теорема.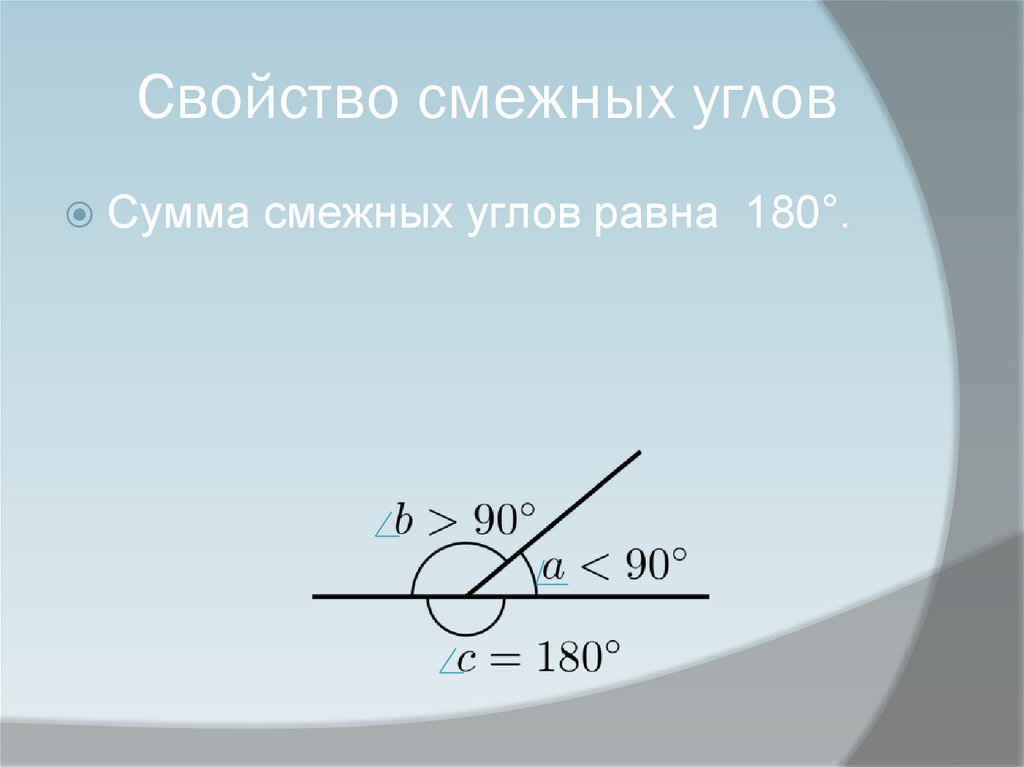
Теорема 3. Из всякой точки, не лежащей на прямой, можно провести перпендикуляр к этой прямой, и притом только один.
Для проведения на чертеже перпендикуляра из точки к прямой используют чертежный угольник (рис.5).
Замечание. Формулировка теоремы обычно состоит из двух частей. В одной части говорится о том, что дано. Эта часть называется условием теоремы. В другой части говорится о том, что должно быть доказано. Эта часть называется заключением теоремы. Например, условие теоремы 2 — углы вертикальные; заключение — эти углы равны.
Всякую теорему можно подробно выразить словами так, что ее условие будет начинаться словом «если», а заключение — словом «то». Например, теорему 2 можно подробно высказать так: «Если два угла вертикальные, то они равны».
Пример 1. Один из смежных углов равен 44°. Чему равен другой?
Решение. Обозначим градусную меру другого угла через x , тогда согласно теореме 1.
44° + х = 180°.
Решая полученное уравнение, находим, что х = 136°. Следовательно, другой угол равен 136°.
Следовательно, другой угол равен 136°.
Пример 2. Пусть на рисунке 21 угол COD равен 45°. Чему равны углы АОВ и АОС?
Решение. Углы COD и АОВ вертикальные, следовательно, по теореме 1.2 они равны, т. е. ∠ АОВ = 45°. Угол АОС смежный с углом COD, значит, по теореме 1.
∠ АОС = 180° — ∠ COD = 180° — 45° = 135°.
Пример 3. Найти смежные углы, если один из них в 3 раза больше другого.
Решение. Обозначим градусную меру меньшего угла через х. Тогда градусная мера большего угла будет Зх. Так как сумма смежных углов равна 180° (теорема 1), то х + Зх = 180°, откуда х = 45°.
Значит, смежные углы равны 45° и 135°.
Пример 4. Сумма двух вертикальных углов равна 100°. Найти величину каждого из четырех углов.
Решение. Пусть условию задачи отвечает рисунок 2. Вертикальные углы COD к АОВ равны (теорема 2), значит, равны и их градусные меры. Поэтому ∠ COD = ∠ АОВ = 50° (их сумма по условию 100°). Угол BOD (также и угол
АОС) смежный с углом COD, и, значит, по теореме 1
Угол BOD (также и угол
АОС) смежный с углом COD, и, значит, по теореме 1
∠ BOD = ∠ АОС = 180° — 50° = 130°.
Смежные углы – два угла, у которых одна сторона общая, а две другие являются продолжениями одна другой.
Сумма смежных углов равна 180°
Вертикальные углы — это два угла, у которых стороны одного угла являются продолжение сторон другого.
Вертикальные углы равны.
2. Признаки равенства треугольников:
I признак : Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
II признак : Если стороны и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.
III признак : Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны
3. Признаки параллельности двух прямых: односторонние углы, накрест лежащие и соответственные:
Признаки параллельности двух прямых: односторонние углы, накрест лежащие и соответственные:
Две прямые на плоскости называются параллельными , если они не пересекаются.
Накрест лежащие углы: 3 и 5, 4 и 6;
Односторонние углы: 4 и 5, 3 и 6; рис. Стр55
Соответственные углы: 1 и 5, 4 и 8, 2 и 6, 3 и 7;
Теорема : Если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны.
Теорема : Если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны.
Теорема : Если при пересечении двух прямых секущей сумма односторонних углов равна 180°, то прямые параллельны.
Теорема : если две параллельные прямые пересечены секущей, то накрест лежащие углы равны
Теорема : если две параллельные прямые пересечены секущей, то соответственные углы равны
Теорема : если две параллельные прямые пересечены секущей, то сумма односторонних углов равна 180°
4. Сумма углов треугольника:
Сумма углов треугольника:
Сумма углов треугольника равна 180°
5. Свойства равнобедренного треугольника:
Теорема: В равнобедренном треугольнике углы при основании равны.
Теорема: В равнобедренном треугольнике биссектриса, проведенная к основанию, являетсямедианой и высотой (медиана наоборот), (биссектриса делит угол пополам, медиана делит сторону пополам, высота образует угол 90°)
Признак: Если два угла треугольника равны, то треугольник равнобедренный.
6. Прямоугольный треугольник:
Прямоугольный треугольник — это треугольник, в котором один угол прямой (то есть составляет 90 градусов)
В прямоугольном треугольнике гипотенуза больше катета
1. Сумма двух острых углов прямоугольного треугольника равна 90°
2. Катет прямоугольного треугольника, лежащий против угла в 30°, равен половине гипотенузы
3. Если катет прямоугольного треугольника равен половине гипотенузы, то угол, лежащий против этого катета, равен 30°
7.
Сумма углов четырёхугольника равна 2 π = 360°.
Четырёхугольник можно вписать в окружность тогда и только тогда, сумма противоположных углов равна 180°
10. Признаки подобия треугольников:
I признак : если два угла одного треугольника соответственно равны двум углам другого, то такие треугольники подобны
II признак : если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключенные между этими сторонами, равны, то такие треугольники подобны.
III признак : если три стороны одного треугольника порциональны трем сторонам другого, то такие треугольники подобны
11. Формулы:
· Теорема Пифагора: a 2 +b 2 =c 2
· Теорема sin:
· Теорема cos:
· 3 формулы площади треугольника:
· Площадь прямоугольного треугольника: S= S=
· Площадь равностороннего треугольника:
· Площадь параллелограмма: S = ah
· Площадь квадрата: S = a2
· Площадь трапеции:
· Площадь ромба:
· Площадь прямоугольника: S=ab
· Равносторонний треугольник.
· Тригонометрическая единица: sin 2 a+cos 2 a=1
· Средняя линия треугольника: S=
· Средняя линия трапеции : МК=
©2015-2019 сайт
Все права принадлежать их авторам. Данный сайт не претендует на авторства, а предоставляет бесплатное использование.
Дата создания страницы: 2017-12-12
Равна двум прямым углам.
Даны два смежных угла : АОВ и ВОС . Требуется доказать, что:
∠АОВ+∠ВОС= d+ d = 2d
Восставим из точки О к прямой АС перпендикуляр OD . Мы разделили угол АОВ на две части AOD и DOB так, что можно написать:
∠AO B = ∠ AO D+∠ D OB
Прибавим к обеим частям этого равенства по одному и тому же углу BOС , отчего равенство не нарушится:
∠ AO B + ∠ BO С = ∠ AOD
+ ∠ D OB + ∠ BO СТак как сумма D OB + BOС составляет прямой угол DO С , то
∠ AO B+ ∠ BO С = ∠ AO D + ∠ DO С = d + d = 2 d,
что и требовалось доказать.
Следствия .
1. Сумма углов (AO B, BOС , СOD , DOE ), расположенных вокруг общей вершины (O ) по одну сторону прямой (AE ) равна 2 d = 180 0 , потому что эта сумма составляет сумму двух смежных углов , например таких: АОС + СОЕ
2. Сумма углов , расположенных вокруг общей вершины
Обратная теорема.
Если сумма двух углов , имеющих общую вершину и общую сторону и не покрывающих друг друга, равна двум прямым углам (2d), то такие углы — смежные , т.е. две другие их стороны составляют прямую линию .
Если из одной точки (O) прямой (AB) восстановить к ней, по каждую ее сторону, перпендикуляры, то эти перпендикуляры образуют одну прямую (СD). Из всякой точки вне прямой можно опустить на эту прямую перпендикуляр и притом только один.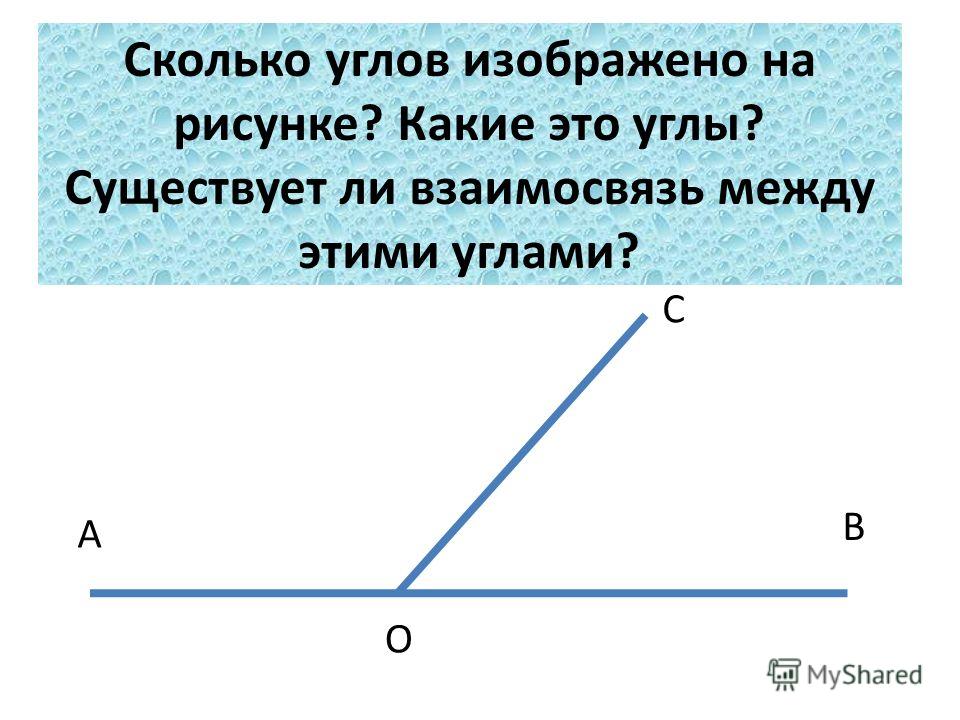 С D .
С D .
Два угла называются вертикальными , если стороны одного составляют продолжение сторон другого.
Так, при пересечении двух прямых AB и С D образуются две пары вертикальных углов: AO D и СOB ; AOС и D OB .
Теорема.
Два вертикальных угла равны.
Пусть даны два вертикальных угла: AOD и С OB т.е. OB есть продолжение OA , а O С продолжение OD .
Требуется доказать, что AOD = С OB.
По свойству смежных углов можем написать:
AO D + D OB = 2 d
DOB + BOС = 2d
Значит: AOD + DOB = DOB + BOС.
Если вычесть из обеих частей этого равенства по углу D OB , получим:
AO D = BOС , что и требовалось доказать.
Аналогично докажем, что AOС = D OB .
Геометрия — это весьма многогранная наука. Она развивает логику, воображение и интеллект. Конечно, из-за своей сложности и огромного количества теорем и аксиом, она не всегда нравится школьникам. Кроме этого, существует необходимость постоянно доказывать свои выводы, используя общепринятые стандарты и правила.
Смежные и вертикальные углы — это неотъемлемая составляющая геометрии. Наверняка многие школьники просто обожают их по той причине, что их свойства понятны и просты в доказательстве.
Образование углов
Любой угол образуется путем пересечения двух прямых или проведения двух лучей из одной точки. Они могут называться либо одной буквой, либо тремя, которые последовательно обозначают точки построения угла.
Углы измеряются в градусах и могут (в зависимости от их значения) по-разному называться. Так, существует прямой угол, острый, тупой и развернутый. Каждому из названий соответствует определенная градусная мера или ее промежуток.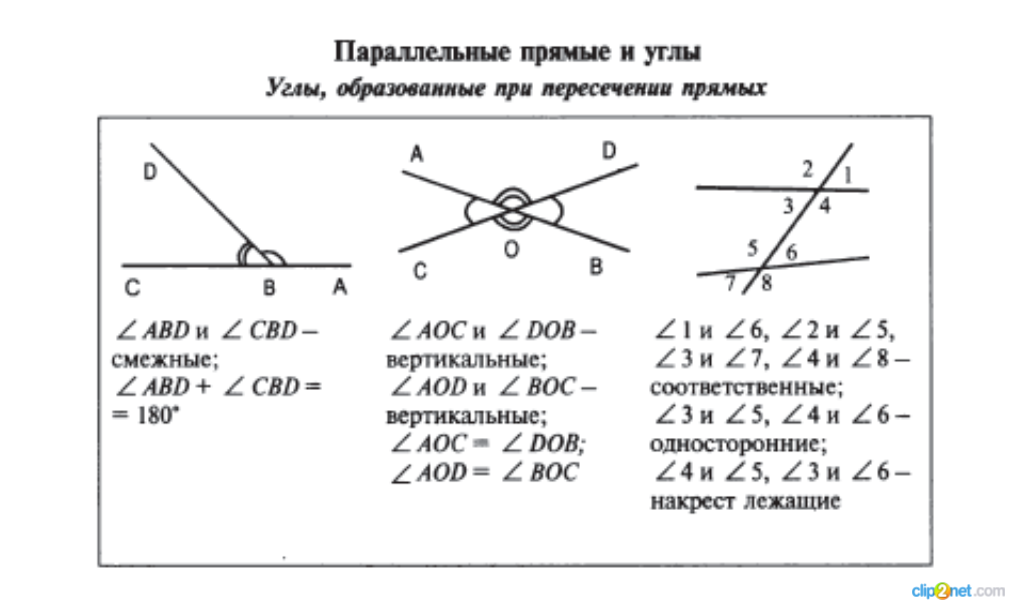
Острым называется угол, мера которого не превышает 90 градусов.
Тупым является угол, превышающий 90 градусов.
Угол называется прямым в том случае, когда его градусная мера равна 90.
В том случае, когда он образован одной сплошной прямой, и его градусная мера равна 180, его называют развернутым.
Углы, имеющие общую сторону, вторая сторона которых продолжает друг друга, называются смежными. Они могут быть как острыми, так и тупыми. Пересечение линией образует смежные углы. Свойства их следующие:
- Сумма таких углов будет равна 180 градусам (существует теорема, доказывающая это). Поэтому можно легко вычислить один из них, если известен другой.
- Из первого пункта следует, что смежные углы не могут быть образованы двумя тупыми или двумя острыми углами.
Благодаря этим свойствам, можно всегда вычислить градусную меру угла, имея значение другого угла или, по крайней мере, отношение между ними.
Вертикальные углы
Углы, стороны которых являются продолжением друг друга, называются вертикальными.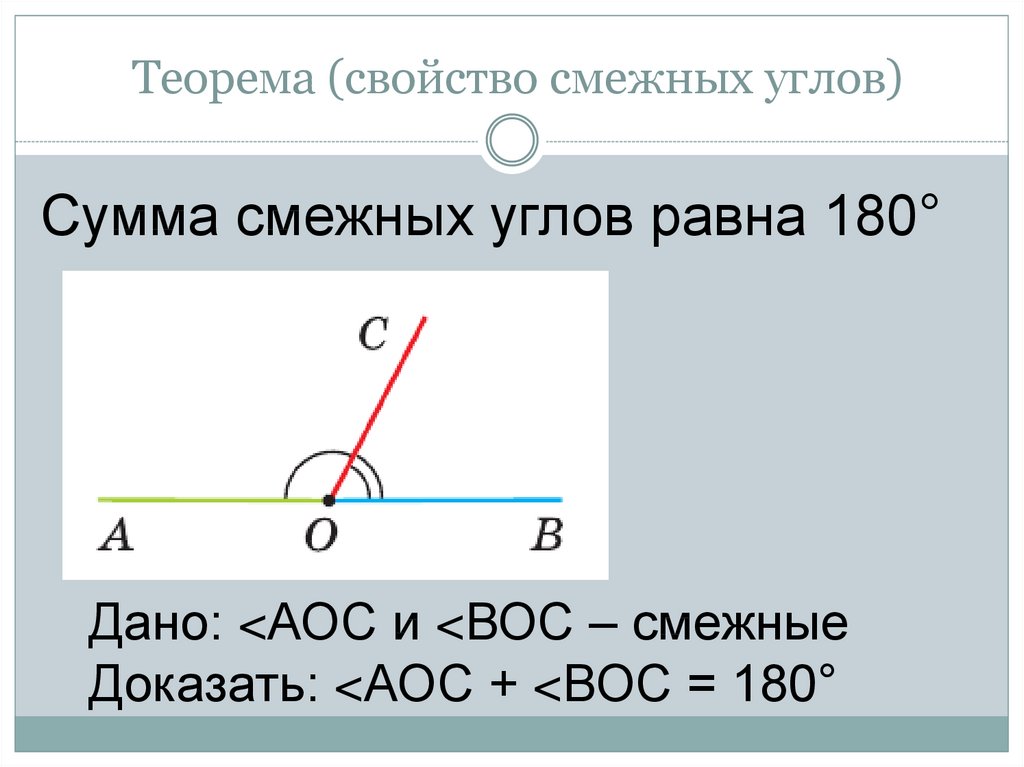 В качестве такой пары могут выступать любые их разновидности. Вертикальные углы всегда равны между собой.
В качестве такой пары могут выступать любые их разновидности. Вертикальные углы всегда равны между собой.
Они образуются при пересечении прямых. Совместно с ними всегда присутствуют и смежные углы. Угол может быть одновременно смежным для одного и вертикальным для другого.
При пересечении произвольной линией также рассматривают еще несколько видов углов. Такая линия называется секущей, она и образует соответственные, односторонние и накрест лежащие углы. Они равны между собой. Их можно рассматривать в свете свойств, которые имеют вертикальные и смежные углы.
Таким образом, тема углов представляется довольно простой и понятной. Все их свойства легко запомнить и доказать. Решение задач не представляется сложным до тех пор, пока углам соответствует числовое значение. Уже дальше, когда начнется изучение sin и cos, придется запоминать множество сложных формул, их выводов и следствий. А до того времени можно просто наслаждаться легкими задачками, в которых необходимо найти смежные углы.
На данном уроке мы рассмотрим и уясним для себя понятие смежные углы. Рассмотрим теорему, которая их касается. Введем понятие «вертикальные углы». Рассмотрим опорные факты, касающиеся этих углов. Далее сформулируем и докажем два следствия об угле между биссектрисами вертикальных углов. В конце занятия рассмотрим несколько задач, посвященных этой теме.
Начнем наш урок с понятия «смежные углы». На рисунке 1 изображен развернутый угол ∠АОС и луч ОВ, который делит данный угол на 2 угла.
Рис. 1. Угол ∠АОС
Рассмотрим углы ∠АОВ и ∠ВОС. Вполне очевидно, что они имеют общую сторону ВО, а стороны АО и ОС являются противолежащими. Лучи ОА и ОС дополняют друг друга, а значит, они лежат на одной прямой. Углы ∠АОВ и ∠ВОС являются смежными.
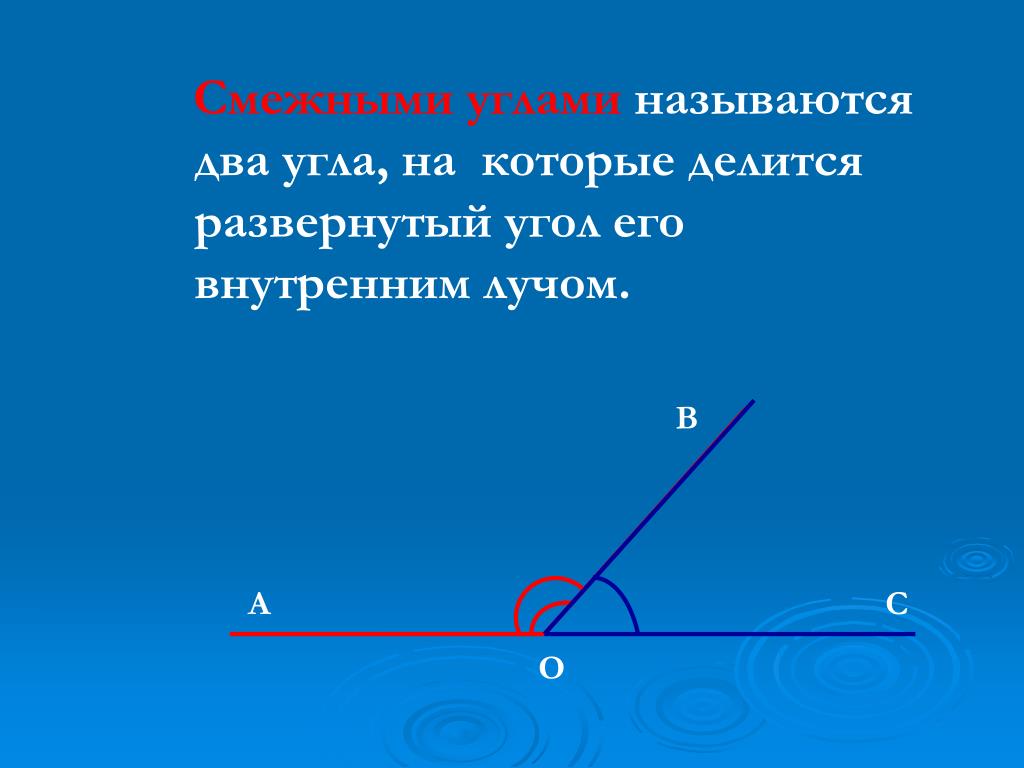
Определение: Если два угла имеют общую сторону, а две другие стороны являются дополняющими лучами, то данные углы называются смежными .
Теорема 1: Сумма смежных углов — 180 о.
Рис. 2. Чертеж к теореме 1
∠МОL + ∠LON = 180 o . Данное утверждение является верным, так как луч OL делит развернутый угол ∠MON на два смежных угла. То есть мы не знаем градусных мер ни одного из смежных углов, а знаем лишь их сумму — 180 о.
Данное утверждение является верным, так как луч OL делит развернутый угол ∠MON на два смежных угла. То есть мы не знаем градусных мер ни одного из смежных углов, а знаем лишь их сумму — 180 о.
Рассмотрим пересечение двух прямых. На рисунке изображено пересечение двух прямых в точке О.
Рис. 3. Вертикальные углы ∠ВОА и ∠СОD
Определение: Если стороны одного угла являются продолжением второго угла, то такие углы называются вертикальными. Именно поэтому на рисунке изображено две пары вертикальных углов: ∠АОВ и ∠СОD, а также ∠AOD и ∠ВОС.
Теорема 2: Вертикальные углы равны.
Используем рисунок 3. Рассмотрим развернутый угол ∠АОС. ∠АОВ = ∠АОС — ∠ВОС = 180 о — β. Рассмотрим развернутый угол ∠ВОD. ∠CОD = ∠BОD — ∠BОС = 180 о — β.
Из этих соображений мы делаем вывод, что ∠АОВ = ∠СОD = α. Аналогично, ∠AOD = ∠ВОС = β.
Следствие 1: Угол между биссектрисами смежных углов равен 90 о.
Рис. 4. Чертеж к следствию 1
Поскольку ОL — биссектриса угла ∠ВОА, то угол ∠LOB = , аналогично ∠ВОК = . ∠LOK = ∠LOB + ∠BOK = + = . Сумма углов α + β равна 180 о, поскольку данные углы — смежные.
∠LOK = ∠LOB + ∠BOK = + = . Сумма углов α + β равна 180 о, поскольку данные углы — смежные.
Следствие 2: Угол между биссектрисами вертикальных углов равен 180 о.
Рис. 5. Чертеж к следствию 2
KO — биссектриса ∠AOB, LO — биссектриса ∠COD. Очевидно, что ∠KOL = ∠KOB + ∠BOC + ∠COL = o . Сумма углов α + β равна 180 о, так как данные углы — смежные.
Рассмотрим некоторые задачи:
Найдите угол, смежный с ∠АOС, если ∠АOС = 111 о.
Выполним чертеж к задаче:
Рис. 6. Чертеж к примеру 1
Поскольку ∠АОС = β и ∠СOD = α смежные углы, то α + β = 180 о. То есть 111 о + β = 180 о.
Значит, β = 69 о.
Этот тип задач эксплуатирует теорему о сумме смежных углов.
Один из смежных углов прямой, каким (острым, тупым или прямым) является другой угол?
Если один из углов прямой, а сумма двух углов 180 о, то и другой угол тоже прямой. Эта задача проверяет знания о сумме смежных углов.
Верно ли, что если смежные углы равны, то они прямые?
Составим уравнение: α + β = 180 о, но поскольку α = β, то β + β = 180 о, значит, β = 90 о.
Ответ: Да, утверждение верно.
Даны два равных угла. Верно ли, что и смежные им углы тоже будут равны?
Рис. 7. Чертеж к примеру 4
Если два угла равны α, то соответствующие им смежные углы будут 180 о — α. То есть они будут равны между собой.
Ответ: Утверждение верно.
- Александров А.Д., Вернер А.Л., Рыжик В.И. и др. Геометрия 7. — М.: Просвещение.
- Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. и др. Геометрия 7. 5-е изд. — М.: Просвещение.
- \Бутузов В.Ф., Кадомцев С.Б., Прасолова В.В. Геометрия 7 / В.Ф. Бутузова, С.Б. Кадомцев, В.В. Прасолова, под редакцией В.А. Садовничего. — М.: Просвещение, 2010.
- Измерение отрезков ().
- Обобщающий урок по геометрии в 7-м классе ().
- Прямая линия, отрезок ().
- № 13, 14. Бутузов В.Ф., Кадомцев С.Б., Прасолова В.В. Геометрия 7 / В.Ф. Бутузова, С.Б. Кадомцев, В.В. Прасолова, под редакцией В.А. Садовничего. — М.: Просвещение, 2010.
- Найдите два смежных угла, если один из них в 4 раза больше другого.

- Дан угол. Постройте для него смежный и вертикальный углы. Сколько таких углов можно построить?
- * В каком случае получается больше пар вертикальных углов: при пересечении трех прямых в одной точке или в трех точках?
Что такое смежные углы? Ответ на webmath.ru
Поможем решить контрольную, написать реферат, курсовую и диплом от 800р
Содержание:
- Определение смежных углов
- Следствия из теоремы о смежных углах
- Свойства (тригонометрические соотношения)
Определение смежных углов
Определение
Смежными углами называются два прилежащих угла, несовпадающие стороны которых образуют прямую (рис. 1).
Определение
Углы называются прилежащими, если они имеют общую вершину и общую сторону, а также, если их внутренние области не покрывают друг друга (рис. 2).
Теорема
Теорема о смежных углах.
Сумма градусных мер смежных углов равна $180^{\circ}$. {\circ}-\angle \beta$$
{\circ}-\angle \beta$$
Так как $\angle \alpha \neq \angle \beta$, то и разности, стоящие в правых частях последних равенств также не равны, причем при равенстве уменьшаемого та разность меньше, где вычитаемое больше, следовательно $\angle \alpha_{1} < \angle \beta_{1}$.
Что и требовалось доказать.
Свойства (тригонометрические соотношения)
- Синусы смежных углов равны. Их косинусы и тангенсы равны по величине, но имеют противоположные знаки (за исключением неопределённых значений).
- Чтобы построить угол, смежный данному, надо одну из сторон рассматриваемого угла продлить за вершину (рис. 3).
Читать дальше: что такое острый угол.
Если смежные углы. Смежные и вертикальные углы, их свойства
1. Смежные углы.
Если продолжить сторону некоторого угла за его вершину, то получим два угла (рис. 72): ∠ABC и ∠CBD, у которых одна сторона BC общая, а две другие, AB и BD, образуют прямая линия.
Два угла, у которых одна сторона общая, а две другие образуют прямую, называются смежными углами.
Смежные углы можно получить и таким образом: если провести из какой-либо точки прямой (не лежащей на данной прямой) луч, то получим смежные углы.
Например, ∠ADF и ∠FDВ — смежные углы (рис. 73).
Смежные углы могут иметь самые разные положения (рис. 74).
Сумма смежных углов составляет прямой угол, поэтому сумма двух смежных углов равна 180°
Следовательно, прямой угол можно определить как угол, равный прилежащему к нему углу.
Зная значение одного из смежных углов, мы можем найти значение другого смежного угла.
Например, если один из смежных углов равен 54°, то второй угол будет:
180° — 54° = l26°.
2. Уголки вертикальные.
Если мы продолжим стороны угла за его вершину, мы получим вертикальные углы. На рисунке 75 углы EOF и AOC вертикальны; углы AOE и COF также вертикальны.
Два угла называются вертикальными, если стороны одного угла являются продолжениями сторон другого угла.
Пусть ∠1 = \(\frac(7)(8)\) ⋅ 90° (рис. 76). ∠2, примыкающий к нему, будет равен 180° — \(\frac(7)(8)\) ⋅ 90°, т.е. 1\(\frac(1)(8)\) ⋅ 90°.
Таким же образом можно вычислить, что такое ∠3 и ∠4.
∠3 = 180° — 1\(\frac(1)(8)\) ⋅ 90° = \(\frac(7)(8)\) ⋅ 90°;
∠4 = 180° — \(\frac(7)(8)\) ⋅ 90° = 1\(\frac(1)(8)\) ⋅ 90° (рис. 77).
Мы видим, что ∠1 = ∠3 и ∠2 = ∠4.
Можно решить еще несколько таких же задач и каждый раз получать один и тот же результат: вертикальные углы равны между собой.
Однако для того, чтобы убедиться, что вертикальные углы всегда равны между собой, недостаточно рассматривать отдельные числовые примеры, так как выводы, сделанные на основании частных примеров, иногда могут быть ошибочными.
Необходимо проверить справедливость свойства вертикальных углов доказательством.
Доказательство можно провести следующим образом (рис. 78):
78):
∠ а + ∠ с = 180°;
∠ б+ ∠ с = 180°;
(так как сумма смежных углов равна 180°).
∠ а + ∠ с = ∠ b+ ∠ с
(поскольку левая часть этого равенства равна 180°, и его правая часть тоже 180°).
В это равенство входит один и тот же угол С .
Если из равных значений вычесть поровну, то и останется поровну. Результат будет: ∠ a = ∠ b , т. е. вертикальные углы равны между собой.
3. Сумма углов, имеющих общую вершину.
На рис. 79 ∠1, ∠2, ∠3 и ∠4 расположены по одну сторону от прямой и имеют общую вершину на этой прямой. В сумме эти углы составляют прямой угол, то есть
∠1 + ∠2 + ∠3 + ∠4 = 180°.
На рисунке 80 ∠1, ∠2, ∠3, ∠4 и ∠5 имеют общую вершину. Сумма этих углов равна полному углу, т. е. ∠1 + ∠2 + ∠3 + ∠4 + ∠5 = 360°.
Прочие материалы
Смежные углы — два угла, у которых одна сторона общая, а два других являются продолжениями один другого.
Сумма смежных углов равна 180°
Вертикальные углы — это два угла, в которых стороны одного угла являются продолжением сторон другого.
Вертикальные углы равны.
2. Признаки равенства треугольников:
I признак : Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны .
II знак : Если стороны и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.
III признак : Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны
3. Признаки параллельности двух прямых: односторонние углы, лежащие накрест и соответствующие:
Две линии на плоскости называются параллельными , если они не пересекаются.
Уголки крестообразно лежащие: 3 и 5, 4 и 6;
Односторонние углы: 4 и 5, 3 и 6; рис. Страница55
Страница55
Соответствующие углы: 1 и 5, 4 и 8, 2 и 6, 3 и 7;
Теорема : Если при пересечении двух прямых секущей лежащие углы равны, то прямые параллельны.
Теорема : Если при пересечении двух прямых секущей соответствующие углы равны, то прямые параллельны.
Теорема : Если при пересечении двух прямых секущей сумма односторонних углов равна 180°, то прямые параллельны.
Теорема : если две параллельные прямые пересекаются секущей, то лежащие накрест углы равны
Теорема : если две параллельные прямые пересекаются секущей, то соответствующие углы равны
Теорема : если две параллельные прямые пересекаются секущей, то сумма односторонних углов равна 180°
4. Сумма углов треугольника:
Сумма углов треугольника равна 180°
5. Свойства равнобедренного треугольника:
Теорема. равный.
Теорема: В равнобедренном треугольнике биссектриса, проведенная к основанию, есть медиана, а высота (медиана наоборот), (биссектриса делит угол пополам, медиана делит сторону пополам, высота образует угол 90° )
Признак: Если два угла треугольника равны, то треугольник равнобедренный.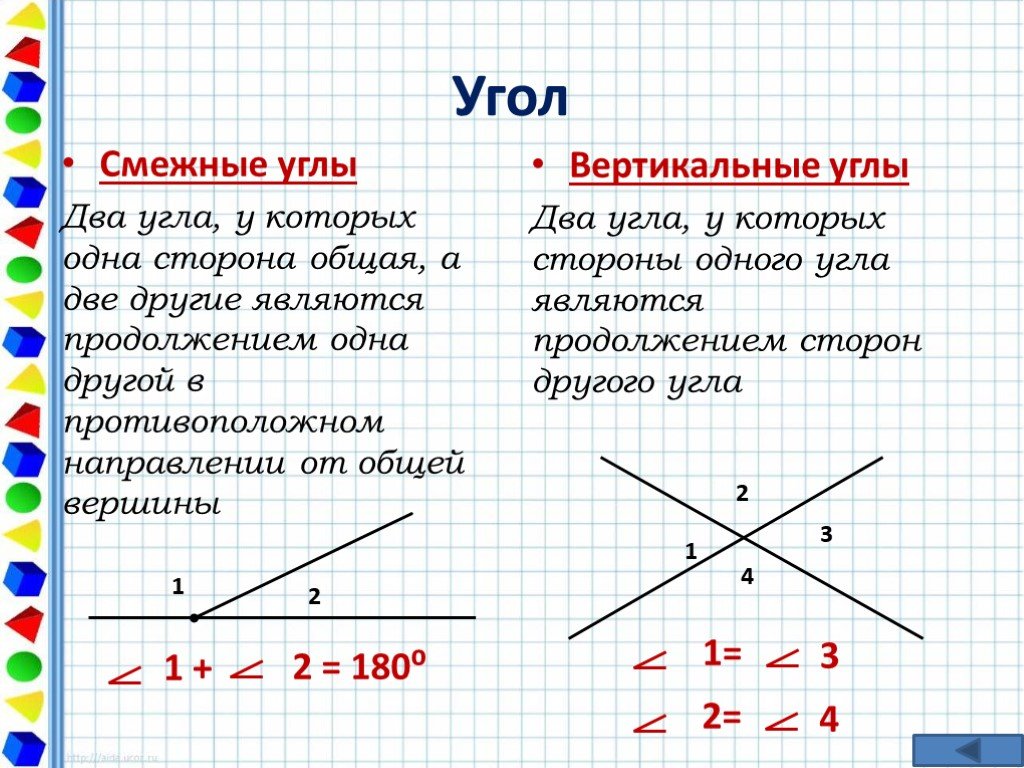
6. Прямоугольный треугольник:
Прямоугольный треугольник – это треугольник, в котором один угол прямой (то есть равен 90 градусам)
В прямоугольном треугольнике гипотенуза длиннее катета
1. Сумма двух острых углов прямоугольного треугольника равна 90°
2. Катет прямоугольного треугольника, лежащий против угла 30°, равен половине гипотенузы
3. Если катет прямоугольного треугольника равен половине гипотенузы, то угол, противолежащий этому катету, равен 30°9
Сумма углов четырехугольника равна 2 π = 360°.
Четырехугольник можно вписать в окружность тогда и только тогда, когда сумма противолежащих ему углов равна 180° равны двум углам другого, то такие треугольники подобны
II признак : если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы между этими сторонами равны, то такие треугольники подобны.
III признак : если три стороны одного треугольника пропорциональны трем сторонам другого, то такие треугольники подобны
11. Формулы:
Формулы:
· Теорема Пифагора: a 2 +b 2 =c 2
· Теорема греха:
· COS Теорема:
· 3 Треугольная площадь. равностороннего треугольника:
· Площадь параллелограмма: S = AH
· Площадь квадратной площадь: S = A2
· Область трапеции:
· SAME:
· .
· Равносторонний треугольник. Высота: h=
· Тригонометрическая единица: sin 2 a+cos 2 a=1
· средняя линия треугольника: S=
· Средняя линия трапеции :MK=
©2015-2019 сайт
Все права принадлежат их авторам. Этот сайт не претендует на авторство, а предоставляет бесплатное использование.
Дата создания страницы: 12.12.2017
ГЛАВА I.
ОСНОВНЫЕ ПОНЯТИЯ.
§одиннадцать. СМЕЖНЫЕ И ВЕРТИКАЛЬНЫЕ УГЛЫ.
1. Смежные углы.
Если продолжить сторону некоторого угла за его вершину, то получим два угла (рис. 72): / Солнце и / СВД, у которого одна сторона ВС общая, а две другие АВ и БД образуют прямую линию.
72): / Солнце и / СВД, у которого одна сторона ВС общая, а две другие АВ и БД образуют прямую линию.
Два угла, у которых одна сторона общая, а две другие образуют прямую, называются смежными углами.
Смежные углы можно получить и таким образом: если провести из какой-либо точки прямой (не лежащей на данной прямой) луч, то получим смежные углы.
Например, / АПД и / FDВ — углы смежные (рис. 73).
Смежные углы могут иметь самые разные положения (рис. 74).
Сумма смежных углов составляет прямой угол, поэтому сумма двух смежных углов равна 2 d.
Следовательно, прямой угол можно определить как угол, равный прилежащему к нему углу.
Зная значение одного из смежных углов, мы можем найти значение другого смежного угла.
Например, если один из смежных углов равен 3/5 d , то второй угол будет равен:
2 d — 3/5 д = 1 2 / 5 д .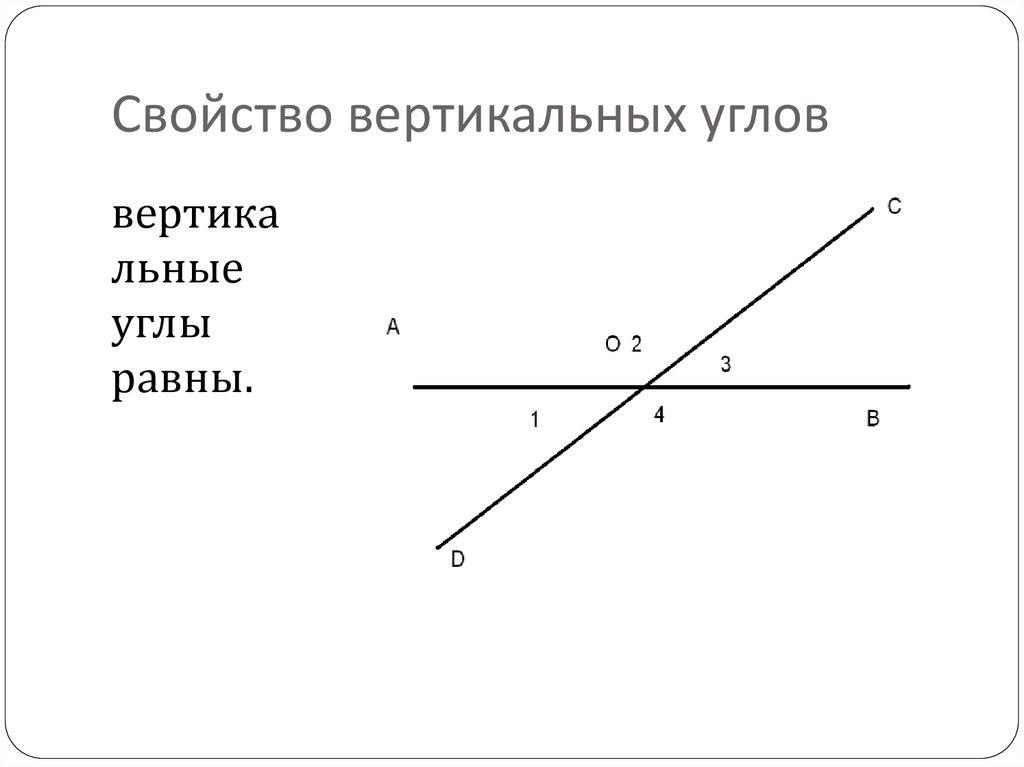
2. Уголки вертикальные.
Если мы продолжим стороны угла за его вершину, мы получим вертикальные углы. На чертеже 75 углы EOF и AOC вертикальны; углы AOE и COF также вертикальны.
Два угла называются вертикальными, если стороны одного угла являются продолжениями сторон другого угла.
Лет / 1 = 7/8 д (рис. 76). Рядом с ним / 2 будет равно 2 d — 7/8 d , т.е. 1 1/8 d .
Таким же образом можно вычислить, чему равны / 3 и / 4.
/ 3 = 2 d — 1 1/8 d = 7/8 d ; / 4 = 2 д — 7/8 д = 1 1/8 д (рис. 77).
Видим, что / 1 = / 3 и / 2 = / 4.
Можно решить еще несколько таких же задач и каждый раз получать один и тот же результат: вертикальные углы равны между собой.
Однако для того, чтобы убедиться, что вертикальные углы всегда равны между собой, недостаточно рассматривать отдельные числовые примеры, так как выводы, сделанные на частных примерах, иногда могут быть ошибочными.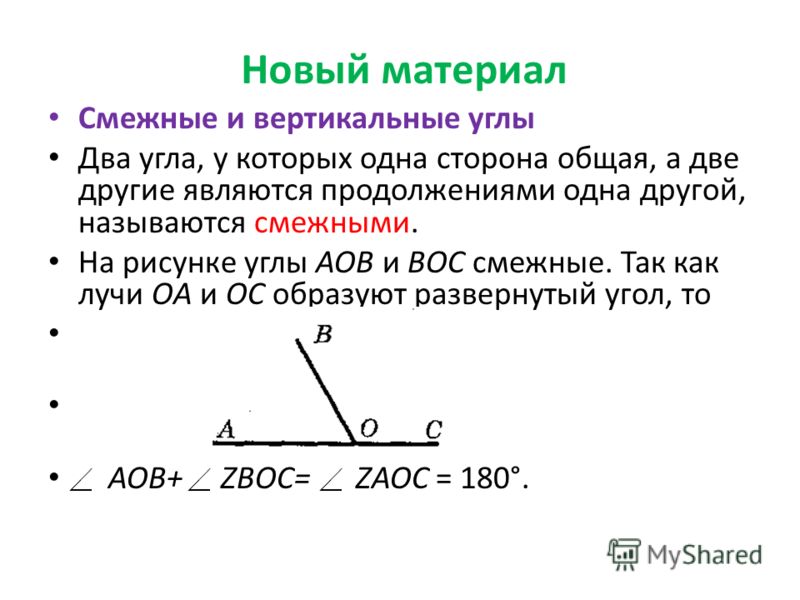
Необходимо проверить справедливость свойства вертикальных углов рассуждениями, доказательством.
Доказательство можно провести следующим образом (рис. 78):
/ а + / с = 2 d ;
/ б+ / с = 2 d ;
(так как сумма смежных углов равна 2 d ).
/ а + / с = / б+ / c
(поскольку левая часть этого равенства равна 2 d , а его правая часть также равна 2 d ).
В это равенство входит один и тот же угол С .
Если из равных значений вычесть поровну, то останется поровну. Результат будет: / а = / b , т. е. вертикальные углы равны между собой.
При рассмотрении вопроса о вертикальных углах мы сначала объяснили, какие углы называются вертикальными, т. е. дали определение вертикальных углов.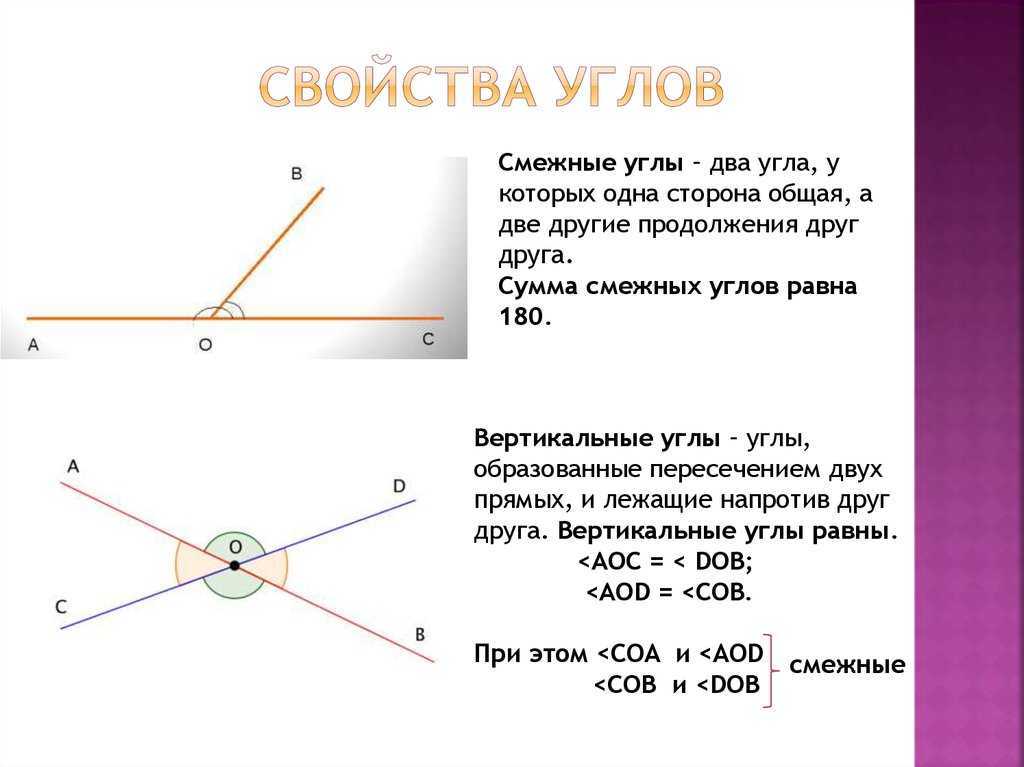
Затем мы сделали суждение (утверждение) о равенстве вертикальных углов и убедились в справедливости этого суждения доказательством. Такие суждения, справедливость которых необходимо доказать, называются теоремами . Таким образом, в этом разделе мы дали определение вертикальных углов, а также сформулировали и доказали теорему об их свойстве.
В дальнейшем при изучении геометрии нам постоянно придется встречаться с определениями и доказательствами теорем.
3. Сумма углов, имеющих общую вершину.
На чертеже 79 / 1, / 2, / 3 и / 4 расположены по одну сторону от прямой и имеют общую вершину на этой прямой. В сумме эти углы составляют прямой угол, т.е.
/ 1+ / 2+ / 3+ / 4 = 2 д .
На чертеже 80 / 1, / 2, / 3, / 4 и / 5 имеют общую вершину. В сумме эти углы составляют полный угол, т.е. / 1 + / 2 + / 3 + / 4 + / 5 = 4 д .
Упражнения.
1. Один из смежных углов равен 0,72 d. Вычислите угол, образованный биссектрисами этих смежных углов.
2. Докажите, что биссектрисы двух смежных углов образуют прямой угол.
3. Докажите, что если два угла равны, то равны и смежные с ними углы.
4. Сколько пар смежных углов на рисунке 81?
5. Может ли пара смежных углов состоять из двух острых углов? из двух тупых углов? под прямым и тупым углами? под прямым и острым углом?
6. Если один из смежных углов прямой, то что можно сказать о величине прилежащего к нему угла?
7. Если на пересечении двух прямых имеется один прямой угол, то что можно сказать о величине остальных трех углов?
На этом уроке мы рассмотрим и поймем для себя понятие смежных углов. Рассмотрим теорему, касающуюся их. Введем понятие «вертикальные углы». Рассмотрим подтверждающие факты, касающиеся этих углов. Далее сформулируем и докажем два следствия об угле между биссектрисами вертикальных углов. В конце урока мы рассмотрим несколько задач, посвященных этой теме.
В конце урока мы рассмотрим несколько задач, посвященных этой теме.
Начнем наш урок с понятия «смежные углы». На рис. 1 показан развернутый угол ∠AOC и луч OB, который делит этот угол на 2 угла.
Рис. 1. Угол ∠AOC
Рассмотрим углы ∠AOB и ∠BOC. Совершенно очевидно, что у них общая сторона VO, а стороны AO и OS противоположны. Лучи ОА и ОС дополняют друг друга, а значит лежат на одной прямой. Углы ∠AOB и ∠BOC смежные.
Определение: Если два угла имеют общую сторону, а две другие стороны являются дополнительными лучами, то такие углы называются связанными .
Теорема 1: Сумма смежных углов равна 180°.
Рис. 2. Рисунок к теореме 1
∠MOL + ∠LON = 180o. Это утверждение верно, поскольку луч OL делит прямой угол ∠MON на два смежных угла. То есть мы не знаем градусных мер ни одного из смежных углов, а знаем только их сумму — 180 o .
Рассмотрим пересечение двух линий. На рисунке показано пересечение двух прямых в точке О.
Рис. 3. Вертикальные углы ∠BOA и ∠COD
Определение: Если стороны одного угла являются продолжением второго угла, то такие углы называются вертикальными. Поэтому на рисунке показаны две пары вертикальных углов: ∠AOB и ∠COD, а также ∠AOD и ∠BOC.
Теорема 2: Вертикальные углы равны.
Воспользуемся рисунком 3. Рассмотрим развернутый угол ∠AOC. ∠АОБ = ∠АОС — ∠ВОС = 180 о — β. Рассмотрим развернутый угол ∠BOD. ∠ХПК = ∠БПК — ∠ВОС = 180 о — β.
Из этих соображений заключаем, что ∠AOB = ∠COD = α. Аналогично, ∠AOD = ∠BOC = β.
Следствие 1: Угол между биссектрисами смежных углов равен 90°.
Рис. 4. Чертеж для следствия 1
Поскольку OL — биссектриса угла ∠BOA, то угол ∠LOB = , аналогично ∠BOK = . ∠LOK = ∠LOB + ∠BOK = + = . Сумма углов α + β равна 180°, так как эти углы смежные.
Следствие 2: Угол между биссектрисами вертикальных углов равен 180°.
Рис. 5. Чертеж для следствия 2
KO – биссектриса ∠AOB, LO – биссектриса ∠COD. Очевидно, ∠KOL = ∠KOB + ∠BOC + ∠COL = o. Сумма углов α + β равна 180°, так как эти углы смежные.
Очевидно, ∠KOL = ∠KOB + ∠BOC + ∠COL = o. Сумма углов α + β равна 180°, так как эти углы смежные.
Рассмотрим несколько задач:
Найдите угол, примыкающий к ∠AOC, если ∠AOC = 111 o.
Сделаем чертеж к заданию:
Рис. 6. Например, чертеж 1
Так как ∠AOC = β и ∠COD = α смежные углы, то α + β = 180°. То есть 111 o + β = 180 o.
Отсюда β = 69 o.
Задачи этого типа основаны на теореме о сумме смежных углов.
Один из смежных углов прямой, какой угол (острый, тупой или прямой) является другим углом?
Если один из углов прямой и сумма двух углов равна 180°, то другой угол тоже прямой. В этом задании проверяются знания о сумме смежных углов.
Верно ли, что если смежные углы равны, то они прямые?
Составим уравнение: α + β = 180°, но так как α = β, то β + β = 180°, значит, β = 90°.
Ответ: Да, утверждение верно.
Даны два равных угла. Верно ли, что смежные с ними углы также будут равны?
Рис.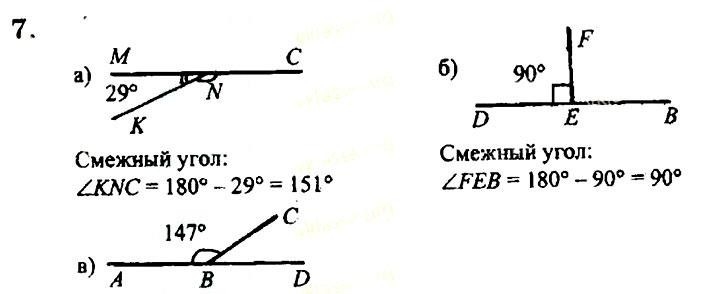 7. Чертеж для примера 4
7. Чертеж для примера 4
Если два угла равны α, то соответствующие им смежные углы будут равны 180 o — α. То есть они будут равны друг другу.
Ответ: Утверждение верно.
- Александров А.Д., Вернер А.Л., Рыжик В.И. и др. Геометрия 7. — М.: Просвещение.
- Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. и другие. Геометрия 7. 5-е изд. — М.: Просвещение.
- \Бутузов В.Ф., Кадомцев С.Б., Прасолова В.В. Геометрия 7 / В.Ф. Бутузова, С.Б. Кадомцев, В.В. Прасолова под редакцией В.А. Садовничий. — М.: Просвещение, 2010.
- Измерение сегментов ().
- Общий урок по геометрии в 7 классе ().
- Прямая линия, сегмент ().
- № 13, 14. Бутузов В.Ф., Кадомцев С.Б., Прасолова В.В. Геометрия 7 / В.Ф. Бутузова, С.Б. Кадомцев, В.В. Прасолова под редакцией В.А. Садовничий. — М.: Просвещение, 2010.
- Найдите два смежных угла, если один из них в 4 раза больше другого.
- Дан угол. Постройте для него смежные и вертикальные углы.
 Сколько таких уголков можно построить?
Сколько таких уголков можно построить? - * В каком случае получается больше пар вертикальных углов: при пересечении трех прямых в одной точке или в трех точках?
на тему: Смежные и вертикальные углы, их свойства.
(3 занятия)
В результате изучения темы Вам необходимо:
УМЕТЬ:
Понятия: смежные и вертикальные углы, перпендикулярные линии
Различать смежные и вертикальные углы
Теоремы о смежных и вертикальных углах
Решение задач с использованием свойств смежных и вертикальных углов
Свойства смежных и вертикальных углов
Построение смежных и вертикальных углов перпендикулярно прямым
ЛИТЕРАТУРА:
1. Геометрия. 7-й класс. ж. Кайдасов, Г. Досмагамбетова, В. Абдиев. Алматы «Мектеп». 2012
2. Геометрия. 7-й класс. К.О. Букубаева, А.Т. Миразов. АлматыАтамура». 2012
3. Геометрия. 7-й класс. Методическое руководство. К.О. Букубаева. АлматыАтамура». 2012
Методическое руководство. К.О. Букубаева. АлматыАтамура». 2012
4. Геометрия. 7 класс. Дидактический материал. А.Н.Шыныбеков. АлматыАтамура». 2012
5. Геометрия. 7-й класс. Сборник задач и упражнений. К.О. Букубаева, А.Т. Миразова. АлматыАтамура». 2012
Помните, что работать нужно по алгоритму!
Не забудьте пройти тест, сделайте пометки на полях,
Пожалуйста, не оставляйте вопросы без ответа.
Будьте объективны во время рецензирования, это поможет и вам, и собеседнику
кого ты проверяешь.
ЖЕЛАЕМ ВАМ УСПЕХОВ!
ЗАДАНИЕ №1.
Прочитайте определение и узнайте (2b):
Определение. Углы, у которых одна сторона общая, а две другие стороны являются дополнительными лучами, называются смежными.
2) Выучите и запишите теорему в тетрадь: (2b)
Сумма смежных углов равна 180.
Дано:
∠ АОД и ∠ DOV — заданные смежные углы
OD — общая сторона
Доказать:
∠ АОД +∠ DOV = 180
Доказательство:
На основании аксиомы III 4:
∠
АОД +∠
ДОВ =∠
АОВ.
∠ АОВ — развернут. Следовательно,
∠ АОД +∠ DOV = 180
Теорема доказана.
3) Из теоремы следует: (2б)
1) Если два угла равны, то равны и прилежащие к ним углы;
2) если смежные углы равны, то градусная мера каждого из них равна 90°.
Помните!
Угол, равный 90°, называется прямым.
Угол меньше 90° называется острым углом.
Угол больше 90° и меньше 180° называется тупым углом.
Прямой угол Острый угол Тупой угол
Так как сумма смежных углов равна 180°, то
1) угол, примыкающий к прямому углу, прямой;
2) угол, примыкающий к острому углу, тупой;
3) угол, примыкающий к тупому углу, острый.
4) Рассмотрим образец раствора хадачи:
а) Дано:∠ хканд∠ kl- смежный;∠ хкмор∠ клац 50°.
Найти:∠ хканд∠ кл.
Решение: Пусть∠
kl= x, тогда∠
hк= х + 50°. По свойству суммы смежных углов∠
кл +
∠
hк= 180°.
х + х + 50° = 180°;
2x = 180° — 50°;
2x = 130°;
х = 65°.
∠ кл= 65°;∠ hk= 65°+ 50° = 115°.
Ответ: 115° и 65°.
б) Пусть∠ kl= x, тогда∠ hk= 3x
x + 3x = 180°; 4х = 180°; х = 45°;∠ кл= 45°;∠ hк= 135°.
Ответ: 135° и 45°.
5) Работа с определением смежных углов: (2 б)
6) Найдите ошибки в определениях: (2b)
Пройти тест №1
Задача номер 2
1) Постройте 2 смежных угла так, чтобы их общая сторона проходила через точку С, а сторона одного из углов совпадала с лучом АВ. (2б)
2). Практическая работа по выявлению свойств смежных углов: (5б)
Прогресс
1. Построить угол примыкающий угол a , если а : острый, прямой, тупой.
2. Измерьте углы.
3. Введите данные измерений в таблицу.
4. Найдите отношение между величинами углов и а также.
5. Сделайте вывод о свойстве смежных углов.
Пройти тест №2
Задание №3
Розыгрыш нерасширенный∠ АОВ и назовите лучи, являющиеся сторонами этого угла.
Тяговая балка O, являющаяся продолжением балки OA, и балка OD, являющаяся продолжением балки OB.
Запиши в тетрадь: углы∠ АОБ и ∠ СОД называются вертикальными. (3б)
Выучить и записать в тетрадь: (4б)
Определение: Углы, стороны одного из которых являются дополнительными лучами другого, называются вертикальными углами.
1 и
RaysOFandOA, OC и OE — попарно дополнительные лучи.
Теорема: Вертикальные углы равны.
Доказательство.
Вертикальные углы образуются при пересечении двух прямых. Пусть прямые a и b пересекаются в точке O.∠ 1 и ∠ 2 — вертикальные углы.
∠ Развернутые средства AOC ∠ АОС= 180°. Однако∠ 1+ ∠ 2= ∠ AOC, т.е.
∠ 3+ ∠ 1= 180°, отсюда имеем:
∠ 1= 180 — ∠ 3. (1)
(1)
У нас тоже есть такое∠ DOV= 180°, следовательно∠ 2+ ∠ 3= 180° или ∠ 2= 180°- ∠ 3. (2)
Так как в равенствах (1) и (2) прямые части равны, то∠ 1= ∠ 2.
Теорема доказана.
5). Работа с определением вертикальных углов: (2б)
6) Найдите ошибку в определении: (2б).
Пройти тест №3
Задание № 4
1) Практикум по выяснению свойств вертикальных углов: (5б)
Прогресс:
1. Построить угол β вертикальный угол α , если α :
острый, прямой, тупой.
2. Измерьте углы.
3. Занести данные измерений в таблицу
4. Найти зависимость между значениями углов α и β.
5. Сделайте вывод о свойстве вертикальных углов.
2) Доказательство свойств смежных и вертикальных углов. (3б)
2) Рассмотрим образец решения ада.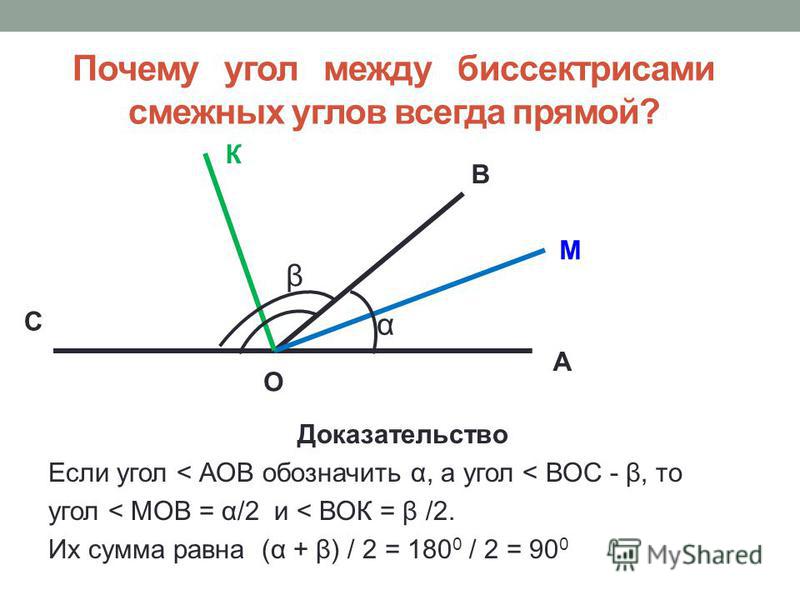
Задача. Прямые AB и CD пересекаются в точке O так, что∠ АОП = 35°. Найдите углы АОС и ВОС.
Решение:
1) Углы AOD и AOC смежные, значит∠ ВОС= 180° — 35° = 145°.
2) Углы AOC и BOC тоже смежные, значит∠ ВОС= 180° — 145° = 35°.
Средства, ∠ ВОС = ∠ AOD = 35°, и эти углы вертикальны. Вопрос: Верно ли, что все вертикальные углы равны?
3) Решение задач по готовым чертежам: (3б)
1. Найти углы AOB, AOD, COD.
3) Найдите углы BOC, FOA.: (3b)
3. Найдите смежный и вертикальный углы на рисунке. Пусть известны значения двух углов, отмеченных на чертеже, 28? и 90?. Можно ли найти значения остальных углов без проведения измерений (2б)
Пройти тест №4
Номер задачи 5
Проверьте свои знания, выполнив проверочную работу №1
Задание № 6
1) Докажите самостоятельно свойства вертикальных углов и запишите эти доказательства в тетрадь. (3б)
(3б)
Учащиеся самостоятельно, используя свойства вертикальных и смежных углов, должны обосновать тот факт, что если при пересечении двух прямых один из образовавшихся углов прямой, то и остальные углы прямые.
2) Решить две задачи на выбор:
1. Градусные меры смежных углов относятся как 7:2. Найдите эти углы. (2б)
2. Один из углов, образованных при пересечении двух прямых, в 11 раз меньше другого. Найдите каждый из углов. (3b)
3. Найдите смежные углы, если их разность и их сумма связаны соотношением 2:9. (3b)
Задача № 7
Молодец! Можно переходить к тестовой работе №2.
Проверочная работа №1.
Определиться с выбором любого из вариантов (10б)
Вариант 1
Г)
Родственные
д) Нарисуйте (на глаз) угол 30° и
е) Какие вертикальные углы?
Два угла называются вертикальными, если углы равны.
г) Из точки А провести две линии, перпендикулярные линии а
Можно провести только одну прямую линию.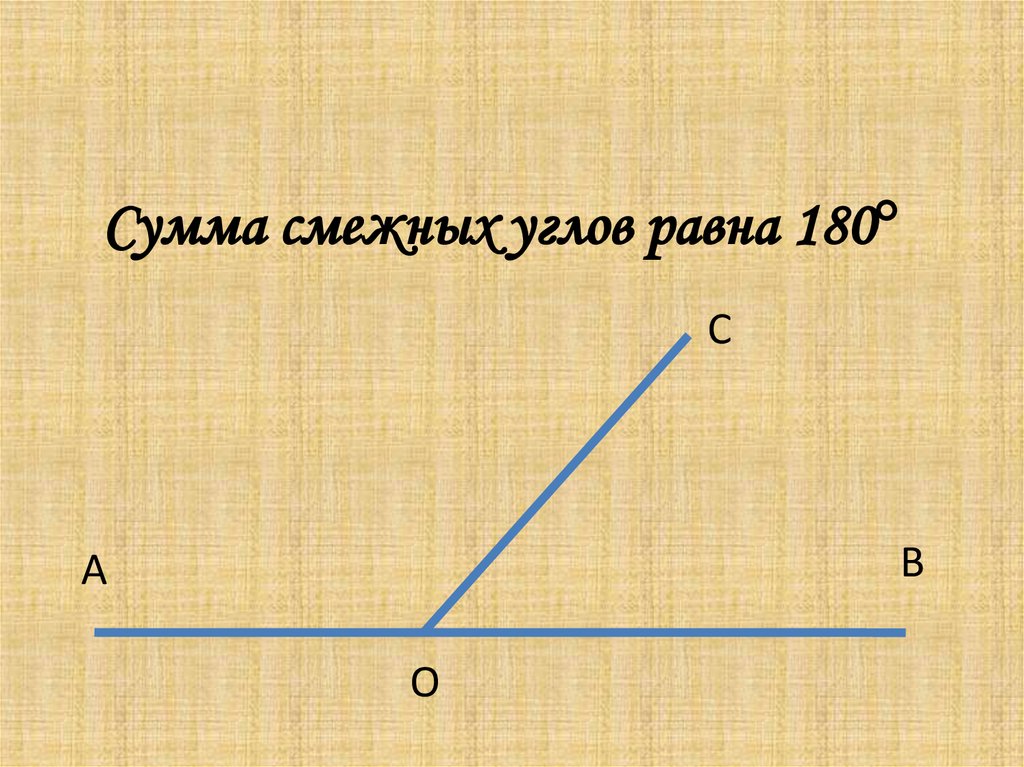
Вариант 2
1. Студент, отвечая на вопросы преподавателя, давал соответствующие ответы. Проверьте их правильность, отметив в третьем столбце слова «ДА», «НЕТ», «НЕ ЗНАЮ». Если «НЕТ», запишите туда правильный ответ или допишите недостающий.
D)
Нет. Они вертикальные
E) Какие прямые называются перпендикулярными?
Две прямые называются перпендикулярными, если они пересекаются под прямым углом.
Ж) Начертите вертикальные углы так, чтобы их стороны были перпендикулярными линиями.
2. Назовите вертикальные углы на этом рисунке.
Итого: 10 баллов
«5» -10 баллов;
«4» -8-9 баллов;
«3» -5-7 баллов.
Проверочная работа № 2.
Выберите любой вариант
Вариант I
Найдите смежные углы, если их разность и их сумма относятся как 2:9. (4b)
Найдите все нерасширенные углы, образованные при пересечении двух прямых, если один из них на 240° меньше суммы двух других. (6б)
(6б)
Вариант II
1) Найдите смежные углы, если их разность и их сумма связаны соотношением 5:8(4b)
2) Найдите все неразвернутые углы, образованные при пересечении двух прямых, если одна из них на 60° больше суммы двух других. (6b)
Итого: 10 баллов
«5» -10 баллов;
«4» -8-9 баллов;
«3» -5-7 баллов.
Углы смежные по вертикали. Н.Никитин Геометрия
Геометрия – очень многогранная наука. Развивает логику, воображение и сообразительность. Конечно, из-за своей сложности и огромного количества теорем и аксиом она не всегда нравится школьникам. Кроме того, возникает необходимость постоянно доказывать свои выводы с использованием общепринятых норм и правил.
Смежные и вертикальные углы являются неотъемлемой частью геометрии. Наверняка многие школьники просто обожают их по той причине, что их свойства понятны и легко доказуемы.
Формирование углов
Любой угол образуется пересечением двух прямых или проведением двух лучей из одной точки.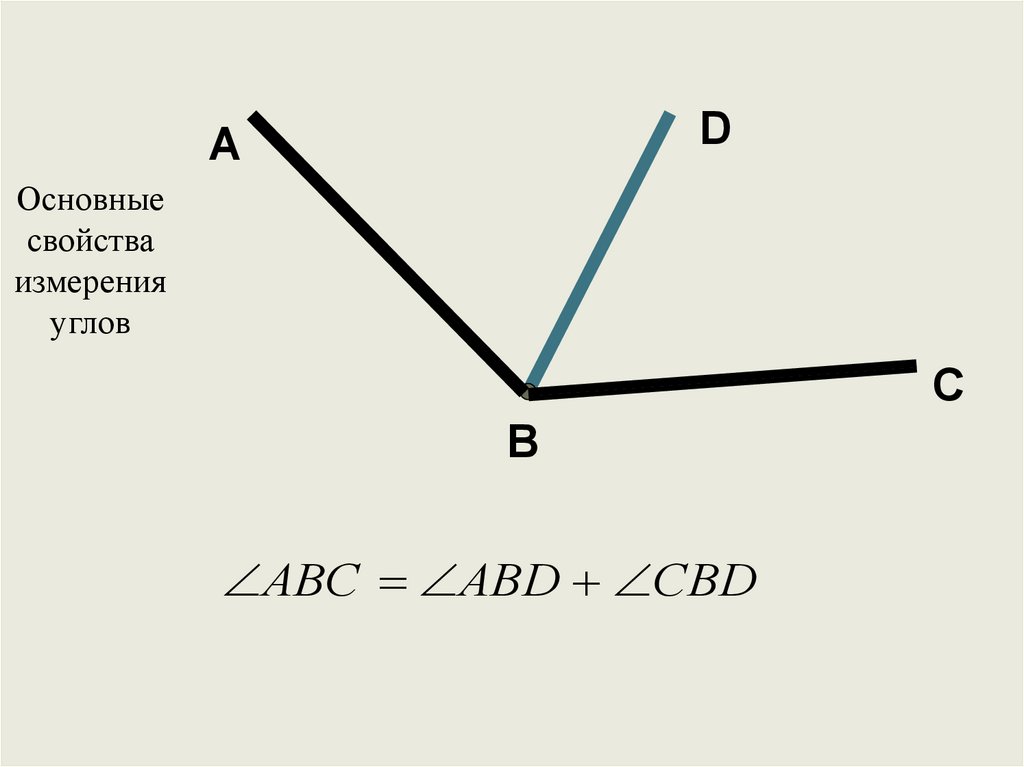 Их можно назвать как одной буквой, так и тремя, которые последовательно обозначают точки построения угла.
Их можно назвать как одной буквой, так и тремя, которые последовательно обозначают точки построения угла.
Углы измеряются в градусах и могут (в зависимости от их значения) называться по-разному. Итак, есть прямой угол, острый, тупой и развернутый. Каждое из названий соответствует определенной градусной мере или ее интервалу.
Острый угол — это угол, градусная мера которого не превышает 90 градусов.
Тупой угол — это угол больше 90 градусов.
Угол называется прямым, если его градусная мера равна 90.
В случае, когда он образован одной непрерывной прямой, а его градусная мера равна 180, он называется развернутым.
Углы, имеющие общую сторону, вторая сторона которых продолжает друг друга, называются смежными. Они могут быть как острыми, так и тупыми. Пересечение прямой образует смежные углы. Их свойства следующие:
- Сумма таких углов будет равна 180 градусам (есть теорема, доказывающая это). Поэтому одно из них легко вычислить, зная другое.

- Из первого пункта следует, что смежные углы не могут быть образованы двумя тупыми или двумя острыми углами.
Благодаря этим свойствам всегда можно вычислить градусную меру угла по значению другого угла или, по крайней мере, отношению между ними.
Уголки вертикальные
Углы, стороны которых являются продолжениями друг друга, называются вертикальными. В качестве такой пары может выступать любая их разновидность. Вертикальные углы всегда равны друг другу.
Образуются при пересечении линий. Вместе с ними всегда присутствуют смежные углы. Угол может быть как смежным для одного, так и вертикальным для другого.
При пересечении произвольной линии также учитываются еще несколько видов углов. Такая линия называется секущей, и она образует соответствующие, односторонний и перекрестно лежащие углы. Они равны друг другу. Их можно рассматривать в свете свойств, которыми обладают вертикальные и смежные углы.
Итак, тема углов кажется достаточно простой и понятной.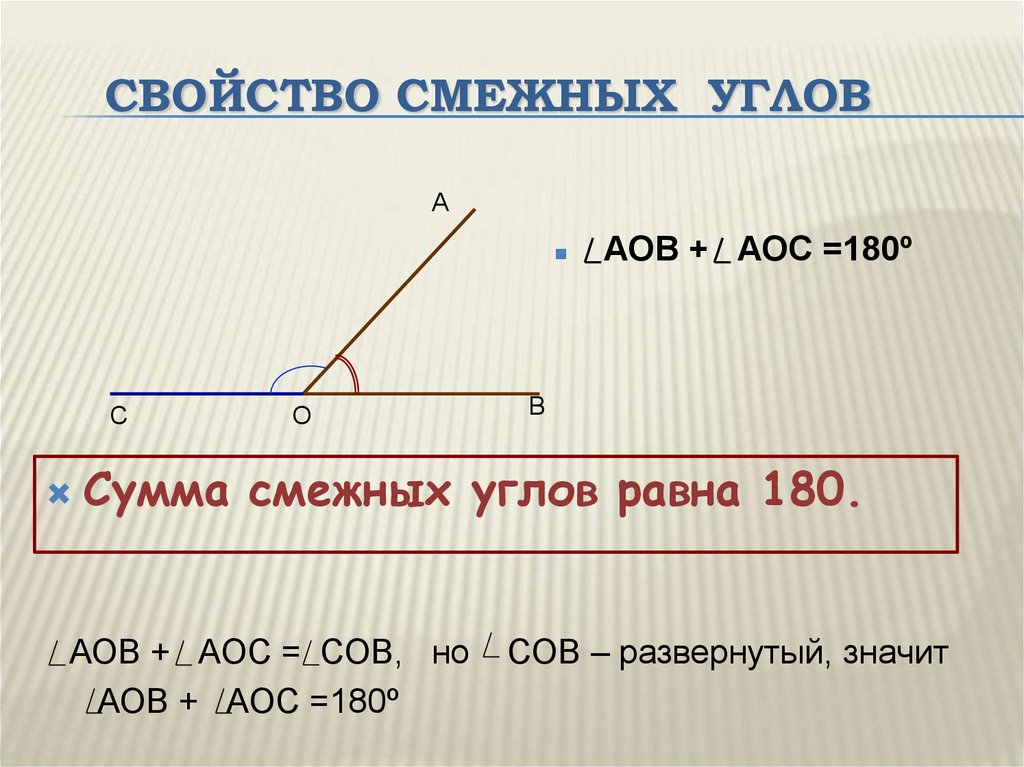 Все их свойства легко запомнить и доказать. Решать задачи несложно, если углы соответствуют числовому значению. Уже дальше, когда начнется изучение sin и cos, вам придется запоминать множество сложных формул, их выводы и следствия. До тех пор вы можете просто наслаждаться легкими головоломками, в которых вам нужно найти соседние углы.
Все их свойства легко запомнить и доказать. Решать задачи несложно, если углы соответствуют числовому значению. Уже дальше, когда начнется изучение sin и cos, вам придется запоминать множество сложных формул, их выводы и следствия. До тех пор вы можете просто наслаждаться легкими головоломками, в которых вам нужно найти соседние углы.
Два угла называются смежными, если они имеют одну общую сторону, а другие стороны этих углов являются дополнительными лучами. На рисунке 20 углы AOB и BOC смежные.
Сумма смежных углов равна 180°
Теорема 1. Сумма смежных углов равна 180°.
Доказательство. Луч ОВ (см. рис. 1) проходит между сторонами развернутого угла. Вот почему ∠ AOB + ∠ BOC = 180° .
Из теоремы 1 следует, что если два угла равны, то равны и смежные с ними углы.
Вертикальные углы равны
Два угла называются вертикальными, если стороны одного угла являются дополнительными лучами сторон другого. Углы AOB и COD, BOD и AOC, образованные при пересечении двух прямых, вертикальны (рис.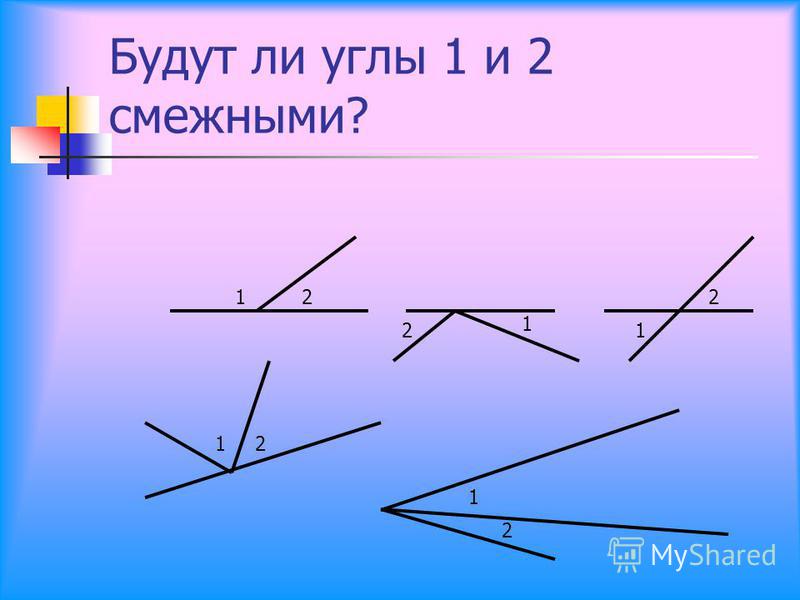 2).
2).
Теорема 2. Вертикальные углы равны.
Доказательство. Рассмотрим вертикальные углы AOB и COD (см. рис. 2). Угол BOD примыкает к каждому из углов AOB и COD. По теореме 1 ∠ AOB + ∠ BOD = 180°, ∠ COD + ∠ BOD = 180°.
Отсюда заключаем, что ∠ AOB = ∠ COD.
Следствие 1. Угол, смежный с прямым углом, является прямым углом.
Рассмотрим две пересекающиеся прямые AC и BD (рис. 3). Они образуют четыре угла. Если один из них прямой (угол 1 на рис. 3), то и остальные углы тоже прямые (углы 1 и 2, 1 и 4 смежные, углы 1 и 3 вертикальные). В этом случае говорят, что эти прямые пересекаются под прямым углом и называются перпендикулярными (или взаимно перпендикулярными). Перпендикулярность прямых AC и BD обозначается следующим образом: AC ⊥ BD.
Биссектриса отрезка — это прямая, перпендикулярная этому отрезку и проходящая через его середину.
AN — перпендикуляр к прямой
Рассмотрим прямую а и не лежащую на ней точку А (рис. 4). Соедините точку А отрезком с точкой Н прямой линией а. Отрезок AH называется перпендикуляром, проведенным из точки A к прямой a, если прямые AN и a перпендикулярны. Точка H называется основанием перпендикуляра.
4). Соедините точку А отрезком с точкой Н прямой линией а. Отрезок AH называется перпендикуляром, проведенным из точки A к прямой a, если прямые AN и a перпендикулярны. Точка H называется основанием перпендикуляра.
Чертежный квадрат
Верна следующая теорема.
Теорема 3. Из любой точки, не лежащей на прямой, можно провести перпендикуляр к этой прямой, и притом только один.
Для проведения перпендикуляра из точки к прямой на чертеже используется чертёжный угольник (рис. 5).
Комментарий. Формулировка теоремы обычно состоит из двух частей. Одна часть говорит о том, что дано. Эта часть называется условием теоремы. Другая часть говорит о том, что нужно доказать. Эта часть называется заключением теоремы. Например, условие теоремы 2 — вертикальные углы; вывод — эти углы равны.
Любую теорему можно подробно выразить словами так, что ее условие будет начинаться со слова «если», а заключение со слова «тогда». Например, теорему 2 можно подробно сформулировать так: «Если два угла вертикальны, то они равны».
Пример 1 Один из смежных углов равен 44°. Чему равно другое?
Раствор. Обозначим градусную меру другого угла через x, тогда согласно теореме 1.
44° + x = 180°.
Решая полученное уравнение, находим, что х = 136°. Следовательно, второй угол равен 136°.
Пример 2 Пусть угол ХПК на рисунке 21 равен 45°. Что такое углы АОВ и АОС?
Раствор. Углы COD и AOB вертикальны, поэтому по теореме 1.2 они равны, т. е. ∠ AOB = 45°. Угол AOC примыкает к углу COD, следовательно, по теореме 1
∠ AOC = 180° — ∠ COD = 180° — 45° = 135°.
Пример 3 Найдите смежные углы, если один из них в 3 раза больше другого.
Раствор. Обозначим градусную меру меньшего угла через x. Тогда градусная мера большего угла будет Zx. Так как сумма смежных углов равна 180° (теорема 1), то x + 3x = 180°, откуда x = 45°.
Значит, смежные углы равны 45° и 135°.
Пример 4 Сумма двух вертикальных углов равна 100°.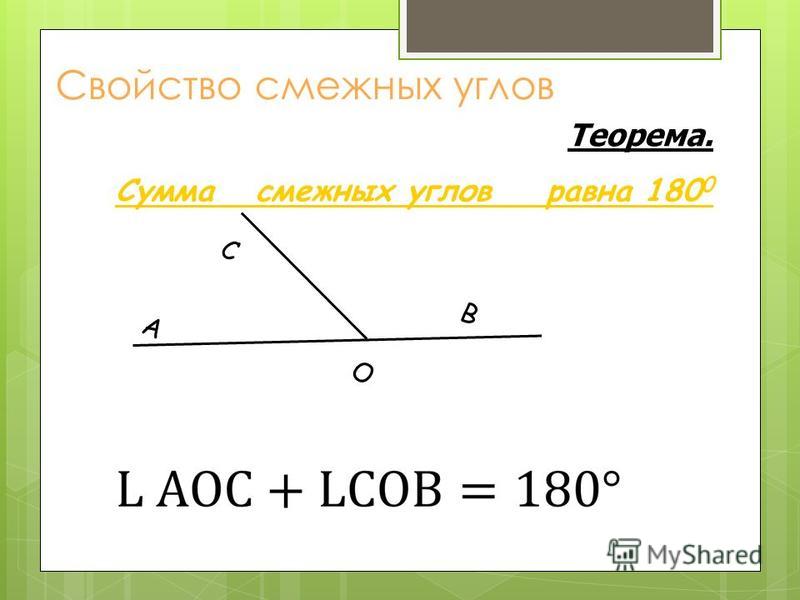 Найдите значение каждого из четырех углов.
Найдите значение каждого из четырех углов.
Решение. Пусть цифра 2 соответствует условию задачи. Вертикальные углы COD и AOB равны (теорема 2), а значит, равны и их градусные меры. Следовательно, ∠ COD = ∠ AOB = 50° (их сумма по условию равна 100°). Угол BOD (он же угол AOC) примыкает к углу COD, а значит, по теореме 1
∠ BOD = ∠ AOC = 180° — 50° = 130°.
Смежные углы — два угла, у которых одна сторона общая, а два других являются продолжением друг друга.
Сумма смежных углов равна 180°
Вертикальные углы — это два угла, в которых стороны одного угла являются продолжением сторон другого.
Вертикальные углы равны.
2. Признаки равенства треугольников:
I признак : Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны .
II признак : Если стороны и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.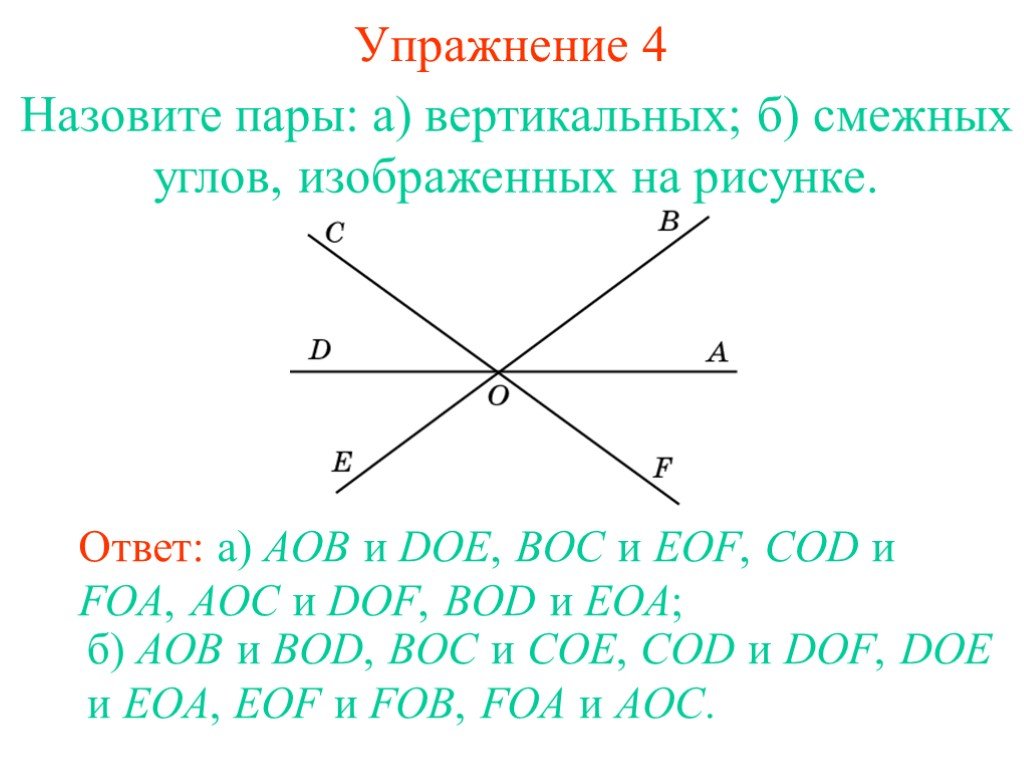
III признак : Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны
3. Признаки параллельности двух прямых: односторонние углы, лежащие накрест и соответствующие:
Две линии на плоскости называются параллельно , если они не пересекаются.
Уголки крестообразно лежащие: 3 и 5, 4 и 6;
Односторонние углы: 4 и 5, 3 и 6; рис. Страница55
Соответствующие углы: 1 и 5, 4 и 8, 2 и 6, 3 и 7;
Теорема : Если при пересечении двух прямых секущей лежащие углы равны, то прямые параллельны.
Теорема : Если при пересечении двух прямых секущей соответствующие углы равны, то прямые параллельны.
Теорема : Если при пересечении двух прямых секущей сумма односторонних углов равна 180°, то прямые параллельны.
Теорема : если две параллельные прямые пересекаются секущей, то лежащие накрест углы равны
Теорема : если две параллельные прямые пересекаются секущей, то соответствующие углы равны
Теорема : если две параллельные прямые пересекаются секущей, то сумма односторонних углов равна 180°
4. Сумма углов треугольника:
Сумма углов треугольника:
Сумма углов треугольника равна 180°
5. Свойства равнобедренного треугольника:
Теорема: В равнобедренном треугольнике углы при основании равны.
Теорема: В равнобедренном треугольнике биссектриса, проведенная к основанию, есть медиана, а высота (медиана наоборот), (биссектриса делит угол пополам, медиана делит сторону пополам, высота образует угол 90° )
Признак: Если два угла треугольника равны, то треугольник равнобедренный.
6. Прямоугольный треугольник:
Прямоугольный треугольник – это треугольник, в котором один угол прямой (то есть равен 90 градусам)
В прямоугольном треугольнике гипотенуза длиннее катета
1. Сумма двух острых углов прямоугольного треугольника равна 90°
2. Катет прямоугольного треугольника, лежащий против угла 30°, равен половине гипотенузы 9
Сумма углов четырехугольника равна 2 π = 360°.
Четырехугольник можно вписать в окружность тогда и только тогда, когда сумма противолежащих ему углов равна 180° равны двум углам другого, то такие треугольники подобны
II признак : если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы между этими сторонами равны, то такие треугольники подобны.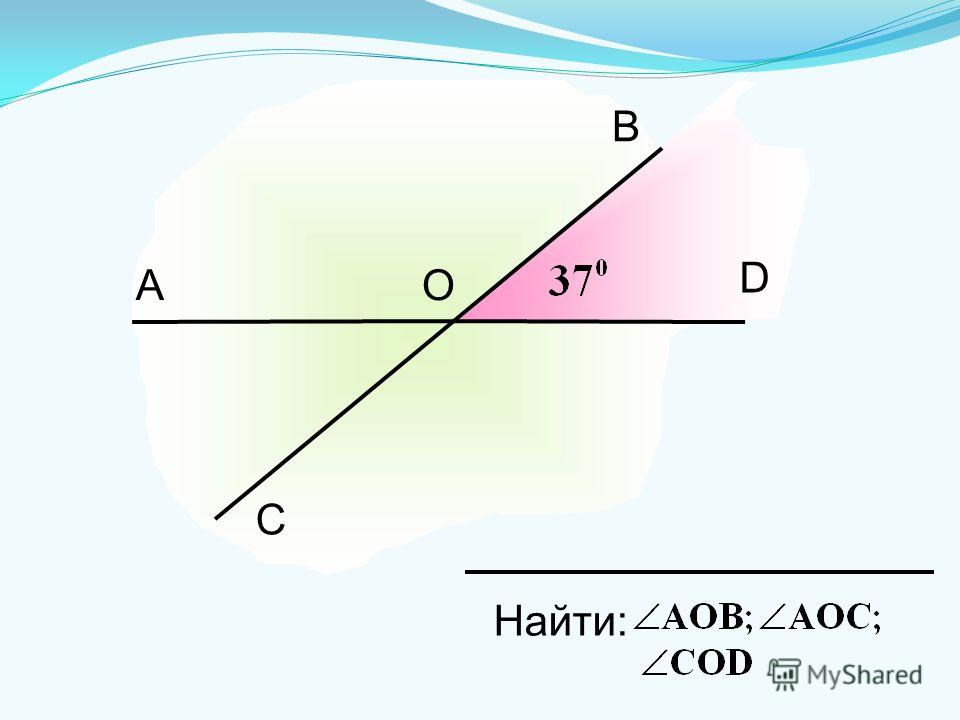
III признак : если три стороны одного треугольника пропорциональны трем сторонам другого, то такие треугольники подобны
11. Формулы:
· Теорема Пифагора: a 2 +b 2 =c 2
· Теорема греха:
· COS Теорема:
· 3 Треугольная площадь. равностороннего треугольника:
· Площадь параллелограмма: S = AH
· Площадь квадратной площадь: S = A2
· Область трапеции:
· SAME:
· .
· Равносторонний треугольник. Высота: h=
· Тригонометрическая единица: sin 2 a+cos 2 a=1
· Средняя линия треугольника: S=
· Средняя линия трапеции :MK=
© 2015-2019 сайт
Все права принадлежат их авторам. Этот сайт не претендует на авторство, а предоставляет бесплатное использование.
Дата создания страницы: 12.12.2017
ГЛАВА I.
ОСНОВНЫЕ ПОНЯТИЯ.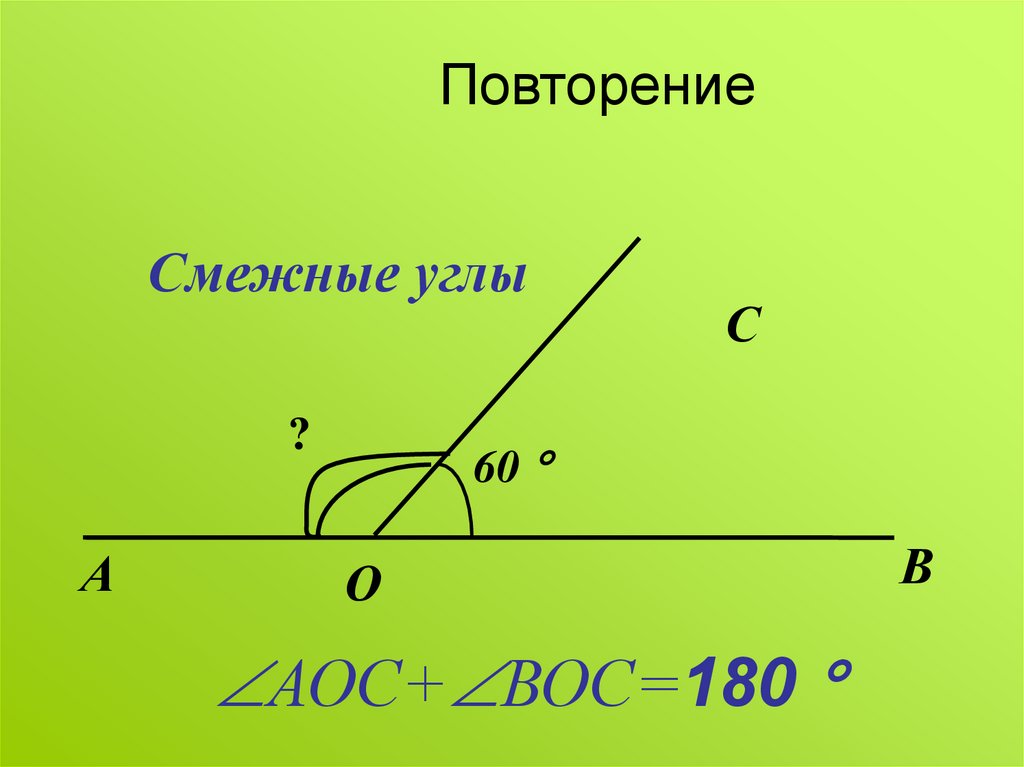
§одиннадцать. СМЕЖНЫЕ И ВЕРТИКАЛЬНЫЕ УГЛЫ.
1. Смежные углы.
Если продолжить сторону некоторого угла за его вершину, то получим два угла (рис. 72): / Солнце и / СВД, у которого одна сторона ВС общая, а две другие АВ и БД образуют прямую линию.
Два угла, у которых одна сторона общая, а две другие образуют прямую, называются смежными углами.
Смежные углы можно получить и таким образом: если провести из какой-либо точки прямой (не лежащей на данной прямой) луч, то получим смежные углы.
Например, / АПД и / FDВ — углы смежные (рис. 73).
Смежные углы могут иметь самые разные положения (рис. 74).
Сумма смежных углов составляет прямой угол, поэтому сумма двух смежных углов равна 2 d.
Следовательно, прямой угол можно определить как угол, равный прилежащему к нему углу.
Зная значение одного из смежных углов, мы можем найти значение другого смежного угла.
Например, если один из смежных углов равен 3/5 d , то второй угол будет равен:
2 d — 3/5 д = 1 2 / 5 д .
2. Уголки вертикальные.
Если мы продолжим стороны угла за его вершину, мы получим вертикальные углы. На чертеже 75 углы EOF и AOC вертикальны; углы AOE и COF также вертикальны.
Два угла называются вертикальными, если стороны одного угла являются продолжениями сторон другого угла.
Лет / 1 = 7/8 д (рис. 76). Рядом с ним / 2 будет равно 2 d — 7/8 d , т.е. 1 1/8 d .
Таким же образом можно вычислить, чему равны / 3 и / 4.
/ 3 = 2 d — 1 1/8 d = 7/8 d ; / 4 = 2 д — 7/8 д = 1 1/8 д (рис. 77).
Видим, что / 1 = / 3 и / 2 = / 4.
Можно решить еще несколько таких же задач и каждый раз получать один и тот же результат: вертикальные углы равны между собой.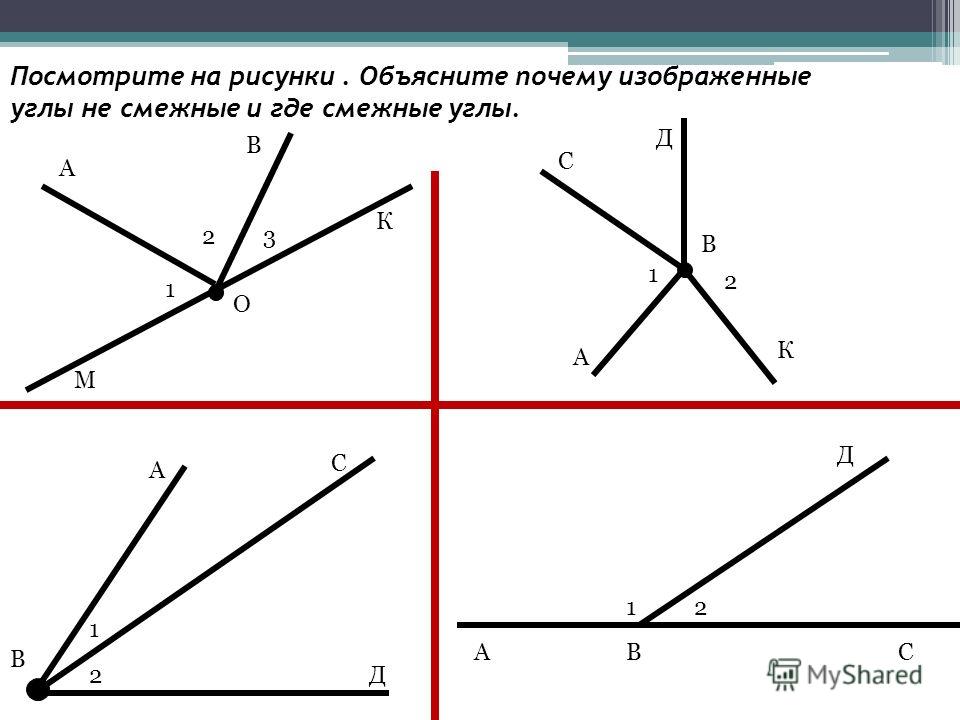
Однако для того, чтобы убедиться, что вертикальные углы всегда равны между собой, недостаточно рассматривать отдельные числовые примеры, так как выводы, сделанные на частных примерах, иногда могут быть ошибочными.
Необходимо проверить справедливость свойства вертикальных углов рассуждениями, доказательством.
Доказательство можно провести следующим образом (рис. 78):
/ а + / с = 2 d ;
/ б + / с = 2 d ;
(так как сумма смежных углов равна 2 d ).
/ а + / с = / б + / c
(поскольку левая часть этого равенства равна 2 d , а его правая часть также равна 2 d ).
В это равенство входит один и тот же угол С .
Если из равных значений вычесть поровну, то останется поровну. Результат будет: / а = / b , т.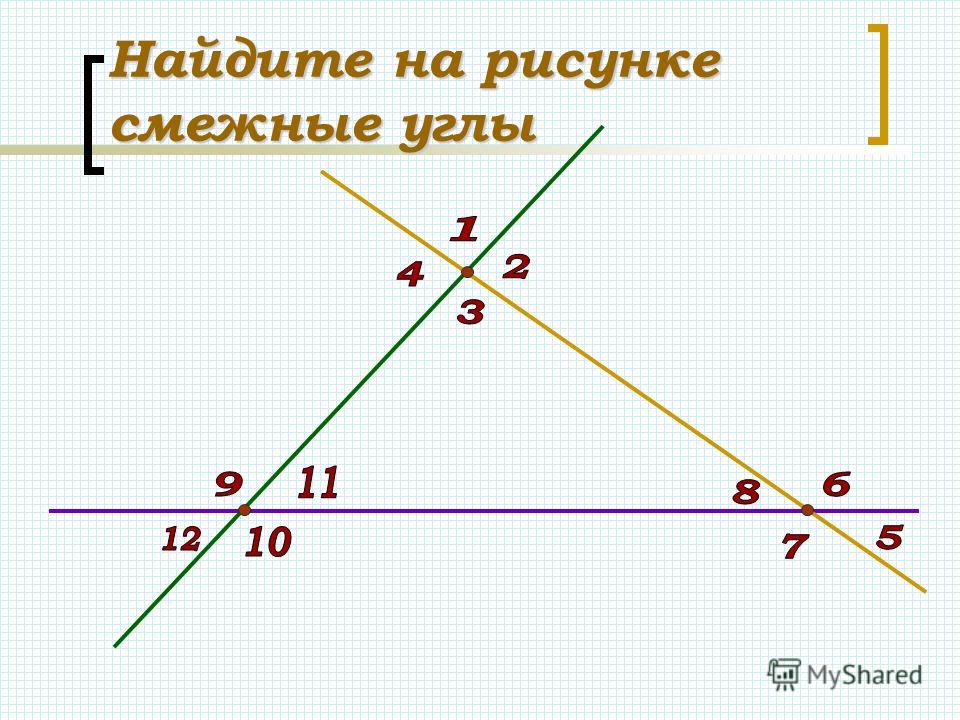 е. вертикальные углы равны между собой.
е. вертикальные углы равны между собой.
При рассмотрении вопроса о вертикальных углах мы сначала объяснили, какие углы называются вертикальными, т. е. дали определение вертикальных углов.
Затем мы сделали суждение (утверждение) о равенстве вертикальных углов и убедились в справедливости этого суждения доказательством. Такие суждения, справедливость которых необходимо доказать, называются теоремами . Таким образом, в этом разделе мы дали определение вертикальных углов, а также сформулировали и доказали теорему об их свойстве.
В дальнейшем при изучении геометрии нам постоянно придется встречаться с определениями и доказательствами теорем.
3. Сумма углов, имеющих общую вершину.
На чертеже 79 / 1, / 2, / 3 и / 4 расположены по одну сторону от прямой и имеют общую вершину на этой прямой. В сумме эти углы составляют прямой угол, т.е.
/ 1+ / 2+ / 3+ / 4 = 2 д .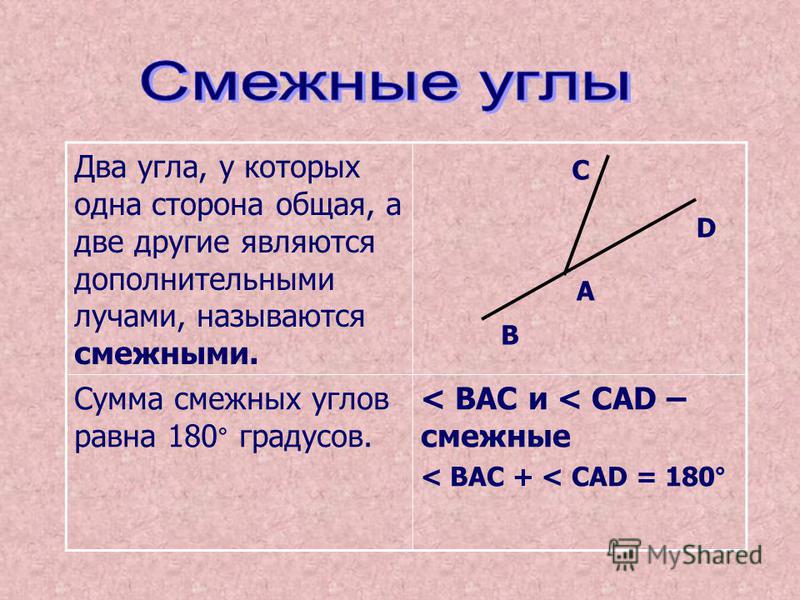


 Сколько таких уголков можно построить?
Сколько таких уголков можно построить?