Раздел недели: Скоропись физического, математического, химического и, в целом, научного текста, математические обозначения. Математический, Физический алфавит, Научный алфавит. | |||||||
| Поиск на сайте DPVA Поставщики оборудования Полезные ссылки О проекте Обратная связь Ответы на вопросы. Оглавление Таблицы DPVA.ru — Инженерный Справочник | Адрес этой страницы (вложенность) в справочнике dpva.ru: главная страница / / Техническая информация/ / Математический справочник / / Таблицы численных значений. Поделиться:
| ||||||
Если Вы не обнаружили себя в списке поставщиков, заметили ошибку, или у Вас есть дополнительные численные данные для коллег по теме, сообщите , пожалуйста. | |||||||
Коды баннеров проекта DPVA.ru Консультации и техническая | Проект является некоммерческим. Информация, представленная на сайте, не является официальной и предоставлена только в целях ознакомления. Владельцы сайта www.dpva.ru не несут никакой ответственности за риски, связанные с использованием информации, полученной с этого интернет-ресурса. | ||||||
|
|
|
|
Тригонометрические функции
Тригонометрические функции — это функции, связанные с углом. Существует шесть тригонометрических функций: синус, косинус, тангенс и их обратные косеканс, секанс и котангенс соответственно. Синус, косинус и тангенс являются наиболее широко используемыми тригонометрическими функциями. Их обратные числа, хотя и используются, менее распространены в современной математике. Тригонометрические функции также называют круговыми функциями.
Существует шесть тригонометрических функций: синус, косинус, тангенс и их обратные косеканс, секанс и котангенс соответственно. Синус, косинус и тангенс являются наиболее широко используемыми тригонометрическими функциями. Их обратные числа, хотя и используются, менее распространены в современной математике. Тригонометрические функции также называют круговыми функциями.
6 тригонометрических функций
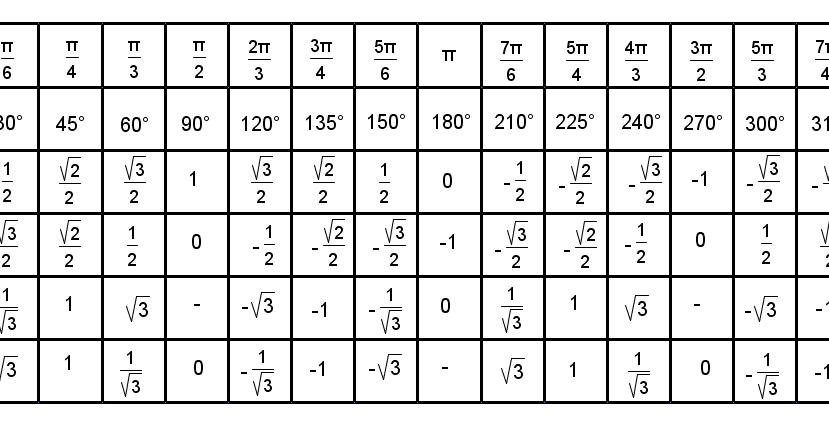
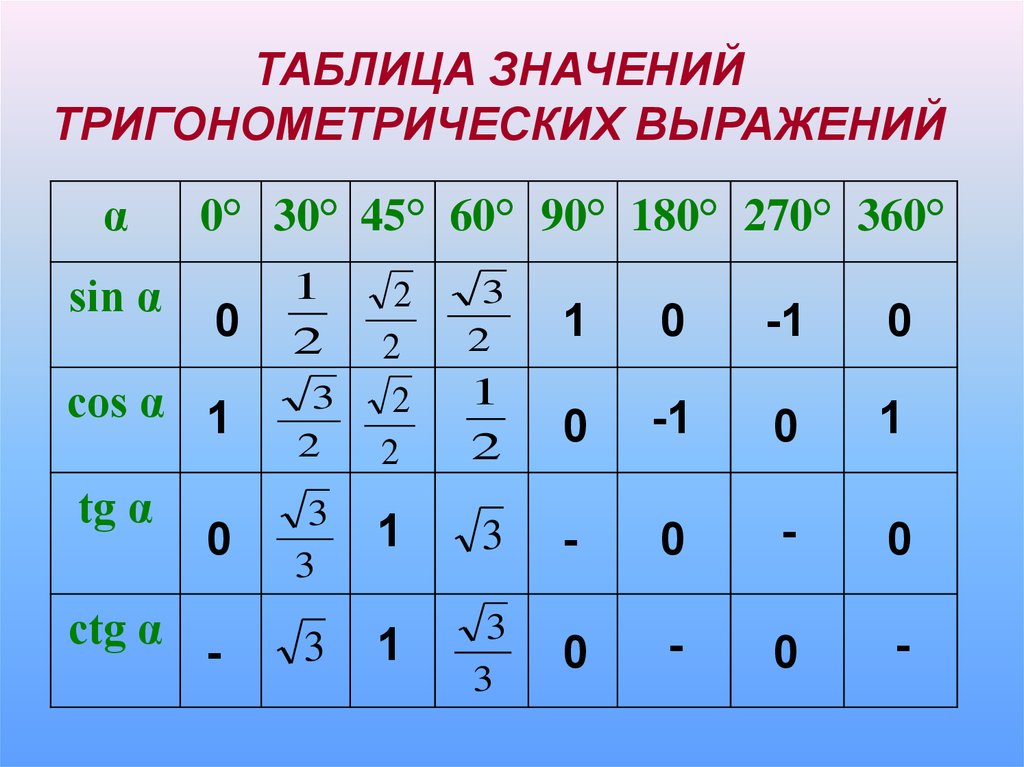
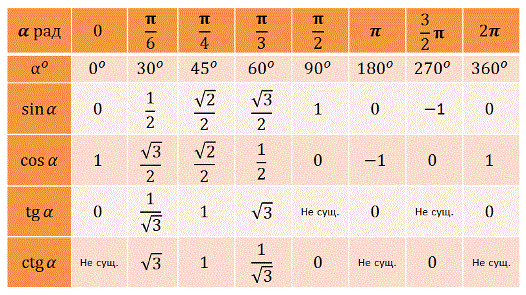
В таблице ниже показаны шесть значений тригонометрических функций для заданных углов в градусах и радианах.
| θ | 0° / 0 | 30° / | 45° / | 60° / | 90° / | 180° / | 270° / | 360° / |
|---|---|---|---|---|---|---|---|---|
| sin(θ) | 0 | 1 | 0 | -1 | 0 | |||
| соз(θ) | 1 | 0 | -1 | 0 | 1 | |||
| тан(θ) | 0 | 1 | Не определено | 0 | Не определено | 0 | ||
| csc(θ) | Не определено | 2 | 1 | Не определено | -1 | Не определено | ||
| сек(θ) | 1 | 2 | Не определено | -1 | Не определено | 1 | ||
| детская кроватка(θ) | Не определено | 1 | 0 | Не определено | 0 | Не определено |
Хотя таблица не включает кратность каждого угла в каждом квадранте, мы можем использовать таблицу, чтобы найти значения других углов; значения одинаковы для каждого соответствующего угла с учетом знака соответствующего квадранта.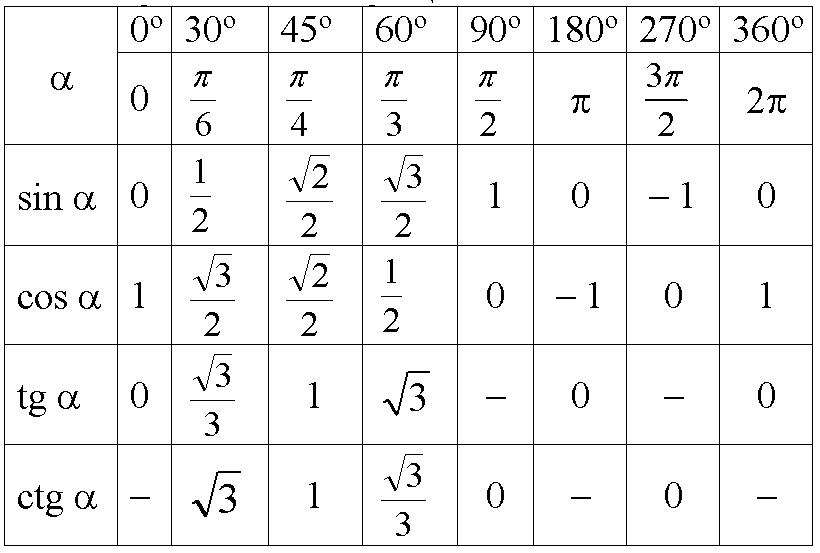 Например, значение косинуса для 30° или в первом квадранте равно . Поскольку значения косинуса в квадрантах II и III отрицательны, значение косинуса для соответствующих углов в квадрантах II и III (150° и 210°) равно . Точно так же, поскольку значение cos(330°) в квадранте IV положительное, оно имеет то же значение, что и cos(30°). Таким же образом можно найти значения других тригонометрических функций. Обратитесь к разделу опорных углов ниже для получения более подробной информации, а также к таблице знаков шести тригонометрических функций в каждом квадранте.
Например, значение косинуса для 30° или в первом квадранте равно . Поскольку значения косинуса в квадрантах II и III отрицательны, значение косинуса для соответствующих углов в квадрантах II и III (150° и 210°) равно . Точно так же, поскольку значение cos(330°) в квадранте IV положительное, оно имеет то же значение, что и cos(30°). Таким же образом можно найти значения других тригонометрических функций. Обратитесь к разделу опорных углов ниже для получения более подробной информации, а также к таблице знаков шести тригонометрических функций в каждом квадранте.
Определения тригонометрических функций
Обычно тригонометрические функции обсуждаются двумя способами: в терминах прямоугольных треугольников и в терминах единичной окружности. Чаще всего вводится определение тригонометрических функций в виде прямоугольного треугольника, за которым следуют их определения в терминах единичной окружности.
Определение прямоугольного треугольника
Выход тригонометрической функции представляет собой отношение длин двух сторон прямоугольного треугольника.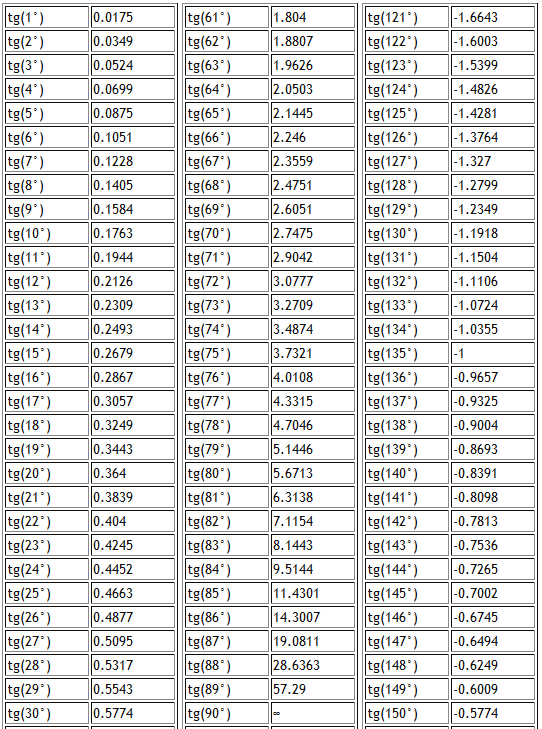 Рассмотрим угол θ как один из углов прямоугольного треугольника. Ниже приведены определения тригонометрических функций. Эти функции часто записываются в сокращенной форме.
Рассмотрим угол θ как один из углов прямоугольного треугольника. Ниже приведены определения тригонометрических функций. Эти функции часто записываются в сокращенной форме.
| синус: | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| косинус: | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| тангенс: | 2 11
Термины, используемые для описания сторон прямоугольного треугольника, — это гипотенуза, прилежащая сторона и противоположная сторона, как показано на рисунке выше.
Обычный метод запоминания вышеупомянутых взаимосвязей — использование мнемонического выражения «soh cah toa». Косеканс, секанс и котангенс являются величинами, обратными синусу, косинусу и тангенсу соответственно. Таким образом, пока мы помним определения синуса, косинуса и тангенса, мы можем взять их обратные значения, чтобы определить определения косеканса, секанса и котангенса. Пример: Найдите значения шести тригонометрических величин для прямоугольного треугольника ниже. Гипотенуза треугольника равна 10, а прилежащая сторона имеет длину 5. Используя теорему Пифагора, находим длину третьей, противоположной, стороны: 5 2 + b 2 = 10 2 25 + B 2 = 100 B 2 = 75 Теперь, когда мы знаем все стороны треугелья со ссылкой на угла, 60 °, мы можем можем подставьте их в тригонометрические функции, как определено выше: Определение единичной окружности Тригонометрические функции также могут быть определены как значения координат на единичной окружности. Учитывая точку (x, y) на единичной окружности, мы можем сформировать прямоугольный треугольник, как показано на рисунке. В таком треугольнике гипотенуза — это радиус единичной окружности, или 1. θ — это угол, образованный между начальной стороной угла вдоль оси x и конечной стороной угла, образованного вращением луча по часовой стрелке или против часовой стрелки. Конечная сторона угла является гипотенузой прямоугольного треугольника и является радиусом единичной окружности. Поэтому его длина всегда равна 1. Точка, в которой конечная сторона угла пересекает единичную окружность, имеет значение x, равное cos(θ), и значение y, равное sin(θ). Таким образом, на единичной окружности косинус и синус можно определить как: синуса, косинуса и тангенса соответственно и определяются как: Значения тригонометрических функций также могут быть представлены длинами отрезков прямых в координатной плоскости с единичным кругом, как показано на рис. диаграмма ниже. Значения тригонометрических функций для специальных угловЗначения тригонометрических функций можно найти через значения координат пересечений на единичной окружности. Хотя мы можем найти значение любой тригонометрической функции для любого значения θ, есть некоторые углы, которые чаще используются в тригонометрии и их стоит запомнить. Опорные углы Острые углы в первом квадранте можно использовать для определения значений тригонометрических функций углов в других квадрантах. Ниже приведена таблица значений функций синуса, косинуса и тангенса для специальных углов в первом квадранте, называемых опорными углами. Эти углы называются эталонными углами, поскольку мы будем ссылаться на их значения для определения других значений. Это всегда наименьший угол (относительно оси абсцисс), который можно составить из конечной стороны угла. На рисунках ниже показан угол θ и его исходный угол θ’ в квадранте, отличном от первого квадранта.
Если один угол является опорным углом другого, то тригонометрические функции этих двух углов имеют одинаковые значения по модулю, и нам нужно только обратить внимание на их знаки исходя из квадранта, в котором лежит крайняя сторона угла , Например, 30° — это опорный угол 210° со значениями синусов sin(30°)= и sin(210°)=. Мы можем видеть, что значения синуса обоих имеют величину , хотя и имеют разные знаки. Ниже приведена таблица, показывающая знаки 6 тригонометрических функций в каждом квадранте.
Как только мы определили исходный угол, мы можем определить значение тригонометрических функций в любом из других квадрантов, применяя соответствующий знак к их значению для исходного угла. Пример: Используйте эталонные углы, чтобы найти значения cos(150°) и sin(315°). Поскольку 150° находится в квадранте II, исходный угол для 150° равен 180°-150°=30°, где cos(30°)=. Кроме того, поскольку 150 ° находится в квадранте II, косинус отрицателен, тогда cos (150 °) =. Поскольку 315° находится в квадранте IV, исходный угол для 315° равен 360°-315°=45°, где sin(45)°=. Кроме того, поскольку 315 ° находится в квадранте IV, синус отрицательный, тогда sin (315 °) =. Тригонометрические функции являются периодическими функциямиПериодическая функция – это функция f, в которой существует некоторое положительное значение p, такое что f(x+p) = f(x) для всех x в области f, p является наименьшим положительное число, для которого f является периодическим, и называется периодом f. Все 6 тригонометрических функций являются периодическими функциями. Независимо от того, с какой точки мы начинаем на единичной окружности, если мы пройдем расстояние 2π (360 °) по единичной окружности от этой точки, мы вернемся в нашу начальную точку, что указывает на то, что тригонометрическая функция имеет то же значение под углом. Функции синуса, косинуса, косеканса и секанса имеют период 2π. Функции тангенса и котангенса имеют период π. sin(θ+2π) = sin(θ) cos(θ+2π) = cos (θ) csc(θ+2π) = csc (θ) сек(θ+2π) = сек (θ) tan(θ+π) = tan (θ) cot(θ+π) = cot (θ) Пример: Найти и использовать их периоды. Тригонометрические функции четные или нечетныеНечетная функция — это функция, в которой -f(x)=f(-x). Он имеет симметрию относительно начала координат. Четная функция — это функция, в которой f(x)=f(-x), что означает, что отображение графика по оси Y даст тот же график. Из 6 тригонометрических функций синус, тангенс, косеканс и котангенс являются нечетными функциями. Косинус и секанс — четные функции. Поэтому:
Обратные тригонометрические функции Обратные тригонометрические функции являются обратными функциями тригонометрических функций.
Обратные тригонометрические функции также записываются как sin -1 (x), cos -1 (x), tan -1 (x), csc -1 (x) ), сек -1 (x) и раскладушка -1 (x). Пример: Учитывая sin(30°) = 0,5, что такое arcsin(0,5)? arcsin(0.5) = 30° Примечание: это дает результат только в первом квадранте. Если рассматривать другие квадранты, arcsin(0.5) также равен 150°. Кроме того, поскольку арксинус является периодической функцией, для учета всех возможных значений арксинуса нам необходимо учитывать его периодичность. 30°+n×360° или 150°+n×360° , где n — целое число. При использовании других обратных тригонометрических функций также необходимо учитывать их периодичность для определения всех решений. Графики тригонометрических функцийНа рисунке ниже показаны графики нескольких периодов шести тригонометрических функций. Обратитесь к страницам синуса, косинуса и тангенса для подробного объяснения того, как построить график тригонометрических функций, подвергшихся определенным преобразованиям (те же объяснения применимы к косекансу, секансу и котангенсу с небольшими отличиями). Функция котангенса Функция котангенса — тригонометрическая функция, одна из трех обратных функций , которые мы рассматриваем на этих страницах, две другие — это функция косеканса и функция секанса . Обратная функция — это функция, которая является обратной (или мультипликативной обратной ) другой функции (см. Котангенс как отрезок единичной окружности Как и другие тригонометрические функции, котангенс может быть представлен в виде отрезка, связанного с единичной окружностью . На диаграмме показан котангенс угла поворота θ сорока пяти градусов (измерено против часовой стрелки от положительной оси x ). Отрезок линии AF (показан красным) является котангенсом и лежит на линии, касательной к окружности в точке 9. Помните, что функция тангенса может быть определена либо как частное противоположной и смежной, либо как частное функций синуса и косинуса. Если вы еще не вывели этот факт из диаграммы, вы увидите в интерактивной демонстрации, что значение sin ( θ ) приближается к единице и значение cos ( θ ) приближается к нулю , значение кроватки ( θ ) также стремится к нулю.
Очевидно, поскольку функция котангенса есть величина, обратная функции тангенса, ее можно выразить через функцию тангенса следующим образом:
Мы также можем определить функцию котангенса в терминах прямоугольного треугольника. В треугольнике ABC раскладушка ( θ ) = б / а В прямоугольном треугольнике ABC тангенс угла θ является частным , противоположного , и , примыкающего к (т. Поскольку функция котангенса есть , обратная функции тангенса, то котангенс угла θ будет частным смежных и напротив . Это дает нам:
Для тех, кто интересуется такими вещами, мы использовали Microsoft Excel для создания собственной таблицы значений котангенса для углов в диапазоне от ноль градусов (0°) до триста шестьдесят градусов (360°) с шагом в одну десятую градуса. Если вы изучите таблицу, то увидите, что существует значительный диапазон углов, сосредоточенных вокруг 90 531 девяносто градусов 90 532 (90°) и 90 531 270 градусов 90 532 (270°), для которых значение, возвращаемое функцией котангенса, довольно невелика и изменяется относительно медленно. Для углов близких к ноль градусов (0°), сто восемьдесят градусов (180°) или триста шестьдесят градусов (360°) однако значение, возвращаемое функцией секанса, быстро увеличивается. Этого следовало ожидать, так как значение тангенса ( θ ) очень мало для этих углов, поэтому его обратное будет соответственно большим. На самом деле значение, возвращаемое функцией котангенса для угла в ноль градусов, сто восемьдесят градусов или триста шестьдесят градусов, считается равным 9.0531 undefined , так как уравнение кроватка ( θ ) = 1 / тангенс ( θ ) будет включать деление на ноль. График функции котангенса для углов в диапазоне от 0° до 720° Как и функция тангенса, значения функции котангенса будут варьироваться от нуля до бесконечности (или, точнее, от нуля до очень большого неопределенного значения). Поскольку функция котангенса является обратной функцией тангенса, значение котангенса будет неопределенным, если значение тангенса равно нулю, и нулем, если значение тангенса не определено. Как видно из таблицы значений котангенса и графика функции котангенса, значение котангенса отрицательно для всех углов, для которых синус и косинус имеют разный знак (т. е. в квадранте II и квадранте IV ), а положительный для всех углов, для которых синус и косинус имеют один и тот же знак (т. Если вы читали страницы о тангенсах, косекансах и секансах (или, возможно, даже если не читали), вы знаете, что вертикальные красные линии на графике — это асимптоты . Асимптота кривой представляет собой линию, которая по мере того, как расстояние между кривой и линией приближается к нулю, когда значение кривой приближается к бесконечности. В этом случае асимптотами можно считать «пробелы» в графике, где значение ctg ( θ ) не определено. Обратите также внимание на то, что по мере того, как график пересекает асимптоту, значение cot ( θ ) переходит от своего максимального положительного значения к максимальному отрицательному значению (или наоборот). Вы также можете увидеть, как различаются значения по обе стороны от асимптоты, изучив таблицу значений котангенса. График функции котангенса может включать несколько очень больших положительных и отрицательных пиков, так как значение тангенса ( θ ) стремится к нулю. Как и в случае с другими тригонометрическими функциями, которые мы рассмотрели, нам не нужно использовать таблицы для нахождения котангенса угла (или угла, соответствующего заданному значению котангенса), так как любой современный научный калькулятор может сделать это за нас, даже хотя в большинстве калькуляторов нет специальной кнопки для функции котангенса. Введите эти нажатия клавиш, чтобы найти котангенс угла 48°. Поскольку функция котангенса является обратной функцией тангенса, все, что мы здесь сделали, это использовали кнопку функции тангенса на калькуляторе, а затем применили встроенную кнопку функции обратной функции калькулятора (обычно помеченную 9). Калькулятор отображает значение раскладушки (48°) Все идет нормально. Теперь давайте предположим, что вы хотите найти размер острого угла в прямоугольном треугольнике, сначала найдя частное смежного и противоположного (т.е. котангенс угла). Если у вас есть значения длин сторон треугольника, вы можете достаточно легко найти значение котангенса угла. Нахождение угла не так просто, как для трех основных тригонометрических функций, поскольку в большинстве калькуляторов нет специальной кнопки для функция арккотангенса (обратная функция котангенса). К счастью, есть относительно простой способ обойти это. Найдем значение угла θ для прямоугольного треугольника, показанного ниже. Мы хотим найти величину угла θ Для угла θ стороны b и a являются смежными и противоположными соответственно. На самом деле мы можем найти размер угла за одну операцию на калькуляторе Windows. Мы делаем это, используя скобки во введенной последовательности клавиш, чтобы заставить калькулятор сначала найти обратное значение частного соседнего и противоположного (т.е. котангенс угла). Затем мы применяем арктангенс функция к результату. Вот последовательность клавиш для использования: Введите эти нажатия клавиш, чтобы найти размер угла θ Возможно, вы уже поняли, что здесь мы находили тангенс угла, взяв обратную котангенса . Затем мы просто применили к результату функцию арктангенс . Если вы правильно ввели нажатия клавиш, вы должны увидеть экран, подобный показанному ниже. Калькулятор отображает значение угла θ Функция котангенса вместе с другими тригонометрическими функциями может быть представлена в виде бесконечного ряда . Значение, возвращаемое тригонометрической функцией для заданного угла, не может быть вычислено с помощью простой алгебраической формулы. Для большинства углов точное значение можно получить только как сумму бесконечного числа слагаемых, чего, очевидно, достичь невозможно. |

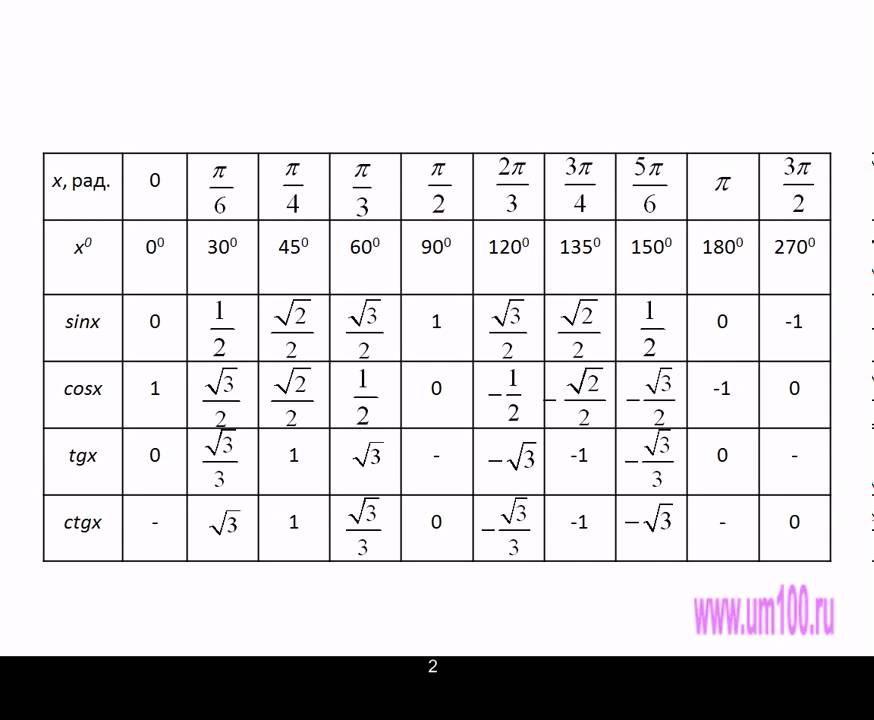
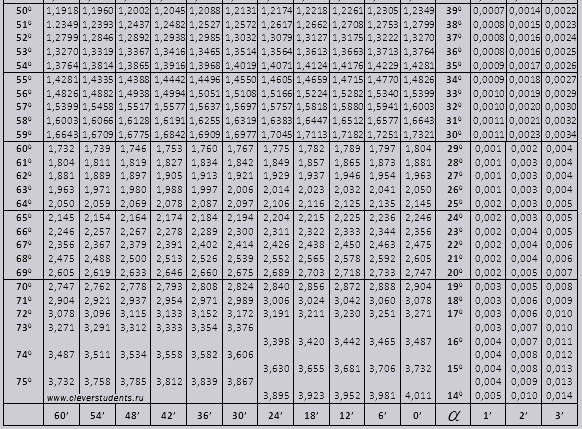
 (Таблица квадратов, кубов, синусов ….) + Таблицы Брадиса / / Углы 0°,30°,45°,60°,90°,180°,270°,360°,(π/6,π/4,π/3,π/2,π,3π/2,2π). Таблица синусов, косинусов, тангенсов и котангенсов 30°,45°,60°,90°,180°,270°,360.
(Таблица квадратов, кубов, синусов ….) + Таблицы Брадиса / / Углы 0°,30°,45°,60°,90°,180°,270°,360°,(π/6,π/4,π/3,π/2,π,3π/2,2π). Таблица синусов, косинусов, тангенсов и котангенсов 30°,45°,60°,90°,180°,270°,360.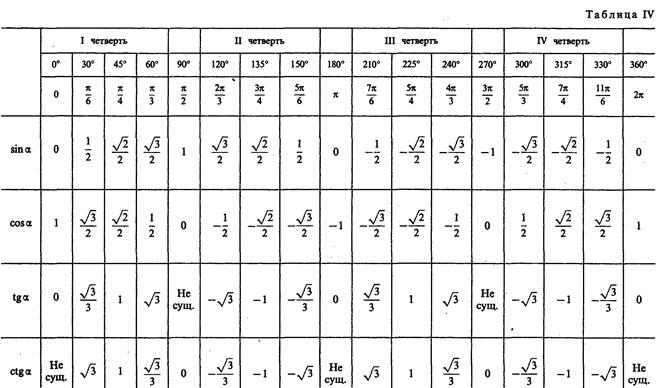 Введите свой запрос:
Введите свой запрос:
 Буквы s, c и t обозначают синус, косинус и тангенс, а o, a и h обозначают противоположное, смежное и гипотенузу.
Буквы s, c и t обозначают синус, косинус и тангенс, а o, a и h обозначают противоположное, смежное и гипотенузу. Единичная окружность — это окружность радиусом 1 с центром в начале координат. Определение тригонометрических функций в виде прямоугольного треугольника допускает углы от 0 ° до 90 ° (0 и в радианах). Использование определений единичного круга позволяет нам расширить область применения тригонометрических функций на все действительные числа. См. рисунок ниже.
Единичная окружность — это окружность радиусом 1 с центром в начале координат. Определение тригонометрических функций в виде прямоугольного треугольника допускает углы от 0 ° до 90 ° (0 и в радианах). Использование определений единичного круга позволяет нам расширить область применения тригонометрических функций на все действительные числа. См. рисунок ниже.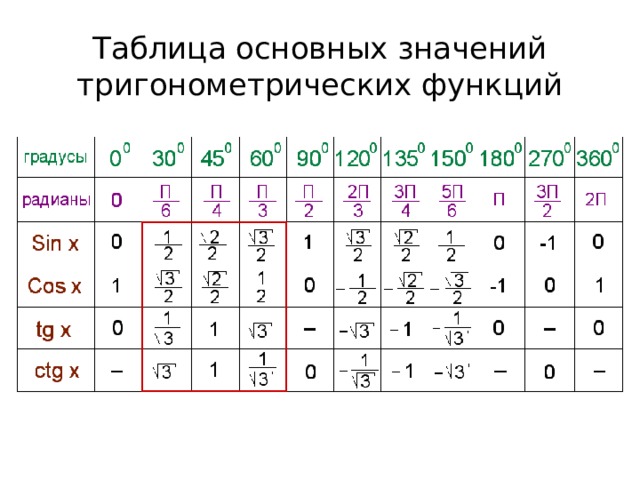

 Это означает, что тригонометрические функции повторяют свои значения.
Это означает, что тригонометрические функции повторяют свои значения. В частности, это арксинус, арккосинус, арктангенс, арккосеканс, арксеканс и арктангенс. Входом обратных тригонометрических функций являются тригонометрические отношения угла, а выходом — угол:
В частности, это арксинус, арккосинус, арктангенс, арккосеканс, арксеканс и арктангенс. Входом обратных тригонометрических функций являются тригонометрические отношения угла, а выходом — угол: Следовательно, решение будет таким:
Следовательно, решение будет таким: ниже). Функция котангенса (обычно сокращенно cot) является обратной функцией функции тангенса . Как и в случае с другими тригонометрическими функциями, используемыми в современном мире, функция котангенса, безусловно, была известна арабским ученым, а таблицы значений котангенса, как известно, существовали к десятому веку нашей эры. Чтобы точно понять, как связаны функция котангенса и функция тангенса, рассмотрим приведенную ниже диаграмму.
ниже). Функция котангенса (обычно сокращенно cot) является обратной функцией функции тангенса . Как и в случае с другими тригонометрическими функциями, используемыми в современном мире, функция котангенса, безусловно, была известна арабским ученым, а таблицы значений котангенса, как известно, существовали к десятому веку нашей эры. Чтобы точно понять, как связаны функция котангенса и функция тангенса, рассмотрим приведенную ниже диаграмму.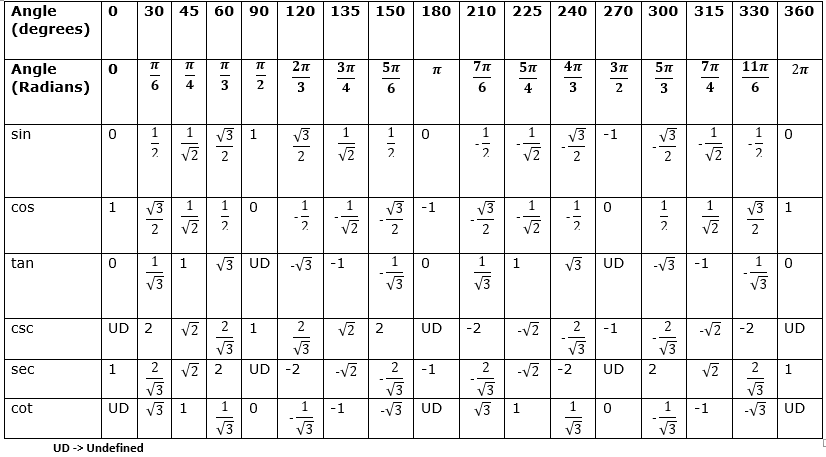 0531 А . Отрезок PF является продолжением отрезка OP (и, кстати, также является секущей ). Помните, что точка P — это точка на окружности единичного круга, координаты которой 90 531 x 90 532 и 90 531 y 90 532 представляют значение cos (90 531 θ 90 532 ) и sin ( θ ) соответственно (отрезки прямой, представляющие синус и косинус также показаны). Помните, что одно из определений функции тангенса — это частное функции синуса и косинуса . Щелкните здесь , чтобы увидеть интерактивную демонстрацию, в которой используется единичный круг, чтобы показать, как функции синуса, косинуса и котангенса соотносятся друг с другом (примечание: чтобы интерактивная страница работала, ваш браузер должен поддерживать Java).
0531 А . Отрезок PF является продолжением отрезка OP (и, кстати, также является секущей ). Помните, что точка P — это точка на окружности единичного круга, координаты которой 90 531 x 90 532 и 90 531 y 90 532 представляют значение cos (90 531 θ 90 532 ) и sin ( θ ) соответственно (отрезки прямой, представляющие синус и косинус также показаны). Помните, что одно из определений функции тангенса — это частное функции синуса и косинуса . Щелкните здесь , чтобы увидеть интерактивную демонстрацию, в которой используется единичный круг, чтобы показать, как функции синуса, косинуса и котангенса соотносятся друг с другом (примечание: чтобы интерактивная страница работала, ваш браузер должен поддерживать Java). Однако при приближении значения sin ( θ ) к нулю и значения cos ( θ ) к единице значение cot ( θ ) стремится к бесконечности. Таким образом, значение кроватки ( θ ), когда cos ( θ ) равно единице, равно undefined . Как упоминалось, тангенс 9Функция 0532 представляет собой частное функций синуса и косинуса. Поскольку функция котангенса является обратной величиной функции тангенса, мы также можем выразить функцию котангенса через функции синуса и косинуса:
Однако при приближении значения sin ( θ ) к нулю и значения cos ( θ ) к единице значение cot ( θ ) стремится к бесконечности. Таким образом, значение кроватки ( θ ), когда cos ( θ ) равно единице, равно undefined . Как упоминалось, тангенс 9Функция 0532 представляет собой частное функций синуса и косинуса. Поскольку функция котангенса является обратной величиной функции тангенса, мы также можем выразить функцию котангенса через функции синуса и косинуса: Если вы прочитали страницы этого раздела, посвященные трем основным тригонометрическим функциям ( синус , косинус и тангенс ), вы уже знакомы с диаграммой ниже.
Если вы прочитали страницы этого раздела, посвященные трем основным тригонометрическим функциям ( синус , косинус и тангенс ), вы уже знакомы с диаграммой ниже.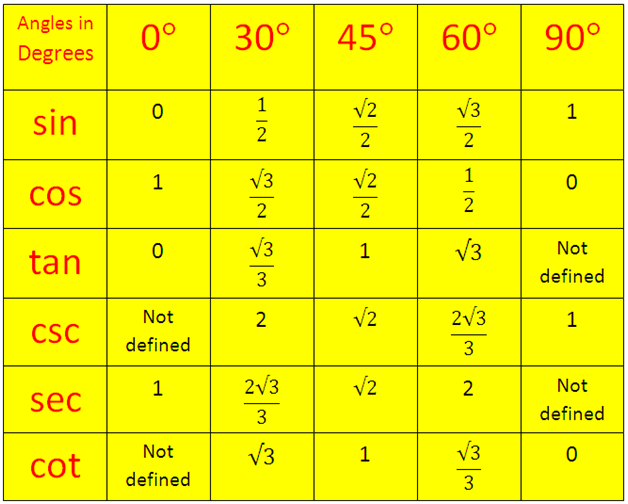 Чтобы увидеть таблицу, нажмите здесь .
Чтобы увидеть таблицу, нажмите здесь . На самом деле, он будет применяться к 90 531 любому углу 90 532, для которого значение тангенса равно нулю. Ниже мы приводим график функции котангенса для углов в диапазоне от ноль до семьсот двадцать градусов (720°).
На самом деле, он будет применяться к 90 531 любому углу 90 532, для которого значение тангенса равно нулю. Ниже мы приводим график функции котангенса для углов в диапазоне от ноль до семьсот двадцать градусов (720°). е. в квадранте I и квадранте III ).
е. в квадранте I и квадранте III ). Как и функция тангенса, период функции котангенса составляет 90 531 сто восемьдесят градусов 90 532 (180°), или π. Возможно, вы помните, что функция тангенса возвращает значение ноль при нуле градусов и достигает своего положительного пика по мере приближения к девяносто градусов. Затем он переходит к своему отрицательному пику, возвращаясь к нулю на 90 531 сто восемьдесят градусов 90 532, после чего цикл повторяется снова. Функция котангенса подобна зеркальному отображению функции тангенса, сдвинутой по фазе на девяносто градусов влево или вправо. Он падает со своего положительного пика по мере удаления от ноль градусов до нулевого значения девяносто градусов , а затем снова падает до своего отрицательного пика, приближаясь к ста восьмидесяти градусам . Затем он переходит к своему положительному пику и снова повторяет цикл.
Как и функция тангенса, период функции котангенса составляет 90 531 сто восемьдесят градусов 90 532 (180°), или π. Возможно, вы помните, что функция тангенса возвращает значение ноль при нуле градусов и достигает своего положительного пика по мере приближения к девяносто градусов. Затем он переходит к своему отрицательному пику, возвращаясь к нулю на 90 531 сто восемьдесят градусов 90 532, после чего цикл повторяется снова. Функция котангенса подобна зеркальному отображению функции тангенса, сдвинутой по фазе на девяносто градусов влево или вправо. Он падает со своего положительного пика по мере удаления от ноль градусов до нулевого значения девяносто градусов , а затем снова падает до своего отрицательного пика, приближаясь к ста восьмидесяти градусам . Затем он переходит к своему положительному пику и снова повторяет цикл. Нахождение котангенса угла с помощью встроенного калькулятора, представленного в Microsoft Windows по-прежнему относительно проста. Предположим, мы хотим найти котангенс угла 90 531 на сорок восемь градусов 90 532 (48°). Вы можете найти встроенный калькулятор Microsoft Windows, нажав кнопку «Пуск» в Windows 7 и выбрав «Все программы»> «Стандартные»> «Калькулятор» (в других версиях Windows может потребоваться другая последовательность нажатий клавиш). Научную версию калькулятора можно выбрать в приложении View 9.0532 меню. Чтобы найти котангенс сорока восьми градусов с помощью калькулятора Windows, введите следующие нажатия клавиш (если у вас нет калькулятора Windows, используйте любой доступный калькулятор, который может выполнять триггерные функции):
Нахождение котангенса угла с помощью встроенного калькулятора, представленного в Microsoft Windows по-прежнему относительно проста. Предположим, мы хотим найти котангенс угла 90 531 на сорок восемь градусов 90 532 (48°). Вы можете найти встроенный калькулятор Microsoft Windows, нажав кнопку «Пуск» в Windows 7 и выбрав «Все программы»> «Стандартные»> «Калькулятор» (в других версиях Windows может потребоваться другая последовательность нажатий клавиш). Научную версию калькулятора можно выбрать в приложении View 9.0532 меню. Чтобы найти котангенс сорока восьми градусов с помощью калькулятора Windows, введите следующие нажатия клавиш (если у вас нет калькулятора Windows, используйте любой доступный калькулятор, который может выполнять триггерные функции): 0863 1/х ) к результату. Убедитесь, кстати, что у вас установлен режим калькулятора градусов (если только вы не планируете вводить значение угла в радианах или градусах). Если вы правильно ввели нажатия клавиш, вы должны увидеть следующий экран:
0863 1/х ) к результату. Убедитесь, кстати, что у вас установлен режим калькулятора градусов (если только вы не планируете вводить значение угла в радианах или градусах). Если вы правильно ввели нажатия клавиш, вы должны увидеть следующий экран: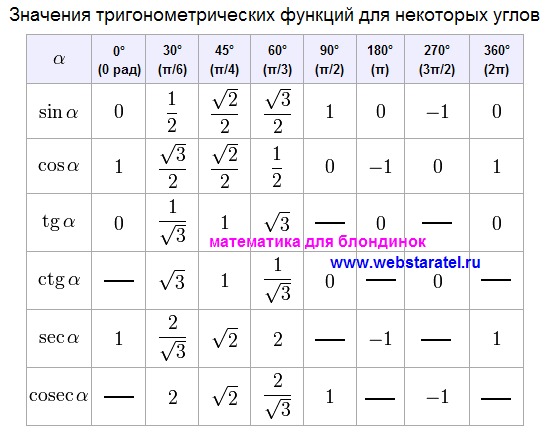
 Если вы читали страницы, посвященные другим тригонометрическим функциям, вы уже поняли, что все они очень тесно взаимосвязаны. Поэтому неудивительно, что графики каждой из трех основных тригонометрических функций так похожи на графики их соответствующих обратных функций. Тот факт, что тригонометрические функции настолько тесно взаимосвязаны, означает, что мы часто можем заменить выражение, включающее одну тригонометрическую функцию, эквивалентным выражением, включающим другую тригонометрическую функцию. Часто это может быть очень полезно.
Если вы читали страницы, посвященные другим тригонометрическим функциям, вы уже поняли, что все они очень тесно взаимосвязаны. Поэтому неудивительно, что графики каждой из трех основных тригонометрических функций так похожи на графики их соответствующих обратных функций. Тот факт, что тригонометрические функции настолько тесно взаимосвязаны, означает, что мы часто можем заменить выражение, включающее одну тригонометрическую функцию, эквивалентным выражением, включающим другую тригонометрическую функцию. Часто это может быть очень полезно.