Таблица значений tg sin cos tg ctg: Таблица значений тригонометрических функций

Содержание

Тригонометрические функции острого и тупого углов

Похожие презентации:

Элементы комбинаторики ( 9-11 классы)

Применение производной в науке и в жизни

Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»

Знакомство детей с математическими знаками и монетами

Тренажёр по математике «Собираем урожай». Счет в пределах 10

Методы обработки экспериментальных данных

Лекция 6. Корреляционный и регрессионный анализ

Решение задач обязательной части ОГЭ по геометрии

Дифференциальные уравнения

Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи

1. Тригонометрические функции острого и тупого углов

Тригонометрические функции острого угла

3. Определение

Если рассмотреть два
прямоугольных
треугольника APQ и ABC, с
общим острым углом α, то
ΔABC ~ ΔAQP по двум
углам, а следовательно,
их стороны
пропорциональны.
Тригонометрические
функции острого угла
определяются
исключительно градусной
мерой самого угла и не
зависят от «надетого» на
него треугольника

4.

ОпределениеСинусом острого угла прямоугольного
треугольника ABC называется отношение
противолежащего катета к гипотенузе
BC
sin
AB
Косинусом острого угла прямоугольного
треугольника ABC называется отношение
прилежащего катета к гипотенузе
AC
cos
AB

5. Определение

Тангенсом острого угла прямоугольного
треугольника ABC называется отношение
противолежащего катета к прилежащему
BC
tg
AC
Котангенсом острого угла прямоугольного
треугольника ABC называется отношение
прилежащего катета к противолежащему
AC
ctg
BC

6. Найдем тригонометрические функции острого угла (90° ‑ α)

Найдем тригонометрические функции
острого угла (90° — α)
AC
sin 90
cos
AB
BC
cos 90
sin
AB
AC
tg 90
ctg
BC
BC
ctg 90
tg
AC

7. «СИНУС»

Слово встречается в индийских трудах IV-V вв.
Линия синуса называлась «джива» – тетива лука.

Позднее термин был переделан в «джаб». При
переводе с арабского на латынь употребили слово
sinus – дословный перевод слово «джайб».
Для обозначения синуса использовались
различные сокращения. Современное
обозначение sin закрепилось в 18 веке (Симпсон,
Эйлер, Д’аламбер, Лагранж), чему способствовал
авторитет Эйлера, который перенял обозначения
от И. Бернулли.
«КОСИНУС». Сокращение выражения complementi sinus
– «дополнительный синус». В трудах арабских
математиков косинус рассматривался как синус
дополнения угла до 90° (18 в.).
«ТАНГЕНС». Тангенс и котангенс фигурировали в науке
о солнечных часах у арабских математиков. В работах
известного математика Ал-Хорезми (9 в.) приведены
таблицы тангенсов и котангенсов. «Тангенс»
происходит от латинского tangere – «касаться» (Финке,
1583)
«КОТАНГЕНС». Котангенсы появились раньше тангенсов
(арабские математики, 9 в.)

9. Тригонометрические тождества

С доказательством

10.

Связь между синусом и косинусом (основное тригонометрическое тождество)sin cos 1
2
2
Доказательство:
BC
AC
BC AC
AB
sin cos
1
2
2
2
2
AB
AB
AB
AB
2
2
2
(по теореме Пифагора)
2
2
2
2

11. Связь между синусом, косинусом и тангенсом

sin
tg
cos
Доказательство:
sin BC AC BC AB BC
:
tg
cos AB AB
AB AC AC

12. Связь между синусом, косинусом и котангенсом

cos
ctg
sin
Доказательство:
cos AC BC AC AB AC
:
ctg
sin
AB AB
AB BC BC

13. Связь между тангенсом и котангенсом

tg ctg 1
Доказательство:
BC AC
tg ctg
1
AC BC

14. Связь между тангенсом и косинусом

1
1 tg
2
cos
2
Доказательство:
Разделим обе части основного тригонометрического
тождества на cos2 0
sin cos
sin cos 1 : cos 0
2
2
cos cos c
1
1
2
tg 1
2
2
cos
cos
2
2
2
2
2

15.

Связь между котангенсом и синусом1
1 ctg
2
sin
2
Доказательство:
Разделим обе части основного тригонометрического
тождества на sin 2 0
2
2
sin
cos
1
2
2
2
sin cos 1 : sin 0 2
2
2
sin sin sin
1
1 ctg
2
sin
2

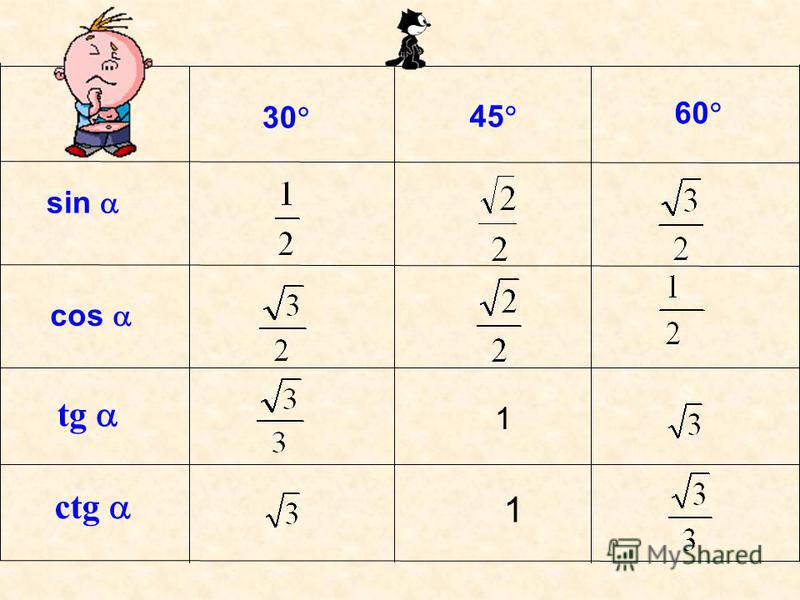
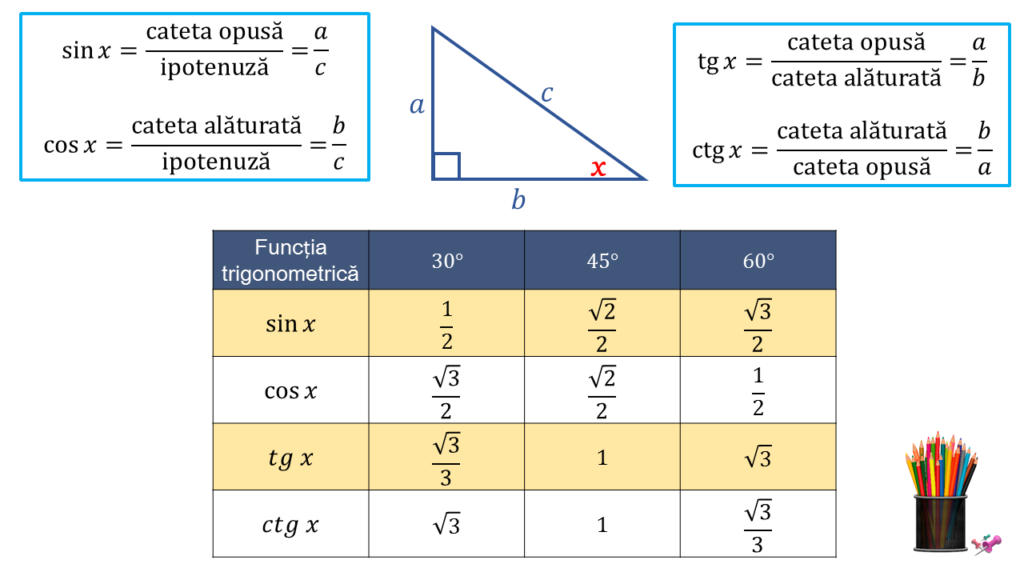
16. Значения тригонометрических функций углов в 30°, 45° и 60°.

Рассмотрим прямоугольный треугольник с острыми
углами в 30° и 60° и меньшим катетом, равным 1.
По свойству прямоугольного треугольника с углом в
30°, AB = 2. Катет AC найдем по теореме Пифагора:
AC AB BC 4 1 3
2
2
Найдем тригонометрические функции углов в 30° и
60°:
BC 1
sin 30 cos 60
AB 2
AC
3
cos30 sin 60
AB
2
BC
1
3
tg 30 ctg 60
AC
3
3
AC
ctg 30 tg 60
3
BC
Теперь рассмотрим равнобедренный прямоугольный
треугольник с катетом, равным 1. Оба его острых угла
равны по 45°. Найдем гипотенузу по теореме
Пифагора: AB AC 2 BC 2 1 1 2
BC
1
2
sin 45 cos 45
AB
2
2
BC
tg 45 ctg 45
1
AC

19.

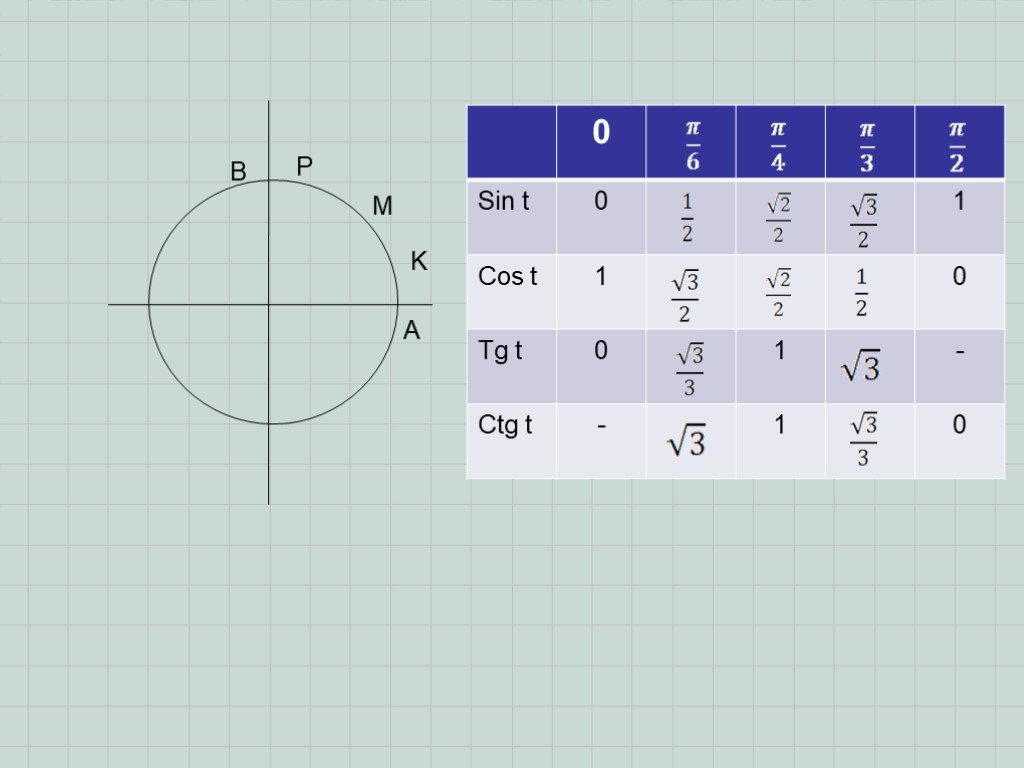
Таблица значений тригонометрических функций sin
cos
30°
1
2
45°
2
2
3
2
2
2
60°
3
2
1
2
tg
3
3
ctg
3
1
1
3
3
3

English Русский Правила

Тригонометричні функції.

Тригонометрические функции

Знаки тригонометрических функций

Знаки чисел

sin α , cos α , tg α , ctg α

определяются тем, в каком квадранте (четверти) координатной плоскости Oxy лежит луч OM (рисунки 1, 2, 3, 4).

Рис.1. Знак sin α


Рис.2. Знак cos α	. Знак cos α

cos α

Рис. 3. Знак tg α Рис.4. Знак сtg α

косинус – четная функция, а синус, тангенс и котангенс – нечетные функции

период косинус, синус -2п, тангенс и котангенс—п

Графики тригонометрических функций

На рисунках 1, 2, 3, 4 приведены графики тригонометрических функций

Рис.1. График функции y = sin x

Рис.2. График функции y = cos x

Рис.3. График функции y = tg x

Рис.4. График функции y = ctg x

Таблица формул приведения

Аргумент	Формула приведения
Аргумент	синус	косинус	тангенс	котангенс
– α	– sin α	cos α
	cos α	sin α
	cos α	– sin α
π – α	sin α	– cos α
π + α	– sin α	– cos α
	– cos α	– sin α
	– cos α	sin α
2π – α	– sin α	cos α
2π + α	sin α	cos α

Связи между тригонометрическими функциями одного угла

sin²α + cos²α = 1

Тригонометрические функции суммы и разности двух углов

Формула	Название формулы
sin (α + β) = sin α cos β + cos α sin β	Синус суммы
sin (α – β) = sin α cos β – cos α sin β	Синус разности
cos (α + β) = cos α cos β – sin α sin β	Косинус суммы
cos (α – β) = cos α cos β + sin α sin β	Косинус разности
	Тангенс суммы
	Тангенс разности

Тригонометрические функции двойного угла

Формула	Название формулы
sin 2α = 2 sin α cos α	Синус двойного угла
cos 2α = cos ²α – sin²α cos 2α = 2cos ²α – 1 cos 2α = 1 – 2sin ²α	Косинус двойного угла
	Тангенс двойного угла

Формулы понижения степени для квадратов тригонометрических функций

Формула	Название формулы
	Выражение квадрата синуса через косинус двойного угла
	Выражение квадрата косинуса через косинус двойного угла
	Выражение квадрата тангенса через косинус двойного угла

Формулы понижения степени для кубов синуса и косинуса

Формула	Название формулы
	Выражение куба синуса через синус угла и синус тройного угла
	Выражение куба косинуса через косинус угла и косинус тройного угла

Выражение тангенса через синус и косинус двойного угла

Преобразование суммы тригонометрических функций в произведение

Формула	Название формулы
	Сумма синусов
	Разность синусов
	Сумма косинусов
	Разность косинусов
	Сумма тангенсов
	Разность тангенсов

Преобразование произведения тригонометрических функций в сумму

Формула	Название формулы
	Произведение синусов
	Произведение косинусов
	Произведение синуса и косинуса

Выражение тригонометрических функций через тангенс половинного угла

Формула	Название формулы
	Выражение синуса угла через тангенс половинного угла
	Выражение косинуса угла через тангенс половинного угла
	Выражение тангенса угла через тангенс половинного угла

Тригонометрические функции тройного угла

Формула	Название формулы
sin 3α = 3sin α – 4sin³α	Синус тройного угла
cos 3α = 4cos³α –3cos α	Косинус тройного угла
	Тангенс тройного угла

Предположим, что число a удовлетворяет неравенству .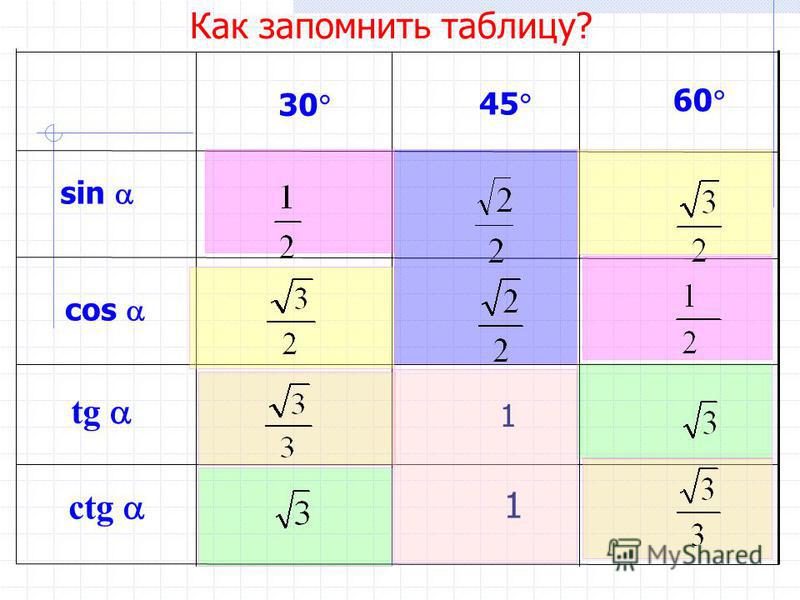 Число x называют арксинусом числа a и обозначают x = arcsin a, если выполнены два условия:

Предположим, что число a удовлетворяет неравенству . Число x называют арккосинусом числа a и обозначают x = arccos a, если выполнены два условия:

Рассмотрим произвольное число a . Число x называют арктангенсом числа a и обозначают x = arctg a, если выполнены два условия:

Рассмотрим произвольное число a . Число x называют арккотангенсом числа a и обозначают x = arcctg a, если выполнены два условия:

Арксинус, арккосинус, арктангенс и арккотангенс удовлетворяют, в частности, следующим соотношениям:

arcsin (– a) = – arcsin a ,

arccos (–

a) = π – arccos a ,

arctg (– a) = – arctg a ,

arcctg (– a) = π – arcctg a .

Простейшие тригонометрические уравнения

Простейшими тригонометрическими уравнениями называют уравнения вида:

sin x = a , cos x = a , tg x = a , ctgx = a .

где a – произвольное число.

Решение уравнения sin x = a

Обычная форма записи решения
Более удобная форма записи решения
Ограничения на число a	В случае, когда , уравнение решений не имеет

Решение уравнения cos x = a

Обычная форма записи решения
Более удобная форма записи решения
Ограничения на число a	В случае, когда , уравнение решений не имеет

Решение уравнения tg x = a

Обычная форма записи решения:
Более удобная форма записи решения
Ограничения на число a	Ограничений нет

Решение уравнения ctg x = a

Обычная форма записи решения
Более удобная форма записи решения
Ограничения на число a	Ограничений нет

градусов — быстрые тригонометрические функции (cos, tan, arcsin, arcos, arctan)

спросил 6 лет, 9 месяцев назад

Изменено 4 года, 4 месяца назад

Просмотрено 53 тысячи раз

здравствуйте, я должен различать вычисления в градусах, и у меня есть следующий код, но я не возвращаю мне точные значения.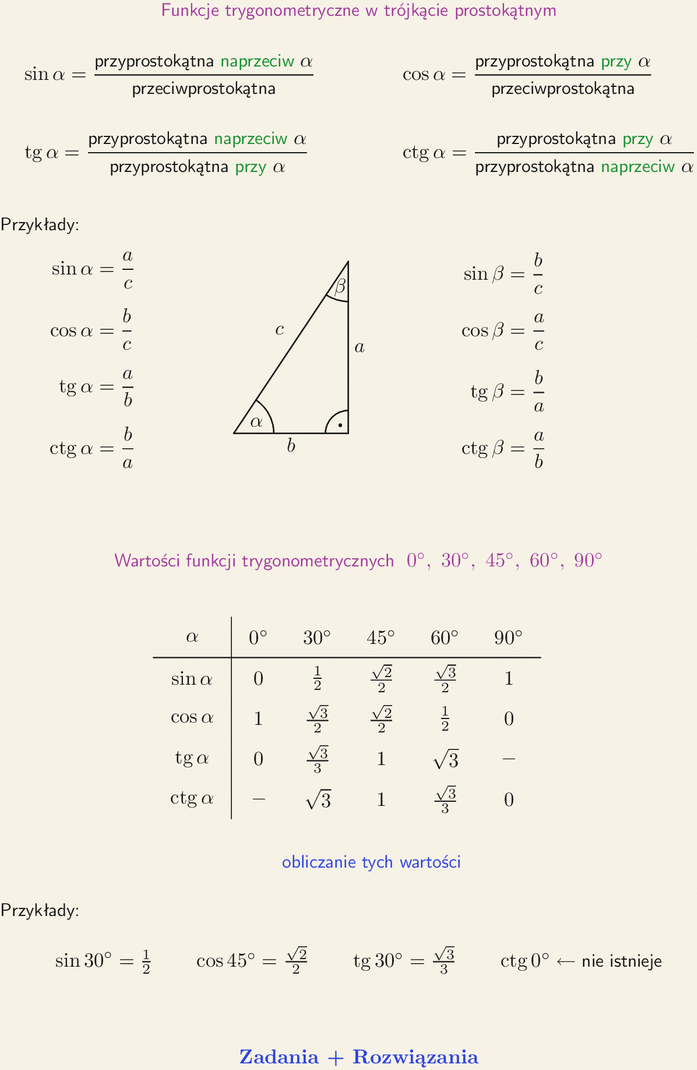 Единственное право — это значение sin90 в градусах = 1

 //////***** ГРАДУСЫ ******//////
вар синус = грех (90,0 * M_PI / 180)
переменная косинус = cos (90 * M_PI / 180)
переменная тангенса = тангенс (90 * M_PI / 180)
var arcsinus = asin(90 * M_PI/180)
var arcosinus = acos (90 * M_PI / 180)
переменная арктангенса = атан (90 * M_PI / 180)

Какая правильная операция возвращает точное значение для каждой операции в градусах для cos, tan и их функций ARC?

свифт
градусов
тригонометрия
радиан

Это скорее математическая задача, чем задача Swift:

 let sinus = sin(90.0 * Double.pi / 180)
print("Синус \(синус)")
пусть косинус = cos(90 * Double.pi / 180)
print("Косинус \(косинус)")
пусть тангенс = тангенс (90 * Double.pi / 180)
print("Касательная \(касательная)")

отпечатков

 Синус 1.0
Косинус 6.12323399573677e-17
Тангенс 1,63312393531954e+16

Синус 90 градусов равен 1 (правильно)

Косинус 90 градусов равен 0.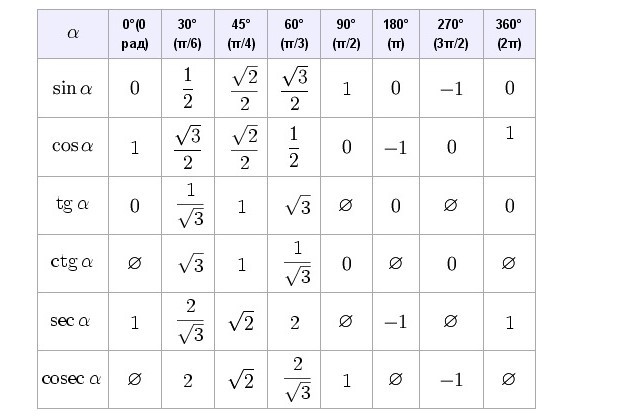 Значение 6e-17 очень мало, любое разумное округление будет считать его равным нулю (верно). Тот факт, что вы не можете получить ровно ноль, связан с ошибками округления при расчете.

Тангенс 90 градусов не определен (sin/tan = 1/0, деление на ноль не определено). Если бы у нас были точные расчеты, вы, вероятно, получили бы бесконечность. В этом случае у нас есть 1 , разделенное на 6e-17 , что становится большим числом 9.0041 1.6e16 . Результат правильный.

Что касается обратных функций, обратите внимание на то, что их параметры не указаны ни в градусах, ни в радианах. Их результат в градусах/радианах, например:

 let arcsinus = asin(1.0) * 180/Double.pi
print("Дуговой синус \(дуговой синус)")