Тесты по теме «Основы тригонометрии»
I. Теоретические сведения
1. Радианная мера угла
2. Тригонометрические функции различных углов
3. Основные формулы тригонометрии и их свойства
4. Функции синус и косинус
5. Графики функций синус и косинус. Синусоида
6. Функции тангенс и котангенс
7. Построение графиков функций тангенса и котангенса
8. Основные тригонометрические функции
1. Радианная мера угла
Угол в 1 радиан — это такой центральный угол,
длина дуги которого равна радиусу окружности (см рисунок ниже). Радианная и
градусная меры угла связаны между собой отношением: 180о =
&pi радиан, а угол nо равен π*n/180 радиан.
Радианная мера угла позволяет упростить некоторые формулы. Например, для окружности радиуса r длина ее дуги l в α радиан вычисляется по формуле: l = α*r. Площать S сектора круга радиуса r, дуга которого содержит α радиан, равна: S=αr2/2. Эти и другие преимущества привели к тому, что в тригонометрии обычно пользуются только радианной мерой угла.
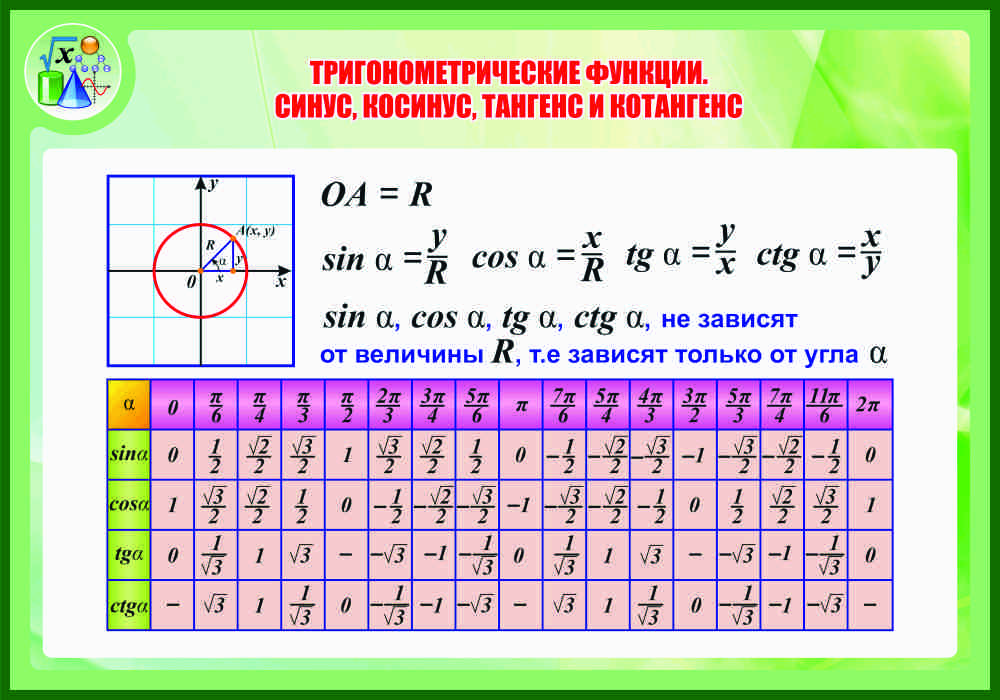
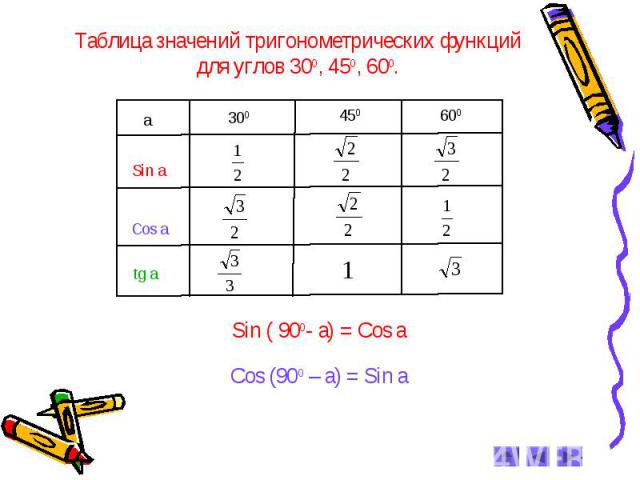
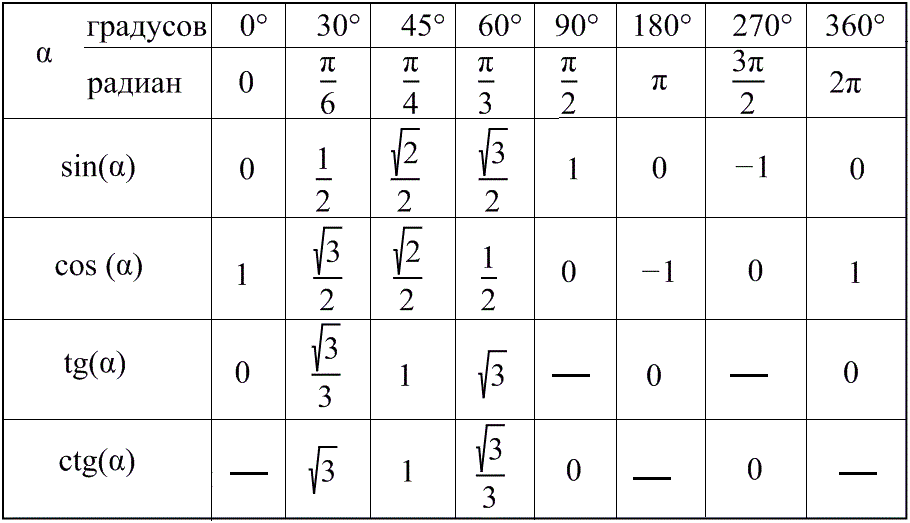
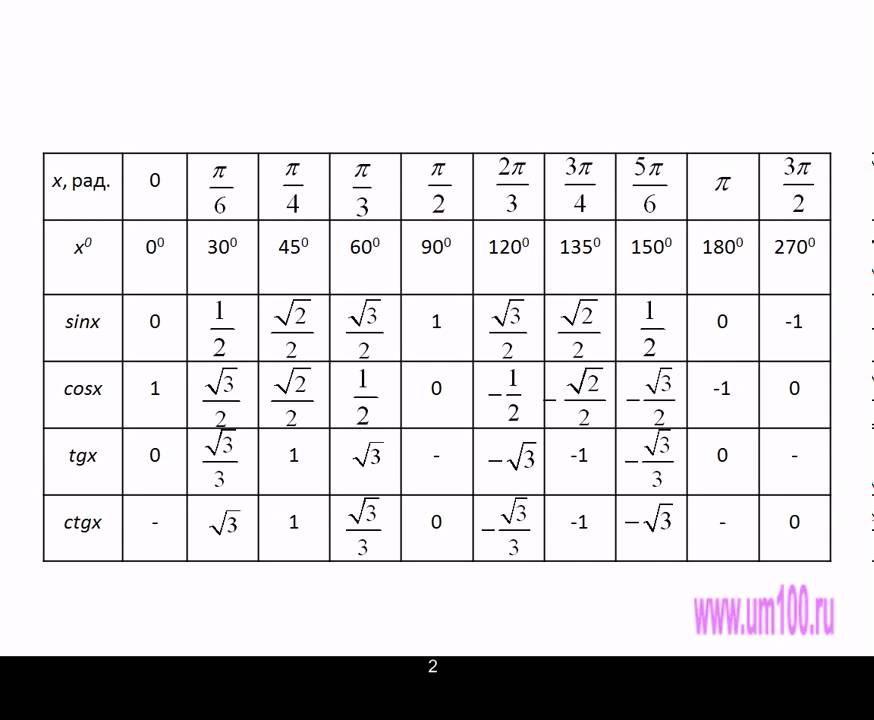
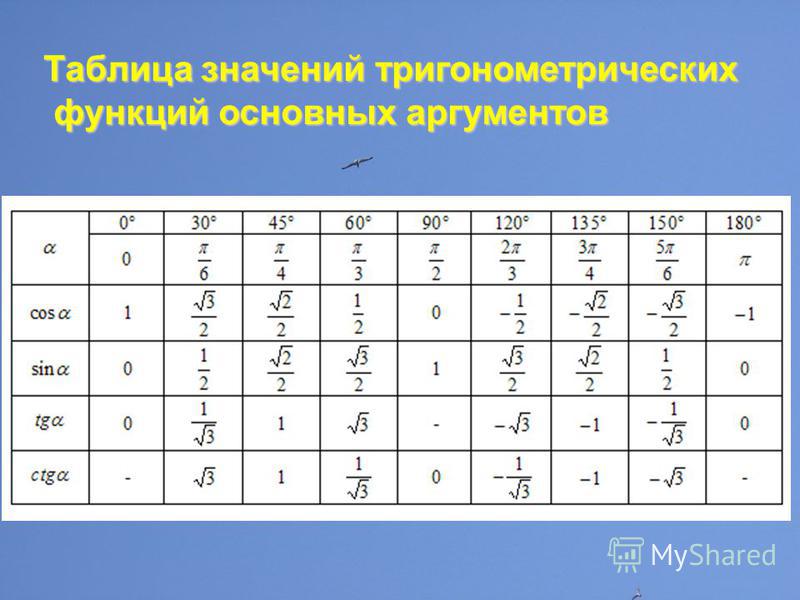
2. Таблица значений тригонометрических функций углов
В нижеприведенной таблице приведены значения тригонометрических функций различных углов, заданных в радианах. Напоминаем, что Π приблизительно равняется 3.14 радиан.
α | 0 | π/6 | π/4 | π/3 | π/2 | 2π/3 | 3π/5 | 5π/6 | π | 7π/6 | 5π/4 | 4π/3 | 3π/2 | 5π/3 | 7π/4 | 11π/6 | 2π |
sin(α) | 0 | 1/2; | √2/2 | √3/2 | 1 | √3/2 | √2/2 | 1/2 | 0 | -1/2 | -√2/2 | -√3/2 | -1 | -√3/2 | -√2/2 | -1/2 | 0 |
cos(α) | 1 | √3/2 | √2/2 | 1/2 | 0 | -1/2 | -√2/2 | -√3/2 | -1 | -√3/2 | -√2/2 | -1/2 | 0 | 1/2 | √2/2 | √3/2 | 1 |
tg(α) | 0 | 1/√3 | 1 | √3 | — | -√3 | -1 | -1/√3 | 0 | 1/√3 | 1 | √3 | — | -√3 | -1 | -1/√3 | 0 |
ctg(α) | — | √3 | 1 | 1/√3 | 0 | -1/√3 | -1 | -√3 | — | √3 | 1 | 1/√3 | 0 | -1/√3 | -1 | -√3 | — |
3. Основные формулы тригонометрии и их свойства
Основные формулы тригонометрии и их свойства
Дадим определения тригонометрическим функциям синуса, косинуса, тангенса и котангенса. возьмем любой прямоугольный треугольник. Из курса геометрии мы знаем, что у него есть два катета и гипотенуза, причем угол между двумя катетами прямой — то есть равен 90o, или π/2 радиан.
Рассмотрим угол α, который образован одним из катетов и гипотенузой.
Синусом угла α называется отношение длин противолежащего катета к гипотенузе.
Косинусом угла α называется отношение длин прилежащего катета к гипотенузе.
Тангенсом угла α называется отношение длин противолежащего катета к прилежащему.
Котангенсом угла α называется отношение длин прилежащего катета к противолежащему.
Из определений тригонометрических функций сразу же следуют тригонометрические тождества:
Немного более сложным путем можно получить формулы сложения тригонометрических функций:
Из формул сложения очевидным образом можно получить формулы приведения тригонометрических функций:
Для запоминания формул приведения можно
воспользоваться следующим правилом:
1.
2. Функция меняется на кофункцию, если n нечетно, и не меняется, если n — четно. Кофункциями для функций синуса, косинуса, тангенса и котангенса соответсвенно являются косинус, синус, котангенс и тангенс.
Так же при решении различных задач, связанных с тригонометрией, часто используются формулы суммы и разности синусов и косинусов:
Из них легко получить формулы двойного аргумента:
При помощи замены переменных легко получить формулы половинного угла:
4. Функции синус и косинус.
Окружность радиуса r=1 с центром в начале
координат называют единичной окружностью. Пусть точка Pα единичной окружности получена путем поворота точки P0 на угол α радиан против часовой стрелки.
Далее и везде будем считать, что значения всех углов задано в радианах, если только специально не указаны другие единицы измерения. Таким образом, если написано α=1, то подразумевается, что угол α равен 1 рад.
Определение. Числовые функции, заданные формулами y=sin(x) и y=cos(x) называют соответсвенно синусом и косинусом (обозначают соответсвенно sin и cos).
Область определения этих функций — вся прямая действительных чисел. Область значения этих функций — отрезок [-1;1]:
D(sin)=D(cos)=R
E(sin)=E(cos)=[-1;1]
Функция sin(x) является нечетной функцией:
sin(-x)=-sin(x)
Функция cos(x) является четной функцией:
cos(-x)=cos(x)
Обе функции sin(x) и cos(x) являются периодическими с периодом T=2π:
sin(x+Tn)=sin(x)
cos(x+Tn)=cos(x), где n — любое целове число.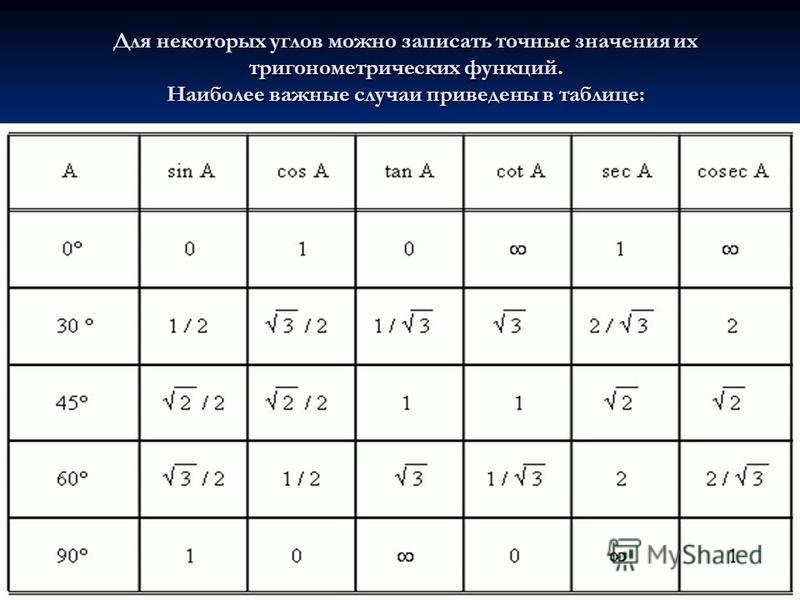
Синусоида.
Построим график функции синус на отрезке [0;2π]. Отметим на оси ордина точки (0;-1) и (0;1), а на оси абсцисс точку с абсциссой 2π (что приблизительно равно 6.28). Слева нарисуем единичную окружность.
Теперь разделим единичную окружность и отрезок [0,2π] на 16 равных частей и воспользуемся определением синуса для построения ее графика. Отметим точку Pα на единичной окружности и проведем через нее линию, параллельную оси абсцисс. Точка пересечения этой линии с прямой x=α и есть искомая точка графика функции синуса. Ее ордината совпадает с ординатой точки Pα, а функция sin по определению и есть ордината точки Pα.
Для продолжения графика по оси ОХ дальше, чем
точка x=2π, необходимо воспользоваться свойством периодичности функции sin(x):
sin(x+2πn)=sin(x), где n — целое число. Таким образом, график синуса на всей
числовой прямой получается путем параллельного переноса его части на отрезке
[0;2π] вдоль оси ОХ на 2π, 4π, 6π, и т.
Графи функции sin(x) называется синусоидой. Отрезок оси ординат [-1;1] иногда называют линия синусов.
Для построения графика функции cos(x) воспользуемся формулой приведения: cos(x)=sin(x+π/2). Следовательно, график функции косинуса получается из графика синуса путем его параллельного переноса на π/2 в отрицателньом направлении оси абсцисс. График функции косинуса так же называется синусоидой. См. рисунок ниже.
6. Функции тангенс и котангенс.
Числовые функции, заданные формулами y=tg(x) и y=ctg(x), называют соответственно тангенсом и котангенсом (и обозначают соответственно tg и ctg).
Областью определения функции тангенс является множество всех чисел x кроме тех, где cos(x)=0: x≠π/2+πn, где n — любое целое число.
Областью определения функции котангенс является
множество всех чисел x кроме тех, где sin(x)=0: x≠πn, где n — любое целое
число.
Проведем касательную l к единичной окружности в точке P0. Пусть α — произвольное число, для которого cos(α)≠0. Тогда точка Pα (cos(α),sin(α)) не лежит на оси ординат, и, следовательно, прямая OPα пересекает l в некоторой точке Tα с абсциссой 1. Необходимо найти ординату этой точки.
Заметим, что прямая OPα проходит через точки О(0,0) и Pα(cos(α),sin(α)), поэтому она имеет уравнение y=xtg(α).
Абсцисса T
Итак, ордината точки пересечения прямых OPα и l равна tg(α). Прямую l иногда называют линией тангенсов.
Нетрудно по аналогии показать, что абсцисса точки Cα пересечения прямой OPα с касательной m к единичной окружности, проведенной через точку Pπ/2, равно ctg(α) при sin(&alpha)≠0. Прямую m называют линией котангенсов.
Область значений тангенса (котангенса) — вся
числовая прямая. Докажем это для функции tg.
Докажем это для функции tg.
Пусть y0 — произвольное действительное число. Рассмотрим точку T(1,y0). Следуя показанному выше, тангенс угла TOX равен y0. Следовательно, функция tg принимает любое действительное значение.
Функции тангенс и котангенс обладают следующими свойствами:
1. tg(-x)=-tg(x), ctg(-x)=-ctg(x) — функции тангенс и котангенс являются нечетными функциями.
2. tg(x+πn)=tg(x), ctg(x+πn)=ctg(x), n — целое.
7. Графики функций тангенса и котангенса.
Построение графика тангенса на интервале (-π/2;π/2) аналогично построению, описанному в случае функции синуса.
Значение функции tg в точке можно найти с помощью линии тангенсов.
Вследствие тождества tg(x+πn)=tg(x), где n —
целое, график функции тангенса на всей области определения получается из
графика на интервале (-π/2;π/2) параллельными переносами вдоль оси ОХ вправо в
влево на π 2π и т.д. График функции тангенс называют тангенсоидой. Получение
графика путем параллельных переносов представлено на рисунке ниже.
Получение
графика путем параллельных переносов представлено на рисунке ниже.
График функции котангенса можно получить аналогичным образом. Он представлен на рисунке ниже.
8. Основные тригонометрические функции.
Синус, косинус, тангенс и котангенс часто называют основными тригонометрическими функциями. Иногда рассматривают еде две основные тригонометрические функции — секанс и косеканс (обозначаются sec и cosec соответственно).
Для того, чтобы понять, почему основных тригонометрический функций именно шесть, заметим, что тригонометрические функции острого угла α можно определить как отношения сторон прямоугольного треугольника с острым углом α.
Таких отношений может быть всего шесть:
sin(α)=a/c
cos(α)=b/c
tg(α)=a/b
ctg(α)=b/a
sec(α)=c/b
cosec(α)=c/a
II. Тесты
Тесты
Тест №1 по теме «Тригонометрия»
Вариант 1
1. Найдите , если
1) -0,8; 2) 0,8; 3) 0,6; 4) -0,6.
2. Вычислите .
1) ; 2); 3); 4).
3. Упростите выражение .
1) ; 2) ; 3) ; 4) 1.
4. Упростите выражение .
1) ; 2) ; 3) 0; 4) 1.
5. Вычислите .
1) ; 2) -2; 3) -2,5; 4) 4.
6. Вычислите .
1) ; 2) 0; 3) 1; 4) ; 5) -.
7. Упростите выражение .
1) ; 2) -; 3) 0; 4) .
8. Вычислите .
1) 48; 2) -96; 3) 96; 4)-48.
9. Чему равен ?
1) ; 2) ; 3) ; 4) .
10. Чему равен ?
1) ; 2) ; 3) ; 4) .
11. Решите уравнение .
1) ; 2) ; 3) ; 4) .
12. Решите уравнение .
1) ; 2) ; 3) ;
4) .
13. Решите уравнение .
1) ; 2) ; 3) ;
4) .
14. Решите уравнение .
1) ; 2) ;
3) ; 4) корней нет.
15. Решите уравнение .
1) ; 2) 4
3) .
Ответы
Вариант 2
1. Вычислите , если .
1) -0,6; 2) 0,8; 3) 0,6; 4) -0,8.
2. Вычислите .
1) ; 2) ; 3) ; 4) .
3. Упростите выражение .
1) ; 2) ; 3) 1; 4) .
4. Упростите выражение .
1) ; 2) 1; 3) ; 4) 0.
5. Вычислите .
1) 0,5; 2) -3,5; 3) -1,5; 4) -5,5.
6. Вычислите .
1) ; 2) ; 3) 0; 4) ; 5) -.
7. Упростите выражение
1) ; 2) ; 3) 0; 4) .
8. Вычислите
1) 2,5; 2) 5; 3) -2,5; 4) -5.
9. Чему равен ?
1) ; 2) ; 3) ; 4) .
10. Чему равен ?
Чему равен ?
1) ; 2) ; 3) ; 4)
11. Решите уравнение .
1) ; 2) ; 3) ; 4) .
12. Решите уравнение .
1) ; 2) ; 3) ;
4) .
13. Решите уравнение .
1) ; 2) ; 3) ;
4) .
14. Решите уравнение .
1) ; 2) корней нет; 3) ;
4) .
15. Решите уравнение .
1) ; 2) ;
3) .
Ответы
Критерии оценивания:
«5» — 14-15 правильных ответов
«4» — 11-13
«3» — 8-10
«2» — менее 8
Тест № 2 по теме: «Распознавание графиков тригонометрических функций»
Вариант №1
1.График какой функции изображен на рисунке?
1) | |
2) | |
3) | |
4) |
2. График
какой функции изображен на рисунке?
График
какой функции изображен на рисунке?
1) | |
2) | |
3) | |
4) |
3.График какой функции изображен на рисунке?
1) | |
2) | |
3) | |
4) |
4. График какой функции изображен на рисунке?
График какой функции изображен на рисунке?
1) | |
2) | |
3) | |
4) |
5.График какой функции изображен на рисунке?
1) | |
2) | |
3) | |
4) |
6. График
какой функции изображен на рисунке?
График
какой функции изображен на рисунке?
1) | |
2) | |
3) | |
4) |
4) |
7. График какой функции изображен на рисунке?
1) | |
2) | |
3) | |
4) |
8. График
какой функции изображен на рисунке?
График
какой функции изображен на рисунке?
1) | |
2) | |
3) | |
4) |
9. График какой функции изображен на рисунке?
1) | |
2) | |
3) | |
4) |
10. График
какой функции изображен на рисунке?
График
какой функции изображен на рисунке?
1) | |
2) | |
3) | |
4) |
Вариант №2
1.График какой функции изображен на рисунке?
1) | |
2) | |
3) | |
4) |
2. График
какой функции изображен на рисунке?
График
какой функции изображен на рисунке?
1) | |
2) | |
3) | |
4) |
3.График какой функции изображен на рисунке?
1) | |
2) | |
3) | |
4) |
4. График
какой функции изображен на рисунке?
График
какой функции изображен на рисунке?
1) | |
2) | |
3) | |
4) |
5.График какой функции изображен на рисунке?
1) | |
2) | |
3) | |
4) |
6. График
какой функции изображен на рисунке?
График
какой функции изображен на рисунке?
1) | |
2) | |
3) | |
4) |
7.График какой функции изображен на рисунке?
1) | |
2) | |
3) | |
4) |
8. График
какой функции изображен на рисунке?
График
какой функции изображен на рисунке?
1) | |
2) | |
3) | |
4) |
9. График какой функции изображен на рисунке?
1) | |
2) | |
3) | |
4) |
10. График
какой функции изображен на рисунке?
График
какой функции изображен на рисунке?
1) | |
2) | |
3) | |
4) |
Ответы
Критерии оценивания:
«5» — 9-10 правильных ответов
«4» — 7-8
«3» — 5-6
«2» — менее 5
рабочих листов | TPT
by
My Teaching Pal
22,00 $
15,00 $
Bundle
Этот комплект содержит 263 ОГРОМНЫХ математических листа для первого класса! Рабочие листы охватывают сложение и вычитание, числа и разрядность, 2D и 3D фигуры, данные и графики, дроби и разбиение на части и время. Эти веселые рабочие листы отлично подходят для использования в течение всего года, они идеально подходят для занятий в классе, математических станций, быстрых финишеров, домашних заданий и повторения. Этот комплект состоит из следующих пакетов: Рабочие листы для сложения и вычитания для первого классаРабочие листы для первого класса 2D и 3D
Этот комплект состоит из следующих пакетов: Рабочие листы для сложения и вычитания для первого классаРабочие листы для первого класса 2D и 3D
Предметы:
Базовые операции, Математика, Числа
Классы:
Типы:
Распечатки, Рабочие тетради, Рабочие листы
by
Внутри вы найдете
03 пассажей! Эти отрывки отлично подходят для детей младшего возраста, а также подойдут для первоклассников или первоклассников, в зависимости от того, как вы их используете. В комплекте много разнообразия. Пожалуйста, проверьте изображения и предварительный просмотр, чтобы увидеть, подойдут ли эти отрывки для ваших учеников. Отрывки разбиты на три категории… Первые 20 отрывков: Основная история с 3 вопросами. Студентам дается два ответа на выбор на каждый вопрос. Вторые 20 отрывков: Базовый
Предметы:
Английский язык искусства, чтение, стратегии чтения
Оценки:
K — 1st
Типы:
Центры, печатные изготовления, рабочие листы
на
приводить в форму навыки самоконтроля детей! Действия сосредоточены на понимании самоконтроля, импульсивного контроля, остановке и обдумывании, чтобы принять решение, ожидании своей очереди, соблюдении правил и указаний, сохранении мотивации, выполнении нашей работы наилучшим образом, управлении эмоциями, использовании стратегий преодоления и практике самоконтроля для укрепления.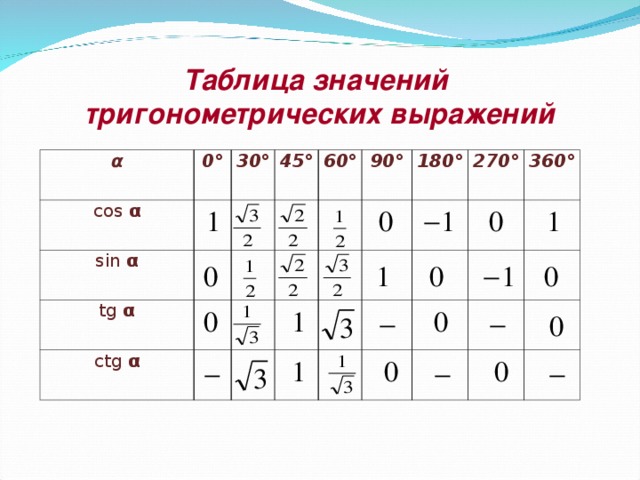 навыки со временем. Также рассматриваются другие навыки, влияющие на самоконтроль, включая планирование, управление временем и настойчивость. Цифровая версия обновлена до 9.0003
навыки со временем. Также рассматриваются другие навыки, влияющие на самоконтроль, включая планирование, управление временем и настойчивость. Цифровая версия обновлена до 9.0003
Тема:
Школьное консультирование, социальное эмоциональное обучение, специальное образование
. шрифты в ZIP-файле! Большинство символов ударения включено во все шрифты. Пожалуйста, проверьте предварительный просмотр, чтобы увидеть все шрифты, включенные в этот набор! Примечания. Включено 5 шрифтов + 1 шрифт для каракулей. Все шрифты с заглавными буквами Elementary. Проверьте предварительный просмотр, чтобы увидеть все шрифты в действии! $ СЭКОНОМЬТЕ ДЕНЬГИ $ БОЛЕЕ 400 ШРИФТОВ + КАЖДЫЙ НОВЫЙ ШРИФТ БЕСПЛАТНО! ПРОВЕРЬТЕ РАСТУЩИЙ НАБОР ШРИФТОВ ЗДЕСЬУсловия использования * Шрифты
Предметы:
Для всех предметов, Товары для продавцов ТРТ, Специальность
Классы:
PreK — 12th, Высшее образование, Образование для взрослых, Персонал by
SunnyDays
12,50 $
9,99 $
Рукописный ввод — это одна из тех областей, в которую трудно вписаться, хотя сейчас она нужна больше, чем когда-либо. С помощью этого пакета вы можете легко проводить полноценную рукописную практику каждый день учебного года всего за несколько минут в день. Каждая страница соответствует одному и тому же формату, поэтому ваши ученики смогут заполнить ее самостоятельно после первого раза.
Отлично подходит для работы со звонком, успокоения после перемены, работы со словами, домашней работы или в любое время, когда у вас есть несколько лишних минут. Распечатать пакет на весь 9 мес.0003
С помощью этого пакета вы можете легко проводить полноценную рукописную практику каждый день учебного года всего за несколько минут в день. Каждая страница соответствует одному и тому же формату, поэтому ваши ученики смогут заполнить ее самостоятельно после первого раза.
Отлично подходит для работы со звонком, успокоения после перемены, работы со словами, домашней работы или в любое время, когда у вас есть несколько лишних минут. Распечатать пакет на весь 9 мес.0003
Тема:
Английский язык искусства, почерк, написание
. предназначен для использования ВМЕСТЕ с Secret Stories, поскольку он НЕ включает постеры и рассказы Secret Stories® Phonics. Узнайте больше о Secret Stories® и загрузите БЕСПЛАТНЫЕ РЕСУРСЫ в файлах группы Secret Facebook! Песня Secret Stories® Better Alphabet™ — это САМЫЙ БЫСТРЫЙ способ выучить отдельные буквы и звуки, используя мышечную память для ускорения овладения языком всего за 2 недели для дошкольников и дошкольников. Этот продукт содержит три видеоверсии Better Alphabet™ 9.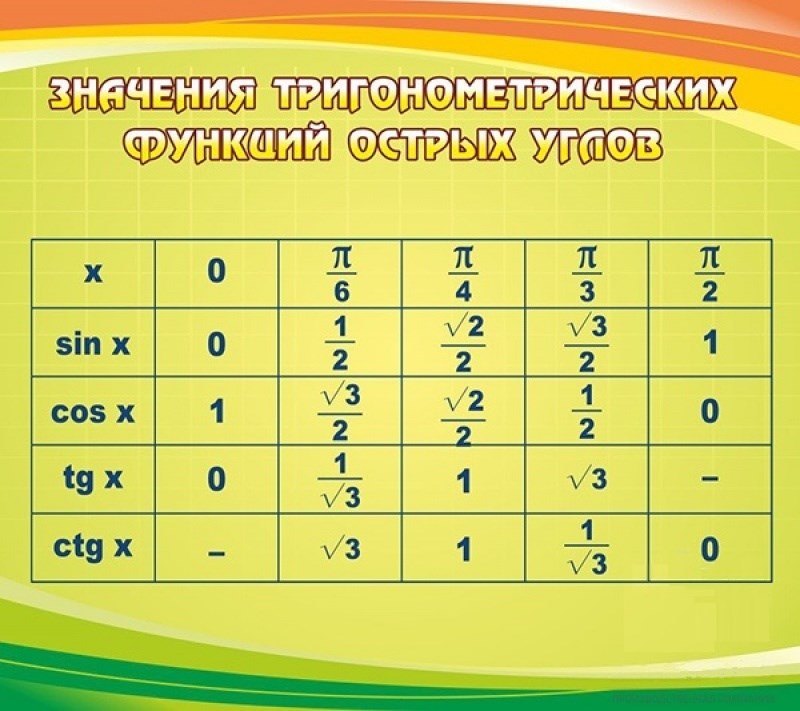 0003
0003
Субъекты:
Фоника, стратегии чтения, написание
Оценки:
Prek — 2nd
Типы:
Учебные программы Homeschool, песни
. Наш комплект брошюр по математике умножения x1-12 Trifold предоставляет учащимся несколько способов попрактиковаться в таблице фактов умножения x1-12 уникальным и интригующим способом, который вызовет интерес у всех учащихся 3-го и 4-го классов. 33 брошюры включены с различными стратегиями и Упражнения:Быстрые факты ПрактикаЗаполнение пробеловЗадачи со словамиЛабиринт множественных Поиск уравнения умножения(как поиск слов)Числовые строкиРавные группыРаскраска по номерамСоответствиеПропустить подсчетМассивыЧисловые связиИстина или F
Субъекты:
Основные операции, математика, номера
. практиковать, в которой они нуждаются, в увлекательной форме. Они будут развивать выносливость при письме, повторять построение букв и цифр и практиковаться в словах, изучая новые шутки и забавные факты! и почерк, который не является «детским»? Глупые шутки и забавные факты привлекут ваших учеников, пока они
Объекты:
Сбалансированная грамотность, почерк, написание
Оценки:
1 -й — 3 -й
Типы:
Независимый рабочий пакет, печатные изделия, рабочие листы
на
Ничего, кроме класса
$ 15,75
. Это новое исследование. for Holes, написанный Луи Сашаром , содержит 124 страницы ресурсов, включая понимание и словарный запас по главам, действия по чтению ответов, оценки и многое другое. Стандарты фокусировки включают образный язык, тему, анализ персонажей, сюжет и написание мнений. Не требующее подготовки, предсказуемое и чрезвычайно удобное для пользователя, это руководство по литературе идеально подходит для всего класса, небольшой группы или самостоятельного изучения. ♥Вы можете использовать печатную или цифровую версию; ОБА входят в комплект поставки Pur 9.0003
Это новое исследование. for Holes, написанный Луи Сашаром , содержит 124 страницы ресурсов, включая понимание и словарный запас по главам, действия по чтению ответов, оценки и многое другое. Стандарты фокусировки включают образный язык, тему, анализ персонажей, сюжет и написание мнений. Не требующее подготовки, предсказуемое и чрезвычайно удобное для пользователя, это руководство по литературе идеально подходит для всего класса, небольшой группы или самостоятельного изучения. ♥Вы можете использовать печатную или цифровую версию; ОБА входят в комплект поставки Pur 9.0003
Субъекты:
Английский язык искусства, литература, чтение
. RL.3.6, RL.3.7…
Также включено в: Holes and The Lion, the Witch, and the Wardrobe | Novel Study Bundle
by
Joanne Miller
Увеличьте вовлеченность и азарт с помощью этих интерактивных игровых досок с помощью стикеров. Эти игровые доски можно использовать с любым предметом или уроком.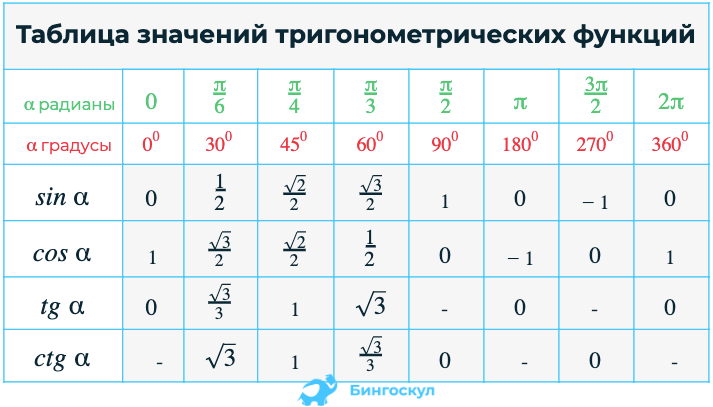 Они идеально подходят для обзора или подготовки к тесту. Учащиеся могут работать как команды, партнеры или весь класс. Используйте свой уже распечатанный рабочий лист или рабочую тетрадь и добавьте эти игровые доски, чтобы заинтересовать и мотивировать своих учеников! Это идеальный способ оживить повторный урок или использовать его для подготовки к экзамену. ***Включены версии PowerPoint и PDF. *Эти игровые доски были дези
Они идеально подходят для обзора или подготовки к тесту. Учащиеся могут работать как команды, партнеры или весь класс. Используйте свой уже распечатанный рабочий лист или рабочую тетрадь и добавьте эти игровые доски, чтобы заинтересовать и мотивировать своих учеников! Это идеальный способ оживить повторный урок или использовать его для подготовки к экзамену. ***Включены версии PowerPoint и PDF. *Эти игровые доски были дези
Предметы:
Английский язык, для всех предметов, математика
Классы:
2-6
Типы:
Занятия, игры, презентации PowerPoint
Также включено в: Комплект интерактивных игр | Вовлечение учащихся
by
Деб Хэнсон
29,50 $
14,75 $
Bundle
В этом наборе документальной текстовой структуры есть все, что вам нужно, чтобы заинтересовать учащихся старших классов начальной и средней школы в изучении ПЯТИ информационных текстовых структур. Он включает в себя 92 нехудожественных отрывка. Упражнения в этом наборе сделают изучение текстовых структур легким и увлекательным! Ученикам нравятся занятия, а учителям нравится удобство этих не требующих подготовки ресурсов, которые можно использовать год за годом! Эти задания по структуре научно-популярного текста можно использовать для подготовки к экзаменам, повторения,
Упражнения в этом наборе сделают изучение текстовых структур легким и увлекательным! Ученикам нравятся занятия, а учителям нравится удобство этих не требующих подготовки ресурсов, которые можно использовать год за годом! Эти задания по структуре научно-популярного текста можно использовать для подготовки к экзаменам, повторения,
Предметы:
Английский язык, информационный текст, чтение
Классы:
4–6
Типы:
Занятия, урок
3 CC:
3 CC: RI.4.5, RI.5.5, RI.5.6, RI.6.5
by
Haley O’Connor
Есть ли в вашем классе учащиеся, нуждающиеся в дополнительной поддержке поведения? Вы тратите драгоценное учебное время, постоянно перенаправляя нескольких трудных учеников, и не знаете, что делать, чтобы поддержать их? Этот пакет ПОЛЕН ресурсов, идей и инструментов, которые помогут каждому учащемуся в вашем классе добиться успеха. Этот ресурс идеально подходит для любого учителя начальных классов, которому нужны дополнительные ресурсы по поведению для поддержки учеников в своем классе! Работая ВМЕСТЕ со студентом, вы сможете создать сильные
Subjects:
Classroom Community, Classroom Management, School Counseling
Grades:
K — 2nd
Types:
Classroom Forms, Printables
by
Especially Education
$21. 00
00
$16.80
Bundle
Перед загрузкой обратите внимание, что эта загрузка включает в себя: Наглядные расписания Полезные раздаточные материалы Наглядные материалы и поддержка позитивного поведения Листы данных Наряду со стрессом обучения специальные преподаватели часто тратят бессчетное количество часов на создание значков, наглядных материалов, расписаний, поддержки позитивного поведения, информационных листов и т. д. Сделайте свою школу год станет немного проще с этим изменяющим жизнь комплектом специального образования: — шаблоны доски с жетонами — поддержка положительного поведения — сначала / затем диаграммы — значки подкрепления — визуальные расписания — s
Субъекты:
Вернуться в школу, управление классом, специальное образование
Оценки:
Prek — 4th
Типы:
Оценка, раздаточные материалы
на
Эми Гроусбек
СОХРАНИТЕ 25% и покупка избранных Ag Fonts. в РАСТУЩЕМ ПАКЕТЕ! Этот пакет шрифтов включает в себя 9 шрифтов истинного типа: AG 180 DaysAG Все, что вам нужно, это SleepAG Я не могуAG Я даже не могуAG Monday BundayAG Нет, не сегодняAG Running Late is My CardioAG Извините, не извинитеAG Third is the WordВсе шрифты включают Испанский, французский, норвежский и немецкий акценты, а также макронизированные гласные. ** ОБНОВЛЕНО: 17 февраля 22 ** Добавлены заглавные буквы в All You Need is Sleep и Third is the Word. Посмотрите предварительный просмотр, чтобы увидеть, что именно ты получишь!W
** ОБНОВЛЕНО: 17 февраля 22 ** Добавлены заглавные буквы в All You Need is Sleep и Third is the Word. Посмотрите предварительный просмотр, чтобы увидеть, что именно ты получишь!W
Субъекты:
Продукты для продавцов TPT
Оценки:
Не специфические оценки
Типы:
от продавцов TPT для продавцов TPT, Fonts
также включены в: Amy Groesbeck Fonts: растущий пучок
на
. Учитель по соседству
18,00 $
14,25 $
Bundle
Ищете способ сделать обучение написанию абзацев намного проще? Хотите помочь своим ученикам писать хорошо продуманные абзацы? Этот полный набор для написания абзацев как в печатном, так и в цифровом виде поможет вам научить каждую часть абзаца напрямую! Он сочетает в себе четыре из моих очень популярных наборов стратегий письма: цветовое кодирование и выделение абзацев, тематические предложения, переходы в письме и заключительные предложения. Здесь есть все, что вам нужно, чтобы помочь вашим ученикам по-настоящему понять, как создавать
Предметы:
Английская словесность, информационный текст, письменное разъяснение
Классы:
3-8
Типы:
Графические органайзеры, плакаты
CCSS:
4, W.
 3.3004, W.30003 .5.2, W.5.2a, W.5.2b…
3.3004, W.30003 .5.2, W.5.2a, W.5.2b… by
Lucky Little Learners
34,00 $
23,00 $
Bundle
Phonics, а также отрывки для чтения без печати или Phonics Mats ресурс, который поможет учащимся превратить отдельные фонетические навыки в чтение текста! Учащиеся практикуют изолированные фонетические навыки, декодирование, беглость речи и понимание в одном ресурсе. *** НОВОЕ ОБНОВЛЕНИЕ *** Этот ресурс обновлен новой версией 2022 года! В новых ковриках для фонетики есть декодируемые отрывки, вопросы на понимание, практика написания слов и страница для разминки для каждого навыка. Обязательно загрузите превью
Предметы:
Акустика, чтение, письмо
Классы:
Типы:
Печатные формы, рабочие листы
CCSS:
RF.2.3, RF.2.3c, RF.2.3b, RF.2.2.2 .2.3d…
by
Peachie Speechie
39,00 $
Этот систематический пошаговый подход к R-терапии — все, что вам нужно для обучения самым угрожающим звукам! Узнайте, почему он получил более 1300 5-звездочных отзывов! Эта тетрадь MUST HAVE у каждого логопеда! Профессиональные иллюстрации учат студентов анатомии рта, а подробные пошаговые изображения помогают врачу и студенту использовать различные методы для получения точных результатов. Вовлекающие действия включены для практики в изоляции, слоги, слова,
Вовлекающие действия включены для практики в изоляции, слоги, слова,
Предметы:
Специальное образование, логопедия
Классы:
1–6
Типы:
Занятия, рабочие тетради, рабочие листы
by
Lucky Little Learners
25,00 $
20,00 $
Bundle
Этот спиральный математический ресурс для 2-го класса С 3 УРОВНЯМИ ДИФФЕРЕНЦИАЦИИ представляет собой идеальные математические рабочие листы для ежедневных математических центров, а также для самостоятельного изучения математики в утренние часы, выполнения домашних заданий. Это хороший спиральный обзор, который проведет вас через весь год и доступен как в печатном, так и в цифровом форматах. Обзор спиральной математики для 2-го класса на ВЕСЬ ГОД включает 40 недель листов спиральной математики с ключами для ответов. Что включено в комплект Spiral Math Review Sheets:►Краткий обзор►40 Weeks of Spiral M
Предметы:
Измерение, разрядность, задачи со словами
Классы:
Типы:
Печатные формы, рабочие листы
CCSS:
2. MD.A.1, 2.2.2.A. MD.A.3, 2.MD.A.4, 2.MD.B.5…
MD.A.1, 2.2.2.A. MD.A.3, 2.MD.A.4, 2.MD.B.5…
по
Специально для образования
Если вы ищете индивидуальное расписание, визуальное расписание или сначала доску, в этом ресурсе поддержки позитивного поведения есть все! Обратите внимание: все редактируемые файлы совместимы с Microsoft PowerPoint. Некоторые страницы теперь можно редактировать с помощью Google Slides. В эту загрузку включены: — Варианты флипбука с 6 и 2 вкладками — Более 200 визуальных значков расписания (они не редактируются) — Сначала доска (отдельно от флипбука) — Сначала затем доска (отдельно от флипбука) — доски жетонов (wi
Предметы:
Снова в школу, Специальное образование, Логопедия
Классы:
PreK — 2nd
Типы:
Расписание мероприятий
реальные фотографии)
на
Речевые размышления
$15.00
Целевая перспектива, делающая выводы и прогнозы, используя реальные фотографии с этим ресурсом! Этот ресурс включает 100 карточек с реальными изображениями, которые позволяют вам обеспечить эффективное, прямое обучение тому, как делать выводы из изображений. Стратегия (вместе с начальными предложениями для студентов, чтобы обеспечить дополнительную поддержку). Рядом с фотографией есть четыре вопроса, которые требуют от ваших учеников
Стратегия (вместе с начальными предложениями для студентов, чтобы обеспечить дополнительную поддержку). Рядом с фотографией есть четыре вопроса, которые требуют от ваших учеников
Субъекты:
Школьное консультирование, специальное образование, речевая терапия
Оценки:
K — 6th
Типы:
Действия, печатные изготовления
также включены в: Real Pictures Resource Bundle для речевой терапии
My Teaching Pal
12,00 $
8,00 $
Bundle
ОГРОМНЫЙ комплект рабочих листов с предложениями поможет вашим учащимся отработать ряд навыков грамотности, связанных с беглостью, редактированием, письмом и грамматикой. Этот комплект идеально подходит для центров обучения грамоте, общеклассных мероприятий, домашних заданий, интервенционных программ и многого другого! В этот комплект входят следующие 4 пакета: 1. Sentence ScrambleСтуденты расшифровывают предложения, чтобы сформировать простое предложение. Это упражнение отлично подходит для изучения и понимания базовой структуры предложения. Есть 20 страниц я
Это упражнение отлично подходит для изучения и понимания базовой структуры предложения. Есть 20 страниц я
Тема:
Английский язык искусства, фонетика, написание
Оценки:
Prek — 1st
Типы:
, Центры, рабочие листы
на
для многих видов, но этот пакет NO PREP наполнен практическими, увлекательными и забавными ресурсами, которые помогут детям освоить эту концепцию. Час⭐️ Время с шагом в десять минут⭐️ Время с шагом в пять минут⭐️ Время с шагом в 1 минутуЛУЧШЕЕ в этом пакете то, что НЕТ ПОДГОТОВКИ! БЕЗ ламинирования, БЕЗ дорогостоящих цветных чернил, БЕЗ резки… просто ПЕЧАТАЙТЕ и УЧИТЕСЬ!
Предметы:
Классы:
1-3
Типы:
Центры, Печатные формы, Рабочие листы
по
Плыть во Вторую Письменность с Aris как важный этап обучения
9004 9004 900 Эти практические занятия по письму помогут вашим учащимся не только улучшить свои навыки письма, но и научатся творческому самовыражению и получат массу удовольствия. ✏️Если вы ищете страницы для практики скорописи, не ищите дальше. Этот пакет содержит более 120 страниц, полных веселых и увлекательных заданий, которые помогут вашим ученикам красиво печатать курсивом! Его используют более 12 000 учителей по всему миру, и он будет
✏️Если вы ищете страницы для практики скорописи, не ищите дальше. Этот пакет содержит более 120 страниц, полных веселых и увлекательных заданий, которые помогут вашим ученикам красиво печатать курсивом! Его используют более 12 000 учителей по всему миру, и он будет
Объекты:
Вернуться в школу, почерк, написание
Оценки:
2 -е — 5 -е
Типы:
, печатные изготовления, рабочие листы
на
Whimsy Workshop Ученик
Здание Senture. предложения! Это всеобъемлющий набор из более чем 80 рабочих листов с практическими упражнениями для практики написания полных простых предложений. Учащиеся вырезают и упорядочивают слова, чтобы построить каждое простое предложение, затем пишут, иллюстрируют, редактируют предложение самостоятельно и редактируют его коллеги. На одной странице собрано множество навыков! Этот продукт является бестселлером TPT! Пожалуйста, ознакомьтесь с тысячами положительных отзывов об этом ресурсе, чтобы увидеть, как его используют другие учителя!»0003
Предметы:
Сбалансированная грамотность, английский язык, письмо
Классы:
K — 2nd
Типы:
Центры, печатные формы, рабочие листы
CC. W. 1, CCRA.L.2
W. 1, CCRA.L.2
Также включено в: Мини-комплект построения предложений 1 — Практика написания предложений, 1-й класс
Решение | Триггерные таблицы | Тригонометрия: треугольники к функциям
Выход из полноэкранного режима
В приведенных ниже таблицах \(0\leq \theta \leq 2\pi\) и любые отсутствующие функции взяты из следующего списка. \[\sin\theta\quad\cos\theta\quad\tan\theta\quad\sec\theta\quad\cosec\theta\quad\cot\theta\]
Отсутствуют заголовки некоторых строк и столбцов. Не используя калькулятор, попробуйте вычислить, какими они могут быть, и заполните таблицу. Функция не появляется дважды в одной и той же таблице.
\(\тета=\ldots\) \(\тета=\ldots\) \(\тета=\ldots\) \(-1\) \(\dfrac{\sqrt{3}}{2}\) \(\dfrac{1}{2}\) \(\ загар \тета\) неопределенный \(\sqrt{3}\) \(\сек\тета\) \(-\dfrac{2}{\sqrt{3}}\)
У нас есть множество инструментов, которые можно использовать для решения этой проблемы, не полагаясь на калькулятор. Например, мы могли бы
Например, мы могли бы
использовать эскизные графики функций
использовать специальные значения функций, такие как \(\cos \tfrac{\pi}{3} = \tfrac{1}{2}\) и \(\tan \tfrac{\pi}{4}= 1\)
использование треугольников или тригонометрических тождеств для определения значений одних функций по значениям других
использовать диаграмму единичного круга и симметрию для определения значений функций для углов больше \(\tfrac{\pi}{2}.\)
Мы будем использовать сочетание этих инструментов при описании двух подходов к заполнению первой таблицы.
Подход 1
Если \(\tan \theta\) не определено, то \(\cos \theta=0.\) Следовательно, \(\sec \theta\) также не определено, и единственные возможности для \(\theta \) в первом столбце: \(\tfrac{\pi}{2}\) и \(\tfrac{3\pi}{2}.\)
Так как \(\cot \tfrac{\pi}{2}=\cot \tfrac{3\pi}{2}=0\) отсутствующая функция должна быть \(\sin \theta\) или \(\ cosec \theta\), оба из которых равны \(-1\) только тогда, когда \(\theta = \tfrac{3\pi}{2}\), поэтому в первом столбце \(\theta = \tfrac{3 \pi}{2}. \)
\)
Нам нужно больше информации, чтобы решить, является ли отсутствующая функция \(\sin \theta\) или \(\cosec \theta.\)
Из верхней строки таблицы мы видим, что значение отсутствующей функции может быть \(\tfrac{1}{2}\), поэтому оно должно быть \(\sin \theta.\)
Теперь \(\tan \theta = \dfrac{\sin \theta}{\cos \theta} = \sin \theta \sec \theta.\) Это означает, что мы можем заполнить оставшиеся ячейки в таблице без зная значения \(\theta.\)
Чтобы найти значения \(\theta\), мы можем распознать в таблице определенные специальные значения, такие как \(\tfrac{\sqrt{3}}{2 } =\sin \tfrac{\pi}{3}\) и \(\tfrac{1}{2}=\sin \tfrac{\pi}{6}\), но нам нужно решить, означает ли это, что значения \(\theta\) равны \(\tfrac{\pi}{3}\) и \(\tfrac{\pi}{6}\) или связанные с ними углы, например \(\tfrac{ \pi}{3}+\pi.\)
Из графиков этих функций мы можем проверить, где функции положительные и отрицательные, чтобы принять решение о значениях \(\theta.\)
Подход 2
Альтернативной отправной точкой было бы отметить, что в третьем столбец, \(\cos\theta = -\tfrac{\sqrt{3}}{2}\), поэтому \(\theta\) должно быть \(\tfrac{5\pi}{6}\) или \ (\tfrac{7\pi}{6}. \) Единственная функция, которая имеет значение \(\tfrac{1}{2}\) при любом из этих значений \(\theta\), это \(\sin\ theta\), и оно принимает это значение только тогда, когда \(\theta = \tfrac{5\pi}{6}.\) Теперь таблицу можно заполнить, используя аргумент, аналогичный приведенному выше.
\) Единственная функция, которая имеет значение \(\tfrac{1}{2}\) при любом из этих значений \(\theta\), это \(\sin\ theta\), и оно принимает это значение только тогда, когда \(\theta = \tfrac{5\pi}{6}.\) Теперь таблицу можно заполнить, используя аргумент, аналогичный приведенному выше.
Как могут измениться ответы, если \(\theta\) может быть любым значением?
Что, если бы для заполнения таблицы можно было использовать такие функции, как \(- \sin \theta\)?
Мы были ограничены \(0\leq \theta \leq 2\pi.\) В противном случае \(\theta\) может принимать любое значение вида \(\dfrac{\pi}{3}+2n\pi \) и \(\dfrac{5\pi}{6}+2n\pi\), где \(n\) — целое число. Если бы нам разрешили использовать такие функции, как \(-\sin\theta\), то проблема не имела бы единственного решения.
На этот раз мы предоставили дополнительную информацию о \(\theta.\) Попробуйте определить недостающие функции и заполнить таблицу. Помните, что нельзя пользоваться калькулятором!
\(\тета\) является рефлексом \(\тета=\ldots\) \(\тета\) тупой \(0\) \(-\dfrac{3}{5}\) \(\косек\тета\) \(1\) \(\dfrac{5}{4}\) \(\dfrac{5}{12}\) \(0\)
Давайте начнем со второго столбца, потому что мы знаем, где находятся определенные функции \(1\) или \(0. \) Опять же, \(\theta\) ограничено \(0\leq \theta \leq 2\pi \), поэтому \(\cosec \theta = 1\) верно только тогда, когда \(\theta\) равно \(\tfrac{\pi}{2}.\) Теперь мы можем подумать о том, какие функции равны \(0 \) когда \(\theta = \tfrac{\pi}{2}.\) Так как \(\tan \tfrac{\pi}{2}\) и \(\sec \tfrac{\pi}{2} \) не определены, единственными возможными вариантами отсутствующих функций являются \(\cos \theta\) и \(\cot \theta.\)
\) Опять же, \(\theta\) ограничено \(0\leq \theta \leq 2\pi \), поэтому \(\cosec \theta = 1\) верно только тогда, когда \(\theta\) равно \(\tfrac{\pi}{2}.\) Теперь мы можем подумать о том, какие функции равны \(0 \) когда \(\theta = \tfrac{\pi}{2}.\) Так как \(\tan \tfrac{\pi}{2}\) и \(\sec \tfrac{\pi}{2} \) не определены, единственными возможными вариантами отсутствующих функций являются \(\cos \theta\) и \(\cot \theta.\)
Как и \(\cos \theta\), так и \(\cot \theta \) может быть \(\tfrac{5}{12}\) и \(-\tfrac{3}{5}\), нам нужно больше информации, чтобы решить, какая функция находится в верхней строке, а какая в нижней. row (помните, что функция не может появляться в таблице дважды). Оба \(\cos \theta\) и \(\cot \theta\) отрицательны, когда \(\theta\) тупые, и оба могут быть отрицательными или положительными, когда \(\theta\) является рефлексом, поэтому знаки не Не помогите нам здесь. 92 \theta.\)
Если \(\cot \theta\) была правильной функцией для верхней строки, то подстановка \(-\tfrac{3}{5}\) вместо \(\cot \theta\) и \(\tfrac{5}{4}\) для \(\cosec \theta\) должны удовлетворять этому тождеству.
 00
00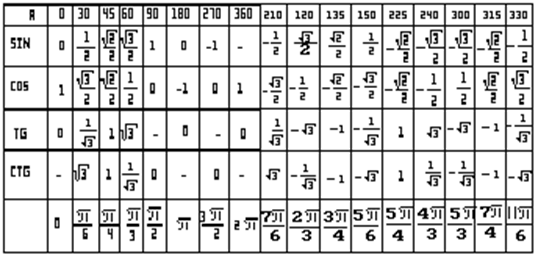 ** ОБНОВЛЕНО: 17 февраля 22 ** Добавлены заглавные буквы в All You Need is Sleep и Third is the Word. Посмотрите предварительный просмотр, чтобы увидеть, что именно ты получишь!W
** ОБНОВЛЕНО: 17 февраля 22 ** Добавлены заглавные буквы в All You Need is Sleep и Third is the Word. Посмотрите предварительный просмотр, чтобы увидеть, что именно ты получишь!W Вовлекающие действия включены для практики в изоляции, слоги, слова,
Вовлекающие действия включены для практики в изоляции, слоги, слова, MD.A.1, 2.2.2.A. MD.A.3, 2.MD.A.4, 2.MD.B.5…
MD.A.1, 2.2.2.A. MD.A.3, 2.MD.A.4, 2.MD.B.5…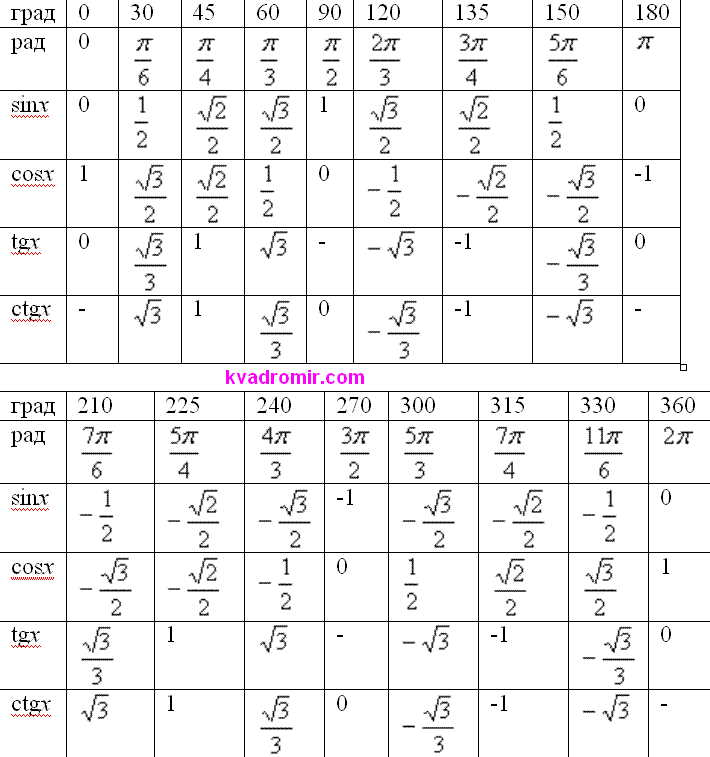 Стратегия (вместе с начальными предложениями для студентов, чтобы обеспечить дополнительную поддержку). Рядом с фотографией есть четыре вопроса, которые требуют от ваших учеников
Стратегия (вместе с начальными предложениями для студентов, чтобы обеспечить дополнительную поддержку). Рядом с фотографией есть четыре вопроса, которые требуют от ваших учеников Это упражнение отлично подходит для изучения и понимания базовой структуры предложения. Есть 20 страниц я
Это упражнение отлично подходит для изучения и понимания базовой структуры предложения. Есть 20 страниц я ✏️Если вы ищете страницы для практики скорописи, не ищите дальше. Этот пакет содержит более 120 страниц, полных веселых и увлекательных заданий, которые помогут вашим ученикам красиво печатать курсивом! Его используют более 12 000 учителей по всему миру, и он будет
✏️Если вы ищете страницы для практики скорописи, не ищите дальше. Этот пакет содержит более 120 страниц, полных веселых и увлекательных заданий, которые помогут вашим ученикам красиво печатать курсивом! Его используют более 12 000 учителей по всему миру, и он будет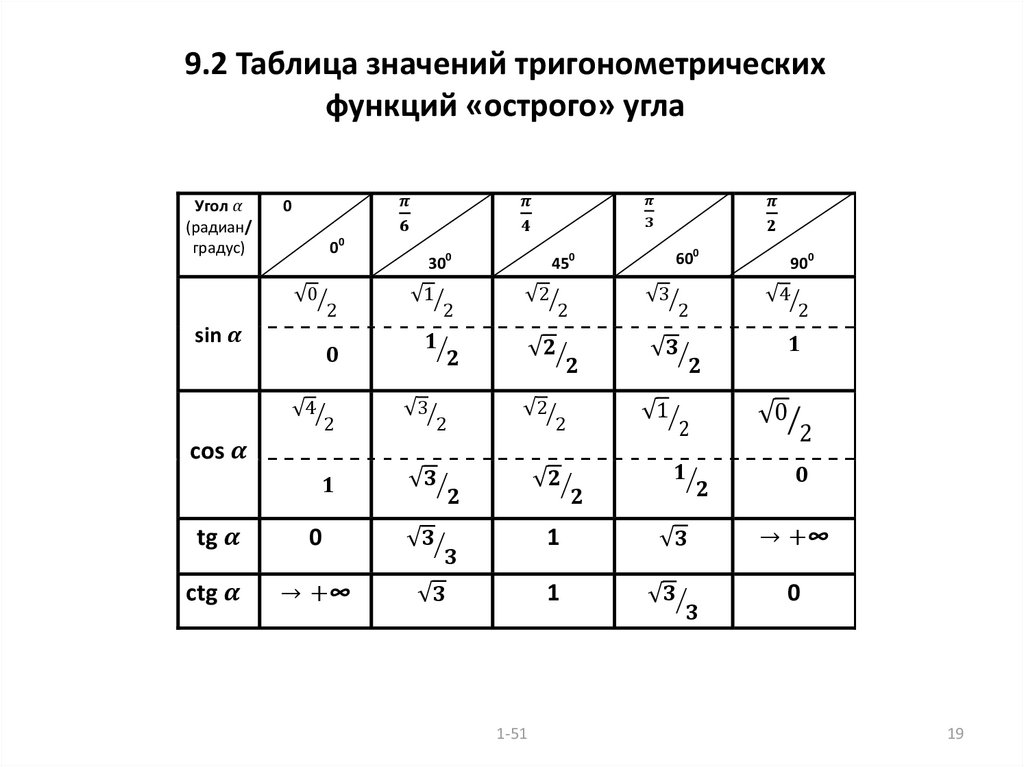 W. 1, CCRA.L.2
W. 1, CCRA.L.2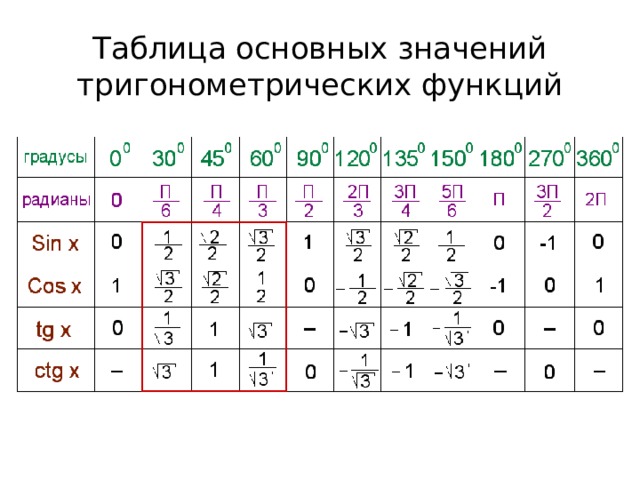 Например, мы могли бы
Например, мы могли быиспользовать эскизные графики функций
использовать специальные значения функций, такие как \(\cos \tfrac{\pi}{3} = \tfrac{1}{2}\) и \(\tan \tfrac{\pi}{4}= 1\)
использование треугольников или тригонометрических тождеств для определения значений одних функций по значениям других
использовать диаграмму единичного круга и симметрию для определения значений функций для углов больше \(\tfrac{\pi}{2}.\)
 \)
\) \) Единственная функция, которая имеет значение \(\tfrac{1}{2}\) при любом из этих значений \(\theta\), это \(\sin\ theta\), и оно принимает это значение только тогда, когда \(\theta = \tfrac{5\pi}{6}.\) Теперь таблицу можно заполнить, используя аргумент, аналогичный приведенному выше.
\) Единственная функция, которая имеет значение \(\tfrac{1}{2}\) при любом из этих значений \(\theta\), это \(\sin\ theta\), и оно принимает это значение только тогда, когда \(\theta = \tfrac{5\pi}{6}.\) Теперь таблицу можно заполнить, используя аргумент, аналогичный приведенному выше. \) Опять же, \(\theta\) ограничено \(0\leq \theta \leq 2\pi \), поэтому \(\cosec \theta = 1\) верно только тогда, когда \(\theta\) равно \(\tfrac{\pi}{2}.\) Теперь мы можем подумать о том, какие функции равны \(0 \) когда \(\theta = \tfrac{\pi}{2}.\) Так как \(\tan \tfrac{\pi}{2}\) и \(\sec \tfrac{\pi}{2} \) не определены, единственными возможными вариантами отсутствующих функций являются \(\cos \theta\) и \(\cot \theta.\)
\) Опять же, \(\theta\) ограничено \(0\leq \theta \leq 2\pi \), поэтому \(\cosec \theta = 1\) верно только тогда, когда \(\theta\) равно \(\tfrac{\pi}{2}.\) Теперь мы можем подумать о том, какие функции равны \(0 \) когда \(\theta = \tfrac{\pi}{2}.\) Так как \(\tan \tfrac{\pi}{2}\) и \(\sec \tfrac{\pi}{2} \) не определены, единственными возможными вариантами отсутствующих функций являются \(\cos \theta\) и \(\cot \theta.\)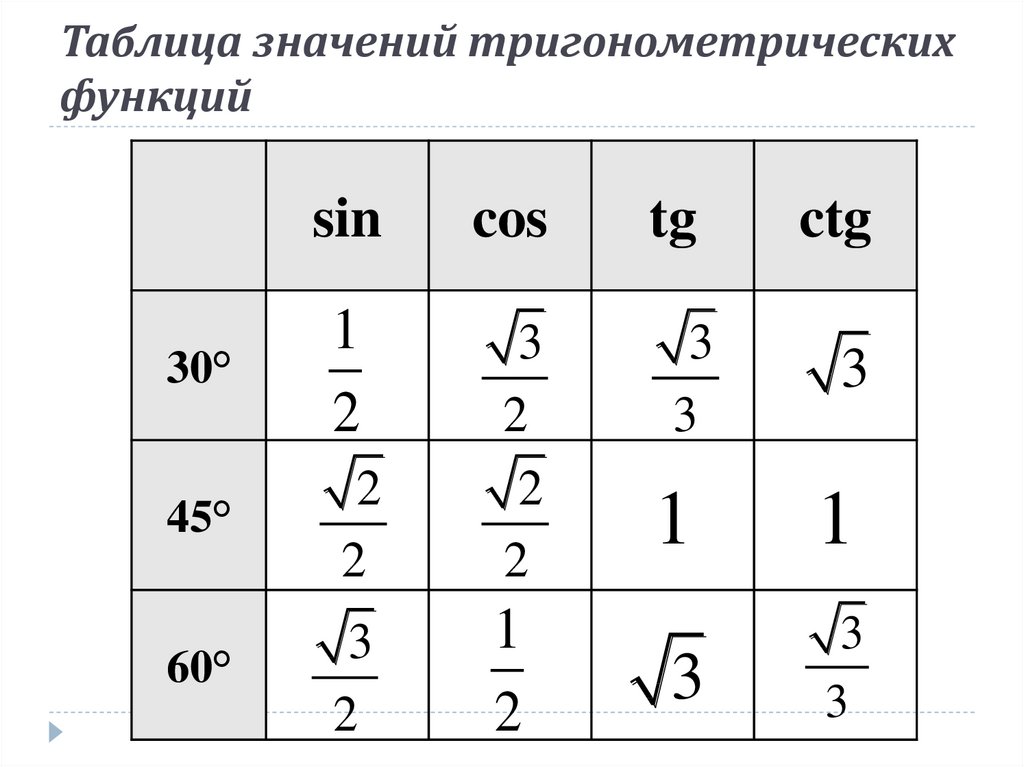

 3.3004, W.30003 .5.2, W.5.2a, W.5.2b…
3.3004, W.30003 .5.2, W.5.2a, W.5.2b…