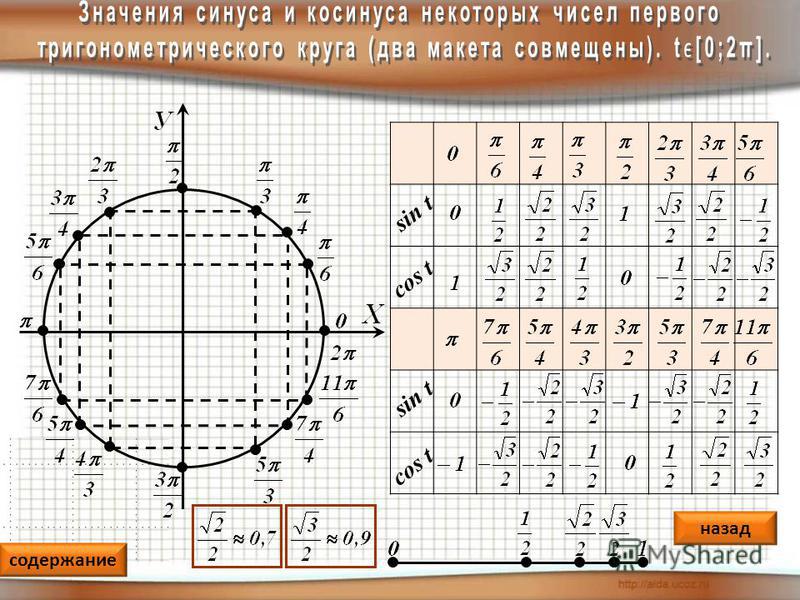
Таблица значений синуса, косинуса и т.д
Функция | Значения | |||||||||
| 00 | | 300 | | 450 | | 600 | | 900 | |
cosx | 1 | 0 | ||||||||
sinx | 0 | 1 | ||||||||
tgx | 0 | 1 | — | |||||||
| ctgx | — | 1 | 0 | |||||||
Соседние файлы в папке Теория по темам
- #
20.
04.201515.87 Кб6Среднее арифметическое.doc - #
20.04.201518.43 Кб6Средняя линия.doc
- #
20.04.201522.53 Кб7Степенная функция.doc
- #
20.04.201528.16 Кб6Степень.doc
- #
20.04.201524.06 Кб6Сумма разность векторов.doc
- #
20.04.201530.72 Кб12Таблица значений синуса, косинуса и т.д..doc
20.04.201519.46 Кб8Теорема Виета.doc
- #
20.04.201520.48 Кб8Теорема косинусов.doc
- #
20.04.201520.48 Кб6Трапеция.doc
- #
20.04.201522.02 Кб6Углы на плоскости.doc
- #
20.04.201518.43 Кб6Уравнение движения.doc
04.201515.87 Кб6Среднее арифметическое.docSine — OeisWiki
Этот сайт поддерживается за счет пожертвований в Фонд OEIS.
Из OeisWiki
Перейти к: навигация, поиск
Эта страница статьи является незавершенной, пожалуйста, помогите, развернув ее.
Функция sine является элементарной трансцендентной функцией. Синус угла
, обозначаемый как
, является одной из важнейших [круговых] тригонометрических функций.Содержание
- 1 Таблица значений синуса и косинуса
- 2 Расширение серии Taylor
- 3 формулы
- 4 См. также
- 5 Примечания
Учитывая угол
дуги на единичной окружности,
— это длина стороны прямоугольного треугольника, противостоящей вершине, совпадающей с центром окружности (две другие стороны треугольника — это гипотенуза, а сторона, это линия вдоль
).
- (ЗАПОЛНИТЕЛЬ ДЛЯ ИЗОБРАЖЕНИЯ) [1]
Per the Pythagorean theorem,
| (sin θ ) 2 + (cos θ ) 2 = 1 |
, usually written
| sin 2 θ + cos 2 θ = 1 |
(где
| SIN 2 θ : = (SIN θ ) 2 |
, т.е. не вну0003
).
График синусоидальной функции дал начало термину «синусоидальная волна», чтобы различать извилистые волны, которые выглядят следующим образом
(синус выделен красным, косинус синим) и пилообразными и треугольными волнами.
Таблица значений синуса и косинуса
Десятичные разложения синуса от 1 до 89 градусов см.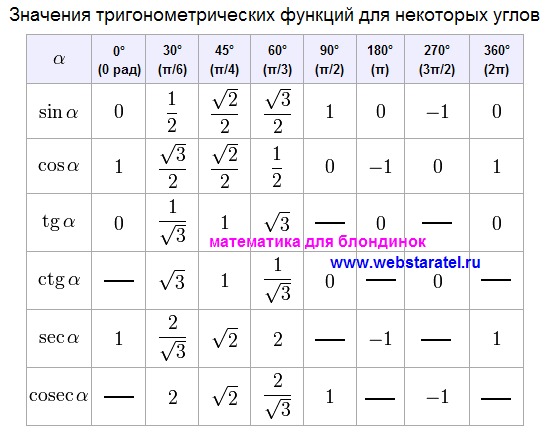
от A019810 до A019898 (число A задается 19809 плюс желаемое количество градусов от 1 до 89, за исключением 30, 45 и 60 градусов). В следующей таблице
| y = 90 − x |
, а все нецелые значения даны с точностью до 8 знаков после запятой (щелкните ссылку для записи последовательности для большей точности).
Расширение ряда Тейлора
Расширение синуса в ряд Тейлора
SIN x = ∑ 9002 9003 9002
x 2 N +1 = x —(−1) N (2 N + 1)!
+x 3 3!
−x 5 5!
+ ⋯.x 7 7!
Формулы
(…)
См. также
- {{ sin }} шаблон математической функции
Примечания
- ↑ Предоставьте иллюстрацию.
Sine Cosine
| void | arm_sin_cos_f32 (float32_t theta, float32_t *pSinVal, float32_t *pCosVal) |
| Функция sin_cos с плавающей запятой. More… | |
| void | arm_sin_cos_q31 (q31_t theta, q31_t *pSinVal, q31_t *pCosVal) |
| Q31 sin_cos function. Подробнее… | |
Вычисляет значения тригонометрического синуса и косинуса, используя комбинацию поиска по таблице и линейной интерполяции. Существуют отдельные функции для Q31 и типов данных с плавающей запятой.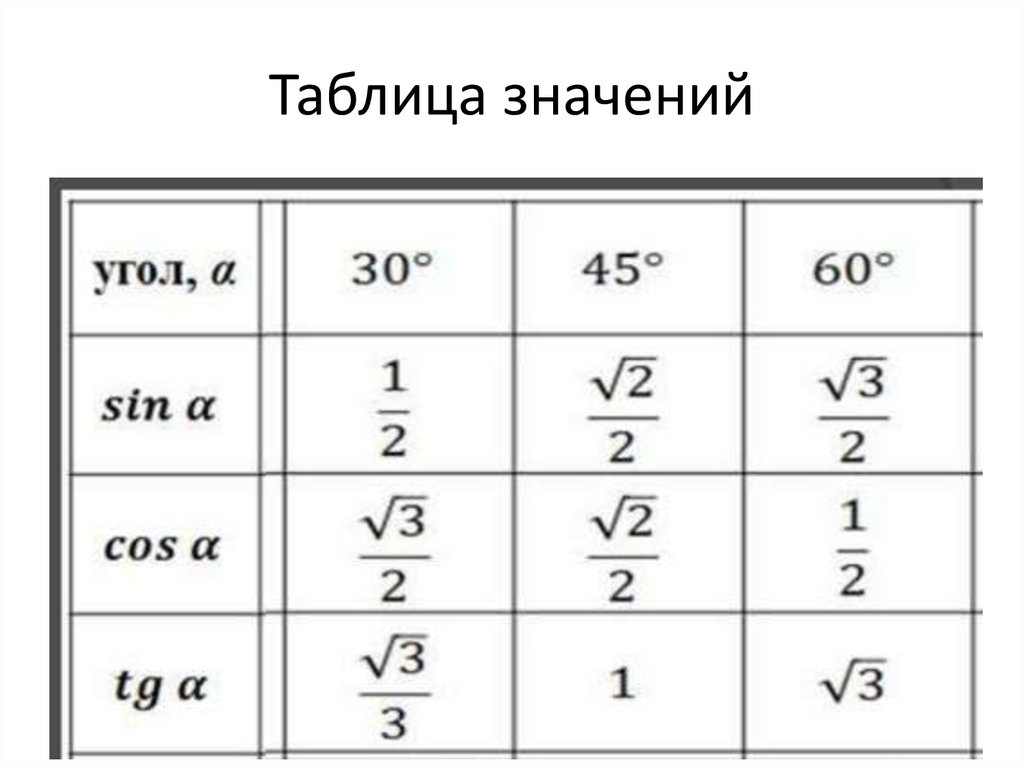
Вход для версии с плавающей запятой находится в градусах, в то время как Q31 с фиксированной точкой имеет масштабированный вход с диапазоном [-1 0,9999] отображение на [-180 +180] градусов.
Функция с плавающей запятой также допускает значения, выходящие за пределы обычного диапазона. Когда это произойдет, функции потребуется дополнительное время, чтобы настроить входное значение в диапазоне [-180 180].
Результат с точностью до 5 знаков после запятой.
Реализация основана на поиске по таблице с использованием 360 значений вместе с линейной интерполяцией. Используемые шаги:
- Вычисление ближайшего целочисленного индекса таблицы.
- Вычислить дробную часть (фракцию) входных данных.
- Получить значение, соответствующее индексу
y0, а также значение изindex+1вy1. - Значение синуса вычисляется как
*psinVal = y0 + (fract * (y1 - y0)). - Получить значение, соответствующее индексу
y0, а также значение изindex+1вy1. - Значение косинуса вычисляется как
*pcosVal = y0 + (fract * (y1 - y0)).
| пустота arm_sin_cos_f32 | ( | float32_t | тета , |
| float32_t * | pSinVal , | ||
| float32_t * | pCosVal | ||
| ) |
- Параметры
[in] theta input value in degrees [out] pSinVal points to processed sine output [out] pCosVal points to processed cosine output
- Возвращает
- нет
| void arm_sin_cos_q31 | ( | q31_t | тета , |
| q31_t * | pSinVal , | ||
| q31_t * | pCosVal | ||
| ) |
- Параметры
[In] THETA Масштабированное входное значение в градусах [Out] PSINVAL POCTIEND SINE [Out Out outs [Out Out outs [Out Out outs [Out outs [Out outs [Out oute oute [Out out oute .
