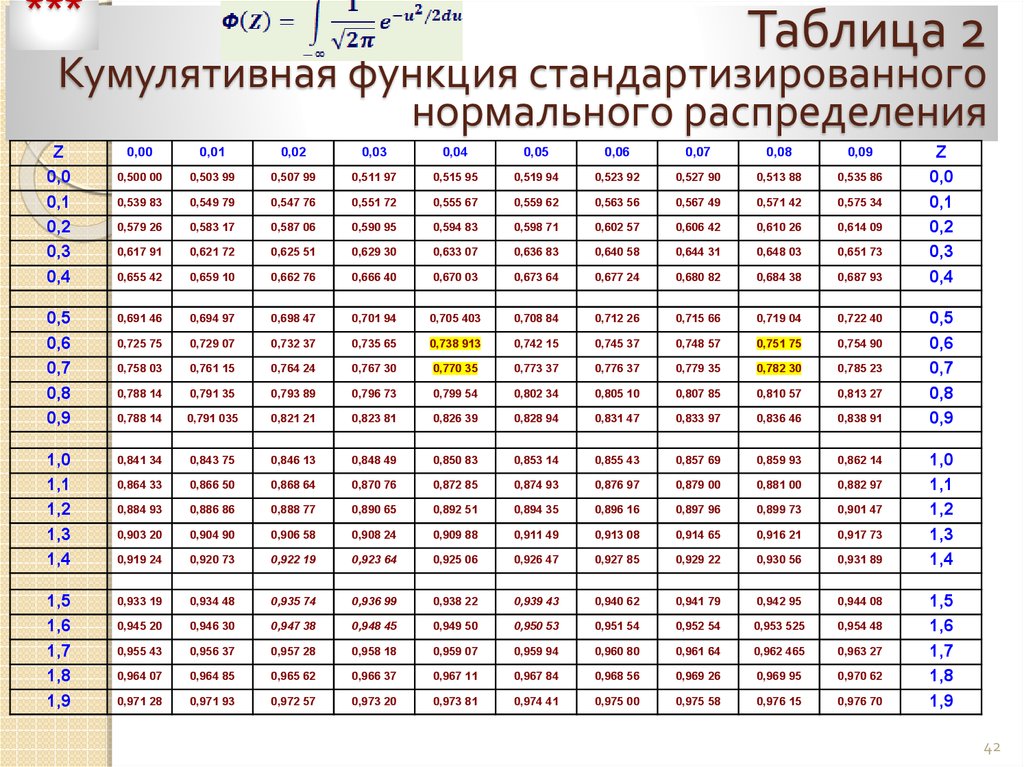
Таблица значений функции Лапласа
Примеры решенийКоэффициент СпирменаКоэффициент Фехнера Множественная регрессияНелинейная регрессия Уравнение регрессии Автокорреляция Расчет параметров трендаОшибка аппроксимации
| x | Ф(x) | x | Ф(x) | x | Ф(x) | x | Ф(x) |
| 0.00 | 0.0000 | 0.32 | 0.1255 | 0.64 | 0.2389 | 0.96 | 0.3315 |
| 0.01 | 0.0040 | 0.33 | 0.1293 | 0.65 | 0.2422 | 0. | 0.3340 |
| 0.02 | 0.0080 | 0.34 | 0.1331 | 0.66 | 0.2454 | 0.98 | 0.3365 |
| 0.03 | 0.0120 | 0.35 | 0.1368 | 0.67 | 0.2486 | 0.99 | 0.3389 |
| 0.04 | 0.0160 | 0.36 | 0.1406 | 0.68 | 0.2517 | 1.00 | 0.3413 |
| 0.05 | 0.0199 | 0.37 | 0.1443 | 0.69 | 0.2549 | 1.01 | 0.3438 |
| 0.06 | 0.0239 | 0.38 | 0.1480 | 0.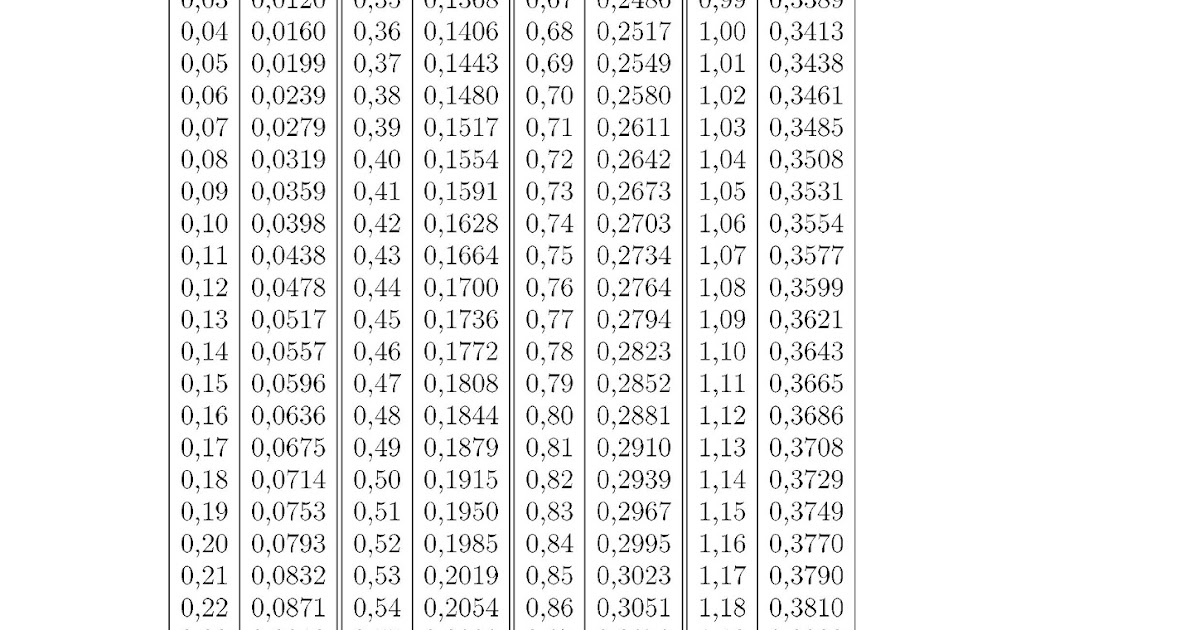 70 70
| 0.2580 | 1.02 | 0.3461 |
| 0.07 | 0.0279 | 0.39 | 0.1517 | 0.71 | 0.2611 | 1.03 | 0.3485 |
| 0.08 | 0.0319 | 0.40 | 0.1554 | 0.72 | 0.2642 | 1.04 | 0.3508 |
| 0.09 | 0.0359 | 0.41 | 0.1591 | 0.73 | 0.2673 | 1.05 | 0.3531 |
| 0.10 | 0.0398 | 0.42 | 0.1628 | 0.74 | 0.2703 | 1.06 | 0.3554 |
| 0.11 | 0.0438 | 0.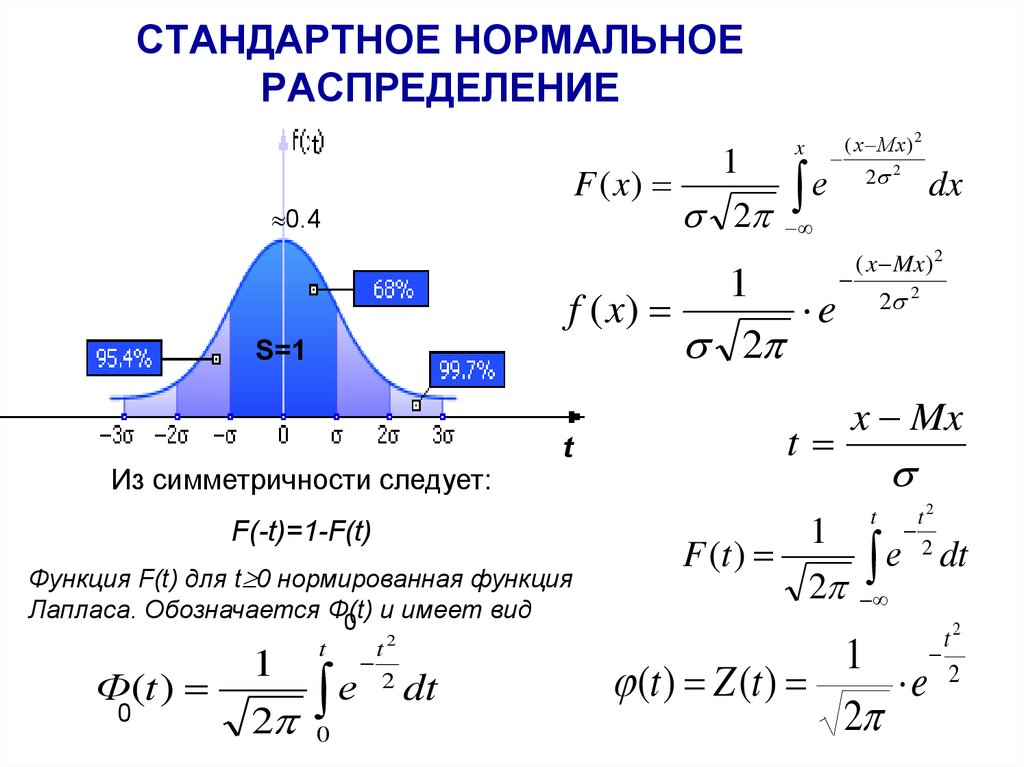 43 43
| 0.1664 | 0.75 | 0.2734 | 1.07 | 0.3577 |
| 0.12 | 0.0478 | 0.44 | 0.1700 | 0.76 | 0.2764 | 1.08 | 0.3599 |
| 0.13 | 0.0517 | 0.45 | 0.1736 | 0.77 | 0.2794 | 1.09 | 0.3621 |
| 0.14 | 0.0557 | 0.46 | 0.1772 | 0.78 | 0.2823 | 1.10 | 0.3643 |
| 0.15 | 0.0596 | 0.47 | 0.1808 | 0.79 | 0.2852 | 1.11 | 0.3665 |
0. 16 16
| 0.0636 | 0.48 | 0.1844 | 0.80 | 0.2881 | 1.12 | 0.3686 |
| 0.17 | 0.0675 | 0.49 | 0.1879 | 0.81 | 0.2910 | 1.13 | 0.3708. |
| 0.18 | 0.0714 | 0.50 | 0.1915 | 0.82 | 0.2939 | 1.14 | 0.3729 |
| 0.19 | 0.0753 | 0.51 | 0.1950 | 0.83 | 0.2967 | 1.15 | 0.3749 |
| 0.20 | 0.0793 | 0.52 | 0.1985 | 0.84 | 0.2995 | 1. 16 16
| 0.3770 |
| 0.21 | 0.0832 | 0.53 | 0.2019 | 0.85 | 0.3023 | 1.17 | 0.3790 |
| 0.22 | 0.0871 | 0.54 | 0.2054 | 0.86 | 0.3051 | 1.18 | 0.3810 |
| 0.23 | 0.0910 | 0.55 | 0.2088 | 0.87 | 0.3078 | 1.19 | 0.3830 |
| 0.24 | 0.0948 | 0.56 | 0.2123 | 0.88 | 0.3106 | 1.20 | 0.3849 |
| 0.25 | 0.0987 | 0.57 | 0.2157 | 0. 89 89
| 0.3133 | 1.21 | 0.3869 |
| 0.26 | 0.1026 | 0.58 | 0.2190 | 0.90 | 0.3159 | 1.22 | 0/3883 |
| 0.27 | 0.1064 | 0.59 | 0.2224 | 0.91 | 0.3186 | 1.23 | 0.3907 |
| 0.28 | 0.1103 | 0.60 | 0.2257 | 0.92 | 0.3212 | 1.24 | 0.3925 |
| 0.29 | 0.1141 | 0.61 | 0.2291 | 0.93 | 0.3238 | 1.25 | 0.3944 |
| 0.30 | 0.1179 | 0. 62 62
| 0.2324 | 0.94 | 0.3264 | ||
| 0.31 | 0.1217 | 0.63 | 0.2357 | 0.95 | 0.3289 |
| x | Ф(x) | x | Ф(x) | x | Ф(x) | x | Ф(x) |
| 1.26 | 0.3962 | 1.59 | 0.4441 | 1.92 | 0.4726 | 2.50 | 0.4938 |
| 1.27 | 0.3980 | 1.60 | 0.4452 | 1.93 | 0.4732 | 2.52 | 0.4941 |
| 1.28 | 0.3997 | 1.61 | 0. 4463 4463
| 1.94 | 0.4738 | 2.54 | 0.4945 |
| 1.29 | 0.4015 | 1.62 | 0.4474 | 1.95 | 0.4744 | 2.56 | 0.4948 |
| 1.30 | 0.4032 | 1.63 | 0.4484 | 1.96 | 0.4750 | 2.58 | 0.4951 |
| 1.31 | 0.4049 | 1.64 | 0.4495 | 1.97 | 0.4756 | 2.60 | 0.4953 |
| 1.32 | 0.4066 | 1.65 | 0.4505 | 1.98 | 0.4761 | 2.62 | 0.4956 |
1. 33 33
| 0.4082 | 1.66 | 0.4515 | 1.99 | 0.4767 | 2.64 | 0.4959 |
| 1.34 | 0.4099 | 1.67 | 0.4525 | 2.00 | 0.4772 | 2.66 | 0.4961 |
| 1.35 | 0.4115 | 1.68 | 0.4535 | 2.02 | 0.4783 | 2.68 | 0.4963 |
| 1.36 | 0.4131 | 1.69 | 0.4545 | 2.04 | 0.4793 | 2.70 | 0.4965 |
| 1.37 | 0.4147 | 1.70 | 0.4554 | 2.06 | 0.4803 | 2.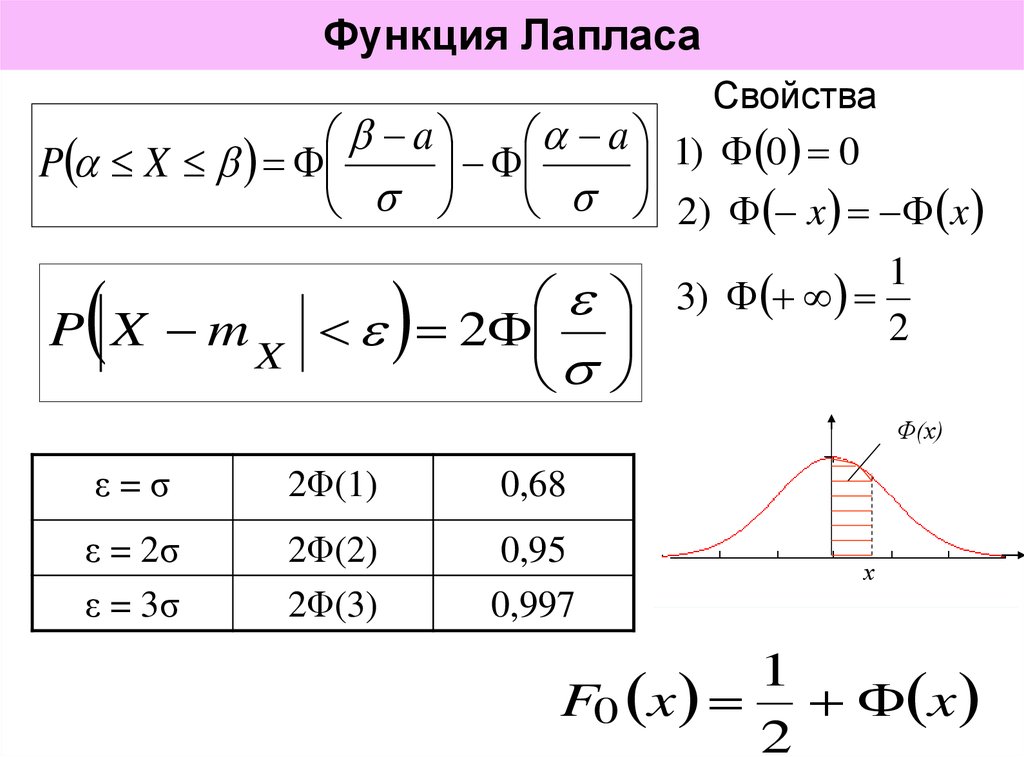 72 72
| 0.4967 |
| 1.38 | 0.4162 | 1.71 | 0.4564 | 2.08 | 0.4812 | -2.74 | 0.4969 |
| 1.39 | 0.4177 | 1.72 | 0.4573 | 2.10 | 0.4821 | 2.76 | 0.4971 |
| 1.40 | 0.4192 | 1.73 | 0.4582 | 2.12 | 0.4830 | 2.78 | 0.4973 |
| 1.41 | 0.4207 | 1.74 | 0.4591 | 2.14 | 0.4838 | 2.80 | 0.4974 |
| 1.42 | 0.4222 | 1.75 | 0. 4599 4599
| 2.16 | 0.4846 | 2.82 | 0.4976 |
| 1.43 | 0.4236 | 1.76 | 0.4608 | 2.18 | 0.4854 | 2.84 | 0.4977 |
| 1.44 | 0.4251 | 1.77 | 0.4616 | 2.20 | 0.4861 | 2.86 | 0.4979 |
| 1.45 | 0.4265 | 1.78 | 0.4625 | 2.22 | 0.4868 | 2.88 | 0.4980 |
| 1.46 | 0.4279 | 1.79 | 0.4633 | 2.24 | 0.4875 | 2.90 | 0.4981 |
1. 47 47
| 0.4292 | 1.80 | 0.4641 | 2.26 | 0.4881 | 2.92 | 0.4982 |
| 1.48 | 0.4306 | 1.81 | 0.4649 | 2.28 | 0.4887 | 2.94 | 0.4984 |
| 1.49 | 0.4319 | 1.82 | 0.4656 | 2.30 | 0.4893 | 2.96 | 0.4985 |
| 1.50 | 0.4332 | 1.83 | 0.4664 | 2.32 | 0.4898 | 2.98 | 0.4986 |
| 1.51 | 0.4345 | 1.84 | 0.4671 | 2.34 | 0.4904 | 3. 00 00
| 0.49865 |
| 1.52 | 0.4357 | 1.85 | 0.4678 | 2.36 | 0.4909 | 3.20 | 0.49931 |
| 1.53 | 0.4370 | 1.86 | 0.4686 | 2.38 | 0.4913 | 3.40 | 0.49966 |
| 1.54 | 0.4382 | 1.87 | 0.4693 | 2.40 | 0.4918 | 3.60 | 0.49984 |
| 1.55 | 0.4394 | 1.88 | 0.4699 | 2.42 | 0.4922 | 3.80 | 0.49992 |
| 1.56 | 0.4406 | 1.89 | 0.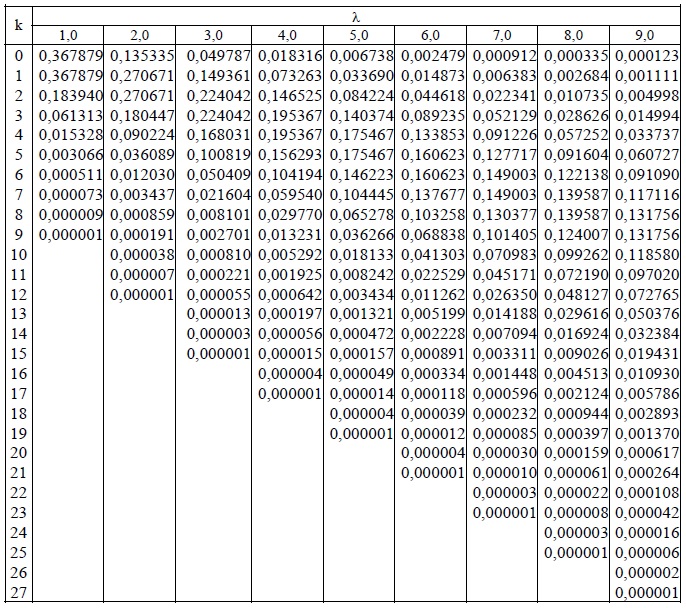 4706 4706
| 2.44 | 0.4927 | 4.00 | 0.49996 |
| 1.57 | 0.4418 | 1.90 | 0.4713 | 2.46 | 0.4931 | 4.50 | 0.49999 |
| 1.58 | 0.4429 | 1 1.91 | 0.4719 | 2.48 | 0.4934 | > 5.00 | 0.49999 |
Задать свои вопросы или оставить замечания можно внизу страницы в разделе Disqus.
Можно также оставить заявку на помощь в решении своих задач у наших проверенных партнеров (здесь или здесь).
Функция Лапласа. Полная таблица значений интегральной функции Лапласа онлайн. Теория вероятностей и математическая статистика
В таблице даны значения функции
для положительных значений
и для
;
для
пользуются той же таблицей, так как функция
нечетна, то есть
. В таблице приведены значения интеграла лишь до
,
так как для
можно принять
.
Эту функцию называют функцией Лапласа.
В таблице приведены значения интеграла лишь до
,
так как для
можно принять
.
Эту функцию называют функцией Лапласа.
Таблица значений функции Лапласа в теории вероятностей и математической статистике используется довольно часто. На сайте можно посмотреть примеры ее использования в следующих задачах:
- Отклонение относительной частоты от постоянной вероятности в независимых испытаниях
- Интегральная теорема Муавра – Лапласа
- Доверительные интервалы для среднего и дисперсии
- Проверка гипотезы о равенстве средних
Цветом в таблице подсвечены аргументы функции Лапласа, рядом, в соседнем столбце — значения функции Лапласа.
| x | Ф(x) | x | Ф(x) | x | Ф(x) | x | Ф(x) |
| 0,00 | 0,0000 | 0,32 | 0,1255 | 0,64 | 0,2389 | 0,96 | 0,3315 |
| 0,01 | 0,0040 | 0,33 | 0,1293 | 0,65 | 0,2422 | 0,97 | 0,3340 |
| 0,02 | 0,0080 | 0,34 | 0,1331 | 0,66 | 0,2454 | 0,98 | 0,3365 |
| 0,03 | 0,0120 | 0,35 | 0,1368 | 0,67 | 0,2486 | 0,99 | 0,3389 |
| 0,04 | 0,0160 | 0,36 | 0,1406 | 0,68 | 0,2517 | 1,00 | 0,3413 |
| 0,05 | 0,0199 | 0,37 | 0,1443 | 0,69 | 0,2549 | 1,01 | 0,3438 |
| 0,06 | 0,0239 | 0,38 | 0,1480 | 0,70 | 0,2580 | 1,02 | 0,3461 |
| 0,07 | 0,0279 | 0,39 | 0,1517 | 0,71 | 0,2611 | 1,03 | 0,3485 |
| 0,08 | 0,0319 | 0,40 | 0,1554 | 0,72 | 0,2642 | 1,04 | 0,3508 |
| 0,09 | 0,0359 | 0,41 | 0,1591 | 0,73 | 0,2673 | 1,05 | 0,3531 |
| 0,10 | 0,0398 | 0,42 | 0,1628 | 0,74 | 0,2703 | 1,06 | 0,3554 |
| 0,11 | 0,0438 | 0,43 | 0,1664 | 0,75 | 0,2734 | 1,07 | 0,3577 |
| 0,12 | 0,0478 | 0,44 | 0,1700 | 0,76 | 0,2764 | 1,08 | 0,3599 |
| 0,13 | 0,0517 | 0,45 | 0,1736 | 0,77 | 0,2794 | 1,09 | 0,3621 |
| 0,14 | 0,0557 | 0,46 | 0,1772 | 0,78 | 0,2823 | 1,10 | 0,3643 |
| 0,15 | 0,0596 | 0,47 | 0,1808 | 0,79 | 0,2852 | 1,11 | 0,3665 |
| 0,16 | 0,0636 | 0,48 | 0,1844 | 0,80 | 0,2881 | 1,12 | 0,3686 |
| 0,17 | 0,0675 | 0,49 | 0,1879 | 0,81 | 0,2910 | 1,13 | 0,3708 |
| 0,18 | 0,0714 | 0,50 | 0,1915 | 0,82 | 0,2939 | 1,14 | 0,3729 |
| 0,19 | 0,0753 | 0,51 | 0,1950 | 0,83 | 0,2967 | 1,15 | 0,3749 |
| 0,20 | 0,0793 | 0,52 | 0,1985 | 0,84 | 0,2995 | 1,16 | 0,3770 |
| 0,21 | 0,0832 | 0,53 | 0,2019 | 0,85 | 0,3023 | 1,17 | 0,3790 |
| 0,22 | 0,0871 | 0,54 | 0,2054 | 0,86 | 0,3051 | 1,18 | 0,3810 |
| 0,23 | 0,0910 | 0,55 | 0,2088 | 0,87 | 0,3078 | 1,19 | 0,3830 |
| 0,24 | 0,0948 | 0,56 | 0,2123 | 0,88 | 0,3106 | 1,20 | 0,3849 |
| 0,25 | 0,0987 | 0,57 | 0,2157 | 0,89 | 0,3133 | 1,21 | 0,3869 |
| 0,26 | 0,1026 | 0,58 | 0,2190 | 0,90 | 0,3159 | 1,22 | 0,3883 |
| 0,27 | 0,1064 | 0,59 | 0,2224 | 0,91 | 0,3186 | 1,23 | 0,3907 |
| 0,28 | 0,1103 | 0,60 | 0,2257 | 0,92 | 0,3212 | 1,24 | 0,3925 |
| 0,29 | 0,1141 | 0,61 | 0,2291 | 0,93 | 0,3238 | 1,25 | 0,3944 |
| 0,30 | 0,1179 | 0,62 | 0,2324 | 0,94 | 0,3264 | ||
| 0,31 | 0,1217 | 0,63 | 0,2357 | 0,95 | 0,3289 |
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Продолжение таблицы
| x | Ф(x) | x | Ф(x) | x | Ф(x) | x | Ф(x) |
| 1,26 | 0,3962 | 1,59 | 0,4441 | 1,92 | 0,4726 | 2,50 | 0,4938 |
| 1,27 | 0,3980 | 1,60 | 0,4452 | 1,93 | 0,4732 | 2,52 | 0,4941 |
| 1,28 | 0,3997 | 1,61 | 0,4463 | 1,94 | 0,4738 | 2,54 | 0,4945 |
| 1,29 | 0,4015 | 1,62 | 0,4474 | 1,95 | 0,4744 | 2,56 | 0,4948 |
| 1,30 | 0,4032 | 1,63 | 0,4484 | 1,96 | 0,4750 | 2,58 | 0,4951 |
| 1,31 | 0,4049 | 1,64 | 0,4495 | 1,97 | 0,4756 | 2,60 | 0,4953 |
| 1,32 | 0,4066 | 1,65 | 0,4505 | 1,98 | 0,4761 | 2,62 | 0,4956 |
| 1,33 | 0,4082 | 1,66 | 0,4515 | 1,99 | 0,4767 | 2,64 | 0,4959 |
| 1,34 | 0,4099 | 1,67 | 0,4525 | 2,00 | 0,4772 | 2,66 | 0,4961 |
| 1,35 | 0,4115 | 1,68 | 0,4535 | 2,02 | 0,4783 | 2,68 | 0,4963 |
| 1,36 | 0,4131 | 1,69 | 0,4545 | 2,04 | 0,4793 | 2,70 | 0,4965 |
| 1,37 | 0,4147 | 1,70 | 0,4554 | 2,06 | 0,4803 | 2,72 | 0,4967 |
| 1,38 | 0,4162 | 1,71 | 0,4564 | 2,08 | 0,4812 | -2,74 | 0,4969 |
| 1,39 | 0,4177 | 1,72 | 0,4573 | 2,10 | 0,4821 | 2,76 | 0,4971 |
| 1,40 | 0,4192 | 1,73 | 0,4582 | 2,12 | 0,4830 | 2,78 | 0,4973 |
| 1,41 | 0,4207 | 1,74 | 0,4591 | 2,14 | 0,4838 | 2,80 | 0,4974 |
| 1,42 | 0,4222 | 1,75 | 0,4599 | 2,16 | 0,4846 | 2,82 | 0,4976 |
| 1,43 | 0,4236 | 1,76 | 0,4608 | 2,18 | 0,4854 | 2,84 | 0,4977 |
| 1,44 | 0,4251 | 1,77 | 0,4616 | 2,20 | 0,4861 | 2,86 | 0,4979 |
| 1,45 | 0,4265 | 1,78 | 0,4625 | 2,22 | 0,4868 | 2,88 | 0,4980 |
| 1,46 | 0,4279 | 1,79 | 0,4633 | 2,24 | 0,4875 | 2,90 | 0,4981 |
| 1,47 | 0,4292 | 1,80 | 0,4641 | 2,26 | 0,4881 | 2,92 | 0,4982 |
| 1,48 | 0,4306 | 1,81 | 0,4649 | 2,28 | 0,4887 | 2,94 | 0,4984 |
| 1,49 | 0,4319 | 1,82 | 0,4656 | 2,30 | 0,4893 | 2,96 | 0,4985 |
| 1,50 | 0,4332 | 1,83 | 0,4664 | 2,32 | 0,4898 | 2,98 | 0,4986 |
| 1,51 | 0,4345 | 1,84 | 0,4671 | 2,34 | 0,4904 | 3,00 | 0,49865 |
| 1,52 | 0,4357 | 1,85 | 0,4678 | 2,36 | 0,4909 | 3,20 | 0,49931 |
| 1,53 | 0,4370 | 1,86 | 0,4686 | 2,38 | 0,4913 | 3,40 | 0,49966 |
| 1,54 | 0,4382 | 1,87 | 0,4693 | 2,40 | 0,4918 | 3,60 | 0,499841 |
| 1,55 | 0,4394 | 1,88 | 0,4699 | 2,42 | 0,4922 | 3,80 | 0,499928 |
| 1,56 | 0,4406 | 1,89 | 0,4706 | 2,44 | 0,4927 | 4,00 | 0,499968 |
| 1,57 | 0,4418 | 1,90 | 0,4713 | 2,46 | 0,4931 | 4,50 | 0,499997 |
| 1,58 | 0,4429 | 1,91 | 0,4719 | 2,48 | 0,4934 | 5,00 | 0,499997 |
Таблица преобразования Лапласа ( F(s) = L{ f(t) } )
- Преобразование Лапласа функция
- Таблица преобразования Лапласа
- Свойства преобразования Лапласа
- Преобразование Лапласа примеры
Преобразование Лапласа преобразует функцию временной области в функцию s-области путем интегрирования от нуля до бесконечности
функции временной области, умноженной на e -st .
Преобразование Лапласа используется для быстрого нахождения решений дифференциальных уравнений и интегралов.
Вывод во временной области преобразуется в умножение на s в s-области.
Интегрирование во временной области преобразуется в деление на s в s-области.
Функция преобразования Лапласа
Преобразование Лапласа определяется оператором L {}:
Обратное преобразование Лапласа
Обратное преобразование Лапласа можно вычислить напрямую.
Обычно обратное преобразование дается из таблицы преобразований.
Таблица преобразования Лапласа
| Имя функции | Функция временной области | преобразование Лапласа |
|---|---|---|
ф ( т ) | F ( s ) = L { f ( t )} | |
| Константа | 1 | |
| Линейный | т | |
| Сила | т н | |
| Мощность | т а | Γ( a +1) ⋅ с -( a +1) |
| Экспонента | и по | |
| Синус | грех на | |
| Косинус | соз на | |
| Гиперболический синус | с по | |
| Гиперболический косинус | кош по | |
| Растущий синус | т син эт | |
| Растущий косинус | т соз в | |
| Затухающий синус | е -ат sin ωt | |
| Затухающий косинус | е -ат cos ωt | |
| Дельта-функция | δ( т ) | 1 |
| Дельта с задержкой | δ( т-а ) | е -как |
Свойства преобразования Лапласа
| Имя свойства | Функция временной области | преобразование Лапласа | Комментарий |
|---|---|---|---|
ф ( т ) | Ф ( с ) | ||
| Линейность | а ф ( т )+ бг ( т ) | аФ ( с ) + бГ ( с ) | а , б а константа |
| Смена шкалы | ф ( по ) | а >0 | |
| Смена | е -ат ф ( т ) | Ф ( с + а ) | |
| Задержка | ф ( т-а ) | e — как F ( с ) | |
| Производная | сф ( с ) — ф (0) | ||
| N-ая производная | с н ф ( с ) — s n -1 f (0) — s n -2 f ‘(0)-. ..- ф ( н -1) (0) ..- ф ( н -1) (0) | ||
| Мощность | т н ф ( т ) | ||
| Интеграция | |||
| Обратный | |||
| Свертка | ф ( т ) * г ( т ) | Ф ( с ) ⋅ Г ( с ) | * это свертка оператор |
| Периодическая функция | ф ( т ) = ф ( т + т ) |
Laplace transform examples
Example #1
Find the transform of f(t):
f ( t ) = 3 t + 2 t 2
Solution:
ℒ{ t } = 1/ s 2
ℒ{ t 2 } = 2/ s 3
F ( s ) = ℒ{ f ( t )} = ℒ{3 t + 2 t 2 } = 3ℒ{ t } + 2ℒ{ t 2 } = 3/ s 2 + 4/ s 3
Example #2
Find the inverse transform of F(s):
F ( с ) = 3 / ( с 2 + s — 6)
Решение:
Чтобы найти обратное преобразование, нам нужно изменить s доменной функции к более простой форме:
F ( с ) = 3 / ( с 2 + s — 6) = 3 / [( s -2)( s +3)] = a / ( s -2) + б / ( с +3)
[ а ( с +3) + б ( с -2)] / [( с -2)] / [( с — +3)] = 3 / [( с -2)( с +3)]
a ( с +3) + b ( с -2) = 3
Чтобы найти a и b, получаем 2 уравнения — одно из s коэффициентов и второе из остальных:
a + b = 0 , 3 a -2 b = 3
a = 3/5 , b = -3/5
F ( s ) = 3 / 5( с -2) — 3 / 5( с +3)
Теперь F(s) можно легко преобразовать с помощью таблицы преобразований для экспоненциальной функции:
f ( t ) = (3/5) e 2 t — (3/5) e -3 t
See also
- Производная
- Символы исчисления
Таблицы обратного преобразования Лапласа функции [Формула: см.
 текст]
текст]. 1990 г., июль-август; 95(4):433-467.
doi: 10.6028/jres.095.036.
Менахем Дишон 1 , Джон Т. Бендлер 2 , Джордж Х. Вайс 3
Принадлежности
- 1 Национальный институт стандартов и технологий, Gaithersburg, MD 20899.
- 2 Корпоративные исследования и разработки General Electric, Schenectady, NY 12301.
- 3 Национальные институты здравоохранения, Bethesda, MD 20892.
- PMID: 28179785
- PMCID: PMC4922407
- DOI:
10.
 6028/jres.095.036
6028/jres.095.036
Бесплатная статья ЧВК
Менахем Дишон и др. J Res Natl Inst Stand Technol. 1990 июль-август.
Бесплатная статья ЧВК
. 1990 г., июль-август; 95(4):433-467.
doi: 10.6028/jres.095.036.
Авторы
Менахем Дишон 1 , Джон Т. Бендлер 2 , Джордж Х. Вайс 3
Принадлежности
- 1 Национальный институт стандартов и технологий, Gaithersburg, MD 20899.

- 2 Корпоративные исследования и разработки General Electric, Schenectady, NY 12301.
- 3 Национальные институты здравоохранения, Бетесда, Мэриленд, 20892.
- PMID: 28179785
- PMCID: PMC4922407
- DOI: 10.6028/jres.095.036
Абстрактный
Обратное преобразование, [формула: см. текст], 0 < β < 1, является устойчивым законом, который возникает в ряде различных приложений в химической физике, физике полимеров, физике твердого тела и прикладной математике. Из-за его важных применений ряд исследователей предложил приближения к г ( т ). Однако до сих пор не было точно рассчитанных значений, доступных для проверки или других целей. Мы приводим здесь таблицы с точностью до шести цифр г ( т ) для ряда значений β от 0,25 до 0,999. Кроме того, поскольку g ( t ), рассматриваемое как функция β , является унимодальным с пиком, приходящимся на t = t max , мы оба заносим в таблицу и рисуем t
Из-за его важных применений ряд исследователей предложил приближения к г ( т ). Однако до сих пор не было точно рассчитанных значений, доступных для проверки или других целей. Мы приводим здесь таблицы с точностью до шести цифр г ( т ) для ряда значений β от 0,25 до 0,999. Кроме того, поскольку g ( t ), рассматриваемое как функция β , является унимодальным с пиком, приходящимся на t = t max , мы оба заносим в таблицу и рисуем t1. max
и 1/ g ( t max ) как функция β , а также дающие полиномиальные приближения к 1/ g ( t max ).
Ключевые слова: численное обращение преобразований Лапласа; релаксационные процессы; стабильные законы; растянутые экспоненты.
Цифры
Рисунок 1а
Кривые г ( т…
Рисунок 1а
Кривые г ( t ) как функция t в…
Рисунок 1а Кривые зависимости г ( t ) от t в окрестности пиковых значений для β =0,25, 0,275 и 0,30.
Рисунок 1b
Кривые г ( т…
Рисунок 1b
Кривые г ( t ) как функция t в…
Рисунок 1бКривые зависимости г ( t ) от t в окрестности пиковых значений для β =0,35(0,1)0,95.
Рисунок 1c
Кривые г ( т…
Рисунок 1c
Кривые g ( t ) как функция плавника окрестности…
Рисунок 1с Кривые зависимости г ( t ) от fin окрестности пиковых значений для β =0,99, 0,995, 0,997, 0,998 и 0,999. Дельта-функция в β =1 обозначено вертикальной линией.
Дельта-функция в β =1 обозначено вертикальной линией.
Рисунок 2а
Кривые t max и…
Рисунок 2а
Кривые т макс и 1/ г ( т макс ) построены как…
Рисунок 2аКривые t max и 1/ g ( t max ), построенные как функция β.
Рисунок 2b
Кривая 1/ г (…
Рисунок 2b
Кривая 1/ г ( т макс ) построена как функция…
Рисунок 2б Кривая 1/ г ( т макс ) построена как функция т макс .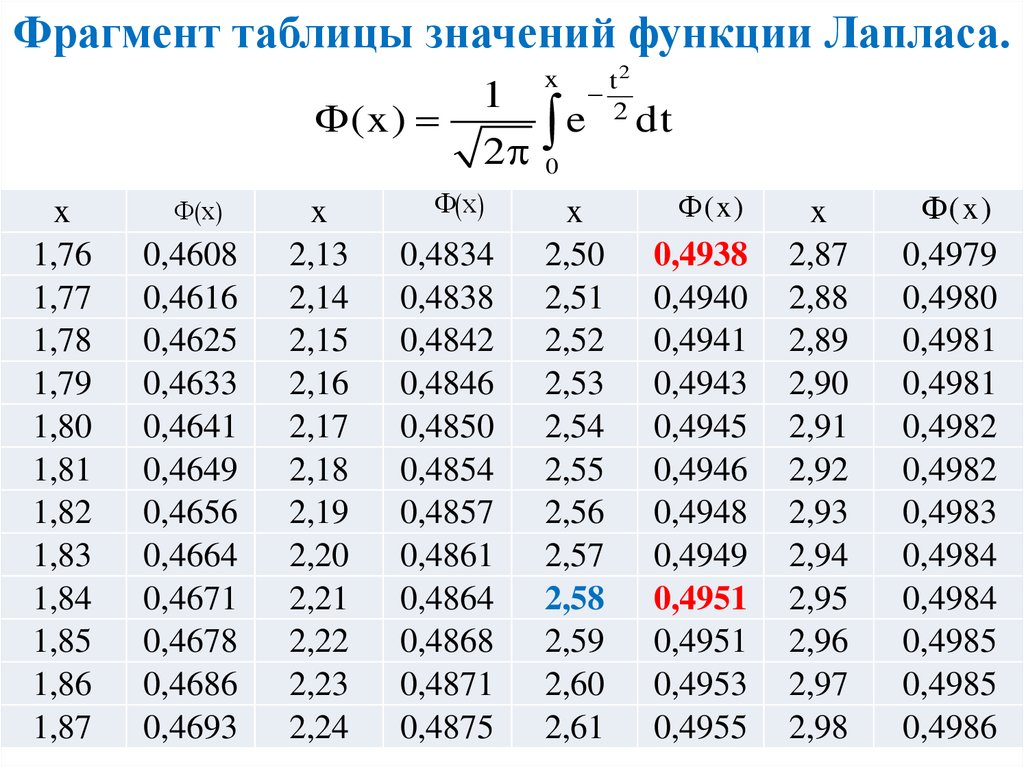
Рисунок 3
Многочлен от второй до четвертой степени…
Рисунок 3
Полиномиальные приближения от второй до четвертой степени до 1/ г ( т макс )…
Рисунок 3Полином второй-четвертой степени приближения к 1/ g ( t max ) как функция β по сравнению с более точно рассчитанным значением этой величины.
См. это изображение и информацию об авторских правах в PMC
Похожие статьи
Анализ обратного преобразования Лапласа растянутой экспоненциальной релаксации.
Чой Х, Виноград И, Чаффи С, Курро, Нью-Джерси.
 Чой Х и др.
Джей Магн Резон. 2021 окт;331:107050. doi: 10.1016/j.jmr.2021.107050. Epub 2021 21 августа.
Джей Магн Резон. 2021.
PMID: 34507236
Чой Х и др.
Джей Магн Резон. 2021 окт;331:107050. doi: 10.1016/j.jmr.2021.107050. Epub 2021 21 августа.
Джей Магн Резон. 2021.
PMID: 34507236Тип задачи обращения в физике: обратная задача коэффициента излучения.
Вэнь Т., Мин Д., Дай Х., Дай Дж., Эвенсон В.Е. Вен Т и др. Phys Rev E Stat Nonlin Soft Matter Phys. 2001, апрель; 63 (4 часть 2): 045601. doi: 10.1103/PhysRevE.63.045601. Epub 2001 19 марта. Phys Rev E Stat Nonlin Soft Matter Phys. 2001. PMID: 11308905
Физические свойства полимерных электролитов [Формула: см. текст]: ядерно-магнитный резонанс и сравнение с [Формулой: см. текст].
Ру С., Горецки В., Санчес Дж. Ю., Жаннин М., Белорицкий Э. Ру С и др.
 J Phys Конденсирует Материю. 1996 г., 16 сентября; 8(38):7005-17. дои: 10.1088/0953-8984/8/38/005.
J Phys Конденсирует Материю. 1996.
PMID: 22146538
J Phys Конденсирует Материю. 1996 г., 16 сентября; 8(38):7005-17. дои: 10.1088/0953-8984/8/38/005.
J Phys Конденсирует Материю. 1996.
PMID: 22146538[Метаанализ итальянских исследований краткосрочных последствий загрязнения воздуха].
Биггери А., Беллини П., Террачини Б.; Итальянская группа MISA. Биггери А. и др. Эпидемиол Пред. 2001 март-апрель; 25 (2 Дополнение): 1-71. Эпидемиол Пред. 2001. PMID: 11515188 итальянский.
Новые вычислительные методы в науке о цунами.
Беренс Дж., Диас Ф. Беренс Дж. и соавт. Philos Trans A Math Phys Eng Sci. 2015 28 октября; 373 (2053): 20140382. doi: 10.1098/rsta.2014.0382. Philos Trans A Math Phys Eng Sci.
 2015.
PMID: 26392612
Обзор.
2015.
PMID: 26392612
Обзор.
Посмотреть все похожие статьи
Рекомендации
Например, исторический обзор содержится в Leader−man
- Упругие свойства ползучести волокнистых материалов и других высокополимеров. Текстильный фонд; Вашингтон: 1943 год.
- Kohlrausch R. Pogg Ann Phys Chem. 1854;91:179.
- Ферри Джей Ди. Вязкоупругие свойства полимеров. Джон Уайли; Нью-Йорк: 1970.
- Маккрам Н.Г., Рид Б.Е., Уильямс Г.

- Маккрам Н.Г., Рид Б.Е., Уильямс Г.

 6028/jres.095.036
6028/jres.095.036
 Чой Х и др.
Джей Магн Резон. 2021 окт;331:107050. doi: 10.1016/j.jmr.2021.107050. Epub 2021 21 августа.
Джей Магн Резон. 2021.
PMID: 34507236
Чой Х и др.
Джей Магн Резон. 2021 окт;331:107050. doi: 10.1016/j.jmr.2021.107050. Epub 2021 21 августа.
Джей Магн Резон. 2021.
PMID: 34507236 J Phys Конденсирует Материю. 1996 г., 16 сентября; 8(38):7005-17. дои: 10.1088/0953-8984/8/38/005.
J Phys Конденсирует Материю. 1996.
PMID: 22146538
J Phys Конденсирует Материю. 1996 г., 16 сентября; 8(38):7005-17. дои: 10.1088/0953-8984/8/38/005.
J Phys Конденсирует Материю. 1996.
PMID: 22146538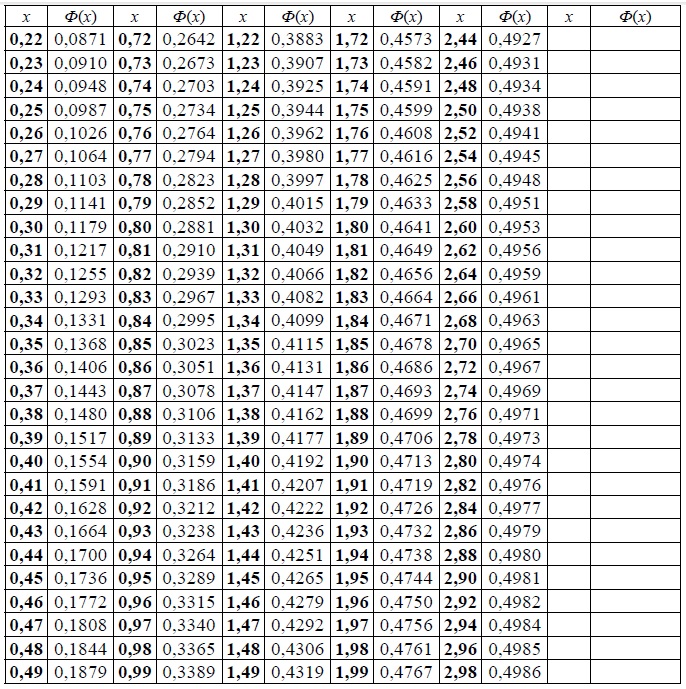 2015.
PMID: 26392612
Обзор.
2015.
PMID: 26392612
Обзор.