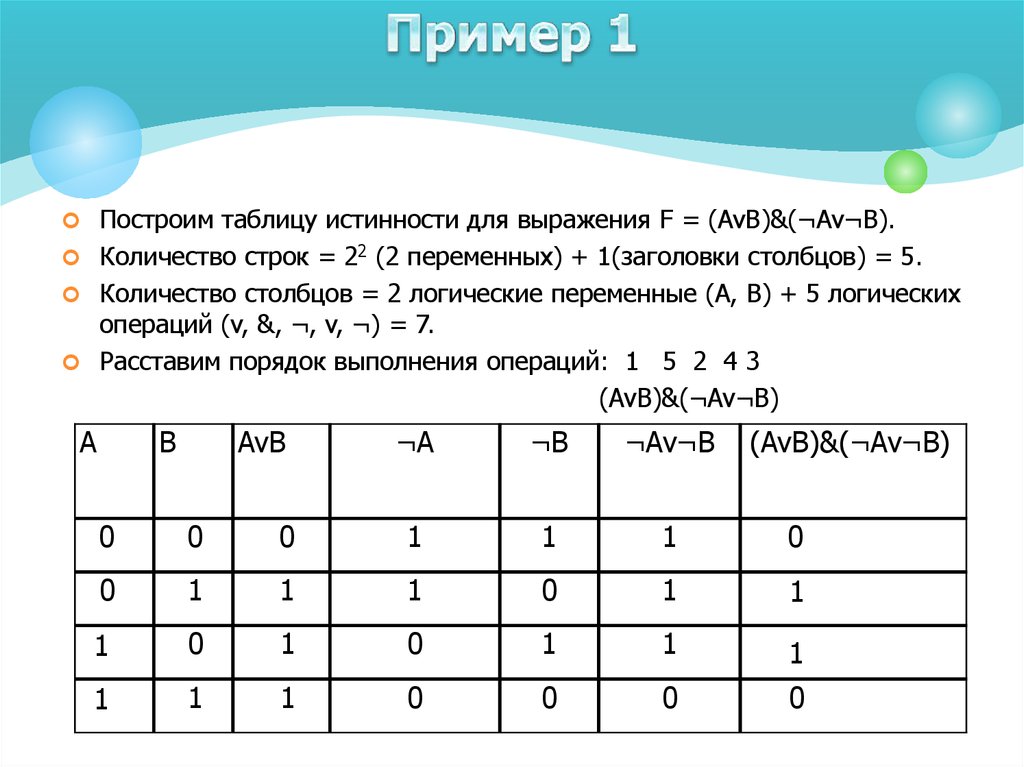
Построение таблиц истинности для логических выражений
Дата: 30.10.2020г
Класс: 8
Учитель: Муртазова Эльмира Вахитова
Ученики:_Мудаева Т., Дайтаева И
________________________________________________________________________________Автор учебника: Л. Л. Босова, А. Ю. Босова
Тема: «Построение таблиц истинности для логических выражений»
Цель урока: сформировать умения строить и заполнять таблицы истинности
Задачи:
Обучающие: изучить последовательность действий построения таблиц истинности, сформировать умение применять алгоритм заполнения таблиц истинности, научить находить значение логических выражений посредством построения таблиц истинности.
Развивающие: развивать логическое мышление и познавательный интерес к предмету, развивать внимание, память, речь учащихся.
Воспитательные: воспитывать культуру общения, формировать интеллектуальную и эмоциональную активность учащихся, воспитывать чувства ответственности за результаты своего труда.
Тип урока: урок изучения и первичного закрепления новых знаний.
План урока:
Организационный момент (2 мин.)
Повторение материала предыдущего урока, проверка ДЗ (5 мин.)
Объяснение нового материала (14 мин.)
Физкультминутка (2 мин.)
Закрепление разбор примера (5 мин.)
Задания для самостоятельной работы (8 мин.)
Подведение итогов, рефлексия (3 мин)
Домашнее задание (1 мин.)
Оборудование и программный материал:
ХОД УРОКА
I. Организационный момент
Здравствуйте ребята. Мы уже несколько уроков изучаем тему (главу) «Математические основы информатики». Слайд 1 И сегодня еще мы узнаем много нового. Вы готовы к этому?
Эпиграфом к уроку являются слова Б.Паскаля: “ВЕЛИЧИЕ ЧЕЛОВЕКА — В ЕГО СПОСОБНОСТИ МЫСЛИТЬ”. Слайд 2
На предыдущем уроке мы увидели, что логика достаточно крепко связана с нашей повседневной жизнью, а также увидели, что почти любое высказывание можно записать в виде формулы. В
В
Рыбу ловят сачком, или ловят крючком, или мухой приманивают, или червячком
А V В V С V В
Давайте вспомним основные определения и понятия, выполните задания в Якласс (4 слайд):
Задания в Якласс
1. Числовые выражения (1 Б.)
Определи, является ли высказыванием: 5⋅2
является высказыванием
не является высказыванием
2. Предложение (2 Б.)
«Капитанская дочь» — самое весёлое стихотворение.
нельзя однозначно определить
истинное
ложное
(Повесть)
3. Высказывания в геометрии (2 Б.)
Определи, высказывание является ложным или истинным.
Площадь прямоугольника с длинами сторон c и d равна c⋅d.
нельзя однозначно определить
истинное
ложное
4. Основные понятия (1 Б. )
)
Выбери верный ответ.
В алгебре логики высказывания обозначают буквами и называют ________________________.
логические переменные
истинное высказывание
геометрия логики
математическое предложение
III. Объяснение нового материала
На Слайде 5 логическое выражение: F = X ИЛИ Y И (НЕ Z). Записать данное выражение, заменяя логические связки на знаки, которые используются для записи логических операций.
(F = X + Y * ¬Z)
Давайте найдем значение данного выражения при значениях переменных Х=1;У=1; Z=0.
Для нахождения значения функции необходимо подставить значении переменных в формулу.
Ответ: F=1+1*(не 0)= 1+1*1=1.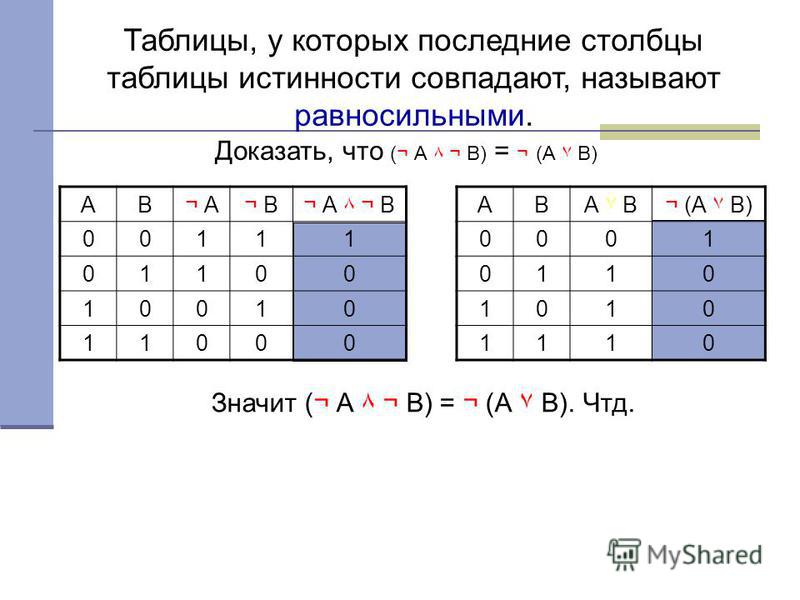
Это единственное значение, которое может принять наша функция? (Нет).
От чего зависит значения функции? (От значений переменных X,Y, Z)
Из ранее изученного материала, нам известно, что для нахождения значения функции логической операции: инверсия, конъюнкция, дизъюнкция мы использовали таблицу истинности. А кто может сформулировать тему нашего урока:
Слайд 7 «ПОСТРОЕНИЕ ТАБЛИЦЫ ИСТИННОСТИ ДЛЯ ЛОГИЧЕСКИХ ВЫРАЖЕНИЙ»
Запишем тему урока в тетрадь. Давайте вместе с вами постараемся дать определение понятию ТАБЛИЦА ИСТИННОСТИ.
Слайд 8 Таблица истинности – это таблица, показывающая, какие значения принимает составное высказывание при всех сочетаниях (наборах) значений входящих в него простых высказываний
Для того, что бы построить ТИ необходимо пользоваться определенным алгоритмом: см. учебник с.29
учебник с.29
Приоритеты операций
скобки
отрицание
конъюнкция
дизъюнкция
Пример: Для формулы A* (B * С) построить таблицу истинности (слайд 9)
Следуя пунктам алгоритма получаем: (слайд 10)
1. посчитаем n: 3
2. посчитаем общее число логических операций в выражении: 3
3. установим последовательность выполнения логических операций с учетом скобок и приоритетов
4. определим число столбцов в таблице: 3 + 3 = 6
5. заполним шапку таблицы, включив в нее и операции в соответствии с последовательностью, установленной в п. 3
6. определим количество строк в таблице (не считая шапки таблицы) m = 2n : 23 = 8
7. выписать наборы входных переменных:
1.разделить колонку значений первой переменной пополам и заполнить верхнюю часть «1», а нижнюю «0»;
2.разделить колонку значений второй переменной на четыре части и заполнить каждую четверть чередующимися группами «1» и «0», начиная с группы «1»;
3. продолжать деление колонок значений последующих переменных на 8, 16 и т.д. частей и заполнение их группами «1» или «0» до тех пор, пока группы «1» и «0» не будут состоять из одного символа.
продолжать деление колонок значений последующих переменных на 8, 16 и т.д. частей и заполнение их группами «1» или «0» до тех пор, пока группы «1» и «0» не будут состоять из одного символа.
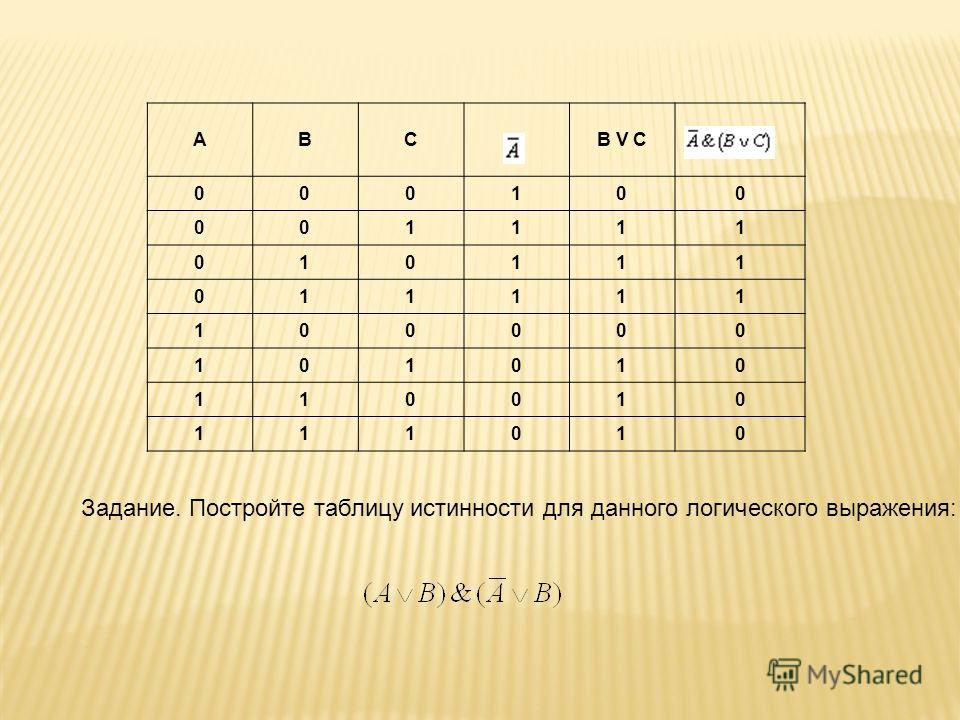
8. провести заполнение таблицы по столбцам, выполняя логические операции в соответствии с установленной последовательностью.
A | B | C | B* | A* (B *) | |
1 | 1 | 1 | 0 | 0 | 0 |
1 | 1 | 0 | 1 | 1 | 1 |
1 | 0 | 1 | 0 | 0 | 0 |
1 | 0 | 0 | 1 | 0 | 0 |
0 | 1 | 1 | 0 | 0 | 0 |
0 | 1 | 0 | 1 | 1 | 0 |
0 | 0 | 1 | 0 | 0 | 0 |
0 | 0 | 0 | 1 | 0 | 0 |
IV. Физкультминутка
Физкультминутка
Гимнастика для глаз (слайд 12)
V. Закрепление новых знаний
Построить таблицы истинности для следующих выражений:
Слайд 13-14
(Задания выведены на слайде)
VI. Контроль знаний (если останется время)
Слайд 15-16
Вариант 1
Составить таблицу истинности для логического выражения
(А + В) * (¬А * А +В)
Вариант 2
Составить таблицу истинности для логического выражения
(А * В) + (¬ В+А)
VII. Рефлексия
Слайд 16
Личностное осмысление каждым учеником результатов урока
Что было наиболее трудным?
Что удалось лучше всего?
Сегодня на уроке мы научились определять истинность составных высказываний, но больше с математической точки зрения, так как вам были даны не сами высказывания, а формулы, отображающие их. На следующих уроках мы закрепим эти умения и постараемся их применить к решению логических задач.
На следующих уроках мы закрепим эти умения и постараемся их применить к решению логических задач.
VIII. Домашнее задание
Слайд 17
Домашняя работа:
§1.3.3
Составить таблицы истинности для логических выражений
Слайд 18 спасибо за урок
Приложение 1
Вариант 1
Составить таблицу истинности для логического выражения
(А + В) * (¬А * А +В)
Вариант 2
Составить таблицу истинности для логического выражения
(А * В) + (¬ В+А)
Приложение 2
Домашняя работа: §1.3.3, №8,10
5.10. Как составить таблицу истинности?
Главная > Справочник по образованию > Энциклопедия де-факто > Математика и компьютерные дисциплины > Информатика > Электронная версия учебника по информатике 10-11 > Глава 1.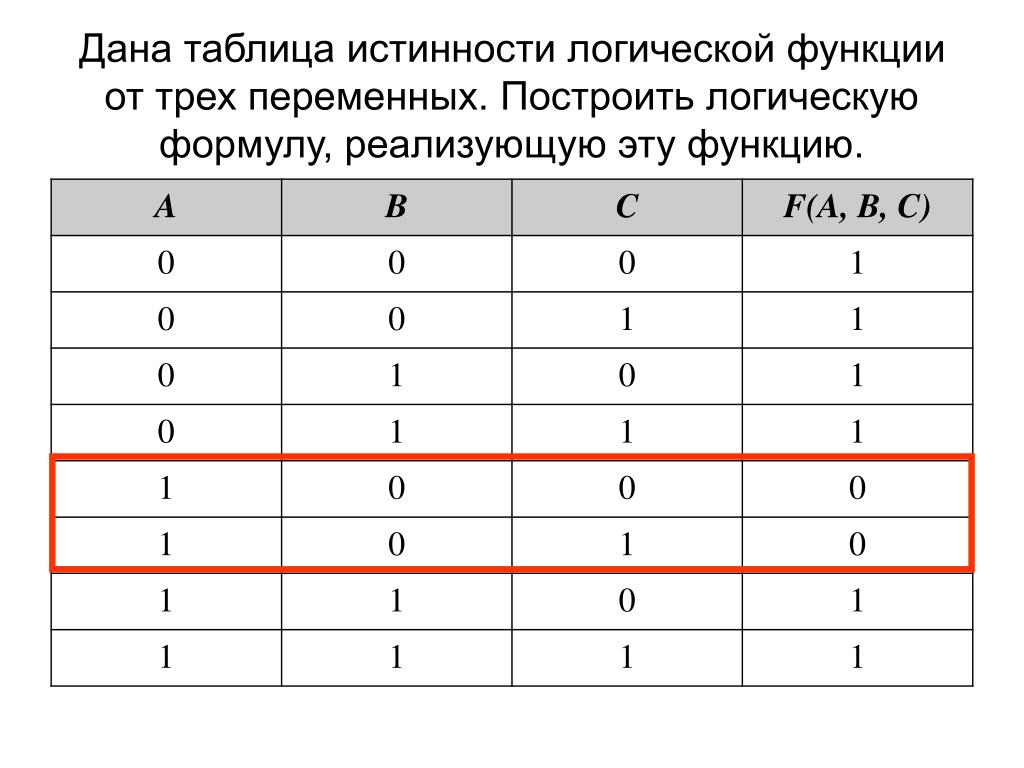 5. Логические основы компьютеров > 5.10. Как составить таблицу истинности?
5. Логические основы компьютеров > 5.10. Как составить таблицу истинности?
Согласно определению, таблица истинности логической формулы выражает соответствие между всевозможными наборами значений переменных и значениями формулы.
Для формулы, которая содержит две переменные, таких наборов значений переменных всего четыре: (0,0), (0,1), (1,0), (1,1).
Если формула содержит три переменные, то возможных наборов значений переменных восемь:
(0,0,0), (0,0,1), (0,1,0), (0,1,1),
(1,0,0), (1,0,1), (1,1,0), (1,1,1).
Количество наборов для формулы с четырьмя переменными равно шестнадцати и т.д.
Удобной формой записи при нахождении значений формулы является таблица, содержащая кроме значений переменных и значений формулы также и значения промежуточных формул.
Примеры.
1. Составим таблицу истинности для формулы ,
которая содержит две переменные x и y.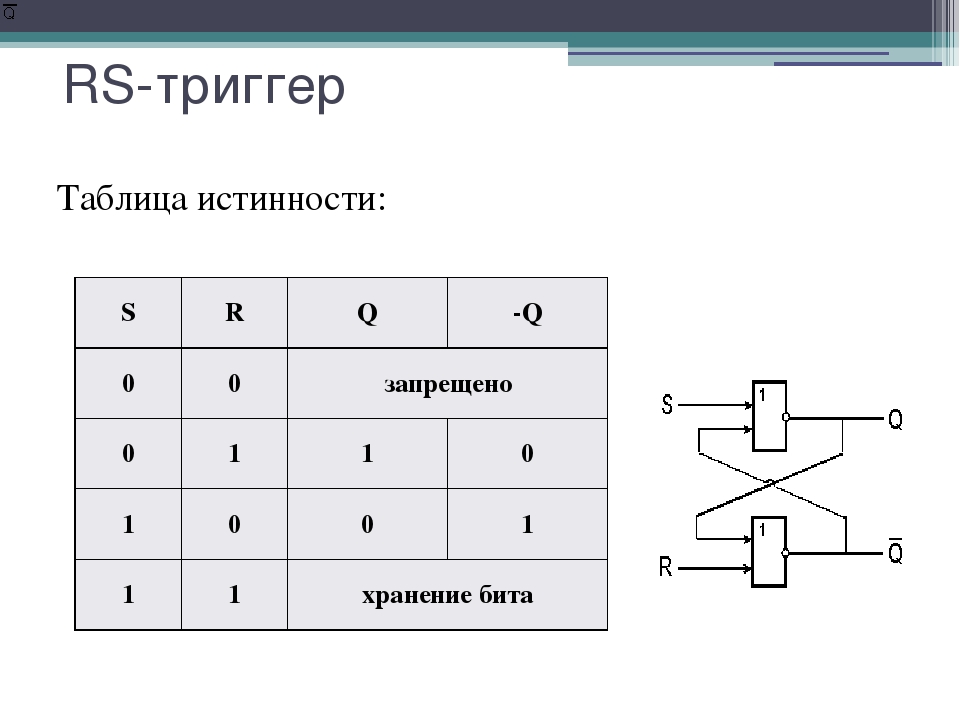 В первых двух столбцах таблицы
запишем четыре возможных пары значений этих переменных, в последующих
столбцах — значения промежуточных формул и в последнем столбце -
значение формулы. В результате получим таблицу:
В первых двух столбцах таблицы
запишем четыре возможных пары значений этих переменных, в последующих
столбцах — значения промежуточных формул и в последнем столбце -
значение формулы. В результате получим таблицу:
| Переменные | Промежуточные логические формулы | Формула | |||||
| 0 | 0 | 1 | 0 | 0 | 1 | 1 | 1 |
| 0 | 1 | 1 | 1 | 1 | 0 | 1 | 1 |
| 1 | 0 | 0 | 0 | 1 | 0 | 0 | |
| 1 | 1 | 0 | 0 | 1 | 0 | 0 | 1 |
Из таблицы видно, что при всех наборах значений переменных x и y формула принимает значение 1, то есть является тождественно истинной.
2. Таблица истинности для формулы :
| Переменные | Промежуточные логические формулы | Формула | ||||
| 0 | 0 | 0 | 1 | 1 | 0 | 0 |
| 0 | 1 | 1 | 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 | 1 | 1 | 0 |
| 1 | 1 | 0 | 0 | 0 | 0 | |
Из таблицы видно, что при всех наборах значений переменных x и y формула принимает значение 0, то есть является тождественно ложной.
3. Таблица истинности для формулы :
| Переменные | Промежуточные логические формулы | Формула | ||||||
| 0 | 0 | 0 | 1 | 1 | 0 | 1 | 0 | 0 |
| 0 | 0 | 1 | 1 | 1 | 0 | 1 | 1 | 1 |
| 0 | 1 | 0 | 0 | 0 | 1 | 1 | 1 | |
| 0 | 1 | 1 | 0 | 0 | 1 | 1 | 1 | 1 |
| 1 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 0 |
| 1 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 0 | 1 | 0 | 0 | 0 | 0 |
Из таблицы видно, что формула в некоторых случаях принимает значение 1, а в некоторых — 0, то есть является выполнимой.
Другие записи
С помощью логических переменных и символов логических операций любое высказывание можно формализовать, то есть заменить логической формулой. Определение логической формулы: 1. Всякая логическая…
10.06.2016. 5.3. Какая связь между алгеброй логики и двоичным кодированием? 5.5. Что такое логический элемент компьютера?
Математический аппарат алгебры логики очень удобен для описания того, как функционируют аппаратные средства компьютера, поскольку основной системой счисления в компьютере является двоичная, в которой…
10.06.2016. 5.6. Что такое схемы И, ИЛИ, НЕ, И-НЕ, ИЛИ-НЕ?
С х е м а И
Схема И реализует конъюнкцию двух или более логических значений.
Условное обозначение на структурных схемах схемы И с двумя входами представлено на рис.
10.06.2016. 5.7. Что такое триггер?
Триггер — это электронная схема, широко применяемая в регистрах компьютера для надёжного запоминания одного разряда двоичного кода. Триггер имеет два устойчивых состояния, одно из которых соответствует…
10.06.2016. 5.8. Что такое сумматор?
Сумматор — это электронная логическая схема, выполняющая суммирование двоичных чисел. Сумматор служит, прежде всего, центральным узлом арифметико-логического устройства компьютера, однако он находит…
О таблицах истинности — Таблицы истинности
- Обновлено 16 июня 2022 г.
-
Распечатать
Поделиться
Темный
Свет
Обзор
A Таблица истинности — это тип правила, которое сравнивает пользовательские данные с несколькими комбинациями входных данных, используемых в условиях, для вывода правильного результата или результата. Каждая строка настроена с несколькими правилами операторов на основе входных данных, используемых в таблице истинности. Эти Правила оператора затем приводят к набору результатов. Если в таблице истинности возвращено несколько строк, будут разные комбинации, которые логика будет оценивать при сравнении входных данных пользователя.
Каждая строка настроена с несколькими правилами операторов на основе входных данных, используемых в таблице истинности. Эти Правила оператора затем приводят к набору результатов. Если в таблице истинности возвращено несколько строк, будут разные комбинации, которые логика будет оценивать при сравнении входных данных пользователя.
Столбцы представляют данные ввода/вывода в каждой строке. Например, таблица истинности с именем и адресом электронной почты в качестве входных данных будет иметь один столбец для правила утверждения имени и другой для адреса электронной почты, а затем столбец результатов для этой строки.
На приведенном ниже снимке экрана Марка, Модель и Год являются входными данными для Правила с условиями, настроенными для каждой строки. Вводимые пользователем данные сравниваются с каждой строкой, чтобы найти строку, в которой данные соответствуют критериям, которые затем выводят соответствующие данные.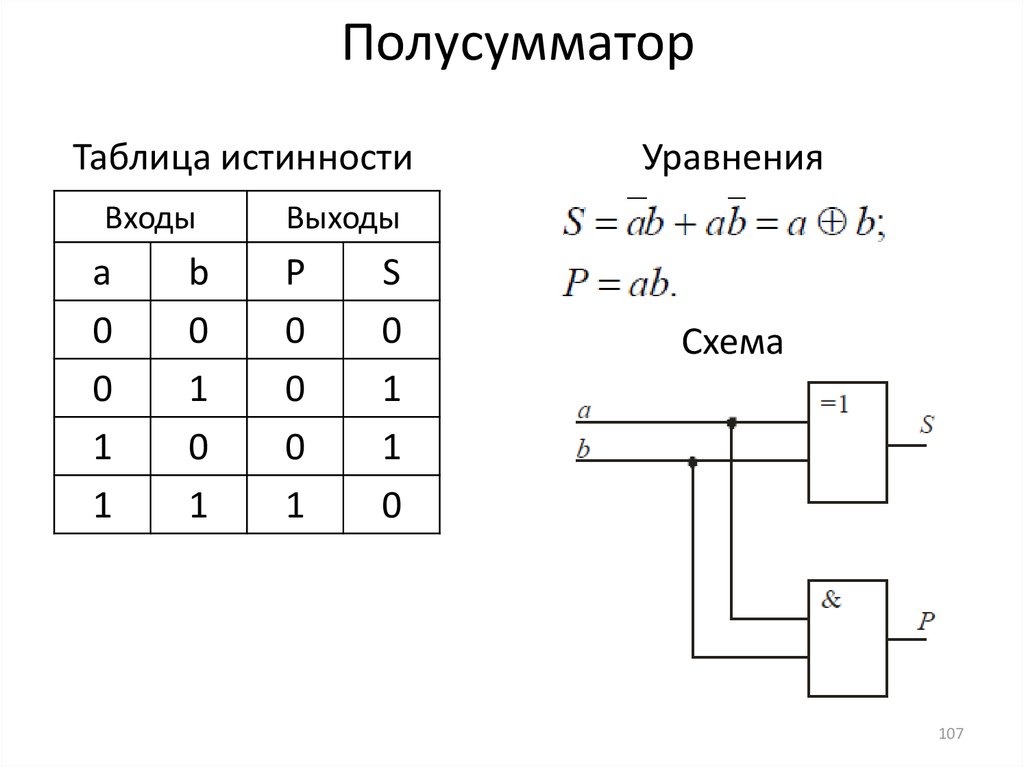
Дополнительные сведения о создании таблицы истинности см. в следующей статье: Создание таблицы истинности.
Типы поведения вывода
- Правило возврата данных (одиночное) : Возвращает одну переменную в поток.
- Правило действия : Передает значение и выполняет поток.
- Правило возврата данных (множественный, составной тип) : Создает новый тип данных на основе полей, указанных в возвращаемых данных. Это позволяет разработчику динамически создавать типы данных для вывода таблицы истинности на основе определенных полей.
- Правило возврата данных (несколько) : Возвращает несколько переменных в поток.
Варианты использования
Таблицы истинности можно использовать для самых разных вариантов использования. Таблицы истинности лучше всего использовать для случаев, в которых используются правила , в которых используются вложенные операторы «если».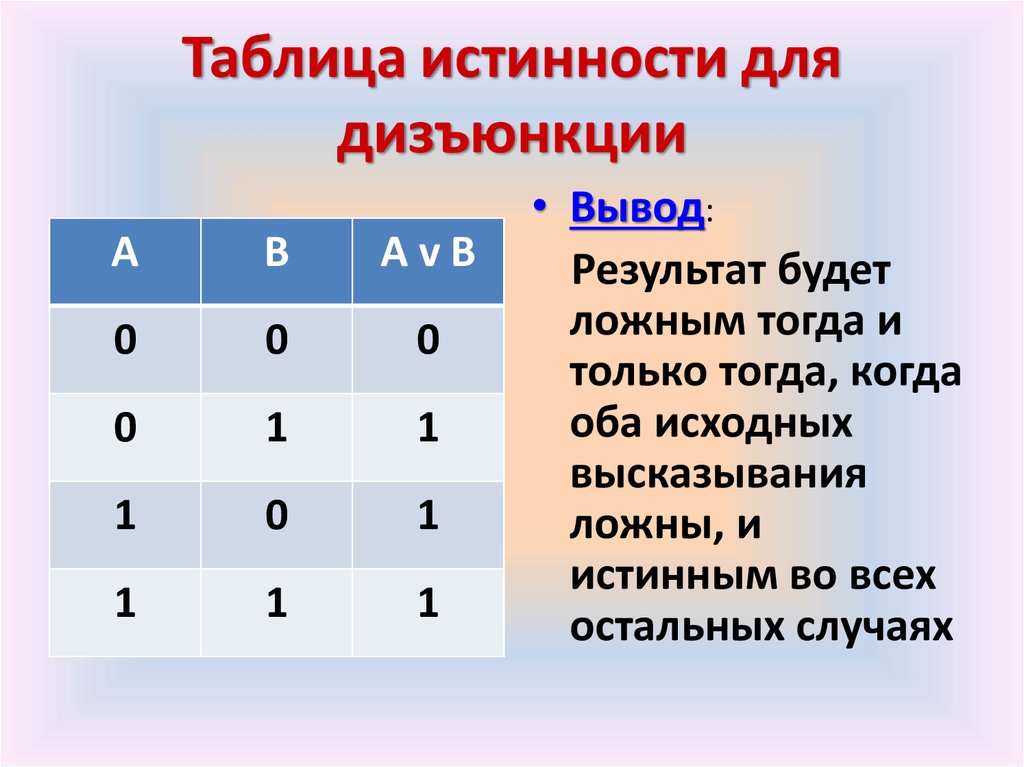 Одна из таких реализаций может включать проверку данных, таких как оценка того, когда следует утвердить аренду автомобиля для компании, путем просмотра времени аренды автомобиля, стоимости для компании и должности лица, запрашивающего аренду. Таким образом, если запрос сделан человеком X, и если он арендован на X дней и стоит компании X долларов, то запрос будет одобрен.
Одна из таких реализаций может включать проверку данных, таких как оценка того, когда следует утвердить аренду автомобиля для компании, путем просмотра времени аренды автомобиля, стоимости для компании и должности лица, запрашивающего аренду. Таким образом, если запрос сделан человеком X, и если он арендован на X дней и стоит компании X долларов, то запрос будет одобрен.
Благодаря тому, что их можно создавать с использованием внутренних или внешних данных, они могут быть полезны для отслеживания данных, относящихся к Системе и/или Учетным записям этой Системы, таким как разрешения Учетной записи. Этого можно добиться, оценив конкретное разрешение в качестве входных данных и сравнив его с учетными записями в системе, которые имеют эти разрешения в качестве выходных данных. Это может быть введено статически через конструктор правил или динамически путем создания таблицы истинности извне через отчет.
Была ли эта статья полезной?
Что дальше
- Действия таблицы истинности
Использование таблиц истинности для моделирования комбинаторной логики — MATLAB & Simulink
Использование таблиц истинности для моделирования комбинаторной логики
Таблицы истинности реализуют комбинаторную логику в табличном формате. Вы можете использовать
Таблицы истинности Stateflow ® для моделирования принятия решений для обнаружения и управления ошибками и
переключение режимов.
Вы можете использовать
Таблицы истинности Stateflow ® для моделирования принятия решений для обнаружения и управления ошибками и
переключение режимов.
Функции таблицы истинности в диаграмме Stateflow выполняются, только когда вы вызываете функцию таблицы истинности. Вы можете определить функция таблицы истинности в диаграмме Stateflow, состоянии или поддиаграмме. Расположение функции определяет множество состояния и переходы, которые могут вызвать функцию.
Если вы хотите вызвать функцию из одного состояния или подграфика и его подсостояния, поместите свою функцию таблицы истинности в это состояние или поддиаграмму. Эта функция переопределяет любые другие функции с тем же именем в родителях и предках этого состояние или подсхема.
Если вы хотите вызвать функцию в любом месте диаграммы, поместите функцию таблицы истинности на уровне диаграммы.
Если вы хотите вызвать функцию из любого графика в вашей модели, поместите свою таблицу истинности на уровне диаграммы и включить экспорт функций уровня диаграммы.
 Для дополнительной информации,
см. Экспорт функций Stateflow для повторного использования.
Для дополнительной информации,
см. Экспорт функций Stateflow для повторного использования.
Функция таблицы истинности может получить доступ к диаграмме и данным состояния над ней в Иерархия потоков состояний.
В качестве альтернативы, для более прямой реализации логики принятия решений, вы можете добавить Истина Блок таблицы непосредственно в вашу модель Simulink ® . Для реализации логики управления блоки таблицы истинности используют MATLAB ® в качестве языка действий.
Структура таблицы истинности
Эта функция таблицы истинности имеет имя ttable . Требуется три
аргументы ( x , y и z ) и возвращает
одно выходное значение ( r ).
Функция состоит из такого расположения условий, решений и действия.
.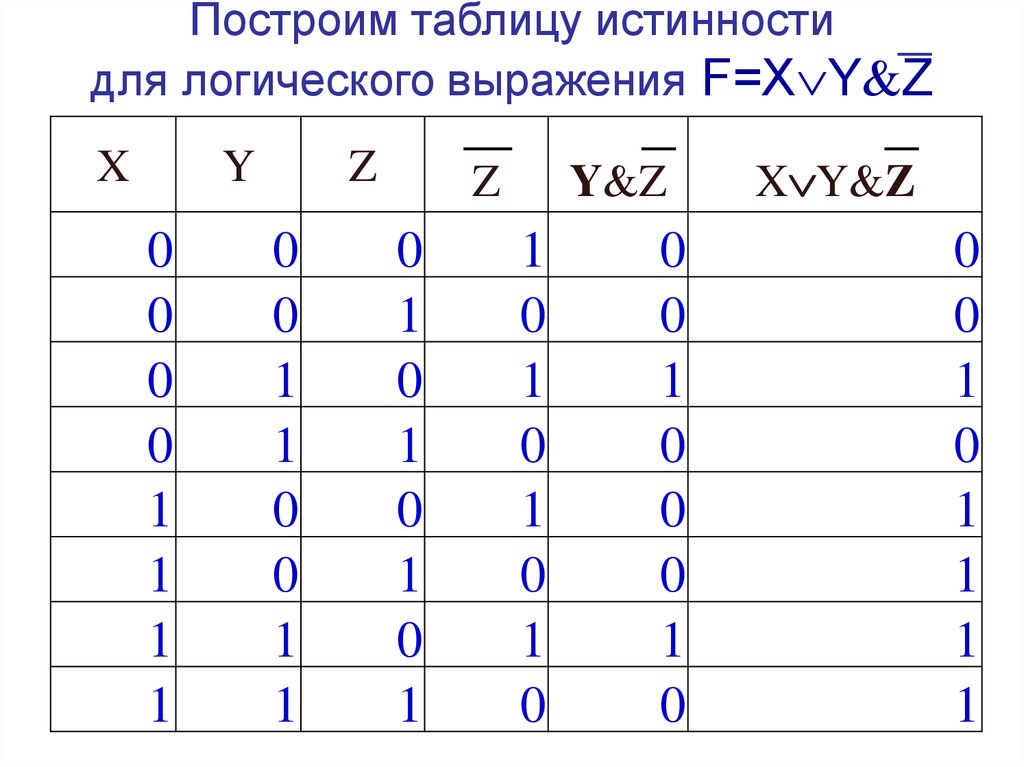 0014 0014 | ||||
|---|---|---|---|---|
x == 1 | T | F | F | — |
y == 1 | F | T | F | — |
z == 1 | F | F | T | — |
Action | r = 1 | r = 2 | r = 3 | r = 4 |
Each of the conditions entered in the Условие столбец обязательно
оценить как true (ненулевое значение) или false (нулевое значение). Результаты для каждого условия
указывается как T (истина), F (ложь) или — (истина или ложь). Каждый из столбцов решений
объединяет результат для каждого условия с помощью логического И в составное условие, которое
называется решением.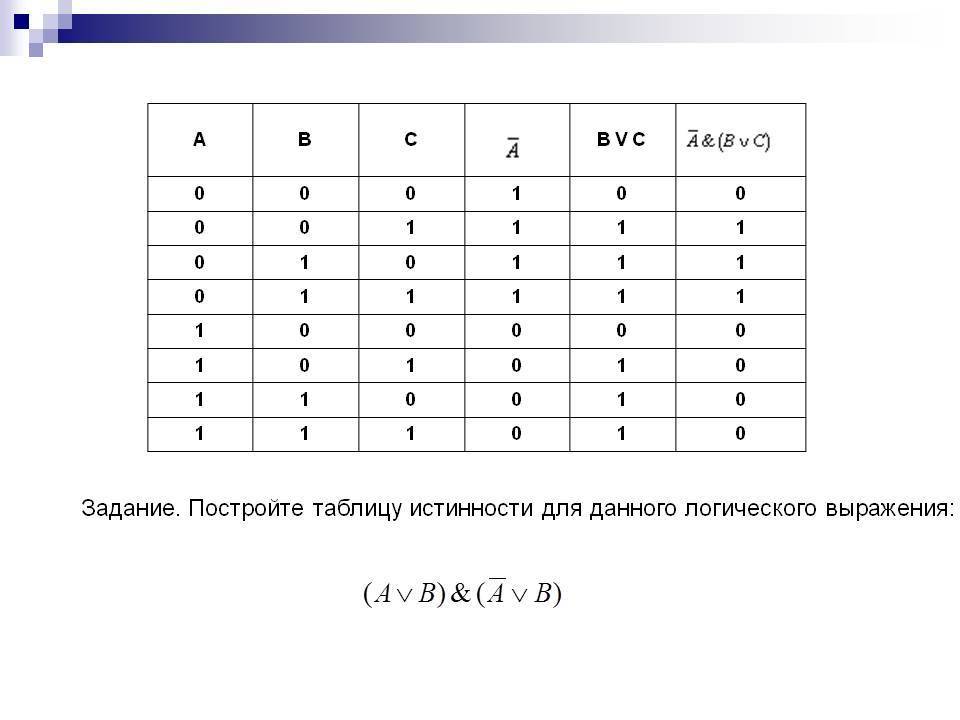
Вы оцениваете таблицу истинности по одному решению за раз, начиная с Решение 1 . Решение 4 охватывает все возможные оставшиеся решения. Если одно из решений истинно, таблица выполняет соответствующее действие, а затем выполнение таблицы истинности завершено.
Например, если выполняются условия x == 1 и y == 1 .
false и условие z == 1 истинно, тогда Решение 3 верно, а переменная r устанавливается равным 3. Остальные решения
не проверено, и оценка таблицы истинности завершена. Если первые три решения
false, то решение по умолчанию автоматически становится истинным, и его действие
( r=4 ) выполняется. В этой таблице перечислены псевдокоды, соответствующие
оценка этого примера таблицы истинности.
Псевдокод | Описание |
|---|---|
если ((x == 1) & !(y == 1) & !(z == 1)) р = 1; | Если Решение 1 верно, то установить |
elseif (!(x == 1) & (y == 1) & !(z == 1)) г = 2; | Если Решение 2 верно, то установить |
elseif (!(x == 1) & !(y == 1) & (z == 1)) г = 3; | Если Решение 3 верно, то установить |
еще г = 4; конец | Если все остальные решения ложны, то решение по умолчанию истинно. Набор |
Определение функции таблицы истинности
Чтобы определить функцию таблицы истинности:
В палитре объектов щелкните значок функции таблицы истинности .
На холсте диаграммы щелкните местоположение новой функции таблицы истинности.

Введите метку подписи для функции.
Метка подписи функции указывает имя для вашего функция и формальные имена для ее аргументов и возвращаемых значений. Этикетка с подписью имеет это синтаксис:
[return_val1,return_val2,...] = имя_функции(arg1,arg2,...)
Вы может указывать несколько возвращаемых значений и несколько входных аргументов. Каждое возвращаемое значение и ввод аргумент может быть скаляром, вектором или матрицей значений. Для функций с одним возвращаемым значением опустить скобки в метке подписи.Вы можете использовать одно и то же имя переменной как для аргументов, так и для возвращаемые значения. Когда вы используете одну и ту же переменную для ввода и вывода, вы создаете оперативные данные . Например, функция с этой меткой подписи использует переменные
y1иy2как входные данные, так и выходы:[y1,y2,y3] = f(y1,u,y2)
Если вы экспортировать эту функцию в код C, сгенерированный код обрабатываетy1иy2как аргументы на месте, передаваемые по ссылке. Использование данных на месте снижает
количество раз, которое сгенерированный код копирует промежуточные данные, что приводит к более
эффективный код.
Использование данных на месте снижает
количество раз, которое сгенерированный код копирует промежуточные данные, что приводит к более
эффективный код.В Панель символов и Model Explorer, аргументы и возвращаемые значения сигнатуры функции отображаются как элементы данных, принадлежащие функция. Аргументы имеют область действия
Вход. Возвращаемые значения имеют областьВыход.Укажите свойства данных для каждого аргумента и возвращаемого значения, как описано в Установите свойства данных. Когда аргумент и возвращаемое значение имеют того же имени, вы можете редактировать свойства только для аргумента. Свойства для возврата значение доступно только для чтения.
Чтобы запрограммировать функцию, откройте редактор таблицы истинности, дважды щелкнув функцию коробка.
В редакторе таблицы истинности добавьте условия, решения и действия.
 Для большего
информацию см. в разделе Программирование таблицы истинности.
Для большего
информацию см. в разделе Программирование таблицы истинности.Создайте любые дополнительные элементы данных, необходимые для вашей функции. Для дополнительной информации, см. Добавление данных через Model Explorer.
Ваша функция может получить доступ к своим собственным данным или данным, принадлежащим родительским состояниям или диаграмма. Элементы данных в функции могут иметь одну из следующих областей:
Константа— Постоянные данные сохраняют свое начальное значение через все вызовы функций.Параметр— Данные параметра сохраняют исходное значение через все вызовы функций.Локальный— Локальные данные сохраняются от одного вызова функции до следующий вызов функции. Действительно только для таблиц истинности, которые используют C в качестве действия язык.
Temporary— Временные данные инициализируются в начале каждого вызов функции. Допустимо только для таблиц истинности, использующих C в качестве языка действий.
В функциях таблицы истинности, которые используют C в качестве языка действий, определяют локальные данные, когда вы хотите, чтобы ваши значения данных сохранялись при вызовах функций на протяжении всей симуляции. Определите временные данные, если вы хотите инициализировать значения данных в начале каждого вызов функции. Например, вы можете определить счетчик с помощью
Локальная область, если вы хотите отслеживать, сколько раз вы вызываете функцию. Напротив, вы можете назначить счетчику цикловВременный прицел, если счетчик не нужен значение, которое будет сохраняться после завершения функции.В функциях таблицы истинности, которые используют MATLAB в качестве языка действий, вам не нужно определять локальные или временные данные функции.
 Вместо этого в этих функциях вы можете использовать неопределенные переменные для хранения
значения, которые доступны только во время остальной части вызова функции. Для хранения значений
которые сохраняются при вызовах функций, используйте локальные данные на уровне диаграммы.
Вместо этого в этих функциях вы можете использовать неопределенные переменные для хранения
значения, которые доступны только во время остальной части вызова функции. Для хранения значений
которые сохраняются при вызовах функций, используйте локальные данные на уровне диаграммы.
Вызов функций таблицы истинности в состояниях и переходах
Вы можете вызывать функции таблицы истинности из действий любого состояния или перехода или из другие функции. Если вы экспортируете функцию таблицы истинности, вы можете вызвать ее из любой диаграммы в модель. Дополнительные сведения об экспорте функций см. в разделе Экспорт функций Stateflow для повторного использования.
Чтобы вызвать функцию таблицы истинности, используйте сигнатуру функции и включите фактический значение аргумента для каждого формального аргумента в сигнатуре функции.
[return_val1,return_val2,...] = имя_функции(arg1,arg2,...)
Если типы данных фактических и формальных аргументов различаются, функция приводит
фактический аргумент к типу формального аргумента.
Задание свойств функций таблицы истинности
Перечисленные ниже свойства определяют, как функция таблицы истинности взаимодействует с другими компоненты в вашей диаграмме Stateflow. Вы можете изменить эти свойства в свойстве . Инспектор , обозреватель моделей или диалоговое окно свойств таблицы истинности.
Для использования Property Inspector :
На вкладке Моделирование в разделе Данные проектирования , выберите Инспектор свойств .
В редакторе Stateflow выберите функцию таблицы истинности.
В Property Inspector отредактируйте функцию таблицы истинности характеристики.
Для использования обозревателя моделей:
На вкладке Моделирование в разделе Данные проектирования , выберите Обозреватель моделей .

На панели Model Hierarchy выберите таблицу истинности функция.
В диалоговом окне отредактируйте функцию таблицы истинности характеристики.
Чтобы использовать диалоговое окно свойств таблицы истинности:
В редакторе Stateflow щелкните правой кнопкой мыши функцию таблицы истинности.
Выбрать .
В диалоговом окне свойств отредактируйте свойства функции таблицы истинности.
Эти свойства также можно изменить программно, используя объекты Stateflow.TruthTable . Для получения дополнительной информации о программном интерфейсе Stateflow см. Обзор API Stateflow.
Имя
Имя функции. Щелкните ссылку с названием функции, чтобы вывести ее на передний план. на родной карте.
Встроенная опция функции
Управляет встраиванием вашей функции в сгенерированный код:
Авто— Определяет, следует ли встраивать вашу функцию на основе внутреннего расчета.
Встроенный— Встраивает вашу функцию, если вы не экспортируете к другим диаграммам и не является частью рекурсии. (Рекурсия существует, если ваш функция вызывает себя прямо или косвенно через вызов другой функции.)Функция— Не встраивает вашу функцию.
Это свойство недоступно в Инспекторе свойств .
Ярлык
Ярлык для вашей функции. Метка сигнатуры функции задает имя для вашей функции и формальные имена для ее аргументов и возвращаемых значений. Это свойство недоступно в Property Inspector .
Заниженная спецификация
Управляет уровнем диагностики неполной спецификации в вашей функции таблицы истинности. Дополнительные сведения см. в разделе Исправление завышенных и недоопределенных таблиц истинности.
Превышение спецификации
Управляет уровнем диагностики завышения спецификации в вашей функции таблицы истинности. Дополнительные сведения см. в разделе Исправление завышенных и недоопределенных таблиц истинности.
Дополнительные сведения см. в разделе Исправление завышенных и недоопределенных таблиц истинности.
Язык действий
Управляет языком действий для вашей функции таблицы истинности Stateflow. Выберите между MATLAB или C. Это свойство доступно только в диаграммах, которые используют C в качестве действия. язык. Для получения дополнительной информации смотрите Различия Между MATLAB и C как Синтаксис Языка Действия.
Описание
Описание функции таблицы истинности.
Ссылка на документ
Ссылка на онлайн-документацию по функции таблицы истинности. Вы можете ввести веб-URL адрес или команду MATLAB, которая отображает документацию в виде файла HTML или в виде текста в Командное окно MATLAB. При нажатии на ссылку Документ гиперссылка, Stateflow оценивает ссылку и отображает документацию.
Задайте свойства для блоков таблицы истинности
Свойства блока таблицы истинности определяют, как ваша таблица истинности взаимодействует с
модель Симулинк.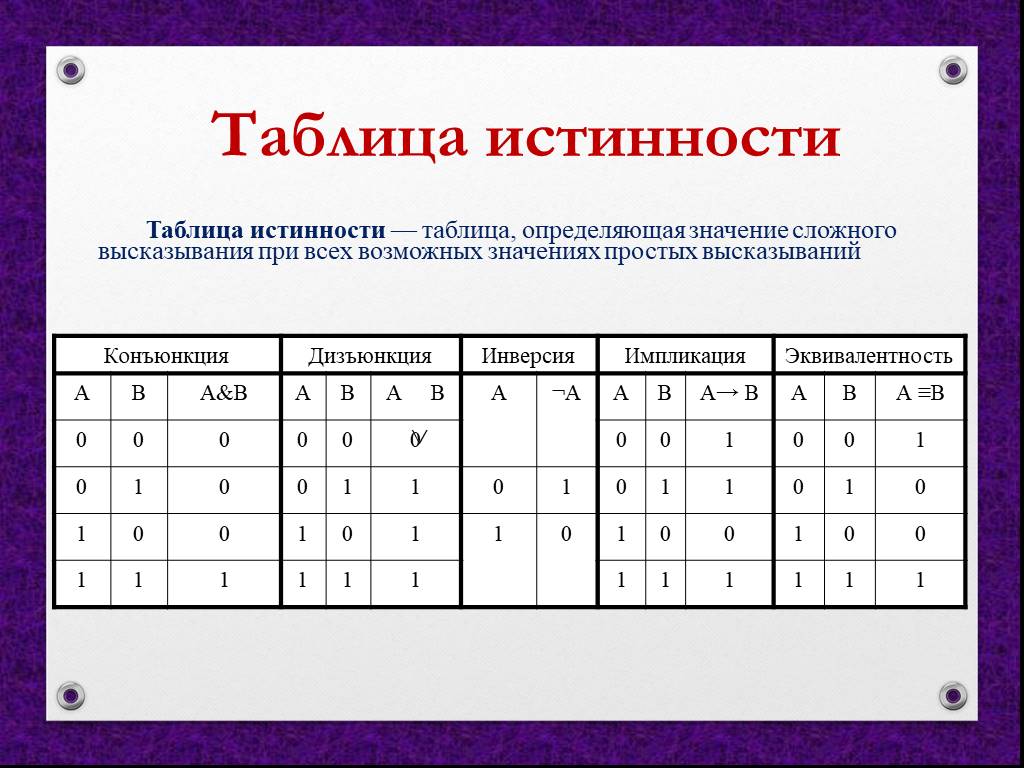 Вы можете изменить эти свойства в свойстве .
Inspector , Model Explorer или диалоговое окно свойств таблицы истинности.
Вы можете изменить эти свойства в свойстве .
Inspector , Model Explorer или диалоговое окно свойств таблицы истинности.
Для использования Property Inspector :
На вкладке Моделирование в разделе Данные проектирования , выберите Инспектор свойств .
В редакторе Stateflow щелкните таблицу истинности.
В Property Inspector отредактируйте таблицу истинности характеристики.
Для использования Model Explorer:
На вкладке Моделирование в разделе Данные проектирования , выберите Обозреватель моделей .
На панели Model Hierarchy выберите таблицу истинности.
В диалоговом окне отредактируйте свойства таблицы истинности.

Чтобы использовать диалоговое окно свойств таблицы истинности:
Откройте редактор Stateflow.
На вкладке Моделирование щелкните Таблица Свойства .
В диалоговом окне свойств отредактируйте свойства таблицы истинности.
Эти свойства также можно изменить программно, используя объекты Stateflow.TruthTableChart . Для получения дополнительной информации о программном интерфейсе Stateflow см. Обзор API Stateflow.
См. также
Блоки
- Таблица истинности
Объекты
-
Stateflow.TruthTable|Stateflow.truthtableChart
Инструменты
- Модель Explorer (Simulink)
Связанные темы
- Программа истины Table
- между Matlab и C. Функции с использованием атомарных блоков
Вы щелкнули ссылку, соответствующую этой команде MATLAB:
Запустите команду, введя ее в командном окне MATLAB.

 Для дополнительной информации,
см. Экспорт функций Stateflow для повторного использования.
Для дополнительной информации,
см. Экспорт функций Stateflow для повторного использования.
 Использование данных на месте снижает
количество раз, которое сгенерированный код копирует промежуточные данные, что приводит к более
эффективный код.
Использование данных на месте снижает
количество раз, которое сгенерированный код копирует промежуточные данные, что приводит к более
эффективный код. Для большего
информацию см. в разделе Программирование таблицы истинности.
Для большего
информацию см. в разделе Программирование таблицы истинности.
 Вместо этого в этих функциях вы можете использовать неопределенные переменные для хранения
значения, которые доступны только во время остальной части вызова функции. Для хранения значений
которые сохраняются при вызовах функций, используйте локальные данные на уровне диаграммы.
Вместо этого в этих функциях вы можете использовать неопределенные переменные для хранения
значения, которые доступны только во время остальной части вызова функции. Для хранения значений
которые сохраняются при вызовах функций, используйте локальные данные на уровне диаграммы.