Как найти область определения функции sin
Статьи › Находится › Как находится область определения функции заданной формулой
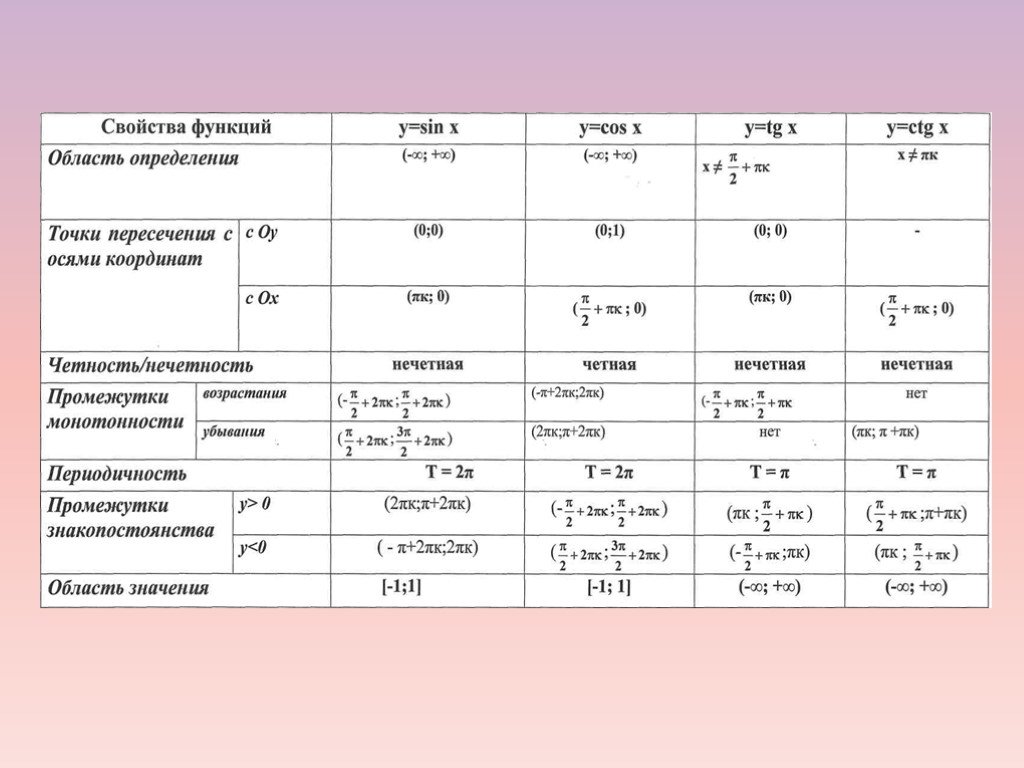
Итак, Областью определения функций y = sin x и y = cos x является множество R всех действительных чисел.
- Как найти область значения функции по формуле
- Как найти область определения функции y sin2x
- Как найти множество значений функции y sinx
- Как найти область определения логарифмической функции
- Как понять область значения функции
- Что такое область определения функции
- Как найти область определения функции y cos2x
- Как найти область определения функции с двумя переменными
- Что является областью определения функции y COSX
- Чему равен основной период функции y sinx
- Как определить четность функции y sinx
- Как найти область определения и множество значений
- Что такое область определения и область значений функции
- Что такое LG
- Чему равна область значений функции
- Как найти область определения квадратичной функции
- Как найти область определения функции гиперболы
- Как найти область определения функции y 4x 8
- Как найти область определения функции y x 3
- Как найти область определения функции y 3x 2
- Какие значения принимает sinx
- Как найти область определения функции тангенса
- Как определить множество значений функции
- Что является графиком логарифмической функции
- Как решать логарифмические уравнения
- Когда логарифмическая функция является убывающей
- Как найти множество значений функции
- Как определить область значения линейной функции
- Что такое область значения функции 9 класс
Как найти область значения функции по формуле
Для того чтобы найти область значений на данном отрезке, необходимо: Найти вершину параболы по формуле: x = -b / (2 * a), подставить ее в формулу и найти y.
Это значение y будет минимальным/максимальным в зависимости от того, куда направлены ветви параболы.
Как найти область определения функции y sin2x
Y = sin 2x. Синус — тригонометрическая функция, непрерывная, значит, область определения функции — любое число. Функция независимо от своего аргумента принимает значения, находящиеся в промежутке от -1 до 1.
Как найти множество значений функции y sinx
Чтобы найти множество значений функции y = sin x, нужно выяснить, какие значения может принимать y при различных значениях x, т. е. установить, для каких значений y есть такие значения x, при которых sin x = y. Известно, что уравнение sin x = a имеет корни, если |a| ≤ 1, и не имеет корней, если |a| > 1.
Как найти область определения логарифмической функции
Зададим аргумент в log(x) большим 0, чтобы узнать, где определено данное выражение. Область определения ― это все значения x, при которых выражение определено.
Как понять область значения функции
Множество всех значений, которые принимает аргумент функции, называется областью определения функции: D(f) т.
е. смотрим по x. Множество всех значений, которые может принять зависимая переменная, называется областью значения функции: E(f) т.
Что такое область определения функции
Область определения — множество, на котором задаётся функция. В каждой точке этого множества значение функции должно быть определено.
Как найти область определения функции y cos2x
Ответы: Функция у = cos2x определена всюду (–∞; +∞), её областью значений является множество [0; 1].
Как найти область определения функции с двумя переменными
Областью определения функции двух переменных называется множество всех пар, для которых существует значение. Графически область определения представляет собой всю плоскость либо её часть. Так, областью определения функции является вся координатная плоскость — по той причине, что для любой точки существует значение.
Что является областью определения функции y COSX
Функция y = cosx определена на всей числовой прямой, и множеством её значений является отрезок − 1; 1.
Поэтому её график не выходит за границы полосы между прямыми y = − 1 и y = 1.
Чему равен основной период функции y sinx
Значит, мы можем сказать, что функции y=sin x, y=cos x — периодические функции, с периодом 2π.
Как определить четность функции y sinx
Синус функция —ограниченная. Для того, чтобы определить чётность функции синус проверим следующие определения: функция чётная, f(−x)=f(x) и функцию нечётная, f(−x)=−f(x). Период функций y=sin x, y=cos xравен 2π, период функций tgx, ctgx равен π. чётной или нечётной?
Как найти область определения и множество значений
Значение y, соответствующее заданному значению x, называют значением функции. Все значения, которые принимает x, образуют область определения функции; все значения, которые принимает y, образуют множество значений функции.
Как найти область определения выражения
Областью определения выражения с одной переменной называется множество значений переменной, при которых это выражение имеет смысл.
Можно вычислить числовое значение алгебраического выражения при любом значении переменной из его области определения.
Что такое область определения и область значений функции
Ответы1. Областью определения функции являются все значения Х, на которых существует функция. Иными словами, те Х, которые можно подставить в уравнение функции и получить в результате Y. Область значения функции определяется значениями, которое принимает Y на всей своей области определения.
Что такое LG
LG (Lucky-Goldstar) — южнокорейская группа компаний, см. также: LG Electronics — южнокорейская компания по производству бытовой техники и электроники; LG Display — южнокорейская компания по производству жидкокристаллических дисплеев.
Чему равна область значений функции
Область значений (или множество значений) функции — множество, состоящее из всех значений, которые принимает функция.
Как найти область определения квадратичной функции
Графиком квадратичной функции является парабола, вершина которой находится в точке (− b 2 a; − b 2 − 4 a c 4 a).
Область определения функции — вся числовая прямая: D (f) = R = (− ∞; ∞). Область значений функции зависит от знака коэффициента.
Как найти область определения функции гиперболы
Область определения — любое число, кроме нуля. Область значения — любое число, кроме нуля. Функция не имеет наибольших или наименьших значений.
Как найти область определения функции y 4x 8
Так как в формуле функции y = 4x — 8 нет ни деления, ни корня, значит допустимы любые значения переменной х. Ответ: D(f) = (-∞; +∞).
Как найти область определения функции y x 3
Область определения функции.
Так как выражение x 3 является степенью с натуральным показателем, то оно имеет смысл для любого действительного числа x, значит, областью определения функции y = x 3 являются все действительные числа: D = R.
Как найти область определения функции y 3x 2
Ответ: D = (-∞;∞).
Какие значения принимает sinx
1) Функция у = sin х определена для всех значений х, так что областью ее определения является совокупность всех действительных чисел.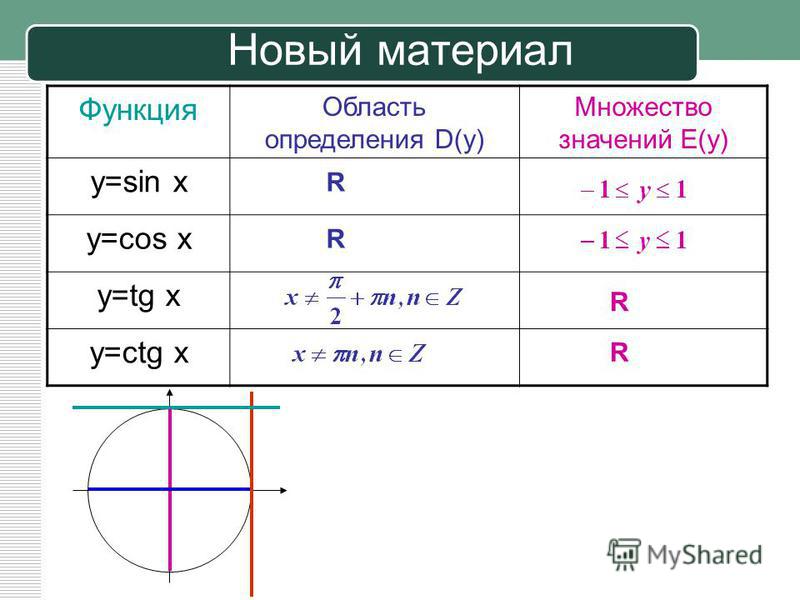
2) Функция у = sin х ограничена. Все значения, которые она принимает, заключены в интервале от —1 до 1, включая эти два числа.
Как найти область определения функции тангенса
Область определения функции y = tgx — множество ℝ действительных чисел, кроме x = π 2 + π n, n ∈ ℤ. Множество значений функции y = tgx — все действительные числа.
Как определить множество значений функции
Множество чисел, пробегаемое функцией у, когда х принимает все возможные значения (т. е. при всех значениях), называется множеством значений функции, или областью значений функции, или областью изменения функции и обозначается через E(f).
Что является графиком логарифмической функции
График логарифмической функции называют логарифмической кривой.
Как решать логарифмические уравнения
Алгоритм решения логарифмического уравнения:
- Написать ОДЗ.
- Упростить выражения слева и справа от знака равенства, используя свойства логарифмов, если это возможно.
- Если основания логарифмов одинаковые, избавиться от логарифмов.
- Решить уравнение и сравнить с ОДЗ, выписать в ответ корни.
Когда логарифмическая функция является убывающей
Область определения: множество всех положительных чисел, т. е. промежуток (0; +). Монотонность: если а > 1, то логарифмическая функция строго возрастает; если 0 < а < 1, то она строго убывает.
Как найти множество значений функции
Найти критические точки функции f(x) и выбрать те из них, которые принадлежат данному отрезку; вычислить значения функции на концах отрезка и в выбранных критических точках; среди найденных значений выбрать наименьшее и наибольшее значения; Множество значений функции заключить между этими значениями.
Как определить область значения линейной функции
Линейной функцией называется функция y = kx + b, где k и b — некоторые числа.Линейная функция:
- Область определения функции — множество R всех действительных чисел.
- Корни — единственный корень x = 0.
- Промежутки постоянного знака зависят от знака параметра k:
Что такое область значения функции 9 класс
Областью определения функции \(y = f(x)\) называют множество всех значений \(x\), для которых функция имеет смысл. Множество всех значений функции \(y = f(x)\), x ∈ X, называют областью значений функции.
Область и диапазон тригонометрических функций
Существует шесть тригонометрических функций sin θ, cos θ, tan θ, cot θ, tan θ, cosec θ и sec θ. Область
В этой статье мы рассмотрим область и диапазон тригонометрических функций, используя таблицу и график, а также область и диапазон обратных тригонометрических функций, а также примеры для лучшего понимания.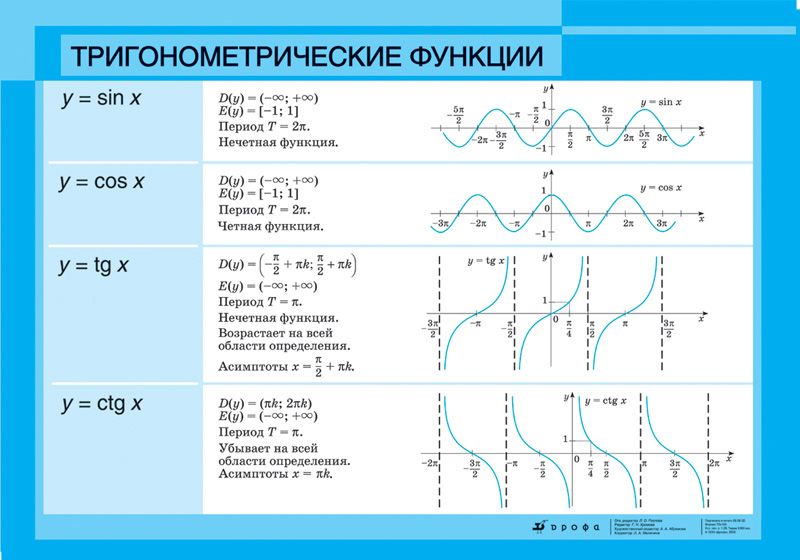
| 1. | Что такое область определения и область значений тригонометрических функций? |
| 2. | ТаблицаОбласть определения и диапазон тригонометрических функций |
| 3. | Область определения и область значений обратных тригонометрических функций |
| 4. | Область определения и диапазон тригонометрических функций с использованием графика |
| 5. | Часто задаваемые вопросы по домену и диапазону тригонометрических функций |
Что такое область определения и область значений тригонометрических функций?
Область определения и диапазон тригонометрических функций — это входные значения и выходные значения тригонометрических функций соответственно. Область определения тригонометрических функций обозначает значения углов, в которых определены тригонометрические функции, а диапазон тригонометрических функций дает результирующее значение тригонометрической функции, соответствующее конкретному углу в области.
Существует шесть основных тригонометрических функций, а именно: sin θ, cos θ, tan θ, cot θ, tan θ, cosec θ и sec θ.
Область и диапазон тригонометрической функции: синус
Мы знаем, что функция синуса представляет собой отношение перпендикуляра к гипотенузе прямоугольного треугольника. Область определения и область значений синуса тригонометрической функции задаются следующим образом:
- Область определения = все действительные числа, т. е. (−∞, ∞)
- Диапазон = [-1, 1]
Область определения и диапазон тригонометрической функции: косинус
Мы знаем, что функция косинуса представляет собой отношение прилежащей стороны и гипотенузы прямоугольного треугольника. Область определения и область значений косинуса тригонометрической функции определяются как:
- Домен = все действительные числа, т. е. (−∞, ∞)
- Диапазон = [-1, 1]
Область определения и диапазон тригонометрической функции: тангенс
Мы знаем, что тангенс представляет собой отношение противолежащих и прилежащих сторон прямоугольного треугольника.
Его также можно записать как отношение функции синуса и косинуса, поэтому область значений tan x не содержит значений, при которых cos x равен нулю. Мы знаем, что cos x равен 0 при нечетных целых числах, кратных π/2, поэтому область определения и область значений тангенса тригонометрической функции определяются выражением:
- Домен = R — (2n + 1)π/2
- Диапазон = (−∞, ∞)
Область определения и область значений тригонометрической функции: котангенс
Мы знаем, что функция котангенса представляет собой отношение прилежащей стороны к противолежащей стороне в прямоугольном треугольнике. Это также может быть записано как отношение функции косинуса и синуса, а cot x является обратной величиной tan x. Поэтому область определения ctg x не содержит значений, при которых sin x равен нулю. Мы знаем, что sin x равен 0 при целых кратных π, следовательно, область определения и область значений котангенса тригонометрической функции определяются как:
- Домен = R — nπ
- Диапазон = (−∞, ∞)
Область и диапазон тригонометрической функции: секущая
Мы знаем, что секущая функция представляет собой отношение гипотенузы к прилежащей стороне в прямоугольном треугольнике.
- Домен = R — (2n + 1)π/2
- Диапазон = (-∞, -1] U [+1, +∞)
Область определения и диапазон тригонометрической функции: косеканс
Мы знаем, что косеканс представляет собой отношение гипотенузы к противолежащему катету в прямоугольном треугольнике. Его также можно записать как обратную функцию синуса. Поэтому область определения тригонометрической функции cosec x не содержит значений, при которых sin x равен нулю. Мы знаем, что sin x равен 0 при целых числах, кратных π, следовательно, область определения и область значений косеканса тригонометрической функции определяются выражением:
- Домен = R — nπ
- Диапазон = (-∞, -1] U [+1, +∞)
Область определения и диапазон тригонометрических функций Таблица
Итак, мы изучили область определения и область значений тригонометрических функций.
В приведенной ниже таблице дано ее краткое изложение, которое поможет лучше понять и использовать для решения различных задач:
| Тригонометрические функции | Домен | Диапазон |
| Синθ | (-∞, + ∞) | [-1, +1] |
| Cosθ | (-∞ +∞) | [-1, +1] |
| Танθ | Р — (2n + 1)π/2 | (-∞, +∞) |
| Кот θ | Р — номер | |
| сек θ | Р — (2n + 1)π/2 | (-∞, -1] U [+1, +∞) |
| Cosecθ | Р — номер | (-∞, -1] U [+1, +∞) |
Область определения и область значений обратных тригонометрических функций
Функция обратима тогда и только тогда, когда она биективна. Обратные тригонометрические функции являются обратными по отношению к тригонометрическим функциям, и, чтобы сделать тригонометрические функции обратимыми, мы ограничиваем их область определения ветвью главного значения.
В таблице ниже представлены область определения и диапазон обратных тригонометрических функций:
| Обратные тригонометрические функции | Домен | Диапазон |
| Грех -1 х | [-1, +1] | [-π/2, π/2] |
| Кос -1 x | [-1, +1] | [0, π] |
| Желто-коричневый -1 x | (-∞, + ∞) | (-π/2, π/2) |
| Детская кроватка -1 x | (-∞, + ∞) | (0, π) |
| сек -1 x | (−∞,−1] U [1,∞) | [0, π/2) U (π/2, π] |
| Косек -1 x | (−∞,−1] U [1,∞) | [-π/2, 0) U (0, π/2] |
Область определения и диапазон тригонометрических функций с использованием графика
Далее мы исследуем область определения и диапазон тригонометрических функций, используя графики тригонометрических функций.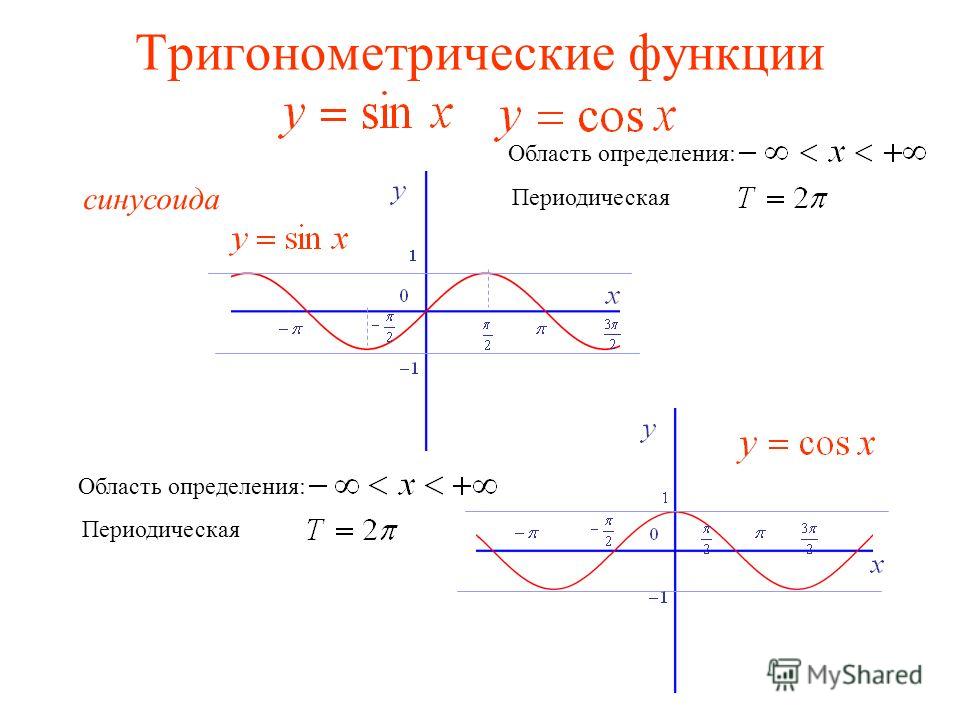
Ниже приведены графики шести тригонометрических функций. Как мы видим на графиках, область определения и диапазон тригонометрических функций представлены осью x и осью y соответственно.
Советы и рекомендации по предметной области и диапазону тригонометрических функций
- Проверить значение ввода, где функция не определена. Значение, в котором функция не определена, может быть исключено из домена.
- Диапазон тригонометрической функции задается выходными значениями для каждого из входных значений (область).
Похожие темы
- Тригонометрия
- Тригонометрические формулы
- Тригонометрические тождества
Часто задаваемые вопросы по домену и диапазону тригонометрических функций
Что такое область и диапазон тригонометрических функций в тригонометрии?
домен и диапазон тригонометрических функций являются входными значениями и выходными значениями тригонометрических функций соответственно.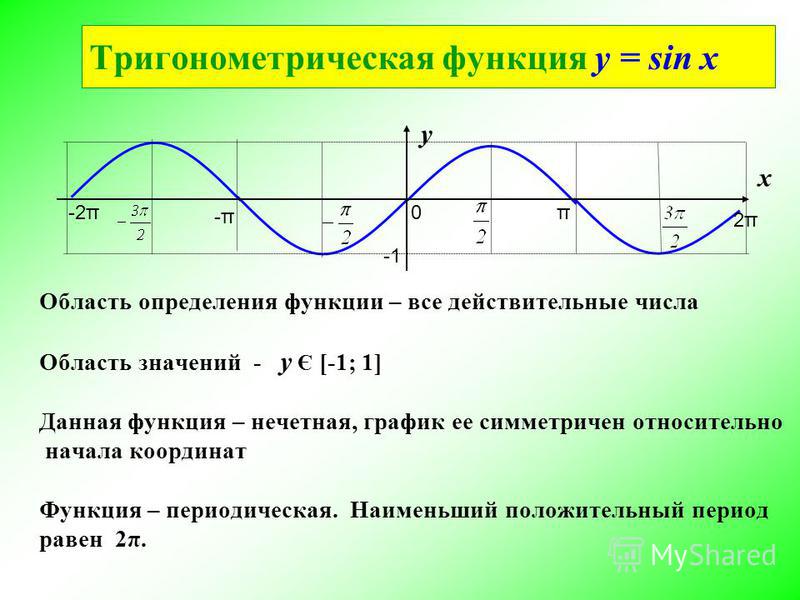
- Для sin θ, домен = (-∞, + ∞), диапазон = [-1, 1]
- Для cos θ, домен = (-∞, + ∞), диапазон = [-1, 1]
- Для тангенса θ, домен = R — (2n + 1)π/2, диапазон = (-∞, +∞)
- Для кроватки θ, домен = R — nπ , диапазон = (-∞, +∞)
- Для сек θ, домен = R — (2n + 1)π/2, диапазон = (-∞, -1] U [+1, +∞)
- Для cosec θ, домен = R — nπ , диапазон = (-∞, -1] U [+1, +∞)
Как найти область определения и диапазон тригонометрических функций?
Домен и диапазон тригонометрических функций можно найти, проверив, где определена функция, и выходные значения функции для каждого входного значения.
Каков диапазон теты Cos Square?
Мы знаем, что диапазон cos θ равен [-1, 1], а cos 2 θ всегда положителен, поэтому диапазон cos квадрат тета равен [0, 1].
Как найти область определения и область значений обратных тригонометрических функций?
Обратные тригонометрические функции являются обратными по отношению к тригонометрическим функциям, и чтобы сделать тригонометрические функции обратимыми, мы ограничиваем их область определения ветвью главного значения.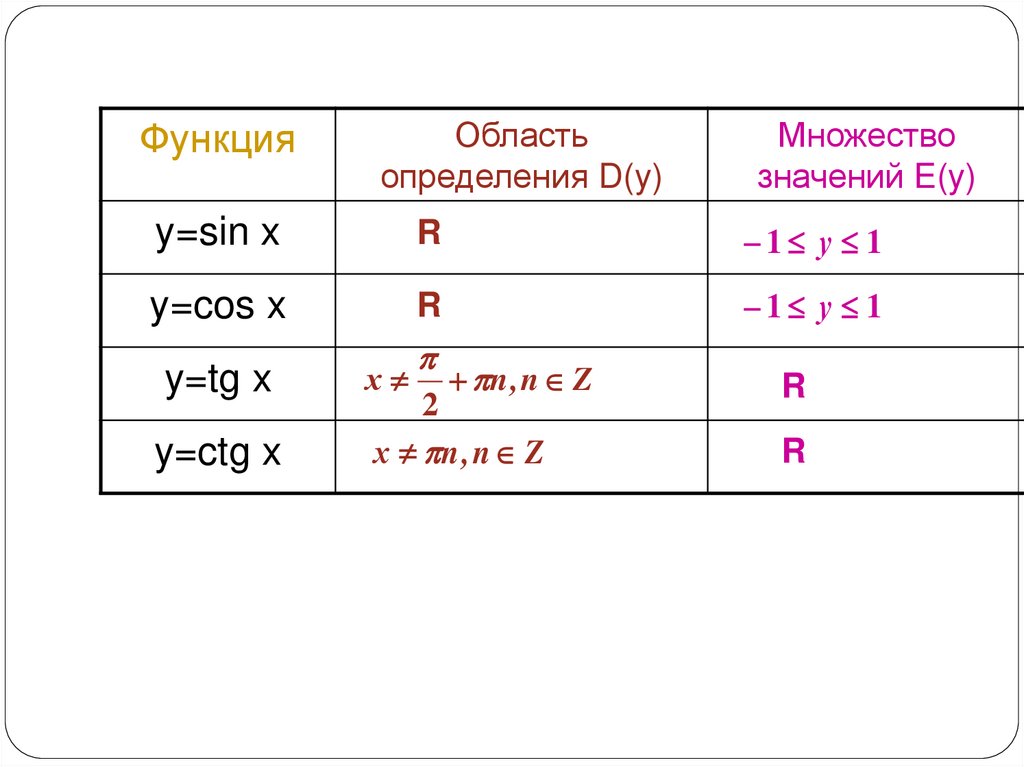
Что такое домен и диапазон Sec Theta?
Область определения sec θ равна R — (2n + 1)π/2, а диапазон равен (-∞, -1] U [+1, +∞), где n — целое число.
Область определения и диапазон тригонометрических функций
Перейти к основному содержанию
Домашняя страница Технологического института Онтарио
nool
Область определения функции — это определенный набор значений, которые может принимать независимая переменная в функции. Диапазон — это результирующие значения, которые зависимая переменная может иметь при изменении x в пределах домена.
Область и диапазон функций синуса и косинуса
Нет ограничений на область определения функций синуса и косинуса; следовательно, их область определения такова, что x ∈ R.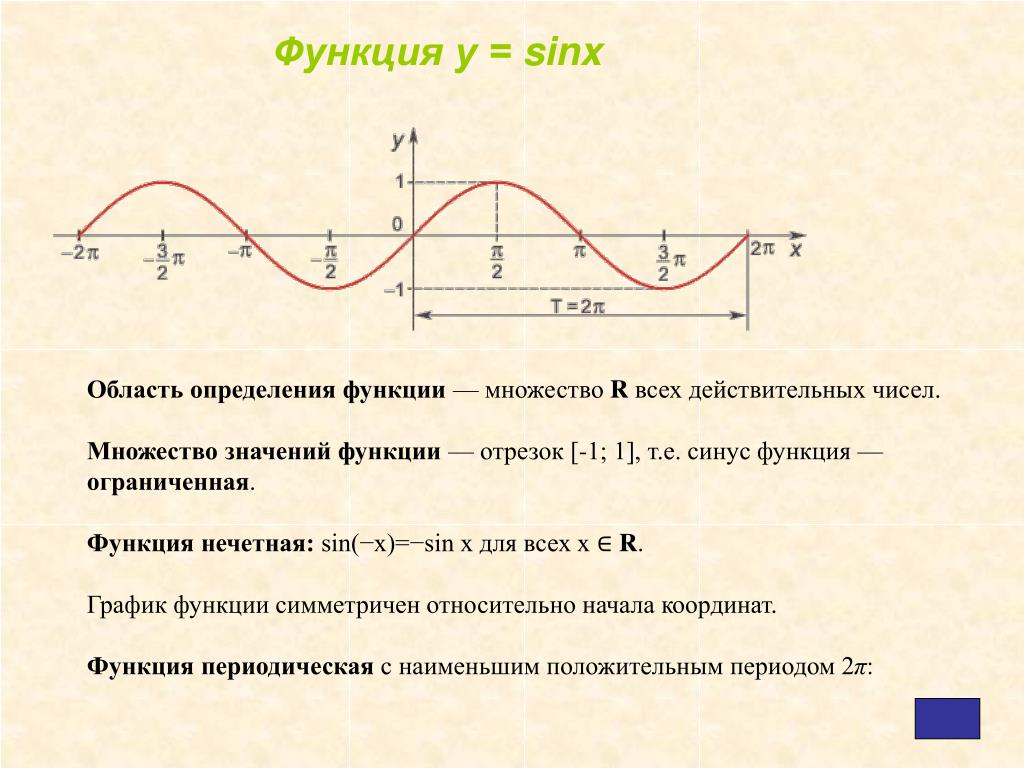
Обратите внимание, однако, что диапазон как для y = sin(x), так и для y = cos(x) находится между -1 и 1. Следовательно, преобразования этих функций в виде сдвиги и растяжения повлияют на диапазон, но не на домен.
Область определения и диапазон для функций тангенса
Обратите внимание, что y = tan(x) имеет вертикальные асимптоты при . Следовательно, его домен таков, что . Однако ее область значений такова при y ∈ R, поскольку функция принимает все значения y. В этом случае преобразования коснутся домена, но не диапазона.
Пример: Найти область определения и диапазон y = cos(x) – 3
Решение:
Область определения: x ∈ R
Диапазон: — 4 ≤ y ∈ R ≤ — 2, y
Обратите внимание, что диапазон просто сдвинут вниз на 3 единицы.
Пример: Найдите домен и диапазон y = 3 tan(x)
Решение:
Домен: , x ∈ R
Обратите внимание, что домен тот же, что и домен для y = tan(x) x), потому что график был растянут по вертикали, что не меняет места расположения вертикальных асимптот.