Таблица тангенсов.
Таблица синусов Таблица косинусов Таблица тангенсов Таблица котангенсов Таблица Брадиса: синусы, косинусы, тангенсы и котангенсы
Скачать таблицу тангенсов
Таблица тангенсов — это записанные в таблицу посчитанные значения тангенсов углов от 0° до 360°. Используя таблицу тангенсов Вы сможете провести расчеты даже если под руками не окажется инженерного калькулятора. Чтобы узнать значение тангенса от нужного Вам угла достаточно найти его в таблице.
Калькулятор — тангенс угла
tg(°) = 0
Калькулятор — арктангенс угла
arctan() = 45°
Таблица тангенсов в радианах
| α | 0 | π6 | π4 | π3 | π2 | π | 3π2 | 2π |
| tg α | 0 | √33 | 1 | √3 | ∞ | 0 | ∞ |
Таблица тангенсов углов от 0° до 180°
| tg(0°) = 0 tg(1°) = 0.  01746 01746tg(2°) = 0.03492 tg(3°) = 0.05241 tg(4°) = 0.06993 tg(5°) = 0.08749 tg(6°) = 0.1051 tg(7°) = 0.12278 tg(8°) = 0.14054 tg(9°) = 0.15838 tg(10°) = 0.17633 tg(11°) = 0.19438 tg(12°) = 0.21256 tg(13°) = 0.23087 tg(14°) = 0.24933 tg(15°) = 0.26795 tg(16°) = 0.28675 tg(17°) = 0.30573 tg(18°) = 0.32492 tg(19°) = 0.34433 tg(20°) = 0.36397 tg(21°) = 0.38386 tg(22°) = 0.40403 tg(23°) = 0.42447 tg(24°) = 0.44523 tg(25°) = 0.46631 tg(26°) = 0.48773 tg(27°) = 0.50953 tg(28°) = 0.53171 tg(29°) = 0.55431 tg(30°) = 0.57735 tg(31°) = 0.60086 tg(32°) = 0.62487 tg(33°) = 0.64941 tg(34°) = 0.67451 tg(35°) = 0.70021 tg(36°) = 0.72654 tg(37°) = 0.75355 tg(38°) = 0.78129 tg(39°) = 0.80978 tg(40°) = 0.8391 tg(41°) = 0.86929 tg(42°) = 0.9004 tg(43°) = 0.93252 tg(44°) = 0.96569 tg(45°) = 1 tg(46°) = 1.03553 tg(47°) = 1.07237 tg(48°) = 1.  11061 11061tg(49°) = 1.15037 tg(50°) = 1.19175 tg(51°) = 1.2349 tg(52°) = 1.27994 tg(53°) = 1.32704 tg(54°) = 1.37638 tg(55°) = 1.42815 tg(56°) = 1.48256 tg(57°) = 1.53986 tg(58°) = 1.60033 tg(59°) = 1.66428 tg(60°) = 1.73205 | tg(61°) = 1.80405 tg(62°) = 1.88073 tg(63°) = 1.96261 tg(64°) = 2.0503 tg(65°) = 2.14451 tg(66°) = 2.24604 tg(67°) = 2.35585 tg(68°) = 2.47509 tg(69°) = 2.60509 tg(70°) = 2.74748 tg(71°) = 2.90421 tg(72°) = 3.07768 tg(73°) = 3.27085 tg(74°) = 3.48741 tg(75°) = 3.73205 tg(76°) = 4.01078 tg(77°) = 4.33148 tg(78°) = 4.70463 tg(79°) = 5.14455 tg(80°) = 5.67128 tg(82°) = 7.11537 tg(83°) = 8.14435 tg(84°) = 9.51436 tg(85°) = 11.43005 tg(86°) = 14.30067 tg(87°) = 19.08114 tg(88°) = 28.63625 tg(89°) = 57.28996 tg(90°) = ∞ tg(91°) = -57.28996 tg(92°) = -28.63625 tg(93°) = -19.  08114 08114tg(94°) = -14.30067 tg(95°) = -11.43005 tg(96°) = -9.51436 tg(97°) = -8.14435 tg(98°) = -7.11537 tg(99°) = -6.31375 tg(100°) = -5.67128 tg(101°) = -5.14455 tg(102°) = -4.70463 tg(103°) = -4.33148 tg(104°) = -4.01078 tg(105°) = -3.73205 tg(106°) = -3.48741 tg(107°) = -3.27085 tg(108°) = -3.07768 tg(109°) = -2.90421 tg(110°) = -2.74748 tg(111°) = -2.60509 tg(112°) = -2.47509 tg(113°) = -2.35585 tg(114°) = -2.24604 tg(115°) = -2.14451 tg(116°) = -2.0503 tg(117°) = -1.96261 tg(118°) = -1.88073 tg(119°) = -1.80405 tg(120°) = -1.73205 | tg(121°) = -1.66428 tg(122°) = -1.60033 tg(123°) = -1.53986 tg(124°) = -1.48256 tg(125°) = -1.42815 tg(126°) = -1.37638 tg(127°) = -1.32704 tg(128°) = -1.27994 tg(129°) = -1.2349 tg(130°) = -1.19175 tg(131°) = -1.15037 tg(132°) = -1.11061 tg(133°) = -1.07237 tg(134°) = -1.03553 tg(135°) = -1 tg(136°) = -0.  96569 96569tg(137°) = -0.93252 tg(138°) = -0.9004 tg(139°) = -0.86929 tg(140°) = -0.8391 tg(141°) = -0.80978 tg(142°) = -0.78129 tg(143°) = -0.75355 tg(144°) = -0.72654 tg(145°) = -0.70021 tg(146°) = -0.67451 tg(147°) = -0.64941 tg(148°) = -0.62487 tg(149°) = -0.60086 tg(150°) = -0.57735 tg(151°) = -0.55431 tg(152°) = -0.53171 tg(153°) = -0.50953 tg(154°) = -0.48773 tg(155°) = -0.46631 tg(156°) = -0.44523 tg(157°) = -0.42447 tg(159°) = -0.38386 tg(160°) = -0.36397 tg(161°) = -0.34433 tg(162°) = -0.32492 tg(163°) = -0.30573 tg(164°) = -0.28675 tg(165°) = -0.26795 tg(166°) = -0.24933 tg(167°) = -0.23087 tg(168°) = -0.21256 tg(169°) = -0.19438 tg(170°) = -0.17633 tg(171°) = -0.15838 tg(172°) = -0.14054 tg(173°) = -0.12278 tg(174°) = -0.1051 tg(175°) = -0.08749 tg(176°) = -0.06993 tg(177°) = -0.05241 tg(178°) = -0.  03492 03492tg(179°) = -0.01746 tg(180°) = 0 |
Таблица тангенсов углов от 181° до 360°
| tg(181°) = 0.01746 tg(182°) = 0.03492 tg(183°) = 0.05241 tg(184°) = 0.06993 tg(185°) = 0.08749 tg(186°) = 0.1051 tg(187°) = 0.12278 tg(188°) = 0.14054 tg(189°) = 0.15838 tg(190°) = 0.17633 tg(191°) = 0.19438 tg(192°) = 0.21256 tg(193°) = 0.23087 tg(194°) = 0.24933 tg(195°) = 0.26795 tg(196°) = 0.28675 tg(197°) = 0.30573 tg(198°) = 0.32492 tg(199°) = 0.34433 tg(200°) = 0.36397 tg(201°) = 0.38386 tg(202°) = 0.40403 tg(203°) = 0.42447 tg(204°) = 0.44523 tg(205°) = 0.46631 tg(206°) = 0.48773 tg(207°) = 0.50953 tg(208°) = 0.53171 tg(209°) = 0.55431 tg(210°) = 0.57735 tg(211°) = 0.60086 tg(212°) = 0.62487 tg(213°) = 0.64941 tg(214°) = 0.67451 tg(215°) = 0.70021 tg(216°) = 0.72654 tg(217°) = 0.  75355 75355tg(218°) = 0.78129 tg(219°) = 0.80978 tg(220°) = 0.8391 tg(221°) = 0.86929 tg(222°) = 0.9004 tg(223°) = 0.93252 tg(224°) = 0.96569 tg(225°) = 1 tg(226°) = 1.03553 tg(227°) = 1.07237 tg(228°) = 1.11061 tg(229°) = 1.15037 tg(230°) = 1.19175 tg(231°) = 1.2349 tg(233°) = 1.32704 tg(234°) = 1.37638 tg(235°) = 1.42815 tg(236°) = 1.48256 tg(237°) = 1.53986 tg(238°) = 1.60033 tg(239°) = 1.66428 tg(240°) = 1.73205 | tg(241°) = 1.80405 tg(242°) = 1.88073 tg(243°) = 1.96261 tg(244°) = 2.0503 tg(245°) = 2.14451 tg(246°) = 2.24604 tg(247°) = 2.35585 tg(248°) = 2.47509 tg(249°) = 2.60509 tg(250°) = 2.74748 tg(251°) = 2.90421 tg(252°) = 3.07768 tg(253°) = 3.27085 tg(254°) = 3.48741 tg(255°) = 3.73205 tg(256°) = 4.01078 tg(257°) = 4.33148 tg(258°) = 4.70463 tg(259°) = 5.14455 tg(260°) = 5.67128 tg(261°) = 6.  31375 31375tg(262°) = 7.11537 tg(263°) = 8.14435 tg(264°) = 9.51436 tg(265°) = 11.43005 tg(266°) = 14.30067 tg(267°) = 19.08114 tg(268°) = 28.63625 tg(269°) = 57.28996 tg(270°) = ∞ tg(271°) = -57.28996 tg(272°) = -28.63625 tg(273°) = -19.08114 tg(274°) = -14.30067 tg(275°) = -11.43005 tg(276°) = -9.51436 tg(277°) = -8.14435 tg(278°) = -7.11537 tg(279°) = -6.31375 tg(280°) = -5.67128 tg(281°) = -5.14455 tg(282°) = -4.70463 tg(283°) = -4.33148 tg(284°) = -4.01078 tg(285°) = -3.73205 tg(286°) = -3.48741 tg(287°) = -3.27085 tg(288°) = -3.07768 tg(289°) = -2.90421 tg(290°) = -2.74748 tg(291°) = -2.60509 tg(292°) = -2.47509 tg(293°) = -2.35585 tg(294°) = -2.24604 tg(295°) = -2.14451 tg(296°) = -2.0503 tg(297°) = -1.96261 tg(298°) = -1.88073 tg(299°) = -1.80405 tg(300°) = -1.73205 | tg(301°) = -1.66428 tg(302°) = -1.60033 tg(303°) = -1. 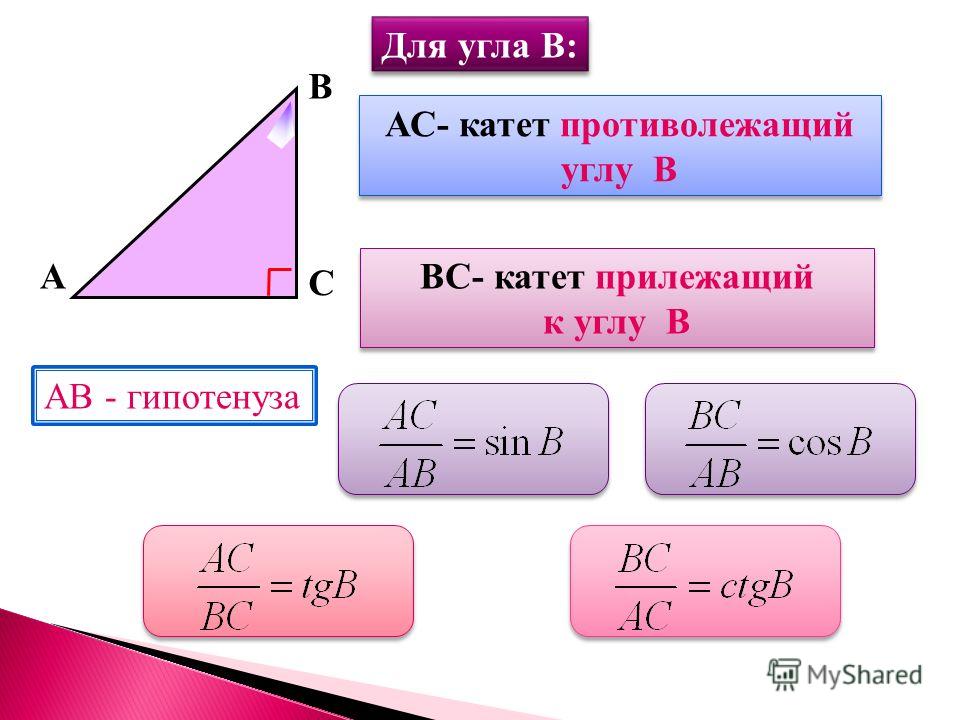 53986 53986tg(304°) = -1.48256 tg(305°) = -1.42815 tg(306°) = -1.37638 tg(307°) = -1.32704 tg(308°) = -1.27994 tg(310°) = -1.19175 tg(311°) = -1.15037 tg(312°) = -1.11061 tg(313°) = -1.07237 tg(314°) = -1.03553 tg(315°) = -1 tg(316°) = -0.96569 tg(317°) = -0.93252 tg(318°) = -0.9004 tg(319°) = -0.86929 tg(320°) = -0.8391 tg(321°) = -0.80978 tg(322°) = -0.78129 tg(323°) = -0.75355 tg(324°) = -0.72654 tg(325°) = -0.70021 tg(326°) = -0.67451 tg(327°) = -0.64941 tg(328°) = -0.62487 tg(329°) = -0.60086 tg(330°) = -0.57735 tg(331°) = -0.55431 tg(332°) = -0.53171 tg(333°) = -0.50953 tg(334°) = -0.48773 tg(335°) = -0.46631 tg(336°) = -0.44523 tg(337°) = -0.42447 tg(338°) = -0.40403 tg(339°) = -0.38386 tg(340°) = -0.36397 tg(341°) = -0.34433 tg(342°) = -0.32492 tg(343°) = -0.30573 tg(344°) = -0.28675 tg(345°) = -0.26795 tg(346°) = -0.  24933 24933tg(347°) = -0.23087 tg(348°) = -0.21256 tg(349°) = -0.19438 tg(350°) = -0.17633 tg(351°) = -0.15838 tg(352°) = -0.14054 tg(353°) = -0.12278 tg(354°) = -0.1051 tg(355°) = -0.08749 tg(356°) = -0.06993 tg(357°) = -0.05241 tg(358°) = -0.03492 tg(359°) = -0.01746 tg(360°) = 0 |
Таблицы значений тригонометрических функций Таблица Брадиса: синусы, косинусы, тангенсы и котангенсы Таблица синусов Таблица косинусов Таблица тангенсов Таблица котангенсов Сводная таблица тригонометрических функций
Тригонометрические формулы
Все таблицы и формулы
TG 46
Р Е Н О К Р И Л TG 46 Futur, Кристалл грунт, для нанесения погружением, белый
Области применения:
РЕНОКРИЛ TG 46 применяется как грунтовка для любых пород древесины, для строительных конструкций с высокими требованиями к сохранению размеров. Для древесины с особыми внутренними веществами должна быть применена изолирующая грунтовка IL 48.
Продукт предназначен для применения на промышленных предприятиях.
Характеристики:
РЕНОКРИЛ TG 46 – шелковисто-матовая, содержащая белые пигменты, не препятствует диффузии водных паров, может наноситься кистью или окунанием. Экологична, имеет нейтральный запах. Не заливать в ёмкости, которые могут ржаветь, оказывает фунгицидное действие, защитное действие согласно DIN EN 152, раздел 1. если после нанесения грунтовки погружением на поверхности проявляются пятна, то необходимо дополнительно обработать грунтом IL 48 L.
Указания по обработке:
Способ нанесения : погружение, облив, нанесение кистью, напыление.
нанесение кистью : Ренокрил TG 46 Futur можно наносить кистью в
неразбавленном виде. Поверхность равномерно
покрыть тонким слоем.
напыление : Ренокрил TG 46 Futur можно наносить в не разведённом виде напылением. Для правильного
высыхания необходимо нанесение ровным слоем.
нанесение погружением : наносится в неразбавленном виде, при этом продукт
имеет вязкость от 11 – до 12 сек. (DIN метал.
(DIN метал.
стаканчик 4 мм). Провести пробное погружение, в
зависимости от стекаемости разбавить с 5% воды.
Очистка : водой или универсальным растворителем.
Температура обработки : 20 °С относит. влажность воздуха – в зависимости от
толщины наносимого слоя, через 30-60 минут
можно шлифовать.
Расход : в зависимости от всасывающей способности
древесины ок. 100-150 мл/м².
Хранение : в прохладном месте, но без замерзания, вскрытые
ёмкости держать плотно закрытыми. для предупреждения образования плёнки на поверхности, впрыснуть в ёмкость немного воды.
В оригинальной упаковке срок хранения 1 год.
Общие указания : перед применением и после длительных пауз
перемешать, не смешивать с продуктами на основе
растворителей.
Не смешивать с другими водорастворимыми
продуктами !!
Точка воспламенения : отсутствует.
Класс опасности : без обозначения.
VbF: отсутствует.
Gef.Stoff V: не требует обозначения.
GGVS / ADR: не требует обозначения.
Создание покрытия для деревянных окон и входных дверей из лиственной и хвойной
древесины:
Предварительные работы : деревянные поверхности тщательно очистить от пыли, смолистые и
загрязнённые поверхности протереть нитрорастворителем.
Rhenocryl TG 46
Грунтовка : нанести Rhenocryl TG 46 Futur (погружением или обливом) на древесину
с особыми внутренними веществами.
Дополнительно нанести (напылением) Rhenocryl IL 48 L как
промежуточное покрытие (толщина мокрой плёнки ок. 175 µ).
Окончательное покрытие : нанести Rhenocryl DL 90 Futur Airless-аппаратом, толщина мокрой
плёнки 300 µ.
(в случае нанесения промежуточного слоя: ок. 125 µ)
В соответствии с директивами о лакокрасочных покрытиях деревянных окон, изданных федеральным комитетом красок и защиты ценностей, строительных норм для открытых строительных элементов (VOB, часть 1), DIN 18363 и рекомендациями IFT (Института оконной техники в Розенхайме) деревянные строительные элементы перед монтажом должны покрываться со всех сторон не менее чем в один слой грунтом и промежуточным грунтом.
Примите во внимание при создании лакокрасочного покрытия так же таблицу «Группы лакокрасочных покрытий для окон и входных дверей», изданную Институтом техники (IFT), Розенхайм, в мае 1983г.
Указания по мерам предосторожности:
Хранить под замком, в местах недоступных для детей. Не допускать попадания в глаза. При попадании промыть большим количеством воды. При работе с малоопасными лаками необходимо соблюдать обычные меры предосторожности.
Утилизация:
Не затвердевшие или не высохшие остатки продукта утилизировать как специальные отходы по согласованию с комитетами по охране окружающей среды (код № 55508 согласно ТА-Abfall). Затвердевшие или высохшие остатки могут быть утилизированы по коду №55513 согласно ТА-Abfall.
Пустые ёмкости должны быть подвергнуты вторичной переработке.
Экология:
WGK (Класс водоопасности): 1 (собственная классификация).
Не допускать попадания в водоёмы, сточные воды и в почву.
Сервис
Наша техническая-информационная служба всегда в Вашем распоряжении.
Тел.: Конкен, +49 — 6384/99 38 — 0, факс: +49 — 6384/99 38 — 126
Эти данные без обязательства, основываются на опыте из практики и на результатах проведённых нами испытаний. Рекомендуется в любом случае провести собственные испытания, так как мы не можем оказывать влияния на многообразие окрашиваемых материалов и возможных способов применения данного материала. За возможные последствия вследствие неправомерного использования материала (не по назначению) изготовитель ответственности не несёт. Содержание технических инструкций не является основанием для ответственности продавца. Данные, не содержащиеся в технической инструкции или не совпадающие с ними, требуют письменного подтверждения заводом.
В любом случае действуют наши общие договорные условия и условия поставок.
Таблица тангенсов углов (углы, значения)
В таблице значения тангенсов от 0° до 360°. Таблица тангенсов нужна, когда у вас под рукой нет калькулятора.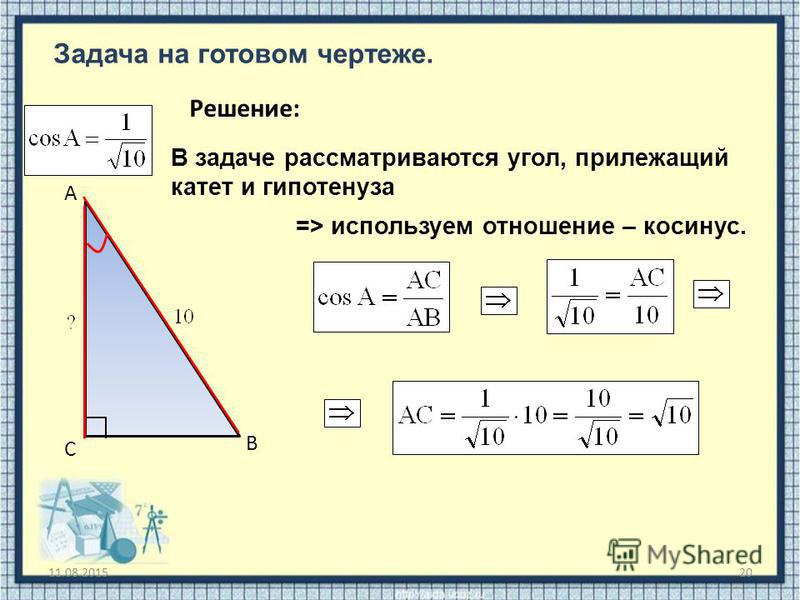 Чтобы узнать, чему равен тангенс угла, просто найдите его в таблице. Для начала короткая версия таблицы:
Чтобы узнать, чему равен тангенс угла, просто найдите его в таблице. Для начала короткая версия таблицы:
https://uchim.org/matematika/tablica-tangensov — uchim.org
Таблица тангенсов для 0°-180°
|
|
|
Таблица тангенсов для 180° — 360°
|
|
|
Существуют также следующие таблицы тригонометрических функций по геометрии: таблица синусов, таблица косинусов и таблица котангенсов.
Всё для учебы » Математика в школе » Таблица тангенсов углов (углы, значения)
Если страница помогла, сохраните её и поделитесь ссылкой с друзьями:
Ссылка: https://uchim.org/matematika/tablica-tangensov
Таблица тангенсов | Онлайн калькуляторы, расчеты и формулы на GELEOT.RU
Тангенс, как отношение катетов в прямоугольном треугольнике, представляет собой функцию которая выглядит как дуга окружности внутри данного треугольника с центром в вершине угла и прилежащим катетом в качестве радиуса.
Значение тангенса показывает не только раскрытие угла α, но и насколько один катет больше другого. При тангенсе угла α, равном 1, катеты равны друг другу и треугольник считается равнобедренным. Значения всех тангенсов и соответствующих им углов можно найти в таблице, приведенной ниже.
Найти тангенс угла tg(α), зная угол
Угол α
Таблица тангенсов от 0° до 180°
|
|
|
|
|
Таблица тангенсов от 181° до 360°
|
|
|
|
|
| ГОСТы, СНиПы Карта сайта TehTab.ru Поиск по сайту TehTab.ru | Навигация по справочнику TehTab.ru: главная страница / / Техническая информация/ / Математический справочник/ / Таблицы численных значений. (Таблица квадратов, кубов, синусов ….) + Таблицы Брадиса / / Таблица тангенсов углов углов от 0° — 360°. Углы с шагом в 1°. Таблица значений тангенса, tg
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Нашли ошибку? Есть дополнения? Напишите нам об этом, указав ссылку на страницу. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
TehTab.ru Реклама, сотрудничество: [email protected] | Обращаем ваше внимание на то, что данный интернет-сайт носит исключительно информационный характер. Информация, представленная на сайте, не является официальной и предоставлена только в целях ознакомления. Все риски за использование информаци с сайта посетители берут на себя. Проект TehTab.ru является некоммерческим, не поддерживается никакими политическими партиями и иностранными организациями. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Таблица тангенсов, найти тангенс угла
Тангенс угла – одна из основных тригонометрических функций. Представляет собой соотношение катетов прямоугольного треугольника. То есть, tg(А)=ВС/АС, где ВС – противолежащий к углу (А) катет, АС – прилежащий катет.
Зачем необходимо знать тангенс угла? Такие данные имеют вполне практическое применение: в геодезии, мореходстве, авиации. Зная одну из сторон треугольника и угол, можно легко получить все остальные данные, используя тригонометрические тождества. Все расчеты легко производить с помощью онлайн-калькулятора на нашем сайте. Данные указаны в таблице тангенсов.
Для практического использования подходят не только таблицы Брадиса. Все тригонометрические функции вычисляются посредством калькулятора. Найдите красивое решение для вашей задачи.
|
|
|
|
|
|
|
|
|
|
Select rating12345
Рейтинг: 3.1 (Голосов 42)
Сообщить об ошибке
Смотрите также
| 1 | Найти точное значение | грех(30) | |
| 2 | Найти точное значение | грех(45) | |
| 3 | Найти точное значение | грех(30 градусов) | |
| 4 | Найти точное значение | грех(60 градусов) | |
| 5 | Найти точное значение | загар (30 градусов) | |
| 6 | Найти точное значение | угловой синус(-1) | |
| 7 | Найти точное значение | грех(пи/6) | |
| 8 | Найти точное значение | cos(pi/4) | |
| 9 | Найти точное значение | грех(45 градусов) | |
| 10 | Найти точное значение | грех(пи/3) | |
| 11 | Найти точное значение | арктан(-1) | |
| 12 | Найти точное значение | cos(45 градусов) | |
| 13 | Найти точное значение | cos(30 градусов) | |
| 14 | Найти точное значение | желтовато-коричневый(60) | |
| 15 | Найти точное значение | csc(45 градусов) | |
| 16 | Найти точное значение | загар (60 градусов) | |
| 17 | Найти точное значение | сек(30 градусов) | |
| 18 | Найти точное значение | cos(60 градусов) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | грех(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | загар (45 градусов) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 градусов) | |
| 25 | Найти точное значение | сек(45 градусов) | |
| 26 | Найти точное значение | csc(30 градусов) | |
| 27 | Найти точное значение | грех(0) | |
| 28 | Найти точное значение | грех(120) | |
| 29 | Найти точное значение | соз(90) | |
| 30 | Преобразовать из радианов в градусы | пи/3 | |
| 31 | Найти точное значение | желтовато-коричневый(30) | |
| 32 | 92|||
| 35 | Преобразовать из радианов в градусы | пи/6 | |
| 36 | Найти точное значение | детская кроватка(30 градусов) | |
| 37 | Найти точное значение | арккос(-1) | |
| 38 | Найти точное значение | арктан(0) | |
| 39 | Найти точное значение | детская кроватка(60 градусов) | |
| 40 | Преобразование градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2 шт. )/3 )/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | тан(пи/2) | |
| 45 | Найти точное значение | грех(300) | |
| 46 | Найти точное значение | соз(30) | |
| 47 | Найти точное значение | соз(60) | |
| 48 | Найти точное значение | соз(0) | |
| 49 | Найти точное значение | соз(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | сек(60 градусов) | |
| 53 | Найти точное значение | грех(300 градусов) | |
| 54 | Преобразование градусов в радианы | 135 | |
| 55 | Преобразование градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5 дюймов)/6 | |
| 57 | Преобразовать из радианов в градусы | (5 дюймов)/3 | |
| 58 | Преобразование градусов в радианы | 89 градусов | |
| 59 | Преобразование градусов в радианы | 60 | |
| 60 | Найти точное значение | грех(135 градусов) | |
| 61 | Найти точное значение | грех(150) | |
| 62 | Найти точное значение | грех(240 градусов) | |
| 63 | Найти точное значение | детская кроватка(45 градусов) | |
| 64 | Преобразовать из радианов в градусы | (5 дюймов)/4 | |
| 65 | Найти точное значение | грех(225) | |
| 66 | Найти точное значение | грех(240) | |
| 67 | Найти точное значение | cos(150 градусов) | |
| 68 | Найти точное значение | желтовато-коричневый(45) | |
| 69 | Оценить | грех(30 градусов) | |
| 70 | Найти точное значение | сек(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | КСК(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | загар((5pi)/3) | |
| 75 | Найти точное значение | желтовато-коричневый(0) | |
| 76 | Оценить | грех(60 градусов) | |
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3 пи)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | угловой синус(-1/2) | |
| 81 | Найти точное значение | sin((4pi)/3) | |
| 82 | Найти точное значение | КСК(45) | |
| 83 | Упростить | арктан(квадратный корень из 3) | |
| 84 | Найти точное значение | грех(135) | |
| 85 | Найти точное значение | грех(105) | |
| 86 | Найти точное значение | грех(150 градусов) | |
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | загар((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | пи/4 | |
| 90 | Найти точное значение | грех(пи/2) | |
| 91 | Найти точное значение | сек(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | угловой синус(0) | |
| 95 | Найти точное значение | грех(120 градусов) | |
| 96 | Найти точное значение | желтовато-коричневый ((7pi)/6) | |
| 97 | Найти точное значение | соз(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразование градусов в радианы | 88 градусов |
Tan 46 градусов — Найти значение Tan 46 градусов
LearnPracticeDownload
Значение tan 46 градусов равно 1,0355303. . . . Тангенс 46 градусов в радианах записывается как тангенс (46° × π/180°), то есть тангенс (23π/90) или тангенс (0,802851…). В этой статье мы обсудим способы нахождения значения тангенса 46 градусов на примерах.
. . . Тангенс 46 градусов в радианах записывается как тангенс (46° × π/180°), то есть тангенс (23π/90) или тангенс (0,802851…). В этой статье мы обсудим способы нахождения значения тангенса 46 градусов на примерах.
- Тан 46° в десятичном формате: 1.0355303. . .
- Желто-коричневый (-46 градусов): -1,0355303. . .
- Tan 46° в радианах: tan (23π/90) или желтовато-коричневый (0,8028514 . . .)
Сколько стоит Тан 46 градусов?
Значение тангенса 46 градусов в десятичной системе равно 1,035530313. . .. Tan 46 градусов также можно выразить, используя эквивалент данного угла (46 градусов) в радианах (0,80285 . . .)
Мы знаем, используя преобразование градусов в радианы, θ в радианах = θ в градусах × (пи/ 180°)
⇒ 46 градусов = 46° × (π/180°) рад = 23π/90 или 0,8028. . .
∴ тангенс 46° = тангенс (0,8028) = 1,0355303. . .
Объяснение:
Для тангенса 46 градусов угол 46° лежит между 0° и 90° (первый квадрант). Поскольку функция тангенса положительна в первом квадранте, значение tan 46° = 1,0355303. . .
Поскольку функция тангенса положительна в первом квадранте, значение tan 46° = 1,0355303. . .
Поскольку функция тангенса является периодической функцией, мы можем представить тангенс 46° как тангенс 46 градусов = тангенс (46° + n × 180°), n ∈ Z.
⇒ тангенс 46° = тангенс 226° = тангенс 406° и так далее.
Примечание: Поскольку тангенс является нечетной функцией, значение тангенса (-46°) = -тангенса (46°).
Методы определения значения Tan 46 градусов
Функция тангенса положительна в 1-м квадранте. Значение тангенса 46° составляет 1,03553. . .. Мы можем найти значение тангенса 46 градусов по:
- Используя единичный круг
- Использование тригонометрических функций
Tan 46 градусов с помощью единичной окружности
Чтобы найти значение tan 46 градусов с помощью единичной окружности:
- Поверните ‘r’ против часовой стрелки, чтобы образовать угол 46° с положительной осью x.
- Тангенс 46 градусов равен координате y (0,7193), деленной на координату x (0,6947) точки пересечения (0,6947, 0,7193) единичной окружности и r.

Следовательно, значение тангенса 46° = y/x = 1,0355 (приблизительно).
Тангенс 46° в терминах тригонометрических функций
Используя формулы тригонометрии, мы можем представить тангенс 46° как:
- sin(46°)/cos(46°)
- ± sin 46°/√(1 — sin²(46°))
- ± √(1 — cos²(46°))/cos 46°
- ± 1/√(косек²(46°) — 1)
- ± √(сек²(46°) — 1)
- 1/кроватка 46°
Примечание. Поскольку 46° лежит в 1-м квадранте, окончательное значение тангенса 46° будет положительным.
Мы можем использовать тригонометрические тождества для представления tan 46° как
- cot(90° — 46°) = cot 44°
- -кроватка(90° + 46°) = -кроватка 136°
- -тангенс (180° — 46°) = -тангенс 134°
☛ Также проверьте:
- загар 50 градусов
- загар 120 градусов
- загар 225 градусов
- загар 4 градуса
- загар 7 градусов
- загар 14 градусов
Примеры использования Tan 46 градусов
Пример 1.
 Найдите значение тангенса 8 (46°)/тангажа 9 (134°).
Найдите значение тангенса 8 (46°)/тангажа 9 (134°). Решение:
Используя тригонометрические тождества, мы знаем, что tan(46°) = -tan(180° — 46°) = -tan 134°.
⇒ тангенс (46°) = -тангенс (134°)
⇒ Значение 8 тангенса (46°)/9 тангенса (134°) = -8/9Пример 2: Используя значение тангенса 46°, найдите: (sec²(46°) — 1).
Решение:
Мы знаем, (сек²(46°) — 1) = (tan²(46°)) = 1,0723
⇒ (сек²(46°) — 1) = 1,0723Пример 3. Найдите значение tan 46°, если cot 46° равно 0,9656.
Решение:
Так как tan 46° = 1/cot 46°
⇒ тангенс 46° = 1/0,9656 = 1,0355
перейти к слайдуперейти к слайдуперейти к слайду
Готовы посмотреть на мир глазами математика?
Математика лежит в основе всего, что мы делаем. Наслаждайтесь решением реальных математических задач на живых уроках и станьте экспертом во всем.
Наслаждайтесь решением реальных математических задач на живых уроках и станьте экспертом во всем.
Запишитесь на бесплатный пробный урок
Часто задаваемые вопросы о Tan 46 Degrees
Что такое Tan 46 Degrees?
Тангенс 46 градусов — значение тангенса тригонометрической функции для угла, равного 46 градусам. Значение тангенса 46° составляет 1,0355 (приблизительно).
Каково значение Tan 46° с точки зрения Sec 46°?
Мы можем представить функцию тангенса в терминах функции секущей, используя тригонометрические тождества, тангенс 46° можно записать как √(sec²(46°) — 1). Здесь значение sec 46° равно 1,4395.
Каково значение Tan 46 градусов по отношению к Cot 46°?
Поскольку функция тангенса является обратной функцией котангенса, мы можем записать тангенс 46° как 1/cot(46°). Значение cot 46° равно 0,96568.
Как найти тангенс 46° с точки зрения других тригонометрических функций?
Используя формулу тригонометрии, значение тангенса 46° можно выразить через другие тригонометрические функции следующим образом:
- sin(46°)/cos(46°)
- ± sin 46°/√(1 — sin²(46°))
- ± √(1 — cos²(46°))/cos 46°
- ± 1/√(cosec²(46°) — 1)
- ± √(сек²(46°) — 1)
- 1/кроватка 46°
☛ Также проверьте: тригонометрическую таблицу
Как найти значение Тан 46 градусов?
Значение тангенса 46 градусов можно рассчитать, построив угол 46° с осью x и затем найдя координаты соответствующей точки (0,6947, 0,7193) на единичной окружности. Значение tan 46° равно координате y (0,7193), деленной на координату x (0,69).47). ∴ tan 46° = 1,0355
Значение tan 46° равно координате y (0,7193), деленной на координату x (0,69).47). ∴ tan 46° = 1,0355
Скачать БЕСПЛАТНЫЕ учебные материалы
Тригонометрия
Рабочие листы по математике и
наглядный учебный план
Портленд — Тангенс — 4 способа добраться на поезде, автобусе и автомобиле
6Найти транспорт к касательной
Путешествие из
Путешествие из
К
Поиск жилья с Booking.com
Нужен номер в отеле в Тангенте?
Забронировать
Есть 4 способа добраться из Портленда в Тангент: автобус, поезд или автомобиль
Выберите один из вариантов ниже, чтобы просмотреть пошаговые инструкции и сравнить цены на билеты и время в пути в планировщике путешествий Rome2rio.
Тренироваться
- Сядьте на поезд из Портленда до станции Albany Amtrak.
Автобус
- Сядьте на автобус от станции Portland Amtrak до станции Albany Amtrak.
Водить машину
- Поездка из Портленда в Тангент
Самый быстрый способ добраться туда Самый дешевый вариант Дистанция между
Портленд в Тангент на автобусе
Время в пути на автобусе между Портлендом и Тангентом составляет около 2 часов 46 минут, а расстояние составляет около 146 км. Это включает в себя среднее время ожидания около 32 минут. Управляемый Greyhound USA и Linn-Benton Loop, автобус Портленд-Тангент отправляется из Портленда и прибывает на шоссе 9.9 в Портерс. Обычно еженедельно курсируют семь автобусов, хотя расписание выходных и праздничных дней может меняться, поэтому уточняйте заранее.
Это включает в себя среднее время ожидания около 32 минут. Управляемый Greyhound USA и Linn-Benton Loop, автобус Портленд-Тангент отправляется из Портленда и прибывает на шоссе 9.9 в Портерс. Обычно еженедельно курсируют семь автобусов, хотя расписание выходных и праздничных дней может меняться, поэтому уточняйте заранее.
7 Еженедельные автобусы
2ч 46м Средняя продолжительность
€18 Самая низкая цена
Посмотреть расписание ПоделитьсяСохраните эту ссылку, чтобы быть в курсе ограничений, связанных с COVID-19
Путешествуйте безопасно во время COVID-19
Правила, которым необходимо следовать в США
ОбязательноОбязательно
Путешествуйте по США
Наблюдайте за COVID-19правила безопасности
Помощь при COVID-19 в США
Если вам нужна помощь, посетите национальный веб-сайт COVID-19 или позвоните по телефону доверия COVID-19 800-232-4636
Часто задаваемые вопросы
Могу ли я путешествовать из Портленда в Тангент?
Каковы ограничения на поездки в Тангенте?
Внутренние поездки не ограничены, но могут применяться некоторые условия
- Маски обязательны
- Необходимо соблюдать социальную дистанцию 2 метра
- Соблюдать правила безопасности COVID-19
Исследуйте варианты путешествий
Что такое национальный COVID-19номер горячей линии в Tangent?
Национальный номер горячей линии COVID-19 в Тангенте: 800-232-4636.
Должен ли я носить маску для лица в общественном транспорте в Тангенте?
Ношение маски в общественном транспорте в Тангенсе обязательно.
Что мне делать, если у меня появятся симптомы COVID-19 по прибытии в Тангент?
Сообщите о себе официальному сотруднику и/или позвоните по телефону горячей линии по коронавирусу 800-232-4636.
Последнее обновление: 13 сентября 2022 г.
Исключения могут применяться, для получения полной информации: Центры по контролю и профилактике заболеваний (CDC).
Мы работаем круглосуточно, чтобы предоставить вам последние новости о поездках в связи с COVID-19.
Информация собрана из официальных источников. Насколько нам известно, это правильно на момент последнего обновления. 909:31 Посетите путеводитель Rome2rio, чтобы получить общую помощь.
Вопросы и ответы
Как дешевле всего добраться из Портленда в Тангент?
Самый дешевый способ добраться из Портленда в Тангент — это проехать на автомобиле, который стоит 14–21 евро и занимает 1 час 25 минут.
Подробнее
Как быстрее всего добраться из Портленда в Тангент?
Самый быстрый способ добраться из Портленда в Тангент — это проехать на автомобиле, который стоит 14–21 евро и занимает 1 час 25 минут.
Подробнее
Есть ли прямой автобус между Портлендом и Тангентом?
Нет, прямого автобуса из Портленда в Тангент нет. Однако есть рейсы, вылетающие из Портленда и прибывающие на шоссе 9.9 в Porters через Downtown Transit Center. Время в пути, включая пересадки, примерно 2 часа 46 минут.
Подробнее
На каком расстоянии Портленд от Тангента?
Расстояние от Портленда до Тангента составляет 114 км. Ехать примерно 124 км.
Ехать примерно 124 км.
Получить маршрут проезда
Как добраться из Портленда в Тангент без машины?
Лучший способ добраться из Портленда в Тангент без машины — это сесть на автобус через Центр транзитных перевозок в центре города, который занимает 2 часа 46 минут и стоит 17–24 евро.
Подробнее
Сколько времени нужно, чтобы добраться из Портленда в Тангент?
Дорога из Портленда в Тангент занимает примерно 2 часа 46 минут, включая пересадки.
Подробнее
Поездом или автобусом из Портленда в Тангент?
Лучший способ добраться из Портленда в Танджент — это сесть на автобус через центр транзитных перевозок в центре города, который занимает 2 часа 46 минут и стоит 17–24 евро. Кроме того, вы можете поехать на поезде, который стоит 28–40 евро и занимает 2 часа 54 минуты.
Кроме того, вы можете поехать на поезде, который стоит 28–40 евро и занимает 2 часа 54 минуты.
Детали режима
Могу ли я проехать из Портленда в Тангент?
Да, расстояние между Портлендом и Тангенсом составляет 124 км. Дорога от Портленда до Тангента занимает примерно 1 час 25 минут.
Получить маршрут проезда
Какие компании осуществляют перевозки между Портлендом, штат Орегон, США, и Тангентом, штат Орегон, США?
Greyhound USA обслуживает автобус из Портленда в Корваллис один раз в день. Билеты стоят 15–22 евро, а время в пути — 1 час 55 минут. Кроме того, Amtrak ходит поездом из Портленда до станции Albany Amtrak 3 раза в день. Билеты стоят 26–40 евро, а время в пути — 1 час 41 минуту.
Амтрак
Amtrak — это железнодорожная служба, которая соединяет США и три провинции Канады. Покрывая 21 000 миль маршрута (34 000 км), Amtrak ежедневно обслуживает более 300 поездов. Эти междугородние перевозки на средние и дальние расстояния осуществляются со скоростью до 240 км/ч по более чем 500 направлениям. Основан в 1971, он базируется в Вашингтоне, округ Колумбия, и предлагает четыре класса обслуживания: первый класс, спальный, бизнес-класс и туристический автобус. Тарифы на билеты делятся на пять подклассов: Saver, Value, Flexible, Business и Premium. Поезда Amtrak известны своими широкими сиденьями, подключаемым питанием, большими окнами и возможностями хранения.
Покрывая 21 000 миль маршрута (34 000 км), Amtrak ежедневно обслуживает более 300 поездов. Эти междугородние перевозки на средние и дальние расстояния осуществляются со скоростью до 240 км/ч по более чем 500 направлениям. Основан в 1971, он базируется в Вашингтоне, округ Колумбия, и предлагает четыре класса обслуживания: первый класс, спальный, бизнес-класс и туристический автобус. Тарифы на билеты делятся на пять подклассов: Saver, Value, Flexible, Business и Premium. Поезда Amtrak известны своими широкими сиденьями, подключаемым питанием, большими окнами и возможностями хранения.
- Телефон
- +1 800-872-7245
- Веб-сайт
- amtrak.com
- Продолжительность
- 1ч 41м
- Частота
- 3 раза в день
- Ориентировочная цена
- €26 — €40
- Веб-сайт
- Амтрак
- Сиденье тренера
- €26 — €40
- Премиум
- €180 — 260 €
- Сиденье Flexi Coach
- €40 — 60 €
- Бизнес-место
- 35 — 55 евро
Грейхаунд США
Greyhound — ведущая автобусная компания, базирующаяся в Далласе, штат Техас, и обслуживающая более 3800 пунктов назначения в Северной Америке, Мексике и Канаде. Greyhound перевозит около 18 миллионов пассажиров в год, которые проезжают 5,4 миллиарда миль (8,6 миллиарда км) в год на своем парке из около 1700 автомобилей. Для гибкости путешествия вы можете сесть или выйти из автобуса Greyhound на официальных станциях Greyhound, станциях-партнерах и остановках у обочины. В США есть около 230 станций Greyhound, где вы можете сесть на автобус и купить билеты, которые также доступны на официальном сайте и через мобильное приложение.
Greyhound перевозит около 18 миллионов пассажиров в год, которые проезжают 5,4 миллиарда миль (8,6 миллиарда км) в год на своем парке из около 1700 автомобилей. Для гибкости путешествия вы можете сесть или выйти из автобуса Greyhound на официальных станциях Greyhound, станциях-партнерах и остановках у обочины. В США есть около 230 станций Greyhound, где вы можете сесть на автобус и купить билеты, которые также доступны на официальном сайте и через мобильное приложение.
- Телефон
- +1 214-849-8100/1-800-231-2222
- Электронная почта
- [email protected]
- Веб-сайт
- greyhound.com
- Продолжительность
- 1ч 55м
- Частота
- Один раз в день
- Ориентировочная цена
- €15 – 22 €
- Веб-сайт
- greyhound.
 com
com
- Эконом
- €15 — 22 €
- Гибкий
- 30 — 50 евро
Точка
- Телефон
- +1 888-846-4183
- Веб-сайт
- oregon-point.com
- Продолжительность
- 1ч 55м
- Частота
- 4 раза в день
- Ориентировочная цена
- €17 — 24 €
- Веб-сайт
- Точка
Хотите узнать больше о путешествиях по Соединенным Штатам
Серия путеводителей Rome2rio содержит жизненно важную информацию для путешественников со всего мира. Наполненные полезной и своевременной информацией о путешествии, гиды отвечают на все сложные вопросы, такие как «Как купить билет?», «Должен ли я бронировать билеты онлайн перед поездкой?» ‘, ‘Сколько я должен заплатить?’, ‘Есть ли в поездах и автобусах Wi-Fi?’ — чтобы помочь вам получить максимальную отдачу от вашей следующей поездки.
Наполненные полезной и своевременной информацией о путешествии, гиды отвечают на все сложные вопросы, такие как «Как купить билет?», «Должен ли я бронировать билеты онлайн перед поездкой?» ‘, ‘Сколько я должен заплатить?’, ‘Есть ли в поездах и автобусах Wi-Fi?’ — чтобы помочь вам получить максимальную отдачу от вашей следующей поездки.
Другие вопросы и ответы
Где остановиться рядом с Тангентом?
В Тангенте доступно 34+ отелей. Цены начинаются от 100 евро за ночь.
Подробнее
Включение внутренних лимфатических узлов молочной железы в стандартные касательные поля молочной железы: влияние габитуса тела
. 2001 март-апрель;7(2):111-6.
doi: 10. 1046/j.1524-4741.2001.007002111.x.
1046/j.1524-4741.2001.007002111.x.
Г М Пру 1 , RJ Lee, PC Stomper
принадлежность
- 1 Отделение радиационной онкологии, Онкологический институт Розуэлл Парк, Школа медицины и биомедицинских наук, Университет штата Нью-Йорк в Буффало, 14263, США. [email protected]
- PMID: 11328318
- DOI: 10.1046/j.1524-4741.2001.007002111.x
GM Proulx et al. Грудь Дж. 2001 март-апрель.
. 2001 март-апрель;7(2):111-6.
doi: 10. 1046/j.1524-4741.2001.007002111.x.
1046/j.1524-4741.2001.007002111.x.
Авторы
Г М Пру 1 , Р. Дж. Ли, ПК Стомпер
принадлежность
- 1 Отделение радиационной онкологии, Онкологический институт Розуэлл Парк, Школа медицины и биомедицинских наук, Университет штата Нью-Йорк в Буффало, 14263, США. [email protected]
- PMID: 11328318
- DOI: 10.1046/j.1524-4741.2001.007002111.x
Абстрактный
Цель этого исследования состояла в том, чтобы определить вариабельность покрытия внутреннего узла молочной железы (IMN) со стандартными касательными полями молочной железы с использованием поверхностной анатомии, определенной с помощью компьютерной томографии (КТ) планирования для пациентов, получавших либо органосохраняющее лечение, либо постмастэктомию, и оценить влияние габитуса и формы тела на покрытие ИМН стандартными касательными полями. В это проспективное исследование были включены последовательные женщины с раком молочной железы, которые подверглись либо локальному иссечению, либо мастэктомии и имели стандартные касательные поля, предназначенные для покрытия груди, плюс край, смоделированный с использованием поверхностной анатомии. При планировании КТ определялось расположение ИМН относительно касательных полей, рассчитанных на основании анатомии поверхности. Внутренние сосуды молочной железы использовались в качестве заменителей IMN. КТ-измерения толщины престернального жира и переднезаднего (AP) и поперечного диаметров скелета были выполнены для определения их связи с включением IMN в касательные поля. Только у семи пациентов (14%) IMN были полностью в пределах касательных полей. Двадцать пациентов (40%) имели частичное покрытие своих IMN, а 23 (46%) имели свои IMN полностью за пределами поля. Включение IMN было обратно пропорционально толщине престернального жира. Грудная форма скелета не была связана с включением IMN.
В это проспективное исследование были включены последовательные женщины с раком молочной железы, которые подверглись либо локальному иссечению, либо мастэктомии и имели стандартные касательные поля, предназначенные для покрытия груди, плюс край, смоделированный с использованием поверхностной анатомии. При планировании КТ определялось расположение ИМН относительно касательных полей, рассчитанных на основании анатомии поверхности. Внутренние сосуды молочной железы использовались в качестве заменителей IMN. КТ-измерения толщины престернального жира и переднезаднего (AP) и поперечного диаметров скелета были выполнены для определения их связи с включением IMN в касательные поля. Только у семи пациентов (14%) IMN были полностью в пределах касательных полей. Двадцать пациентов (40%) имели частичное покрытие своих IMN, а 23 (46%) имели свои IMN полностью за пределами поля. Включение IMN было обратно пропорционально толщине престернального жира. Грудная форма скелета не была связана с включением IMN. Стандартные тангенциальные поля обычно не покрывают IMN полностью, но могут покрывать их, по крайней мере, частично у большинства пациентов. Толщина престернального жира обратно пропорциональна включению IMN в касательные поля.
Стандартные тангенциальные поля обычно не покрывают IMN полностью, но могут покрывать их, по крайней мере, частично у большинства пациентов. Толщина престернального жира обратно пропорциональна включению IMN в касательные поля.
Похожие статьи
Покрытие внутренних лимфатических узлов молочной железы (ВМН) стандартными тангенциальными полями облучения у пациентов с дренированием ВМН на лимфосцинтиграфии: терапевтические последствия.
Заяц GB, Proulx GM, Lamonica DM, Stomper PC. Харе ГБ и др. Am J Clin Oncol. 2004 июнь; 27 (3): 274-8. doi: 10.1097/01.coc.00000
.03967.80. Am J Clin Oncol. 2004. PMID: 15170147
Использование ПЭТ-КТ 18 F-FDG для определения расположения внутренних лимфатических узлов молочной железы при планировании лучевой терапии у пациентов с раком молочной железы.

Дэвидсон Т., Бен-Дэвид М., Гальпер С., Хаскин Т., Хоус М., Скейф Р., Канана Н., Амит У., Вейцман Н., Чикман Б., Гошен Э., Бен-Хаим С., Саймон З., Гольдштейн Дж. Дэвидсон Т. и др. Практика Radiat Oncol. 2017 ноябрь-декабрь;7(6):373-381. doi: 10.1016/j.prro.2016.11.001. Epub 2016 5 ноября. Практика Radiat Oncol. 2017. PMID: 28989000
Стандартные поля тангенциального излучения не обеспечивают случайного покрытия внутренних узлов молочной железы.
Loganadane G, Kassick M, Kann BH, Young MR, Knowlton CA, Evans SB, Higgins SA, Belkacemi Y, Potenziani M, Saltmarsh N, Wilson LD, Moran MS. Логанадан Г. и соавт. Практика Radiat Oncol. 2020 янв-февраль;10(1):21-28. doi: 10.1016/j.prro.2019.07.014. Epub 2019 5 августа. Практика Radiat Oncol. 2020. PMID: 31394256
Картирование сигнальных лимфатических узлов при раке молочной железы: критическая переоценка проблемы внутренней цепи молочной железы.

Манка Г., Вольтеррани Д., Маццарри С., Дуче В., Свириденко А., Джулиано А., Мариани Г. Манка Г. и др. Q J Nucl Med Mol Imaging. 2014 июнь;58(2):114-26. Q J Nucl Med Mol Imaging. 2014. PMID: 24835288 Обзор.
Должны ли внутренние молочные лимфатические узлы при раке молочной железы быть мишенью для онколога-радиолога?
Фридман Г.М., Фаубл Б.Л., Николау Н., Сигурдсон Э.Р., Торосян М.Х., Бораас М.С., Хоффман Д.П. Фридман Г.М. и соавт. Int J Radiat Oncol Biol Phys. 2000 март 1;46(4):805-14. doi: 10.1016/s0360-3016(99)00481-2. Int J Radiat Oncol Biol Phys. 2000. PMID: 10705000 Обзор.
Посмотреть все похожие статьи
Цитируется
Дозиметрическая оценка случайного облучения внутренней цепи молочной железы после операции у больных раком молочной железы.

Ван В, Сунь Т, Мэн И, Сюй М, Чжан И, Шао Ц, Сун И, Ли Дж. Ван В и др. Фронт Онкол. 2022 2 марта; 12:839831. doi: 10.3389/fonc.2022.839831. Электронная коллекция 2022. Фронт Онкол. 2022. PMID: 35311065 Бесплатная статья ЧВК.
Факторы, влияющие на случайное распределение дозы во внутренних узлах молочной железы: сравнительное исследование.
Ван В, Ван Дж, Цю П, Сунь Т, Чжан Ю, Шао Ц, Сю М, Лю С, Ли Дж. Ван В и др. Фронт Онкол. 2020 9 апр; 10:456. doi: 10.3389/fonc.2020.00456. Электронная коллекция 2020. Фронт Онкол. 2020. PMID: 32328459 Бесплатная статья ЧВК.
Дозиметрическое сравнение случайного облучения внутренних узлов молочной железы после органосохраняющей операции с использованием 3 методов: лучевая терапия с обратной модуляцией интенсивности, лучевая терапия с модулированной интенсивностью поле-в-поле и трехмерная конформная лучевая терапия: ретроспективное клиническое исследование.

Сун Ю, Ю Т, Ван В, Ли Дж, Сунь Т, Цю П, Сюй М, Шао К. Сонг Ю и др. Медицина (Балтимор). 2019 окт;98(41):e17549. doi: 10.1097/MD.0000000000017549. Медицина (Балтимор). 2019. PMID: 31593136 Бесплатная статья ЧВК. Клиническое испытание.
Внеплановое облучение внутренних молочных лимфатических узлов при раке молочной железы.
Канилмаз Г., Актан М., Коч М., Демир Х., Демир Л.С. Каньилмаз Г. и др. Радиол Мед. 2017 июнь; 122(6):405-411. doi: 10.1007/s11547-017-0747-5. Epub 2017 3 марта. Радиол Мед. 2017. PMID: 28255809
Случайное облучение внутренних молочных лимфатических узлов при раке молочной железы: обычная двухмерная лучевая терапия по сравнению с конформной трехмерной лучевой терапией.

Лейте Э.Т., Угино Р.Т., Сантана М.А., Феррейра Д.В., Лопес М.Р., Пелоси Э.Л., да Силва Х.Л., Карвалью Хде А. Лейте Э.Т. и др. Радиол Бюстгальтеры. 2016 май-июнь;49(3):170-5. дои: 10.1590/0100-3984.2015.0003. Радиол Бюстгальтеры. 2016. PMID: 27403017 Бесплатная статья ЧВК.
Просмотреть все статьи «Цитируется по»
термины MeSH
Калькулятор кофункций
Создано Maciej Kowalski, кандидатом наук
Отзыв Стивена Вудинга
Последнее обновление: 05 сентября 2022 г.
Содержание:- Тригонометрические функции
- Графики кофункций: sin и cos, tan и cot, sec и csc
- Тождества кофункций
- Пример: использование калькулятора кофункций тождества кофункций и как их использовать.
 По сути, в тригонометрии существует шесть функций, полностью описывающих отношения между углами и сторонами треугольника. Таким образом, они связаны друг с другом, поэтому мы часто думаем о них как о парах: sin и cos, tan и cot, sec и csc . Сегодня мы рассмотрим эти отношения и узнаем, как перейти от одной карты к ее паре, то есть к ее кофункции .
По сути, в тригонометрии существует шесть функций, полностью описывающих отношения между углами и сторонами треугольника. Таким образом, они связаны друг с другом, поэтому мы часто думаем о них как о парах: sin и cos, tan и cot, sec и csc . Сегодня мы рассмотрим эти отношения и узнаем, как перейти от одной карты к ее паре, то есть к ее кофункции .Так что расслабьтесь, расслабьтесь и насладитесь хорошей математикой !
Тригонометрические функции
Прежде чем мы узнаем, что такое кофункция, нам нужно начать с основ . А в геометрии мы не можем пойти дальше, чем треугольники: три стороны, три вершины, три внутренних угла. В каком-то смысле проще полигона быть не может.
Нас, однако, больше всего интересует конкретный тип треугольников: прямоугольных треугольников (вы знаете, о которых говорит теорема Пифагора). Один из их углов всегда равен
90градусов (отсюда и название), поэтому у нас уже есть некоторая информация о нашей фигуре еще до того, как мы ее нарисуем.
Кроме того, мы можем наблюдать некоторые другие зависимости , которые заставляют треугольник выглядеть так, как он есть. Ведь если мы увеличим один из острых углов, то легко увидим, что противоположная сторона тоже должна стать длиннее. Это наблюдение является более или менее идеей тригонометрии: каким-то образом соотнести внутренние углы треугольника с его сторонами .
Определим тригонометрических функций как отношение сторон прямоугольного треугольника. Ниже вы можете найти картинку с формулами для всех шести из них. (Обратите внимание, что в калькуляторе кофункций для каждой из них есть по одному идентификатору.)
🔎 Все тригонометрические функции (sin, cos, tan) являются отношениями. Таким образом, вы можете найти недостающие члены, используя только наш калькулятор отношений!
Например, мы видим, что синус равен катету, противоположному углу, деленному на гипотенузу. Обратите внимание, что мы никогда не упоминаем, насколько велик треугольник.
 На самом деле там важнейшее свойство тригонометрии заключается в следующем: даже если мы удвоим размер треугольника, если мы сохраним углы нетронутыми, значения тригонометрических функций не изменятся .
На самом деле там важнейшее свойство тригонометрии заключается в следующем: даже если мы удвоим размер треугольника, если мы сохраним углы нетронутыми, значения тригонометрических функций не изменятся .Однако приведенные выше формулы, при всем их изяществе, имеют существенный недостаток. Мы определили их с помощью прямоугольного треугольника, поэтому угол может быть только между
0и90градусов (или0иπ/2в радианах). Но не дуйся! К счастью для нас, для математики и всего мира, есть способ это исправить ! Единственное, что нам нужно сделать, это перенести рассуждения на двумерное евклидово пространство, т. е. на плоскость.Пусть
A = (x,y)— точка на плоскости, и определимαкак угол, идущий против часовой стрелки от положительной половины горизонтальной оси к отрезку, конечные точки которого равны(0 ,0)иА. (Обратите внимание, как мы сказали, что
(Обратите внимание, как мы сказали, что αпроходит от одной линии к другой, а не то, что это просто угол между ними. Вот почему мы часто называемαнаправленный угол .)Очевидно, что
αтеперь может быть больше, чем90градусов. На самом деле, может даже выйти за пределы360градусов . Для таких углов мы просто считаем первые360градусов первым кругом вокруг(0,0), и от этого значения мы продолжаем со вторым (и, если нужно, с третьим, четвертым, так далее.). На самом деле даже больше —αтоже может быть отрицательным . В конце концов, мы сказали, что это направленный угол, поэтому для отрицательных значений мы просто меняем направление на противоположное, то есть идем по часовой стрелке, а не против часовой стрелки.Теперь, когда мы понимаем углы всех размеров, мы можем определить для них тригонометрические функции и точку
A = (x,y). Правило здесь довольно простое: повторяем формулы с рисунка выше , но подставляем
Правило здесь довольно простое: повторяем формулы с рисунка выше , но подставляем bвместоx,aвместоy, и 92}}{x}sec(α)=xx2+y2Итак, мы познакомились с тригонометрическими функциями с точки зрения их определений, так что мы готовы копнуть глубже . В конце концов, имя « калькулятор кофункций » привело нас сюда, и мы до сих пор не знаем, как найти кофункцию. Для этого лучше всего использовать графики функций .
Графики кофункций: sin и cos, tan и cot, sec и csc
Шесть тригонометрических функций равны синус и косинус (обозначаются sin и cos), тангенс и котангенс (tan и cot) и секанс и косеканс (sec и csc).
Вы, наверное, уже понимаете, почему мы объединили их так, как , только по именам. В каждой паре у нас есть «базовая» функция и карта с таким же названием, но с дополнительным префиксом « co-».
 Сходство со словом « кофункция » далеко не случайно. В каждой из пар мы говорим, что один является кофункцией другого .
Сходство со словом « кофункция » далеко не случайно. В каждой из пар мы говорим, что один является кофункцией другого .» Но что значит быть кофункцией? » Что ж, мы рады, что вы спросили! Мы подробно рассмотрим тождества кофункций в следующем разделе. Однако сначала попробуем мотивировать их, посмотрев на графики функций в парах и выявив сходство.
Начнем с sin и cos .
Они выглядят почти одинаково, не так ли? Синус — это просто косинус, сдвинутый на
90градусов (илиπ/2в радианах) вправо.Для наших целей сосредоточимся на области от
0до90градусов и представим, что вы проходите это расстояние по наклону обеих кривых, но в разных направлениях: синус от0до90и косинус от90до0. Видите ли вы, что пути тогда одинаковы?
Видите ли вы, что пути тогда одинаковы?Попробуем сделать нечто подобное для графиков tan и cot .
Опять же, если мы проследим касательную от
0до90и котангенс от90до0, мы заметим, что мы идем по тому же пути .Наконец, у нас есть функции sec и csc .
Как вы могли догадаться, история повторяется для секанса и косеканса.
По существу, это то, что характеризует кофункции . Можно было бы сказать, что их графики являются взаимными отражениями, если мы поместим зеркало в середину интервала
(0°,90°), т. е. на45градусов. Это, в свою очередь, означает, что значение тригонометрической функции в точкеxдолжно быть таким же, как значение кофункции в точке90° - x. И это именно то, что утверждают тождества кофункций.
Кофункциональные тождества
Как упоминалось в предыдущем разделе, мы делим тригонометрические функции на пары . В каждом из них одно является кофункцией другого. Это означает, что их графики (а значит, и значения) являются взаимными отражениями в интервале
(0°,90°). Следовательно, значение первого в точкехсовпадает с другим в90° - хдляхиз интервала.Если вы хотите порадовать нескольких высокомерных ученых, мы можем написать приведенный выше абзац эквивалентно, используя математические обозначения. Это будет выглядеть так:
Однако помните, что работают только для углов между
0и90градусов . Приведенные выше формулы основаны на том факте, что углы по обе стороны от знака 91 626 = 91 627 дополняют друг друга, т. е. в сумме дают 91 626 90 91 627 градусов.
На самом деле, есть способ рассмотреть и другие углы . Однако это сложно. Здесь мы имели то удобство, что все функции принимают положительные значения в интервале
(0°,90°). За его пределами все может стать негативным. Также возникает вопрос, куда поставить « зеркало », что отражает кофункции.Несмотря на препятствия, в результате многочасовой напряженной работы математики смогли вывести формул, обобщающих тождества кофункций . Они называются формулами тригонометрического приведения (заметьте, не формулы приведения в степени). Хотя мы не будем приводить их здесь, мы с радостью рекомендуем вам найти их и наслаждайтесь дополнительными математическими знаниями . Если вы спросите нас, это, безусловно, лучше, чем пролистывание социальных сетей.
И на этом мы объявляем конец теории на сегодня ! Возможно, мы потратили довольно много времени на изучение определений и формул.
 Почему бы не взять несколько примеров и не использовать тождества кофункций с пользой для ?
Почему бы не взять несколько примеров и не использовать тождества кофункций с пользой для ?Пример: использование калькулятора кофункций
Скажите, что вы решили сделать ремонт в своей гостиной . В конце концов, у карантина из-за коронавируса есть как минимум один положительный момент — у вас много свободного времени .
Вы планируете починить пол, может быть, заменить плитку на деревянную? Проблема в том, что вам нужны измерения , а комната не является идеальным прямоугольником; есть пара наклонных стен. К счастью, вы еще кое-что помните из колледжа и, немного почесав голову, понимаете, что для вам понадобится косинус
45градусов и котангенс30градусов для дальнейших расчетов.Однако есть проблема. Прошло несколько лет с вашего последнего урока тригонометрии, а вы не можете вспомнить формулы для косинуса или котангенса.
 Что вы помните, так это синус и тангенс. О, как хорошо вписывается в этот сценарий калькулятор тождеств кофункций!
Что вы помните, так это синус и тангенс. О, как хорошо вписывается в этот сценарий калькулятор тождеств кофункций! (Ладно, признаем, что подробности немного притянуты за уши 909:10, но, пожалуйста, дайте нам перерыв. Воображение разработчиков контента Omni может только простираться.)
Прежде всего, давайте посмотрим насколько легко задача, когда у нас есть калькулятор кофункций под рукой . Там мы начинаем с , выбирая функцию, которая у нас есть . Во-первых, мы выбираем косинус, то есть
cos(x)из списка. Получив это, мы переходим к переменному полю ниже, которое содержит угол. Мы вводим45°из нашей задачи, и в тот момент, когда мы это делаем, калькулятор кофункций выдает ответ внизу: кофункция вместе со значением . Аналогично, для второго случая мы выбираем котангенс (cot(x)) из списка и вводим30°.Обратите внимание, как каждый раз, когда инструмент дает нам точное значение (т.
 е. в виде дроби с квадратными корнями), кроме округленного в большую сторону. Мы объясним, почему это так, через секунду. Кроме того, хотя калькулятор кофункций стремится к точности , вы можете уменьшить количество значащих цифр в ответе для любых дальнейших вычислений.
е. в виде дроби с квадратными корнями), кроме округленного в большую сторону. Мы объясним, почему это так, через секунду. Кроме того, хотя калькулятор кофункций стремится к точности , вы можете уменьшить количество значащих цифр в ответе для любых дальнейших вычислений.Теперь оставим в стороне инструмент Omni и посмотрим как найти ответ самостоятельно . Мы выполним следующие шаги:
- Нарисуйте прямоугольный треугольник с заданным углом;
- Используйте тождества кофункций , чтобы преобразовать искомую функцию в ее кофункцию; и
- Рассчитайте значение кофункции, взяв отношения сторон треугольника.
Начнем с угла
45°.Заметим, что это пример совершенно особого треугольника, в котором мы знаем отношения между сторонами , то есть мы знаем, что если катет имеет длину
x, то гипотенуза должна бытьx√2. Это потому, что наша фигура на самом деле является половиной квадрата, где длинная сторона является диагональю квадрата.
Это потому, что наша фигура на самом деле является половиной квадрата, где длинная сторона является диагональю квадрата.Теперь мы вспоминаем тождества кофункций из предыдущего раздела и используем их для преобразования
cos(45°)в синус:cos(45°) = sin(90° - 45°) = sin(45°).Таким образом, мы можем использовать формулу синуса , чтобы найти ответ. В первом разделе мы сказали, что это катет, противоположный углу, деленному на гипотенузу. Это дает:
cos(45°) = sin(45°) = x / x√2 = 1 / √2 = √2 / 2.Перейдем к случаю
30градусов. Снова начинаем с чертежа .Как и прежде, нам посчастливилось знать отношения между сторонами . На этот раз это потому, что наша фигура на самом деле является половиной равностороннего треугольника.
Мы используем тождества кофункций для преобразования
cot(30°)в тангенс:cot(30°) = tan(90° - 30°) = tan(60°).
Обратите внимание, что хотя рассматриваемый угол изменился, мы все еще можем использовать ту же картинку . Это всегда будет иметь место с тождествами кофункций, поскольку мы всегда имеем дело с дополнительными углами , то есть с углами, образующими острые углы одного и того же прямоугольного треугольника.
Наконец, вспоминаем формулу тангенса из первого раздела: функция возвращает катет, противоположный углу, деленному на другой. В нашем случае это:
cot(30°) = tan(60°) = x√3 / x = √3.Готово! Мы нашли нужные нам тригонометрические функции; мы готовы позаботиться об этой плитке и обновить гостиную. Конечно, с установкой фанеры будет намного уютнее. И когда вы закончите, почему бы не пойти дальше и придумать что-нибудь для спальни ?
Часто задаваемые вопросы
Как использовать тождества кофункций?
Тождества кофункций позволяют определить значение тригонометрической функции по значению кофункции (вашей функции) под углом, дополнительным к вашему углу.
 Например, вы можете легко найти
Например, вы можете легко найти cos(20°), если знаетеsin(70°), потому что синус и косинус являются кофункциями, а70° + 20° = 90°.Для какого x выполняется sin(x)=cos(15°)?
Ответ:
x = 75°. Мы знаем, что синус и косинус являются кофункциями, т. е. их значения совпадают на дополнительных углах. Итак,хи15°должны быть дополнительными:х + 15° = 90°. Следовательно,x = 75°, как и утверждалось.Как найти синус с косинусом?
Чтобы определить
sin(x)поcos(x), выполните следующие действия:- Вычислите квадрат
cos(x). - Вычесть
cos²(x)из1. - Извлеките квадратный корень из результата шага 2. Помните, что есть два возможных результата: один положительный и один отрицательный.
- У вас есть два возможных значения
sin(x). Если вы знаете, например, что ваш угол
Если вы знаете, например, что ваш угол xострый, то его синус положителен. - Полная форма формулы, которую мы применили:
sin²(x) + cos²(x) = 1.
Как найти синус с помощью косинуса и тангенса?
Чтобы определить синус угла по его косинусу и тангенсу, нужно умножить косинус на тангенс . Вам нужна формула
sin(α) = tan(α) × cos(α).Maciej Kowalski, кандидат в PhD
Функция
Угол (x)
. Для визуального сравнения COFUNCTIONS Будьте проверены на их графиках:
.
AC Приближение касательной линии
Мотивирующие вопросы
Какова формула общей аппроксимации касательной к дифференцируемой функции \(y = f(x)\) в точке \((a,f(a))\text{?}\)
Что такое принцип локальной линейности и что такое локальная линеаризация дифференцируемой функции \(f\) в точке \((a,f(a))\text{?}\)
Каким образом знание только аппроксимации касательной дает нам информацию о поведении самой исходной функции вблизи точки аппроксимации? Каким образом знание значения второй производной в этот момент дает нам дополнительные сведения о поведении исходной функции?
Среди всех функций линейные функции самые простые.
 Одно из важных следствий дифференцируемости функции \(y = f(x)\) в точке \((a,f(a))\) заключается в том, что вблизи функция \(y = f(x )\) локально линейна и имеет вид своей касательной в этой точке. В определенных обстоятельствах это позволяет нам аппроксимировать исходную функцию \(f\) более простой функцией \(L\), которая является линейной: это может быть выгодно, когда у нас есть ограниченная информация о \(f\) или когда \(f \) является вычислительно или алгебраически сложным. Далее мы рассмотрим все эти ситуации. 92+3x+2\текст{.}\)
Одно из важных следствий дифференцируемости функции \(y = f(x)\) в точке \((a,f(a))\) заключается в том, что вблизи функция \(y = f(x )\) локально линейна и имеет вид своей касательной в этой точке. В определенных обстоятельствах это позволяет нам аппроксимировать исходную функцию \(f\) более простой функцией \(L\), которая является линейной: это может быть выгодно, когда у нас есть ограниченная информация о \(f\) или когда \(f \) является вычислительно или алгебраически сложным. Далее мы рассмотрим все эти ситуации. 92+3x+2\текст{.}\)Использовать предельное определение производной для вычисления формулы для \(y = g'(x)\text{.}\)
Определить наклон касательной к \(y = g(x)\) при значении \(x = 2\text{.}\)
Вычислить \(g(2)\text{.}\)
Найдите уравнение для касательной к \(y = g(x)\) в точке \((2,g(2))\text{.}\) Запишите результат в виде точка-наклон.
На осях, показанных на рисунке 1.8.1, нарисуйте точный помеченный график \(y = g(x)\) вместе с его касательной в точке \((2,g(2))\text{ .
 }\)
}\)
Подраздел 1.8.1 Касательная линия
Для данной функции \(f\), которая дифференцируема в точке \(x = a\text{,}\), мы знаем, что можем определить наклон касательной к \(y = f(x)\) в точке \ ((a,f(a))\) путем вычисления \(f'(a)\text{.}\) Уравнение полученной касательной линии задается в форме точка-наклон как
\begin{уравнение*} y — f(a) = f'(a)(x-a) \ \ \text{or} \ \ y = f'(a)(x-a) + f(a)\text{.} \end{уравнение*}
Обратите внимание: в этом контексте между \(f(a)\) и \(f(x)\) есть большая разница. Первая — это константа, полученная в результате использования заданного фиксированного значения \(a\text{,}\), а вторая — это общее выражение для правила, определяющего функцию. То же верно и для \(f'(a)\) и \(f'(x)\text{:}\), мы должны тщательно различать эти выражения. Каждый раз, когда мы находим касательную, нам нужно вычислять функцию и ее производную при фиксированном \(a\)-значении.

На рисунке 1.8.2 мы видим график функции \(f\) и ее касательную в точке \((a,f(a))\text{.}\). Обратите внимание, что при увеличении масштаба мы см. более четко выделенную локальную линейность \(f\). Функция и ее касательная почти неразличимы вблизи. Локальная линейность также может наблюдаться динамически в этом апплете 2 .
Рисунок 1.8.2. Функция \(y = f(x)\) и ее касательная в точке \((a,f(a))\text{:}\) слева на расстоянии и справа вблизи. Справа мы обозначаем функцию касательной через \(y = L(x)\) и замечаем, что для \(x\) вблизи \(a\text{,}\) \(f(x) \ приблизительно L( х)\текст{.}\)Подраздел 1.8.2 Локальная линеаризация
Небольшое изменение перспективы и обозначений позволит нам более точно обсуждать, как касательная аппроксимирует \(f\) вблизи \(x = a\text{.}\). Решая для \(y\text{, }\) мы можем написать уравнение для касательной как
\begin{уравнение*} у = f'(а)(х-а) + f(а) \end{уравнение*}
Эта строка сама является функцией \(x\text{.
 }\) Заменив переменную \(y\) выражением \(L(x)\text{,}\), мы назовем
}\) Заменив переменную \(y\) выражением \(L(x)\text{,}\), мы назовем\begin{уравнение*} L(x) = f'(a)(x-a) + f(a) \end{уравнение*}
локальная линеаризация \(f\) в точке \((a,f(a))\text{.}\) В этих обозначениях \(L(x)\) есть не что иное, как новая имя касательной линии. Как мы видели выше, для \(x\) близких к \(a\text{,}\) \(f(x) \ приблизительно L(x)\text{.}\)
Пример 1.8.3.
Предположим, что функция \(y = f(x)\) имеет аппроксимацию касательной, заданную выражением \(L(x) = 3 — 2(x-1)\) в точке \((1,3)\ text{,}\), но мы ничего не знаем о функции \(f\text{.}\) Чтобы оценить значение \(f(x)\) для \(x\) около 1, например \(f(1.2)\text{,}\) мы можем использовать тот факт, что \(f(1.2) \ приблизительно L(1.2)\) и, следовательно,
\begin{уравнение*} f(1.2) \приблизительно L(1.2) = 3 — 2(1.2-1) = 3 — 2(0.2) = 2.6\text{.} \end{equation*}
Подчеркнем, что \(y = L(x)\) — это просто новое название функции касательной. Используя это новое обозначение и наше наблюдение, что \(L(x) \ приблизительно f(x)\) для \(x\) вблизи \(a\text{,}\), следует, что мы можем написать
\begin{уравнение*} f(x) \ приблизительно f(a) + f'(a)(x-a) \ \text{for} \ x \ \text{рядом} \ a\text{.
 }
\end{уравнение*}
}
\end{уравнение*}Мероприятие 1.8.2.
. Предположим, что известно, что для данной дифференцируемой функции \(y = g(x)\text{,}\) ее локальная линеаризация в точке, где \(a = —1\), определяется выражением \(L(x) = -2 + 3(х+1)\текст{.}\)
Вычислить значения \(L(-1)\) и \(L'(-1)\text{.}\)
Какими должны быть значения \(g(-1)\) и \(g'(-1)\text{?}\) Почему?
Ожидаете ли вы, что значение \(g(-1.03)\) будет больше или меньше значения \(g(-1)\text{?}\) Почему?
Используйте локальную линеаризацию для оценки значения \(g(-1.03)\text{.}\)
Предположим, что вы также знаете, что \(g»(-1) = 2\text{.}\) Что это говорит вам о графике \(y = g(x)\) в точке \(a = -1\текст{?}\)
Для \(x\) вблизи \(-1\text{,}\) нарисуйте график локальной линеаризации \(y = L(x)\), а также возможный график \(y = g( x)\) по осям, указанным на рисунке 1.8.4.
 4. Оси построения \(y = L(x)\) и \(y = g(x)\text{.}\)
4. Оси построения \(y = L(x)\) и \(y = g(x)\text{.}\)Из упражнения 1.8.2 мы видим, что локальная линеаризация \(y = L(x)\) является линейной функцией, которая имеет два общих значения с функцией \(y = f(x)\), полученной из . В частности,
, так как \(L(x) = f(a) + f'(a)(x-a)\text{,}\) следует, что \(L(a) = f(a)\text{;} \) и
, поскольку \(L\) — линейная функция, ее производная — это наклон.
Следовательно, \(L'(x) = f'(a)\) для любого значения \(x\text{,}\) и, в частности, \(L'(a) = f'(a)\text {.}\) Таким образом, мы видим, что \(L\) является линейной функцией, которая имеет и то же значение, и тот же наклон, что и функция \(f\) в точке \((a,f(a)) \текст{.}\)
Таким образом, если мы знаем линейную аппроксимацию \(y = L(x)\) для функции, мы знаем исходное значение функции и ее наклон в точке касания. Однако остается неизвестным форма функции \(f\) в точке касания. По сути, есть четыре возможности, как показано на рисунке 1.
Рисунок 1.8.5. Четыре возможных графика нелинейной дифференцируемой функции и то, как она может располагаться относительно своей касательной в точке. 8.5.
8.5.Эти возможные формы являются результатом того, что есть три варианта значения второй производной: либо \(f»(a) \lt 0\text{,}\) \(f»(a) = 0 \text{,}\) или \(f»(a) \gt 0\text{.}\)
Если \(f»(a) \gt 0\text{,}\), то мы знаем, что график \(f\) вогнут вверх, и мы видим первую возможность слева, где касательная линия лежит полностью ниже кривой.
Если \(f»(a) \lt 0\text{,}\), то \(f\) вогнута вниз и касательная лежит выше кривой, как показано на втором рисунке.
Если \(f»(a) = 0\) и \(f»\) меняет знак при \(x = a\text{,}\), то вогнутость графика изменится, и мы увидим либо третья, либо четвертая фигура. 3 .
Пятый вариант (который не очень интересен) может иметь место, если сама функция \(f\) является линейной, так что \(f(x) = L(x)\) для всех значений \(x\text {.
 }\)
}\)
Графики на рис. 1.8.5 подчеркивают еще одну важную вещь, которую мы можем узнать из вогнутости графика вблизи точки касания: лежит ли касательная выше или ниже самой кривой. Это ключевой момент, потому что он говорит нам, будут ли значения аппроксимации касательной слишком большими или слишком маленькими по сравнению с истинным значением \(f\text{.}\). Например, в первой ситуации на крайнем левом графике на рисунке 1.8.5, где \(f»(a) > 0\text{,}\), поскольку касательная опускается ниже кривой, мы знаем, что \(L(x) \le f(x)\) для все значения \(x\) рядом с \(a\text{.}\)
Мероприятие 1.8.3.
Это действие касается функции \(f(x)\), о которой известна следующая информация:
\(f\) — дифференцируемая функция, определенная для каждого действительного числа \(x\)
\(\displaystyle f(2) = -1\)
\(y = f'(x)\) имеет график, показанный на рисунке 1.8.6
 }\)
}\)Ваша задача — найти как можно больше информации о \(f\) (особенно вблизи значения \(a = 2\)) с помощью ответов на приведенные ниже вопросы.
Найдите формулу аппроксимации касательной от \(L(x)\text{,}\) до \(f\) в точке \((2,-1)\text{.}\)
Используйте аппроксимацию касательной для оценки значения \(f(2.07)\text{.}\) Внимательно и ясно покажите свою работу.
Нарисуйте график \(y = f»(x)\) в правой сетке на рисунке 1.8.6; обозначьте его соответствующим образом.
Является ли наклон касательной к \(y = f(x)\) возрастающим, убывающим или ни тем, ни другим, когда \(x = 2\text{?}\) Объясните.
Нарисуйте возможный график \(y = f(x)\) вблизи \(x = 2\) в левой сетке на рисунке 1.8.6. Включите набросок \(y=L(x)\) (найден в части (a)). Объясните, откуда вы знаете, что график \(y = f(x)\) выглядит так, как будто вы его нарисовали.
Ваша оценка в (b) завышает или занижает истинное значение \(f(2.
 07)\text{?}\) Почему?
07)\text{?}\) Почему?
Идея о том, что дифференцируемая функция выглядит линейной и может быть хорошо аппроксимирована линейной функцией, является важной и находит широкое применение в исчислении. Например, аппроксимируя функцию ее локальной линеаризацией, можно разработать эффективный алгоритм оценки нулей функции. Локальная линейность также помогает нам лучше понять некоторые сложные ограничения. Например, мы видели, что предел
\begin{уравнение*} \lim_{x \to 0} \frac{\sin(x)}{x} \end{уравнение*}
является неопределенным, потому что его числитель и знаменатель стремятся к 0. Хотя нет никакой алгебры, которую мы могли бы сделать, чтобы упростить \(\frac{\sin(x)}{x}\text{,}\), это просто покажите, что линеаризация \(f(x) = \sin(x)\) в точке \((0,0)\) определяется выражением \(L(x) = x\text{.}\) Следовательно , для значений \(x\) около 0, \(\sin(x) \ приблизительно x\text{,}\) и, следовательно,
\begin{уравнение*} \ frac {\ sin (x)} {x} \ приблизительно \ frac {x} {x} = 1 \ text {,} \end{уравнение*}
, что делает правдоподобным тот факт, что
\begin{уравнение*} \lim_{x \to 0} \frac{\sin(x)}{x} = 1\text{.
 }
\end{уравнение*}
}
\end{уравнение*}Подраздел 1.8.3 Резюме
Касательная к дифференцируемой функции \(y = f(x)\) в точке \((a,f(a))\) задается в виде точки-наклона уравнением
\begin{уравнение*} y — f(a) = f'(a)(x-a)\text{.} \end{уравнение*}
Принцип локальной линейности говорит нам, что если мы увеличим масштаб точки, где функция \(y = f(x)\) дифференцируема, функция будет неотличима от своей касательной. То есть дифференцируемая функция выглядит линейной при ближайшем рассмотрении. Мы переименовываем касательную в функцию \(y = L(x)\text{,}\), где \(L(x) = f(a) + f'(a)(x-a)\text{.} \) Таким образом, \(f(x) \ приблизительно L(x)\) для всех \(x\) вблизи \(x = a\text{.}\)
Если мы знаем приближение касательной \(L(x) = f(a) + f'(a)(x-a)\) к функции \(y=f(x)\text{,}\), то поскольку \(L(a) = f(a)\) и \(L'(a) = f'(a)\text{,}\) мы также знаем значения как функции, так и ее производной в точке где \(x = a\text{.}\) Другими словами, линейная аппроксимация сообщает нам высоту и наклон исходной функции.
 Если, кроме того, мы знаем значение \(f»(a)\text{,}\), то мы знаем, лежит ли касательная выше или ниже графика \(y = f(x)\text{ ,}\) в зависимости от вогнутости \(f\text{.}\)
Если, кроме того, мы знаем значение \(f»(a)\text{,}\), то мы знаем, лежит ли касательная выше или ниже графика \(y = f(x)\text{ ,}\) в зависимости от вогнутости \(f\text{.}\)
Упражнения 1.8.4 Упражнения
1. Приближение \(\sqrt{x}\).
Используйте линейную аппроксимацию для аппроксимации \(\sqrt {36.1}\) следующим образом.
Пусть \(f(x) = \sqrt x\text{.}\) Уравнение касательной к \(f(x)\) в точке \(x = 36\) можно записать в виде \ (y = mx+b\text{.}\) Вычислить \(m\) и \(b\text{.}\)
\(m=\)
\(b=\)
Используя это найдите приближение для \(\sqrt {36.1}\text{.}\)
Ответ:
2. Локальная линеаризация графа.
На рисунке ниже показано \(f(x)\) и его локальная линеаризация при \(x=a\text{,}\) \(y = 4 x — 4\text{.}\) (Локальная линеаризация показано синим цветом.)
Каково значение \(a\text{?}\)
\(a =\)
Каково значение \(f(a)\text{?}\)
\(f(a) =\)
Используйте линеаризацию для аппроксимации значения \(f(3.
 2)\text{.}\)
2)\text{.}\)\(f(3.2) =\)
Является приближением заниженная или завышенная оценка?
(Введите вместо или вместо .)
3. Оценка с локальной линеаризацией.
Предположим, что \(f(x)\) является функцией с \(f(130) = 46\) и \(f'(130) = 1\text{.}\). Оценка \(f(125,5)\ текст{.}\)
\(f(125.5) =\)
4. Прогнозирование поведения по локальной линеаризации.
Температура, \(H\text{,}\) в градусах Цельсия, чашки кофе, стоящей на кухонном столе, определяется выражением \(H = f(t)\text{,}\), где \(t \) в минутах с момента подачи кофе на прилавок.
(a) Является ли \(f'(t)\) положительным или отрицательным?
положительный
отрицательный
(Убедитесь, что вы можете обосновать свой ответ.)
(b) Каковы единицы измерения \(f'(30)\text{?}\)
Предположим, что \(|f'(30)| = 0,9\) и \(f(30) = 51\text{.}\) Заполните пропуски (включая единицы измерения, где это необходимо) и выберите соответствующие термины, чтобы завершить следующее утверждение о температура кофе в данном случае.

Через несколько минут после того, как кофе был поставлен на прилавок, его
есть и будет
увеличение
уменьшение
примерно за следующие 75 секунд.
5.
Некоторая функция \(y=p(x)\) имеет локальную линеаризацию в точке \(a = 3\), заданную выражением \(L(x) = -2x + 5\text{.}\)
Каковы значения \(p(3)\) и \(p'(3)\text{?}\) Почему?
Оценить значение \(p(2,79)\текст{.}\)
Предположим, что \(p»(3) = 0\) и вы знаете, что \(p»(x) \lt 0\) для \(x \lt 3\text{.}\) Ваша оценка в (б) слишком большой или слишком маленький?
Предположим, что \(p»(x) \gt 0\) для \(x \gt 3\text{.}\) Используйте этот факт и приведенную выше дополнительную информацию, чтобы нарисовать точный график \(y = p (x)\) рядом с \(x = 3\text{.}\) Включите набросок \(y = L(x)\) в свою работу.
6.

Картофель помещают в печь, измеряют температуру картофеля \(F\) (в градусах по Фаренгейту) в различные моменты времени и записывают в следующую таблицу. Время \(t\) измеряется в минутах.
Таблица 1.8.7. Температурные данные для картофеля.\(т\) \(Ф(т)\) \(0\) \(70\) \(15\) \(180.5\) \(30\) \(251\) \(45\) \(296\) \(60\) \(324.5\) \(75\) \(342.8\) \(90\) \(354,5\) Используйте центральную разность для оценки \(F'(60)\text{.}\) При необходимости используйте эту оценку в последующих вопросах.
Найти локальную линеаризацию \(y = L(t)\) функции \(y = F(t)\) в точке, где \(a = 60\text{.}\)
Определите оценку для \(F(63)\), используя локальную линеаризацию.

Как вы думаете, ваша оценка в (c) слишком велика или слишком мала? Почему?
7.
Объект, движущийся по прямолинейному пути, имеет дифференцируемую функцию положения \(y = s(t)\text{;}\) \(s(t)\) измеряет положение объекта относительно начала координат в момент времени \(t \text{.}\) Известно, что в момент времени \(t = 9\) секунд объект находится в \(s(9) = 4\) футах (т.е. на 4 фута правее начала координат). Кроме того, мгновенная скорость объекта при \(t = 9\) составляет \(-1,2\) фута в секунду, а его ускорение в тот же момент составляет \(0,08\) фута в секунду в секунду.
Использовать локальную линейность для оценки положения объекта в точке \(t = 9,34\text{.}\)
Возможно, ваша оценка слишком велика или слишком мала? Почему?
Обычным языком опишите поведение движущегося объекта в точке \(t = 9\text{.}\) Он движется к началу координат или от него? Его скорость увеличивается или уменьшается?
8.


 364
364 0355
0355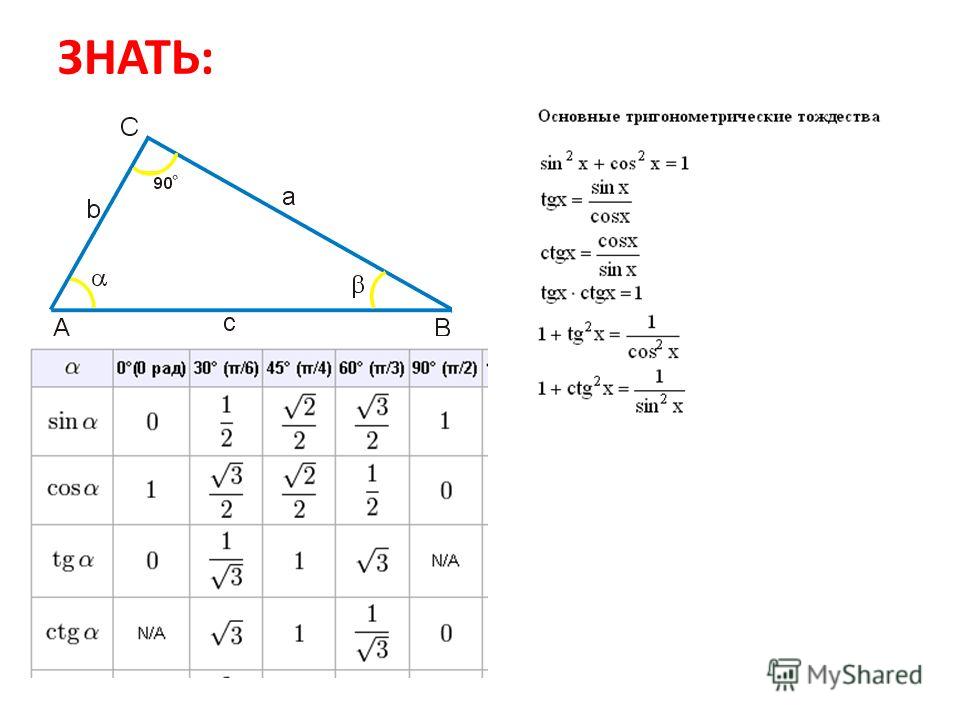 9042
9042 5144
5144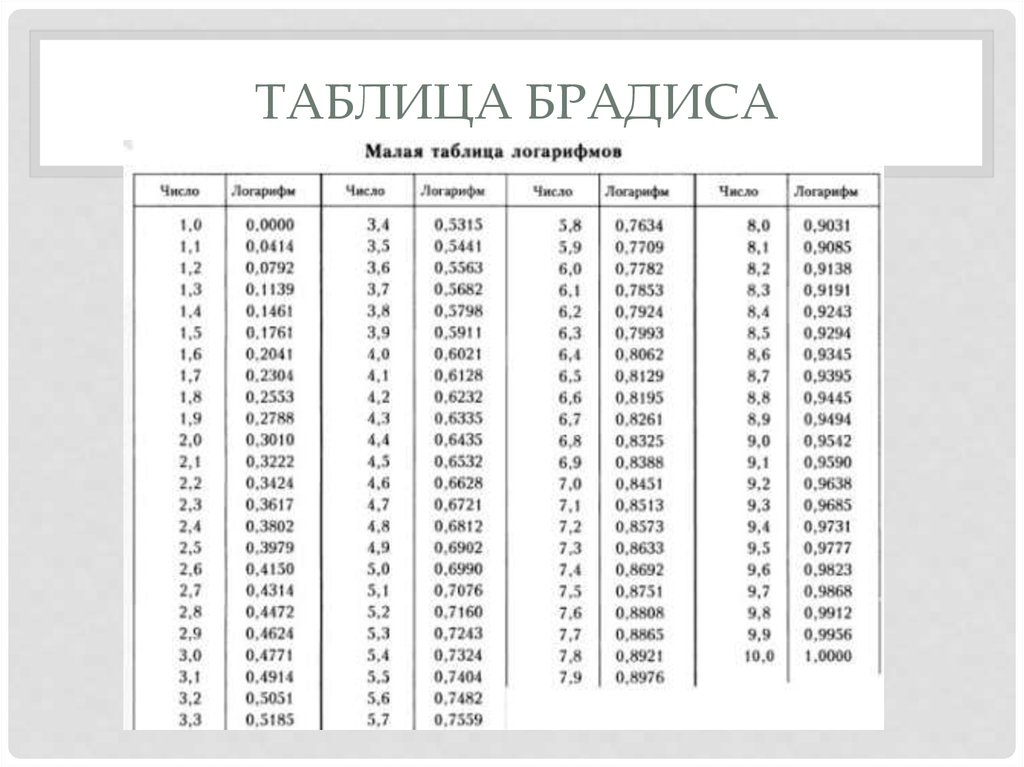 7321
7321 7265
7265 2126
2126 1763
1763 7002
7002 7321
7321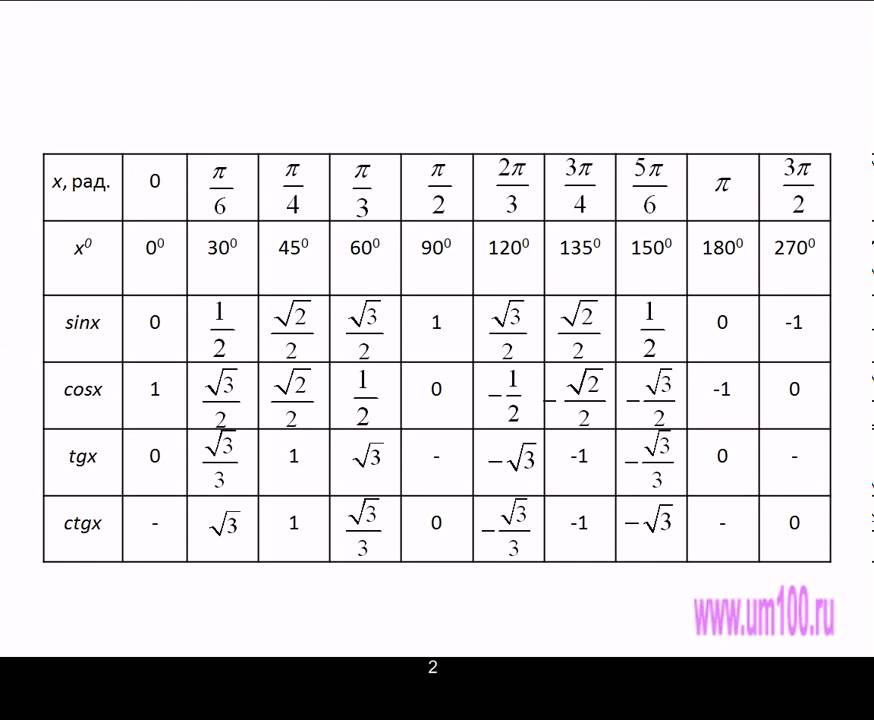 5144
5144 0777
0777 1106
1106 4452
4452 0175
0175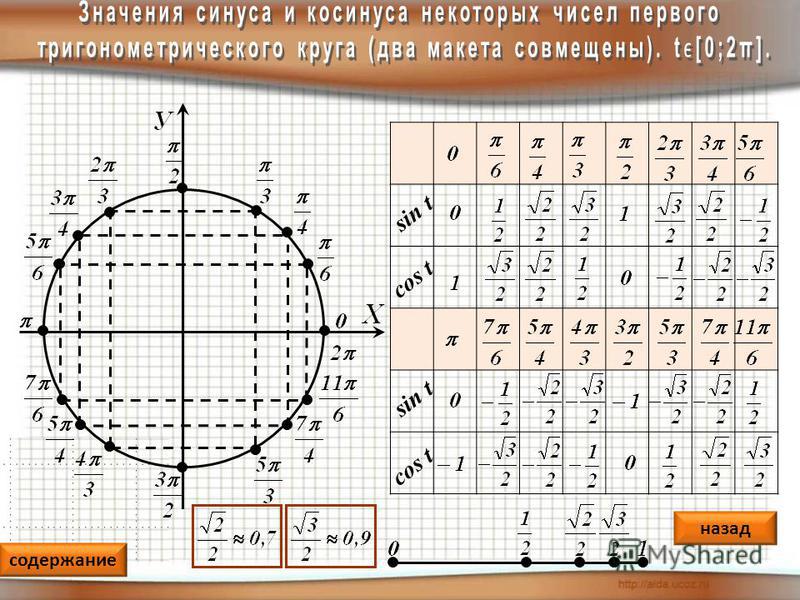 5095
5095 2799
2799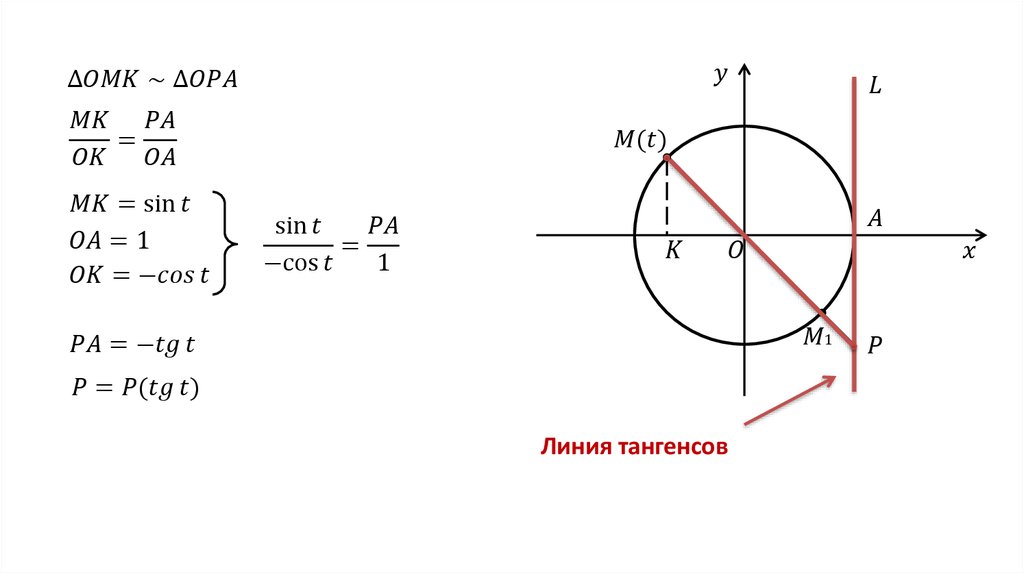 3315
3315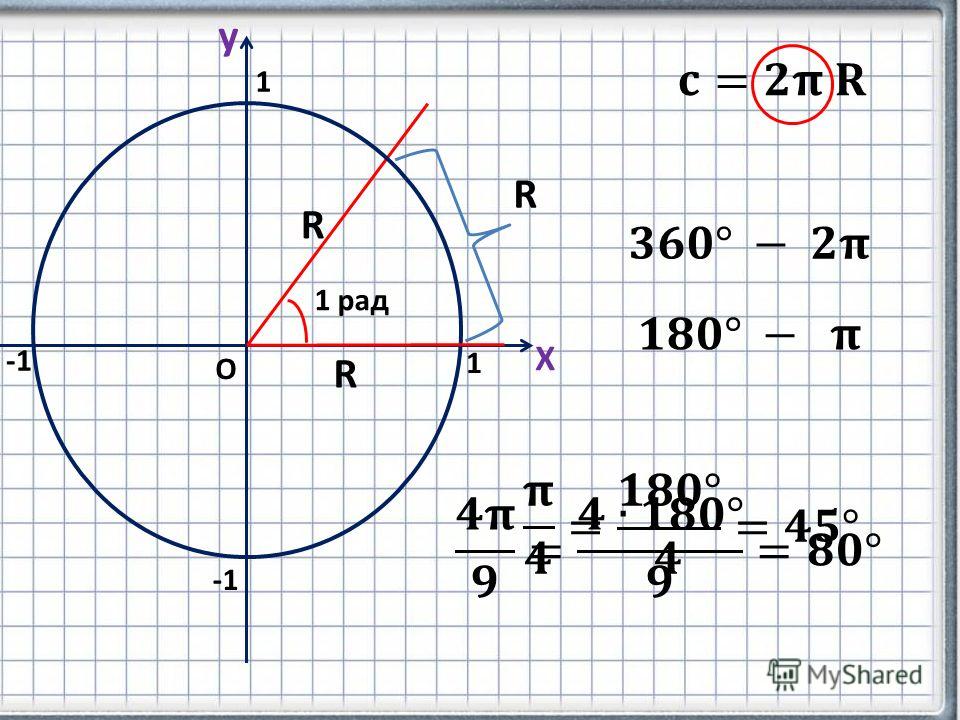 7046
7046 4281
4281 6249
6249 1405
1405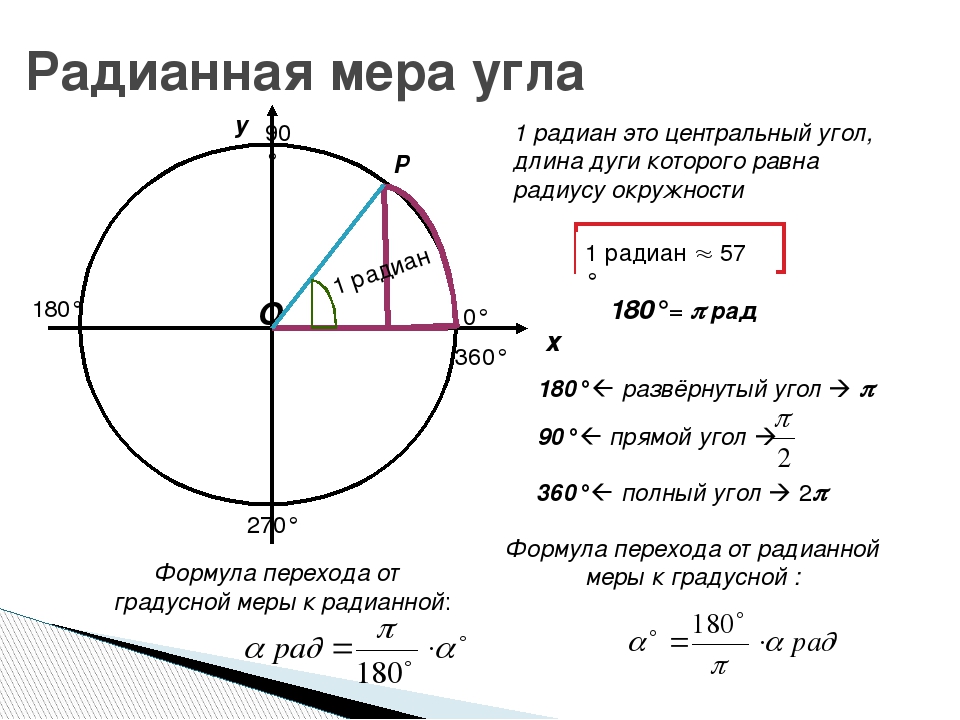 2309
2309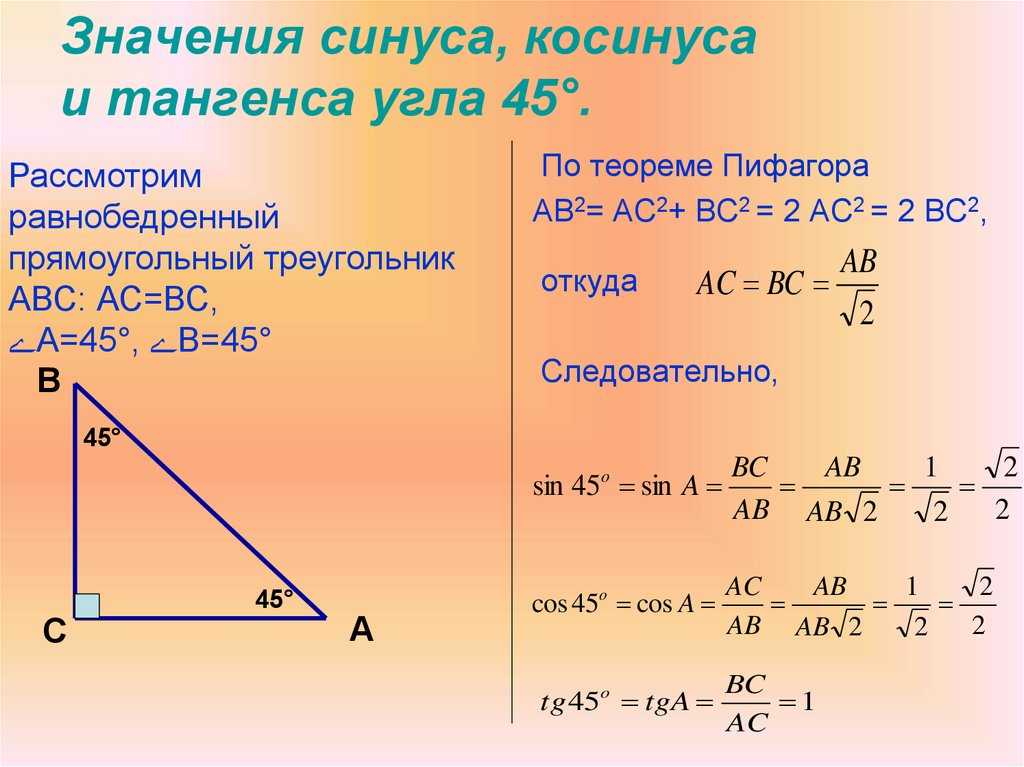 7536
7536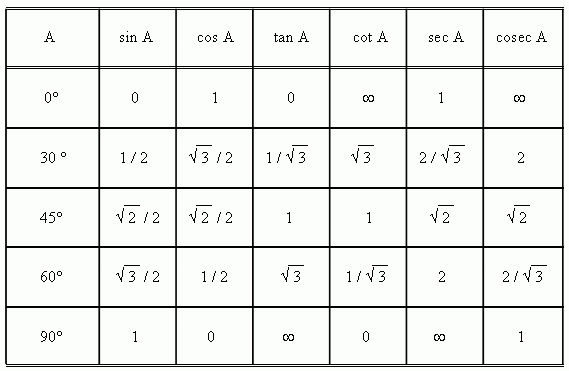 8807
8807 3007
3007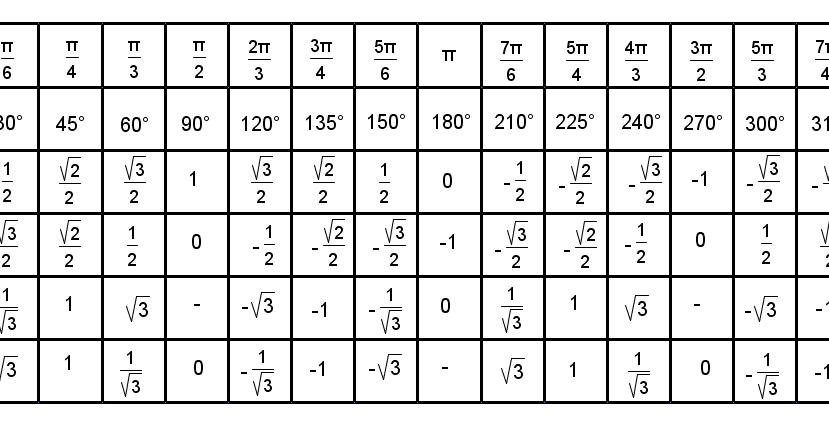 9042
9042 0724
0724 4452
4452 Углы с шагом в 1°. Таблица значений тангенса, tg
Углы с шагом в 1°. Таблица значений тангенса, tg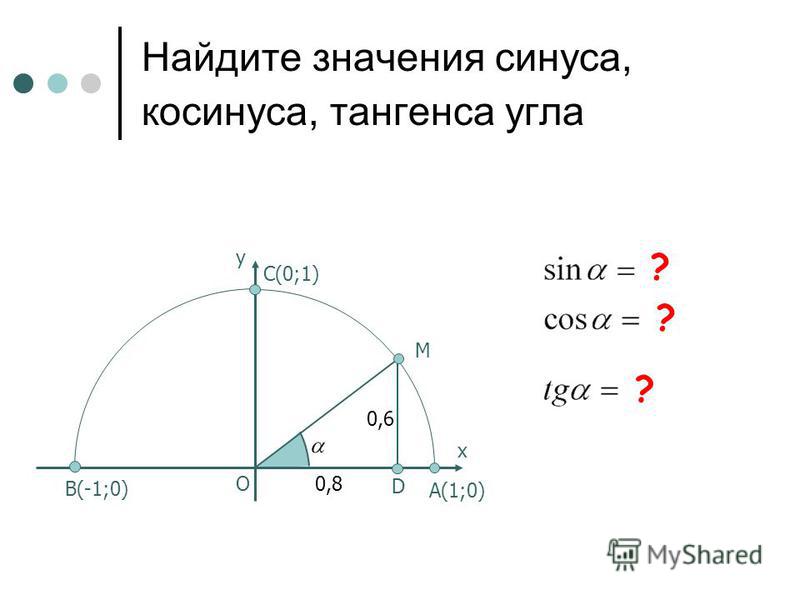 0174
0174 2308
2308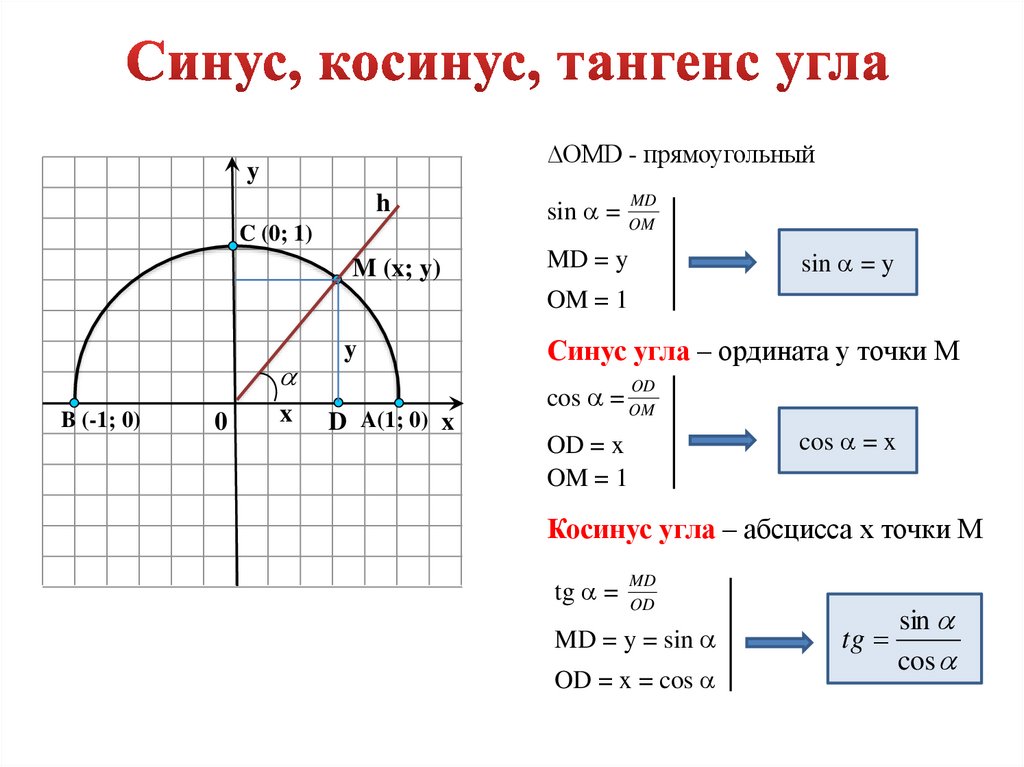 4663
4663 7535
7535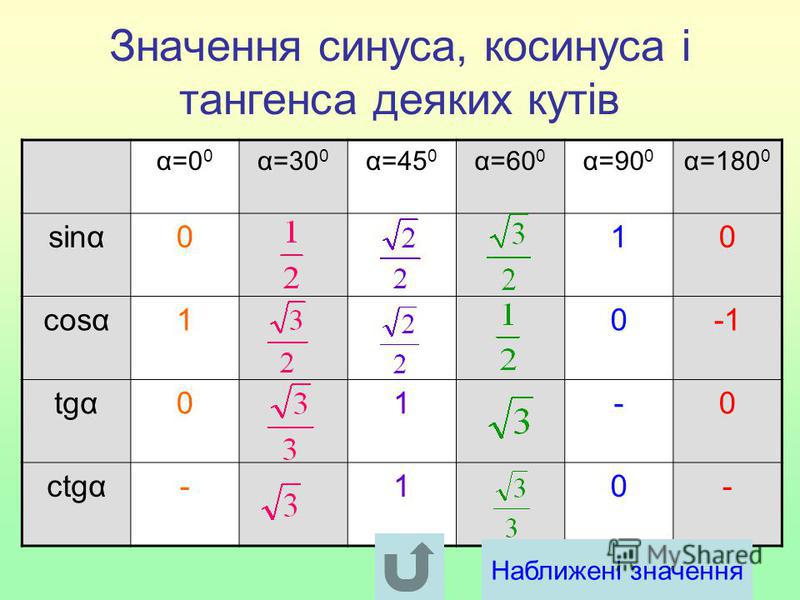 1504
1504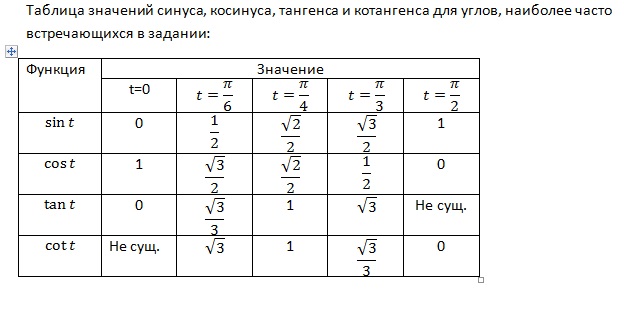 804
804 2709
2709 4301
4301 3007
3007 4874
4874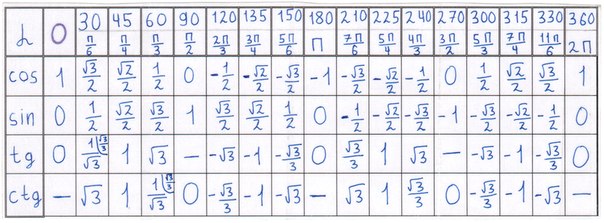 8807
8807