| 1 | Найти точное значение | sin(30) | |
| 2 | Найти точное значение | sin(45) | |
| 3 | Найти точное значение | sin(30 град. ) | |
| 4 | Найти точное значение | sin(60 град. ) | |
| 5 | Найти точное значение | tan(30 град. ) | |
| 6 | Найти точное значение | arcsin(-1) | |
| 7 | Найти точное значение | sin(pi/6) | |
| 8 | cos(pi/4) | ||
| 9 | Найти точное значение | sin(45 град. ) ) | |
| 10 | Найти точное значение | sin(pi/3) | |
| 11 | Найти точное значение | arctan(-1) | |
| 12 | Найти точное значение | cos(45 град. ) | |
| 13 | Найти точное значение | cos(30 град. ) | |
| 14 | Найти точное значение | tan(60) | |
| 15 | Найти точное значение | csc(45 град. ) | |
| 16 | Найти точное значение | tan(60 град. ) | |
| 17 | Найти точное значение | sec(30 град.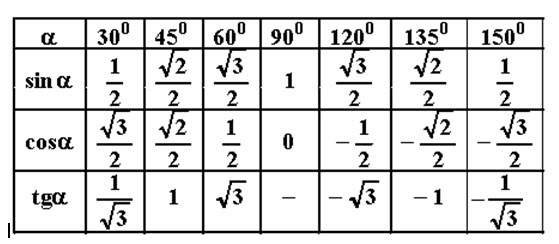 ) ) | |
| 18 | Найти точное значение | cos(60 град. ) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | sin(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | tan(45 град. ) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 град. ) | |
| 25 | Найти точное значение | sec(45 град.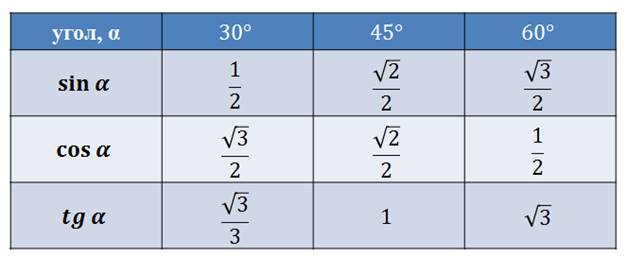 ) ) | |
| 26 | Найти точное значение | csc(30 град. ) | |
| 27 | Найти точное значение | sin(0) | |
| 28 | Найти точное значение | sin(120) | |
| 29 | Найти точное значение | cos(90) | |
| 30 | Преобразовать из радианов в градусы | pi/3 | |
| 31 | Найти точное значение | tan(30) | |
| 32 | Преобразовать из градусов в радианы | 45 | |
| 33 | Найти точное значение | cos(45) | |
| 34 | Упростить | ||
| 35 | Преобразовать из радианов в градусы | pi/6 | |
| 36 | Найти точное значение | cot(30 град. ) ) | |
| 37 | Найти точное значение | arccos(-1) | |
| 38 | Найти точное значение | arctan(0) | |
| 39 | Найти точное значение | cot(60 град. ) | |
| 40 | Преобразовать из градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2pi)/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | tan(pi/2) | |
| 45 | Найти точное значение | sin(300) | |
| 46 | Найти точное значение | cos(30) | |
| 47 | Найти точное значение | cos(60) | |
| 48 | Найти точное значение | cos(0) | |
| 49 | Найти точное значение | cos(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | sec(60 град.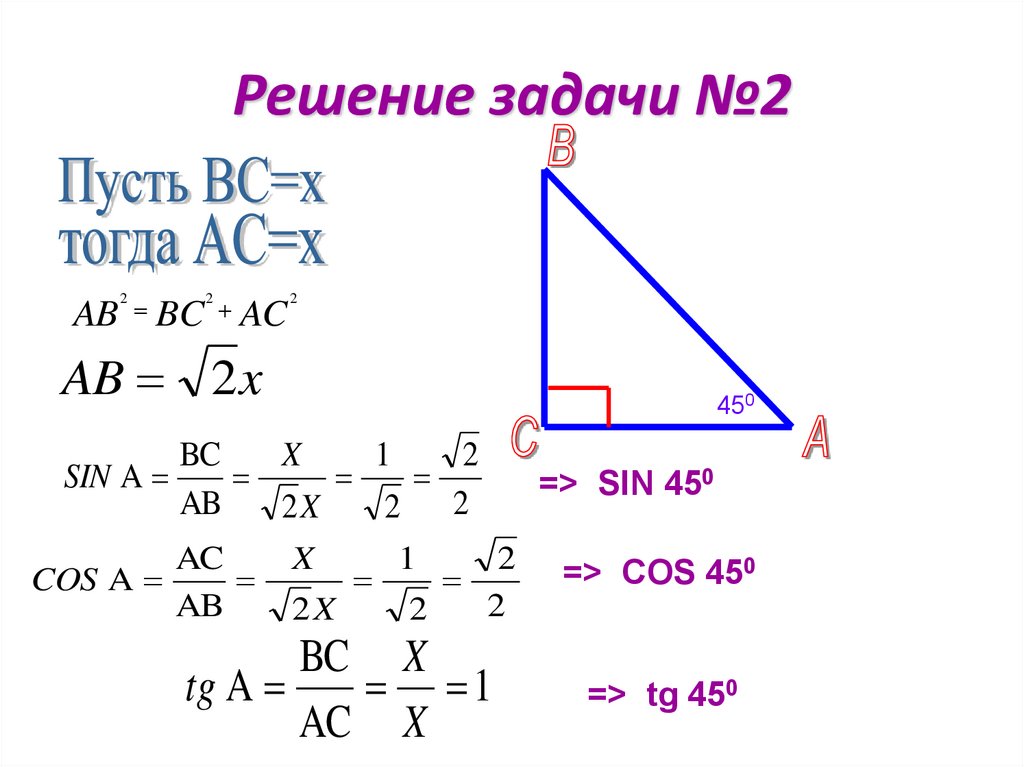 ) ) | |
| 53 | Найти точное значение | sin(300 град. ) | |
| 54 | Преобразовать из градусов в радианы | 135 | |
| 55 | Преобразовать из градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5pi)/6 | |
| 57 | Преобразовать из радианов в градусы | (5pi)/3 | |
| 58 | Преобразовать из градусов в радианы | 89 град. | |
| 59 | Преобразовать из градусов в радианы | 60 | |
| 60 | Найти точное значение | sin(135 град.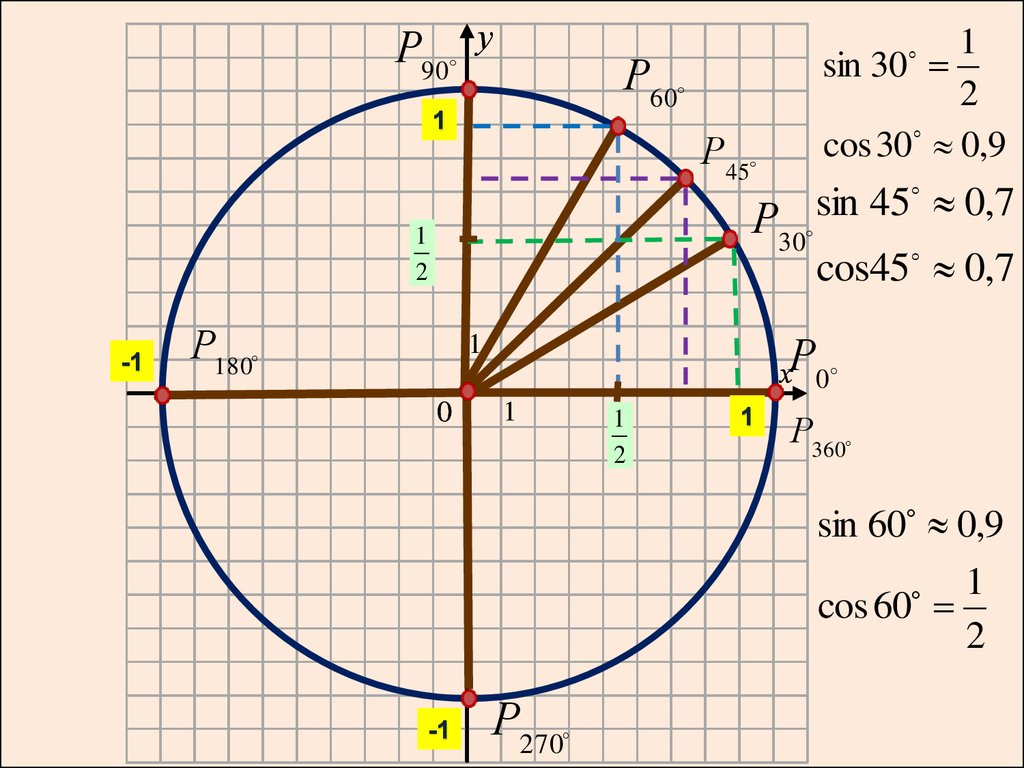 ) ) | |
| 61 | Найти точное значение | sin(150) | |
| 62 | Найти точное значение | sin(240 град. ) | |
| 63 | Найти точное значение | cot(45 град. ) | |
| 64 | Преобразовать из радианов в градусы | (5pi)/4 | |
| 65 | Найти точное значение | sin(225) | |
| 66 | Найти точное значение | sin(240) | |
| 67 | Найти точное значение | cos(150 град. ) | |
| 68 | Найти точное значение | tan(45) | |
| 69 | Вычислить | sin(30 град.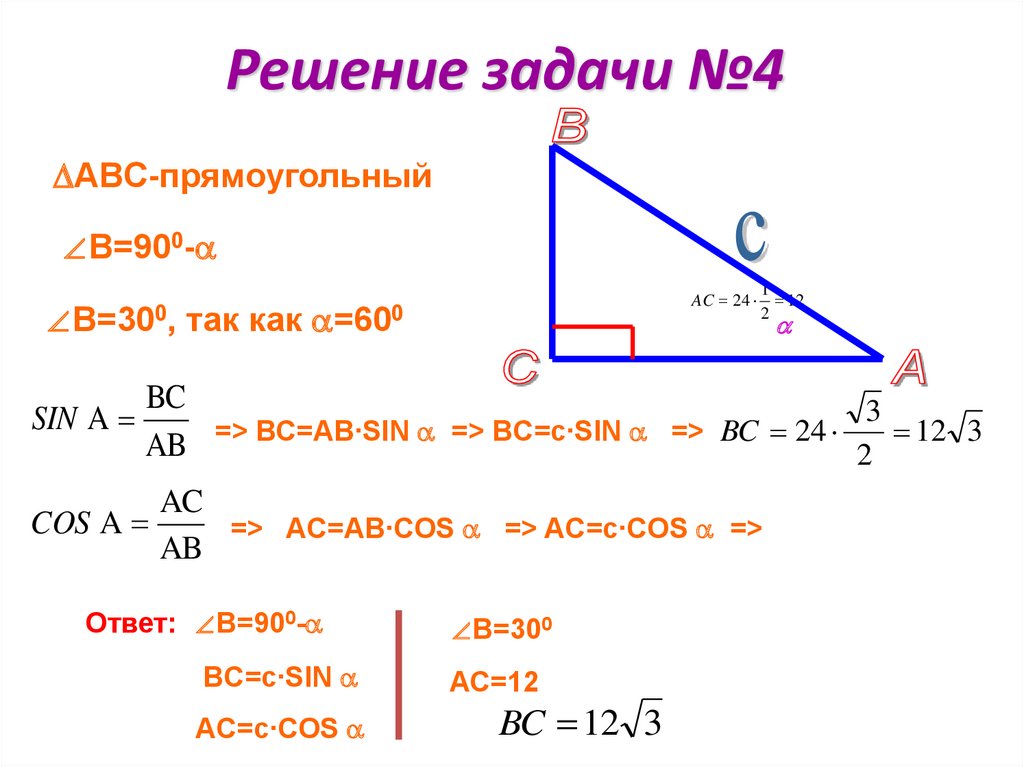 ) ) | |
| 70 | Найти точное значение | sec(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | csc(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | tan((5pi)/3) | |
| 75 | Найти точное значение | tan(0) | |
| 76 | Вычислить | sin(60 град. ) | |
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3pi)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | arcsin(-1/2) | |
| 81 | Найти точное значение | sin((4pi)/3) | |
| 82 | Найти точное значение | csc(45) | |
| 83 | Упростить | arctan( квадратный корень из 3) | |
| 84 | Найти точное значение | sin(135) | |
| 85 | Найти точное значение | sin(105) | |
| 86 | Найти точное значение | sin(150 град.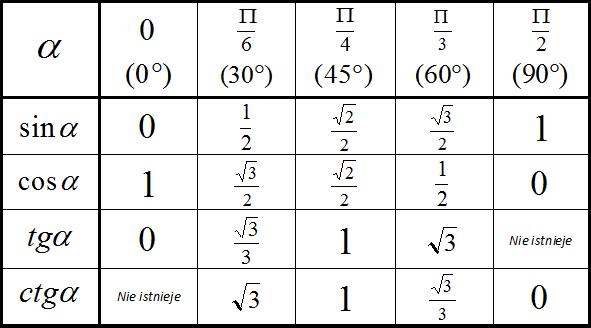 ) ) | |
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | tan((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | pi/4 | |
| 90 | Найти точное значение | sin(pi/2) | |
| 91 | Найти точное значение | sec(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | arcsin(0) | ||
| 95 | Найти точное значение | sin(120 град. ) ) | |
| 96 | Найти точное значение | tan((7pi)/6) | |
| 97 | Найти точное значение | cos(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразовать из градусов в радианы | 88 град. |
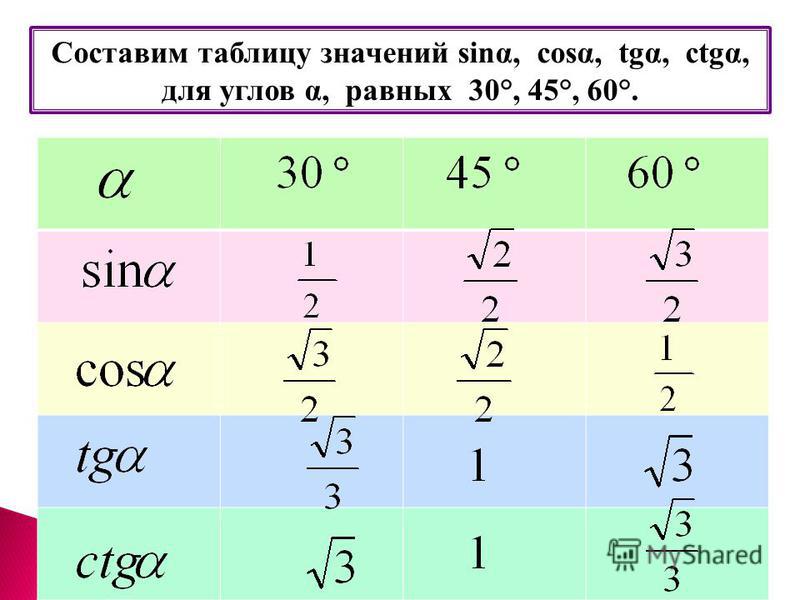
Значения синуса, косинуса и тангенса для углов 30, 45 и 60 градусов 8 класс презентация, доклад, проект
Методическая разработка урока
по геометрии 8 класса
учителя ГБОУ СОШ № 277
города Санкт-Петербурга
Протасовой Светланы Михайловны
Значения синуса, косинуса и тангенса
для углов 300, 450 и 600
Цели урока
Научить учащихся вычислять значения синуса, косинуса и тангенса для углов 300, 450 и 600.
Формировать навыки решения прямоугольных треугольников, используя синус, косинус и тангенс острого угла.
Содержание
Проверка домашнего задания
Устная работа
Вычисление значений синуса, косинуса и тангенса для углов 300, 450 и 600 в ходе решения задач
Решение задач
Итоги урока
Домашнее задание
Проверка домашнего задания
Задача № 591(в)
Дано:
ΔАВС
∠С=900
ВС=1
АС=2
Найти:
Sin A, cos A, tg A,
Sin B, cos B, tg B.
Ответ:
Проверка домашнего задания
Ответы к тесту:
А
2) А
3) В
4) Б
5) Б
Устная работа
1. Сформулируйте теорему Пифагора для прямоугольного треугольника.
Сформулируйте теорему Пифагора для прямоугольного треугольника.
2.Что называют синусом, косинусом, тангенсом острого угла прямоугольного треугольника?
3. Как найти площадь параллелограмма?
4. Как найти катет прямоугольного треугольника, лежащий напротив угла в 300?
C2=a2+b2
S=a∙h
Устная работа
Дано:
ΔАВС
∠С=900
ВС=5
АВ=13
Найти:
Sin A, cos A, tg A,
Sin B, cos B, tg B.
Решение задачи
По теореме Пифагора:
АВ2=ВС2+АС2
АС2=169-25
АС2=144
АС=12
SIN A=
BC
AB
COS A=
AC
AB
tg A=
BC
AC
SIN B =
AC
AB
COS B=
BC
AB
tg B =
AC
BC
Устная работа
Дано:
АВСD-параллелограмм
∠E=900
∠A=600
AE=4
ED=5
Найти:
SABCD.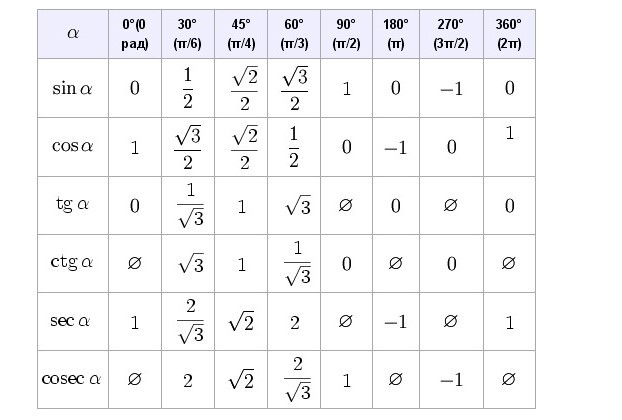
Решение задачи
По теореме Пифагора:
AB2=AE2+BE2
BE2=64-16=48
∠ABE=300
SABCD=BE·AD
AD=4+5=9
AE=0,5∙AB => AB=8
Вычисление значений синуса, косинуса и тангенса для углов 300, 450 и 600 в ходе решения задач
Дано:
ΔАВС
∠А=300
∠С=900
Найти:
Sin A, cos A, tg A,
Sin B, cos B, tg B.
Задача №1
300
Решение задачи №1
Пусть ВС=х
тогда АВ=2х
300
Вычисление значений синуса, косинуса и тангенса для углов 300, 450 и 600 в ходе решения задач
Задача №2
Дано:
ΔАВС
∠А=450
∠С=900
Найти:
Sin A, cos A, tg A.
Решение задачи №2
Пусть ВС=х
тогда АC=х
=> SIN 450
=> tg 450
=> COS 450
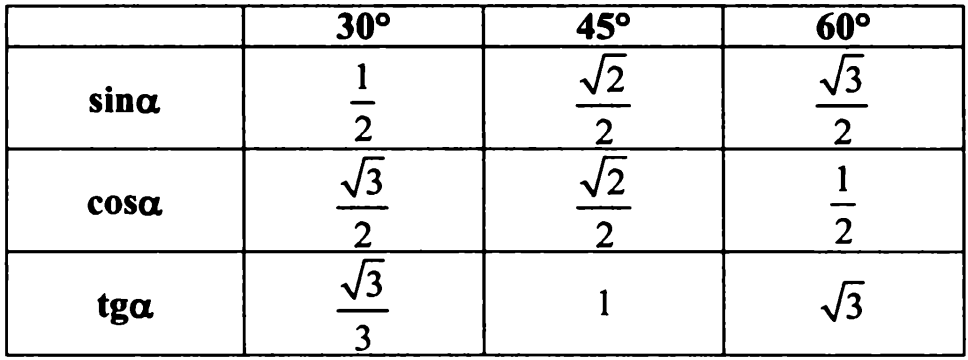
Таблица значений синуса, косинуса и тангенса для углов 300, 450 и 600
Решение задач
Задача №3
В прямоугольной трапеции основания равны 6 и 11, меньшая боковая сторона равна 4.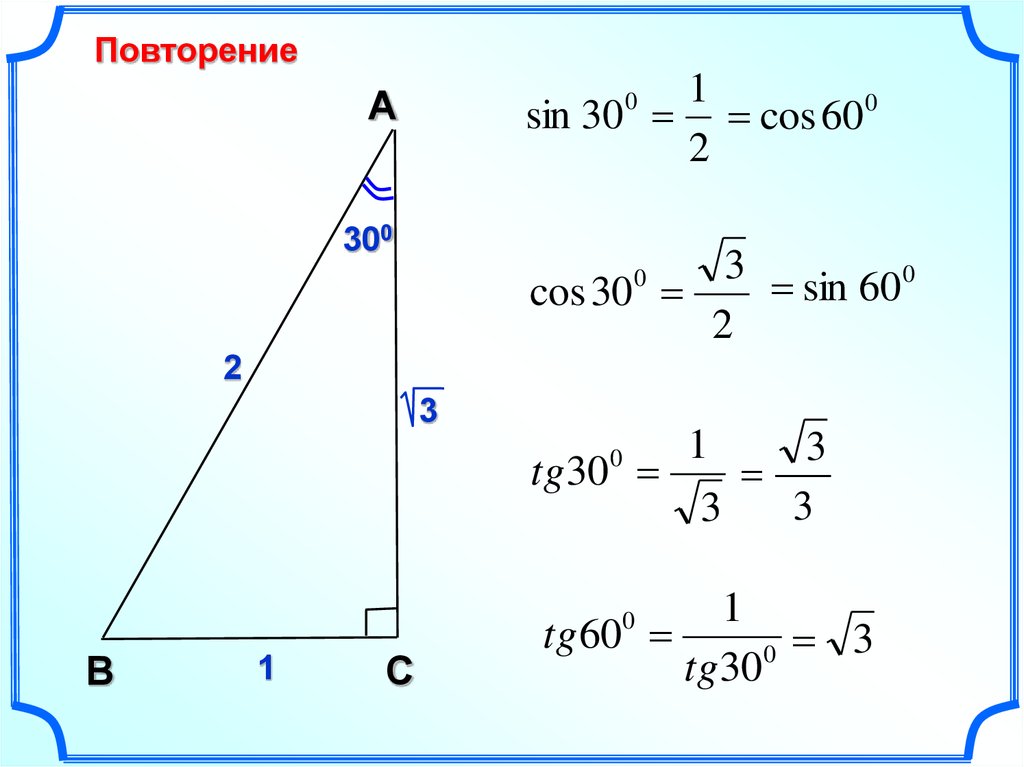 Найдите синус, косинус и тангенс острого угла трапеции.
Найдите синус, косинус и тангенс острого угла трапеции.
Дано:
АВСD-трапеция
CD⊥AD
CD=4
AD=11
BC=6
Найти:
Sin A, cos A, tg A.
Решение задачи №3
Проведем ВН⊥AD
BH=CD=4
AH=AD – HD=5
ΔABH-прямоугольный
ПО ТЕОРЕМЕ ПИФАГОРА:
АВ2=ВН2+АН2
Решение задач
В прямоугольном треугольнике гипотенуза равна с, а один из острых углов равен α. Выразите второй острый угол и катеты через с и α и найдите их значения, если с=24, а α=600.
Задача № 4
Дано:
ΔАВС
∠А=α=600
AВ=24
Найти:
∠В, АС, ВС,
Выразить через
α и с.
Решение задачи №4
ΔABС-прямоугольный
∠В=900-α
∠В=300, так как α=600
=> ВС=АВ∙SIN α => BС=c∙SIN α =>
=> AС=АВ∙COS α => AС=c∙COS α =>
Ответ: ∠В=900-α
BС=c∙SIN α
AС=c∙COS α
∠В=300
АС=12
Итоги урока
Как найти острый угол прямоугольного треугольника, если другой острый угол равен α?
2. Какая связь существует между катетом, противолежащим ему углом и гипотенузой?
Какая связь существует между катетом, противолежащим ему углом и гипотенузой?
Итоги урока
3. Как взаимосвязаны два катета прямоугольного треугольника и один из его острых углов?
4. Какая связь существует между катетом, прилежащим к нему острым углом и гипотенузой?
5. Для каких углов сегодня узнали значения синуса, косинуса и тангенса?
Домашнее задание
Выучить значения синуса, косинуса и тангенса для углов 300, 450 и 600;
№ 595; № 597; № 598(б).
Скачать презентацию
Примечание . В данной таблице значений тригонометрических функций используется знак √ для обозначения квадратного корня. См. также полезные материалы: Для определения значения тригонометрической функции , найдите его на пересечении строки с указанием тригонометрической функции. Например, синус 30 градусов — ищем колонку с заголовком sin (синус) и находим пересечение этой колонки таблицы со строкой «30 градусов», на их пересечении считываем результат — одна вторая. Аналогично находим косинус 60 градусов, синус 60 градусов (еще раз, в пересечении колонки sin (синус) и строки 60 градусов находим значение sin 60 = √3/2) и т.д. Точно так же находятся значения синусов, косинусов и тангенсов других «популярных» углов. Синус пи, косинус пи, тангенс пи и других углов в радианахПриведенная ниже таблица косинусов, синусов и тангенсов также подходит для нахождения значения тригонометрических функций, аргумент которых задан в радианах . Для этого воспользуйтесь второй колонкой значений угла. Благодаря этому можно перевести значение популярных углов из градусов в радианы. Число пи однозначно выражает зависимость длины окружности от градусной меры угла. Таким образом, пи радиан равны 180 градусам. Любое число, выраженное через пи (радиан) можно легко перевести в градусную меру, заменив число пи (π) на 180 . Примеры : 2. Косинус пи . 3. Тангенс пи Таблица значений синуса, косинуса, тангенса для углов 0 — 360 градусов (часто встречающиеся значения)
Если в таблице значений тригонометрических функций вместо значения функции указан прочерк (тангенс (tg) 90 градусов, котангенс (ctg) 180 градусов) значит при данном значении градусной меры угла функция не имеет определенного значения. Таблица значений тригонометрических функций sin, cos, tg для наиболее популярных углов0, 15, 30, 45, 60, 90 … 360 градусов (цифровые значения «как по таблицам Брадиса»)
|
| 1 | Найти точное значение | грех(30) | |
| 2 | Найти точное значение | грех(45) | |
| 3 | Найти точное значение | грех(30 градусов) | |
| 4 | Найти точное значение | грех(60 градусов) | |
| 5 | Найти точное значение | загар (30 градусов) | |
| 6 | Найти точное значение | угловой синус(-1) | |
| 7 | Найти точное значение | грех(пи/6) | |
| 8 | Найти точное значение | cos(pi/4) | |
| 9 | Найти точное значение | грех(45 градусов) | |
| 10 | Найти точное значение | грех(пи/3) | |
| 11 | Найти точное значение | арктан(-1) | |
| 12 | Найти точное значение | cos(45 градусов) | |
| 13 | Найти точное значение | cos(30 градусов) | |
| 14 | Найти точное значение | желтовато-коричневый(60) | |
| 15 | Найти точное значение | csc(45 градусов) | |
| 16 | Найти точное значение | загар (60 градусов) | |
| 17 | Найти точное значение | сек(30 градусов) | |
| 18 | Найти точное значение | cos(60 градусов) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | грех(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | загар (45 градусов) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 градусов) | |
| 25 | Найти точное значение | сек(45 градусов) | |
| 26 | Найти точное значение | csc(30 градусов) | |
| 27 | Найти точное значение | грех(0) | |
| 28 | Найти точное значение | грех(120) | |
| 29 | Найти точное значение | соз(90) | |
| 30 | Преобразовать из радианов в градусы | пи/3 | |
| 31 | Найти точное значение | желтовато-коричневый(30) | |
| 32 | 92|||
| 35 | Преобразовать из радианов в градусы | пи/6 | |
| 36 | Найти точное значение | детская кроватка(30 градусов) | |
| 37 | Найти точное значение | арккос(-1) | |
| 38 | Найти точное значение | арктан(0) | |
| 39 | Найти точное значение | детская кроватка(60 градусов) | |
| 40 | Преобразование градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2 шт. )/3 )/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | тан(пи/2) | |
| 45 | Найти точное значение | грех(300) | |
| 46 | Найти точное значение | соз(30) | |
| 47 | Найти точное значение | соз(60) | |
| 48 | Найти точное значение | соз(0) | |
| 49 | Найти точное значение | соз(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | сек(60 градусов) | |
| 53 | Найти точное значение | грех(300 градусов) | |
| 54 | Преобразование градусов в радианы | 135 | |
| 55 | Преобразование градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5 дюймов)/6 | |
| 57 | Преобразовать из радианов в градусы | (5 дюймов)/3 | |
| 58 | Преобразование градусов в радианы | 89 градусов | |
| 59 | Преобразование градусов в радианы | 60 | |
| 60 | Найти точное значение | грех(135 градусов) | |
| 61 | Найти точное значение | грех(150) | |
| 62 | Найти точное значение | грех(240 градусов) | |
| 63 | Найти точное значение | детская кроватка(45 градусов) | |
| 64 | Преобразовать из радианов в градусы | (5 дюймов)/4 | |
| 65 | Найти точное значение | грех(225) | |
| 66 | Найти точное значение | грех(240) | |
| 67 | Найти точное значение | cos(150 градусов) | |
| 68 | Найти точное значение | желтовато-коричневый(45) | |
| 69 | Оценить | грех(30 градусов) | |
| 70 | Найти точное значение | сек(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | КСК(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | загар((5pi)/3) | |
| 75 | Найти точное значение | желтовато-коричневый(0) | |
| 76 | Оценить | грех(60 градусов) | |
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3 пи)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | угловой синус(-1/2) | |
| 81 | Найти точное значение | sin((4pi)/3) | |
| 82 | Найти точное значение | КСК(45) | |
| 83 | Упростить | арктан(квадратный корень из 3) | |
| 84 | Найти точное значение | грех(135) | |
| 85 | Найти точное значение | грех(105) | |
| 86 | Найти точное значение | грех(150 градусов) | |
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | загар((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | пи/4 | |
| 90 | Найти точное значение | грех(пи/2) | |
| 91 | Найти точное значение | сек(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | угловой синус(0) | |
| 95 | Найти точное значение | грех(120 градусов) | |
| 96 | Найти точное значение | желтовато-коричневый ((7pi)/6) | |
| 97 | Найти точное значение | соз(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразование градусов в радианы | 88 градусов |
Tan 60 градусов — расчет, вывод, примеры решений и часто задаваемые вопросы
Тригонометрия — раздел математики, изучающий треугольники. Слово тригонометрия состоит из двух греческих слов Trigōnon (что означает треугольник) и Metron (что означает мера). Короче говоря, мы можем сказать, что измерение треугольника (особенно прямоугольного треугольника) — это тригонометрия. Тригонометрия — это исследование отношений между углами, высотами и длинами треугольников, а также отношений между различными частями круга и другими геометрическими фигурами. В области астрономии, инженерии, архитектурного дизайна и физики можно найти приложения тригонометрии. Тригонометрические тождества очень полезны и помогают лучше решать проблемы, изучая приведенные ниже формулы. Существует огромное количество областей, в которых используются эти тригонометрические тождества и тригонометрические уравнения.
Слово тригонометрия состоит из двух греческих слов Trigōnon (что означает треугольник) и Metron (что означает мера). Короче говоря, мы можем сказать, что измерение треугольника (особенно прямоугольного треугольника) — это тригонометрия. Тригонометрия — это исследование отношений между углами, высотами и длинами треугольников, а также отношений между различными частями круга и другими геометрическими фигурами. В области астрономии, инженерии, архитектурного дизайна и физики можно найти приложения тригонометрии. Тригонометрические тождества очень полезны и помогают лучше решать проблемы, изучая приведенные ниже формулы. Существует огромное количество областей, в которых используются эти тригонометрические тождества и тригонометрические уравнения.
Tan 60 Degrees Value
Прямоугольный треугольник — это замкнутая фигура, имеющая три стороны, три угла и три ребра, так что один из трех углов треугольника равен 90 градусов.
Чтобы найти значение тангенса 60 градусов, возьмем один из углов равным 60 градусам.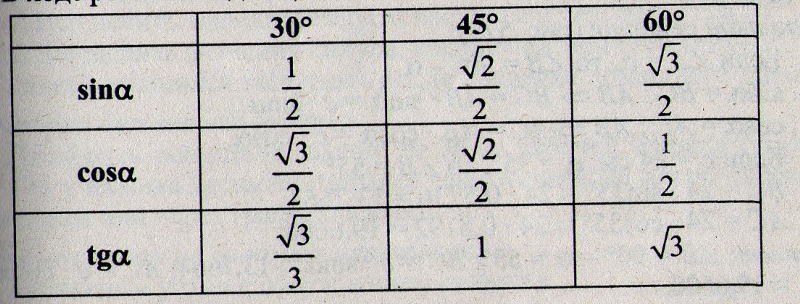
Гипотенуза: самая длинная сторона из всех трех сторон прямоугольного треугольника, которая также противоположна прямому углу, называется гипотенузой.
Основание или примыкание: сторона, содержащая 60 градусов, а также 90 градусов, называется основанием.
Перпендикулярный или противоположный: Сторона, перпендикулярная основанию, не содержащая 60 градусов, называется перпендикулярной или противоположной стороной прямоугольного треугольника.
\[\sin \left( \theta \right) = \frac{{opposite}}{{Гипотенуза}}\]
\[\cos \left( \theta \right) = \frac{{ Смежный}}{{Гипотенуза}}\]
Здесь = 60 градусов. 9
Таким образом, frac{{\sin\left(\theta \right)}}{{\cos\left(\theta \right)}} = \frac{{\frac{{напротив}}{{гипотенуза}}}}{{ \frac{{Смежный}}{{Гипотенуза}}}} = \frac{{Противоположный}}{{Смежный}} = \tan \left( \theta \right)\]
\[\tan \left ( \theta \right) = \frac{{Противоположный}}{{Смежный}}\]
Следовательно, значение tan 60 = Противоположный / Смежный. 9\circ \]Это означает, что AD=AD
9\circ \]Это означает, что AD=AD
Теперь возникает вопрос, каково значение тангенса 60 градусов. Итак, мы знаем, что согласно AAS Congruence,
\[\Delta {\text{ }}ABD{\text{ }} \cong {\text{ }}\Delta {\text{ }}ACD\]
Отсюда мы можем сказать, что
BD = DC
Возьмем AB = BC = 2a
Тогда
BD = ½ (BC) = ½ (2a) =a
Используя теорему Пифагора,
AB 2 = AD 2 — BD 2
AD 2 = AB 2 — BD 2
AD 2 = (2a) 2 — a 2
AD 2 = 4A 2 — A 2
г.
 н.э. √3/a = √3
н.э. √3/a = √3Следовательно, точное значение тангенса 60 градусов равно √3. Мы также можем получить значения Tan 0°, 30°, 45°, 90°, 180°, 270° и 360° таким же образом.
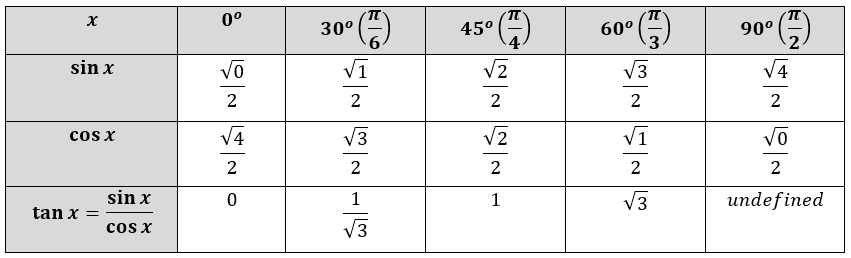
The values of the imporTant Functions of Sin can also be determined by the given method:
Simplifying in a tabular form:
0°
30°
45°
60°
90°
9 09007 9 09090 Sin06 0 \[\frac{1}{2}\]
\[\frac{1}{{\sqrt 2 }}\]
\[\frac{{\sqrt 3 }}{2}\]
1
Значение косинуса функции противоположно, если синус функции как в:
Сводная таблица значений углов синуса и косинуса:
10500°
30°
45°
60°
90°
Sin
0
\[\frac{1}{2}\]
\[\frac{{\sqrt 1}}{{\sqrt 2}}\]
\[\frac{{\sqrt 3}}{2}\]
1
Cos
1
\[\frac{{\sqrt 3}}{2}\]
\[\frac{1}{{\sqrt 2 }}\]
\[\frac{1}{2}\]
0
Отсюда мы можем найти
Угол
0o
9 30°0907
45o
60o
90o
Sin \[\theta \]
0
\[\frac{1}{2}\]
\[\frac{1}{{\sqrt 2 }}\]
\[\frac{{\sqrt 3 }}{2}\]
1
1
\[\ frac {{\ sqrt 3 }} {2} \]
\[\frac{1}{{\sqrt 2 }}\]
\[\frac{1}{2}\]
0
0 \theta \]
0
\[\frac{1}{{\sqrt 3 }}\]
1
\[\sqrt 3 \]
\ [\infty \]
Cosec \[\theta \]
\[\infty \]
2
\[\sqrt 2 \]
\[\frac{2}{{\sqrt 3 }}\]
1
Sec \[\theta \ ]
1
\[\frac{2}{{\sqrt 3 }}\]
\[\sqrt 2 \]
2
\[\infty \]
Детская кроватка \[\theta \]
\[\infty \]
\[\sqrt 3 \]
1
\[\frac{1}{{\sqrt 3 }}\]
0
Решенные Примеры:
Вопрос: Рассчитайте значение тангенса 75 градусов.

Решение: Значение тангенса 75 градусов можно рассчитать разными способами. Один из способов приведен ниже:
75 также можно рассматривать как сумму 30 и 45 (поскольку значение Tan 30 nd Tan 45 можно легко разместить в соответствии с таблицей)
tan75 = tan(30+45)
Кроме того,
tan(A+B) = (tanA + tanB)/(1 — tanATanB)
Итак, tan(30+45) = (tan30+tan45) /(1+tan30tan45)
Теперь, tan30 = 1/✓3
И, tan45 = 1
tan(30+45) = (1/✓3 + 1)/(1+ 1/✓3)
Следовательно, tan75 = (1 + 1/✓3)²
Итак, tan75 = 1 + 1/3 + 2/✓3
tan75 = 4/3 + 2/✓3
Таким образом, tan75 = (4 ✓3 + 6)/3✓3
Значение ✓3 равно 1,73205
Итак, tan75 = 12,9282/5,19615 = 2,4880344
Таким образом, приблизительное значение tan75 равно 2,4880344
Tan 60 градусов — Найдите значение Tan 60 градусов
LearnPracticeDownload
Значение tan 1,5 60320 градусов .
 . . Тангенс 60 градусов в радианах записывается как тангенс (60° × π/180°), то есть тангенс (π/3) или тангенс (1,047197…). В этой статье мы обсудим методы определения значения тангенса 60 градусов на примерах.
. . Тангенс 60 градусов в радианах записывается как тангенс (60° × π/180°), то есть тангенс (π/3) или тангенс (1,047197…). В этой статье мы обсудим методы определения значения тангенса 60 градусов на примерах.- Желто-коричневый 60°: √3
- Tan 60° в десятичной системе: 1,7320508. . .
- Желто-коричневый (-60 градусов): -1,7320508. . . или -√3
- Tan 60° в радианах: tan (π/3) или tan (1,0471975 . . .)
Сколько стоит Тан 60 градусов?
Значение тангенса 60 градусов в десятичном виде равно 1,732050807. . .. Tan 60 градусов также можно выразить с помощью эквивалента заданного угла (60 градусов) в радианах (1,04719 . . .)
Мы знаем, используя преобразование градусов в радианы, что θ в радианах = θ в градусах × (пи/ 180°)
⇒ 60 градусов = 60° × (π/180°) рад = π/3 или 1,0471. . .
∴ тангенс 60° = тангенс (1,0471) = √3 или 1,7320508. . .
. .Пояснение:
Для тангенса 60 градусов угол 60° лежит между 0° и 90° (первый квадрант). Поскольку функция тангенса положительна в первом квадранте, значение тангенса 60° = √3 или 1,7320508. . .
Поскольку функция тангенса является периодической функцией, мы можем представить тангенс 60° как тангенс 60 градусов = тангенс (60° + n × 180°), n ∈ Z.
⇒ тангенс 60° = тангенс 240° = тангенс 420° и так далее.
Примечание: Поскольку тангенс является нечетной функцией, значение тангенса (-60°) = -тангенса (60°).Методы определения значения Tan 60 градусов
Функция тангенса положительна в 1-м квадранте. Значение тангенса 60° указано как 1,73205. . .. Мы можем найти значение тангенса 60 градусов по:
- Используя тригонометрические функции
- Использование единичного круга
Тангенс 60° в терминах тригонометрических функций
Используя формулы тригонометрии, мы можем представить тангенс 60° как:
- sin(60°)/cos(60°)
- ± sin 60°/√(1 — sin²(60°))
- ± √(1 — cos²(60°))/cos 60°
- ± 1/√(косек²(60°) — 1)
- ± √(сек²(60°) — 1)
- 1/кровать 60°
Примечание.
 Поскольку 60° лежит в 1-м квадранте, окончательное значение тангенса 60° будет положительным.
Поскольку 60° лежит в 1-м квадранте, окончательное значение тангенса 60° будет положительным.Мы можем использовать тригонометрические тождества для представления tan 60° как
- cot(90° — 60°) = cot 30°
- -кроватка(90° + 60°) = -cot 150°
- -тангенс (180° — 60°) = -тангенс 120°
Tan 60 градусов с использованием единичной окружности
Чтобы найти значение tan 60 градусов с помощью единичной окружности:
- Поверните ‘r’ против часовой стрелки, чтобы образовать угол 60° с положительной осью x.
- Тангенс 60 градусов равен координате y (0,866), деленной на координату x (0,5) точки пересечения (0,5, 0,866) единичной окружности и r.
Следовательно, значение тангенса 60° = y/x = 1,7321 (приблизительно).
☛ Также проверьте:
- загар 53 градуса
- загар 40 градусов
- загар 12 градусов
- загар 210 градусов
- загар 900 градусов
- загар 1260 градусов
Примеры использования Tan 60 градусов
Пример 1: Упростить: 4 (tan 60°/cot 30°)
Решение:
Мы знаем, что tan 60° = cot 30°
⇒ 4 tan 60°/cot 30° = 4 (tan 60°/tan 60°)
= 4(1) = 4Пример 2.
 Найдите значение tan 60°, если cot 60° равно 0,5773.
Найдите значение tan 60°, если cot 60° равно 0,5773. Решение:
Так как tan 60° = 1/cot 60°
⇒ тангенс 60° = 1/0,5773 = 1,7321Пример 3: Используя значение tan 60°, найдите: (sec²(60°) — 1).
Решение:
Мы знаем, (sec²(60°) — 1) = (tan²(60°)) = 3
⇒ (сек²(60°) — 1) = 3
перейти к слайдуперейти к слайдуперейти к слайду
Готовы увидеть мир глазами математика?
Математика лежит в основе всего, что мы делаем. Наслаждайтесь решением реальных математических задач на живых уроках и станьте экспертом во всем.
Запишитесь на бесплатный пробный урок
Часто задаваемые вопросы о Tan 60 Degrees
Что такое Tan 60 Degrees?
Тангенс 60 градусов — значение тангенса тригонометрической функции для угла, равного 60 градусам.


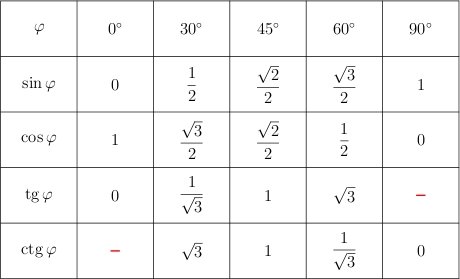 После этого мы дадим таблицу синусов и косинусов, а также таблицу тангенсов и котангенсов В. М. Брадиса, и покажем, как использовать эти таблицы при нахождении значений тригонометрических функций.
После этого мы дадим таблицу синусов и косинусов, а также таблицу тангенсов и котангенсов В. М. Брадиса, и покажем, как использовать эти таблицы при нахождении значений тригонометрических функций.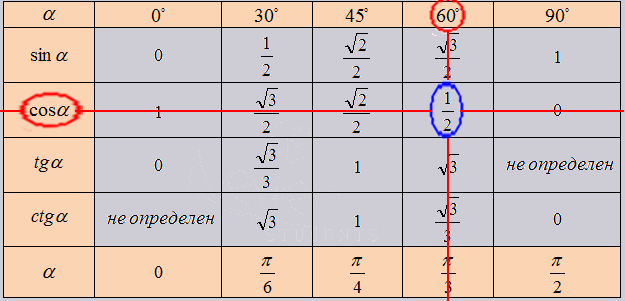 Математика (пособие для поступающих в техникумы): Учеб. пособие.- М.; Высш. шк., 1984.-351 с., ил.
Математика (пособие для поступающих в техникумы): Учеб. пособие.- М.; Высш. шк., 1984.-351 с., ил.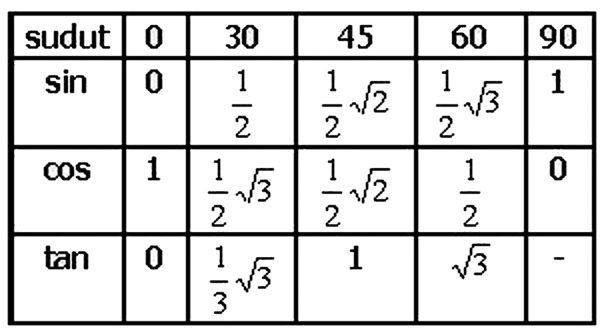 Получим:
Получим: 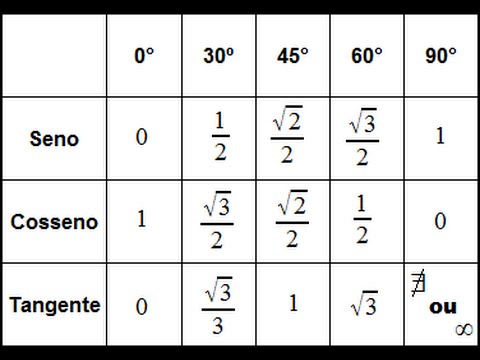 Но в данной таблице возможно узнать сколько составит тангенс от угла в 1020 градусов, он = -√3 Проверим 1020 0 = 300 0 +360 0 *2. Найдем по таблице.
Но в данной таблице возможно узнать сколько составит тангенс от угла в 1020 градусов, он = -√3 Проверим 1020 0 = 300 0 +360 0 *2. Найдем по таблице.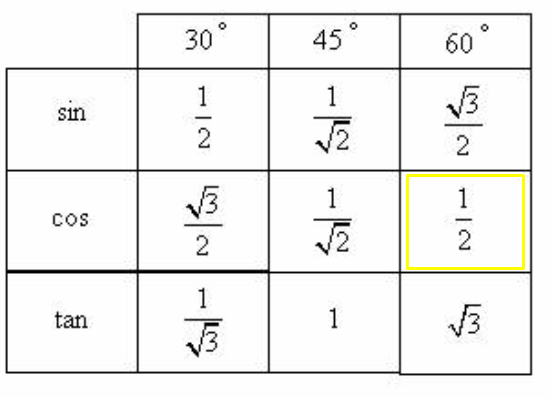 Берем за основу 42 и воспользуемся добавочными столбцами в правой стороне, берем 2 поправку и добавляем к 0,3040 + 0,0006 получаем 0,3046.
Берем за основу 42 и воспользуемся добавочными столбцами в правой стороне, берем 2 поправку и добавляем к 0,3040 + 0,0006 получаем 0,3046.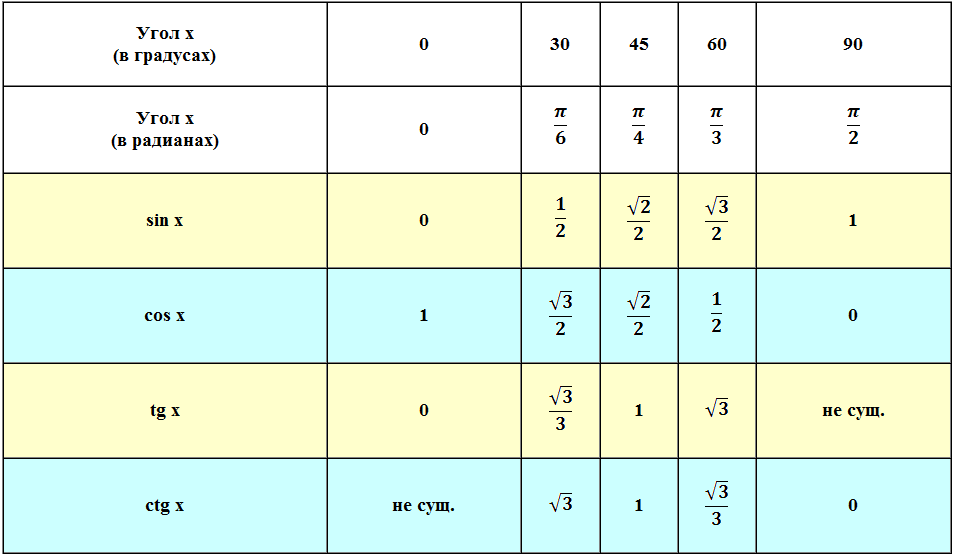 Для обозначения дроби — символ «/».
Для обозначения дроби — символ «/».  Например, найдем угол 60 градусов в первой строке и под ним прочитаем его значение в радианах. 60 градусов равно π/3 радиан.
Например, найдем угол 60 градусов в первой строке и под ним прочитаем его значение в радианах. 60 градусов равно π/3 радиан. Если же прочерка нет — клетка пуста, значит мы еще не внесли нужное значение. Мы интересуемся, по каким запросам к нам приходят пользователи и дополняем таблицу новыми значениями, несмотря на то, что текущих данных о значениях косинусов, синусов и тангенсов самых часто встречающихся значений углов вполне достаточно для решения большинства задач.
Если же прочерка нет — клетка пуста, значит мы еще не внесли нужное значение. Мы интересуемся, по каким запросам к нам приходят пользователи и дополняем таблицу новыми значениями, несмотря на то, что текущих данных о значениях косинусов, синусов и тангенсов самых часто встречающихся значений углов вполне достаточно для решения большинства задач. н.э. √3/a = √3
н.э. √3/a = √3
 . . Тангенс 60 градусов в радианах записывается как тангенс (60° × π/180°), то есть тангенс (π/3) или тангенс (1,047197…). В этой статье мы обсудим методы определения значения тангенса 60 градусов на примерах.
. . Тангенс 60 градусов в радианах записывается как тангенс (60° × π/180°), то есть тангенс (π/3) или тангенс (1,047197…). В этой статье мы обсудим методы определения значения тангенса 60 градусов на примерах. . .
. . Поскольку 60° лежит в 1-м квадранте, окончательное значение тангенса 60° будет положительным.
Поскольку 60° лежит в 1-м квадранте, окончательное значение тангенса 60° будет положительным.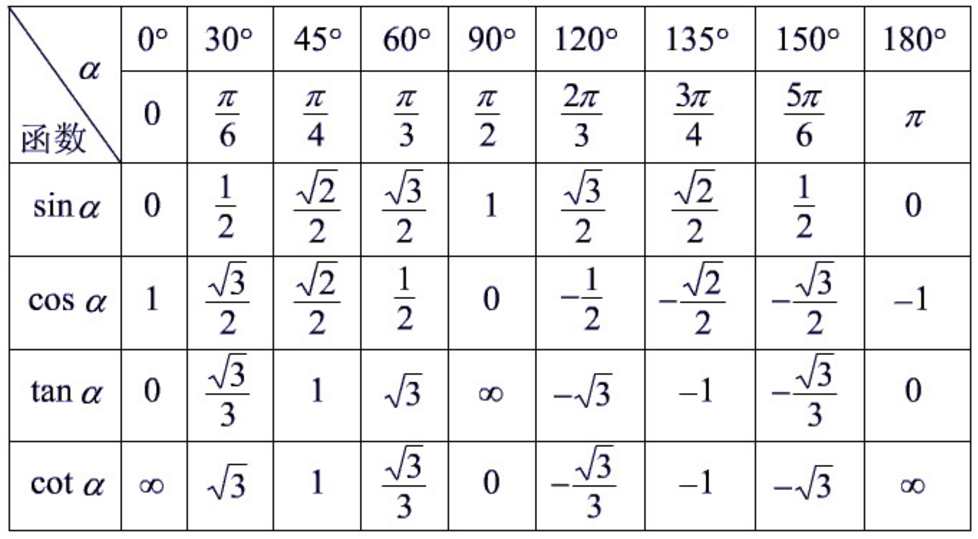 Найдите значение tan 60°, если cot 60° равно 0,5773.
Найдите значение tan 60°, если cot 60° равно 0,5773.