Лучший ответ по мнению автора | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||
Другие ответы
| ||||||||||||
| ||||||||||||
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||
Посмотреть всех экспертов из раздела Учеба и наука > Математика
| Похожие вопросы |
до перерыва шахматисты играли 4/5. ..
..
Решено
В саду растут 128 деревьев груш,что в 3 раза меньше, чем яблонь.На сколько больше в саду яблонь,чем деревьев груш.
по норме маляр за 4…
Решено
Через вершину конуса проведена плоскость, пересекающая основание по хорде, длина которой равна 3 см, и стягивающей дугу 120°. Плоскость сечения…
Решено
Высота конуса равна 6 см, угол при вершин осевого сечения равен 120 градусов. Найдите 1) площадь сечения конуса плоскостью проходящей через две…
Пользуйтесь нашим приложением
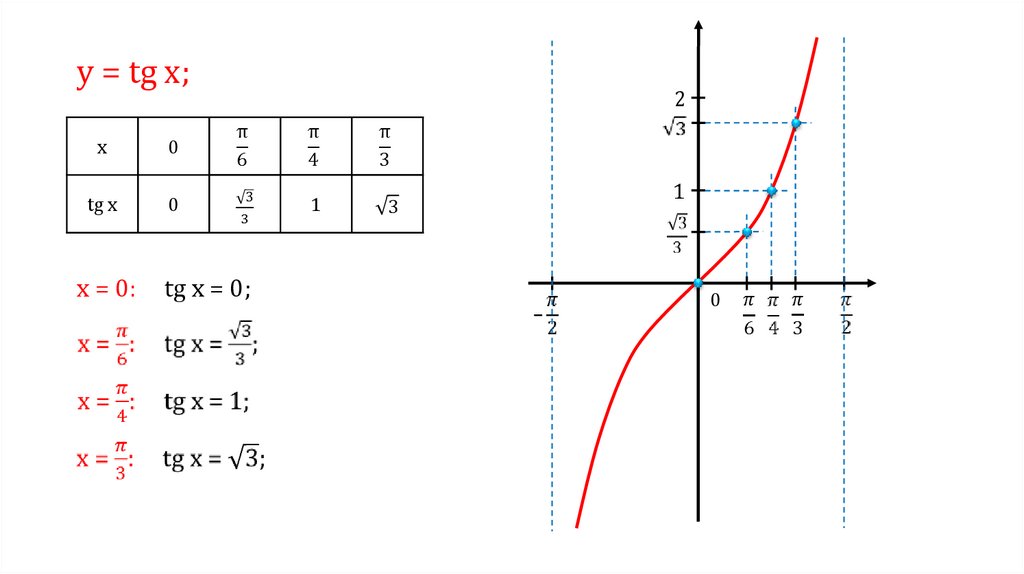
график и свойства функции, область определения, уравнение функции и его решение
Что такое функция y = tgx
ОпределениеТангенсом угла α называют такое число, которое равно отношению синуса угла α к косинусу данного угла, при α≠π/2+π,k∈Z.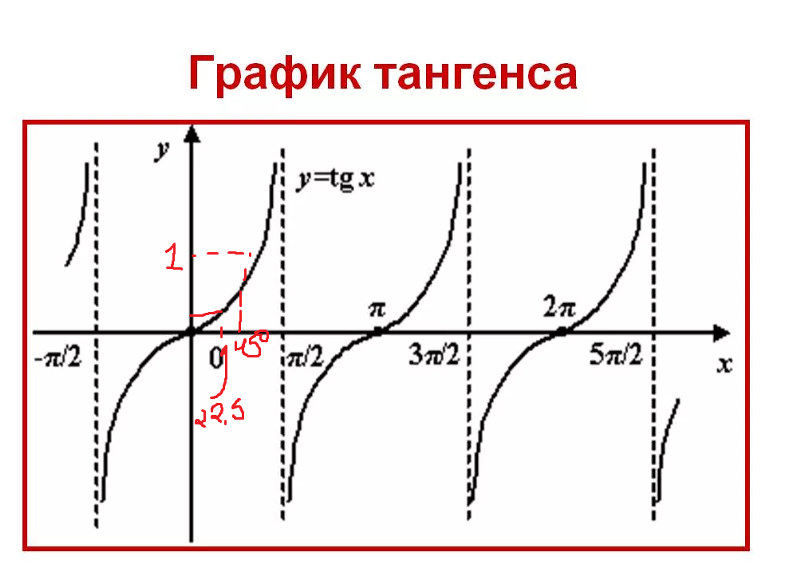
Тангенс угла α обозначают, как tgα.
Любое значение х, за исключением x=π/2+π,k∈Z, взаимно и однозначно соответствует значению у = tg x. Таким образом, будет задана функция у = tg x. Данная функция обладает определенными свойствами, которые являются следствием свойств функций у = sin x и у = cos x.
Перечислим типичные для функции у = tg x свойства:
- Область определения x≠π2+πk являются числа из множества действительных, за исключением таких точек, в которых cos x принимает нулевые значения.
- У функции отсутствуют какие-либо ограничения в нижней и верхней частях. Область значений соответствует y∈ℝ.
- Функция является нечетной tg (-x)=-tg x.
- Функция является периодической, период равен pi; при этом tg(x+πk)=tgx.
- Сближение с левой стороны с точками x=π2+πk демонстрирует стремление функции к+∞. Сближение с левой стороны с точкой а принято записывать в виде x→a-0limx→π2+πk-0tgx=+∞. Сближение с правой стороны с точками x=π2+πk демонстрирует стремление функции -∞.
 Сближение с правой стороны с точкой а принято записывать в виде x→a+0limx→π2+πk+0tgx=-∞. Нулями функции y0=0 являются точки x0=πk.
Сближение с правой стороны с точкой а принято записывать в виде x→a+0limx→π2+πk+0tgx=-∞. Нулями функции y0=0 являются точки x0=πk. - Можно наблюдать возрастание функции на всей области определения.
- Функция разрывается в точках x=π2+πk, данные точки пересекают вертикальные асимптоты. На отрезках, разделяющих асимптоты, -π2+πk; π2+πk функция не прерывается.
Источник: belmathematics.by
Графическое изображение функции у = tg x можно наблюдать на рисунке выше. Заметим, что график имеет вид совокупности линий, которые симметричны по отношению к точке начала координат, и обладает асимптотами, расположенными вертикально, x=π/2+πn,n∈Z.
Таблица значений для функции y = tgx
В процессе решения задач часто требуется определить значение функции у = tg x, когда известно значение х, либо наоборот. Тогда пригодится простая таблица:
Источник: ppt-online.org
Как решать уравнение y = tgx
Пример 1Решением уравнения вида:
tg x = a
является:
x=arctga+πk,k∈Z
Например, представим, что:
tg x = 2
Воспользуемся формулой:
x=arctga+πk,k∈Z
В результате:
x=arctg2+πk,k∈Z
Алгоритм решения уравнения y = tgx с помощью тригонометрической окружности:
- построение окружности, оси синусов, косинусов, тангенсов;
- перенос на ось тангенсов значения, которому соответствует тангенс по условию;
- построение прямой через центральную точку окружности и точку, расположенную на оси тангенсов;
- определить, чему равна одна из точек на окружности;
- записать ответ с помощью соотношения x=t0+πn,n∈Z, при t0, которое равно значению, найденному на шаге алгоритма.

При решении тригонометрических уравнений пригодятся специальные формулы, объясняющие связь между тригонометрическими функциями.
Пример 2К примеру:
tg x=sinxcosx
Рассмотрим несколько самых простых тригонометрических тождеств. Известно, что синус и косинус представляют собой обозначение ординаты и абсциссы точки соответственно. Данная точка соответствует на единичной окружности углу α. Если воспользоваться уравнением единичной окружности x2+y2=1) или теоремой Пифагора, то получим следующее соотношение:
sin2α+cos2α=1.
В итоге получилось записать основное тригонометрическое тождество. Данную формулу можно применять с целью выражения тригонометрических функций, в том числе tg x. При делении данного тождества на квадрат косинуса и синуса соответственно, можно вывести следующие справедливые равенства:
Если вспомнить, что обозначают термины тангенса и котангенса, то получится следующее:
При неизменном аргументе допустимо выражать какую-либо тригонометрическую функцию с помощью другой тригонометрической функции с таким же аргументом. Если 0<x<π/2, то:
Если 0<x<π/2, то:
tgx= sinx1-sin2x
tgx= 1-cos2xcosx
tgx= 1ctgx
tgx= sec2x-1
tgx= 1cosec2x-1
Важным соотношением тригонометрических функций, которое пригодится при решении заданий, является:
tg x=sinxcosx=2tgx21-tg2x2,
Примеры решения заданий
Задача 1Найти корни уравнения:
tgx=-3
Решение
В данном случае решения соответствуют бесконечному множеству:
x=2π3+πk, k∈ℤ
Ответ: x=2π3+πk, k∈ℤ
Задача 2Найти корни уравнения:
tgx-π2=0
Решение
x-π2=πk
Корни уравнения соответствуют бесконечному множеству:
x=π2+πk, k∈ℤ
Ответ: x=π2+πk, k∈ℤ
Задача 3Требуется решить следующее уравнение:
tg(2x)=1
Решение
2x=π4+πk
Решением данного уравнения является бесконечное множество:
x=π8+πk2, k∈ℤ
Ответ: x=π8+πk2, k∈ℤ
Задача 4Дано уравнение, которое требуется решить:
tgx3-1=-1
Решение
x3-1=-π4+πk
x3=1-π4+πk
Уравнение обладает бесконечным множеством решений:
x=3-3π4+3πk, k∈ℤ
Ответ: x=3-3π4+3πk, k∈ℤ
Задача 5Дана функция, четность которой необходимо определить:
y(x)=4tgx+5sinx
Решение
y(-x)=4tg(-x)+5sin(-x)=-4tg x-5 sin x=-(4tg x+5sin x)=-y(x)
Ответ: функция является нечетной.
Имеется функция, четность которой необходимо определить:
y(x)=tg x-2cos x
Решение
Ответ: функция не является ни четной, ни нечетной.
Задача 7Нужно определить четность следующей функции:
y(x)=tg2x+cos5x
Решение
y(-x)=tg2(-x)+cos(-5x)=(-tgx)2+cos5x=tg2x+cos5x)=y(x)
Ответ: данная функция является четной.
Задача 8Требуется определить, является ли четной данная функция:
y(x)=x2-tgx
Решение
Ответ: функция не является ни четной, ни нечетной.
Задача 9Требуется вычислить значения tgx, ctgx при условии, что:
tg(7π-x)=34
Решение
Зная, что период тангенса составляет pi, запишем, что:
Ответ: -34, -43.
| 1 | Найти точное значение | грех(30) | |
| 2 | Найти точное значение | грех(45) | |
| 3 | Найти точное значение | грех(30 градусов) | |
| 4 | Найти точное значение | грех(60 градусов) | |
| 5 | Найти точное значение | загар (30 градусов) | |
| 6 | Найти точное значение | угловой синус(-1) | |
| 7 | Найти точное значение | грех(пи/6) | |
| 8 | Найти точное значение | cos(pi/4) | |
| 9 | Найти точное значение | грех(45 градусов) | |
| 10 | Найти точное значение | грех(пи/3) | |
| 11 | Найти точное значение | арктан(-1) | |
| 12 | Найти точное значение | cos(45 градусов) | |
| 13 | Найти точное значение | cos(30 градусов) | |
| 14 | Найти точное значение | желтовато-коричневый(60) | |
| 15 | Найти точное значение | csc(45 градусов) | |
| 16 | Найти точное значение | загар (60 градусов) | |
| 17 | Найти точное значение | сек(30 градусов) | |
| 18 | cos(60 градусов) | ||
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | грех(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | загар (45 градусов) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 градусов) | |
| 25 | Найти точное значение | сек(45 градусов) | |
| 26 | Найти точное значение | csc(30 градусов) | |
| 27 | Найти точное значение | грех(0) | |
| 28 | Найти точное значение | грех(120) | |
| 29 | Найти точное значение | соз(90) | |
| 30 | Преобразовать из радианов в градусы | пи/3 | |
| 31 | Найти точное значение | желтовато-коричневый(30) | |
| 32 | 92|||
| 35 | Преобразовать из радианов в градусы | пи/6 | |
| 36 | Найти точное значение | детская кроватка(30 градусов) | |
| 37 | Найти точное значение | арккос(-1) | |
| 38 | Найти точное значение | арктан(0) | |
| 39 | Найти точное значение | детская кроватка(60 градусов) | |
| 40 | Преобразование градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2 шт. )/3 )/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | тан(пи/2) | |
| 45 | Найти точное значение | грех(300) | |
| 46 | Найти точное значение | соз(30) | |
| 47 | Найти точное значение | соз(60) | |
| 48 | Найти точное значение | соз(0) | |
| 49 | Найти точное значение | соз(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | сек(60 градусов) | |
| 53 | Найти точное значение | грех(300 градусов) | |
| 54 | Преобразование градусов в радианы | 135 | |
| 55 | Преобразование градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5 дюймов)/6 | |
| 57 | Преобразовать из радианов в градусы | (5 дюймов)/3 | |
| 58 | Преобразование градусов в радианы | 89 градусов | |
| 59 | Преобразование градусов в радианы | 60 | |
| 60 | Найти точное значение | грех(135 градусов) | |
| 61 | Найти точное значение | грех(150) | |
| 62 | Найти точное значение | грех(240 градусов) | |
| 63 | Найти точное значение | детская кроватка(45 градусов) | |
| 64 | Преобразовать из радианов в градусы | (5 дюймов)/4 | |
| 65 | Найти точное значение | грех(225) | |
| 66 | Найти точное значение | грех(240) | |
| 67 | Найти точное значение | cos(150 градусов) | |
| 68 | Найти точное значение | желтовато-коричневый(45) | |
| 69 | Оценить | грех(30 градусов) | |
| 70 | Найти точное значение | сек(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | КСК(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | загар((5pi)/3) | |
| 75 | Найти точное значение | желтовато-коричневый(0) | |
| 76 | Оценить | грех(60 градусов) | |
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3 пи)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | угловой синус(-1/2) | |
| 81 | Найти точное значение | sin((4pi)/3) | |
| 82 | Найти точное значение | КСК(45) | |
| 83 | Упростить | арктан(квадратный корень из 3) | |
| 84 | Найти точное значение | грех(135) | |
| 85 | Найти точное значение | грех(105) | |
| 86 | Найти точное значение | грех(150 градусов) | |
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | загар((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | пи/4 | |
| 90 | Найти точное значение | грех(пи/2) | |
| 91 | Найти точное значение | сек(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | угловой синус(0) | |
| 95 | Найти точное значение | грех(120 градусов) | |
| 96 | Найти точное значение | желтовато-коричневый ((7pi)/6) | |
| 97 | Найти точное значение | соз(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразование градусов в радианы | 88 градусов |
тригонометрия — Что означает $\tan x = 1$?
спросил
Изменено 9 лет, 3 месяца назад
Просмотрено 3к раз
$\begingroup$
Я могу найти $x$, взяв арктангенс обеих сторон, но я не понимаю, что означает уравнение.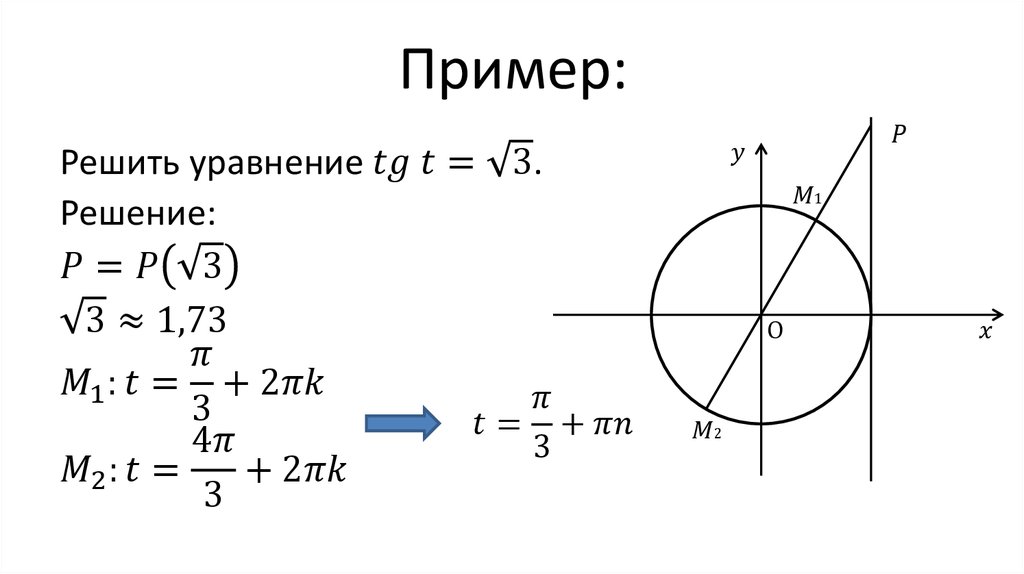 Представляет ли уравнение пересечение между $y = \tan x$ и $y =1$? Точно так же $\sin x = 2$ считается неопределенным, поскольку две кривые не пересекаются ни при каком действительном $x$ (они не пересекают друг друга?). Я чувствую, что мне не хватает ключевого понятия в тригонометрических уравнениях.
Представляет ли уравнение пересечение между $y = \tan x$ и $y =1$? Точно так же $\sin x = 2$ считается неопределенным, поскольку две кривые не пересекаются ни при каком действительном $x$ (они не пересекают друг друга?). Я чувствую, что мне не хватает ключевого понятия в тригонометрических уравнениях.
Также, чтобы найти другие решения $\tan x = 1$, нужно ли просто вычесть или добавить $\pi$ к основному значению?
Спасибо
- тригонометрия
$\endgroup$
6
$\begingroup$
Решить уравнение $\tan x=1$ означает найти каждый угол $x$, тангенс которого равен $1$. Вы можете начать с $\frac{\pi}4$, главного арктангенса $1$; тангенс имеет период $\pi$, поэтому (как вы сказали) вам нужно добавить к нему целые числа, кратные $\pi$, чтобы получить весь набор решений:
$$\left\{\frac{\pi}4+n\pi:n\in\Bbb Z\right\}\;.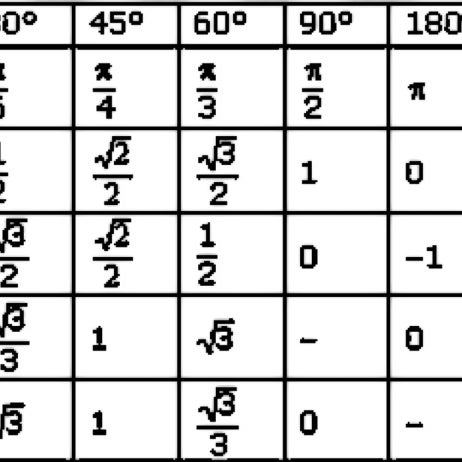 $$
$$
Если вас попросят решить $\sin x=2 $ можно с уверенностью сказать, что множество решений пусто ($\varnothing$), так как $|\sin x|\le 1$ для всех $x\in\Bbb R$.
Ни в том, ни в другом случае на самом деле нет необходимости думать в терминах графов, хотя это, безусловно, возможно: множество решений $\tan x=1$ на самом деле является множеством $x\in\Bbb R$, где графики $y=\tan x$ и $y=1$ пересекаются, и аналогично для $\sin x=1$.
$\endgroup$
3
$\begingroup$
$\tan{x}$ — отношение $\sin{x}$ к $\cos{x}$. Наличие $\tan{x}=1$ означает, что $\sin{x}=\cos{x}$.
Теперь, какие углы дают этот результат?
$\endgroup$
$\begingroup$
Каково ваше определение касательной функции? Это синус, деленный на косинус, что точно так же, как знаменитая формула наклона «подъем относительно пробега».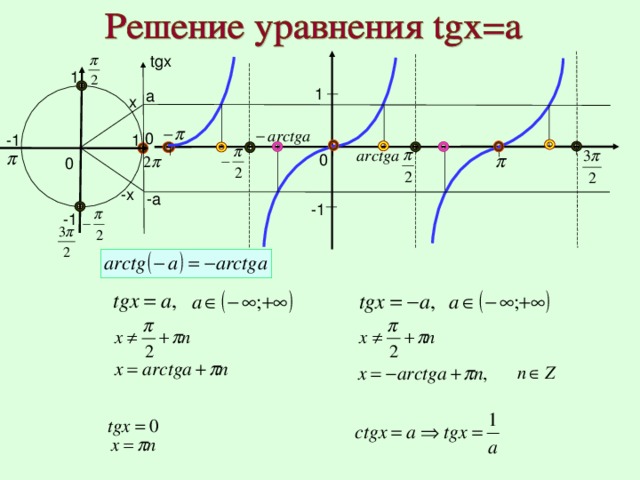

 01.15
01.15 01.15
01.15 01.15
01.15 Сближение с правой стороны с точкой а принято записывать в виде x→a+0limx→π2+πk+0tgx=-∞. Нулями функции y0=0 являются точки x0=πk.
Сближение с правой стороны с точкой а принято записывать в виде x→a+0limx→π2+πk+0tgx=-∞. Нулями функции y0=0 являются точки x0=πk.