Лучший ответ по мнению автора | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||
03.16Другие ответы
| ||||||||||||
03.16
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||
Посмотреть всех экспертов из раздела Учеба и наука
| Похожие вопросы |
решение задачи: масса трёх моржей на 170 кг больше, чем масса трёх морских котиков и на 50 кг меньше, чем масса 4 котиков.
2-4 в точке x нулевое = 4…
Математика
Литература
Алгебра
Геометрия
Английский язык
Химия
Физика
Биология
Другие предметы
История
Обществознание
Окружающий мир
География
Українська мова
Українська література
Қазақ тiлi
Беларуская мова
Информатика
Экономика
Музыка
Право
Французский язык
Немецкий язык
МХК
ОБЖПсихология
Исчисление III.
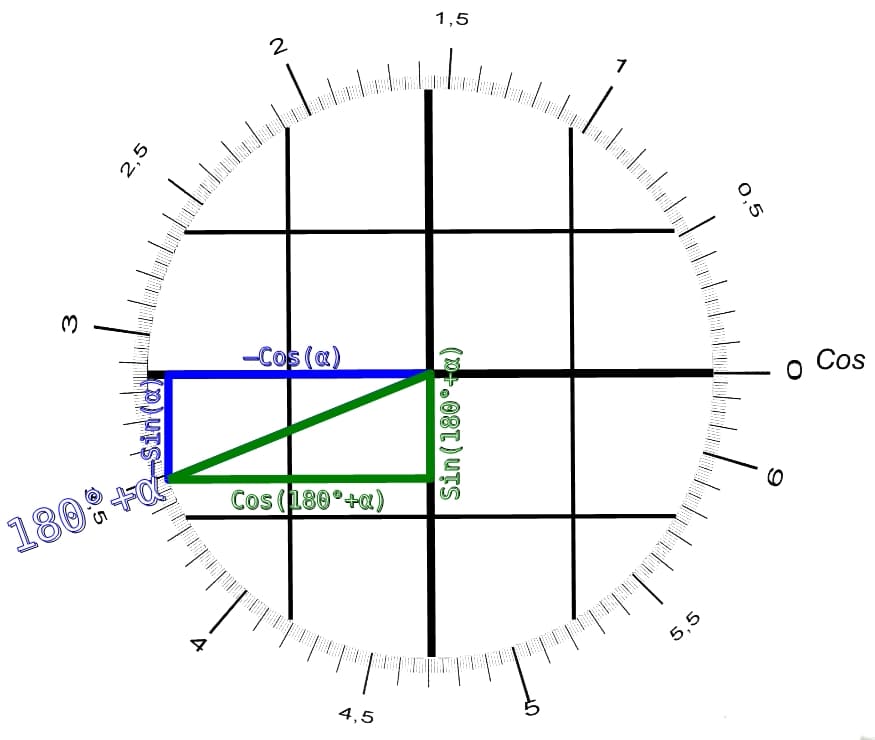Касательные, нормальные и бинормальные векторы Онлайн-заметки Пола
Главная
/
Исчисление III
/
Трехмерное пространство
/ Касательные, нормальные и бинормальные векторы
Показать мобильное уведомление Показать все примечания Скрыть все примечания
Мобильное уведомление
Похоже, вы используете устройство с «узкой» шириной экрана ( т. е. вы, вероятно, используете мобильный телефон). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.
Раздел 1-8: Касательные, нормальные и бинормальные векторы
В этом разделе мы хотим рассмотреть применение производных для векторных функций. На самом деле есть пара приложений, но все они возвращаются к необходимости первого.
В прошлом мы использовали тот факт, что производной функции был наклон касательной. С векторными функциями мы получаем точно такой же результат, за одним исключением.
Учитывая векторную функцию \(\vec r\left( t \right)\), мы называем \(\vec r’\left( t \right)\) касательным вектором , если он существует и если \(\vec r’\left( t \right) \ne \vec 0\). Касательная линия к \(\vec r\left( t \right)\) в \(P\) — это линия, которая проходит через точку \(P\) и параллельна касательному вектору, \(\vec г’\влево( т \вправо)\). Обратите внимание, что нам действительно нужно требовать \(\vec r’\left( t \right) \ne \vec 0\) для того, чтобы иметь касательный вектор. Если бы у нас было
\[\vec r’\left( t \right) = \vec 0\]у нас был бы вектор, который не имел величины и поэтому не мог бы дать нам направление касательной.
2}\,\vec i + 2\sin t\,\ vec j + 2\cos t\,\vec k\).
Показать решение
Во-первых, под общей формулой мы подразумеваем, что мы не будем подставлять конкретную \(t\), и поэтому мы найдем формулу, которую мы сможем использовать позже, если мы хотим найти тангенс в точке любую точку на кривой. С учетом сказанного, на данный момент на самом деле не так уж много нужно сделать, кроме как выполнять работу.
Вот касательный вектор к кривой.
\[\vec r’\left( t \right) = 2t\,\vec i + 2\cos t\,\vec j — 2\sin t\,\vec k\] 92}\,\vec i + 2\sin t\,\vec j + 2\cos t\,\vec k\) в \(\displaystyle t = \frac{\pi} {3}\).
Показать решение
Во-первых, нам нужен касательный вектор, и, поскольку это функция, с которой мы работали в предыдущем примере, мы можем просто повторно использовать касательный вектор из этого примера и подставить \(t = \frac{\pi }{3}\ ).
\[\ vec r ‘\ влево ( {\ frac {\ pi} {3}} \ right) = \ frac {{2 \ pi}} {3} \, \ vec i + 2 \ cos \ влево ( {\ frac{\pi} {3}} \right)\,\vec j — 2\sin \left( {\frac{\pi} {3}} \right)\,\vec k = \frac{{2\ pi }}{3}\,\vec i + \vec j — \sqrt 3 \,\vec k\] 92}}}{9},\sqrt 3 ,1} \right\rangle + t\left\langle {\ frac{{2\pi}}}{3},1, — \sqrt 3} \right\rangle \ ]
Прежде чем двигаться дальше, давайте отметим пару вещей о предыдущем примере. Во-первых, мы могли бы использовать единичный касательный вектор, если бы захотели, для параллельного вектора. Однако это привело бы к более сложному уравнению для касательной.
Во-вторых, обратите внимание, что мы использовали \(\vec r\left( t \right)\) для представления касательной линии, несмотря на то, что мы использовали ее и для функции. Не волнуйтесь по этому поводу. \(\vec r\left( t \right)\) здесь очень похоже на \(y\) с нормальными функциями. В случае нормальных функций \(y\) — это общая буква, которую мы использовали для обозначения функций, а \(\vec r\left( t \right)\) имеет тенденцию использоваться таким же образом с векторными функциями.
Далее нам нужно поговорить о единичных нормальных и бинормальных векторах.
Единичный вектор нормали определен как
\[\vec N\left( t \right) = \frac{{\vec T’\left( t \right)}}{{\left\| {\ vec T ‘\ влево ( т \ вправо)} \ вправо \ |}} \]
Единичная нормаль ортогональна (или нормальна, или перпендикулярна) к единичному касательному вектору и, следовательно, к кривой. Мы уже видели векторы нормалей, когда имели дело с уравнениями плоскостей. Они будут появляться с некоторой регулярностью в нескольких темах Calculus III.
Определение единичного вектора нормали всегда кажется немного загадочным, когда вы впервые видите его. Это следует непосредственно из следующего факта.
Факт
Предположим, что вектор \(\vec r\left( t \right)\) такой, что \(\left\| {\vec r\left( t \right)} \right\| = c \) для всех \(t\). Тогда \(\vec r’\left( t \right)\) ортогонален \(\vec r\left( t \right)\).
Доказать этот факт довольно просто.
Из утверждения факта и отношения между величиной вектора и скалярным произведением мы имеем следующее. 92}} \справа) = 0\]
Также, вспоминая факт из предыдущего раздела о дифференцировании скалярного произведения, мы видим, что
\[\ frac{d}{{dt}}\left( {\vec r\left( t \right)\,\centerdot \,\vec r\left( t \right)} \right) = \vec r ‘\left( t \right)\,\centerdot \,\vec r\left( t \right) + \vec r\left( t \right)\,\centerdot \,\vec r’\left( t \ справа) = 2\vec r’\left( t \right)\,\centerdot \,\vec r\left( t \right)\]
Или, сложив все вместе, получим
\[2\vec r’\left( t \right)\,\centerdot \,\vec r\left( t \right) = 0\hspace{0.25in}\hspace{0.25in} \Rightarrow \hspace{0.25 in}\hspace{0.25in}\vec r’\left( t \right)\,\centerdot \,\vec r\left( t \right) = 0\]
Следовательно, \(\vec r’\left( t \right)\) ортогонален \(\vec r\left( t \right)\).
Определение единицы нормального затем вытекает непосредственно из этого. Поскольку \(\vec T\left( t \right)\) является единичным вектором, мы знаем, что \(\left\| {\vec T\left( t \right)} \right\| = 1\) для всех \(t\) и, следовательно, по факту \(\vec T’\left( t \right)\) ортогонален \(\vec T\left( t \right)\). Однако, поскольку \(\vec T\left( t \right)\) касается кривой, \(\vec T’\left( t \right)\) также должен быть ортогонален или нормален к кривой. и, таким образом, быть нормальным вектором для кривой. Все, что нам нужно сделать, это разделить на \(\left\| {\vec T’\left( t \right)} \right\|\), чтобы получить единичный вектор нормали.
Далее идет вектор бинормалей. Вектор бинормалей определяется как
\[\vec B\left( t \right) = \vec T\left( t \right) \times \vec N\left( t \right)\]
Поскольку вектор бинормалей определяется как векторное произведение единичного касательного и единичного вектора нормали, мы знаем, что вектор бинормали ортогонален как касательному вектору, так и вектору нормали.
Пример 3 Найдите вектор нормали и бинормали для \(\vec r\left( t \right) = \left\langle {t,3\sin t,3\cos t} \right\rangle \). 92}t} = \sqrt {10} \end{align*}\]
Тогда единичный касательный вектор равен
\[\ vec T \ left( t \ right) = \ left \ langle {\ frac {1} {{\ sqrt {10}}}, \ frac {3} {\ sqrt {10}}} \ cos t , — \frac{3}{{\sqrt {10} }}\sin t} \right\rangle \]
Единичный вектор нормали теперь требует производной единичного тангенса и его модуля.
\[\begin{align*}\vec T’\left( t \right) & = \left\langle {0, — \ frac {3}{{\ sqrt {10}}} \ sin t, — \ frac {3}{{\sqrt {10}}}\cos t} \right\rangle \\ \left\| {\ vec T ‘\ влево ( т \ вправо)} \ вправо \ | & знак равно \ sqrt {\ гидроразрыва {92} t} = \ sqrt {\ frac {9} {{10}}} = \ frac {3} {{\ sqrt {10}}} \ end {align *} \]
Тогда единичный вектор нормали равен
\[\vec N\left( t \right) = \frac{{\sqrt {10}}}}{3}\left\langle {0, — \frac{3}{{\sqrt {10}}}\ sin t, — \frac{3}{{\sqrt {10} }}\cos t} \right\rangle = \left\langle {0, — \sin t, — \cos t} \right\rangle \]
Наконец, вектор бинормалей равен
\[\begin{align*}\vec B\left( t \right) & = \vec T\left( t \right) \times \vec N\left( t \right)\\ & = \left| {\ begin {array} {* {20} {c}} {\ vec i} & {\ vec j} & {\ vec k} \\ {\ frac {1} {{\ sqrt {10}}}} &{\ frac {3} {{\ sqrt {10}}} \ cos t} & { — \ frac {3} {{\ sqrt {10}}} \ sin t} \\ 0 & { — \ sin t} &{ — \cos t}\end{массив}} \right|\,\,\,\,\,\begin{массив}{*{20}{c}}{\vec i}&{\vec j }\\{\frac{1}{{\sqrt {10}}}}&{\frac{3}{{\sqrt {10}}}\cos t}\\0&{ — \sin t}\end {массив}\\ & = — \frac{3}{{\sqrt {10}}}{\cos ^2}t\,\vec i — \frac{1}{{\sqrt {10}}}\ sin t \,\vec k + \frac{1}{{\sqrt {10}}}\cos t\,\,\vec j — \frac{3}{{\sqrt {10}}}}{\sin ^ 2} t \, \ vec i \\ & = — \ frac {3} {{\ sqrt {10} }} \, \ vec i + \ frac {1} {{\ sqrt {10}}} \ cos t \,\,\vec j — \frac{1}{{\sqrt {10}}}\sin t\,\,\vec k\end{align*}\]
исчисление — Найти значения m и n в функции по касательной в точке
Задавать вопрос
спросил
Изменено 4 года, 7 месяцев назад
Просмотрено 267 раз
$\begingroup$
Вопрос: Если $y = m\sqrt{1-nx}$, (где m и n — константы), имеет касательную $6x + 2y = 10$ в точке $x = -1$.
Найдите значения m и n.
Попытка решения:
Я выделил y в обоих уравнениях и приравнял их, чтобы получить одно уравнение для m через n:
$5 — 3x = m\sqrt{1-nx}$
$m = \frac {8}{\sqrt{1+n}}$
Чтобы получить второе уравнение, я приравнял производные двух исходных уравнений и решил относительно m: 9{\frac{-1}{2}}$
$m = -6\sqrt{1+n}$
Но когда я пытаюсь найти m, я не получаю правильного ответа. Кроме того, если я помещу правильные решения для n и m во второе уравнение, это приведет к неверному утверждению.
Как найти правильное второе уравнение?
Решения: $m = 4, n = 3$
- исчисление
- производные
$\endgroup$
$\begingroup$
При различении градиент должен быть 9{-\frac12}$$
Ваша ошибка в том, что вы забыли применить цепное правило и пропустили множитель $-n$ в правой части.
Из первого уравнения имеем
$$m = \frac{8}{\sqrt{1+n}}$$
Следовательно, имеем
$$-3=-\frac{4n}{ 1+n}$$
и имеем
$$3+3n=4n$$
Отсюда $n=3$.