математика — Python | Почему тангенс π/2 = 1.633123935319537e+16?
Вопрос задан
Изменён 2 года 4 месяца назад
Просмотрен 226 раз
Почему тангенс π/2 = 1.633123935319537e+16?
Код:
import math print(math.tan(math.pi / 2))
Результат: 1.633123935319537e+16
- python
- математика
7
потому что pi — это 180 градусов, pi / 2 — это 90 градусов, а тангенс стремится к бесконечности при стремлении к 90 градусам
кроме того тангенс — это синус делить на косинус, а точность float значений все таки не абсолютная, поэтому деление на 0 может и не происходить, поэтому могут получаться какие-то конечные значения
ну и в третьих синус, косинус, тангенс и т.
д. можно вычислять (а возможно так и вычисляются) как ряд тейлора
а значит учитывая точность float будет лишь приближенное значение и в вашем случае это 1.633123935319537e+16
кстати из-за алгоритма вычисления тригонометрических функций и cos(math.pi / 2) равен не 0, а 6.123233995736766e-17
P.S.
попробовал подсчитать cos(pi / 2) через ряд Тейлора:
import math
value = math.pi / 2
res = 0
for i in range(50):
res += (-1)**i * (value**(2*i + 1) / math.factorial(2 * i))
print(res)
Вместо 0 получил 1.2246167519384833e-16 как и ожидалось
Вот график значений lg(|cos(x)|) (для удобства взял логарифмическую шкалу, чтобы лучше показать) от кол-ва шагов вычисления — видно, что после 10 шага точность не меняется (достигли предела точности чисел с плавающей запятой):
1
Можно использовать более точные библиотеки, например:
from sympy import pi, tan print(tan(pi / 2))
Вывод:
zoo (complex infinity)
Зарегистрируйтесь или войдите
Регистрация через Google
Регистрация через Facebook
Регистрация через почту
Отправить без регистрации
Почта
Необходима, но никому не показывается
Отправить без регистрации
Почта
Необходима, но никому не показывается
Нажимая на кнопку «Отправить ответ», вы соглашаетесь с нашими пользовательским соглашением, политикой конфиденциальности и политикой о куки
| 1 | Найти точное значение | грех(30) | |
| 2 | Найти точное значение | грех(45) | |
| 3 | Найти точное значение | грех(30 градусов) | |
| 4 | Найти точное значение | грех(60 градусов) | |
| 5 | Найти точное значение | загар (30 градусов) | |
| 6 | Найти точное значение | угловой синус(-1) | |
| 7 | Найти точное значение | грех(пи/6) | |
| 8 | Найти точное значение | cos(pi/4) | |
| 9 | Найти точное значение | грех(45 градусов) | |
| 10 | Найти точное значение | грех(пи/3) | |
| 11 | Найти точное значение | арктан(-1) | |
| 12 | Найти точное значение | cos(45 градусов) | |
| 13 | Найти точное значение | cos(30 градусов) | |
| 14 | Найти точное значение | желтовато-коричневый(60) | |
| 15 | Найти точное значение | csc(45 градусов) | |
| 16 | Найти точное значение | загар (60 градусов) | |
| 17 | Найти точное значение | сек(30 градусов) | |
| 18 | Найти точное значение | cos(60 градусов) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | грех(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | загар (45 градусов) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | csc(60 градусов) | ||
| 25 | Найти точное значение | сек(45 градусов) | |
| 26 | Найти точное значение | csc(30 градусов) | |
| 27 | Найти точное значение | грех(0) | |
| 28 | Найти точное значение | грех(120) | |
| 29 | Найти точное значение | соз(90) | |
| 30 | Преобразовать из радианов в градусы | пи/3 | |
| 31 | Найти точное значение | желтовато-коричневый(30) | |
| 32 | 92|||
| 35 | Преобразовать из радианов в градусы | пи/6 | |
| 36 | Найти точное значение | детская кроватка(30 градусов) | |
| 37 | Найти точное значение | арккос(-1) | |
| 38 | Найти точное значение | арктан(0) | |
| 39 | Найти точное значение | ||
| 40 | Преобразование градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2 шт. )/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | тан(пи/2) | |
| 45 | Найти точное значение | грех(300) | |
| 46 | Найти точное значение | соз(30) | |
| 47 | Найти точное значение | соз(60) | |
| 48 | Найти точное значение | соз(0) | |
| 49 | Найти точное значение | соз(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | сек(60 градусов) | |
| 53 | Найти точное значение | грех(300 градусов) | |
| 54 | Преобразование градусов в радианы | 135 | |
| 55 | Преобразование градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5 дюймов)/6 | |
| 57 | Преобразовать из радианов в градусы | (5 дюймов)/3 | |
| 58 | Преобразование градусов в радианы | 89 градусов | |
| 59 | Преобразование градусов в радианы | 60 | |
| 60 | Найти точное значение | грех(135 градусов) | |
| 61 | Найти точное значение | грех(150) | |
| 62 | Найти точное значение | грех(240 градусов) | |
| 63 | Найти точное значение | детская кроватка(45 градусов) | |
| 64 | Преобразовать из радианов в градусы | (5 дюймов)/4 | |
| 65 | Найти точное значение | грех(225) | |
| 66 | Найти точное значение | грех(240) | |
| 67 | Найти точное значение | cos(150 градусов) | |
| 68 | Найти точное значение | желтовато-коричневый(45) | |
| 69 | Оценить | грех(30 градусов) | |
| 70 | Найти точное значение | сек(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | КСК(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | загар((5pi)/3) | |
| 75 | Найти точное значение | желтовато-коричневый(0) | |
| 76 | Оценить | грех(60 градусов) | |
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3 пи)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | угловой синус(-1/2) | |
| 81 | Найти точное значение | sin((4pi)/3) | |
| 82 | Найти точное значение | КСК(45) | |
| 83 | Упростить | арктан(квадратный корень из 3) | |
| 84 | Найти точное значение | грех(135) | |
| 85 | Найти точное значение | грех(105) | |
| 86 | Найти точное значение | грех(150 градусов) | |
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | загар((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | пи/4 | |
| 90 | Найти точное значение | грех(пи/2) | |
| 91 | Найти точное значение | сек(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | угловой синус(0) | |
| 95 | Найти точное значение | грех(120 градусов) | |
| 96 | Найти точное значение | желтовато-коричневый ((7pi)/6) | |
| 97 | Найти точное значение | соз(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразование градусов в радианы | 88 градусов |
анализ — Значение тангенса (пи/2)
спросил
Изменено 6 лет, 7 месяцев назад
Просмотрено 14 тысяч раз
$\begingroup$
Я понимаю, что это очень глупый вопрос, но я не получаю ответа.
При $x=\pi/2$ каково значение $tan(x)$? Должно ли это быть $-\infty$ или $+\infty$?
Текст говорит, что это $+\infty$. Но почему?
С точки зрения геометрии получается $+\infty$. Но как объяснить график, у которого оба значения равны $\pi/2$?
- анализ
- тригонометрия
$\endgroup$
4
$\begingroup$
Ничего не должно быть, потому что там это не определено.
$\endgroup$
$\begingroup$
Вместо того, чтобы пытаться «оценить» $\tan(\pi/2)$, просто наблюдая за его графиком, почему бы не вернуться к старым добрым триггерным аргументам? Если бы вам нужно было оценить значение $\tan(\pi/2)$ на единичной окружности, вы бы, по сути, построили этот аргумент: $$ \tan(\pi/2) = \frac{\sin(\pi /2)}{\cos(\pi/2)} = \frac{1}{0} $$ Обратите внимание, что это то же самое, что запрашивать $y$-координату точки (0,1) на единице окружность, которую нужно разделить на ее $x$-координату.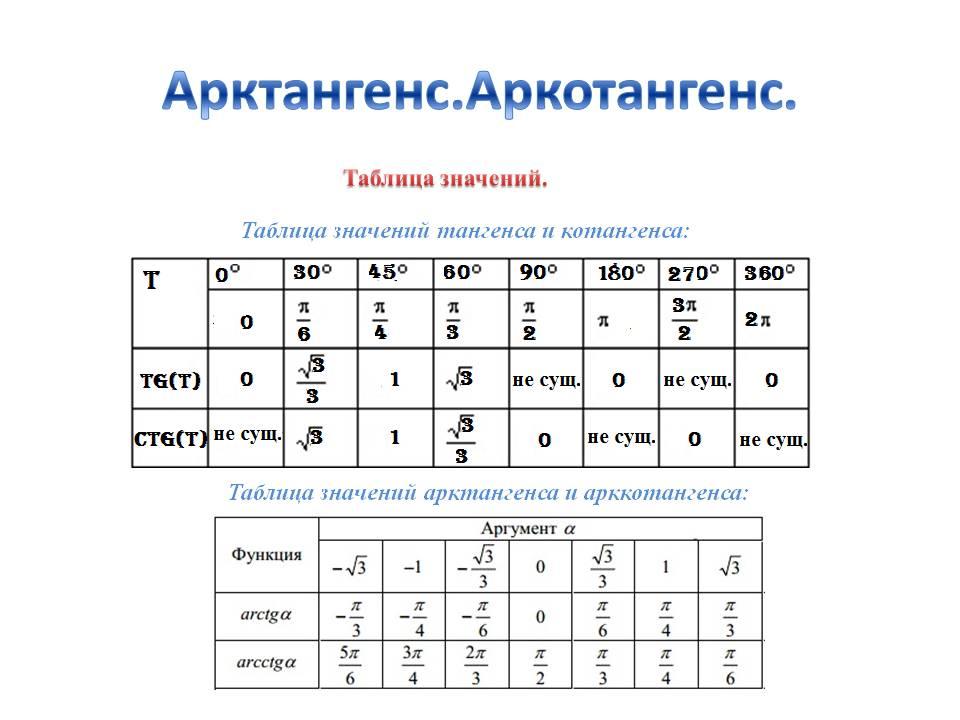
По разным причинам (см. http://en.wikipedia.org/wiki/Division_by_zero или удивительно информативное видео 9 от Numberphile).0945 Проблемы с нулем http://www.youtube.com/watch?v=BRRolKTlF6Q) математики не определили, что значит делить на ноль, потому что это значение несовместимо в различных контекстах. Таким образом, деление на ноль просто «не определено», что приводит к вашей неуверенности в том, является ли $\tan(\pi/2) = +\infty$ или $\tan(\pi/2)=-\infty$ (! )
$\endgroup$
$\begingroup$
Существует два распространенных способа «компактификации» вещественных чисел.
Первый из них вам, вероятно, больше знаком. Вы добавляете две дополнительные точки, $+\infty$ и $-\infty$, расположенные на двух «концах» числовой прямой. Это называется расширенной реальной линией. Обычно вместо $+\infty$ используется обозначение $\infty$: это вызывает некоторую путаницу с….
Вторая называется проективной вещественной прямой.