Графики тригонометрических функций. Все углы А по умолчанию приведены в градусах. Все таблицы значений и формулы синусов, косинусов, тангенсов, котангенсов (здесь). Во всех формулах пределов и разложений в ряд — углы в радианах. Графики функций y=sinA, y=cosA, y=tgA,построенные для диапазона от 0o до 360o, показаны на рисунках ниже.
Из графиков видно что:
Углы произвольной величины На рис. слева показаны перпендикулярные оси ХХ’ и YY’; пересекающиеся в начале координат О. При работе с графиками измерения вправо и вверх от О считаются положительными, влево и вниз от О — отрицательными. Пусть ОА свободно вращается относительно О. При повороте ОА против часовой стрелки измеряемый угол считается положительным, а при повороте по часовой стрелке — отрицательным.
Пусть ОА вращается против часовой стрелки таким образом, что Θ1 — любой угол в первом квадранте, и построим перпендикуляр АВ для получения прямоугольного треугольника ОАВ на рис. слева. Поскольку все три стороны треугольника положительны, тригонометрические функции синус, косинус и тангенс в первом квадранте будут положительны. (Отметим, что длина ОА всегда положительна, поскольку является радиусом круга.)  Тогда sin Θ2=+/+ = +; cos Θ2=+/- = -; tg Θ2=+/- = -. Пусть ОА вращается дальше таким образом, что Θ3 — любой угол в третьем квадранте, и построим АD так, чтобы образовался прямоугольный треугольник ОАD. Тогда sin Θ3= -/+ = -; cos Θ3= -/+ = -; tg Θ3 = -/- =+ . Тогда sin Θ2=+/+ = +; cos Θ2=+/- = -; tg Θ2=+/- = -. Пусть ОА вращается дальше таким образом, что Θ3 — любой угол в третьем квадранте, и построим АD так, чтобы образовался прямоугольный треугольник ОАD. Тогда sin Θ3= -/+ = -; cos Θ3= -/+ = -; tg Θ3 = -/- =+ .График. Поcтроение углов в различных квадрантах. Пусть ОА вращается дальше таким образом, что Θ4— любой угол в четвертом квадранте, и построим АЕ так, чтобы образовался прямоугольный треугольник ОАЕ. Тогда sin Θ4= -/+= -; cos Θ4=+/+=+; tg Θ4= -/+= -. В первом квадранте все тригонометрические функции имеют положительные значения, во втором положителен только синус, в третьем — только тангенс, в четвертом только косинус, что и показано на рис. слева. График. Положительные и отрицательные
Будьте внимательны! Калькулятор дает только одно из этих значений. Второе значение следует определить согласно теории углов произвольной величины. Пример 1 Найти все углы в диапазоне от 0o до 360o , синус которых равен -0,7071 Решение: График. Нахождение всех углов по Из следующего рисунка Θ = arcsin 0,7071 = 45o. Два угла в диапазоне от 0o до 360o, синус которых равен -0,7071, это 180o +45o =225o и 360o — 45 o = 315o .
Пример 2 Найти все углы между 0o и 360 Решение: Из рис ниже Θ = arctg1,327= 53o . Построение синусоиды и косинусоиды Пусть ОR на рис. слева- это вектор единичной длины, свободно вращающийся против часовой стрелки вокруг О. За один оборот получается круг, показанный на рис. и разделенный секторами по 15 o. Каждый радиус имеет горизонтальную и вертикальную составляющую. Например, для 30o вертикальная составляющая — это ТS, а горизонтальная — ОS.
График. Из определения тригонометрических функций
Вертикальную составляющую TS можно перенести на график в виде T’S’, что равно значению, соответствующему углу 30o на графике зависимости y от угла х. Если все вертикальные составляющие, подобно TS, перенести на график, то получится синусоида, показанная на рис. выше.
Если все горизонтальные составляющие, подобные OS, спроецировать на график зависимости у от угла х, получится косинусоида. Эти проекции легко визуализировать, перерисовывая круг с радиусом OR и началом отсчета углов от вертикали, как показано на рисунке слева. График. Построение косинусоиды. 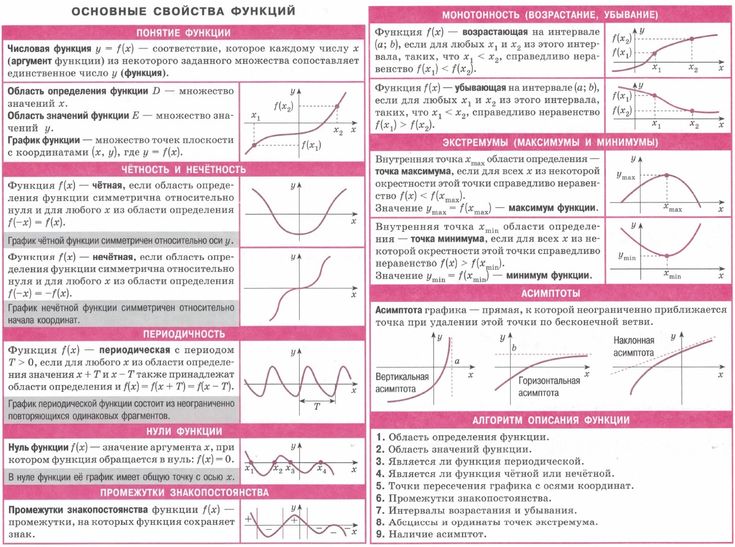
Синусоидальные и косинусоидальные графики
Периодические функции и период Амплитуда Пример 3. Решение: Пример 4. Решение: График. Построение y=4cos2x (косинусоида).
Углы запаздывания и опережения Составив таблицу значений, можно построить график функции y=sin(A-60o), показанный на рис. слева. Если кривая y=sinA начинается в 0o, то кривая y=sin(A-60o) начинается в 60o (т.е. ее нулевое значение на 60o правее ). Таким образом, говорят, что y=sin(A-60o) запаздывает относительно y=sinA на 60o. Составив таблицу значений, можно построить график функции y=cos(A+45o), показанный на рис. ниже. В общем виде, график y=sin(A-α) запаздывает относительно y=sinAна угол α. Пример 5.
Решение: Пример 6. Решение: Синусоида вида Asin(ωt±α). Фазовый угол. Сдвиг по фазе.
Если фазовый вектор OR делает один оборот (т.е. 2π радиан) за Т секунд, то угловая скорость ω=2π/Т рад/с, откуда Если в общем виде синусоидальная функция выглядит, как y=sin(ωt± α), то Пример 7. Решение: Пример 8. Решение Пример 9. График. v=350sin(40πt-0,542) Следовательно, (40πt-0,542)=arcsin200/350=35o или 0,611 рад. | ||||||||
Дополнительная информация от TehTab.ru: | ||||||||
Графики тригонометрических функций. Все углы А по умолчанию приведены в градусах. Все таблицы значений и формулы синусов, косинусов, тангенсов, котангенсов (здесь). Во всех формулах пределов и разложений в ряд — углы в радианах. Графики функций y=sinA, y=cosA, y=tgA,построенные для диапазона от 0o до 360o, показаны на рисунках ниже.
Из графиков видно что:
Углы произвольной величины На рис. слева показаны перпендикулярные оси ХХ’ и YY’; пересекающиеся в начале координат О. При работе с графиками измерения вправо и вверх от О считаются положительными, влево и вниз от О — отрицательными. Пусть ОА свободно вращается относительно О. При повороте ОА против часовой стрелки измеряемый угол считается положительным, а при повороте по часовой стрелке — отрицательным.
Пусть ОА вращается против часовой стрелки таким образом, что Θ1 — любой угол в первом квадранте, и построим перпендикуляр АВ для получения прямоугольного треугольника ОАВ на рис. слева. Поскольку все три стороны треугольника положительны, тригонометрические функции синус, косинус и тангенс в первом квадранте будут положительны. (Отметим, что длина ОА всегда положительна, поскольку является радиусом круга.)
График. Поcтроение углов в Пусть ОА вращается дальше таким образом, что Θ4— любой угол в четвертом квадранте, и построим АЕ так, чтобы образовался прямоугольный треугольник ОАЕ. Тогда sin Θ4= -/+= -; cos Θ4=+/+=+; tg Θ4= -/+= -. В первом квадранте все тригонометрические функции имеют положительные значения, во втором положителен только синус, в третьем — только тангенс, в четвертом только косинус, что и показано на рис. слева. График. Положительные и отрицательные
Будьте внимательны! Калькулятор дает только одно из этих значений. Второе значение следует определить согласно теории углов произвольной величины. Пример 1 Найти все углы в диапазоне от 0o до 360o , синус которых равен -0,7071 Решение: График. Нахождение всех углов по Из следующего рисунка Θ = arcsin 0,7071 = 45o. Два угла в диапазоне от 0o до 360o, синус которых равен -0,7071, это 180o +45o =225o и 360o — 45 o = 315o .
Пример 2 Найти все углы между 0o и 360o , тангенс которых равен 1, 327. Решение: Из рис ниже Θ = arctg1,327= 53o . Построение синусоиды и косинусоиды Пусть ОR на рис. слева- это вектор единичной длины, свободно вращающийся против часовой стрелки вокруг О. За один оборот получается круг, показанный на рис. и разделенный секторами по 15 o. Каждый радиус имеет горизонтальную и вертикальную составляющую. Например, для 30o вертикальная составляющая — это ТS, а горизонтальная — ОS.
График. Из определения тригонометрических функций
Вертикальную составляющую TS можно перенести на график в виде T’S’, что равно значению, соответствующему углу 30o на графике зависимости y от угла х. Если все вертикальные составляющие, подобно TS, перенести на график, то получится синусоида, показанная на рис. выше.
Если все горизонтальные составляющие, подобные OS, спроецировать на график зависимости у от угла х, получится косинусоида. Эти проекции легко визуализировать, перерисовывая круг с радиусом OR и началом отсчета углов от вертикали, как показано на рисунке слева. Синусоидальные и косинусоидальные графики
Периодические функции и период Амплитуда Пример 3. Решение: Пример 4. Решение: График. Построение y=4cos2x (косинусоида).
Углы запаздывания и опережения Составив таблицу значений, можно построить график функции y=sin(A-60o), показанный на рис. слева. Если кривая y=sinA начинается в 0o, то кривая y=sin(A-60o) начинается в 60o (т.е. ее нулевое значение на 60o правее ). Таким образом, говорят, что y=sin(A-60o) запаздывает относительно y=sinA на 60o. Составив таблицу значений, можно построить график функции y=cos(A+45o), показанный на рис. ниже. В общем виде, график y=sin(A-α) запаздывает относительно y=sinAна угол α. Пример 5.
Решение: Пример 6. Решение: Синусоида вида Asin(ωt±α). Фазовый угол. Сдвиг по фазе.
Если фазовый вектор OR делает один оборот (т.е. 2π радиан) за Т секунд, то угловая скорость ω=2π/Т рад/с, откуда Если в общем виде синусоидальная функция выглядит, как y=sin(ωt± α), то Пример 7. Решение: Пример 8. Решение Пример 9. График. v=350sin(40πt-0,542) Следовательно, (40πt-0,542)=arcsin200/350=35o или 0,611 рад. | ||||||||
Дополнительная информация от TehTab.ru: | ||||||||
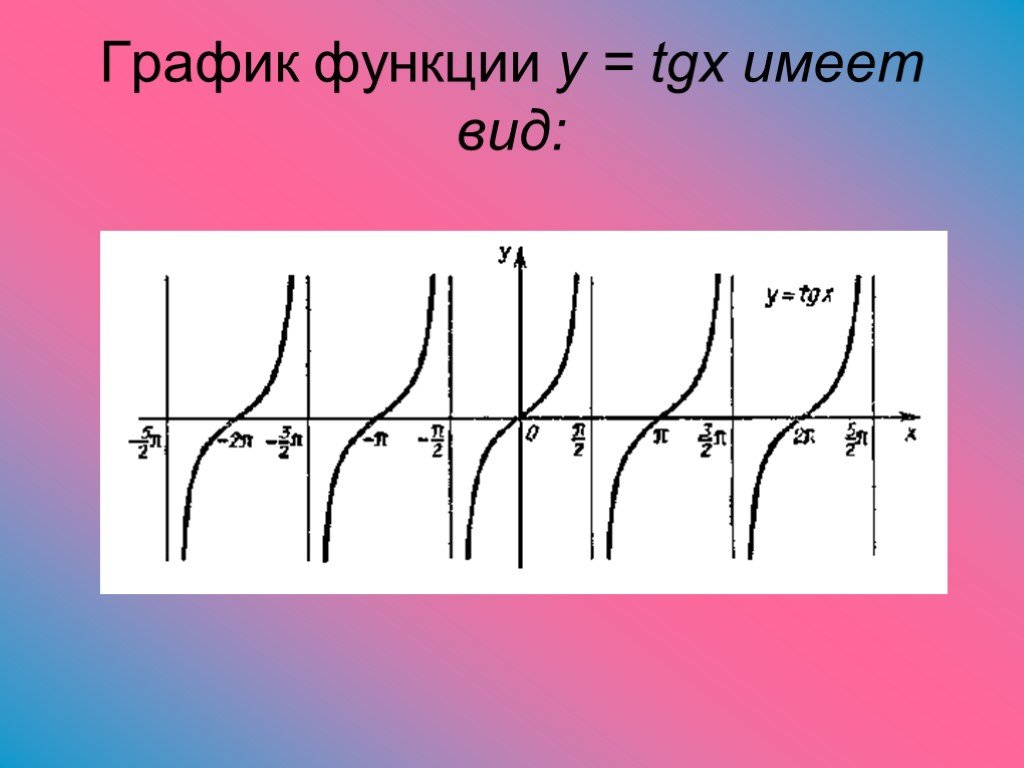
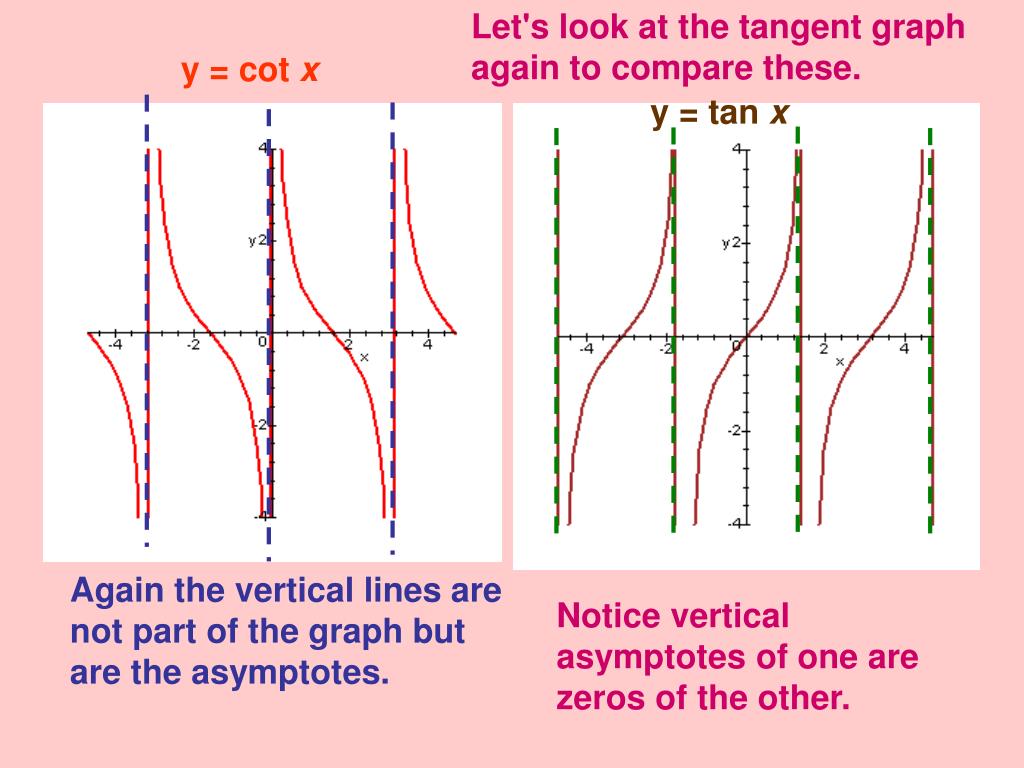
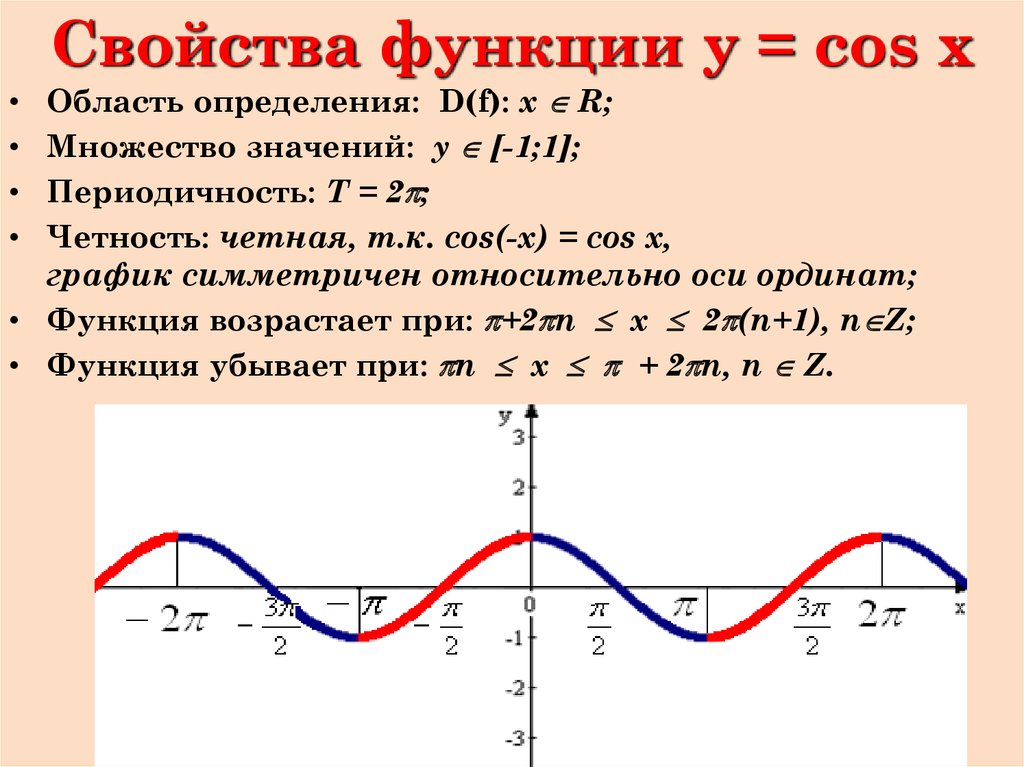
Давайте изучим графики функций тангенса и котангенса
¶График \(y=\tan(t)\).
Изучение влияния факторной идентичности \(\tan(t)=\frac{\sin(t)}{\cos(t)}\) на поведение функции тангенса даст нам много информации о graph \(y=\tan(t)\text{.}\) Давайте сделаем некоторые начальные наблюдения.
Везде есть \(t\)-перехват \(\sin(t)=0\text{.}\) Это дает нам следующие \(t\)-перехваты.
\begin{уравнение*} …,\,(-2\pi,0),\,(-\pi,0),\,(0,0),\,(\pi,0),\,(2\pi,0 ),\,… \end{уравнение*}
Вертикальная асимптота при каждом значении \(t\), где \(\cos(t)=0\text{.}\) Это дает нам следующие вертикальные асимптоты.

\begin{уравнение*} …,\,t=-\frac{5\pi}{2},\,t=-\frac{3\pi}{2},\,t=-\frac{\pi}{2} ,\,t=\frac{\pi}{2},\,t=\frac{3\pi}{2},\,t=\frac{5\pi}{2},\,… \end{уравнение*}
\(y\)-координата точки на графике \(y=\tan(t)\) равна \(1\) или \(-1\) при каждом значении \(t\) где функции синуса и косинуса имеют равные или противоположные значения. Это дает нам следующие моменты.
\begin{уравнение*} …,\,\влево(-\frac{5\pi}{4},-1\вправо),\,\влево(-\frac{3\pi}{4},1\вправо),\ ,\left(-\frac{\pi}{4},-1\right),\,\left(\frac{\pi}{4},1\right),\,\left(\frac{3 \pi}{4},-1\вправо),\,\влево(\frac{5\pi}{4},1\вправо),\,… \end{уравнение*}
Давайте продолжим и построим то, что мы обсуждали до сих пор. Это показано на рисунке 16.5.1.
Рисунок 16.5.1. Точки и асимптоты для графика \(y=\tan(t)\) Знак значения тангенса может меняться только тогда, когда \(t\) перемещается из одного квадранта в другой. На рис. 16.5.1 это происходит на асимптотах и \(t\)-перехватах. Мы можем использовать этот факт, чтобы сделать вывод о поведении функции, когда \(t\) приближается к асимптоте с любой стороны, что дает нам график функции, показанный на рисунке 16.5.2.
Мы можем использовать этот факт, чтобы сделать вывод о поведении функции, когда \(t\) приближается к асимптоте с любой стороны, что дает нам график функции, показанный на рисунке 16.5.2.
Мы должны сделать так, чтобы в отличие от функций синуса и косинуса период \(y=\tan(t)\) составлял всего \(\pi\text{.}\)
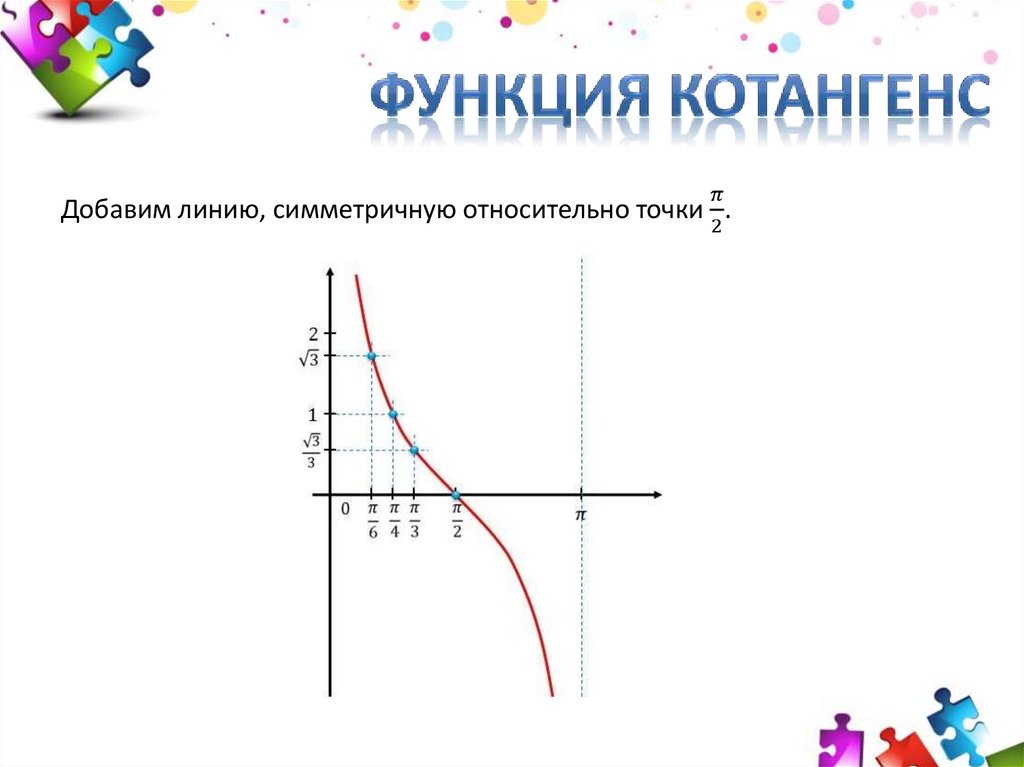
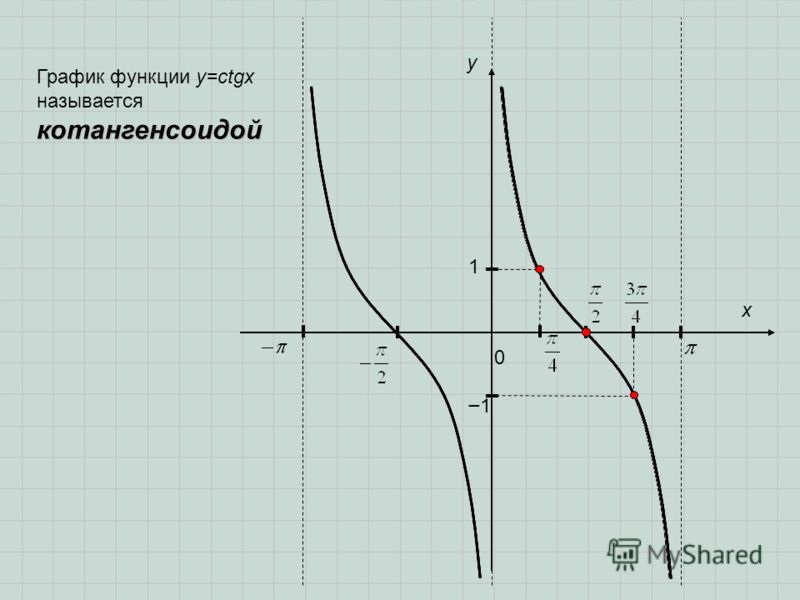
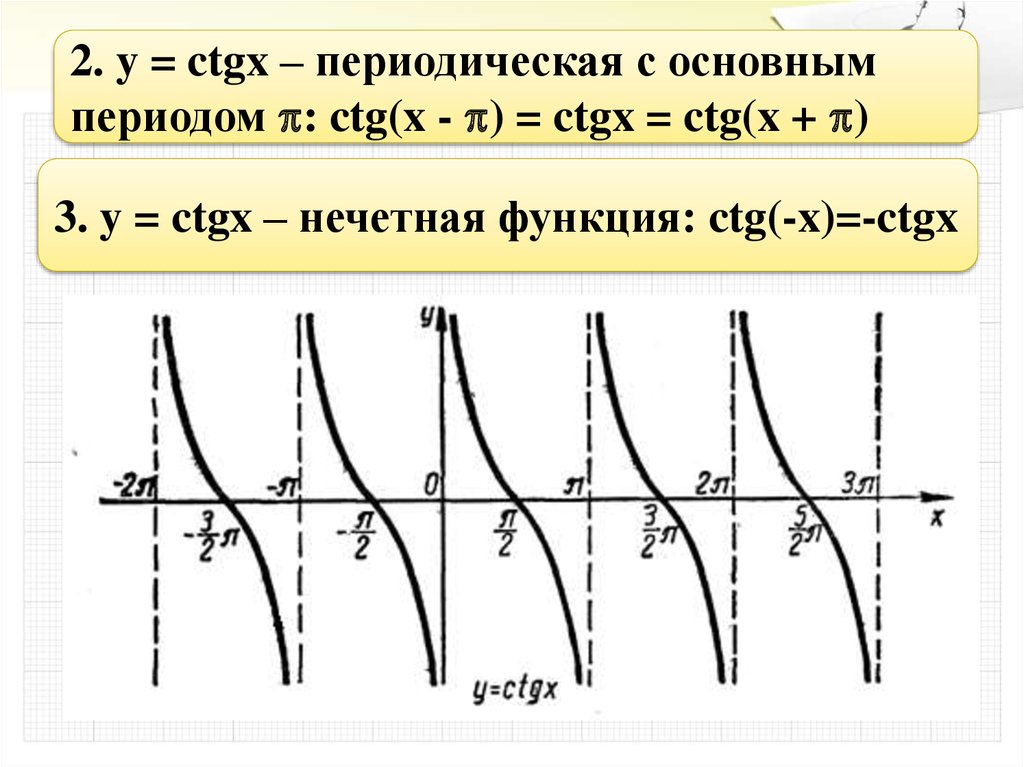
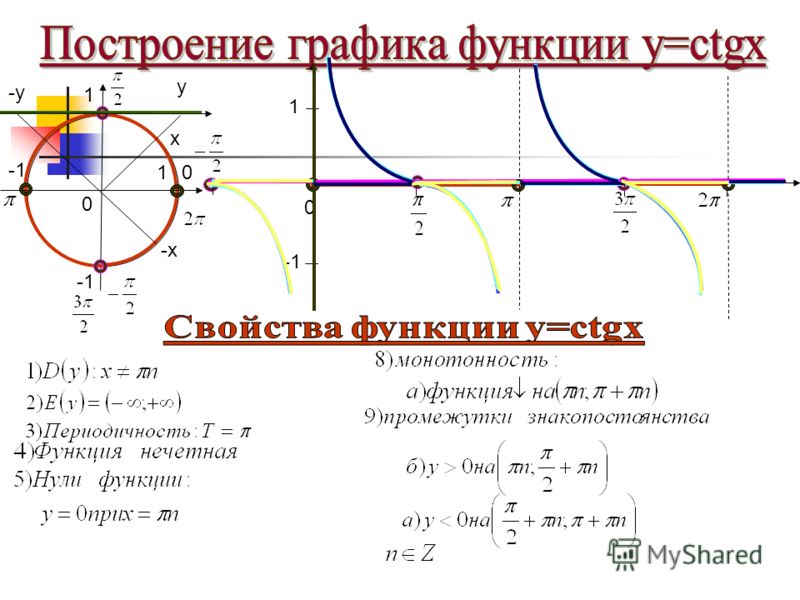
График \(y=\cot(t)\).
Изучение влияния факторной идентичности \(\cot(t)=\frac{\cos(t)}{\sin(t)}\) на поведение функции котангенса даст нам много информации о graph \(y=\cot(t)\text{.}\) Давайте сделаем некоторые начальные наблюдения.
Везде есть \(t\)-перехват \(\cos(t)=0\text{.}\) Это дает нам следующие \(t\)-перехваты.
\begin{уравнение*} …,\,\влево(-\frac{5\pi}{2},0\вправо),\,\влево(-\frac{3\pi}{2},0\вправо),\, \left(-\frac{\pi}{2},0\right),\,\left(\frac{3\pi}{2},0\right),\,\left(\frac{5\ pi}{2},0\вправо),\,\влево(\frac{7\pi}{2},0\вправо),\,… \end{уравнение*}
Вертикальная асимптота при каждом значении \(t\), где \(\sin(t)=0\text{.
 }\) Это дает нам следующие вертикальные асимптоты.
}\) Это дает нам следующие вертикальные асимптоты.\begin{уравнение*} …,\,t=-2\pi,\,t=-\pi,\,t=0,\,t=\pi,\,t=2\pi,\,t=3\pi, \,… \end{уравнение*}
\(y\)-координата точки на графике \(y=\cot(t)\) равна \(1\) или \(-1\) при каждом значении \(t\) где функции синуса и косинуса имеют равные или противоположные значения. Это дает нам следующие моменты.
\begin{уравнение*} …,\,\влево(-\frac{5\pi}{4},-1\вправо),\,\влево(-\frac{3\pi}{4},1\вправо),\ ,\left(-\frac{\pi}{4},-1\right),\,\left(\frac{\pi}{4},1\right),\,\left(\frac{3 \pi}{4},-1\вправо),\,\влево(\frac{5\pi}{4},1\вправо),\,… \end{уравнение*}
Давайте продолжим и построим то, что мы обсуждали до сих пор. Это показано на рисунке 16.5.3.
Рисунок 16.5.3. Точки и асимптоты для графика \(y=\cot(t)\) Знак значения котангенса может меняться только тогда, когда \(t\) перемещается из одного квадранта в другой. На рис. 16.5.3 это происходит на асимптотах и \(t\)-перехватах.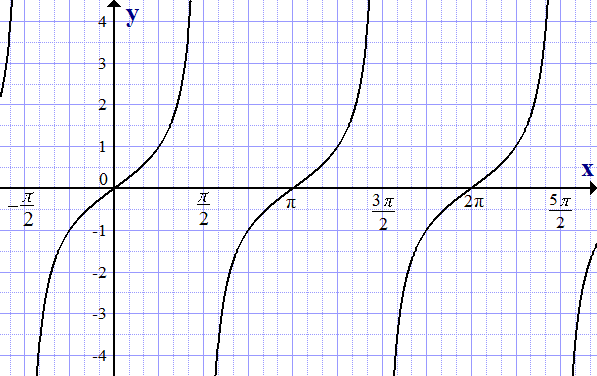 Мы можем использовать этот факт, чтобы сделать вывод о поведении функции, когда \(t\) приближается к асимптоте с любой стороны, что дает нам график функции, показанный на рисунке 16.5.4.
Мы можем использовать этот факт, чтобы сделать вывод о поведении функции, когда \(t\) приближается к асимптоте с любой стороны, что дает нам график функции, показанный на рисунке 16.5.4.
Следует отметить, что, как и функция тангенса, период \(y=\cot(t)\) равен \(\pi\text{.}\)
Давайте двигаться дальше и обсудить графические преобразования, произведенные над \(y=\tan(t)\) и \(y=\cot(t)\text{.}\)
Период функции тангенса или котангенса.
Как и в случае с функцией синуса и косинуса, если \(\omega\) ненулевая константа, не равная \(1\) или \(-1\text{,}\), то график \ (y=\tan(\omega t)\) или \(y=\cot(\omega t)\) будут отличаться от периодов графиков \(y=\tan(t)\) и \( y=\cot(t)\text{.}\) Однако в этом случае новый период равен \(\frac{\pi}{\abs{\omega}}\) (в отличие от \(\frac{ 2\pi}{\abs{\omega}}\), что является периодом либо \(y=\sin(\omega t)\), либо \(y=\cos(\omega t)\)). Давайте посмотрим на пару примеров.
Пример 16.
 5.5.
5.5.Нарисуйте три периода функции \(y=\tan(2t)\text{.}\)
Решение
Мы видим, что \(\omega=2\text{,}\) поэтому период этой функции равен \(\frac{\pi}{2}\text{.}\)
Когда есть нет смещения по горизонтали, функция касательной имеет вертикальные асимптоты по половине периода как слева, так и справа от оси \(y\). В данном случае это означает, что и \(t=-\frac{\pi}{4}\), и \(t=\frac{\pi}{4}\) являются вертикальными асимптотами. Каждый раз, когда мы перемещаемся на один полный период влево или вправо от вертикальной асимптоты, мы сталкиваемся с другой вертикальной асимптотой. Это означает, что и \(t=-\frac{3\pi}{4}\), и \(t=\frac{3\pi}{4}\) являются вертикальными асимптотами. Эти вертикальные асимптоты показаны на рисунке 16.5.6. Обратите внимание, что шкала по оси \(t\) равна \(\frac{\pi}{4}\text{.}\). Это связано с тем, что \(\frac{\pi}{4}\) равно единице. -половина полного периода.
Рисунок 16.5.6. Вертикальные асимптоты для графика \(y=\tan(2t)\) На полпути между каждой парой асимптот есть \(t\)-отрезок.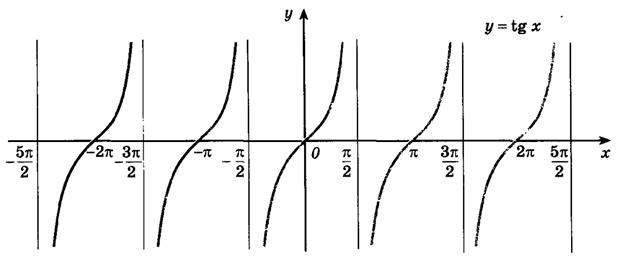 В четверти периода слева от каждого \(t\)перехвата находится точка с \(y\)-координатой \(-1\text{.}\) В четверти периода справа от на каждом \(t\)-перехвате есть точка с \(y\)-координатой \(1\text{.}\). Все эти точки добавлены на график на рисунке 16.5.7.
В четверти периода слева от каждого \(t\)перехвата находится точка с \(y\)-координатой \(-1\text{.}\) В четверти периода справа от на каждом \(t\)-перехвате есть точка с \(y\)-координатой \(1\text{.}\). Все эти точки добавлены на график на рисунке 16.5.7.
Осталось только соединить точки таким образом, чтобы продемонстрировать асимптотическое поведение функции. Это показано на рисунке 16.5.8.
Рисунок 16.5.8. Точки и асимптоты для графика \(y=\tan(2t)\)Пример 16.5.9.
Нарисуйте три периода функции \(y=\cot\left(\frac{\pi}{3}\right)\text{.}\)
Решение
Начнем с того, что \(\frac{t}{3}=\frac{1}{3}t\text{,}\) поэтому \(\omega=\frac{1}{3} \text{.}\) Период для \(y=\cot\left(\frac{pi}{3}\right)\) получен ниже.
\begin{выравнивание*} \ гидроразрыва {\ пи} {\ абс {\ омега}} \ amp = \ гидроразрыва {\ пи} {\ гидроразрыва {1} {3}} \\ \amp=\frac{\pi}{1} \cdot \frac{3}{1} \end{align*}
При отсутствии смещения по горизонтали ось \(y\) представляет собой вертикальную асимптоту графика функции котангенса. Каждый раз, когда мы перемещаемся на один полный период влево от вертикальной асимптоты, мы сталкиваемся с другой вертикальной асимптотой. В данном случае это означает, что \(t=-3\pi\text{,}\) \(t=3\pi\text{,}\) и \(t=6\pi\) также являются вертикальными асимптотами. Эти вертикальные асимптоты показаны на рисунке 16.5.10. Обратите внимание, что масштаб по оси \(t\) равен \(\frac{3\pi}{2}\text{.}\). Это потому, что \(\frac{3\pi}{2}\) составляет половину периода.
Каждый раз, когда мы перемещаемся на один полный период влево от вертикальной асимптоты, мы сталкиваемся с другой вертикальной асимптотой. В данном случае это означает, что \(t=-3\pi\text{,}\) \(t=3\pi\text{,}\) и \(t=6\pi\) также являются вертикальными асимптотами. Эти вертикальные асимптоты показаны на рисунке 16.5.10. Обратите внимание, что масштаб по оси \(t\) равен \(\frac{3\pi}{2}\text{.}\). Это потому, что \(\frac{3\pi}{2}\) составляет половину периода.
На полпути между каждой парой асимптот есть \(t\)-отрезок. В четверти периода слева от каждого \(t\)перехвата находится точка с \(y\)-координатой \(1\text{.}\) В четверти периода справа от каждого \(t\)-перехват есть точка с \(y\)-координатой \(-1\text{.}\) Все эти точки были добавлены на график на рисунке 16.5.7.
Рисунок 16.5.11. Точки и асимптоты для графика \(y=\cot\left(\frac{\pi}{3}\right)\) Осталось только соединить точки таким образом, чтобы продемонстрировать асимптотическое поведение функции.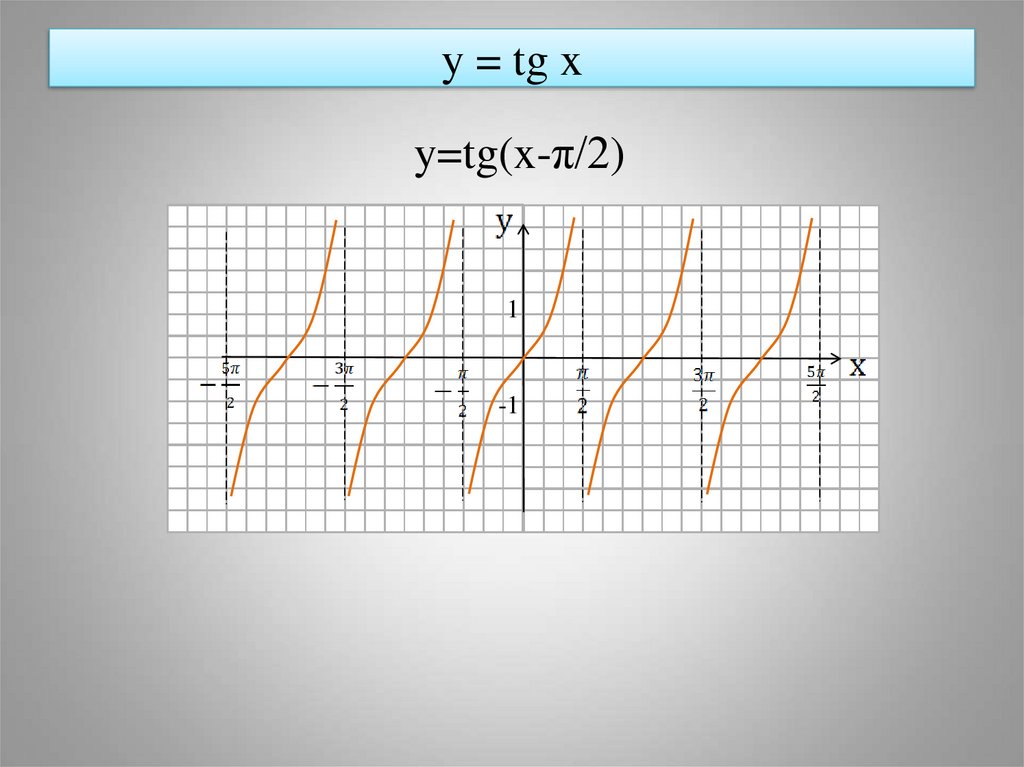 Это показано на рисунке 16.5.12.
Это показано на рисунке 16.5.12.
Горизонтальный сдвиг функции тангенса или котангенса.
Как и для любой другой функции, ненулевая константа \(h\) в выражении \(y=\tan(\omega(t-h))\) или \(y=\cot(\omega(t-h))\) влияет на горизонтальный сдвиг \(\abs{h}\) относительно их родительской функции (\(y=\tan(\omega t)\) или \(y=\cot(\omega t)\)). Когда \(h\) положителен, сдвиг вправо, а когда \(h\) отрицателен, сдвиг влево.
Например, \(y=\tan\left(t-\frac{\pi}{3}\right)\) лежит \(\frac{\pi}{3}\) справа от \(y =\tan(t)\), тогда как \(y=\tan\left(t+\frac{\pi}{3}\right)\) лежит \(\frac{\pi}{3}\) слева из \(y=\tan(t)\text{.}\)
Давайте посмотрим на пару примеров графического процесса, когда есть сдвиг по горизонтали.
Пример 16.5.13.
Эскиз трех периодов функции \(y=\tan\left(t-\frac{\pi}{3}\right)\text{.}\)
Решение
Функция \(y=\tan(t)\) имеет вертикальную асимптоту в точке \(t=-\frac{3\pi}{2}\text{,}\) \(t=-\frac {\pi}{2}\text{,}\) \(t=\frac{\pi}{2}\text{,}\) и \(t=\frac{3\pi}{2}\ text{. }\) Функция \(y=\tan\left(t-\frac{\pi}{3}\right)\) лежит \(\frac{\pi}{3}\) справа функции \(y=\tan(t)\text{.}\) Влияние, которое это оказывает на расположение вертикальных асимптот графика \(y=\tan\left(t-\frac{\pi {3}\right)\) вычисляется ниже
}\) Функция \(y=\tan\left(t-\frac{\pi}{3}\right)\) лежит \(\frac{\pi}{3}\) справа функции \(y=\tan(t)\text{.}\) Влияние, которое это оказывает на расположение вертикальных асимптот графика \(y=\tan\left(t-\frac{\pi {3}\right)\) вычисляется ниже
\begin{выравнивание*} t\amp=-\frac{3\pi}{2}+\frac{\pi}{3}\\ t\amp=-\frac{7\pi}{6} \end{выравнивание*}
\begin{выравнивание*} t \ amp = — \ frac {\ pi} {2} + \ frac {\ pi} {3} \\ т \ амп = — \ гидроразрыва {\ пи} {6} \end{выравнивание*}
\begin{выравнивание*} t \ amp = — \ frac {\ pi} {2} + \ frac {\ pi} {3} \\ t\amp=-\frac{5\pi}{6} \end{выравнивание*}
\begin{выравнивание*} t \ amp = — \ frac {\ pi} {2} + \ frac {\ pi} {3} \\ t\amp=-\frac{11\pi}{6} \end{align*}
Еще один способ определить положение этих вертикальных асимптот — применить сдвиг к \(t=\frac{\pi}{2}\) (в результате получается \(t= \frac{5\pi}{6})\), а затем многократно добавляя или вычитая полную точку (в данном случае \(\pi\)) к \(\frac{5\pi}{6}\text{.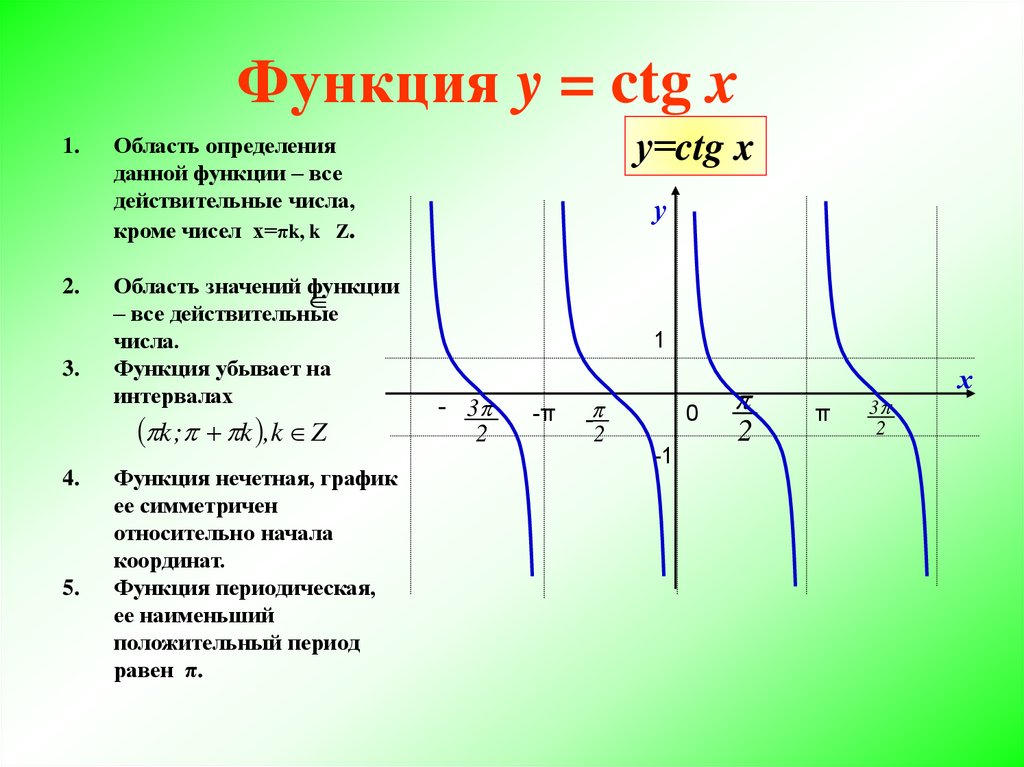 }\)
}\)
Независимо от стратегии определения вертикальных асимптот, в данном случае они равны \(t=-\frac{7\pi}{6}\text{,}\) \(t=-\frac{\pi {6}\text{,}\) \(t=\frac{5\pi}{6}\text{,}\) и \(t=\frac{11\pi}{6}\text{ .}\) Эти асимптоты показаны на рисунке 16.5.14. Обратите внимание, что средняя точка между каждой парой последовательных асимптот также была определена. Это точки, в которых касательные кривые будут пересекать ось \(t\).
Рисунок 16.5.14. Асимптоты для графика \(y=\tan\left(t-\frac{\pi}{6}\right)\)На полпути между каждой парой асимптот есть \(t\)-отрезок. В четверти периода слева от каждого \(t\)перехвата находится точка с \(y\)-координатой \(-1\text{.}\) В четверти периода справа от на каждом \(t\)-перехвате есть точка с \(y\)-координатой \(1\text{.}\). Все эти точки добавлены на график на рис. 16.5.15.
Рисунок 16.5.15. Точки и асимптоты для графика \(y=\tan\left(t-\frac{\pi}{6}\right)\) Все, что осталось сделать, это соединить точки таким образом, чтобы продемонстрировать асимптотику поведение функции.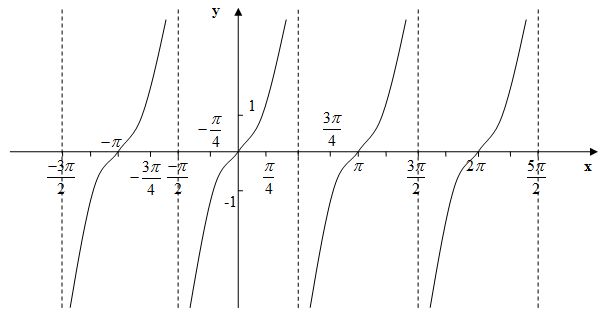 Это показано на рисунке 16.5.16.
Это показано на рисунке 16.5.16.
Пример 16.5.17.
Эскиз трех периодов функции \(y=\cot\left(2t+\frac{\pi}{2}\right)\text{.}\)
Решение
Начнем с того, что период этой функции равен \(\frac{\pi}{2}\text{.}\). вдали от \(t\) и \(\frac{\pi}{2}\text{.}\) Это делается ниже.
\begin{уравнение*} \ кроватка \ влево (2t + \ frac {\ pi} {2} \ справа) = \ кроватка \ влево (2 \ влево (t + \ frac {\ pi} {4} \ вправо) \ вправо) \end{уравнение*}
Теперь мы можем видеть сдвиг влево на \(\frac{\pi}{4}\text{.}\)
Линии \(t=-\frac{\pi}{2}\ text{,}\) \(t=0\text{,}\) \(t=\frac{\pi}{2}\text{,}\) и \(t=\pi\) все вертикальны асимптоты для функции \(y=\cot(2t)\text{.}\) Функция \(y=\cot\left(2t+\frac{\pi}{2}\right)\) лежит \(\ frac{\pi}{4}\) слева от \(y=\cot(2t)\text{,}\), поэтому он имеет вертикальные асимптоты \(t=-\frac{3\pi}{4 }\text{,}\) \(t=-\frac{\pi}{4}\text{,}\) \(t=\frac{\pi}{4}\text{,}\) и \(t=\frac{3\pi}{4}\text{. }\) Эти асимптоты показаны на рисунке 16.5.18. Обратите внимание, что средняя точка между каждой парой последовательных асимптот также была определена. Это точки, в которых касательные кривые будут пересекать ось \(t\).
}\) Эти асимптоты показаны на рисунке 16.5.18. Обратите внимание, что средняя точка между каждой парой последовательных асимптот также была определена. Это точки, в которых касательные кривые будут пересекать ось \(t\).
На полпути между каждой парой асимптот есть \(t\)-отрезок. В четверти периода слева от каждого \(t\)перехвата находится точка с \(y\)-координатой \(-1\text{.}\) В четверти периода справа от на каждом \(t\)-перехвате есть точка с \(y\)-координатой \(1\text{.}\). Все эти точки добавлены на график на рис. 16.5.19.
Рисунок 16.5.19. Точки и асимптоты для графика \(y=\cot\left(2t+\frac{\pi}{2}\right) \)Осталось только соединить точки таким образом, чтобы продемонстрировать асимптотическое поведение функции. Это показано на рисунке 16.5.20.
Рисунок 16.5.20. \(y=\cot\left(2t+\frac{\pi}{2}\right) \)Вертикальные растяжения, сжатия, отражения и сдвиги.
Вертикальные растяжения, сжатия, отражения и сдвиги работают точно так же для функций тангенса и котангенса, как и для любой другой функции. А именно:
А именно:
График \(y=A \tan(t)\text{,}\) \(A \neq 0\text{,}\) \(A \neq \pm 1\text{,}\ ) является либо вертикальным растяжением, либо вертикальным сжатием графика \(y=\tan(t)\text{.}\) Если \(\abs{A} \gt 1\text{,}\) эффект является отклонением от оси \(t\) в \(A\text{.}\) Если \(\abs{A} \lt 1\text{,}\) эффект представляет собой вертикальный сжатие по оси \(t\) в \(\abs{A}\text{.}\) Кроме того, если \(A \lt 0\text{,}\) кривые \(y =\tan(t)\) отражаются поперек оси \(t\).
График \(y=\tan(t)+k\text{,}\) \(k \neq 0\text{,}\) является вертикальным сдвигом графика \(y=\tan (t)\text{.}\) Когда \(k \gt 0\text{,}\) сдвиг вверх на \(k\text{.}\) Когда \(k \lt 0\text{, }\) сдвиг вниз на \(\abs{k}\text{.}\)
Давайте рассмотрим пример.
Пример 16.5.21.
Зарисовать три периода функции \(y=-3\cot(t)+2\text{.}\)
Решение
Говоря словами, графические преобразования, затрагивающие родительскую функцию \(y=\cot(t)\), являются растяжением в \(3\text{,}\) раз отражения через \(t \)-ось и, наконец, сдвиг вверх на \(2\text{. }\)
}\)
При построении графика \(y=\cot(t)\text{,}\) между каждой парой последовательных пар асимптот есть три ключевые точки. Точки слева направо имеют вид
\begin{equation*} (t,1),\,\,(t,0),\,\,(t,-1). \end{equation*}
На графике \(y=-3\cot(2)+2\) эти точки становятся
\begin{equation*} (t,3(1)+2),\,\,(t,3(0)+2),\,\,(t,3(-1)+2) \end{equation*}
, которые упрощаются до
\begin{equation*} (t,5),\,\,(t,2),\,\,(t,-2). \end{уравнение*}
Поскольку в горизонтальном направлении изменений нет, мы знаем, что \(t=-\pi\text{,}\) \(t=0\text{,}\) \(t=\pi\text{ ,}\) и \(t=2\pi\) — вертикальные асимптоты функции. Эти асимптоты и вышеупомянутые точки представлены на рисунке 16.5.22.
Рисунок 16.5.22. Точки и асимптоты для графика \(y=-3\cot(t)+2\)Все, что осталось сделать, это соединить точки таким образом, чтобы продемонстрировать асимптотическое поведение функции. Это показано на рисунке 16.5.23.
Рисунок 16.5.23. \(у=-3\кроватка(т)+2\)Упражнения Упражнения
Нарисуйте три периода каждой функции.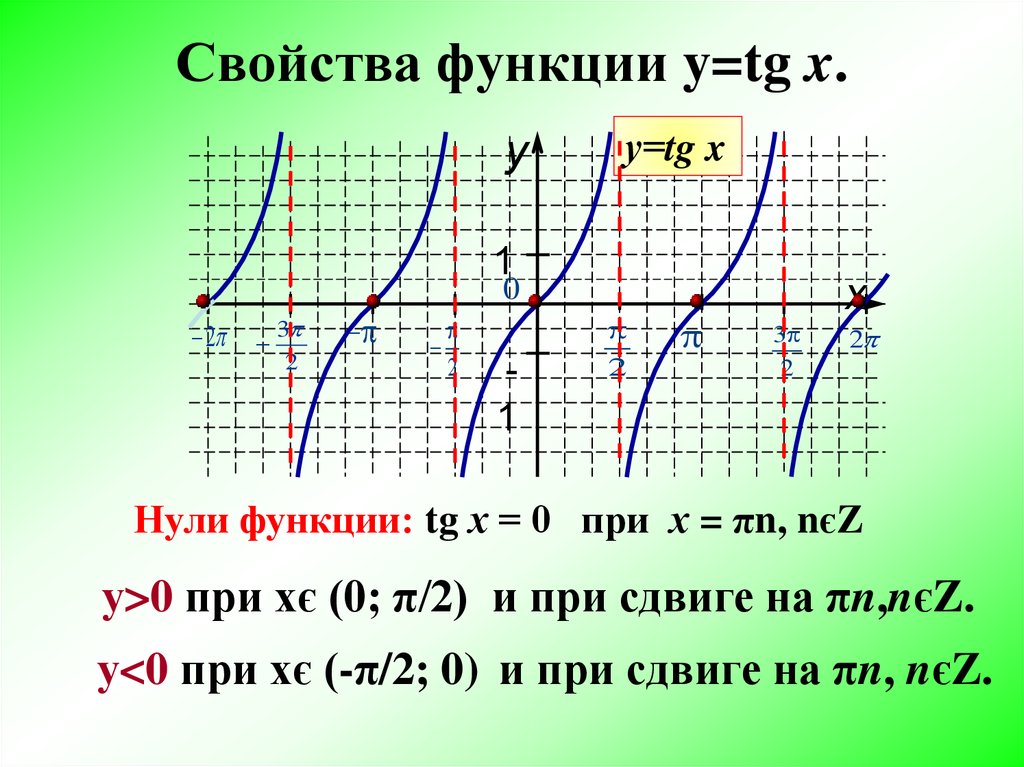
1.
\(у=\кроватка(3т)\)
Решение
Единственным преобразованием, затрагивающим функцию \(y=\cot(t)\), является изменение периода. Новый период равен \(\frac{\pi}{3}\text{.}\) Строки \(t=-\frac{\pi}{3}\text{,}\) \(t=0 \text{,}\) \(t=\frac{\pi}{3}\text{,}\) и \(t=\frac{2\pi}{3}\) будут вертикальными асимптотами для график. На полпути между каждой последовательной парой асимптот кривая будет пересекать ось \(t\). В четверти периода левее каждого \(t\)-перехвата находится точка с \(y\)-координатой \(1\) и в четверти периода правее каждого \(t\) )-перехват есть точка с \(y\)-координатой \(-1\text{.}\) Все это показано на рисунке 16.5.24.
Рисунок 16.5.24. Точки и асимптоты для графика \(y=\cot(3t)\)Все, что осталось сделать, это соединить точки таким образом, чтобы продемонстрировать асимптотическое поведение функции. Это показано на рисунке 16.5.24.
Рисунок 16.5.25. \(y=\cot(3t)\)2.
\(y=\tan\left(t-\frac{\pi}{8}\right)\)
Решение
Единственным преобразованием, затрагивающим график \(y=\tan(t)\), является сдвиг вправо \(\frac{\pi}{8}\text{.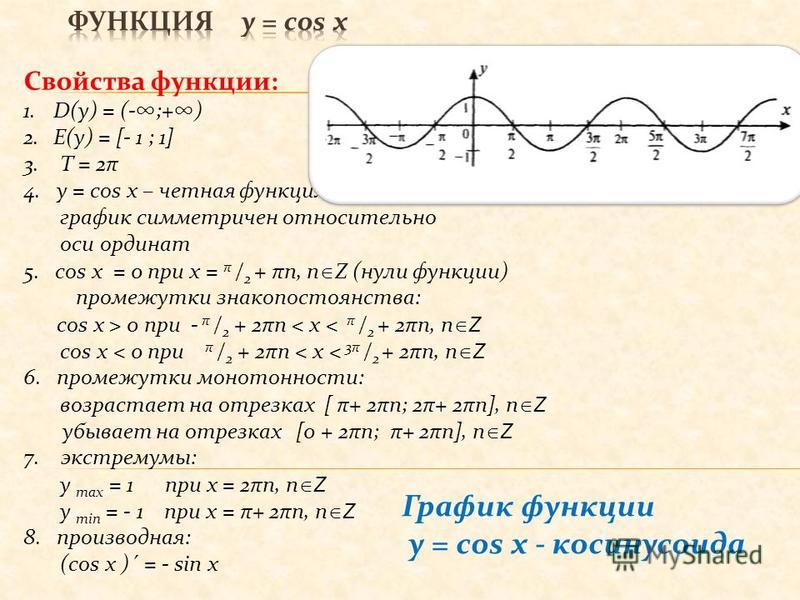 }\) Эффект этого на вертикальных асимптотах вычисляется ниже.
}\) Эффект этого на вертикальных асимптотах вычисляется ниже.
\begin{выравнивание*} t\amp=-\frac{3\pi}{2}+\frac{\pi}{8}\\ t\amp=-\frac{11\pi}{8} \end{выравнивание*}
\begin{выравнивание*} t \ amp = — \ frac {\ pi} {2} + \ frac {\ pi} {8} \\ t\amp=-\frac{3\pi}{8} \end{выравнивание*}
\begin{выравнивание*} t\amp=\frac{\pi}{2}+\frac{\pi}{8}\\ t\amp=\frac{5\pi}{8} \end{выравнивание*}
\begin{выравнивание*} t\amp=\frac{3\pi}{2}+\frac{\pi}{8}\\ t\amp=-\frac{13\pi}{8} \end{align*}
На полпути между каждой последовательной парой асимптот кривая пересекает ось \(t\). В четверти периода слева от каждого \(t\)-перехвата находится точка с \(y\)-координатой \(-1\) и в четверти периода справа от каждого \(t \)-перехват есть точка с \(y\)-координатой \(1\text{.}\) Все это показано на рисунке 16.5.26.
Рисунок 16.5.26. Точки и асимптоты для графика \(y=\tan\left(t-\frac{\pi}{8}\right)\) Все, что осталось сделать, это соединить точки таким образом, чтобы продемонстрировать асимптотику поведение функции.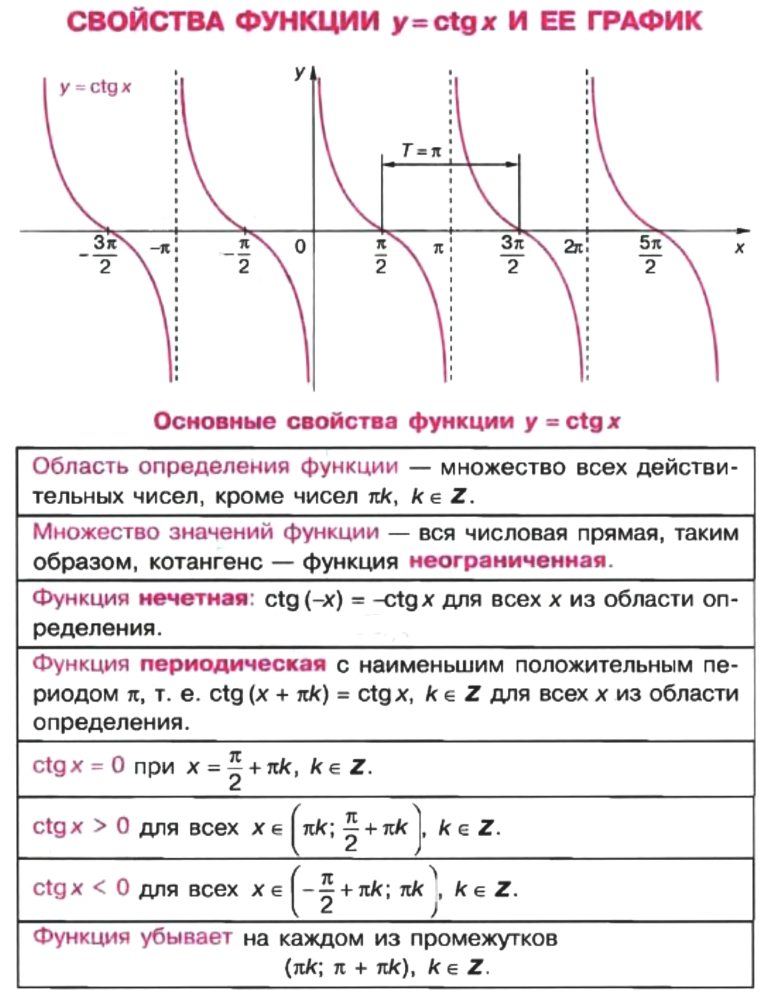 Это показано на рисунке 16.5.27.
Это показано на рисунке 16.5.27.
3.
\(y=\frac{2}{3}\cot(t)-2\)
Решение
Все модификации графика \(y=\cot(t)\) выполняются в вертикальном направлении. Происходит вертикальное сжатие в \(\frac{2}{3}\) с последующим сдвигом вниз в 2,9 раза.0005
При построении графика \(y=\cot(t)\text{,}\) между каждой парой последовательных пар асимптот есть три ключевые точки. Точки слева направо имеют вид
\begin{equation*} (t,1),\,\,(t,0),\,\,(t,-1). \end{equation*}
На графике \(y=y=\frac{2}{3}\cot(t)-2\) эти точки становятся
\begin{equation*} (t,\frac{2}{3}(1)-2),\,\,(t,\frac{2}{3}(0)-2),\,\,(t,\frac{ 2}{3}(-1)-2) \end{equation*}
, которые упрощаются до
\begin{equation*} (t,-\frac{4}{3}),\,\,(t,-2),\,\,(t,-\frac{8}{3}). \end{уравнение*}
Давайте построим наши асимптоты, \(t=-\pi\text{,}\) \(t=0\text{,}\) \(t=\pi\text{,}\) и \(t=2\pi\text{. }\) Давайте также нанесем точки, о которых говорилось выше. Это показано на рисунке 16.5.28.
}\) Давайте также нанесем точки, о которых говорилось выше. Это показано на рисунке 16.5.28.
Все, что осталось сделать, это соединить точки таким образом, чтобы продемонстрировать асимптотическое поведение функции . Это показано на рисунке 16.5.29.
Рисунок 16.5.29. \(y=\frac{2}{3}\cot(t)-2\)4.
\(y=-\tan\left(3\left(t+\frac{\pi}{6}\right)\right)\)
Решение
Начнем с того, что период равен \(\frac{\pi}{3}\text{.}\)
Линии \(y=-\frac{3\pi}{2}\ text{,}\) \(y=-\frac{\pi}{2}\text{,}\) \(y=\frac{\pi}{2}\text{,}\) и \( y=\frac{3\pi}{2}\) — все вертикальные асимптоты для графика \(y=\tan(t)\text{.}\). Все эти линии должны быть сжаты по направлению к \(y \) по оси в \(\frac{1}{3}\text{.}\) Результирующие вертикальные асимптоты для графика \(y=\tan(3t)\) равны \(y=-\ frac{\pi}{2}\text{,}\) \(y=-\frac{\pi}{6}\text{,}\) \(y=\frac{\pi}{6}\ text{,}\) и \(y=\frac{\pi}{2}\text{.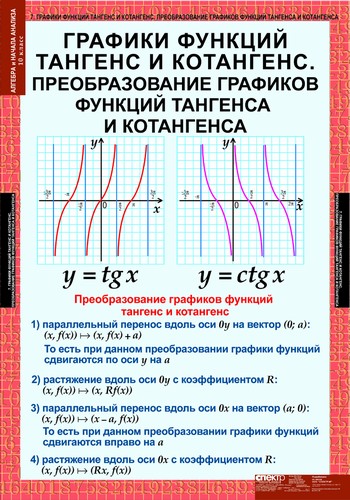 }\) Все эти строки сдвинуты влево на \(\frac{\pi}{6}\) на график \(y=-\tan\left(3\left(t+\frac{\pi}{6}\right)\right)\text{.}\) Эффект, который это оказывает на вертикальные асимптоты, вычисляется ниже.
}\) Все эти строки сдвинуты влево на \(\frac{\pi}{6}\) на график \(y=-\tan\left(3\left(t+\frac{\pi}{6}\right)\right)\text{.}\) Эффект, который это оказывает на вертикальные асимптоты, вычисляется ниже.
\begin{выравнивание*} t \ amp = — \ frac {\ pi} {2} — \ frac {\ pi} {6} \\ t\amp=-\frac{2\pi}{3} \end{выравнивание*}
\begin{выравнивание*} t \ amp = — \ frac {\ pi} {6} — \ frac {\ pi} {6} \\ т \ амп = — \ гидроразрыва {\ пи} {3} \end{выравнивание*}
\begin{выравнивание*} t\amp=\frac{\pi}{6}-\frac{\pi}{6}\\ т\ампер=0 \end{выравнивание*}
\begin{выравнивание*} t\amp=\frac{\pi}{2}-\frac{\pi}{6}\\ т \ амп = \ гидроразрыва {\ пи} {3} \end{align*}
Давайте построим вертикальные асимптоты. Это показано на рисунке 16.5.30.
Рисунок 16.5.30. Асимптоты для графика \(y=-\tan\left(3\left(t+\frac{\pi}{6}\right)\right)\) Существует кривая, пересекающая ось \(t\) на полпути между каждой парой последовательных асимптот. На графике \(y=\tan(t)\) есть точка в четверти периода слева от каждого \(t\)-перехвата с \(y\)-координатой \(1 \) и точка на четверть периода справа от каждого \(t\)-перехвата с \(y\)-координатой \(1\text{. }\) Поскольку функция, которую мы рисуем, имеет отрицательный знак перед выражением касательной, точки с \(y\)-координатой \(1\) попадут левее \(t\)-перехвата, а точки с \(y\)-координатой )-координата \(-1\) будет падать правее \(t\)-перехватов. Эти точки были добавлены на график на рисунке 16.5.31.
}\) Поскольку функция, которую мы рисуем, имеет отрицательный знак перед выражением касательной, точки с \(y\)-координатой \(1\) попадут левее \(t\)-перехвата, а точки с \(y\)-координатой )-координата \(-1\) будет падать правее \(t\)-перехватов. Эти точки были добавлены на график на рисунке 16.5.31.
Осталось только соединить точки способом, демонстрирующим асимптотическое поведение функции. Это показано на рисунке 16.5.32.
Рисунок 16.5.32. Точки и асимптоты для графика \(y=-\tan\left(3\left(t+\frac{\pi}{6}\right)\right)\)5.
\(y=\cot\left(\frac{t}{2}-\frac{\pi}{4}\right)-3\)
Решение
Сначала заметим, что \(\frac{t}{2}=\frac{1}{2}t\text{,}\), поэтому значение \(\omega\) равно \(\frac {1}{2}\text{.}\) Период рассчитывается ниже.
\begin{выравнивание*} \ гидроразрыва {\ пи} {\ абс {\ омега}} \ amp = \ гидроразрыва {\ пи} {\ гидроразрыва {1} {2}} \\ \amp=\frac{\pi}{1} \cdot \frac{2}{1}\\ \амп=2\пи \end{align*}
Прежде чем мы сможем установить сдвиг по горизонтали, нам нужно разложить \(\frac{1}{2}\) как на \(t\), так и на \(\frac{\pi}{ 4}\text{.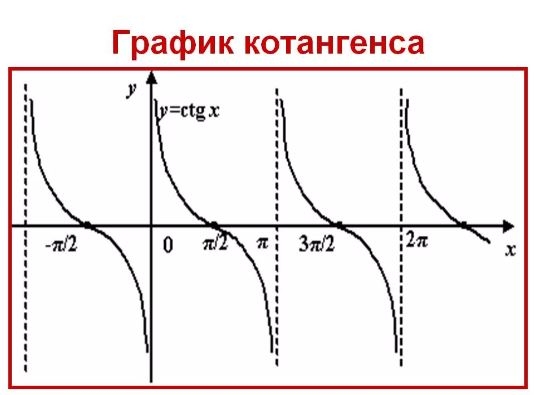 }\) Это делается ниже.
}\) Это делается ниже.
\begin{уравнение*} \cot\left(\frac{t}{2}-\frac{\pi}{4}\right)-3=\cot\left(\frac{1}{2}\left(t-\frac{ \pi}{2}\справа)\справа)-3 \end{equation*}
Теперь мы можем видеть, что имеет место сдвиг вправо \(\frac{\pi}{2}\text{.}\)
Строки \(y=-2\pi\text{,}\) \(y=0\text{,}\) \(y=2\pi\text{,}\) и \(y= 4\pi\) все вертикальные асимптоты на графике \(y=\cot\left(\frac{t}{2}\right)\text{.}\) На графике \(y=\cot\ left(\frac{t}{2}-\frac{\pi}{4}\right)-3\) все эти асимптоты нужно сдвинуть вправо на \(\frac{\pi}{2}\text {.}\) Результирующие асимптоты равны \(y=-\frac{3\pi}{2}\text{,}\) \(y=\frac{\pi}{2}\text{,}\ ) \(y=\frac{5\pi}{2}\text{,}\) и \(y=\frac{9\pi}{2}\text{.}\) Эти асимптоты представлены на рис. 16.5.33.
Рисунок 16.5.33. Асимптоты для графика \(y=\cot\left(\frac{t}{2}-\frac{\pi}{4}\right)-3\) Между асимптотами через равные промежутки в один- четверть периода координаты \(y\) немодифицированной функции котангенса следуют схеме \(1\text{,}\) \(0\text{,}\) \(-1\text{. } \) Функция котангенса, которую мы рисуем, имеет сдвиг вниз на \(3\text{,}\), так что шаблон смещается вниз на \(-2\text{,}\) \(-3\text{,} \) \(-4\text{.}\) Полученные точки добавлены к графику на рисунке 16.5.34.
} \) Функция котангенса, которую мы рисуем, имеет сдвиг вниз на \(3\text{,}\), так что шаблон смещается вниз на \(-2\text{,}\) \(-3\text{,} \) \(-4\text{.}\) Полученные точки добавлены к графику на рисунке 16.5.34.
Осталось только соединить точки таким образом, который демонстрирует асимптотическое поведение функции. Это показано на рисунке 16.5.35.
Рисунок 16.5.35. Точки и асимптоты для графика \(y=\cot\left(\frac{t}{2}-\frac{\pi}{4}\right)-3\)Графики: другие тригонометрические функции
Тангенс — нечетная функция, потому что
Тангенс имеет период π, потому что
Тангенс не определен, если cos x = 0. Это происходит, когда x = q π/2, где q — нечетное целое число. В этих точках значение тангенса стремится к бесконечности и не определено. При графическом изображении касательной пунктирная линия используется, чтобы показать, где значение касательной не определено. Эти линии называются асимптотами . Значения тангенса для различных величин угла показаны в Таблице 1 .
Эти линии называются асимптотами . Значения тангенса для различных величин угла показаны в Таблице 1 .
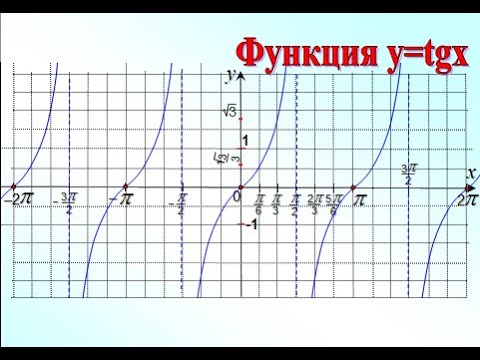
График функции тангенса в интервале от 0 до π/2 показан на рисунке 1 .
Рис. 1
Часть функции касательной.
Тангенс является нечетной функцией и симметричен относительно начала координат. График касательной за несколько периодов показан на рисунке 2 . Обратите внимание, что асимптоты показаны пунктирными линиями, а значение касательной в этих точках не определено.
Рисунок 2
Несколько периодов функции тангенса.
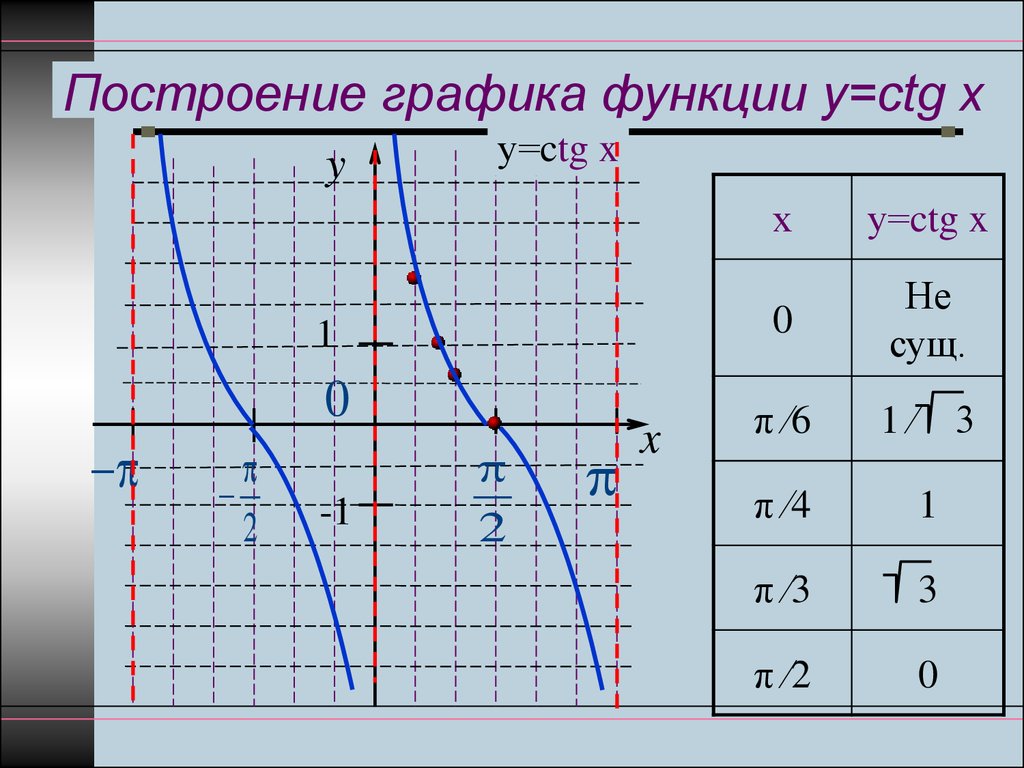
Котангенс является обратной величиной тангенса, и его график показан на рисунке 3. Обратите внимание на разницу между графиком тангенса и котангенса в интервале от 0 до π/2.
Рисунок 3
Часть функции котангенса.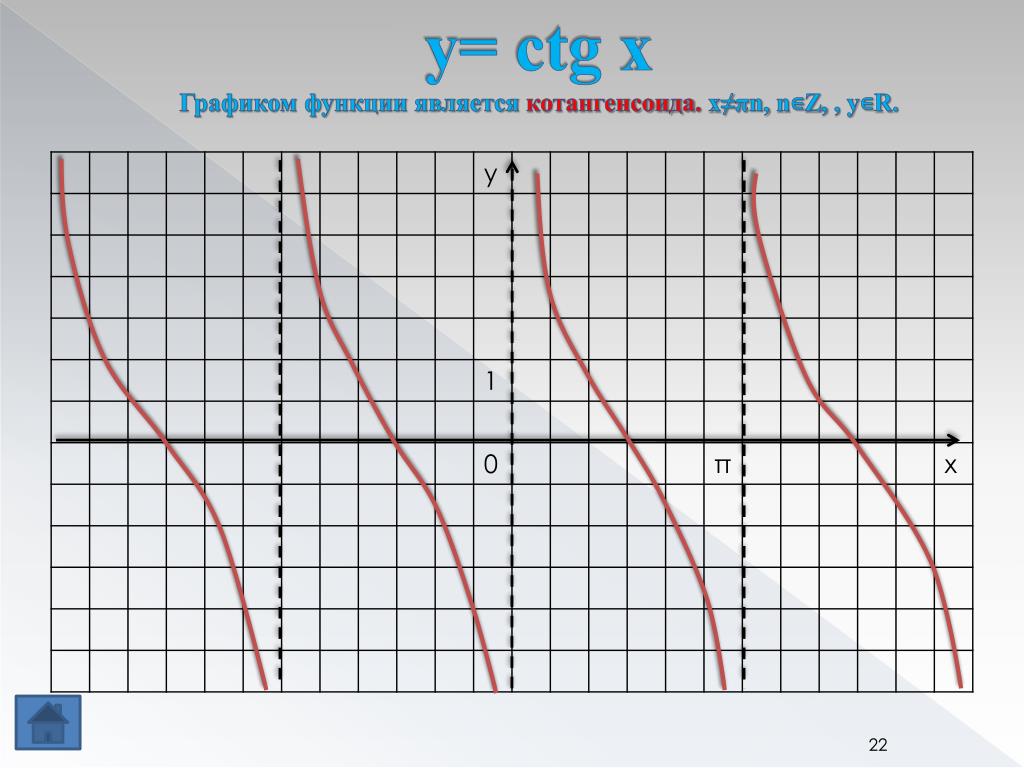
Как показано на рис. 4, на графике котангенса асимптоты расположены на кратных π.
Рисунок 4 Несколько периодов функции котангенса.
Поскольку графики тангенса и котангенса неограниченно простираются как выше, так и ниже оси x , амплитуда тангенса и котангенса не определена.
Общие формы функций тангенса и котангенса
Переменные C и D определяют период и фазовый сдвиг функции, как и в функциях синуса и косинуса. Период равен π/ C , а фазовый сдвиг равен |D/C|. Сдвиг вправо, если | Д/Ц | < 0 и влево, если | Д/Ц | > 0. Переменная B не представляет амплитуду, поскольку тангенс и котангенс не ограничены, но она показывает, насколько график «растянут» в вертикальном направлении. Переменная A представляет сдвиг по вертикали.
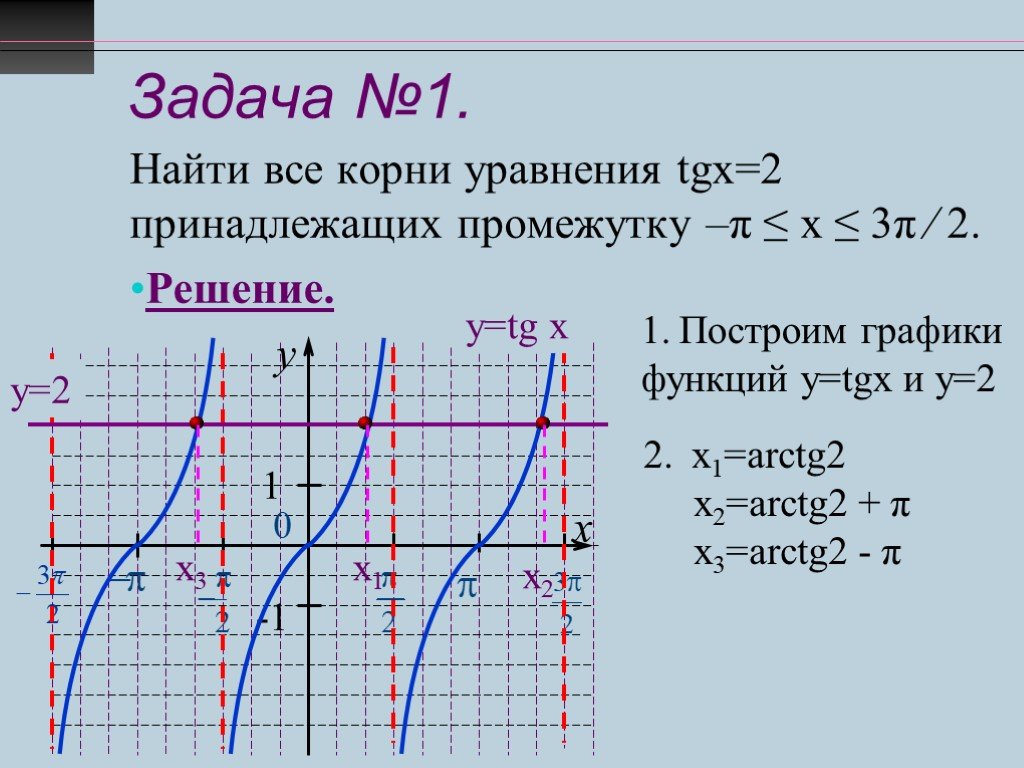
Пример 1: Определить период, фазовый сдвиг и расположение асимптот функции
и построить график не менее двух полных периодов функции.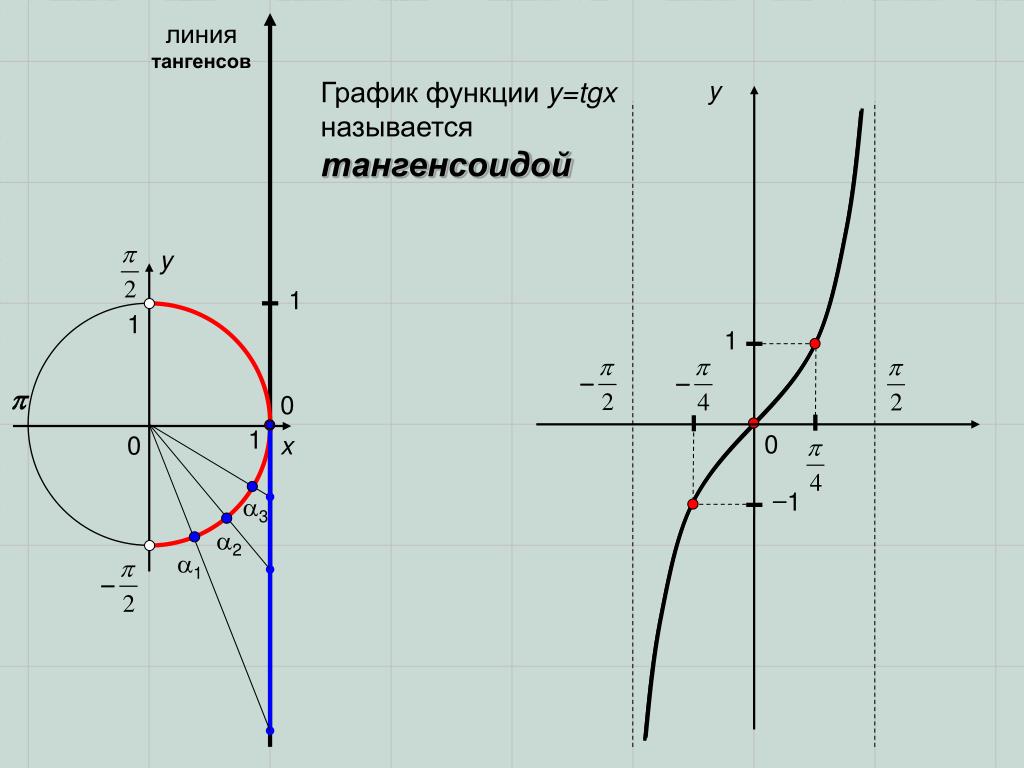
Асимптоты можно найти, решив Cx + D = π/2 и Cx + D = −π/2 для X .
Период функции
Фазовый сдвиг функции равен
Поскольку фазовый сдвиг положительный, он находится влево (рис. 5).
Рисунок 5 Фазовый сдвиг функции касательной.
Амплитуда не определена для секанса или косеканса. Секанс и косеканс изображаются как обратные величины косинуса и синуса соответственно и имеют одинаковый период (2π). Поэтому фазовый сдвиг и период этих функций находятся путем решения уравнений Cx + D = 0 и Cx + D = 2π для x .
Пример 2: Определите период, фазовый сдвиг и расположение асимптот функции
и построить график не менее двух периодов функции.
Асимптоты можно найти, решая Cx + D = 0, Cx + D = π и Cx + D = 2π для x .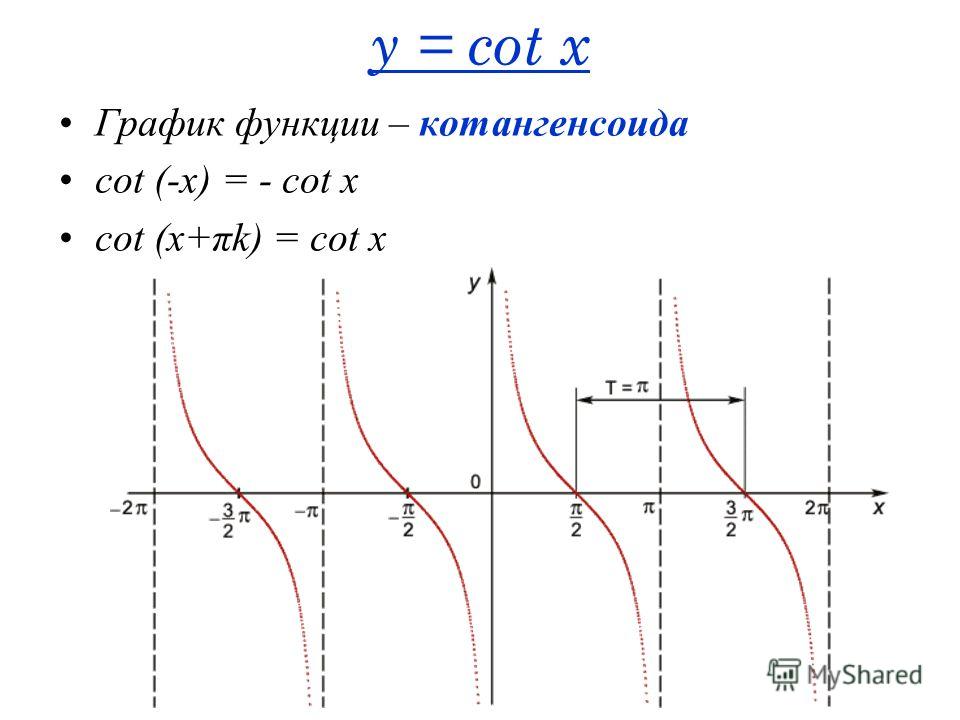

 Фазовый угол. Сдвиг по фазе.
Фазовый угол. Сдвиг по фазе.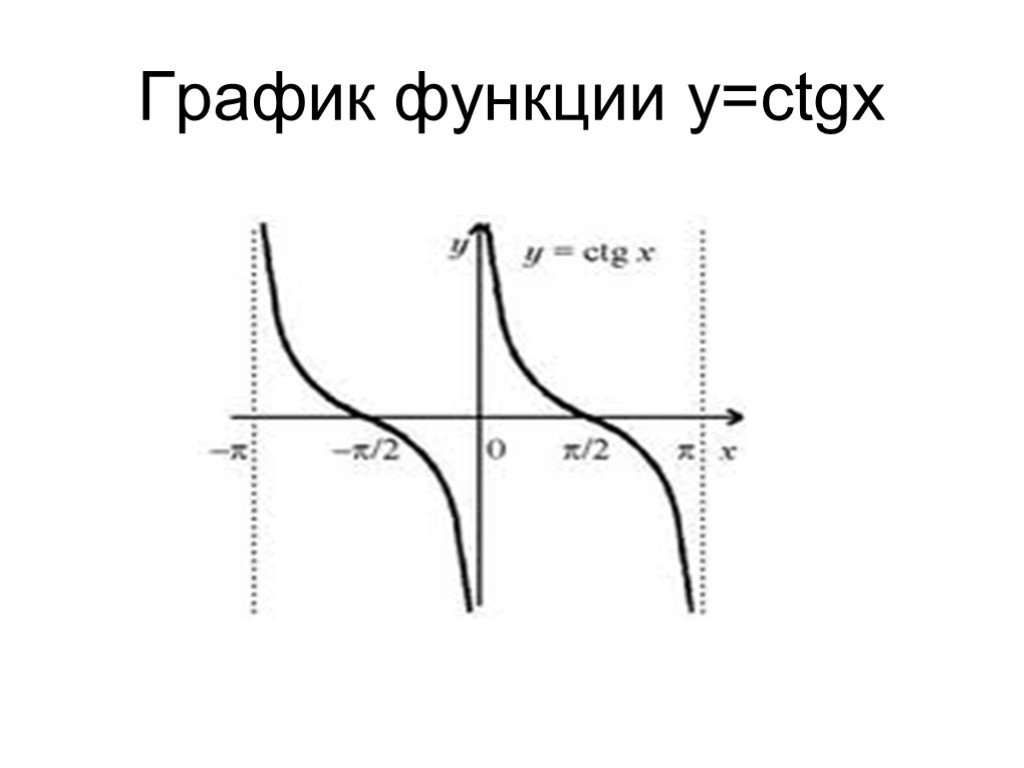

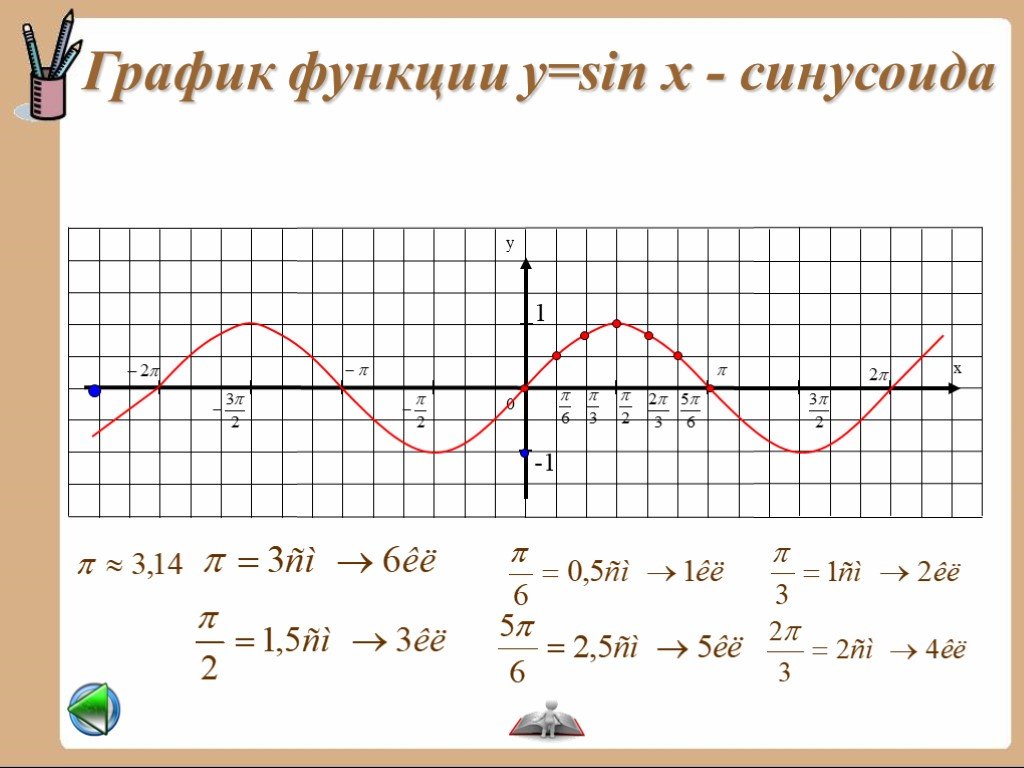
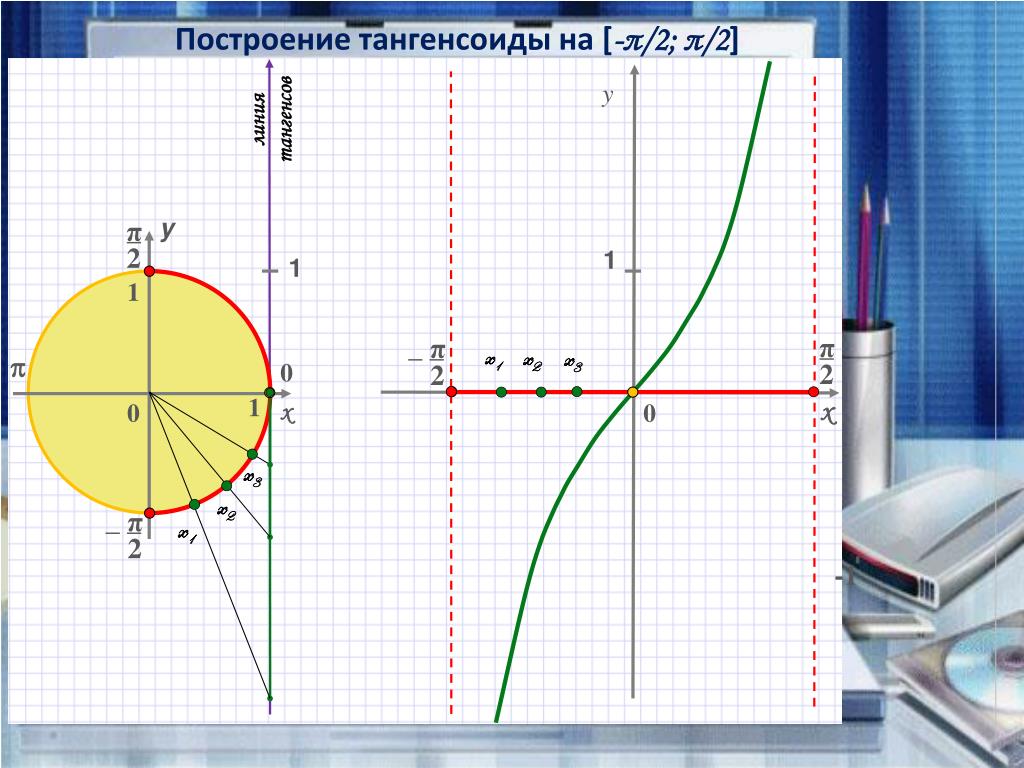
 Построение синусоиды.
Построение синусоиды.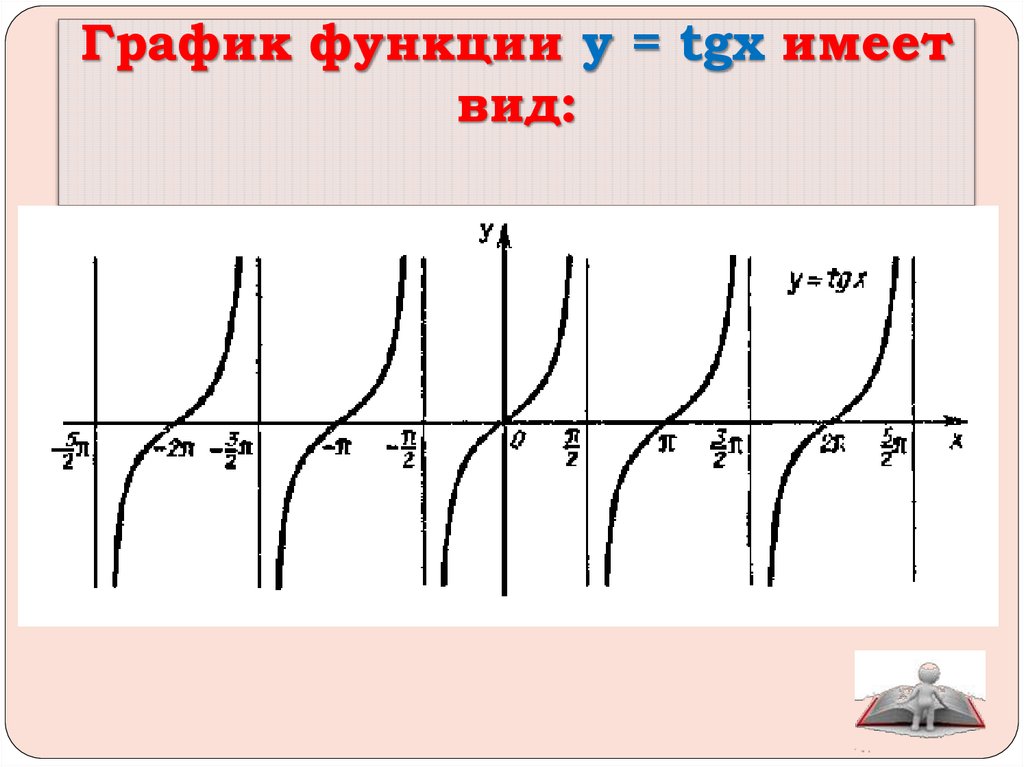
 y=sin(A-60o) (синусоида).
y=sin(A-60o) (синусоида).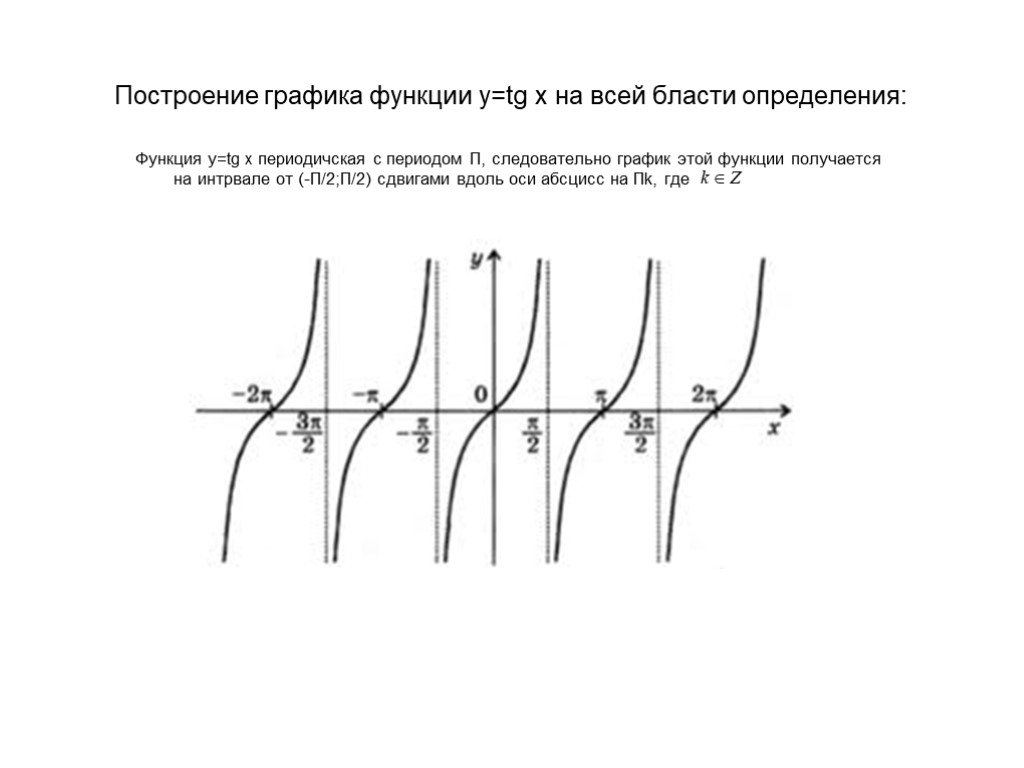
 слева это угол TOR). Если перпендикулярно к OR построить ST, то sinωt=ST/OT, т.e. ST=OTsinωt.
слева это угол TOR). Если перпендикулярно к OR построить ST, то sinωt=ST/OT, т.e. ST=OTsinωt.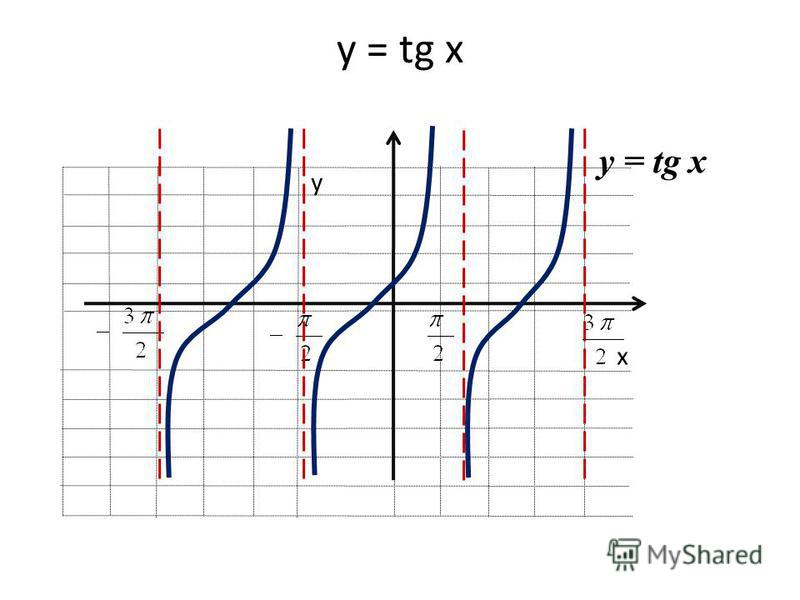
 Колебательный механизм
Колебательный механизм Фазовый угол. Сдвиг по фазе.
Фазовый угол. Сдвиг по фазе.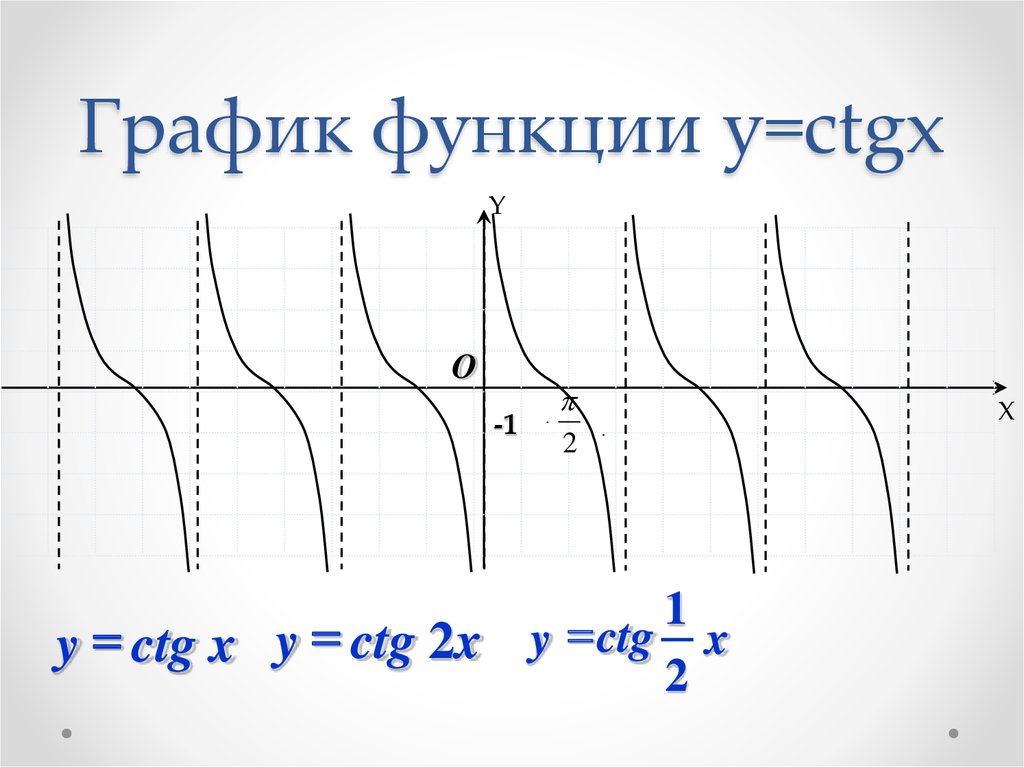
 Тогда sin Θ2=+/+ = +; cos Θ2=+/- = -; tg Θ2=+/- = -. Пусть ОА вращается дальше таким образом, что Θ3 — любой угол в третьем квадранте, и построим АD так, чтобы образовался прямоугольный треугольник ОАD. Тогда sin Θ3= -/+ = -; cos Θ3= -/+ = -; tg Θ3 = -/- =+ .
Тогда sin Θ2=+/+ = +; cos Θ2=+/- = -; tg Θ2=+/- = -. Пусть ОА вращается дальше таким образом, что Θ3 — любой угол в третьем квадранте, и построим АD так, чтобы образовался прямоугольный треугольник ОАD. Тогда sin Θ3= -/+ = -; cos Θ3= -/+ = -; tg Θ3 = -/- =+ . Построение синусоиды.
Построение синусоиды.

 y=sin(A-60o) (синусоида).
y=sin(A-60o) (синусоида).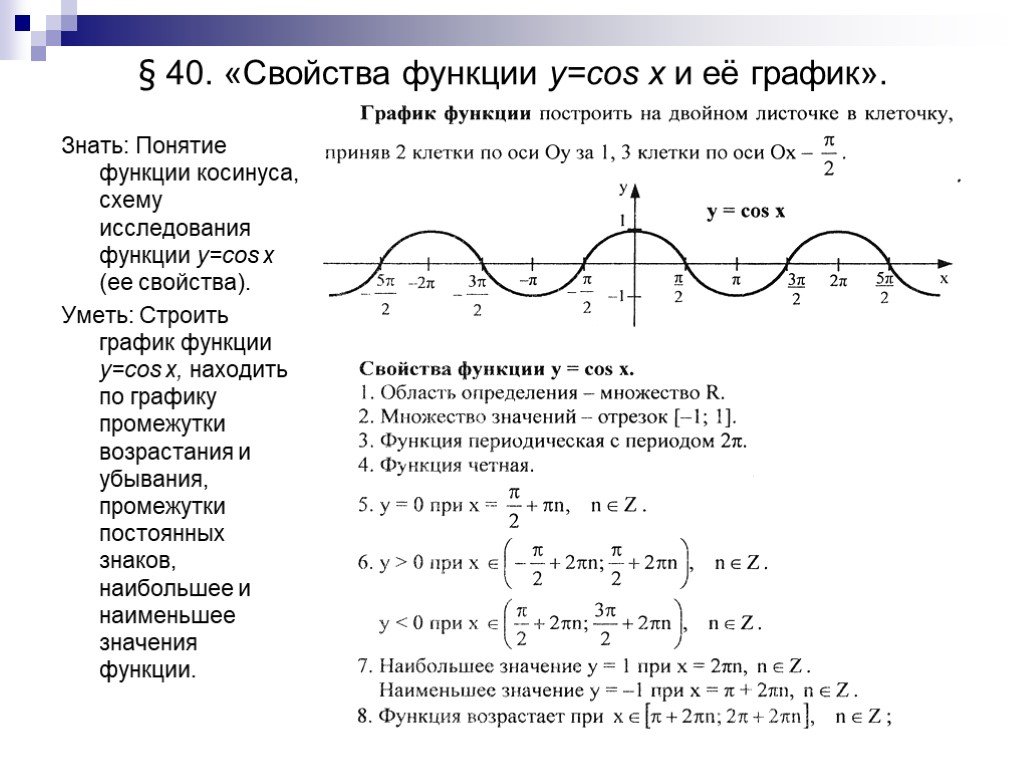
 слева это угол TOR). Если перпендикулярно к OR построить ST, то sinωt=ST/OT, т.e. ST=OTsinωt.
слева это угол TOR). Если перпендикулярно к OR построить ST, то sinωt=ST/OT, т.e. ST=OTsinωt.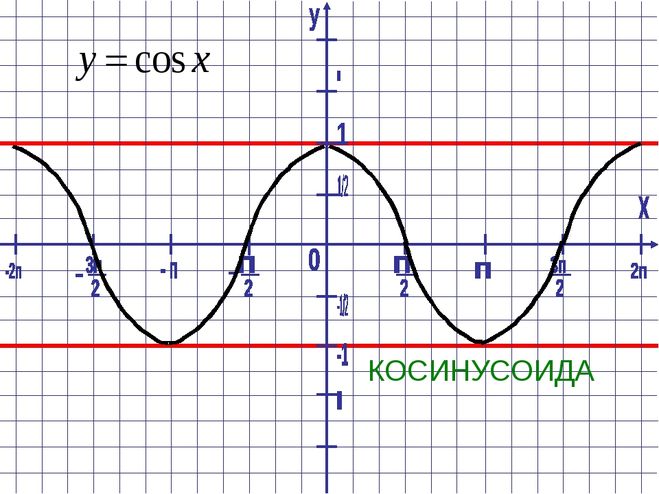
 Колебательный механизм
Колебательный механизм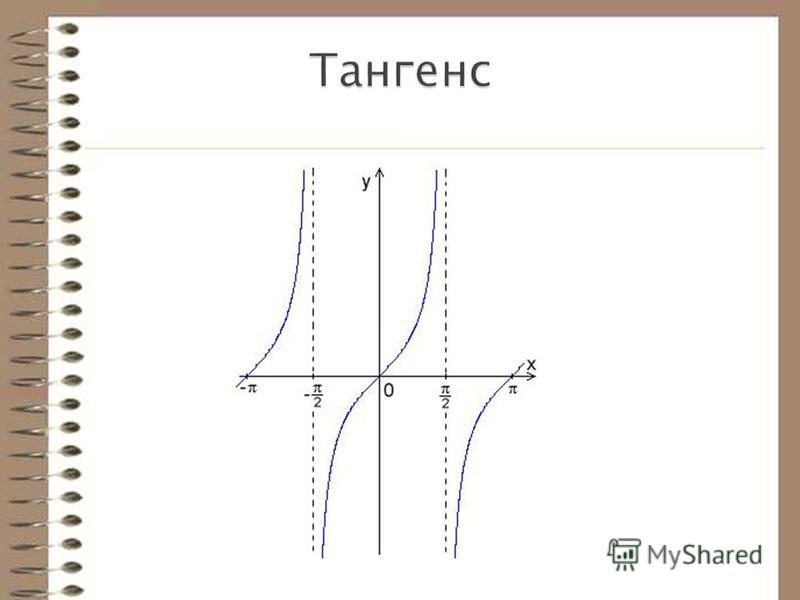
 }\) Это дает нам следующие вертикальные асимптоты.
}\) Это дает нам следующие вертикальные асимптоты.