Теорема фалеса ударение куда. Вариации и обобщения
Великий физик начала двадцатого века Эрнест Резерфорд высказался так: «Вся наука — это либо физика, либо коллекционирование марок». В предыдущей статье мы с Вами как раз убедились в том, что физика и собирание фактов находятся на разных полюсах развития моделей. А сегодня у нас с Вами первый экскурс в прошлое.
Начнем с Фалеса Милетского, ибо по мнению историков именно он заложил первый кирпич в основание здания современной науки.
Небольшое отступление по поводу собственно имени героя нашего сегодняшнего повествования. Не знаю, как у Вас, а мне лично в советской школе преподавали теорему Фалеса с ударением на первом слоге. На самом деле изначальное греческое Θαλῆς имеет на первом месте букву Θ, что на греческом произносится как английское th в think. Эта буква (фита) в чистом виде присутствовала в русском языке до 1918, пока ее не сократили вкупе с ятью и ижицей. После реформы ее заменяли как рука возьмет — обычно как Ф (в данном случае), но часто и как Т (теория, тезис, театр).
С Милетом все значительно проще, обошлись заменой очередного «и» на «е». Город этот располагался на побережье Малой Азии, может кто на тот дальний берег турецкий ездил отдыхать? Основали его по легенде выходцы (или беженцы) с Крита, и нарекли в честь Милитуса, сына Аполлона и критской красавицы. В описываемые нами времена (шесть сотен лет до нашей эры) это был самый богатый город эллинистического мира с многочисленными колониями — самая известная для нас из которых город Феодосия (опять же изначально с фитой). Греками к этому времени уже была построена настоящая цивилизация — и одним из следствий этого было то, что у отдельных индивидумов стало оставаться время от тупой борьбы за существование.
Фалес был одним из таких счастливчиков — сыном богатых родителей. Секунду — вот это не случайно. В ту далекую эпоху наукой заработать себе на жизнь было непросто, не было тебе не только нобелевских премий, но и даже теплых местечек в многочисленных университетах или НИИ. В философы (а это тогда был синоним ученого) шли почти исключительно люди, которые уже предварительно решили для себя все материальные проблемы. Почему почти — поскольку спустя пару столетий наука стала настолько уважаться (и в этом во многом заслуга Фалеса), что за мудрость стали платить некоторые деньги (например, для целей образования золотой молодежи). Тем не менее если сосчитать всех древнегреческих философов, то их будет числом поменьше, чем младших научных сотрудников в любом нашем провинциальном ВУЗе. Вот только пользы от них было куда побольше — не из-за правильной мотивации ли? Они ведь алкали истины и знания, а не тринадцатой зарплаты.
Тем не менее родительские деньги Фалес судя по всему промотал … на науку, за которой он отправился из Милета в Египет, типа как наш Ломоносов из Холмогор в Москву. Во всяком случае известно, что по возвращению домой над ним издевались — мол, какой прок от твоей учености. Своих простодушных критиков Фалес поставил на место следующим образом.
Во всяком случае известно, что по возвращению домой над ним издевались — мол, какой прок от твоей учености. Своих простодушных критиков Фалес поставил на место следующим образом.
Высчитав (непонятным образом) по звездам, что ожидается большой урожай оливков, он заранее скупил все прессы в округе, а потом, сдавая их в аренду по спекулятивной цене, заработал на этом себе целое состояние.
Сила человека (его интеллекта) в умении предвидеть (а иногда и создать) будущее, комбинируя известные ему модели. Настоящую известность принесло Фалесу предсказанное им солнечное затмение, которое даже остановило войну между лидийцами и мидянами. Пришлось древнегреческим горячим парням поспешно заключить мир, дабы боги сменили гнев на милость. С богами все обошлось, как Вы уже догадались.
Помочь предугадать солнечное затмение Фалесу могло знание так называемого сароса или драконического периода (примерно каждые 18 лет луна и солнце в точности повторяют свое местоположение). Об этом знали халдеи (Вавилон) и египтяне.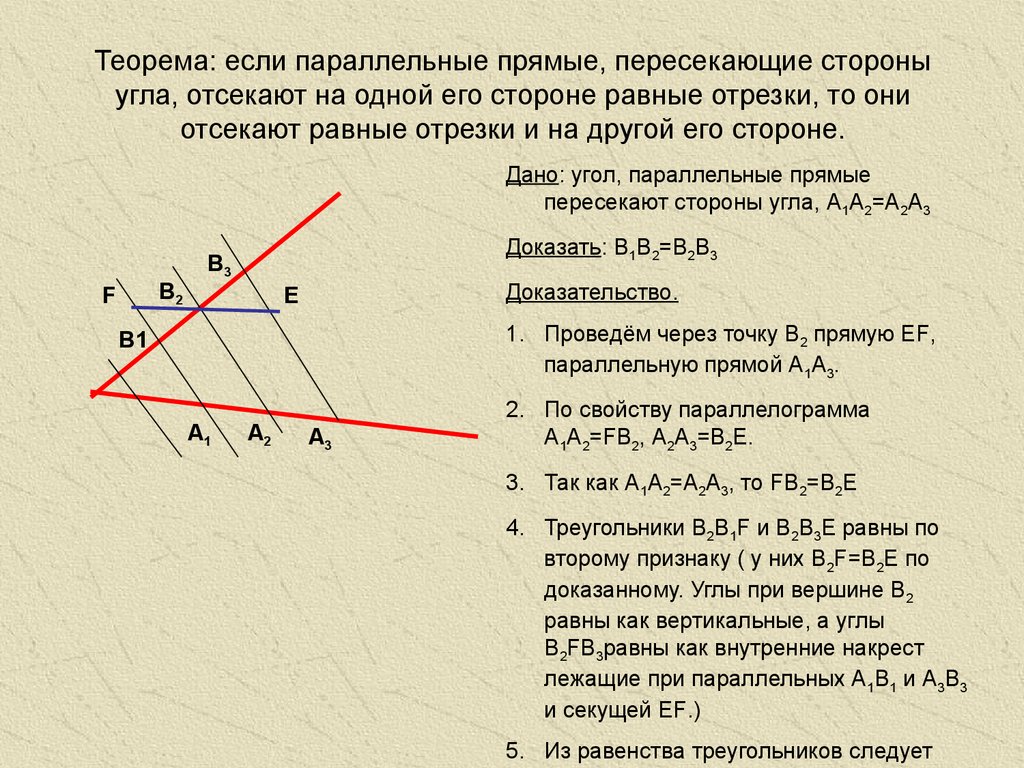 Это в нашей терминологии модель каузальной фазы — то есть работает, но непонятно почему. Вообщем-то с точки зрения прагматики это и неважно, хоть на кофейной гуще гадай (или как тогда было модно — изучая потроха домашних животных или консультируясь с оракулами), лишь бы был требуемый результат.
Это в нашей терминологии модель каузальной фазы — то есть работает, но непонятно почему. Вообщем-то с точки зрения прагматики это и неважно, хоть на кофейной гуще гадай (или как тогда было модно — изучая потроха домашних животных или консультируясь с оракулами), лишь бы был требуемый результат.
Так что учился человек как видите не зря. Однако там, в Египте, его обучали жрецы в храмах после ритуалов посвящений. А он, вернувшись домой, в русле своего демократического мировоззрения (а он ведь был на короткой ноге с легендарным законодателем Афин Солоном) начал раздавать священное знание налево и направо, кому попало. На манер Прометея. И не оказалось в окрестностях ни единого Зевса его за это наказать.
(она верна как для пересекающихся прямых, так и для параллельных). Также не важно, где находятся отрезки на секущих.
Доказательство в случае секущих
Ошибка создания миниатюры: Файл не найден
Доказательство теоремы Фалеса
Рассмотрим вариант с несвязанными парами отрезков: пусть угол пересекают прямые texvc не найден; См. math/README — справку по настройке.): AA_1||BB_1||CC_1||DD_1 и при этом Невозможно разобрать выражение (Выполняемый файл
math/README — справку по настройке.): AA_1||BB_1||CC_1||DD_1 и при этом Невозможно разобрать выражение (Выполняемый файл texvc не найден; См. math/README — справку по настройке.): AB=CD .
- Проведём через точки Невозможно разобрать выражение (Выполняемый файл
texvcне найден; См. math/README — справку по настройке.): A и Невозможно разобрать выражение (Выполняемый файлtexvcне найден; См. math/README — справку по настройке.): C прямые, параллельные другой стороне угла. Невозможно разобрать выражение (Выполняемый файлtexvcне найден; См. math/README — справку по настройке.): AB_2B_1A_1 и Невозможно разобрать выражение (Выполняемый файлtexvcне найден; См. math/README — справку по настройке.): CD_2D_1C_1 . Согласно свойству параллелограмма: Невозможно разобрать выражение (Выполняемый файлtexvcне найден; См. math/README — справку по настройке.): AB_2=A_1B_1 и Невозможно разобрать выражение (Выполняемый файлtexvcне найден; См. math/README — справку по настройке.): CD_2=C_1D_1 .
math/README — справку по настройке.): CD_2=C_1D_1 . - Треугольники Невозможно разобрать выражение (Выполняемый файл
texvcне найден; См. math/README — справку по настройке.): \bigtriangleup ABB_2 и Невозможно разобрать выражение (Выполняемый файлtexvcне найден; См. math/README — справку по настройке.): \bigtriangleup CDD_2 равны на основании второго признака равенства треугольников
Доказательство в случае параллельных прямых
Проведем прямую BC. Углы ABC и BCD равны как внутренние накрест лежащие при параллельных прямых AB и CD и секущей BC, а углы ACB и CBD равны как внутренние накрест лежащие при параллельных прямых AC и BD и секущей BC. Тогда по второму признаку равенства треугольников треугольники ABC и DCB равны. Отсюда следует, что AC = BD и AB = CD. ■
Также существует теорема о пропорциональных отрезках
:Параллельные прямые отсекают на секущих пропорциональные отрезки : Невозможно разобрать выражение (Выполняемый файл texvc не найден; См.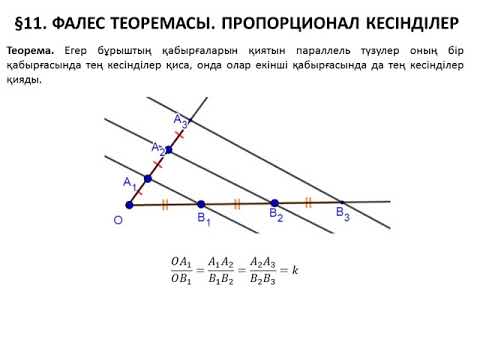 math/README — справку по настройке.): \frac{A_1A_2}{B_1B_2}=\frac{A_2A_3}{B_2B_3}=\frac{A_1A_3}{B_1B_3}.
math/README — справку по настройке.): \frac{A_1A_2}{B_1B_2}=\frac{A_2A_3}{B_2B_3}=\frac{A_1A_3}{B_1B_3}.
Теорема Фалеса является частным случаем теоремы о пропорциональных отрезках, поскольку равные отрезки можно считать пропорциональными отрезками с коэффициентом пропорциональности, равным 1.
Обратная теорема
Если в теореме Фалеса равные отрезки начинаются от вершины (часто в школьной литературе используется такая формулировка), то обратная теорема также окажется верной. Для пересекающихся секущих она формулируется так:
В обратной теореме Фалеса важно, что равные отрезки начинаются от вершины
Таким образом (см. рис.) из того, что Невозможно разобрать выражение (Выполняемый файл texvc не найден; См. math/README — справку по настройке. ): A_1B_1||A_2B_2||\ldots .
): A_1B_1||A_2B_2||\ldots .
Если секущие параллельны, то необходимо требовать равенство отрезков на обеих секущих между собой, иначе данное утверждение становится неверным (контрпример — трапеция, пересекаемая линией, проходящей через середины оснований).
Вариации и обобщения
Следующее утверждение, двойственно к лемме Соллертинского :
Пусть Невозможно разобрать выражение (Выполняемый файл |
В случае теоремы Фалеса коникой будет бесконечно удалённая точка, соответствующая направлению параллельных прямых.
Это утверждение, в свою очередь, является предельным случаем следующего утверждения:
Теорема Фалеса в культуре
Аргентинская музыкальная группа Les Luthiers представила песню, посвящённую теореме .
- Теорема Фалеса до сих пор используется в морской навигации в качестве правила о том, что столкновение судов, двигающихся с постоянной скоростью, неизбежно, если сохраняется курс судов друг на друга.
- Вне русскоязычной литературы теоремой Фалеса иногда называют другую теорему планиметрии, а именно, утверждение о том , что вписанный угол , опирающийся на диаметр окружности , является прямым. Открытие этой теоремы действительно приписывается Фалесу, о чём есть свидетельство Прокла .
Напишите отзыв о статье «Теорема Фалеса»
Литература
- Атанасян Л. C. и др. Геометрия 7-9. — Изд.
 3-е. — М
.: Просвещение, 1992.
3-е. — М
.: Просвещение, 1992.
Примечания
См. также
- Теорема Фалеса об угле, опирающемся на диаметр окружности
Отрывок, характеризующий Теорема Фалеса
Я не поняла, куда девалась вся моя усталость, и почему это я вдруг совершенно забыла данное себе минуту назад обещание не вмешиваться ни в какие, даже самые невероятные происшествия до завтрашнего дня, или хотя бы уж, пока хоть чуточку не отдохну. Но, конечно же, это снова срабатывало моё ненасытное любопытство, которое я так и не научилась пока ещё усмирять, даже и тогда, когда в этом появлялась настоящая необходимость…
Поэтому, стараясь, насколько позволяло моё измученное сердце, «отключиться» и не думать о нашем неудавшемся, грустном и тяжёлом дне, я тут же с готовностью окунулась в «новое и неизведанное», предвкушая какое-нибудь необычное и захватывающее приключение…
Мы плавно «притормозили» прямо у самого входа в потрясающий «ледяной» мир, как вдруг из-за сверкавшего искрами голубого дерева появился человек. .. Это была очень необычная девушка – высокая и стройная, и очень красивая, она казалась бы совсем ещё молоденькой, почти что если бы не глаза… Они сияли спокойной, светлой печалью, и были глубокими, как колодец с чистейшей родниковой водой… И в этих дивных глазах таилась такая мудрость, коей нам со Стеллой пока ещё долго не дано было постичь… Ничуть не удивившись нашему появлению, незнакомка тепло улыбнулась и тихо спросила:
.. Это была очень необычная девушка – высокая и стройная, и очень красивая, она казалась бы совсем ещё молоденькой, почти что если бы не глаза… Они сияли спокойной, светлой печалью, и были глубокими, как колодец с чистейшей родниковой водой… И в этих дивных глазах таилась такая мудрость, коей нам со Стеллой пока ещё долго не дано было постичь… Ничуть не удивившись нашему появлению, незнакомка тепло улыбнулась и тихо спросила:
– Что вам, малые?
– Мы просто рядом проходили и захотели на вашу красоту посмотреть. Простите, если потревожили… – чуть сконфузившись, пробормотала я.
– Ну, что вы! Заходите внутрь, там наверняка будет интереснее… – махнув рукой в глубь, опять улыбнулась незнакомка.
Мы мигом проскользнули мимо неё внутрь «дворца», не в состоянии удержать рвущееся наружу любопытство, и уже заранее предвкушая наверняка что-то очень и очень «интересненькое».
Внутри оказалось настолько ошеломляюще, что мы со Стеллой буквально застыли в ступоре, открыв рты, как изголодавшиеся однодневные птенцы, не в состоянии произнести ни слова. ..
..
Никакого, что называется, «пола» во дворце не было… Всё, находящееся там, парило в искрящемся серебристом воздухе, создавая впечатление сверкающей бесконечности. Какие-то фантастические «сидения», похожие на скопившиеся кучками группы сверкающих плотных облачков, плавно покачиваясь, висели в воздухе, то, уплотняясь, то почти исчезая, как бы привлекая внимание и приглашая на них присесть… Серебристые «ледяные» цветы, блестя и переливаясь, украшали всё вокруг, поражая разнообразием форм и узорами тончайших, почти что ювелирных лепестков. А где-то очень высоко в «потолке», слепя небесно-голубым светом, висели невероятной красоты огромнейшие ледяные «сосульки», превращавшие эту сказочную «пещеру» в фантастический «ледяной мир», которому, казалось, не было конца…
– Пойдёмте, гостьи мои, дедушка будет несказанно рад вам! – плавно скользя мимо нас, тепло произнесла девушка.
И тут я, наконец, поняла, почему она казалась нам необычной – по мере того, как незнакомка передвигалась, за ней всё время тянулся сверкающий «хвост» какой-то особенной голубой материи, который блистал и вился смерчами вокруг её хрупкой фигурки, рассыпаясь за ней серебристой пыльцой. ..
..
Не успели мы этому удивиться, как тут же увидели очень высокого, седого старца, гордо восседавшего на странном, очень красивом кресле, как бы подчёркивая этим свою значимость для непонимающих. Он совершенно спокойно наблюдал за нашим приближением, ничуть не удивляясь и не выражая пока что никаких эмоций, кроме тёплой, дружеской улыбки.
Белые, переливающиеся серебром, развевающиеся одежды старца сливались с такими же, совершенно белыми, длиннющими волосами, делая его похожим на доброго духа. И только глаза, такие же таинственные, как и у нашей красивой незнакомки, потрясали беспредельным терпением, мудростью и глубиной, заставляя нас ёжиться от сквозящей в них бесконечности…
– Здравы будете, гостюшки! – ласково поздоровался старец. – Что привело вас к нам?
– И вы здравствуйте, дедушка! – радостно поздоровалась Стелла.
И тут впервые за всё время нашего уже довольно-таки длинного знакомства я с удивлением услышала, что она к кому-то, наконец, обратилась на «вы». ..
..
У Стеллы была очень забавная манера обращаться ко всем на «ты», как бы этим подчёркивая, что все ею встреченные люди, будь то взрослый или совершенно ещё малыш, являются её добрыми старыми друзьями, и что для каждого из них у неё «нараспашку» открыта душа… Что конечно же, мгновенно и полностью располагало к ней даже самых замкнутых и самых одиноких людей, и только очень чёрствые души не находили к ней пути.
– А почему у вас здесь так «холодно»? – тут же, по привычке, посыпались вопросы. – Я имею в виду, почему у вас везде такой «ледяной» цвет?
Девушка удивлённо посмотрела на Стеллу.
– Я никогда об этом не думала… – задумчиво произнесла она. – Наверное, потому, что тепла нам хватило на всю нашу оставшуюся жизнь? Нас на Земле сожгли, видишь ли…
В теореме нет ограничений на взаимное расположение секущих (она верна как для пересекающихся прямых, так и для параллельных). Также не важно, где находятся отрезки на секущих.
Доказательство в случае параллельных прямых
Проведем прямую BC.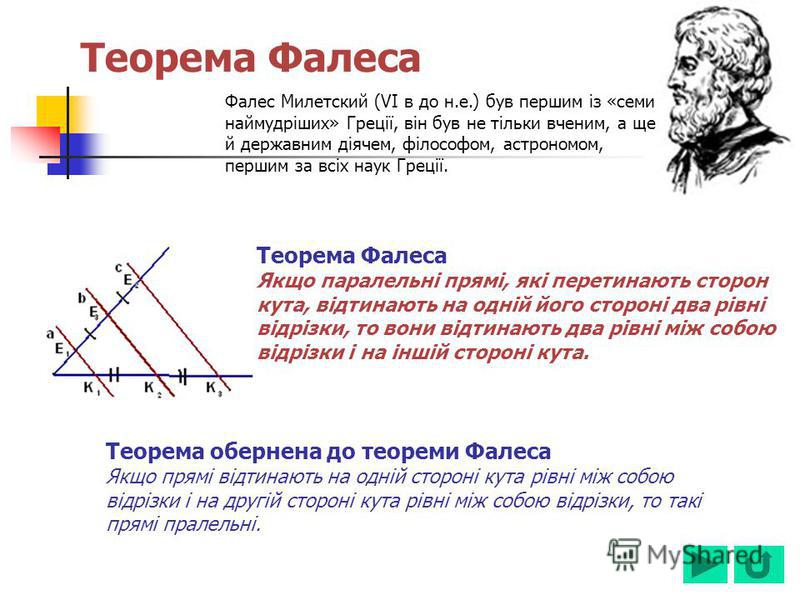 Углы ABC и BCD равны как внутренние накрест лежащие при параллельных прямых AB и CD и секущей BC, а углы ACB и CBD равны как внутренние накрест лежащие при параллельных прямых AC и BD и секущей BC. Тогда по второму признаку равенства треугольников треугольники ABC и DCB равны. Отсюда следует, что AC = BD и AB = CD. ■
Углы ABC и BCD равны как внутренние накрест лежащие при параллельных прямых AB и CD и секущей BC, а углы ACB и CBD равны как внутренние накрест лежащие при параллельных прямых AC и BD и секущей BC. Тогда по второму признаку равенства треугольников треугольники ABC и DCB равны. Отсюда следует, что AC = BD и AB = CD. ■
Также существует теорема о пропорциональных отрезках :
Параллельные прямые отсекают на секущих пропорциональные отрезки :
\frac{A_1A_2}{B_1B_2}=\frac{A_2A_3}{B_2B_3}=\frac{A_1A_3}{B_1B_3}.
Теорема Фалеса является частным случаем теоремы о пропорциональных отрезках, поскольку равные отрезки можно считать пропорциональными отрезками с коэффициентом пропорциональности, равным 1.
Обратная теорема
Если в теореме Фалеса равные отрезки начинаются от вершины (часто в школьной литературе используется такая формулировка), то обратная теорема также окажется верной. Для пересекающихся секущих она формулируется так:
Таким образом (см.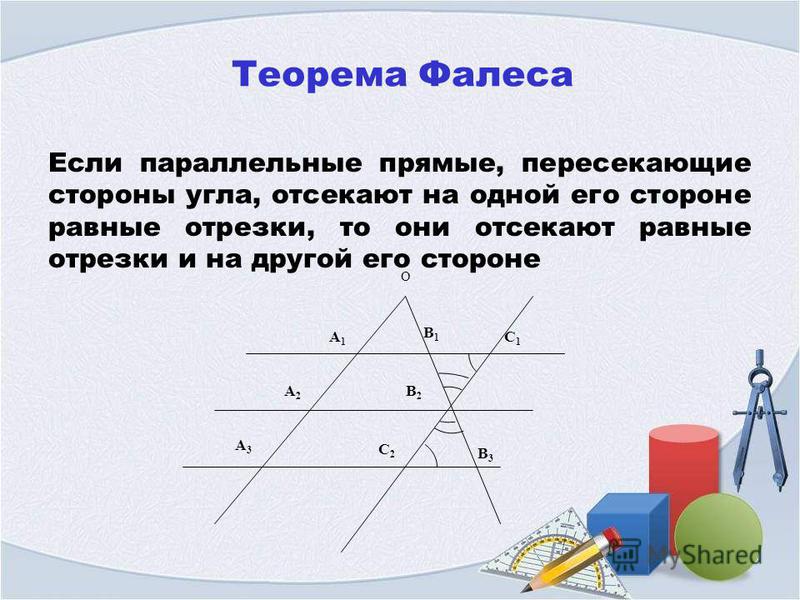 рис.) из того, что \frac{CB_1}{CA_1}=\frac{B_1B_2}{A_1A_2}=\ldots = {\rm idem} следует, что прямые A_1B_1||A_2B_2||\ldots.
рис.) из того, что \frac{CB_1}{CA_1}=\frac{B_1B_2}{A_1A_2}=\ldots = {\rm idem} следует, что прямые A_1B_1||A_2B_2||\ldots.
Если секущие параллельны, то необходимо требовать равенство отрезков на обеих секущих между собой, иначе данное утверждение становится неверным (контрпример — трапеция, пересекаемая линией, проходящей через середины оснований).
Вариации и обобщения
Следующее утверждение, двойственно к лемме Соллертинского :
Напишите отзыв о статье «Теорема Фалеса»Литература
ПримечанияСм. также
Отрывок, характеризующий Теорема Фалеса– Я ничего не думаю, я только не понимаю этого…– Подожди, Соня, ты всё поймешь. Увидишь, какой он человек. Ты не думай дурное ни про меня, ни про него. – Я ни про кого не думаю дурное: я всех люблю и всех жалею. Но что же мне делать? Соня не сдавалась на нежный тон, с которым к ней обращалась Наташа. Чем размягченнее и искательнее было выражение лица Наташи, тем серьезнее и строже было лицо Сони. – Наташа, – сказала она, – ты просила меня не говорить с тобой, я и не говорила, теперь ты сама начала. Наташа, я не верю ему. Зачем эта тайна? – Опять, опять! – перебила Наташа. – Наташа, я боюсь за тебя. – Чего бояться? – Я боюсь, что ты погубишь себя, – решительно сказала Соня, сама испугавшись того что она сказала. Лицо Наташи опять выразило злобу.  – И погублю, погублю, как можно скорее погублю себя. Не ваше дело. Не вам, а мне дурно будет. Оставь, оставь меня. Я ненавижу тебя. – Наташа! – испуганно взывала Соня. – Ненавижу, ненавижу! И ты мой враг навсегда! Наташа выбежала из комнаты. Наташа не говорила больше с Соней и избегала ее. С тем же выражением взволнованного удивления и преступности она ходила по комнатам, принимаясь то за то, то за другое занятие и тотчас же бросая их. Как это ни тяжело было для Сони, но она, не спуская глаз, следила за своей подругой. Накануне того дня, в который должен был вернуться граф, Соня заметила, что Наташа сидела всё утро у окна гостиной, как будто ожидая чего то и что она сделала какой то знак проехавшему военному, которого Соня приняла за Анатоля. Соня стала еще внимательнее наблюдать свою подругу и заметила, что Наташа была всё время обеда и вечер в странном и неестественном состоянии (отвечала невпопад на делаемые ей вопросы, начинала и не доканчивала фразы, всему смеялась).  После чая Соня увидала робеющую горничную девушку, выжидавшую ее у двери Наташи. Она пропустила ее и, подслушав у двери, узнала, что опять было передано письмо. И вдруг Соне стало ясно, что у Наташи был какой нибудь страшный план на нынешний вечер. Соня постучалась к ней. Наташа не пустила ее. «Она убежит с ним! думала Соня. Она на всё способна. Нынче в лице ее было что то особенно жалкое и решительное. Она заплакала, прощаясь с дяденькой, вспоминала Соня. Да это верно, она бежит с ним, – но что мне делать?» думала Соня, припоминая теперь те признаки, которые ясно доказывали, почему у Наташи было какое то страшное намерение. «Графа нет. Что мне делать, написать к Курагину, требуя от него объяснения? Но кто велит ему ответить? Писать Пьеру, как просил князь Андрей в случае несчастия?… Но может быть, в самом деле она уже отказала Болконскому (она вчера отослала письмо княжне Марье). Дяденьки нет!» Сказать Марье Дмитриевне, которая так верила в Наташу, Соне казалось ужасно. «Но так или иначе, думала Соня, стоя в темном коридоре: теперь или никогда пришло время доказать, что я помню благодеяния их семейства и люблю Nicolas.  Нет, я хоть три ночи не буду спать, а не выйду из этого коридора и силой не пущу ее, и не дам позору обрушиться на их семейство», думала она. Нет, я хоть три ночи не буду спать, а не выйду из этого коридора и силой не пущу ее, и не дам позору обрушиться на их семейство», думала она.Анатоль последнее время переселился к Долохову. План похищения Ростовой уже несколько дней был обдуман и приготовлен Долоховым, и в тот день, когда Соня, подслушав у двери Наташу, решилась оберегать ее, план этот должен был быть приведен в исполнение. Наташа в десять часов вечера обещала выйти к Курагину на заднее крыльцо. Курагин должен был посадить ее в приготовленную тройку и везти за 60 верст от Москвы в село Каменку, где был приготовлен расстриженный поп, который должен был обвенчать их. В Каменке и была готова подстава, которая должна была вывезти их на Варшавскую дорогу и там на почтовых они должны были скакать за границу. |
Эпонимы в классе: как связаны теорема Пифагора и русский язык
Метапредметность вызывает много вопросов у педагогов. Как объединить физику и пение или географию и физкультуру? А вот с русским языком всё легко объединяется эпонимами! Наш блогер Марк Блау рассказывает, что это такое и как связать географию, физику, биологию и другие науки с русским языком.
С точки зрения школьника, скучнее занятия, чем изучение грамматики, не придумаешь. Особенно грамматики такого языка, как русский, где на каждое правило по нескольку исключений. В конце концов, оказывается, что, если много читал или памятью обладаешь фотографической, никакие правила тебе не нужны. Смотришь на слово и видишь, правильно или неправильно оно написано. Ну а если не повезло, вряд ли спасёт свод правил с прилагаемым к нему сводом исключений. Учи его или не учи — результат один, и результат грустный: «Как ниграмотно песал, так песать и будиш»!
Хорошо, что всё чаще приходится писать не рукой и не ручкой, а с помощью компьютера или телефона. В этом случае к нашим услугам различные программы-корректоры, которые и правописание поправят, а иногда и покажут, как лучше построить предложение. Ещё чуть-чуть, и письма за нас станет писать искусственный интеллект. То-то станет весело, то-то хорошо!
Впрочем, языкознание изучением грамматики не исчерпывается. Есть в нём очень интересные разделы. Один из таких разделов — этимология, наука о происхождении слов. Будет время (а оно будет!) — расскажу об этом разделе подробнее. А пока о самом интересном, пожалуй, — о способе образования новых слов, об эпонимии.
Один из таких разделов — этимология, наука о происхождении слов. Будет время (а оно будет!) — расскажу об этом разделе подробнее. А пока о самом интересном, пожалуй, — о способе образования новых слов, об эпонимии.
Что такое эпонимия
Этим красивым термином называется процесс словообразования, при котором имя нарицательное образуется из имени собственного. Имена людей (знаменитых и не очень) переходят на те предметы, которые эти люди изобрели, создали, построили, а иной раз просто пользовались ими, как, например, граф Сэндвич, придумавший способ наскоро перекусить. В результате появляется целый класс имён нарицательных, образовавшихся из имён собственных. Такие слова называются эпонимами.
Здесь стоит ненадолго остановиться и попытаться придумать несколько слов, названных по имени людей. Сразу приходят в голову рентген, автомат Калашникова, а также его коллега и, скорее всего, старший брат «шмайсер». А марки многих современных автомобилей, от простодушной «Шкоды» до роскошного «Роллс-Ройса»? А единицы измерения: джоули, ватты, амперы и омы? В общем, современный человек без особенного напряжения составит весьма большой список таких слов.
Доблестные предки
«Эпоним» — это слово древнегреческого происхождения. ἐπώνῠμος в буквальном переводе означает «давший имя». Древние греки называли города, реки, горы и другие географические объекты именами богов, легендарных героев или реальных людей.
Например, город Византий, согласно легенде, основал герой-мореплаватель Визант, которого мифы называли сыном бога Посейдона. Визант, таким образом, стал эпонимом Византия, а через него также и эпонимом Византийской империи, возникшей на том же месте гораздо позже.
Геенна огненная сейчас место совершенно идиллическоеЕщё один пример из совсем другого времени и совсем другого языка. У подножия Иерусалима находится долина Гей Бен Хинном, что в переводе с иврита означает «долина сынов Еннома». Во времена царя Соломона и библейских пророков эта долина пользовалась нехорошей славой: здесь приносили человеческие жертвы языческим богам. Позже долина стала муниципальной территорией, свалкой. Сюда свозили из города и сжигали мусор. Огонь горел здесь и днём, и ночью. Зрелище пугающее и дурнопахнущее! Так иерусалимская мусорка, находившаяся на земле, названной по имени давно, казалось бы, забытого Еннома, стала прообразом вечно пылающего ада, геенной огненной. Этот пример показывает, какой извилистой может быть жизнь обычного слова-эпонима.
Огонь горел здесь и днём, и ночью. Зрелище пугающее и дурнопахнущее! Так иерусалимская мусорка, находившаяся на земле, названной по имени давно, казалось бы, забытого Еннома, стала прообразом вечно пылающего ада, геенной огненной. Этот пример показывает, какой извилистой может быть жизнь обычного слова-эпонима.
К легендарным предкам-эпонимам различные народы и племена зачастую возводили свои названия. Например, эпонимом племени латинян считают мифического царя Латина. По другой легенде, названия народов чехов и поляков (ляхов) происходят от имён легендарных князей Чеха и Леха.
Памятник основателям Киева на берегу ДнепраЭпонимом города Киева стал легендарный князь Кий. Один из братьев Кия, Щек, стал эпонимом горы Щекавица, возвышающейся над Подолом, а их сестра Лыбедь — эпонимом реки Лыбедь (правого притока Днепра), которая протекает по территории нынешнего Киева.
Имена собственные становились также названиями промежутков времени. Так, в античных Афинах год назывался по имени первого из девяти правителей-архонтов, который поэтому назывался «архонтом-эпонимом». По этой причине в официальных хрониках датировка была такой: «в год, когда архонтом был такой-то». В истории Китая выделяются времена правления различных императорских династий (например, Цинь, Хань, Мин).
По этой причине в официальных хрониках датировка была такой: «в год, когда архонтом был такой-то». В истории Китая выделяются времена правления различных императорских династий (например, Цинь, Хань, Мин).
Слишком много эпонимов?
Со временем появлялось всё большее количество понятий и явлений, наименования которых образовывали от имён собственных самых разных людей. Всё чаще эпонимами становились реальные, а не легендарные личности. Так, уже в 332 году до нашей эры в Египте на берегу Средиземного моря был построен город Александрия, эпонимом которого стал Александр Македонский. В 330 году нашей эры уже упомянутый Византий переименовали в Константинополь. Таким образом, произошла смена эпонима, старый город принял новое имя, имя императора Константина.
Количество географических объектов, для которых понадобилось придумывать названия, резко возросло в эпоху Великих географических открытий. Когда началась научно-техническая революция, появилось огромное число новых предметов, явлений и понятий. Всем им требовались наименования, и их стали называть по имени реальных людей: первооткрывателей, изобретателей, учёных, предпринимателей, владельцев или властителей.
Всем им требовались наименования, и их стали называть по имени реальных людей: первооткрывателей, изобретателей, учёных, предпринимателей, владельцев или властителей.
Почему эпонимы
Эверест — самая высокая гора в миреИной раз кажется, что эпонимы — это только дань человеческому тщеславию. Самую высокую вершину мира британские геодезисты, работавшие в Индии, назвали в честь начальника всей геодезической службы колонии сэра Джорджа Эвереста. Ещё чаще (особенно в биологических науках, где количество обнаруженных человеком живых организмов упрямо стремится к бесконечности) называют не ради славы, а просто для того, чтобы назвать. Ведь у всякого предмета должно быть название, и желательно короткое. Так что «эффект Мёссбауэра», без сомнения, более удачный научный термин, чем «резонансное поглощение гамма-фотонов». Во-первых, на два слова короче, а во-вторых, хоть какая-то информация для профанов: этот непонятный широкой публике эффект открыл Рудольф Мёссбауэр.
Как язык производит эпонимы
Эпонимия оказалась удачным способом образования слов. Эпоним может быть не одним словом, а парой слов (болезнь Боткина, теорема Пифагора) или даже несколькими словами. В русском языке эпонимия совершила интересный кульбит. Если раньше эпонимом называлась персона, дававшая своё имя некоторому предмету или понятию, то сейчас эпонимом чаще всего называют само слово, имя нарицательное, произведённое от имени собственного. То есть сейчас эпонимами являются джоуль, а не Джоуль, рентген, а не Рентген, и «Форд», а не Форд.
Эпоним может быть не одним словом, а парой слов (болезнь Боткина, теорема Пифагора) или даже несколькими словами. В русском языке эпонимия совершила интересный кульбит. Если раньше эпонимом называлась персона, дававшая своё имя некоторому предмету или понятию, то сейчас эпонимом чаще всего называют само слово, имя нарицательное, произведённое от имени собственного. То есть сейчас эпонимами являются джоуль, а не Джоуль, рентген, а не Рентген, и «Форд», а не Форд.
Эпонимы — удивительные кентавры
Эпонимы — тема интересная ещё и потому, что один эпоним всегда объединяет некоторую персону и некоторый материальный или духовный объект. Сам по себе объект может быть весьма интересным. Например, автомобили, компьютеры, оружие — о них можно говорить бесконечно. Но ведь и биография человека-эпонима может быть потрясающей. Цветок бугенвиллия красив, но и биография капитана Бугенвилля, в честь которого этот цветок назван, может быть основой интереснейшего сериала. Жюль Верн эту биографию оценил и подробно описал.
Поэтому эпонимы — одна из самых интересных для учащихся тем в изучении языка. Одна из возможностей показать им, что языкознание — не набор скучных и ненужных правил.
Вы находитесь в разделе «Блоги». Мнение автора может не совпадать с позицией редакции.
Подробный обзор теоремы Фалеса
Содержание
Введение в теорему Фалеса:Теорема Фалеса — фундаментальная теорема геометрии, приписываемая древнегреческому математику Фалесу Милетскому, жившему в 6 веке до н.э. . Теорема утверждает, что если A, B и C являются точками на окружности, где прямая AC является диаметром окружности, то угол ABC является прямым углом.
Теорема была впервые записана Евклидом в его «Началах», сборнике математических доказательств, написанном около 300 г. до н.э. В «Началах» Евклид утверждает, что это древняя теорема, но не приводит никаких подробностей о ее происхождении.
В 19 веке ученые начали более подробно изучать историю Теоремы Фалеса. Считается, что теорему впервые открыл Фалес, философ и математик из Милета. Ему приписывают то, что он первым использовал дедуктивное рассуждение для доказательства теоремы, которая в то время была революционным способом мышления.
Считается, что теорему впервые открыл Фалес, философ и математик из Милета. Ему приписывают то, что он первым использовал дедуктивное рассуждение для доказательства теоремы, которая в то время была революционным способом мышления.
Теорема Фалеса остается важной математической теоремой с момента ее открытия. Теорема использовалась во многих различных областях математики, включая тригонометрию, исчисление и геометрию.
Он также использовался в физике и технике для решения задач. Теорема до сих пор изучается как часть основной учебной программы во многих школах и университетах. Это одна из самых важных математических теорем, которая считается краеугольным камнем современной математики.
Теорема Фалеса Доказательство теоремы Фалеса: Теорема Фалеса утверждает, что если A, B и C являются тремя различными точками на окружности с центром O и радиусом r, то угол AOB равен углу ВОС. Эта теорема может быть легко доказана с помощью базовой геометрии.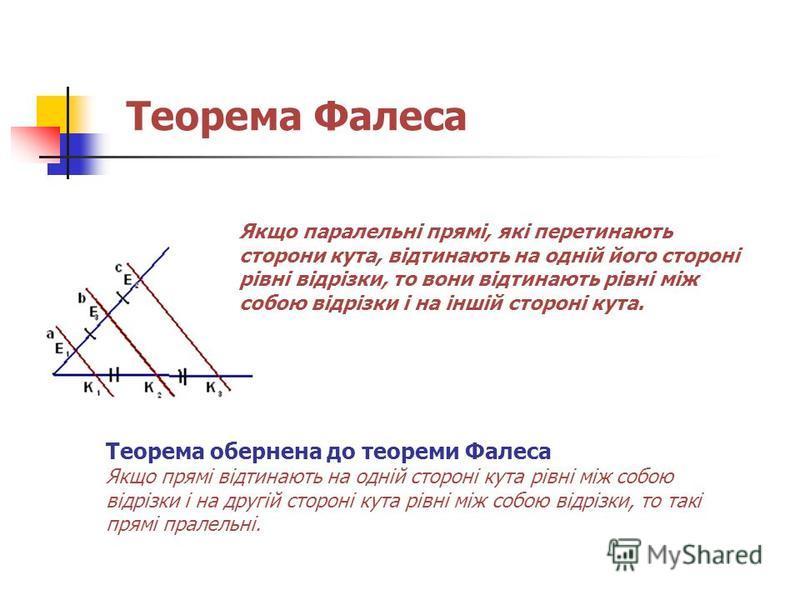 Сначала нарисуйте окружность с центром O и радиусом r и обозначьте точки A, B и C.
Сначала нарисуйте окружность с центром O и радиусом r и обозначьте точки A, B и C.
Теперь проведите линию от A до B и от B до C. Это образует два угла, AOB и BOC. Затем нарисуйте две линии от A до O и от B до O. Это образует два прямых угла, OAB и OBC. Так как сумма углов в треугольнике всегда равна 180°, угол AOB должен быть равен углу BOC.
Чтобы доказать это, воспользуемся тем фактом, что сумма углов вокруг окружности равна 360°. Поскольку оба угла OAB и OBC прямые, каждый из них равен 90°, поэтому сумма трех углов AOB, BOC и OAB равна 180° + 90° + 90° = 360°.
Следовательно, углы AOB и BOC должны быть равны. Это доказывает теорему Фалеса.
Обратная теорема Фалеса:Обратная теорема Фалеса утверждает, что если треугольник имеет две стороны и угол между ними равны, то треугольник равнобедренный. Это означает, что если две стороны треугольника равны, то и угол между ними должен быть равен.
Чтобы доказать это обращение теоремы Фалеса, мы сначала нарисуем треугольник ABC с двумя сторонами, AB и AC, которые равны по длине.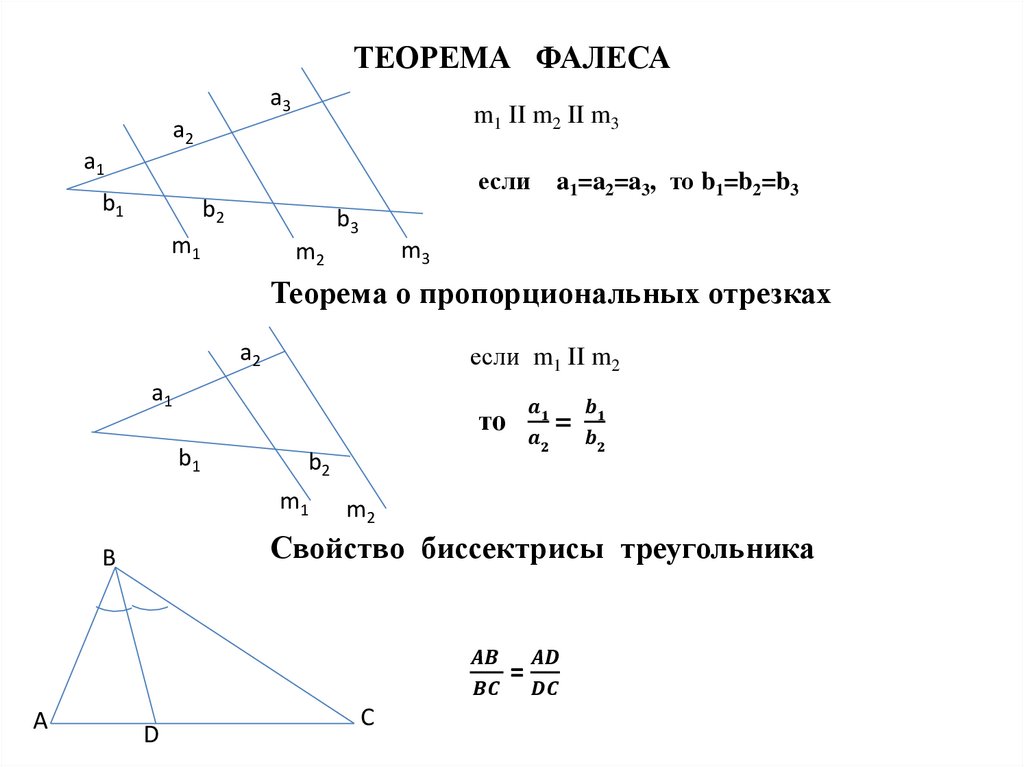 Затем мы проводим линию из точки B в точку C, которая образует угол ABC.
Затем мы проводим линию из точки B в точку C, которая образует угол ABC.
Используя обратную теорему Фалеса, мы должны быть в состоянии доказать, что этот угол равен углу BAC. Так как АВ и АС равны, то точка А является серединой прямой ВС.
Это означает, что углы BAC и ABC прямые. Так как прямой угол имеет градусную меру 90 градусов, то оба угла равны. Таким образом, мы доказали обратную теорему Фалеса. Если две стороны треугольника равны, то и угол между ними равен.
Обобщения и родственные результаты теоремы Фалеса:Теорема Фалеса утверждает, что если треугольник вписать в окружность, то сумма углов треугольника составит 180 градусов. Эта теорема является фундаментальным результатом евклидовой геометрии и имеет множество обобщений и связанных результатов.
Первое обобщение теоремы Фалеса заключается в том, что теорема верна для любого многоугольника, а не только для треугольников. Это означает, что если многоугольник вписан в окружность, то сумма углов многоугольника составит в сумме 180 (n-2) градусов, где n — количество сторон многоугольника.
Другим родственным результатом теоремы Фалеса является теорема о вписанном угле. Эта теорема утверждает, что если угол вписан в окружность, то мера угла равна половине меры дуги, на которую он опирается. Эту теорему можно использовать для доказательства теоремы Фалеса, поскольку углы треугольника можно разделить на два угла, вписанных в окружность.
Теорема Фалеса также связана с теоремой об обратной касательной. Эта теорема утверждает, что если две прямые пересекаются по окружности, то мера угла, образованного этими прямыми, равна арктангенсу отношения длин прямых.
Эту теорему можно использовать для нахождения углов треугольника, вписанного в окружность, которые затем можно использовать для доказательства теоремы Фалеса. Наконец, теорема Фалеса связана с теоремой о внешнем угле. Эта теорема утверждает, что для любого треугольника мера внешнего угла равна сумме мер двух удаленных друг от друга внутренних углов.
Эту теорему можно использовать для нахождения углов треугольника, вписанного в окружность, которые затем можно использовать для доказательства теоремы Фалеса. Таким образом, теорема Фалеса имеет много обобщений и связанных результатов.
Таким образом, теорема Фалеса имеет много обобщений и связанных результатов.
Эти связанные результаты можно использовать для доказательства теоремы Фалеса и для нахождения углов треугольника, вписанного в окружность.
Применение теоремы Фалеса:Теорема Фалеса — это фундаментальная теорема геометрии, которая утверждает, что если A, B и C — три точки на окружности, где линия AC — это диаметр окружности, то угол АВС прямой.
Эта теорема названа в честь древнегреческого математика Фалеса Милетского, который, как говорят, открыл ее. Есть несколько приложений теоремы Фалеса в математике и естественных науках.
1. В геометрии теорему можно использовать для доказательства теоремы Пифагора и для построения прямоугольных треугольников и других фигур. Его также можно использовать для доказательства теорем о окружностях, таких как теорема о вписанном угле и теорема о внешнем угле.
2. В физике теорема Тале может быть использована для доказательства закона отражения и закона преломления.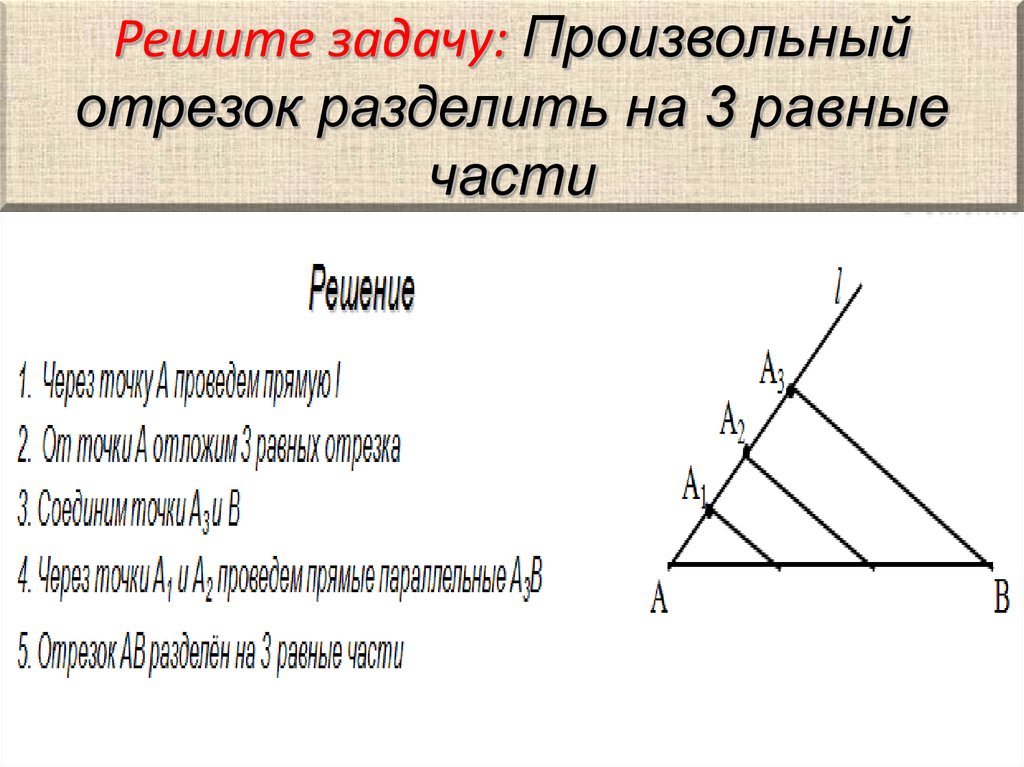
3. В астрономии теорема Тале используется для расчета углового расстояния между двумя точками на небесной сфере, такими как звезды.
4. В технике теорема Фалеса используется для вычисления углов треугольника, образованного тремя точками на плоскости, такими как углы треугольника.
5. В информатике теорема Фалеса используется для вычисления углов треугольника, образованного тремя точками в трехмерном пространстве, такими как углы куба.
6. В математике теорема Фалеса используется для вычисления углов треугольника, образованного тремя точками на поверхности сферы, такими как вершины сферического треугольника.
7. В теории графов теорема Фалеса может использоваться для вычисления углов треугольника, образованного тремя точками на графе, такими как вершины треугольника графа.
В целом, теорема Тале является фундаментальной теоремой в геометрии, которая имеет множество приложений в математике, естественных науках, технике, информатике и теории графов.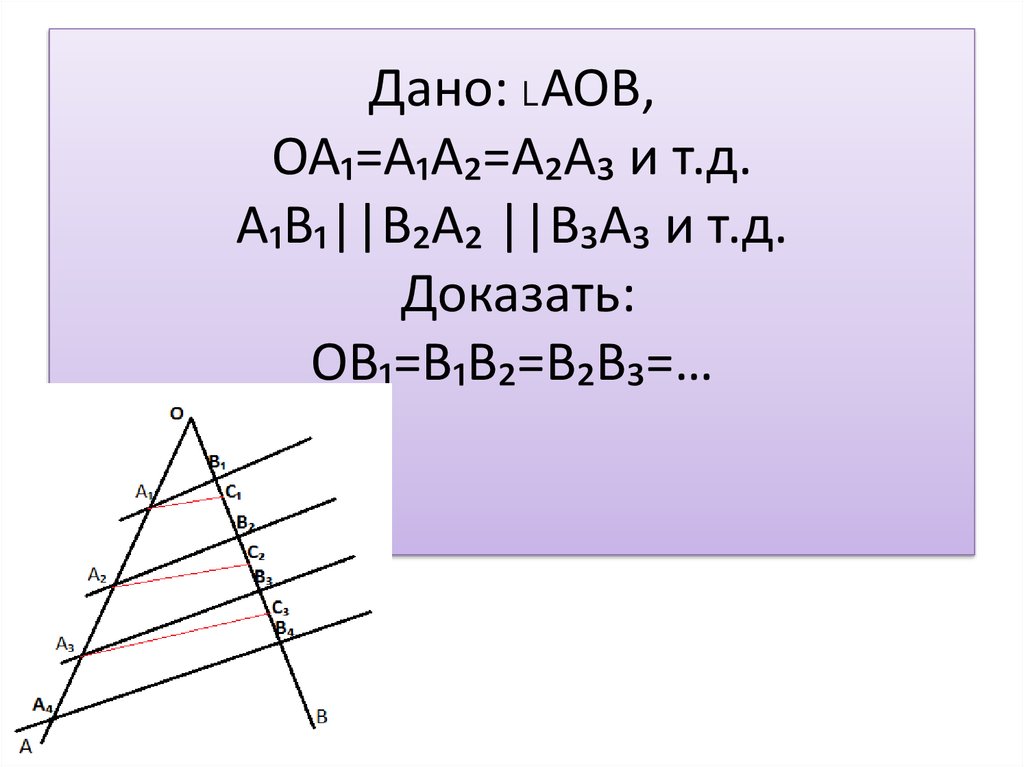
Теорема Фалеса утверждает, что «если A, B и C — точки на окружности, где линия AC — это диаметр, то угол ABC — прямой угол». Эта теорема была впервые введена греческим математиком Фалесом Милетским.
Один из самых популярных примеров этой теоремы касается круга диаметром 8 единиц. Если провести линию из точки А в точку С по диаметру, то можно вычислить угол в точке В. Так как длина линии АС равна 8 единицам, то угол АВС должен быть прямым или равен 90°.
Другой пример теоремы Фалеса касается круга диаметром 10 единиц. Если провести прямую из точки А в точку С по диаметру, то можно вычислить угол в точке В. Так как длина прямой АС 10 единиц, то угол АВС должен быть прямым или 90°.
В заключение, теорема Фалеса утверждает, что если отрезок провести по диаметру окружности, то угол, образованный в любой точке окружности окружности, будет прямым углом. Эта теорема полезна для решения задач, связанных с окружностями и углами.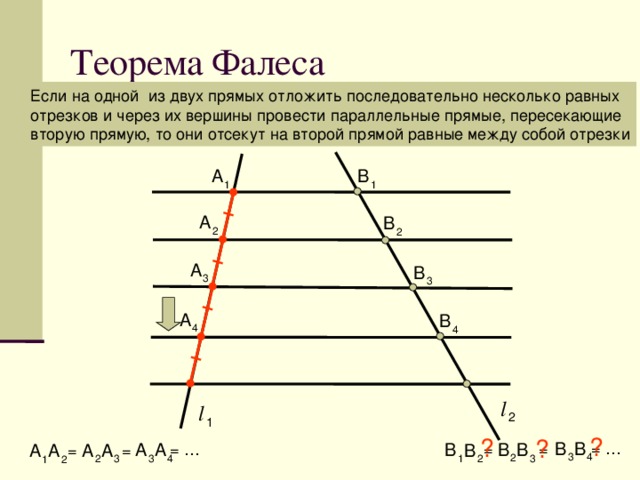
Также прочитайте Раби урожай
Просмотров: 94
Преодоление страха перед математикой
Математика является причиной многих нервов и слез, пролитых студентами на протяжении всей их образовательной карьеры. Мысль о контрольной по математике может даже вызвать приступ тревоги или другие симптомы беспокойства.
От начальной школы до колледжа любой ученик может застрять перед, казалось бы, неразрешимыми математическими вопросами .
Эта тревога и стресс усугубляются тем фактом, что математика является ключевой дисциплиной в учебной программе по математике, а математические навыки, умение рассуждать и понимать математические понятия являются важной частью образования.
Это не только позволяет учащимся понять окружающий мир и решить реальных задач, но является обязательным требованием для многих профессиональная карьера . Хороший уровень A по математике — это высоко ценимая квалификация , которая открывает множество различных возможностей для дальнейшего образования .
Все это означает, что очень важно преодолеть свою боязнь математики , но как?
Лучшие репетиторы по математике
Поехали
Помощь в преодолении страха перед математикой
Все учащиеся, начиная с KS1 и заканчивая средней школой и после окончания A Level, хорошо знакомы с важность математики не только в школьной программе на каждом этапе их образования, но и для профессиональной и повседневной жизни .
Умственные блокировки — частое явление от начальной школы до университета (источник: Superprof.fr).Учащиеся знают, что им нужно быть внимательными на уроках математики и слушать своих учителей . Но что, если математика вызывает у вас настоящее беспокойство?
Именно из-за этой важности математика вызывает стресс, тревогу и панику.
Короче говоря, то, что известно как « боязнь математики «. В худшем случае это может способствовать психическим блокам, тревожным расстройствам и паническим атакам, так что это не шутки. Наши 5 советов помогут вам преодолеть страх перед математикой:
В худшем случае это может способствовать психическим блокам, тревожным расстройствам и паническим атакам, так что это не шутки. Наши 5 советов помогут вам преодолеть страх перед математикой:
- Возьмите частных уроков математики с частным репетитором. Этот особый тип преподавания прикладной математики может помочь разблокировать некоторых студентов, которые испытывают проблемы. Благодаря персонализированным учебным ресурсам такой репетитор, будь то из обычной школы или самоучка (например, студент или аспирант), будет знать, как преодолеть глубоко укоренившиеся препятствия, связанные с математикой.
- Используйте практических, актуальных материалов : Страх перед математикой можно преодолеть с помощью альтернативных подходов к обучению и использования практических материалов. Думайте о математике с точки зрения объектов, круговых диаграмм и даже камешков, чтобы логически понимать концепции и преодолевать точки преткновения.

- Избавьтесь от беспокойства по поводу математики, читая специализированные книги . Избегание трудных тем не поможет вам в долгосрочной перспективе.
- Определить умственных блоков : Они часто возникают в результате семейного окружения учащегося. Учитель в этом случае может выступать и в роли психолога.
- вернуться к основам математики : сложение и вычитание, арифметика в уме, задачи на умножение, десятичные числа, целые числа, задачи на деление, решение задач по геометрии, теорема Фалеса, теорема Пифагора, симметрия, окружности, углы, тригонометрия, алгебра, арифметика, квадратный корень…. Короче говоря, все основы, необходимые для подготовки к математике или естественным наукам уровня A! Это поможет вам построить свою логику.
Вы также можете уменьшить беспокойство по поводу математики, используя приложения и инструменты для решения математических задач…
Понимание страха перед математикой
Опыт начальной и средней школы, колледжа и университета может привести к отсутствию интереса или страха к математике. Но если у вас был неудачный опыт в математике, еще не поздно изменить свое мышление.
Но если у вас был неудачный опыт в математике, еще не поздно изменить свое мышление.
Это может произойти в результате беспокойства, стресса и разочарования из-за того, что вы не усвоили ключевую концепцию на любом уроке математики. Другие просто думают, что тригонометрия, алгебра, исчисление и т. д. скучны и «непривлекательны».
Что, если любовь к математике — это то, с чем вы родились? Может показаться, что для того, чтобы справиться с линейными уравнениями, упражнениями по решению математических задач, геометрией или теоремой Пифагора, нужно быть мечтателем типа Альберта Эйнштейна: творческим, интуитивным студентом, наделенным способностью синтезировать. разные области знаний .
Для других математика может быть болезненной! Одно исследование показало, что простое ожидание сложных математических задач можно преобразовать в физическую боль . Точно так же математика может быть связана с болезненными прошлыми эмоциями. Во-вторых, стыд, который испытывает ученик, не сумевший решить сложные уравнения на доске.
Во-вторых, стыд, который испытывает ученик, не сумевший решить сложные уравнения на доске.
В общем, эта паника, тревога, мыслительные блоки и боязнь позора со стороны других могут вызвать безнадежное отвращение и отвращение к математике. Уроки математики могут даже привести к слезам, потере самооценки и негативным эмоциям. Однако есть несколько вспомогательных математических методов, которые можно использовать, и решать математические задачи :
- Подчеркивать и хвалить хорошие стороны,
- Поощрять его или ее попытки,
- Не наказывать,
- panic,
- Превратите математику в увлекательное занятие с помощью игр, викторин и головоломок.
Лучшие репетиторы по математике
Поехали
Вы можете преодолеть свой страх перед математикой!
В толпе лишь незначительное меньшинство не может добиться успеха в математике (источник: Unsplash).
Когда мы делаем шаг назад и смотрим на все стрессы, создаваемые прикладной математикой , наукой (биологией, науками о жизни, науками о земле), физикой, химией, инженерией, технологиями, оказывается, что математика не такая уж пугающая или недоступная после все.
Исследования показали, что мозг может увеличиваться или уменьшаться. Также теперь известно, что совершение ошибок в математике позволяет мозгу соответственно развиваться: фактически учиться на своих ошибках. Таким образом, хотя тревога и паника могут быть нерациональными, стрессовые и неприятные ошибки могут привести к тому, что мозг станет умнее. Получение математических задач ошибок на самом деле дает мозгу возможность умножать нейроны и связи.
Более того, благодаря эксперименту, проведенному Джо Боалер, мы теперь знаем, что только от 2 до 3% населения действительно испытывают трудности в изучении математики. Остальные способны преодолевать стресс и решать математические задачи, в том числе и высокого уровня. Поэтому мы должны попытаться превратить это чувство паники и беспокойства в «хороший стресс»: нечто, способное стимулировать успеваемость по математике .
Поэтому мы должны попытаться превратить это чувство паники и беспокойства в «хороший стресс»: нечто, способное стимулировать успеваемость по математике .
Боулер доказал, что при постоянном давлении в условиях временных ограничений мозг не способен нормально функционировать. Устраняя ограничение по времени, учащиеся могут значительно продвинуться в вопросах алгебры, решении задач с дробями, геометрии, арифметике в уме, вычислении простых чисел и т. д.
Добейтесь успеха в математике, развлекаясь
Изучение математики не должно вызывать у вас беспокойства!
Чтобы исключить элемент давление , можно также сделать математику веселой, используя математические игры. Вам не нужно сидеть и мучиться на уроках математики, пытаясь выучить таблицу умножения наизусть.
Многие веб-сайты уже обслуживают этот особый подход к обучению с помощью игр для решения математических задач для детей и взрослых:
- Математические игры BBC Bitesize
- ICT Games
- Математические игры BBC Skillswise для взрослых
- Mind Games 4
- Topmarks Игровая зона
- Математическая площадка
 .. это редко слышимая фраза (источник: Jisc)
.. это редко слышимая фраза (источник: Jisc)Существуют также отличные математические приложения для использования в классе, включающие задания по решению задач и забавные математические задачи, которые помогут вам преодолеть стресс, беспокойство или панику, которые вы испытываете при изучении математики, включая Math Master, Edupad и iTooch. Превращение математических концепций в игру действительно может помочь уменьшить распространенный страх и тревогу.
Отличные бесплатные онлайн-ресурсы по математике для студентов и преподавателей можно найти в NRICH Maths Кембриджского университета. Еще один хороший ресурс — Funmaths.
Повторное изучение и повторение математики для взрослых
Если метод «учить математику — это весело» вас не убедил, то, возможно, повторное изучение математики понравится вам больше.
Многие скажут, что изучение математики похоже на изучение нового языка. Если это так, то пренебрежение освоением основ этого языка останется принципиальным недостатком.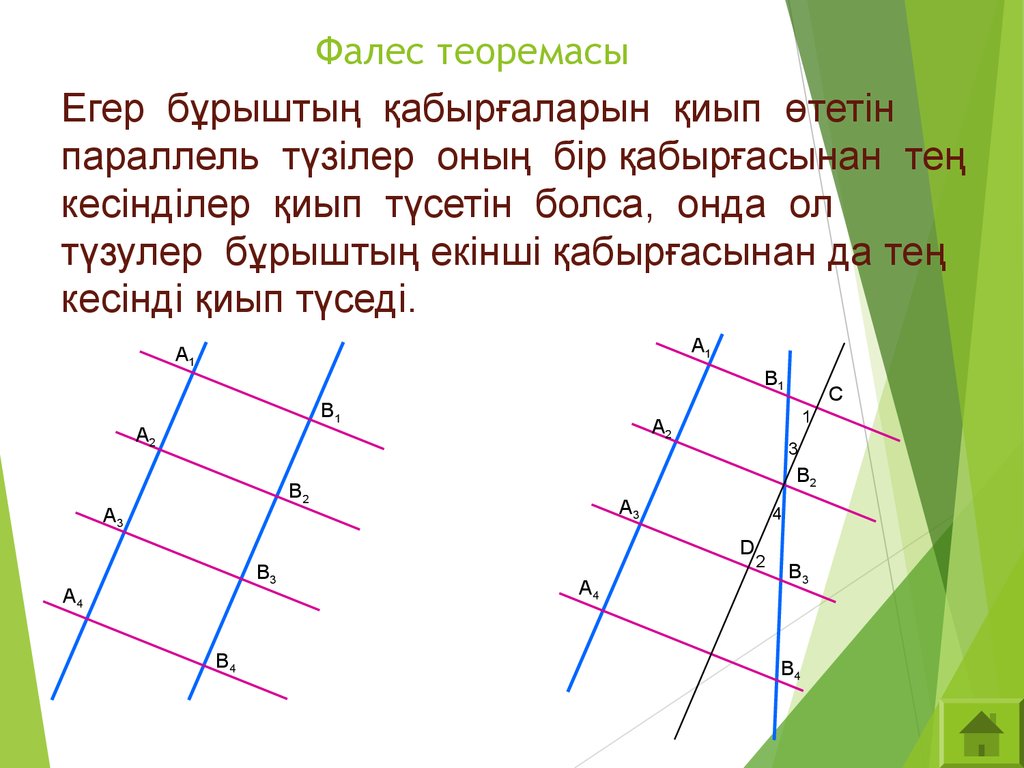



 3-е. — М
.: Просвещение, 1992.
3-е. — М
.: Просвещение, 1992. C. и др. Геометрия 7-9. — Изд. 3-е. — М
.: Просвещение, 1992.
C. и др. Геометрия 7-9. — Изд. 3-е. — М
.: Просвещение, 1992.
