Теорема фалеса в каком классе проходят: Теорема Фалеса и теорема о пропорциональных отрезках — что это, определение и ответ

Теоремы, которые точно пригодятся на ЕГЭ — 5 теорем

Поможем понять и полюбить математику

Начать учиться

Геометрия без теорем не была бы геометрией. Поэтому подготовили самые нужные теоремы для ЕГЭ по математике.

Получите +50 баллов на экзаменах

Дарим до 5 уроков на подготовку к ОГЭ и ЕГЭ по новым предметам

Подготовка к ЕГЭ с преподавателем

Теорема Пифагора

Теорема Пифагора — одна из основополагающих теорем евклидовой геометрии. Она устанавливает соотношение между сторонами прямоугольного треугольника. И звучит так:

В прямоугольном треугольнике сумма квадратов длин катетов равна квадрату длины гипотенузы.

c² = a² + b².

Теорема Пифагора — это частный случай теоремы косинусов. Это объясняется тем, что косинус 90 градусов равен нулю.

Узнай, какие профессии будущего тебе подойдут

Пройди тест — и мы покажем, кем ты можешь стать, а ещё пришлём подробный гайд, как реализовать себя уже сейчас

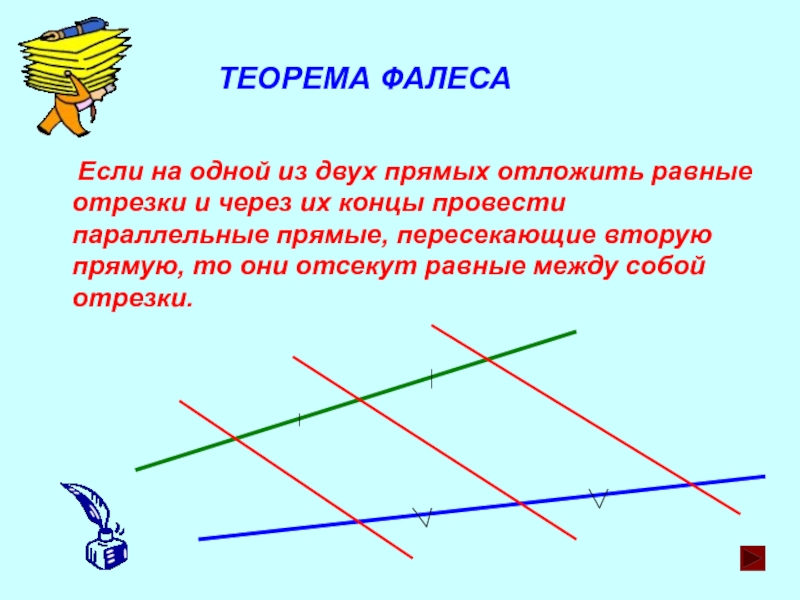
Теорема Фалеса

Теорема Фалеса — это свойство параллельных прямых, которые пересекают две секущие с общей точкой.

Вообще, есть две теоремы Фалеса — общая, на все случаи жизни, и частная — то, что нужно для решения задач на ЕГЭ по математике.

Через произвольные точки A₁, A₂, … A_n–1, A_n, лежащие на стороне AO угла AOB, проведены параллельные прямые, пересекающие сторону угла OB в точках B₁, B₂, … B_n–1, B_n, соответственно. Тогда справедливы равенства:

В ЕГЭ по математике теорема Фалеса встречается чаще всего в параллелограмме, у которого проведена диагональ, — будьте начеку.

Теорема косинусов

Теорема Пифагора — кайф, легко запомнить, часто встречается, применяем только тогда, когда у нас есть прямоугольный треугольник. Но на самом деле теорема Пифагора работает для любого треугольника, только называется она в этом случае теоремой косинусов.

Квадрат длины стороны треугольника равен сумме квадратов длин других сторон минус удвоенное произведение длин этих сторон на косинус угла между ними.

a² = b² + c² – 2bc cos A

Собственно, по формуле сразу становится понятно, почему это соотношение называется теоремой косинусов. Ещё она крайне похожа на разность квадратов с учётом косинуса, поэтому запомнить её не очень сложно. И если вспомнить, что косинус 90 градусов — это 0, то мы увидим знакомую теорему Пифагора.

Теорема синусов

Казалось бы, синус — это что-то про тригонометрию, но на самом деле совсем не только. Планиметрия может с этим смело поспорить, и теорема синусов — явный аргумент в этом воображаемом споре. Если коротко, теорема синусов — это формула связи угла с противолежащей ему стороной в треугольнике.

Для любого треугольника справедливы равенства:

,

где R — радиус описанной около треугольника окружности.

По теореме синусов, во-первых, можно быстро найти радиус описанной окружности по известной стороне и противолежащему ей углу.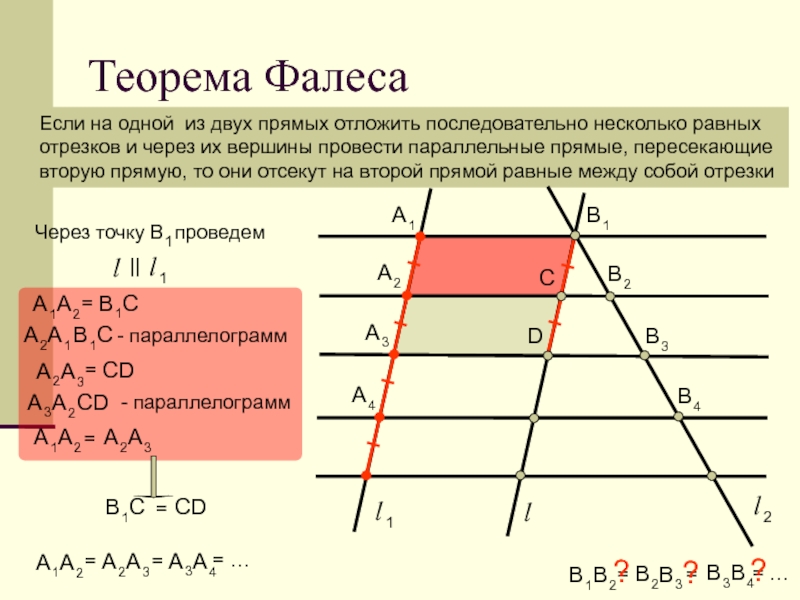 Во-вторых, если треугольник не прямоугольный, то в нём можно просто найти синус угла по известным стороне и радиусу описанной окружности. Ну и в конце концов, можно использовать отношение двух любых сторон и углов. Формула синусов в ЕГЭ по математике используется нечасто, но иметь её в своем арсенале полезно и обязательно.

Теорема Менелая

Её также называют теоремой о треугольнике и секущей, и звучит она так:

Если на сторонах AB и BC треугольника ABC взяты соответственно точки C₁ и A₁, а точка B₁ взята на продолжении стороны AC за точку C, то точки C₁, A₁ и B₁ лежат на одной прямой тогда и только тогда, когда выполнено равенство:

Теорема Менелая пригодится для решения 2-й части ЕГЭ по математике. Она поможет уменьшить огромную кучу исписанных листочков при решении и сохранить время на экзамене, ведь помогает решать в несколько действий.

Чтобы с лёгкостью запомнить все основные теоремы из геометрии для ЕГЭ по математике, скачайте и распечатайте удобную шпаргалку. Кроме теорем из этой статьи, там есть ещё две редкие — теоремы Чевы и Вариньона, а также задачи на доказательства.

Математика — обязательный для сдачи на ЕГЭ предмет, без которого не получишь аттестат. Это также один из самых сложных экзаменов для выпускников. Делимся типичными ошибками в ЕГЭ по математике, а также ресурсами, которые помогут отработать теорию на практике.

Скачивайте бесплатно шпаргалки для экзаменов

Бонус: чек-лист для подготовки к экзаменам. Чтобы ничего не упустить и получить высокие баллы

Эйджей Гаусс

К предыдущей статье

Угол между прямой и плоскостью

К следующей статье

255.3K

Теорема косинусов и синусов

Получите план обучения, который поможет понять и полюбить математику

На вводном уроке с методистом

1. Выявим пробелы в знаниях и дадим советы по обучению

2. Расскажем, как проходят занятия

3. Подберём курс

Пропорциональные отрезки в треугольнике.

(открытый урок, 8 класс) | План-конспект урока геометрии (8 класс) по теме:

Пропорциональные отрезки в треугольнике

Землякова Ольга Владимировна, учитель математики
Осетрова Надежда Евгеньевна, учитель математики
Одинец Ирина Валентиновна, учитель математики
Лосева Алевтина Николаевна, учитель математики 

Статья отнесена к разделу: Преподавание математики 

1-й урок

Повторение тем “Подобие треугольников. Свойство биссектрисы треугольника.
Среднее пропорциональное. Теорема Фалеса. Обобщённая теорема Фалеса”

Цели:

1. Закрепить навык определения хода решения задач;
2. Закрепить умение проводить доказательные рассуждения в ходе решения типичных задач;
3. Закрепить умения и навыки решения типичных задач по данной теме.

Задачи:

1. Закрепить умения и навыки решения типичных задач по данной теме;
2. Формирование у учащихся устойчивого интереса к предмету;
3. Развитие познавательной и исследовательской деятельности учащихся.

Оборудование: мультимедийный проектор.

Ход урока

I. Устно:

1) Формулировки всех теорем, связанных с пропорциональными отрезками.

2) Задачи по готовым чертежам (на мультимедийном проекторе).

№ 1. Найти подобные треугольники на чертежах:

Сформулировать признаки подобия треугольников, применяемые для решения данных задач.

№ 2. Найти подобные треугольники на чертежах:

Сформулировать признаки подобия треугольников, применяемые для решения данных задач.

№ 3. Стороны угла пересечены параллельными прямыми. Отрезки, отсечённые прямыми на одной стороне угла, относятся как . Как относятся отрезки, отсечённые на другой стороне угла?

Сформулировать обобщённую теорему Фалеса.

№ 4. Дано: АВС – прямоугольный (С=90°), СD – высота, АD=4 см, ВD=9 см.

Найти: а) СD; б) АС; в) ВС.

Сформулировать теорему о средних пропорциональных.

II. Решение задач:

1. В треугольнике АВС АВ=8 см, ВС=9 см, АС=2 см. На сколько надо продолжить сторону АС до пересечения с биссектрисой внешнего угла при вершине В?
2. В треугольнике АВС ВС=а, АС=b, АВ=с. Докажите, что если , то А=2В.
3. Постройте прямоугольный треугольник по отношению катетов 2 : 3 и его периметру.
4. В трапеции АВСD и , АС=15 см, АЕ=9 см. Найти площадь трапеции.

III. Итог урока:

Объявление отметок и домашнего задания.

2-й урок

“Теоремы Чевы и Менелая”

Цели:

1. Формирование исследовательского подхода к решению задач;
2. Формирование у учащихся устойчивого интереса к предмету и его истории;
3. Сформулировать и доказать теоремы Чевы и Менелая;
4. Добиваться осознанного восприятия отдельных шагов при доказательстве теорем, а также логического перехода от одного шага к другому;
5. Формирование навыка решения задач “в один шаг” на непосредственное применения изученных теорем.

Задачи:

1. Решение задач, подводящих к формулировке теорем Чевы и Менелая;
2. Сформулировать и доказать теоремы Чевы и Менелая;
3. Добиваться осознанного восприятия отдельных шагов при доказательстве теорем, а также логического перехода от одного шага к другому;
4. Формирование навыка решения задач “в один шаг” на непосредственное применения изученных теорем.

Оборудование: мультимедийный проектор.

Ход урока

I. Решение задачи с помощью обобщённой теоремы Фалеса.

№ 1. В треугольнике АВС АN – медиана. На стороне АС взята точка М так, что АМ : МС = 1 : 3. Отрезки AN и ВМ пересекаются в точке О, а луч СО пересекает АВ в точке К. В каком отношении точка К делит отрезок АВ.

(Указание: через точки N и С провести параллельные прямые, пересекающие АВ; и через точки М и С провести параллельные прямые, пересекающие АВ).

Эту задачу можно решить более рациональным способом, но для этого нужны дополнительные знания.

II. Доклад о математике Джованни Чева.

Джованни Чева — итальянский математик. Родился в 1648 г. и умер в 1734 г. Главными предметами его занятий были геометрия и механика. Старался возродить греческую геометрию. Основной заслугой является построение учения о секущих, которое положило начало новой синтетической геометрии. Оно изложено в сочинении “О взаимопересекающихся прямых”. В первой его части автор доказывает теорему Менелая и ряд сходных с нею теорем при помощи статического метода, основанного на свойствах центра тяжести системы точек. Прилагаемый к вопросам, в которых рассматриваются отношения между отрезками, образованными пересекающимися линиями друг на друге, он состоит в помещении в точках пересечения тяжестей, обратно пропорциональных соответствующим отрезкам, и в последующем за тем выводе отношения между тяжестями на основании принципа рычага в статике. Достаточно назвать известное в геометрии под именем теоремы Чевы предложение о произведениях отрезков, образованных на сторонах треугольника трансверсалями, проходящими через общую точку (произведение трех отрезков, не сходящихся попарно в одной общей точке, равно произведению трех других отрезков), и на подобное же предложение об отрезках, образованных на сторонах четырехугольника плоскостью, их пересекающею, если не все вершины четырехугольника лежат в одной плоскости. Во второй части идеи и теоремы, изложенные в 1-й, прилагаются к коническим сечениям. Наконец, прибавление занимается теоремами о площадях некоторых плоских фигур и об объемах и центрах тяжести тел вращения второго порядка. Чева был инженером-гидравликом и в качестве такового несколько раз служил правительству Мантуи. Смерть его последовала во время осады Мантуи. Считался выдающимся автором в области экономики — первым проницательным математическим писателем по этому предмету. Его брат, Томмазо Чева, математик (1648—1737), иезуит. В 1695 г. изобрел инструмент для механического деления угла на три части.

III. Определение чевианы и доказательство теоремы Чевы.

Определение. Чевианой называется отрезок, соединяющий вершину треугольника с любой точкой на противоположной стороне этого треугольника.

Теорема Чевы.

Пусть на сторонах треугольника ABC выбраны точки .  Отрезки АА1 , ВВ1 и СС1 пересекаются в одной точке тогда и только тогда, когда выполняется равенство:.

Доказательство:

Необходимость.

Пусть отрезки АА1, ВВ1 и СС1 пересекаются в одной точке O. Проведем через вершину B треугольника прямую a¦AC. Пусть прямые АА1 и ВВ1 пересекают прямую a в точках M и N соответственно. Тогда из подобия треугольников АА1С и МА1В1 по двум углам (А1СА = А1ВМ как накрест лежащие и ВА1М = АА1С как вертикальные) имеем: . (1)

Аналогично из подобия треугольников АС1С и ВС1N по двум углам (С1СА = С1NB и С1АС = С1BN – как пары накрест лежащих): . (2)

Наконец, из подобия треугольников OAC и OMN по двум углам (ОСА = ONP и ОАС = OMN) получаем . (3)

Перемножив соответственно правые и левые части выписанных равенств (1), (2) и (3), получим необходимое равенство.

Достаточность.

Пусть выполнено равенство. Покажем, что отрезки АА1, ВВ1 и СС1 проходят через одну точку.

Пусть O – точка пересечения отрезков АА1 и СС1, а C2 – точка пересечения отрезка AB с лучом CO. Тогда из только что доказанного следует, что .

Сравнивая с условием теоремы, получим . Следовательно, точки C2 и С1 совпадают.

IV. Решение задач.

№ 2. Решить задачу №1 с помощью теоремы Чевы.

№ 3. На стороне ВС треугольника АВС взята точка D такая, что ВD : DC = 2:5, а на стороне АС точка Е такая, что . В каком отношении делятся отрезки ВЕ и АD точкой К их пересечения?

V. Презентация о математике Менелае Александрийском.

VI. Доказательство теоремы Менелая. (Доказательство ведётся с помощью мультимедийного аппарата в программе “Живая геометрия”).

VII. Решение задач.

№ 4. В треугольнике АВС точка М – середина АВ, точка N такая, что BN : NC = 3 : 2.

Прямая МN пересекает прямую АС в точке К. Найти отношение КС : АК.

№ 5. В треугольнике АВС отрезки AD и ВЕ, проведённые из вершин А и В к сторонам ВС и АС соответственно, делятся точкой пересечения Q в соотношении AQ : QD = 7 : 5, BQ : QE = 3 : 4. В каков отношении точки D и Е делят сторону треугольника?

VIII. Итог урока:

Объявление отметок и домашнего задания.

3-й урок

Решение задач по теме “Пропорциональные отрезки в треугольнике”
с использованием теорем Чевы и Менелая

Цели:

1. Уйти от традиционных подходов к решению задач, приводящих к громоздким преобразованиям.
2. Сформировать умения и навыки применять теоремы Чевы и Менелая к решению задач, позволяющих получать короткое и эффективное решение.
3. Формирование у учащихся устойчивого интереса к предмету и его истории.
4. Добиваться осознанного восприятия отдельных шагов при решении задач, а также логического перехода от одного шага к другому.
5. Формирование умения решать выделенные подзадачи.

Задачи:

1. Уйти от традиционных подходов к решению задач, приводящих к громоздким преобразованиям.
2. Сформировать умения и навыки применять теоремы Чевы и Менелая к решению задач, позволяющих получать короткое и эффективное решение.
3. Добиваться осознанного восприятия отдельных шагов при решении задач, а также логического перехода от одного шага к другому и умения решать выделенные подзадачи.
4. Формирование навыков работы в группах.

Оборудование: мультимедийный проектор.

В результате учащиеся должны:

— прочно усвоить теоремы, связанные с данной темой;

— уметь решать задачи, связанные с данной темой, рациональным способом;

— повысить качество знаний.

Ход урока

I. Повторить формулировки теорем Чевы и Менелая.

II. Работа в группах (4 группы по 5-6 человек).

1. Каждая группа получает задачу на данную тему и решает её.
2. Обсуждение решений задач каждой группы по готовым чертежам (готовит учитель на мультимедийном проекте).
3. Выработка рационального способа решения каждой задачи.

Задачи для урока:

№ 1. В треугольнике АВС на стороне АВ взята точка К так, что АК : ВК = 1 : 3, а на стороне ВС – точка L так, что CL : BL = 2 : 1. Пусть Q – точка пересечения прямых AL и СК. Найти площадь треугольника АВС, если площадь треугольника BQC равна 2. (Ответ: 3)

№ 2. В треугольнике АВС, площадь которого равна 5, на стороне АВ взята точка К, делящая эту сторону в отношении АК : ВК = 2 : 3, а на стороне АС – точка L, делящая её в отношении AL : АС = 5 : 8. Точка Q пересечения прямых CK и BL удалена от прямой АВ на расстояние 1. Найти длину стороны АВ. (Ответ: 5)

№ 3. В треугольнике АВС на стороне АС взята точка К, а на стороне ВС точка М так, что СК : КА = 5 : 1, . Найти СМ : МВ. (Ответ: 6 : 5)

№ 4. На медианах АК, BL и CN треугольника АВС взяты точки Р, Q и R так, что AP : PK = 1 : 1, BQ : QL = 1 : 2, CR : CN = 9 : 4. Найти площадь треугольника PQR, если площадь треугольника АВС равна 1. (Ответ: )

III. Итог урока.

Выставление оценок группам. Домашнее задание.

Литература

1. Б.Г.Зив, В.М. Мейлер “Дидактические материалы по геометрии для 8 класса” (Москва, “Просвещение” 2008 г.)
2. Л.С. Атанасян “Дополнительные главы” (Москва, “Просвещение” 2002 г.)
3. Д. Шноль, А. Сгибнев, Н. Нетрусова “Система открытых задач по геометрии” (библиотечка “1 сентября” 2009 г.)
4. О.Ю. Черкасов “Планиметрия на вступительном экзамене” (изд-во “Московский лицей” 1996 г.)
5. В.И. Жохов, Г.Д. Карташева, Л.Б. Крайнева “Уроки геометрии в 7-9 классах” (Москва, “Мнемозина” 2005 г.)

Основная теорема о пропорциональности | Теорема Фалеса | Утверждение и доказательство

Основная теорема пропорциональности была предложена известным греческим математиком Фалесом, поэтому ее также называют теоремой Фалеса

. По мнению известного математика, для любых двух равноугольных треугольников отношение любых двух соответствующих сторон данных треугольников всегда одинаково. На основе этой концепции была предложена основная теорема пропорциональности (BPT). Он дает отношение между сторонами любых двух равноугольных треугольников.

Понятие теоремы Фалеса было введено в подобных треугольниках. Если данные два треугольника подобны друг другу, то

• Соответствующие углы обоих треугольников равны
• Соответствующие стороны обоих треугольников пропорциональны друг другу

Таким образом, эта теорема также помогает нам лучше понять концепцию подобных треугольников. Теперь давайте попробуем понять основную теорему пропорциональности.

1.	Формулировка основной теоремы пропорциональности
2.	Доказательство основной теоремы о пропорциональности
3.	Обратное из основной теоремы пропорциональности
4.	Часто задаваемые вопросы

Доказательство основной теоремы о пропорциональности

Теперь попробуем доказать основное утверждение теоремы о пропорциональности (BPT).

Утверждение:  Линия, проведенная параллельно одной стороне треугольника и пересекающая две другие стороны, делит две другие стороны в равных пропорциях.

Дано:  Рассмотрим треугольник ΔABC, как показано на данном рисунке. В этом треугольнике мы проводим линию DE, параллельную стороне BC треугольника ΔABC и пересекающую стороны AB и AC в точках D и E соответственно.

Конструкция:  На приведенной выше диаграмме создайте воображаемые линии, где вы можете соединить C с D и B с E. Нарисуйте перпендикуляр DP перпендикулярно AE и EQ перпендикулярно AD.

Доказательство:

Рассмотрим треугольники ADE и BDE. Оба эти треугольника находятся на одном основании AB и имеют одинаковую высоту EQ.

(Площадь ADE)/(Площадь BDE) = (1/2 × AD × EQ)/(1/2 × BD × EQ) 

(Площадь ADE)/(Площадь BDE) = AD/BD

Теперь рассмотрим треугольники CDE и ADE. Оба эти треугольника лежат на одном основании AC и имеют одинаковую высоту DP.

(Площадь ADE)/(Площадь CDE) = (1/2 × AE × DP)/(1/2 × CE × DP)

(Площадь ADE)/(Площадь CDE) = AE/CE

Оба треугольника BDE и CDE находятся между одним и тем же набором параллельных прямых.

Площадь треугольника BDE = Площадь треугольника CDE

Применяя это, мы имеем (Площадь треугольника ADE)/(Площадь треугольника BDE) = (Площадь треугольника ADE)/(Площадь треугольника CDE)

AD/BD = AE/CE

Следствие:

Приведенное выше доказательство также помогает доказать другую важную теорему, называемую теоремой о средней точке. Теорема о средней точке утверждает, что отрезок, проведенный параллельно одной стороне треугольника, и половина этой стороны делит две другие стороны посередине.

Вывод:

Таким образом, мы доказываем основную теорему о пропорциональности. Следовательно, прямая DE, проведенная параллельно стороне BC треугольника ABC, делит две другие стороны AB, AC в равной пропорции. Кроме того, обратная теорема BPT о средней точке также остается верной. В нем говорится, что линия, проведенная через середину стороны треугольника и параллельная другой стороне, делит пополам третью сторону треугольника.

Обращение к основной теореме пропорциональности

В соответствии с обратной теоремой о пропорциональности: «Если отрезок нарисован так, чтобы разделить две стороны треугольника в равных пропорциях, то он параллелен третьей стороне».

Дано:

ABC — треугольник, и прямая DE пересекает стороны AB и AC в равных пропорциях. AD/BD = AE/CE

Доказательство:

Предположим, что DE не параллелен BC. Поэтому проведем еще одну прямую DF, параллельную ВС. Применяя основную теорему пропорциональности, мы имеем: AD/BD = AF/CF. Но уже дано, что: AD/BD = AE/CE. Соблюдая равенство левых частей двух приведенных выше утверждений, мы заключаем следующее утверждение: AE/CE = AF/CF. Добавьте 1 с обеих сторон этого утверждения.

(AE/CE) + 1= (AF/CF)  + 1

(AE + CE)/CE = (AF + CF)/CF

AC/CE = AC/CF 

∴ CE = CF

Для приведенного выше утверждения точки E и F являются одними и теми же точками, и они совпадают. Следовательно, прямая DE параллельна BC, что доказывает обратное утверждение основной теоремы о пропорциональности.

Важные примечания

• Основная теорема пропорциональности. Линия, проведенная параллельно одной стороне треугольника и пересекающая две другие стороны, делит две другие стороны в равной пропорции.
• Обратное из основной теоремы о пропорциональности: линия, проведенная для разрезания двух сторон треугольника в равных пропорциях, параллельна третьей стороне.
• Теорема о средней точке. Линия, проведенная параллельно одной стороне треугольника и половине этой стороны, делит две другие стороны в своей середине.

Контрольные вопросы

• Диагонали четырехугольника PQRS пересекаются в точке O, так что PO/QO = RO/SO. Докажите, что PQRS — трапеция.

 

---

Часто задаваемые вопросы по основной теореме пропорциональности

Что такое Теорема Фалеса?

Теорема Фалеса, которую также называют основной теоремой пропорциональности, утверждает, что линия, проведенная параллельно одной стороне треугольника и пересекающая две другие стороны, делит эти две стороны в равной пропорции.

Каковы применения основной теоремы пропорциональности?

Основная теорема о пропорциональности помогает найти длины, на которые две стороны треугольника делятся линией, проведенной параллельно третьей стороне. Кроме того, у него есть приложения, чтобы найти взаимосвязь между двумя равноугольными треугольниками.

Что такое История Теоремы Фалеса?

Теорема Фалеса была предложена Фалесом, греческим математиком и философом около 625 г. до н.э. Сейчас ее называют основной теоремой пропорциональности, и она помогает найти соотношение между сторонами двух равноугольных треугольников.

Что такое формула основной теоремы пропорциональности?

Базовая формула теоремы пропорциональности для треугольника ABC с точкой D на AB, точкой E на AC и DE // BC выглядит следующим образом,

AD/DB = AE/EC

Что вы подразумеваете под основной теоремой пропорциональности?

Основная теорема о пропорциональности гласит, что если прямая проведена параллельно одной стороне треугольника и пересекает две другие стороны, то две другие стороны она делит в равной пропорции.

Как доказать основную теорему о пропорциональности, вырезая бумагу?

Чтобы показать основную теорему о пропорциональности, вырежьте из цветной бумаги треугольник и обозначьте его вершины как ABC. Поместите его на разлинованную бумагу так, чтобы одна сторона BC совпадала с линией на разлинованной бумаге. Теперь отметьте точки D на АВ и Е на АС так, чтобы DE была параллельна стороне ВС. Теперь измерьте длины AD, BD, AE и CE и проверьте, пропорциональны ли они.

AD/DB = AE/EC

Как решить теорему Фалеса?

Теорема Фалеса аналогична основной теореме о пропорциональности. Чтобы решить ее, нам нужно доказать, что прямая, проведенная параллельно одной стороне треугольника, делит две другие стороны в равной пропорции.

Основная теорема о пропорциональности Класс 10 Math Notes

Теорема 1:

Если провести прямую, параллельную одной стороне треугольника, чтобы пересечь две другие стороны в разных точках, то две другие стороны делятся в том же отношении.

Дано: треугольник ABC, в котором прямая, параллельная стороне BC, пересекает две другие стороны AB и AC в точках D и E соответственно.

Доказать:

Конструкция: Соедините BE и CD и начертите DM ⊥ AC и EN ⊥ AB.

Доказательство: площадь Δ ADE

(Взяв AD за базу)

Итак, [Площадь Δ ADE обозначается как ar (ADE)].

Аналогично,

[Δ BDE и DEC находятся на одном основании DE и между одними и теми же параллелями BC и DE.]

Следовательно, из (i), (ii) и (iii) имеем:

.

Следствие: Из приведенного выше уравнения мы имеем

.

Добавляя 1 к обеим сторонам, мы получаем

.

Теорема 2:

(Обратное из теоремы BPT) Если прямая делит любые две стороны треугольника в одинаковом отношении, докажите, что она параллельна третьей стороне.

Дано: В ΔABC DE — прямая такая, что .

Доказать: DE || ДО Н.Э.

Построение: Если DE не параллелен BC, нарисуйте DF, пересекающий AC в точке F.

Доказательство. Пусть в ∆ABC DF || БК

[∴ Линия, проведенная параллельно одной стороне Δ, делит две другие стороны в том же отношении.]

Но . …(ii) [дано]

Из (i) и (ii) мы получаем

.

⇒ ФК = ЭК.

Это возможно только при совпадении E и F

Следовательно, ДЭ || ДО Н.Э.

НЕКОТОРЫЕ ВАЖНЫЕ РЕЗУЛЬТАТЫ И ТЕОРЕМЫ:

(i) Внутренняя биссектриса угла треугольника делит противолежащую сторону внутри в отношении сторон, содержащих этот угол.

(ii) В треугольнике ABC, если D — точка на BC такая, что D делит BC в отношении AB : AC, то AD — биссектриса ∠A.

(iii) Внешняя биссектриса угла треугольника делит противоположные стороны внешне в отношении сторон, содержащих этот угол.

(iv) Линия, проведенная из середины одной стороны треугольника параллельно другой стороне, делит третью сторону пополам.

(v) Прямая, соединяющая середины двух сторон треугольника, параллельна третьей стороне.

(vi) Диагонали трапеции пропорционально делят друг друга.

(vii) Если диагонали четырехугольника делят друг друга пропорционально, то это трапеция.

(viii) Любая линия, параллельная параллельным сторонам трапеции, пропорционально делит непараллельные стороны.

(ix) Если три или более параллельных прямых пересекаются двумя секущими, то пересечения ими на секущей пропорциональны.

Если каким-либо учащимся необходимо пройти онлайн-тест, чтобы проверить свои концепции или понимание, они могут посетить вопрос по базовой теории пропорциональности .

Вопрос 1. В ΔABC точки D и E на сторонах AB и AC соответственно такие, что DE || ДО Н.Э. Если AD = 4x – 3, AE = 8x – 7, BD = 3x – 1 и CE = 5x – 3, найдите значение x.

Решение: В ΔABC мы имеем

DE||БК.

∴ . [По основной теореме пропорциональности]

⇒ 20x ² – 15x – 12x + 9 = 24x ² – 21x – 8x + 7

⇒ 20x ² – 27x + 9 = 24x ² – 29x + 7

⇒ 4×2 – 2x – 2 = 0

⇒ 2х2 – х – 1 = 0

⇒ (2х + 1) (х – 1) = 0

⇒ х = 1 или х = –1/2

Итак, искомое значение x равно 1.

[x = — 1/2 пренебрегается, так как длина не может быть отрицательной].

Вопрос 2. D и E — точки на сторонах AB и AC ΔABC соответственно, такие что AB = 12 см, AD = 8 см, AE = 12 см и AC = 18 см, покажите, что DE || ДО Н.Э.

Решение: У нас есть,

AB = 12 см, AC = 18 м, AD = 8 см и AE = 12 см.

∴ ВД = АВ — АД = (12 – 8) см = 4 см.

CE = AC – AE = (18 12) см = 6 см.

.

Таким образом, DE делит стороны AB и AC треугольника ΔABC в одинаковом отношении. Следовательно, по обратной теореме о пропорциональности имеем DE||BC.

Вопрос 3. В трапеции ABCD AB||DC и DC = 2AB. EF, проведенный параллельно AB, пересекает AD в F и BC в E так, что. Диагональ DB пересекает EF в точке G. Докажите, что 7FE = 10AB.

Решение: В ΔDFG и ΔDAB,

∠1 = ∠2 [Соответствующее ∠s ∴ AB || ФГ]

∠FDG = ∠ADB [Общий]

∴ ΔDFG ~ ΔDAB [По правилу подобия АА]

Из (i) и (ii) мы получаем

FG/AB = 4/7 т. е. FG = 4/7 AB ……(iii)

В ΔBEG и ΔBCD имеем

∠BEG = ∠BCD [Соответствующий угол ∴ EG||CD]

∠GBE = ∠DBC [Общий]

∴ ΔBEG ~ ΔBCD [По правилу подобия АА]

Значит доказано.

Вопрос 4. В ΔABC, если AD является биссектрисой ∠A, докажите, что .

Решение: В ΔABC AD является биссектрисой ∠A.

∴ AB/AC = BD/DC….(i) [По теореме о внутренней биссектрисе]

Из розыгрыша A AL⊥BC

.

[Из (i)] Следовательно Доказано.

Вопрос 5. ∠BAC = 90°, AD — его биссектриса. ЕСЛИ DE⊥ AC, докажите, что DE × (AB + AB) = AB × AC.

Решение: Дано, что AD является биссектрисой ∠A треугольника ΔABC.

В CDE и CBA Δ у нас есть

∠DCE = ∠BCA [Общий]

∠DEC = ∠BAC. [Каждый равен 90o]

Значит по АА-критерию подобия

Δ CDE ~ Δ CBA

⇒ DE × (AB + AC) = AB × AC.