Теорема синусов онлайн калькулятор. Теорема синусов и теорема косинусов
Построим произвольный треугольник, вписанный в окружность. Обозначим его как ABC.
Для доказательства всей теоремы, поскольку размеры треугольника выбраны произвольным образом, достаточно доказать, что соотношение одной произвольной стороны к противолежащему ей углу равно 2R. Пусть это будет 2R = a / sin α, то есть если взять по чертежу 2R = BC / sin A.
Проведем диаметр BD для описанной окружности. Образовавшийся треугольник BCD является прямоугольным, поскольку его гипотенуза лежит на диаметре описанной окружности (свойство углов, вписанных в окружность).
Поскольку, углы, вписанные в окружность, опирающиеся на одну и ту же дугу, равны, то угол CDB либо равен углу CAB (если точки A и D лежат по одну сторону от прямой BC), либо равен π — CAB (в противном случае).
Обратимся к свойствам тригонометрических функций. Поскольку sin(π − α) = sin α, то указанные варианты построения треугольника все равно приведут к одному результату.
Вычислим значение 2R = a / sin α, по чертежу 2R = BC / sin A. Для этого заменим sin A на соотношение соответствующих сторон прямоугольного треугольника.
2R = BC / sin A
2R = BC / (BC / DB)
2R = DB
А, поскольку, DB строился как диаметр окружности, то равенство выполняется.
Повторив то же рассуждение для двух других сторон треугольника, получаем:
Теорема синусов доказана.
Теорема синусов
Примечание . Это часть урока с задачами по геометрии (раздел теорема синусов). Если Вам необходимо решить задачу по геометрии, которой здесь нет — пишите об этом в форуме. В задачах вместо символа «квадратный корень» применяется функция sqrt(), в которой sqrt — символ квадратного корня, а в скобках указано подкоренное выражение .
Теорема синусов:
Стороны треугольника пропорциональны синусам противолежащих углов, или, в расширенной формулировке:
a / sin α = b / sin β = c / sin γ = 2R
где R — радиус описанной окружности
Теорию — формулировку и доказательство теоремы подробно см.
в главе «Теорема синусов» .
Задача
В треугольнике XYZ угол Х=30 угол Z=15. Перпендикуляр YQ к ZY делит сторону ХZ на части XQ и QZ.Найти XY, если QZ=1.5м
Решение .
Высота образовала два прямоугольных треугольника XYQ и ZYQ.
Для решения задачи воспользуемся теоремой синусов.
QZ / sin(QYZ) = QY / sin(QZY)
QZY = 15 градусов, Соответственно, QYZ = 180 — 90 — 15 = 75
Поскольку длина высоты треугольника теперь известна, найдем XY по той же теореме синусов.
QY / sin(30) = XY / sin(90)
Примем во внимание табличные значения некоторых тригонометрических функций:
- синус 30 градусов равен sin(30) = 1 / 2
- синус 90 градусов равен sin(90) = 1
QY = XY sin (30)
3/2 (√3 — 1) / (√3 + 1) = 1/2 XY
XY = 3 (√3 — 1) / (√3 + 1) ≈ 0.8 м
Ответ : 0,8 м или 3 (√3 — 1) / (√3 + 1)
Теорема синусов (часть 2)
Примечание . Это часть урока с задачами по геометрии (раздел теорема синусов).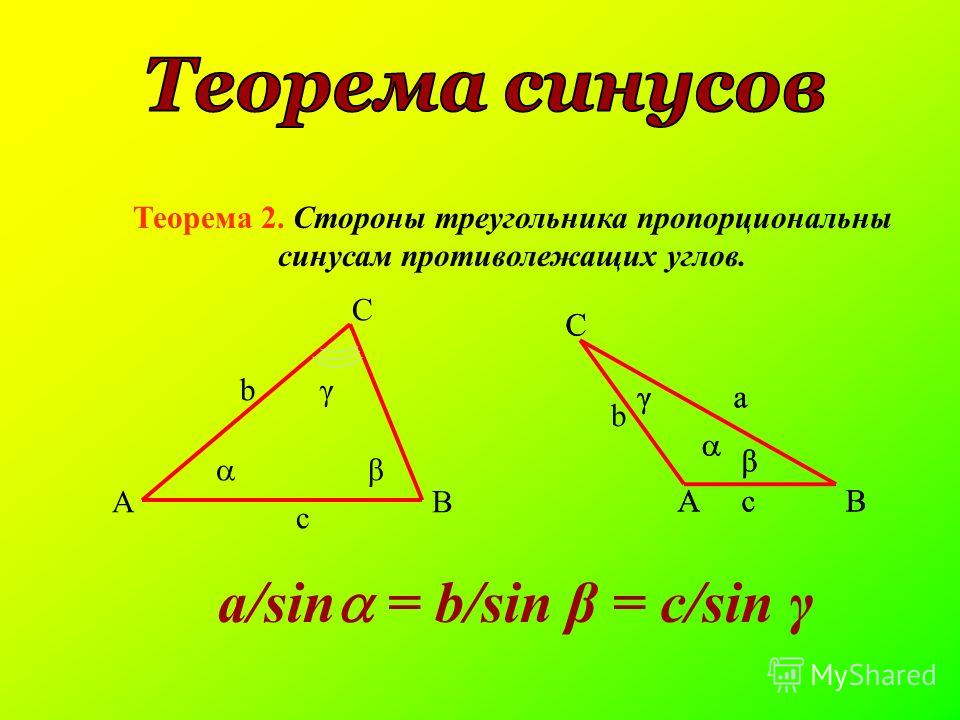
Если Вам необходимо решить задачу по геометрии, которой здесь нет — пишите об этом в форуме .
Теорию подробно см. в главе «Теорема синусов» .
Задача
Сторона АВ треугольника ABC равна 16см. Угол А равен 30 градусам. Угол В равен 105 градусам. Вычислите длину стороны ВС.
Решение .
Согласно теореме синусов, стороны треугольника пропорциональны синусам противолежащих углов:
a / sin α = b / sin β = c / sin γ
Таким образом
BC / sin α = AB / sin γ
Величину угла С найдем, исходя из того, сумма углов треугольника равна 180 градусам.
С = 180 — 30 -105 = 45 градусов.
Откуда:
BC / sin 30° = 16 / sin 45°
BC = 16 sin 30° / sin 45°
Обратившись к таблице тригонометрических функций, находим:
BC = (16 * 1 / 2) / √2/2 = 16 / √2 ≈ 11,3 см
Ответ : 16 / √2
Задача .
В треугольнике ABC угол А = α, угол С = β, ВС = 7см, ВН — высота треугольника.
Найти АН
Тригонометрия широко применяется не только в разделе алгебра — начала анализа, но также и в геометрии.
В связи с этим, разумно предположить о существовании теорем и их доказательств, связанных с тригонометрическими функциями. Действительно, теоремы косинусов и синусов выводят очень интересные, а главное полезные соотношения между сторонами и углами треугольников.
С помощью данной формулы можно вывести любую из сторон треугольника:
Доказательство утверждения выводится на основе теоремы Пифагора: квадрат гипотенузы равен сумме квадратов катетов.
Рассмотрим произвольный треугольник ABC. Из вершины C опустим высоту h к основанию фигуры, в данном случае абсолютно не важна ее длина. Теперь, если рассмотреть произвольный треугольник AСВ, то можно выразить координаты точки C через тригонометрические функции cos и sin.
Вспомним определение косинуса и распишем соотношение сторон треугольника ACD: cos α = AD/AC | умножим обе стороны равенства на AC; AD = AC * cos α.
Длину AC примем за b и получим выражение для первой координаты точки С:
x = b * cosα.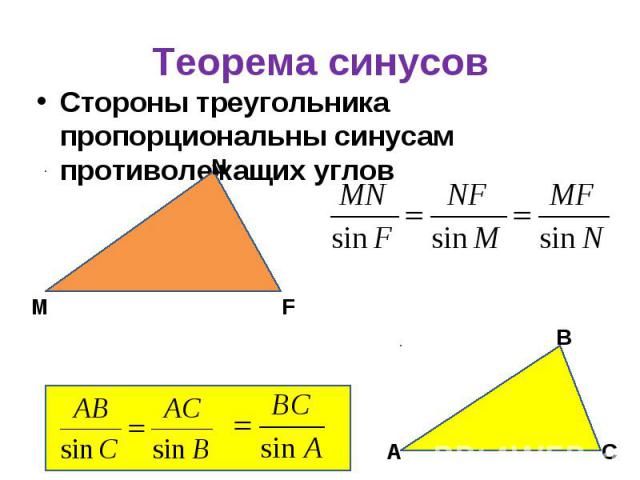
Аналогично, находим значение ординаты С: y = b * sin α. Далее применим теорему Пифагора и выразим h поочередно для треугольника ACD и DCB:
Очевидно, что оба выражения (1) и (2) равны между собой. Приравняем правые части и приведем подобные:
На практике данная формула позволяет найти длину неизвестной стороны треугольника по заданным углам. Теорема косинусов имеет три следствия: для прямого, острого и тупого угла треугольника.
Заменим величину cos α привычной переменной x, тогда для острого угла треугольника ABC получим:
Если же угол окажется прямым, то 2bx исчезнет из выражения, так как cos 90° = 0. Графически второе следствие можно представить следующим образом:
В случае тупого угла знак «-»перед двойным аргументом в формуле сменится на «+»:
Как видно из объяснения, ничего сложного в соотношениях нет. Теорема косинусов есть не что иное, как переложение теоремы Пифагора в тригонометрических величинах.
Практическое применение теоремы
Задание 1 .
Дан треугольник ABC, у которого сторона BC = a = 4 см, AC = b = 5 см, а cos α = ½. Необходимо найти длину стороны AB.
Чтобы правильно произвести расчет, нужно определить угол α. Для этого стоит обратиться к таблице значений для тригонометрических функций, согласно которой арккосинус равен 1/ 2 для угла в 60°. Исходя из этого, воспользуемся формулой первого следствия теоремы:
Задание 2 . Для треугольника ABC известны все стороны: AB =4√2,BC=5,AC=7. Требуется найти все углы фигуры.
В данном случае не обойтись без чертежа условий задачи.
Так как значения углов остаются неизвестными, для поиска решений следует использовать полную формулу для острого угла.
По аналогии нетрудно составить формулы и рассчитать значения и других углов:
В сумме три угла треугольника должны составить 180 °: 53 + 82 + 45 = 180, следовательно, решение найдено.
Теорема синусов
Теорема гласит, что все стороны произвольного треугольника пропорциональны синусам противолежащих углов.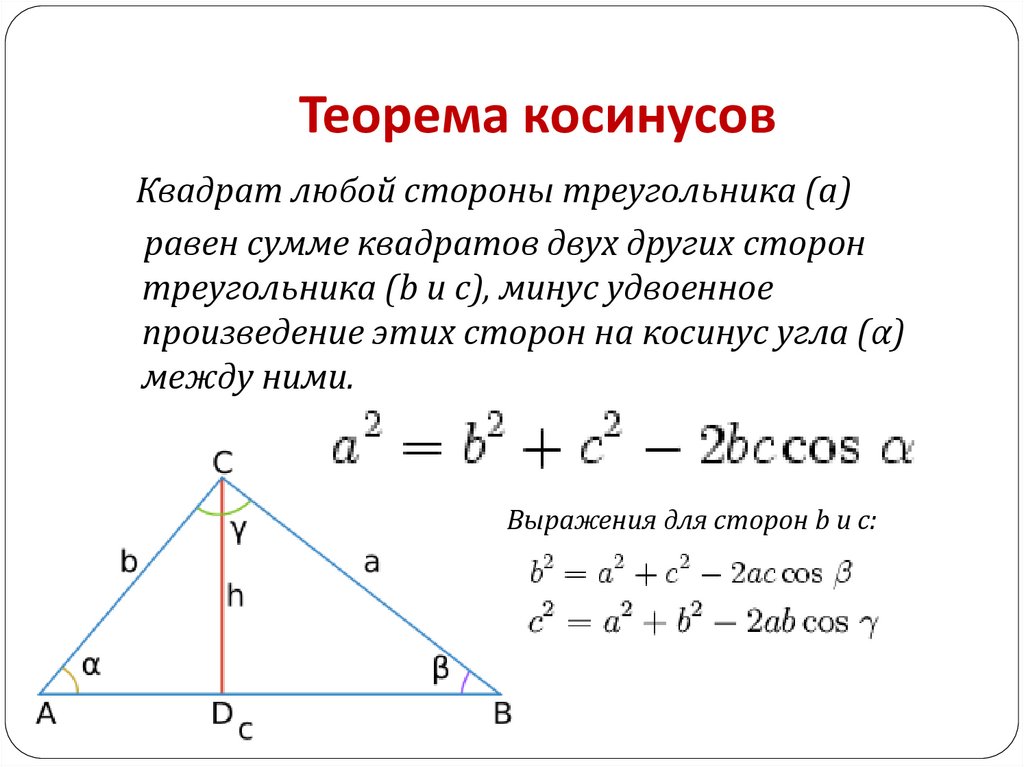
Записываются соотношения в виде тройного равенства:
Классическое доказательство утверждения проводят на примере фигуры вписанной в окружность.
Чтобы убедиться в правдивости высказывания на примере треугольника ABC на рисунке, необходимо подтвердить тот факт, что 2R = BC / sin A. Затем доказать, что и прочие стороны соотносятся с синусами противоположных углов, как 2R или D окружности.
Для этого проводим диаметр круга из вершины B. Из свойства углов вписанных в окружность ∠GCB – прямой, а ∠CGB либо равен ∠CAB, либо (π — ∠CAB). В случае с синусом последнее обстоятельство не значительно, так как sin (π –α) = sin α. На основании приведенных умозаключений можно утверждать, что:
sin ∠CGB = BC/ BG или sin A = BC/2R,
Если рассматривать другие углы фигуры, получим расширенную формулу теоремы синусов:
Типовые задания на отработку знания теоремы синусов сводятся к поиску неизвестной стороны или угла треугольника.
Как видно из примеров, решение подобных задач не вызывает затруднений и заключается в проведении математических расчетов.
Первая часть теоремы : стороны произвольного треугольника пропорциональный синусам противоположных углов, то есть:
Вторая часть теоремы : каждая дробь равна диаметру окружности, описанной около данного треугольника, то есть: .
Комментарий репетитора по математике : использование второй части теоремы синусов закладывается чуть ли не в каждой второй конкурсной задаче на окружность. Почему? Дело в том, что равенство позволяет находить радиус окружности имея в наличие только два элемента треугольника. Это очень часто используют составители сильных задач, которые специально так подбирают условие, чтобы никакие другие элементы треугольника (и всего рисунка) не находились бы вообше! «Картинка» при этом будет плавующей. Это обстоятельство сильно усложняет работу на экзамене, ибо не дает возможность действовать в обход заложенному свойству.
Доказательство теоремы синусов:
по учебнику Атанасяна
Докажем, что для любого треугольника со сторонами a, b, c и противолежащими углами A, B и С выполняется равенство: .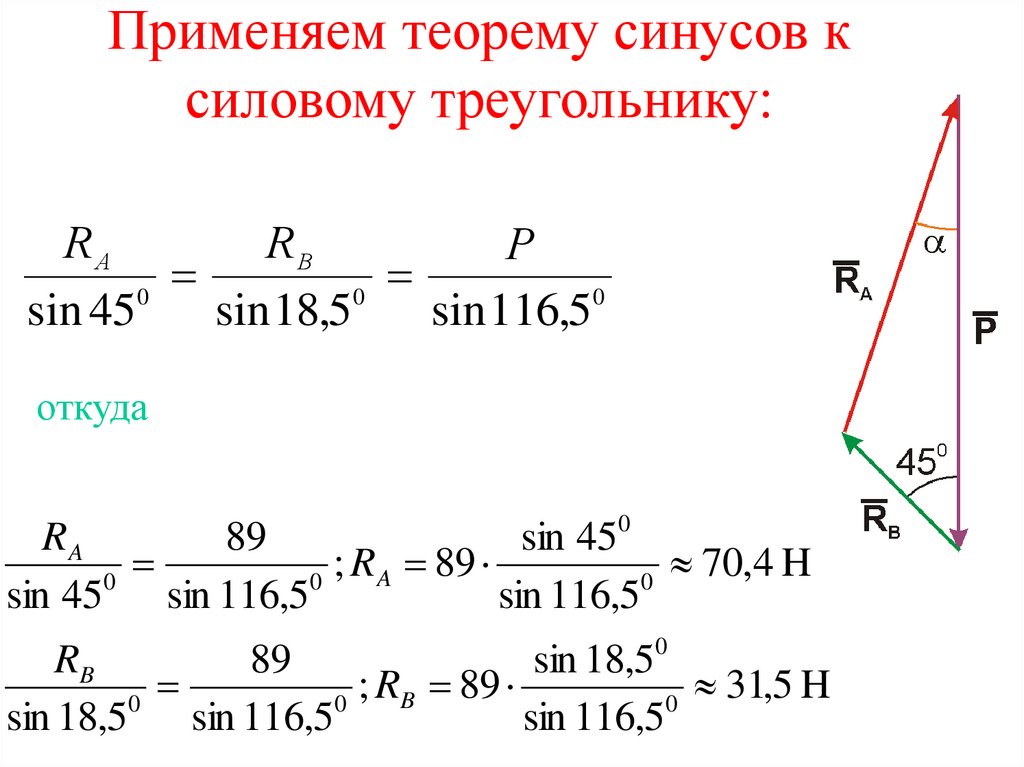
Проведем высоту BH из вершины В. Возможны два случая:
1) Точка H лежит на стороне AC (это возможно когда и — острые).
По определению синуса острого угла в прямоугольном треугольнике ABH запишем
Аналогично в треугольнике CBH имеем . Приравнивая выражения для BH друг к другу получим:
2) Пусть H лежит на продолжении стороны AC (например слева от А). Это произойдет, если – тупой. Аналогично по определению синуса острого угла А в треугольнике ABH запишем равенство , но так как синусы смежных углов равны, то заменив в этом равенстве на , получим как и в первом случае. Поэтому независимо от величин углов А и С равенство верное.
Доказательство теоремы синусов по учебнику Погорелова:
Применим формулу площади треугольника для двух углов A и C:
После приравнивания правых частей и сокращения на получим тоже самое равенство , как и в доказательстве первым способом.
Из него тем же путем получаем равенство дробей.
Доказательство второй части теоремы синусов:
Опишем около данного треугольника окружность и через В проведем ее диаметр BD. Так как углы D и C опираются на одну дугу, то они равны (следствие из теоремы о вписанных углах). Тогда . Применим в треугольнике ABD определение синуса угла D: Что и требовалось доказать.
Задачи на вторую часть теоремы синусов:
1) В окружность радиуса 15 вписана трапеция. Длины диагонали и высоты трапеции соответственно равны 20 и 6. Найти боковую сторону.
2) Радиус окружность, описанной около трапеции, равен 25, а косинус ее тупого угла равен -0,28 (минус!!!). Диагональ трапеции образует с основанием угол . Найти высоту трапеции.
3) В окружность радиуса 10 вписана трапеция. Длины диагонали и средней линии трапеции соответственно равны 15 и 12. Найти длину боковой стороны трапеции.
4) Олимпиада в Финансовой академии 2009г. Хорды окружности пересекаются в точке Q. Известно, что а радиус окружности равен 4см.
Найдите длину хорды PN. Олимпиада в Финансовой академии 2009г.
5) В треугольнике PST . Вокруг точки пересечения его биссектрис и вершин P и T описана окружность с радиусом 8см. Найдите радиус окружности, описанной около треугольника PST (авторская задача).
Детально разобрать теорему синусов и получить необходимую практику ее использования в задачах вам всегда поможет репетитор по математике . Ее плановое школьное изучение происходит в курсе геометрии 9 класса в теме решение треугольников (по всем программам). Если вам нужна подготовка к ЕГЭ по математике для сдачи экзамена не менее чем на 70 баллов — придется тренироваться в решении крепких планиметрических задач с номеров С4. В них теорему синусов часто применяют к вписанным треугольникам учитывая соотношение . Помните об этом!
С уважением, Колпаков Александр Николаевич,
репетитор по математике
При изучении треугольников невольно встаёт вопрос о вычислении зависимости между их сторонами и углами. В геометрии и синусов дает наиболее полный ответ для решения этой проблемы.
В изобилии различных математических выражений и формул, законов, теорем и правил встречаются такие, что отличаются необычайной гармоничностью, лаконичностью и простотой подачи заключённого в них смысла. Теорема синусов является ярким примером подобной математической формулировки. Если в словесной трактовке ещё и возникает определённое препятствие в осмыслении данного математического правила, то при взгляде на математическую формулу всё сразу становится на свои места.
Первые сведения о данной теореме были обнаружены в виде доказательства её в рамках математического труда Насир ад-Дин Ат-Туси, датированного тринадцатым веком.
Приближаясь ближе к рассмотрению соотношения сторон и углов в любом треугольнике, стоит отметить, что теорема синусов позволяет решать массу математических задач, при этом данный закон геометрии находит себе применение в различных видах практической деятельности человека.
Сама теорема синусов гласит, что для любого треугольника характерна пропорциональность сторон к синусам противоположных углов.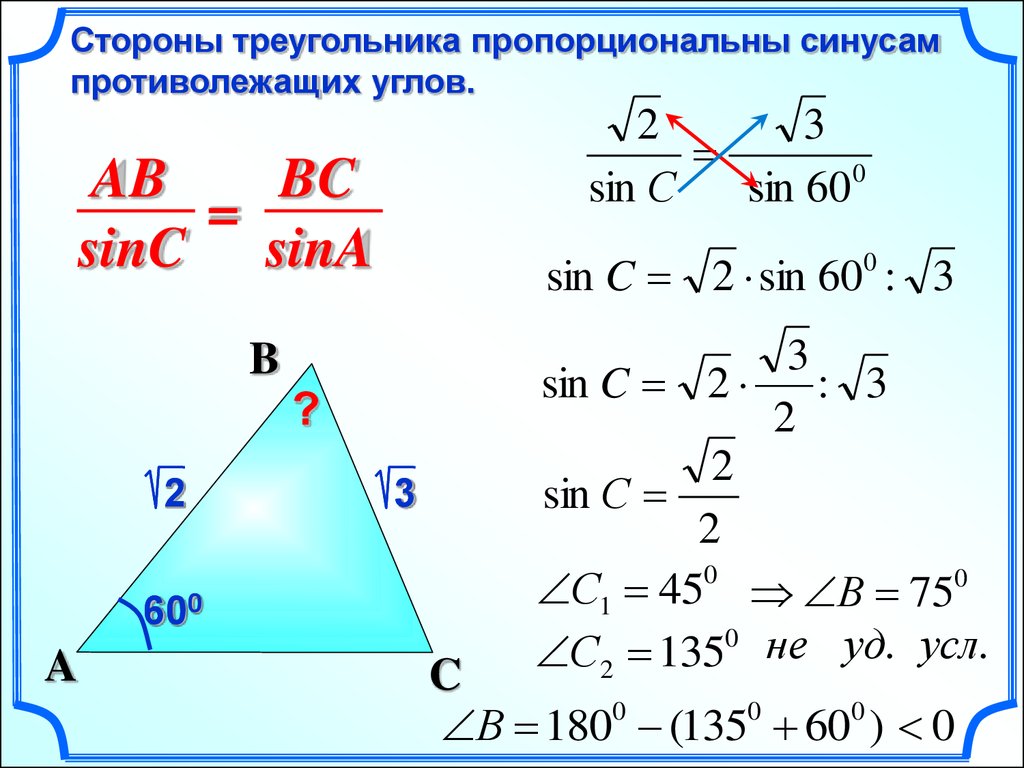
Также имеется и вторая часть этой теоремы, согласно которой отношение любой стороны треугольника к синусу противоположного угла равно описанной около рассматриваемого треугольника.
В виде формулы это выражение выглядит, как
a/sinA = b/sinB = c/sinC = 2R
Имеет теорема синусов доказательство, которое в различных вариантах учебников предлагается в богатом разнообразии версий.
Для примера рассмотрим одно из доказательств, дающих объяснение первой части теоремы. Для этого зададимся целью доказать верность выражения a sinC = c sinA.
В произвольном треугольнике ABC построим высоту BH. В одном из вариантов построения H будет лежать на отрезке AC, а в другом за его пределами, в зависимости от величины углов при вершинах треугольников. В первом случае высоту можно выразить через углы и стороны треугольника, как BH = a sinC и BH = c sinA, что и является требуемым доказательством.
В случае, когда точка H окажется за пределами отрезка AC, можем получить следующие варианты решений:
ВН = a sinC и ВН = c sin(180-A)= c sinA;
либо ВН = a sin(180-C) = а sinC и ВН = c sinA.
Как видим, в независимости от вариантов построения, мы приходим к желаемому результату.
Доказательство второй части теоремы потребует от нас описать вокруг треугольника окружность. Через одну из высот треугольника, к примеру B, построим диаметр круга. Полученную точку на окружности D соединим с одной из высотой треугольника, пусть это будет точка A треугольника.
Если рассмотреть полученные треугольники ABD и ABC, то можно заметить равенство углов C и D (они опираются на одну дугу). А учитывая, что угол А равен девяносто градусов то sin D = c/2R, или же sin C = c/2R, что и требовалось доказать.
Теорема синусов является отправной точкой для решения широкого спектра различных задач. Особая привлекательность заключается в практическом её применении, как следствие из теоремы мы получаем возможность связать между собой величины сторон треугольника, противолежащих углов и радиуса (диаметра) описанной вокруг треугольника окружности. Простота и доступность формулы, описывающей данное математическое выражение, позволяли широко использовать эту теорему для решения задач при помощи различных механических счётных приспособлений таблицы и пр.
), но даже приход на службу человека мощных вычислительных устройств не снизил актуальность данной теоремы.
Эта теорема не только входит в обязательный курс геометрии средней школы, но и в дальнейшем применяется в некоторых отраслях практической деятельности.
Официальный сайт МБОУ СОШ с.Паниковец
| Размер шрифта: | Межстрочный интервал: стандартный средний большой |
| Цвет фона: | Межбуквенный интервал: стандартный средний большой |
Версия для слабовидящих Отключить версию для слабовидящих
Липецкая область, Задонский район, с. Пани́ковец, ул. Запрудная, д. 18. Телефон: 8 (47471) 4-72-12
Электронная почта школы: sc-panikovets@schools48.
ru
02.02.2023
Сталинград. Победа, изменившая мир
С 1995 года 2 февраля в России отмечают как день Победы советского народа в Сталинградской битве.
Читать далее
31.01.2023
Изобретательно и занимательно
В современном творчестве очень популярным стало lego – конструирование.
Читать далее
30.01.2023
Помни. Не забывай…
Хотя уже прошло две трети века, я не нашел ответа на вопрос:
Читать далее
27.01.2023
Девятьсот дней мужества
На окне моем горит свеча
Читать далее
26.01.2023
Предстоит учиться мне в университете
25 января в России отмечается день студента. История праздника студенчества тесно связана с историей Московского государственного университета.
Так случилось, что именно в Татьянин день, 25 января в 1775 году императрица Елизавета Петровна подписала указ «Об учреждении Московского университета», и Татьянин день стал официальным праздником всех студентов, Святая Татьяна их небесной покровительницей.
Читать далее
20.01.2023
Дорожная азбука
Липецкая область один из немногих регионов России, где проводится профильная Олимпиада по основам дорожной безопасности. Организаторами «Дорожной азбуки» являются областные Госавтоинспекция и управление образования и науки, а целями – повышение знаний учащихся школ в области транспортной безопасности и культуры. Мероприятие проводится в рамках реализации федерального проекта «Безопасность дорожного движения» национального проекта «Безопасные качественные дороги».
Читать далее
01.01.2023
Год педагога и наставника
2023 год Указом Президента России Владимира Путина объявлен Годом педагога и наставника.
Миссия Года – признание особого статуса педагогических работников, в том числе выполняющих наставническую деятельность. Мероприятия Года педагога и наставника будут направлены на повышение престижа профессии учителя.
Читать далее
28.12.2022
Акция «Дед Мороз за БДД»
В канун новогодних праздников традиционно проводятся профилактические мероприятия. Наша школа охотно поддержала акцию по безопасности дорожного движения «Дед Мороз за БДД». Дед Мороз с ребятами из отряда ЮИД в игровом занятии проверили свои знания по ПДД, призывали всех позаботиться о своей безопасности, быть внимательными и осторожными при переходе дороги, а автомобилистам напомнили о том, что скоро зимние каникулы, когда нужно быть особенно внимательными. Дед Мороз поздравил всех с наступающим Новым годом.
Читать далее
23.12.2022
Этой силе имя есть – Россия!
25 декабря 2000 года президент России Владимир Владимирович Путин подписал федеральные законы о государственных символах Российской Федерации – флаге, гербе и гимне.
Читать далее
20.12.2022
Правила поведения на водоёмах в зимний период
1. Необходимо помнить, что выходить на лед можно только в крайнем случае с максимальной осторожностью.
Читать далее
Все новости >>>
Калькулятор закона синусов — Найдите закон синусов по формуле
Онлайн-калькулятор закона синусов позволяет найти неизвестные углы и длины сторон треугольника. Когда мы имеем дело с простыми и сложными тригонометрическими функциями sin(x), этот калькулятор использует формулу закона синусов, которая помогает найти недостающие стороны и углы треугольника.
Итак, читайте дальше, чтобы получить полное руководство по законам синусов.
Что такое закон синусов? Законы синусов — это соотношение между углами и сторонами треугольника, которое определяется как отношение длины стороны треугольника к синусу противоположного угла.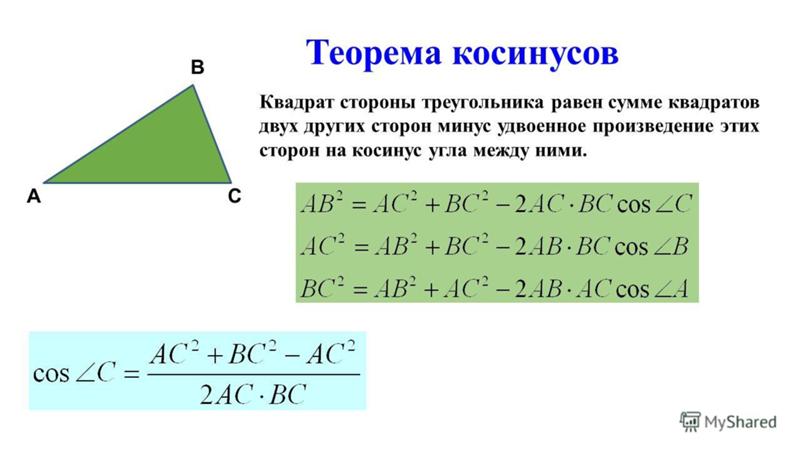
Где:
Стороны треугольника:
$$a = сторона a, b = сторона b, c = сторона c$$
Углы треугольника:
$$A = угол A , B = угол B, C = угол C$$
Характеристики треугольника:
P = периметр треугольника, s = полупериметр, K = площадь, r = радиус вписанной окружности, R = радиус описанной окружности
Если a, b и c — длины сторон треугольника, а противолежащие углы равны A, B и C соответственно; тогда закон грехов показывает: 90}$$
Из калькулятора получаем:
$$a = 15,427$$
Итак, длина сторон b и c равна \(15,427 мм\).
Однако онлайн-калькулятор синуса рассчитает тригонометрические функции синуса для заданного угла в градусах, радианах или π радианах.
Уравнения, полученные из закона синусов для углов A, B и C:Вот некоторые уравнения, которые используются калькулятором закона синусов, полученные из закона грехов:
$$A=sin ^{−1}[\frac{asinB}{b}]$$ 9{−1}[\frac{csinB}{b}]$$
Производные уравнения по закону синусов Решение для сторон a, b и c:Чтобы найти любую сторону треугольника по закону синусов калькулятор извлек некоторые значения из формулы закона синусов:
$$a=\frac{bsinA}{sinB}$$
$$a=\frac{csinA}{sinC}$$
$$b=\frac {asinB}{sinA}$$
$$b=\frac{csinB}{sinC}$$
$$c=\frac{asinC}{sinA}$$
$$c=\frac{bsinC }{sinB}$$
Кроме того, вы можете найти альфа (α), используя значения \(a=n/a, b=n/a, бета (β ) =n/a\), а значение бета рассчитывается с помощью \(a=n/a, alpha=n/a, b=n/a\).
90\).
Кроме того, онлайн-калькулятор CSC определит косеканс и обратную тригонометрическую функцию синуса для заданного угла в градусах, радианах или пи (π) радианах.
Как работает калькулятор закона синусов?Калькулятор синусоиды, специально используемый для вычисления пропущенных значений треугольника, связанных с синусоиды, с помощью следующих шагов:
Ввод:- Вы должны выбрать опцию, чтобы найти любой угол или сторону треугольника из выпадающего списка, даже калькулятор отображает уравнение для выбранной опции
- Теперь вам нужно добавить значения углов и сторон в соответствующие поля
- Затем необходимо выбрать единицы для введенных значений
- Наконец, нажмите на заданную кнопку расчета
Калькулятор синусов вычисляет:
- Значение углов и сторон для данного уравнения
- Значения различных характеристик треугольника
- Диаграмма
Когда у вас есть две стороны и один угол или два угла и одна сторона треугольника, мы используем законы синусов.
Согласно теореме о неравенстве треугольника, сумма любых двух сторон должна быть больше третьей стороны треугольника, и это правило должно удовлетворять всем трем условиям сторон.
Что такое косой треугольник в тригонометрии?Косоугольный треугольник не является прямоугольным, поэтому основные тригонометрические соотношения не применяются, их можно изменить, чтобы покрыть косоугольность с помощью закона синусов и косинусов.
Каковы характеристики треугольника?Существуют различные способы определения характеристик треугольника:
- Радиус окружности вокруг треугольника \(R = (abc) / (4K)\)
- Радиус вписанной окружности в треугольник \(r = \sqrt{(s-a)*(s-b)*(s-c) / s}\)
- Площадь треугольника \(K = \sqrt{s*(s-a)*(s-b)*(s-c)}\)
- Полупериметр треугольника \(s = 0,5 * (a + b + c)\)
- Периметр \(P = a + b + c\)
Калькулятор закона синусов настоятельно рекомендуется для оценки недостающих значений треугольника с использованием формулы закона синусов.
Нахождение всех этих значений вручную является сложной задачей, а также увеличивает риск получения точных результатов. Используя калькулятор закона синуса, вы можете найти все значения закона синуса мгновенно и на 100% безошибочно. Кроме того, этот инструмент полезен для людей, которые работают с тригонометрической функцией, связанной с законом синуса.
Из источника Википедии: Неоднозначный случай решения треугольника, Отношение к описанной окружности, Отношение к площади треугольника.
Из источника Краткий курс триггеров Дейва: косые треугольники, теорема Пифагора, характеристики треугольника.
Из источника Академии Хана: Обзор законов синусов и косинусов, Решение треугольников по закону синусов, Недостающий угол.
.tb_button {padding:1px;курсор:указатель;граница справа: 1px сплошная #8b8b8b;граница слева: 1px сплошная #FFF;нижняя граница: 1px сплошная #fff;}.tb_button.hover {сверлильный станок: 2px отступ #def; background-color: #f8f8f8 !important;}.
ws_toolbar {z-index:100000} .ws_toolbar .ws_tb_btn {курсор:указатель;граница:1px сплошная #555;padding:3px} .tb_highlight{background-color:yellow} .tb_hide {visibility:hidden} .ws_toolbar img {padding:2px;margin:0px}
Калькулятор синусов
- Дом
- Расчет
- Математика
- Калькулятор закона синусов
Калькулятор закона синусов
Расчет с входными данными: &Угол;А, &угол;В, сторона b&угла;А, &угол;С, сторона с&угол;В, &угол А, сторона а&угол;В, &угол;С, сторона с&угол;С, &угол;А, сторона а&угол;С, &угол. ;B, сторона b, сторона a, ∠B, сторона b, сторона a, ∠C, сторона c, сторона b, ∠A, сторона, сторона b, ∠C, сторона c, сторона c, ∠A, сторона, сторона c, ∠B , сторона б
Входы:
и угол; A:
& Angle; B:
& Angle; C:
РЕЗУЛЬТАТ:
1113
|
Чтобы найти неизвестное значение, необходимо знать три значения.