Подборка задач ОГЭ по теме «Площадь» для 8 класса
Квадрат
1. Сторона квадрата равна 10. Найдите его площадь.
2. Периметр квадрата равен 40. Найдите площадь квадрата.
3.Из квадрата вырезали прямоугольник. Найдите площадь получившейся фигуры.
4. Периметр квадрата равен 160. Найдите площадь квадрата.
5. Найдите площадь квадрата, если его диагональ равна 1.
6. Найдите площадь квадрата, описанного вокруг окружности радиуса 83.
Прямоугольник
1. В прямоугольнике одна сторона равна 10, другая сторона равна 12. Найдите площадь прямоугольника.
2. В прямоугольнике диагональ равна 10, а угол между ней и одной из сторон равен 30°. Найдите площадь прямоугольника, делённую на .
3. В прямоугольнике диагональ равна 10, угол между ней и одной из сторон равен 30°, длина этой стороны . Найдите площадь прямоугольника, деленную на
Найдите площадь прямоугольника, деленную на
4. Найдите площадь прямоугольника, если его периметр равен 44 и одна сторона на 2 больше другой.
5. Найдите площадь прямоугольника, если его периметр равен 60, а отношение соседних сторон равно 4:11.
6. Найдите площадь прямоугольника, если его периметр равен 58 и одна сторона на 5 больше другой.
7. В прямоугольнике одна сторона равна 96, а диагональ равна 100. Найдите площадь прямоугольника.
8. На стороне BC прямоугольника ABCD, у которого AB = 12 и AD = 17, отмечена точка E так, что ∠EAB = 45°. Найдите ED.
Треугольник
В прямоугольном треугольнике один из катетов равен 10, а угол, лежащий напротив него, равен 45°. Найдите площадь треугольника.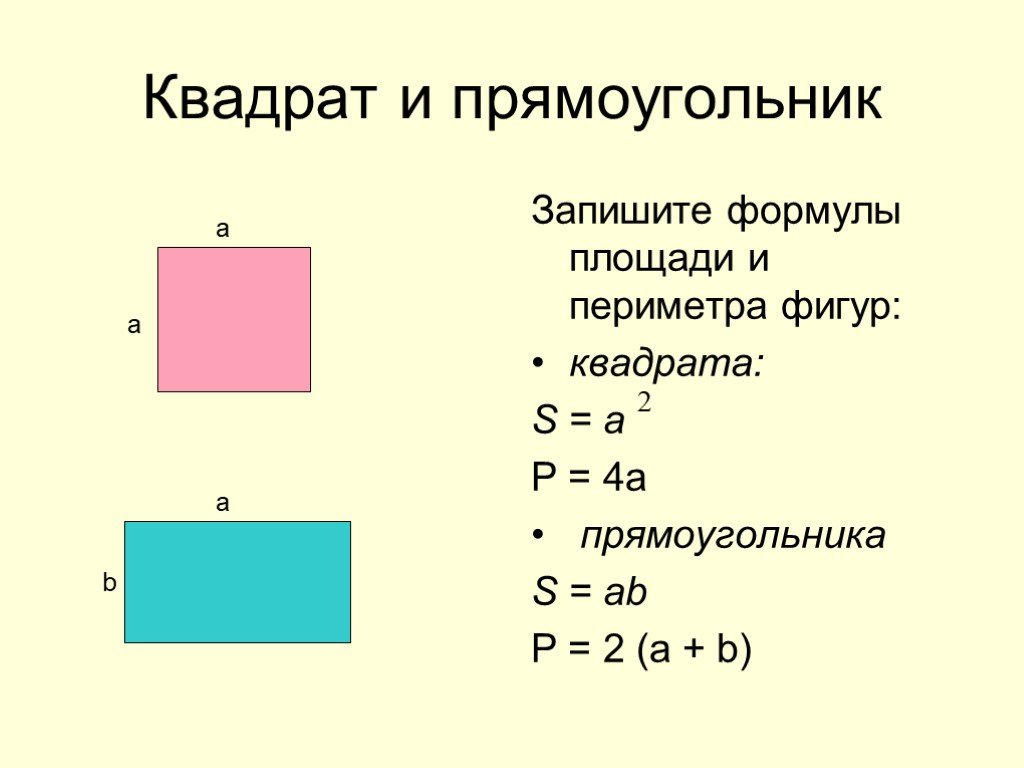
Найдите площадь прямоугольного треугольника, если его катет и гипотенуза равны соответственно 28 и 100.
В прямоугольном треугольнике один из катетов равен 4, а острый угол, прилежащий к нему, равен 45°. Найдите площадь треугольника.
В прямоугольном треугольнике гипотенуза равна 70, а один из острых углов равен 45°. Найдите площадь треугольника.
Катеты прямоугольного треугольника равны 8 и 15. Найдите гипотенузу этого треугольника.
Два катета прямоугольного треугольника равны 4 и 9. Найдите площадь этого треугольника.
Сторона равностороннего треугольника равна 10. Найдите его площадь, делённую на .
Периметр равностороннего треугольника равен 30. Найдите его площадь, делённую на .
Высота равностороннего треугольника равна 10. Найдите его площадь, делённую на
Найдите его площадь, делённую на
В равнобедренном треугольнике боковая сторона равна 10, а угол, лежащий напротив основания, равен 120°. Найдите площадь треугольника, делённую на
Периметр равнобедренного треугольника равен 16, а боковая сторона — 5. Найдите площадь треугольника.
В равнобедренном треугольнике боковая сторона равна 10, основание — , а угол, лежащий напротив основания, равен 30°. Найдите площадь треугольника.
Боковая сторона равнобедренного треугольника равна 34, а основание равно 60. Найдите площадь этого треугольника.
Периметр равнобедренного треугольника равен 216, а боковая сторона — 78. Найдите площадь треугольника.
В треугольнике одна из сторон равна 10, а опущенная на нее высота — 5. Найдите площадь треугольника.
В треугольнике одна из сторон равна 10, другая равна , а угол между ними равен 60°. Найдите площадь треугольника.
Найдите площадь треугольника, изображённого на рисунке.
В треугольнике ABC отрезок DE — средняя линия. Площадь треугольника CDE равна 97. Найдите площадь треугольника ABC.
Сторона треугольника равна 12, а высота, проведённая к этой стороне, равна 33. Найдите площадь этого треугольника.
Трапеция
1. Найдите площадь трапеции, изображённой на рисунке.
2. Основания трапеции равны 18 и 12, одна из боковых сторон равна , а угол между ней и одним из оснований равен 135°. Найдите площадь трапеции.
3. Основания трапеции равны 18 и 12, одна из боковых сторон равна 6, а синус угла между ней и одним из оснований равен . Найдите площадь трапеции.
Найдите площадь трапеции.
4. Основания трапеции равны 18 и 12, одна из боковых сторон равна 6, а косинус угла между ней и одним из оснований равен . Найдите площадь трапеции.
5. Основания трапеции равны 18 и 12, одна из боковых сторон равна 6, а тангенс угла между ней и одним из оснований равен . Найдите площадь трапеции.
6. Средняя линия трапеции равна 11, а меньше основание равно 5. Найдите большее основание трапеции.
7. Боковая сторона трапеции равна 5, а один из прилегающих к ней углов равен 30°. Найдите площадь трапеции, если её основания равны 3 и 9.
8. В равнобедренной трапеции основания равны 3 и 9, а один из углов между боковой стороной и основанием равен 45°. Найдите площадь трапеции.
9. Основания равнобедренной трапеции равны 5 и 17, а ее боковые стороны равны 10. Найдите площадь трапеции.
Найдите площадь трапеции.
10. Основания трапеции равны 7 и 49, одна из боковых сторон равна 18 , а косинус угла между ней и одним из оснований равен Найдите площадь трапеции.
11.Основания трапеции равны 1 и 13, одна из боковых сторон равна , а угол между ней и одним из оснований равен 135°. Найдите площадь трапеции.
12. В трапеции ABCD AD = 5, BC = 2, а её площадь равна 28. Найдите площадь трапеции BCNM, где MN – средняя линия трапеции ABCD.
13. В трапеции ABCD AD = 3, BC = 1, а её площадь равна 12. Найдите площадь треугольника ABC.
14. Тангенс острого угла прямоугольной трапеции равен Найдите её большее основание, если меньшее основание равно высоте и равно 58.
15. Основания трапеции равны 9 и 54, одна из боковых сторон равна 27, а косинус угла между ней и одним из оснований равен .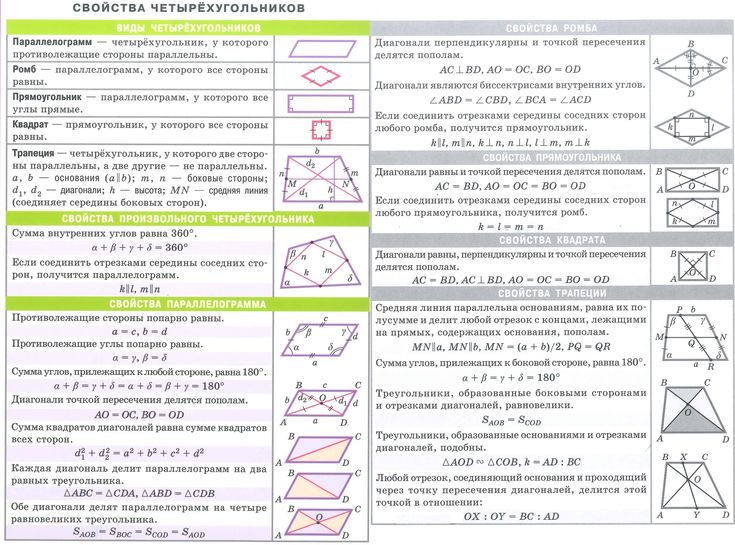 Найдите площадь трапеции.
Найдите площадь трапеции.
16.В трапеции ABCD известно, что AD = 6, BC = 2, а её площадь равна 32. Найдите площадь трапеции BCNM, где MN – средняя линия трапеции ABCD.
17. В трапеции ABCD известно, что AD = 5, BC = 1, а её площадь равна 51. Найдите площадь трапеции BCNM, где MN – средняя линия трапеции ABCD.
18. Основания трапеции равны 6 и 24, одна из боковых сторон равна 11, а синус угла между ней и одним из оснований равен . Найдите площадь трапеции.
19. Основания трапеции равны 7 и 63, одна из боковых сторон равна 18, а косинус угла между ней и одним из оснований равен . Найдите площадь трапеции.
Параллелограмм, ромб
1. Найдите площадь параллелограмма, изображённого на рисунке.
2. Сторона ромба равна 5, а диагональ равна 6. Найдите площадь ромба.
Найдите площадь ромба.
3. Периметр ромба равен 40, а один из углов равен 30°. Найдите площадь ромба.
4. Периметр ромба равен 24, а синус одного из углов равен . Найдите площадь ромба.
5. Одна из сторон параллелограмма равна 12, а опущенная на нее высота равна 10. Найдите площадь параллелограмма.
6. Одна из сторон параллелограмма равна 12, другая равна 5, а один из углов — 45°. Найдите площадь параллелограмма, делённую на .
7. Одна из сторон параллелограмма равна 12, другая равна 5, а синус одного из углов равен . Найдите площадь параллелограмма.
8. Одна из сторон параллелограмма равна 12, другая равна 5, а косинус одного из углов равен . Найдите площадь параллелограмма.
9. Одна из сторон параллелограмма равна 12, другая равна 5, а тангенс одного из углов равен . Найдите площадь параллелограмма.
10. Найдите площадь ромба, если его диагонали равны 14 и 6.
11. В ромбе сторона равна 10, одна из диагоналей — , а угол, лежащий напротив этой диагонали, равен 30°. Найдите площадь ромба.
12. Площадь параллелограмма ABCD равна 56. Точка E — середина стороны CD. Найдите площадь трапеции AECB.
13. Сторона ромба равна 9, а расстояние от центра ромба до неё равно 1. Найдите площадь ромба.
14. Периметр ромба равен 116, а один из углов равен 30°. Найдите площадь ромба.
15. Сторона ромба равна 50, а диагональ равна 80. Найдите площадь ромба.
17. Высота BH параллелограмма ABCD делит его сторону AD на отрезки AH = 1 и HD = 28. Диагональ параллелограмма BD равна 53. Найдите площадь параллелограмма.
Фигуры на квадратной решётке
На клетчатой бумаге с размером клетки 1см × 1см найти площадь фигуры
100 ballov.
 kz образовательный портал для подготовки к ЕНТ и КТА
kz образовательный портал для подготовки к ЕНТ и КТА
Хотите купить новую квартиру и уже нашли несколько подходящих под ваш бюджет вариантов? Не забудьте добавить к стоимости жилья ряд дополнительных расходов, которые вам придется оплатить при покупке недвижимости в Казахстане. Квартиры в Астане и квартиры в Алматы можно посмотреть на korter.kz, где с помощью фильтров можно максимально точно подобрать желаемые варианты.
Что оплачивает покупатель?Договор купли-продажи недвижимости включает в себя ряд обязательных платежей, независимо от того, где было куплено жилье — на вторичном рынке или в новостройке. Определенную часть расходов должен погасить покупатель. Сумма платежей рассчитывается в зависимости от особенностей сделки и может достигать значительных размеров, поэтому важно перед покупкой подсчитать все расходы.
Дополнительные платежи покупателя при оформлении права собственности:
- услуги нотариуса;
- оплата госпошлины за регистрацию.

Нотариальное оформление договора купли-продажи не является обязательной процедурой, но специалисты рынка недвижимости советуют не пренебрегать услугами нотариуса. Нотариус проверяет стороны сделки, контролирует процесс заключения договора и выступает гарантом безопасности.
Нотариальные услуги имеют фиксированную стоимость. Средняя стоимость нотариального оформления объекта недвижимости в 2023 году составляет 12 МРП, т.е. около 37000 тг. Следует обращать внимание на то, что сумма платы зависит от того, кто является участниками сделки. Если сделка заключается с близким родственником – сумма уменьшается, если с юридическим лицом – увеличивается.
Как правило, участники сделки делят расходы на оформление поровну. Однако, лучше заранее согласовать этот момент с продавцом недвижимости.
Прямые сделки также предусматривают дополнительные расходы, например, оформление задатка.
Регистрация прав на имуществоПри покупке недвижимости покупатель обязуется оплатить государственную пошлину за регистрацию своих прав на имущество в ЦОН. Процедура оформления занимает до 3 рабочих дней. Стоимость данной услуги — 1 073,7 тг.
Процедура оформления занимает до 3 рабочих дней. Стоимость данной услуги — 1 073,7 тг.
Покупатель может заказать услугу ускоренной регистрации права собственности. Процесс внесения информации в реестр займет 1 день. Стоимость ускоренной регистрации — 5000 тг.
Дополнительные расходыЗачастую дополнительных трат требуют услуги опытных специалистов: риелторов, оценщиков, юристов. Однако в зависимости от типа сделки могут появиться и другие дополнительные издержки:
- Ипотечный налог. Если вы покупаете квартиру в ипотеку, вы должны совершить платеж, размер которого зависит от условий кредитования, налоговых вычетов и т.д.
- Банковские услуги. Плата за совершение операций, использование банковской ячейки, аренда сейфа, страховка и т.д.
- Увеличение фактической площади. Это относится к покупке квартиры в новостройке. Когда конечная площадь жилья превышает предусмотренную проектом.
- Оплата коммунальных. Управляющая компания жилого комплекса может взимать оплату своих услуги наперед.

Следовательно, в понятие конечной стоимости жилья входит не только цена квадратных метров, но ряд дополнительных расходов, сумма которых может составлять около 10% стоимости самого объекта.
Площадь треугольника — УРОКИ МАТЕМАТИИ КЕЙТ
Что такое площадь?Площадь – это пространство внутри формы. Измеряется в квадратных единицах. Если вы поместите фигуру на сетку, площадь — это количество квадратов, которые могут поместиться внутри фигуры.
Вместо подсчета квадратов вы также можете использовать формулу для нахождения площади прямоугольника. | Добро пожаловать на уроки математики у Кейт! Учителя, обязательно ознакомьтесь с учебными пособиями и заданиями. |
Как найти площадь треугольника?
Есть формула, по которой можно найти площадь треугольника. Она похожа на формулу площади прямоугольника, за исключением того, что вместо длины и ширины в ней используются основание и высота. Треугольник занимает вдвое меньше места, чем прямоугольник, поэтому в формуле стоит 1/2.
Треугольник занимает вдвое меньше места, чем прямоугольник, поэтому в формуле стоит 1/2.
Что делать, если треугольник не похож на нарисованный? Иногда высота не является одной из сторон треугольника. Основание и высота треугольника всегда перпендикулярны друг другу, поэтому ищите прямоугольник, который отмечает число 9.угол 0 градусов.
Основанием может быть любая из трех сторон треугольника. Как правило, мы выбираем сторону «снизу» для основы, но вы можете повернуть бумагу, и другая сторона окажется внизу. Неважно, какую сторону вы выберете для основания, но высота и основание должны быть перпендикулярны друг другу. Высотой может быть одна из сторон треугольника (если это прямоугольный треугольник). Высота может быть внутри треугольника (например, треугольник в середине ниже) или высота может быть вне треугольника (например, треугольник справа внизу).
Пример 1
Найдите площадь треугольника.
Шаг 1: Определите основание и высоту. Основание и высота должны быть под углом 90 градусов. Это означает, что
Шаг 2: Подставьте основание и высоту в формулу площади треугольника.
Шаг 3: Упрощение. Сначала возьмите половину 12, чтобы получить 6. Затем умножьте 6 на 10, чтобы получить 60 квадратных единиц. Если вы используете калькулятор, вы можете ввести 0,5 вместо 1/2 или сначала умножить основание и высоту, а затем разделить на 2.
Пример 2
Найдите площадь треугольника.
Шаг 1: Определите основание и высоту треугольника. Не забудьте найти прямоугольник, который отмечает угол 90 градусов. Основание и высота должны быть перпендикулярны друг другу. Это означает, что основание = 15 , а высота = 6 .
Шаг 2: Подставьте основание и высоту в формулу площади треугольника.
Шаг 3: Упрощение. Вы можете ввести 0,5 для 1/2, если используете калькулятор. Или вы можете сначала умножить основание и высоту, а затем разделить на 2. В любом случае вы получите один и тот же ответ.
Практика
Готовы решить некоторые задачи самостоятельно? Нажмите кнопку СТАРТ ниже, чтобы пройти пробный тест.
Работает на Interact |
Хотите узнать, как найти площадь круга?
Прямоугольник и треугольник . Прямоугольник и треугольник имеют одинаковую площадь. При размещении на одном уровне вершина треугольника касается верхнего края…
Цитата страницы Начать эссе значок-вопрос Спросите репетитораНачать бесплатную пробную версию
Скачать PDF PDF Цитата страницы Цитировать Поделиться ссылкой ДелитьсяУкажите эту страницу следующим образом:
«Прямоугольник и треугольник.
Ответы экспертов
Ответ Нилы отличный .
Чтобы треугольник (высота которого равна ширине прямоугольника) имел ту же площадь, что и прямоугольник, основание должно быть в два раза длиннее прямоугольника.
[ Сравнение формулы площади прямоугольника ( длина x ширина ) и площадь треугольника ( 1/2 x основание x высота ), чтобы эти два выражения были равны, когда ширина прямоугольника равна высоте треугольника, отсюда следует, что основание должно быть 2xlength прямоугольника ]
См.
 eNotes без рекламы
eNotes без рекламыНачните с 48-часовой бесплатной пробной версией , чтобы получить доступ к более чем 30 000 дополнительных руководств и более чем 350 000 вопросов помощи при выполнении домашних заданий, на которые наши эксперты ответили.
Получите 48 часов бесплатного доступаУже зарегистрированы? Войдите здесь.
Утверждено редакцией eNotes
Математика
Последний ответ опубликован 07 сентября 2010 г. в 12:47:25.
Что означают буквы R, Q, N и Z в математике?
14 Ответы педагога
Математика
Последний ответ опубликован 07 октября 2013 г. в 20:13:27.
Как определить, является ли это уравнение линейной или нелинейной функцией?
84 Ответы воспитателя
Математика
Последний ответ опубликован 09 октября 2017 г.



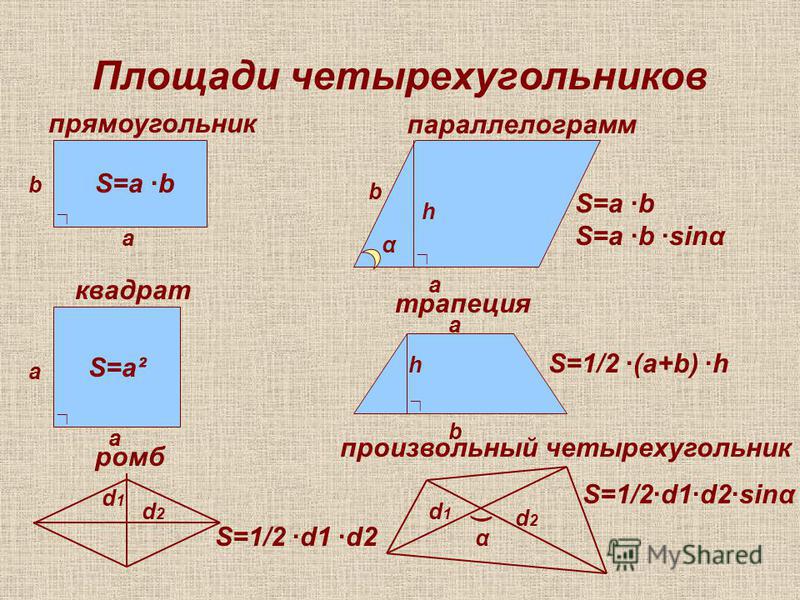 Формула площади прямоугольника: Площадь = длина х ширина. Для прямоугольника выше мы могли бы также умножить 4 x 3, чтобы найти площадь.
Формула площади прямоугольника: Площадь = длина х ширина. Для прямоугольника выше мы могли бы также умножить 4 x 3, чтобы найти площадь.