Презентация на тему средняя линия трапеции. Теорема о средней линии трапеции
«Урок площадь трапеции» — В прямоугольной трапеции основания 5см. и 17см., а меньшая боковая сторона 10см. Учитель подводит итоги, задавая вопросы: Кто получил 5, 4, 3 балла? В каждом случае формулируют теорему, которую доказали. Решение поставленной задачи. Как вычислить площадь трапеции? Какие элементы плоских фигур используются в формулах площадей?
«Задачи на теорему Пифагора» — №21 Найти: Х. №18 Найти: Х. №27 Найти: Х. Задачи на готовых чертежах («Теорема Пифагора»). №23 Найти: Х. №25 Найти: Х. №26 Найти: Х. №13 Найти: Х. №20 Найти: Х. №19 Найти: Х. №14 Найти: Х. Вы справились со всеми предложенными заданиями. №29 Найти: Х. №28 Найти: Х. №30 Найти: Х. №22 Найти: Х.
«Теорема Фалеса» — Фалес широко известен как геометр. Астрономия. Милетский материалист. Проведем через точку В2 прямую ЕF, параллельную прямой А1А3. Из равенства треугольников следует равенство сторон В1В2=В2В3. Теорема Фалеса. Считается, что Фалес первым изучил движение Солнца по небесной сфере. Треугольники В2В1F и В2В1Е равны по второму признаку равенства треугольников.
Считается, что Фалес первым изучил движение Солнца по небесной сфере. Треугольники В2В1F и В2В1Е равны по второму признаку равенства треугольников.
«Теорема синусов» — Стороны треугольника пропорциональны синусам противолежащих углов. Решение: Устная работа: Ответы к задачам по чертежам: Проверка домашнего задания. Тема урока: Теорема синусов. Теорема синусов:
«Урок теорема Пифагора» — Определить вид треугольника: Знакомства с теоремой. Доказательство теоремы. Разминка. Теорема Пифагора. И обрете лестницу долготою 125стоп. План урока: Исторический экскурс. Показ картинок. Решение простейших задач. Вычислите высоту CF трапеции ABCD. Доказательство. Определить вид четырехугольника KMNP.
«Теорема Пифагора 8 класс» — ФИГУРЫ. Деление чисел на четные и нечетные, простые и составные. Дано: прямоугольный треугольник a,b катеты с- гипотенуза. Высота. Доказательство Бхаскари. Открытия пифагорийцев в математике. Дано: Прямоугольный треугольник, a, b – катеты, с — гипотенуза Доказать: c2 = a2 + b2.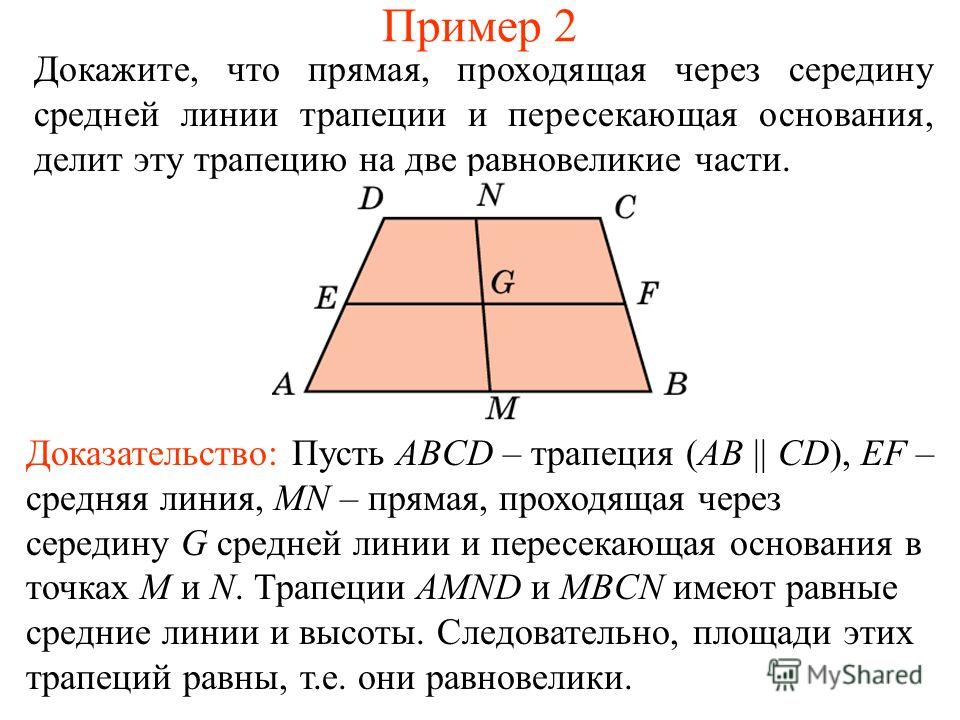 Меньшая сторона прямоугольного треугольника.
Меньшая сторона прямоугольного треугольника.
Чтобы пользоваться предварительным просмотром презентаций создайте себе аккаунт (учетную запись) Google и войдите в него: https://accounts.google.com
Подписи к слайдам:
Средняя линия (8 класс)
Средняя линия треугольника
Средняя линия треугольника. Определение: Отрезок, соединяющий середины двух сторон треугольника, называют СРЕДНЕЙ ЛИНИЕЙ ТРЕУГОЛЬНИКА.
Теорема Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны. т.е.: КМ ║ АС КМ = ½ АС A B C K M
Решить задачу устно: A B C K M 7 см Дано: M К – сред. линия Найти: АС?
Работа в парах:
Решим задачу: Дано: MN – сред. линия Найти: P ∆ АВС M N A B C 3 4 3, 5
Работа в парах:
Средняя линия трапеции
Вспомним: Трапеция – это четырехугольник, у которого две стороны параллельны, а две другие стороны не параллельны A D B C BC || AD — основания AB łł CD – боковые стороны
Средняя линия трапеции.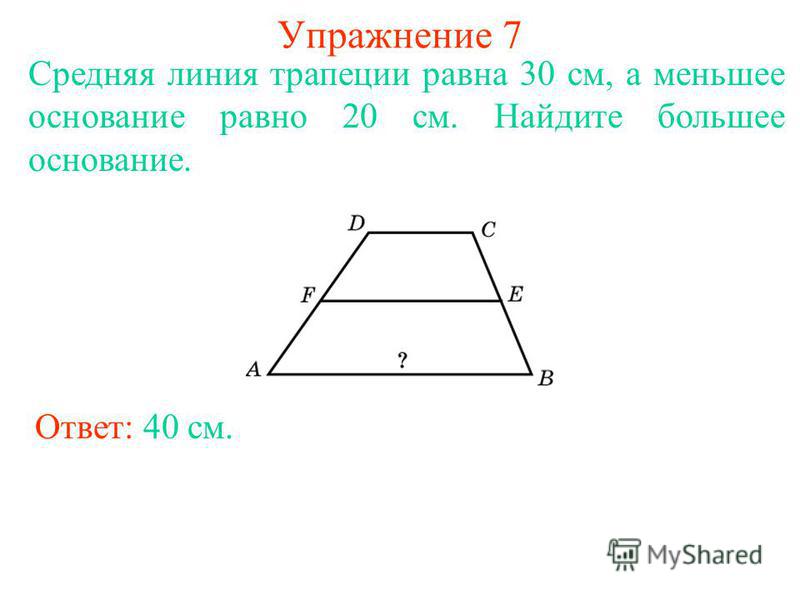 Определение: Средней линией трапеции называется отрезок, соединяющий середины её боковых сторон. A D B C M N MN – средняя линия трапеции ABCD
Определение: Средней линией трапеции называется отрезок, соединяющий середины её боковых сторон. A D B C M N MN – средняя линия трапеции ABCD
Теорема о средней линии трапеции Средняя линия трапеции параллельна её основаниям и равна их полусумме. т.е.: М N ║ВС║А D М N = ½ (ВС+А D) M N A D B C
Решить устно: M N A D B C 6,3 см 18,7 см?
Решить устно в парах: Дано: AB = 16 см; CD = 1 8 см; М N = 15 см Найти: P ABCD = ? M N A D B C
Самостоятельная работа Задача: Средняя линия трапеции равна 5 см. Найти основания трапеции, если известно, что нижнее основание больше верхнего основания в 1,5 раз. Решение: A D B C 5 см Пусть BC = Х см тогда AD = 1.5X см BC+AD = 10 см X + 1.5X = 10 X = 4 Значит: BC = 4 см AD = 6 см
СПАСИБО ЗА УРОК!!!
Презентация разработана учителем математики ГБОУ СОШ №467 Г. Санкт-Петербурга, Колпинского района Лугвиной Натальей Анатольевной
По теме: методические разработки, презентации и конспекты
Урок обобщения и закрепления знаний по теме «Средняя линия треугольника. Средняя линия трапеции» в 8 классе с использованием ИКТ….
Средняя линия трапеции» в 8 классе с использованием ИКТ….
Рабочая тетрадь — это индивидуальное творческое задание ученика. которое предполагает самостоятельную работу с текстом по теме «Трапеция. Средняя линия трапеции», применение знаний при решении задач. …
Определение: средней линией треугольника называется отрезок, соединяющий середины двух его сторон. АК = КС ВЕ = СЕ КЕ – средняя линия АВС Определение: средней линией трапеции называется отрезок, соединяющий середины боковых её сторон. А ВС К Н Е АН = НВ КЕ = СЕ НЕ – средняя линия АВСК А В С К Е Сколько средних линий в треугольнике? Сколько средних линий в трапеции?
Средняя линия треугольника Теорема. Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны. А С В М К Дано: АВС, МК – средняя линия Доказательство: Т. к. по условию МК – средняя линия, то АМ = МВ = ½ АВ, СК = КВ = ½ ВС, Значит, ВМ АВ ВК ВС 1 2 В – общий для АВС и МВК, значит, АВС и МВК подобны по второму признаку подобия, следовательно, ВМК = А, значит, МК АС.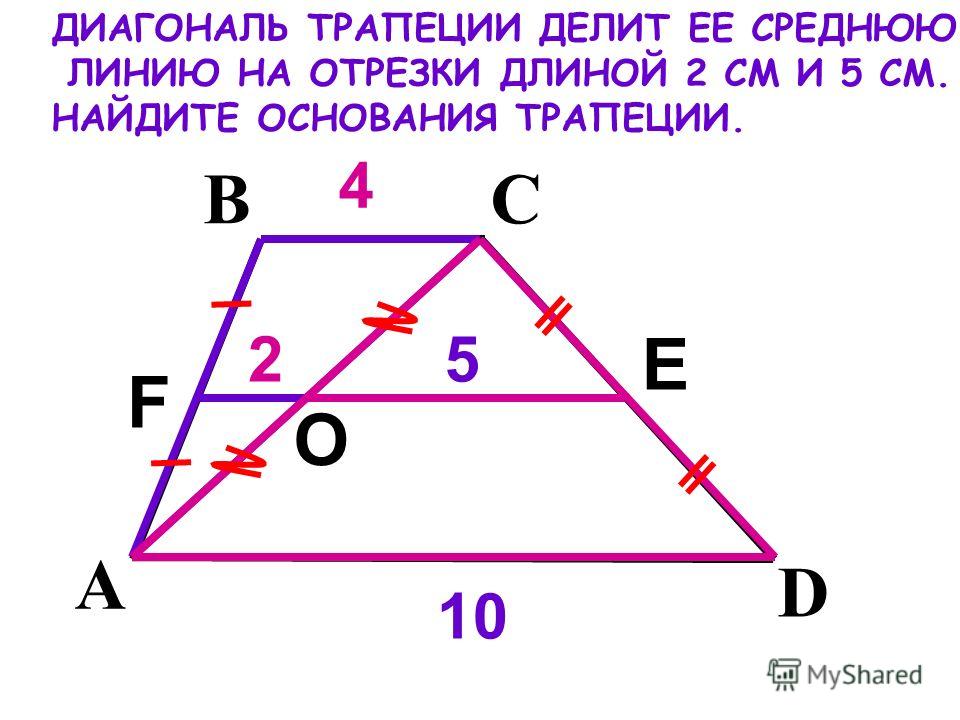
Реши задачу F R N ? А В
Доказательство: Проведём А 1 В 1 А В С А1А1 В1В1 О С1С1 По условию АА 1, ВВ 1 – медианы значит, ВА 1 = СА 1, АВ 1 = СВ 1, т. е. А 1 В 1 – средняя линия. Значит, А 1 В 1 АВ, поэтому 1 = 2, 3 = 4. Следовательно, треугольники АОВ и А 1 ОВ 1 подобны по двум углам. Значит, их стороны пропорциональны: АО ВО АВ А1ОА1О В1ОВ1О А1В1А1В1 По свойству средней линии треугольника АВ = 2 А 1 В 1, т. е. АО ВО АВ А1ОА1О В1ОВ1О А1В1А1В1 2 1 Аналогично, СО С1ОС1О 2 1 Получим: С1ОС1О АОВОСО А1ОА1ОВ1ОВ1О 2 1
Средняя линия трапеции Теорема. Средняя линия трапеции параллельна основаниям и равна их полусумме. А В С К М Р Дано: АВСК – трапеция МР – средняя линия Доказать: МР АК, МР ВС МР = Доказательство: О Проведём через точку М прямую МЕ АК, докажем, что МЕ пройдёт через Р. Т. к. АВСК – трапеция, то ВС АК, а, значит, ВС МЕ АК Т. к. МР – средняя линия, то АМ= МВ, КР = СР Е Следовательно, МР лежит на МЕ, значит, МР АК, МР ВС. Проведём ВК. По теореме Фалеса О – середина ВК, значит, МО – средняя линия АВК, ОР – средняя линия ВСК МР = МО + ОР = ½ АК + ½ ВС = ½ (АК + ВС) = По теореме Фалеса МЕ пересечёт СК в середине СК, т. е. в точке Р.
к. МР – средняя линия, то АМ= МВ, КР = СР Е Следовательно, МР лежит на МЕ, значит, МР АК, МР ВС. Проведём ВК. По теореме Фалеса О – середина ВК, значит, МО – средняя линия АВК, ОР – средняя линия ВСК МР = МО + ОР = ½ АК + ½ ВС = ½ (АК + ВС) = По теореме Фалеса МЕ пересечёт СК в середине СК, т. е. в точке Р.
Тема «Средняя линия трапеции» относится к одной из важных тем курса геометрии. Данная фигура довольно часто встречается в различных задачах, как и ее средняя линия. Задания, содержащие данные этой темы часто встречаются в итоговых контрольных и аттестационных работах. Знание по данной теме могут также пригодиться при обучении в средних и высших заведениях.
Хотя и в теме заявлена фигура трапеция, но рассмотрение данной темы может проходить в период изучения темы «Векторы» и «Применение векторов при решении задач». Это можно понять, глядя на слайд презентации.
Автор здесь определяет среднюю линию, как отрезок, который соединяет середины боковых сторон. Более того, здесь же отмечено, что средняя линия трапеции параллельна ее основаниям, а также равна их полусумме. Вот именно в ходе доказательства этого утверждения и пригодятся знания, связанные с векторами. Применяя правила сложения векторов по чертежу, который показан, как иллюстрация условия, получаются равенства. Эти равенства имеют одинаковую левую часть, и она является средней линией трапеции в виде вектора. Складывая эти равенства, получаются большое выражение в правой части равенства.
Вот именно в ходе доказательства этого утверждения и пригодятся знания, связанные с векторами. Применяя правила сложения векторов по чертежу, который показан, как иллюстрация условия, получаются равенства. Эти равенства имеют одинаковую левую часть, и она является средней линией трапеции в виде вектора. Складывая эти равенства, получаются большое выражение в правой части равенства.
слайды 1-2 (Тема презентации «Средняя линия трапеции», определение средней линии трапеции)
Если внимательно рассмотреть, то в двух случаях получается сложение противоположных векторов, дающих в результате нуль. Тогда остается, что двойной вектор, содержащий среднюю линию трапеции, равен сумме векторов, содержащий основания. Разделив это равенство на 2, получается, что вектор, содержащий среднюю линию, равен половине суммы векторов, содержащих основания. Теперь идет сравнение векторов. Получается, что все эти векторы одинаково направленные. Это значит, что знаки векторов можно смело опускать.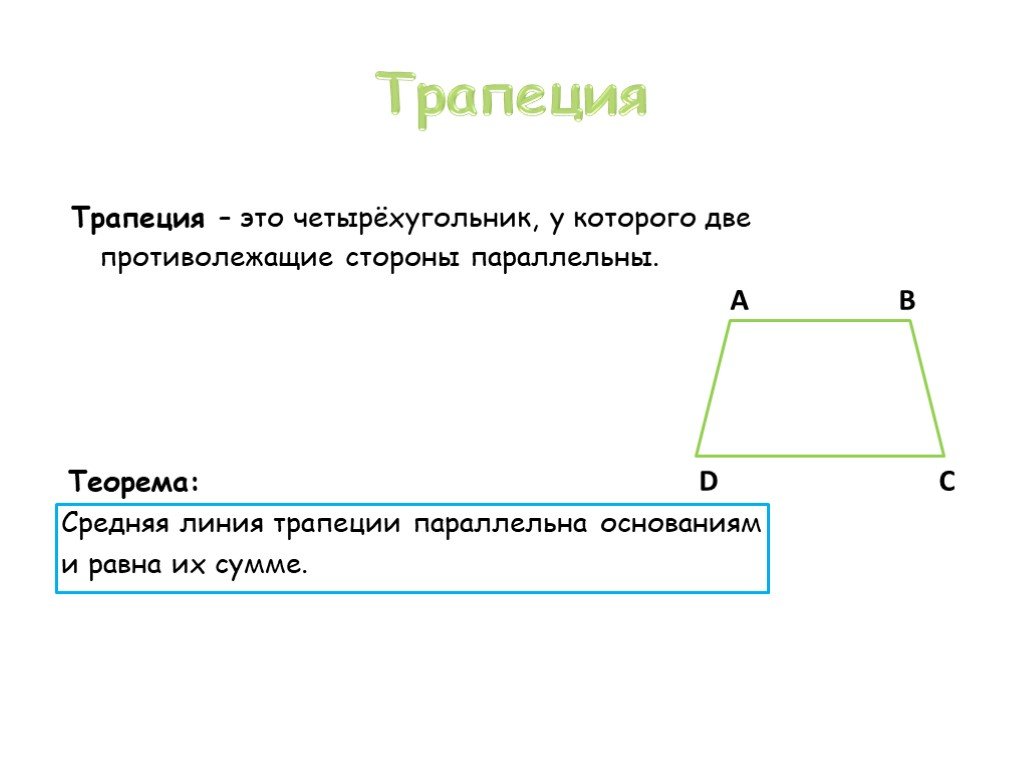 И тогда получается, что сама средняя линия трапеции равна полусумме оснований.
И тогда получается, что сама средняя линия трапеции равна полусумме оснований.
Презентация содержит единственный слайд, который несет в себе большое количество информации. Здесь дано определение средней линии трапеции, а также указано ее основное свойство. В курсе геометрии это свойство является теоремой. Так здесь доказана теорема с использованием знаний понятия векторов и действий над ними.
Учитель может данную презентацию дополнить своими примерами и задачами, но все, что требуется для среднего уровня знаний по данному предмету здесь опубликовано. Более того, так автор оставил возможность учителю пофантазировать, доработать то, что ему самому захочется для того,чтобы создать соответствующую атмосферу на уроке. Не стоит забывать и про сам настрой на урок. Тогда с помощью данной презентации точно можно добиться желаемого результата.
краткое содержание других презентаций
«Построение правильных многоугольников» — ?=60?. ·180?. Геометрия. ?=. n. n — 2. Работу выполнила учитель математики МОУ «Гимназия №11» Лисицына Е.Ф.
?=. n. n — 2. Работу выполнила учитель математики МОУ «Гимназия №11» Лисицына Е.Ф.
«Теорема Фалеса» — Теорема Фалеса. Именем Фалеса названа геометрическая теорема. Астрономия. Проведем через точку В2 прямую ЕF, параллельную прямой А1А3. Считается, что Фалес первым изучил движение Солнца по небесной сфере. Презентация по геометрии Ученицы 9 «А» класса Сорогиной Полины. Милетский материалист. Геометрия. По свойству параллелограмма А1А2=FВ2, А2А3=В2Е. Фалес широко известен как геометр. И так как А1А2=А2А3, то FВ2=В2Е.
«Разложение вектора по двум неколлинеарным» — Пусть р коллинеарен b . Доказательство: Разложение вектора по двум неколлинеарным векторам. Доказательство: Пусть а и b — неколлинеарные векторы. Лемма: Если векторы а и b коллинеарны и а? 0, то существует такое число k, что b = ka. Докажем, что любой вектор р можно разложить по векторам а и b. Геометрия 9 класс. Тогда р = уb , где у – некоторое число.
«Правильные многоугольники 9 класс» — Урок геометрии в 9 классе. Луковникова Н.М., учитель математики. Построение правильного пятиугольника 1 способ. МОУ гимназия №56 г.Томск-2007. Правильные многоугольники.
Луковникова Н.М., учитель математики. Построение правильного пятиугольника 1 способ. МОУ гимназия №56 г.Томск-2007. Правильные многоугольники.
«Симметрия фигур» — Прямая а называется осью симметрии фигуры. D. Одна фигура получена из другой преобразованием. Оглавление. Преобразование, обратное движению, также является движением. А1. Выполнил:Пантюков Е. А. Существует множество различных видов симметрии. М1. Преобразование фигур.
«Симметрия относительно прямой» — Фигура может иметь одну или несколько осей симметрии. Симметрия в природе. Савченко Миша, 9В класс. Угол. Кто же изображен на фотографии оригинале? Л.С. Атанасян «Геометрия 7-9». Равнобедренная трапеция. Построить отрезок А1В1 симметричный отрезку АВ относительно прямой. Сколько осей симметрии имеет каждая фигура? Прямоугольник.
Трапеция. Виды трапеции. Доказать теорему о средней линии трапеции.
Трапеция – четырехугольник, у
которого только две противолежащие
стороны параллельны.
Виды трапеции: прямоугольная, равнобедренная (равнобокая), разнобокая.
Средняя линия трапеции – отрезок, соединяющий середины боковых сторон.
Теорема о средней линии трапеции.
Средняя линия трапеции параллельна основаниям и равна их полусумме.
Д-ть:
EF || AB, EF || CD; EF= (AB + CD).
Д-во:
A E = ED (теор. Фалеса)
BF = FC
EF- ср. линия.
EF || AB; EF || DC
EO = AB; OF = DC.
EF = EO + OF = (AB + CD).
Параллельный перенос. Свойства параллельного переноса.
Параллельный перенос фигуры Ф называется такое преобразование фигуры Ф, при котором все ее точки смещаются в одном и том же направлении на одно и то же расстояние.
Свойства параллельного переноса в пространстве.
Параллельный перенос есть движение.
При параллельном переносе

При параллельном переносе плоскость переходит либо в себя, либо в параллельную ей плоскость.
Параллельный перенос задается парой соответствующих точек, т.е. каковы бы ни были точки и , существует единственный параллельный перенос, при котором точка переходит в точку .
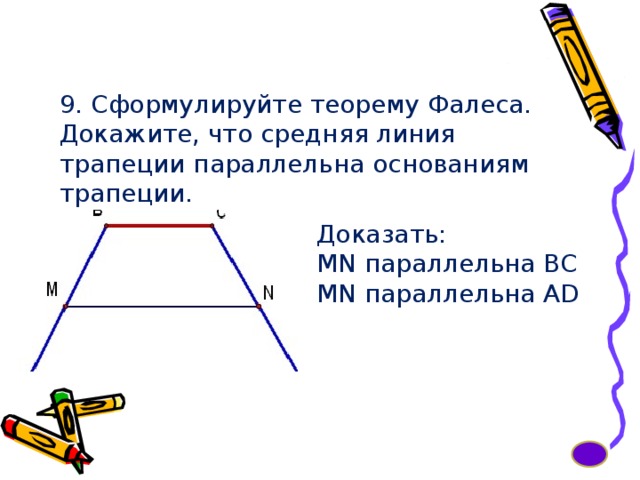
Доказать теорему Фалеса.
Теорема.
Если
параллельные прямые, пересекающие
стороны угла, отсекают на одной его
стороне равные отрезки, то они отсекают
равные отрезки и на другой его
стороне. Доказательство. Пусть
точки A1, A2, A3 – точки пересечения
параллельных прямых с одной из сторон
угла. А точки B1, B2, B3 – соответствующие
точки пересечения этих прямых с другой
стороной угла. Докажем, что если A1A2 =
A2A3, то B1B2=B2B3.
Проведем
через точку В2 прямую С1С2, параллельную
прямой A1A2. Получаем параллелограммы
A1C1B2A2 и A2B2C2A3. По свойствам параллелограмма,
A1A2 = C1B2 и A2A3 = B2C2.
Гомотетия. Свойства гомотетии.
Гомотетия с центром в точке О и коэффициентом k 0 называется такое преобразование, при котором каждая точка М отображается в такую точку М1, что выполняется равенство:
Свойства.
Если коэффициент гомотетии равен 1, то гомотетия является тождественным преобразованием: образ каждой точки совпадает с ней самой.
Если коэффициент гомотетии равен -1, то гомотетия является центральной симметрией.
Как и любое преобразование подобия, гомотетия преобразует прямую в прямую, отрезок в отрезок, луч в луч, угол в угол, окружность в окружность.

Как и любое преобразование подобия, гомотетия сохраняет величины углов между кривыми.
Параллельна ли средняя линия трапеции ее основаниям? Средняя линия трапеции
Ваша конфиденциальность важна для нас. По этой причине мы разработали Политику конфиденциальности, в которой описывается, как мы используем и храним вашу информацию. Пожалуйста, ознакомьтесь с нашей политикой конфиденциальности и сообщите нам, если у вас есть какие-либо вопросы.
Сбор и использование личной информации
Личная информация относится к данным, которые могут быть использованы для идентификации конкретного лица или связи с ним.
Вас могут попросить предоставить личную информацию в любое время, когда вы свяжетесь с нами.
Ниже приведены некоторые примеры типов личной информации, которую мы можем собирать, и того, как мы можем использовать такую информацию.
Какую личную информацию мы собираем:
- Когда вы подаете заявку на сайте, мы можем собирать различную информацию, включая ваше имя, номер телефона, адрес электронной почты и т.
 д.
д.
Как мы используем вашу личную информацию:
- Собираемая нами личная информация позволяет нам связываться с вами по поводу уникальных предложений, рекламных акций и других событий и предстоящих событий.
- Время от времени мы можем использовать вашу личную информацию для отправки вам важных уведомлений и сообщений.
- Мы также можем использовать личную информацию для внутренних целей, таких как проведение аудитов, анализ данных и различные исследования, чтобы улучшить предоставляемые нами услуги и предоставить вам рекомендации относительно наших услуг.
- Если вы участвуете в розыгрыше призов, конкурсе или аналогичном поощрении, мы можем использовать предоставленную вами информацию для управления такими программами.
Раскрытие информации третьим лицам
Мы не раскрываем полученную от вас информацию третьим лицам.
Исключения:
- В случае необходимости — в соответствии с законом, судебным приказом, в порядке судопроизводства и/или на основании публичных запросов или запросов государственных органов на территории Российской Федерации — раскрыть свои Персональные данные.
 Мы также можем раскрывать информацию о вас, если решим, что такое раскрытие необходимо или уместно в целях безопасности, правоохранительных органов или по другим причинам, представляющим общественный интерес.
Мы также можем раскрывать информацию о вас, если решим, что такое раскрытие необходимо или уместно в целях безопасности, правоохранительных органов или по другим причинам, представляющим общественный интерес. - В случае реорганизации, слияния или продажи мы можем передать личную информацию, которую мы собираем, соответствующему правопреемнику третьей стороны.
Защита личной информации
Мы принимаем меры предосторожности, в том числе административные, технические и физические, для защиты вашей личной информации от потери, кражи и неправомерного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения.
Обеспечение конфиденциальности на уровне компании
Чтобы обеспечить безопасность вашей личной информации, мы сообщаем нашим сотрудникам о правилах конфиденциальности и безопасности и строго следим за соблюдением правил конфиденциальности.
Понятие средней линии трапеции
Для начала вспомним, какая фигура называется трапецией.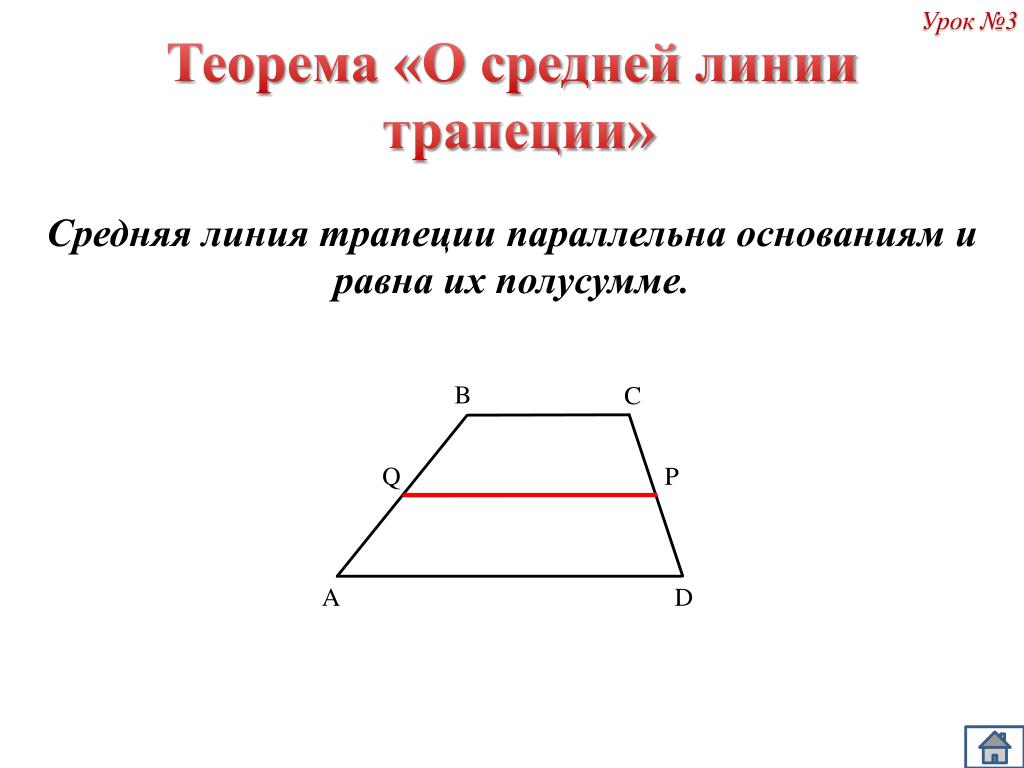
Определение 1
Трапеция – это четырехугольник, у которого две стороны параллельны, а две другие не параллельны.
При этом параллельные стороны называются основаниями трапеции, а не параллельные — сторонами трапеции.
Определение 2
средняя линия Трапеция — это отрезок, соединяющий середины сторон трапеции.
Теорема о средней линии трапеции
Теперь введем теорему о средней линии трапеции и докажем ее векторным методом.
Теорема 1
Средняя линия трапеции параллельна основаниям и равна половине их суммы.
Доказательство.
Дана трапеция $ABCD$ с основаниями $AD\ и\ BC$. И пусть $MN$ — средняя линия этой трапеции (рис. 1).
Рис. 1. Средняя линия трапеции
Докажем, что $MN||AD\ и \ MN=\frac(AD+BC)(2)$.
Рассмотрим вектор $\overrightarrow(MN)$. Далее мы используем правило многоугольника для сложения векторов. С одной стороны получаем, что
С другой стороны
Складывая два последних равенства, получаем
Так как $M$ и $N$ — середины сторон трапеции, то
Получаем :
Следовательно
Из того же равенства (поскольку $\overrightarrow(BC)$ и $\overrightarrow(AD)$ сонаправлены и, следовательно, коллинеарны), получаем, что $MN||AD$.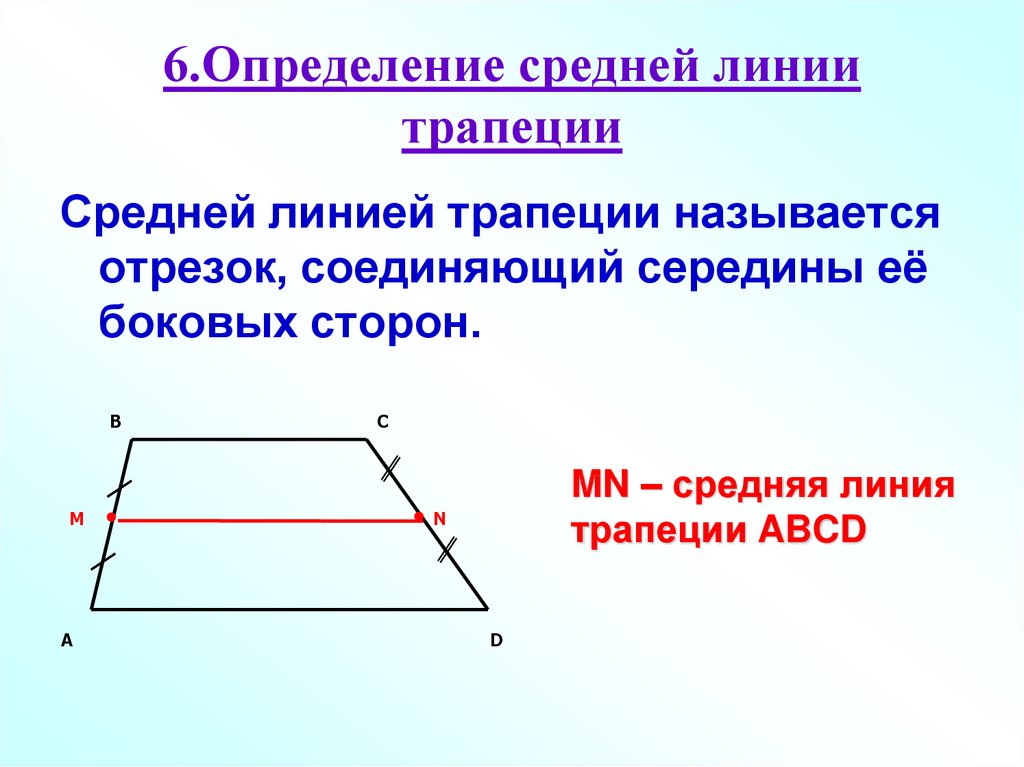
Теорема доказана.
Примеры задач на понятие средней линии трапеции
Пример 1
Стороны трапеции равны $15\см$ и $17\см$ соответственно. Периметр трапеции равен $52\см$. Найдите длину средней линии трапеции.
Раствор.
Обозначим среднюю линию трапеции через $n$.
Сумма сторон равна
Следовательно, поскольку периметр равен $52\см$, сумма оснований равна
Отсюда по теореме 1 получаем
Ответ: $10\см$.
Пример 2
Концы окружности диаметром $9$ см и $5$ см соответственно от касательной. Найдите диаметр этого круга.
Раствор.
Дана окружность с центром $O$ и диаметром $AB$. Проведите касательную $l$ и постройте расстояния $AD=9\ см$ и $BC=5\ см$. Проведем радиус $OH$ (рис. 2).
Рисунок 2.
Поскольку $AD$ и $BC$ — расстояния до касательной, то $AD\bot l$ и $BC\bot l$, а поскольку $OH$ — радиус, то $OH\bot l$, следовательно, $ OH |\left|AD\right||BC$. Из всего этого получаем, что $ABCD$ — трапеция, а $OH$ — ее средняя линия. По теореме 1 получаем
Из всего этого получаем, что $ABCD$ — трапеция, а $OH$ — ее средняя линия. По теореме 1 получаем
Понятие средней линии трапеции
Для начала вспомним, какая фигура называется трапецией.
Определение 1
Трапеция – это четырехугольник, у которого две стороны параллельны, а две другие не параллельны.
При этом параллельные стороны называются основаниями трапеции, а не параллельные — сторонами трапеции.
Определение 2
Средняя линия трапеции — это отрезок, соединяющий середины сторон трапеции.
Теорема о средней линии трапеции
Теперь введем теорему о средней линии трапеции и докажем ее векторным методом.
Теорема 1
Средняя линия трапеции параллельна основаниям и равна половине их суммы.
Доказательство.
Дана трапеция $ABCD$ с основаниями $AD\ и\ BC$. И пусть $MN$ — средняя линия этой трапеции (рис. 1).
Рис. 1. Средняя линия трапеции
Докажем, что $MN||AD\ и \ MN=\frac(AD+BC)(2)$.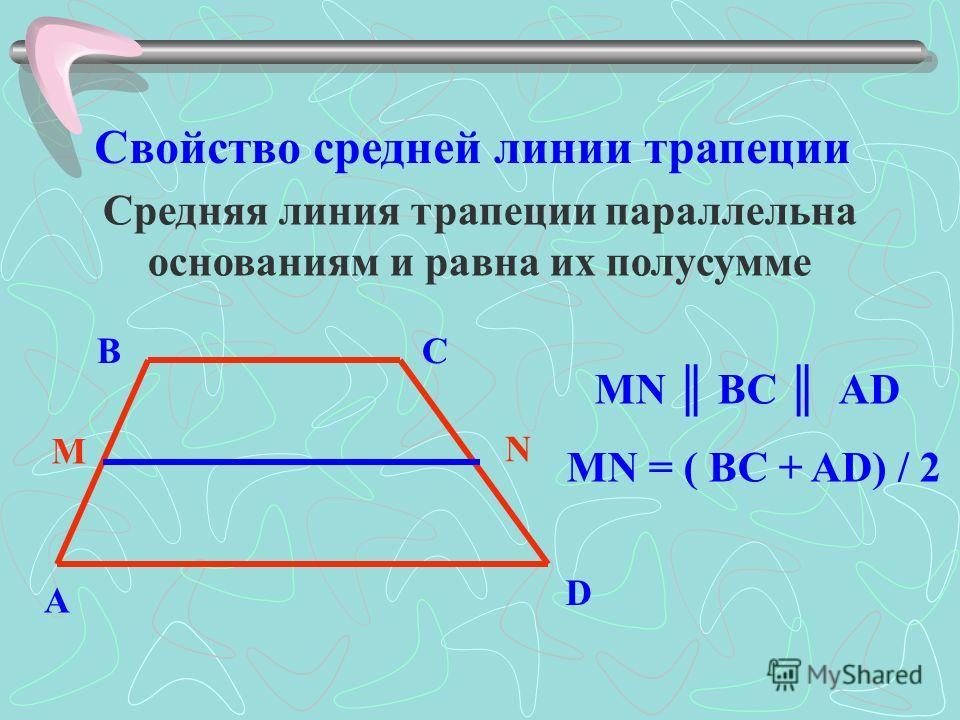
Рассмотрим вектор $\overrightarrow(MN)$. Далее мы используем правило многоугольника для сложения векторов. С одной стороны получаем, что
С другой стороны
Складывая два последних равенства, получаем
Так как $M$ и $N$ являются серединами сторон трапеции, то
Получаем:
Следовательно
Из того же равенства (поскольку $\overrightarrow(BC)$ и $\overrightarrow( AD)$ сонаправлены и, следовательно, коллинеарны), получаем, что $MN||AD$.
Теорема доказана.
Примеры задач на понятие средней линии трапеции
Пример 1
Стороны трапеции равны $15\см$ и $17\см$ соответственно. Периметр трапеции равен $52\см$. Найдите длину средней линии трапеции.
Раствор.
Обозначим среднюю линию трапеции через $n$.
Сумма сторон равна
Следовательно, поскольку периметр равен $52\см$, сумма оснований равна
Отсюда по теореме 1 получаем
Ответ: $10\см$.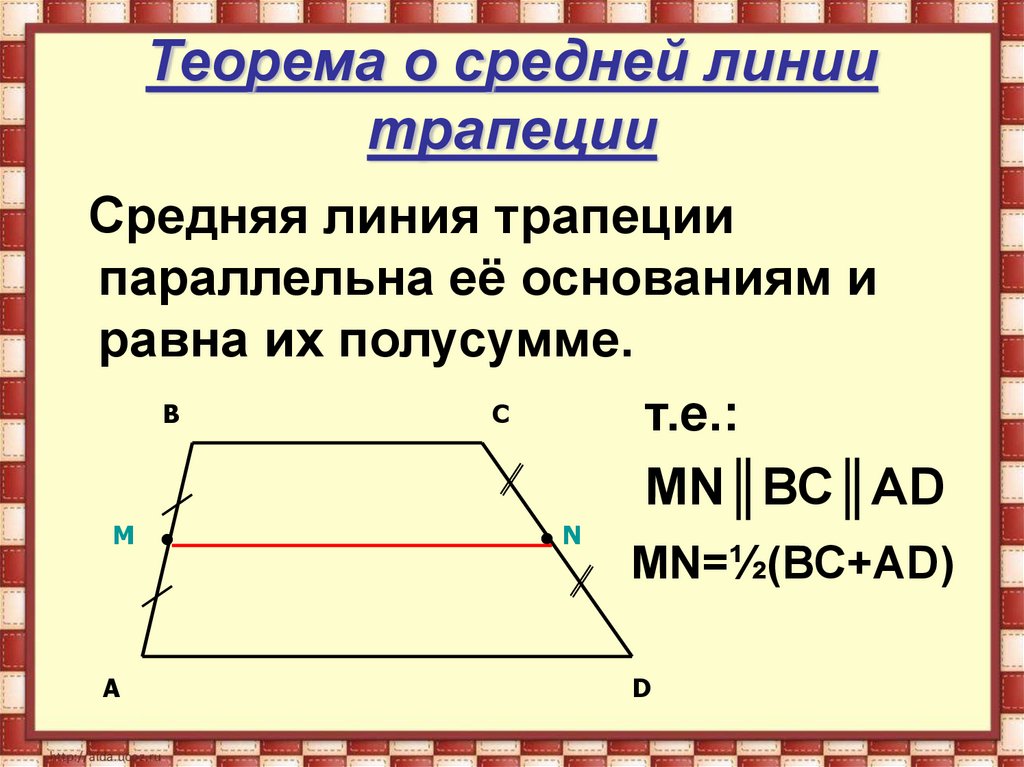
Пример 2
Концы окружности диаметром $9$ см и $5$ см соответственно от касательной. Найдите диаметр этого круга.
Раствор.
Дана окружность с центром $O$ и диаметром $AB$. Проведите касательную $l$ и постройте расстояния $AD=9\ см$ и $BC=5\ см$. Проведем радиус $OH$ (рис. 2).
Рис. 2.
Поскольку $AD$ и $BC$ — расстояния до касательной, то $AD\bot l$ и $BC\bot l$, а так как $OH$ — радиус, то $OH \bot l$, следовательно, $OH |\left|AD\right||BC$. Из всего этого получаем, что $ABCD$ — трапеция, а $OH$ — ее средняя линия. По теореме 1 получаем
- Отрезок, соединяющий середины диагоналей трапеции, равен половине разности оснований
- Треугольники, образованные основаниями трапеции и отрезками диагоналей до точки их пересечения, подобны
- Треугольники, образованные отрезками диагоналей трапеции, стороны которых лежат на сторонах трапеции — равновеликие (имеют одинаковую площадь)
- Если мы продолжим стороны трапеции в сторону меньшего основания, то они пересекутся в одной точке с прямой, соединяющей середины оснований
- Отрезок, соединяющий основания трапеции, и проходящий через точку пересечения диагоналей трапеции, делится этой точкой в пропорции, равной отношению длин оснований трапеции
- Отрезок, параллельный основаниям трапеции и проведенный через точку пересечения диагоналей, делится этой точкой пополам, и его длина равна 2ab/(a+b), где а и b — основания трапеции
Свойства отрезка, соединяющего середины диагоналей трапеции
Соединим середины диагоналей трапеции ABCD, в результате чего у нас получится отрезок LM.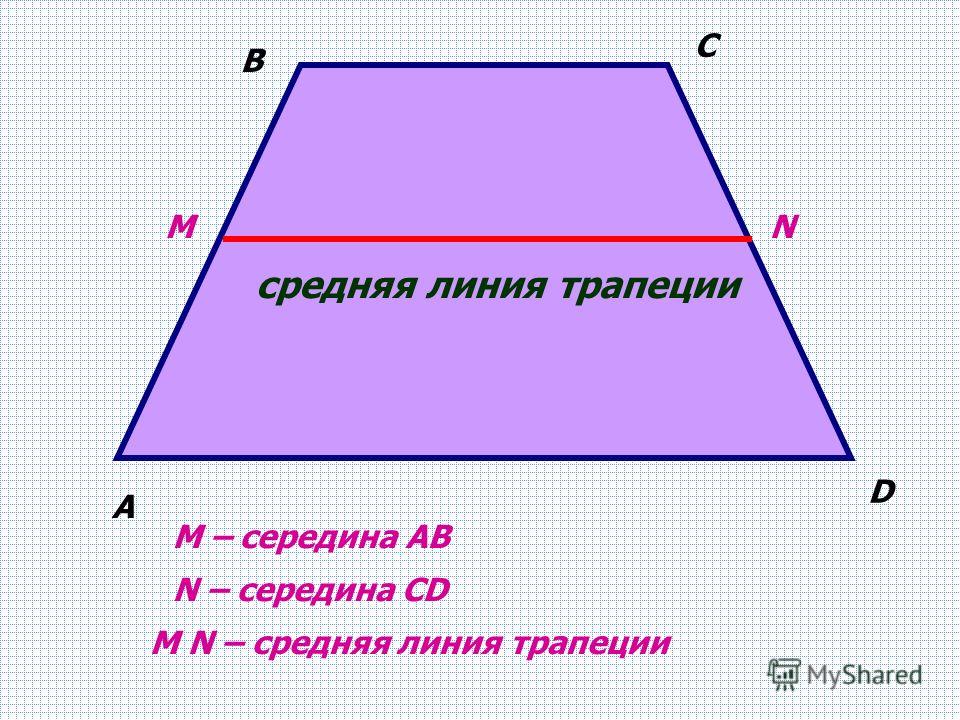
Отрезок, соединяющий середины диагоналей трапеции , лежит на средней линии трапеции .
Этот отрезок параллелен основаниям трапеции .
Длина отрезка, соединяющего середины диагоналей трапеции, равна полуразности ее оснований.
LM = (AD — BC)/2
или
LM = (a-b)/2
Свойства треугольников, образованных диагоналями трапеции
Треугольники, образованные основаниями трапеции и точкой пересечения диагоналей трапеции трапеция — аналогичны .
Треугольники BOC и AOD подобны. Поскольку углы BOC и AOD вертикальны, они равны.
Углы OCB и OAD внутренние крест-накрест, лежащие на параллельных прямых AD и BC (основания трапеций параллельны друг другу) и секущей AC, следовательно, равны.
Углы OBC и ODA равны по той же причине (внутреннее пересечение).
Поскольку все три угла одного треугольника равны соответствующим углам другого треугольника, эти треугольники подобны.
Что из этого следует?
Для решения задач по геометрии подобие треугольников используется следующим образом. Если известны длины двух соответствующих элементов подобных треугольников, то находим коэффициент подобия (делим одно на другое). Откуда длины всех остальных элементов связаны друг с другом точно такой же величиной.
Свойства треугольников, лежащих на боковой стороне и диагоналях трапеции
Рассмотрим два треугольника, лежащих на сторонах трапеции AB и CD. Это треугольники AOB и COD. Несмотря на то, что размеры отдельных сторон этих треугольников могут быть совершенно разными, но площади треугольников, образованных сторонами и точкой пересечения диагоналей трапеции, равны , то есть треугольники равны.
Если стороны трапеции продолжить в сторону меньшего основания, то точка пересечения сторон будет совпадать с прямой линией, проходящей через середины оснований .
Таким образом, любую трапецию можно продолжить до треугольника. При этом:
При этом:
- Треугольники, образованные основаниями трапеции с общей вершиной в точке пересечения продолженных сторон, подобны
- Прямая, соединяющая середины оснований трапеции, является одновременно медианой построенного треугольника
Свойства отрезка, соединяющего основания трапеции
Если провести отрезок, концы которого лежат на основаниях трапеции, лежащей в точке пересечения диагоналей трапеции (КН), то отношение составляющих ее отрезков от стороны основания до точки пересечения диагоналей (КО/ОН) будет равно отношению оснований трапеции (ВС/АД).
КО/ОН=БК/АД
Это свойство следует из подобия соответствующих треугольников (см. выше).
Свойства отрезка, параллельного основаниям трапеции
Если провести отрезок, параллельный основаниям трапеции и проходящий через точку пересечения диагоналей трапеции, то он будет иметь следующее свойства:
- Заданное расстояние (км) делит пополам точку пересечения диагоналей трапеции
- Длина отрезка , проходящая через точку пересечения диагоналей трапеции и параллельная основаниям, равна км = 2ab/(a + b)
Формулы для поиска диагонали трапеции
A, B — основания трапеции
C, D — стороны трапеции
D1 — DiAGONASOD
9000 D1 — DiAGONASOD9000 D1 — DiAGONASOD 9000D1 — DiAGONASOD
9000 D1 — DiAGONASOD 9000 2 D1 — DiAGONASOD 9000D1 — DIASIOD 9000
D1 — DIA.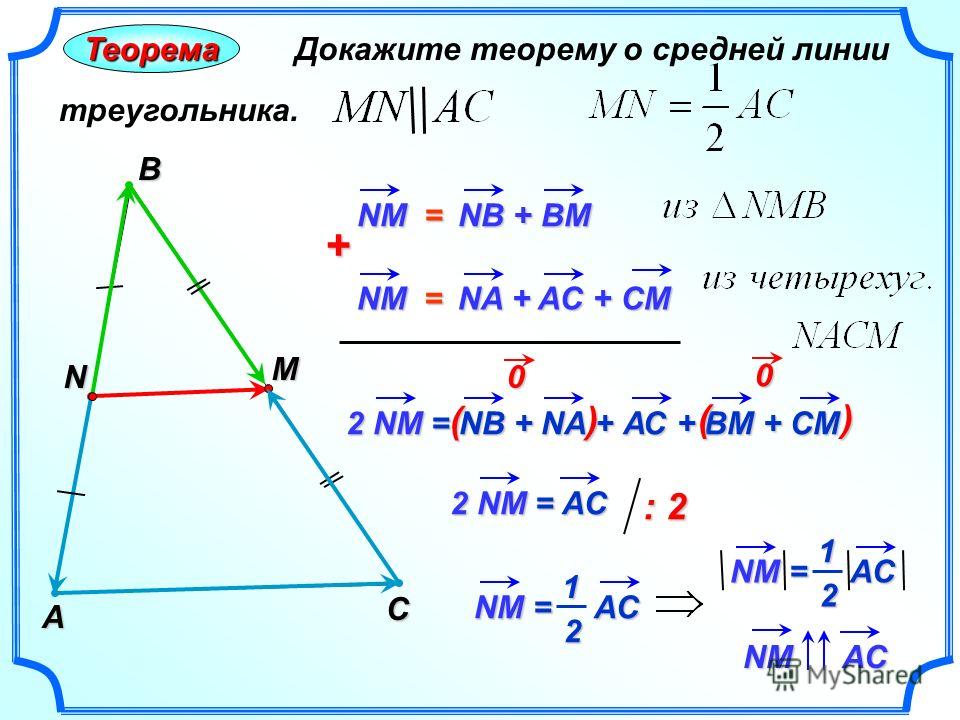 α β — уголки с большим основанием трапеции
α β — уголки с большим основанием трапеции
Формулы нахождения диагоналей трапеции через основания, стороны и углы при основании
Первая группа формул (1-3) отражает одно из основных свойств диагоналей трапеции:
1 . Сумма квадратов диагоналей трапеции равна сумме квадратов сторон плюс удвоенное произведение ее оснований. Это свойство диагоналей трапеции можно доказать в виде отдельной теоремы
2 . Эта формула получается преобразованием предыдущей формулы. Квадрат второй диагонали набрасывается на знак равенства, после чего из левой и правой частей выражения извлекается квадратный корень.
3 . Эта формула нахождения длины диагонали трапеции аналогична предыдущей, с тем отличием, что в левой части выражения
оставлена еще одна диагональ. Следующая группа формул (4-5) аналогична по смыслу и выражает подобное отношение.
Группа формул (6-7) позволяет найти диагональ трапеции, если известны большее основание трапеции, одна сторона и угол при основании.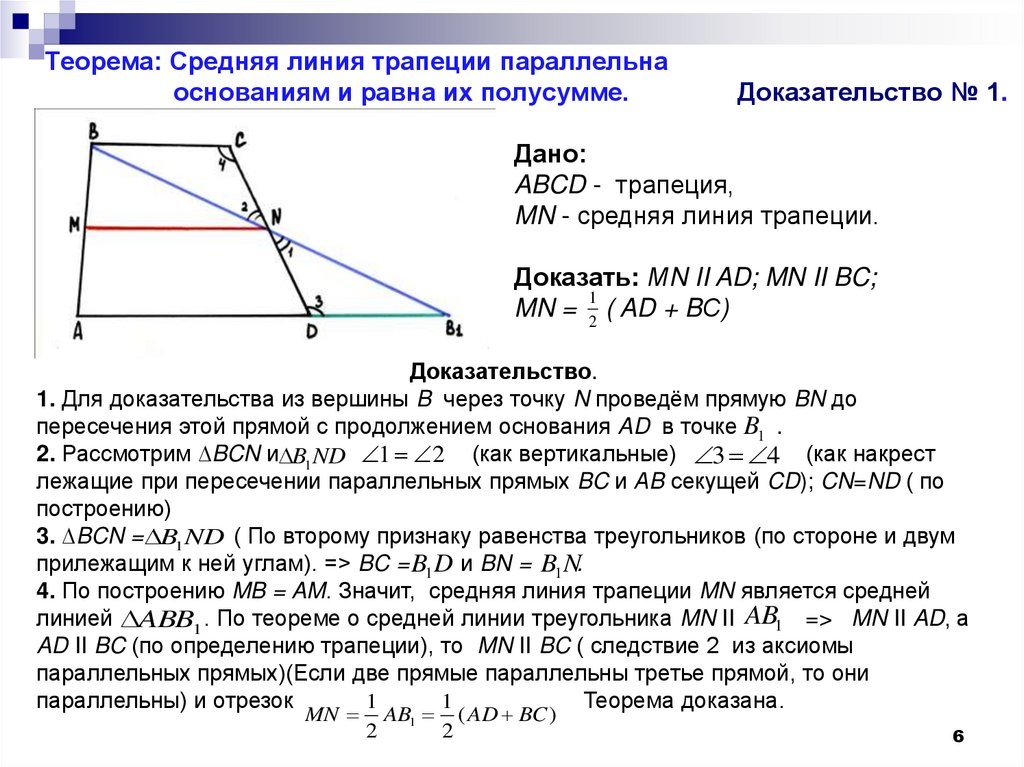
Формулы нахождения диагоналей трапеции через высоты
Примечание . В этом уроке дается решение задач по геометрии о трапециях. Если Вы не нашли решение задачи по геометрии интересующего Вас типа — задайте вопрос на форуме .
Задача .
Диагонали трапеции ABCD (AD | | BC) пересекаются в точке O. Найдите длину основания BC трапеции, если основание AD = 24 см, длина AO = 9 см, длина OS = 6 см.
Решение .
Решение этой задачи по идеологии абсолютно идентично предыдущим задачам.
Треугольники AOD и BOC подобны по трем углам — AOD и BOC вертикальны, а остальные углы попарно равны, так как образованы пересечением одной прямой и двух параллельных прямых.
Так как треугольники подобны, то все их геометрические размеры связаны друг с другом, как известные нам по условию задачи геометрические размеры отрезков АО и ОС. То есть
AO/OC=AD/BC
9 / 6 = 24 / B.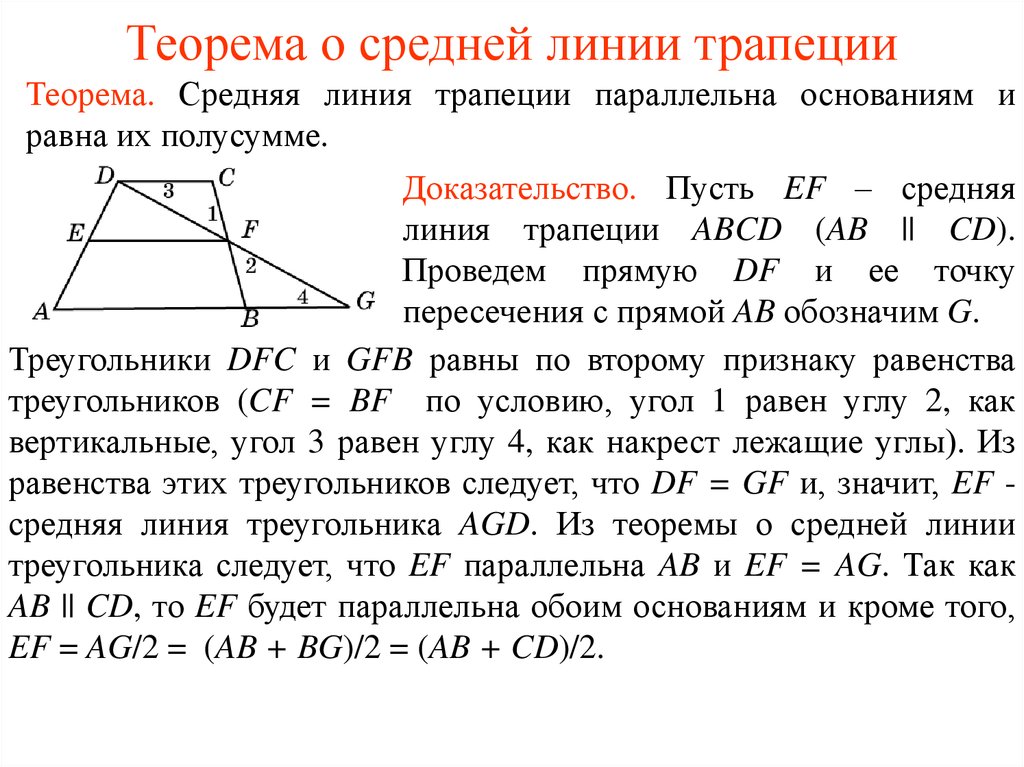 C.
C.
БК = 24 * 6 / 9 = 16
Ответ : 16 см
Задача .
В трапеции ABCD известно, что AD=24, BC=8, AC=13, BD=5√17. Найдите площадь трапеции.
Решение .
Чтобы найти высоту трапеции из вершин меньшего основания В и С, опускаем две высоты на большее основание. Так как трапеция неравнополочная, обозначим длину АМ = а, длину КД = b (не путать с символами в формуле нахождения площади трапеции). Так как основания трапеции параллельны и мы опустили две высоты, перпендикулярные большему основанию, то MBCK является прямоугольником.
Средства
AD=AM+BC+KD
a + 8 + b = 24
a = 16 — b
Треугольники DBM и ACK прямоугольные, поэтому их прямые углы образованы высотами трапеции. Обозначим высоту трапеции через h. Тогда по теореме Пифагора
H 2 + (24 — a) 2 = (5√17) 2
и
h 2 + (24 — b) 2 = 13 2
Считаем, что a = 16 — b , то в первое уравнение
ч 2 + (24 — 16 + b) 2 = 425
ч 2 = 425 — (8 + b) 2
Подставляем во второе уравнение значение квадрата высоты, получается по теореме Пифагора.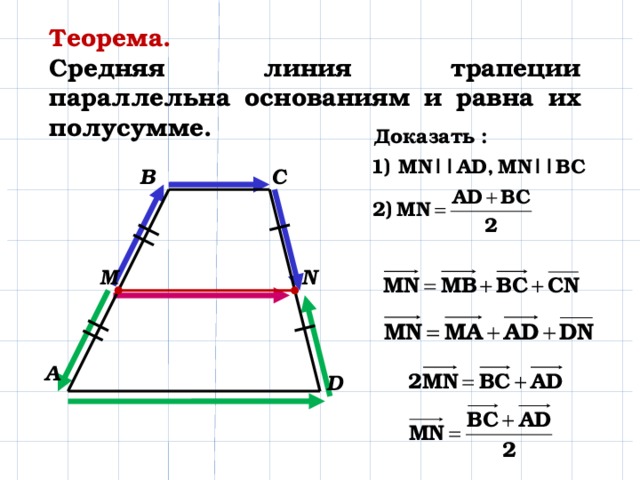 Получаем:
Получаем:
425 — (8 + b) 2 + (24 — b) 2 = 169
-(64 + 16b + b) 2 + (24 — b) 2 = -256
-64 — 16b — b 2 + 576 — 48b + b 2 = -256
-64b = -768
b = 12
Таким образом, KD = 12
Где
h 2 = 425 — (8 + b) 2 = 425 — (8 + 12) 2 = 25
h = 5
Найдите площадь трапеции, используя ее высоту и половину суммы оснований
, где a b — основания трапеции, h — высота трапеции
S = (24 + 8) * 5/2 = 80 см 2
Ответ : площадь трапеции 80 см2.
Четырехугольник только с двумя параллельными сторонами называется трапецией .
Параллельные стороны трапеции называются ее основаниями , а те стороны, которые не параллельны, называются сторонами . Если стороны равны, то такая трапеция равнобедренная. Расстояние между основаниями называется высотой трапеции.
Средняя линия трапеции
Срединная линия представляет собой отрезок, соединяющий середины сторон трапеции. Средняя линия трапеции параллельна ее основаниям.
Теорема:
Если прямая, пересекающая середину одной стороны, параллельна основаниям трапеции, то она делит вторую сторону трапеции пополам.
Теорема:
Длина средней линии равна среднему арифметическому длин ее оснований
МН || АБ || DC
AM=MD; БН=НЗ
MN средняя линия, AB и CD — основания, AD и BC — стороны
MN=(AB+DC)/2
Теорема:
Длина средней линии трапеции равна среднему арифметическому длин ее оснований.
Основная задача : Докажите, что средняя линия трапеции делит пополам отрезок, концы которого лежат на середине оснований трапеции.
Средняя линия треугольника
Отрезок, соединяющий середины двух сторон треугольника, называется средней линией треугольника. Он параллелен третьей стороне и его длина равна половине длины третьей стороны.
Теорема : Если прямая, пересекающая середину одной стороны треугольника, параллельна другой стороне данного треугольника, то она делит третью сторону пополам.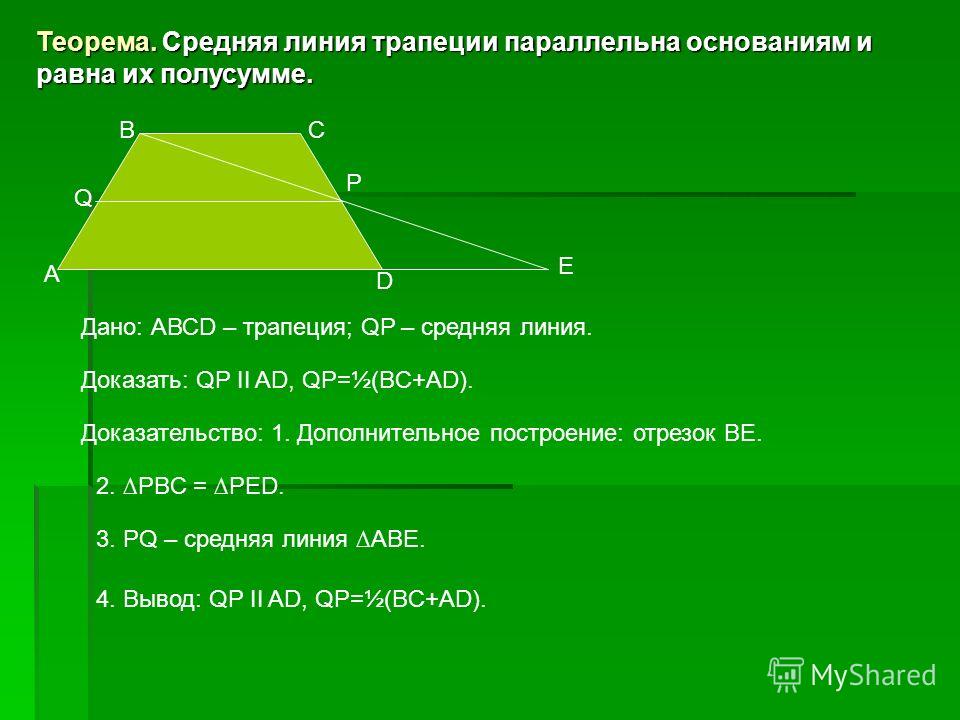
AM = MC и BN = NC =>
Применение свойств средней линии треугольника и трапеции
Деление сегмента на определенное количество равных частей.
Задание: Разделите отрезок АВ на 5 равных частей.
Решение:
Пусть p — случайный луч, начало которого находится в точке A и который не лежит на прямой AB. Откладываем последовательно 5 равных отрезков на р АА 1 = А 1 А 2 = А 2 А 3 = А 3 А 4 = А 4 А 5
Соединим А 5 с В и проведем через А 4 , А 3 , А 2 и А 1 прямые, параллельные А 5 В. Они пересекают АВ в точках В 4 , В 3 , В 2 и В 1 соответственно. Эти точки делят отрезок АВ на 5 равных частей. Действительно, из трапеции BB 3 A 3 A 5 мы видим, что BB 4 = B 4 B 3 . Точно так же из трапеции B 4 B 2 A 2 A 4 получаем B 4 B 3 = B 3 B 2
А из трапеции B 3 B 1 A 1 A 3 , B 3 B 2 = B 2 Б 1 .
Тогда из B 2 AA 2 следует, что B 2 B 1 = B 1 A. В заключение получаем:
AB 1 = B 1 B 2 = B 2 B 3 = B 3 B 4 = B 4 B
Понятно, что для того, чтобы разделить отрезок AB на другое количество равных частей, нужно спроецировать такое же количество равных частей отрезки на луч p.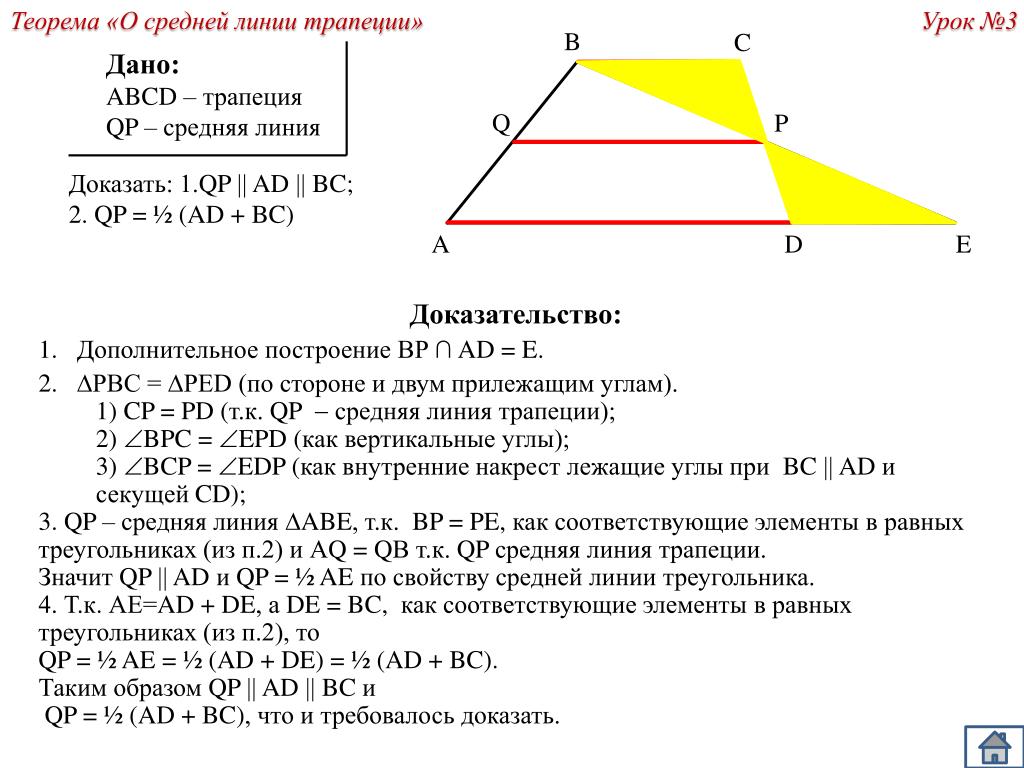 А затем продолжить в порядке, описанном выше.
А затем продолжить в порядке, описанном выше.
9 класс – Геометрия – Страница ресурсов Math Plus
Щелкните значок – – , чтобы загрузить и установить приложение на Android-устройство (например, смартфон, планшет). У некоторых приложений есть версия для ПК: нажмите на значок – – , чтобы загрузить программу установки для вашего ПК с Windows.
| НАЗВАНИЕ ПРИЛОЖЕНИЯ | ОПИСАНИЕ | СКАЧАТЬ | |
|---|---|---|---|
| Это приложение | Prove It | — Последнее обновление: 23 февраля 2022 г. | |
| GeoMatch | Будут показаны различные типы треугольников и четырехугольников. Игроку необходимо выбрать объект на основе определения или свойства, указанного в нижней части экрана. Это необходимо сделать до того, как будут заполнены все 16 позиций.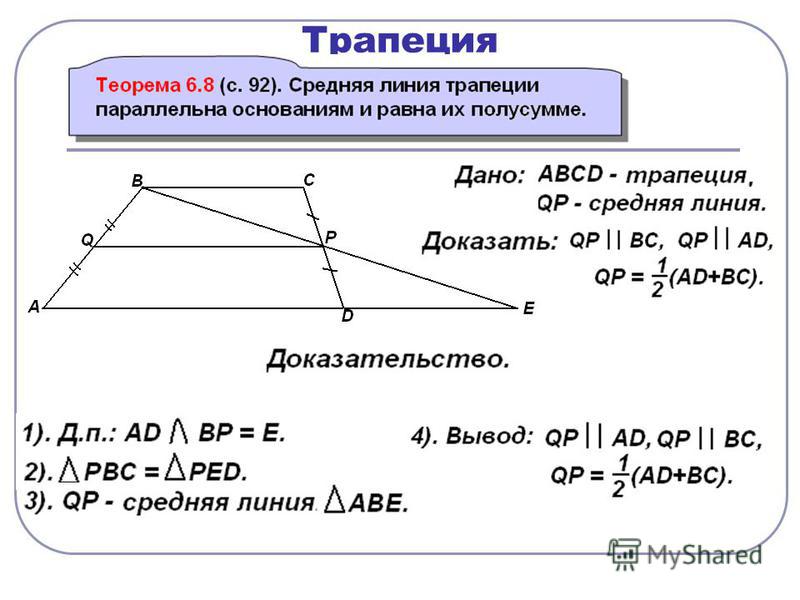 Игроку дается 3 «жизни», чтобы насладиться игрой в трех скоростных режимах (медленно, нормально, быстро). Игроку дается 3 «жизни», чтобы насладиться игрой в трех скоростных режимах (медленно, нормально, быстро). | Последнее обновление: 4 октября 2021 г. | |
| Доказательство с двумя столбцами | Это приложение относится к проверке с двумя столбцами. Это помогает учащемуся понять и сформулировать доказательство теоремы в два столбца, позволяя им визуализировать данные утверждения доказательства. | — Последнее обновление: 8 февраля 2022 г. |
Если вы подключены к Интернету, щелкните значок ––, чтобы открыть апплет Geogebra в браузере.
Если вы хотите использовать апплет в автономном режиме, загрузите и сохраните файл .ggb ; затем вы можете открыть его в автономном режиме с помощью Geogebra Classic (бесплатно: для настольных / портативных компьютеров, для устройств Android и для iPad).
| Тема | Важнейшая учебная компетенция | Руководство для преподавателей | Приложение |
|---|---|---|---|
| Свойства параллелограммов, образующих 9 параллелограммов | 130553|||
| Opposite Sides of a Parallelogram are Congruent | Determines the conditions that guarantee a quadrilateral is a parallelogram | ||
| Opposite Angles of a Parallelogram are Congruent | Determines the conditions that guarantee a четырехугольник является параллелограммом | ||
| Условия, делающие четырехугольник параллелограммом | Determines the conditions that guarantee a quadrilateral is a parallelogram | ||
| Quadrilateral with Pairs of Opposite Sides Congruent | Determines the conditions that guarantee a quadrilateral is a parallelogram | ||
| Quadrilateral with a Pair противоположных сторон, которые параллельны и конгруэнтны | Определяет условия, гарантирующие, что четырехугольник является параллелограммом | ||
| Conditions that Make a Quadrilateral a Parallelogram Part 2 | Conditions that Make a Quadrilateral a Parallelogram Part 2 | ||
| Diagonals of Quadrilaterals | Proves theorems on the different kinds of parallelograms | ||
| Свойства различных видов четырехугольников | Иллюстрирует и применяет свойства различных видов четырехугольников. |


 д.
д.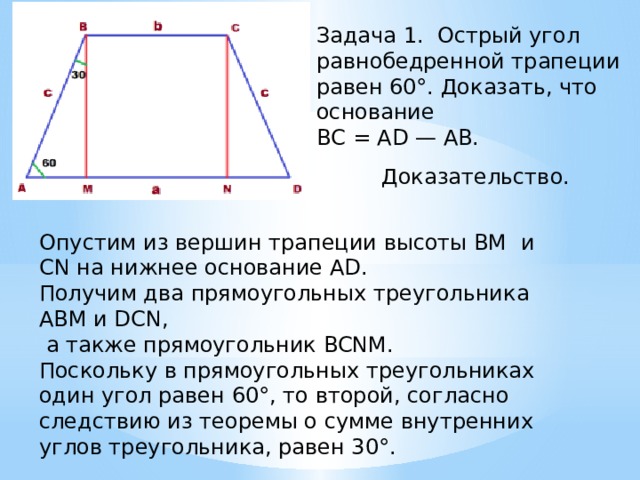 Мы также можем раскрывать информацию о вас, если решим, что такое раскрытие необходимо или уместно в целях безопасности, правоохранительных органов или по другим причинам, представляющим общественный интерес.
Мы также можем раскрывать информацию о вас, если решим, что такое раскрытие необходимо или уместно в целях безопасности, правоохранительных органов или по другим причинам, представляющим общественный интерес.