| 1 | Найти точное значение | sin(30) | |
| 2 | Найти точное значение | sin(45) | |
| 3 | Найти точное значение | sin(30 град. ) | |
| 4 | Найти точное значение | sin(60 град. ) | |
| 5 | Найти точное значение | tan(30 град. ) | |
| 6 | Найти точное значение | arcsin(-1) | |
| 7 | Найти точное значение | sin(pi/6) | |
| 8 | cos(pi/4) | ||
| 9 | Найти точное значение | sin(45 град. ) | |
| 10 | Найти точное значение | sin(pi/3) | |
| 11 | Найти точное значение | arctan(-1) | |
| 12 | Найти точное значение | cos(45 град. ) | |
| 13 | Найти точное значение | cos(30 град. ) | |
| 14 | Найти точное значение | tan(60) | |
| 15 | Найти точное значение | csc(45 град. ) | |
| 16 | Найти точное значение | tan(60 град. ) | |
| 17 | Найти точное значение | sec(30 град. ) | |
| 18 | Найти точное значение | cos(60 град. ) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | sin(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | tan(45 град. ) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 град. ) | |
| 25 | Найти точное значение | sec(45 град. ) | |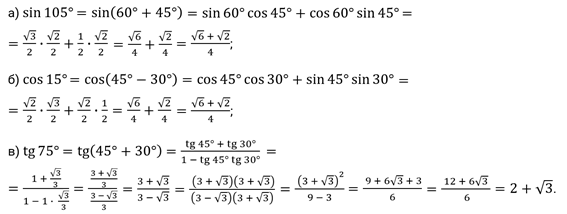
| 26 | Найти точное значение | csc(30 град. ) | |
| 27 | Найти точное значение | sin(0) | |
| 28 | Найти точное значение | sin(120) | |
| 29 | Найти точное значение | cos(90) | |
| 30 | Преобразовать из радианов в градусы | pi/3 | |
| 31 | Найти точное значение | tan(30) | |
| 32 | Преобразовать из градусов в радианы | 45 | |
| 33 | Найти точное значение | cos(45) | |
| 34 | Упростить | sin(theta)^2+cos(theta)^2 | |
| 35 | Преобразовать из радианов в градусы | pi/6 | |
| 36 | Найти точное значение | cot(30 град. ) | |
| 37 | Найти точное значение | arccos(-1) | |
| 38 | Найти точное значение | arctan(0) | |
| 39 | Найти точное значение | cot(60 град. ) | |
| 40 | Преобразовать из градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2pi)/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | tan(pi/2) | |
| 45 | Найти точное значение | sin(300) | |
| 46 | Найти точное значение | cos(30) | |
| 47 | Найти точное значение | cos(60) | |
| 48 | Найти точное значение | cos(0) | |
| 49 | Найти точное значение | cos(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | sec(60 град. ) | |
| 53 | Найти точное значение | sin(300 град. ) | |
| 54 | Преобразовать из градусов в радианы | 135 | |
| 55 | Преобразовать из градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5pi)/6 | |
| 57 | Преобразовать из радианов в градусы | (5pi)/3 | |
| 58 | Преобразовать из градусов в радианы | 89 град. | |
| 59 | Преобразовать из градусов в радианы | 60 | |
| 60 | Найти точное значение | sin(135 град. ) | |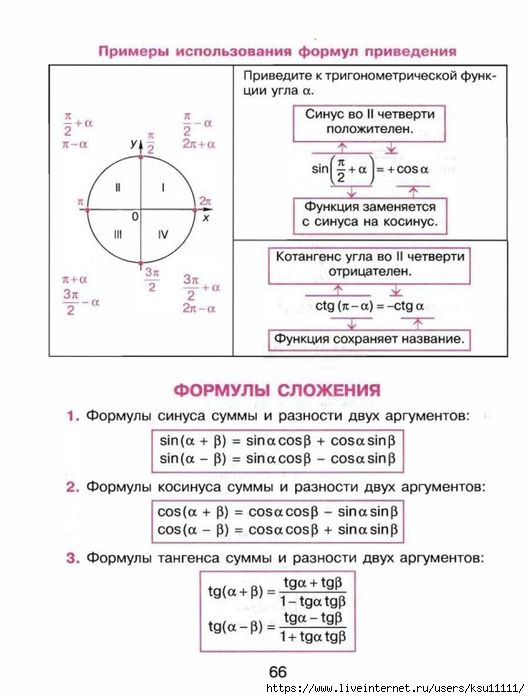
| 61 | Найти точное значение | sin(150) | |
| 62 | Найти точное значение | sin(240 град. ) | |
| 63 | Найти точное значение | cot(45 град. ) | |
| 64 | Преобразовать из радианов в градусы | (5pi)/4 | |
| 65 | Найти точное значение | sin(225) | |
| 66 | Найти точное значение | sin(240) | |
| 67 | Найти точное значение | cos(150 град. ) | |
| 68 | Найти точное значение | tan(45) | |
| 69 | Вычислить | sin(30 град. ) | |
| 70 | Найти точное значение | sec(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | csc(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | tan((5pi)/3) | |
| 75 | Найти точное значение | tan(0) | |
| 76 | Вычислить | sin(60 град. ) | |
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3pi)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | arcsin(-1/2) | |
| 81 | sin((4pi)/3) | ||
| 82 | Найти точное значение | csc(45) | |
| 83 | Упростить | arctan( квадратный корень из 3) | |
| 84 | Найти точное значение | sin(135) | |
| 85 | Найти точное значение | sin(105) | |
| 86 | Найти точное значение | sin(150 град. ) | |
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | tan((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | pi/4 | |
| 90 | Найти точное значение | sin(pi/2) | |
| 91 | Найти точное значение | sec(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | arcsin(0) | |
| 95 | Найти точное значение | sin(120 град. ) | |
| 96 | Найти точное значение | tan((7pi)/6) | |
| 97 | Найти точное значение | cos(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразовать из градусов в радианы | 88 град. |
Формулы сложения синусов и косинусов. Формулы сложения: доказательство, примеры
Я не буду убеждать вас не писать шпаргалки. Пишите! В том числе, и шпаргалки по тригонометрии. Позже я планирую объяснить, зачем нужны шпаргалки и чем шпаргалки полезны.
А здесь — информация, как не учить, но запомнить некоторые тригонометрические формулы. Итак — тригонометрия без шпаргалки!Используем ассоциации для запоминания.1. Формулы сложения:
косинусы всегда «ходят парами»: косинус-косинус, синус-синус. И еще: косинусы — «неадекватны». Им «все не так», поэтому они знаки меняют: «-» на «+», и наоборот.
Синусы — «смешиваются» : синус-косинус, косинус-синус.
2. Формулы суммы и разности:
косинусы всегда «ходят парами». Сложив два косинуса — «колобка», получаем пару косинусов- «колобков». А вычитая, колобков точно не получим. Получаем пару синусов. Еще и с минусом впереди.
Синусы — «смешиваются» :
3. Формулы преобразования произведения в сумму и разность.
Когда мы получаем пару косинусов? Когда складываем косинусы. Поэтому
Когда мы получаем пару синусов? При вычитании косинусов.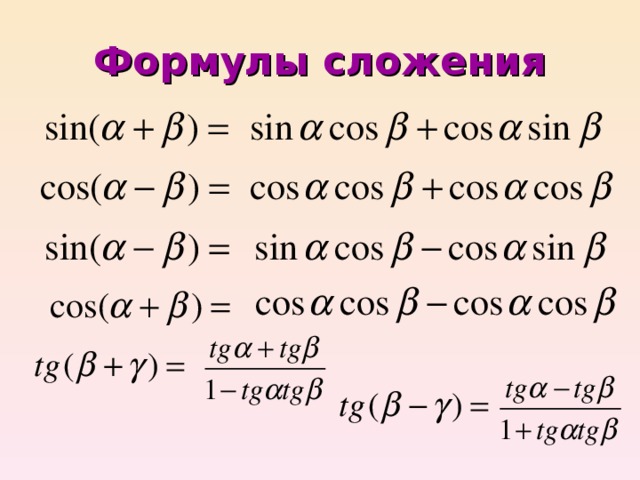
Отсюда:
«Смешение» получаем как при сложении, так и при вычитании синусов. Что приятнее: складывать или вычитать? Правильно, складывать. И для формулы берут сложение:
В первой и в третьей формуле в скобках — сумма. От перестановки мест слагаемых сумма не меняется. Принципиален порядок только для второй формулы. Но, чтобы не путаться, для простоты запоминания мы во всех трех формулах в первых скобках берем разность
а во вторых — сумму
Шпаргалки в кармане дают спокойствие: если забыл формулу, можно списать. А дают уверенность: если воспользоваться шпаргалкой не удастся, формулы можно легко вспомнить.
Продолжаем наш разговор про наиболее употребляемые формулы в тригонометрии. Важнейшие из них – формулы сложения.
Определение 1
Формулы сложения позволяют выразить функции разности или суммы двух углов с помощью тригонометрических функций этих углов.
Для начала мы приведем полный список формул сложения, потом докажем их и разберем несколько наглядных примеров.
Yandex.RTB R-A-339285-1
Выделяют восемь основных формул: синус суммы и синус разности двух углов, косинусы суммы и разности, тангенсы и котангенсы суммы и разности соответственно. Ниже приведены их стандартные формулировки и вычисления.
1.Синус суммы двух углов можно получить следующим образом:
Вычисляем произведение синуса первого угла на косинус второго;
Умножаем косинус первого угла на синус первого;
Складываем получившиеся значения.
Графическое написание формулы выглядит так: sin (α + β) = sin α · cos β + cos α · sin β
2. Синус разности вычисляется почти так же, только полученные произведения нужно не сложить, а вычесть друг из друга. Таким образом, вычисляем произведения синуса первого угла на косинус второго и косинуса первого угла на синус второго и находим их разность. Формула пишется так: sin (α — β) = sin α · cos β + sin α · sin β
3. Косинус суммы. Для него находим произведения косинуса первого угла на косинус второго и синуса первого угла на синус второго соответственно и находим их разность: cos (α + β) = cos α · cos β — sin α · sin β
4.
Косинус разности: вычисляем произведения синусов и косинусов данных углов, как и ранее, и складываем их. Формула: cos (α — β) = cos α · cos β + sin α · sin β
5. Тангенс суммы. Эта формула выражается дробью, в числителе которой – сумма тангенсов искомых углов, а в знаменателе – единица, из которой вычитается произведение тангенсов искомых углов. Все понятно из ее графической записи: t g (α + β) = t g α + t g β 1 — t g α · t g β
6. Тангенс разности. Вычисляем значения разности и произведения тангенсов данных углов и поступаем с ними схожим образом. В знаменателе мы прибавляем к единице, а не наоборот: t g (α — β) = t g α — t g β 1 + t g α · t g β
7. Котангенс суммы. Для вычислений по этой формуле нам понадобятся произведение и сумма котангенсов данных углов, с которыми мы поступаем следующим образом: c t g (α + β) = — 1 + c t g α · c t g β c t g α + c t g β
8. Котангенс разности. Формула схожа с предыдущей, но в числителе и знаменателе – минус, а не плюс c t g (α — β) = — 1 — c t g α · c t g β c t g α — c t g β .
Вы, наверное, заметили, что эти формулы попарно схожи. При помощи знаков ± (плюс-минус) и ∓ (минус-плюс) мы можем сгруппировать их для удобства записи:
sin (α ± β) = sin α · cos β ± cos α · sin β cos (α ± β) = cos α · cos β ∓ sin α · sin β t g (α ± β) = t g α ± t g β 1 ∓ t g α · t g β c t g (α ± β) = — 1 ± c t g α · c t g β c t g α ± c t g β
Соответственно, мы имеем одну формулу записи для суммы и разности каждого значения, просто в одном случае мы обращаем внимание на верхний знак, в другом – на нижний.
Определение 2
Мы можем взять любые углы α и β , и формулы сложения для косинуса и синуса подойдут для них. Если мы можем правильно определить значения тангенсов и котангенсов этих углов, то формулы сложения для тангенса и котангенса будут также для них справедливы.
Как и большинство понятий в алгебре, формулы сложения могут быть доказаны. Первая формула, которую мы докажем, — формула косинуса разности. Из нее потом можно легко вывести остальные доказательства.
Уточним основные понятия. Нам понадобится единичная окружность. Она получится, если мы возьмем некую точку A и повернем вокруг центра (точки O) углы α и β . Тогда угол между векторами O A 1 → и O A → 2 будет равняться (α — β) + 2 π · z или 2 π — (α — β) + 2 π · z (z – любое целое число). Получившиеся вектора образуют угол, который равен α — β или 2 π — (α — β) , или он может отличаться от этих значений на целое число полных оборотов. Взгляните на рисунок:
Мы воспользовались формулами приведения и получили следующие результаты:
cos ((α — β) + 2 π · z) = cos (α — β) cos (2 π — (α — β) + 2 π · z) = cos (α — β)
Итог: косинус угла между векторами O A 1 → и O A 2 → равняется косинусу угла α — β , следовательно, cos (O A 1 → O A 2 →) = cos (α — β) .
Вспомним определения синуса и косинуса: синус — функция угла, равная отношению катета противолежащего угла к гипотенузе, косинус – это синус дополнительного угла. Следовательно, точки A 1 и A 2 имеют координаты (cos α , sin α) и (cos β , sin β) .
Получим следующее:
O A 1 → = (cos α , sin α) и O A 2 → = (cos β , sin β)
Если непонятно, взгляните на координаты точек, расположенных в начале и конце векторов.
Длины векторов равны 1 , т.к. у нас единичная окружность.
Разберем теперь скалярное произведение векторов O A 1 → и O A 2 → . В координатах оно выглядит так:
(O A 1 → , O A 2) → = cos α · cos β + sin α · sin β
Из этого мы можем вывести равенство:
cos (α — β) = cos α · cos β + sin α · sin β
Таким образом, формула косинуса разности доказана.
Теперь мы докажем следующую формулу – косинуса суммы. Это проще, поскольку мы можем воспользоваться предыдущими расчетами. Возьмем представление α + β = α — (- β) . У нас есть:
cos (α + β) = cos (α — (- β)) = = cos α · cos (- β) + sin α · sin (- β) = = cos α · cos β + sin α · sin β
Это и есть доказательство формулы косинуса суммы. В последней строчке использовано свойство синуса и косинуса противоположных углов.
Формулу синуса суммы можно вывести из формулы косинуса разности.
Возьмем для этого формулу приведения:
вида sin (α + β) = cos (π 2 (α + β)) . Так
sin (α + β) = cos (π 2 (α + β)) = cos ((π 2 — α) — β) = = cos (π 2 — α) · cos β + sin (π 2 — α) · sin β = = sin α · cos β + cos α · sin β
А вот доказательство формулы синуса разности:
sin (α — β) = sin (α + (- β)) = sin α · cos (- β) + cos α · sin (- β) = = sin α · cos β — cos α · sin β
Обратите внимание на использование свойств синуса и косинуса противоположных углов в последнем вычислении.
Далее нам нужны доказательства формул сложения для тангенса и котангенса. Вспомним основные определения (тангенс – отношение синуса к косинусу, а котангенс –наоборот) и возьмем уже выведенные заранее формулы. У нас получилось:
t g (α + β) = sin (α + β) cos (α + β) = sin α · cos β + cos α · sin β cos α · cos β — sin α · sin β
У нас получилась сложная дробь. Далее нам нужно разделить ее числитель и знаменатель на cos α · cos β , учитывая что cos α ≠ 0 и cos β ≠ 0 , получаем:
sin α · cos β + cos α · sin β cos α · cos β cos α · cos β — sin α · sin β cos α · cos β = sin α · cos β cos α · cos β + cos α · sin β cos α · cos β cos α · cos β cos α · cos β — sin α · sin β cos α · cos β
Теперь сокращаем дроби и получаем формулу следующего вида: sin α cos α + sin β cos β 1 — sin α cos α · s i n β cos β = t g α + t g β 1 — t g α · t g β .
У нас получилось t g (α + β) = t g α + t g β 1 — t g α · t g β . Это и есть доказательство формулы сложения тангенса.
Следующая формула, которую мы будем доказывать – формула тангенса разности. Все наглядно показано в вычислениях:
t g (α — β) = t g (α + (- β)) = t g α + t g (- β) 1 — t g α · t g (- β) = t g α — t g β 1 + t g α · t g β
Формулы для котангенса доказываются схожим образом:
c t g (α + β) = cos (α + β) sin (α + β) = cos α · cos β — sin α · sin β sin α · cos β + cos α · sin β = = cos α · cos β — sin α · sin β sin α · sin β sin α · cos β + cos α · sin β sin α · sin β = cos α · cos β sin α · sin β — 1 sin α · cos β sin α · sin β + cos α · sin β sin α · sin β = = — 1 + c t g α · c t g β c t g α + c t g β
Далее:
c t g (α — β) = c t g (α + (- β)) = — 1 + c t g α · c t g (- β) c t g α + c t g (- β) = — 1 — c t g α · c t g β c t g α — c t g β
Доказательство формулы сложения и вычитания для тригонометрических функций: CCSS.Math.Content.HSF-TF.
C.9 — Common Core: High SchoolAll Common Core: High School — Functions Resources
6 диагностических тестов 82 практических теста Вопрос дня Карточки Learn by Concept
← Предыдущая 1 2 Следующая →
Common Core: High School — Помощь по функциям » Тригонометрические функции » Докажите формулу сложения и вычитания для тригонометрических функций: CCSS.Math.Content.HSF-TF.C.9
Используя формулу сложения для синуса и вычисления специальных опорных углов,
.
Возможные ответы:
Правильный ответ:
Объяснение:
Этот тип вопросов проверяет глубокое понимание геометрии, прямоугольных треугольников, тригонометрии и работы с доказательствами. Такие вопросы не предназначены для проверки, а вместо этого используются для получения знаний, которые помогут в курсах математики более высокого уровня.
В соответствии с Общими базовыми стандартами «доказать формулы сложения и вычитания для синуса, косинуса и тангенса и использовать их для решения задач» относится к кластеру C «доказать и применить тригонометрические тождества» (CCSS.MATH. СОДЕРЖАНИЕ.HSF.TF.C).
Зная стандарт и концепцию, к которой он относится, теперь мы можем выполнить пошаговый процесс решения рассматриваемой проблемы.
Шаг 1: Разбейте угол на два угла, которые соответствуют специальным эталонным углам.
Шаг 2: Напишите общую формулу сложения для синуса.
Шаг 3: Подставьте опорные углы в общую формулу сложения для синуса.
Чтобы рационализировать знаменатель, умножьте числитель и знаменатель на квадратный корень из двух.
Сообщить об ошибке
Используя формулу сложения для вычисления синуса и специальных опорных углов,
.
Возможные ответы:
Правильный ответ:
Объяснение:
Этот тип вопросов проверяет глубокое понимание геометрии, прямоугольных треугольников, тригонометрии и работы с доказательствами.
Такие вопросы не предназначены для проверки, а вместо этого используются для получения знаний, которые помогут в курсах математики более высокого уровня.
В соответствии с Общими базовыми стандартами «доказать формулы сложения и вычитания для синуса, косинуса и тангенса и использовать их для решения задач» относится к кластеру C «доказать и применить тригонометрические тождества» (CCSS.MATH. СОДЕРЖАНИЕ.HSF.TF.C).
Зная стандарт и концепцию, к которой он относится, теперь мы можем выполнить пошаговый процесс решения рассматриваемой проблемы.
Шаг 1: Разбейте угол на два угла, которые соответствуют специальным эталонным углам.
Шаг 2: Напишите общую формулу сложения для синуса.
Шаг 3: Подставьте опорные углы в общую формулу сложения для синуса.
Сообщить об ошибке
Используя формулу сложения для вычисления синуса и специальных опорных углов,
.
Возможные ответы:
Правильный ответ:
Объяснение:
Этот тип вопросов проверяет глубокое понимание геометрии, прямоугольных треугольников, тригонометрии и работы с доказательствами.
Такие вопросы не предназначены для проверки, а вместо этого используются для получения знаний, которые помогут в курсах математики более высокого уровня.
В соответствии с Общими базовыми стандартами «доказать формулы сложения и вычитания для синуса, косинуса и тангенса и использовать их для решения задач» относится к кластеру C «доказать и применить тригонометрические тождества» (CCSS.MATH. СОДЕРЖАНИЕ.HSF.TF.C).
Зная стандарт и концепцию, к которой он относится, теперь мы можем выполнить пошаговый процесс решения рассматриваемой проблемы.
Шаг 1: Разбейте угол на два угла, которые соответствуют специальным эталонным углам.
Шаг 2: Напишите общую формулу сложения для синуса.
Шаг 3: Подставьте опорные углы в общую формулу сложения для синуса.
Сообщить об ошибке
Используя формулу сложения для синуса и вычисления специальных опорных углов,
.
Возможные ответы:
Правильный ответ:
Объяснение:
Этот тип вопросов проверяет глубокое понимание геометрии, прямоугольных треугольников, тригонометрии и работу с доказательствами.
Такие вопросы не предназначены для проверки, а вместо этого используются для получения знаний, которые помогут в курсах математики более высокого уровня.
В соответствии с Общими базовыми стандартами «доказать формулы сложения и вычитания для синуса, косинуса и тангенса и использовать их для решения задач» относится к кластеру C «доказать и применить тригонометрические тождества» (CCSS.MATH. СОДЕРЖАНИЕ.HSF.TF.C).
Зная стандарт и концепцию, к которой он относится, теперь мы можем выполнить пошаговый процесс решения рассматриваемой проблемы.
Шаг 1: Разбейте угол на два угла, которые соответствуют специальным эталонным углам.
Шаг 2: Напишите общую формулу сложения для синуса.
Шаг 3: Подставьте опорные углы в общую формулу сложения для синуса.
Сообщить об ошибке
Используя формулу сложения для вычисления синуса и специальных опорных углов,
.
Возможные ответы:
Правильный ответ:
Объяснение:
Этот тип вопросов проверяет глубокое понимание геометрии, прямоугольных треугольников, тригонометрии и работы с доказательствами.
Такие вопросы не предназначены для проверки, а вместо этого используются для получения знаний, которые помогут в курсах математики более высокого уровня.
В соответствии с Общими базовыми стандартами «доказать формулы сложения и вычитания для синуса, косинуса и тангенса и использовать их для решения задач» относится к кластеру C «доказать и применить тригонометрические тождества» (CCSS.MATH. СОДЕРЖАНИЕ.HSF.TF.C).
Зная стандарт и концепцию, к которой он относится, теперь мы можем выполнить пошаговый процесс решения рассматриваемой проблемы.
Шаг 1: Разбейте угол на два угла, которые соответствуют специальным эталонным углам.
Шаг 2: Напишите общую формулу сложения для синуса.
Шаг 3: Подставьте опорные углы в общую формулу сложения для синуса.
Сообщить об ошибке.
Возможные ответы:
Правильный ответ:
Объяснение:
Этот тип вопросов проверяет глубокое понимание геометрии, прямоугольных треугольников, тригонометрии и работы с доказательствами.
Такие вопросы не предназначены для проверки, а вместо этого используются для получения знаний, которые помогут в курсах математики более высокого уровня.
В соответствии с Общими базовыми стандартами «доказать формулы сложения и вычитания для синуса, косинуса и тангенса и использовать их для решения задач» относится к кластеру C «доказать и применить тригонометрические тождества» (CCSS.MATH. СОДЕРЖАНИЕ.HSF.TF.C).
Зная стандарт и концепцию, к которой он относится, теперь мы можем выполнить пошаговый процесс решения рассматриваемой проблемы.
Шаг 1: Разбейте угол на два угла, которые соответствуют специальным эталонным углам.
Шаг 2: Напишите общую формулу сложения для синуса.
Шаг 3: Подставьте опорные углы в общую формулу сложения для синуса.
Теперь, чтобы рационализировать знаменатель, умножьте числитель и знаменатель на квадратный корень из двух.
Сообщить об ошибке
Используя формулу вычитания для косинуса и вычисления специальных опорных углов,
.
Возможные ответы:
Правильный ответ:
Объяснение:
Этот тип вопросов проверяет глубокое понимание геометрии, прямоугольных треугольников, тригонометрии и работы с доказательствами. Такие вопросы не предназначены для проверки, а вместо этого используются для получения знаний, которые помогут в курсах математики более высокого уровня.
В соответствии с Общими базовыми стандартами «доказать формулы сложения и вычитания для синуса, косинуса и тангенса и использовать их для решения задач» относится к кластеру C «доказать и применить тригонометрические тождества» (CCSS.MATH. СОДЕРЖАНИЕ.HSF.TF.C).
Зная стандарт и концепцию, к которой он относится, теперь мы можем выполнить пошаговый процесс решения рассматриваемой проблемы.
Шаг 1: Разбейте угол на два угла, которые соответствуют специальным эталонным углам.
Шаг 2: Напишите общую формулу сложения для косинуса.
Шаг 3: Подставьте опорные углы в общую формулу сложения для косинуса.
Чтобы рационализировать знаменатель, умножьте числитель и знаменатель на квадратный корень из двух.
Сообщить об ошибке
Используя формулу сложения для косинуса и вычисления специальных опорных углов,
.
Возможные ответы:
Правильный ответ:
Объяснение:
Этот тип вопросов проверяет глубокое понимание геометрии, прямоугольных треугольников, тригонометрии и работы с доказательствами. Такие вопросы не предназначены для проверки, а вместо этого используются для получения знаний, которые помогут в курсах математики более высокого уровня.
В соответствии с Общими базовыми стандартами «доказать формулы сложения и вычитания для синуса, косинуса и тангенса и использовать их для решения задач» относится к кластеру C «доказать и применить тригонометрические тождества» (CCSS.
MATH. СОДЕРЖАНИЕ.HSF.TF.C).
Зная стандарт и концепцию, к которой он относится, теперь мы можем выполнить пошаговый процесс решения рассматриваемой проблемы.
Шаг 1: Разбейте угол на два угла, которые соответствуют специальным эталонным углам.
Шаг 2: Напишите общую формулу сложения для косинуса.
Шаг 3: Подставьте опорные углы в общую формулу сложения для косинуса.
Чтобы рационализировать знаменатель, умножьте числитель и знаменатель на квадратный корень из двух.
Сообщить об ошибке
Используя формулу сложения для косинуса и вычисления специальных опорных углов,
.
Возможные ответы:
Правильный ответ:
Объяснение:
Этот тип вопросов проверяет глубокое понимание геометрии, прямоугольных треугольников, тригонометрии и работы с доказательствами.
Такие вопросы не предназначены для проверки, а вместо этого используются для получения знаний, которые помогут в курсах математики более высокого уровня.
В соответствии с Общими базовыми стандартами «доказать формулы сложения и вычитания для синуса, косинуса и тангенса и использовать их для решения задач» относится к кластеру C «доказать и применить тригонометрические тождества» (CCSS.MATH. СОДЕРЖАНИЕ.HSF.TF.C).
Зная стандарт и концепцию, к которой он относится, теперь мы можем выполнить пошаговый процесс решения рассматриваемой проблемы.
Шаг 1: Разбейте угол на два угла, которые соответствуют специальным эталонным углам.
Шаг 2: Напишите общую формулу сложения для косинуса.
Шаг 3: Подставьте опорные углы в общую формулу сложения для косинуса.
Отчет о ошибке
Используя формулу добавления для косинуса и специальных эталон0005
Объяснение:
Этот тип вопросов проверяет глубокое понимание геометрии, прямоугольных треугольников, тригонометрии и работы с доказательствами.
Такие вопросы не предназначены для проверки, а вместо этого используются для получения знаний, которые помогут в курсах математики более высокого уровня.
В соответствии с Общими базовыми стандартами «доказать формулы сложения и вычитания для синуса, косинуса и тангенса и использовать их для решения задач» относится к кластеру C «доказать и применить тригонометрические тождества» (CCSS.MATH. СОДЕРЖАНИЕ.HSF.TF.C).
Зная стандарт и концепцию, к которой он относится, теперь мы можем выполнить пошаговый процесс решения рассматриваемой проблемы.
Шаг 1: Разбейте угол на два угла, которые соответствуют специальным эталонным углам.
Шаг 2: Напишите общую формулу сложения для косинуса.
Шаг 3: Подставьте опорные углы в общую формулу сложения для косинуса.
Чтобы рационализировать знаменатель, умножьте на квадратный корень из двух.
Сообщить об ошибке
← Предыдущая 1 2 Следующая →
Уведомление об авторских правах 82 практических теста Вопрос дня Карточки Learn by Concept
Аналитическая тригонометрия Sin Addition Formula
Мы знаем точное значение всех триггерных функций для благодаря специальным треугольникам.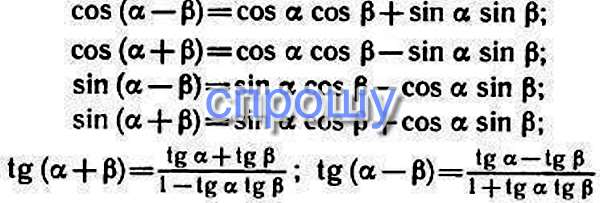
Мы также знаем значения на каждой оси. Но нам нужно знать больше, и нам нужно сделать это без калькулятора.
Начнем с формулы сложения для синуса. Это не так просто, как просто сложить несколько чисел; это тригонометрия, и это делает ее более сложной, чем обычно. Итак, возьмите нас за руку, и мы вместе пройдем доказательство формулы. Это может показаться немного пугающим, но знание того, откуда берется формула, поможет нам понять, почему она выглядит именно так.
Давайте посмотрим на изображение двух углов, которые мы хотим сложить, образуя два отдельных треугольника.
Мы можем найти sin(α + β), используя эти треугольники… почти. Давайте добавим туда еще одну строку, чтобы помочь нам:
Итак, мы добавили две строки, достаточно близко. Мы сделали треугольник ADE с ∠DAE, измеряющим α + β, а затем еще несколько треугольников ближе к вершине, которые будут полезны.
Теперь, когда фигурка на месте, давайте потыкаем ее, чтобы посмотреть, что выпадет.
К счастью, вероятность появления пчел, ос или шершней из такой математической задачи равна 0%. Видите ли, не все доказательства плохи; они могут быть намного хуже и гораздо более болезненными.
Давайте посмотрим на ∠CAB (мы знаем, что это α) и ∠FCA. Они очень похожи на альтернативные внутренние углы, потому что, эй, так оно и есть. Будучи альтернативными внутренними углами, они имеют одинаковую величину, поэтому мы знаем, что ∠FCA также является α.
Куда мы идем с этим? Когда-нибудь мы собираемся в Мир Диснея. Мы также собираемся треугольник FDC. ∠FCD должен быть равен 90° – α, потому что вместе ∠FCD и ∠FCA составляют угол 90°. Это важно из-за ∠FDC. Мы знаем, что сумма всех углов треугольника равна 180°, поэтому:
∠FDC + ∠FCD + 90° = 180°
∠FDC + (90° – α) + 90° = 180°
Немного алгебры и ба-бах-о, ∠FCD тоже α . Давайте поместим их на нашу диаграмму. В основном потому, что мы устали так много прокручивать каждый раз, когда забываем, какой угол есть какой.
Чтобы найти sin(α + β), мы можем использовать триггерное отношение треугольника ADE:
Кажется достаточно простым, не так ли? Проблема в том, что мы не знаем длины всех этих новых линий. На самом деле мы ничего не знаем ни о каких линиях. Что делать в такой ситуации? Мы не знаем, но мы собираемся что-то сделать со всеми этими углами, которые у нас есть.
Это означает использование большего количества триггерных функций, а , что означает, что нам нужно разбить некоторые из наших строк на более мелкие строки:
Вот кое-что хитрое, что мы можем сделать: заменить на его равенство на другом конце прямоугольника, .
Теперь, когда мы разобрали это, давайте вернемся к нашей формуле:
Линии и обе живут в треугольниках с углом α в них. Мы попросим их соседей по комнате помочь нам с небольшим триггером.
Спасибо, что пригласили нас в свои дома, но нам нужно немного изменить ситуацию, чтобы мы могли продолжить эту проблему.
Давайте поставим кушетку вдоль другой стены, поставим телевизор рядом с книжным шкафом и изолируем и, чтобы мы могли заменить их в нашей формуле.
С этим покончено, давайте воткнем это в
Мы почти у цели. Оставайтесь с нами. Все линии являются частями треугольника DAC. И в этом треугольнике есть угол β. Ча-цзин, мы попали в беду. Мы можем заменить отношения в формуле на тригонометрические функции, используя β, и немного изменить его, чтобы получить:
sin (α + β) = sin (α) cos (β) + cos (α) sin (β)
Мы сделали это; мы доказали, что эта формула верна. Теперь нам просто нужно уметь помнить об этом, когда мы работаем над нашими проблемами. Давайте посмотрим, синус и косинус появляются дважды, один раз с альфой и один раз с бетой. Они никогда не делят один и тот же угол, угол. В формуле синус стоит первым. Хорошо, это должно помочь нам вспомнить.
Пример задачи
Найдите точное значение sin (75°).
Убери этот калькулятор, приятель.