Теория графов. Термины и определения в картинках / Хабр
В этой статье мы познакомимся с основными терминами и определениями Теории графов. Каждый термин схематично показан на картинках.
Самый объёмный модуль на курсе «Алгоритмы и структуры данных» посвящён теории графов.
Граф — это топологичекая модель, которая состоит из множества вершин и множества соединяющих их рёбер. При этом значение имеет только сам факт, какая вершина с какой соединена.
Например, граф на рисунке состоит из 8 вершин и 8 рёбер.
Очень многие задачи могут быть решены используя богатую библиотеку алгоритмов теории графов. Для этого достаточно лишь принять объекты за вершины, а связь между ними — за рёбра, после чего весь арсенал алгоритмов теории графов к вашим услугам: нахождение маршрута от одного объекта к другому, поиск связанных компонент, вычисление кратчайших путей, поиск сети максимального потока и многое другое.
В этой статье мы познакомимся с основными терминами и определениями теории графов.
На курсе “Алгоритмы и Структуры данных” в компании Отус “Теория графов” изучается в самом объёмном модуле из 6 вебинаров, где мы изучаем десяток самых популярных алгоритмов.
Вершина — точка в графе, отдельный объект, для топологической модели графа не имеет значения координата вершины, её расположение, цвет, вкус, размер; однако при решении некоторых задачах вершины могут раскрашиваться в разные цвета или сохранять числовые значения.
Ребро — неупорядоченная пара двух вершин, которые связаны друг с другом. Эти вершины называются концевыми точками или концами ребра. При этом важен сам факт наличия связи, каким именно образом осуществляется эта связь и по какой дороге — не имеет значения; однако рёбра может быть присвоен “вес”, что позволит говорить о “нагруженном графе” и решать задачи оптимизации.
Инцидентность — вершина и ребро называются инцидентными, если вершина является для этого ребра концевой. Обратите внимание, что термин “инцидентность” применим только к вершине и ребру.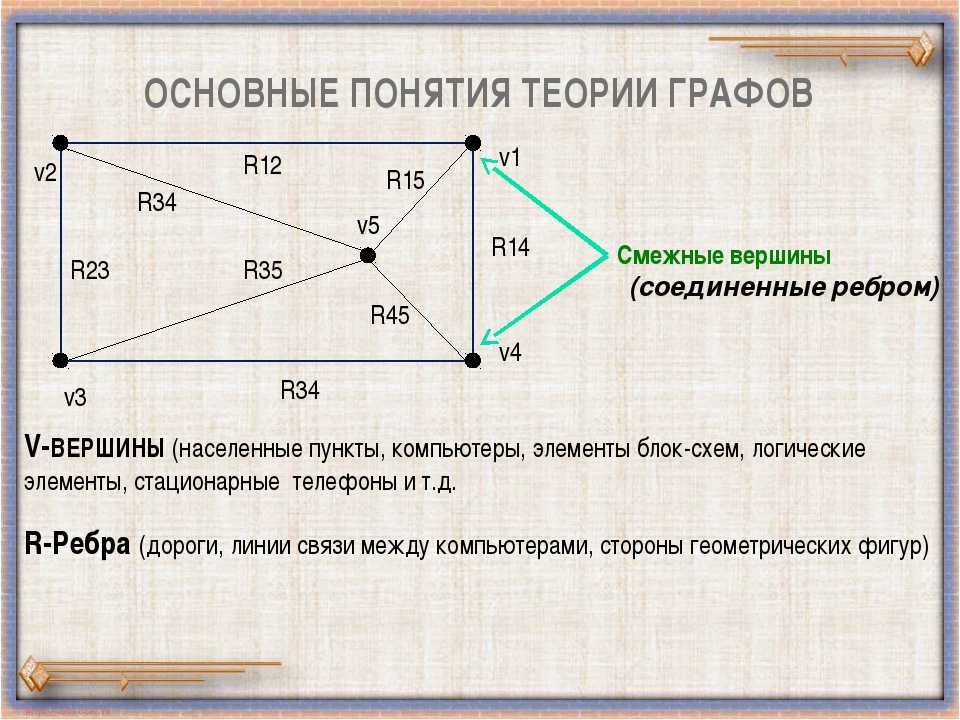
Смежность вершин — две вершины называются смежными, если они инцидентны одному ребру.
Смежность рёбер — два ребра называются смежными, если они инцедентны одной вершине.
Говоря проще — две вершины смежные, если они соединены ребром, два ребра смежные — если они соединены вершиной.
Петля — ребро, инцидентное одной вершине. Ребро, которое замыкается на одной вершине.
Псевдограф — граф с петлями. С такими графами не очень удобно работать, потому что переходя по петле мы остаёмся в той же самой вершине, поэтому у него есть своё название.
Кратные рёбра — рёбра, имеющие одинаковые концевые вершины, по другому их называют ещё параллельными.
Мультиграф — граф с кратными рёбрами.
Псевдомультиграф — граф с петлями и кратными рёбрами.
Степень вершины — это количество рёбер, инцидентных указанной вершине. По-другому — количество рёбер, исходящих из вершины.
Петля увеливает степень вершины на 2.
Изолированная вершина — вершина с нулевой степенью.
Висячая вершина — вершина со степенью 1.
Подграф. Если в исходном графе выделить несколько вершин и несколько рёбер (между выбранными вершинами), то мы получим подграф исходного графа.
Идея подграфов используется во многих алгоритмах, например, сначала создаётся подграф их всех вершин без рёбер, а потом дополняется выбранными рёбрами.
Полный граф — это граф, в котором каждые две вершины соединены одним ребром.
Сколько рёбер в полном графе? Это известная задача о рукопожатиях: собралось N человек (вершин) и каждый с каждым обменялся рукопожатием (ребро), сколько всего было рукопожатий? Вычисляется как сумма чисел от 1 до N — каждый новый участник должен пожать руку всем присутствующим, вычисляется по формуле: N * (N — 1) / 2.
Регулярный граф — граф, в котором степени всех вершин одинаковые.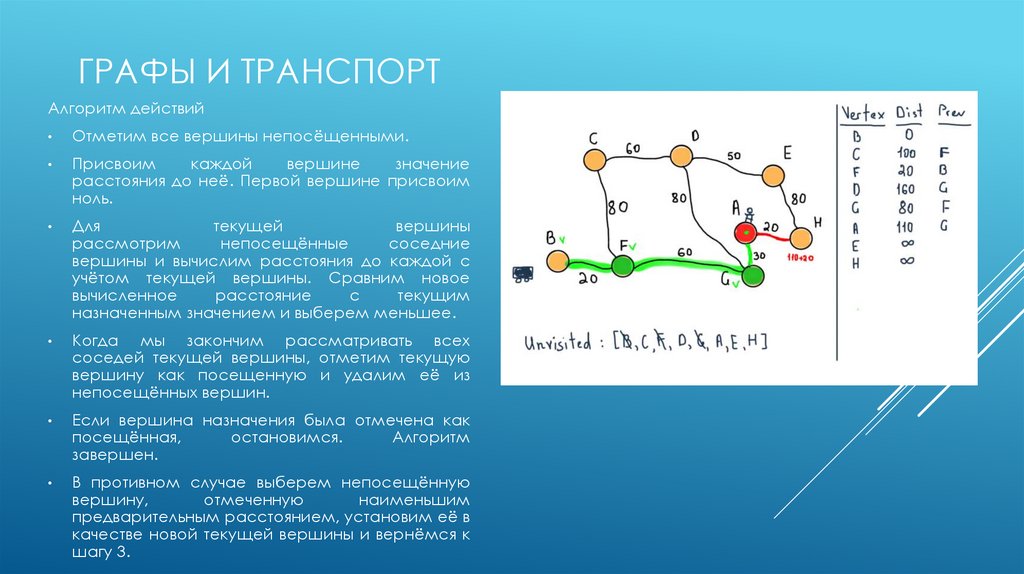
Двудольный граф — если все вершины графа можно разделить на два множества таким образом, что каждое ребро соединяет вершины из разных множеств, то такой граф называется двудольным. Например, клиент-серверное приложение содержит множество запросов (рёбер) между клиентом и сервером, но нет запросов внутри клиента или внутри сервера.
Планарный граф. Если граф можно разместить на плоскости таким образом, чтобы рёбра не пересекались, то он называется “планарным графом” или “плоским графом”.
Если это невозможно сделать, то граф называется “непланарным”.
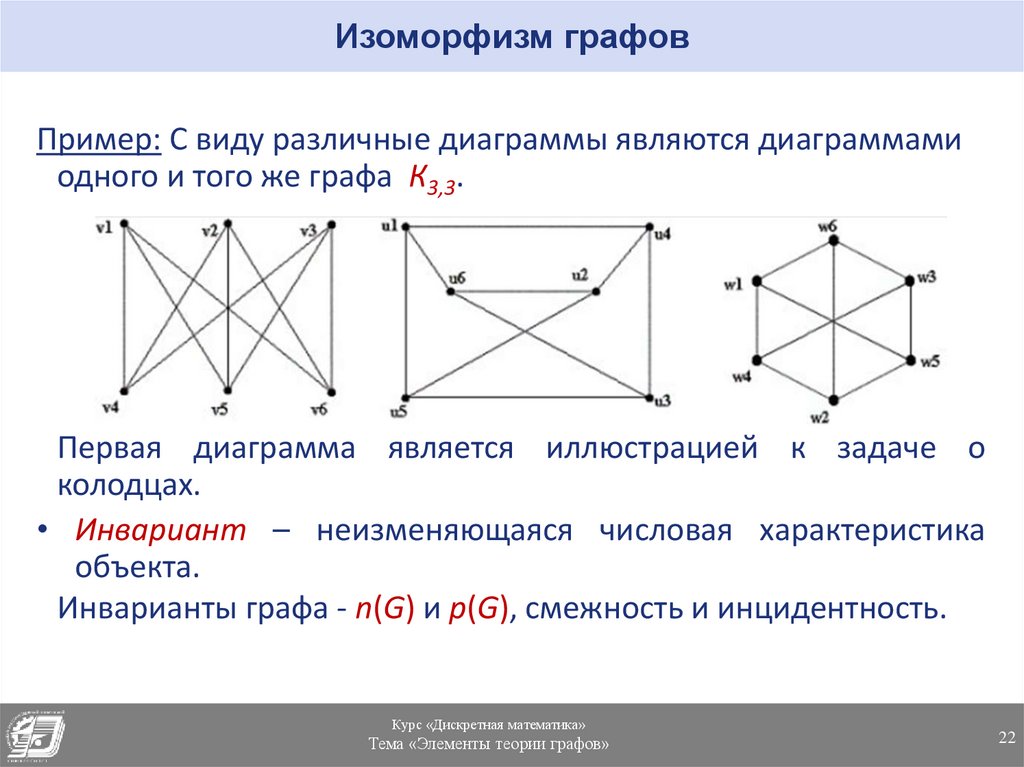
Минимальные непланарные графы — это полный граф К5 из 5 вершин и полный двудольный граф К3,3 из 3+3 вершин (известная задача о 3 соседях и 3 колодцах). Если какой-либо граф в качестве подграфа содержит К5 или К3,3, то он является непланарным.
Путь или Маршрут — это последовательность смежных рёбер. Обычно путь задаётся перечислением вершин, по которым он пролегает.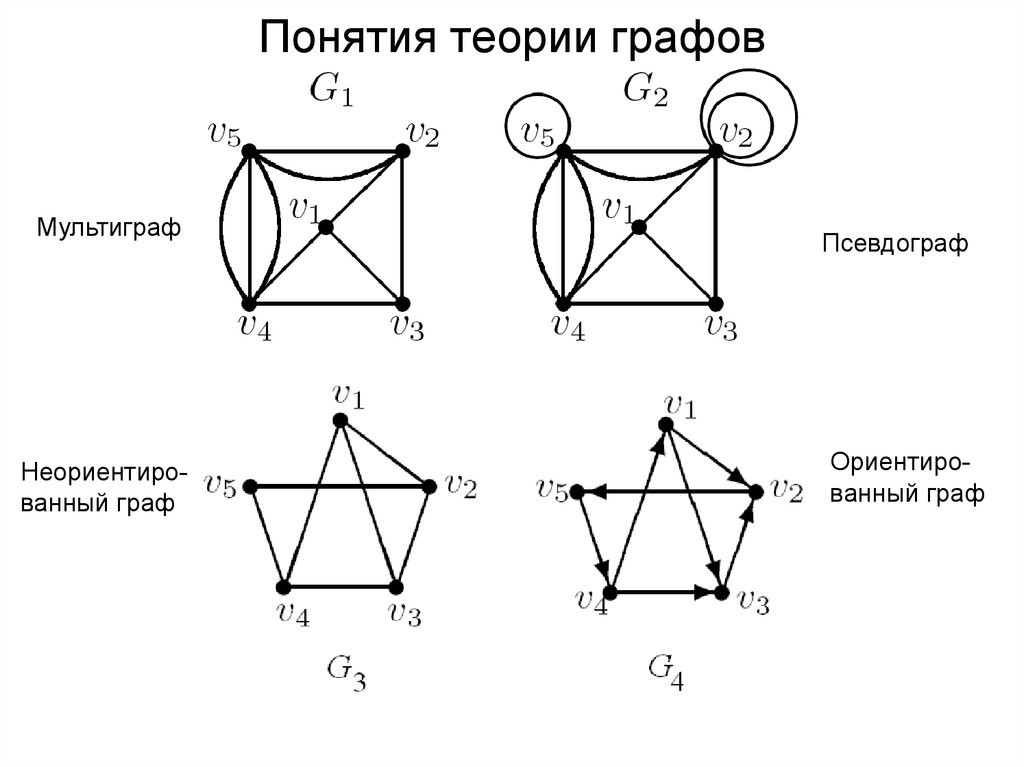
Длина пути — количество рёбер в пути.
Цепь — маршрут без повторяющихся рёбер.
Простая цепь — цепь без повторяющихся вершин.
Цикл или Контур — цепь, в котором последняя вершина совпадает с первой.
Длина цикла — количество рёбер в цикле.
Самый короткий цикл — это петля.
Цикл Эйлера — цикл, проходящий по каждому ребру ровно один раз. Эйлер доказал, что такой цикл существует тогда, и только тогда, когда все вершины в связанном графе имеют чётную степень.
Цикл Гамильтона — цикл, проходящий через все вершины графа по одному разу. Другими словами — это простой цикл, в который входят все вершины графа.
Взвешенный граф — граф, в котором у каждого ребра и/или каждой вершины есть “вес” — некоторое число, которое может обозначать длину пути, его стоимость и т. п. Для взвешенного графа составляются различные алгоритмы оптимизации, например поиск кратчайшего пути.
Пока ещё не придуман алгоритм, который за полиномиальное время нашёл бы кратчайший цикл Гамильтона в полном нагруженном графе, однако есть несколько приближённых алгоритмов, которые за приемлимое время находят если не кратчайший, то очень короткий цикл, эти алгоритмы мы также рассматриваем на курсе Отуса — “Алгоритмы и структуры данных”.
Связный граф — граф, в котором существует путь между любыми двумия вершинами.
Дерево — связный граф без циклов.
Между любыми двумя вершинами дерева существует единственный путь.
Деревья часто используются для организации иерархической структуры данных, например, при создании двоичных деревьев поиска или кучи, в этом случае одну вершину дерева называют корнем.
Лес — граф, в котором несколько деревьев.
Ориентированный граф или Орграф — граф, в котором рёбра имеют направления.
Дуга — направленные рёбра в ориентированном графе.
Полустепень захода вершины — количество дуг, заходящих в эту вершину.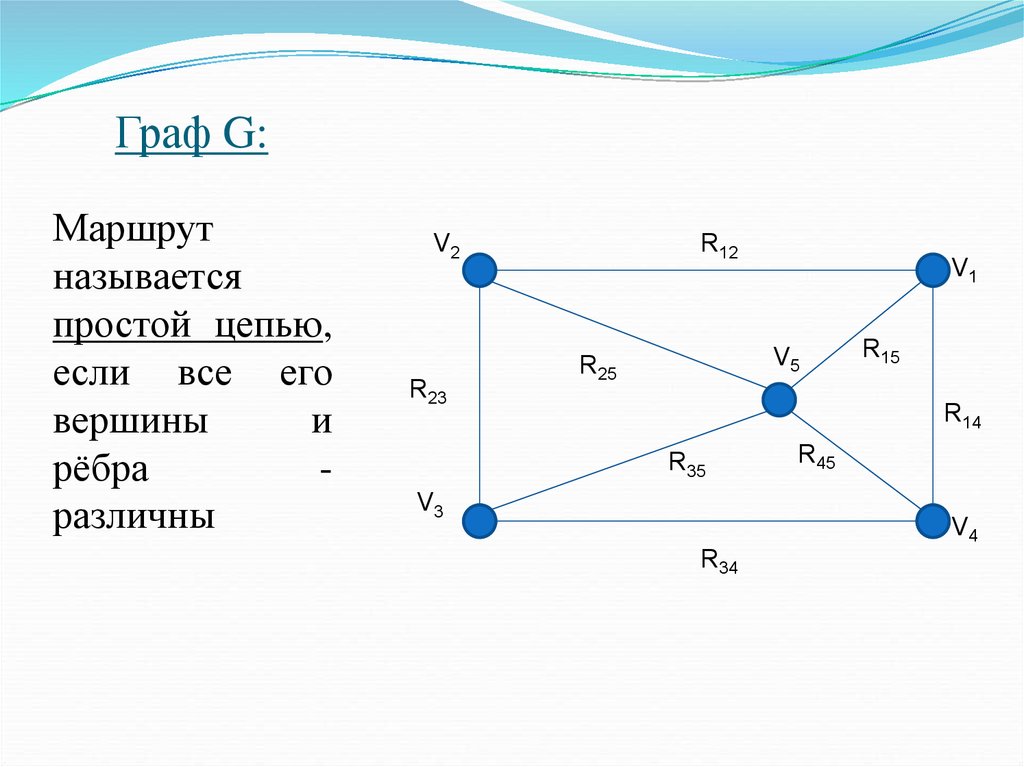
Исток — вершина с нулевой полустепенью захода.
Полустепень исхода вершины — количество дуг, исходящих из этой вершины
Сток — вершина с нулевой полустепенью исхода.
Компонента связности — множество таких вершин графа, что между любыми двумя вершинами существует маршрут.
Компонента сильной связности — максимальное множество вершин орграфа, между любыми двумя вершинами которого существует путь по дугам.
Компонента слабой связности — максимальное множество вершин орграфа, между любыми двумя вершинами которого существует путь по дугам без учёта направления (по дугам можно двигаться в любом направлении).
Мост — ребро, при удалении которого, количество связанных компонент графа увеличивается.
Это только основные термины и определения теории графов, которые мы рассматриваем на первом вебинаре модуля “Теория графов”. Цель статьи — дать наглядное и понятное представление об этих терминах, для чего и были нарисованы эти картинки.
Узнать о курсе подробнее
Записаться на интенсив: «Алгоритм сжатия данных — код Хаффмана. Создание Архиватора.». День 1
Записаться на интенсив: «Алгоритм сжатия данных — код Хаффмана. Создание Архиватора.». День 2
Теория графов | Комбинаторика
Зарегистрируйтесь для доступа к 15+ бесплатным курсам по программированию с тренажером
В этом курсе мы изучили базовые темы комбинаторики — области математики, занимающаяся проблемами выбора, расположения и работы в конечной или дискретной системе. Но пока мы не затрагивали один важный аспект этой темы — комбинаторную геометрию. В этом уроке мы обсудим, как комбинаторика связана с геометрией и какие темы стоит изучать дальше.
Как углубить знания в комбинаторике
Одной из основных задач комбинаторики — определить число возможных конфигураций заданного типа. Даже если конфигурация задается простыми правилами, перечисление иногда может представлять огромные трудности.
В таких случаях математик довольствуется приблизительным ответом или диапазоном с нижней и верхней границей. Это одна из сложностей, которая есть в комбинаторике.
В математике обычно говорят о «существовании». Сущность существует, если математический пример удовлетворяет абстрактным свойствам, определяющим сущность. Неочевидно, что существует даже единственная конфигурация с определенными заданными свойствами. Такая ситуация порождает проблемы существования и конструирования. Эти абстрактные формулировки используются и в комбинаторных задачах, и в этом состоит вторая сложность.
Считается, что комбинаторика нужна только для счета, но на деле она шире. Она решает и неожиданные вопросы, например, «Возможна ли определенная комбинация?». Но чтобы отвечать на такие вопросы с помощью комбинаторики, нужно добавить в нее конкретики. В этом помогает теория графов.
Что такое теория графов
Теория графов занимается графами — различными типами сетей или моделями сетей. Сами графы выглядят как точки, соединенные линиями:
Вместо точек и линий в теории графов используются другие термины — вершины и ребра.
Рассмотрим несколько примеров графов, чтобы лучше понять, о чем речь.
Задача с домино и шахматной доской
Предположим, у нас есть шахматная доска и набор домино, в котором каждая костяшка занимает два квадрата на шахматной доске. Можно ли покрыть всю доску этими костяшками? Сначала уточним правила:
Доска покрыта, если костяшки уложены так, что каждая из них покрывает ровно два квадрата доски
Ни одна костяшка не пересекается с другой
Каждая клетка доски в итоге покрыта
Ответ на эту задачу прост: чтобы покрыть доску, надо выложить 32 костяшки в ряд. Чтобы сделать задачу более интересной, добавим два новых условия:
Доска может быть примерно такой:
Можно ли ее покрыть целиком? Вот простое наблюдение: каждая костяшка должна покрывать две клетки, поэтому общее количество клеток должно быть четным; при этом доска имеет четное количество клеток. Достаточно ли этого? Нетрудно убедить себя, что эта доска не может быть покрыта, но все не так просто.
Теперь мы узнали кое-что новое — у нас есть четыре белых и шесть серых плиток. Каждая плитка должна покрывать один белый и один серый квадрат, но это невозможно. Теперь у нас есть полная картина? Снова неочевидно:
Серый квадрат в правом верхнем углу явно не может быть покрыт, потому что у него нет пары.
К сожалению, нелегко сформулировать условие, чтобы оно полностью характеризовало доски, которые можно покрыть — мы еще встретимся с этой проблемой. Отметим, что эту задачу можно представить в виде графа. Введем вершину, соответствующую каждому квадрату. Затем соединим две вершины ребром, если связанные с ними квадраты могут быть покрыты одним домино. Вот предыдущая доска в виде графа:
Расшифруем, что здесь обозначено:
Верхний ряд вершин — серые квадраты
Нижний ряд вершин — белые квадраты
Ребра — костяшки домино
Теперь мы можем размышлять так: «Костяшки соответствует набору ребер, которые не имеют общих конечных точек и касаются всех шести вершин.
Ни одно ребро не касается левой верхней вершины, поэтому эта клетка на шахматной доске не закроется».
Задача с раскраской
Возможно, самая известная задача в теории графов связана с раскраской карт. Она сформулирована так: «Если дана карта некоторых стран, то сколько цветов необходимо, чтобы раскрасить карту так, чтобы страны с общей границей имели разные цвета? Долгое время предполагалось, что любую карту можно раскрасить четырьмя цветами, и это было окончательно доказано в только 1976 году. Вот пример небольшой карты, раскрашенной четырьмя цветами:
Обычно эту проблему превращают в задачу теории графов. Предположим, что мы добавим к каждой стране столицу и соединим столицы через общие границы. Раскрашивание столиц так, чтобы ни одна из двух соединенных столиц не имела общего цвета — это та же проблема. Для предыдущей карты схема со столицами будет выглядеть так:
Открыть доступ
Курсы программирования для новичков и опытных разработчиков. Начните обучение бесплатно
- 130 курсов, 2000+ часов теории
- 1000 практических заданий в браузере
- 360 000 студентов
Электронная почта *
Отправляя форму, вы принимаете «Соглашение об обработке персональных данных» и условия «Оферты», а также соглашаетесь с «Условиями использования»
Наши выпускники работают в компаниях:
Нежное введение в теорию графов | Вайдехи Джоши | basecs
Так много всего в мире никогда бы не появилось, если бы не проблема, требующая решения.
Эта истина применима ко всему, но мальчик, разве это очевидно в мире информатики.
Кому-то нужен был способ отслеживать порядок вещей, поэтому они экспериментировали и создавали различные структуры данных, пока не нашли ту, которая лучше всего подходит для конкретной проблемы, которую они пытались решить. Кому-то еще нужен был хороший способ хранения данных, поэтому они экспериментировали с различными системами счисления, пока не нашли ту, которая лучше всего подходит для той информации, которую они хотели содержать. Людям нужен был хороший способ маркировки и обработки задач, поэтому они нашли способ опираться на имеющиеся у них инструменты и создали способ жонглировать всеми задачами, которые должна была делать одна система, в любой момент времени.
Конечно, информатика — это не единственная область, где можно внедрять инновации и развивать то, что было до нее, но я действительно думаю, что она уникальна в одном отношении: инновации в области информатики опираются на ее собственные абстракции и строятся на них.
Я много говорил об абстракциях в этой серии, потому что, в конечном счете, эта серия о заключается в том, чтобы находить радость в абстракциях, лежащих в основе вещей, которыми мы все пользуемся каждый божий день. И, что бы там ни было, когда я говорю «нас», я лишь частично говорю о нас как программистов, производителей технологий — я также имею в виду нас как пользователей, потребителей технологий.
Итак, о какой удивительной абстракции мы узнаем дальше? Что ж, теперь, когда мы являемся экспертами в древовидных структурах данных, кажется правильным понять, откуда взялись деревья. Деревья на самом деле являются подмножеством того, о чем вы, возможно, уже слышали: графов . Но чтобы по-настоящему узнать, почему мы используем графики и что они из себя представляют, нам нужно углубиться в самые корни того, что происходит из дискретной математики: теория графов .
Если это ваше первое знакомство с дискретной математикой, не бойтесь — это и мое! Давайте решать эту проблему вместе — и постарайтесь не потерять рассудок в процессе.
Когда мы впервые начали изучать нелинейные структуры, мы узнали об их самой фундаментальной характеристике: их данные не следуют порядку — по крайней мере, не очевидному числовому порядку, как мы видим в массивах или связанных списках. Как мы узнали, деревья начинаются с корневого узла и могут соединяться с другими узлами, что означает, что они могут содержать поддеревья внутри себя. Деревья определяются определенным набором правил: один корневой узел может соединяться или не соединяться с другими, но в конечном итоге все они происходят из одного определенного места. У некоторых деревьев даже более конкретных правил, таких как бинарные деревья поиска, которые могут иметь только две ссылки на два узла в любой момент времени.
Но что, если мы сделаем что-нибудь безумное и просто… выбросим эти правила в окно? Что ж, как оказалось, мы в сумме можем сделать это! Просто мы больше не будем иметь дело с деревьями — мы будем иметь дело с чем-то, что называется графом .
Деревья — это не что иное, как ограниченные типы графов, но с гораздо большим количеством правил, которым нужно следовать. Дерево всегда будет графом, но не все графы будут деревьями.
Итак, что отличает дерево от большого зонтика графов?
Ну, во-первых, дерево может течь только в одном направлении, от корневого узла либо к листовым узлам, либо к дочерним узлам. Дерево также может иметь только односторонние соединения — у дочернего узла может быть только один родитель, а в дереве не может быть петель или циклических связей.
Древовидные структуры данных по сравнению со структурами данных графа С графами все эти ограничения исчезают. Графы не имеют понятия «корневой» узел. А зачем им? На самом деле узлы могут быть связаны любым возможным способом. Один узел может быть подключен к пяти другим! У графиков также нет понятия «однонаправленного» потока — вместо этого они могут иметь направление или вообще не иметь направления. Или, чтобы еще больше усложнить ситуацию, у них могут быть некоторые ссылки, которые имеют направление, а другие — нет! Но мы не будем вдаваться в это сегодня.
Для начала остановимся на самом простом.
Итак, мы знаем, что графики в значительной степени нарушают все известные нам правила. Однако есть одна характеристика, которой должен обладать каждый граф и : каждый граф всегда должен иметь, по крайней мере, один-единственный узел. Точно так же, как деревьям нужен хотя бы один корневой узел, чтобы считаться «деревом», точно так же графу нужен хотя бы один узел, чтобы считаться «графом». Граф только с одним узлом обычно называют singleton graph , хотя на самом деле мы не будем иметь дело с ними.
Большинство графиков, с которыми мы будем иметь дело, немного сложнее. Но не волнуйтесь — сегодня мы не будем погружаться в сверхсложных графика . И поверьте мне, некоторые графики действительно сложны!
Вместо этого давайте рассмотрим два типа графов, которые довольно легко обнаружить и которые также довольно часто встречаются в задачах теории графов: ориентированные графы и неориентированные графы.
Как мы знаем, не существует реальных правил в отношении того, как один узел соединяется с другим узлом в графе. Края (иногда их называют ссылки ) могут соединять узлы в любым возможным способом.
Edges могут соединять узлы любым возможным способом!Различные типы ребер очень важны, когда дело доходит до распознавания и определения графов. На самом деле, это одно из самых больших и очевидных различий между одним графом и другим: типы ребер, которые у него есть. По большей части (кроме одного исключения, которое мы сегодня не будем рассматривать) графы могут иметь два типа ребер: ребро, имеющее направление или поток, и ребро, не имеющее направления или потока. Мы называем их направленный и ненаправленный края, с уважением.
В направленном ребре два узла соединены очень специфическим образом. В приведенном ниже примере узел A соединяется с узлом B; между этими двумя узлами есть только один способ перемещения — только одно направление , в котором мы можем двигаться.
Довольно часто узел, с которого мы начинаем, называют источником , а узел, к которому мы направляемся , — пунктом назначения 9.0004 . В направленном ребре мы можем пройти только от источника к месту назначения , и никогда наоборот.
Однако с ненаправленными ребрами дело обстоит совсем по-другому. В ненаправленном ребре путь, по которому мы можем пройти, идет в обе стороны. Другими словами, путь между двумя узлами является двунаправленным , что означает, что исходный и конечный узлы не фиксированы .
Это различие на самом деле очень важно, потому что ребра в графе определяют, как называется граф. Если все ребра в графе ориентированы , граф называется ориентированным графом , также называемым орграфом . Если все ребра в графе неориентированные , то говорят, что граф — как вы уже догадались — неориентированный граф ! Поди разберись, да?
Ориентированные графы по сравнению с неориентированными графамиВсе это очень круто, но на данный момент я хочу знать две вещи — откуда взялись все эти графы происходит от , точно? И… какое нам дело?
Давайте разберемся.
Информатика любит брать взаймы. В частности, он позаимствовал множество понятий из логики и математики. Как оказалось, это относится и к графикам.
Структуры графовых данных, какими мы их знаем в компьютерных науках, на самом деле происходят из математики и изучения графов, которые называются теорией графов .
В математике графы — это способ формального представления сети, которая, по сути, представляет собой просто набор взаимосвязанных объектов.
Как оказалось, когда ученые-компьютерщики применили теорию графов к коду (и, в конечном счете, реализовали графы как структуры данных), они мало что изменили. Таким образом, многие термины, которые мы используем для описания и реализации графов, являются точными терминами, которые мы найдем в математических справочниках по теории графов.
Например, в математических терминах мы описываем графы как упорядоченных пар . Помните школьную алгебру, когда мы узнали о (x, y) упорядоченных парных координатах? Аналогичная сделка здесь, с одним отличием: вместо x и y , части графа вместо этого: v , для вершин , и e , для его ребер .
Формальное математическое определение графа таково: G = (V, E) . Вот и все! Действительно. Обещаю.
Очень краткое введение в теорию графовНо подождите секунду — что, если наш граф имеет более одного узла и более одного ребра! На самом деле… будет почти всегда имеют несколько ребер, если у него более одного узла. Как же работает это определение?
Ну, это работает, потому что эта упорядоченная пара — (V, E) — на самом деле состоит из двух объектов : набор из вершин и набор из ребер.
Хорошо, теперь это имеет для меня больше смысла. Но было бы намного яснее, если бы у меня был пример и я действительно записал определение графа! Так что мы сделаем именно это. В приведенном ниже примере у нас есть неориентированный граф с 8 вершинами и 11 ребрами.
Формальное определение неориентированного графаТак что же здесь происходит?
Итак, мы записали нашу упорядоченную пару (V, E) , но поскольку каждый из этих элементов является объектом, нам пришлось выписать и их.
Мы определили V как неупорядоченных набора ссылок на наши 8 вершин. «Неупорядоченная» часть здесь действительно важна, потому что помните, в отличие от деревьев, нет иерархии узлов ! Это означает, что нам не нужно их упорядочивать, так как порядок здесь не имеет значения.
Мы также должны были определить E как объект, который содержит множество граничных объектов внутри себя. Заметьте еще раз, что наши краевые объекты также являются неупорядоченными . Почему это может быть? Ну и что это за график? Есть ли какое-то направление или течение? Существует ли фиксированное значение «происхождения» и «назначения»?
Нет, нет! Это неориентированный граф , что означает, что ребра являются двунаправленными, а исходный узел и узел назначения равны , а не 9.0004 исправлено. Итак, каждый из наших реберных объектов также представляет собой неупорядоченных пары .
Эта особенность, конечно, заставляет задуматься: а что, если бы это был -ориентированный -граф? Время для другого примера! Вот ориентированный граф с тремя вершинами и тремя ребрами:
Формальное определение ориентированного графа Способ, которым мы определяем вершины, ничем не отличается, но давайте более внимательно рассмотрим определение нашего ребра.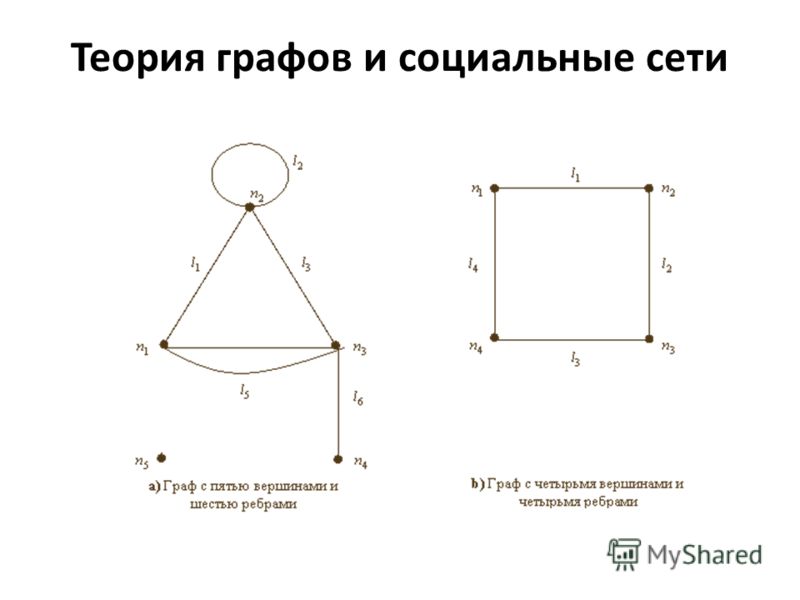
Наши граничные объекты в этом случае — это упорядоченных пары, потому что в этом случае направление действительно имеет значение! Поскольку мы можем путешествовать только от исходного узла к узлу назначения, наши ребра должен быть упорядочен , чтобы исходный узел был первым из двух узлов в каждом из наших определений ребер.
Круто, вот как мы определяем графики. Но… когда мы будем использовать графов ? Ну, вы, вероятно, использовали один из них сегодня. Возможно, вы еще этого не знаете! Время изменить это.
Графики окружают нас повсюду, просто мы не всегда видим их такими, какие они есть.
На самом деле, читая этот пост, вы буквально находитесь на графике прямо сейчас. Сеть — это массивная графовая структура! Когда мы щелкаем между веб-сайтами и перемещаемся между URL-адресами, мы на самом деле просто перемещаемся по графику. Иногда эти графы имеют узлы с ненаправленными ребрами — я могу переходить с одной веб-страницы на другую — и другие, которые являются направленными — я могу переходить только с веб-страницы А на веб-страницу Б и никогда наоборот.
Но есть еще лучший пример, прекрасно иллюстрирующий наше ежедневное взаимодействие с графами: социальные сети.
Facebook, огромная социальная сеть, представляет собой тип графа. И если мы больше подумаем об этом на самом деле, мы начнем лучше понимать , как мы можем определить , и что именно представляет собой тип графа. На Facebook, если я добавлю вас в друзья, вы должны принять мой запрос. Я не могу быть твоим другом в сети, если ты не будешь моим. Отношение между двумя пользователями (читай: узлы или вершины в терминах графа!) равно двунаправленным . Нет понятия «источник» и «пункт назначения» — вместо этого ты мой друг, а я твой.
Угадайте, какой тип графа реализован в Facebook?
Facebook как структура неориентированного графа Если вы угадали неориентированный граф , то вы правы! Отличная работа. Отношения двусторонние, поэтому, если бы мы определили сеть друзей Facebook как граф, все ее ребра оказались бы неупорядоченными парами, когда мы их записали.
Twitter, с другой стороны, работает совершенно иначе, чем Facebook. Я могу следовать за тобой, но ты можешь не следовать за мной в ответ. Показательный пример: я слежу за Бейонсе, но она определенно не следует за мной в ответ (к сожалению).
Twitter как структура ориентированного графаМы можем представить Twitter как направленный граф. Каждое ребро, которое мы создаем, представляет собой односторонних отношений . Когда вы подписываетесь на меня в Твиттере, вы создаете ребро на графике, где ваша учетная запись выступает в качестве исходного узла, а моя учетная запись — в качестве конечного узла.
Что произойдет, если я пойду за тобой? Могу ли я изменить край, который вы создали, когда следовали за мной? Он вдруг становится двунаправленным? Ну, нет, потому что я могу отписаться от тебя в любой момент. Когда я иду за тобой назад в Твиттере, я создаю второе ребро, с моей учетной записью в качестве исходного узла и вашей в качестве конечного узла.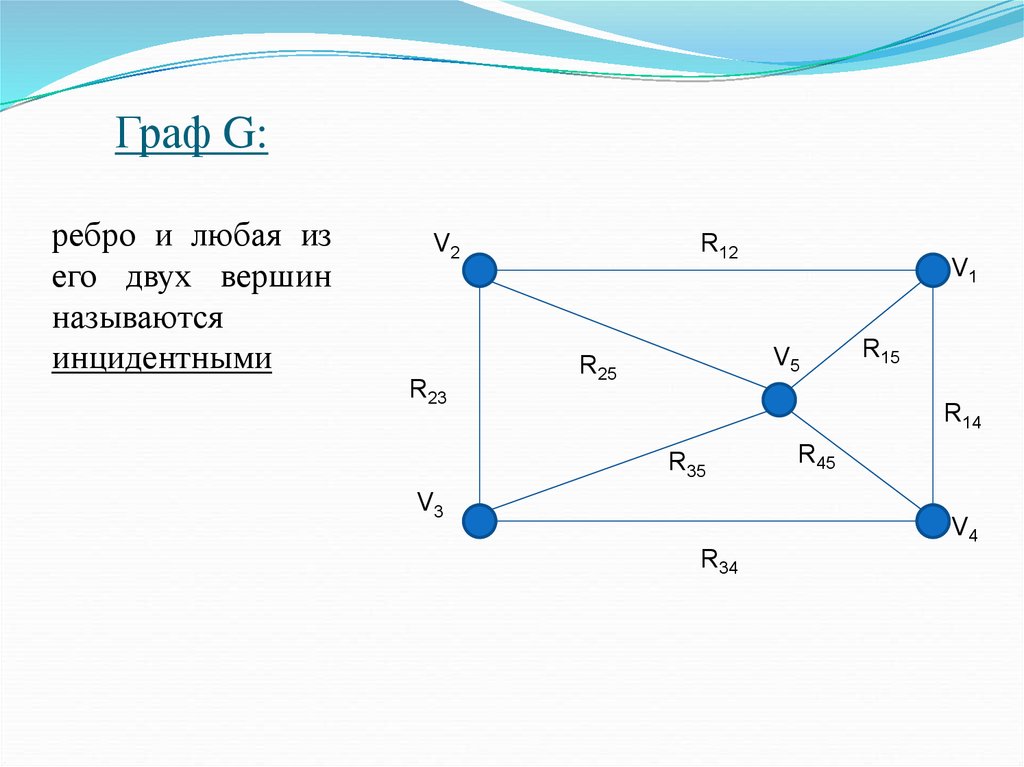
Та же модель применима и к Medium, что позволяет вам подписываться на авторов и отписываться от них! На самом деле эта сетевая модель вместо . И все это, как только мы абстрагируем все слои, — это граф. И действительно, какая это мощная штука.
О графах написано множество целых книг . Я, конечно, не предоставил здесь достаточно информации, чтобы заполнить книгу, но это не значит, что вы не можете продолжать изучать графики! Наполните свой разум еще большим количеством удивительной теории графов, начиная с замечательных ссылок ниже.
- Разница между деревьями и графами, Пунам Дханвани
- В чем разница между деревом структуры данных и графом?, StackOverflow
- Применение теории графов в компьютерных науках: обзор, С.Г.Ширинивас и др. др.
- Обход графа, профессор Джонатан Коэн
- Структуры данных: введение в графы, mycodeschool
Искусство решения проблем
В теории графов граф представляет собой (обычно конечный) непустой набор вершин, которые соединены количество (возможно, ноль) ребер.
Здесь должно быть изображение. Вы можете помочь нам, создав и отредактировав его. Спасибо.
Формально граф — это пара множества вершин вместе с классом подмножеств, состоящим из пар элементов из . Обратите внимание, что это определение описывает простых графов без петель : существует не более одного ребра, соединяющего две вершины, ни одно ребро не может соединять вершину с собой, и ребра не являются направленными. Для графов с несколькими ребрами см. мультиграф. Если ребра направлены, то их можно определить с помощью упорядоченных пар из набора произведений .
Содержание
- 1 Определения
- 2 типа графиков и подграфов
- 2.1 Полный граф или клика
- 2.2 Дополнительные графики
- 2.3 Нулевой график или независимый набор
- 2.4 Подключенный график
- 2.
5 Сильно связный граф - 2.6 Планарные графики
- 2.7 Двудольный граф
- 3 прогулки
- 3.1 Пути и циклы
- 3.2 След Эйлера
- 3.3 Деревья и леса
- 4 взвешенных графика
- 5 Гиперграф
- 6 См. также
5 Сильно связный графОпределения
- Если , и тогда мы говорим и являются инцидентами. Если и мы говорим, что ребра и совпадают с в .
- Количество ребер в содержании равно степени и часто обозначается .
- Вершина является изолированной если , т.е. если нет ребер, инцидентных .
- Если и такие графы, что и тогда мы говорим, что это подграф
Типы графов и подграфов
Полный граф или клика
Полный граф — это граф, в котором есть ребро, соединяющее каждую пару вершин.
Полный граф по вершинам обозначается и имеет ребра. Если является полным подграфом, то говорят, что его вершины образуют клик в .
Дополнительные графы
Если два графа в одном и том же наборе вершин таковы, что это полный граф, то говорят, что он является дополнением и наоборот.
Нулевой граф или независимый набор
Нулевой граф (или независимый набор ) является дополнением полного графа. То есть нулевой граф — это граф, в котором каждая вершина изолирована. При обычном рисовании нулевой граф представляет собой просто набор разбросанных точек (вершин) без соединяющих их ребер. Термин «независимый набор» чаще всего используется для обозначения подграфа. Другими словами, говорят, что это независимое множество в тогда и только тогда, когда это клика в дополнении к .
Связный граф
Неориентированный граф является связным , если для всех существует путь из в с использованием только ребер в . То есть не существует изолированных вершин, из которых не исходят пути, и множество вершин не может быть разделено на две части без ребра между ними.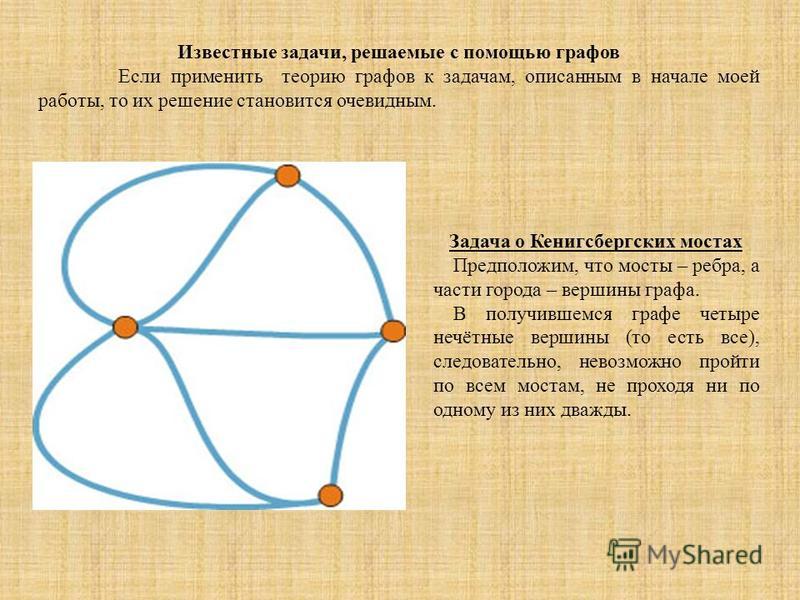
Родственное понятие — это компонент связности , который является максимально связным подграфом графа.
Сильно связный граф
Ориентированный граф сильно связный если для всех существует направленный путь из в с использованием только ребер в .
Планарные графы
Граф называется планарным, если его можно нарисовать на плоскости без пересекающихся ребер. Например, и плоские, а и не плоские.
Здесь должно быть изображение. Вы можете помочь нам, создав и отредактировав его. Спасибо.
В плоском графе мы можем определить грани графа или наименьшие области, ограниченные ребрами. (Альтернативное определение — это области, ограниченные ребрами, через которые не проходят никакие ребра.) Обратите внимание, что область за пределами плоского графа также является гранью, называемой неограниченной гранью. Степень грани — это количество ребер, ограничивающих грань. (Обратите внимание, что тот же термин используется для вершин, что может привести к путанице.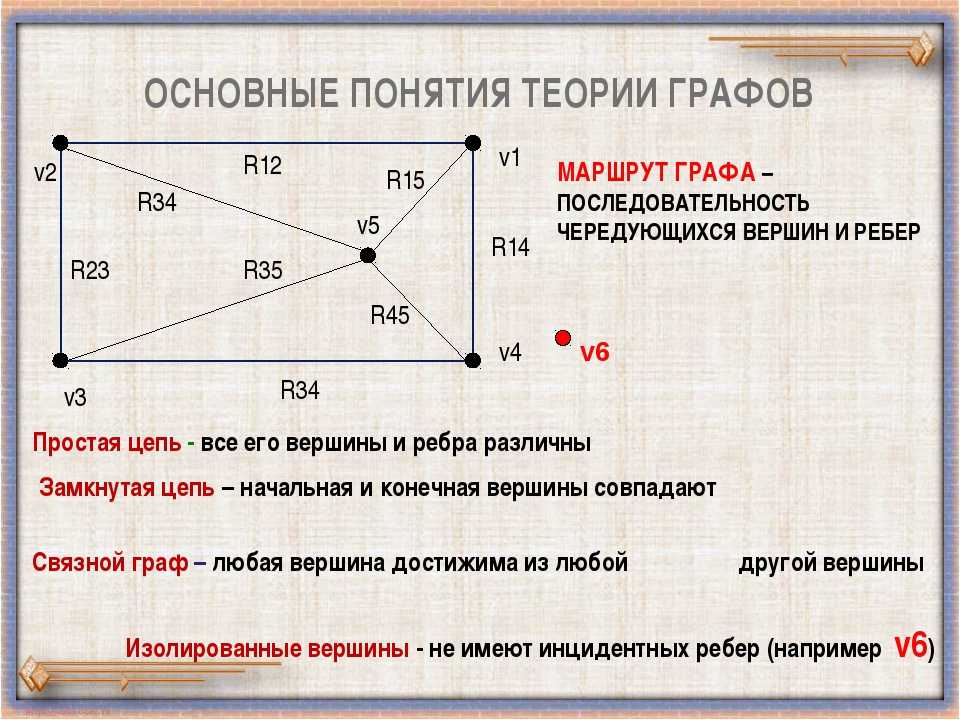
)
Все планарные графы имеют двойственные графы, в которых плоскости одного графа превращаются в вершины, а вершины — в плоскости, причем ребра соединяются, если две плоскости смежны. Двойник двойственного графа возвращает исходный граф.
Интересным результатом является многогранная формула Эйлера, которая утверждает, что в плоском графе с вершинами, ребрами и гранями тогда Доказательство этого просто с помощью индукции, но вывод формулы гораздо сложнее.
Другие интересные результаты для плоских графов:
- если сумма степеней граней графа равна , то .
Двудольный граф
Граф называется двудольным , если его множество вершин можно разделить на два непересекающихся подмножества и такое, что каждое ребро соединяет вершину в с вершиной в (по этому определению, пустой граф на вершинах является двудольным ). Граф двудольный тогда и только тогда, когда он не имеет нечетных циклов, тогда и только тогда, когда он раскрашивается в 2 цвета.
Двудольные графы имеют множество приложений, включая задачи на сопоставление.
Полный двудольный граф (обозначается целыми числами и ) — это двудольный граф, где , , и существует ребро, соединяющее каждый с каждым (так что ребра есть).
Здесь должно быть изображение. Вы можете помочь нам, создав и отредактировав его. Спасибо.
Обходы
Обход — это общий процесс перемещения по ребрам графа. Путь не проходит через любую вершину более одного раза, а след не проходит через любое ребро более одного раза.
Пути и циклы
Путь в графе представляет собой последовательность такую, что и для всех . Цикл — это путь, в котором начальная и конечная вершины совпадают.
Путь Эйлера
Путь Эйлера — это граф, в котором можно сформировать след, использующий все ребра. Путь Эйлера имеет не более двух вершин с нечетными степенями. Сумма всех степеней вершин равна удвоенному количеству ребер в графе.