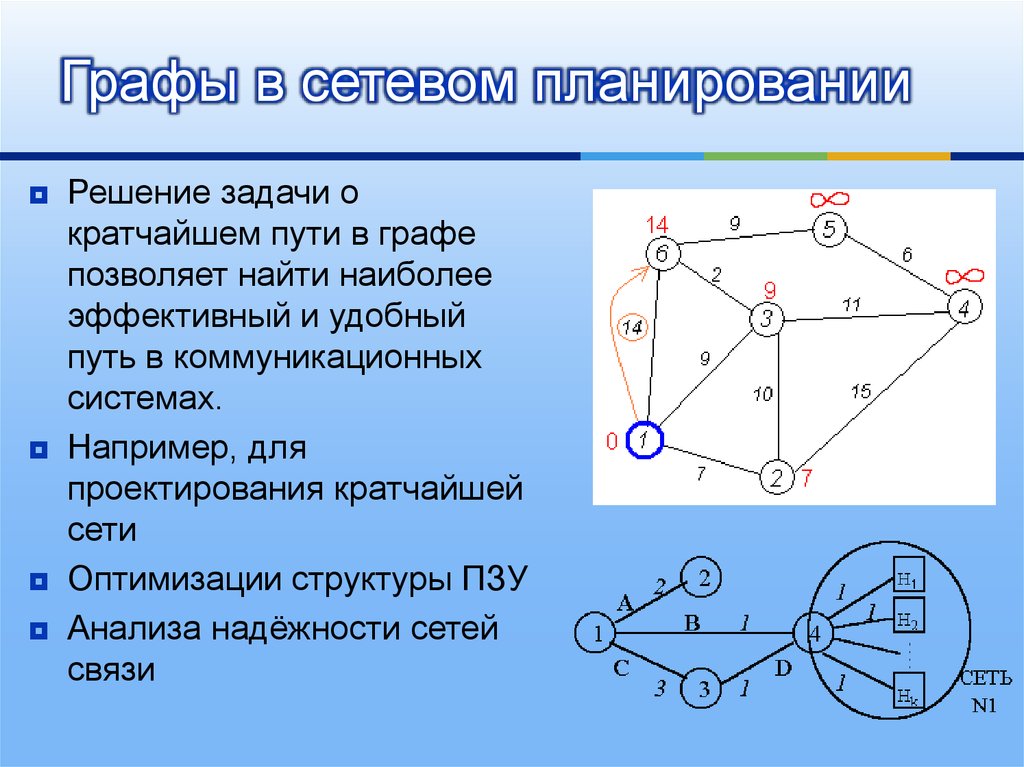
Теория графов при решении задач
ВведениеТеория графов — раздел математики и информатики, нашедший широкое применение в современных прикладных задачах. В первую очередь, это задачи поиска маршрута на картах, но её применение не ограничивается навигационными приложениями. Графы возникают там, где между данными существуют какие-либо нелинейные связи. Например, это могут быть компьютеры, соединённые в сеть. Или же это могут быть задачи, которые надо выполнить в каком-то порядке, причём некоторые задачи надо выполнять строго после каких-то других. Существуют алгоритмы, позволяющие вычислить оптимальный порядок выполнения таких задач.
История возникновения теории графов. Леонард Эйлер и задача о Кёнигсберских мостах Родоначальником теории графов считается Леонард Эйлер. В 1736 году в одном из своих писем он формулирует и предлагает решение задачи о семи кёнигсбергских мостах, ставшей впоследствии одной из классических задач теории графов.
Издавна среди жителей Кёнигсберга (теперь Калининграда) была распространена такая загадка: как пройти по всем мостам, не проходя ни по одному из них дважды? Многие кёнигсбержцы пытались решить эту задачу как теоретически, так и практически, во время прогулок. Но никому это не удавалось, однако не удавалось и доказать, что это даже теоретически невозможно.
В 1736 году задача о семи мостах заинтересовала выдающегося математика, члена Петербургской академии наук Леонарда Эйлера, о чём он написал в письме итальянскому математику и инженеру Мариони от 13 марта 1736 года. В этом письме Эйлер пишет о том, что он смог найти правило, пользуясь которым легко определить, можно ли пройти по всем мостам, не проходя дважды ни по одному из них (в случае семи мостов Кёнигсберга это невозможно).
Для того, чтобы решить эту задачу, Эйлер сделал специальные обозначения. Каждую часть суши (остров или берег реки) он обозначил кружком на бумаге, а затем соединил линиями те кружки, между которыми существуют мосты.
- Число нечётных вершин (вершин, к которым ведёт нечётное число рёбер) графа должно всегда быть чётно. То есть, просто не может существовать графа, который имел бы нечётное число нечётных вершин.
- Если все вершины графа чётные, то его можно начертить не отрывая карандаша от бумаги, при этом начинать можно с любой вершины графа и завершить его в ней же.
- Граф с более чем двумя нечётными вершинами невозможно начертить одним росчерком.
Доказательство. Вначале заметим, что если все вершины графа имеют степень не меньше двух, то в нем существует хотя бы один цикл.
Рассмотрим случай, когда все вершины четны. Применим «метод стирания». Выберем некоторую точку и начнем строить путь. Так как степени всех вершин четны, то они не меньше двух. Поэтому, войдя по некоторому ребру в данную точку, мы всегда можем выйти из нее по второму ребру. Будем отмечать пройденные вершины. Так как число вершин конечно, то на каком-то шаге мы перейдем в одну из уже отмеченных вершин и таким образом замкнем цикл. Теперь сотрем этот цикл (естественно, запомнив его где-то) и рассмотрим получившийся граф. Он может оказаться несвязным, но, тем не менее, все его вершины будут иметь четную степень. Применим к этому графу ту же процедуру, и будем это делать до тех пор, пока остается хотя бы один нетривиальный подграф. В результате мы получим несколько циклов, которые не имеют общих ребер, а все вместе образуют исходный граф. Нам остается только склеить эти циклы в один. Возьмем два цикла (… ВАС…) и (…НАМ…), имеющие общую вершину А, разрежем их в этой вершине и склеим по такому правилу: сначала выписываем вершины первого цикла, потом, дойдя до точки А, записываем все вершины второго цикла, а затем продолжаем выписывать оставшиеся вершины первого цикла. Очевидно, что в итоге у нас получится один цикл, который содержит все ребра исходного графа.
Очевидно, что в итоге у нас получится один цикл, который содержит все ребра исходного графа.
Предположим теперь, что в исходном графе ровно две нечетных вершины А и В. Соединим их дополнительных ребром АВ, и получим граф, все вершины которого четны. Построим для него эйлеров цикл по указанному выше алгоритму. Перепишем его так, чтобы вершина
Предположим теперь, что граф уникурсален. Докажем, что в нем не более двух нечетных вершин. Очевидно, что рисовать такой граф нужно, начиная с нечетной вершины. Причем завершить маршрут нужно в другой нечетной вершине. Если же имеется еще одна нечетная вершина, то она не может быть ни начальной, ни конечной. Поэтому, когда мы в нее заходим, то должны обязательно выйти. Каждый проход через вершину уменьшает число не пройденных ребер, связанных с этой вершиной, ровно на два. В итоге, на каком то шаге в нечетной вершине останется только одно не пройденное ребро, зайдя по которому в вершину мы уже не сможем из нее выйти. Теорема доказана полностью.
В итоге, на каком то шаге в нечетной вершине останется только одно не пройденное ребро, зайдя по которому в вершину мы уже не сможем из нее выйти. Теорема доказана полностью.
Граф кёнигсбергских мостов имел четыре нечётные вершины (т.е. все), следовательно, невозможно пройти по всем мостам, не проходя ни по одному из них дважды.
Определения теории графов
Граф — конечное множество вершин, природа которых не важна, и конечно множество рёбер, соединяющих между собой какие-либо вершины.
Графы могут быть ориентированными и неориентированными. Если в рамках задачи по рёбрам можно перемещаться в обоих направлениях, то граф называется неориентированным. Если же по каждому ребру можно пройти только в одну сторону, то граф ориентированный. В таком случае рёбра обычно обозначаются стрелками, а не просто линиями.
Пример ориентированного графа
Иногда бывает полезно связать с ребрами графа какие-то числа. Это могут быть длины дорог или плата за проезд, если граф моделирует карту какой-то местности. В таком случае граф называется взвешенным, а сами числа — весами.
Это могут быть длины дорог или плата за проезд, если граф моделирует карту какой-то местности. В таком случае граф называется взвешенным, а сами числа — весами.
Пример: граф с шестью вершинами и семью рёбрами
Граф, в котором каждая пара вершин соединена ребром, называется полным. Обозначение: Kn — граф, состоящий из n вершин и ребер, соединяющих всевозможные пары этих вершин. Такой граф можно представить как n-угольник, в котором проведены все диагонали.
Ниже приведены полные графы с числом вершин от 1 до 8 и количества их рёбер.
Степенью вершины называется число ребер, которым принадлежит вершина (число рёбер с концом в данной вершине).
Дополнением данного графа называется граф, состоящий из всех ребер и их концов, которые необходимо добавить к исходному графу, чтобы получить полный граф.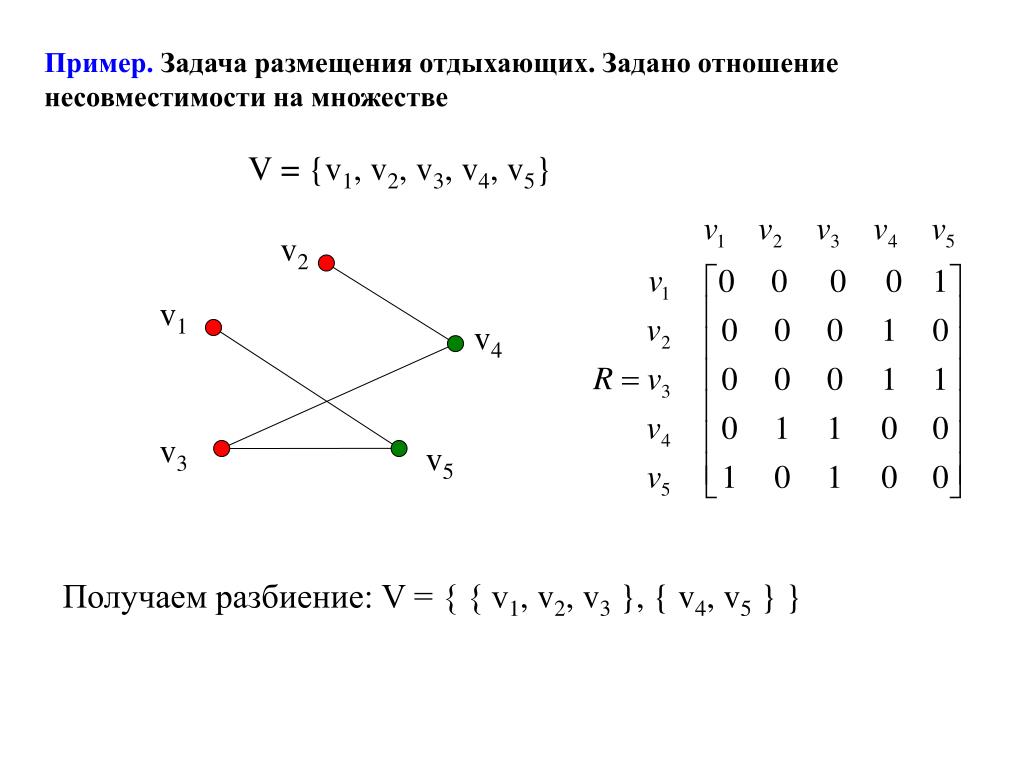
Граф, который можно представить на плоскости в таком виде, когда его ребра пересекаются только в вершинах, называется плоским.
Многоугольник плоского графа, не содержащий внутри себя никаких вершин или ребер графа, называют его гранью.
Понятия плоского графа и грани графа применяется при решении задач на «правильное» раскрашивание различных карт.
Путем от вершины A до вершины X называется последовательность ребер, ведущая от A к X, такая, что каждые два соседних ребра имеют общую вершину, и никакое ребро не встречается более одного раза.
Циклом называется путь, в котором совпадают начальная и конечная точка (т.е. можно «ходить по циклу» — «ходить по кругу»).
Простым циклом называется цикл, не проходящий ни через одну из вершин графа более одного раза.
Длиной пути, проложенного на цикле, называется число ребер этого пути.
Две вершины A и B в графе называются связными (несвязными), если в нем существует (не существует) путь, ведущий из A в B.
Граф называется связным, если каждые две его вершины связны; если же в графе найдется хотя бы одна пара несвязных вершин, то граф называется несвязным.
https://habr.com/ru/company/otus/blog/568026/
Специальным типом графов является дерево. В дереве выделяется особая вершина — корень, которая соединена рёбрами с другими вершинами — своими потомками, которые в свою очередь могут иметь своих потомков. Вершина, не имеющая потомков, называется листом. Наглядный пример дерева — иерархия файлов и папок в файловой системе компьютера или систематика живых организмов
Если не выделять особым образом корень, то дерево — это просто любой связный граф, не имеющий циклов.
Представление графов в памяти
Чтобы решать задачи, связанные с графами, нужно сначала научиться сохранять его в памяти, а ещё лучше — сохранять оптимально. Существует несколько способов сделать это, и для каждой конкретной задачи оптимальным будет свой способ.
Существует несколько способов сделать это, и для каждой конкретной задачи оптимальным будет свой способ.
Матрица смежности
Самый простой способ сохранить граф в памяти — матрица смежности. Нарисуем таблицу, которая чем-то напоминает таблицу умножения: в первой строчке и в первом столбце будут стоять номера (или любые названия) вершин, а на пересечении столбца и строки будем ставить, например, 1 если между этими вершинами есть ребро и 0 если нет. Кроме 1 и 0 можно ставить, например, вес ребра, а для обозначения отсутствия ребра — просто очень большое число. Какой именно вариант использовать, зависит от каждой конкретной задачи. Также задача определяет, что ставить на диагонали получившейся матрицы.
Граф и его матрица смежности.
Матрица смежности элементарно реализуется в большинстве языков программирования, достаточно лишь объявить двумерный массив.
Другие способы
Существуют и другие способы хранения графа в памяти, например, матрица инцидентости, которая удобна при использовании методов линейной алгебры в задачах на графах, или списки рёбер, но практическое применение в задачах обычно находят описанные выше два способа.
Обходы графа
Часто требуется обойти все вершины графа в определённом порядке, например, для проверки его на связность или упорядочения задач при планировании (топологическая сортировка графа). Существует два стандартных метода обхода графа — обход в глубину и обход в ширину.
Обход в глубину (DFS)
Обход в глубину можно описать так: представьте, что вы в лабиринте. Идите всегда прямо, а на всех развилках выбирайте самый левый путь. Упёршись в тупик, возвращайтесь обратно до последней развилки и выбирайте следующий путь слева. Продолжайте, пока не обойдёте весь лабиринт.
Обход в ширину (BFS)
Обход в ширину можно наглядно представить себе так: в какой-то стартовой точке лабиринта разливается жидкость, и она начинает равномерно заполнять все его помещения, продвигаясь все дальше. При этом в каждый момент времени все точки края разливающейся воды находятся на одном расстоянии от начала.
Этот обход, как и обход DFS, можно применять для поиска путей в графах. Основное его отличие в том, что поиск не уходит сразу далеко от начала, а продвигается вглубь графа постепенно, неким «фронтом».
Его реализация немного сложнее, чем DFS. Для этого нам понадобится такая структура данных, как очередь. Очередь, как видно из названия, моделирует обычную очередь в магазине. Обычно это список, в которой можно класть элементы с одной стороны, а забирать — с другой. Обход в ширину хранит в очереди вершины, которые еще предстоит просмотреть.
Другие задачи
Другими классическими задачами теории графов являются, например, задача топологической сортировки и задача поиска наименьшего остовного дерева.
Проблема четырёх красок
Проблема четырёх красок — математическая задача, предложенная Гутри в 1852 году.
Выяснить, можно ли всякую расположенную на сфере карту раскрасить четырьмя красками так, чтобы любые две области, имеющие общий участок границы, были раскрашены в разные цвета.
Иначе говоря, показать что хроматическое число плоского графа не превосходит 4.
О доказательстве
К.Аппель и В.Хакен доказали в 1976 г., что так можно раскрасить любую карту. Это была первая крупная математическая теорема, для доказательства которой был применён компьютер. Несмотря на последующие упрощения, доказательство практически невозможно проверить, не используя компьютер. Поэтому некоторые математики отнеслись к этому доказательству с недоверием, что объяснялось не только использованием компьютера, но и громоздкостью описания алгоритма первых доказательств (741 страница), впоследствии были предложены более компактные алгоритмы и скорректирован ряд ошибок. Проблема четырех красок является одним из известнейших прецедентов неклассического доказательства в современной математике.
Исторически планарные графы связаны с одной знаменитой задачей.
Задача о домиках и колодцах. В некоторой деревне есть три колодца. Трое жителей, живущие в трех стоящих рядом домиках перессорились, и решили так протоптать тропинки от своих домов к каждому из трех колодцев, чтобы они не пересекались. Удастся ли им выполнить свой план?
Трое жителей, живущие в трех стоящих рядом домиках перессорились, и решили так протоптать тропинки от своих домов к каждому из трех колодцев, чтобы они не пересекались. Удастся ли им выполнить свой план?
Решим эту задачу. Проведем тропинки так, как это показано на рисунке 8. Как видно, нам удалось провести только восемь тропинок, а девятая должна пересечься хотя бы с одной. Можно доказать (мы не будем приводить строгое доказательство), что эта задача не имеет решения. Дело в том, что по мере проведения тропинок из двух первых домиков, будет получаться некоторый замкнутый контур, внутри которого будет стоять один из колодцев, при этом третий домик будет находиться снаружи от этого контура. Для того чтобы соединить этот домик с колодцем, обязательно потребуется пересечь новой тропинкой одну из уже проложенных.
Задача о четырех красках. На политической карте мира нарисовано несколько государств. Карту нужно раскрасить так, что бы две страны, имеющие общую границу, были покрашены в разные цвета.
В классическом варианте предполагалось, что карту можно раскрасить четырьмя цветами. Покажем, как эта задача связана с графами. Обозначим каждую страну на карте точкой, вершины, отвечающие странам, имеющим общую границу, соединим ребрами. Теперь задачу о раскрашивании можно сформулировать так: раскрасить вершины планарного графа так, чтобы любые две смежные были покрашены в разные цвета. Эта задача может быть решена для графов с малым количеством вершин. Если же число вершин достаточно велико, то гипотеза четырех красок оказывается неверной. (Этот факт установлен с помощью мощных компьютеров.)
Вместе с тем, довольно простыми средствами была доказана теорема о пяти красках.
Теорема. Планарный граф можно раскрасить пятью красками так, что любые смежные вершины будут окрашены в разные цвета.
Еще одна интересная проблема: сколькими способами можно раскрасить граф, если имеется n красок.
Оказывается, что число способов раскрашивания является многочленом от n, коэффициенты этого многочлена можно вычислить с помощью специального алгоритма. зу науково! лггератури вiдмiчаeться, що теореми й алгоритми, як1 викорис-товуються в теорiях графiв i автомапв, можуть служити основою для уточнення та розвитку загальноприй-нятих теорш i методiв в механiцi стержневих систем.
зу науково! лггератури вiдмiчаeться, що теореми й алгоритми, як1 викорис-товуються в теорiях графiв i автомапв, можуть служити основою для уточнення та розвитку загальноприй-нятих теорш i методiв в механiцi стержневих систем.
На основе проведенного анализа научной литературы отмечается, что используемые в теориях графов и автоматов теоремы и алгоритмы могут служить основой для уточнения и развития общепринятых теорий и методов в механике стержневых систем.
On the basis of conducted analysis of scientific literature it is noted that the theorems and algorithms used in theories of graphs and automata can serve as a basis for the refinement and development of generally accepted theories and methods in the mechanics of beam systems.
Наряду с традиционными методами, позволяющими рассчитывать свободные и вынужденные колебания стержневых систем, все более широкое применение находят топологические методы, связанные с исследованиями структуры графов, представляющих такие системы [1 — 8]. Появилась возможность получить эффективное средство формализации современных инженерных задач, возникающих при изучении сложных механических систем, и разработки оптимальных вычислительных алгоритмов.
Появилась возможность получить эффективное средство формализации современных инженерных задач, возникающих при изучении сложных механических систем, и разработки оптимальных вычислительных алгоритмов.
В настоящее время имеется множество публикаций, посвященных приложениям теории графов в различных областях исследований. Их детальный обзор и тематическая классификация приведены в работе J. Montbrun-DiFilippo и M. Delgado [9]. Следует также назвать монографии М. Свами, К. Тхуласираман [10], В. П. Сигорского [11], Р. Басакер, Т. Саати [12], В. А. Горбатова [13], в которых излагаются как основы теории графов, так и примеры их практического применения, в частности, в задачах сетевого планирования и управления, построения систем связи и передачи информации, выбора оптимальных маршрутов и потоков в сетях, проектировании механических систем, построении электрических цепей и других. Отметим работы, в которых применялись связные графы для изучения динамики транспортных средств [14 — 16], моделирования механических систем [5, 17, 18], стержневых конструкций [8, 19 — 22], динамики твердого тела [7, 23 — 25] и др. Кроме того, графы широко используются в различных разделах математики, теории конечных автоматов и теории групп [26 — 28].
Кроме того, графы широко используются в различных разделах математики, теории конечных автоматов и теории групп [26 — 28].
В свою очередь, конечные автоматы, являясь составной частью теории систем, применяются в самых разнообразных областях науки и техники, таких как электротехника, механика, физиология, лингвистика, а также в задачах анализа и синтеза различных технических устройств, систем и процессов, разработке программ и алгоритмов [11, 29 — 31].
O. Shai, K. Preiss [17], подводя итоги различных исследований, на примере плоской фермы, возвратно-поступательного механизма и планетарной передачи показали, что дискретные математические представления теории графов, матроидов и линейного программирования содержат элементы и структуры, изоморфные многим техническим системам. В следующей работе [18] авторы переходят к логическому выводу, имеющему важное практическое применение. Представляя элементы различных технических систем в виде математического графа, несложно определить, насколько обоснована топология данного графа и, следовательно, топология данной технической системы. Проведение такого анализа до перехода к основному статическому расчету дает явные преимущества, сокращает время на проектирование и исключает вероятность ошибки. Кроме того, дальнейшие исследования N. Ta’aseh, O. Shai [8] открывают новые перспективы для использования известных теорем сопряженных структур в механике, которые могут быть выведены из принципа теоретической двойственности графов, представляющих реальные конструкции.
Проведение такого анализа до перехода к основному статическому расчету дает явные преимущества, сокращает время на проектирование и исключает вероятность ошибки. Кроме того, дальнейшие исследования N. Ta’aseh, O. Shai [8] открывают новые перспективы для использования известных теорем сопряженных структур в механике, которые могут быть выведены из принципа теоретической двойственности графов, представляющих реальные конструкции.
F. F. Tsai, J. E. Hang [14, 15] вводят понятие топологического анализа, под которым понимается исследование структуры графа, описы-
© Распопов А. С., 2010
вающего систему твердых тел. Разработанная методика позволяет приводить граф к структуре дерева и находить пути оптимизации вычислительных процедур для расчета кинематических и динамических характеристик механической системы. Для конкретных примеров многозвенного механизма и четырехколесного экипажа получены матрицы ориентации, скорости и ускорения точек тел.
Работа Е. Г. Кузовкова, А. А. Тырымова [32] посвящена изучению возможностей графового подхода к разработке статических расчетных схем повышенной точности, в частности, при построении дискретной модели упругой орто-тропной среды. Вначале среда рассекается на элементы (подграфы), имеющие известное математическое описание. Затем с помощью матриц, гарантирующих структуру графа-модели и уравнений, описывающих отдельные элементы, получают уравнения системы в целом.
Тырымова [32] посвящена изучению возможностей графового подхода к разработке статических расчетных схем повышенной точности, в частности, при построении дискретной модели упругой орто-тропной среды. Вначале среда рассекается на элементы (подграфы), имеющие известное математическое описание. Затем с помощью матриц, гарантирующих структуру графа-модели и уравнений, описывающих отдельные элементы, получают уравнения системы в целом.
Практически из той же идеи исходит метод Г. Крона [33], получивший название «диакоп-тика». Проводя аналогию между электрическими сетями и системами самой различной физической природы, автор с помощью топологических моделей, матричного и тензорного исчисления получает общее решение по уравнениям отдельных ее частей.
В работе В. А. Баженова, В. Ф. Оробей и др. [4] для рассчитываемой методом граничных элементов стержневой системы составляется ориентированный граф, который практически не отличается от принятой расчетной схемы и содержит номера узлов с указанием начала и конца каждого стержня. Для составления разрешающих уравнений используются топологические матрицы, связанные с переносом конечных параметров и сохраняющие свою структуру в задачах статики, динамики и устойчивости стержневых систем.
Для составления разрешающих уравнений используются топологические матрицы, связанные с переносом конечных параметров и сохраняющие свою структуру в задачах статики, динамики и устойчивости стержневых систем.
На основе применения теории графов K. Watanuki, H. Ohtaki и др. [16] предложили аналитический метод, позволяющий с помощью специальных средств компьютерной алгебры автоматизировать расчет динамических характеристик многомассовых механических систем. На примере моделей с двумя и тремя степенями свободы вычерчивается граф системы, составляются уравнения движения и рассчитываются параметры колебаний. Аналогичный подход использовали в своих работах J. J. McPhee, S. M. Redmond, P. Shi [7, 34, 35] для представления топологии системы твердых тел и составления уравнений движения с по-
мощью специальной компьютерной программы в символьной форме.
Ma Zheng-Dong, N. Kikuchi и др. [6] методы топологической оптимизации относят к одним из самых перспективных направлений оптимального проектирования конструкций, в частности, при отыскании показателей наилучшего распределения конструкционного материала. Предлагается также использовать способ топологической оптимизации в задачах расчета собственных значений однопролетных балок и плоских рам с различными граничными условиями. Развитие этот метод получил в работах
Предлагается также использовать способ топологической оптимизации в задачах расчета собственных значений однопролетных балок и плоских рам с различными граничными условиями. Развитие этот метод получил в работах
G. Guo, N. Morita, T. Torii [21], Y. Dong,
H. Huang [20], в которых используется генетический алгоритм для топологической оптимизации ферменной конструкции и определения оптимальных динамических характеристик плоского четырехзвенного механизма, а также в работе K. Shea, J. Cagan, S. J. Fenves [22], где рассматривается топологическая задача оптимального проектирования стержневых конструкций с целью наилучшей группировки структурных звеньев.
Одной из важнейших проблем, возникающих при расчете колебаний стержневых и балочных конструкций на ЭВМ, является формализация ее топологии и автоматизация формирования коэффициентов системы уравнений. И. П. Осолотков, Е. К. Резников [3] для формализации топологии таких конструкций предложили выделение типовых структурных элементов (звено, связь, включение) и присвоение им векторов признаков. Эффективная методика для идентификации изоморфных графов разработана Ch.-H. Hsu, K.-T. Lam [36], где также приведен простой алгоритм перемаркировки вершин графа и получения его топологического кода.
Эффективная методика для идентификации изоморфных графов разработана Ch.-H. Hsu, K.-T. Lam [36], где также приведен простой алгоритм перемаркировки вершин графа и получения его топологического кода.
G. Bojadziev, L. Lilov [24] представили уравнения движения системы твердых тел, которые можно разделить на две группы: первая описывает топологию, т.е. совокупность связей между подсистемами, а вторая — физические процессы, происходящие в этих подсистемах. В монографии А. И. Телегина [37] разработана методика формального составления уравнений механики систем твердых тел с помощью таблиц структурных, кинематических и массо-инерционных параметров. В результате использования теории графов K. P. Arczewski, F. A. Dul [23] получили матричное выражение для угловых скоростей отдельных твердых тел системы. Показано, что абсолютная скорость любого тела зависит от топологической струк-
туры системы, которую удобно представить в виде системного и размерного графов. Первый определяет взаимосвязь элементов системы, а второй — прослеживает возможные переходы к основанию от каждого тела.
T. F. Brown [25] для анализа относительно простых динамических систем использует методы прямого моделирования. Такой подход приводит к тому, что специалист создает модель в виде связного графа, который раскрывает сущность конструкции и содержание самой модели, тем самым предотвращает возможность совершения разного рода ошибок и ускоряет процесс благодаря получению набора легко решаемых алгебраических уравнений. Для расчета сложных систем автор предлагает методы непрямого моделирования, основанные на расчетах энергии с помощью уравнений Ла-гранжа и Гамильтона, которые также совместимы с основными связными графами. Как доказательство приведены многочисленные примеры в виде плоского двухзвенного механизма, системы с переменной регулируемой массой, гиросистемы и др.
Статьи D. Karnopp [5] и B. Maschke [38] развивают предшествовавшие работы, посвященные применению связных графов к исследованию энергетических потоков в физических системах. В частности, предлагается способ построения графа при нелинейных характеристиках конечных связей, который демонстрируется для механического дифференциала при помощи полей инерции и податливости конструкции с последующим аналитическим описанием движения системы уравнениями Лагранжа и Гамильтона.
Топологические аспекты механики стержневых систем, а также основные понятия теории графов использованы А. П. Филиным, О. Д. Тананайко и др. [19] в статических расчетах строительных конструкций с применением классических методов сил и перемещений. Графовая модель и функция Грина использовались в работе М. Абдульмаджида и В. А. Прядиева [39] при расчете колебаний упругой сетки из струн, сочлененных пружинами.
Приложение булевой алгебры, математической логики и некоторых понятий теории конечных автоматов к решению плоской задачи изгибных колебаний пластин и цепных стержневых систем можно найти в работах В. Л. Рвачева [40] и Г. Н. Эйхе [41]. В первом случае для описания сложных краевых условий в расчеты вводятся специальные R -функции, которые являются функциями обычных непре-
рывных аргументов и обладают рядом свойств функций алгебры Буля. Во втором — применяется метод прогонки в сочетании с ассоциированными матрицами, действия над которыми сведены к простым и наглядным операциям.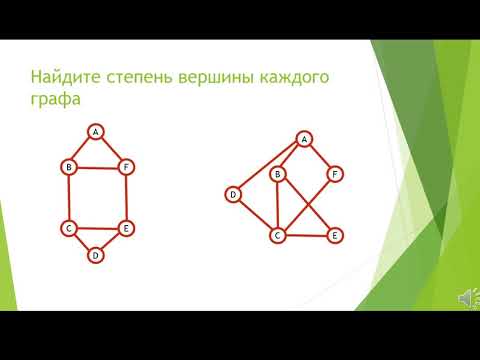
A. С. Галиуллин [42], анализируя основные задачи динамики механических систем, отметил, что они как по постановке, так и по методике их решения могут быть рассмотрены в виде прямой и обратной задач теории симметрии, предполагающей существование исходного и отображенного множеств. Особенно четкое представление составляющих симметрии наблюдается в системах динамической аналогии между процессами различного физического содержания.
Как известно [43, 44], формальное сходство дифференциальных уравнений, описывающих колебательное движение механических, электрических, акустических и других систем позволяет провести динамические аналогии между ними.
К примеру, уравнения Лагранжа второго рода для электрической системы (уравнения Ла-гранжа-Максвелла) по аналогии «сила-напряжение» выражают второй закон Кирхгофа, а по аналогии «сила-ток» — первый. Поэтому выводы, полученные при исследовании уравнений одной системы, могут быть распространены на другие динамически аналогичные системы.
B. Ю. Бобыльченко, П. М. Чеголин [45] использовали метод электромеханических аналогий для определения собственных изгибных колебаний балок с сосредоточенными регулярными массами. Электрическая схема замещения колеблющейся балки представлена в виде четырехполюсника, а динамические уравнения — в форме метода начальных параметров, содержащие в качестве неизвестных либо углы поворота и изгибающие моменты, либо линейные перемещения и перерезывающие силы. В статье С. В. Кудинова [46] показана возможность электрического моделирования связанных изгибно-крутильных и поперечно-продольных колебаний простой балки. Проведены аналогии между уравнениями в электромагнитных цепях и дифференциальными уравнениями, полученными для механических систем. В работе Г. Крона [33] упругая балка рассматривается как шестифазная линия передачи. При этом линейные и угловые смещения балки возникают под действием приложенных сил точно так же, как и электрические токи в трехфазной линии передачи под действием приложенных напряжений.
В свою очередь, анализ электрических цепей удобно проводить с помощью теории графов [10, 12]. В этом случае соотношения между токами и напряжениями на элементах цепи вытекают из законов Кирхгофа и отношения ортогональности между цикломатической матрицей и матрицей сечений соответствующего ориентированного графа. Излагаемые в работах Ю. Г. Минкина, К. Ю. Красносельского [1, 2] методы исследования колебаний некоторых механических систем обобщают результаты, полученные в теории электрических цепей. Стержень представляется в виде двухполюсника, соединенных дугой графа. Составление дифференциальных уравнений производится по методу интегральных координат. Однако следует отметить сложность формирования разрешающей системы уравнений даже для простых конструкций, а также большой порядок получаемых матриц, включающий до нескольких тысяч строк (столбцов).
Дальнейшее развитие этого направления предложено O. Shai [47] для решения задач проектирования с помощью дискретных математических моделей.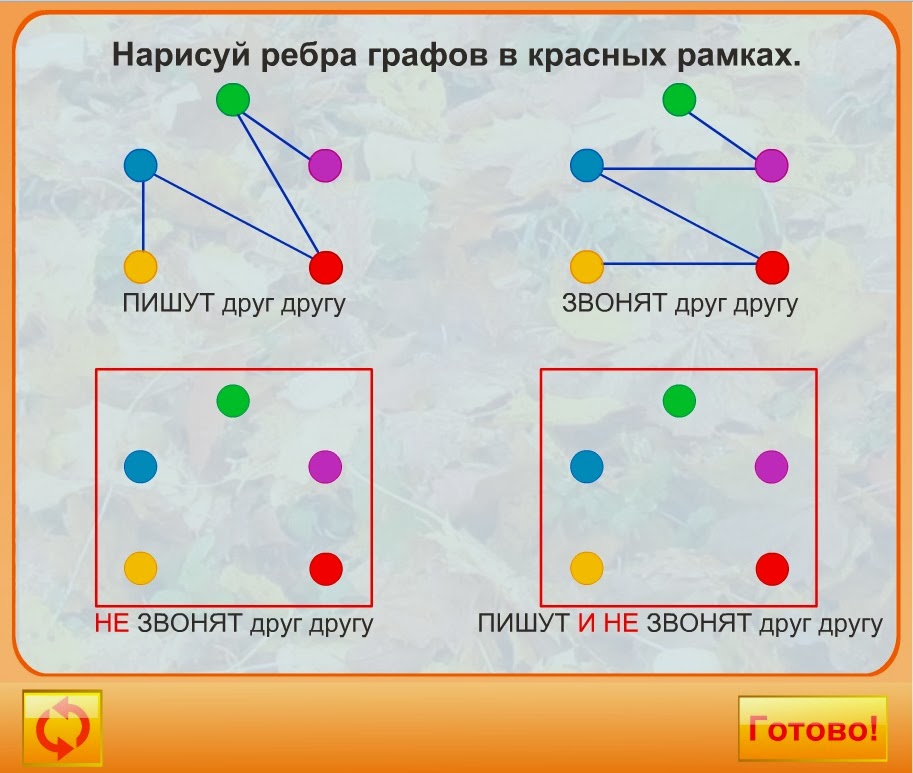 Когда различные технические системы представляются в виде одного и того же графа, существует возможность обмена информацией между ними через каналы связи. Это свойство автор использует для преобразования задач по проектированию из одной области в другую с последующим поиском решения в этой вторичной области. Как только решение найдено, оно трансформируется обратно в первоначальную задачу и возвращается в исходную область.
Когда различные технические системы представляются в виде одного и того же графа, существует возможность обмена информацией между ними через каналы связи. Это свойство автор использует для преобразования задач по проектированию из одной области в другую с последующим поиском решения в этой вторичной области. Как только решение найдено, оно трансформируется обратно в первоначальную задачу и возвращается в исходную область.
Как известно [33], разработанная математиками фундаментальная наука о структурах (комбинаторная топология) послужила мощным толчком в развитии теории электрических цепей. В связи с этим можно ожидать, что использование основных понятий комбинаторной топологии для анализа и расчета механических систем также будет служить развитию существующих и созданию новых более мощных методов их исследования.
Имеющийся опыт позволяет предположить, что интеграция топологических и автоматных методов наиболее перспективна по отношению к методам решения краевых задач на базе граничных интегральных уравнений [48].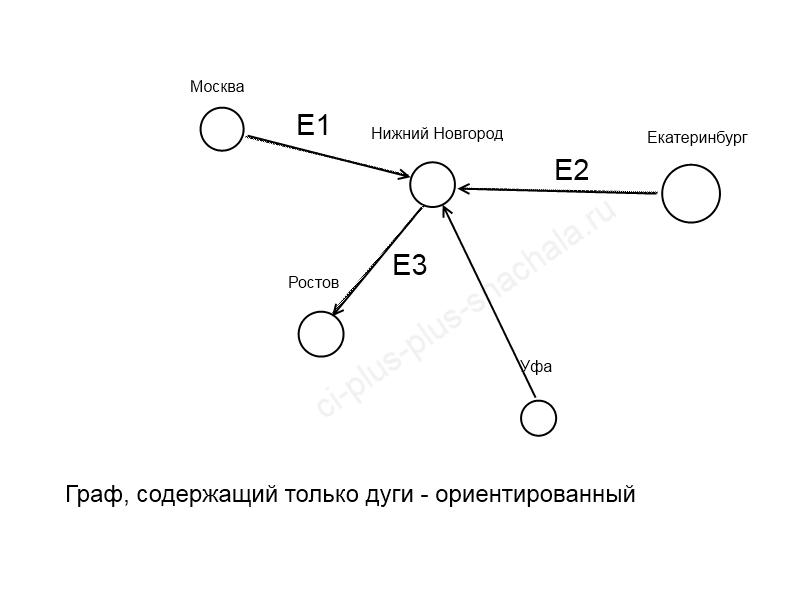 В числе работ, использующих модели стержневых систем с распределенными параметрами, все чаще применяется метод граничных элементов [4, 48 — 51], который превосходит многие методы по точности получаемых результатов, про-
В числе работ, использующих модели стержневых систем с распределенными параметрами, все чаще применяется метод граничных элементов [4, 48 — 51], который превосходит многие методы по точности получаемых результатов, про-
стоте алгоритма, экономичности использования ресурсов ЭВМ, времени подготовки данных и времени счета и т.д. Среди упомянутых обращают на себя внимание работы отечественных ученых В. А. Баженова, В. Ф. Оробея и др. [4, 51], в которых основные соотношения метода начальных параметров используются в задачах динамики стержневых систем на качественно более высоком уровне. Дальнейшее развитие МГЭ возможно за счет решения некоторых проблем, связанных с точным учетом сосредоточенных масс и сил инерции подвижных элементов, исключением из матриц нулевых ведущих элементов, раскрытием определителей высоких порядков, а также с детальной проработкой вопросов расчета совместных колебаний двух- и трехмерных стержневых систем, учетом различных факторов реальных конструкций и других.
По результатам краткого анализа научной литературы можно отметить, что многие стержневые конструкции могут быть представлены в виде графов и автоматов, однако лишь небольшое число публикаций посвящено использованию понятий комбинаторной топологии в решении инженерных задач, возникающих при изучении сложных механических систем. Тем не менее, ряд научных исследований показывает, что используемые в теориях графов и автоматов теоремы и алгоритмы могут служить основой для уточнения и развития общепринятых теорий и методов в механике стержневых систем.
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
1. Красносельский, К. Ю. Новый алгоритм исследования динамики сложных пространственных конструкций [Текст] / К. Ю. Красносельский, Ю. Г. Минкин // Пробл. прочн. матер. и сооруж. на трансп. — 1989. — С. 49-59.
2. Минкин, Ю. Г. Топологические методы исследования колебаний некоторых механических систем [Текст] / Ю. Г. Минкин // 3-й Всесоюзн. съезд по теор. и прикл. механике: Сб. аннотац. докл. (Москва — 1968). — Изд-во АН СССР, 1968. — С. 16-20.
— Изд-во АН СССР, 1968. — С. 16-20.
3. Осолотков, И. П. Матричный метод расчета динамических характеристик систем с упругими звеньями [Текст] / И. П. Осолотков, Е. К. Резников // Сб. науч. тр. Челяб. политехн. ин-та. -1981. — № 254. — С. 74-78.
4. Строительная механика. Применение метода граничных элементов: [спец. курс] [Текст] / под ред. В. А. Баженова. — Одесса: Астропринт, 2001. — 288 с.
5. Karnopp, D. An approach to derivative causality in bond graph models of mechanical systems [Text] /
D. Karnopp // J. of the Franklin Institute. — 1992. -vol. 329, № 1. — Р. 65-75.
6. Ma, Zh.-D. Topological optimization technique for free vibration problems [Text] / Zh.-D. Ma [et al.] // Trans. ASME J. Appl. Mech. — 1995. — vol. 62, № 1. — P. 200-207.
7. McPhee, J. J. On the use of linear graph-theory in multibody system dynamics [Text] / J. J. McPhee // Nonlinear Dynamics. — 1996. — vol. 9, № 1-2. -P. 73-90.
8. Ta’aseh, N. Graph theoretical duality perspective on conjugate structures and its applications [Text] / N. Ta’aseh, O. Shai // Eur. J. Mech. A. — 2005. -vol. 24, № 6. — P. 974-986.
Ta’aseh, O. Shai // Eur. J. Mech. A. — 2005. -vol. 24, № 6. — P. 974-986.
9. Montbrun-Di Filippo, J. A survey of bond graphs: theory, applications and programs [Text] / J. Mont-brun-Di Filippo, M. Delgado // J. of the Franklin Institute. — 1991. — vol. 328, № 5-6. — P. 565-606.
10. Свами, М. Графы, сети и алгоритмы [Текст] / М. Свами, К. Тхуласираман. — М.: Мир, 1984. -455 с.
11. Сигорский, В. П. Математический аппарат инженера [Текст] / В. П. Сигорский. — К.: Техника, 1975. — 768 с.
12. Басакер, Р. Конечные графы и сети [Текст] / Р. Басакер, Т. Саати. — М.: Наука, Гл. ред. физ.-мат. лит., 1973. — 368 с.
13. Горбатов, В. А. Фундаментальные основы дискретной математики. Информационная математика [Текст] / В. А. Горбатов. — М.: Наука, Физ-матлит, 2000. — 544 с.
14. Tsai, F.-F. Real-time multibody system dynamic simulation. P. I. A modified recursive formulation and topological analysis [Text] / F.-F. Tsai,
E. J. Huag // Mech. Struct. and Mach. — 1991.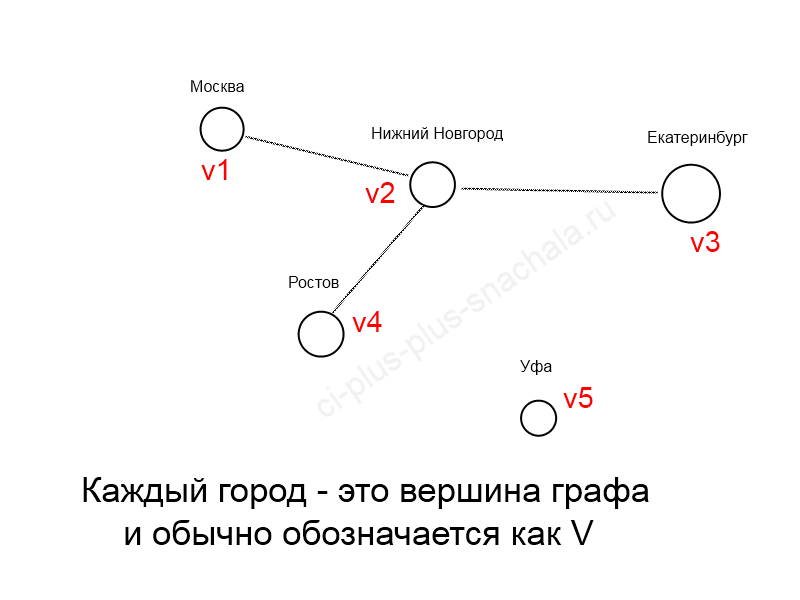 -vol. 19, № 1. — Р. 99-127.
-vol. 19, № 1. — Р. 99-127.
15. Tsai, F.-F. Real-time multibody system dynamic simulation. P. II. A parallel algorithm and numerical results [Text] / F.-F. Tsai, E. J. Huag // Mech. Struct. and Mach. — 1991. — vol. 19, № 2. -Р. 129-162.
16. Watanuki, K. Automation to mechanical vibration systems [Text] / K. Watanuki [et al.] // Nihon kikai gakkai ronbunshu. C. = Trans. Jap. Soc. Mech. Eng. C. — 1993. — vol. 59, № 562. — P. 1960-1965.
17. Shai, O. Graph theory representations of engineering systems and their embedded knowledge [Text] / O. Shai, K. Preiss // Artificial Intelligence in Engineering. — 1999. — № 13. — P. 273-285.
18. Shai, O. Isomorphic representations and Well-Formedness of engineering systems [Text] / O. Shai, K. Preiss // Engineering with computers. — 1999. -№ 15. — P. 303-314.
19. Алгоритмы построения разрешающих уравнений механики стержневых систем [Текст] / под ред. А. П. Филина. — Л.: Стройиздат, 1983. -232 с.
20. Dong, Y. The optimization of topology of the frame construction through the approximation of suspension points and the genetic algorithm [Text] / Y. Dong, H. Huang // Jisuan lixue xuebao = Chin.
Dong, H. Huang // Jisuan lixue xuebao = Chin.
J. Comput. Mech. — 2004. — vol. 21, № 6. -P. 746-751.
21. Guo, G. Optimum dynamic design of planar linkage using genetic algorithms [Text] / G. Guo, N. Mo-rita, T. Torii // JSME Int. J. C. — 2000. — vol. 43, № 2. — P. 372-377.
22. Shea, K. A shape annealing approach to optimal truss design with dynamic grouping of members [Text] / K. Shea, J. Cagan, S. J. Fenves // Trans. ASME. J. Mech. Des. [Trans. ASME. J. Mech., Transmiss., and Autom. Des.] — 1997. — vol. 119, № 3. — P. 388-394.
23. Arczewski, K. P. Determination of angular velocities within a multibody system by means of graphs [Text] / K. P. Arczewski, F. A. Dul // Z. angew. Math. Und Mech. — 1995. — vol. 75, Suppl. № 1. -P. 105-106.
24. Bojadziev, G. Dynamics of multicomponent systems based on the orthogonality principle [Text] / G. Bojadziev, L. Lilov // 1st Eur. Solid Mech. Conf. «EUROMECH» : Abstr. (München, 09-13 Sept. 1991). — 1991. — Sec. 1. — P. 33-34.
25. Brown, F. T. Hamiltonian and Lagrangian bond graphs [Text] / F. T. Brown // J. of the Franklin Institute. — 1991. — vol. 328, № 5-6. — P. 809-831.
26. Татт, У. Теория графов [Текст] / У. Татт. — М.: Мир, 1988. — 424 с.
27. Харари, Ф. Теория графов [Текст] / Ф. Харари. -М.: Едиториал УРСС, 2003. — 296 с.
28. Хопкрофт, Дж. Э. Введение в теорию автоматов, языков и вычислений [Текст] / Дж. Э. Хопкрофт., Р. Мотвани, Дж. Д. Ульман. — М.: Изд. дом «Вильямс», 2002. — 528 с.
29. Брауэр, В. В. Введение в теорию конечных автоматов [Текст] / В. В. Брауэр. — М.: Радио и связь, 1987. — 392 с.
30. Гилл, А. Введение в теорию конечных автоматов [Текст] / А. Гилл. — М.: Наука, 1966. — 272 с.
31. Кудрявцев, В. Б. Введение в теорию автоматов [Текст] / В. Б. Кудрявцев, С. В. Алешин, А. С. Подколзин. — М.: Наука, Гл. ред. физ.-мат. лит., 1985. — 320 с.
32. Кузовков, Е. Г. Графовая модель упругой ортотропной среды [Текст] / Е. Г. Кузовков, А. А. Тырымов // 2-я Межресп. конф. «Мех. и технол. изделий из мет. и металлокерам. компо-зиц. матер.» : Мат. конф. (Волгоград, 25.0901.10.1995 г.). — 1996. — С. 95-101.
конф. «Мех. и технол. изделий из мет. и металлокерам. компо-зиц. матер.» : Мат. конф. (Волгоград, 25.0901.10.1995 г.). — 1996. — С. 95-101.
33. Крон, Г. Исследование сложных систем по частям (диакоптика) [Текст] / Г. Крон. — М.: Наука, 1972. — 544 с.
34. McPhee, J. J. Modeling multibody systems with indirect coordinates [Text] / J. J. McPhee, S. M. Redmond // Computer methods in app. mech. and eng. — 2006. — vol. 195, № 50-51. -P. 6942-6957.
35. Shi, P. Dynamics of flexible multibody systems using virtual work and linear graph theory [Text] / P. Shi, J. J. McPhee // Multibody System Dynamics. — 2000. — vol. 4, № 4. — P. 355-381.
36. Hsu, Ch.-H. Topological Code of Graphs [Text] / Ch.-H. Hsu, K.-T. Lam // J. of the Franklin Institute. — 1992. — № 329. — P. 99-109.
37. Телегин, А. И. Системы твердых тел. Математическое обеспечение решения задач механики и управления [Текст] / А. И. Телегин. — Челябинск: ЧГТУ, 1995. — 202 с.
38. Maschke, B. Geometrical formulation of bond graph dynamics with application to mechanism [Text] / B. Maschke // J. of the Franklin Institute. -1991. — vol. 328, № 5-6. — P. 723-740.
Maschke // J. of the Franklin Institute. -1991. — vol. 328, № 5-6. — P. 723-740.
39. Абдульмаджид, М. О спектре разрывной задачи Дирихле на графе [Текст] / М. Абдульмаджид,
B. Л. Прядиев // Воронеж. ун-т. — 1992. — 10 с. -Деп. в ВИНИТИ 27.07.92, № 2473-В92.
40. Рвачев, В. Л. Геометрические приложения алгебры логики [Текст] / В. Л. Рвачев. — К.: Техника, 1967. — 212 с.
41. Эйхе, Г. Н. Особенности структуры уравнений частот и форм установившихся колебаний рамных мостов и других плоских ортогональных стержневых систем [Текст] / Г. Н. Эйхе // Вопросы статики и динамики мостов: Межвуз. сб. науч. тр. — 1987. — С. 83-94.
42. Галиуллин, А. С. Симметрия и основные задачи динамики [Текст] / А. С. Галиуллин // Вестник Рос. ун-та дружбы народов. — 1999. — № 1. —
C. 6-11.
43. Вибрации в технике : Справочник в 6 т. — Т. 1: Колебания линейных систем [Текст] / под ред. В. В. Болотина. — М.: Машиностроение, 1978. -352 с.
44. Яблонский, А. А. Курс теории колебаний [Текст] / А. А. Яблонский, С. С. Норейко. — М.: Высш. шк., 1975. — 248 с.
А. Яблонский, С. С. Норейко. — М.: Высш. шк., 1975. — 248 с.
45. Бобыльченко, В. Ю. Определение собственных колебаний балок с сосредоточенными регулярными массами методом электромеханических аналогий [Текст] / В. Ю. Бобыльченко,
П. М. Чеголин // Рост. гос. акад. стр-ва. -1996. — 12 с. — Деп. в ВИНИТИ 09.08.96, № 2652-В96.
46. Кудинов, С. В. Электрическое моделирование связанных колебаний стержневых конструкций [Текст] / С. В. Кудинов // III Междунар. науч.-практ. конф. «Моделирование. Теория, методы и средства»: Мат. конф. (Новочеркасск, 11 апр. 2003 г.) — ЮРГТУ, 2003. — Ч. 5. — С. 43-45.
47. Shai, O. Design through common graph representations [Text] / O. Shai // «Design Engineering Technical Conf.» and «Computers and Information in Engineering Conf.»: DETC’03 ASME 2003: Proc. (Chicago, Illinois, USA. Sept. 02-06, 2003). — 2003. — P. 1-10.
48. Бенерджи, П. Метод граничных элементов в прикладных науках [Текст] / П. Бенерджи, Р. Баттерфилд. — М.: Мир, 1984. — 494 с.
— 494 с.
49. Барановская, Л. В. Расчет балки непрямым методом граничных элементов [Текст] / Л. В. Барановская // Проблемы прочности и надежности строительных и машиностроительных конструкций: Межвуз. сб. науч. тр. — Саратов: Изд-во СГТУ, 2005. — С. 63-67.
50. Давидчак, О. Р. Динашчний розрахунок пере-хресно-ребристо! системи на основi дискретно-неперервно! моделi [Текст] / О. Р. Давидчак, Р. М. Тацш // Мехашка i фiзика руйнування будiвельних матерiалiв та конструкцш. -2007. — Вип. 7. — С. 17-22.
51. Оробей, В. Ф. Расчет неразрезной балки на устойчивость и динамику численными методами [Текст] / В. Ф. Оробей, Н. Г. Сурьянинов, Д. В. Лазарева // Тр. Одес. политехн. ун-та. -2005. — № 1. — С. 14-16.
Поступила в редколлегию 11.05.2010.
Принята к печати 20.05.2010.
Решение задач с помощью графов
Похожие презентации:
Теория графов. Его величество граф
Элементы теории графов
Элементы теории графов
Решение комбинаторных задач с помощью графов
Теория графов
Решение задач с помощью графов
Введение в теорию графов
Графы. Элементы графов. Виды графов и операции над ними
Элементы графов. Виды графов и операции над ними
Элементы теории графов
Дискретные структуы. Теория графов. Основные понятия
Презентация подготовлена
учителем математики МБОУ
«Лицей №35» Шепталенко Т.Н.
В последнее время интерес к комбинаторике в
школьном курсе математики заметно возрос. Элементы
комбинаторики, статистики и теории вероятностей
включены в новые стандарты по математике для
основной и профильной школ. Формирование
комбинаторных представлений и развитие
комбинаторного мышления школьников входит в число
основных целей обучения математике.
Однако обычно, когда говорят об элементах
комбинаторики, имеют в виду задачи алгебраического
содержания. Здесь мы рассмотрим комбинаторные
задачи, которые можно решать с помощью графов.
Пусть задано некоторое непустое множество V и множество E пар
различных элементов из V. Элементы множества V называются вершинами
графа, элементы множества E – ребрами графа. Множество вершин и
Множество вершин и
множество ребер называют графом.
Будем использовать геометрическое представление графа. Вершины
графа изображаются в виде точек на плоскости. Если две вершины образуют
ребро, то соответствующую пару точек соединяют линией.
Например, на рис.1 изображен граф G, заданный
множеством вершин V={1,2,3,4,5} и множеством ребер
E ={(1,2), (2,3), (4,3), (4,2)}
Число ребер, выходящих из вершины v, называют
степенью вершины v и обозначается d(v). Вершина
степени 0 называется изолированной, вершина
степени 1 – висячей.
0≤ d(v) ≤ n-1, где n- число вершин графа.
Рис.1
Задача 1. Сколько диагоналей имеет пятиугольник? n-угольник?
Решение.
Всего отрезков, соединяющих 2 вершины n-угольника равно
Из них n отрезков являются сторонами, остальные – диагонали.
Получим формулу для нахождения числа диагоналей:
Замечание:
Сумма степеней вершин графа равна удвоенному числу ребер.
Для пятиугольника :
Рис.2
Задача 2. В шахматном турнире по круговой системе
В шахматном турнире по круговой системе
участвуют 7 школьников.
Информация о сыгранных партиях представлена
в таблице. С кем сыграл Леша?
Решение.
Построим граф встреч игроков, в котором каждая
вершина соответствует участнику.
В
Л
Д С
И
Имя
Ваня
Толя
Леша
Дима
Семен
Илья
Женя
Количество
игр
6
5
3
3
2
2
1
Ж
Т
По графу видно, что Леша встречался с Ваней, Толей и Димой.
Кроме этого можно сказать, с кем встречались остальные школьники.
Задача 3. Соревнование проводится по круговой системе. Это
означает, что каждая пара игроков встречается между собой ровно
один раз. Докажите, что в любой момент времени найдутся хотя бы
два игрока, проведшие одинаковое количество встреч.
Решение.
Поставим в соответствие каждому игроку точку плоскости – вершину
графа. Если 2 игрока встретились между собой, то соединим
соответствующие вершины графа ребром.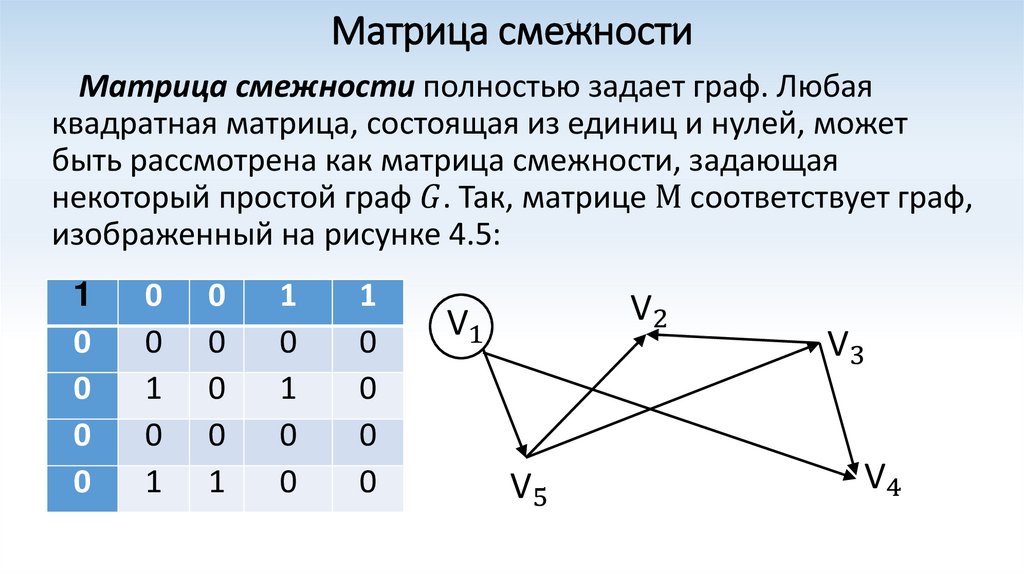 Получим граф встреч
Получим граф встреч
игроков. Надо доказать, что существуют 2 игрока, проведших
одинаковое количество встреч, т.е.
в графе обязательно найдутся 2 вершины,
степени которых одинаковы.
Рис.3
Доказательство (от противного). Допустим, что существует граф H, степени
всех вершин которого различны. В промежутке от 0 до n-1 существует ровно n
целых чисел: 0,1, 2,…, n-1. Степени n вершин графа тоже расположены в этом
промежутке. Поэтому должны существовать такие вершины v1, v2, …, vn , что
d(v1)=0, d(v2)=1, …, d(vn)=n-1. Т.к. d(v1)=0 , то вершина v1 не соединена ребром
ни с какой другой вершиной. d(vn)=n-1, следовательно, вершина vn соединена
со всеми остальными вершинами, в том числе и с v1 . Пришли к противоречию.
Существование графа H, степени всех вершин которого различны,
невозможно.
Вывод: Хотя бы два игрока проведут одинаковое количество встреч.
Задача 4. Андрей пошел с отцом в тир. Уговор был такой: Андрей
делает 5 выстрелов и за каждое попадание получает еще по 2
выстрела. Андрей выстрелил 25 раз. Сколько раз он попал?
Андрей выстрелил 25 раз. Сколько раз он попал?
Решение.
Стрельбу Андрея можно описать деревом, которое называется корневым
деревом.
В этом дереве все вершины, кроме верхней, соответствуют выстрелам. Если
Андрей попал, то степень соответствующей вершины равна 3, если
промахнулся -1. Степень верхней вершины равна 5. Дерево имеет 26
вершин и 25 ребер.
Пусть n — число попаданий. Тогда граф содержит n вершин степени 3, (25-n)
вершин степени 1 и одну вершину степени 5.
Т.к. сумма степеней вершин графа равна
удвоенному числу ребер, получим :
3·n+1·(25-n)+5=2·25
n=10
Ответ: Андрей попал 10 раз.
Следует отметить, что применение графов для решения
задач не всегда целесообразно. Например, большое
количество ребер графа может запутать учеников.
Однако, с помощью графов можно
наглядно
моделировать
задачу,
что несомненно важно для развития комбинаторного
мышления учащихся.
English Русский Правила
| Муниципальное общеобразовательное учреждение средняя общеобразовательная школа № 37 Практический проект по теме «Графы» Выполнила: Брель Юлия Вениаминовна обучающаяся 6 А класса МОУСОШ № 37 Руководитель: Баталова Е. Учитель математики МОУСОШ № 37 ТОМСК — 2008 Содержание
Введении. Теория графов является частью как топологии, так и комбинаторики. То, что это топологическая теория, следует из независимости свойств графа. А удобство формулировок комбинаторных задач в терминах графов привела к тому, что теория графов стала одним из мощнейших аппаратов комбинаторики. Теория графов позволяет решать наиболее легким способом, наглядно многие логические задачи, которые способствуют развитию мышления и интеллекта. Поэтому тема выбранная мною актуальна и интересна. Целью работы является: Изучить понятие граф и его элементы, продемонстрировать решение задач с помощью графов. На основании поставленной цели, сформулируем задачи:
исследования, рассмотреть основные понятия. 2. Подобрать и решить задачи с использованием понятия графа. 3. Доказать и показать обучающимся 6 А класса, что используя понятие граф можно упростить и рационально решать многие логические задачи. Графы — это замечательные математические объекты, с помощью, которых можно решать математические, экономические и логические задачи. Также можно решать различные головоломки и упрощать условия задач по физике, химии, электронике, автоматике. Графы используют при составлении карт и генеалогических древ. В математике даже есть специальный раздел, который так и называется: «Теория графов». Слово «граф» в математике означает картинку, где нарисовано несколько точек, некоторые из которых соединены линиями. С дворянским титулом «граф» их связывает общее происхождение от латинского слова «графио» — пишу. В математике графом называется конечное множество точек, некоторые из которых соединены линиями. Примерами графов могут служить схемы авиалиний, дорог, электросхемы, чертежи многоугольников. Одними из самых распространённых графов являются схемы линий метрополитена. Используют графы и при построении генеалогических деревьев (рис.1). На рисунке приведена часть генеалогического дерева знаменитого дворянского рода. Его вершины – члены этого рода, а связывающие их отрезки – отношения родственности, ведущие от родителей к детям. Схема графа, состоящая из «изолированных» вершин, называется нулевым графом. (рис.2) Графы, в которых не построены все возможные ребра, называются неполными графами. (рис.3) Графы, в которых построены все возможные ребра, называются полными графами. (рис.4) рис. 1 Граф, который можно нарисовать, не отрывая карандаша от бумаги, называется эйлеровым. Такими графы названы в честь учёного Леонарда Эйлера. Граф называется связным, если любые две его вершины могут быть соединены путем, т. е. последовательностью ребер, каждое следующее из которых начинается в конце предыдущего. Граф называется несвязным, если это условие не выполняется. Висячей вершиной называется вершина, из которой выходит ровно одно ребро. Граф, на рёбрах которого расставлены стрелки, называется ориентированным или направленным. Использует графы и дворянство. На рисунке 2 приведена часть генеалогического дерева знаменитого дворянского рода. Здесь его вершины – члены этого рода, а связывающие их отрезки – отношения родственности, ведущие от родителей к детям. Слово «дерево» в теории графов означает граф, в котором нет циклов, то есть в котором нельзя из некоторой вершины пройти по нескольким различным ребрам и вернуться в ту же вершину. Не трудно понять, что граф – дерево всегда можно изобразить так, чтобы его ребра не пересекались. Тем же свойством обладают графы, образованные вершинами и ребрами выпуклых многогранников. На рисунке 3 приведены графы, соответствующие пяти правильным многогранникам. В графе соответствующем тетраэдру, все четыре вершины попарно соединены ребрами.
Они жили в трех домиках, неподалеку от них находились три колодца: один с водой, другой с маслом, а третий с повидлом, и ходили к ним по тропинкам, изображенным на рисунке 5. Однажды эти люди перессорились и решили провести тропинки от своих домов к колодцам так, чтобы эти тропинки не пересекались. Графы, изображенные на рисунках 4 и 5, как оказалось, играют решающую роль при определение для каждого графа – является ли он плоским, то есть может ли он быть изображен на плоскости без пересечения его ребер. Польский математик Г. Куратовский и академик Л. С. Понтрягин независимо доказали, что если граф не является плоским, то в нем «сидит» хотя бы один из графов, изображенных на рисунках 4 и 5, то есть «полный пятивершинник» или граф «домики – колодцы». Графами являются блок – схемы программ для ЭВМ, сетевые графики строительства, где вершины – события, означающие окончания работ на некотором участке, а ребра, связывающие эти вершины, — работы, которые возможно начать по совершении одного события и необходимо выполнить для совершения следующего. Если на ребрах графа нанесены стрелочки, указывающие направление ребер, то такой граф называют направленным. Свойство графов не зависят от того, соединены вершины отрезками или кривыми линиями, что дает возможность изучения их свойств с помощью одной из молодых наук – топологии. Впервые основы теории графов появились в работе Л. Эйлера, где он описывал решение головоломок и математических развлекательных задач. Широкое развитие теория графов получила с 50-х гг. 20 в. в связи со становлением кибернетики и развитием вычислительной техники. Решение задач с применением понятия граф. В терминах графов легко формулируется и решается задача о назначении на должности. А именно: если имеется несколько вакантных должностей и группа лиц, желающих их занять, причем каждый из претендентов имеет квалификацию для нескольких должностей, то при каких условиях каждый из претендентов сможет получить работу по одной из своих специальностей? Свойства графов не зависят от того, соединены вершины отрезками или кривыми линиями. Это дает возможность изучения их свойств с помощью одной из молодых наук – топологии, хотя сами задачи теории графов являются типичными задачами комбинаторики. Вот несколько задач теории графов. Задача об эйлеровом пути: найти путь по ребрам графа, проходящий по каждому ребру ровно один раз. Хроматическим числом графа называется наименьшее количество красок, с помощью которых можно так раскрасить вершины графа, что любые две вершины, соединенные ребром, окрашиваются при этом в разные цвета. Долгое время математики не могли решить эту проблему: достаточно ли четырех красок, для того чтобы раскрасить произвольную графическую карту так, чтобы любые две стороны, имеющие общую границу, были окрашены разными красками? Если изобразить страны точками – вершинами графа, соединив ребрами те вершины, для которых соответствующие им страны граничат , то задача сведется к следующей: верно ли, что хроматическое число любого графа, расположенного на плоскости, не больше четырех? Положительный ответ на этот вопрос был лишь недавно получен с помощью ЭВМ. Используя графы можно решать задачи. Вот, например, как выглядит последняя американская версия известной задачи Дьюдени: 1. Смит, Джонс и Робинсон работают в одной поездной бригаде машинистом, кондуктором и кочегаром. Профессии их названы не обязательно в том же порядке, что и фамилии. В поезде, который обслуживает бригада, едут трое пассажиров с теми же фамилиями. В дальнейшем каждого пассажира мы будем почтительно называть «мистер» (м-р) 2. М-р Робинсон живет в Лос-Анджелесе. 3. Кондуктор живет в Омахе. 4. М-р Джонс давно позабыл всю алгебру, которой его учили в колледже. 5. Пассажир – однофамилец кондуктора живет в Чикаго. 6. Кондуктор и один из пассажиров, известный специалист по математической физике, хотя в одну церковь. 7. Смит всегда выигрывает у кочегара, когда им случается встречаться за партией в бильярд. Как фамилия машиниста? Здесь 1-5 – номера ходов, в скобках – номера пунктов задачи, на основании которых сделаны ходы (выводы). Далее следует из п.7, что кочегар не Смит, следовательно, Смит-машинист. Графы часто используют для решения логических проблем, связанных с перебором вариантов. Для примера рассмотрим такую задачу. В ведре 8 л воды, и имеется две кастрюли емкостью 5 и 3 л. требуется отлить в пятилитровую кастрюлю 4 л воды и оставить в ведре 4 л, т. е. разлить воду поровну в ведро и большую кастрюлю. Ситуацию в каждый момент можно описать тремя числами, где А-количество литров воды в ведре, Б- в большой кастрюле, В — в меньшей. В начальный момент ситуация описывалась тройкой чисел ( 8, 0, 0), от нее мы можем перейти в одну из двух ситуаций: ( 3, 5, 0),если наполним водой большую кастрюлю, или ( 5, 0, 3), если наполним меньшую кастрюлю. В результате получаем два решения: одно в 7 ходов, другое в 8 ходов. Подобным образом можно ставить граф любой позиционной игры: шахмат, шашек, «крестиков – ноликов», где позиции станут вершинами, а направленные отрезки между ними будут означать, что одним ходом можно перейти от одной позиции к другой, по направлению стрелки. Однако для шахмат и шашек такой граф будит очень большим, поскольку различные позиции в этих играх исчисляются миллионами. А вот для игры «крестики – нолики» на доске 3 * 3 соответствующий граф нарисовать не так уж трудно, хотя и он будет содержать несколько десятков (но не миллионов) вершин. Рассмотрим еще некоторые задачи: Между планетами введено космическое сообщение по следующим маршрутам: З-К, П-В, З-П, П-К, К-В, У-М, М-С, С-Ю, Ю-М, М-У. Можно ли добраться с З до М? Решение: Составим схему-граф маршрутов: Мы видим, что от З до М добраться нельзя. Вашему вниманию предложена еще одна задача Мальчики 10 б класса Андрей, Витя, Сережа, Валера, Дима при встрече обменялись рукопожатиями (каждый пожал руку каждому по одному разу). Сколько всего рукопожатий было сделано? Решение: Пусть каждому из пяти молодых людей соответствует определенная точка на плоскости, названная первой буквой его имени, а производимому рукопожатию — отрезок или часть кривой, соединяющая конкретные точки — имена. Если подсчитать число ребер графа, изображенного на рисунке справа, то это число и будет равно количеству совершенных рукопожатий между пятью молодыми людьми. Их 10. В спортивном зале собрались Витя, Коля, Петя, Сережа и Максим. Каждый из мальчиков знаком только с двумя другими. Кто с кем знаком. Решение: Построим граф
Список литературы
Каталог: proekt жүктеу/скачать 1. Достарыңызбен бөлісу: |
Факультативный курс по математике «Графы» для 5-6 классов
Муниципальное бюджетное общеобразовательное учреждение
Средняя общеобразовательная школа №2
города Азова Ростовской области
Факультативный курс по математике
«Графы» для 5-6 классов
подготовила
учитель математики
Данькова Валентина Николаевна
г. Азов
Тема графов очень интересна при изучении, что позволяет привлечь школьников к активной познавательной деятельности. Графы, как никакая другая модель, позволяет изучать свойства отношений в «чистом виде», а графическое представление решения логических задач делает этот процесс более наглядным. С помощью графов решать задачи очень удобно, интересно, увлекательно, можно рассмотреть несколько вариантов решения одной и той же задачи и выбрать наиболее легкое, удобное, красивое, интересное решение задачи.
Начальные сведения о графах как геометрических схемах, состоящих из точек (вершин) и соединяющих их линий (ребер), достаточно просты, а работа с ними вызывает у детей большой интерес.
В школьном курсе математики теория графов не рассматривается, но в учебниках начальных классов и основной школы, можно встретить задачи, которые намного проще решить с помощью графов, нежели другими способами. Олимпиадные задачи и некоторые задачи ЕГЭ тоже наполнены заданиями, которые легче решить, применяя графический способ. Но что мешает учителю включить в факультативный курс теорию графов и показать, как с ее помощью можно быстро решать «сложные» задачи. Тем более, что некоторый теоретический материал доступен для понимания детей уже даже начальной школы.
Задачи по теории графов можно предлагать не только детям, посещающим факультативы, но и на некоторых уроках математики для развития логического мышления. Но вводить такие задачи нужно постепенно, начиная с элементарных заданий, даже почти с устных, и постепенно повышать уровень их сложности.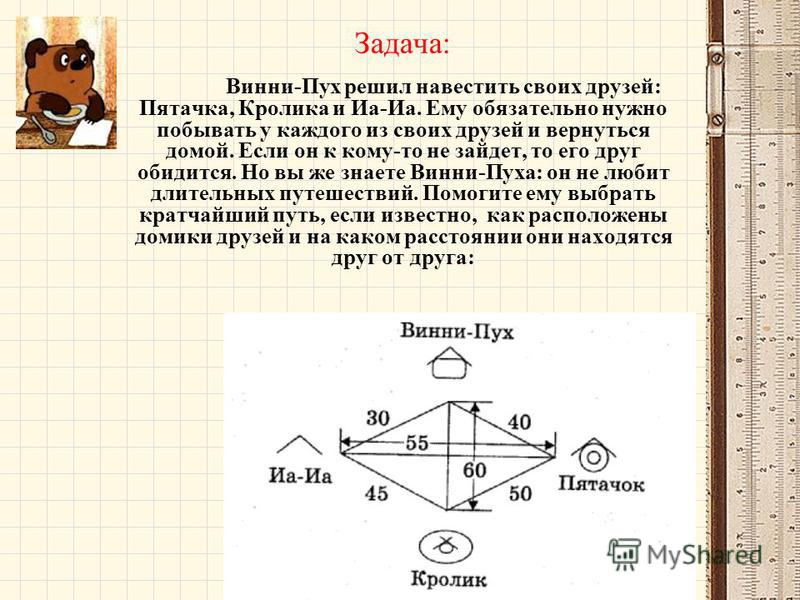 Конечно, для неподготовленных детей, такие задачи сначала вызовут затруднения в решении, и поиск решения может занимать достаточно долгое время. Поэтому на первых этапах задачи по графам лучше всего задавать, как дополнительное домашнее задание, но не обязательное для всех учащихся. При первом «домашнем» знакомстве с такими упражнениями учителю не обязательно сообщать детям, что при их решении применяется теория графов. Новый неизвестный термин может психологически оттолкнуть детей от поиска решения: «я не решу, ведь мы этого не проходили», хотя и решение может быть совсем легким, элементарным. Лишь только когда дети почувствуют силу при решении задач, можно сказать детям, что эти задания выделяют в особый раздел математики – топологию, теорию графов. Особенно важно, на этом этапе, похвалить тех детей, которые решали или пытались решать задачи, и сказать всему классу, что в их силах решать даже некоторые задачи по неизвестной теме. В дальнейшем можно раз в неделю уделять по 5 минут в конце уроке для дальнейшего изучения теории графов.
Конечно, для неподготовленных детей, такие задачи сначала вызовут затруднения в решении, и поиск решения может занимать достаточно долгое время. Поэтому на первых этапах задачи по графам лучше всего задавать, как дополнительное домашнее задание, но не обязательное для всех учащихся. При первом «домашнем» знакомстве с такими упражнениями учителю не обязательно сообщать детям, что при их решении применяется теория графов. Новый неизвестный термин может психологически оттолкнуть детей от поиска решения: «я не решу, ведь мы этого не проходили», хотя и решение может быть совсем легким, элементарным. Лишь только когда дети почувствуют силу при решении задач, можно сказать детям, что эти задания выделяют в особый раздел математики – топологию, теорию графов. Особенно важно, на этом этапе, похвалить тех детей, которые решали или пытались решать задачи, и сказать всему классу, что в их силах решать даже некоторые задачи по неизвестной теме. В дальнейшем можно раз в неделю уделять по 5 минут в конце уроке для дальнейшего изучения теории графов. Но более детальное рассмотрение темы, всё же, надо вынести на факультативный курс.
Но более детальное рассмотрение темы, всё же, надо вынести на факультативный курс.
Для школьника не обязательно давать строгое определение графа, как математического объекта. Им вполне достаточно будет сформулировать несколько определений и теорем и показать, как они работают при решении задач.
Итак, сформулируем основные определения и теоремы на которых можно построить факультативный курс по графам.
Граф – это набор точек, некоторые из которых соединены линиями.
Особо важно обратить внимание детей в определении на том, что могут соединяться не все точки друг с другом и соединяются не обязательно отрезками, а произвольными линиями-дугами. Далее целесообразно подкрепить новое определение примерами – наглядными рисунками.
рис.1 рис.2 рис.3 рис.4 рис.5
На вышеприведенных примерах очень удобно ввести следующие понятия: вершины (точки) и ребра (линии, соединяющие вершины) графа и закрепить эти понятия на примерах. Четкого, строгого обозначения вершин не существует, обозначают из контекста задачи: или буквами (русскими, латинскими) или цифрами. Причем нужно особо подчеркнуть, что бывают графы, состоящие только из одних вершин (рис.5), что две вершины могут быть соединены несколькими ребрами одновременно (рис.4) и что ребро может «выходить и заходить» в одну и ту же вершину (рис.3) – такое ребро называют петлей.
Причем нужно особо подчеркнуть, что бывают графы, состоящие только из одних вершин (рис.5), что две вершины могут быть соединены несколькими ребрами одновременно (рис.4) и что ребро может «выходить и заходить» в одну и ту же вершину (рис.3) – такое ребро называют петлей.
Можно рассказать детям, что графы используются не только в математике и привести примеры «нематематических графов». Так, например, люди часто пользуются графами, не догадываясь об этом, когда изображают различные объекты: населенные пункты, карты городов, схемы электроприборов, атомы. Схема метро это тоже граф: вершины конечные станции и станции пересадок, ребра – пути, соединяющие эти станции. Дворянство тоже применяло графы для создания генеалогического дерева. В них вершины – это члены рода, а связывающие их линии — отношения родственности, ведущие от родителей к детям. Ниже приведен фрагмент родословной А.С. Пушкина.
Графы бывают конечные (число его ребер конечно) и бесконечные (число его ребер бесконечно). В начальной школе и 5-6 классах задачи на бесконечные графы не предлагают, но для детей постарше можно привести пример такого графа. Например, когда каждой вершине графа соответствует натуральное число, т.е. вершины графа нумеруются числами 1, 2, 3… Но так как ряд натуральных чисел бесконечен, то и граф тоже бесконечный. Конечно, полностью изобразить бесконечный граф нельзя, но можно изобразить его частично.
В начальной школе и 5-6 классах задачи на бесконечные графы не предлагают, но для детей постарше можно привести пример такого графа. Например, когда каждой вершине графа соответствует натуральное число, т.е. вершины графа нумеруются числами 1, 2, 3… Но так как ряд натуральных чисел бесконечен, то и граф тоже бесконечный. Конечно, полностью изобразить бесконечный граф нельзя, но можно изобразить его частично.
рис.6
Степень вершины – число ребер выходящих из вершины графа. Если ребро является петлей, то его считают дважды. Закрепляем определение примерами (см. рис.1-5).
Иногда степень вершины записывают в виде таблицы, а иногда пишут рядом с самой вершиной. Важно подчеркнуть, что одно и тоже ребро считается дважды (один раз – для одной вершины, второй – для другой), так как оно соединяет две вершины.
Вершины бывают четные (степень вершины четна) и нечетные (степень вершины нечетна).
Первые задания, которые можно предлагать по теме графы, связаны как раз с этими понятиями: построить граф, определить по рисунку, сколько вершин, ребер у граф, какова степень вершины графа, посчитать сколько четных и нечетных вершин и тому подобные задания.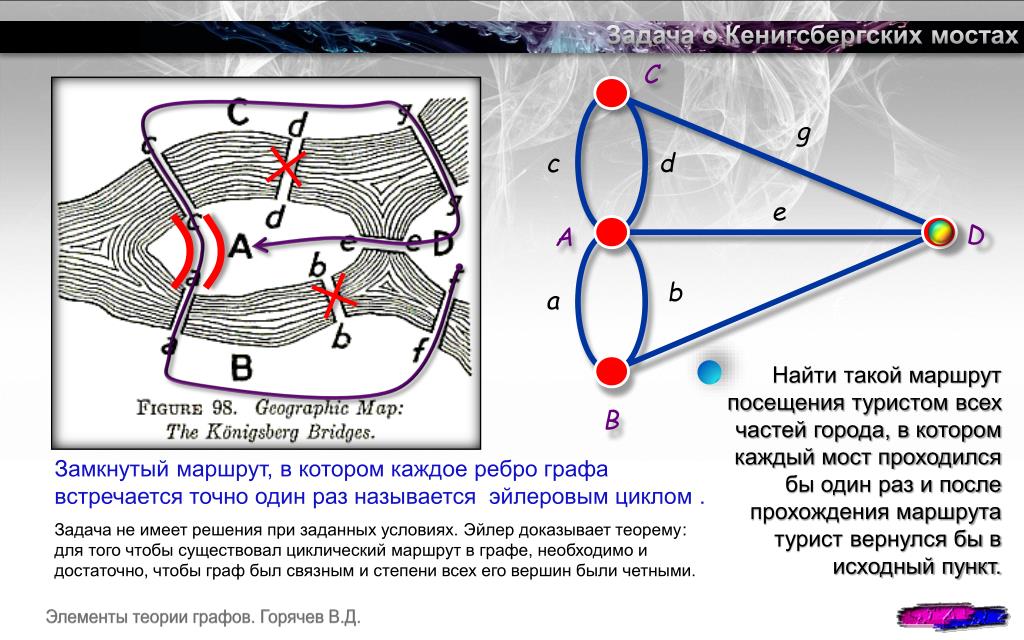 Такие задания можно предлагать и в начальной школе, так как они вполне доступны детям 3-4 классов.
Такие задания можно предлагать и в начальной школе, так как они вполне доступны детям 3-4 классов.
Задание: По рисунку определить: сколько вершин, ребер у графа и какова степень каждой вершины графа?
рис.7
Решение: Сначала посчитаем количество вершин. Для наглядности на первых порах их можно выделить другим цветом – 8 вершин (рис.8). Для подсчета ребер удобно посчитанное ребро выделять черточкой, чтобы не посчитать его дважды – 9 ребер (рис.9)
рис.8 рис.9 рис.10
Для определения степени вершины графа лучше все вершины обозначить буквами (рис.10), а потом результаты записать в таблицу.
Первое свойство, которое вводим детям без доказательства: «Число нечетных вершин графа – четно». И в дальнейшем, все свойства и теоремы даются без строгого доказательства. Закрепление данного свойства происходит так же на решении задач.
Задание: Построить граф у которого вершины имеют следующие степени:
а) А – 7, Б – 3, С – 1; б) А – 5, Б – 1, С – 4.
Решение: При решении задач на построение графов, надо объяснить детям, что сначала необходимо проверить, возможно ли вообще построение заданного графа. Для этого учащиеся должны применить первое свойство. Сколько бы дети не пытались построить граф а), у них ничего не получится. Построение графа а) невозможно, так как все его вершины нечетные, и число их нечетно. А вот граф б) построить можно, так как у него две нечетных вершины. Причем у детей могут получаться различные по конфигурации графы (рис.11-13). Именно на таких заданиях и закрепляется, что число нечетных вершин графа – четно.
Поучительная сторона этих задач состоит в исследовании, возможно или нет решение данной задачи, прежде чем приниматься за само решение.
Обратите внимание детей, что построение графа следует начинать с изображения всех его вершин, и лишь потом соединять их ребрами. Причем лучше всего начинать соединять ребрами вершины с наименьшей и наибольшей степенью.
рис.11 рис.12 рис. 13
13
Далее лучше всего дать задания такого плана: «без построения графа, определить число ребер графа».
Свойство 2: Для того чтобы найти количество ребер в графе, надо просуммировать степени вершин и результат разделить пополам.
Задание: Даны степени вершин графа: А – 2, Б – 5, С – 1, Д – 4. Без построения графа, определить число ребер графа.
Решение: Первое, что должны проверить дети: возможно ли построение такого графа. Чтобы проверить это, надо сосчитать число нечетных вершин – их должно быть четно. По условию задачи 2 нечетных вершины Б и С, значит построение возможно. Теперь можно ответить на вопрос задачи, используя второе свойство: (2+5+1+4):2=6.
После решения задачи можно предложить детям построить этот граф и проверить решение. Причем рисунки могут получиться совершенно разные, в зависимости от того, какие вершины будут соединены (рис.14-16). Самое главное, чтобы степени вершин соответствовали условию задачи. Эти задания не сложные и доступны учащимся 5 классов. рис.14 рис.15 рис.16 Связный граф – граф, у которого любые две его вершины можно соединить непрерывной последовательностью ребер. Другими словами: из любой вершины можно пройти в другую вершину по ребрам (рис.17-18). Несвязный граф – граф, который состоит из нескольких частей, каждая из которых или связный граф, или отдельные вершины (рис.19). рис.17 рис.18 рис.19 Предложенный выше теоретический материал по графам вполне доступен детям 5-6 классов. Рассмотрим ниже основные задачи, опираясь на которые можно построить факультативный курс по математике. Такие задачи, как правило, встречаются в математических олимпиадах или в разделе задач со звездочками.
Эти задания не сложные и доступны учащимся 5 классов. рис.14 рис.15 рис.16 Связный граф – граф, у которого любые две его вершины можно соединить непрерывной последовательностью ребер. Другими словами: из любой вершины можно пройти в другую вершину по ребрам (рис.17-18). Несвязный граф – граф, который состоит из нескольких частей, каждая из которых или связный граф, или отдельные вершины (рис.19). рис.17 рис.18 рис.19 Предложенный выше теоретический материал по графам вполне доступен детям 5-6 классов. Рассмотрим ниже основные задачи, опираясь на которые можно построить факультативный курс по математике. Такие задачи, как правило, встречаются в математических олимпиадах или в разделе задач со звездочками.
- Десять человек приветствовали друг друга рукопожатиями. Пять человек сделали по семь рукопожатий, трое – по пять, двое – по четыре. Сколько всего было сделано рукопожатий?
Решение: Вначале надо разобраться с детьми, правильно ли они понимают понятие рукопожатие на языке графов. Одно рукопожатие – это две вершины соединены одним ребром. То есть, два человека и у них одно рукопожатие на двоих. Данную задачу можно переформулировать на язык графов следующим образом: дано 10 вершин, известны степени каждой вершины и нужно узнать, сколько ребер в этом графе. Чтобы узнать количество ребер в графе надо сложить степени каждой вершины и разделить пополам – применить второе свойство . Так как пять человек сделали по семь рукопожатий, то это значит, что из пяти вершин выходят по семь ребер, а всего ребер: 5+5+5+5+5+5+5=5*7. Аналогично рассуждаем и с остальными вершинами, получаем: (5*7+3*5+2*4)/2=(35+15+8)/2=58/2=29
Одно рукопожатие – это две вершины соединены одним ребром. То есть, два человека и у них одно рукопожатие на двоих. Данную задачу можно переформулировать на язык графов следующим образом: дано 10 вершин, известны степени каждой вершины и нужно узнать, сколько ребер в этом графе. Чтобы узнать количество ребер в графе надо сложить степени каждой вершины и разделить пополам – применить второе свойство . Так как пять человек сделали по семь рукопожатий, то это значит, что из пяти вершин выходят по семь ребер, а всего ребер: 5+5+5+5+5+5+5=5*7. Аналогично рассуждаем и с остальными вершинами, получаем: (5*7+3*5+2*4)/2=(35+15+8)/2=58/2=29
- Можно ли организовать футбольный турнир девяти команд так, чтобы каждая команда провела по четыре встречи?
Решение: Переформулируем задачу на язык графов: можно ли построить такой граф, у которого 9 вершин и степень каждой вершины равна 4. По свойству два, найдем число ребер и если оно будет целым числом, то такой турнир можно организовать, в противном случае – нельзя. (9*4)/2=18. Да, можно и будет сыграно 18 игр.
(9*4)/2=18. Да, можно и будет сыграно 18 игр.
- Можно ли 15 телефонов соединить между собой так, чтобы каждый из них был связан ровно с 11 другими?
Решение: Переформулируем задачу на язык графов: можно ли построить такой граф, у которого 15 вершин и степень каждой вершины равна 11. Применим второе свойство: 15*11/2=82,5. Получили не натуральное число, значит нельзя соединить телефоны.
- В государстве 100 городов, из каждого выходит 4 дороги. Сколько всего дорог в государстве?
Решение: Одна дорога соединяет два города, т.е. две вершины соединены одним ребром. Применим второе свойство: 100*4/2=200.
- Может ли в государстве, в котором из каждого города выходит 3 дороги, быть ровно 100 дорог?
Решение: Решим задачу, составив уравнение: х*3/2=100, где х – число городов в государстве. Х*3=200, х=66,(6) – число не натуральное, значит в таком государстве не может быть ровно 100 дорог. После отработки выше изложенного материала на задачах можно приступать к дальнейшему изучению теоретического материала по теме графы. Цикл – замкнутый путь в графе. Графы бывают с циклом (рис.20 цикл выделен голубым цветом) и без цикла (рис.21). рис.20 рис.21 рис.22 Дерево – связный граф, не имеющий циклов (рис.22). Перед введением этого определения обязательно надо повторить понятие связный граф. Далее предлагаем задания следующего типа: Задание: Среди предложенных графов (рис.23-26) найти графы-деревья и графы с циклом. Укажите, сколько вершин входит в цикл? рис.23 рис.24 рис.25 рис.26 Решение: Графы-деревья изображены на рис.24 и рис.25; графы с циклом – рис.23 (цикл состоит из 3 вершин) и рис. 26 (цикл состоит из 4 вершин). Далее вводим еще одно важное свойство, которое очень часто применяется при решении логических задач. Свойство 3: Если граф связный и нечетных вершин у него 0 или 2, то его можно обойти, пройдя по каждому ребру только один. По-другому можно переформулировать это свойство так: Если граф связный и нечетных вершин у него 0 или 2, то его можно начертить, не отрывая карандаш от бумаги и не проходя по любому ребру дважды.
После отработки выше изложенного материала на задачах можно приступать к дальнейшему изучению теоретического материала по теме графы. Цикл – замкнутый путь в графе. Графы бывают с циклом (рис.20 цикл выделен голубым цветом) и без цикла (рис.21). рис.20 рис.21 рис.22 Дерево – связный граф, не имеющий циклов (рис.22). Перед введением этого определения обязательно надо повторить понятие связный граф. Далее предлагаем задания следующего типа: Задание: Среди предложенных графов (рис.23-26) найти графы-деревья и графы с циклом. Укажите, сколько вершин входит в цикл? рис.23 рис.24 рис.25 рис.26 Решение: Графы-деревья изображены на рис.24 и рис.25; графы с циклом – рис.23 (цикл состоит из 3 вершин) и рис. 26 (цикл состоит из 4 вершин). Далее вводим еще одно важное свойство, которое очень часто применяется при решении логических задач. Свойство 3: Если граф связный и нечетных вершин у него 0 или 2, то его можно обойти, пройдя по каждому ребру только один. По-другому можно переформулировать это свойство так: Если граф связный и нечетных вершин у него 0 или 2, то его можно начертить, не отрывая карандаш от бумаги и не проходя по любому ребру дважды.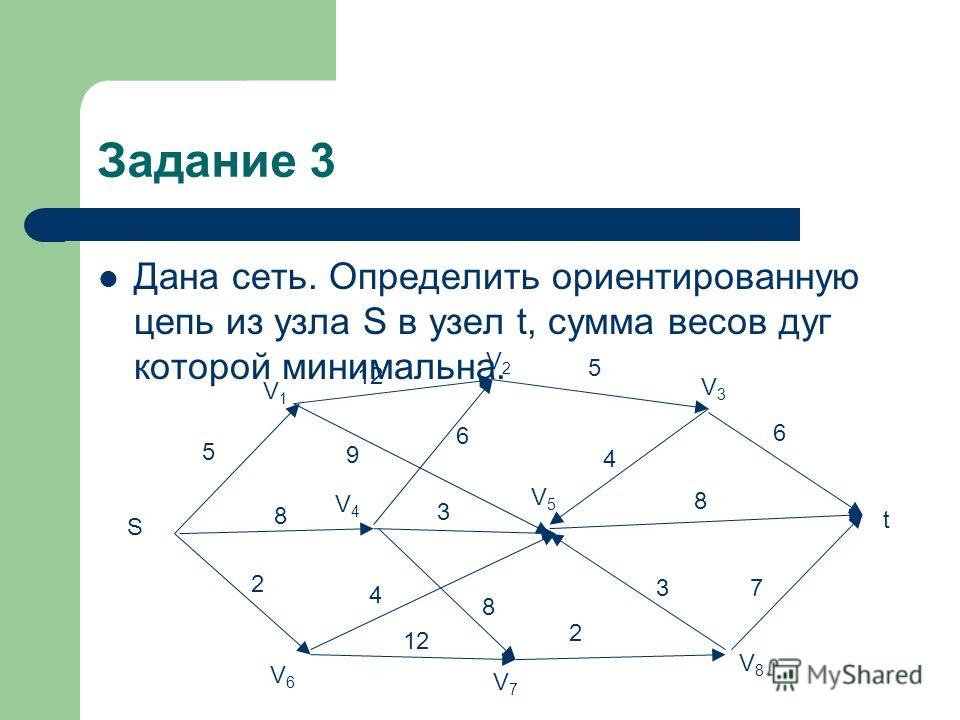 Если можно начертить граф, не отрывая карандаш от бумаги и не проходя по любому ребру дважды, то такой граф называют уникурсальным или Эйлеровым графом. Как правило, задания на это свойство вызывают у детей наибольший интерес. Задание: Из предложенных графов (рис.27- 33) найти те, которые можно изобразить одним росчерком (т.е. не отрывая карандаш от бумаги и не проходя по любому ребру дважды) и нарисовать их в тетради. рис.27 рис.28 рис.29 рис.30 рис.31 рис.32 рис.33 Решение: Для решения этого задания необходимо посчитать степени всех вершин, определить нечетные вершины и посчитать их количество. Если их 2 или 0, то граф построить можно в противном случае – нет. Перед тем, как изображать графы в тетради необходимо рассказать детям, что для более быстрого и правильного способа изображения графов надо знать: если граф имеет две нечетных вершины, то его изображение надо начинать из одной нечетной вершины, а заканчивать – в другой. Если же все вершины графа четные, то начало и конец графа совпадают.
Если можно начертить граф, не отрывая карандаш от бумаги и не проходя по любому ребру дважды, то такой граф называют уникурсальным или Эйлеровым графом. Как правило, задания на это свойство вызывают у детей наибольший интерес. Задание: Из предложенных графов (рис.27- 33) найти те, которые можно изобразить одним росчерком (т.е. не отрывая карандаш от бумаги и не проходя по любому ребру дважды) и нарисовать их в тетради. рис.27 рис.28 рис.29 рис.30 рис.31 рис.32 рис.33 Решение: Для решения этого задания необходимо посчитать степени всех вершин, определить нечетные вершины и посчитать их количество. Если их 2 или 0, то граф построить можно в противном случае – нет. Перед тем, как изображать графы в тетради необходимо рассказать детям, что для более быстрого и правильного способа изображения графов надо знать: если граф имеет две нечетных вершины, то его изображение надо начинать из одной нечетной вершины, а заканчивать – в другой. Если же все вершины графа четные, то начало и конец графа совпадают.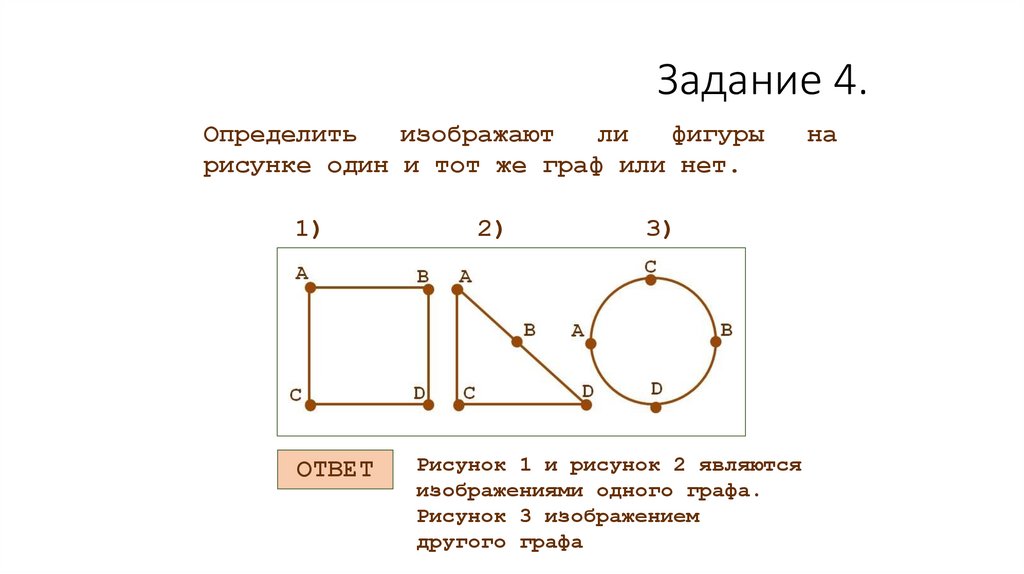 Графы, изображенные на рис.27, 28, 33 нельзя нарисовать, а остальные можно. В качестве домашнего задания можно предложить детям проанализировать печатные буквы русского алфавита и найти среди них те, которые можно написать одним росчерком, а какие нельзя и объяснить почему? Если применить немного фантазии и воображения, то одним росчерком можно изобразить много необычных рисунков (рис.34-36). рис.34 рис.35 рис.36 Для отработки понятия Эйлеров граф полезно дать задание следующего типа: Задание: Достроить графы до Эйлеровых (рис.37-39) рис. 37 рис. 38 рис.39 Решение: Чтобы решить это задание, надо сначало посчитать степень каждой вершины и дополнить ребрами граф так, чтобы стало две нечетных вершины или ни одной. На рис. 40-42 представлен один из вариантов решения. рис.40 рис.41 рис.42 Детям постарше, начиная с 7 класса, можно ввести понятия ориентированный, неориентированный графы и мультиграф. Если ребро соединяет вершину А с вершиной В и пара (А,В) считается упорядоченной, то это ребро называют ориентированным, вершину А – его началом, вершину В – его концом, а само ребро изображают в виде стрелки.
Графы, изображенные на рис.27, 28, 33 нельзя нарисовать, а остальные можно. В качестве домашнего задания можно предложить детям проанализировать печатные буквы русского алфавита и найти среди них те, которые можно написать одним росчерком, а какие нельзя и объяснить почему? Если применить немного фантазии и воображения, то одним росчерком можно изобразить много необычных рисунков (рис.34-36). рис.34 рис.35 рис.36 Для отработки понятия Эйлеров граф полезно дать задание следующего типа: Задание: Достроить графы до Эйлеровых (рис.37-39) рис. 37 рис. 38 рис.39 Решение: Чтобы решить это задание, надо сначало посчитать степень каждой вершины и дополнить ребрами граф так, чтобы стало две нечетных вершины или ни одной. На рис. 40-42 представлен один из вариантов решения. рис.40 рис.41 рис.42 Детям постарше, начиная с 7 класса, можно ввести понятия ориентированный, неориентированный графы и мультиграф. Если ребро соединяет вершину А с вершиной В и пара (А,В) считается упорядоченной, то это ребро называют ориентированным, вершину А – его началом, вершину В – его концом, а само ребро изображают в виде стрелки.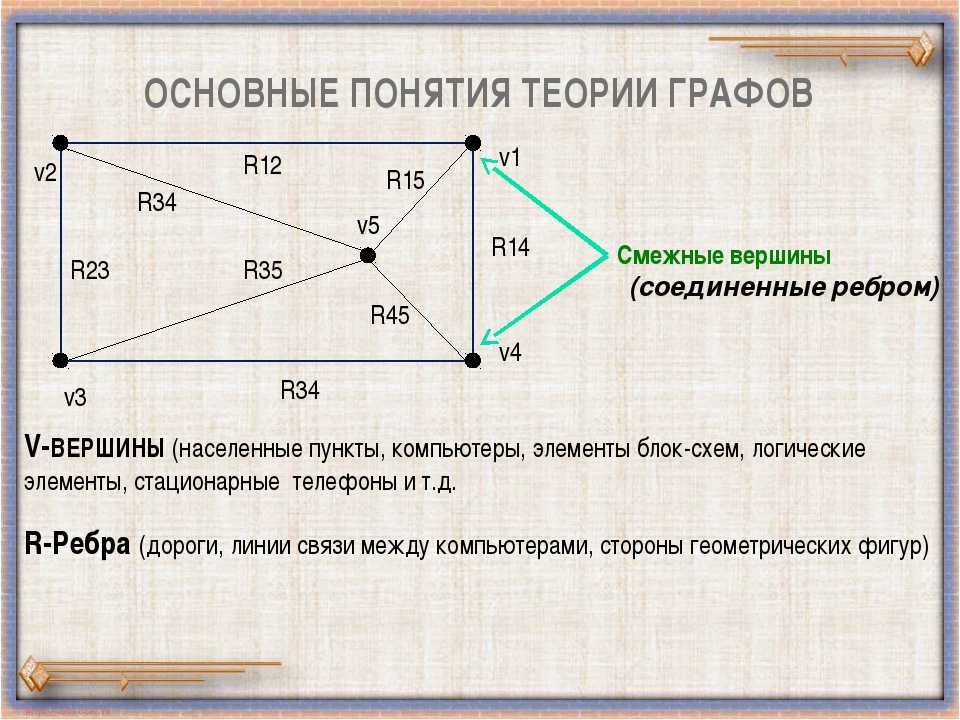 Если же эта пар считается неупорядоченной, то ребро называют неориентированным, а обе вершины – его концами. Граф с ориентированными ребрами называется ориентированный. Граф с неориентированными ребрами называется неориентированный. Например, только из города А в город В едет автобус №1, а из города Д в город С и обратно едет автобус №2. Изображением маршрута автобуса №1 будет ориентированный граф, вершина А будет его началом, а вершина В будет его концом (рис. 43). Изображением маршрута автобуса №2 будет неориентированный граф, и вершины С и Д будут называться его концами (рис.44). рис.43 рис.44 Кратные ребра – это разные ребра, но имеющие одинаковые начала и концы. Граф с кратными ребрами называют мультиграфом (рис.45). рис.45 В 5-6 классах, как правило, решаются задачи, в которых используются обыкновенные графы, то есть неориентированные графы без петель и без кратных ребер.
Если же эта пар считается неупорядоченной, то ребро называют неориентированным, а обе вершины – его концами. Граф с ориентированными ребрами называется ориентированный. Граф с неориентированными ребрами называется неориентированный. Например, только из города А в город В едет автобус №1, а из города Д в город С и обратно едет автобус №2. Изображением маршрута автобуса №1 будет ориентированный граф, вершина А будет его началом, а вершина В будет его концом (рис. 43). Изображением маршрута автобуса №2 будет неориентированный граф, и вершины С и Д будут называться его концами (рис.44). рис.43 рис.44 Кратные ребра – это разные ребра, но имеющие одинаковые начала и концы. Граф с кратными ребрами называют мультиграфом (рис.45). рис.45 В 5-6 классах, как правило, решаются задачи, в которых используются обыкновенные графы, то есть неориентированные графы без петель и без кратных ребер.
- Встретились три друга – Белов, Серов и Чернов. Чернов сказал другу, одетому в серый костюм: «На одном из нас белый костюм, на другом – серый и на третьем – черный, но на каждом костюм цвета, не соответствующего фамилии».
 Какой цвет костюма у каждого?
Какой цвет костюма у каждого?
Решение: Начнем решать задачу с построения графа. Первые три вершины будут обозначать фамилии трех друзей. Вторые три вершины – цвета их костюмов. Причем, для большей наглядности, вторая тройка вершин должна находиться справа от первой тройки. Наша задача построить три ребра, то есть соединить фамилию с цветом костюма. Так как цвет костюма не соответствует фамилии, то пунктиром покажем, куда нельзя проводить ребра. Далее анализируем условие задачи: «Чернов сказал другу, одетому в серый костюм», значит на Чернове не серый костюм. Покажем это условие так же пунктиром. Остается, что на Чернове белый костюм, покажем это условие ребром. Так как белый костюм уже занят, то остается Серову – черный, а Белову – серый, покажем это тоже ребрами. Итак, мы решили задачу с построением несвязного графа (рис.46), который содержит 6 вершин и 3 ребра. рис.46
- В одном классе учатся Иван, Петр и Сергей. Их фамилии Иванов, Петров и Сергеев.
 Установи фамилию каждого из ребят, если известно, что Иван не Иванов, Петр не Петров и Сергей не Сергеев и что Сергей живет в одном доме Петровым.
Установи фамилию каждого из ребят, если известно, что Иван не Иванов, Петр не Петров и Сергей не Сергеев и что Сергей живет в одном доме Петровым.
Решение: Задача решается аналогично предыдущей задачи с построением несвязного графа (рис.47), который содержит 6 вершин и 3 ребра. Ключевая фраза, которая помогает решить задачу: «Сергей живет в одном доме Петровым», значит Сергей не Петров. Ребра и показывают ответ задачи. рис.47
Три друга Алеша, Боря и Вова после школы едут домой на различном транспорте: автобусе, маршрутке, трамвае. Однажды после уроков Алеша пошел проводить своего друга до остановки автобуса. Когда мимо них проходила маршрутка, третий друг крикнул из окна: «Боря, ты забыл в школе тетрадку!» Кто на чем ездит домой?
Решение: Задача отличается от предыдущей задачи тем, что в ней несколько ключевых фраз, но решается тоже с построением несвязного графа (рис.48), который содержит 6 вершин и 3 ребра. Первая ключевая фраза, которая помогает решить задачу: «Алеша пошел проводить своего друга до остановки автобуса», значит Алеша ездит не на автобусе. Вторая ключевая фраза: «Когда мимо них проходила маршрутка», значит Алеша ездит не на маршрутке. Остается – Алеша на трамвае. Третья ключевая фраза: «третий друг крикнул из окна: «Боря, ты забыл в школе тетрадку!»», значит друг, которого провожал Алеша до автобуса – Боря, а Вова едет на маршрутке. Ребра и показывают ответ задачи.
Первая ключевая фраза, которая помогает решить задачу: «Алеша пошел проводить своего друга до остановки автобуса», значит Алеша ездит не на автобусе. Вторая ключевая фраза: «Когда мимо них проходила маршрутка», значит Алеша ездит не на маршрутке. Остается – Алеша на трамвае. Третья ключевая фраза: «третий друг крикнул из окна: «Боря, ты забыл в школе тетрадку!»», значит друг, которого провожал Алеша до автобуса – Боря, а Вова едет на маршрутке. Ребра и показывают ответ задачи.
рис.48
- Андрей, Борис, Витя и Гриша – друзья. Один из них – врач, другой – журналист, третий – тренер, четвертый – строитель. Журналист написал статьи об Андрее, Борисе и Грише. Тренер и журналист вместе с Борисом ходили в поход. Андрей и Борис были на приеме у врача. У кого какая профессия?
Решение: В данной задаче граф будет состоять из 8 вершин и 4 ребер. Первая ключевая фраза, которая помогает решить задачу: «Журналист написал статьи об Андрее, Борисе и Грише», значит журналист это Витя. Вторая ключевая фраза: «Тренер и журналист вместе с Борисом ходили в поход», значит Борис не тренер и не журналист. Третья ключевая фраза: «Андрей и Борис были на приеме у врача», значит врач не Андрей и не Борис. Так как больше с условием задачи работать нельзя, то будем работать по графу. По графу видно, что Борис не врач, не журналист, не тренер, а значит – строитель (рис.49). Андрей – не врач, но и не журналист (Витя) и не строитель (Борис), а значит – тренер. А Грише остается врач. Ребра и показывают ответ задачи (рис.50).
Вторая ключевая фраза: «Тренер и журналист вместе с Борисом ходили в поход», значит Борис не тренер и не журналист. Третья ключевая фраза: «Андрей и Борис были на приеме у врача», значит врач не Андрей и не Борис. Так как больше с условием задачи работать нельзя, то будем работать по графу. По графу видно, что Борис не врач, не журналист, не тренер, а значит – строитель (рис.49). Андрей – не врач, но и не журналист (Витя) и не строитель (Борис), а значит – тренер. А Грише остается врач. Ребра и показывают ответ задачи (рис.50).
рис.49 рис.50
- Три подруги Тамара, Валя и Лида были в белом, красном и голубом платьях. Их туфли были тех же цветов. Только у Тамары цвета платья и туфель совпадали. Валя была в белых туфлях. Ни платье, ни туфли Лиды не были красными. Определите цвет платья и цвет туфель каждой из подруг.
Решение: В данной задаче граф будет состоять из 9 вершин и 6 ребер. Причем вершины надо разбить на три тройки: первая – имена, вторая – цвет туфель, третья – цвет платья и разместить их для наглядности в разных плоскостях (рис. 51). Первая ключевая фраза, которая помогает решить задачу: «Валя была в белых туфлях», значит проводим первое ребро от Вали до белых туфель. Вторая ключевая фраза: «Ни платье, ни туфли Лиды не были красными», значит проводим пунктиры от Лиды до красных туфель и красного платья. Третья ключевая фраза: «Только у Тамары цвета платья и туфель совпадали», значит у Вали не белое платье (так как у нее белые туфли). Так как больше с условием задачи работать нельзя, то будем работать по графу (рис.52). По графу видно, что у Лиды голубые туфли (так как красные быть не могут, а белые у Вали), значит, проводим второе ребро. Далее видно, что Тамаре остаются красные туфли и значит и красное платье (третья ключевая фраза), проводим еще два ребра. У Вали голубое платье (так так красное у Тамары, а белое не может быть по графу). Остается Лиде белое платье, проводим последнее ребро. Ребра и показывают ответ задачи (рис.53).
51). Первая ключевая фраза, которая помогает решить задачу: «Валя была в белых туфлях», значит проводим первое ребро от Вали до белых туфель. Вторая ключевая фраза: «Ни платье, ни туфли Лиды не были красными», значит проводим пунктиры от Лиды до красных туфель и красного платья. Третья ключевая фраза: «Только у Тамары цвета платья и туфель совпадали», значит у Вали не белое платье (так как у нее белые туфли). Так как больше с условием задачи работать нельзя, то будем работать по графу (рис.52). По графу видно, что у Лиды голубые туфли (так как красные быть не могут, а белые у Вали), значит, проводим второе ребро. Далее видно, что Тамаре остаются красные туфли и значит и красное платье (третья ключевая фраза), проводим еще два ребра. У Вали голубое платье (так так красное у Тамары, а белое не может быть по графу). Остается Лиде белое платье, проводим последнее ребро. Ребра и показывают ответ задачи (рис.53).
рис. 51 рис.52 рис. 53
- Три друга – Леша, Сергей и Денис – купили щенков разной породы: щенка такса, щенка колли и щенка овчарки.
 Известно, что: щенок Леши темнее по окрасу, чем такса, Леси и Гриф; щенок Сергея старше Грифа, овчарки и таксы; Джек и такса всегда гуляют вместе. У кого какой породы щенок? Назовите клички щенков.
Известно, что: щенок Леши темнее по окрасу, чем такса, Леси и Гриф; щенок Сергея старше Грифа, овчарки и таксы; Джек и такса всегда гуляют вместе. У кого какой породы щенок? Назовите клички щенков.
Решение: В данной задаче граф будет состоять из 9 вершин и 6 ребер. Причем вершины надо разбить на три тройки: первая – имена, вторая – клички, третья – порода и разместить их для наглядности в разных плоскостях. Первая ключевая фраза, которая помогает решить задачу: «: щенок Леши темнее по окрасу, чем такса, Леси и Гриф», значит у Леши не такса, не Леси, не Гриф. Вторая ключевая фраза: «щенок Сергея старше Грифа, овчарки и таксы», значит у Сергея не Гриф, не овчарка, не такса. Третья ключевая фраза: «Джек и такса всегда гуляют вместе», значит Джек это не такса. Так как больше с условием задачи работать нельзя, то будем работать по графу. По графу видно, что у Сережи не такса и не овчарка, а значит – колли, поэтому проводим первое ребро. Далее видно, что у Леши не такса и не колли, а значит — овчарка, проводим еще ребра. Денису осталась такса. У Леши не Леси и не Гриф, значит Джек. У Сережи не Гриф и не Джек, а Леси. Остается Денису Гриф, проводим последнее ребро. Ребра и показывают ответ задачи (рис.54).
Денису осталась такса. У Леши не Леси и не Гриф, значит Джек. У Сережи не Гриф и не Джек, а Леси. Остается Денису Гриф, проводим последнее ребро. Ребра и показывают ответ задачи (рис.54).
рис.54
- В столовой на горячее можно заказать щуку, грибы и баранину, на гарнир – картофель и рис, а из напитков – чай и кофе. Сколько различных вариантов обедов можно составить из указанных блюд?
Решение: Решением задачи будет несвязный граф, состоящий из трех граф-деревьев (рис.55). Первым звеном графа будут горячие блюда, вторым – гарнир, третьим – напитки. По графу легко составить все возможные комбинации обедов: Щ-К-Ч, Щ-К-К, Щ-Р-Ч, Щ-Р-К, Г-К-Ч, Г-К-К, Г-Р-Ч, Г-Р-К, Б-К-Ч, Б-К-К, Б-Р-Ч, Б-Р-К – 12 вариантов. рис.55
Алла решила маме на день рождения подарить букет цветов (розы, тюльпаны или гвоздики) и поставить их или в вазу или в кувшин. Сколькими способами это можно сделать?
Решение: Решением задачи будет несвязный граф, состоящий из трех граф-деревьев (рис. 56). Первым звеном графа будут цветы, вторым – сосуды. По графу легко составить все возможные комбинации букетов: Р-В, Р-К, Т-В, Т-К, Г-В, Г-К – 6 способов. рис.56
56). Первым звеном графа будут цветы, вторым – сосуды. По графу легко составить все возможные комбинации букетов: Р-В, Р-К, Т-В, Т-К, Г-В, Г-К – 6 способов. рис.56
- Из наборного полотна взяли две карточки с цифрой 1 и три карточки с цифрой 5. Сколько различных пятизначных чисел можно составить из этих карточек?
Решение: Решением задачи будет несвязный граф, состоящий из двух граф-деревьев (рис.57). В каждом граф-дереве будет по 5 звеньев, так как надо составить пятизначное число. По графу легко посчитать, что можно составить 10 чисел. рис.57
- У Левы 2 конверта: обычный и авиа и 3 марки: прямоугольная, квадратная и треугольная. Сколькими способами он может выбрать конверт и марку, чтобы отправить письмо?
Решение: Решением задачи будет несвязный граф, состоящий из двух граф-деревьев (рис.58). В каждом граф-дереве будет по 2 звена. Первое звено – тип конверта, второе – тип марки. По графу легко посчитать, что возможно 6 вариантов. рис.58
По графу легко посчитать, что возможно 6 вариантов. рис.58
.
Проанализировав выше предложенный практический материал, приходим к выводу, что для решения задач, с применением теории графов, можно выделить следующие этапы:
Анализ условия задачи и перевод ее на язык графов;
Геометрическая интерпретация условия, построение графа. Именно на этом этапе очень важен элемент творчества потому, что далеко не просто найти соответствия между элементами условия и соответствующими элементами графа;
Точками обозначают объекты задачи (вершины графа). Если в задачах дано несколько групп объектов, то лучше их изображать в разных плоскостях и различными цветами;
Линиями (отрезками, дугами) обозначают отношения между объектами (рёбра графа). Отношения могут быть двух типов: принадлежит и не принадлежит. Если отношение «принадлежит», то линии сплошные, если отношение «не принадлежит» — пунктирные;
Выделяем ключевые фразы задач и, анализируя их, проводим ребра;
Если ключевых фраз не достаточно для решения задачи, то анализируем граф и проводим недостающие ребра;
Выбираем нужные отношения (сплошные линии) и записываем ответ.

Использование графов в качестве некоторого вспомогательного средства позволяет облегчить процесс обучения и подготовить учеников к восприятию сложных тем в курсе школьной математики. Графовые задачи, без сомнения, нужно использовать не только на математических кружках, при подготовке к олимпиадам для развития сообразительности учеников, но и использовать теорию графов как языка на уроках математики, алгебры, геометрии, информатики для повышения качества обучения.
Таким образом, применяя теорию графов в школьном курсе математики, решение многих математических задач и доказательств упрощается, придает им наглядность и простоту.
Использованные материалы и Интернет-ресурсы
Нагибин Ф.Ф. Применение графов для решения логических задач.
// Математика в школе. — 1964. — № 3.
Гуровиц В.М., Ховрина В.В. Графы.-М.:МЦНМО, 2008.- 32 с.:ил.
П.В. Севрюков Подготовка к решению олимпиадных задач по математике: Илекса, 2001
http://sch316.
 narod.ru/nayka/doc/graf.htm
narod.ru/nayka/doc/graf.htmhttp://dok.opredelim.com/docs/index-3239.html
http://festival.1september.ru/articles/416943/
http://kk.docdat.com/docs/index-487830.html
http://pandia.ru/text/78/009/77971.php
http://player.myshared.ru/4/191256/data/images/img4.png
http://www.vevivi.ru/best/Obuchenie-resheniyu-matematicheskikh-zadach-s-pomoshchyu-grafov-ref43062.html
http://www.igry-detei.ru/uploads/24.png
http://nsportal.ru/shkola/algebra/library/2013/03/09/teoriya-grafov-teoriya-i-zadachi
Приложения:
- Ранним утром Оля, Маша, Катя обменялись приветствиями каждый с каждым. Сколько всего было приветствий.
- Андрей, Борис, Виктор и Георгий играли в шахматы. Каждый сыграл с каждым по одной партии. Сколько партий было сыграно?
Аркадий, Борис, Георгий, Владимир и Дмитрий при встрече обменялись рукопожатиями (каждый пожал руку каждому один раз).
 Сколько всего рукопожатий сделано?
Сколько всего рукопожатий сделано?Несколько мальчиков встретились на вокзале, чтобы поехать за город в лес. При встрече все они поздоровались друг с другом за руку. Сколько мальчиков поехало за город, если всего было 10 рукопожатий?
- На лесной опушке встретились заяц, белка, лиса, волк, медведь и куница. Каждый, здороваясь, пожал каждому лапу. Сколько всего рукопожатий было сделано?
В шахматном турнире участвовало семь человек. Каждый с каждым сыграл по одной партии. Сколько партий они сыграли?
В первенстве класса по шашкам 5 участников: Аня, Боря, Влад, Гриша, Даша. Первенство проводится по круговой системе – каждый из участников играет с каждым из остальных один раз. К настоящему времени некоторые игры уже проведены: Аня сыграла с Борей, Владом и Дашей. Боря сыграл с Аней и Гришей, Влад – с Аней и Дашей, Гриша – с Борей, Даша – с Аней и Гришей. Сколько игр проведено к настоящему времени и сколько еще осталось?
В стране алфавит 8 городов: А, Б, В, Г, Д, Е, Ж, З и 8 непересекающихся дорог между городами А и Б, Е и Д, Б и Ж, З и А, В и Г, Г и Д, Ж и З, В и Е.
 Можно ли по этим дорогам проехать из А в Г?
Можно ли по этим дорогам проехать из А в Г?Красный, синий, желтый и зеленый карандаши лежат в четырех коробках по одному. Цвет карандаша отличается от цвета коробки. Известно, что зеленый карандаш лежит в синей коробке, а красный не лежит в желтой. В какой коробке лежит каждый карандаш?
На столе лежат в ряд четыре фигуры: треугольник, ромб, круг, квадрат. Цвета этих фигур – зеленый, желтый, синий, красный. В каком порядке лежат фигуры и каков цвет каждой из них, если фигура красного цвета лежит между зеленой и синей. Справа от желтой фигуры лежит ромб, круг лежит правее треугольника и ромба, причем треугольник лежит не с краю, и, наконец, фигура синего цвета не лежит рядом с фигурой желтого цвета?
В квартирах №1,2,3 жили три друга: Айдар, Тима и Саша. Известно, что в квартирах №1 и 2 жил не Айдар. Тима жил не в квартире №1. В какой квартире жил каждый из друзей.
На улице, став в кружок, беседуют четыре девочки: Аня, Валя, Галя и Надя.
 Девочка в зеленом платье (не Аня и не Валя) стоит между девочкой в голубом платье и Надей. Девочка в белом платье стоит между девочкой в розовом и Валей. Какое платье носит каждая девочка?
Девочка в зеленом платье (не Аня и не Валя) стоит между девочкой в голубом платье и Надей. Девочка в белом платье стоит между девочкой в розовом и Валей. Какое платье носит каждая девочка?На одном заводе работают три друга: слесарь, токарь и сварщик. Их фамилии Борисов, Иванов и Семенов. У слесаря нет ни братьев, ни сестер, он самый младший из друзей. Семенов старше токаря и женат на сестре Борисова. Назовите фамилии слесаря, токаря и сварщика.
В пионерский лагерь приехали три друга Миша, Володя и Петя. Известно, что каждый из них имеет одну из фамилий: Иванов, Семенов и Герасимов. Миша не Герасимов, отец Володи инженер, Володя учится в 6-м классе. Герасимов учится в 5-м классе. Отец Иванова слесарь. Какая фамилия у каждого из ребят?
В бутылке, стакане, кувшине и банке находятся молоко, лимонад, квас и вода. Известно, что вода и молоко не в бутылке, сосуд с лимонадом стоит между кувшином и сосудом с квасом, в банке не лимонад и не вода.
 Стакан стоит около банки и сосуда с молоком. В какой сосуд налита каждая жидкость?
Стакан стоит около банки и сосуда с молоком. В какой сосуд налита каждая жидкость?В нашем лесу каждый занят своим делом: одни плетут корзины, другие ловят рыбу. Ремеслу мы учились друг у друга. Кот учился у Выдры, Еж — у Зайца, Лиса- у Волка, а Мышь- у Ежа. Бобер учил Волка и Выдру, Заяц- Белку, а Барсук- Зайца. Бобер был учеником Медведя, а Еж учителем Дятла. Лучше всех плетет корзины Еж. Чем занимались Заяц, Дятел, Волк, и Лиса? Кто из зверей нашего леса раньше всех научился ловить рыбу, а кто — плести корзины?
На карточке нарисованы: отрезок, круг, треугольник, звезда, квадрат. В каком порядке они нарисованы, если известно, что отрезок располагается не рядом с треугольником, треугольник — не рядом с кругом, круг — не рядом со звездой, а звезда- не рядом с отрезком, треугольник- не рядом с квадратом, а квадрат- не рядом с кругом, звезда- рядом с квадратом, слева от него?
- Ужасные грабители Кнопка и Скрёпка решили украсть из сейфа золотой ключик Буратино, который знает пока 4 цифры:1,2,3,4.
 Сколько вариантов придется перебрать им, чтобы подобрать двузначный код?
Сколько вариантов придется перебрать им, чтобы подобрать двузначный код? - Сколько трехзначных чисел можно составить из цифр 1,3,5,7, используя в записи числа каждую из них не более одного раза?
- Антон, Борис и Василий купили 3 билета на 1-е, 2-е, 3-е места первого ряда на футбольный матч. Сколькими способами они могут занять места?
В пятницу 4 урока: алгебра, русский, физика и история. Сколькими способами можно составить расписание на пятницу?
Катя, Галя и Оля, играя, спрятали по игрушке. Они играли с медвежонком, зайчиком и слоником. Известно, что Катя не прятала зайчика, а Оля не прятала ни зайчика, ни медвежонка.
У кого какая игрушка?Коля, Боря, Вова и Юра заняли первые четыре места в соревновании, причём никакие два мальчика не делили между собой одно и тоже место. На вопрос, какие места заняли ребята, трое ответили: Коля — не первое и не четвёртое; Боря — второе; Вова — не был последним.
Какое место занял каждый из мальчиков?Три поросенка построили три домика из соломы, из прутьев, из камней.
 Каждый из них получил один домик: Ниф-Ниф – не из камней, и не из прутьев; Нуф-Нуф не из камней.
Каждый из них получил один домик: Ниф-Ниф – не из камней, и не из прутьев; Нуф-Нуф не из камней.
Какой домик достался Наф-Нафу.Четыре брата Юра, Петя, Вова, Коля учатся в 1,2,3,4 классах. Петя- отличник, младшие братья стараются брать с него пример. Вова учится в 4 классе. Юра помогает решать задачи брату.
Кто в каком класе учится?В семье трое детей: 2 мальчика и девочка. Их имена начинаются с букв А,В,Г. Среди А и В есть начальная буква имени одного мальчика, а среди В и Г – начальная буква имени другого мальчика.
С какой буквы начинается имя девочки?Нюша , Бараш, Копатыч и Лосяш играли с мячами синим, зелёным, жёлтым и красным.
Каким из мячей играл каждый из них, если мяч Бараша не синий, у Нюши не синий и не красный, а у Копатыча желтый мяч?Старый гном разложил свои сокровища в 3 разноцветных сундука, стоящих у стены.
В один – драгоценные камни, в другой – золотые монеты, а в третий – магические книги.
Он помнит, что красный сундук правее, чем драгоценные камни.
А магические книги правее, чем красный сундук.
В каком сундуке лежат магические книги, если зелёный сундук стоит левее, чем синий?
Решение задач маршрутизации и путевых разбиений графов методами раскрасок и весовых перераспределений
Автореферат диссертациина тему «Решение задач маршрутизации и путевых разбиений графов методами раскрасок и весовых перераспределений»
РОССИЙСКАЯ АКАДЕМИЯ НАУК СИБИРСКОЕ ОТДЕЛЕНИЕ ИНСТИТУТ МАТЕМАТИКИ им. С. Л. СОБОЛЕВА
ЗАМБАЛАЕВА Долгор Жамьяновна
РЕШЕНИЕ ЗАДАЧ МАРШРУТИЗАЦИИ И ПУТЕВЫХ РАЗБИЕНИЙ ГРАФОВ МЕТОДАМИ РАСКРАСОК И ВЕСОВЫХ ПЕРЕРАСПРЕДЕЛЕНИЙ
(01.01.09 — дискретная математика и математическая кибернетика)
На правах рукописи
1 О НОЯ 2011
Автореферат диссертации на соискание ученой степени кандидата физико-математических наук
Новосибирск 2011
4859188
Работа выполнена в Учреждении Российской академии наук Институте математики им. С. Л. Соболева Сибирского отделения РАН.
С. Л. Соболева Сибирского отделения РАН.
Научный руководитель: Официальные оппоненты:
Ведущая организация:
кандидат физико-математических наук Глебов Алексей Николаевич доктор физико-математических наук, профессор Гимади Эдуард Хайрутдинович кандидат физико-математических наук Аксенов Валерий Анатольевич Учреждение Российской академии наук Институт математики и механики Уральского отделения РАН (ИММ УрО РАН)
Защита состоится 30 ноября 2011 г. в 17 часов на заседании диссертационного совета Д 003.015.01 при Учреждении Российской академии наук Институте математики им. С. Л. Соболева СО РАН (пр. Академика Коп-тюга, 4, 630090 Новосибирск).
С диссертацией можно ознакомиться в библиотеке Учреждения Российской академии наук Института математики СО РАН.
Автореферат разослан октября 2011 г.
Ученый секретарь диссертационного совета доктор физ.-мат. наук
Ю. В. Шамардин
ОБЩАЯ ХАРАКТЕРИСТИКА РАБОТЫ
Актуальность темы.
Направление исследований данной диссертации относится к задачам дискретной оптимизации и экстремальным задачам на графах. Объектами исследования диссертации являются путевые разбиения планарных графов, то есть их вершинные разбиения на два подграфа с заданными ограничениями на длины цепей, а также некоторые разновидности задач маршрутизации, а именно задачи о двух коммивояжерах на минимум и на максимум.
Исследования в области дискретной оптимизации за последние полвека приобрели особую актуальность в связи с фундаментальными проблемами полиномиальной разрешимости задач из классов NP-полных и NP-трудных задач. Было установлено, что полиномиальная разрешимость хотя бы одной NP-полной проблемы влечет полиномиальную разрешимость любой другой задачи из класса NP. Драматизм ситуации состоит в том, что доказать (или опровергнуть) совпадение классов Р и NP к настоящему времени не удается. Большинство исследователей склоняются к пессимистической гипотезе несовпадения этих классов.
В этих условиях актуальными становятся исследования по разработке и обоснованию полиномиальных приближенных алгоритмов решения трудных задач комбинаторной оптимизации с возможно более лучшими оценками их качества. Основные усилия специалистов по методам комбинаторной оптимизации направлены в сторону развития новых методов построения малотрудоемких приближенных алгоритмов и получения как положительных, так и отрицательных результатов, касающихся существования полиномиальных приближенных схем (SNP-трудность). Это направление исследований является составной частью раздела математики, известного за рубежом под названием «Computer science». Оно сопровождается большим количеством международных симпозиумов и конференций, множеством специальных журналов и монографий, интенсивно развивается во многих научных школах (Кук С., Карп Р., Гэри М., Джонсон Д., Яннакакис М. и Пападимитриу X. — США, Ленстра Дж., Скрайвер А. — Нидерланды, Эрдеш П., Ловас Л. — Венгрия, Эдмондс Дж. — Канада, Грётшель М. — Германия, Буркард Р. — Австрия др.).
— Германия, Буркард Р. — Австрия др.).
В диссертационной работе большое внимание уделено построению полиномиальных алгоритмов с гарантированными оценками точности для задачи о двух коммивояжерах на минимум и на максимум. Этим исследованиям посвящены главы 2 и 3 диссертации. Актуальность построения и анализа подобных алгоритмов обусловлена возможностью их применения
при разработке эффективных методов решения практически значимых и сложных задач, для которых не известно точных полиномиальных алгоритмов решения. В частности, это касается ИР-трудных задач дискретной оптимизации. Особенностью построения приближенных алгоритмов в диссертации является активное применение методов теории графов, таких как техника раскрасок вершин и ребер и метод перераспределения зарядов между вершинами графа.
В связи с этим следует отметить, что теория графов за последние 30-40 лет оформилась в самостоятельную математическую дисциплину, с присущими ей задачами и подходами, и активно развивается. Идеи и методы теории конечных графов востребованы во многих областях дискретной математики и их приложениях. Одно из центральных мест в современной теории графов занимает теория раскраски, то есть разбиения дискретного объекта на проще устроенные подобъекты. В частности, внимание ведущих графистов мира привлекают задачи о вершинных раскрасках и разбиениях планарных графов. Одной из разновидностей таких задач являются задачи о путевых разбиениях графов, при которых каждая часть разбиения (цветовой класс) порождает подграф с заданными ограничениями на длины цепей. В диссертации путевые разбиения планарных графов изучаются в главе 1, а в главе 2 при разработке алгоритмов для задачи о двух коммивояжерах на максимум применяются реберные раскраски графов в 2 и 3 цвета.
Идеи и методы теории конечных графов востребованы во многих областях дискретной математики и их приложениях. Одно из центральных мест в современной теории графов занимает теория раскраски, то есть разбиения дискретного объекта на проще устроенные подобъекты. В частности, внимание ведущих графистов мира привлекают задачи о вершинных раскрасках и разбиениях планарных графов. Одной из разновидностей таких задач являются задачи о путевых разбиениях графов, при которых каждая часть разбиения (цветовой класс) порождает подграф с заданными ограничениями на длины цепей. В диссертации путевые разбиения планарных графов изучаются в главе 1, а в главе 2 при разработке алгоритмов для задачи о двух коммивояжерах на максимум применяются реберные раскраски графов в 2 и 3 цвета.
Цель исследования диссертации состоит в получении новых результатов о путевой разбиваемости планарных графов и в построении и анализе приближенных полиномиальных алгоритмов с гарантированными оценками точности для некоторых модификаций задачи о двух коммивояжерах.
Методы исследований. Для получения результатов о путевых разбиениях планарных графов, равно как и при построении алгоритмов с гарантированными оценками качества для задач маршрутизации применялись общие методы исследований, такие как техника раскрасок вершин и ребер графа, а также техника перераспределения весов (зарядов) между вершинами (и/или гранями) графа.
Научная новизна. В диссертации получен ряд новых важных результатов. В частности, частично подтверждена гипотеза о т-разбиваемости для планарных графов. Впервые доказана возможность разбиения вершин любого плоского графа с обхватом не менее 7 на два подмножества, каждое из которых порождает звездный лес, что эквивалентно путевой
(3,3)-разбиваемости таких графов. Разработаны новые алгоритмы для задачи о двух коммивояжерах на минимум и на максимум, обладающие лучшими, в сравнении с ранее известными, оценками точности.
Практическая ценность. Результаты работы носят преимущественно теоретический характер. Разработанные алгоритмы могут использоваться для решения соответствующих прикладных задач.
Разработанные алгоритмы могут использоваться для решения соответствующих прикладных задач.
Основные результаты.
1. Доказана r-разбиваемость планарных графов с обхватом не менее 5.
2. Доказано, что множество вершин планарного графа с обхватом не менее 7 можно разбить на два подмножества, каждое из которых порождает звездный лес, что эквивалентно путевой (3,3)-разбиваемости таких графов.
3. Построен полиномиальный приближенный алгоритм решения задачи о двух коммивояжерах на максимум (задача 2-PSP-max) с оценкой точности | и оценкой временной сложности 0(п3).
4. Для решения задачи о двух коммивояжерах на минимум с весами ребер 1 и 2 и различными весовыми функциями (задача 2-PSP(l,2)-min-2w) построены следующие приближенные алгоритмы:
4.1. алгоритм с оценкой точности | и временной сложностью 0(п3).
4.2. алгоритм с оценкой точности | и временной сложностью 0(п5).
Оценки точности последних двух алгоритмов приведены без учета аддитивной константы.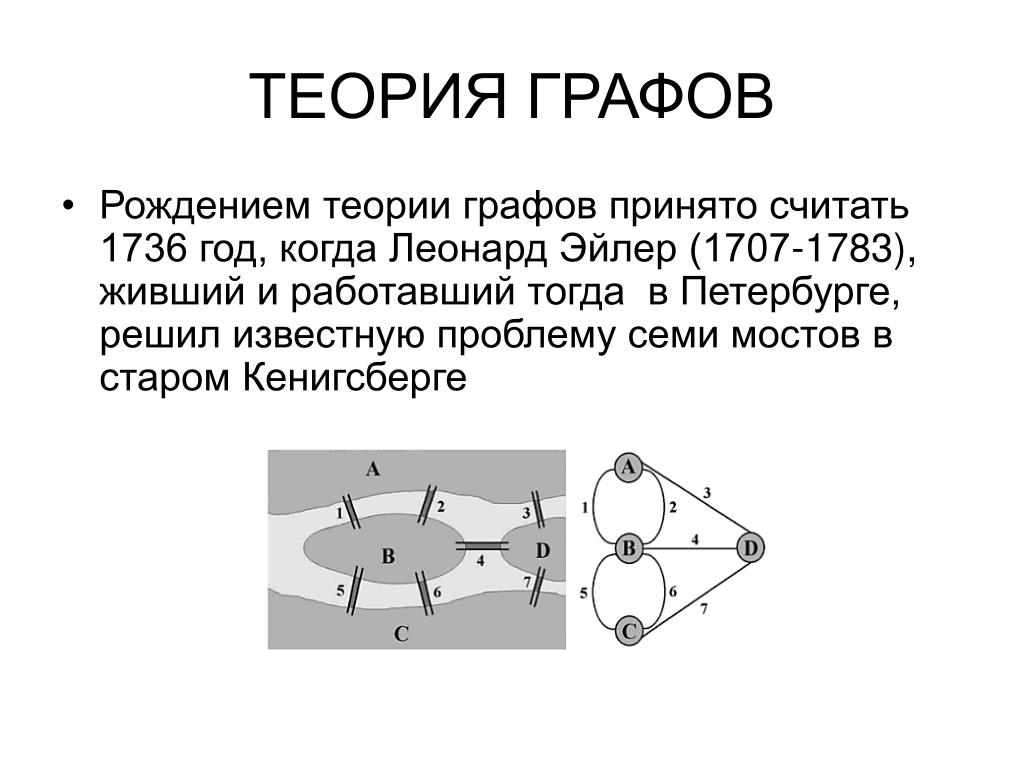
Апробация работы. Результаты диссертации докладывались на международных научных студенческих конференциях «Студент и научно-технический прогресс» (Новосибирск, 2007, 2008), на Всероссийских конференциях «Методы оптимизации и экономические приложения» (Омск, 2009), «Дискретная оптимизация и исследование операций» (Алтай, 2010), «Математическое программирование и приложения» (Екатеринбург, 2011), на Международных конференциях по исследованию операций «European Conference on Operational Research» (Бонн, 2009), «Optimal Discrete Structures and Algorithms» (Росток, 2010), на научных семинарах Института математики им. С.Л. Соболева СО РАН.
Публикации. По теме диссертации автором опубликовано 11 работ, из них 5 публикаций в научных журналах [16-20] и 6 публикаций в трудах и тезисах конференций [21-26]. Результаты разделов 1.2, 3.3 и главы 2 получены в соавторстве с А.Н. Глебовым. Результат раздела 3.2. получен в соавторстве с А.Н. Глебовым и A.B. Гордеевой. Конфликт интересов с соавторами отсутствует.
Структура и объем работы. Диссертация изложена на 138 страницах, содержит введение, три главы и список литературы, содержащий 70 наименований.
СОДЕРЖАНИЕ ДИССЕРТАЦИОННОЙ РАБОТЫ
Во введении приводится обзор известных результатов, посвященных рассматриваемым задачам, обосновывается актуальность темы исследования и кратко излагается содержание диссертационной работы.
В первой главе исследуются путевые разбиения планарных графов, понятие которых было введено в [10], то есть вершинные разбиения графа на два подграфа с заданными ограничениями на длины цепей. Такие путевые разбиения интерпретируются как раскраски вершин графа в два цвета с ограниченными длинами одноцветных цепей. При доказательстве результатов первой главы, а именно: т-разбиваемости и путевой (3,3)-разбиваемости планарных графов с обхватом не менее 5 и 7 соответственно, осуществляется построение раскрасок, соответствующих рассматриваемым путевым разбиениям. Получение таких раскрасок становится возможным благодаря использованию’метода перераспределения зарядов, основанного на формуле Эйлера.
В разделе 1.1 вводятся основные определения и обозначения. Пусть а > 1, Ь > 1 — целые числа. Граф G называется (а,Ъ)-разбиваемым, если существует такое разбиение множества его вершин V = Vi U V2, что в подграфе Gi = G[Vi], порожденном подмножеством Vu длина наибольшей простой цепи не превосходит а, а в подграфе G2 = G[V2] — не превосходит Ь, где под длиной цепи понимается число ее вершин. Граф G называется т-разбиваемым, если он (а, Ь)-разбиваем для любых натуральных а, Ь таких, что а + Ь = т, где т = r(G) — наибольшая длина простой цепи в G.
В работах [10, 12] высказывалась гипотеза о том, что любой граф является r-разбиваемым. В [11, 12, 13, 14] и ряде других работ справедливость этой гипотезы была подтверждена для некоторых специальных классов графов. В [6] было доказано, что любой граф является (а, г — а)-разбиваемым при а < 8. Вопрос о т-разбиваемости планарных графов ранее специально не исследовался.
В разделе 1.2 диссертации гипотеза о т-разбиваемости частично подтверждена для специального подкласса пленарных графов, а именно доказана
Теорема 1. Любой планарный граф с обхватом не менее 5 является т-разбиваемым.
Любой планарный граф с обхватом не менее 5 является т-разбиваемым.
Помимо задачи выделения классов т-разбиваемых графов представляет интерес вопрос об (а, 6)-разбиваемости при небольших фиксированных значениях параметров а и Ь. В указанной постановке задача об (а, Ь)-разбиваемое™ оказывается тесно связана с такой активно исследуемой областью теории графов как разложение на вырожденные подграфы. Наиболее часто рассматриваются разбиения графов на леса (ациклические подграфы) и звездные леса. Напомним, что звездным лесом, называется такой лес, в котором каждая компонента связности является звездой.
В разделе 1.3 доказана
Теорема 2. Множество вершин любого плоского графа с обхватом не менее 7 можно разбить на два подмножества, каждое из которых порождает звездный лес.
Иначе это утверждение можно сформулировать так: множество вершин графа можно разбить на два подмножества, каждое из которых порождает подграф, не содержащий циклов и простых цепей с более чем тремя вершинами.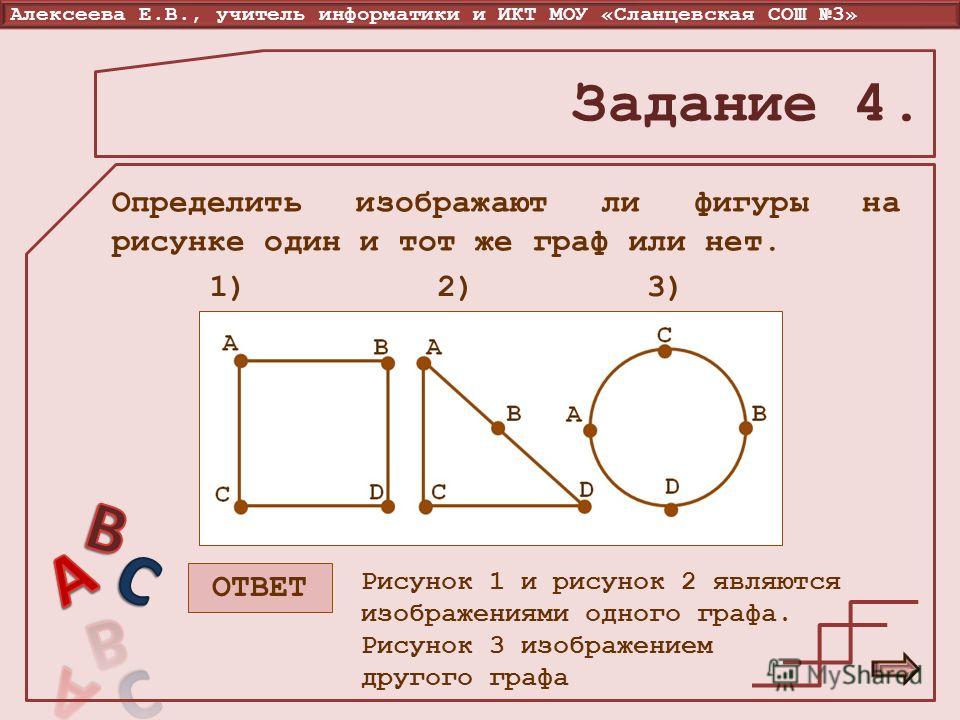 Здесь обнаруживается связь полученного результата с понятием путевой разбиваемости. В силу того, что (3,3)-разбиваемость графа эквивалентна его разбиваемости на два звездных леса (для графов без 3-циклов), утверждение теоремы 2 равносильно тому, что любой плоский граф с обхватом не менее 7 является (3,3)-разбиваемым.
Здесь обнаруживается связь полученного результата с понятием путевой разбиваемости. В силу того, что (3,3)-разбиваемость графа эквивалентна его разбиваемости на два звездных леса (для графов без 3-циклов), утверждение теоремы 2 равносильно тому, что любой плоский граф с обхватом не менее 7 является (3,3)-разбиваемым.
В [10, 11, 12] и ряде других работ исследовались (о, 6)-разбиения для некоторых специальных классов (непланарных) графов. Уже для планар-ных графов Глебовым и Замбалаевой [19] было доказано, что такие графы с обхватом не менее 8, 9 и 16 являются (2,3)-, (2,2)- и (1,2)-разбиваемыми соответственно. Эти результаты были усилены Бородиным и Ивановой [3, 4], которые установили, что планарные графы с обхватом не менее 14 являются (1,2)-разбиваемыми, а с обхватом не менее 8 — (2,2)-разбиваемыми.
С другой стороны, Михоком [15] было показано, что для любых фиксированных значений параметров а, Ь существуют плоские графы, не являющиеся (а, Ь)-разбиваемыми. При этом во всех примерах графов, приводимых в [15], содержится большое число циклов длины 3. 0.778 и кубическую временную сложность, что улучшает результат Агеева, Бабурина и Гимади [1], ранее построивших для данной задачи алгоритм с оценкой §.
0.778 и кубическую временную сложность, что улучшает результат Агеева, Бабурина и Гимади [1], ранее построивших для данной задачи алгоритм с оценкой §.
В основе алгоритма А7/9 лежит идея, впервые реализованная Сердю-ковым [7] при построении приближенного алгоритма для задачи одного коммивояжера на максимум (ТБР-тах) с оценкой точности На первом этапе алгоритма Сердюкова в графе находятся 2-фактор и паросочетание максимального веса, суммарный вес которых составляет не менее 5 от веса оптимального решения. Далее алгоритм разбивает найденные 2-фактор и паросочетание на два частичных тура (то есть на два набора из вершинно непересекающихся цепей, покрывающих все вершины графа), каждый из которых дополняется до гамильтонова цикла. Максимальный по весу из этих циклов дает решение 2-Р8Р-тах с оценкой точности §.
В представленном в диссертации алгоритме Л7/9 реализован аналогичный подход, однако в качестве исходного подграфа, подвергающегося разбиению на непересекающиеся по ребрам частичные туры, используется 4-регулярный остовный подграф максимального веса в (3. При этом
При этом
представленный алгоритм развивает идеи, ранее использованные в работе Гимади, Глазкова и Глебова [5] при построении приближенного алгоритма с оценкой | для задачи 2-Р8Р на минимум с весами ребер 1 и 2. Ключевым этапом алгоритма Л7/9 является построение двух реберных раскрасок начальной пары частичных туров в два и в три цвета, что позволяет получить шесть альтернативных пар реберно непересекающихся частичных туров, наилучшая из которых имеет суммарный вес ребер не менее |ОРТ. Благодаря структурным свойствам начальной пары частичных туров, полученные туры удается дополнить до пары реберно непересекающихся гамильтоновых циклов, что не всегда возможно в случае произвольных реберно непересекающихся частичных туров.
Для построенного алгоритма в диссертации доказана следующая
Теорема 3. Алгоритм А7/д находит, в полном п-вершинном графе С? пару реберно непересекающихся гамильтоновых циклов Нг,Н2, для которых выполняется оценка ш(#1 иЯ2) > 1<ЭРТ. (ЯО 4- №2(Я2), где и>ДЯ*) = ‘Шг(е), минимален. Для приближен-
(ЯО 4- №2(Я2), где и>ДЯ*) = ‘Шг(е), минимален. Для приближен-
ного решения данной задачи построены два полиномиальных алгоритма, для каждого из которых получены оценка временной сложности и гарантированная оценка точности.
Как и в первой главе диссертации, в главе 3 используются весовые перераспределения. При помощи таких перераспределений обосновывается оценка точности полученного алгоритмом решения. В отличие от доказательства структурных результатов о плоских графах, в рассматриваемом случае использование зарядов (весов) вершин и последующее их перераспределение с сохранением суммы является нетипичным для задач такого плана, и ранее применялось только Берманом и Карпински [9] в задаче одного коммивояжера на минимум с весами ребер 1 и 2.
Для приближенного решения задачи 2-Р8Р-тт-2\у-(1,2) в разделах 3.2 и 3.3 представлены полиномиальные алгоритмы Л7/5 и Л4/3 соответственно. Последний алгоритм имеет наилучшую на сегодняшний день гарантированную оценку точности для данной задачи, равную | (без учета аддитивной константы) и оценку временной сложности 0(п°). Алгоритм Л7/5 обладает худшей по сравнению с алгоритмом Л4/3 оценкой точности 7/5, зато имеет лучшую (кубическую) оценку временной сложности. Оба алгоритма улучшают оценку точности уч ранее полученную в [8].
Алгоритм Л7/5 обладает худшей по сравнению с алгоритмом Л4/3 оценкой точности 7/5, зато имеет лучшую (кубическую) оценку временной сложности. Оба алгоритма улучшают оценку точности уч ранее полученную в [8].
В основу обоих алгоритмов положена идея метода из [9], заключающаяся в построении и последовательном «улучшении» двух реберно непересекающихся частичных туров из ребер единичного веса, и последующем замыкании этих туров в непересекающиеся гамильтоновы циклы. Под «улучшением» туров понимается такое их локальное преобразование, при котором уменьшается либо общее число цепей и циклов, составляющих туры, либо число одновершинных цепей (синглов). Для того, чтобы гарантировать возможность улучшающего преобразования в случае, если нужное качество решения еще не достигнуто, применяется введенная в [9] модификация метода перераспределения зарядов вершин. Аналогично тому, как это делается при работе с плоскими графами, для каждой вершины графа определяется ее заряд, то есть число, определяемое на основе туров оптимального решения. -вершиной (б-, д)-дерева (независимо для каждого тура).
-вершиной (б-, д)-дерева (независимо для каждого тура).
Следует отметить, что в разделе 3.3, посвященном построению и анализу алгоритма Л4/3, понятие частичного тура, традиционно используемое при построении алгоритмов для задач одного и двух коммивояжеров, существенно модифицировано за счет включения в туры наряду с цепями и циклами так называемых (в, д)-деревьев, определение и свойства которых даются в разделе 3.3.1 диссертации.
Для построенных алгоритмов доказаны следующие результаты:
Теорема 5. Алгоритм А7/5 за время 0(п3) находит в полном п-вершинном графе С пару реберно непересекающихся гамилътоновых циклов Н1, Н2, для веса которых выполняется неравенство
■шх{Н1) + -ш2{Нг) < {ОРТ+1.
Теорема 6. Алгоритм Л4/3 за время 0(п5) находит в полном п-вершинном графе С пару реберно непересекающихся гамилътоновых циклов Нг, #2, для веса которых выполняется неравенство
1И1(#1) + »02(Яа) < §ОРГ+1.
Есть все основания полагать, что разработанные в диссертации методы, связанные с применением раскрасок вершин и ребер, перераспределением зарядов и использованием принципиально новых объектов, таких как («, д)-деревья, окажется полезными при разработке других алгоритмов решения задач маршрутизации, главным образом, задач одного, двух и более коммивояжеров на минимум и на максимум.
Автор выражает искреннюю признательность своему научному руководителю Алексею Николаевичу Глебову за постоянную поддержку и внимание к работе.
Список литературы
[1] Агеев A.A., Бабурин А.Е., Гимади Э.Х. Полиномиальный алгоритм с оценкой точности 3/4 для отыскания двух непересекающих-
ся гамильтоновых циклов максимального веса. // Дискрет, анализ и исслед. операций. — 2006. — Сер. 1. Т. 13, № 2. — С. 11-20.
[2] Бабурин А. Е., Гимади Э.Х., Коркишко Н.М. Приближенные алгоритмы для нахождения двух реберно непересекающихся гамильтоновых цикла минимального веса. // Дискрет, анализ и исслед. операций. — 2004. — Сер. 2. Т. 11, № 1. — С. 11-25.
[3] Бородин О. В., Иванова А. О. Почти правильные 2-раскраски вершин разреженных графов // Дискретный анализ и исследование операций. — 2009. — Т. 16, № 2. — С. 16-20.
[4] Бородин О. В., Иванова А. О. Разбиение разреженных плоских графов на два подграфа малой степени // Сибирские электронные математические известия, (http://semr. raath.nsc.ru). — 2009. — Т. 6.
raath.nsc.ru). — 2009. — Т. 6.
— С. 13-16.
[5] Гимади Э. X., Глазков Ю. В., Глебов А. Н. Приближенные алгоритмы решения задачи о двух коммивояжерах в полном графе с весами ребер 1 и 2 // Дискрет, анализ и исслед. операций. — Сер. 2. 2007. — Т. 14, № 2. — С. 41-61.
[6] Мельников JI.C., Петренко И.В. О путевых ядрах и разбиениях в неориентированных графах// Дискретный анализ и исследование операций. — 2002. — Сер. 1. Т. 9, № 2. — С. 21-35.
[7] Сердюков А. И. Алгоритм с оценкой для задачи коммивояжера на максимум. // Управляемые системы. Сб. науч. тр. — 1984. — Вып. 25.
— С.80-86.
[8] А.Е. Baburin, F.Della Croce, Е.К. Gimadi, Y.V. Glazkov and V.Th. Paschos. Approximation algorithms for the 2-peripatetic salesman problem with edge weights 1 and 2 // Discrete Applied Mathematics, Vol. 157, No 9, 2009, P. 1988-1992.
[9] Berman P., Karpinski M. 8/7-approximation algorithm for (1,2)-TSP // Proc. of the 17th annual ACM-SIAM symposium on discrete algorithms, SODA 2006 (Miami, January 22-26, 2006).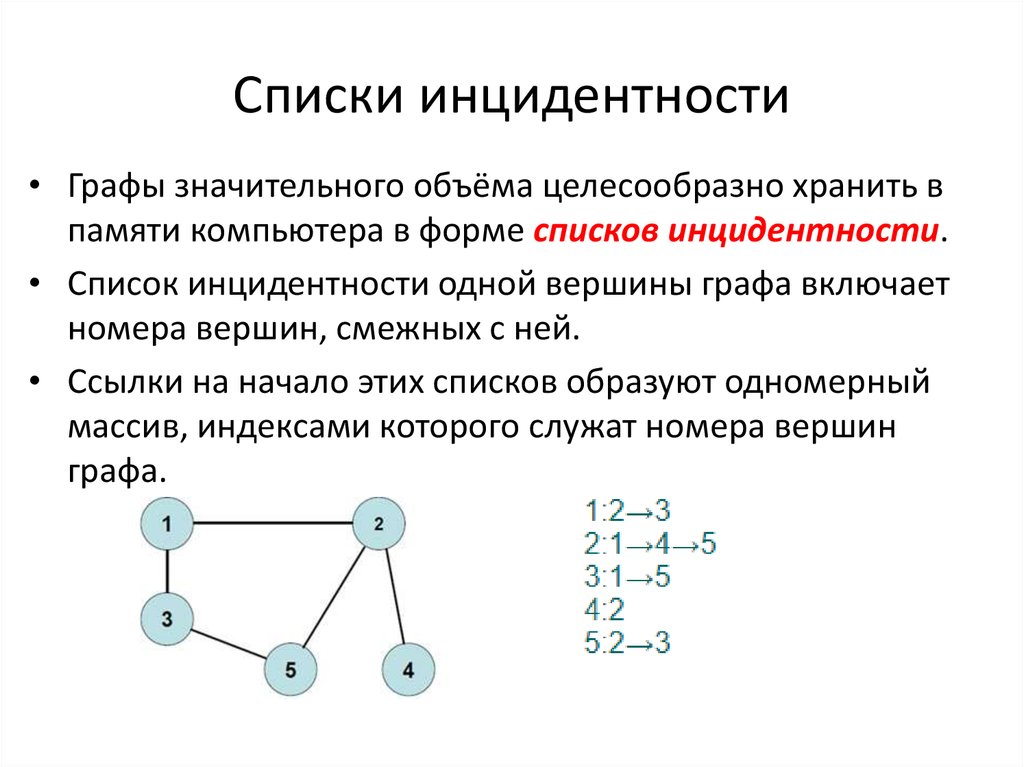 New York: ACM Press, 2006. P. 641-648.
New York: ACM Press, 2006. P. 641-648.
[10] Borowiecki M., Broere I., Frick M., Mihok P., Semanisin G. A
survey of hereditary properties of graphs // Discussiones Mathematicae Graph Theory. 1997. V. 17, N 1 P. 5-50.
[11] Broere I., Dorfling M., Dunbar J. E., Frick M. A path(ological) partition problem // Discussiones Mathematicae Graph Theory. 1998. V. 18, N 1 P. 113-125.
[12] Broere I., Hajnal P., Mihok P., Semanisin G. Partition problems and kernels of graphs // Discussiones Mathematicae Graph Theory. 1997. V. 17, N 2 P. 311-313.
[13] Dunbar J. E., Frick M. Path kernels and partitions // Math. Combin. Comput. 1999. V. 31. P. 137-149.
[14] Dunbar J. E., Frick M., Bullock F. Path partitions and Pn-free sets // Discrete Math. 2004. V. 289. N 1-3, P. 145-155.
[15] Mihok J. Graphs, hypergraphs and matroids. Zielon Gora: Higher College Engrg., 1985.
Публикации автора по теме диссертации
Статьи в журналах
[16] Глебов А. Н., Гордеева А.В., Замбалаева Д.Ж. Алгоритм с оценкой 7/5 для задачи о двух коммивояжерах на минимум с различными весовыми функциями // Сибирские электронные математические известия (htpp://semr.math.nsc.ru). — 2011. — Т. 8. — С. 296-309.
Н., Гордеева А.В., Замбалаева Д.Ж. Алгоритм с оценкой 7/5 для задачи о двух коммивояжерах на минимум с различными весовыми функциями // Сибирские электронные математические известия (htpp://semr.math.nsc.ru). — 2011. — Т. 8. — С. 296-309.
[17] Глебов А.Н., Замбалаева Д.Ж. Полиномиальный алгоритм с оценкой точности 7/9 для задачи о двух коммивояжерах на максимум // Дискретный анализ и исследование операций. — 2011. — Т. 18, № 4. — С. 17-48.
[18] Глебов А.Н., Замбалаева Д.Ж. Приближенный алгоритм решения задачи о двух коммивояжерах на минимум с различными весовыми функциями // Дискретный анализ и исследование операций. — 2011. — Т. 18, № 5. — С. 11-37.
[19] Глебов А.Н., Замбалаева Д.Ж. Путевые разбиения планар-ных графов // Сибирские электронные математические известия (htpp://semr.math.nsc.ru). — 2007. — Т. 4. — С. 450-459.
[20] Замбалаева Д.Ж. Разбиение плоского графа с обхватом 7 на два звездных леса// Дискретный анализ и исследование операций. — 2009. — Т. 16, № 3. — С. 20-46
— 2009. — Т. 16, № 3. — С. 20-46
Прочие публикации
[21} Глебов А.Н., Замбалаева Д.Ж. Путевые и звездные разбиения плоских графов // Материалы IV Всероссийской конференции «Проблемы оптимизации и экономические приложения» (Омск, 29 июня -4 июля 2009). Омск: Полиграфический центр К АН, 2009. С. 121.
[22] Глебов А.Н., Замбалаева Д.Ж. Задача о двух коммивояжерах на минимум в полном графе с различными весовыми функциями // Материалы Российской конференции «Дискретная оптимизация и исследование операций«- (Республика Алтай, 27 июня — 3 июля 2010). Новосибирск: Издательство Института математики, 2010. С. 131.
[23] Глебов А.Н., Замбалаева Д.Ж. Эффективный алгоритм с оценкой точности 7/9 для задачи о двух коммивояжерах на максимум // Информационный бюллетень Ассоциации математического программирования. № 12. XIV Всероссийская конференция «Математическое программирование и приложения» (Екатеринбург, 28 февраля — 4 марта 2011). Екатеринбург: УрО РАН, 2011. С. 168.
С. 168.
[24] Глебов А.Н., Замбалаева Д.Ж., Ивонина Е.В. Эффективные алгоритмы с гарантированными оценками точности для задач одного и двух коммивояжеров на максимум // Труды XV Байкальской международной школы-семинара «Методы оптимизации и их приложения» (пос. Листвянка, 23-29 июня 2011). Т. 4: Дискретная оптимизация. Иркутск: РИО ИДСТУ СО РАН, 2011. С. 82-87.
[25] Zambalaeva D. Decomposing planar graphs into degenerate subgraphs // Abstracts of European conference on Operational Research, Bonn, July 5-8, 2009. P. 183.
[26] Zambalaeva D. 4/3-approximation algorithm for the minimum 2-PSP with different weight functions valued 1 and 2 // Abstracts of International conference on Optimal Discrete Structures and Algorithms (ODSA), Rostok, September 13-15, 2010. P. 66.
Замбалаева Долгор Жамьяновна
Решение задам маршрутизации и путевых разбиений графов методами раскрасок и весовых перераспределений
Автореферат диссертации на соискание ученой степени кандидата физико-математических наук
Подписано в печать 24.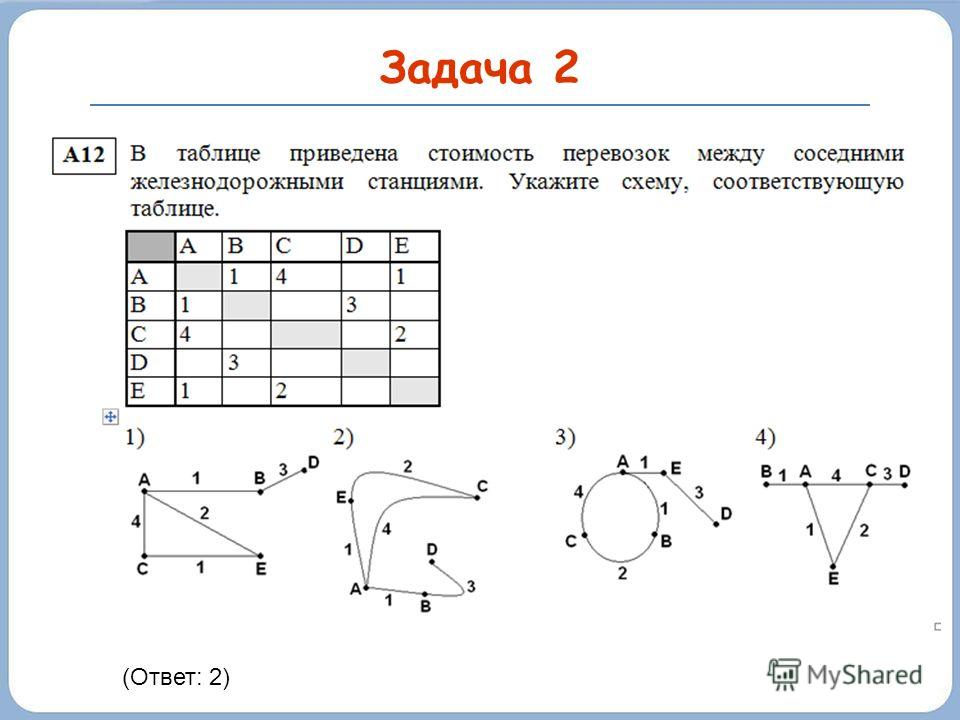 10.2011 г. Формат 60×84 1\1б Усл. печ. л. 1.2 Объем 32 стр. Тираж 80 экз. Заказ № 205
10.2011 г. Формат 60×84 1\1б Усл. печ. л. 1.2 Объем 32 стр. Тираж 80 экз. Заказ № 205
Отпечатано Омега Принт
общих задач по теории графов. Этот пост призван дать обширный, но… | by Kelvin Jose
Этот пост призван предоставить обширный, но интуитивно понятный набор формулировок задач и возможных решений с использованием теории графов.
Многие проблемы, с которыми мы сталкиваемся каждый день, можно было бы перефразировать в виде задачи с графом или близкой к ней подзадачи. Поэтому необходимо иметь некоторое представление о различных вариациях графов и их приложениях. Если вы хотите освежить в памяти основы теории графов — еще раз обязательно посетите это. Последнее даст вам краткое представление о различных типах графиков и их представлениях.
Проблема кратчайшего пути
Одной из наиболее распространенных задач графа является не что иное, как задача кратчайшего пути. Учитывая взвешенный граф, мы должны вычислить кратчайший путь от узла A до G. Сокращенный путь из всех возможных путей определенно будет тем, который оптимизирует функцию стоимости.
Сокращенный путь из всех возможных путей определенно будет тем, который оптимизирует функцию стоимости.
Например, рассмотрим узлы приведенного выше графа в разных городах мира. Если вы внимательно посмотрите на рисунок, мы увидим стоимость, связанную с каждым ребром. Итак, это ориентированно-взвешенный граф. Возвращаясь к нашей интуиции, веса, связанные с каждой парой городов, считаются затратами на путешествие между городами. Чтобы было удобнее, давайте умножим каждую стоимость на 100 долларов, чтобы получить реальную цифру. Таким образом, стоимость проезда между городами A и B составляет 300 долларов, между городами B и F — 600 долларов и так далее. Если мы хотим спланировать экономически эффективное путешествие между двумя городами, мы должны свериться с этим графиком, чтобы оценить общую стоимость. Между двумя городами может быть несколько путей, но путь, который мы ищем больше всего, будет тот, который снижает стоимость до минимума. Это действительно простой, но понятный пример задачи о кратчайшем пути.
К счастью, существует пара алгоритмов, которые могут привести нас из узла A в узел B с минимальными затратами. LADGHT PRIMULE , Dijksra’s , Bellman — Ford , Floyd — Warshall , A* и SolsEST SoldSEST SoldSEST.
Связность
Несмотря на простое название, связность является большой проблемой в теории графов, что указывает на существует ли путь от узла A к узлу B . Следует отметить одну вещь: нас волнует не минимальная стоимость, а только путь.
Фото автораСамый простой подход к решению этой проблемы состоит в том, чтобы выполнить либо поиск в ширину , либо поиск в глубину .
Отрицательные циклы Иногда наш граф может иметь отрицательные ребра, которые могут оборвать весь поток графа. Я бы сказал, что негативный цикл — это бесконечная ловушка. Итак, мы исследуем, существует ли ребро с отрицательным весом между любой парой узлов, и если да, то как оно образует цикл.
Итак, мы исследуем, существует ли ребро с отрицательным весом между любой парой узлов, и если да, то как оно образует цикл.
В данном графе находится отрицательное ребро. Очевидно, это вносит свой вклад в формирование отрицательных циклов. Один из таких циклов (B, C, D) . Если мы будем циклически проходить через эти ребра, мы будем бесконечны с минимальными затратами навсегда. Тем не менее, есть некоторые контексты, в которых отрицательные циклы играют ангельскую роль. Например, если мы запустим игру с обменом денег из одной валюты в другую валюту и еще в одну, мы могли бы использовать такой отрицательный график, который, в свою очередь, мог бы дать некоторую экономическую выгоду. Это всего лишь гипотеза, которая может сбыться, а может и не сбыться, потому что курсы валют не будут оставаться неизменными так долго. Существуют определенные алгоритмы, такие как Bellman — Ford и Floyd — Warshall для обнаружения отрицательных циклов.
Сильно связанные компоненты
Это автономные циклы с ориентированным графом, так что — каждый узел в цикле может достигать всех других узлов в том же цикле.
Фото автораВажно видеть, есть ли сильно связанные компоненты или нет. Циклы, заключенные в красные прямоугольники, являются примерами таких компонентов. Различные алгоритмы, используемые для обнаружения этих компонентов, Алгоритмы Тарьяна и Косараджу.
Задача коммивояжера
Никто не получил бы степень в области информатики, не услышав этот термин. Мне очень жаль, если ты этого не сделал. Но его совершенно легко понять, и он имеет множество приложений в реальном мире.
Фото из блога Essay Corp. Задача структурирована в виде заданного списка городов и стоимости или расстояния между всеми возможными парами городов. Затем продавец должен начать и закончить в одном и том же узле, но должен посетить каждый город ровно один раз на траектории с минимальными затратами или расстоянием — в зависимости от целевой функции. Проблема выглядит очень простой и привлекла большое внимание в задачах оценки пути и оптимизации затрат. Для решения этой проблемы доступны несколько алгоритмов, таких как ветвь и граница и Хелда-Карпа. Это по-прежнему сложная вычислительная задача, но исследования продолжаются.
Проблема выглядит очень простой и привлекла большое внимание в задачах оценки пути и оптимизации затрат. Для решения этой проблемы доступны несколько алгоритмов, таких как ветвь и граница и Хелда-Карпа. Это по-прежнему сложная вычислительная задача, но исследования продолжаются.
Мосты
Мосты — это ребра в графе, удаление которых может увеличить количество связанных компонентов в графе. Мосты действительно важны, потому что они представляют уязвимости и узкие места на графике.
Фото с сайта onion-router.netУдаление ребра, соединяющего узлы G и N, приведет к соединению двух отдельных компонентов. Если это настоящий мост, то его снос приведет к двум изолированным городам. Таким образом, мост всегда является слабым местом, потому что его разъединение создаст дополнительные болевые точки.
Точно так же точка сочленения представляет собой узел, удаление которого приводит к увеличению общего количества связанных компонентов.
Минимальное остовное дерево
Минимальное остовное дерево — это подмножество ребер, которые соединяют все вершины вместе, образуя дерево с минимальной стоимостью.
Как видите, данный график взвешен и ненаправлен. Более жирные ребра показывают остовное дерево с минимальной стоимостью, которое соединяет все вершины, но с минимальной стоимостью. Мы формулируем различные проблемы, такие как планирование маршрута, проектирование схем и многое другое, в виде минимального связующего дерева, которое может быть решено с помощью Алгоритмы Крускала и Прима.
Максимальный сетевой поток
Как видно из названия, эти задачи можно использовать для оценки максимального объема (в зависимости от задачи), который может вместить график. Например, если мы рассмотрим электрическую сеть как наш граф, а столбы электропередач — как разные узлы графа. У нас могут быть предположения о том, сколько электроэнергии может быть отправлено по сети, не затрагивая энергосистему. Другой пример — мобильная сеть, в которой каждый пользователь действует как узел графа. Как и в предыдущем примере, мы можем вычислить максимальное количество пользователей, которые могут оставаться в сети без сетевого трафика.
Эта формулировка может ответить на максимум всех и предсказать потенциальные узкие места. Используются различные алгоритмы: Форда-Фулкерсона и Алгоритмы Эдмондса Карпа и Диника.
Мы рассмотрели почти все проблемы теории графов. Мы обсудим каждый алгоритм, упомянутый здесь, в следующих постах. Я очень рад поделиться всеми ими с вами. А пока, увидимся!
4.E: Теория графов (упражнения) — Математика LibreTexts
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 15224
1
Если 10 человек пожали друг другу руки, сколько рукопожатий произошло? Какое отношение этот вопрос имеет к теории графов?
- Ответить
Здесь запрашивается количество ребер в \(K_{10}\text{.
 }\) Каждая вершина (человек) имеет степень (рукопожатие) 9 (человек). Таким образом, сумма степеней равна \(90\text{.}\). Однако степени учитывают каждое ребро (рукопожатие) дважды, поэтому в графе 45 ребер. Именно столько рукопожатий произошло.
}\) Каждая вершина (человек) имеет степень (рукопожатие) 9 (человек). Таким образом, сумма степеней равна \(90\text{.}\). Однако степени учитывают каждое ребро (рукопожатие) дважды, поэтому в графе 45 ребер. Именно столько рукопожатий произошло.
2
В группе из 5 человек каждый может дружить ровно с двумя людьми в группе? А как насчет 3 человек в группе?
- Ответить
Каждый может дружить ровно с двумя людьми. Вы можете расположить 5 человек по кругу и сказать, что все дружат с двумя людьми по обе стороны от них (таким образом вы получите график \(C_5\)). Однако не каждый может дружить с тремя людьми. Это привело бы к графу с нечетным числом вершин нечетной степени, что невозможно, поскольку сумма степеней должна быть четной.
3
Возможно ли, чтобы два различных (неизоморфных) графов имели одинаковое количество вершин и одинаковое количество ребер? Что, если степени вершин в двух графах одинаковы (например, оба графа имеют вершины со степенями 1, 2, 2, 3 и 4)? Нарисуйте два таких графика или объясните, почему нет.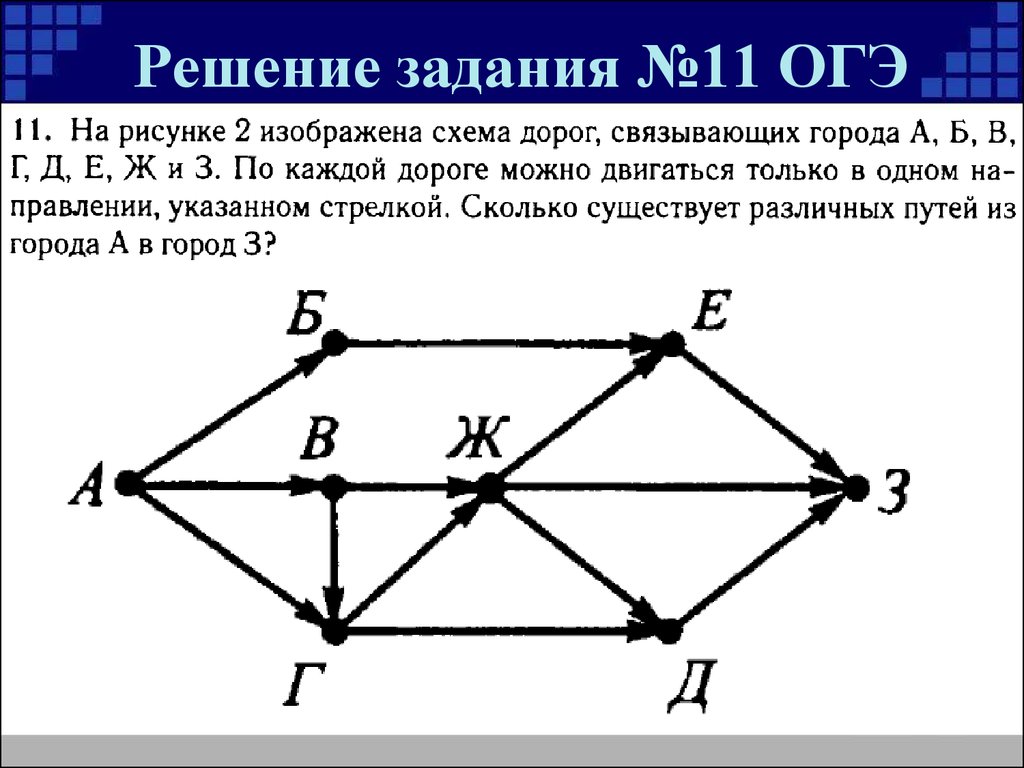
- Ответить
Да. Например, оба приведенных ниже графа содержат 6 вершин, 7 ребер и имеют степени (2,2,2,2,3,3).
4
Два приведенных ниже графика равны? Являются ли они изоморфными? Если они изоморфны, укажите изоморфизм. Если нет, объясните.
- График 1: \(V = \{a,b,c,d,e\}\text{,}\) \(E = \{\{a,b\}, \{a,c\ }, \{a,e\}, \{b,d\}, \{b,e\}, \{c,d\}\}\text{.}\)
- График 2:
- Ответить
Графики не равны. Например, у графа 1 есть ребро \(\{a,b\}\), а у графа 2 этого ребра нет. Они изоморфны. Один из возможных изоморфизмов: \(f:G_1\to G_2\), определяемый формулой \(f(a) = d\text{,}\) \(f(b) = c\text{,}\) \(f( c) = e\text{,}\) \(f(d) = b\text{,}\) \(f(e) = a\text{.}\)
5
Рассмотрим следующие два графика:
\(G_1\)
- \(V_1=\{a,b,c,d,e,f,g\}\)
- \(E_1=\{\{a,b\},\{a,d\},\{b,c\},\{b,d\},\{b,e\},\{b ,f\},\{c,g\},\{d,e\},\)
- \(\{е,е\},\{е,г\}\}\текст{.
 }\)
}\)
\(G_2\)
- \(V_2=\{v_1,v_2,v_3,v_4,v_5,v_6,v_7\}\text{,}\)
- \(E_2=\{\{v_1,v_4\},\{v_1,v_5\},\{v_1,v_7\},\{v_2,v_3\},\{v_2,v_6\},\)
- \(\{v_3,v_5\},\{v_3,v_7\},\{v_4,v_5\},\{v_5,v_6\},\{v_5,v_7\}\}\)
- Пусть \(f:G_1 \rightarrow G_2\) будет функцией, которая переводит вершины графа 1 в вершины графа 2. Эта функция задается следующей таблицей:
\(х\) \(а\) \(б\) \(с\) \(д\) \(д\) \(ф\) \(г\) \(ф(х)\) \(v_4\) \(v_5\) \(v_1\) \(v_6\) \(v_2\) \(v_3\) \(v_7\) Определяет ли \(f\) изоморфизм между Графиком 1 и Графиком 2? Объяснять.

- Определите новую функцию \(g\) (с \(g\not=f\)), которая определяет изоморфизм между графиком 1 и графиком 2.
- Является ли график, изображенный ниже, изоморфным графикам 1 и 2? Объяснять.
6
Какие из приведенных ниже графов являются двудольными? Обоснуйте свои ответы.
- Ответить
Три графа двудольные. Тот, который не является \(C_7\) (второй справа). Чтобы увидеть, что эти три графа являются двудольными, мы можем просто разделить их на два множества \(A\) и \(B\text{,}\), как показано ниже:
Граф \(C_7\) не является двудольным, потому что это нечетных циклов. Вы хотели бы поместить каждую вторую вершину в набор \(A\text{,}\), но если вы будете двигаться таким образом по часовой стрелке, последняя вершина также будет помещена в набор \(A\text{,}\) оставляя две вершины \(A\) смежными (что делает его не двудольным).

7
Для чего \(n \ge 3\) граф \(C_n\) двудольный?
8
За каждое из следующего постарайтесь дать два различных непомеченных графов с заданными свойствами или объяснить, почему это невозможно.
- Два разных дерева с одинаковым количеством вершин и одинаковым количеством ребер. Дерево — это связный граф без циклов.
- Два различных графа с 8 вершинами степени 2.
- Два различных графа с 5 вершинами степени 4.
- Два различных графа с 5 вершинами степени 3.
- Ответ
- Например:
- Это невозможно, если мы требуем, чтобы графы были связаны. Если нет, мы могли бы взять \(C_8\) в качестве одного графа и две копии \(C_4\) в качестве другого.
- Невозможно. Если у вас есть граф с 5 вершинами степени 4, то каждая вершина должна быть смежной с любой другой вершиной.
 Это граф \(K_5\text{.}\)
Это граф \(K_5\text{.}\) - Это невозможно. На самом деле нет ни одного графа с таким свойством (такой граф имел бы \(5\cdot 3/2 = 7,5\) ребер).
1
Может ли планарный граф иметь 6 вершин, 10 ребер и 5 граней? Объяснять.
- Ответить
Нет. Планарный (связный) граф должен удовлетворять формуле Эйлера: \(v — e + f = 2\text{.}\) Здесь \(v — e + f = 6 — 10 + 5 = 1\text{. }\)
2
Граф \(G\) имеет 6 вершин со степенями \(2, 2, 3, 4, 4, 5\text{.}\) Сколько ребер имеет \(G\)? Может ли \(G\) быть плоским? Если да, то сколько лиц у него будет. Если нет, объясните.
- Ответить
\(G\) имеет 10 ребер, так как \(10 = \frac{2+2+3+4+4+5}{2}\text{.}\) может быть плоским, и тогда 6 граней, используя формулу Эйлера: \(6-10+f = 2\) означает \(f = 6\text{.}\) Однако, чтобы убедиться, что она действительно плоская, нам нужно нарисовать график с этими степени вершины без пересечения ребер.
 Это можно сделать методом проб и ошибок (и возможно).
Это можно сделать методом проб и ошибок (и возможно).
3
Я думаю о многограннике с 12 гранями. Семь треугольников и четыре четырехугольника. Многогранник имеет 11 вершин, включая вершины вокруг загадочной грани. Сколько сторон у последней грани?
- Ответить
Допустим, последний многогранник имеет \(n\) ребер, а также \(n\) вершин. Тогда общее количество ребер многогранника равно \((7 \cdot 3 + 4 \cdot 4 + n)/2 = (37 + n)/2\text{.}\) В частности, мы знаем последнюю грань должно иметь нечетное число ребер. Мы также имеем, что \(v = 11 \text{.}\) По формуле Эйлера мы имеем \(11 — (37+n)/2 + 12 = 2\text{,}\) и решая для \(n \) мы получаем \(n = 5\text{,}\), поэтому последняя грань представляет собой пятиугольник.
4
Рассмотрим некоторые классические многогранники.
- Октаэдр — правильный многогранник, состоящий из 8 равносторонних треугольников (похож на две пирамиды со склеенными основаниями).
 Нарисуйте плоское графическое представление октаэдра. Сколько вершин, ребер и граней у октаэдра (и вашего графа)?
Нарисуйте плоское графическое представление октаэдра. Сколько вершин, ребер и граней у октаэдра (и вашего графа)? - Традиционный дизайн футбольного мяча на самом деле представляет собой (сферическую проекцию) усеченного икосаэдра. Он состоит из 12 правильных пятиугольников и 20 правильных шестиугольников. Никакие два пятиугольника не являются смежными (поэтому ребра каждого пятиугольника являются общими только для шестиугольников). Сколько вершин, ребер и граней имеет усеченный икосаэдр? Объясните, как вы пришли к своим ответам. Бонус: нарисуйте представление усеченного икосаэдра на плоской диаграмме.
- Ваш «друг» утверждает, что построил выпуклый многогранник из 2 треугольников, 2 квадратов, 6 пятиугольников и 5 восьмиугольников. Докажите, что ваш друг лжет. Подсказка: каждая вершина выпуклого многогранника должна граничить не менее чем с тремя гранями.
5
Докажите формулу Эйлера, используя индукцию по количеству ребер в графе.
- Ответить
Доказательство
Пусть \(P(n)\) будет утверждением «каждый планарный граф, содержащий \(n\) ребер, удовлетворяет \(v — n + f = 2\text{.
 }\)». Мы покажем \(P( n)\) верно для всех \(n \ge 0\text{.}\) Базовый случай: существует только один граф с нулевыми ребрами, а именно одна изолированная вершина. В этом случае \(v = 1\text{,}\) \(f = 1\) и \(e = 0\text{,}\), поэтому формула Эйлера верна. Индуктивный случай: предположим, что \(P(k)\) верно для некоторого произвольного \(k \ge 0\text{.}\). Теперь рассмотрим произвольный граф, содержащий \(k+1\) ребер (и \(v\ ) вершины и \(f\) грани). Независимо от того, как выглядит этот граф, мы можем удалить одно ребро, чтобы получить граф с \(k\) ребер, к которому мы можем применить индуктивную гипотезу. Есть две возможности. Во-первых, ребро, которое мы удаляем, может быть инцидентно вершине степени 1. В этом случае также удалите эту вершину. Меньший граф теперь будет удовлетворять \(v-1 — k + f = 2\) по предположению индукции (удаление ребра и вершины не уменьшило количество граней). Добавление ребра и вершины назад дает \(v — (k+1) + f = 2\text{,}\) по мере необходимости. Второй случай состоит в том, что удаляемое нами ребро инцидентно вершинам степени больше единицы.
}\)». Мы покажем \(P( n)\) верно для всех \(n \ge 0\text{.}\) Базовый случай: существует только один граф с нулевыми ребрами, а именно одна изолированная вершина. В этом случае \(v = 1\text{,}\) \(f = 1\) и \(e = 0\text{,}\), поэтому формула Эйлера верна. Индуктивный случай: предположим, что \(P(k)\) верно для некоторого произвольного \(k \ge 0\text{.}\). Теперь рассмотрим произвольный граф, содержащий \(k+1\) ребер (и \(v\ ) вершины и \(f\) грани). Независимо от того, как выглядит этот граф, мы можем удалить одно ребро, чтобы получить граф с \(k\) ребер, к которому мы можем применить индуктивную гипотезу. Есть две возможности. Во-первых, ребро, которое мы удаляем, может быть инцидентно вершине степени 1. В этом случае также удалите эту вершину. Меньший граф теперь будет удовлетворять \(v-1 — k + f = 2\) по предположению индукции (удаление ребра и вершины не уменьшило количество граней). Добавление ребра и вершины назад дает \(v — (k+1) + f = 2\text{,}\) по мере необходимости. Второй случай состоит в том, что удаляемое нами ребро инцидентно вершинам степени больше единицы. В этом случае удаление ребра сохранит количество вершин прежним, но уменьшит количество граней на единицу. Таким образом, по индуктивному предположению мы будем иметь \(v — k + f-1 = 2\text{.}\) Добавление ребра обратно даст \(v — (k+1) + f = 2\) по мере необходимости. Следовательно, по принципу математической индукции формула Эйлера верна для всех плоских графов.
В этом случае удаление ребра сохранит количество вершин прежним, но уменьшит количество граней на единицу. Таким образом, по индуктивному предположению мы будем иметь \(v — k + f-1 = 2\text{.}\) Добавление ребра обратно даст \(v — (k+1) + f = 2\) по мере необходимости. Следовательно, по принципу математической индукции формула Эйлера верна для всех плоских графов.
6
Докажите формулу Эйлера, используя индукцию по количеству вершин в графе.
7
Формула Эйлера (\(v — e + f = 2\)) верна для всех связных плоских графов. Что делать, если граф несвязен? Предположим, что планарный граф состоит из двух компонентов. Каково теперь значение \(v — e + f\)? Что, если он имеет \(k\) компонент?
8
Докажите, что граф Петерсена (ниже) не является плоским.
- Ответить
Какова длина самого короткого цикла? (Эта величина обычно называется обхватом графика.
 )
)
9
Докажите, что любой планарный граф с \(v\) вершинами и \(e\) ребрами удовлетворяет \(e \le 3v — 6\text{.}\)
- Ответ
Доказательство
Мы знаем, что в любом плоском графе число граней \(f\) удовлетворяет условию \(3f \le 2e\), так как каждая грань ограничена по крайней мере тремя ребрами, но каждое ребро граничит с двумя гранями. Объедините это с формулой Эйлера:
\begin{equation*} v — e + f = 2 \end{equation*} \begin{equation*} v — e + \frac{2e}{3} \ge 2 \end{equation*} \begin{ уравнение*} 3v — e \ge 6 \end{equation*} \begin{equation*} 3v — 6 \ge e. \end{уравнение*}
10
Докажите, что любой планарный граф должен иметь вершину степени 5 или меньше.
1
Какое наименьшее количество цветов нужно, чтобы правильно раскрасить вершины \(K_{4,5}\text{?}\) То есть найти хроматическое число графа.
- Ответить
2, так как граф двудольный.
 Один цвет для верхнего набора вершин, другой цвет для нижнего набора вершин.
Один цвет для верхнего набора вершин, другой цвет для нижнего набора вершин.
2
Нарисуйте граф с хроматическим числом 6 (т. е. для правильного окрашивания вершин требуется 6 цветов). Может ли ваш график быть планарным? Объяснять.
- Ответить
Например, \(K_6\text{.}\) Если хроматическое число равно 6, то граф не является плоским; Теорема о четырех цветах утверждает, что все планарные графы можно раскрасить в четыре или меньше цветов.
3
Найдите хроматическое число каждого из следующих графиков.
- Ответить
Хроматические числа 2, 3, 4, 5 и 3 соответственно слева направо.
4
Группа из 10 друзей решает отправиться в хижину в лесу (где ничего не может пойти не так). К сожалению, некоторые из этих друзей встречались друг с другом в прошлом, и все еще немного неловко. Чтобы получить кабину, им нужно разбиться на какое-то количество машин, причем никакие два человека, которые встречались, не должны находиться в одной машине.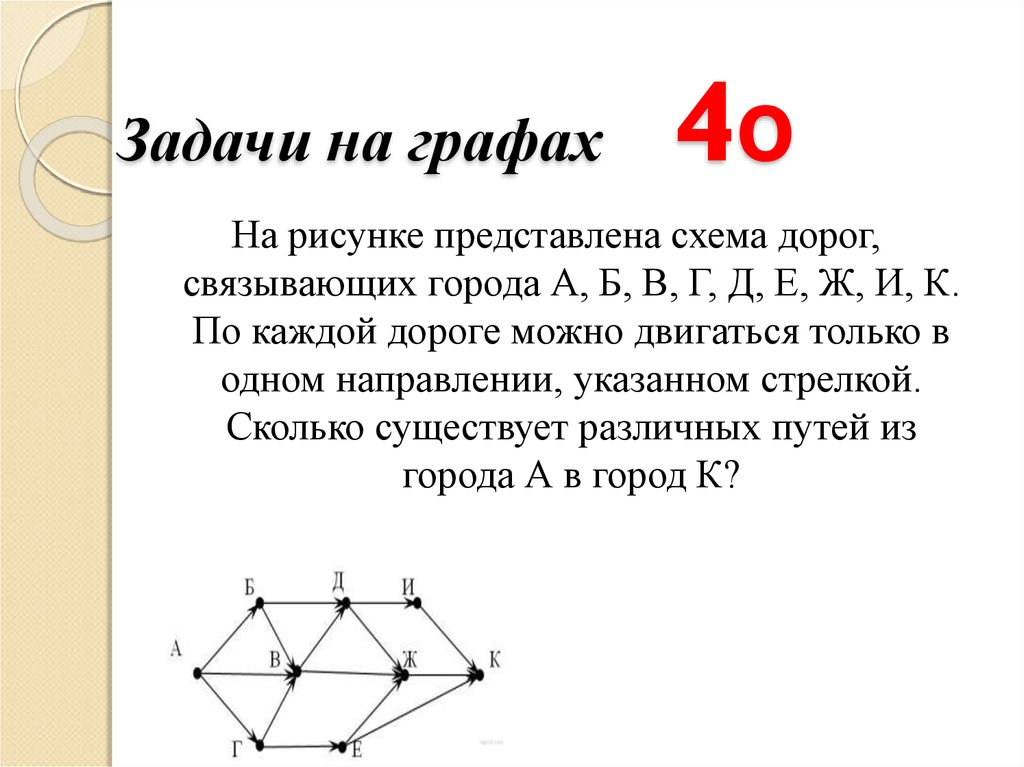
- Какое наименьшее количество автомобилей вам нужно, если все отношения были строго гетеросексуальными? Представьте пример такой ситуации с помощью графика. Какой график у вас получился?
- Поскольку некоторые из этих друзей встречаются, между друзьями одного пола также возникают конфликты, перечисленные ниже. Какое наименьшее количество бесконфликтных машин они могли взять в салон?
Друг А Б С Д Э Ф Г Х я Дж Конфликты с БЭЖ АДГ ХДЖ БФ АИ ДЖ Б ДИ ЭХДЖ АКФИ - Какое отношение эти вопросы имеют к раскрашиванию?
5
Какое наименьшее количество цветов можно использовать для раскраски вершин куба так, чтобы никакие две соседние вершины не были окрашены одинаково?
- Ответить
Куб можно представить в виде плоского графа и раскрасить двумя цветами следующим образом:
Поскольку покрасить вершины в один цвет было бы невозможно, мы видим, что куб имеет хроматическое число 2 (он двудольный).

6
Докажите, что хроматическое число любого дерева равно двум. Напомним, дерево — это связный граф без циклов.
- Опишите процедуру раскрашивания дерева ниже.
- Хроматическое число \(C_n\) равно двум, когда \(n\) четно. Что пойдет не так, если \(n\) нечетно?
- Докажите, что ваша процедура из пункта (а) всегда работает для любого дерева.
- Теперь докажите по индукции, что каждое дерево имеет хроматическое число 2.
7
Докажите теорему о шести красках: каждый планарный граф имеет хроматическое число 6 или меньше. Не принимайте теорему о четырех красках (доказательство которой НАМНОГО сложнее), но вы можете предположить, что каждый планарный граф содержит вершину степени не выше 5,9.0005
8
Не все графики идеальны. Приведите пример графа с хроматическим числом 4, который не содержит копии \(K_4\text{. }\) То есть не должно быть 4 вершин, все попарно смежные.
}\) То есть не должно быть 4 вершин, все попарно смежные.
- Ответить
Колесо графа ниже имеет это свойство. Внешняя часть колеса образует нечетный цикл, поэтому требуется 3 цвета, центр колеса должен отличаться от всех внешних вершин.
9
Докажите индукцией по вершинам, что любой граф \(G\), содержащий хотя бы одну вершину степени меньше \(\Delta(G)\) (максимальная степень всех вершин в \(G\) ) имеет хроматическое число не более \(\Delta(G)\text{.}\)
10
У вас есть набор букв магнитного алфавита (по одной из 26 букв алфавита), которые вам нужно поставить в ящики. По очевидным причинам вы не хотите помещать две последовательные буквы в одну и ту же ячейку. Какое наименьшее количество коробок вам нужно (при условии, что коробки могут вместить столько писем, сколько им нужно)?
- Ответить
Если бы мы нарисовали граф, в котором каждая буква представляет собой вершину, а каждое ребро соединяет две последовательные буквы в алфавите, у нас был бы граф, содержащий две вершины степени 1 (A и Z), а остальные 24 вершины имели бы степень 2 (например, \(D\) будет смежным как с \(C\), так и с \(E\)).
 По теореме Брукса этот граф имеет хроматическое число не более 2, так как это максимальная степень в графе, а граф не является полным графом или нечетным циклом. Таким образом, нужны только две коробки.
По теореме Брукса этот граф имеет хроматическое число не более 2, так как это максимальная степень в графе, а граф не является полным графом или нечетным циклом. Таким образом, нужны только две коробки.
11
Докажите, что если вы покрасите каждое ребро \(K_6\) в красный или синий цвет, вы гарантированно получите одноцветный треугольник (то есть полностью красный или полностью синий треугольник).
1
Вы и ваши друзья хотите совершить поездку на юго-запад на машине. Вы посетите девять штатов ниже, со следующим довольно странным правилом: вы должны пересечь каждую границу между соседними штатами ровно один раз (так, например, вы должны пересечь границу Колорадо-Юта ровно один раз). Ты можешь сделать это? Если да, имеет ли значение, где вы начнете свое путешествие? Какой факт из теории графов решает эту проблему?
- Ответить
Это вопрос о нахождении путей Эйлера. Нарисуйте граф с вершиной в каждом состоянии и соедините вершины, если их состояния имеют общую границу.
 Ровно две вершины будут иметь нечетную степень: вершины для Невады и Юты. Таким образом, вы должны начать свое путешествие в одном из этих штатов, а закончить его в другом.
Ровно две вершины будут иметь нечетную степень: вершины для Невады и Юты. Таким образом, вы должны начать свое путешествие в одном из этих штатов, а закончить его в другом.
2
Какой из следующих графов содержит путь Эйлера? Какие из них содержат схему Эйлера?
- \(К_4\)
- \(К_5\текст{.}\)
- \(К_{5,7}\)
- \(К_{2,7}\)
- \(С_7\)
- \(P_7\)
- Ответить
- \(K_4\) не имеет эйлерова пути или схемы.
- \(K_5\) имеет эйлерову схему (а значит, и эйлеров путь).
- \(K_{5,7}\) не имеет эйлерова пути или схемы.
- \(K_{2,7}\) имеет эйлеров путь, но не эйлерову схему.
- \(C_7\) имеет схему Эйлера (это граф цепи!)
- \(P_7\) имеет путь Эйлера, но не имеет схемы Эйлера.
3
Эдвард А. Маус только что закончил свой новый дом. План этажа показан ниже:
Маус только что закончил свой новый дом. План этажа показан ниже:
- Эдвард хочет провести экскурсию по своей новой квартире подруге-мышке. Могут ли они пройти через каждый дверной проем ровно один раз? Если да, то в каких комнатах они должны начинать и заканчивать экскурсию? Объяснять.
- Можно ли обойти дом, посетив каждую комнату ровно один раз (не обязательно через каждый дверной проем)? Объяснять.
- Спустя несколько мышиных лет Эдвард решает перестроиться. Он хотел бы добавить несколько новых дверей между комнатами, которые у него есть. Конечно, он не может добавить двери снаружи дома. Может ли в каждой комнате быть нечетное количество дверей? Объяснять.
4
Для каких \(n\) граф \(K_n\) содержит эйлеров цикл? Объяснять.
- Ответить
Когда \(n\) нечетно, \(K_n\) содержит схему Эйлера. Это связано с тем, что каждая вершина имеет степень \(n-1\text{,}\), поэтому нечетное \(n\) приводит к тому, что все степени четные.

5
Для каких \(m\) и \(n\) граф \(K_{m,n}\) содержит путь Эйлера? Цепь Эйлера? Объяснять.
- Ответить
Если оба числа \(m\) и \(n\) четны, то \(K_{m,n}\) имеет эйлеров цикл. Когда оба нечетны, пути или цепи Эйлера не существует. Если одно равно 2, а другое нечетно, то существует эйлерова путь, но не эйлерова схема.
6
Для каких \(n\) \(K_n\) содержит путь Гамильтона? Цикл Гамильтона? Объяснять.
- Ответить
Добавьте сюда текст. Не удаляйте этот текст первым.
Все значения \(n\text{.}\) В частности, \(K_n\) содержит \(C_n\) в качестве подгруппы, которая представляет собой цикл, включающий каждую вершину.
7
Для каких \(m\) и \(n\) граф \(K_{m,n}\) содержит путь Гамильтона? Цикл Гамильтона? Объяснять.
- Ответить
Пока \(|m-n| \le 1\text{,}\) граф \(K_{m,n}\) будет иметь путь Гамильтона.
 Чтобы иметь цикл Гамильтона, мы должны иметь \(m=n\text{.}\)
Чтобы иметь цикл Гамильтона, мы должны иметь \(m=n\text{.}\)
8
В Кенигсберг приехал строитель мостов и хочет добавить мосты так, чтобы можно было пройти по каждому мосту ровно один раз. Сколько мостов нужно построить?
- Ответить
Если мы построим один мост, у нас может быть путь Эйлера. Для схемы Эйлера необходимо построить два моста.
9
Ниже приведен график дружбы между группой студентов (каждая вершина — студент, а каждое ребро — дружба). Возможно ли, чтобы ученики сидели за круглым столом так, чтобы каждый ученик сидел между двумя друзьями? Какое отношение этот вопрос имеет к путям?
- Ответить
Мы ищем гамильтонов цикл, и на этом графе он есть:
10
- Предположим, что граф имеет путь Гамильтона. Какое максимальное количество вершин степени один может иметь граф? Объясните, почему ваш ответ правильный.

- Найдите граф, в котором нет пути Гамильтона, даже если ни одна вершина не имеет степени один. Объясните, почему ваш пример работает.
11
Рассмотрим следующий график:
- Найдите путь Гамильтона. Можно ли расширить ваш путь до цикла Гамильтона?
- Является ли граф двудольным? Если да, то сколько вершин в каждой «части»?
- Используйте свой ответ на пункт (b), чтобы доказать, что в графе нет цикла Гамильтона.
- Предположим, у вас есть двудольный граф \(G\), в одной части которого как минимум на две вершины больше, чем в другой. Докажите, что \(G\) не имеет пути Гамильтона.
1
Найдите паросочетание двудольных графов ниже или объясните, почему паросочетания не существует.
- Ответить
Первый и третий графики имеют паросочетание, выделенное жирным шрифтом (есть и другие паросочетания). Средний граф не имеет паросочетания.
 Если вы посмотрите на три обведенные вершины, то увидите, что они имеют только двух соседей, что нарушает условие соответствия \(\card{N(S)} \ge \card{S}\) (три обведенные вершины образуют множество \(С\)).
Если вы посмотрите на три обведенные вершины, то увидите, что они имеют только двух соседей, что нарушает условие соответствия \(\card{N(S)} \ge \card{S}\) (три обведенные вершины образуют множество \(С\)).
2
Двудольный граф, у которого нет паросочетания, все еще может иметь частичное совпадение . Под этим мы подразумеваем набор из ребер , для которого ни одна вершина не принадлежит более чем одному ребру (но, возможно, не принадлежит ни одному). Каждый двудольный граф (с хотя бы одним ребром) имеет частичное паросочетание, поэтому мы можем искать наибольшее частичное паросочетание в графе.
Ваш «друг» утверждает, что нашел наибольшее частичное совпадение для графика ниже (ее совпадение выделено жирным шрифтом). Она объясняет, что никакое другое ребро не может быть добавлено, потому что все ребра, не используемые в ее частичном сопоставлении, соединяются с совпавшими вершинами. Она правильная?
3
Один из способов проверить, является ли частичное совпадение максимальным, — построить чередующийся путь .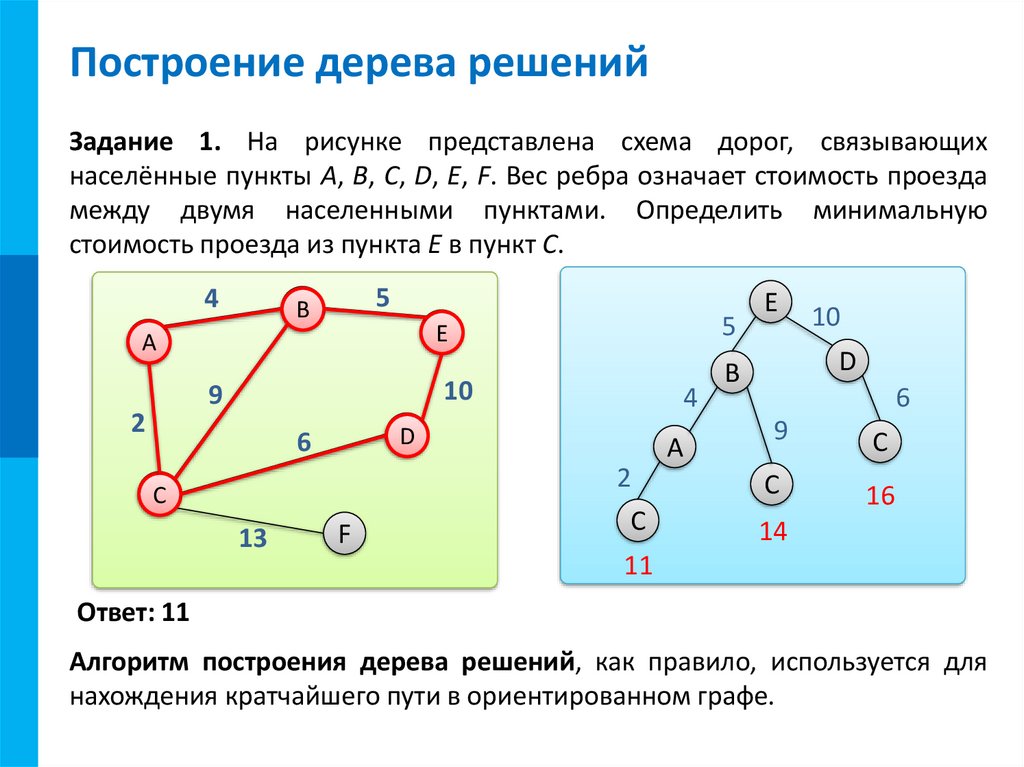 Это последовательность смежных ребер, которые чередуются между ребрами в совпадении и ребрами, не входящими в соответствие (ни одно ребро не может использоваться более одного раза). Если чередующийся путь начинается и заканчивается с ребром , а не в паросочетании, то он называется увеличивающим путем .
Это последовательность смежных ребер, которые чередуются между ребрами в совпадении и ребрами, не входящими в соответствие (ни одно ребро не может использоваться более одного раза). Если чередующийся путь начинается и заканчивается с ребром , а не в паросочетании, то он называется увеличивающим путем .
- Найдите максимально возможный чередующийся путь для частичного совпадения графа вашего друга. Это увеличивающий путь? Как это поможет вам найти большее соответствие?
- Найдите максимально возможный чередующийся путь для приведенного ниже частичного совпадения. Есть ли увеличивающие пути? Является ли частичное совпадение самым большим из существующих в графе?
4
Две богатейшие семьи Вестероса решили заключить союз посредством брака. В первой семье 10 сыновей, во второй 10 девочек. Возраст детей в обеих семьях совпадает. Чтобы избежать неуместности, семьи настаивают на том, чтобы каждый ребенок женился на ком-то своего возраста или на одной позиции младше или старше. На самом деле график, представляющий приятные браки, выглядит так:
На самом деле график, представляющий приятные браки, выглядит так:
Вопрос: сколько различных допустимых брачных союзов, при которых выдаются замуж все 20 детей, возможны?
- Сколько брачных союзов возможно, если мы настаиваем на том, что ровно 6 мальчиков женятся на девочках не их возраста?
- Не могли бы вы обобщить предыдущий ответ, чтобы получить общее количество заключенных браков?
- Откуда вы знаете, что вы правы? Попробуйте считать по-другому. Посмотрите на меньшие размеры семьи и получите последовательность.
- Можете ли вы дать рекуррентное соотношение, соответствующее задаче?
5
Мы говорим, что множество вершин \(A \subseteq V\) является вершинным покрытием , если каждое ребро графа инцидентно вершине в покрытии (таким образом, вершинное покрытие покрывает ребер ). Так как \(V\) сам является вершинным покрытием, каждый граф имеет вершинное покрытие. Интересен вопрос о нахождении минимального покрытия из вершин, которое использует наименьшее возможное количество вершин.
Интересен вопрос о нахождении минимального покрытия из вершин, которое использует наименьшее возможное количество вершин.
- Предположим, у вас есть сопоставление графа. Как вы можете использовать это, чтобы получить минимальное вершинное покрытие? Всегда ли будет работать ваш метод?
- Предположим, у вас есть минимальное вершинное покрытие для графа. Как вы можете использовать это, чтобы получить частичное совпадение? Всегда ли будет работать ваш метод?
- Какая связь между размером минимального покрытия вершин и размером максимального частичного паросочетания в графе?
6
Для многих приложений паросочетаний имеет смысл использовать двудольные графы. Однако вы можете задаться вопросом, есть ли вообще способ находить соответствия на графах.
- Для какого \(n\) есть паросочетание в полном графе \(K_n\)?
- Докажите, что если в графе есть паросочетание, то \(\card{V}\) четно.
- Верно ли обратное? То есть все ли графы с \(\card{V}\) вообще имеют соответствие?
- Что, если нам также потребуется условие соответствия? Докажите или опровергните: если граф с четным числом вершин удовлетворяет условию \(\card{N(S)} \ge \card{S}\) для всех \(S \subseteq V\text{,}\), то граф имеет соответствие.

4.E: Теория графов (упражнения) распространяется по незаявленной лицензии и была создана, изменена и/или курирована LibreTexts.
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или страница
- Показать страницу TOC
- нет
- Метки
Самая простая нерешенная задача теории графов | Сергей Иванов
Умница Уилл Хантинг, дворник и математик-любитель, рисует все гомоморфно неприводимые деревья по призыву профессора Массачусетского технологического института. © 1997 Мирамакс Пикчерз
© 1997 Мирамакс ПикчерзЭтот пост написан совместно с Екатериной Воробьевой .
В десять лет я однажды сказал своему другу, как было бы здорово, если бы наш учитель поставил перед нами нерешенные математические задачи. Было бы намного интереснее подходить к ним в классе, а не выполнять упражнения из учебника. Это было время, когда у нас не было легкодоступного интернета, и информации о нерешенных проблемах было мало. Сегодня, 20 лет спустя, когда я гуглю нерешенные задачи по математике, я получаю огромный список задач. Но, к сожалению, большинство из них выше моего понимания. Тем не менее, есть нерешенные проблемы, которые легко понять и дать возможность энтузиасту решить их.
Я достаточно давно практикуюсь в этой сфере. Я решал головоломки, публиковал статьи и даже получил докторскую степень. И я прекрасно знаю, что есть люди вне профессии математика, которые заинтересованы в решении еще нерешенных математических задач. Этот пост посвящен интересной математической задаче, с которой справится даже 10-летний ребенок.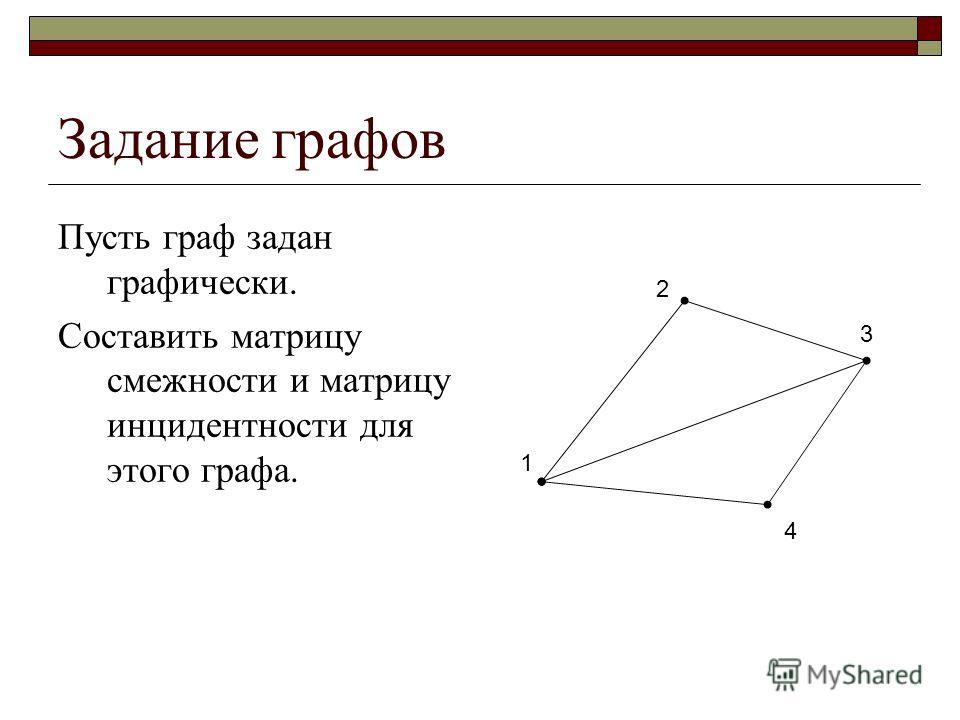
Проблема, о которой я буду говорить, — это проблема теории графов. Теория графов имеет долгую историю решения задач увлеченными любителями. В 1879 г., юрист Альфред Кемпе попытался решить теорему о четырех красках, введя концепции, которые использовались сто лет спустя, чтобы окончательно доказать теорему с помощью компьютеров. В 1950-х годах художник Энтони Хилл открыл минимальное число пересечений для любого рисунка полных графов и вывел общую формулу, которая до сих пор остается недоказанной. В 2018 году геронтолог Обри де Грей улучшил нижнюю границу раскраски произвольных графов — 60-летняя открытая задача в теории графов.
Теория графов имеет множество открытых проблем. Здесь я опишу конкретный «простой» случай гипотезы реконструкции (RC), также известной как гипотеза Келли-Улама. Несмотря на множество «доказательств» в Интернете, эта проблема остается нерешенной уже около 80 лет, что представляет собой грандиозную задачу.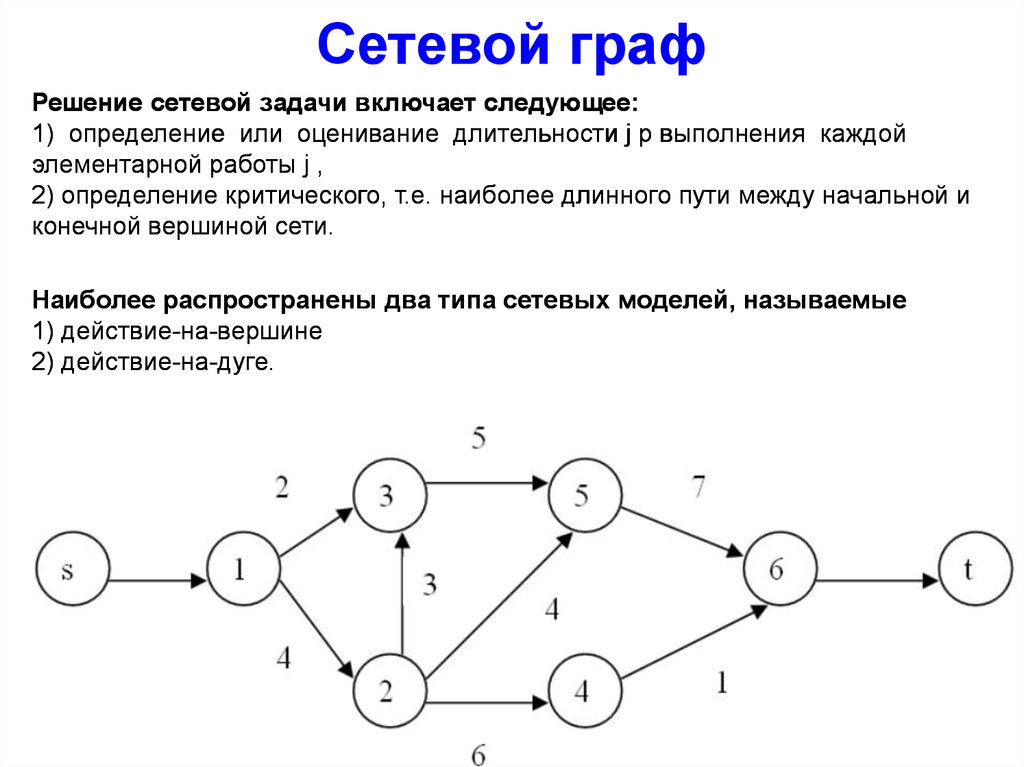 Так что, хотя и заманчиво решить эту проблему в целом, это может быть слишком сложно. Я объясню это шаг за шагом, описывая графы, для которых гипотеза реконструкции уже доказана, и закончу конкретным «легким» набором графов, для которых RC все еще открыт.
Так что, хотя и заманчиво решить эту проблему в целом, это может быть слишком сложно. Я объясню это шаг за шагом, описывая графы, для которых гипотеза реконструкции уже доказана, и закончу конкретным «легким» набором графов, для которых RC все еще открыт.
Можно сначала попытаться решить конкретный случай, прежде чем подходить к гипотезе в ее общей формулировке.
Проблема Святого ГрааляГипотезу реконструкции очень легко сформулировать: имеют ли разные графы разные наборы подграфов с удаленными вершинами? Давайте уточним, что это значит.
На рисунке ниже у нас есть граф G. Если мы удалим красную вершину, то получим некоторый подграф слева. Или мы можем удалить синюю вершину вместо красной и получить другой подграф. Мы можем сделать это для любого узла в графе и получить n различных подграфов, по одному на каждую удаленную вершину. Каждый из полученных подграфов называется картой , а их совокупность называется колодой .
Проблема, сформулированная Келли и его научным руководителем Уламом в 1942 году, может считаться проблемой Святого Грааля в теории графов:
Задача 1 [Гипотеза реконструкции, RC] : Два неориентированных графа G и H по крайней мере с тремя узлами одинаковы тогда и только тогда, когда их колоды одинаковы.
Примечание: на математическом языке два одинаковых графа изоморфны, т. е. базовая связность узлов остается неизменной независимо от порядка узлов.
Причина, по которой RC формулируется для графов по крайней мере с тремя узлами, заключается в том, что для графов с двумя узлами RC не выполняется. Рисунок 4 иллюстрирует это.
Единственное известное исключение из гипотезы реконструкции. Разные графы G и H имеют одинаковые колоды . Как подойти к гипотезе реконструкции? Один из способов понять это — рассмотреть простые семейства графов, в которых выполняется RC. Простой пример — регулярные графы, т. е. графы, в которых каждая вершина имеет одинаковую степень. Предположим, у нас есть колода для некоторого графа G . Легко показать, что можно получить последовательность степеней графа из его колоды. Следовательно, мы можем определить, является ли граф правильным по его колоде. Если она обычная, мы можем взять любую карту из колоды и найти узлы со степенью любой из д или степень д-1 . Итак, для восстановления исходного графа нам достаточно добавить еще одну вершину и соединить ее с вершинами, имеющими степень d-1 .
Простой пример — регулярные графы, т. е. графы, в которых каждая вершина имеет одинаковую степень. Предположим, у нас есть колода для некоторого графа G . Легко показать, что можно получить последовательность степеней графа из его колоды. Следовательно, мы можем определить, является ли граф правильным по его колоде. Если она обычная, мы можем взять любую карту из колоды и найти узлы со степенью любой из д или степень д-1 . Итак, для восстановления исходного графа нам достаточно добавить еще одну вершину и соединить ее с вершинами, имеющими степень d-1 .
Другие семейства реконструируемых графов включают, среди прочего, деревья и несвязные графы, т. е. графы с несколькими компонентами связности.
Гипотеза о реконструкции была решена для деревьев, несвязных графов и многого другого. Тем не менее, многие интересные дела до сих пор не раскрыты.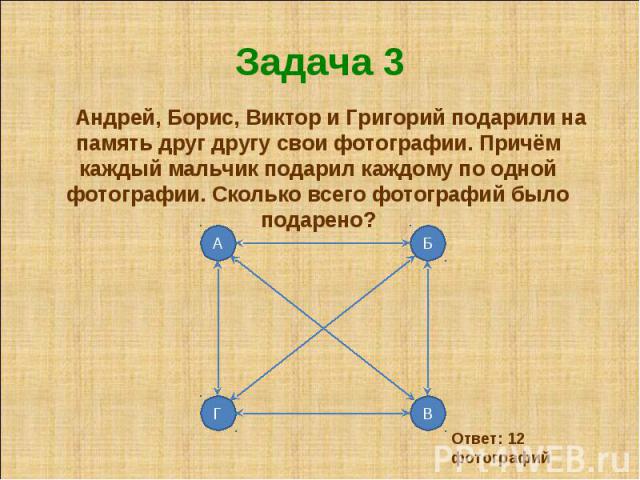 Падение в кроличью нору
Падение в кроличью нору Еще одним шагом будет рассмотрение графов только с двумя возможными значениями степени узлов. Такие графы называются двустепенными . Например, в приведенном ниже графе есть вершины с 2 или 4 соседями.
Пример двустепенного графа, где каждая вершина имеет степень 4 или 2 .Двустепенные графы со степенями a и b имеют одну особенность. Если b-a>1 , они реконструируемы. Другими словами, если граф имеет степени 2 и 4, как в приведенном выше примере, гипотеза реконструкции верна. Этот результат следует тому же аргументу, что и для обычных графов.
Двустепенные графы с последовательными степенями a и a+1 называются двустепенными последовательными . Здесь предыдущий аргумент не выполняется, но известно несколько результатов. Во-первых, можно видеть, что если вершина двустепенного графа соединена только с вершинами со степенью a , то такой граф также реконструируем. Точно так же, если есть только одна вершина степени a или только одна вершина степени a+1 , граф также реконструируется. И, наконец, Кочай доказал, что если a=2 , то двустепенный граф с двумя вершинами степени a и оставшимися n-2 степени a+1 реконструируем. Более общее правило пока неизвестно. Таким образом, самой простой версией RC было бы ограничиться двустепенными последовательными графами. В конце концов, кажется, что это очень простые экземпляры графов.
Точно так же, если есть только одна вершина степени a или только одна вершина степени a+1 , граф также реконструируется. И, наконец, Кочай доказал, что если a=2 , то двустепенный граф с двумя вершинами степени a и оставшимися n-2 степени a+1 реконструируем. Более общее правило пока неизвестно. Таким образом, самой простой версией RC было бы ограничиться двустепенными последовательными графами. В конце концов, кажется, что это очень простые экземпляры графов.
Иголка в стоге сенаЗадача 2 (более простая) [Гипотеза реконструкции двустепенных графов] : Два неориентированных двустепенных последовательных графов G и H со степенями $a$ и $a+1$ одинаковы тогда и только тогда, когда их колоды одинаковы.
Мнения специалистов по реконструкции разделились. Большинство считает RC правильным, и мы просто не обнаружили дополнительных инструментов и теорий, которые нужны, чтобы доказать это. Другие эксперты считают, что контрпримеры RC существуют, но поле поиска настолько велико, что найти их практически невозможно. Итак, давайте рассмотрим причины RC, истинны они или нет.
Другие эксперты считают, что контрпримеры RC существуют, но поле поиска настолько велико, что найти их практически невозможно. Итак, давайте рассмотрим причины RC, истинны они или нет.
Основания для принятия RC
Веским аргументом в пользу того, что гипотеза реконструкции верна, является теорема Боллобаса. В нем говорится, что почти все графики можно восстановить, используя только три карты колоды. Другими словами, по мере роста числа вершин в случайном графе вероятность стремится к единице, что для восстановления графа достаточно знания трех карт.
Другая веская причина заключается в том, что RC был проверен алгоритмически для всех графов до n=13 вершин. Если вы думаете, что это очень маленькие графы, посчитайте общее количество таких графов. Например, для n=13 существует примерно 50 триллионов графов, и может потребоваться поиск по всем возможным парам, которые могут расти пропорционально квадрату этого числа. Алгоритмические результаты также подтвердили вышеупомянутую теорему Боллобаса, показав, что большинство чисел реконструкции равны 3 для графов с 11 вершинами.
Наконец, как показано на рисунке выше, существует гораздо больше семейств графов, для которых известно, что RC верен. Сюда входят деревья, полные многодольные графы, графы единичных интервалов, унициклические графы, графы кактусов и многое другое. Хотя это не охватывает пространство всех возможных графов, растущее число таких семейств является обнадеживающим признаком того, что RC однажды будет доказано. 9n +1 такие, что их колоды эквивалентны. Позднее этот результат был распространен на нетурниры, показав, что в общем случае можно построить ориентированный граф с достаточно большим порядком, который не определяется однозначно своей колодой.
Турниры Стокмейера являются контрпримерами к RC в направленном случае. Подграф с черными ребрами встраивается в больший граф путем добавления одной дополнительной вершины двумя разными способами. Мы можем убедиться, что колоды этих графов одинаковы, даже если графы не изоморфны. Аналогичным образом было показано, что обобщения гипотезы реконструкции для 3-гиперграфов (где каждое ребро соединяет 3 вершины), а также для бесконечных графов (включая графы с конечными степенями) имеют контрпримеры.
Итак, резюмируя, вот различные причины, чтобы принять или отклонить гипотезу о реконструкции:
Причины, чтобы принять или отклонить гипотезу о реконструкции. Хотя есть веские основания полагать, что RC выполняется, аналогичные версии RC для других типов графов демонстрируют противоположные примеры.Сокращение пространства кандидатов
Заманчиво перенести известные контрпримеры в область неориентированных графов. В конце концов, турниры Стокмейера и неориентированные графы тесно связаны (общее количество турниров и неориентированных графов одинаково), однако прямых адаптаций пока не найдено. Например, турниры Стокмейера обладают рекурсивным свойством, которое позволяет построить пару подобных графов из меньшего базового графа. Поиск неориентированных графов с похожими свойствами представляет собой ключевую проблему для опровержения RC, и на эту проблему было пролито много чернил.
Одна из наиболее успешных попыток была предпринята Kimble et al. которые показали, как строить неориентированные графы, все вершины которых сгруппированы в пары из псевдоподобных вершин, т. е. вершин, которые производят одну и ту же карту после ее удаления. Аналогичным свойством обладает контрпример Стокмейера. Аллен Швенк, профессор Университета Западного Мичигана, описывает, что такой граф — самое близкое к опровержению предположение о неориентированных графах. Однако после почти 40 лет обширных исследований контрпримеры найдены не были.
которые показали, как строить неориентированные графы, все вершины которых сгруппированы в пары из псевдоподобных вершин, т. е. вершин, которые производят одну и ту же карту после ее удаления. Аналогичным свойством обладает контрпример Стокмейера. Аллен Швенк, профессор Университета Западного Мичигана, описывает, что такой граф — самое близкое к опровержению предположение о неориентированных графах. Однако после почти 40 лет обширных исследований контрпримеры найдены не были.
Интересно, что графы с псевдоподобными вершинами, построенные Kimble et al. также двустепенны, определены выше в задаче 2, и авторы предполагают, что это правильная окрестность для поиска контрпримера. Действительно, графы с узлами, имеющими различные значения степеней, легко реконструируются, так как вершины легко идентифицируются. С другой стороны, регулярные графы, как мы видели, также легко реконструируются. С другой стороны, двустепенные графы представляют наибольшую путаницу. В качестве наименьшего графа, который Kimble et al. имеет 20 вершин, самый простой нерешенный случай гипотезы реконструкции следующий.
имеет 20 вершин, самый простой нерешенный случай гипотезы реконструкции следующий.
Задача 3 (наконец-то простая!) [Гипотеза реконструкции для малых двустепенных графов]: Два неориентированных двустепенных последовательных графа G и H с 20 вершинами и степенями $a$ и $a+1$ совпадают, если и только если их колоды одинаковы.
Из-за относительно небольшого количества вершин можно попытаться просмотреть пространство двустепенных графов с 20 вершинами и проверить, есть ли два неизоморфных графа с одинаковыми колодами. Сколько времени это может занять? Итак, Брендан Маккей недавно проверил гипотезу реконструкции для всех графов с 13 вершинами, и это заняло у него 1,5 года. Так что, может быть, хотя бы для небольшой степени , можно проверить и двустепенные графы с 20 вершинами.
Итак, кто знает, может быть, однажды какой-нибудь гений полностью докажет гипотезу о реконструкции или найдет к ней контрпример, как это недавно произошло с другой задачей на графах, называемой Гипотеза Хедетниеми . Но, по крайней мере, теперь мы знаем самый простой нерешенный случай великой задачи 80-летней давности в математике, и любой энтузиаст математики может попытаться доказать это.
Но, по крайней мере, теперь мы знаем самый простой нерешенный случай великой задачи 80-летней давности в математике, и любой энтузиаст математики может попытаться доказать это.
П.С. Если вам нравится эта история, рассмотрите возможность подписки на мои телеграмм канал , твиттер и новостная рассылка graphML .
Открытые задачи по теории графов
Открытые задачи по теории графов| Единица измерения расстояния
Графики — хроматическое число Графики единичных расстояний — обхват Гипотеза Барнетта Число пересечений K(7,7) Вершины и соседи в цикле Квадрат ориентированного графа |
Графики единичных расстояний — хроматическое число
ИССЛЕДОВАТЕЛЬ: Роберт ХохбергОФИС: Core 414
Эл.
 плоскости назначается один из цветов, нет двух точек, которые находятся точно на расстоянии
1 обособленно будет присвоен тот же цвет? Эта проблема была открыта с
1956. Известно, что ответ либо 4, либо 5, либо 6, либо 7—это не слишком
трудно показать. Вы должны попробовать это сейчас, чтобы получить представление о том, что это
проблема действительно просит. Это число также называют «хроматическим числом».
плоскости.»
плоскости назначается один из цветов, нет двух точек, которые находятся точно на расстоянии
1 обособленно будет присвоен тот же цвет? Эта проблема была открыта с
1956. Известно, что ответ либо 4, либо 5, либо 6, либо 7—это не слишком
трудно показать. Вы должны попробовать это сейчас, чтобы получить представление о том, что это
проблема действительно просит. Это число также называют «хроматическим числом».
плоскости.»Граф, который можно вложить в плоскость так, чтобы вершины соответствовали точкам на плоскости, а ребра соответствуют отрезкам единичной длины называется «графом единичного расстояния». Приведенный выше вопрос эквивалентен спрашивая, каким может быть хроматическое число графов единичного расстояния.
Вот несколько вопросов для разминки, ответы на которые известны: двудольные графы являются графами с единичным расстоянием? Какой самый маленький 4-хроматический граф единичного расстояния? Покажите, что граф Петерсена является графом единичного расстояния.
Диаграммы расстояний между единицами измерения — обхват
ИССЛЕДОВАТЕЛЬ: Роберт ХохбергОФИС: Core 414
Эл.
 обратили свое внимание на смежные проблемы в надежде получить некоторое
разобраться в этом сложном вопросе.
обратили свое внимание на смежные проблемы в надежде получить некоторое
разобраться в этом сложном вопросе.В этой задаче нас интересует, какое единичное расстояние графы, которые мы можем построить, в частности, можем ли мы найти 4-хроматические графы, которые имеют большой обхват? Пол О’Доннелл нашел граф единичных расстояний обхвата 12. который не может быть трехцветным, но этот граф имеет невероятно большое количество точек. Хохберг и О’Доннелл нашли 4-хроматические графы единичного расстояния. обхватов 4 и 5 с 23 (показано справа) и 45 вершинами соответственно. Есть поменьше? Существуют ли 4-хроматические графы единичных расстояний произвольно большого обхвата? Ответ на этот вопрос может помочь решить «хроматическое число задача «плоскость».
Гипотеза Барнетта
ИССЛЕДОВАТЕЛЬ: Питер ГамбургерОФИС: Core 442
Электронная почта: [email protected]
ОПИСАНИЕ: двудольный граф является гамильтоновым?
Известно, что это неверно, если убрать условие «двудольности»,
но наименьший известный такой граф, который не является гамильтоновым, имеет 38 вершин,
как показано справа.
Номер пересечения K(9, 9)
ИССЛЕДОВАТЕЛЬ: Роберт ХохбергОФИС: Core 414
Эл. граф K(9, 9)? Предполагается, что их 256, но никто не знает.
Еще один способ задать этот вопрос: если вы поместите 9 красных точек в плоскости и 9 синих точек на плоскости, а затем соедините каждую красную точку на каждую синюю точку с кривыми (всего 81 кривая), то какой минимум количество точек пересечения, которые должны появиться на вашем чертеже?
Справа показан пример для K(4,4) с 8 пересечениями. Фактически, этот график можно нарисовать всего за 4 пересечения… сможете ли вы его найти?
Для этих чертежей предполагается, что кривые не касаются точек (вершины), за исключением их конечных точек, и что никакие три кривые не пересекаются в точка.
Вершины и соседи по циклу
ИССЛЕДОВАТЕЛЬ: Нейт ДинОФИС: Кафедра математики, Южный Техасский университет
Эл. не имеет гамильтонова цикла имеет цикл, содержащий k независимых вершины и их соседи? Известно, что это верно для k = 2 и 3.
 Например, граф справа является 3-связным, но не гамильтоновым.
Показанный пунктиром цикл содержит 3 независимые вершины (три вершины
которые светлее) и их соседи. Чтобы увидеть, что это не гамильтониан,
обратите внимание, что этот граф является полным двудольным графом K(3,4).
Например, граф справа является 3-связным, но не гамильтоновым.
Показанный пунктиром цикл содержит 3 независимые вершины (три вершины
которые светлее) и их соседи. Чтобы увидеть, что это не гамильтониан,
обратите внимание, что этот граф является полным двудольным графом K(3,4).Квадрат ориентированного графа
ИССЛЕДОВАТЕЛЬ: Нейт ДинОФИС: Кафедра математики Южного Техасского университета
Эл. Ориентированный граф — это простой граф (без петель и кратных ребер), в котором каждое ребро заменяется дугой. Таким образом, вы создаете простой ориентированный граф без пар «перевернутых дуг».
Чтобы получить квадрат ориентированного графа (или любого ориентированного графа), вы оставляете вершину установить одинаковой, сохранить все дуги, и для каждой пары дуг форму (u,v), (v,w), вы добавляете дугу (u,w), если эта дуга еще не была подарок. Пример ориентированного графа и его квадрата показан выше.
Вот открытая задача: Докажите, что для каждого ориентированного графа D существует
существует вершина, исходящая степень которой по крайней мере удваивается, когда вы возводите в квадрат ориентированную
график. В приведенном выше примере вершины A, B, C, E и G удовлетворяют этому
имущество. (Для вершин A и G 2*0=0). Нейт узнал об этой проблеме
от Пола Сеймура. Дэвид Фишер доказал эту теорему для турниров, т.е.
ориентации полных графов.
В приведенном выше примере вершины A, B, C, E и G удовлетворяют этому
имущество. (Для вершин A и G 2*0=0). Нейт узнал об этой проблеме
от Пола Сеймура. Дэвид Фишер доказал эту теорему для турниров, т.е.
ориентации полных графов.
Основы теории графов | Математика для гуманитарных наук
Результаты обучения
- Определение вершин, ребер и петель графа
- Определить степень вершины
- Определить и нарисовать как путь, так и цепь через граф
- Определить, является ли граф связным или несвязанным
- Найдите кратчайший путь в графе с помощью алгоритма Дейкстры
На этом уроке мы познакомим вас с теорией графов, областью математики, которая началась примерно 300 лет назад, чтобы помочь решить такие задачи, как поиск кратчайшего пути между двумя точками.
Теперь элементы теории графов используются для оптимизации широкого спектра систем, предложения друзей в социальных сетях и планирования сложных морских и воздушных маршрутов.
Элементы теории графов
В современном мире планирование эффективных маршрутов имеет важное значение для бизнеса и промышленности, с такими разнообразными приложениями, как распространение продуктов, прокладка новых волоконно-оптических линий для широкополосного доступа в Интернет и предложение новых друзей в социальных сетях, таких как Facebook. .
Эта область математики зародилась почти 300 лет назад как разгадка математической головоломки (мы рассмотрим ее чуть позже). Важность этой области резко возросла в прошлом веке как из-за растущей сложности бизнеса в глобальной экономике, так и из-за вычислительной мощности, которую нам предоставили компьютеры.
Графики чертежей
Пример
Это часть жилого комплекса в Миссуле, штат Монтана. В рамках своей работы инспектор по газонам застройки должен пройтись по каждой улице застройки, чтобы убедиться, что озеленение домовладельцев соответствует требованиям сообщества.
Естественно, она хочет свести к минимуму количество пеших прогулок. Возможно ли, чтобы она прошла по каждой улице в этом развитии, не возвращаясь назад? Хотя вы можете ответить на этот вопрос, просто взглянув некоторое время на изображение, было бы идеально иметь возможность ответить на вопрос для любого изображения, независимо от его сложности.
Возможно ли, чтобы она прошла по каждой улице в этом развитии, не возвращаясь назад? Хотя вы можете ответить на этот вопрос, просто взглянув некоторое время на изображение, было бы идеально иметь возможность ответить на вопрос для любого изображения, независимо от его сложности.
Для этого нам сначала нужно упростить изображение, придав ему форму, с которой будет легче работать. Мы можем сделать это, нарисовав простую линию для каждой улицы. Там, где улицы пересекаются, мы поставим точку.
Этот тип упрощенного изображения называется графиком .
Графы, вершины и ребра
Граф состоит из набора точек, называемых вершинами , и набора ребер , соединяющих пары вершин.
Хотя мы нарисовали наш первоначальный график, чтобы он соответствовал изображению, которое у нас было, нет ничего особенно важного в компоновке, когда мы анализируем график. Оба приведенных ниже графика эквивалентны приведенному выше.
Вы, наверное, уже заметили, что мы используем термин график иначе, чем вы, возможно, использовали этот термин в прошлом для описания графика математической функции.
Посмотрите видео ниже, чтобы увидеть другой взгляд на рисование графика уличной сети.
Пример
Еще в 18 веке в прусском городе Кенигсберге через город протекала река, а развилки реки пересекали семь мостов. Река и мосты выделены на картинке справа. [1]
В качестве развлечения на выходных горожане хотели посмотреть, смогут ли они найти маршрут, который проведет их по одному разу через каждый мост и вернет туда, откуда они начали.
В следующем видео мы представляем другой взгляд на проблему Кенигсбергского моста.
youtube.com/embed/yn-OD8OBSDM?feature=oembed&rel=0″ frameborder=»0″ allow=»accelerometer; autoplay; encrypted-media; gyroscope; picture-in-picture» allowfullscreen=»»>Леонард Эйлер (произносится как OY-lur), один из самых плодовитых математиков всех времен, рассматривал эту проблему в 1735 году, заложив основу теории графов как области математики. Чтобы проанализировать эту проблему, Эйлер ввел ребра, представляющие мосты:
Поскольку размер каждого массива суши не имеет отношения к вопросу о мостовых переходах, каждый из них может быть сжат до вершины, представляющей местоположение: остров, соответствующий двум мостам на исходном рисунке. В зависимости от интерпретации ребер и вершин, соответствующей сценарию, вполне возможно и разумно иметь более одного ребра, соединяющего две вершины.
Хотя мы еще не ответили на вопрос о том, существует ли маршрут, который пересекает все мосты по одному разу и возвращается в исходное положение, граф обеспечивает основу для изучения этого вопроса.
Определения
Хотя ранее мы в общих чертах определили некоторую терминологию, теперь мы постараемся быть более конкретными.
Вершина
Вершина — это точка на графике, которая может обозначать пересечение улиц, участок земли или общее место, например «работа» или «школа». Вершины часто соединяются ребрами. Обратите внимание, что вершины появляются только при явном размещении точки, а не при пересечении двух ребер. Представьте эстакаду на автостраде — пересечение автострады и переулка, но в этой точке невозможно перейти с переулка на автостраду, поэтому пересечения нет, и вершина не будет размещена.
Ребра
Ребра соединяют пары вершин. Ребро может представлять собой физическую связь между местоположениями, например улицу, или просто наличие маршрута, соединяющего два местоположения, например рейс авиакомпании.
Петля
Петля — это ребро особого типа, соединяющее вершину с самой собой. Петли не часто используются в графах уличных сетей.
Степень вершины
Степень вершины — это количество ребер, сходящихся в этой вершине. Степень вершины может быть равна нулю или больше.
| Степень 0 | Степень 1 | Степень 2 | Степень 3 | Степень 4 |
|---|---|---|---|---|
Путь
Путь — это последовательность вершин, использующих ребра. Обычно нас интересует путь между двумя вершинами. Например, путь из вершины A в вершину M показан ниже. Это один из многих возможных путей на этом графе.
Цепь
Цепь — это путь, который начинается и заканчивается в одной вершине. Схема, начинающаяся и заканчивающаяся в вершине A, показана ниже.
Связный
Граф является связным, если существует путь из любой вершины в любую другую вершину. Каждый граф, нарисованный до сих пор, был связан. График ниже: отключено ; нет никакого способа попасть из вершин слева в вершины справа.
Веса
В зависимости от решаемой задачи ребрам иногда присваиваются веса. Веса могут представлять расстояние между двумя точками, время в пути или стоимость поездки. Важно отметить, что расстояние между вершинами в графе не обязательно соответствует весу ребра.
Попробуйте
1. На приведенном ниже графике показаны 5 городов. Веса по краям представляют собой стоимость авиабилета на рейс в один конец между городами.
а. Сколько вершин и ребер имеет граф?
б. Связан ли граф?
с. Какова степень вершины, представляющей LA?
д. Если вы летите из Сиэтла в Даллас в Атланту, это путь или круг?
эл. Если вы летите из Лос-Анджелеса в Чикаго, из Далласа в Лос-Анджелес, это путь или схема.
Кратчайший путь
Когда вы посещаете веб-сайт, такой как Google Maps, или используете свой смартфон, чтобы узнать дорогу от дома до дома вашей тети в Пасадене, вы обычно ищете кратчайший путь между двумя точками. Эти компьютерные приложения используют представления карт улиц в виде графиков с расчетным временем в пути в качестве весовых коэффициентов.
Эти компьютерные приложения используют представления карт улиц в виде графиков с расчетным временем в пути в качестве весовых коэффициентов.
Хотя часто можно найти кратчайший путь на небольшом графе методом угадывания и проверки, наша цель в этой главе — разработать методы систематического решения сложных задач, следуя алгоритмы . Алгоритм — это пошаговая процедура решения проблемы. Алгоритм Дейкстры (произносится как дайк-стра) найдет кратчайший путь между двумя вершинами.
Алгоритм Дейкстры
1. Отметьте конечную вершину нулевым расстоянием. Назовите эту вершину текущей.
2. Найти все вершины, ведущие к текущей вершине. Вычислите их расстояния до конца. Поскольку мы уже знаем, на каком расстоянии от конца находится текущая вершина, потребуется просто добавить самое последнее ребро. Не записывайте это расстояние, если оно больше, чем ранее записанное расстояние.
3. Отметить текущую вершину как посещенную. Мы больше никогда не будем смотреть на эту вершину.
Мы больше никогда не будем смотреть на эту вершину.
4. Отметьте вершину с наименьшим расстоянием как текущую и повторите действия, начиная с шага 2.
ПРИМЕР
Предположим, вам нужно проехать из Такомы, штат Вашингтон (вершина T), в Якиму, штат Вашингтон (вершина Y). Глядя на карту, кажется, что ехать через Оберн (A), а затем через Маунт-Рейнир (MR) может быть кратчайшим, но это не совсем ясно, поскольку эта дорога, вероятно, медленнее, чем ехать по главному шоссе через Норт-Бенд (NB). Ниже показан график времени в пути в минутах. Также показан альтернативный маршрут через Итонвилль (E) и Паквуд (P).
Шаг 1: Отметьте конечную вершину нулевым расстоянием. Расстояния будут записаны в [скобках] после имени вершины
Шаг 2: Для каждой вершины, ведущей к Y, мы вычисляем расстояние до конца. Например, NB — это расстояние 104 от конца, а MR — 96 от конца. Помните, что расстояния в данном случае относятся к времени в пути в минутах.
Шаг 3 и 4: Мы отмечаем Y как посещенную и отмечаем вершину с наименьшим записанным расстоянием как текущую. В этот момент P будет обозначаться текущим. Вернуться к шагу 2.
В этот момент P будет обозначаться текущим. Вернуться к шагу 2.
Шаг 2 (#2): Для каждой вершины, ведущей в P (и не ведущей в посещенную вершину), мы находим расстояние от конца. Поскольку E находится в 96 минутах от P, и мы уже вычислили, что P находится в 76 минутах от Y, мы можем вычислить, что E составляет 96+76 = 172 минуты от Y.
Шаг 3 и 4 (#2): Отмечаем P как посещенную, и обозначьте вершину с наименьшим зарегистрированным расстоянием как текущую: MR. Вернемся к шагу 2.
Шаг 2 (#3): Для каждой вершины, ведущей в MR (и не ведущей в посещенную вершину), мы находим расстояние до конца. Единственная рассматриваемая вершина — это A, так как мы уже посетили Y и P. Добавляем расстояние MR 96 к длине от A до MR дает расстояние 96+79 = 175 минут от A до Y.
Шаги 3 и 4 (#3): Мы помечаем MR как посещенную и обозначаем вершину с наименьшим зарегистрированным расстоянием как текущую: NB. Вернемся к шагу 2.
Шаг 2 (№4): Для каждой вершины, ведущей к NB, мы находим расстояние до конца. Мы знаем, что кратчайшее расстояние от NB до Y равно 104, а расстояние от A до NB равно 36, поэтому расстояние от A до Y через NB равно 104+36 = 140. Так как это расстояние короче рассчитанного ранее расстояния от Y до А через MR, заменяем.
Мы знаем, что кратчайшее расстояние от NB до Y равно 104, а расстояние от A до NB равно 36, поэтому расстояние от A до Y через NB равно 104+36 = 140. Так как это расстояние короче рассчитанного ранее расстояния от Y до А через MR, заменяем.
Шаги 3 и 4 (#4): Мы помечаем NB как посещенный и обозначаем A как текущий, так как теперь он имеет кратчайшее расстояние.
Шаг 2 (#5): T — единственная непосещенная вершина, ведущая к A, поэтому мы вычисляем расстояние от T до Y через A: 20+140 = 160 минут.
Шаг 3 и 4 (#5): Мы помечаем A как посещенный, а E — как текущий.
Шаг 2 (#6): Единственная непосещенная вершина, ведущая к E, — это T. Вычисляя расстояние от T до Y через E, мы вычисляем 172+57 = 229минут. Поскольку это больше, чем существующее отмеченное время, мы не заменяем его.
Шаг 3 (#6): Мы отмечаем E как посещенный. Поскольку все вершины были посещены, мы закончили.
Отсюда мы знаем, что кратчайший путь из Такомы в Якиму займет 160 минут. Отслеживая, какая последовательность ребер дала 160 минут, мы видим, что кратчайший путь — это T-A-NB-Y.
Отслеживая, какая последовательность ребер дала 160 минут, мы видим, что кратчайший путь — это T-A-NB-Y.
Алгоритм Дейкстры является оптимальным алгоритмом , а это означает, что он всегда выдает фактический кратчайший путь, а не просто довольно короткий путь, если он существует. Этот алгоритм тоже эффективен , что означает, что его можно реализовать за разумное время. Алгоритм Дейкстры требует около V2 вычислений, где V — количество вершин в графе[1]. Граф со 100 вершинами потребует около 10 000 вычислений. В то время как это было бы много, чтобы сделать вручную, это не так уж много для компьютера. Именно благодаря этой эффективности GPS-устройство вашего автомобиля может вычислить направление движения всего за несколько секунд.
[1] Его можно ускорить за счет различных оптимизаций реализации.
Напротив, неэффективный алгоритм может попытаться перечислить все возможные пути, а затем вычислить длину каждого пути. Попытка перечислить все возможные пути может легко потребовать 1025 вычислений для вычисления кратчайшего пути всего с 25 вершинами; это 1 с 25 нулями после нее! Для сравнения, самый быстрый компьютер в мире все равно потратил бы более 1000 лет на анализ всех этих путей.
Попытка перечислить все возможные пути может легко потребовать 1025 вычислений для вычисления кратчайшего пути всего с 25 вершинами; это 1 с 25 нулями после нее! Для сравнения, самый быстрый компьютер в мире все равно потратил бы более 1000 лет на анализ всех этих путей.
ПРИМЕР
Транспортной компании необходимо направить посылку из Вашингтона, округ Колумбия, в Сан-Диего, Калифорния. Чтобы свести к минимуму затраты, посылка сначала будет отправлена в их центр обработки в Балтиморе, штат Мэриленд, а затем отправлена в рамках массовых поставок между их различными центрами обработки и в конечном итоге окажется в их центре обработки в Бейкерсфилде, Калифорния. Оттуда он будет доставлен на небольшом грузовике в Сан-Диего.
Время в пути в часах между их центрами обработки показано в таблице ниже. К каждому времени в пути было добавлено три часа для обработки. Найдите кратчайший путь из Балтимора в Бейкерсфилд.
| Балтимор | Денвер | Даллас | Чикаго | Атланта | Бейкерсфилд | |
| Балтимор | * | 15 | 14 | |||
| Денвер | * | 18 | 24 | 19 | ||
| Даллас | * | 18 | 15 | 25 | ||
| Чикаго | 15 | 18 | 18 | * | 14 | |
| Атланта | 14 | 24 | 15 | 14 | * | |
| Бейкерсфилд | 19 | 25 | * |
Хотя мы могли бы нарисовать график, мы также можем работать непосредственно с таблицей.
Шаг 1: Конечная вершина Бейкерсфилд помечается как текущая.
Шаг 2: Все города, связанные с Бейкерсфилдом, в данном случае Денвер и Даллас, рассчитываются по расстоянию; мы отметим эти расстояния в заголовках столбцов.
Шаг 3 и 4: Отметьте Бейкерсфилд как посещенный. Здесь мы делаем это, затеняя соответствующую строку и столбец таблицы. Мы помечаем Денвер как текущий, выделенный жирным шрифтом, так как это вершина с кратчайшим расстоянием.
| Балтимор
| Денвер [19] | Даллас [25] | Чикаго | Атланта | Бейкерсфилд [0] | |
| Балтимор | * | 15 | 14 | |||
| Денвер | * | 18 | 24 | 19 | ||
| Даллас | * | 18 | 15 | 25 | ||
| Чикаго | 15 | 18 | 18 | * | 14 | |
| Атланта | 14 | 24 | 15 | 14 | * | |
| Бейкерсфилд | 19 | 25 | * |
Шаг 2 (#2): Для городов, связанных с Денвером, рассчитайте расстояние до конца. Например, Чикаго находится в 18 часах от Денвера, а Денвер — в 19 часах от конца, расстояние от Чикаго до конца составляет 18+19 = 37 (от Чикаго до Денвера до Бейкерсфилда). Атланта находится в 24 часах от Денвера, поэтому расстояние до конца равно 24+19 = 43 (от Атланты до Денвера до Бейкерсфилда).
Например, Чикаго находится в 18 часах от Денвера, а Денвер — в 19 часах от конца, расстояние от Чикаго до конца составляет 18+19 = 37 (от Чикаго до Денвера до Бейкерсфилда). Атланта находится в 24 часах от Денвера, поэтому расстояние до конца равно 24+19 = 43 (от Атланты до Денвера до Бейкерсфилда).
Шаг 3 и 4 (#2): Мы отмечаем Денвер как посещенный, а Даллас — как текущий.
| Балтимор
| Денвер [19] | Даллас [25] | Чикаго [37] | Атланта [43] | Бейкерсфилд [0] | |
| Балтимор | * | 15 | 14 | |||
| Денвер | * | 18 | 24 | 19 | ||
| Даллас | * | 18 | 15 | 25 | ||
| Чикаго | 15 | 18 | 18 | * | 14 | |
| Атланта | 14 | 24 | 15 | 14 | * | |
| Бейкерсфилд | 19 | 25 | * |
Шаг 2 (#3): Для городов, связанных с Далласом, рассчитайте расстояние до конца. Для Чикаго расстояние от Чикаго до Далласа равно 18, а от Далласа до конца — 25, поэтому расстояние от Чикаго до конца через Даллас будет 18 + 25 = 43. Поскольку это больше, чем отмеченное в настоящее время расстояние для Чикаго, мы не заменяем его. Для Атланты мы вычисляем 15+25 = 40. Так как это меньше, чем текущее отмеченное расстояние для Атланты, мы заменяем существующее расстояние.
Для Чикаго расстояние от Чикаго до Далласа равно 18, а от Далласа до конца — 25, поэтому расстояние от Чикаго до конца через Даллас будет 18 + 25 = 43. Поскольку это больше, чем отмеченное в настоящее время расстояние для Чикаго, мы не заменяем его. Для Атланты мы вычисляем 15+25 = 40. Так как это меньше, чем текущее отмеченное расстояние для Атланты, мы заменяем существующее расстояние.
Шаги 3 и 4 (#3): Мы отмечаем Даллас как посещенный, а Чикаго как текущий.
| Балтимор
| Денвер [19] | Даллас [25] | Чикаго [37] | Атланта [40] | Бейкерсфилд [0] | |
| Балтимор | * | 15 | 14 | |||
| Денвер | * | 18 | 24 | 19 | ||
| Даллас | * | 18 | 15 | 25 | ||
| Чикаго | 15 | 18 | 18 | * | 14 | |
| Атланта | 14 | 24 | 15 | 14 | * | |
| Бейкерсфилд | 19 | 25 | * |
Шаг 2 (#4): Балтимор и Атланта — единственные непосещаемые города, связанные с Чикаго. Для Балтимора мы вычисляем 15+37 = 52 и отмечаем это расстояние. Для Атланты мы вычисляем 14+37 = 51. Поскольку это больше, чем существующее расстояние 40 для Атланты, мы не заменяем это расстояние.
Для Балтимора мы вычисляем 15+37 = 52 и отмечаем это расстояние. Для Атланты мы вычисляем 14+37 = 51. Поскольку это больше, чем существующее расстояние 40 для Атланты, мы не заменяем это расстояние.
Шаг 3 и 4 (#4): Отметьте Чикаго как посещенный, а Атланту как текущий.
| Балтимор [52] | Денвер [19] | Даллас [25] | Чикаго [37] | Атланта [40] | Бейкерсфилд [0] | |
| Балтимор | * | 15 | 14 | |||
| Денвер | * | 18 | 24 | 19 | ||
| Даллас | * | 18 | 15 | 25 | ||
| Чикаго | 15 | 18 | 18 | * | 14 | |
| Атланта | 14 | 24 | 15 | 14 | * | |
| Бейкерсфилд | 19 | 25 | * |
Шаг 2 (#5): Расстояние от Атланты до Балтимора равно 14. Прибавив это к расстоянию, уже рассчитанному для Атланты, мы получим общее расстояние 14+40 = 54 часа от Балтимора до Бейкерсфилда через Атланту. Так как это больше рассчитываемого в настоящее время расстояния, мы не заменяем расстояние для Балтимора.
Прибавив это к расстоянию, уже рассчитанному для Атланты, мы получим общее расстояние 14+40 = 54 часа от Балтимора до Бейкерсфилда через Атланту. Так как это больше рассчитываемого в настоящее время расстояния, мы не заменяем расстояние для Балтимора.
Шаг 3 и 4 (#5): Мы отмечаем Атланту как посещенную. Все города были посещены, и мы закончили.
Самый короткий маршрут из Балтимора в Бейкерсфилд займет 52 часа и пройдет через Чикаго и Денвер.
ПОПРОБУЙТЕ СЕЙЧАС
- Найдите кратчайший путь между вершинами A и G на графике ниже.
В следующем видео обобщены темы, затронутые на этой странице.
- Богдан Джушка. http://en.wikipedia.org/wiki/File:Konigsberg_bridges.png ↵
Леонард Эйлер. Решение проблемы Кенигсбергского моста
Автор(ы):
Тео Паолетти (Колледж Нью-Джерси)
Редакция Примечание
Следующий студенческий исследовательский отчет был подготовлен для класса 255 профессора Юдит Кардос по математике в Колледже Нью-Джерси. Это был 3-кредитный вводный курс по истории математики. Этот отчет был засчитан в 30% итоговой оценки. Это пример того, какие исторические исследования студенты могут проводить с использованием вторичных источников.
Это был 3-кредитный вводный курс по истории математики. Этот отчет был засчитан в 30% итоговой оценки. Это пример того, какие исторические исследования студенты могут проводить с использованием вторичных источников.
Решение Леонардом Эйлером проблемы Кенигсбергского моста
Кенигсберг
Наша история начинается в 18 веке в причудливом городе Кенигсберге, Пруссия, на берегу реки Прегель. В 1254 году тевтонские рыцари основали город Кенигсберг под предводительством чешского короля Оттокера II после своего второго крестового похода против пруссаков. В средние века Кенигсберг стал очень важным городом и торговым центром благодаря своему расположению на берегу реки. Произведения искусства восемнадцатого века изображают Кенигсберг как процветающий город, где флотилии кораблей заполняют Прегель, а их торговля обеспечивает комфортный образ жизни как для местных купцов, так и для их семей. Здоровая экономика позволила горожанам построить семь мостов через реку, большинство из которых соединялись с островом Кнайпхоф; их расположение можно увидеть на прилагаемой картинке [источник: MacTutor History of Mathematics Archive].
Поскольку река текла вокруг Кнайпхофа, что буквально означает паб, и другого острова, она делила город на четыре отдельных района. Семь мостов назывались Мост Кузнеца, Соединительный мост, Зеленый мост, Купеческий мост, Деревянный мост, Высокий мост и Медовый мост. Согласно преданиям, жители Кенигсберга проводили воскресные дни, гуляя по своему прекрасному городу. Во время прогулки жители города решили создать для себя игру, их цель состояла в том, чтобы придумать способ, которым они могли бы ходить по городу, пересекая каждый из семи мостов только один раз. Хотя никто из жителей Кенигсберга не мог придумать маршрут, который позволил бы им пересечь каждый из мостов только один раз, но они не могли доказать, что это невозможно. К счастью для них, Кенигсберг находился недалеко от Санкт-Петербурга, где жил знаменитый математик Леонард Эйлер.
Эйлер и проблема моста
Зачем Эйлеру интересоваться проблемой, столь не связанной с областью математики? Зачем такому выдающемуся математику тратить много времени на решение тривиальной задачи вроде проблемы Кенигсбергского моста? Эйлер, очевидно, был занятым человеком, опубликовавшим за свою жизнь более 500 книг и статей. Только в 1775 году он писал в среднем одну математическую статью в неделю, а в течение своей жизни он писал на множество тем, помимо математики, включая механику, оптику, астрономию, навигацию и гидродинамику. Неудивительно, что Эйлер считал эту проблему тривиальной, заявив в письме 1736 года Карлу Леонхарду Готлибу Элеру, мэру Данцига, который попросил его решить проблему [цитируется по Hopkins, 2]:
Только в 1775 году он писал в среднем одну математическую статью в неделю, а в течение своей жизни он писал на множество тем, помимо математики, включая механику, оптику, астрономию, навигацию и гидродинамику. Неудивительно, что Эйлер считал эту проблему тривиальной, заявив в письме 1736 года Карлу Леонхарду Готлибу Элеру, мэру Данцига, который попросил его решить проблему [цитируется по Hopkins, 2]:
. . . Таким образом, вы видите, благороднейший сэр, как этот тип решения имеет мало отношения к математике, и я не понимаю, почему вы ожидаете, что его даст математик, а не кто-либо другой, ибо решение основано только на разуме, и его открытие не зависит ни от какого математического принципа. Из-за этого я не знаю, почему даже вопросы, имеющие столь малое отношение к математике, математики решают быстрее, чем другие.
Несмотря на то, что Эйлер нашел проблему тривиальной, он все равно был заинтригован ею. В письме, написанном в том же году Джованни Маринони, итальянскому математику и инженеру, Эйлер сказал [цитируется по Хопкинсу, 2],
Этот вопрос так банален, но показался мне достойным внимания тем, что [ни] геометрии, ни алгебры, ни даже искусства счета не было достаточно для его решения.
Эйлер полагал, что эта проблема связана с темой, которую Готфрид Вильгельм Лейбниц когда-то обсуждал и над которой очень хотел поработать, и которую Лейбниц называл geometria situs , или геометрия положения. Эта так называемая геометрия положения — это то, что теперь называется теорией графов, которую Эйлер вводит и использует при решении этой знаменитой проблемы.
Доказательство Эйлера
26 августа 1735 года Эйлер представил статью, содержащую решение проблемы Кенигсбергского моста. Он обращается как к этой конкретной проблеме, так и к общему решению с любым количеством участков суши и любым количеством мостов. Эта статья под названием «Solutio Problematis ad geometriam situs pertinentis» была позже опубликована в 1741 г. [Hopkins, 2]. Статья Эйлера разделена на двадцать один пронумерованный абзац, и далее будет представлена упрощенная версия абзацев Эйлера.
В первых двух абзацах доказательства Эйлера он вводит проблему Кенигсбергского моста. В параграфе 1 Эйлер заявляет, что, по его мнению, эта проблема касается геометрии, но не той геометрии, которая хорошо известна его современникам и включает в себя измерения и расчеты, а нового вида геометрии, которую Лейбниц называл геометрией положения. Затем в параграфе 2 Эйлер объясняет своей аудитории, как работает проблема Кенигсберга. Эйлер набросал проблему (см. 9).0015 Рисунок Эйлера 1 ), и назвал семь различных мостов: a, b, c, d, e, f и, g. В этом абзаце он формулирует общий вопрос задачи: «Можно ли узнать, можно ли пересечь каждый мост ровно один раз?»
В параграфе 1 Эйлер заявляет, что, по его мнению, эта проблема касается геометрии, но не той геометрии, которая хорошо известна его современникам и включает в себя измерения и расчеты, а нового вида геометрии, которую Лейбниц называл геометрией положения. Затем в параграфе 2 Эйлер объясняет своей аудитории, как работает проблема Кенигсберга. Эйлер набросал проблему (см. 9).0015 Рисунок Эйлера 1 ), и назвал семь различных мостов: a, b, c, d, e, f и, g. В этом абзаце он формулирует общий вопрос задачи: «Можно ли узнать, можно ли пересечь каждый мост ровно один раз?»
Рисунок Эйлера 1 из «Solutio Problematis ad geometriam situs pertinentis», Eneström 53 [источник: архив MAA Euler] нахождения решения. В параграфе 3 Эйлер говорит читателю, что для решения этой конкретной проблемы он мог бы записать все возможные пути, но этот метод занял бы много времени и не работал бы для более крупных конфигураций с большим количеством мостов и участков суши. Из-за этих проблем Эйлер решил выбрать другой метод решения этой проблемы.
Из-за этих проблем Эйлер решил выбрать другой метод решения этой проблемы.
В параграфе 4 он начинает упростить задачу, изобретая удобную систему для представления пересечения моста. Эйлер решает, что вместо того, чтобы использовать строчные буквы для обозначения пересечения моста, он будет писать заглавными буквами, обозначающими массивы суши. Например, ссылаясь на его Рисунок 1 , AB будет означать путешествие, которое началось на суше A и закончилось на B. Более того, если после путешествия с суши A на B кто-то решит переместиться на сушу D, это будет просто обозначено , АБД. В параграфе 5 Эйлер продолжает свое обсуждение этого процесса, объясняя, что в ABDC, хотя есть четыре заглавных буквы, было пересечено только три моста. Эйлер объясняет, что сколько бы ни было мостов, будет еще одна буква для обозначения необходимого перехода. Из-за этого вся проблема Кенигсбергского моста требовала пересечения семи мостов и, следовательно, восьми заглавных букв.
В параграфе 6 Эйлер продолжает объяснять детали своего метода. Он говорит читателю, что если есть более одного моста, который можно пересечь при переходе с одного участка суши на другой, не имеет значения, какой мост используется. Например, даже если есть два моста, a и b, которые могут привести путешественника из A в B, в системе обозначений Эйлера не имеет значения, какой мост будет взят. В этом абзаце Эйлер также обсуждает конкретную проблему, с которой он имеет дело. Он объясняет, используя свой исходный рисунок, что в задаче Кёнигсберга требуется ровно восемь букв, где пары (A, B) и (A, C) должны стоять рядом друг с другом ровно два раза, независимо от того, какая буква появляется первой. Кроме того, пары (A,D), (B,D) и (C,D) должны встречаться вместе ровно один раз, чтобы путь, пересекающий каждый мост один и только один раз, существовал.
Он говорит читателю, что если есть более одного моста, который можно пересечь при переходе с одного участка суши на другой, не имеет значения, какой мост используется. Например, даже если есть два моста, a и b, которые могут привести путешественника из A в B, в системе обозначений Эйлера не имеет значения, какой мост будет взят. В этом абзаце Эйлер также обсуждает конкретную проблему, с которой он имеет дело. Он объясняет, используя свой исходный рисунок, что в задаче Кёнигсберга требуется ровно восемь букв, где пары (A, B) и (A, C) должны стоять рядом друг с другом ровно два раза, независимо от того, какая буква появляется первой. Кроме того, пары (A,D), (B,D) и (C,D) должны встречаться вместе ровно один раз, чтобы путь, пересекающий каждый мост один и только один раз, существовал.
Рисунки Эйлера 2 и 3 из «Solutio problematis ad geometriam situs pertinentis», Eneström 53 [источник: Архив Эйлера MAA]
последовательность букв, которая удовлетворяет задаче, или ему нужно доказать, что такой последовательности не существует. Прежде чем сделать это для проблемы Кенигсбергского моста, он решает найти правило, чтобы выяснить, существует ли путь для более общей задачи. Он делает это в параграфе 8, рассматривая гораздо более простой пример массивов суши и мостов. Эйлер рисует Рисунок 2 , и он начинает оценивать ситуации, в которых проходит область А. Эйлер утверждает, что если мост а пройден один раз, то путь А либо начинался, либо заканчивался, и поэтому использовался только один раз. Если все мосты a, b и c пройдены один раз, A используется ровно дважды, независимо от того, является ли он начальным или конечным местом. Точно так же, если пять мостов ведут к А, участок суши А будет встречаться на пути ровно три раза. Эйлер утверждает, что «в общем случае, если количество мостов равно любому нечетному числу и если его увеличить на единицу, то количество вхождений A составляет половину результата». Другими словами, если существует нечетное количество мостов, соединяющих A с другими массивами суши, добавьте один к количеству мостов и разделите его на два, чтобы узнать, сколько всего раз A должно быть использовано на пути, где каждый мост используется один и только один раз (т.
Прежде чем сделать это для проблемы Кенигсбергского моста, он решает найти правило, чтобы выяснить, существует ли путь для более общей задачи. Он делает это в параграфе 8, рассматривая гораздо более простой пример массивов суши и мостов. Эйлер рисует Рисунок 2 , и он начинает оценивать ситуации, в которых проходит область А. Эйлер утверждает, что если мост а пройден один раз, то путь А либо начинался, либо заканчивался, и поэтому использовался только один раз. Если все мосты a, b и c пройдены один раз, A используется ровно дважды, независимо от того, является ли он начальным или конечным местом. Точно так же, если пять мостов ведут к А, участок суши А будет встречаться на пути ровно три раза. Эйлер утверждает, что «в общем случае, если количество мостов равно любому нечетному числу и если его увеличить на единицу, то количество вхождений A составляет половину результата». Другими словами, если существует нечетное количество мостов, соединяющих A с другими массивами суши, добавьте один к количеству мостов и разделите его на два, чтобы узнать, сколько всего раз A должно быть использовано на пути, где каждый мост используется один и только один раз (т. е. общее количество вхождений A, где A имеет нечетное количество мостов = (количество мостов — 1) / 2 ).
е. общее количество вхождений A, где A имеет нечетное количество мостов = (количество мостов — 1) / 2 ).
Используя этот факт, Эйлер решает задачу Кенигсбергского моста в параграфе 9. В этом случае, поскольку есть пять мостов, ведущих к А, это должно произойти три раза (см. его рис. 1 выше). Точно так же B, C и D должны появиться дважды, так как все они имеют три моста, ведущих к ним. Следовательно, 3 (для A) + 2 (для B) + 2 (для C) + 2 (для D) = 9, но Эйлер уже заявил, что для семи мостов должно быть только восемь вхождений. Это противоречие! Поэтому по мостам в городе Кёнигсберг нельзя проехать один и только один раз. Конец или нет? В то время как жители Кенигсберга могут быть довольны этим решением, великий математик Леонард Эйлер не был удовлетворен. Эйлер продолжает свое доказательство, чтобы иметь дело с более общими ситуациями.
Обобщение Эйлера
В параграфе 10 Эйлер продолжает свое обсуждение, отмечая, что если ситуация включает все массивы суши с нечетным числом мостов, можно сказать, можно ли совершить путешествие, используя каждый мост только один раз. Эйлер утверждает, что если сумма количества раз, которое должна появиться каждая буква, на единицу больше, чем общее количество мостов, путешествие можно совершить. Однако, если количество вхождений более чем на один больше, чем количество мостов, путешествие невозможно, как в задаче о Кенигсбергском мосту. Это потому, что правило, которое Эйлер дает для нечетного числа мостов, используя свой рисунок 2, верно для общей ситуации, есть ли только один другой массив суши или более одного.
Эйлер утверждает, что если сумма количества раз, которое должна появиться каждая буква, на единицу больше, чем общее количество мостов, путешествие можно совершить. Однако, если количество вхождений более чем на один больше, чем количество мостов, путешествие невозможно, как в задаче о Кенигсбергском мосту. Это потому, что правило, которое Эйлер дает для нечетного числа мостов, используя свой рисунок 2, верно для общей ситуации, есть ли только один другой массив суши или более одного.
В абзацах 11 и 12 Эйлер рассматривает ситуацию, когда к региону прикреплено четное число мостов. Эта ситуация не возникает в кенигсбергской задаче и поэтому до сих пор игнорировалась. В ситуации с массивом суши X с четным числом мостов могут возникнуть два случая. Первый случай, когда X является отправной точкой путешествия. В этом случае X появится дважды, один раз как начальная точка и еще раз как конечная точка. В другом случае X не является отправной точкой. Если бы это произошло, X появился бы только один раз, так как путешествие должно было бы начинаться через один мост и немедленно выходить через единственный другой доступный мост. Точно так же, если к X подключено четыре моста, количество вхождений X зависит от того, является ли он начальной точкой. Если путешествие начинается в X, оно должно появиться три раза, но если оно не начинается в X, оно появится только дважды. Таким образом, в общем, если к X подключено четное количество мостов, то, если путешествие не начинается в X, X появляется в половине случаев как мосты (т.е. Вхождения X, где X четное, а не начальная точка = (# мостов) / 2). Если путешествие действительно начинается в X, то X появляется в половине случаев в виде мостов плюс один (т. е. число вхождений X, где X четно, а начальная точка = ((количество мостов) / 2) + 1).
Точно так же, если к X подключено четыре моста, количество вхождений X зависит от того, является ли он начальной точкой. Если путешествие начинается в X, оно должно появиться три раза, но если оно не начинается в X, оно появится только дважды. Таким образом, в общем, если к X подключено четное количество мостов, то, если путешествие не начинается в X, X появляется в половине случаев как мосты (т.е. Вхождения X, где X четное, а не начальная точка = (# мостов) / 2). Если путешествие действительно начинается в X, то X появляется в половине случаев в виде мостов плюс один (т. е. число вхождений X, где X четно, а начальная точка = ((количество мостов) / 2) + 1).
В абзацах с 13 по 15 Эйлер объясняет, как выяснить, существует ли путь, использующий каждый мост один и только один раз, и представляет свой собственный пример, чтобы показать, как это работает. Эйлер сначала объясняет свой простой шестишаговый метод решения любой общей ситуации с массивами суши, разделенными реками и соединенными мостами. Первый Эйлер обозначает каждый массив суши с заглавной буквы. Во-вторых, он берет общее количество мостов, добавляет один и записывает это над таблицей, которую собирается составить. Далее он берет заглавные буквы, ставит их в столбик, а рядом пишет количество мостов. В-четвертых, он указывает звездочками участки суши, на которых имеется четное число мостов. Затем рядом с каждым четным числом он пишет ½ числа, а рядом с каждым нечетным числом ставит ½ числа плюс один. Наконец, Эйлер складывает числа, записанные в крайнем правом столбце, и если сумма на единицу меньше или равна количеству мостов плюс один, то требуемое путешествие возможно. Однако важно отметить, что если сумма на один меньше, чем количество мостов плюс один, то путешествие должно начинаться с одного из участков суши, отмеченных звездочкой. Если сумма равна количеству мостов плюс один, путешествие должно начинаться в регионе, не отмеченном звездочкой.
Первый Эйлер обозначает каждый массив суши с заглавной буквы. Во-вторых, он берет общее количество мостов, добавляет один и записывает это над таблицей, которую собирается составить. Далее он берет заглавные буквы, ставит их в столбик, а рядом пишет количество мостов. В-четвертых, он указывает звездочками участки суши, на которых имеется четное число мостов. Затем рядом с каждым четным числом он пишет ½ числа, а рядом с каждым нечетным числом ставит ½ числа плюс один. Наконец, Эйлер складывает числа, записанные в крайнем правом столбце, и если сумма на единицу меньше или равна количеству мостов плюс один, то требуемое путешествие возможно. Однако важно отметить, что если сумма на один меньше, чем количество мостов плюс один, то путешествие должно начинаться с одного из участков суши, отмеченных звездочкой. Если сумма равна количеству мостов плюс один, путешествие должно начинаться в регионе, не отмеченном звездочкой.
Примеры
Использование задачи Конигсберга в качестве своего первого примера Эйлера показывает следующее:
Количество мостов = 7, количество мостов плюс один = 8
Область мостов. 2
2
C 3 2
D 3 2
Однако 3 + 2 + 2 + 2 = 9, что больше 8 невозможно, поэтому путешествие невозможно.
Поскольку этот пример довольно простой, Эйлер решает создать свою собственную ситуацию с двумя островами, четырьмя реками и пятнадцатью мостами. Ситуацию, созданную Эйлером, можно увидеть на его Рис. 3 выше. Теперь Эйлер пытается выяснить, существует ли путь, позволяющий пройти по каждому мосту один и только один раз. Эйлер следует тем же шагам, что и выше, называя пять различных областей заглавными буквами и создавая таблицу, чтобы проверить это, если это возможно, например:0005
Количество мостов = 15, количество мостов плюс один = 16
Область мостов.0005
E 5 3
F*6 3
Кроме того . Поскольку сумма равна количеству мостов плюс один, путешествие должно начинаться либо в D, либо в E. Теперь, когда Эйлер знает, что путешествие возможно, все, что ему нужно сделать, это указать, каким будет путь. Эйлер выбирает путь EaFbBcFdAeFfCgAhCiDkAmenApBoElD, где он указывает, какие мосты пересекаются между буквами, представляющими массивы суши. Хотя эта информация является лишней, поскольку точный мост не имеет значения для понимания того, что путешествие возможно, она полезна при выборе пути. Это хороший пример, показывающий метод, которым воспользовался бы Эйлер при решении любой задачи такого рода.
Теперь, когда Эйлер знает, что путешествие возможно, все, что ему нужно сделать, это указать, каким будет путь. Эйлер выбирает путь EaFbBcFdAeFfCgAhCiDkAmenApBoElD, где он указывает, какие мосты пересекаются между буквами, представляющими массивы суши. Хотя эта информация является лишней, поскольку точный мост не имеет значения для понимания того, что путешествие возможно, она полезна при выборе пути. Это хороший пример, показывающий метод, которым воспользовался бы Эйлер при решении любой задачи такого рода.
Выводы Эйлера
В следующих нескольких абзацах Эйлер предлагает еще один способ выяснить, можно ли совершить путешествие по любому набору участков суши, мостов и рек. В параграфе 16 Эйлер указывает, что сумма чисел, перечисленных непосредственно справа от суши, в сумме в два раза превышает общее количество мостов. Позже этот факт станет известен как лемма о рукопожатии. По сути, лемма о рукопожатии утверждает, что каждый мост считается дважды, по одному разу для каждого участка суши, к которому он прикреплен. В параграфе 17 Эйлер продолжает утверждать, что сумма всех мостов, ведущих в каждую область, четна, поскольку половина этого числа равна общему количеству мостов. Однако это невозможно, если есть нечетное количество участков суши с нечетным количеством мостов. Таким образом, Эйлер доказывает, что если есть нечетные числа, связанные с массивами суши, то должно быть четное количество этих массивов суши.
В параграфе 17 Эйлер продолжает утверждать, что сумма всех мостов, ведущих в каждую область, четна, поскольку половина этого числа равна общему количеству мостов. Однако это невозможно, если есть нечетное количество участков суши с нечетным количеством мостов. Таким образом, Эйлер доказывает, что если есть нечетные числа, связанные с массивами суши, то должно быть четное количество этих массивов суши.
Однако этого недостаточно, чтобы доказать, когда существует путь, на котором каждый мост используется один и только один раз, поскольку в задаче о Кенигсбергском мосту есть четное количество массивов суши с нечетным количеством мостов, ведущих к ним. Из-за этого Эйлер добавляет дополнительные ограничения в параграфах 18 и 19. Эйлер объясняет, что, поскольку общее количество мостов, прикрепленных к каждому массиву суши, равно удвоенному количеству мостов (как видно из леммы о рукопожатии), поэтому, если вы добавьте два к этой сумме, а затем разделите на два, вы получите общее количество мостов плюс один. Этот номер такой же, как тот, который использовался ранее, и используется, чтобы сказать, возможен ли путь. Если все числа четные, то сумма в третьем столбце таблицы будет на единицу меньше, чем общее количество мостов плюс один.
Этот номер такой же, как тот, который использовался ранее, и используется, чтобы сказать, возможен ли путь. Если все числа четные, то сумма в третьем столбце таблицы будет на единицу меньше, чем общее количество мостов плюс один.
Затем Эйлер объясняет, что очевидно, что если есть два массива суши с нечетным числом мостов, то путешествие всегда будет возможно, если путешествие начинается в одном из регионов с нечетным числом мостов. Это потому, что если четные числа разделить пополам, а каждое из нечетных увеличить на единицу и разделить пополам, то сумма этих половинок будет на единицу больше, чем общее количество мостов. Однако если имеется четыре или более массивов суши с нечетным числом мостов, то пути быть не может. Это потому, что сумма половин нечетных чисел плюс один вместе с суммой всех половинок четных чисел сделает сумму третьего столбца больше, чем общее количество мостов плюс один. Следовательно, Эйлер только что доказал, что может быть не более двух участков суши с нечетным числом мостов.
После этого Эйлер может сделать выводы относительно более общих форм проблемы Кенигсбергского моста. В параграфе 20 Эйлер дает три рекомендации, которые можно использовать, чтобы выяснить, существует ли путь, использующий каждый мост один и только один раз. Во-первых, он утверждал, что если существует более двух участков суши с нечетным числом мостов, то такое путешествие невозможно. Во-вторых, если количество мостов нечетно ровно для двух участков суши, то путешествие возможно, если оно начинается на одном из двух участков суши с нечетными номерами. Наконец, Эйлер утверждает, что если нет регионов с нечетным количеством суши, то путешествие можно совершить, начав с любого региона. Установив эти три факта, Эйлер завершает свое доказательство параграфом 21, в котором просто говорится, что после того, как кто-то выяснил, что путь существует, он все равно должен приложить усилия, чтобы написать работающий путь. Эйлер считал, что метод достижения этого тривиален, и не хотел тратить на него много времени. Однако Эйлер действительно предлагал сконцентрироваться на том, как добраться с одного массива суши на другой, вместо того, чтобы сначала концентрироваться на конкретных мостах.
Однако Эйлер действительно предлагал сконцентрироваться на том, как добраться с одного массива суши на другой, вместо того, чтобы сначала концентрироваться на конкретных мостах.
Доказательство Эйлера и теория графов
Читая оригинальное доказательство Эйлера, можно обнаружить относительно простую и понятную математическую работу; однако не фактическое доказательство, а промежуточные шаги делают эту проблему известной. Великое нововведение Эйлера заключалось в том, что он рассматривал проблему Кенигсбергского моста абстрактно, используя линии и буквы для представления более крупной ситуации с массивами суши и мостами. Он использовал заглавные буквы для обозначения массивов суши и строчные буквы для обозначения мостов. Это был совершенно новый тип мышления для того времени, и в своей статье Эйлер случайно запустил новую область математики, названную теорией графов, где граф — это просто набор вершин и ребер. Сегодня путь в графе, который содержит каждое ребро графа один и только один раз, называется эйлеровым путем из-за этой проблемы. С тех пор, как Эйлер решил эту проблему, и до сегодняшнего дня теория графов стала важным разделом математики, лежащим в основе наших представлений о сетях.
С тех пор, как Эйлер решил эту проблему, и до сегодняшнего дня теория графов стала важным разделом математики, лежащим в основе наших представлений о сетях.
Проблема Кенигсбергского моста — вот почему Биггс заявляет [Biggs, 1],
Истоки теории графов скромны, даже легкомысленны… Проблемы, которые привели к развитию теории графов, часто были не более чем головоломками, предназначенными для проверки изобретательности, а не для стимулирования воображения. Но, несмотря на кажущуюся тривиальность таких головоломок, они привлекли внимание математиков, в результате чего теория графов стала предметом, богатым теоретическими результатами удивительного разнообразия и глубины.
Как следует из заявления Биггса, эта проблема настолько важна, что упоминается в первой главе каждой книги по теории графов, которую просматривали в библиотеке.
После открытия Эйлера (или изобретения, в зависимости от того, как на это смотрит читатель) теория графов бурно развивалась благодаря значительным вкладам, внесенным такими великими математиками, как Огюстен Коши, Уильям Гамильтон, Артур Кэли, Густав Кирхгоф и Джордж Полиа. Все эти люди внесли свой вклад в раскрытие «практически всего, что известно о больших, но упорядоченных графах, таких как решетка, образованная атомами в кристалле, или гексагональная решетка, созданная пчелами в улье [9].0016 ScienceWeek, 2]. Другие известные задачи теории графов включают в себя поиск способа выхода из лабиринта или лабиринта или поиск порядка ходов коня на шахматной доске, при котором каждое поле попадает только один раз, а конь возвращается на место, с которого он начал. [ ScienceWeek, 2]. Некоторые другие проблемы теории графов оставались нерешенными на протяжении столетий [ ScienceWeek, 2].
Все эти люди внесли свой вклад в раскрытие «практически всего, что известно о больших, но упорядоченных графах, таких как решетка, образованная атомами в кристалле, или гексагональная решетка, созданная пчелами в улье [9].0016 ScienceWeek, 2]. Другие известные задачи теории графов включают в себя поиск способа выхода из лабиринта или лабиринта или поиск порядка ходов коня на шахматной доске, при котором каждое поле попадает только один раз, а конь возвращается на место, с которого он начал. [ ScienceWeek, 2]. Некоторые другие проблемы теории графов оставались нерешенными на протяжении столетий [ ScienceWeek, 2].
Судьба Кенигсберга
В то время как теория графов процветала после того, как Эйлер решил проблему Кенигсбергского моста, у города Кенигсберга была совсем другая судьба. В 1875 году жители Кенигсберга решили построить новый мост между узлами B и C, увеличив количество соединений этих двух массивов суши до четырех. Это означало, что только два массива суши имели нечетное количество связей, что давало довольно простое решение проблемы. Создание дополнительного моста могло быть или не быть подсознательно вызвано желанием найти путь, чтобы решить известную проблему города.
Создание дополнительного моста могло быть или не быть подсознательно вызвано желанием найти путь, чтобы решить известную проблему города.
Однако новый мост не решил всех будущих проблем Кенигсберга, так как город не ожидал еще в девятнадцатом веке «печальной и истерзанной войной судьбы, которая ожидала его как место проведения одного из самых ожесточенных сражений Второй мировой войны. ” В течение четырех дней августа 1944 года британские бомбардировщики уничтожили как старый город, так и северную часть Кенигсберга. В январе и феврале 1945 года район Кенигсберга окружен русскими войсками. Немецкое гражданское население начинает эвакуацию из города, но слишком поздно. Тысячи людей гибнут, пытаясь бежать на лодках и пешком по ледяным водам Куршского залива. 19 апреля45 года Красная Армия захватывает Кенигсберг, около девяноста процентов старого города лежат в руинах.
Текущая карта улиц Кенигсберга представлена ниже [источник: MacTutor History of Mathematics Archive]. Эта карта показывает, насколько сильно изменился город. Многие мосты были разрушены во время бомбардировок, и город больше не может задавать тот же интригующий вопрос, что и в восемнадцатом веке. Наряду с принципиально иной планировкой город Кенигсберг носит новое название Калининград, а река Прегель переименована в Преголю [Гопкинс, 6]. В то время как судьба Кенигсберга ужасна, старая кофейная проблема горожан пройти каждый из своих старых семи мостов ровно по одному разу привела к формированию совершенно нового раздела математики, теории графов.
Многие мосты были разрушены во время бомбардировок, и город больше не может задавать тот же интригующий вопрос, что и в восемнадцатом веке. Наряду с принципиально иной планировкой город Кенигсберг носит новое название Калининград, а река Прегель переименована в Преголю [Гопкинс, 6]. В то время как судьба Кенигсберга ужасна, старая кофейная проблема горожан пройти каждый из своих старых семи мостов ровно по одному разу привела к формированию совершенно нового раздела математики, теории графов.
Ссылки
Биггс, Норман Л., Э. К. Ллойд и Робин Дж. Уилсон. Теория графов: 1736-1936 . Оксфорд: Clarendon Press, 1976.
Данэм, Уильям. Эйлер: Повелитель всех нас . Вашингтон: Математическая ассоциация Америки, 1999.
Эйлер, Леонхард, «Solutio Problematis ad geometriam situs pertinentis» (1741), Eneström 53, MAA Euler Archive.
«История математики: о Леонарде Эйлере (1707–1783)». ScienceWeek (2003).

 А.
А. С 2006 года раздел математики комбинаторику ввели в школьный курс. Многие задачи по комбинаторики можно просто решить используя понятие граф.
С 2006 года раздел математики комбинаторику ввели в школьный курс. Многие задачи по комбинаторики можно просто решить используя понятие граф. Типичными графами являются схемы авиалиний, которые часто вывешивается в аэропортах, схемы метро, а на географических картах – изображение железных дорог. Выбранные точки графа называются его вершинами, а соединяющие их линии – ребрами.
Типичными графами являются схемы авиалиний, которые часто вывешивается в аэропортах, схемы метро, а на географических картах – изображение железных дорог. Выбранные точки графа называются его вершинами, а соединяющие их линии – ребрами.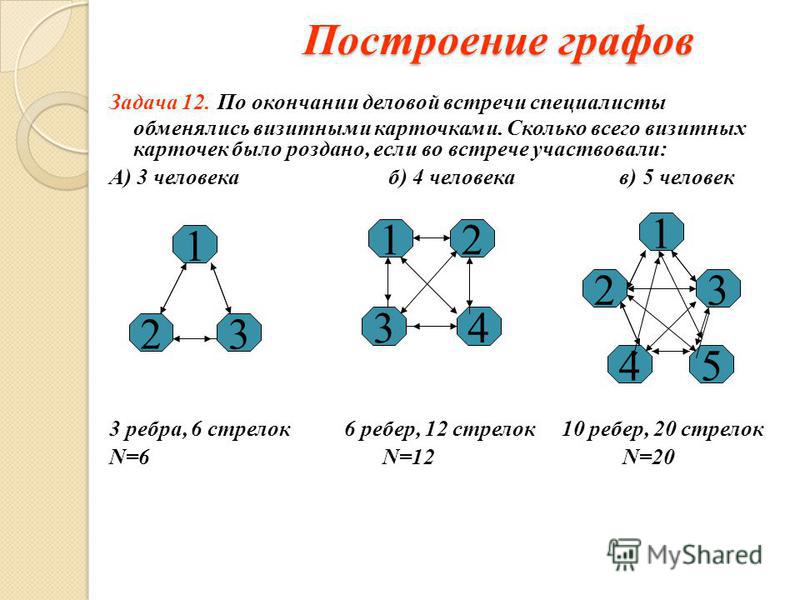 Точки называются вершинами графа, а соединяющие линии – рёбрами.
Точки называются вершинами графа, а соединяющие линии – рёбрами.
 Генеалогическое дерево будет деревом и в смысле теории графов, если в этом семействе не было браков между родственниками.
Генеалогическое дерево будет деревом и в смысле теории графов, если в этом семействе не было браков между родственниками.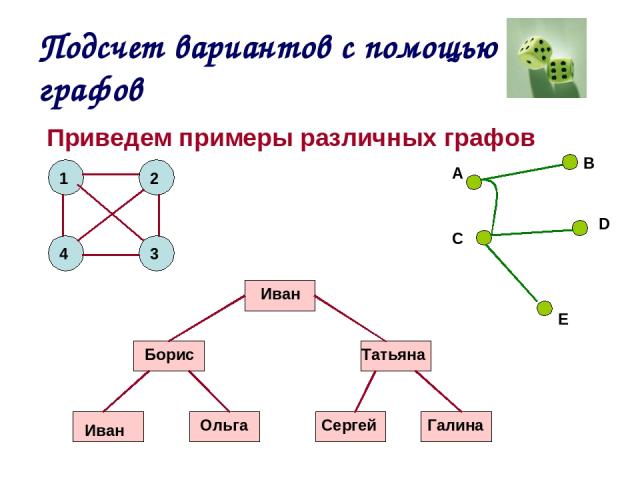 На рисунке 6 изображена очередная попытка проложить такие тропы.
На рисунке 6 изображена очередная попытка проложить такие тропы.
 Такой путь существует лишь в том случае, если граф – связный, т. е. от каждой его вершины к каждой другой можно пройти по ребрам графа, и из каждой вершины, кроме, может быть, двух, выходит четное число ребер. На графе, изображенном на рис. 3,а, он есть, а на рис. 3,б его нет.
Такой путь существует лишь в том случае, если граф – связный, т. е. от каждой его вершины к каждой другой можно пройти по ребрам графа, и из каждой вершины, кроме, может быть, двух, выходит четное число ребер. На графе, изображенном на рис. 3,а, он есть, а на рис. 3,б его нет.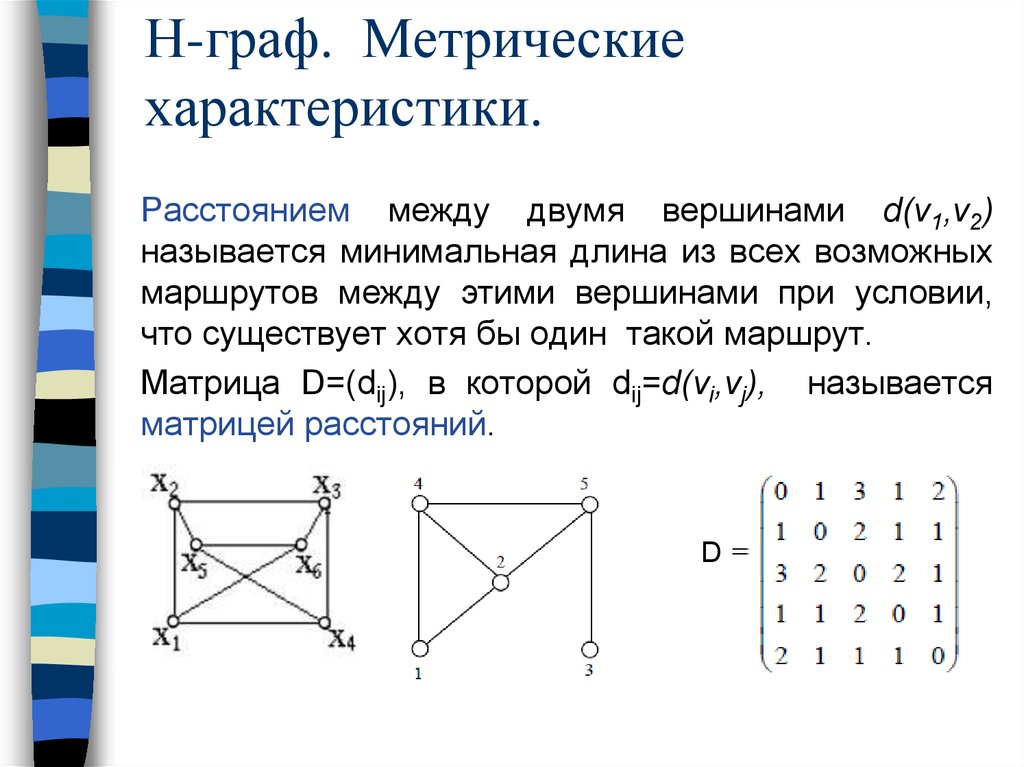




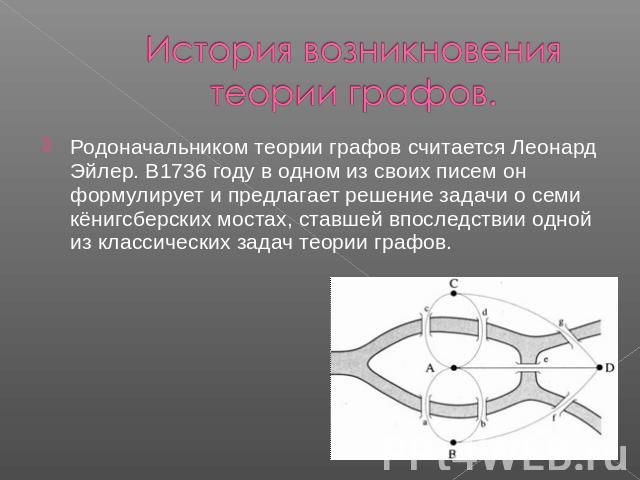 47 Mb.
47 Mb. Какой цвет костюма у каждого?
Какой цвет костюма у каждого? Установи фамилию каждого из ребят, если известно, что Иван не Иванов, Петр не Петров и Сергей не Сергеев и что Сергей живет в одном доме Петровым.
Установи фамилию каждого из ребят, если известно, что Иван не Иванов, Петр не Петров и Сергей не Сергеев и что Сергей живет в одном доме Петровым. Известно, что: щенок Леши темнее по окрасу, чем такса, Леси и Гриф; щенок Сергея старше Грифа, овчарки и таксы; Джек и такса всегда гуляют вместе. У кого какой породы щенок? Назовите клички щенков.
Известно, что: щенок Леши темнее по окрасу, чем такса, Леси и Гриф; щенок Сергея старше Грифа, овчарки и таксы; Джек и такса всегда гуляют вместе. У кого какой породы щенок? Назовите клички щенков.
 narod.ru/nayka/doc/graf.htm
narod.ru/nayka/doc/graf.htm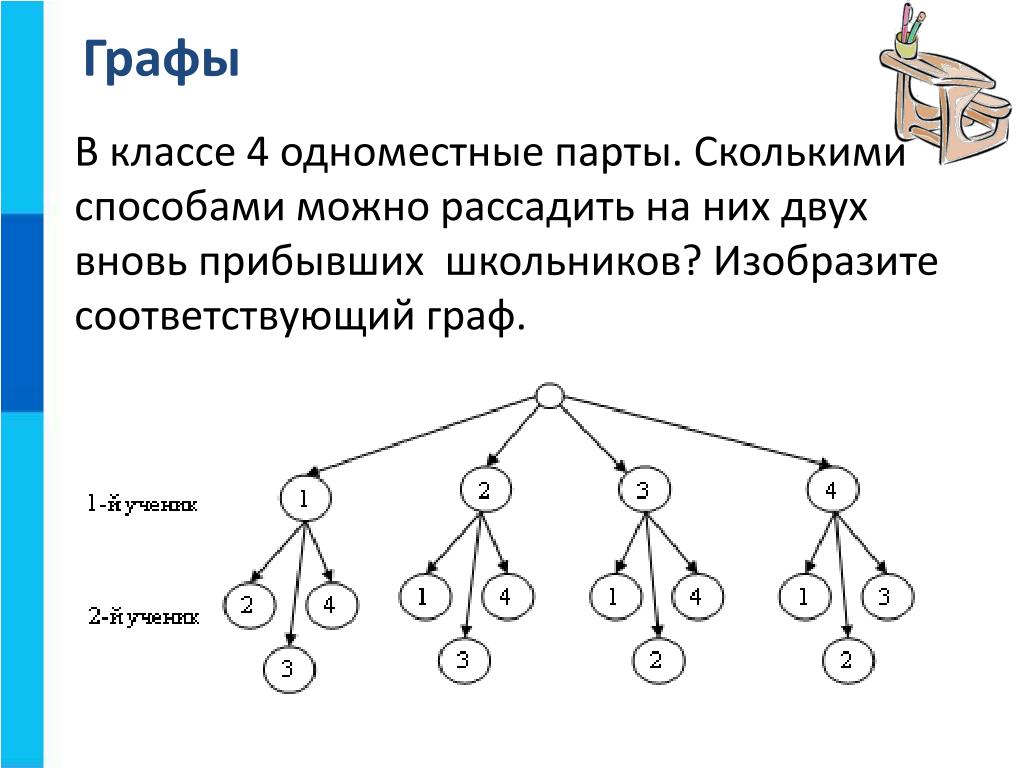 Сколько всего рукопожатий сделано?
Сколько всего рукопожатий сделано?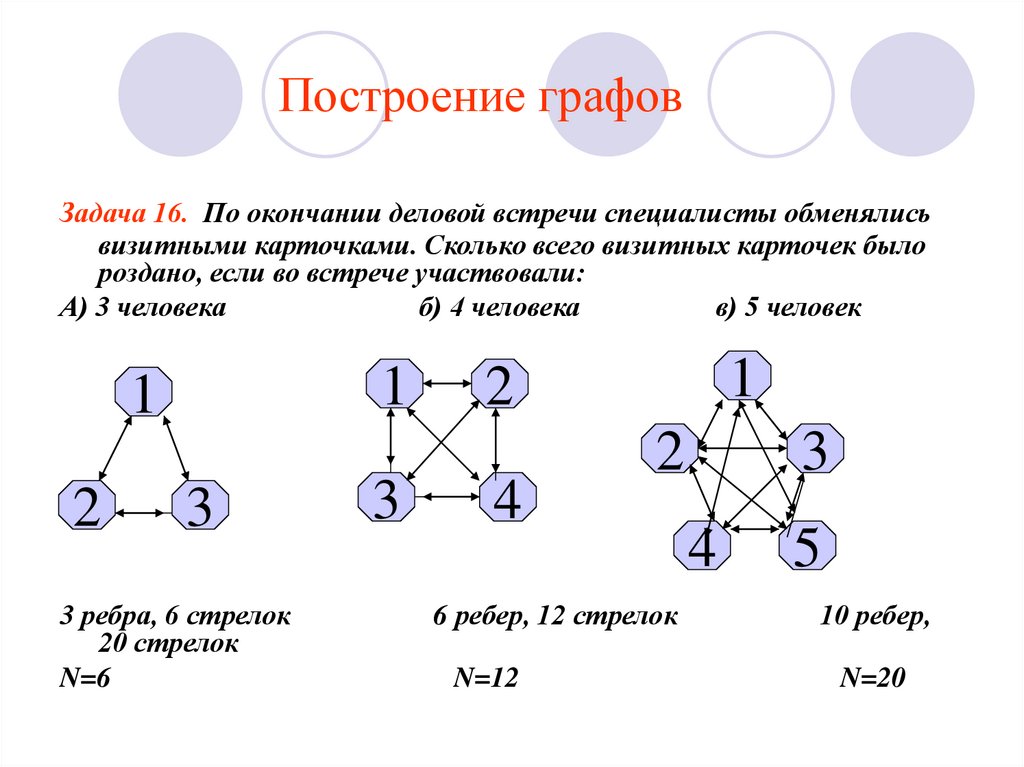 Можно ли по этим дорогам проехать из А в Г?
Можно ли по этим дорогам проехать из А в Г?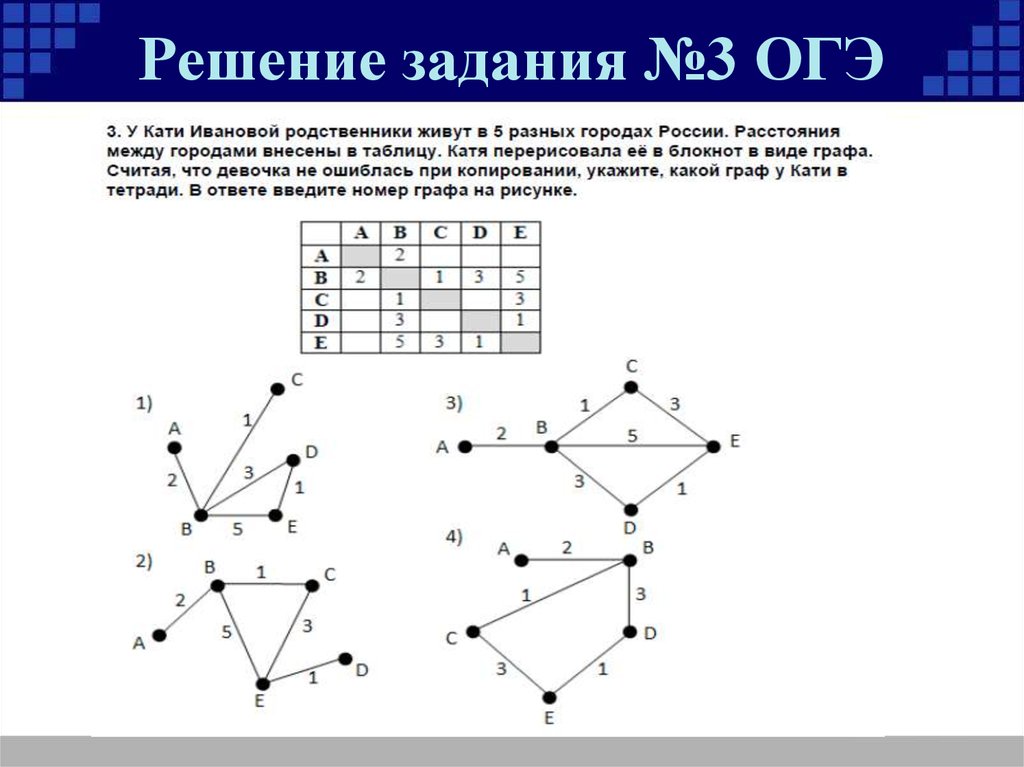 Девочка в зеленом платье (не Аня и не Валя) стоит между девочкой в голубом платье и Надей. Девочка в белом платье стоит между девочкой в розовом и Валей. Какое платье носит каждая девочка?
Девочка в зеленом платье (не Аня и не Валя) стоит между девочкой в голубом платье и Надей. Девочка в белом платье стоит между девочкой в розовом и Валей. Какое платье носит каждая девочка? Стакан стоит около банки и сосуда с молоком. В какой сосуд налита каждая жидкость?
Стакан стоит около банки и сосуда с молоком. В какой сосуд налита каждая жидкость? Сколько вариантов придется перебрать им, чтобы подобрать двузначный код?
Сколько вариантов придется перебрать им, чтобы подобрать двузначный код?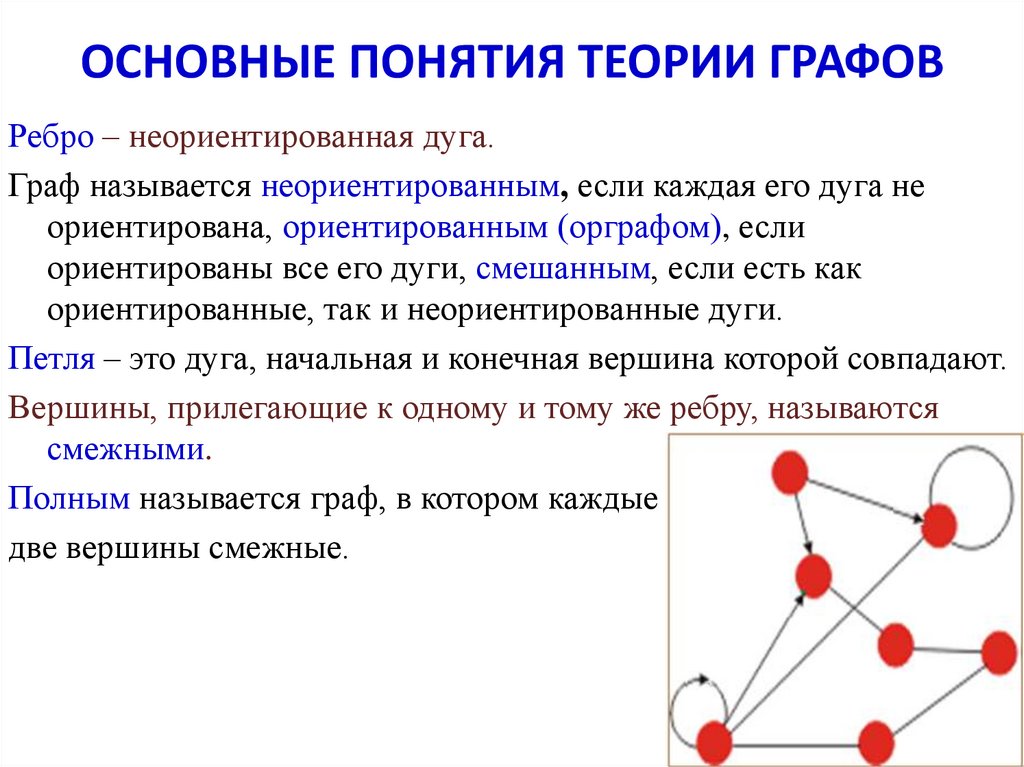 Каждый из них получил один домик: Ниф-Ниф – не из камней, и не из прутьев; Нуф-Нуф не из камней.
Каждый из них получил один домик: Ниф-Ниф – не из камней, и не из прутьев; Нуф-Нуф не из камней.
 }\) Каждая вершина (человек) имеет степень (рукопожатие) 9 (человек). Таким образом, сумма степеней равна \(90\text{.}\). Однако степени учитывают каждое ребро (рукопожатие) дважды, поэтому в графе 45 ребер. Именно столько рукопожатий произошло.
}\) Каждая вершина (человек) имеет степень (рукопожатие) 9 (человек). Таким образом, сумма степеней равна \(90\text{.}\). Однако степени учитывают каждое ребро (рукопожатие) дважды, поэтому в графе 45 ребер. Именно столько рукопожатий произошло. }\)
}\)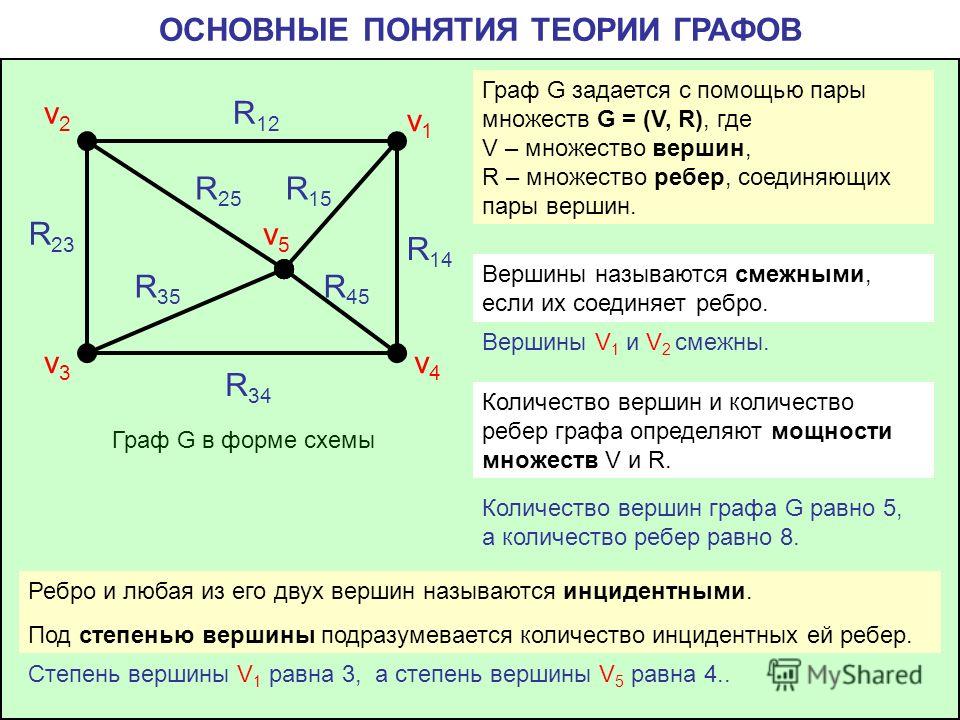
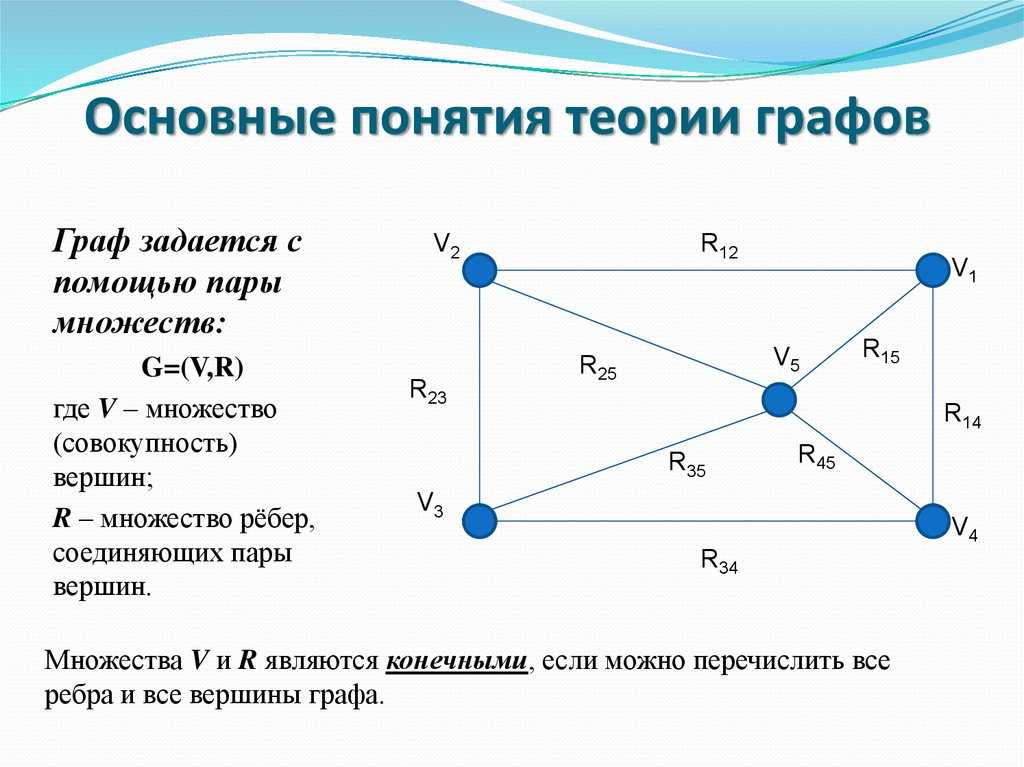 Это граф \(K_5\text{.}\)
Это граф \(K_5\text{.}\) Это можно сделать методом проб и ошибок (и возможно).
Это можно сделать методом проб и ошибок (и возможно). Нарисуйте плоское графическое представление октаэдра. Сколько вершин, ребер и граней у октаэдра (и вашего графа)?
Нарисуйте плоское графическое представление октаэдра. Сколько вершин, ребер и граней у октаэдра (и вашего графа)? }\)». Мы покажем \(P( n)\) верно для всех \(n \ge 0\text{.}\) Базовый случай: существует только один граф с нулевыми ребрами, а именно одна изолированная вершина. В этом случае \(v = 1\text{,}\) \(f = 1\) и \(e = 0\text{,}\), поэтому формула Эйлера верна. Индуктивный случай: предположим, что \(P(k)\) верно для некоторого произвольного \(k \ge 0\text{.}\). Теперь рассмотрим произвольный граф, содержащий \(k+1\) ребер (и \(v\ ) вершины и \(f\) грани). Независимо от того, как выглядит этот граф, мы можем удалить одно ребро, чтобы получить граф с \(k\) ребер, к которому мы можем применить индуктивную гипотезу. Есть две возможности. Во-первых, ребро, которое мы удаляем, может быть инцидентно вершине степени 1. В этом случае также удалите эту вершину. Меньший граф теперь будет удовлетворять \(v-1 — k + f = 2\) по предположению индукции (удаление ребра и вершины не уменьшило количество граней). Добавление ребра и вершины назад дает \(v — (k+1) + f = 2\text{,}\) по мере необходимости. Второй случай состоит в том, что удаляемое нами ребро инцидентно вершинам степени больше единицы.
}\)». Мы покажем \(P( n)\) верно для всех \(n \ge 0\text{.}\) Базовый случай: существует только один граф с нулевыми ребрами, а именно одна изолированная вершина. В этом случае \(v = 1\text{,}\) \(f = 1\) и \(e = 0\text{,}\), поэтому формула Эйлера верна. Индуктивный случай: предположим, что \(P(k)\) верно для некоторого произвольного \(k \ge 0\text{.}\). Теперь рассмотрим произвольный граф, содержащий \(k+1\) ребер (и \(v\ ) вершины и \(f\) грани). Независимо от того, как выглядит этот граф, мы можем удалить одно ребро, чтобы получить граф с \(k\) ребер, к которому мы можем применить индуктивную гипотезу. Есть две возможности. Во-первых, ребро, которое мы удаляем, может быть инцидентно вершине степени 1. В этом случае также удалите эту вершину. Меньший граф теперь будет удовлетворять \(v-1 — k + f = 2\) по предположению индукции (удаление ребра и вершины не уменьшило количество граней). Добавление ребра и вершины назад дает \(v — (k+1) + f = 2\text{,}\) по мере необходимости. Второй случай состоит в том, что удаляемое нами ребро инцидентно вершинам степени больше единицы. В этом случае удаление ребра сохранит количество вершин прежним, но уменьшит количество граней на единицу. Таким образом, по индуктивному предположению мы будем иметь \(v — k + f-1 = 2\text{.}\) Добавление ребра обратно даст \(v — (k+1) + f = 2\) по мере необходимости. Следовательно, по принципу математической индукции формула Эйлера верна для всех плоских графов.
В этом случае удаление ребра сохранит количество вершин прежним, но уменьшит количество граней на единицу. Таким образом, по индуктивному предположению мы будем иметь \(v — k + f-1 = 2\text{.}\) Добавление ребра обратно даст \(v — (k+1) + f = 2\) по мере необходимости. Следовательно, по принципу математической индукции формула Эйлера верна для всех плоских графов. )
) Один цвет для верхнего набора вершин, другой цвет для нижнего набора вершин.
Один цвет для верхнего набора вершин, другой цвет для нижнего набора вершин.
 По теореме Брукса этот граф имеет хроматическое число не более 2, так как это максимальная степень в графе, а граф не является полным графом или нечетным циклом. Таким образом, нужны только две коробки.
По теореме Брукса этот граф имеет хроматическое число не более 2, так как это максимальная степень в графе, а граф не является полным графом или нечетным циклом. Таким образом, нужны только две коробки. Ровно две вершины будут иметь нечетную степень: вершины для Невады и Юты. Таким образом, вы должны начать свое путешествие в одном из этих штатов, а закончить его в другом.
Ровно две вершины будут иметь нечетную степень: вершины для Невады и Юты. Таким образом, вы должны начать свое путешествие в одном из этих штатов, а закончить его в другом.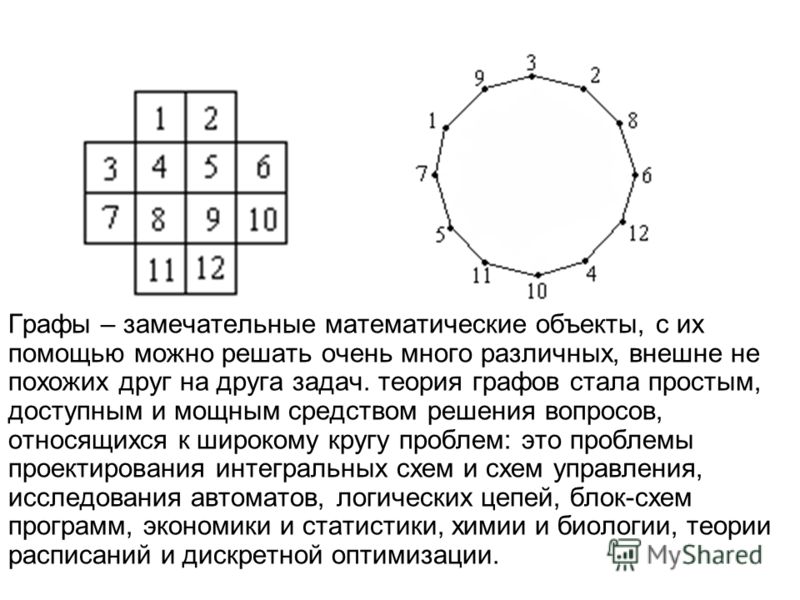
 Чтобы иметь цикл Гамильтона, мы должны иметь \(m=n\text{.}\)
Чтобы иметь цикл Гамильтона, мы должны иметь \(m=n\text{.}\)
 Если вы посмотрите на три обведенные вершины, то увидите, что они имеют только двух соседей, что нарушает условие соответствия \(\card{N(S)} \ge \card{S}\) (три обведенные вершины образуют множество \(С\)).
Если вы посмотрите на три обведенные вершины, то увидите, что они имеют только двух соседей, что нарушает условие соответствия \(\card{N(S)} \ge \card{S}\) (три обведенные вершины образуют множество \(С\)).