Теория лапласа матрицы: Теорема Лапласа

Теорема Лапласа (без доказательства) — ПриМат

Итак, прежде чем перейти к методу использования теоремы Лапласа, необходимо рассмотреть несколько важных определений.

Определение Пусть дана матрица $A \in M_{m \times n}(P).$ Возьмем в ней любые $i$ строк и $i$ столбцов, причем $i > 0$ и $i$ меньше минимального из $m$ и $n.$ Элементы, которые располагаются на пересечении выбранных строк и столбцов, образуют матрицу $i-$го порядка. Определитель этой матрицы называется минором $i-$го порядка исходной матрицы. Если порядок минора равен единице, то минор является элементом исходной матрицы.

Пример 1 Пусть дан определитель четвертого порядка $$ \begin{vmatrix} -8 & -5 & 2 & 7 \\ 1 & 3 & -9 & -3 \\ 4 & -4 & -1 & 9 \\ -5 & 3 & -4 & 8 \end{vmatrix}.$$ Выберем, например, $2$-й и $4$-й столбцы и $1$-ю и $3$-ю строки. Таким образом, элементы, стоящие на пересечении этих столбцов и строк образуют минор $2-$го порядка: $$ \begin{vmatrix} -5 & 7 \\ -4 & 9 \end{vmatrix} = -45 + 28 = -17.

{S_1 + S_2}$, в котором $S_1$ — это сумма номеров строк, а $S_2$ — это сумма номеров столбцов, в которых лежит исходный минор, то мы получим алгебраическое дополнение к этому минору.

Пример 3 Пусть дан определитель пятого порядка $$ \begin{vmatrix} -7 & 5 & 3 & -2 & 6 \\ 9 & -8 & 7 & 3 & -4 \\ 0 & 1 & -1 & -5 & 9 \\ -3 & 2 & -2 & -4 & -8 \\ 4 & 9 & 5 & -1 & 1 \end{vmatrix}.$$ Выберем в нем, к примеру $1-$ю и $4-$ю строки, а также $2-$й и $5-$й столбцы. Тогда на пересечении выбранных строк и столбцов образуется минор $2-$го порядка $$ \begin{vmatrix} 5 & 6 \\ 2 & -8 \end{vmatrix} = -40-12 = -52.$$ Дополнительным минором к нему будет $$ \begin{vmatrix} 9 & 7 & 3 \\ 0 & -1 & -5 \\ 4 & 5 & -1 \end{vmatrix} = 9 + 0-140 + 12 + 0 + 225 = 106.$$ Наконец, алгебраическим дополнением к минору будет $$ \begin{vmatrix} 9 & 7 & 3 \\ 0 & -1 & -5 \\ 4 & 5 & -1 \end{vmatrix} \cdot (-1)^{(1 + 4) + (2 + 5)} = 106 \cdot (-1)^{12} = 106,$$ где степени $-1$ являются таковыми, так как элементы минора исходного определителя располагаются в $1-$й и $4-$й строках и во $2-$м и в $5-$м столбцах.

Итак, разобравшись с приведенными выше определениями, можно приступать к формулированию теоремы.

Теорема (Лапласа) Если в определителе порядка $m$ выбрать $i$ строк (столбцов), где $i > 0$ и $i < m,$ то данный определитель будет равняться сумме миноров, которые расположены в этих строках (столбцах), умноженных на их алгебраические дополнения. Эти миноры будут иметь $i-$й порядок.

Таким образом, благодаря теореме Лапласа, при вычислении определителя $m-$го порядка, мы можем вычислить несколько определителей более малых порядков ($i$), что упрощает нам задачу.

Следствием (а также частным случаем, для которого $i = 1$) из теоремы Лапласа является Теорема о разложении определителя по строке.

Пример 4 Найти определитель матрицы $4-$го порядка $$\begin{pmatrix} 3 & 5 & 6 & 9 \\ -1 & 7 & 2 & -5 \\ 0 & 4 & 1 & 2 \\ -3 & -6 & 5 & 0 \end{pmatrix}.$$ Разложим определитель этой матрицы по теореме Лапласа, выбрав $1-$ю и $3-$ю строки: $$\begin{vmatrix} 3 & 5 & 6 & 9 \\ -1 & 7 & 2 & -5 \\ 0 & 4 & 1 & 2 \\ -3 & -6 & 5 & 0 \end{vmatrix} = (-1)^{(1 + 3) + (1 + 2)} \cdot \begin{vmatrix} 3 & 5 \\ 0 & 4 \end{vmatrix} \cdot \begin{vmatrix} 2 & -5 \\ 5 & 0 \end{vmatrix} +$$ $$+ (-1)^{(1 + 3) + (1 + 3)} \cdot \begin{vmatrix} 3 & 6 \\ 0 & 1 \end{vmatrix} \cdot \begin{vmatrix} 7 & -5 \\ -6 & 0 \end{vmatrix} + (-1)^{(1 + 3) + (1 + 4)} \cdot \begin{vmatrix} 3 & 9 \\ 0 & 2 \end{vmatrix} \cdot \begin{vmatrix} 7 & 2 \\ -6 & 5 \end{vmatrix} +$$ $$+ (-1)^{(1 + 3) + (2 + 4)} \cdot \begin{vmatrix} 5 & 9 \\ 4 & 2 \end{vmatrix} \cdot \begin{vmatrix} -1 & 2 \\ -3 & 5 \end{vmatrix} + (-1)^{(1 + 3) + (3 + 4)} \cdot \begin{vmatrix} 6 & 9 \\ 1 & 2 \end{vmatrix} \cdot \begin{vmatrix} -1 & 7 \\ -3 & -6 \end{vmatrix} +$$ $$+ (-1)^{(1 + 3) + (2 + 3)} \cdot \begin{vmatrix} 5 & 6 \\ 4 & 1 \end{vmatrix} \cdot \begin{vmatrix} -1 & -5 \\ -3 & 0 \end{vmatrix} = (-1)^7 \cdot (12-0) \cdot (0 + 25) +$$ $$+ (-1)^8 \cdot (3-0) \cdot (0-30) + (-1)^9 \cdot (6-0) \cdot (35 + 12) +$$ $$+ (-1)^{10} \cdot (10-36) \cdot (-5 + 6) + (-1)^{11} \cdot (12-9) \cdot (6 + 21) +$$ $$+ (-1)^9 \cdot (5-24) \cdot (0-15) = -(12 \cdot 25)-3 \cdot 30-6 \cdot 47-26 \cdot 1-3 \cdot 27-$$ $$-(19 \cdot 15) = -300-90-282-26-81-285 = -1064. $$

Как мы могли заметить, для нахождения определителя $4-$го порядка нам понадобилось искать лишь определители $2-$го порядка, что намного легче. Разберем этот пример подробнее.

Для начала, вторым множителем каждого слагаемого является минор, расположенный в выбранных в начале решения строках. Мы берем все существующие в данных строках миноры. Далее, первым множителем каждого слагаемого является $(-1)$ в степени, которая является суммой номеров строк и столбцов, в которых расположен соответствующий минор. Третьим же множителем является дополнительный минор к соответствующему. Произведение дополнительного минора и $(-1)$ в соответствующей степени образует алгебраическое дополнение к своему минору.

Таким образом мы расписываем все миноры, находящиеся в выбранных строках, умножаем на их алгебраические дополнения и суммируем полученные произведения. После этого решаем полученное выражение, приходя к ответу, который является значением определителя исходной матрицы.

Пример 5 Найти определитель матрицы $4-$го порядка $$\begin{pmatrix} 1 & 4 & -3 & 0 \\ 5 & -2 & 1 & 7 \\ 0 & 2 & -6 & 4 \\ -5 & 1 & 0 & 2 \end{pmatrix}.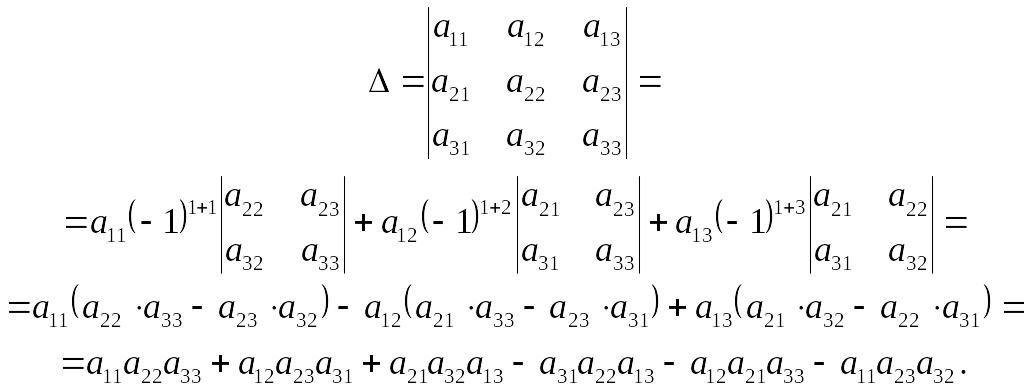 {10} \cdot (-2-60) \cdot (120-0) = -67 \cdot 47-89 \cdot 110 + 23 \cdot 28 + 169 \cdot 60-$$ $$-3 \cdot 36-62 \cdot 120 = -3149-9790 + 644 + 10140-108-7440 = -9703. $$

[свернуть]

1. А. И. Кострикин Введение в алгебру М.: Наука, 1994, Глава 3, §3, «Упражнения» (стр. 150)
2. Курош А.Г. Курс высшей алгебры М.: Наука, 1968, Глава 1, §6, «Вычисление определителей» (стр. 51)
3. Личный конспект, составленный на основе лекций Г. С. Белозерова.

Тест на проверку знаний о теореме Лапласа и определений, необходимых для формулировки данной теоремы.

Открытое образование — Алгебра и геометрия

Select the required university:

———

Закрыть

• About
• Format
• Requirements
• Course program
• Knowledge
• Skills
• Abilities
• Education directions

About

I часть. Матрицы, теоретико-множественные понятия, геометрические векторы, линейные пространства, системы линейных алгебраических уравнений.
Курс рассчитан на студентов университетов и вузов, обучающихся по специальностям «Математика», «Прикладная математика», «Информатика», «Физика», «Экономика».

Format

Форма обучения: дистанционная. 

Еженедельные занятия будут включать:

• тематические видеолекции, на которых излагается теоретический материал курса, каждая лекция сопровождается тестами;
• семинарские занятия, ориентированные на усвоение лекционного материала, приобретение навыков решения задач и умение пользоваться алгоритмами;
• тренажеры (в интерактивном формате) для самостоятельного решения простейших задач с автоматизированной проверкой результатов;
• дополнительные семинарские занятия по решению задач повышенной трудности: будут изложены основные приемы математических доказательств, их применение будет иллюстрироваться на примерах задач по текущему разделу курса.

Requirements

Курс рассчитан на студентов университетов и вузов, обучающихся по специальностям «Математика», «Прикладная математика», «Информатика», «Физика», «Экономика».

Course program

Лекция 1.
Глава I. Основы теории матриц
§ 1. Понятие матрицы
Компактная форма записи матрицы. Матрицы специального вида.
§ 2. Операции над матрицами
Линейные операции. Умножение матриц. Транспонирование матрицы.

Лекция 2.
§ 3. Элементарные преобразования матрицы и матрицы элементарных
преобразований
Приведение к ступенчатому виду. Матрицы элементарных преобразований.
§ 4. Определитель матрицы
Перестановки. Построение определителя n-го порядка. Простейшие свойства.
Лекция 3.
§ 4. Определитель матрицы (продолжение)
Миноры и алгебраические дополнения. Теорема Лапласа, общая схема доказательства.
Лекция 4.
§ 4. Определитель матрицы (продолжение)
Доказательство теоремы Лапласа. Разложение определителя по строке (столбцу).
Блочные матрицы. Определитель произведения матриц.
Лекция 5.
§ 5. Обратная матрица
Определение и простейшие свойства. Присоединенная матрица. Критерий обратимости. Явный вид обратной матрицы.
Глава II. Теоретико-множественные понятия
§ 6. Понятие множества.
О понятии множества. Операции над множествами. Декартово произведение множеств.
§ 7. Бинарные отношение. Отношение эквивалентности
§ 8. Отображения
Определение. Биективное (взаимно-однозначное) отображение. Обратное отображение.
Критерий обратимости.
Лекция 6.
Глава III. Геометрические векторы
§ 9. Направленные отрезки
§ 10. Свободный вектор. Линейные операции над векторами
Определение и терминология. Линейные операции над векторами. Множества векторов на прямой, на плоскости и в пространстве.
Лекция 7.
Глава IV. Введение в теорию линейных пространств
§ 11. Вещественное линейное пространство.
Определение. Примеры: геометрические пространства, арифметическое пространство, пространство матриц, пространства многочленов.
§ 12. Линейная зависимость
§ 13. Геометрический смысл линейной зависимости

Лекция 8.
§ 14. Ранг матрицы
Ранг матрицы и линейная зависимость. Ранг матрицы и элементарные преобразования. Вычисление ранга. Эквивалентные матрицы.
§ 15. Базис и размерность линейного пространства
Определения. Координаты вектора. Переход к другому базису.
Лекция 9.
Глава V. Векторная алгебра
§ 16. Координаты вектора на оси
§ 17. Аффинная (общая декартова) система координат. Координаты точки
§ 18. Проекции вектора
Проекции вектора на плоскости. Проекции вектора в пространстве. Проекции вектора и координаты.
Лекция 10.
§ 19. Скалярное произведение
Определение и основные свойства. Ортонормированный базис. Координаты вектора и скалярное произведение в ортонормированном базисе.
§ 20. Векторное и смешанное произведения векторов
Ориентация в вещественном пространстве. Основные факты. Векторное и смешанное произведения в прямоугольных координатах.
§ 21. Преобразование прямоугольной декартовой системы координат
Ортогональная матрица. Матрица перехода от одного ортонормированного базиса к другому ортонормированному базису. Преобразование прямоугольной декартовой системы координат на плоскости.
Лекция 11.
Глава VI. Системы линейных алгебраических уравнений
§ 22. Основные задачи теории решения систем линейных алгебраических уравнений
Терминология. Компактная запись системы. Эквивалентность систем.
§ 23. Системы с квадратной невырожденной матрицей
§ 24. Системы общего вида. Общее решение системы
Совместность системы. Схема исследования совместной системы. Общее решение системы. Однородные системы.
§ 25. Метод Гаусса исследования и решения систем уравнений
Системы с трапециевидной матрицей. Элементарные преобразования системы уравнений. Приведение системы общего вида к системе с верхней трапециевидной матрицей.
Лекция 12.
Глава VII. Геометрические свойства решений системы линейных алгебраических уравнений
§ 26. Линейное подпространство решений однородной системы
Линейное подпространство линейного пространства. Множество решений однородной системы линейных алгебраических уравнений как линейное подпространство арифметического пространства. Фундаментальная система решений. Общее решение системы.
§ 27. Линейное многообразие решений неоднородной системы
Линейное многообразие в линейном пространстве. Множество решений неоднородной системы линейных алгебраических уравнений как линейное многообразие в арифметическом пространстве. Общее решение системы

Education directions

01.03.02 Прикладная математика и информатика

Knowledge

Знать определения понятий и формулировки теорем по программе курса

Skills

Уметь доказывать теоремы, ориентироваться в логической структуре курса, уметь пользоваться алгоритмами.

Abilities

Овладеть навыками математических доказательств и навыками решения задач

Московский государственный университет имени М.В. Ломоносова

Мокроусов Илья Сергеевич

Кандидат физико-математических наук
Position: Асистент кафедры общей математики факультета вычислительной математики и кибернетики МГУ имени М. В. Ломоносова

Ким Галина Динховна

Кандидат физико-математических наук
Position: Доцент кафедры общей математики МГУ имени М.В.Ломоносова

Similar courses

12 September 2022 — 1 January 2030 г.

Геометрия и группы

МФТИ

12 September 2022 — 1 January 2030 г.

Религия и наука: христианская апологетика

МФТИ

New course

1 November 2022 — 1 November 2030 г.

Компьютерное зрение

НИУ ВШЭ

К сожалению, мы не гарантируем корректную работу сайта в вашем браузере. Рекомендуем заменить его на один из предложенных.

Также советуем ознакомиться с полным списком рекомендаций.

Google Chrome

Mozilla Firefox

Apple Safari

Разложения Лапласа для определителя

Используя определение определителя, в примере 5 было получено следующее выражение: 

Это уравнение можно переписать следующим образом:

  

Каждый термин справа имеет следующую форму:

 

В частности, обратите внимание, что

 

Если A = [ a _ij ] является матрицей n x n , то определитель ( n − 1) x ( n − 1) матрица, которая остается после удаления строки и столбца, содержащих запись a _ij , называется a _ij второстепенной , обозначается mnr( а _ij ). Если a _ij минор умножить на (−1) ^{i + j} , то результат называется кофактором a _ij 9 0042 , обозначаемый cof( a _ij ). То есть

Используя эту терминологию, приведенное выше уравнение для определителя матрицы 3 x 3 A равно сумме произведений элементов первой строки и их сомножителей:

 

Это называется расширением Лапласа по первой строке. Можно также показать, что определитель равен разложению Лапласа по второй -й строке,

   

или по третьему ряду ,

Верно даже больше. Определитель также равен разложению Лапласа по первому столбцу  

по второму столбцу или по третьему столбцу. Хотя формула разложения Лапласа для определителя была явно проверена только для матрицы 3×3 и только для первой строки, можно доказать, что определитель любой матрицы nxn равен разложению Лапласа по любой строке или любому столбцу .

Пример 1 : Оцените определитель следующей матрицы, используя разложение Лапласа по второму столбцу:

 

Записи во втором столбце: a ₁₂ = −1, a

22 = 2 и a ₃₂ = 0. Миноры этих записей, mnr( а ₁₂ ), mnr( a ₂₂ ) и mnr( a ₃₂ ), вычисляются следующим образом:

 

Поскольку кофакторы записей второго столбца равны

   

расширение Лапласа по второму столбцу становится

Обратите внимание, что не нужно было вычислять минор или кофактор записи (3, 2) в A , поскольку эта запись была равна 0. В общем случае при вычислении определителя методом разложения Лапласа выберите строку или столбец с наибольшим количеством нулей. Миноры этих записей не нужно оценивать, потому что они ничего не дадут в определителе.

Множитель (−1) ^{i + j} , который умножает a _ij минор, чтобы получить кофактор a _ij , приводит к шахматной доске узор знаков; каждый знак дает значение этого фактора при вычислении кофактора

a _ij из минора a _ij . Например, шахматная доска для матрицы 3 х 3 выглядит так:

.

 

Для матрицы 4 x 4 шахматная доска имеет вид

   

и так далее.

Пример 2 : Вычислите определитель следующей матрицы:

 

Сначала найдите строку или столбец с наибольшим количеством нулей. Здесь это третья строка, содержащая два нуля; разложение Лапласа по этой строке будет содержать только два ненулевых члена. Шаблон шахматной доски, показанный выше для матрицы 4 на 4, подразумевает, что минор записи a ₃₁ = 1 будет умножен на +1, а минор записи a ₃₄ = 2 будут умножены на -1, чтобы получить соответствующие кофакторы:

Теперь каждый из этих кофакторов, которые сами по себе являются детерминантами, можно оценить с помощью разложения Лапласа. Расширение по третьему столбцу,

 

Другой кофактор оценивается путем расширения его первой строки: 

Следовательно, вычисление det A с помощью разложения Лапласа по третьей строке A дает

Пример 3 : Перекрестное произведение двух 3-векторов, x = x ₁ i + x ₂ j 900 42 + x ₃ к и у = у ₁ я + у ₂ у + у ₃ 90 041 k , проще всего вычислить, выполнив разложение Лапласа по первой строке символического определителя

 

Это расширение дает

 

Для иллюстрации, векторное произведение векторов x = 3

j − 3 k и y = −2 i + 2 j − k

 

Пример 4 : Есть ли связь между определителем числа A ^T и определителем числа A ?

В случае 2 на 2 легко видеть, что det ( А ^Т ) = det А :

 

В случае 3 по 3 разложение Лапласа по первой строке A дает тот же результат, что и разложение Лапласа по первому столбцу A ^T , подразумевая, что det ( A 9002 0 ^T ) = det A :

 

Начиная с расширения

   

для определителя, нетрудно привести общее доказательство того, что det ( А ^Т ) = det А .

Пример 5 : Примените результат det ( A ^T ) = det A для вычисления

   

при том, что

(где a, e, g, n, o, p и r — скаляры).

Поскольку замена одной строки меняет знак определителя (свойство 2), замена двух строк,

   

оставит определитель без изменений:

Но определитель матрицы равен определителю ее транспонирования, поэтому

 

Следовательно,

 

Пример 7 : Учитывая, что числа 1547, 2329, 3893 и 4471 делятся на 17, докажите, что определитель числа

   

также делится на 17 без фактического вычисления.

Из-за результата det ( A ^T ) = det A каждое свойство определителя, которое включает строки из A подразумевает другое свойство определителя, включающее столбцы A . Например, определитель является линейным в каждом столбце , меняет знак, если два столбца меняются местами, не меняется, если число, кратное одному столбцу , добавляется к другому столбцу и так далее.

Для начала умножьте первый столбец А на 1000, второй столбец на 100 и третий столбец на 10. Определитель полученной матрицы будет в 1000·100·10 раз больше определителя А :

 

Затем добавьте второй, третий и четвертый столбцы этой новой матрицы к ее первому столбцу. Ни одна из этих операций со столбцами не изменяет определитель; таким образом,

 

Поскольку каждый элемент в первом столбце этой последней матрицы делится на 17, каждый член разложения Лапласа по первому столбцу будет делиться на 17, и, таким образом, сумма этих членов, которая дает определитель, будет делиться на 17. 17. Так как 17 делит 10 ⁶ det A , 17 должно делить det A , потому что 17 простое число и не делится на 10 ⁶ .

Пример 7 : Полезным понятием в многомерном исчислении (например, в связи с формулой замены переменных для кратных интегралов) является понятие Якобиана отображения. Пусть x и y заданы как функции независимых переменных u и v :

.

 

Якобиан отображения ( u, v ) ↦ ( x, y ), величина, обозначаемая символом δ( x, y )/δ( u, v ), определяется как следующий определитель: 

Для иллюстрации рассмотрим преобразование полярных координат ,

 

Якобиан этого отображения ( r , θ) ↦ ( x, y ) равен

.

Тот факт, что якобиан этого преобразования равен r учитывает коэффициент r в известной формуле

.

   

, где R ′ представляет собой область в плоскости r −θ, отображаемую (*) в область интегрирования R в плоскости x−y .

Якобиан также может быть расширен до трех переменных. Например, точку в трехмерном пространстве можно задать, задав ее сферических координат —ϕ и θ, которые связаны с обычными прямоугольными координатами — x, y и z — по уравнениям

 

См. рис.

Рисунок 1

Якобиан отображения (ρ, ϕ, θ) ↦ ( x, y, z ) равен

Разложением Лапласа по третьей строке,

 

Тот факт, что якобиан этого преобразования равен ρ ² sin ϕ, объясняет множитель ρ ² sin ϕ в формуле замены переменных в тройном интеграле от прямоугольных координат к сферическим:

Расширения Лапласа после сокращения строк . Полезность метода разложения Лапласа для вычисления определителя повышается, когда ему предшествуют элементарные операции со строками. Если такие операции выполняются над матрицей, количество нулей в данном столбце может быть увеличено, тем самым уменьшая количество ненулевых членов в разложении Лапласа вдоль этого столбца.

Пример 8 : вычислить определитель матрицы

 

Следующие операции редукции строк, поскольку они просто включают в себя добавление кратного одной строки к другой, не изменяют значение определителя:

 

Теперь, когда определитель этой последней матрицы вычисляется с использованием разложения Лапласа по первому столбцу, остается только один ненулевой член:

 

Следовательно, det A = −5.

Пример 9 : Вычисление определителя матрицы

 

Чтобы избежать создания большого количества нецелочисленных записей в процессе сокращения строк, первая строка делится на коэффициент 2 из нижней строки. Поскольку при умножении строки на скаляр определитель умножается на этот скаляр,

 

Теперь, потому что элементарные операции со строками

   

не изменяют определитель, разложение Лапласа по первому столбцу этой последней матрицы завершает вычисление определителя A :

[PDF] Применение метода недель для численного обращения преобразования Лапласа к матричной экспоненте

• 60

 @статья{ Brio2005ПриложениеOW,
  title={Применение метода Уикса для численного обращения преобразования Лапласа к матричной экспоненте},
  автор = {Мойси Брио, Патрик О. Кано и Джером В. Молони},
  journal={Коммуникации в математических науках},
  год = {2005},
  объем = {3},
  страницы = {335-372}
} 

• M. Brio, P. Kano, J. Moloney
• Опубликовано 1 июня 2005 г.
• Mathematics
• Communications in Mathematical Sciences

Метод Уикса — хорошо зарекомендовавший себя алгоритм числовой инверсии скалярных пространственных функций Лапласа. В этой статье мы распространяем метод на обращение матричных функций одной переменной времени и оцениваем качества этого подхода. Чтобы проиллюстрировать и дать количественную оценку нашего обсуждения, мы вычисляем экспоненциальную матрицу с помощью алгоритма на основе БПФ. Особое внимание уделено сравнению алгоритмов автоматизированного подбора двух параметров настройки. В дополнение к… 

Просмотр через Publisher

intlpress.com

Обзор алгоритмов обратного преобразования Лапласа для численных подходов в пространстве Лапласа для повторного использования прямой оценки функции изображения, по крайней мере, в течение логарифмического цикла времени.

Выбор оптимального параметра в методе Уикса для численной инверсии преобразования Лапласа на основе машинного обучения

Метод Уикса для численного обращения преобразования Лапласа использует преобразование Мёбиуса, которое параметризуется двумя действительными величинами, σ и b.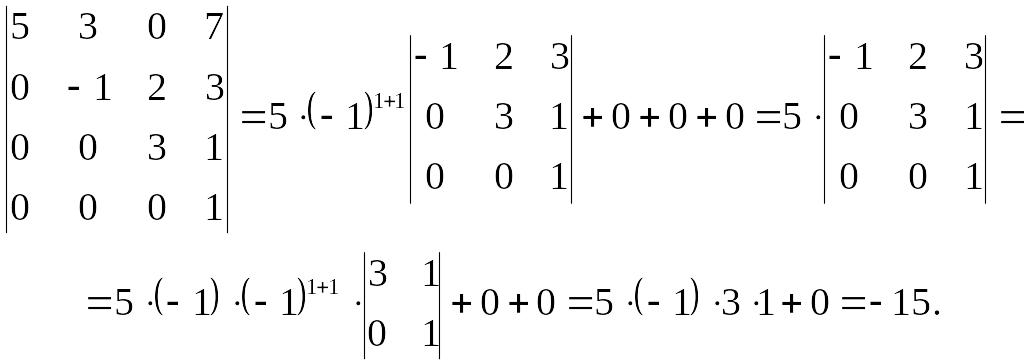 Правильный выбор этих параметров…

Инверсия Лапласа для решения абстрактного уравнения теплопроводности без прямого преобразования исходного члена

• Шулин Ву

• Математика

  J. Num. Мат.

• 2017

По сравнению с существующими контурными квадратурами анализ ошибок показывает, что новая квадратура обладает конкурентоспособным асимптотическим порядком точности, а численные результаты показывают, что при несоблюдении регулярности начального члена и/или дифференцируемости f(t) новая квадратура точнее.

Три эффективных алгоритма обратного преобразования Лапласа для вычисления электромагнитных откликов во временной области 3

В этой работе применена арифметика переменной точности в вычислительной среды MATLAB к реализации алгоритма Гавера-Штефеста и обратила внимание на два других алгоритма вычисления обратных преобразований Лапласа, а именно на алгоритмы Эйлера и Тальбота.

Разработка и анализ высокоточных численных методов для вычислительной оптики

• М. Брио, П. Кано

• Физика

• 2005

Данная работа связана с разработкой и применением высокоточных численные методы вычислительной оптики. Три основные темы составляют ядро ​​текста. Во-первых, это применение конечных…

Метод аналитического элемента с преобразованием Лапласа для моделирования нестационарного потока подземных вод

• Кристофер Л. Кульман

• Математика

• 2008

Метод аналитического элемента с преобразованием Лапласа (LT-AEM) применяет традиционный стационарный метод аналитического элемента (AEM) к преобразованному Лапласом уравнению диффузии (Fur человек and Neuman, 2003).…

Роль преобразования Лапласа в цифровой обработке сигналов

• Д. Рамеш, Рашми. Б. Бхави, Ашвини. Н. Кемпаннавар

• Информатика

• 2018

Основная цель этой статьи — продемонстрировать, как методы преобразования Лапласа могут быть полезны в обработке сигналов, свертке, анализе Фурье, и показать, что линейную систему можно полностью понять по ее импульсной или частотной характеристике с возрастающей сложностью инженерные проблемы.

Доказательная теория Демпстера-Шейфера для автоматизированного выбора параметров для контуров метода Талбота и применения к матричному возведению в степень

• П. Кано, М. Брио, П. Достерт, Джон Кейн

• Информатика

  Вычисл. Мат. заявл.

• 2012

ОЦЕНКА МАКСИМАЛЬНОЙ ВЕРОЯТНОСТИ И ВЫЧИСЛЕНИЕ ДЛЯ ПРОЦЕССА ОРНШТЕЙНА-УЛЕНБЕКА

• П. Маллоуни, С. Айенгар
• 90 002 Математика, информатика

• 2006

Алгоритм вычисления оценок максимального правдоподобия ( MLE) и соответствующие им доверительные области для трех идентифицируемых параметров процесса Орнштейна-Уленбека путем численного обращения преобразования Лапласа.

Проектирование системы управления с использованием теории конечных преобразований Лапласа

• Субхенду К. Дас

• Инженерное дело

• 2011

Теория преобразования Лапласа нарушает очень фундаментальное требование всей инженерии системы. Мы показываем, что эта теория предполагает, что все сигналы должны существовать в течение бесконечного интервала времени. Поскольку в…

Подробнее о методе недель для численного обращения преобразования Лапласа

• Г. Джунта, Г. Лаччетти, М. Риццарди

• Математика

• 1988

Резюме Большинство численных методов обращения преобразования Лапласа требуют значений нескольких дополнительных параметров. Как правило, эти параметры связаны со свойствами…

Алгоритмы выбора параметров в методе недель для обращения преобразования Лапласа

• J. Weideman

• Информатика, математика

  SIAM J. Sci. вычисл.

• 1999

В сложных численных тестах оба алгоритма успешно предсказали значения параметров, близкие к оптимальным, и оба реализованы с помощью БПФ.

Улучшенный метод численного обращения преобразований Лапласа

• Ф. Хуг, Дж. Найт, А. Н. Стоукс

• Математика

• 1982

90 002 Предложена усовершенствованная процедура численного обращения преобразований Лапласа, основанная на ускорении сходимость ряда Фурье, полученного из интеграла обращения с помощью трапециевидной…

О численном обращении преобразований Лапласа: сравнение трех новых методов характеристических задач из приложений

• Д. Даффи

• Математика

  TOMS

• 1993
9 0563

Три часто используемых метода численного обращения преобразования Лапласа: протестирован на сложных преобразованиях, взятых из литературы, и у Talbot есть точный метод выбора необходимых параметров.

Инверсия преобразования Лапласа повышенной точности

• J. Abate, P. Valko

• Математика

• 2004

Для численного обращения преобразований Лапласа мы предлагаем использовать многоточечные вычисления с уровнем точности, определяемым алгоритмом. Приведем две такие процедуры. The…

Численное обращение преобразований Лапласа с использованием функций Лагерра

• В. Уикс

• Математика

  JACM

• 1966
9 0563

Описан метод численного обращения преобразований Лапласа, в котором обратное получается как разложение по ортонормированным функциям Лагерра. Чтобы это было…

Точная числовая инверсия преобразований Лапласа

• А. Талбот

• Математика

• 1979

Инверсия почти произвольное преобразование Лапласа осуществляется трапециевидным интегрированием по специальному контуру.

No related posts.