Теория вероятностей задачи: Сборник задач по теории вероятностей (с решениями) | Материал для подготовки к ЕГЭ (ГИА) по алгебре (9, 11 класс):

Задачи теории вероятностей. Основные понятия

Теорией вероятностей называется математическая наука, изучающая закономерности случайных событий, которые наблюдаются при многократном повторении опыта. На ее основе построены математическая и прикладная статистика. Ниже введен ряд основных понятий, которые Вам нужно понять при изучении курса теории вероятностей.

Под испытанием (экспериментом) понимают некоторую совокупность условий, при которых наблюдается то или иное явление, фиксируется тот или иной результат. Опыт может проводиться многократно в подобных (неизменных основных) условиях, однако ряд второстепенных условий и факторов, которые невозможно проконтролировать изменяется от испытания к испытанию и приводят к разным результатам последствий эксперимента.

Случайным событием (событием) называется любой факт, который в результате эксперимента может состояться или не состояться. Случайные события обозначают большими латинскими буквами .

Вероятностью события называется численная мера свободы уверенности в появлении данного события вследствие нового испытания.

Вероятность события обозначается как .

Вероятной (достоверностью) называется событие , которое в результате испытания непременно должно произойти. Для достоверного события вероятность равна единице .

Невозможным называется такое событие , которое в результате опыта не может произойти.
Для невозможного события вероятность равна нулю .

Вероятность любого случайного события принимает значения между нулем и единицей:

.

Полной группой событий называется ряд таких событий , что в результате испытания непременно должно произойти хотя бы одно из них. Несколько событий в опыте называются несовместимыми, если никакие два из них не могут появиться одновременно.

Несколько событий в испытании называются равновозможными, если они имеют равные шансы появления в результате испытания. Примерами равновозможных событий можно отметить появление: герба или цифры при одном подбрасывании монеты; четного и нечетного числа очков при одном подбрасывании игрального кубика и т. д.

Если последствия испытания образуют полную группу несовместных равновозможных событий, то они называются случаями.

Множество всех результатов эксперимента, которое рассматривается называется пространством элементарных событий.

Следствие (случай) называется благоприятным событию , если оно приводит к обязательному появлению события .

Классическое определения вероятности

Если результаты испытания сводятся к схеме случаев, то вероятность события вычисляется по формуле

Где – общее число случаев; – число случаев, благоприятствующих событию .

Приведенное соотношение является классической формулой вычисления вероятности событий.

———————————————-

Приведем несколько типичных примеров.

Пример 1. В цеху по изготовлению мячей для гольфа в одной коробке было 67 мячей правильной формы и 23 мяча неправильной формы в другой. Мячи ссыпали в одну коробку. Какова вероятность того, что наугад извлечен мяч будет неправильной формы ?

Решение

Общее число равновозможных событий равна количеству всех мячей

Число способствующих событий, которые заключается в извлечении бракованного мяча — равны их количеству

По формуле вычисляем

———————————————-

Пример 2. На столе выложены кубики с номерами от единицы до девяти. Ученик наугад вытаскивает один кубик. Какова вероятность того, что:

— число из кубика делится на 3?

— число делится на 2?

Решение

Общее число случайных событий равно количеству кубиков

Число способствующих событию можно изобразить в виде множества , для В множество благоприятных событий будет следующим На основе этого число принимает значение и для первого и второго события соответственно. Вероятность их появления определяем по известной формуле

Пример 3. В группе 17 ребят и 13 девушек. Преподавателю нужно вызвать кого-то для проверки выполнения домашних заданий. Какова вероятность того, что к доске выйдет девушка?

Решение

Общее число равносильных событий равно количеству учащихся

Число девушек равно

Тогда искомая вероятность

 

Аналитика vs моделирование. Задача по теории вероятностей / Хабр

На примере хорошей задачки по теории вероятностей мы сравним что круче — аналитические решения или моделирование. Вначале я хотел написать только аналитическую часть и попросить заинтересованных читателей запрограммировать симуляцию задачи. Но нехорошо перекладывать на других свои дела, поэтому, в меру способностей, постарался сделать и вторую часть. Попутно знакомясь с Питончиком. Если что-то в коде получилось коряво, милости просим наставить на путь истинный.

Задачка такая:

В ящике 4 белых 10 черных шаров. Из него наудачу вынимают шар, фиксируют его цвет и возвращают шар назад в ящик. Назовем «белым пулом» любую максимальную цепочку подряд вынутых белых шаров. Найти математическое ожидание количества «белых пулов» при извлечении из ящика 20 шаров.

Аналитический подход

Чтобы решить такую задачку, нужно прочувствовать ее изнутри — представить себя белым шаром, черным шаром, всеми шарами сразу вместе… Картинка поможет настроиться на нужный лад и не подглядывать в решение, если захотелось порешать сначала самому.

Внимание, мой вариант решения. Возможны арифметические ошибки, но ответ похож на правду и будет проверен моделированием.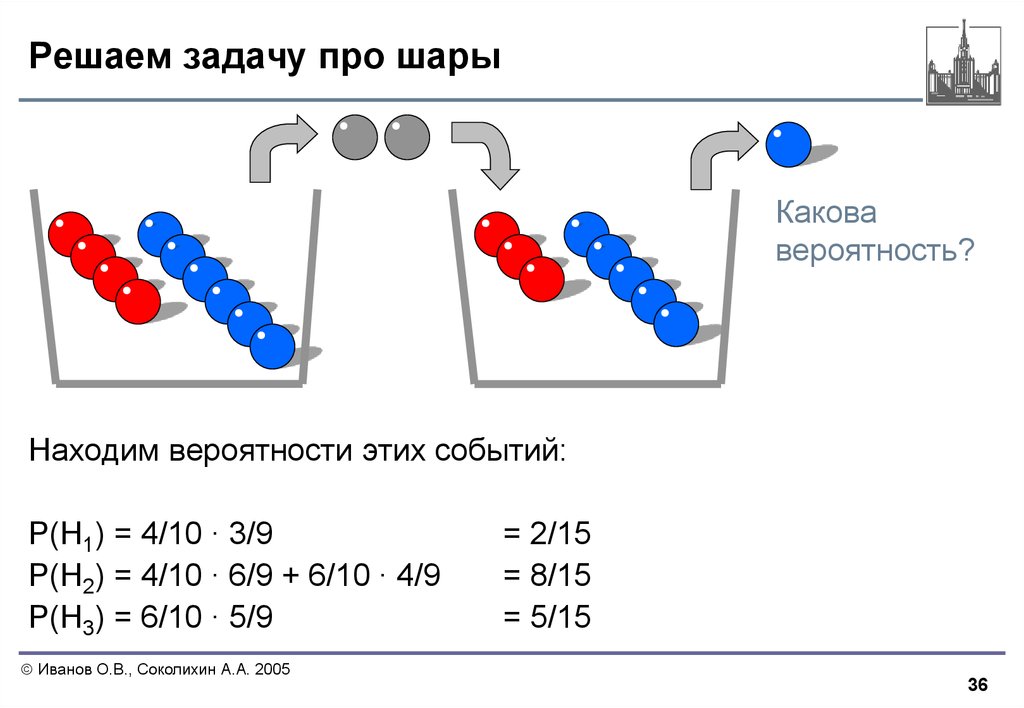

Мне кажется, задачка нетривиальная. По крайне мере, все виденные мной на просторах интернета попытки решения были весьма плачевны. Люди получали в ответе математическое ожидание числа белых пулов, большее чем их максимально возможное число…

Первый шаг, который я сделал — интуитивно почувствовал, что нужно использовать индуктивный подход, начав с небольшого числа извлеченных шаров. Хорошо бы еще формализовать задачу. Сделать это проще всего перейдя к рассмотрению двоичных последовательностей см.также предыдущий пост про слоистые среды. Ноль у меня будет обозначать черный шар, единичка — белый. Тогда, например, в последовательности 1-0-1-0-111-0-11-0-1-000 будет 5 белых пулов с длиной от 1 до 3. Изолированная с двух сторон нулями единичка — уже белый пул! Поэтому при вытаскивании 20 шаров максимальное число пулов будет равно 10 чередование нулей и единиц. Соответственно ответ, который хитрый студент найдет в гугле = 100/7, будет весьма далек от правды.

Идем дальше. При извлечении 2х шаров нам нужно рассмотреть 4 варианта: 0=00, 1=01, 2=10, 3=11. Соответственно, при извлечении 3х шаров нужно рассматривать двоичные последовательности задающие числа от 0 до 7, и т.д.

В случае последовательности из 2х шаров матожидание числа белых пулов найти просто. У нас есть ноль пулов, и три раза по одному пулу. А дальше мы делаем твист, который может сбить с толку. Обозначим это матожидание как <N(2)>, но вычислять его не будем — вдруг и не понадобится потом!

Если взять большее число испытаний, то возникает сложность с одновременным подсчетом числа пулов и соответствующих вероятностей. Понятно, что для каждой двоичной последовательности вероятности появления нулей и единиц нужно перемножить. Но их нужно как-то подсчитать. К счастью, в задаче есть повторяющаяся структура. При увеличении числа испытаний сначала все двоичные последовательности повторяются, потом слева появляется дополнительная единичка и снова все повторяется.

Черновик решения задачи. Обнаружена повторяющаяся структура!

Логично попробовать вывести рекуррентную формулу для матожидания <N((n))>. Сделать это можно так — при n испытаниях вы должны выписать двоичные представления чисел от 0 до

Обозначим

Следующий шаг уже вполне предсказуем. Наша стратегия заключается в том, чтобы не выводить формулы для числа пулов и числа единичек! Используем аналог ленивых вычислений — ленивую аналитику. Запишем матожидание числа пулов

Тоже самое сделаем для матожидания при увеличенном на 1 числе испытаний

Теперь нужно в формуле для <N((n+1))> попытаться выделить <N((n))>. Для этого нужно понять как работает число пулов, при добавлении еще одного двоичного разряда. Если число i по прежнему может быть представлено n разрядами, то добавление нового двоичного разряда просто соответствует приписыванию 0 слева. Число белых пулов и число единичек не меняется

Дальше в двоичном разложении слева появляется изолированная единичка, что увеличивает число белых пулов и число единиц на, простите, единицу

И в оставшемся диапазоне, левая единичка сливается с предыдущей единичкой, в итоге

Теперь все это добро надо подставить в формулу для математического ожидания длины белых пулов при n+1 испытаниях. После некоторых алгебраических преобразований, у меня получилось, что

Это уже замечательно! Число белых пулов вычислять не надо. Но есть сумма, в которую входит выражение для числа единиц. Для оставшейся суммы я не придумал ничего лучше, чем снова найти рекуррентное соотношение

Теперь если мы увеличим число испытаний на единичку, число слагаемых вырастет в два раза. Первая половина суммы не поменяется, а у вторая половина будет точно такая же как первая, только с дополнительным множителем за счет добавления одной единички

Получилась геометрическая прогрессия!

Теперь можно выписать искомое рекуррентное соотношение без наших вспомогательных функций p и u:

Это арифметическая прогрессия! Значит см. UPD1.

И, окончательно, <N(20)>=200/49~4, то есть в среднем мы ожидаем 4 белых пула. Ответ похож на правду, если учесть что число возможных пулов от 0 до 10.

Моделирование

Давайте теперь решим задачу с помощью моделирования! Надо запустить генератор двоичных последовательностей длиной в 20 символов с вероятностью появления нулей и единичек из задачи. Я просто сделал ящик=последовательность с 10 нулями и 4 единичками и случайным образом вытаскиваю 20 раз по одному элементу. Появление и исчезновение белого пула я подсчитываю по изменению следующего элемента. При этом каждый пул кроме, возможно, последнего, будет учтен два раза.

import random
box = [1,1,1,1,0,0,0,0,0,0,0,0,0,0]
def poolnumber():
    unitcount=0
    poolcount=0
    pooldelim=0
    for i in range(20):
        ball=random.choice(box)
        #print(ball) 
        unitcount=unitcount+ball
        if ball!= pooldelim:
            poolcount+=1
        pooldelim=ball
        res=round((poolcount+0.1)/2)
    #print(unitcount)
    #print(round((poolcount+0.1)/2))
    return res

Ну а теперь много раз вызовем функцию подсчета пулов и найдем среднее

totalpoolnumber=0
size=5000
for i in range(size):
    totalpoolnumber=totalpoolnumber+poolnumber()
    
print(totalpoolnumber/size)
print(204/49)

Удивительно, но вероятные арифметические ошибки в аналитической части не случились! И 500 и 20000 испытаний дают 4. 0xxx — близкий ответ к аналитическому решению! Однако, насколько проще и быстрее реализовать модель! К тому же, можно уже полученную модель применить для решения более сложных задач — искать, например, среднюю длину белого пула, или среднюю длину пула максимальной длины. Так что, хоть я и занимаюсь «точно решаемыми» задачами, но должен признаться — использование программирования и моделирования является мощным и универсальным инструментом.

PS: Моделирование сначала давало заниженный ответ, близкий к 3.8. И только знание точного ответа, хотя я в нем и засомневался, позволило мне найти ошибку — шарик я вытаскивал не 20 раз, а всего 19. Когда это поправил, сразу добился замечательного согласия теории и эксперимента! И в защиту аналитического метода решения, скажу, что ответ у нас получился для любого числа испытаний — мы нашли, что среднее число белых пулов растет с числом вытащенных шаров линейно. В принципе, этого и следует ожидать от аналитического подхода — попадание в общие свойства решения.

UPD 1. В развертывании арифметической прогрессии я потерял начальное слагаемое. Правильная формула

приводит к ответу 204/49~4.16.

Да, такая простая формула наталкивает на мысли, что все можно сделать проще, и действительно в комментариях есть простой вывод рекуррентного соотношения. Нужно сразу думать о том, что может происходить с математическим ожиданием числа пулов, если будет вытягиваться на один шарик больше. А также есть альтернативное решение строго в парадигме теории вероятностей.

В моделировании я поправил пределы в цикле для подсчета пулов, но опять ошибся на единичку в подсчете среднего. Эта ошибка не должна была влиять для большого размера выборки, но ответ получался систематически ниже. Конечно, это из-за корявого использования округления, которое я исправил «регуляризацией» вместо корректного решения. Зато теперь точно все сходится. Спасибо за примеры корректных реализаций модели на самых разных языках программирования!

Искусство решения задач

Вероятность традиционно считается одной из самых сложных областей математики, поскольку вероятностные аргументы часто приводят к явно парадоксальным или нелогичным результатам. Примеры включают парадокс Монти Холла и проблему дня рождения. Вероятность можно приблизительно определить как вероятность того, что событие произойдет.

Содержание

• 1 Видео для начинающих!
• 2 Начальная вероятность
• 3 Формальное определение вероятности
  • 3.1 Типы вероятности
  • 3.2 Примеры проблем
    • 3.2.1 Введение
    • 3.2.2 Промежуточный уровень
• 4 Ресурсы

Видео для начинающих!

Введение в теорию вероятности

Прежде чем читать по следующим темам, учащийся, изучающий теорию вероятности, должен ознакомиться с вводными методами счета.

• зависимая вероятность
• независимая вероятность

Формальное определение вероятности

Основы вероятности лежат в области анализа, известной как теория меры. Теория меры в целом имеет дело с интеграцией, в частности, с тем, как определить и расширить понятие «площадь» или «объем». Таким образом, интуитивно можно сказать, что вероятность учитывает, какой «объем» событие занимает в пространстве результатов. Теория меры предполагает значительную математическую зрелость, поэтому ее обычно игнорируют до тех пор, пока человек не достигнет продвинутого уровня бакалавриата. После изучения теории меры вероятность становится намного проще в использовании и понимании.

На языке теории меры вероятность формально определяется как тройка, известная как вероятностное пространство, обозначаемое . Вот набор, называемый выборочным пространством, и класс событий, заданный определенными подмножествами . должны удовлетворять определенным свойствам (это должна быть -алгебра), чтобы квалифицироваться как класс событий. Вместе они образуют то, что известно как измеримое пространство. — это задание с определенными свойствами (это особый вид меры), называемое вероятностной функцией или вероятностной мерой. Каждому возможному событию присваивается «объем».

В качестве простого примера рассмотрим подбрасывание монеты.

В этом случае , , и присваивает событиям в : ,

,

,

.

Мы можем интерпретировать это как утверждение, что событие выпадения орла и событие выпадения решки занимают равную половину множества возможных результатов; событие выпадения орла или решки несомненно, и точно так же событие выпадения ни орла, ни решки имеет вероятность 0.

Конечно, чтобы понять этот пример, не нужна теория меры, но он показывает, как перевести очень простую ситуацию на язык теории меры. Более того, если бы кто-то захотел определить, является ли монета честной или взвешенной, было бы трудно сделать это без использования методов вывода, полученных из теории меры.

Типы вероятности

Часть всестороннего понимания базовой вероятности включает понимание различий между различными видами вероятностных задач.

• алгебраическая вероятность
• комбинаторных вероятностных задач включают подсчет результатов.
• геометрическая вероятность

Важные подразделения вероятности включают

• случайные процессы
• математическая статистика

Примеры задач

Введение

• 2006 AMC 10B Задача 17
• 2006 AMC 10B Задача 21

Промежуточный

• 2006 AIME II Проблема 5
• 2007 AIME II Задача 10

Ресурсы

• Введение в счет и теорию вероятности Дэвид Патрик

• Промежуточный счет и вероятность Дэвид Патрик

Сборник задач по теории вероятностей0001

Полезно для учителей, у которых нет времени решать задачи для своих классам или исследователям, которые могут захотеть проверить, не получен ли уже какой-либо результат. известен.

— Mathematical Reviews

Базовый код продукта Список ключевых слов: ммоно; ММОНО; ммоно/163; ММОНО/163; ммоно-163; MMONO-163

Распечатать код продукта: MMONO/163.S

Онлайн-код продукта: MMONO/163.E

Заголовок (HTML): Теория вероятностей: Сборник задач

Автор(ы) (показать товар): А. Я. Дороговцев; Д. С. Сильвестров; А. В. Скороход; М. И. Ядренко

Организация(и) (HTML): , Киев, Украина; Киевский государственный университет; Украинская академия наук; Киевский государственный университет

Абстрактный:

Сборник задач предназначен для студентов, изучающих чистую и прикладную математику. Существуют проблемы в традиционных областях теории вероятностей и проблемы в теории случайных процессов, имеющей широкое применение в теории автоматического управления, теории массового обслуживания и надежности, а также во многих других областях современной науки и техники. Даются ответы на большинство задач, а в книге даны советы и решения для более сложных задач.

Название серии книг: Переводы математических монографий

Месяц и год публикации: 21.06.2011

Год авторского права: 1997

Количество страниц: 347

Тип крышки: Мягкая обложка

Печать ISBN-13: 978-0-8218-6866-9

Интернет ISBN 13: 978-1-4704-4578-2

Распечатать ISSN: 0065-9282

Интернет-ISSN: 0065-9282

Основной MSC: 60

Учебник?: false

Прикладная математика?: false

Книга MAA?: ложь

Обучение на основе запросов?: false

Электронные носители?: false

Одежда или подарок: ложь

SXG Тема: PR

Онлайн-цена 1 Этикетка: Список

Цена онлайн 1: 105.00

Цена печати 1 Этикетка: Список

Цена печати 1: 105.00

Цена онлайн 2 Этикетка: Участник AMS

Цена онлайн 2: 84.00

Цена печати 2 Этикетка: Участник AMS

Цена печати 2: 84.00

Цена онлайн 3 Этикетка: Член МАА

Цена онлайн 3: 94.50

Цена печати 3 Этикетка: Член MAA

Цена печати 3: 94.

50

Цена комплекта 1 Этикетка: Список

Цена комплекта 1: 157.50

Цена комплекта 2 Этикетка: Участник AMS

Цена комплекта 2: 126.00

Цена комплекта 3: 141.75

Цена комплекта 3 Этикетка: Член MAA

Распечатать Добавить в корзину URL: /some/url/at/AMS/MMONO-163.S

Электронный адрес Добавить в корзину: /some/url/at/AMS/MMONO-163.E

Распечатать Доступно для заказа: правда

Копия обзора: https://www.ams.org/exam-desk-review-request?&eisbn=978-1-4704-4578-2&pisbn=978-0-8218-6866-9&epc=MMONO/163.E&ppc=MMONO/163. S&title=Вероятность%20Теория%3А%20Сборник%20%20Проблемы&автор=А.%20Я.%20Дороговцев%3Б%20Д.%20С.%20Сильвестров%3Б%20А.%20В.%20Скороход%3Б%20М.%20И.% 20Ядренко&type=R

Читательская аудитория:

Аспиранты и математики-исследователи, интересующиеся теория вероятности.

Отзывы:

Полезно для учителей, которые не могут найти время, чтобы решить задачи для своих классам или исследователям, которые могут захотеть проверить, не получен ли уже какой-либо результат.