Тест 4 прямоугольник ромб квадрат ответы: Прямоугольник. Ромб. Квадрат. Вариант 1

Прямоугольник, ромб, квадрат тест по геометрии (8 класс)

Последний раз тест пройден 7 часов назад.

Для учителя

Материал подготовлен совместно с учителем высшей категории Харитоненко Натальей Владимировной.

Опыт работы учителем математики — более 33 лет.

1. Вопрос 1 из 10

   Чему равна сумма углов прямоугольника?

   • 90

   • 180

   • 360

   Подсказка

   Правильный ответ

   Неправильный ответ

   В вопросе ошибка?

2. Вопрос 2 из 10

   Выберите верное утверждение:

   • параллелограмм обладает всеми свойствами прямоугольника

   • прямоугольник обладает всеми свойствами параллелограмма

   • общих свойств у параллелограмма и прямоугольника нет

   Подсказка
   Правильный ответ

   Неправильный ответ

   В вопросе ошибка?

3. Вопрос 3 из 10

   Диагонали пересекаются под прямым углом.

   Это верно:

   • только для прямоугольника

   • только для ромба

   • для ромба и квадрата

   Подсказка

   Правильный ответ

   Неправильный ответ

   В вопросе ошибка?

4. Вопрос 4 из 10

   Выберите верное утверждение:

   • ромб обладает всеми свойствами параллелограмма

   • ромб обладает всеми свойствами прямоугольника

   • ромб обладает всеми свойствами квадрата

   Подсказка

   Правильный ответ

   Неправильный ответ

   В вопросе ошибка?

5. Вопрос 5 из 10

   Могут ли углы квадрата быть равными 100⁰?

   • Да, все 4 угла

   • Нет

   • Только один угол
   Подсказка

   Правильный ответ

   Неправильный ответ

   В вопросе ошибка?

6. Вопрос 6 из 10

   Ось симмтерии – это:

   • точка

   • отрезок

   • прямая

   Подсказка

   Правильный ответ

   Неправильный ответ

   В вопросе ошибка?

7. Вопрос 7 из 10

   Сколько осей симметрии имеет неразвернутый угол?

   • 2

   • 1

   • Нет осей симметрии

   Подсказка

   Правильный ответ

   Неправильный ответ

   В вопросе ошибка?

8. Вопрос 8 из 10

   Точка О является центром симметрии отрезка АВ, если:

   Подсказка

   Правильный ответ

   Неправильный ответ

   В вопросе ошибка?

9. Вопрос 9 из 10

   Какие из четырехугольников всегда имеют 4 равных угла?

   • Параллелограмм и ромб

   • Ромб и трапеция

   • Квадрат и прямоугольник

   Подсказка

   Правильный ответ

   Неправильный ответ

   В вопросе ошибка?

10. Вопрос 10 из 10

    Является ли прямоугольником параллелограмм, у которго есть прямой угол?

    • Да

    • Нет

    • Не всегда

    Подсказка

    Правильный ответ

    Неправильный ответ

    В вопросе ошибка?

Доска почёта

Чтобы попасть сюда — пройдите тест.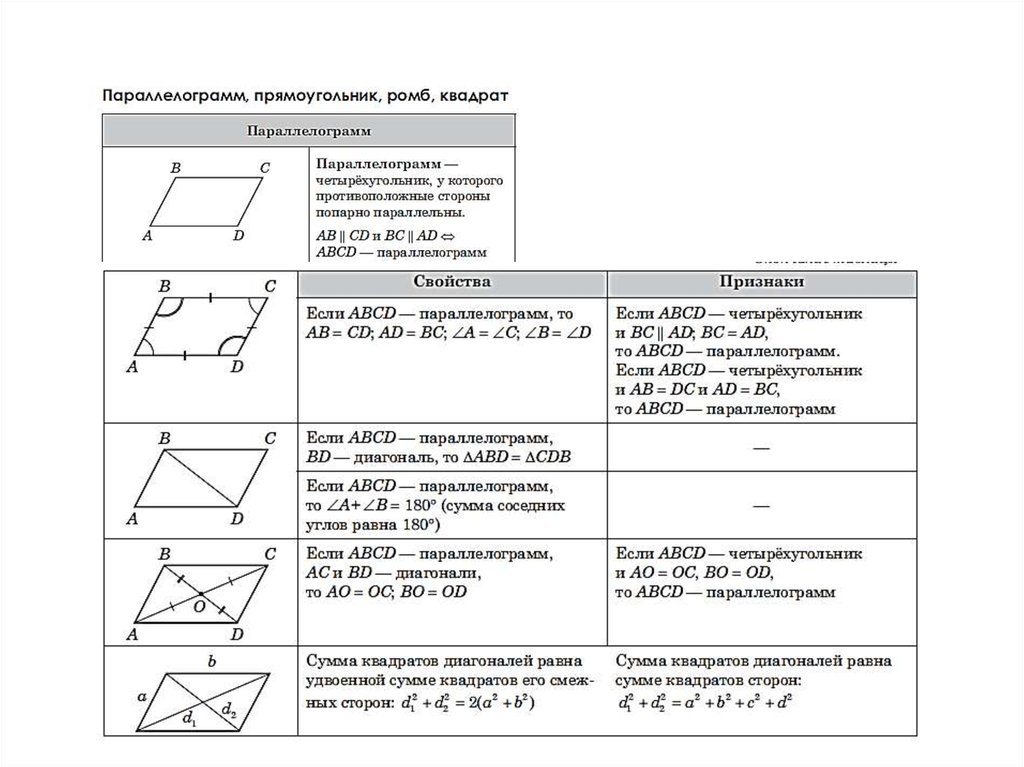

Тест «Прямоугольник, ромб, квадрат» (8 класс), соответствующий министерским требованиям, поможет школьникам получить «отлично» за текущий урок или проверочную работу. Представленные вопросы охватывают всю теоретическую базу раздела. Более сложные задания являют собой задачи, требующие применения формул, теорем.

Прохождение теста подразумевает только выбор одного варианта из нескольких, поэтому справиться с ним можно очень быстро. Тематического вопросы разного уровня сложности позволяют самостоятельно, а главное объективно оценить свое владение материалом. Для удобства к подборке подаются правильные ответы, что позволяет сразу восполнять “пробелы”. При необходимости желательно дополнять ответы информацией из учебников. К заданиям легко получить онлайн доступ с любого гаджета. Представленные тесты могут использовать и старшие ученики (8-9 классы), если нужно повторить материал.

Тест по геометрии «Прямоугольник. Ромб. Квадрат» – отличный инструмент для самостоятельного оценивания. Вопросы подобраны так, чтобы их можно было использовать не только для подготовки к тематическим контрольным, но и к итоговым промежуточным проверкам.

Рейтинг теста

3.9

Средняя оценка: 3.9

Всего получено оценок: 1825.

---

А какую оценку получите вы? Чтобы узнать — пройдите тест.

Вариативные тестовые вопросы по геометрии (Варианты 1-4 по 12 вопросов с отметками правильных ответов)

Математика \ Геометрия

Страницы работы

11 страниц (Word-файл)

Посмотреть все страницы

Скачать файл

Фрагмент текста работы

Тест 5. Тема: Параллелограмм, прямоугольник, ромб, квадрат

Цель данного теста — проверить, умеет ли учащийся:

¾  при анализе геометрических конфигураций пользоваться определением и свойствами параллелограмма, ромба, прямоугольника, квадрата для нахождения их элементов.

Вариант 1

Записывая ответы на задания теста, обведите буквы, отвечающие утверждениям, которые вы считаете правильными, и зачеркните буквы, отвечающие утверждениям, которые вы считаете неправильными. Например, если вы считаете правильными утверждения А и В, а неправильными — утверждения Б и Г, запишите . Если хотя бы одна буква из 4-х будет не отмечена, задание считается

невыполненным.

1. Дан параллелограмм ABCD, в котором AB = 5 см, AD = 7 см, A = 30°. Выберите правильное утверждение. –А. DC = 7 см. +Б. BC = 7 см. –В. ÐC = 150°.  –Г. D > B.

2. Дан прямоугольник ABCD, у которого диагональ АС = 10 см, точка O  — точка пересечения диагоналей. Выберите правильное утверждение. –А. OB = 6 см. –Б. AO > BO. –В. BAD > ABC.  +Г. BD = 10 см.

3. Дан ромб ABCD, у которого АВ = 7 см. Выберите правильное утверждение. –А. Треугольник ABC неравнобедренный.  +Б. Периметр ромба равняется 28 см. –В. AD может равняться 6 см. –Г. ВС > CD.

4. Дан параллелограмм ABCD, у которого a = 35°, g = 45° (см. рисунок). Отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные. –А. ÐB > ÐD. –Б. AB + BC > AD + DC.  +В. d = .  +Г. ÐBAD = 80°.

5. Диагонали прямоугольника ABCD пересекаются в точке О. Известно, что AD = 9 м, AO = 6 м. Отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные. +А. AC = 2AO. –Б. BD < 11 м. –В. BC = 6 м. +Г. Периметр треугольника BOC больше 18 м.

6. Четырехугольник ABCD — ромб, в котором O — точка пересечения диагоналей, OD = 6 м, OC = = 8 м. Отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные. –А. AC < 15 м. +Б. ÐBAC = ÐCAD. –В. BC + AD может быть больше AB + CD. +Г. АО — высота треугольника ABD.

7. Дан параллелограмм ABCD. На сторонах ВС и AD взяты соответственно точки

Е и F так, что BE = DF, О — точка пересечения BD и EF. Отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные.

–А. BEFА — параллелограмм.

–Б. BO > OD.

+В. Прямая AC проходит через точку О.

–Г. BE + AF < AD.

8. Дан прямоугольный треугольник АВС. Через точку М, принадлежащую гипотенузе, проведены прямые, параллельные катетам и пересекающие катет AC в точке K и катет ВС в точке L. Отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные.

+А. CKML —прямоугольник.

–Б. KL > MC.

+В. Если KM = ML, то отрезок KL перпендикулярен

MC.

–Г. KM + LB < CB.

9. Дан квадрат ABCD. На диагонали AC взяты точки М и N так, что AM = CN, причем AM < 0,5 AC. Отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные.

–А. Треугольники АМВ и CND могут быть не равными.

–Б. Четырехугольник BMDN — обязательно является квадратом. 

–В. ÐBNC < ÐDNC.

–Г. ÐDBN + ÐBDM = 90°.

10. На сторонах параллелограмма ABCD взяты точки K, L, M, N так, что AK : KB = CL : LB = CM : MD = AN : ND, О — точка пересечения AC и KM. Отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные.

+А. Середины отрезков LN и KM обязательно совпадают.

+Б. Прямые KM, LN и BD обязательно пересекаются в точке O.

–В. KO обязательно равно LO.

+Г. Если KМ — биссектриса угла LKN, то LN — биссектриса угла KLM.

11. Дан прямоугольник ABCD, не являющийся квадратом. Биссектриса угла А пересекает биссектрисы углов B и D соответственно в точках K и L, биссектриса угла С пересекает биссектрисы углов B и D соответственно в точках N и M. Отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные.

–А. Угол между биссектрисами углов А и В может быть острым.

+Б. KLMN — прямоугольник. 

+В. Отрезок KM обязательно перпендикулярен LN.

+Г. KМ обязательно равно LN.

12. Дан параллелограмм ABCD, у которого угол A острый. Из вершины угла B на стороны AD и CD опущены перпендикуляры, основаниями которых являются соответственно точки K и L. Отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные.

+А. BK может равняться BL.

+Б. Если треугольники BKA и BLC равны, то ABCD — ромб.

–В. ÐKBL = 2A.

–Г. ÐBKL всегда равно .

Вариант 2

Записывая ответы на задания теста, обведите буквы, отвечающие утверждениям, которые вы считаете правильными, и зачеркните буквы, отвечающие утверждениям, которые вы считаете неправильными. Например, если вы считаете правильными утверждения А и В, а неправильными — утверждения Б и Г, запишите . Если хотя бы одна буква из 4-х будет не отмечена, задание считается невыполненным.

1. Дан параллелограмм ABCD, в котором О — точка пересечения диагоналей, АО = 6 мм. Выберите правильное утверждение. –А. BО > OD. –Б. BO < OD. –В. АВ ¹ DC. +Г. AC = 12 мм.

2. Дан прямоугольник ABCD, в котором О — точка пересечения диагоналей, a = 25°. Выберите правильное утверждение. –А. AC ¹ BD. +Б. b = 65°. –В. a + g = 60°. –Г. OB < OA.

3.  Дан ромб KLMN, в котором a = 35°. Выберите правильное утверждение. +А. b = 35°. –Б. KN¹ NM. –В. KL < NM. –Г.  ¹ .

4. Сумма длин всех сторон параллелограмма ABCD равна 24 м, а сумма длин

Похожие материалы

Информация о работе

Скачать файл

Как проверить, образуют ли заданные четыре точки кортежа квадрат, прямоугольник, параллелограмм или ромб в питоне?

Попытка редактирования 2: Вместо этого вычислите векторы между точками и найдите количество уникальных векторов и углов между векторами, которые встречаются в одной и той же точке, чтобы определить, какая форма из четырех требуется, если таковая имеется (обратите внимание, что этот метод требует, чтобы точки были упорядочены в порядке их соединения). ):

 импортировать numpy как np
по определению четырехугольник2 (*аргументы):
    если len(аргументы) != 4:
        return 'Не четырехугольник'
    аргументы = np.массив (аргументы)
    векторы = np.array([args[i-1]-j для i, j в enumerate(args)])
    unique_vectors = np.unique(np.round(np.abs(vectors), 6), axis=0) #Округлить, чтобы избежать числовых ошибок: можно изменить количество цифр на округление до
    если len(unique_vectors) != 2:
        return 'Не квадрат, прямоугольник, ромб или параллелограмм'
    norms = [np.linalg.norm(i) для i в векторах]
    norm_vectors = [i/j для i, j в zip (векторы, нормы)]
    unique_norms = set(round(i, 6) for i в нормах) # Опять округляем числовые ошибки
    углы = [np.arccos (np.dot (norm_vectors [i-1], j)) для i, j в перечислении (norm_vectors)]
    если все (i == np.pi/2 для i в углах):
        если len(unique_norms) == 1:
            вернуть «Квадрат»
        если len(unique_norms) == 2:
            вернуть «Прямоугольник»
    
    elif len(set(round(i, 6) for i в углах)) == 2: #Опять же, округлить числовые ошибки
        если len(unique_norms) == 1:
            вернуть «Ромб»
        если len(unique_norms) == 2:
            вернуть 'Параллелограмм'
    еще:
        return 'Не квадрат, прямоугольник, ромб или параллелограмм'
 

Тест с предыдущими тестами и приведенными в качестве комментариев:

 квадрат = [(2, 2), (2, 4), (4,4), (4, 2)]
прямоугольник = [(2, 2), (2,8), (4, 8), (4, 2)]
ромб = [(0, 0), (np. sqrt(8), 0), (2+np.sqrt(8), 2), (2, 2)]
параллелограмм = [(2,2), (5, 2), (6,4), (3,4)]
печать (четырехугольник2 (* квадрат))
печать (четырехугольник2 (* прямоугольник))
печать (четырехугольник2 (* ромб))
печать (четырехугольник2 (* параллелограмм))
print(четырехугольник2(*[[2, -3], [6, 5], [-2, 1], [-6, -7]]))
печать (четырехугольник2 (* [(0, 0), (0, -5), (3,2,5), (3, -2,5)]))
печать (четырехугольник2 (* [(0, 2), (0, -2), (-1,0), (1, 0)]))
 

Вывод:

 Квадрат
Прямоугольник
Ромб
Параллелограмм
Ромб
Не квадрат, прямоугольник, ромб или параллелограмм
Не квадрат, прямоугольник, ромб или параллелограмм
 

Отказ от ответственности: не работает для любого ввода, но я думаю, что он работает, если ввод гарантированно является квадратом, прямоугольником, параллелограммом или ромбом. Хорошо, я думаю, что это работает, но я не проверял это много. По сути, вам нужно вычислить уникальные расстояния и уникальные углы между всеми заданными точками, а затем использовать свои знания о желаемых формах, чтобы решить по этим расстояниям и углам, какая форма, если таковая имеется:0003

 импорт itertools
импортировать numpy как np
четырехугольник по определению (*аргументы):
    тол = 1e-4
    если не len(аргументы) == 4:
        return 'Не четырехугольник'
    #Рассчитать все перестановки координат
    перестановки = np. array (список (itertools.permutations (args, r = 2)))
    #Рассчитать все расстояния
    расстояния = np.array(list(np.sqrt(sum((i[0]-i[1])**2)) для i в перестановках))
    #Выберите уникальные расстояния в пределах допуска
    расстояния = расстояния [~ (np.triu (np.abs (расстояния [:, нет]] - расстояния) <= tol, 1)). любой (0)]
    #Рассчитать все абсолютные углы
    angulars = np.array(list(abs(np.arctan2(*(i[0]-i[1])[::-1])) для i в перестановках))
    #Выберите уникальные углы в пределах допуска
    angulars = sorted(angles[~(np.triu(np.abs(angles[:,None] - angles) <= tol,1)).any(0)])
    если len (расстояния) == 2 и все (np.pi * i/4 == j для i, j в перечислении (углы)):
            вернуть "Это квадрат"
    elif len(расстояния) == 3:
        если len(углы) == 5:
            вернуть "Это прямоугольник"
        elif len(углы) == 8:
            вернуть "Это ромб"
        еще:
            return 'Не квадрат, прямоугольник, ромб или параллелограмм'
    elif len(расстояния) == 4 и len(углы) == 8:
        вернуть "Это параллелограмм"
    еще:
        return 'Не квадрат, прямоугольник, ромб или параллелограмм'
 

Простые тестовые примеры:

 квадрат = [(2, 2), (2, 4), (4,2), (4, 4)]
прямоугольник = [(2, 2), (4, 2), (2,8), (4, 8)]
ромб = [(0, 0), (2, 2), (np. sqrt(8), 0), (2+np.sqrt(8), 2)]
параллелограмм = [(2,2), (3,4), (5, 2), (6,4)]
печать (четырехугольник (* квадрат))
печать (четырехугольник (* прямоугольник))
печать (четырехугольник (* ромб))
печать (четырехугольник (* параллелограмм))
 

Вывод:

 Это квадрат
это прямоугольник
это ромб
это параллелограмм
 

Почему ромб не квадрат?

Возможно, вы изучали квадраты и ромбы на уроках геометрии. Эти две формы имеют странное сходство, поскольку принадлежат к одному и тому же семейству параллелограммов или четырехугольников. Основное различие между квадратом и ромбом заключается в том, что у квадрата все углы равны 90 градусам, а у ромба - нет. Однако все стороны обеих форм равны.

Что такое квадрат?

Квадрат считается правильным четырехугольником, у которого все четыре стороны имеют одинаковую длину и все равны четыре угла. Углы, опирающиеся на смежные стороны квадрата, прямые. Кроме того, диагонали квадрата равны и делят друг друга пополам в точке 9. 0 ^или . Квадрат — это частный случай параллелограмма с двумя смежными равными сторонами и одним прямым углом при вершине. Кроме того, квадрат можно рассматривать как частный случай прямоугольника с одинаковой длиной и шириной.

Свойства квадрата

Квадрат — это замкнутая фигура со следующими свойствами:

• Квадрат — это замкнутый четырехугольник с 4 сторонами и 4 вершинами.
• Все стороны квадрата равны друг другу.
• Длины обеих диагоналей равны.
• Противоположные стороны параллельны друг другу, поэтому он называется параллелограммом.
• Сумма внутренних углов ромба равна 360°.
• Диагонали квадрата делятся пополам под углом 90°.
• Диагонали делят квадрат на два равных треугольника.
• Противоположные стороны квадрата параллельны друг другу.
• Внутренний угол, образованный при каждой вершине квадрата, равен 90°.
• Длина диагонали со сторонами s равна √2 × s
• Длина диагоналей в квадрате больше его сторон.

Площадь квадрата: Область, заключенная в двумерную плоскость, называется площадью фигуры. В случае квадрата площадь эквивалентна квадрату сторон. Измеряется в квадратных единицах.

Площадь = (сторона) ²  

Примем «а» к длине стороны квадрата, тогда имеем;

Площадь = a ²  

Периметр квадрата: Сумма всех четырех сторон квадрата называется его периметром. Измеряется в тех же единицах, что и длина. Таким образом, мы знаем,

Периметр = 4 × Сторона квадрата

Примем «а» к длине стороны квадрата, тогда имеем;

Периметр = 4 × a  

Формула для диагонали квадрата: Обе диагонали квадрата равны друг другу. Примем «а» за длину стороны квадрата. По теореме Пифагора имеем

Hypotenuse ²  = Base ²  + Perpendicular ²

Hypotenuse ²  = a ²  + a ²

Hypotenuse ²  = 2a ²  + Perpendicular ²

Гипотенуза = a√2

Длина диагоналей квадрата равна a√2.

Диагональ - это гипотенуза, а две стороны треугольника образованы диагональю квадрата.

Therefore, 

Diagonal ²  = Side ²  + Side ²

Diagonal = √2(side) ²  

or

d = a√2

где d — длина диагонали квадрата, а — сторона.

Что такое ромб?

Ромб также известен как четырехугольник с четырьмя сторонами. Считается частным случаем параллелограмма. Ромб имеет параллельные противоположные стороны и равные противоположные углы. Ромб также известен под названием алмаз или ромбовидный алмаз. Ромб содержит все стороны ромба равные по длине. Кроме того, диагонали ромба пересекаются пополам под прямым углом.

Свойства ромба

Ромб обладает следующими свойствами: 

• У ромба все стороны равны.
• Диагонали ромба делят друг друга пополам под прямым углом.
• Противоположные стороны ромба по своей природе параллельны.
• Сумма двух смежных углов ромба равна 180 ^o .
• В ромбе нет вписанной окружности.
• Вокруг ромба нет описанной окружности.
• Диагонали ромба образуют четыре прямоугольных треугольника.
• Эти треугольники конгруэнтны друг другу.
• Противоположные углы ромба равны.
• При соединении середины сторон ромба образуется прямоугольник.
• При соединении середины половины диагонали образуется еще один ромб.

Периметр ромба: Периметр ромба определяется как сумма длин его границ, образующих фигуру. Его также можно обозначить как общую сумму длин четырех сторон ромба. Периметр ромба определяется: 

Периметр, P = 4a 

, где диагонали ромба обозначены d ₁ и d ₂ , а «а» — сторона.

Площадь ромба: Площадь ромба определяется как область, заключенная в двумерную плоскость. Площадь ромба равна произведению диагоналей ромба на 2. Площадь ромба можно определить по следующей формуле:

Площадь, A = (d ₁ × d ₂ ) / 2

Является ли квадрат ромбом?

Квадраты и ромбы имеют некоторые сходства и различия. Обе замкнутые фигуры обладают определенными свойствами, отличающимися числом диагоналей, длиной, формой и диагоналями. И ромб, и квадрат имеют схожие свойства, поскольку оба они подпадают под категорию параллелограмма.

Однако ромб и квадрат обладают разными свойствами: в ромбе одна пара противоположных углов в ромбе острая, а другая пара тупая. Однако в случае квадрата каждый из четырех углов равен 9.0о. Кроме того, обе диагонали ромба имеют разную длину. И диагонали в квадрате имеют одинаковую длину.

Таким образом, квадрат всегда является ромбом, но ромб не обязательно может быть квадратом.

Квадрат всегда является ромбом, так как все стороны квадрата равны по длине. Кроме того, диагонали обеих замкнутых фигур, квадрата и ромба, перпендикулярны друг другу и делят противоположные углы пополам. Таким образом, квадрат всегда является ромбом.

Аналогичные вопросы

Вопрос 1: Рассчитайте периметр и площадь парка со стороной и , равной 500 м?

Ответ:

Здесь

Длина одной стороны квадратного парка = 500 м

Так как парк квадратный, все стороны парков равны, т.е. 500 м.

Таким образом,

Периметр сквера-парка = 4 × сторона сквера-парка

= 4 × 500 = 2000 м

Отсюда периметр парка 2000 м.

Теперь,

Площадь квадратного парка = сторона ² за квадратную единицу

сторона = 500 м

Область = 500 ² = 500 × 500 = 250000 кв. М

Вопрос 2: Мы имеют квадратный парк со стороной равной 12 см. Вычислите площадь, периметр и длину диагонали квадрата.

Ответ:

Дано,

Сторона квадрата, s = 12 см

Известно,

Площадь квадрата = Сторона ²

Подставляя значения,

Площадь = 12 × 12 = 144 кв. см

Площадь квадрата равна 144 кв.

Периметр квадрата = 4 × сторона

Периметр = 4 × 12 см = 48 см

Периметр квадрата = 48 см

Длина диагонали квадрата =

Длина диагонали квадрат = 12 × 1,414 = 16,9705 см

Вопрос 3: Найдите длину стороны квадрата, площадь которого равна 25 см². Также найдите периметр квадрата?

Ответ: 

Нам дано, 

Площадь квадрата = 25 кв.см.

Площадь квадрата = сторона ² = s × s

Таким образом,

Подставив значения, получим:

Получим;

25 = сторона ²

сторона =  =  = 5 см

Следовательно, 

Длина стороны квадрата равна 5 см.

No related posts.