Math Tricks — Behavioral Sciences Research Core
Page MenuЭта веб-страница посвящена
невероятно умной
идее о том, что математика может быть интересной!
Попробуйте эти трюки:
- Easy Magic Addition
- Магический квадрат #15
- Магический квадрат #34
- Создайте свой собственный магический квадрат
- Перевернутый магический квадрат
- Антимагический квадрат
- Выиграйте ставки с этим квадратом
- Магический фокус с картами
- Калькулятор молний
- Таблицы забавных чисел
- Знаете ли вы…?
- Уловка на этот год
- Где нить?
- Огромный магический квадрат
Вот несколько интересных ссылок:
- Список книг по хитрой математике для чтения, большинство из которых я использовал для этого сайта.
- Узнайте об оригинальном компьютере: The Abacus (http://www.
 ee.ryerson.ca:8080/~elf/abacus/)
ee.ryerson.ca:8080/~elf/abacus/) - Сыграйте в математическую игру (http://dev.eyecon.com/marcia) — для одного или двух игроков. (Если вы используете Netscape,
- Играйте в Shoot Balls (http://www.fi.uu.nl/wisweb/en/applets/bollen/Welcome.html).
- Играйте в Flippo 24 (http://www.fi.uu.nl/wisweb/en/applets/bollen/Welcome.html).
- Проверьте свои знания таблицы умножения (http://www.fi.uu.nl/wisweb/en/applets/tafels/Welcome.html)
- Попробуйте свои силы в оценке (http://www.fi.uu.nl/wisweb/en/applets/bollen/Welcome.html).
- Исследуйте геометрию в увлекательной интерактивной форме.
- Попробуйте загадку «Ханойская башня» (http://www.eng.auburn.edu/~fwushan/Hanoi1.html).
- Посмотрите, что такое Spriographis (http://www.mainstrike.com/mstservices/handy/Spiro/).
- Посмотрите, что такое набор Мандельброта (http://www.franceway.com/java/fractale/mandel_b.
 htm).
htm). - Если вы хотите больше задач по математике , попробуйте новый сайт PBS MATHLINE MATH CHALLENGES. Попробуйте, вам понравится. (Но помните, что мы были первыми.)
Волшебный трюк №1
Удивите пеонов этим. Все просто. Это эффективно. Он получает их каждый раз.
- Спросите свою оценку выберите три (3) разных номеров от 1 до 9.
- Скажите ему или ей (или ей или ему) записать три числа рядом друг с другом, начиная с самого большого и заканчивая наименьшим, чтобы получилось одно трехзначное число. Скажите ему/ей, чтобы он не говорил вам, что это за числа.
- Затем попросите ее или его составить новое трехзначное число, переставив цифры местами, поставив наименьшее первым, а самое большое последним. И напишите это число прямо под первым числом.
- Теперь попросите его или ее вычесть меньшее (и меньшее) трехзначное число из старшего (и большего) трехзначного числа. Скажи им, чтобы они не говорили тебе, каков результат.

- Теперь у вас есть выбор оберток:
- Попросите вашего друга сложить три цифры числа, которое получается в результате вычитания меньшего из большего трехзначного числа. Затем удивите его или ее, сказав, какова сумма этих трех чисел. Сумма трехзначного ответа всегда будет 18!
- Скажите своему другу, что если он или она скажет вам, какая первая ИЛИ последняя цифра ответа, вы скажете ей или ему, какие две другие цифры. Это возможно, потому что средняя цифра всегда будет 9, а сумма двух других цифр всегда будет 9! Таким образом, чтобы получить цифру, отличную от средней (которая равна 9) и отличную от цифры, которую сказал вам ваш друг, просто вычтите цифру, которую ваш друг сказал вам, из 9, и это будет неизвестная цифра.
Вернуться к началу
Магический квадрат #15
Каждая строка и столбец в этом магическом квадрате в сумме дают 15. Так сделайте обе диагонали!
| 8 | 3 | 4 |
| 1 | 5 | 9 |
| 6 | 7 | 2 |
Вернуться к началу
Магический квадрат #34
Каждая строка и столбец в этом магическом квадрате в сумме дают 34. Так сделайте обе диагонали!
Так сделайте обе диагонали!
| 1 | 15 | 14 | 4 |
| 12 | 6 | 7 | 9 |
| 8 | 10 | 11 | 5 |
| 13 | 3 | 2 | 16 |
Вернуться к началу
Рецепт собственного магического квадрата 3 X 3
Некоторые необходимые правила и определения:
- Пусть буквы a , b и c обозначают целые числа (то есть целые числа).

- Всегда выбирайте a так, чтобы оно было больше суммы b и c . То есть a > b + c . Это гарантирует отсутствие записи в магический квадрат отрицательного числа.
- Не допускайте 2 X b = c . Это гарантирует, что вы не получите одно и то же число в разных ячейках.
- Используя формулы, приведенные в таблице ниже, вы можете составить магический квадрат, в котором сумма строк, столбцов и диагоналей равна 3 X независимо от числа или .
Чтобы создать первый магический квадрат #15 выше, пусть 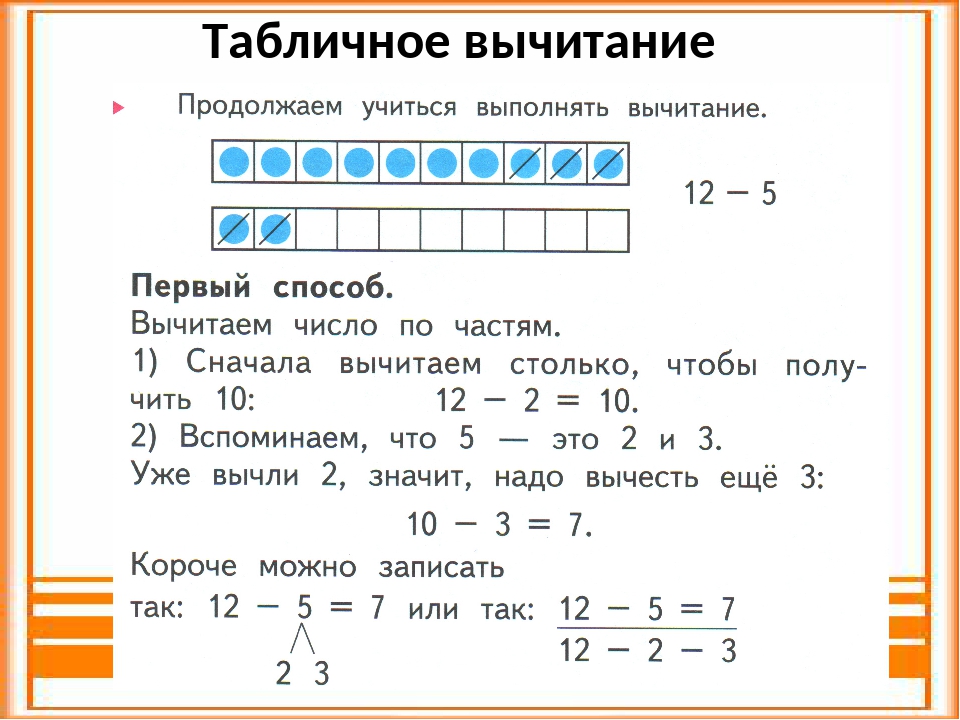 Вот некоторые другие:
Вот некоторые другие:
- а = 6, б = 3, в = 2
- а = 6, б = 3, в = 1
- а = 7, б = 3, в = 2
- а = 7, б = 4, в = 2
- а = 8, б = 6, в = 1
- а = 8, б = 5, в = 2
- а = 8, б = 4, в = 3
Попробуйте придумать что-нибудь свое.
Вернуться к началу
Перевернутый магический квадрат
Вот магический квадрат, который не только дает в сумме 264 по всем направлениям, но и делает это, даже когда он перевернут! Если не веришь мне, посмотри на это, стоя на голове! (Или просто скопируйте его и переверните вверх ногами.)
| 96 | 11 | 89 | 68 |
| 88 | 69 | 91 | 16 |
| 61 | 86 | 18 | 99 |
| 19 | 98 | 66 | 81 |
Вернуться к началу
Антимагический квадрат
Вот магический квадрат с максимально возможным количеством различных сумм .
| 5 | 1 | 3 |
| 4 | 2 | 6 |
| 8 | 7 | 9 |
Эта таблица дает 8 разных итого.
Вернуться к началу
Выиграть ставки с помощью магического квадрата
Итак, вот отличный способ выиграть ставки с помощью магического квадрата. Позвоните другу по телефону. Пусть он или она возьмет карандаш и бумагу и поднесет их к телефону, чтобы он или она могли записать цифры от 1 до 9. Скажите своему другу, что вы будете по очереди называть цифры от 1 до 9. Никто из вас не может повторить номер, который называет другой. Затем вы оба запишите числа от 1 до 9.. Затем, когда ваш друг называет одно из чисел, он обводит это число кружком, и вы тоже. Когда вы называете число, вы рисуете квадрат вокруг этого числа, и ваш друг делает то же самое. Выигрывает тот, кто первым наберет три числа, сумма которых точно равна 15.
Допустим, вы идете первым и называете 8. Ваш друг может назвать 6. Затем вы называете 2. Ваш друг называет 5, и вы называете 4. Ваш друг называет 7, а вы называете 3. Затем вы говорите своему другу, что вы только что выиграли, потому что назвали 8, 3 и 4, что в сумме дает 15.
Ваш друг снова захочет поиграть. Так что на этот раз вы можете поспорить с ним, что выиграете, с условием, что в случае ничьей (когда вы используете числа от 1 до 9, но ни один из вас не получает в сумме 15) никто ничего не должен.
Если вы знаете хитрость, вы никогда не проиграете, и, вероятно, проиграете в большинстве случаев.
Фокусы На самом деле фокус основан как на крестиках-ноликах, так и на магическом квадрате. Магический квадрат выглядит так:
| 8 | 1 | 6 |
| 3 | 5 | 7 |
| 4 | 9 | 2 |
Поскольку это магический квадрат, каждая строка, каждый столбец и каждая диагональ в сумме дают 15.
Итак, в приведенном выше примере, когда вы называете 8, вы ставите X в верхнем левом углу. Когда ваш друг говорит 6, вы ставите ) в правом верхнем углу. И так далее.
Наверх
Математический фокус с картами
Для этого задания вам понадобится обычная колода карт. Никаких причудливых перетасовок не требуется. Просто следуйте этим простым шагам:
- Перемешайте карты, чтобы тщательно их перемешать.
- Разложите 36 карт стопкой.
- Попросите друга выбрать одну из 36 карт, посмотреть на нее и запомнить, а затем положить ее обратно в стопку, не показывая ее вам.
- Перемешайте 36 карт.
- Разложите 36 карт в 6 рядов по 6 карт в каждом.
 Обязательно сдавайте верхний ряд слева направо. Затем нанесите второй ряд под ним слева направо. И так далее, каждый последующий ряд кладется под предыдущий.
Обязательно сдавайте верхний ряд слева направо. Затем нанесите второй ряд под ним слева направо. И так далее, каждый последующий ряд кладется под предыдущий. - Попросите друга посмотреть на карточки и сказать, в каком ряду находится выбранная карточка. Запомните, под каким номером находится ряд.
- Аккуратно поднимите карты в том же порядке, в котором вы их положили . Таким образом, первая карта слева в верхнем ряду находится наверху стопки, а последняя карта справа в нижнем ряду — внизу стопки.
- Теперь разложите карты в 6 рядов по 6 карт в каждом, но на этот раз разложите карты по одному столбцу за раз . Вместо того, чтобы переходить от одной строки к другой, переходите от одного столбца к другому. Разложите первые шесть карт в столбце сверху вниз в крайний левый угол. Затем выложите следующие шесть карт во второй столбец из шести карт справа от первого столбца из шести карт. Продолжайте делать это, пока у вас не будет 6 столбцов по 6 карт в каждом (что выглядит так же, как 6 рядов по 6 карт в каждом, потому что это 9).
 0004 это то же самое).
0004 это то же самое). - Еще раз спросите у друга, в каком ряду находится выбранная карта.
- Когда ваш друг говорит вам, в каком ряду находится карта, вы можете сказать, какая именно выбранная карта. Как? Если ваш друг сказал, что карта была в строке 2 в первый раз, а в строке 5 во второй раз, то выбранная карта — это карта во втором столбце пятой строки. Это связано с тем, что при расположении карточек то, что в первый раз было строками, во второй раз становится столбцами.
Вернуться к началу
Калькулятор молний
Вот уловка, чтобы удивлять их каждый раз! Попросите кого-нибудь записать свой номер социального страхования. Затем попросите их переписать его так, чтобы все было перемешано. (Если у них нет номера социального страхования, попросите их записать любые 9 цифр от 1 до 9.) Если есть нули, попросите заменить их на любую другую цифру от 1 до 9. Затем попросите их скопировать свои девять цифр. числа в том же порядке рядом с исходными девятью числами. Это даст им число с 18 цифрами, первая половина которого такая же, как вторая половина. Далее измените вторую цифру на 7 и измените одиннадцатую цифру (это будет то же число, что и вторая цифра, но во вторых девяти цифрах) также на 7. Тогда поспорьте с ними, что вы сможете сказать им, что останется после деления числа на 7, быстрее, чем они сообразят это вручную. Ответ: 0 — 7 делится на это новое число ровно без остатка!
Это даст им число с 18 цифрами, первая половина которого такая же, как вторая половина. Далее измените вторую цифру на 7 и измените одиннадцатую цифру (это будет то же число, что и вторая цифра, но во вторых девяти цифрах) также на 7. Тогда поспорьте с ними, что вы сможете сказать им, что останется после деления числа на 7, быстрее, чем они сообразят это вручную. Ответ: 0 — 7 делится на это новое число ровно без остатка!
Вернуться к началу
Таблицы забавных чисел
Следующие забавные таблицы взяты из одной из моих любимых книг всех времен, Recreations in the Theory of Numbers , Альберт Х. Бейлер, опубликовано Dover Publications. Эта книга на самом деле объясняет математические причины, по которым эти трюки работают.
900 40 9 х 37 = 333 и 3 + 3 + 3 = 9
900 79
90 079
 д.
д.
Наверх
Знаете ли вы…?
Каждое двузначное число, оканчивающееся на 9, представляет собой сумму, кратную двум цифрам, плюс сумму двух цифр. Так, например, 29 = (2 х 9) + (2 + 9). 2 X 9 = 18. 2 + 9 = 11. 18 + 11 = 29.
40 — уникальное число, потому что, когда оно записано как «сорок», это единственное число, буквы которого расположены в алфавитном порядке.
А премьер число — это целое число больше 1, которое не делится без остатка ни на какое другое целое число, кроме самого себя (и 1). 2, 3, 5, 7, 11, 13 и 17 являются примерами простых чисел.
139 и 149 — первые последовательные простые числа, отличающиеся на 10.
69 — единственное число, в квадрате и кубе которого между ними используются все цифры от 0 до 9 по одному разу:
69 2 = 4761 и 69 3 = 328 509.
Один фунт железа содержит примерно 4 891 500 000 000 000 000 000 000 атомов.
Существует около 318 979 564 000 возможных способов сыграть первые четыре хода с каждой стороны в игре в шахматы.
Земля проходит более полутора миллионов миль каждый день.
В Эйфелевой башне 2 500 000 заклепок.
Если бы все кровеносные сосуды в человеческом теле были сложены встык, они растянулись бы на 100 000 миль.
Вернуться к началу
Математический трюк для этого года
Предполагается, что этот трюк будет работать только в 1998 году, но на самом деле одно изменение позволит ему работать в течение любого года.
1. Выберите количество дней в неделю, когда вы хотели бы выходить на улицу (1-7).
2. Умножьте это число на 2.
3. Прибавьте 5.
4. Умножьте полученную сумму на 50.
5. В 1998 году, если у вас уже был день рождения в этом году, прибавьте 1748. Если нет , добавьте 1747. В 1999 году просто добавьте 1 к этим двум числам (поэтому добавьте 1749, если у вас уже был день рождения, и добавьте 1748, если нет). В 2000 году номер меняется на 1749 и 1748. И так далее.
В 2000 году номер меняется на 1749 и 1748. И так далее.
6. Вычтите из четырех цифр год вашего рождения (19ХХ).
Результаты:
У вас должно быть трехзначное число.
Первая цифра этого номера — это количество дней, в течение которых вы хотите выходить на улицу каждую неделю (1–7).
Последние две цифры — ваш возраст.
(Спасибо, что передали мне это, Джуди.)
Вернуться к началу
Где нить?
В следующий раз, когда вы будете с группой людей и захотите произвести на них впечатление своими экстрасенсорными способностями, попробуйте это. Пронумеруйте всех в группе от 1 до любого числа. Возьмите кусок веревки и скажите, чтобы он привязал ее кому-нибудь к пальцу, пока вы выходите из комнаты или поворачиваетесь спиной. Затем скажите, что вы можете сказать им не только, у кого он есть, но и на какой руке и на каком пальце он находится, если они просто посчитают за вас и дадут вам ответы. Затем попросите одного из них ответить на следующие вопросы:
1. Умножьте номер человека со строкой на 2.
Умножьте номер человека со строкой на 2.
2. Прибавьте 3.
3. Умножьте результат на 5.
4. Если строка справа, добавьте 8.
Если струна находится на левой руке, добавьте 9.
5. Умножьте на 10.
6. Добавьте номер пальца (большой палец = 1).
7. Добавить 2.
Попросите их сказать вам ответ. Затем мысленно вычтите 222. Остаток дает ответ, начиная с правой цифры ответа.
Например, предположим, что струна находится на безымянном пальце левой руки Игрока №6:
1. Умножить на 2 = 12.
2. Прибавить 3 = 15.
3. Умножить на 5 = 75
4. Поскольку струна находится на левой руке, прибавьте 9 = 84.
5. Умножьте на 10 = 840.
6. Прибавьте номер пальца (3) = 843.
7. Прибавьте 2 = 845.
Теперь мысленно вычтите 222 = 623. Цифра справа (3) говорит о том, что струна находится на безымянном пальце. Средняя цифра говорит о том, что он находится на левой руке (правая рука = 1). Цифра слева говорит о том, что строка принадлежит Игроку №6.
Цифра слева говорит о том, что строка принадлежит Игроку №6.
Кстати, когда номер человека больше 9, вы получите ЧЕТЫРЕХзначное число, а ДВЕ левые цифры будут номером Игрока.
В чем секрет?
(Это из замечательной книги под названием Giant Book of Puzzles & Games, Шейлы Энн Бэрри. Опубликовано Sterling Publishing Co., Inc., Нью-Йорк, 1978 г., недавно переиздано в мягкой обложке.)
Оставайтесь с нами. больше математических трюков. Они будут добавляться время от времени, так что не забудьте проверить снова.
Полное руководство по гистограммам
Что такое гистограмма?
Гистограмма — это диаграмма, отображающая распределение значений числовой переменной в виде ряда столбцов. Каждая полоса обычно охватывает диапазон числовых значений, называемый ячейкой или классом; высота столбца указывает частоту точек данных со значением в соответствующем бине.
На приведенной выше гистограмме показано частотное распределение времени ответа на запросы, отправленные в вымышленную систему поддержки.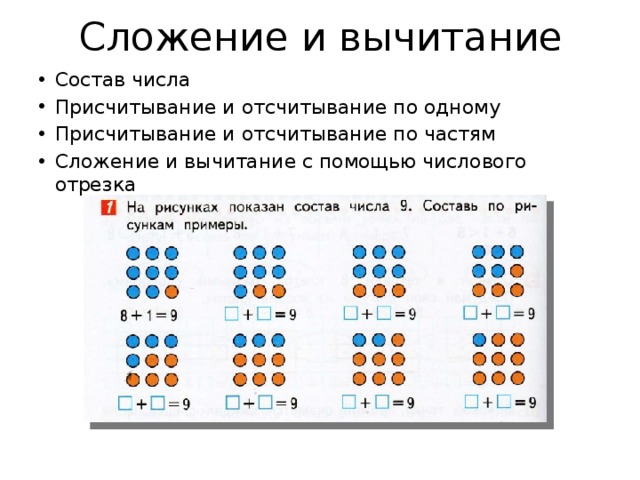 Каждая полоса охватывает один час времени, а высота указывает количество билетов в каждом временном диапазоне. Мы видим, что наибольшая частота ответов была в диапазоне 2-3 часов, с более длинным хвостом справа, чем слева. Есть также холм поменьше, пик (режим) которого находится в диапазоне 13-14 часов. Если бы мы смотрели только на числовую статистику, такую как среднее значение и стандартное отклонение, мы могли бы упустить тот факт, что эти два пика внесли свой вклад в общую статистику.
Каждая полоса охватывает один час времени, а высота указывает количество билетов в каждом временном диапазоне. Мы видим, что наибольшая частота ответов была в диапазоне 2-3 часов, с более длинным хвостом справа, чем слева. Есть также холм поменьше, пик (режим) которого находится в диапазоне 13-14 часов. Если бы мы смотрели только на числовую статистику, такую как среднее значение и стандартное отклонение, мы могли бы упустить тот факт, что эти два пика внесли свой вклад в общую статистику.
Когда следует использовать гистограмму
Гистограммы удобны для отображения общих характеристик распределения переменных набора данных. Вы можете примерно увидеть, где находятся пики распределения, является ли распределение асимметричным или симметричным, и есть ли какие-либо выбросы.
Чтобы использовать гистограмму, нам просто нужна переменная, которая принимает непрерывные числовые значения. Это означает, что различия между значениями постоянны независимо от их абсолютных значений. Например, даже если оценка за тест может принимать только целочисленные значения от 0 до 100, разрыв одинакового размера имеет одинаковое значение независимо от того, где мы находимся на шкале: разница между 60 и 65 равна той же 5-балльной шкале. размер как разница между 9от 0 до 95.
Например, даже если оценка за тест может принимать только целочисленные значения от 0 до 100, разрыв одинакового размера имеет одинаковое значение независимо от того, где мы находимся на шкале: разница между 60 и 65 равна той же 5-балльной шкале. размер как разница между 9от 0 до 95.
Информация о количестве бинов и их границах для подсчета точек данных не является неотъемлемой частью самих данных. Вместо этого настройка бинов — это отдельное решение, которое мы должны принять при построении гистограммы. То, как мы указываем бины, будет иметь большое влияние на то, как можно интерпретировать гистограмму, как будет видно ниже.
Когда значение находится на границе бина, оно будет последовательно назначено бину справа или слева от него (или в конечные бины, если оно находится в конечных точках). Какая сторона выбрана, зависит от инструмента визуализации; некоторые инструменты имеют возможность переопределить настройки по умолчанию. В этой статье предполагается, что значения на границе бина будут присвоены бину справа.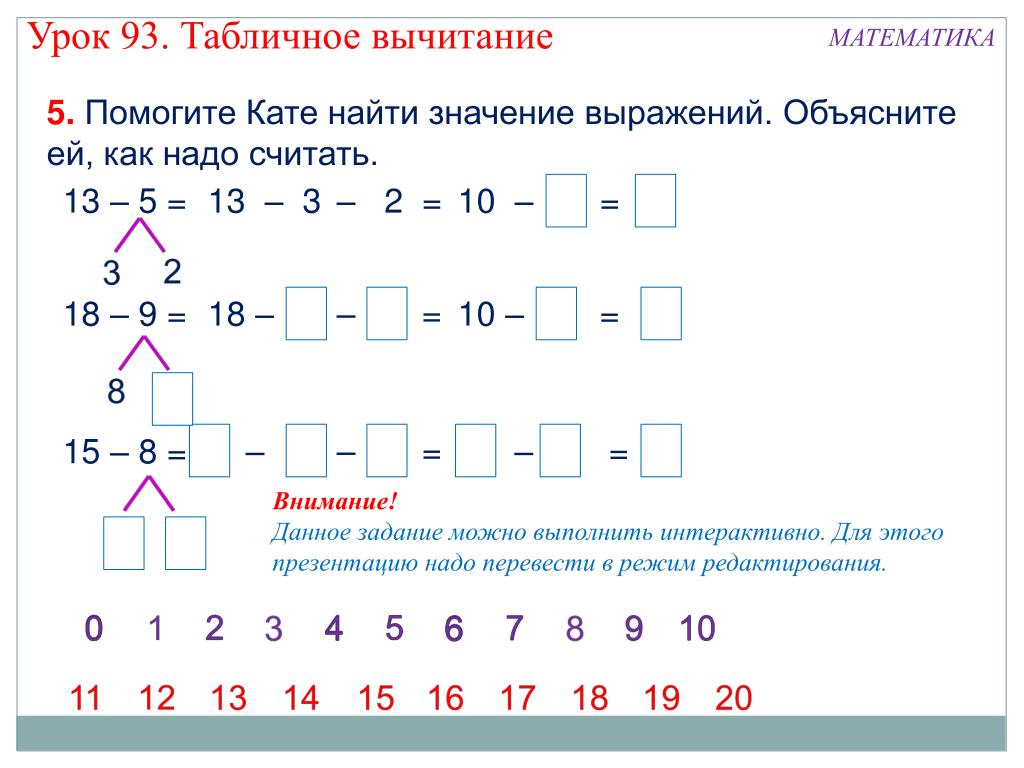
Пример структуры данных
Один из способов, которым инструменты визуализации могут работать с данными, которые должны быть визуализированы в виде гистограммы, — это сводная форма, как показано выше. Здесь первый столбец указывает границы бина, а второй — количество наблюдений в каждом бине. Кроме того, некоторые инструменты могут просто работать с исходным столбцом неагрегированных данных, а затем применять к данным заданные параметры группирования при создании гистограммы.
Рекомендации по использованию гистограммы
Использовать базовую линию с нулевым значением
Важным аспектом гистограмм является то, что они должны быть построены с базовой линией с нулевым значением. Поскольку частота данных в каждом бине определяется высотой каждого столбца, изменение базовой линии или введение пробела в шкале исказят восприятие распределения данных.
Отсечение 80 точек от вертикальной оси делает распределение оценок производительности намного лучше, чем оно есть на самом деле.
Выберите подходящее количество ячеек
Хотя инструменты, которые могут генерировать гистограммы, обычно имеют некоторые алгоритмы по умолчанию для выбора границ бинов, вы, вероятно, захотите поиграть с параметрами биннинга, чтобы выбрать что-то, что репрезентативно для ваших данных. В Википедии есть обширный раздел, посвященный эмпирическим правилам выбора подходящего количества ячеек и их размеров, но, в конечном счете, стоит использовать знание предметной области, а также изрядно поэкспериментировать с различными вариантами, чтобы узнать, что лучше всего подойдет для ваших целей.
Выбор размера ячейки обратно пропорционален количеству ячеек. Чем больше размеры бинов, тем меньше бинов будет для охвата всего диапазона данных. Чем меньше размер корзины, тем больше корзин должно быть. Стоит потратить некоторое время на то, чтобы протестировать различные размеры бинов, чтобы увидеть, как выглядит распределение в каждом из них, а затем выбрать график, который лучше всего представляет данные. Если у вас слишком много бинов, то распределение данных будет выглядеть грубым, и будет сложно отличить сигнал от шума. С другой стороны, при слишком малом количестве бинов на гистограмме будет не хватать деталей, необходимых для выделения какой-либо полезной закономерности из данных.
Если у вас слишком много бинов, то распределение данных будет выглядеть грубым, и будет сложно отличить сигнал от шума. С другой стороны, при слишком малом количестве бинов на гистограмме будет не хватать деталей, необходимых для выделения какой-либо полезной закономерности из данных.
Выберите интерпретируемые границы бинов
Метки и метки обычно должны располагаться на границах бинов, чтобы наилучшим образом сообщить, где лежат границы каждого столбца. Метки не нужно устанавливать для каждого бара, но наличие их между каждыми несколькими барами помогает читателю отслеживать значение. Кроме того, полезно, если метки представляют собой значения с небольшим количеством значащих цифр, чтобы их было легко читать.
Это говорит о том, что бины размера 1, 2, 2,5, 4 или 5 (которые делят 5, 10 и 20 поровну) или их степени десяти являются хорошими размерами бинов, чтобы начать с эмпирического правила. Это также означает, что бины размером 3, 7 или 9, вероятно, будет труднее читать, и их не следует использовать, если контекст не имеет для них смысла.
Это также означает, что бины размером 3, 7 или 9, вероятно, будет труднее читать, и их не следует использовать, если контекст не имеет для них смысла.
Небольшое предостережение: убедитесь, что вы учитываете типы значений, которые принимает интересующая вас переменная. В случае дробного размера ячейки, такого как 2,5, это может быть проблемой, если ваша переменная принимает только целые значения. Ячейка от 0 до 2,5 имеет возможность собрать три разных значения (0, 1, 2), но следующая ячейка от 2,5 до 5 может собрать только два разных значения (3, 4 — 5 попадут в следующую ячейку). Это означает, что ваша гистограмма может выглядеть неестественно «ухабистой» просто из-за количества значений, которые может принимать каждый бин.
На рисунке выше показано распределение результатов при суммировании результата пяти бросков кубика, повторенных 20 000 раз. Ожидаемая форма колокола выглядит остроконечной или кривобокой, когда выбираются размеры ячеек, которые охватывают различное количество целочисленных результатов.
Ожидаемая форма колокола выглядит остроконечной или кривобокой, когда выбираются размеры ячеек, которые охватывают различное количество целочисленных результатов.Распространенное неправильное использование
Измеряемая переменная не является непрерывной числовой переменной
Как отмечалось во вступительных разделах, гистограмма предназначена для отображения частотного распределения непрерывной числовой переменной. Когда интересующая нас переменная не соответствует этому свойству, вместо этого нам нужно использовать другой тип диаграммы: гистограмму. Переменная, которая принимает категориальные значения, такие как тип пользователя (например, гость, пользователь) или местоположение, явно не является числовой, и поэтому должна использовать гистограмму. Однако существуют определенные типы переменных, которые сложнее классифицировать: те, которые принимают дискретные числовые значения, и те, которые принимают значения, зависящие от времени.
Переменные, принимающие дискретные числовые значения (например, целые числа 1, 2, 3 и т. д.), могут отображаться либо в виде гистограммы, либо в виде гистограммы, в зависимости от контекста. Использование гистограммы будет более вероятным, когда есть много разных значений для построения. Когда диапазон числовых значений велик, тот факт, что значения являются дискретными, как правило, не имеет значения, и хорошей идеей будет непрерывная группировка.
д.), могут отображаться либо в виде гистограммы, либо в виде гистограммы, в зависимости от контекста. Использование гистограммы будет более вероятным, когда есть много разных значений для построения. Когда диапазон числовых значений велик, тот факт, что значения являются дискретными, как правило, не имеет значения, и хорошей идеей будет непрерывная группировка.
Одна важная вещь, на которую следует обращать внимание, это то, что цифры представляют реальную стоимость. Если числа на самом деле являются кодами категориальной или неупорядоченной переменной, то это признак того, что следует использовать гистограмму. Например, если у вас есть ответы на опрос по шкале от 1 до 5, кодирующие значения от «полностью не согласен» до «полностью согласен», то частотное распределение следует визуализировать в виде гистограммы. Причина в том, что различия между отдельными значениями могут быть непоследовательными: мы на самом деле не знаем, что значимая разница между 1 и 2 («совершенно не согласен» и «не согласен») такая же, как разница между 2 и 3. («не согласен» на «ни согласен, ни не согласен»).
(«не согласен» на «ни согласен, ни не согласен»).
Более сложный случай, когда интересующая нас переменная является характеристикой, зависящей от времени. Когда значения соответствуют относительным периодам времени (например, 30 секунд, 20 минут), тогда имеет смысл группировать по периодам времени для гистограммы. Однако, когда значения соответствуют абсолютному времени (например, 10 января, 12:15), различие становится размытым. Когда записываются новые точки данных, значения обычно попадают во вновь созданные ячейки, а не в существующий диапазон ячеек. Кроме того, некоторые естественные варианты группирования, например, по месяцам или кварталам, приводят к немного неравным размерам ячеек. По этим причинам нередко можно увидеть другой тип диаграммы, такой как гистограмма или линейная диаграмма.
Использование бинов разного размера
Хотя во всех примерах до сих пор гистограммы демонстрировались с использованием бинов одинакового размера, на самом деле это не является техническим требованием. Когда данных мало, например, когда есть длинный хвост данных, может прийти в голову идея использовать бины большей ширины, чтобы покрыть это пространство. Однако создание гистограммы с бинами разного размера не является ошибкой, но требует значительных изменений в способе создания гистограммы и может вызвать много трудностей при интерпретации.
Когда данных мало, например, когда есть длинный хвост данных, может прийти в голову идея использовать бины большей ширины, чтобы покрыть это пространство. Однако создание гистограммы с бинами разного размера не является ошибкой, но требует значительных изменений в способе создания гистограммы и может вызвать много трудностей при интерпретации.
Техническая особенность гистограмм заключается в том, что общая площадь столбцов представляет собой целое, а площадь, занимаемая каждым столбцом, представляет долю целого, содержащуюся в каждом ячейке. Когда размеры корзин одинаковы, это делает площадь и высоту измеряемой полосы эквивалентными. Однако в гистограмме с переменными размерами ячеек высота больше не может соответствовать общей частоте появления. Это исказило бы представление о том, сколько точек находится в каждом бине, поскольку увеличение размера бина только заставит его выглядеть больше. На центральном графике рисунка ниже ячейки 5-6, 6-7 и 7-10 в конечном итоге выглядят так, как будто они содержат больше точек, чем на самом деле.
. Вместо этого вертикальная ось должна кодировать частоту плотность на единицу размера бина. Например, на правой панели рисунка выше ячейка 2–2,5 имеет высоту около 0,32. Умножьте на ширину бина, 0,5, и мы можем оценить около 16% данных в этом бине. Высота более широких бинов была уменьшена по сравнению с центральной панелью: обратите внимание, как общая форма выглядит похожей на исходную гистограмму с одинаковыми размерами бинов. Плотность — это непростая концепция для понимания, и такой сюжет, представленный другим, незнакомым с этой концепцией, будет трудно его интерпретировать.
Из-за всего этого лучший совет — просто придерживаться абсолютно одинаковых размеров контейнеров. Наличие пустых интервалов и некоторый повышенный уровень шума в диапазонах с разреженными данными, как правило, стоят увеличения интерпретируемости вашей гистограммы. С другой стороны, если есть неотъемлемые аспекты отображаемой переменной, которые предполагают неравные размеры ячеек, то вместо использования гистограммы с неравномерными ячейками вам может быть лучше использовать гистограмму.
С другой стороны, если есть неотъемлемые аспекты отображаемой переменной, которые предполагают неравные размеры ячеек, то вместо использования гистограммы с неравномерными ячейками вам может быть лучше использовать гистограмму.
Общие параметры гистограммы
Абсолютная частота по сравнению с относительной частотой
В зависимости от целей вашей визуализации вы можете изменить единицы измерения на вертикальной оси графика как в терминах абсолютной частоты или относительной частоты. Абсолютная частота — это просто естественное количество вхождений в каждом бине, а относительная частота — это доля вхождений в каждом бине. Выбор единиц оси будет зависеть от того, какие виды сравнений вы хотите выделить в распределении данных.
Преобразуя первый пример в терминах относительной частоты, гораздо проще сложить первые пять тактов, чтобы обнаружить, что примерно на половину заявок отвечают в течение пяти часов.Отображение неизвестных или отсутствующих данных
На самом деле это , а не особенно распространенный вариант, но его стоит учитывать, когда дело доходит до настройки графиков. Если в строке данных отсутствует значение для интересующей нас переменной, оно часто будет пропущено при подсчете для каждого бина. Если важно показать количество пропущенных или неизвестных значений, вы можете объединить гистограмму с дополнительной полосой, отображающей частоту этих неизвестных. При построении этого столбца рекомендуется поместить его на параллельную ось основной гистограммы и другого нейтрального цвета, чтобы точки, собранные на этом столбце, не путались с числовыми значениями.
Если в строке данных отсутствует значение для интересующей нас переменной, оно часто будет пропущено при подсчете для каждого бина. Если важно показать количество пропущенных или неизвестных значений, вы можете объединить гистограмму с дополнительной полосой, отображающей частоту этих неизвестных. При построении этого столбца рекомендуется поместить его на параллельную ось основной гистограммы и другого нейтрального цвета, чтобы точки, собранные на этом столбце, не путались с числовыми значениями.
Гистограмма
Как отмечалось выше, если интересующая переменная не является непрерывной и числовой, а дискретной или категориальной, то вместо нее нам понадобится гистограмма. В отличие от гистограммы, столбцы гистограммы обычно имеют небольшой разрыв между собой: это подчеркивает дискретный характер отображаемой переменной.
Линейная диаграмма
Если вы группируете числовые данные, но хотите, чтобы вертикальная ось вашего графика отображала что-то другое, кроме информации о частоте, вам следует рассмотреть возможность использования линейной диаграммы. Вертикальное положение точек на линейной диаграмме может отображать значения или статистические сводки второй переменной. Когда линейная диаграмма используется для изображения частотных распределений, таких как гистограмма, это называется полигон частот .
Вертикальное положение точек на линейной диаграмме может отображать значения или статистические сводки второй переменной. Когда линейная диаграмма используется для изображения частотных распределений, таких как гистограмма, это называется полигон частот .
Кривая плотности
Кривая плотности, или оценка плотности ядра (KDE), является альтернативой гистограмме, которая дает каждой точке данных непрерывный вклад в распределение. На гистограмме вы можете представить себе каждую точку данных как выливание жидкости из ее значения в серию цилиндров ниже (контейнеры). В KDE каждая точка данных добавляет небольшой объем вокруг своего истинного значения, которое складывается по точкам данных для создания окончательной кривой. Форма куска объема — это «ядро», и существует безграничный выбор. Из-за огромного количества опций при выборе ядра и его параметров кривые плотности обычно являются областью программных инструментов визуализации.
Толстые черные штрихи обозначают точки данных, которые влияют на гистограмму (слева) и кривую плотности (справа). Обратите внимание, как каждая точка вносит небольшую кривую в форме колокола в общую форму.
Обратите внимание, как каждая точка вносит небольшую кривую в форме колокола в общую форму.Коробчатая диаграмма и диаграмма для скрипки
Гистограммы хорошо показывают распределение одной переменной, но проводить сравнения между гистограммами довольно сложно, если мы хотим сравнить эту переменную между различными группами. Для двух групп одним из возможных решений является построение гистограмм двух групп вплотную друг к другу. Специфическая для предметной области версия этого типа сюжета — 9Пирамида населения 0050 , которая отображает возрастное распределение мужчин и женщин в стране или другом регионе в виде последовательных вертикальных гистограмм.
Однако, если у нас есть три или более групп, параллельное решение не будет работать. Одним из решений может быть создание многогранных гистограмм, отображающих по одной для каждой группы в строке или столбце. Другой альтернативой является использование другого типа сюжета, например, коробчатого или скрипичного сюжета.

 ee.ryerson.ca:8080/~elf/abacus/)
ee.ryerson.ca:8080/~elf/abacus/) htm).
htm).

 Обязательно сдавайте верхний ряд слева направо. Затем нанесите второй ряд под ним слева направо. И так далее, каждый последующий ряд кладется под предыдущий.
Обязательно сдавайте верхний ряд слева направо. Затем нанесите второй ряд под ним слева направо. И так далее, каждый последующий ряд кладется под предыдущий. 0004 это то же самое).
0004 это то же самое).