Tg 2pi: Tg(2pi-x)= -корень из 3 — ответ на Uchi.ru

Здравствуйте, нужно помочь решить: arcctg(tg 2pi/5)

Лучший ответ по мнению автора

27. 03.16 Лучший ответ по мнению автора

Другие ответы

arcctg(tg 2pi/5)=pi/2-arctg(tg 2pi/5)=pi/2-2pi/5=pi/10 27. 03.16

Михаил Александров Читать ответы

Андрей Андреевич Читать ответы

Eleonora Gabrielyan Читать ответы

Посмотреть всех экспертов из раздела Учеба и наука

Похожие вопросы

Маша сложила нить пополам, получившуюся двойную нить снова сложила пополам, а затем еще раз пополам. После этого она разрезала в некотором месте

Строки прямоугольного поля 2015×5000 пронумерованы от 1 до 2015 снизу вверх, а столбцы пронумерованы от 1 до 5000 слева направо. Змейка

Предположив, что корона царя Гиерона в воздухе весит 20н, а в воде 18,75 н, вычислите плотность вещества короны. Полагая, что к золоту было подмешано только серебро, определите, сколько в короне было

Решено

Помогите, пожалуйста!!! Очень важно!!! 1)В коробке вперемешку лежат чайные пакетики с черным и зеленым чаем, одинаковые на вид, причем пакетиков с черным чаем в 9 раз больше, чем с зеленым. Найдите

Решено

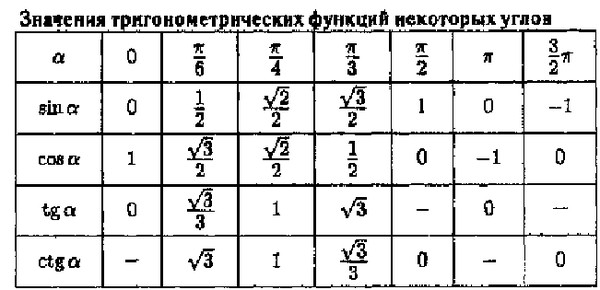
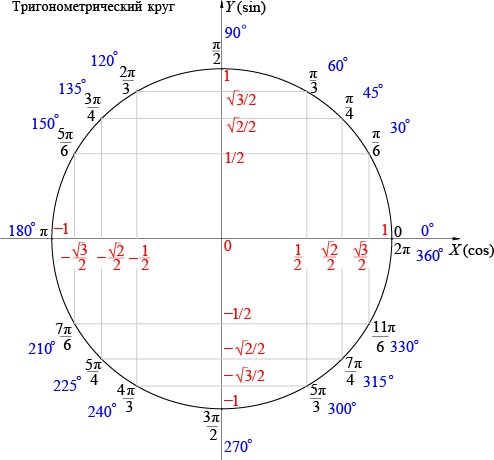
арктангенс 4/3 в градусах

Пользуйтесь нашим приложением

Методы решения тригонометрических уравнений — презентация онлайн

1. Методы решения тригонометрических уравнений

МБОУ СОШ №5 – «Школа здоровья и развития» г.  Радужный
Методы решения
тригонометрических уравнений
Учитель математики: Семёнова Елена Юрьевна

2. Содержание

Метод замены переменной 
Метод разложения на множители
Однородные тригонометрические уравнения
С помощью тригонометрических формул:
−Формул сложения
−Формул приведения
−Формул двойного аргумента

3. Метод замены переменной

С  помощью  замены  t  =  sinx  или  t  =  cosx,  где  t  ∈  [−1;1] 
решение  исходного  уравнения  сводится  к  решению 
квадратного или другого алгебраического уравнения.
См. примеры 1 – 3 
Иногда  используют  универсальную  тригонометрическую 
подстановку:  t = tg x
2
α
1 tg
1 t2
2
cos α
2
1
t
2 α
1 tg
2
2
sin α
α
2tg
2
1 tg 2
α
2
2t
1 t2

4. Пример 1

2 sin 2 x 5 sin x 2 0
Пусть sin x t , где t 1; 1 , тогда
2t 2 5t 2 0
t1 2, не удовлетвор яет условию t 1; 1
t 2 1 ;
2
Вернемся к исходной переменной
1
sin x
2
1
n
x 1 arcsin π n , n Z
2
n π
x 1
πn, n Z
6
n π
Ответ : 1
πn, n Z.
6

5. Пример 2

cos 2 x sin 2 x cos x 0
Поскольку sin 2 x 1 cos 2 x , то
cos 2 x 1 соs 2 x cos x 0
2cos 2 x cos x 1 0
Пусть соsx t , где t 1; 1 , тогда
2t 2 t 1 0
t1 1,
t 2 1 ;
2
Вернемся к исходной переменной :
x 2π k , k Z
соsx 1,
x 2π k , k Z
1
1
x arccos 2π n , n Z
cos x ;
x 2π 2π n , n Z
2
3
2
Ответ : 2π k , k Z ;
2π
2π n , n Z .
3

6. Пример 3

tg
x
x
3ctg 4
2
2
Пример 3
Вернемся к исходной переменной
x
x
tg
1
,
x
1
2
2 arctg1 π n , n Z
Поскольку ctg
, то
2 tg x
tg x 3;
x arctg 3 π k , k Z
2
x
3
2
2
tg
4
2 tg x
x
arctg1 π n , n Z
2
x
2
Пусть tg t , где t 0, тогда
2
x arctg 3 π k , k Z
2
3
t 4
t
t
x π
πn, n Z
2
2 4
t 4t 3 0
x 2arctg 3 π k , k Z
t1 1
t 3
π
2
x
2π n , n Z
2
x 2arctg 3 2π k , k Z
π
Ответ :
2π n ; 2arctg 3 2π k ; n , k Z .
2

7. Метод разложения на множители

Суть  этого  метода  заключается  в  том,  что 
произведение  нескольких  множителей  равно  нулю, 
если  хотя  бы  один  из  них  равен  нулю,  а  другие  при 
этом не теряют смысл:
f(x) ∙ g(x) ∙ h(x) ∙ … = 0    ⟺   f(x) = 0  или  g(x) = 0  или  h(x) = 0 
 
и  т.д. при условии существования каждого из сомножителей
См. примеры 4 – 5 

8. Пример 4

1
2
sin x cos x 0
3
5
1
sin x 3 0,
cos x 2 0;
5
x
x
1
sin
x
,
3
cos x 2 ;
5
1
1
n
n
x 1 arcsin π n , n Z
1 arcsin π n , n Z
3
3
2
x π arccos 2 2π k , k Z
arccos 2π k , k Z
5
5
Ответ : 1 arcsin
n
1
2
π n ; π arccos 2π k ; n , k Z .
3
5

9. Пример 5

2 sin x cos 5x cos 5x 0
cos 5x 2 sin x 1 0
2 sin x 1 0,
cos 5x 0;
1
sin
x
,
2
cos 5x 0;
1
n
x
1
arcsin
πn, n Z
2
5x π π k , k Z
2
n π
x
1
πn, n Z
6
x π π k , k Z
10
5
π πk
n π
Ответ : 1
πn, n Z ;
, k Z.
6
10
5

10. Однородные тригонометрические уравнения

Уравнение вида a sin x + b cos x = 0 называют 
однородным тригонометрическим уравнением 
первой степени.
a sin x + b cos x = 0  
a sin x    b cos x         0  
+ cos x = cos x
cos x
    
a tg x + b = 0  
b
tg x = –   
a
: cos x
Замечание. 
Деление на cos x допустимо, поскольку решения 
уравнения cos x = 0 не являются решениями 
уравнения a sin x + b cos x = 0.

11. Однородные тригонометрические уравнения

Уравнение вида a sin2x + b sin x cos x + c cos2x = 0 
называют однородным тригонометрическим 
уравнением второй степени.
: cos2x
a sin2x + b sin x cos x + c cos2x = 0
a sin2x      b sin x cos x      c cos2x         0
+
+
=
2
cos2x
cos x
cos2x
cos2x
a tg2x + b tg x + c = 0 
 
Далее, вводим новую  переменную tg x  = t и 
решаем 
методом замены переменной.
Замечание.  Если в данном уравнении а = 0 или с = 0 
то, уравнение решается методом разложения 
на множители.

12. Пример 6

2 sin x 3 cos x 0
: cos x
2 sin x 3 cos x
0
cos x
cos x
cos x
2tgx 3 0
3
tgx
2
3
x arctg π n , n Z
2
Ответ : arctg
3
πn, n Z .
2
Пример 7
: cos 2x
sin 2x cos 2x 0
sin 2x cos 2x
0
cos 2x cos 2x cos 2x
tg 2x 1 0
tg 2x 1
π
2x π n , n Z
4
π πn
x
, n Z
8
2
π πn
Ответ :
, n Z.
8
2

13. Пример 8

sin 2 x 3 sin x cos x 2cos 2 x 0
sin 2 x 3 sin x cos x 2cos 2 x
0
2
2
2
cos x
cos x
cos x
: cos 2 x
tg 2 x 3tgx 2 0
Пусть tgx t , тогда
t 2 3t 2 0
t1 1
t 2
2
Вернемся к исходной переменной :
π
tgx 1,
x πn, n Z
4
tgx 2;
x arctg 2 π k , k Z
Ответ :
π
π n ; arctg 2 π k ; n ,k Z .
4

14. Пример 9

3 sin x cos x cos 2 x 0
cos x 3 sin x cos x 0
3 sin x cos x 0,
cos x 0;
: cos x
1
tgx
,
3
π
x
πn, n Z ;
2
1
π
arctg
πk, k Z ,
x πk, k Z ,
3
6
π
π
x πn, n Z .
πn, n Z ;
2
2
3tgx 1 0,
x π π n , n Z ;
2
x
x
Ответ :
π
πk ;
6
π
π n ; n ,k Z .
2

15. Пример 10

sin 3 x sin 2 x cos x 3 sin x cos 2 x 3 cos 3 x 0
: cos 3 x
sin 3 x sin 2 x cos x 3 sin x cos 2 x 3 cos 3 x
0
3
3
3
3
cos x
cos x
cos x
cos x
tg 3 x tg 2 x 3tgx 3 0
tg 2 x tgx 1 3 tgx 1 0
tg
2
x 3 tgx 1 0
tg x 3 0,
tgx 1 0;
2
tg x 3,
tgx 1;
2
x arctg 3 π k , k Z ,
x π π n , n Z ;
4
Ответ :
tgx 3 ,
x π π n , n Z ;
4
π
x
πk, k Z ,
3
x π π n , n Z .
4
π
π
πn ; πk ; n, k Z .
4
3

16. Пример 11

3 sin 2 3x 2 3 sin 3x cos 3x 5 cos 2 3x 2
cos 2 3x sin 2 3x
3 sin 2 3x 2 3 sin 3x cos 3x 5 cos 2 3x 2 cos 2 3x sin 2 3x
3 sin 2 3x 2 3 sin 3x cos 3x 5 cos 2 3x 2cos 2 3x 2 sin 2 3x 0
sin 2 3x 2 3 sin 3x cos 3x 3 cos 2 3x 0
: cos 2 3x
sin 2 3x 2 3 sin 3x cos 3x 3 cos 2 3x
0
2
2
2
cos 3x
cos 3x
cos 3x
tg 2 3x 2 3tg 3x 3 0
Вернемся к исходной переменной
Пусть tg 3x t , тогда
tg 3x 3
3x arctg 3 π n , n Z
t 2 2 3t 3 0
3
t 3 0
π
πn, n Z
3
π πn
x
,n Z
9
3
t 3
Ответ :
t 2 3t
2
t 3
2
0
2
0
3x
π πn
, n Z.
9
3

17. С помощью тригонометрических формул

1. Формулы сложения:
sin (x + y) = sinx cosy + cosx siny
sin (x − y) = sinx cosy + cosx siny
cos (x + y) = cosx cosy − sinx siny
cos (x − y) = cosx cosy + sinx siny
tg (x + y) =
tg (x − y) =
tgx + tgy
1 − tgx tgy
tgx − tgy
1 + tgx tgy
сtgx  сtgy − 1 
сtg (x + y) =
сtgу + с tgх
сtgx  сtgy + 1 
сtg (x − y) =
сtgу − с tgх

18. Пример 12

3 cos x sin x 1
:2
3
1
1
cos x sin x
2
2
2
3
π 1
π
Заметим , что
cos ,
sin , тогда
2
6 2
6
π
π
1
cos cos x sin sin x
6
6
2
π
1
cos x
6
2
π
1
x arccos 2π n , n Z
6
2
π π
x 2π n , n Z
3 6
π π
Ответ : 2π n , n Z .
3 6

19. Пример 13

π
π
sin x cos x 3
3
6
π
π
π
π
π
π
sin x cos x sin cos x cos sin x cos cos x sin sin x
3
3
6
6
3
6
3
1
3
1
cos x sin x
cos x sin x 3 cos x
2
2
2
2
3 cos x 3
cos x 1
x 2π n , n Z
Ответ : 2π n , n Z

20.

С помощью тригонометрических формул2. Формулы приведения:
π
sin t cos t
2
sin π t sin t
π
cos t sin t
2
cos π t cos t
3π
sin
t cos t
2
3π
cos
t sin t
2
sin 2π t sin t
cos 2π t cos t
π
tg t ctg t
2
tg π t tg t
π
ctg t tg t
2
ctg π t ctg t
3π
tg
t ctg t
2
tg 2π t tg t
3π
ctg
t tg t
2
ctg 2π t ctg t

21. Лошадиное правило

В  старые  добрые  времена  жил 
рассеянный  математик,  который  при 
поиске  ответа  менять  или  не  менять 
название  функции  (синус  на  косинус), 
смотрел  на  свою  умную  лошадь,  а  она 
кивала  головой  вдоль  той  оси 
координат, 
которой 
принадлежала 
точка, 
соответствующая 
первому 
слагаемому аргумента π/ 2 + α или π  + α.
Если  лошадь  кивала  головой  вдоль  оси 
ОУ,  то  математик  считал,  что  получен 
ответ «да, менять», если вдоль оси ОХ, 
то «нет, не менять».  
 

22. С помощью тригонометрических формул

3. Формулы двойного аргумента:
sin 2x = 2sinx cosx
cos 2x = cos2x – sin2x
2tgx
tg 2x =
1 – tg2x
ctg2x – 1
ctg 2x =
2ctgx
cos 2x = 2cos2x – 1
cos 2x = 1 – 2sin2x

23. Пример 14

sin 4x cos 2x 0
2 sin 2x cos 2x cos 2x 0
cos 2x 2 sin 2x 1 0
cos 2x 0,
2 sin 2x 1 0;
cos 2x 0,
sin 2x 1 ;
2
π
2
x
πn, n Z
2
2x 1 k arcsin 1 π k , k Z
2
Ответ :
π πn
,n Z;
4
2
1 k
π πn
x
,n Z
4
2
x 1 k π π k , k Z
12
2
π πk
, k Z.
12
2

24. С помощью тригонометрических формул

4. Формулы понижения степени:
sin 2 α
1
1 cos 2α
2
1
cos α 1 cos 2α
2
2
sin α cos α
1
sin 2α
2
sin α cos α 2 1 sin 2α
5. Формулы половинного угла:
α
1 cos α
sin
2
2
α
sin α
1 cos α
tg
2 1 cos α
sin α
α
1 cos α
2
2
α
sin α
1 cos α
ctg
2 1 cos α
sin α
cos

25.

С помощью тригонометрических формул6. Формулы суммы и разности:
cos α cos β 2cos
α β
α β
cos
2
2
cos α cos β 2 sin
α β
β α
sin
2
2
sin α sin β 2 sin
α β
α β
cos
2
2
α β
α β
sin α sin β 2 sin
cos
2
2
sin( α β )
tg α tg β
cos α cos β
sin( α β )
tg α tg β
cos α cos β
sin( α β )
ctg α ctg β
sin α sin β
ctg α ctg β
sin( β α )
sin α sin β

26. С помощью тригонометрических формул

7. Формулы произведения:
1
cos α cos β cos α β cos α β
2
1
sin α sin β cos α β cos α β
2
1
sin α cos β sin α β sin α β
2

27. Мнемоническое правило “Тригонометрия на ладони”

Очень часто требуется знать 
наизусть значения cos, sin, tg, ctg 
для углов 0°, 30°, 45°, 60°, 90°. 
Но если вдруг какое­либо значение 
забудется, то можно 
воспользоваться правилом руки.
Правило: Если провести линии 
через мизинец и большой палец,
то они пересекутся в точке, 
называемой “лунный бугор”.  
Образуется угол 90°. Линия мизинца образует угол 0°. 
Проведя  лучи  из  “лунного  бугра”  через  безымянный,  средний, 
указательный пальцы, получаем углы соответственно 30°, 45°, 60°. 
Подставляя  вместо  n:  0,  1,  2,  3,  4,  получаем  значения  sin,  для 
углов 0°, 30°, 45°, 60°, 90°.
Для cos отсчет происходит в обратном порядке. 

28. Не закончено!

Тангенте 2π/3 радиано(ов) | tg(2π/3)

Расчет прямого действия

Цифра гм доблесть. Пример: 60, -30, пи/3, 3π/2 и т. д.

Английский: Использование калькулятора Чтобы использовать этот калькулятор, просто введите значение угла, затем нажмите «Рассчитать». Вы можете выбрать радианы (rad) или градусы (°) в качестве единицы измерения угла. Единицей измерения по умолчанию является градус (°) Примеры допустимых входных значений 30 → sin(30°) = 0,5 пи → грех(пи рад ) = 0 3pi/4 → sin(3pi/4) = 0,707 . .. (обратите внимание на звездочку как символ умножения) 1/(2pi) → sin(1/(2pi) рад ) = 0,158 … (обратите внимание на скобки в знаменателе) 1/2pi → sin(1/2pi рад ) = sin((1/2) x pi рад ) = 1 ровно Примечание: этот калькулятор принимает числа, дроби, ‘пи’, ‘π’, ‘+’, ‘-‘, ‘*’, ‘/’, ‘(‘, ‘)’ и некоторые (не все) комбинации их в качестве входных данных. Используйте его с осторожностью!

Выбор в один конец:

граус (°) радиан (рад)

Репоста:

Use nossa calculadora de tg(x) para calcular o valor da tangente de 2π/3 radiano(s) — tg(2pi/3 rad) — ou de qualquer outro ângulo em graus ou em radianos.

Tabela de valores de funções trigonométricas para angulos mais usados ​​

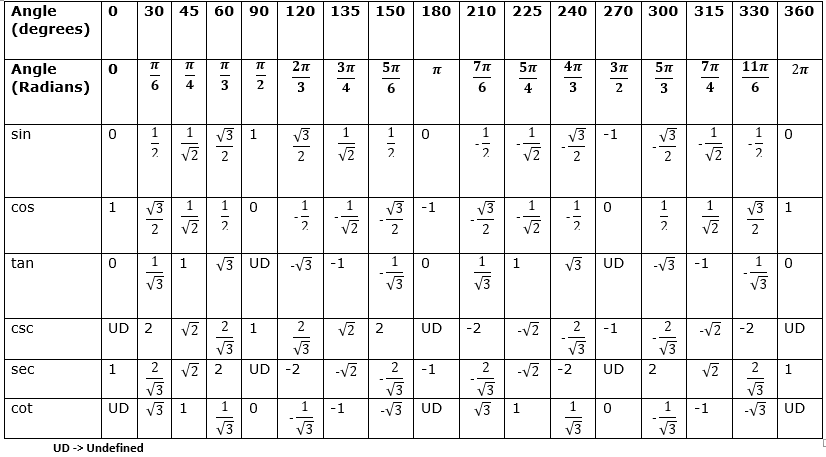
х°	x рад	сен(х)	кос(х)	тг(х)	КСК(х)	сек(х)	детская кроватка(x)
0°	0	0	1	0	0	1	0
30°	№/6	1/2	√3/2	√3/3	2	2√3/3	√3
45°	№/4	√2/2	√2/2	1	√2	√2	1
60°	№/3	√3/2	1/2	√3	2√3/3	2	√3/3
90°	№/2	1	0	(*)	1	0	0
120°	2π/3	√3/2	-1/2	-√3	2√3/3	-2	-√3/3
135°	3π/4	√2/2	-√2/2	-1	√2	-√2	-1
150°	5π/6	1/2	-√3/2	-√3/3	2	-2√3/3	-√3
180°	№	0	-1	0	0	-1	(*)
210°	7π/6	-1/2	-√3/2	√3/3	-2	-2√3/3	-√3
225°	5π/4	-√2/2	-√2/2	1	-√2	-√2	1
240°	4π/3	-√3/2	-1/2	-√3	-2√3/3	-2	-√3/3
270°	3π/2	-1	0	(*)	-1	0	(*)
300°	5π/3	-√3/2	1/2	-√3	-2√3/3	2	-√3/3
315°	7π/4	-√2/2	√2/2	-1	-√2	√2	-1
330°	11π/6	-1/2	√3/2	-√3/3	-2	2√3/3	-√3

(*) siginifica um valor não definido para função.

Ссылки:

• Таблицы триггеров – некоторые точные значения и числовая таблица
• Точные значения тригонометрической функции
• Бесконечность или не определено?

Aviso de responsabilidade:

Nós nos esforçamos ao maximo para assegurar que nossas calculadoras e conversores sejam tão precisos Quanto possível, porém não podemos garantir isso. Антес-де-usar qualquer uma де nossas ferramentas, qualquer informação ou didos, por пользу verifique sua exatidão эм outras fontes.

2PI INTERACTIVE PRIVATE LIMITED — Компания, директора и контактная информация

Главная › 2pi Interactive Private Limited

Дата: 25 июня 2022 г.

Отследить эту компанию

Дата: 25 июня 2022 г.
Размер компании: Войдите для просмотра

Отслеживайте эту компанию

5

2pi Interactive Private Limited является частной компанией, зарегистрированной 29 августа 2011 года. Она классифицируется как негосударственная компания и зарегистрирована в Реестре компаний Хайдарабада. Его разрешенный акционерный капитал составляет рупий. 10 000 000, а его оплаченный капитал составляет рупий. 2 415 000. Он занимается публикацией программного обеспечения, консультированием и поставкой [Издание программного обеспечения включает производство, поставку и документирование готового (неиндивидуализированного) программного обеспечения, программного обеспечения для операционных систем, программного обеспечения для бизнеса и других приложений, программного обеспечения для компьютерных игр для всех платформ. Консультации включают в себя предоставление наилучшего решения в виде заказного программного обеспечения после анализа потребностей и проблем пользователя. Программное обеспечение на заказ также включает программное обеспечение, изготовленное на заказ на основе заказов конкретных пользователей. Также сюда входит написание программного обеспечения любого рода в соответствии с указаниями пользователей; сопровождение программного обеспечения, дизайн веб-страниц].

Ежегодное общее собрание (ГОСА) 2pi Interactive Private Limited в последний раз проводилось 30 ноября 2021 года, и, согласно отчетам Министерства корпоративных дел (MCA), его балансовый отчет был в последний раз подан 31 марта 2021 года.

Директора 2pi Interactive Private Limited Ограниченными являются Venkatarama Reddy Burri, Siddhartha Burri и .

Корпоративный идентификационный номер 2pi Interactive Private Limited — (CIN) U72200TG2011PTC076217, регистрационный номер — 76217. Адрес электронной почты — [email protected], а зарегистрированный адрес — H.No.8-2-624/A/B. /3/1, дорога № 11 Banjarahills Hyderabad TG 500034 IN .

Текущий статус 2pi Interactive Private Limited — Активен.

Информация о компании

CIN	U72200TG2011PTC076217
Название компании	2PI INTERACTIVE PRIVATE LIMITED
Статус компании	Активный
РП	RoC-Хайдарабад
Регистрационный номер	76217
Категория компании	Компания с ограниченной ответственностью
Подкатегория компании	Негосударственная компания
Класс компании	Частный
Дата регистрации	29 августа 2011 г.
Возраст компании	11 лет, 3 месяца, 17 дней
Деятельность	Издание программного обеспечения, консультирование и поставка [Издание программного обеспечения включает производство, поставку и документирование готового (неадаптированного) программного обеспечения, программного обеспечения для операционных систем, программного обеспечения для бизнеса и других приложений, программного обеспечения для компьютерных игр для всех платформ. Консультации включают в себя предоставление наилучшего решения в виде заказного программного обеспечения после анализа потребностей и проблем пользователя. Программное обеспечение на заказ также включает программное обеспечение, изготовленное на заказ на основе заказов конкретных пользователей. Также сюда входит написание программного обеспечения любого рода в соответствии с указаниями пользователей; сопровождение программного обеспечения, дизайн веб-страниц]. Нажмите здесь, чтобы увидеть другие компании, занимающиеся тем же видом деятельности.
Количество членов	—

Предыдущие имена

Войдите для просмотра предыдущих имен

Предыдущие CINS

Войдите для просмотра предыдущих номеров

Акционерный капитал и количество сотрудников

Уставный капитал	₹ 10 000 000
Оплаченный капитал	₹ 2 415 000
Количество сотрудников	Войдите для просмотра

Сведения о листинге и ежегодном соблюдении требований

Статус листинга	Нет в списке
Дата последнего годового общего собрания	30 ноября 2021 г.
Дата последнего баланса	31 марта 2021 г.

Финансовый отчет

Бухгалтерский баланс
Оплаченный капитал
Резервы и излишки
Долгосрочные займы
Краткосрочные займы
Торговая кредиторская задолженность
Текущие инвестиции
Запасы
Торговая дебиторская задолженность
Денежные средства и остатки на счетах в банках

Прибыли и убытки
Общий доход (оборот)
Всего расходов
Расходы на вознаграждения работникам
Финансовые расходы
Амортизация
Прибыль до налогообложения
Прибыль после налогообложения

Разблокируйте полный отчет с историческими финансовыми данными и просмотрите все 38 документов всего за 499 фунтов стерлингов

Добавить в корзину

Графический отчет, содержащий исторические финансовые показатели. Щелкните здесь, чтобы просмотреть финансовый отчет Infosys Ltd.

Пожизненный доступ ко всем документам

Загрузить все 38 документов одним щелчком мыши

Просмотр хронологии событий — Список всех событий компании с момента основания. Щелкните здесь, чтобы просмотреть хронологию событий Infosys Ltd.

Контактная информация

Идентификатор электронной почты: [email protected]

Веб-сайт: »> Нажмите здесь, чтобы добавить. /B/3/1, Road No.11 Banjarahills Hyderabad TG 500034 IN

Сведения о директоре

DIN	Имя директора	Обозначение	Дата назначения
03571639	ВЕНКАТАРАМА РЕДДИ БУРРИ	Директор	29 августа 2011 г.	Посмотреть другие директораты
Другие компании, связанные с Предыдущие компании, связанные с Компания Обозначение Дата назначения Дата прекращения действия Войдите, чтобы просмотреть эту информацию.
03571642	СИДДХАРТА БУРРИ	Директор	29 августа 2011 г.	Посмотреть другие директораты
Другие компании, связанные с Предыдущие компании, связанные с Компания Обозначение Дата назначения Дата прекращения действия Войдите, чтобы просмотреть эту информацию.

Данные бывшего директора

DIN	Имя директора	Дата назначения	Дата прекращения действия
Войдите, чтобы просмотреть прошлых директоров.

Компании с похожим адресом

CIN	Имя	Адрес
U01119TG1995PTC020305	GENESIS CROP SCIENCES (INDIA) PRIVATE LIMITED	R.No.1, F.No.C3/B, H.No.8-2-350/6/2, 3-й этаж, PNo.16 Vamshiram Jyothi Square, Sy.No.360, Road No.3, Банджарахиллс Хайдарабад TG 500034 IN
U45208TG2019PTC137253	РАМАНИЯ ИНФРА ПРОДЖЕКТС ПРИВЕЙТ ЛИМИТЕД	H NO: 8 — 2 — 624/A/B/3/1, ROAD NO — 11, BANJARA HILLS, HYDERABAD Hyderabad TG 500034 IN
U72900TG2002PTC062694	SKYWORKS SOLUTIONS INDIA PRIVATE LIMITED	Участок № 8-2-277/A/3/1–3/3, 3A и 3B, II этаж, улица № 2, дорога № 2, Banjara Hills Hyderabad Hyderabad TG 500034 IN
U01122TG2004PTC043767	SRI SATHYA AGRI BIO-TECH PRIVATE LIMITED	F. No.C3/B, H.No.8-2-350/6/2, 3-й этаж, Vamshiramjyoti Square, Plot No.16, Sy.No.360, Road No.3, Banjarahills HYDERABAD Hyderabad TG 500034 IN
U85191TG2010PTC069349	АМБРОЗИЯ ВЕЛНЕС ПРИВАТ ЛИМИТЕД	М.№8-2-293/174/4/Б/Б,П.№4,3,3/А,1/А,Дорога №14 Сы №129/82, Колония Б.Н.Редди, Банджара Хиллз, Хайдарабад Хайдарабад TG 500034 IN
U33110TG2011PTC075308	АКШАЯ АГРИБИОМЕД ПРИВЕЙТ ЛИМИТЕД	УЧАСТОК № 682 (10A), H. № 8-2-268/A/4/B/1, СРИНИКЕТАНСКАЯ КОЛОНИЯ, дорога № 3, БАНДЖАРАХИЛЛС ХАЙДАРАБАД TG 500034 IN
U45209TG2013PTC0		SAICHARAN REALTORS PRIVATE LIMITED	# Костюм № 1, H № 8-2-693/2/1A/1B/S1, обследование первого этажа № 129/77, дорога № 12, Банджара Хиллз, Хайдарабад Хайдарабад TG 500034 IN
U22130TG2014PTC093907	PIXEL DIGITAL PRINT SOLUTIONS PRIVATE LIMITED	Дом № 8-2-624/A/B/3/1, участок A Road No. 11, Banjara Hills Hyderabad Hyderabad TG 500034 IN
U72900TG2022PTC167799	БСА ТЕХНОЛОДЖИ ПРИВЕЙТ ЛИМИТЕД	8-2-624/A/B/2, 8-2-624/B/2/1, First Floor Road No.11, Banjara Hills Hyderabad Hyderabad TG 500034 IN

Просмотреть все 8 392 компаний с похожими адресами

Детали судебного преследования

S.No.	Субъекты-дефолты	Название суда	Прокуратура	Дата заказа	Статус
Преследований не обнаружено

Сведения о платежах/займах

Идентификатор платежа	Дата создания	Дата модификации	Дата закрытия	Заложенные активы	Сумма	Зарядный держатель
Платежи не найдены

Сведения об учреждениях

Название учреждения	Город	Пин-код	Адрес
Предприятия не найдены

*Отраслевая классификация получена из Национальной отраслевой классификации. Если компания изменила направление деятельности без уведомления Регистратора или является диверсифицированным бизнесом, классификация может быть другой. Мы не даем никаких гарантий относительно точности промышленной классификации.

Обновление информации

Мы ежедневно добавляем и обновляем информацию о сотнях тысяч компаний и периодически добавляем компании в очередь на обновление. Вы можете попросить добавить компанию в начало очереди на обновление, особенно полезно, если адрес, директора или другая важная информация изменились. Просто нажмите кнопку «Обновить информацию» ниже, чтобы начать процесс.

Смена директоров
Подача финансовой отчетности
Регистрация новых кредитов
Регистрация долговых обязательств
Преобразование компании в LLP
Выплата кредитов
Изменение адреса
Форма заявления на изменение названия
Заявление о преобразовании публичной компании в частную
Уведомление о постановление суда или совета по правовым вопросам компаний
Преобразование публичной компании в частную или частной компании в публичную компанию
Выделение капитала (ESOP, привлечение средств и т.