Типовые задачи по теории графов: Математическое Бюро. Страница 404

Содержание

Задачи, которые можно решить с помощью графов

Типичные задачи Теории Графов

Теория графов содержит множество алгоритмов, которые были созданы для решения конкретных задач. Типичная область их применения ясна из названия. Рассмотрим основные из них.

Поиск кратчайшего пути

Одной из таких задач является поиск кратчайшего пути.

Например алгоритм Дейкстры находит кратчайший путь из одной вершины до другой, если он существует. Стоит отметить, что этот алгоритм не работает с графами, где есть циклы с отрицательным весом дуг.
Алгоритм Беллмана — Форда может искать кратчайший путь в графах и с отрицательным весом дуг, но он медленнее, чем алгоритм Дейкстры.
Например, Алгоритм поиска A* часто используется в компьютерных играх. Так как в алгоритме А* используется эвристическое правило, он не всегда найдёт самый короткий пусть, но найдёт близкий к самому короткому. Алгоритм поиска A* работает быстрее алгоритма Дейкстры.

Таким образом, алгоритмов поиска кратчайшего пути много и каждый из них обладает своей особенностью.

Сервис Graphonline использует алгоритмы Дейкстры и с его помощью можно найти кратчайший путь до вершины и минимальное расстояние до всех остальных вершин.

Поиск максимального потока

Алгоритмы поиска максимального потока находят максимальный поток из источника в сток. С помощью этого алгоритма можно решить задачи максимальной пропускной способности трубопровода или дорожной сети или компьютерной сети.

Сервис Graphonline использует алгоритм Проталкивания Предпотока. Например, если у вас есть граф, где вершины это — города, а вес дуг задаёт пропускную способность дорог между городами (например автомобилей в час), то можно легко посчитать сколько машин может доехать из города А в город N за час.

Поиск минимального остовного дерева

Алгоритм ищет дерево минимального веса в графе, которое бы соединяло все вершины. Этот алгоритм можно применять для дорожной или компьютерной сети, где вы хотите оптимизировать стоимость.

Предположим, имеются 7 компьютеров и разные способы проложить локальную сеть.

Используя алгоритм поиска минимального остовного дерева, можно легко посчитать, где стоит проложить кабель, чтобы понадобилось минимальное количество кабеля.

Прикладные задачи, решаемые с помощью Теории Графов

Распределение рабочих

В распоряжении имеются N работников и M различных типов работ. Разные работники могут выполнять разные типы работ. Необходимо распределить работников, чтобы максимальное количество из их было занято.

Для решения строим граф, где соединяем работников с теми работами, которые они могут выполнять. Создаём псевдоисток, который соединяется со всеми работниками и сток, с которым соединены все типы работ. После этого ищем максимальный поток от истока к стоку.

Теория 6 рукопожатий

Существует социологическая теория, которая гласит, что два любых человека на Земле разделены не более чем пятью уровнями общих знакомых. Таким образом можно говорить о шести уровнях связей. В графе вершинами является человек, а дугой — факт его знакомства с другим человеком. После этого необходимо найти кратчайший путь от одного человека до другого. Длина пути покажет через сколько рукопожатий знакомы эти два человека.

Самый быстрый способ

Предположим, что что-то можно сделать разными способами. Например, добраться от дома до работы мы можем разными способами: поехать на машине, пойти пешком или воспользоваться самокатом. Все эти действия можно представить в виде графа, где дугами будет являться продолжительность определённых действий. Для поиска самого быстрого способа необходимо найти кратчайший путь между начальной и конечной вершиной.

Задачи, приводящие к теории графов. Основные понятия и определения. (Лекция 13)

1. Задачи, приводящие к теории графов. Основные понятия и определения.

2. Историческая записка

• Леонард Эйлер (1707-1783)- швейцарец по
происхождению. Приехал в Санкт-Петербург в
1727 году. Не было такой области математики
XVIII века, в которой Эйлер не достиг бы
заметных результатов. Например, решая
головоломки и развлекательные задачи, Эйлер
заложил основы теории графов, ныне широко
используемой во многих приложениях
математики.
• Напряженная работа повлияла на зрение ученого,
в 1766 году он ослеп, но и после этого
продолжал работу, диктуя ученикам свои статьи.

• Эйлер умер в 76 лет и был похоронен на
Смоленском кладбище Санкт-Петербурга. В 1957
году его прах был перенесен в АлександроНевскую лавру.

3. Приложения теории графов

— Задача о кратчайшей цепи
составление расписания движения транспортных средств,
размещение пунктов скорой помощи,
размещение телефонных станций.
— Задача о максимальном потоке
анализ пропускной способности коммуникационной сети
организация движения в динамической сети
оптимальный подбор интенсивностей выполнения работ
задача о распределении работ
— Задача об упаковках и покрытиях
оптимизация структуры ПЗУ
размещение диспетчерских пунктов городской транспортной сети
— Раскраска в графах
распределение памяти в ЭВМ
проектирование сетей телевизионного вещания
— Связность графов и сетей
проектирование кратчайшей коммуникационной сети
синтез структурно-надежной сети циркуляционной связи
анализ надежности стохастических сетей связи
— Изоморфизм графов и сетей
структурный синтез линейных избирательных цепей
автоматизация контроля при проектировании БИС
— Изоморфное вхождение и пересечение графов
локализация неисправности с помощью алгоритмов поиска МИПГ
покрытие схемы заданным набором типовых подсхем
— Автоморфизм графов
конструктивное перечисление структурных изомеров для
производных органических соединений
синтез тестов цифровых устройств

4.

Задачи, приводящие к теории графов• Попробуйте нарисовать закрытый конверт одним росчерком, т.е.,
не отрывая карандаша от бумаги и не проводя дважды один и тот
же отрезок.
• А если конверт распечатать?

5. Задача о Кёнигсбергских мостах

Впервые над задачей описанного выше типа задумался Леонард Эйлер после
посещения города Кенигсберга (ныне Калининград).
В городе было семь мостов через реку Прегель.
A
D
B
C
Гостям города предлагали задачу: пройти по всем мостам ровно один раз. Никому
из гостей не удавалось справиться с задачей.
Эйлер отметил на карте города по одной точке на каждом берегу реки и на каждом
острове.
Затем он соединил эти точки в соответствии с расположением мостов. Задача
обхода мостов свелась к задаче изображения одним росчерком следующей
картинки
A
B
C
D

6. Задача о трех домах и трех колодцах

Всегда ли можно изобразить граф на плоскости так, чтобы его ребра не
пересекались? Впервые этот вопрос возник при решении старой
головоломки.

Вот как ее описывает Льюис Кэрролл.
В трех домиках жили три человека, неподалеку находилось три колодца:
один с водой, другой с маслом, а третий с повидлом. Однако хозяева
домиков перессорились и решили провести тропинки от своих домиков к
колодцам так, чтобы эти тропинки не пересекались. Первоначальный
вариант по этой причине их не устраивал.
Основные понятия и определения
Определение 1
V
Под графом будем понимать пару (V , E ) , где
– произвольное
непустое множество, аE – подмножество множества
V ( 2) ( E V ( 2) )
Если множество V конечно, то граф называется конечным,
иначе – бесконечным.
Элементы множества V называются вершинами графа, а
элементы множества E – ребрами графа.
Вершины графа обозначают точками на плоскости, а ребра
графа – кривыми на плоскости, соединяющими
соответствующие точки. Такие рисунки называют графами.
Множество вершин и ребер графа G обозначают V(G) и E(G)
соответственно.
Пример
b
a
g
c
f
e
d
G
V (G ) a, b, c, d , e, f , g , E (G ) (a, b), (a, c), (a, d ), (a, f ), (b, c),
(b, g ), (b, e), (c, e), (d , f ) .

Определение 2
a) Если в графе допускается существование повторяющихся
(кратных) ребер, то граф называется мультиграфом.
a) Если в графе, кроме того, допускается существование петель, т.е.
ребер, соединяющих вершину саму с собой, то граф называется
псевдографом.
Пример
G1
G — мультиграф, G — псевдограф
1
2
G2
Определение 3
Если мощность множества V
порядком графа.
равнаn
, то число
n
называется
Определение 4
Если мощность множества V равна n, а мощность множества E
равна m, то граф называется (n,m) — графом.
Определение 5
Две вершины графа называются смежными, если они соединены
ребром.
Определение 6
Два ребра называются смежными, если они выходят из
одной вершины.
Определение 7
Ребро и вершина называются инцидентными, если данная
вершина является концом данного ребра.
Определение 8
Окружением вершины v в графе G называется множество смежных
с ней вершин графа G.

Обозначают: N (v), N (v) .
G
Вернемся к примеру.
Пример
b
a
g
c
f
e
d
G
N ( a ) ? Смежны ли вершины a и b , a и g ?
Смежны ли ребра ( a , b ) и ( a , d ), ( a , b ) и ( c , e ) ?
Являются ли инцидентны ми вершина f и ребро ( f , d ) ?
Определение 9
Граф называется пустым, если в нем нет ребер.
n
Обозначают:On илиEn – пустой граф порядка
.
Определение 10
Граф называется полным, если любые две его вершины
соединены ребром.
n
Обозначают: K n илиFn – полный граф порядка
.
Определение 11
Два графа G и H называются равными, если
V(G)=V(H) и E(G)=E(H).
Обозначают: G=H.
Пример
. O1
. . O2
K4
K3
Теорема 12
n
Число ребер в полном графе порядка
n(n 1)
равно
.
2

16. Дополнительные графы. Самодополнительные графы

Дополнительные графы.
Самодополнительные графы.
Определение 1
Пусть дан граф
G
G (V , E ) . Дополнением графа
(или допо лнительным графом G
к
) называется граф G
(V , E V ( 2 ) ) ,
Gв
V (G ) V (G ) и любые две несовпадающие вершины смежны
тогда и только то гда, ко гда они не смежныG
в
.

т.е.
Пример
1
2
3
1
4
G
2
3
4
G
Определение 2
Два графа называются изоморфными, если существует биекция
между множествами их вершин, со храняющая отношение смежности.
То есть, две вершины в о дном графе будут смежны тогда и только тогда,
когда их образы (прообразы) при данной биекции смежны в другом графе.
Обозначают: G H -G изоморфен
H .
Пример
b
3
a
2
c
4
1
5
G1
f
d
G2
G1 G2 , так как существует со храняющая отношение смежности биекция
: V (G1 ) V (G2 ) .
(1) b, (2) a, (3) c, (4) f , (5) d .
Определение 3
Граф называется сомодополнительным, если он изоморфен
своему дополнению.
Пример
3
2
2
4
1
5
G
4
5
1
3
G
G G , G -самодополнительный.
Теорема 4
1) G G .
2) G
H G H .
3)Для любого
(n, m) — графаG
G
, граф
является
n(n 1)
m — графом.
n,
2
n
4)Если G – самодополнительный граф порядка
n n 1
то G является n,
— графом.

4
,

теория графов | Проблемы и приложения

мосты Кенигсберга

Смотреть все СМИ

Ключевые люди:: Пол Эрдёш Эндре Семереди Леонард М. Адлеман Авраам Трахтман

Похожие темы:: график задача коммивояжера Схема Гамильтона линейный график теория сетей

Просмотреть весь соответствующий контент →

Резюме

Прочтите краткий обзор этой темы

теория графов , раздел математики, связанный с сетями точек, соединенных линиями. Предмет теории графов зародился в развлекательных математических задачах ( см. числовая игра ), но он превратился в значительную область математических исследований с приложениями в химии, исследовании операций, социальных науках и информатике.

Историю теории графов можно проследить до 1735 года, когда швейцарский математик Леонард Эйлер решил проблему Кенигсбергского моста. Проблема Кенигсбергского моста была старой головоломкой, касающейся возможности найти путь через каждый из семи мостов, пересекающих разветвленную реку, протекающую мимо острова, но без пересечения какого-либо моста дважды. Эйлер утверждал, что такого пути не существует. Его доказательство включало только ссылки на физическое расположение мостов, но по существу он доказал первую теорему теории графов.

Britannica Quiz

Числа и математика

A-B-C, 1-2-3… Если вы считаете, что считать числа — это то же самое, что читать алфавит, проверьте, насколько свободно вы владеете языком математики в этом тесте.

Используемый в теории графов термин график не относится к диаграммам данных, таким как линейные графики или гистограммы. Вместо этого он относится к набору вершин (то есть точек или узлов) и ребер (или линий), которые соединяют вершины. Когда любые две вершины соединены более чем одним ребром, граф называется мультиграфом. Граф без петель и с не более чем одним ребром между любыми двумя вершинами называется простым графом.

Если не указано иное, 9Предполагается, что граф 0027 относится к простому графу. Когда каждая вершина соединена ребром с каждой другой вершиной, граф называется полным графом. При необходимости каждому ребру может быть назначено направление для создания так называемого ориентированного графа или орграфа.

Важным числом, связанным с каждой вершиной, является ее степень, которая определяется как количество ребер, которые входят или выходят из нее. Таким образом, петля вносит 2 в степень своей вершины. Например, все вершины простого графа, показанного на диаграмме, имеют степень 2, тогда как все вершины показанного полного графа имеют степень 3. Знание количества вершин в полном графе характеризует его существенную природу. По этой причине полные графы обычно обозначают K _n , где n относится к числу вершин, а все вершины K _n имеют степень n 91.028 Теорему Эйлера о проблеме Кенигсбергского моста можно было бы переформулировать следующим образом: если существует путь по ребрам мультиграфа, пересекающий каждое ребро один и только один раз, то существует не более двух вершин нечетной степени; кроме того, если путь начинается и заканчивается в одной и той же вершине, то никакие вершины не будут иметь нечетную степень.

)
Другим важным понятием в теории графов является путь, то есть любой маршрут вдоль ребер графа. Путь может следовать по одному ребру непосредственно между двумя вершинами или может следовать по нескольким ребрам через несколько вершин. Если существует путь, соединяющий любые две вершины графа, то этот граф называется связным. Путь, который начинается и заканчивается в одной и той же вершине, не пересекая ни одно ребро более одного раза, называется замкнутым путем. Схема, которая проходит по каждому ребру ровно один раз при посещении каждой вершины, называется эйлеровой схемой, а граф называется эйлеровым графом. Эйлеров граф связен и, кроме того, все его вершины имеют четную степень.

В 1857 году ирландский математик Уильям Роуэн Гамильтон изобрел головоломку (Икосианскую игру), которую позже продал производителю игр за 25 фунтов стерлингов. Загадка заключалась в том, чтобы найти особый тип пути, позже известный как гамильтонов контур, вдоль ребер додекаэдра (платоново тело, состоящее из 12 пятиугольных граней), который начинается и заканчивается в одном и том же углу, проходя через каждый угол ровно один раз. Путешествие коня ( см. числовая игра: задачи на шахматной доске) — еще один пример развлекательной задачи, включающей гамильтонову схему. Гамильтоновы графы было сложнее охарактеризовать, чем эйлеровы графы, поскольку необходимые и достаточные условия существования гамильтоновой цепи в связном графе до сих пор неизвестны.

Оформите подписку Britannica Premium и получите доступ к эксклюзивному контенту. Подпишитесь сейчас
История теории графов и топологии тесно связана, и эти две области имеют много общих проблем и методов. Эйлер сослался на свою работу над проблемой Кенигсбергского моста как на пример geometria situs — «геометрии положения», а развитие топологических идей во второй половине XIX века стало известно как analysis situs — «геометрия положения». анализ положения». В 1750 году Эйлер открыл формулу многогранника V – E + F = 2 отношение количества вершин ( V ), ребер ( E ) и граней ( F ) многогранника (тела, подобного упомянутому выше додекаэдру , грани которого являются многоугольниками). Вершины и ребра многогранника образуют граф на его поверхности, и это понятие привело к рассмотрению графов на других поверхностях, таких как тор (поверхность твердого бублика), и того, как они делят поверхность на дискообразные грани. Формула Эйлера вскоре была обобщена на поверхности как
V – E + F = 2 – 2 g , где g обозначает род или число «дырок от бублика» поверхности ( см. Эйлерова характеристика). Рассмотрев поверхность, разделенную на многоугольники вложенным графом, математики начали изучать способы построения поверхностей, а затем и более общих пространств путем склеивания многоугольников. Это было началом области комбинаторной топологии, которая позже, благодаря работам французского математика Анри Пуанкаре и других, переросла в то, что известно как алгебраическая топология.
Связь между теорией графов и топологией привела к появлению подполя, называемого топологической теорией графов. Важная проблема в этой области касается плоских графов.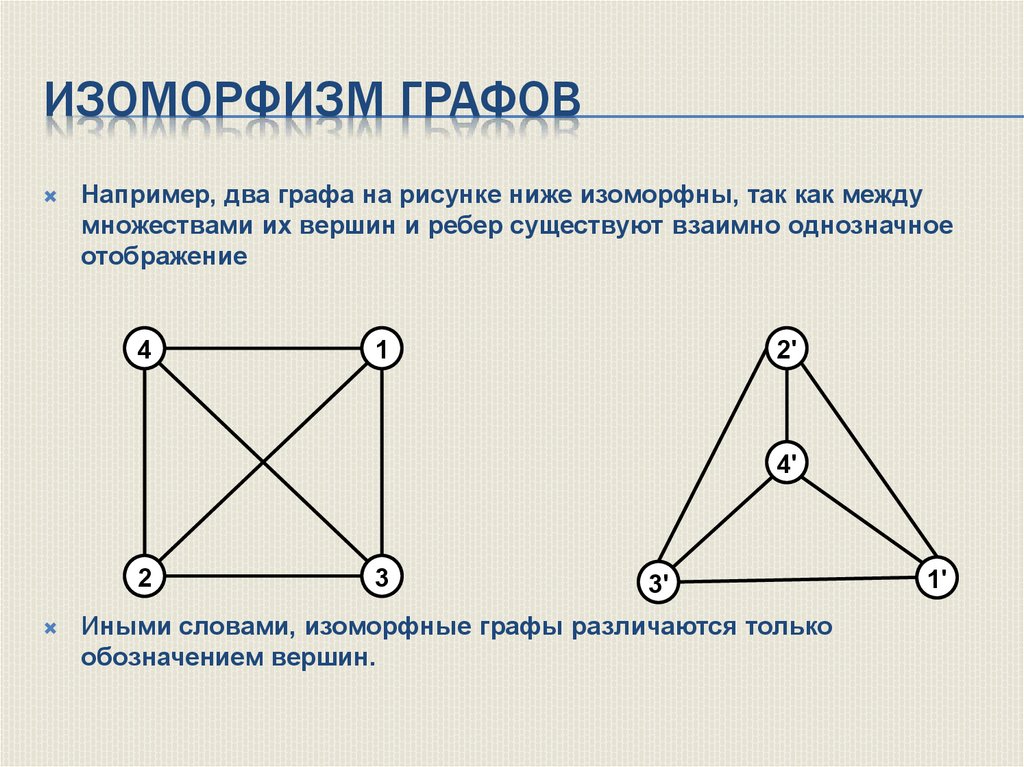 Это графы, которые можно изобразить в виде точечно-линейных диаграмм на плоскости (или, что то же самое, на сфере) без каких-либо пересечений ребер, кроме как в вершинах, где они встречаются. Полные графы с четырьмя или менее вершинами являются планарными, а полные графы с пятью вершинами ( K ₅ ) или более — нет. Непланарные графы нельзя рисовать на плоскости или на поверхности сферы без ребер, пересекающих друг друга между вершинами. Использование диаграмм точек и линий для представления графиков выросло из 19химия 19-го века, где буквенные вершины обозначали отдельные атомы, а соединительные линии обозначали химические связи (со степенью, соответствующей валентности), в которой планарность имела важные химические последствия. Первое использование в этом контексте слова граф приписывается англичанину 19-го века Джеймсу Сильвестру, одному из нескольких математиков, заинтересованных в подсчете особых типов диаграмм, представляющих молекулы.
Другой класс графов — совокупность полных двудольных графов K _{m , n} , которые состоят из простых графов, которые можно разбить на два независимых множества по m и n вершин, так что между вершинами нет ребер внутри каждого множества и каждой вершины. в одном наборе соединен ребром с каждой вершиной в другом наборе. Как и K ₅ , двудольный граф K _3,3 не является планарным, что опровергает сделанное в 1913 году английским рекреационным проблематиком Генри Дьюдени заявление о решении проблемы «газ-вода-электричество». В 1930 польский математик Казимеж Куратовский доказал, что любой непланарный граф должен содержать определенный тип копии K ₅ или K _3,3 . В то время как K ₅ и K _3,3 нельзя вложить в сферу, их можно вложить в тор. Задача вложения графа касается определения поверхностей, в которые может быть вложен граф, и тем самым обобщает проблему планарности. Только в конце 19В 60-х годах задача вложения для полных графов K _n была решена для всех n .
Другой проблемой топологической теории графов является проблема раскраски карты. Эта задача является результатом хорошо известной задачи о четырех цветах карты, в которой спрашивается, можно ли раскрасить страны на каждой карте, используя всего четыре цвета, таким образом, чтобы страны, имеющие общее ребро, имели разные цвета. Первоначально поставленная в 1850-х годах Фрэнсисом Гатри, в то время студентом Университетского колледжа Лондона, эта проблема имеет богатую историю, полную ошибочных попыток ее решения. В эквивалентной теоретико-графовой форме эту проблему можно перевести так: всегда ли вершины планарного графа можно раскрасить, используя всего четыре цвета, таким образом, чтобы вершины, соединенные ребром, имели разные цвета. Результат был окончательно доказан в 1976 с помощью компьютерной проверки почти 2000 специальных конфигураций. Интересно, что соответствующая проблема раскраски, касающаяся количества цветов, необходимых для раскрашивания карт на поверхностях более высокого рода, была полностью решена несколькими годами ранее; например, для карт на торе может потребоваться до семи цветов. Эта работа подтвердила, что формула английского математика Перси Хевуда от 1890 года правильно дает эти числа окраски для всех поверхностей, кроме односторонней поверхности, известной как бутылка Клейна, для которой правильное число окраски было определено в 1990 году. 34.
К числу актуальных интересов теории графов относятся проблемы, связанные с эффективными алгоритмами поиска оптимальных путей (в зависимости от различных критериев) в графах. Двумя хорошо известными примерами являются задача китайского почтальона (кратчайший путь, который проходит через каждое ребро хотя бы один раз), которая была решена в 1960-х годах, и задача коммивояжера (кратчайший путь, который начинается и заканчивается в одной и той же вершине и посещает каждую вершину). edge ровно один раз), который продолжает привлекать внимание многих исследователей из-за его приложений для маршрутизации данных, продуктов и людей. Работа над такими задачами связана с областью линейного программирования, которая была основана в середине 20 века американским математиком Джорджем Данцигом.
Стефан С. Карлсон
()
%PDF-1.4 % 1 0 объект > эндообъект 6 0 объект /Заголовок /Предмет /Автор /Режиссер /Ключевые слова /CreationDate (D:20221005164041-00’00’) /ModDate (D:20130402111717+02’00’) >> эндообъект 2 0 объект > эндообъект 3 0 объект > эндообъект 4 0 объект > эндообъект 5 0 объект > ручей GPL Ghostscript 9.
No related posts.