Локальный экстремум функции. Примеры
Отыскание локальных максимумов и минимумов не обходится без дифференцирования и является необходимым при исследовании функции и построении ее графика.
Точка называется точкой локального максимума (или минимума) функции , сли существует такой окрестность этой точки, принадлежащий области определения функции, и для всех из этого окрестности выполняется неравенство (или ).
Точки максимума и минимума называются точками экстремума функции, а значения функции в экстремальных точках — ее экстремальными значениями.
НЕОБХОДИМОЕ УСЛОВИЕ ЛОКАЛЬНОГО ЭКСТРЕМУМА:
Если функция имеет в точке локальный экстремум, то либо производная равна нулю , либо не существует.
Точки которые удовлетворяют выписанным выше требованиям называют критическими точками.
Однако в каждой критической точке функция имеет экстремум. Ответ на вопрос: будет критическая точка точкой экстремума дает следующая теорема.
ДОСТАТОЧНОЕ УСЛОВИЕ СУЩЕСТВОВАНИЯ ЭКСТРЕМУМА ФУНКЦИИ
Теорема І. Пусть функция непрерывна в некотором интервале, содержащем критическую точку и дифференцированная во всех точках этого интервала (за исключением, возможно, самой точки ).
Пусть функция непрерывна в некотором интервале, содержащем критическую точку и дифференцированная во всех точках этого интервала (за исключением, возможно, самой точки ).
Тогда для точки функция имеет максимум, если для аргументов выполняется условие, что производная больше нуля , а для условие — производная меньше нуля .
Если же для производная меньше нуля , а для больше нуля , то для точки функция имеет минимум.
Теорема ІІ. Пусть функция дважды дифференцируема в окрестности точки и производная равна нулю . Тогда в точке функция имеет локальный максимум, если вторая производная меньше нуля и локальный минимум, если наоборот .
Если же вторая производная равна нулю , то точка может и не быть точкой экстремума.
При исследовании функций на экстремумы используют обе теоремы. Первая на практике проще, поскольку не требует нахождения второй производной.
ПРАВИЛА НАХОЖДЕНИЯ ЕКСТРЕМУМОВ (МАКСИМУМОВ И МИНИМУМОВ) С ПОМОЩЬЮ ПЕРВОЙ ПРОИЗВОДНОЙ
1) найти область определения ;
2) найти первую производную ;
3) найти критические точки;
4) исследовать знак производной на интервалах, которые получили от разбиения критическими точками области определения .
При этом критическая точка является точкой минимума, если при переходе через нее слева направо производная меняет знак с отрицательного на положительный , в противном случаэ является точкой максимума.
Вместо данного правила можно определять вторую производную и исследовать согласно второй теоремы.
5) вычислить значения функции в точках экстремума.
Рассмотрим теперь исследование функции на экстремумы на конкретных примерах.
————————————
Примеры.
Сборник В.Ю. Клепко, В.Л. Голец «Высшая математика в примерах и задачах»
1. (4.53.7)
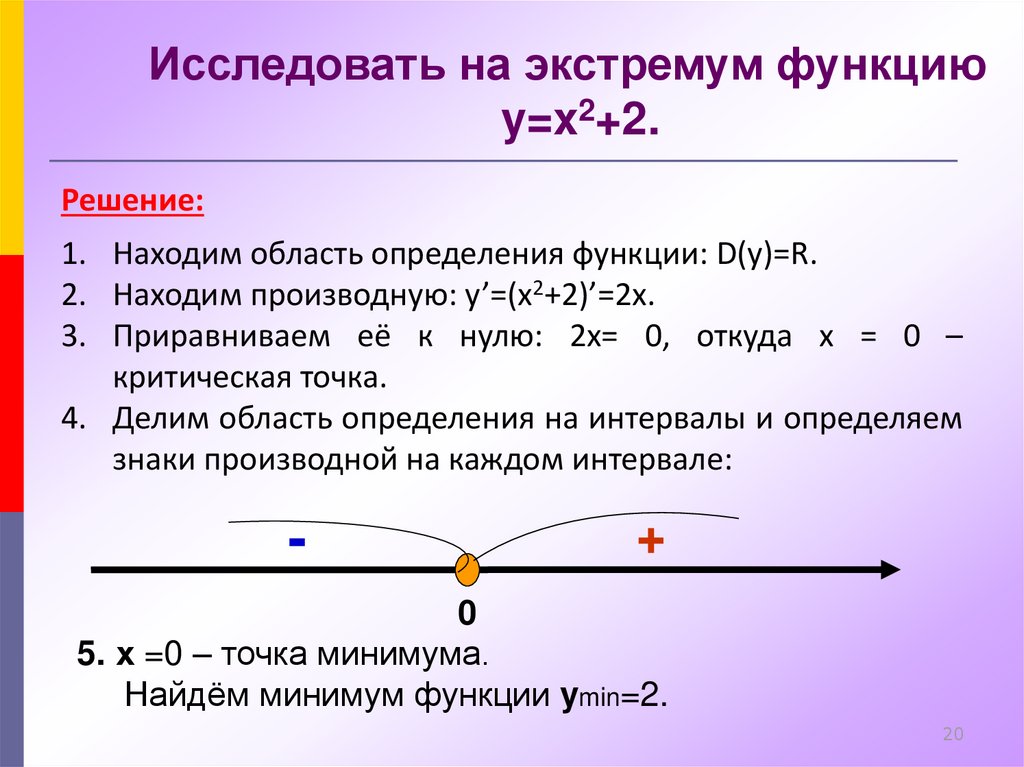
1) Областью определения будет множество действительных чисел
;
2) Находим производную
3) Вычисляем критические точки
Они разбивают область определения на следующие интервалы
4) Исследуем знак производной на найденных интервалах методом подстановки значений
Таким образом первая точка является точкой минимума, а вторая — точкой максимума.
5) Вычисляем значение функции
——————————
2. (4.53.9)
1) Областью определения будет множество действительных чисел , так корень всегда больше единицы
и функция арктангенс определена на всей действительной оси.
2) Находим производную
3) С условия равенства производной нулю находим критическую точку
Она разбивает область определения на два интервала
4) Определим знак производной в каждой из областей
Таким образом находим, что в критической точке функция принимает минимальное значение.
5) Вычислим экстремум функции
——————————
3. (4.53.13)
1) Функция определена когда знаменатель не превращается в ноль
Из этого следует, что область определения состоит из трех интервалов
2) Вычисляем производную
3) Приравниваем производную к нулю и находим критические точки.
4) Устанавливаем знак производной в каждой из областей, подстановкой соответствующих значений.
Таким образом точка является точкой локального максимума, а локального минимума. В имеем перегиб функции, но о нем будет больше материала в следующих статьях.
5) Находим значение в критических точках
Несмотря на то, что значение функции , первая точка является точкой локального максимума, а дуга — минимума. Не бойтесь, если у Вас выйдут подобные результаты, при определении локальных экстремумов такие ситуации допустимы.
———————————————-
Посмотреть материалы:
- Исследования функции и построения графика
- Интервалы монотонности функции
- Наибольшее и наименьшее значение функции на отрезке
- Выпуклость и вогнутисть графика функции
- Асимптоты функции
- Область определения функции
Точки экстремума функции, необходимые и достаточные условия экстремума
Содержание:
- Необходимое условие экстремума
- Первое достаточное условие экстремума
- Второе достаточное условие экстремума
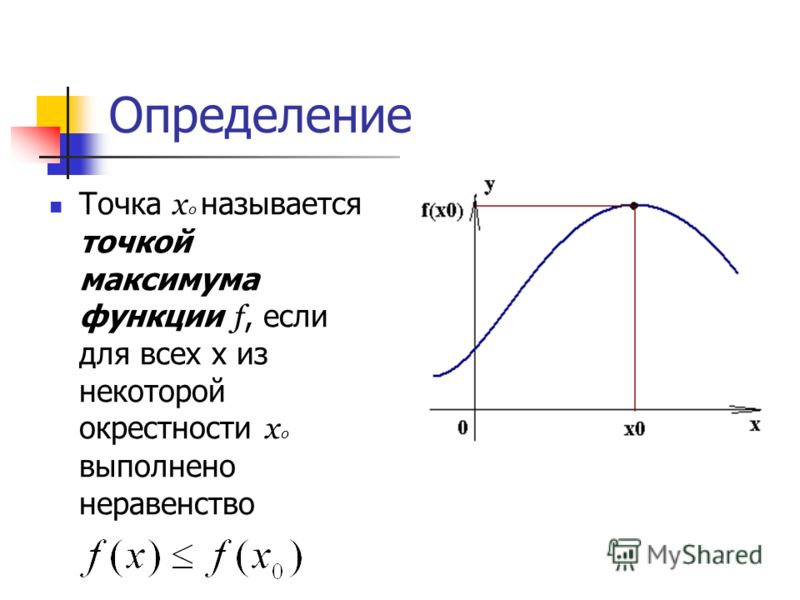
Определение
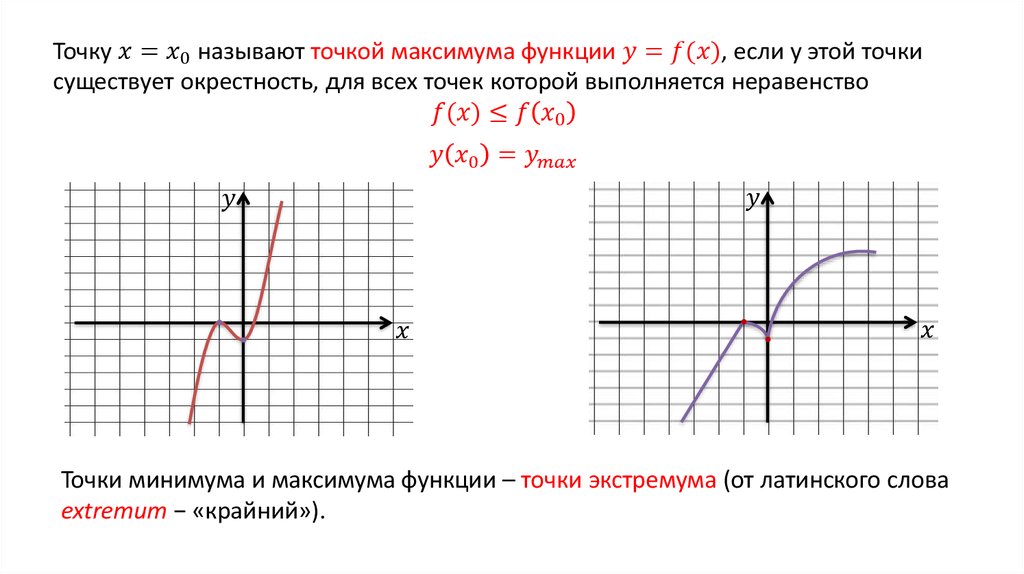
Точка $x_{0}$ называется точкой локального максимума функции $f(x)$, если существует такая окрестность
этой точки, что для всех $x$ из этой окрестности
выполняется неравенство: $f(x) \leq f\left(x_{0}\right)$.
Точка $x_{0}$ называется точкой локального минимума функции $f(x)$, если существует такая окрестность этой точки, что для всех $x$ из этой окрестности $f(x) \geq f\left(x_{0}\right)$.
Значение функции в точке максимума называется локальным максимумом, значение функции в точке минимума — локальным минимумом данной функции. Локальные максимум и минимум функции называются
Точка $x_{0}$ называется точкой строгого локального максимума функции $y=f(x)$, если для всех $x$ из окрестности этой точки будет справедливо строгое неравенство $f(x) \lt f\left(x_{0}\right)$.
Точка $x_{0}$ называется точкой строгого локального минимума функции $y=f(x)$, если для всех $x$ из окрестности этой точки будет справедливо строгое неравенство $f(x)>f\left(x_{0}\right)$.
Наибольшее или наименьшее значение функции на промежутке называется глобальным экстремумом. {2}+1}=-1$.
{2}+1}=-1$.
Ответ. $y_{\min }=y(0)=-1$
Остались вопросы?
Здесь вы найдете ответы.
Что подразумевается под понятием «экстремум»?
Экстремум представляет собой значение функции на определенном интервале в момент достижения им минимального или максимального показания. Под понятием «экстремумы» или по-другому минимумы/максимумы подразумевается значение функции (у).
Точка экстремума – что это такое?
Если в определенной точке достигается экстремум или, иными словами,
максимальное/минимальное значение функции на заданном интервале, то эта
точка носит название точки экстремума. Из этого следует, что при
достижении минимума, точка экстремума будет названа точкой минимума, и,
наоборот, при достижении максимума эта точка будет называться точкой
максимума. В случае, когда указываются точки экстремумов (или
минимумов/максимумов) подразумеваются иксы, в которых достигаются
минимальные или максимальные значения.
Что имеется в виду под понятием «точка минимума функции»?
Любая точка x₀ будет определена в качестве точки минимума функции y = f(x) при соблюдении условия о том, что имеется такая V, представляющая собой окрестность (x₀ — V; x₀+V) упомянутой ранее точки, из которой для каждого значения x x₀ действительно следующее неравенство:
f(x)>f(x₀).
Как описать точку минимума функции?
Под понятием «минимум функции» имеется в виду та точка на ней, в которой функция имеет значение, являющееся наименьшим среди всех значений, приобретаемых ею в любой из других соседних точек. Другими словами, это означает, что в случае, когда функция, достигнув определенной точки, прекращает падать, а, наоборот, наблюдается ее рост, то данная точка и представляет собой точку ее минимума.
Каким образом можно вычислить значение функции y=x⁴-4x³+6x²-4x, которого она достигает в точке своего минимума?
Для ответа на поставленный вопрос нужно отыскать точку минимума указанной
функции, в которой ее значение перестает падать.
y’ = 4x³ — 12x² + 12x – 4
Предположив, что минимальное значение данной функции равно 0, можно переписать равенство в следующем виде:
4x³ — 12x² + 12x — 4 = 0
Сократим данное уравнение на 4:
x³ — 3x² + 3x — 1 = 0
Получившееся равенство также может быть записано в следующем виде после перемены местами слагаемых:
(x³ — 1) + (-3x² + 3x) = 0
Распишем слагаемые в ином виде, чтобы избавиться от третьей степени:
(x — 1)(x² + x + 1) -3x(x — 1) = 0
Это же уравнение может выглядеть так:
(x -1)(x² + x + 1- 3x) = 0
Произведем сложение слагаемых х и -3х:
(x — 1) (x² -2x + 1) = 0
Теперь для упрощения можно переписать уравнение в таком виде:
(x — 1)(x-1)² = 0
Получившееся равенство:
(x — 1)³ = 0
В этом случае х = 1
-∞ 1 +∞
Знаками «+» и «-» обозначены значения производной.
После проведенных вычислений было установлено, что х = 1, что является точкой минимума функции:
у = 1⁴- 4*1³ + 6*1² — 4*1 = 1 — 4 +6 — 4 = -1
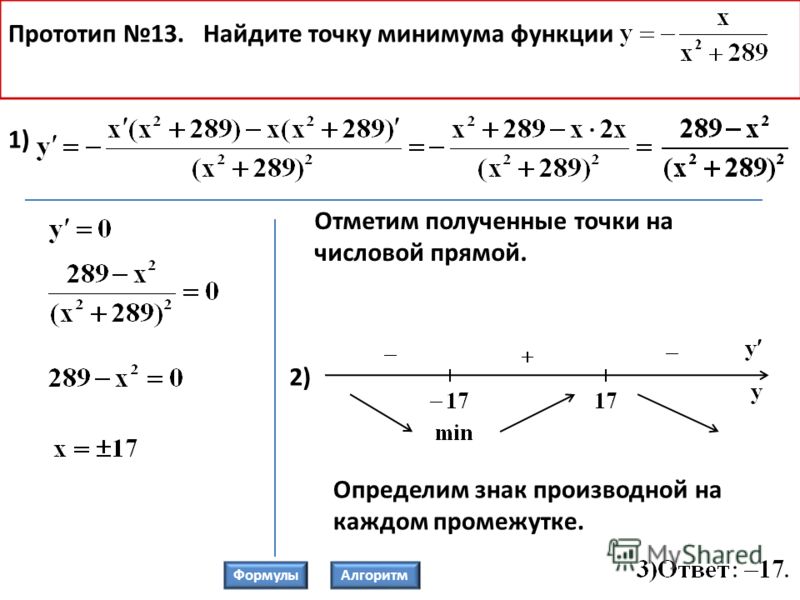
Какие расчеты нужно произвести, для того чтобы вычислить точку максимума для функции y = -x/x²+484?
Точкой максимума называется то значение х, достигнув которого, производная
начинает менять свой знак с плюса на минус. Зная это, можно перейти к
поиску точки максимума для функции, указанной в задании.
Зная это, можно перейти к
поиску точки максимума для функции, указанной в задании.
Для этого нужно начать с поиска производной, используя следующую формулу:
(U/V)’ = (U’V — UV’)/V²
Подставляем приведенные в задании значения и получаем:
y’ = (-(x² + 484) — 2x)/(x² + 484)² = (-x²-484 -2x)/(x² +484)²
Теперь следует приравнять производную к 0 и начать решать получившееся уравнение:
(-x²-484 -2x)/(x² +484)² = 0
Упростим уравнение и получим:
(-x²-484 -2x) = 0(x² +484)² ≠ 0
-x²-484 -2x = 0
Избавимся от минусов в уравнении:
x² + 2x +484 = 0
D
В результате вычислений стало ясно, что корней нет. Это значит, что невозможно поставить их на числовой прямой, для того чтобы проверить знаки производной по соседству с этими точками. На основании этого можно сделать вывод о том, что указанная в задании функция не имеет точек экстремума.
Что представляет собой точка максимума функции?
Под точкой максимума функции понимается та точка, в которой она достигает
значения, являющегося наибольшим среди тех значений, что достигаются ею в
соседних точках.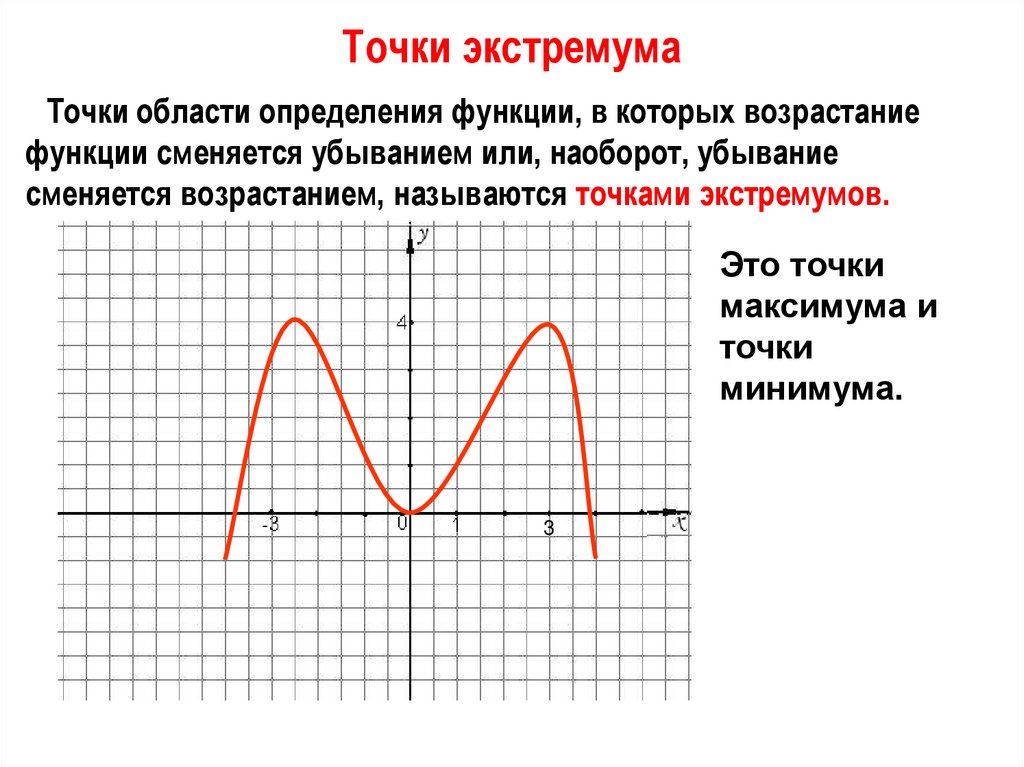 Это означает, что в точке, при пересечении которой
функция прекращает расти, и наблюдается ее падение, и достигается ее
максимум.
Это означает, что в точке, при пересечении которой
функция прекращает расти, и наблюдается ее падение, и достигается ее
максимум.
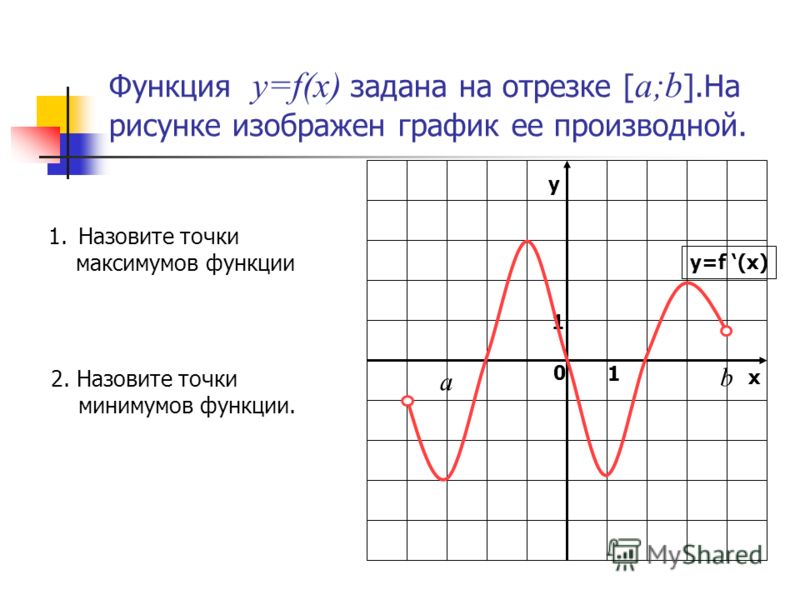
Имеется график производной функции. Каким образом можно вычислить точки ее максимума и минимума?
В случае, если имеется график производной функции, и при этом требуется
определить ее экстремумы, то необходимо вычислить точки пересечения этого
графика производной с осью Ох. По-другому они называются «нулями»
производной. В случае, когда, пересекая конкретную точку, график
производной восходит из области со знаком «-» в область со знаком «+», и в
это время производная меняет свой знак на противоположный, функция также
изменяется с убывания на рост. В этом случае данная точка, которая
пересекается графиком производной, представляет собой точку минимума. Если
же при пересечении графиком производной какой-либо точки он идет из
положительной в отрицательную область, а функция из возрастания меняется
на убывание, то речь идет о точке ее максимума.
Как можно вычислить экстремумы и точки экстремума функции y=4x⁴+2x²+1?
Для того чтобы найти ответ на поставленный вопрос, сначала нужно приравнять функцию к 0:
у = 0
Это же означает, что:
4X⁴ + 2X² + 1 = 0
Введем обозначения:
Х2 = А, при этом А больше 0.
С учетом введенных обозначений равенство будет иметь следующий вид:
4A² + 2A + 1 = 0
D = 4 — 4 = 0 ; √ D = 0
A = (- 2) : 4 = (- 0,5) (
Очевидно, что корней нет.
Ответ: х = 0, у = 1.
Дана функция y = x² -3x+2. Как можно вычислить экстремум этой функции?
Имеется функция y = x² -3x+2, которую также можно переписать в следующем виде:
у = -0,25+ (x-1,5)²
Отсюда следует, что:
miny = — 0,25 при условии, что х-1,5 = 0
Можно сделать вывод о том, что х = 1,5.
Запишем производную данной функции:
y ‘= (x² -3x+2)’ =2x -3
А затем приравняем ее к 0:
y ‘ = 0, значит:
2x -3 = 0.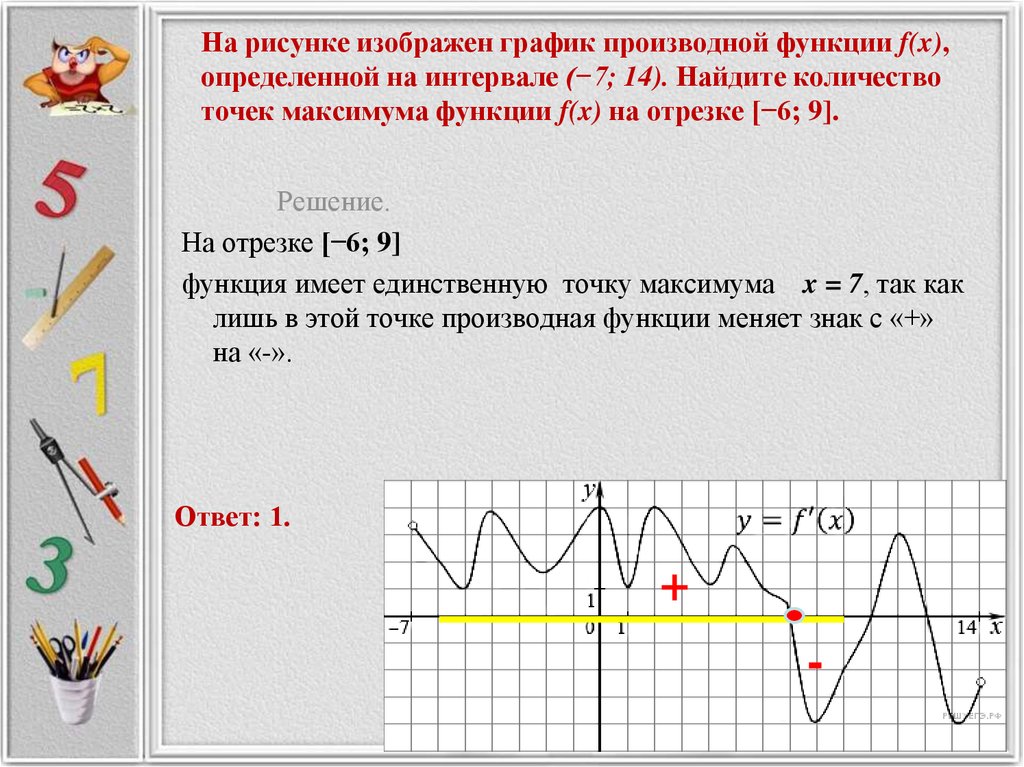
Это позволяет сделать вывод о том, что:
x = 3/2.
Получается, что, если x
Если же x >3/2, то производная y’ > 0, и в этом случае функция возрастает.
x =3/2=1,5 – это единственная точка экстремума, которая является точкой минимума.
miny =(1,5)² -3*1,5+2 = -0,25.
Как раскрыть понятие «критическая точка функции»?
Критическая точка функции представляет собой ту точку, при пересечении с которой производная данной функции становится равной 0, либо она вовсе не существует.
Возможно ли привести доказательства того, что функция f(x) =2x — 3/x не может иметь критической точки?
Для начала нужно определить, что под критической точкой функции
подразумевается та точка, при пересечении с которой производная
приобретает нулевое значение, либо же эта производная просто не существует
в этой точке, что означает, что функцию в данной точке невозможно
дифференцировать.
Проверим, применимо ли это утверждение к упомянутой в задании функции:
f ‘(x) =(sin2x — 3x)’ = 2sin2x-3
Приравняем производную функции к 0:
f ‘(x) = 0, это значит, что 2sin2x-3 = 0.
Следовательно:
sin2x= 3 2 не имеет решения
Ответ: заданная функция не имеет критических точек и существует при любых х.
Каким способом можно определить критические точки функции y=|x|/1+x²?
Под критическими точками функции понимаются те точки, в которых ее производная равна 0 или вовсе не существует.
В задании дана функция:
y=|x|/(1+x²)
Предположим, что x
y=-x/(1+x²)
Запишем производную функции и приравняем ее к 0:
y`=(-1-x²+2x²)/(1+x²)²=(x²-1)/(1+x²)²=(x-1)(x+1)/(1+x²)²=0
х = 1 не соответствует условию, значит х = -1.
Теперь предположим, что x≥0.
Снова записываем производную имеющейся функции и приравниваем ее к 0:
y`=(1+x²-2x²)/(1+x²)²=(1-x²)/(1+x²)²=(1-x)(x+1)/(1+x²)²=0
х = — 1 не отвечает условию, значит х = 1.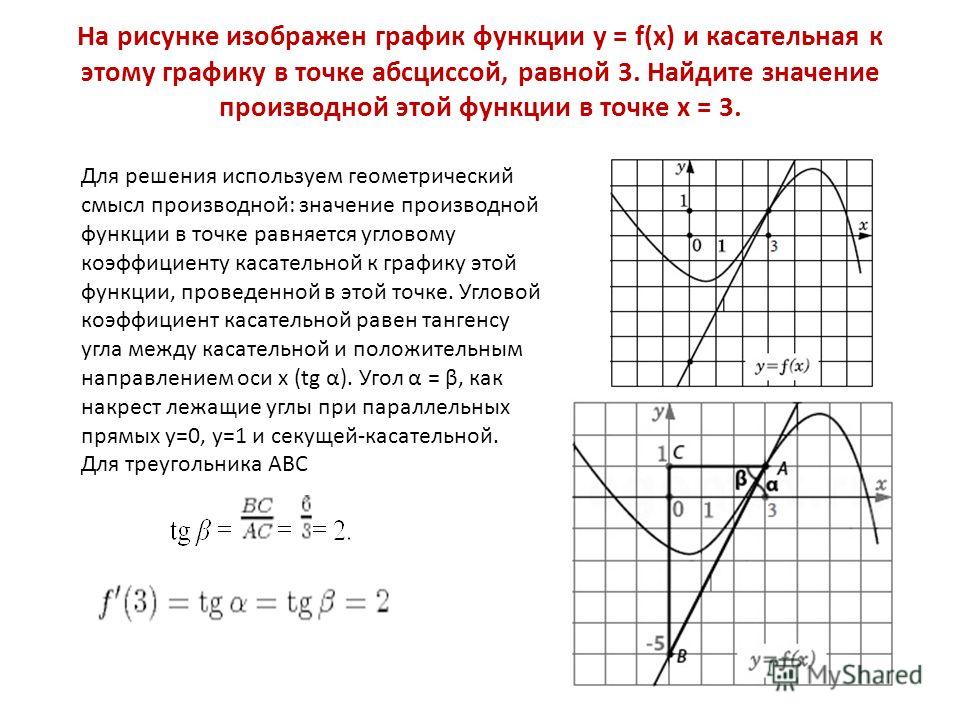
Ответ: х = 1, х = -1.
Читать дальше: наибольшее и наименьшее значение функции.
Найти экстремум функции f x. Экстремумы функции
Функцияy = f(x) называется возрастающей (убывающей ) в некотором интервале, если при x 1 f(x 2)).
Если дифференцируемая функцияy = f(x) на отрезке возрастает (убывает), то ее производная на этом отрезке f » (x) > 0 , (f » (x)
Точкаx о называется точкой локального максимума (минимума ) функции f(x), если существует окрестность точки x о , для всех точек которой верно неравенство f(x) ≤ f(x о), (f(x) ≥f(x о)).
Точки максимума и минимума называются точками экстремума , а значения функции в этих точках — ее экстремумами.
Точки экстремума
Необходимые условия экстремума . Если точка x о является точкой экстремума функции f(x), то либо f » (x о) = 0, либо f (x о) не существует. Такие точки называют критическими, причем сама функция в критической точке определена. Экстремумы функции следует искать среди ее критических точек.
Экстремумы функции следует искать среди ее критических точек.
Первое достаточное условие. Пусть x о — критическая точка. Если f » (x) при переходе через точку x о меняет знак плюс на минус, то в точке x о функция имеет максимум, в противном случае — минимум. Если при переходе через критическую точку производная не меняет знак, то в точке x о экстремума нет.
Второе достаточное условие. Пусть функция f(x) имеет f » (x) в окрестности точки x о и вторую производную f «» (x 0) в самой точке x о . Если f » (x о) = 0, f «» (x 0)>0, (f «» (x 0) x о является точкой локального минимума (максимума) функции f(x). Если же f «» (x 0)=0, то нужно либо пользоваться первым достаточным условием, либо привлекать высшие .
На отрезке функция y =f(x) может достигать наименьшего или наибольшего значения либо в критических точках, либо на концах отрезка .
Пример 3.22. Найти экстремумы функции f(x) = 2x 3 — 15x 2 + 36x — 14.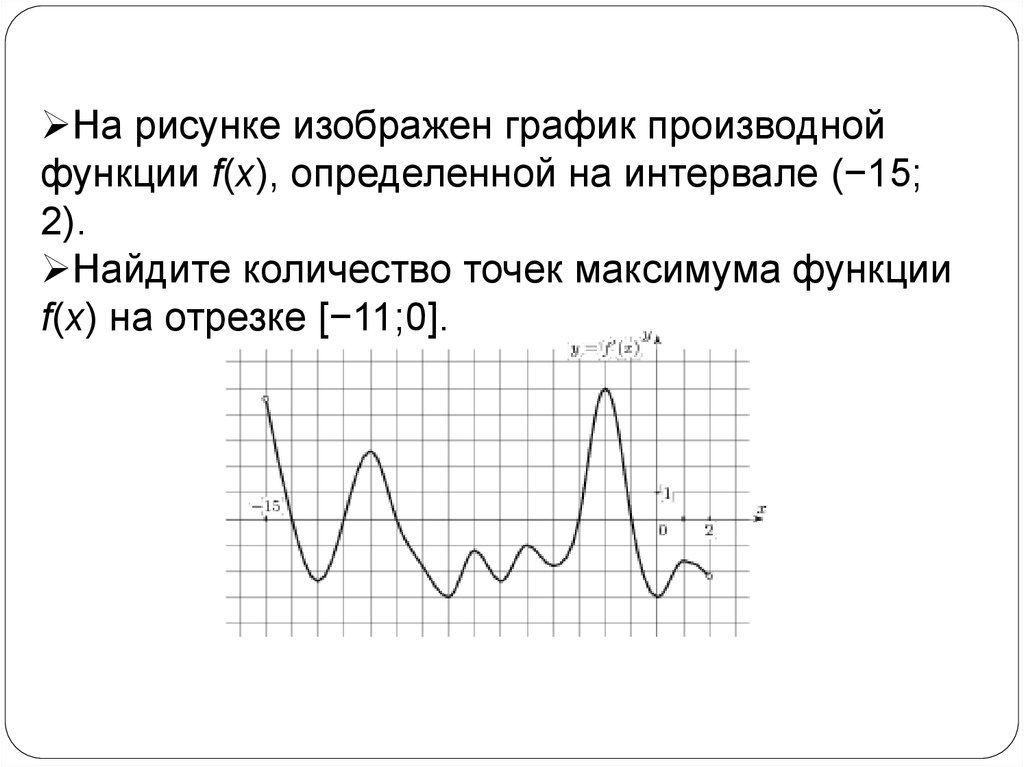
Решение. Так как f » (x) = 6x 2 — 30x +36 = 6(x -2)(x — 3), то критические точки функции x 1 = 2 и x 2 = 3. Экстремумы могут быть только в этих точках. Так как при переходе через точку x 1 = 2 производная меняет знак плюс на минус, то в этой точке функция имеет максимум. При переходе через точку x 2 = 3 производная меняет знак минус на плюс, поэтому в точке x 2 = 3 у функции минимум. Вычислив значения функции в точках x 1 = 2 и x 2 = 3, найдем экстремумы функции: максимум f(2) = 14 и минимум f(3) = 13.
Задачи на нахождения экстремума функции
Пример 3.23. a
Решение. x и y . Площадь площадки равна S =xy. Пусть y — это длина стороны, примыкающей к стене. Тогда по условию должно выполняться равенство 2x +y =a. Поэтому y = a — 2x и S =x(a — 2x), где
0 ≤x ≤a/2 (длина и ширина площадки не могут быть отрицательными).
S » = a — 4x, a — 4x = 0 при x = a/4, откуда
y = a — 2×a/4 = a/2. Поскольку x = a/4 — единственная критическая точка, проверим, меняется ли знак производной при переходе через эту точку. При x 0, а при x > a/4, S »
При x 0, а при x > a/4, S »
Пример 3.24.
Решение.
R = 2, Н = 16/4 = 4.
Пример 3.22. Найти экстремумы функцииf(x) = 2x 3 — 15x 2 + 36x — 14.
Решение. Так как f » (x) = 6x 2 — 30x +36 = 6(x -2)(x — 3), то критические точки функции x 1 = 2 и x 2 = 3. Экстремумы могут быть только в этих точках. Так как при переходе через точку x 1 = 2 производная меняет знак плюс на минус, то в этой точке функция имеет максимум. При переходе через точку x 2 = 3 производная меняет знак минус на плюс, поэтому в точке x 2 = 3 у функции минимум. Вычислив значения функции в точках x 1 = 2 и x 2 = 3, найдем экстремумы функции: максимумf(2) = 14 и минимумf(3) = 13.
Пример 3.23. Нужно построить прямоугольную площадку возле каменной стены так, чтобы с трех сторон она была отгорожена проволочной сеткой, а четвертой стороной примыкала к стене. Для этого имеетсяa погонных метров сетки. При каком соотношении сторон площадка будет иметь наибольшую площадь?
Решение. Обозначим стороны площадки черезx иy . Площадь площадки равна S = xy. Пусть y — это длина стороны, примыкающей к стене. Тогда по условию должно выполняться равенство 2x +y =a. Поэтому y = a — 2x и S = x(a — 2x), где
Обозначим стороны площадки черезx иy . Площадь площадки равна S = xy. Пусть y — это длина стороны, примыкающей к стене. Тогда по условию должно выполняться равенство 2x +y =a. Поэтому y = a — 2x и S = x(a — 2x), где
0 ≤x ≤a/2 (длина и ширина площадки не могут быть отрицательными). S » = a — 4x, a — 4x = 0 при x = a/4, откуда
y = a — 2a/4 = a/2. Поскольку x = a/4 — единственная критическая точка, проверим, меняется ли знак производной при переходе через эту точку. Приx 0, а при x >a/4 S »
Пример 3.24. Требуется изготовить закрытый цилиндрический бак вместимостью V=16p ≈ 50 м 3 . Каковы должны быть размеры бака (радиус R и высота Н), чтобы на его изготовление пошло наименьшее количество материала?
Решение. Площадь полной поверхности цилиндра равна S = 2pR(R+Н). Мы знаем объем цилиндра V = pR 2 Н Þ Н = V/pR 2 =16p/ pR 2 = 16/ R 2 . Значит, S(R) = 2p(R 2 +16/R). Находим производную этой функции:
S » (R) = 2p(2R- 16/R 2) = 4p (R- 8/R 2). S » (R) = 0 при R 3 = 8, следовательно,
S » (R) = 0 при R 3 = 8, следовательно,
R = 2, Н = 16/4 = 4.
Рассмотрим график непрерывной функции y=f(x) , изображенной на рисунке.
Значение функции в точке x 1 будет больше значений функции во всех соседних точках как слева, так и справа от x 1 . В этом случае говорят, что функция имеет в точке x 1 максимум. В точке x 3 функция, очевидно, также имеет максимум. Если рассмотреть точку x 2 , то в ней значение функции меньше всех соседних значений. В этом случае говорят, что функция имеет в точке x 2 минимум. Аналогично для точки x 4 .
Функция y=f(x) в точке x 0 имеет максимум , если значение функции в этой точке больше, чем ее
значения во всех точках некоторого интервала, содержащего точку x 0 , т.е. если существует такая
окрестность точки x 0 , что для всех x ≠x 0 , принадлежащих этой окрестности, имеет место неравенство f(x) f(x
0 ) .
Функция y=f(x) имеет минимум в точке x 0 , если существует такая окрестность точки x 0 , что для всех x ≠x 0 , принадлежащих этой окрестности, имеет место неравенство f(x) >f(x 0 .
Точки, в которых функция достигает максимума и минимума, называются точками экстремума, а значения функции в этих точках экстремумами функции.
Обратим внимание на то, что функция, определенная на отрезке, может достигать максимума и минимума только в точках, заключенных внутри рассматриваемого отрезка.
Отмети, что если функция
имеет в точке максимум, то это не означает, что в этой точке функция имеет
наибольшее значение во всей области определения. На рисунке, рассмотренном выше,
функция в точке x 1 имеет максимум, хотя
есть точки, в которых значения функции больше, чем в точке x 1 . В частности, f (x 1) f
(x 4)
т.е. минимум функции больше максимума. Из определения максимума следует только,
что это самое большое значение функции в точках, достаточно близкихк точке максимума.
Теорема 1. (Необходимое условие существования экстремума.) Если дифференцируемая функция y=f(x) имеет в точке x= x 0 экстремум, то ее производная в этой точке обращается в нуль.
Доказательство . Пусть для определенности в точке x 0 функция имеет максимум. Тогда при достаточно малых приращениях Δx имеем f(x 0 + Δx) 0 ) , т.е. Но тогда
Переходя в этих неравенствах к пределу при Δx → 0 и учитывая, что производная f «(x 0) существует, а следовательно предел, стоящий слева, не зависит от того как Δx → 0, получаем: при Δx → 0 – 0 f» (x 0) ≥ 0 а при Δx → 0 + 0 f» (x 0) ≤ 0. Так как f » (x 0) определяет число, то эти два неравенства совместны только в том случае, когда f » (x 0) = 0.
Доказанная
теорема утверждает, что точки максимума и минимума могут находиться только
среди тех значений аргумента, при которых производная обращается в нуль.
Мы рассмотрели случай, когда функция во всех точках некоторого отрезка имеет производную. Как же обстоит дело в тех случаях, когда производная не существует? Рассмотрим примеры.
Примеры .
- y =|x |.
Функция не имеет производной в точке x =0 (в этой точке график функции не имеет определенной касательной), но в этой точке функция имеет минимум, так как y (0)=0, а при всех x ≠ 0y > 0.
- Пусть x 0 . Тогда c 0 и f «(c)> 0. Поэтомуf «(c)(x- x 0) 0и, следовательно,
f(x) — f(x 0 ) 0,т.е. f(x) 0 ).
- Пусть x > x 0 . Тогда c> x 0
и f «(c) 0. Значитf «(c)(x- x 0) 0.
 Поэтому f(x) — f(x 0 ) f(x) f(x 0 ) .
Поэтому f(x) — f(x 0 ) f(x) f(x 0 ) . - Найти область определения
функции f(x).

- Найти первую производную функции f «(x) .
- Определить критические
точки, для этого:
- найти действительные корни уравнения f «(x) =0;
- найти все значения x при которых производная f «(x) не существует.
- Определить знак производной слева и справа от критической точки. Так как знак производной остается постоянным между двумя критическими точками, то достаточно определить знак производной в какой-либо одной точке слева и в одной точке справа от критической точки.
- Вычислить значение функции в точках экстремума.
- Найти все критические точки функции в интервале (a, b ) и вычислить значения функции в этих точках.
- Вычислить значения функции на концах отрезка при x = a, x = b .
- Из всех полученных значений выбрать наибольшее и наименьшее.
Функция не имеет производной при x =0, так как обращается в бесконечность приx =0. Но в этой точке функция имеет максимум.
Функция не имеет производной при x =0, так как при x →0. В этой точке функция не имеет ни максимума, ни минимума. Действительно, f(x) =0 и при x f(x) x >0f(x) >0.
Таким образом, из
приведенных примеров и сформулированной теоремы видно, что функция может иметь
экстремум лишь в двух случаях: 1) в точках, где производная существует и равна
нулю; 2) в точке, где производная не существует.
Однако, если в некоторой точке x 0 мы знаем, что f «(x 0 ) =0, то отсюда нельзя делать вывод, что в точке x 0 функция имеет экстремум.
Например . .
Но точка x =0 не является точкой экстремума, поскольку слева от этой точки значения функции расположены ниже оси Ox , а справа выше.
Значения аргумента из области определения функции, при которых производная функции обращается в нуль или не существует, называются критическими точками .
Из всего вышесказанного следует, что точки экстремума функции находятся среди критических точек, и, однако, не всякая критическая точка является точкой экстремума. Поэтому, чтобы найти экстремум функции, нужно найти все критические точки функции, а затем каждую из этих точек исследовать отдельно на максимум и минимум. Для этого служит следующая теорема.
Теорема 2. (Достаточное
условие существования экстремума.) Пусть функция непрерывна на некотором
интервале, содержащем критическую точку x 0 , и дифференцируема
во всех точках этого интервала (кроме, быть может, самой точки x 0). Если при
переходе слева направо через эту точку производная меняет знак с плюса на
минус, то в точке x = x 0
функция имеет максимум. Если же при переходе через x 0
слева направо производная меняет знак с минуса на плюс, то функция имеет в этой
точке минимум.
Если при
переходе слева направо через эту точку производная меняет знак с плюса на
минус, то в точке x = x 0
функция имеет максимум. Если же при переходе через x 0
слева направо производная меняет знак с минуса на плюс, то функция имеет в этой
точке минимум.
Таким образом, если
Доказательство . Предположим сначала, что при переходе через x 0 производная меняет знак с плюса на минус, т.е. при всех x , близких к точке x 0 f «(x)> 0 для x 0 , f «(x) 0 для x> x 0 . Применим теорему Лагранжа к разности f(x) — f(x 0 ) = f «(c)(x- x 0), где c лежит между x и x 0 .
Таким образом, для всех значений x достаточно близких к x 0 f(x) f(x 0 ) . А это значит, что в точке x 0 функция имеет максимум.
Аналогично доказывается вторая часть теоремы о минимуме.
Проиллюстрируем смысл этой теоремы на рисунке. Пусть f «(x 1 ) =0 и для любых x, достаточно близких к x 1 , выполняются неравенства
f «(x) 0 при x 1 , f «(x)> 0 при x> x 1 .
Тогда слева от точки x 1 функция возрастает, а справа убывает, следовательно, при x = x 1 функция переходит от возрастания к убыванию, то есть имеет максимум.
Аналогично можно рассматривать точки x 2 и x 3 .
Схематически все вышесказанное можно изобразить на картинке:
Правило исследования функции y=f(x) на экстремум
Примеры . Исследовать функции на минимум и максимум.
НАИБОЛЬШЕЕ И НАИМЕНЬШЕЕ ЗНАЧЕНИЯ ФУНКЦИИ НА ОТРЕЗКЕ
Наибольшим значением функции на отрезке называется самое большое из всех ее значений на этом отрезке, а наименьшим – самое маленькое из всех ее значений.
Рассмотрим функцию y=f(x) непрерывную
на отрезке [a, b ]. Как известно, такая функция достигает своего наибольшего и наименьшего
значений, либо на границе отрезка, либо внутри него. Если наибольшее или
наименьшее значение функции достигается во внутренней точке отрезка, то это
значение является максимумом или минимумом функции, то есть достигается в
критических точках.
Как известно, такая функция достигает своего наибольшего и наименьшего
значений, либо на границе отрезка, либо внутри него. Если наибольшее или
наименьшее значение функции достигается во внутренней точке отрезка, то это
значение является максимумом или минимумом функции, то есть достигается в
критических точках.
Таким образом, получаем следующее правило нахождения наибольшего и наименьшего значений функции на отрезке[a, b ] :
Это довольно-таки занятный раздел математики, с которым сталкиваются абсолютно все ученики выпускных классов и студенты. Тем не менее далеко не каждому нравится матан. Некоторые не могут понять даже элементарных вещей наподобие, казалось бы, стандартного исследования функции. Данная статья призвана исправить подобную оплошность. Хотите поподробнее узнать об анализе функции? Желаете узнать, что такое точки экстремума и как их найти? Тогда данная статья для вас.
Данная статья призвана исправить подобную оплошность. Хотите поподробнее узнать об анализе функции? Желаете узнать, что такое точки экстремума и как их найти? Тогда данная статья для вас.
Исследование графика функции
Для начала стоит понять, зачем вообще необходимо анализировать график. Существуют простые функции, начертить которые не составит труда. Ярким примером подобной функции может служить парабола. Начертить ее график не составит труда. Все что необходимо, так это с помощью простого преобразования найти числа, при которых функция принимает значение 0. И в принципе это все что знать для того, чтобы начертить график параболы.
Но что делать, если функция, график которой нам нужно начертить, намного сложнее? Поскольку свойства сложных функций довольно-таки неочевидны, необходимо проводить целый анализ. Только после этого можно изобразить функцию графически. Как же это сделать? Ответ на этот вопрос вы сможете найти в данной статье.
План анализа функции
Первое, что необходимо сделать, так это провести поверхностное исследование функции, в ходе которого мы найдем область определения. Итак, начнем по порядку. Область определения — это совокупность тех значений, которыми функция задается. Проще говоря, это те числа, которые можно использовать в функции вместо х. Для того чтобы определить область определения, необходимо просто взглянуть на запись. К примеру, очевидно, что у функции у (х) = х 3 + х 2 — х + 43 область определения — множество действительных чисел. Ну а с функцией наподобие (х 2 — 2х)/х все немного иначе. Поскольку число в знаменателе не должно равняться 0, то областью определения данной функции будут все действительные числа, помимо нуля.
Итак, начнем по порядку. Область определения — это совокупность тех значений, которыми функция задается. Проще говоря, это те числа, которые можно использовать в функции вместо х. Для того чтобы определить область определения, необходимо просто взглянуть на запись. К примеру, очевидно, что у функции у (х) = х 3 + х 2 — х + 43 область определения — множество действительных чисел. Ну а с функцией наподобие (х 2 — 2х)/х все немного иначе. Поскольку число в знаменателе не должно равняться 0, то областью определения данной функции будут все действительные числа, помимо нуля.
Далее необходимо найти так называемые нули функции. Это те значения аргумента, при которых вся функция принимает значения ноль. Для этого необходимо приравнять функцию к нулю, подробно ее рассмотреть и совершить некоторые преобразования. Возьмём уже знакомую нам функцию у(х) = (х 2 — 2х)/х. Из школьного курса мы знаем, что дробь равна 0 тогда, когда числитель равен нулю. Поэтому знаменатель мы отбрасываем и начинаем работать с числителем, приравнивая его к нулю. Получаем х 2 — 2х = 0 и выносим х за скобочки. Отсюда х (х — 2) = 0. В итоге получаем, что наша функция равна нулю тогда, когда х равняется 0 или же 2.
Получаем х 2 — 2х = 0 и выносим х за скобочки. Отсюда х (х — 2) = 0. В итоге получаем, что наша функция равна нулю тогда, когда х равняется 0 или же 2.
Во время исследования графика функции многие сталкиваются с проблемой в виде точек экстремума. И это странно. Ведь экстремумы — это довольно-таки простая тема. Не верите? Убедитесь сами, прочитав данную часть статьи, в которой мы поговорим о точках минимума и максимума.
Для начала стоит разобраться в том, что собой представляет экстремум. Экстремум — это предельное значений, которое достигает функция на графике. Отсюда получается, что существует два крайних значения — максимум и минимум. Для наглядности можно посмотреть на картинку, что расположена выше. На исследованной области точка -1 является максимумом функции у (х) = х 5 — 5х, а точка 1, соответственно, минимумом.
Также не стоит путать между собой понятия. Точки экстремума функции — это те аргументы, при которых заданная функция приобретает крайние значения. В свою очередь, экстремумом называют значение минимумов и максимумов функции. К примеру, вновь рассмотрим рисунок выше. -1 и 1 — это точки экстремума функции, а 4 и -4 — это сами экстремумы.
В свою очередь, экстремумом называют значение минимумов и максимумов функции. К примеру, вновь рассмотрим рисунок выше. -1 и 1 — это точки экстремума функции, а 4 и -4 — это сами экстремумы.
Нахождение точек экстремума
Но как все-таки найти точки экстремума функции? Все довольно-таки просто. Первое, что необходимо сделать — найти производную уравнения. Допустим, мы получили задание: «Найдите точки экстремума функции y (x), x — аргумент. Для наглядности возьмем функцию у (х) = х 3 + 2х 2 + х + 54. Проведем дифференцирование и получим следующее уравнение: 3х 2 + 4х + 1. В итоге мы получили стандартное квадратное уравнение. Все, что необходимо сделать дальше — приравнять его к нулю и найти корни. Поскольку дискриминант больше нуля (D = 16 — 12 = 4), данное уравнение определяется двумя корнями. Находим их и получаем два значения: 1/3 и -1. Это и будут точки экстремума функции. Однако как все-таки определить, кто есть кто? Какая точка является максимумом, а какая минимумом? Для этого нужно взять соседнюю точку и узнать ее значение. К примеру, возьмем число -2, которое находится слева по координатной прямой от -1. Подставляем это значение в наше уравнение у(-2) = 12 — 8 + 1 = 5. В итоге мы получили положительное число. Это значит, что на промежутке от 1/3 до -1 функция возрастает. Это, в свою очередь, обозначает, что на промежутках от минус бесконечности до 1/3 и от -1 до плюс бесконечности функция убывает. Таким образом, можно сделать вывод, что число 1/3 — точка минимума функции на исследованном промежутке, а -1 — точка максимума.
К примеру, возьмем число -2, которое находится слева по координатной прямой от -1. Подставляем это значение в наше уравнение у(-2) = 12 — 8 + 1 = 5. В итоге мы получили положительное число. Это значит, что на промежутке от 1/3 до -1 функция возрастает. Это, в свою очередь, обозначает, что на промежутках от минус бесконечности до 1/3 и от -1 до плюс бесконечности функция убывает. Таким образом, можно сделать вывод, что число 1/3 — точка минимума функции на исследованном промежутке, а -1 — точка максимума.
Также стоит отметить, что на ЕГЭ требуют не просто найти точки экстремума, Но и провести с ними какую-то операцию (прибавить, умножить и т.д.). Именно по этой причине стоит обратить особое внимание на условия задачи. Ведь из-за невнимательности можно потерять баллы.
Урок на тему: «Нахождение точек экстремумов функций. Примеры»
Дополнительные материалы
Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания! Все материалы проверены антивирусной программой.
Пособия и тренажеры в интернет-магазине «Интеграл» для 10 класса от 1С
Решаем задачи по геометрии. Интерактивные задания на построение для 7-10 классов
Программная среда «1С: Математический конструктор 6.1»
Что будем изучать:
1. Введение.
2. Точки минимума и максимума.
4. Как вычислять экстремумы?
5. Примеры.
Введение в экстремумы функций
Ребята, давайте посмотрим на график некоторой функции:
Заметит, что поведение нашей функции y=f (x) во многом определяется двумя точками x1 и x2. Давайте внимательно посмотрим на график функции в этих точках и около них. До точки x2 функция возрастает, в точке x2 происходит перегиб, и сразу после этой точки функция убывает до точки x1. В точке x1 функция опять перегибается, и после этого — опять возрастает. Точки x1 и x2 пока так и будем называть точками перегиба. Давайте проведем касательные в этих точках:
Касательные в наших точках параллельны оси абсцисс, а значит, угловой коэффициент касательной равен нулю. Это значит, что и производная нашей функции в этих точках равна нулю.
Это значит, что и производная нашей функции в этих точках равна нулю.
Посмотрим на график вот такой функции:
Касательные в точках x2 и x1 провести невозможно. Значит, производной в этих точках не существует. Теперь посмотрим опять на наши точки на двух графиках. Точка x2 — это точка, в которой функция достигает наибольшего значения в некоторой области (рядом с точкой x2). Точка x1 — это точка, в которой функция достигает своего наименьшего значения в некоторой области (рядом с точкой x1).
Точки минимума и максимума
Определение: Точку x= x0 называют точкой минимума функции y=f(x), если существует окрестность точки x0, в которой выполняется неравенство: f(x) ≥ f(x0).
Определение: Точку x=x0 называют точкой максимума функции y=f(x), если существует окрестность точки x0, в которой выполняется неравенство: f(x) ≤ f(x0).
Ребята, а что такое окрестность?
Определение: Окрестность точки — множество точек, содержащее нашу точку, и близкие к ней.
Окрестность мы можем задавать сами. Например, для точки x=2, мы можем определить окрестность в виде точек 1 и 3.
Вернемся к нашим графикам, посмотрим на точку x2, она больше всех других точек из некоторой окрестности, тогда по определению — это точка максимума. Теперь посмотрим на точку x1, она меньше всех других точек из некоторой окрестности, тогда по определению — это точка минимума.
Ребята, давайте введем обозначения:
Y min — точка минимума,
y max — точка максимума.
Важно! Ребята, не путайте точки максимума и минимума с наименьшим и наибольшим значение функции. Наименьшее и наибольшее значения ищутся на всей области определения заданной функции, а точки минимума и максимума в некоторой окрестности.
Экстремумы функции
Для точек минимума и максимума есть общей термин – точки экстремума.
Экстремум (лат. extremum – крайний) – максимальное или минимальное значение функции на заданном множестве. Точка, в которой достигается экстремум, называется точкой экстремума.
Соответственно, если достигается минимум – точка экстремума называется точкой минимума, а если максимум – точкой максимума.
Как же искать экстремумы функции?
Давайте вернемся к нашим графикам. В наших точках производная либо обращается в нуль (на первом графике), либо не существует (на втором графике).
Тогда можно сделать важное утверждение: Если функция y= f(x) имеет экстремум в точке x=x0, то в этой точке производная функции либо равна нулю, либо не существует.
Точки, в которых производная равна нулю называются стационарными.
Точки, в которых производной функции не существует, называются критическими.
Как вычислять экстремумы?
Ребята, давайте опять вернемся к первому графику функции:
Анализируя этот график, мы говорили: до точки x2 функция возрастает, в точке x2 происходит перегиб, и после этой точки функция убывает до точки x1. В точке x1 у функции опять перегибается, и после этого функция опять возрастает.
На основании таких рассуждений, можно сделать вывод, что функция в точках экстремума меняет характер монотонности, а значит и производная функция меняет знак. Вспомним: если функция убывает, то производная меньше либо равно нулю, а если функция возрастает, то производная больше либо равна нулю.
Вспомним: если функция убывает, то производная меньше либо равно нулю, а если функция возрастает, то производная больше либо равна нулю.
Обобщим полученные знания утверждением:
Теорема: Достаточное условие экстремума: пусть функция y=f(x) непрерывна на некотором промежутке Х и имеет внутри промежутка стационарную или критическую точку x= x0. Тогда:
Для решении задач запомните такие правила: Если знаки производных определены то:
Алгоритм исследования непрерывной функции y= f(x) на монотонность и экстремумы:
- Найти производную y’.
- Найти стационарные(производная равна нулю) и критические точки (производная не существует).

- Отметить стационарные и критические точки на числовой прямой и определить знаки производной на получившихся промежутках.
- По указанным выше утверждениям сделать вывод о характере точек экстремума.
Примеры нахождения точки экстремумов
1) Найти точки экстремума функции и определить их характер: y= 7+ 12*x — x 3
Решение: Наша функция непрерывна, тогда воспользуемся нашим алгоритмом:
а) y»= 12 — 3x 2 ,
б) y»= 0, при x= ±2,
Точка x= -2 — точка минимума функции, точка x= 2 — точка максимума функции.
Ответ: x= -2 — точка минимума функции, x= 2 — точка максимума функции.
2) Найти точки экстремума функции и определить их характер.
Решение: Наша функция непрерывна. Воспользуемся нашим алгоритмом:
а)
б) в точке x= 2 производная не существует, т.к. на нуль делить нельзя, Область определения функции: , в этой точки экстремума нет, т.к. окрестность точки не определена. Найдем значения, в которой производная равна нулю: в) Отметим стационарные точки на числовой прямой и определим знаки производной: г) посмотрим на наш рисунок, где изображены правила определения экстремумов.
Точка x= 3 — точка минимума функции.
Ответ: x= 3 — точка минимума функции.
3) Найти точки экстремума функции y= x — 2cos(x) и определить их характер, при -π ≤ x ≤ π.
Решение: Наша функция непрерывна, воспользуемся нашим алгоритмом:
а) y»= 1 + 2sin(x),
б) найдем значения в которой производная равна нулю: 1 + 2sin(x)= 0, sin(x)= -1/2,
т.к. -π ≤ x ≤ π, то: x= -π/6, -5π/6,
в) отметим стационарные точки на числовой прямой и определим знаки производной: г) посмотрим на наш рисунок, где изображены правила определения экстремумов.
Точка x= -5π/6 — точка максимума функции.
Точка x= -π/6 — точка минимума функции.
Ответ: x= -5π/6 — точка максимума функции, x= -π/6 — точка минимума функции.
4) Найти точки экстремума функции и определить их характер:
Решение: Наша функция имеет разрыв только в одной точке x= 0. Воспользуемся алгоритмом:
а)
б) найдем значения в которой производная равна нулю: y»= 0 при x= ±2,
в) отметим стационарные точки на числовой прямой и определим знаки производной:
г) посмотрим на наш рисунок, где изображены правила определения экстремумов.
Точка x= -2 точка минимума функции.
Точка x= 2 — точка минимума функции.
В точке x= 0 функция не существует.
Ответ: x= ±2 — точки минимума функции.
Задачи для самостоятельного решения
а) Найти точки экстремума функции и определить их характер: y= 5x 3 — 15x — 5.
б) Найти точки экстремума функции и определить их характер:
в) Найти точки экстремума функции и определить их характер: y= 2sin(x) — x при π ≤ x ≤ 3π.
г) Найти точки экстремума функции и определить их характер:
Из данной статьи читатель узнает о том, что такое экстремум функционального значения, а также об особенностях его использования в практической деятельности. Изучение такого концепта крайне важно для понимания основ высшей математики. Эта тема является основополагающей для более глубокого изучения курса.
Вконтакте
Что такое экстремум?
В школьном курсе дается множество определений понятия «экстремум». Данная статья призвана дать самое глубокое и четкое представление о термине для несведущих в вопросе лиц. Итак, под термином понимают, насколько функциональный промежуток приобретает минимальное либо максимальное значение на том или ином множестве.
Итак, под термином понимают, насколько функциональный промежуток приобретает минимальное либо максимальное значение на том или ином множестве.
Экстремум – это и минимальное значение функции, и максимальное одновременно. Различают точку минимума и точку максимума, то есть крайние значения аргумента на графике. Основные науки, в которых используют данный концепт:
- статистика;
- машинное управление;
- эконометрика.
Точки экстремума играют важную роль в определении последовательности заданной функции. Система координат на графике в лучшем виде показывает изменение экстремального положения в зависимости от изменения функциональности.
Экстремумы производной функции
Имеет также место такое явление, как «производная». Она необходима для определения точки экстремума. Важно не путать точки минимума либо максимума с наибольшим и наименьшим значением. Это разные понятия, хотя могут показаться похожими.
Значение функции является основным фактором для определения того, как найти точку максимума. Производная не образуется от значений, а исключительно от крайнего ее положения в том или ином его порядке.
Производная не образуется от значений, а исключительно от крайнего ее положения в том или ином его порядке.
Сама же по себе производная определяется на основе данных точек экстремума, а не наибольшего или наименьшего значения. В российских школах недостаточно четко проводят грань между этими двумя концептами, что влияет на понимание данной темы вообще.
Давайте теперь рассмотрим такое понятие как «острый экстремум». На сегодняшний день выделяют острый минимум значения и острый максимум значения. Определение дано в соответствии с российской классификацией критических точек функции. Концепт точки экстремума лежит в основе нахождения критических точек на графике.
Для определения такого понятия прибегают к использованию теоремы Ферма. Она является важнейшей в ходе изучения крайних точек и дает четкое представление об их существовании в том или ином их виде. Для обеспечения экстремальности важно создать определенные условия для убывания либо возрастания на графике.
Для точного ответить на вопрос «как найти точку максимума», необходимо следовать таким положениям:
- Нахождение точной области определения на графике.

- Поиск производной функции и точки экстремума.
- Решать стандартные неравенства на область нахождения аргумента.
- Уметь доказывать, в каких функциях точка на графике определена и непрерывна.
Внимание! Поиск критической точки функции возможен только в случае существования производной не менее второго порядка, что обеспечивается высокой долей наличия точки экстремума.
Необходимое условие экстремума функции
Для того чтобы существовал экстремум, важно, чтобы были как точки минимума, так и точки максимума. В случае если это правило соблюдено лишь частично, то условие существование экстремума нарушается.
Каждая функция в любом положении должна быть продифференцирована с целью выявления ее новых значений. Важно понимать, что случай обращения точки в ноль не является основным принципом нахождения дифференцируемой точки.
Острый экстремум, также как и минимум функции – это крайне важный аспект решения математической задачи с использованием экстремальных значений. Для того чтобы лучше понимать данную составляющую, важно обратиться к табличным значениям по заданию функционала.
Для того чтобы лучше понимать данную составляющую, важно обратиться к табличным значениям по заданию функционала.
| Полное исследование значения | Построение графика значения |
| 1. Определение точек возрастания и убывания значений. 2. Нахождение точек разрыва, экстремума и пересечение с координатными осями. 3. Процесс определения изменений положения на графике. 4. Определение показателя и направления выпуклости и выгнутости с учетом наличия асимптот. 5. Создание сводной таблицы исследования с точки зрения определения ее координат. 6. Нахождение промежутков возрастания и убывания крайних и острых точек. 7. Определение выпуклости и вогнутости кривой. 8. Построение графика с учетом исследования позволяет найти минимум либо максимум. | Основным элементом при необходимости работы с экстремумами является точное построение его графика. Школьные учителя не часто уделяют столь важному аспекту максимум внимания, что является грубейшим нарушением учебного процесса. Построение графика происходит только по итогам исследования функциональных данных, определения острых экстремумов, а также точек на графике. Острые экстремумы производной функции отображаются на графике точных значений, с использованием стандартной процедуры определения асимптот. Точки максимума и минимума функции сопровождаются более сложными построениями графика. Это обусловлено более глубокой необходимостью прорабатывать проблему острого экстремума. Необходимо также находить производную сложной и простой функции, так как это одно из самых главных понятий проблематики экстремума. |
Экстремум функционала
Для того чтобы отыскать вышеозначенное значение, необходимо придерживаться следующих правил:
- определить необходимое условие экстремального отношения;
- учитывать достаточное условие крайних точек на графике;
- осуществлять расчет острого экстремума.
Используются также такие понятия, как слабый минимум и сильный минимум. Это необходимо учитывать при определении экстремума и точного его расчета. При этом острый функционал – это поиск и создание всех необходимых условий для работы с графиком функции.
Это необходимо учитывать при определении экстремума и точного его расчета. При этом острый функционал – это поиск и создание всех необходимых условий для работы с графиком функции.
Калькулятор локальных максимумов и минимумов с шагами
Онлайн-калькулятор локальных максимумов и минимумов был специально разработан для ученых и математиков, чтобы получать мгновенные результаты относительно максимумов и минимумов.
Ниже в этом чтении мы обсудим, что такое локальные максимумы, локальные минимумы и как вычислить эти параметры вручную или с помощью бесплатного калькулятора локальных минимумов и максимумов.
Развлекаемся вместе!
Что такое локальные максимумы и минимумы?
В контексте математического анализа мы имеем:
Локальные максимумы:
Точка (x, y) на функции f(x), координата y которой больше, чем все координаты y других точек, которые фактически близко к (х, у).
Локальные минимумы:
Конкретная точка (x, y) на графике функции, координата y которой является наименьшей для всех других координат y других точек, близких к (x, y).
Определение локальных максимумов и минимумов:
Самый надежный метод нахождения локальных максимумов и минимумов любой функции — калькулятор локальных максимумов и минимумов. Но вы должны быть в состоянии понять ручные расчеты. Ниже приведены ключевые моменты, которые вы должны иметь в виду при нахождении локальных максимумов и минимумов функции:
Взять производную функции:
Когда у вас есть функция, вы сначала смотрите, является ли эта функция дифференцируемой или нет. Если да, то определить производную функции. Кроме того, вы также можете использовать наш лучший калькулятор производных, чтобы найти производную любой функции за несколько секунд. Это определенно поможет вам минимизировать время вычислений и повысить точность.
Разложить полученную производную функцию на множители:
После дифференцирования функции на меньшие значения приступайте к поиску множителей функции. Одна вещь здесь заключается в том, что факторинг может потребовать некоторого дополнительного времени, чтобы обдумать числа, которые могут удовлетворять данной функции. Именно поэтому вы можете воспользоваться нашим калькулятором факторинга, чтобы сразу определить коэффициенты любой функции. Как это звучит?
Именно поэтому вы можете воспользоваться нашим калькулятором факторинга, чтобы сразу определить коэффициенты любой функции. Как это звучит?
Определение критических точек:
Итак, следующий метод — это определение критических точек, точек, в которых функция не может дифференцироваться. Вы можете найти эти точки, приравняв множители к нулю, и решить для определенного значения x. Но если вам это покажется сложным, наш калькулятор критических точек сделает это за вас за считанные секунды.
Поиск локальных максимумов и минимумов:
В конце подставьте значения критических точек в исходное уравнение одно за другим, чтобы определить локальные максимумы и минимумы функции. Но, воспользовавшись нашим лучшим онлайн-калькулятором локальных максимумов и минимумов, вы определенно сможете определить все вышеперечисленные параметры за пару кликов.
Как найти локальные максимумы и минимумы?
Хорошо, давайте перейдем к решению примера, который прояснит ваше представление об обсуждаемых параметрах.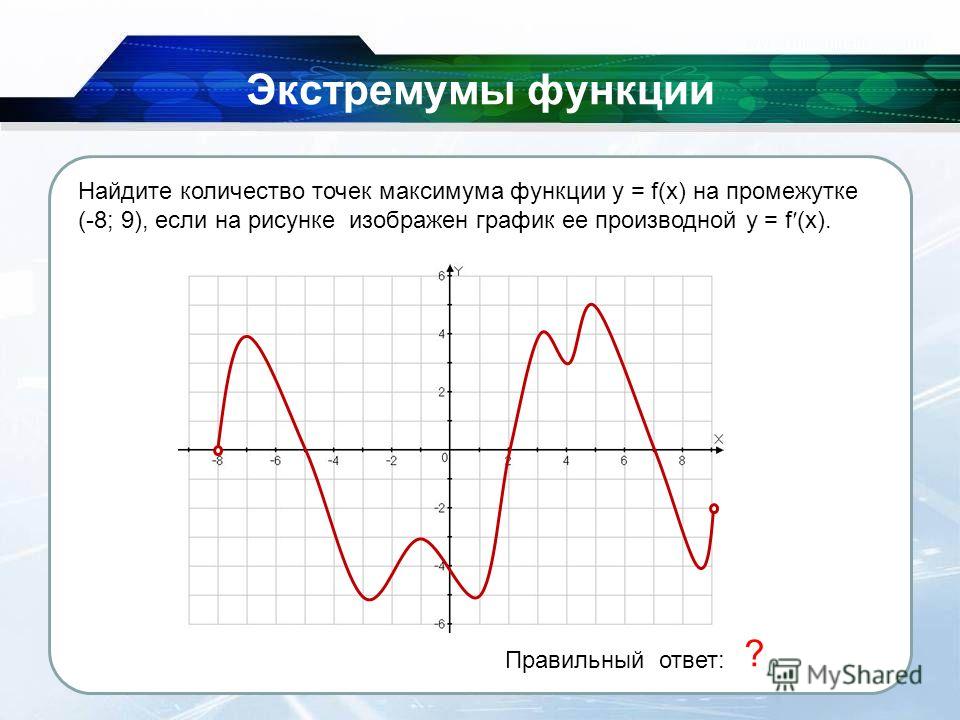 9{2} + 6x $$
9{2} + 6x $$
$$ 6x\влево(2x + 1\вправо) $$
$$ Факторы = 6x \hspace{0,025in} и \hspace{0,025in} 2x+1 $$
Бесплатно Онлайн-калькулятор локальных максимумов и минимумов также найдет эти ответы, но за считанные секунды, что сэкономит вам много времени.
Критические точки:
Обнуление множителей:
$$ 6x = 0 $$
$$ x = 0 $$
И
$$ 2x+1 =0 $$
$$ x = — \frac{1}{2} $$
Локальные максимумы и локальные минимумы:
Здесь имеем: 9{2} $$
$$ \frac{-4}{8} + \frac{3}{4} $$
$$ \frac{-4+6}{8} $$
$$ \frac{ 2}{8} $$
$$ \frac{1}{4} $$
Результат:
Локальные максимумы: (-½, ¼)
Локальные минимумы: (0, 0)
Как Локальные максимумы А калькулятор минимумов работает?
Пусть этот бесплатный калькулятор минимального максимума найдет наименьшее и наибольшее значение любой функции за пару секунд. Хотите знать, как это работает на самом деле? Давайте идти!
Ввод:
- Что вам нужно сделать, так это просто написать уравнение функции в специально отведенном поле
- После этого нажмите кнопку расчета
Вывод:
Бесплатный локальный калькулятор минимума и максимума определяет:
- Производная функции
- Факторы производной функции
- Критические точки функции
- Локальные максимумы и минимумы
Часто задаваемые вопросы:
В чем разница между локальными максимумами и абсолютными максимумами?
Абсолютные максимумы — это значение функции, которое является наибольшим и сохраняется во всей области определения функции. С другой стороны, локальные максимумы — это максимальное значение функции, но оно лежит в подмножестве области. Интересным фактом является то, что вы можете сразу найти все эти параметры, воспользовавшись бесплатным локальным калькулятором максимума и минимума.
С другой стороны, локальные максимумы — это максимальное значение функции, но оно лежит в подмножестве области. Интересным фактом является то, что вы можете сразу найти все эти параметры, воспользовавшись бесплатным локальным калькулятором максимума и минимума.
Что такое абсолютный минимум?
Абсолютные минимумы – это точки, соответствующие наименьшему значению функции, которое остается постоянным во всей области. Вы также можете легко определить абсолютный минимум с помощью бесплатного онлайн-калькулятора максимума и минимума.
В чем смысл инверсии?
Любое значение x в области определения функции, которое не является ни максимальным, ни минимальным, называется точкой инверсии. Имейте в виду, что самые ближайшие точки слева или справа от точки инверсии имеют нулевой наклон.
Что такое теорема об экстремальных значениях?
Если функция определена и непрерывна в пределах интервала [a, b], существуют точки c и d, которые присутствуют в интервале [a, b]. Для этих значений функция f получает максимальное и минимальное значения.
Для этих значений функция f получает максимальное и минимальное значения.
f(c) > f(x) > f(d)
Каков локальный минимум функции, как показано ниже:
f(x) = 2
Поскольку производная функции равна 0, локальный минимум равен 2, что также может быть подтверждено калькулятором относительного минимума и показано на следующем графике:
Можем ли мы рассматривать все глобальные максимумы как локальные максимумы?
Глобальные максимумы всегда равны одному значению соответственно. Но когда мы говорим о локальных максимумах, их больше одного. Другая причина заключается в том, что глобальные максимумы являются наибольшим значением, в то время как локальные максимумы являются наибольшим значением в области подмножества. Поэтому глобальные максимумы нельзя считать локальными максимумами.
Что такое локальные минимумы в массиве?
Если число в массиве является наименьшим как из левых, так и из правых его частей, то оно называется локальным минимумом в массиве.
Например:
Посмотрите на следующий массив чисел:
4, 4, 6, 3, 3, 2, 4, 5, 7
В приведенном выше массиве число 2 рассматривается как локальные минимумы массива, так как числа слева и справа от него больше его и равны 3 и 4 соответственно.
Примечание: процесс получает наоборот, если вас интересует определение локальных максимумов массива.
Вывод:
Итак, пока мы имели краткий обзор концептуальной теории максимальных и минимальных значений функции. Основной факт, стоящий за этим контекстом и дизайном этого бесплатного калькулятора локальных максимумов и минимумов, заключается в том, что он широко используется для оценки различных явлений. Наиболее важными из них являются оценка высоты ракеты, которую она достигнет после запуска, максимальное или минимальное количество алюминия, которое потребуется для изготовления консервных банок, и решение многих других задач оптимизации.
Ссылки:
Из источника википедии: Максимумы и минимумы, Функции более чем одной переменной, По отношению к множествам
Из источника академии хана: Абсолютные максимумы и минимумы, Относительные максимумы и минимумы
Из источника изучения светового потока: максимумы и минимумы, абсолютные экстремумы, локальные экстремумы и критические точки, поиск абсолютных экстремумов
Критические точки и тест первой производной — Криста Кинг Математика
Что такое критические точки и как их найти?
Процесс оптимизации заключается в поиске наименьшего и наибольшего значений функции. Если мы воспользуемся калькулятором, чтобы нарисовать график функции, мы обычно сможем определить наименьшее и наибольшее значения.
Если мы воспользуемся калькулятором, чтобы нарисовать график функции, мы обычно сможем определить наименьшее и наибольшее значения.
Привет! Я Криста.
Я создаю онлайн-курсы, чтобы помочь вам в учебе по математике. Читать далее.
Например, для функции, показанной ниже, мы можем увидеть, просто взглянув на график, что функция достигает своего наименьшего значения в точке ???A???. Эта нижняя возможная точка является 9 функцией.0015 глобальный минимум .
Есть причина, по которой важно найти этот глобальный минимум. Давайте на мгновение представим, что функция, показанная на графике, на самом деле моделирует вероятность того, что продукты испортятся в морозильной камере ресторана при разных температурах.
Если я владелец бизнеса этого ресторана и хочу свести к минимуму вероятность того, что моя еда испортится, то мне очень интересно найти этот глобальный минимум. Если я знаю, как посчитать это значение, то я буду знать точную температуру, на которую следует установить морозильник, чтобы свести к минимуму вероятность того, что моя еда испортится.
Если я знаю, как посчитать это значение, то я буду знать точную температуру, на которую следует установить морозильник, чтобы свести к минимуму вероятность того, что моя еда испортится.
И это действительно ценно! Правильное соблюдение этого правила может сэкономить мне время и деньги, а также поможет обеспечить бесперебойную работу моего ресторана и добиться успеха в долгосрочной перспективе.
Вот что такое оптимизация. Это позволяет нам рассчитать точку, в которой функция максимизируется или минимизируется, и у этого есть все виды реальных приложений, о которых мы подробно поговорим позже в курсе.
В этом разделе мы поговорим о процессе оптимизации, начиная с того, как найти наименьшее и наибольшее значения функции. Мы закончим раздел, переведя эти шаги оптимизации в изучение того, как рисовать график функции.
Локальные и глобальные экстремумы
В общем случае наименьшее и наибольшее значения функции являются ее экстремумами . Думайте об экстремумах как о «экстремальных точках» функции.
Думайте об экстремумах как о «экстремальных точках» функции.
Экстремумы функции состоят из ее наименьших точек, которые мы называем минимумами , и ее наибольших точек, которые мы называем максимумами .
Внутри минимумов функции различают локальные (относительные) минимумы и глобальные (абсолютные) минимумы. А внутри максимумов функции мы различаем локальные (относительные) максимумы и глобальные (относительные) максимумы.
В качестве примера давайте снова посмотрим на тот же график, что и раньше.
Мы уже сказали, что абсолютный/глобальный минимум функции находится в точке ???A???, и это потому, что ???A??? это точка, в которой функция имеет наименьшее значение во всей области определения. Но функция также имеет локальный минимум при ???C???, потому что ???C??? является низшей точкой функции в области вблизи ???C???.
Функция также имеет локальный максимум в точке ???B???, потому что ???B??? является наивысшей точкой функции в районе ???B???.
Мы бы не определили абсолютный максимум для функции, потому что он стремится к ???\infty??? оба слева от ???A??? и справа от ???C???, так что мы не можем назвать конечную точку, которая описывала бы наибольшее значение, которое когда-либо достигает функция.
Таким образом, в общем случае
локальный/относительный максимум существует везде, где функция меняет направление с возрастания на убывание. Если локальный максимум также оказывается наивысшей точкой функции в любом месте ее области определения, то это также глобальный/абсолютный максимум . Функция может иметь бесконечно много локальных/относительных максимумов, но у нее будет только один (или ни одного) глобальный/абсолютный максимум.
Локальный/относительный минимум существует везде, где функция меняет направление с убывающего на возрастающее. Если локальный минимум также является самой низкой точкой функции в любом месте ее области определения, то это также глобальный/абсолютный минимум .
 У функции может быть бесконечно много локальных/относительных минимумов, но у нее будет только один (или ни одного) глобальный/абсолютный минимум. 92???, которая представляет собой параболу с вершиной в начале координат, которая раскрывается. Эта парабола имеет только один локальный минимум при ???x=0???, этот локальный минимум также является глобальным минимумом, но парабола не имеет ни локального максимума, ни глобального максимума.
У функции может быть бесконечно много локальных/относительных минимумов, но у нее будет только один (или ни одного) глобальный/абсолютный минимум. 92???, которая представляет собой параболу с вершиной в начале координат, которая раскрывается. Эта парабола имеет только один локальный минимум при ???x=0???, этот локальный минимум также является глобальным минимумом, но парабола не имеет ни локального максимума, ни глобального максимума.Возьмем другой пример: строка ???y=x??? это линия, которая проходит через начало координат с наклоном ???m=1???, и у нее вообще нет экстремумов (нет локальных максимумов или минимумов, а также нет глобальных максимумов или минимумов), потому что она никогда не меняет направление.
Итак, какие экстремумы вы сможете классифицировать, всегда будет зависеть от конкретной функции, с которой вы работаете.
Критические точки
Первым шагом в любом процессе оптимизации всегда является поиск критических точек функции.

Критические точки существуют, где производная равна ???0??? (или, возможно, где производная не определена), и они представляют собой точки, в которых график функции изменит направление либо с убывания на возрастание, либо с увеличения на убывание.
Поскольку функция меняет направление в критических точках, функция всегда будет иметь по крайней мере локальный максимум или минимум в критической точке, если не глобальный максимум или минимум там.
Чтобы найти критические точки, мы просто берем производную, устанавливаем ее равной ???0???, а затем находим переменную.
Как использовать критические точки для поиска локальных и глобальных экстремумов
Пройти курс
Хотите узнать больше об исчислении 1? У меня есть пошаговый курс для этого. 🙂
Учить больше
Пошаговый пример поиска критических точек и применения теста первой производной 92=4???
???x=\pm2???
Это критические точки ???f(x)???.

Критические точки существуют там, где производная равна 0, и представляют собой точки, в которых график функции меняет направление с убывающего на возрастающее и наоборот.
Возрастание и убывание
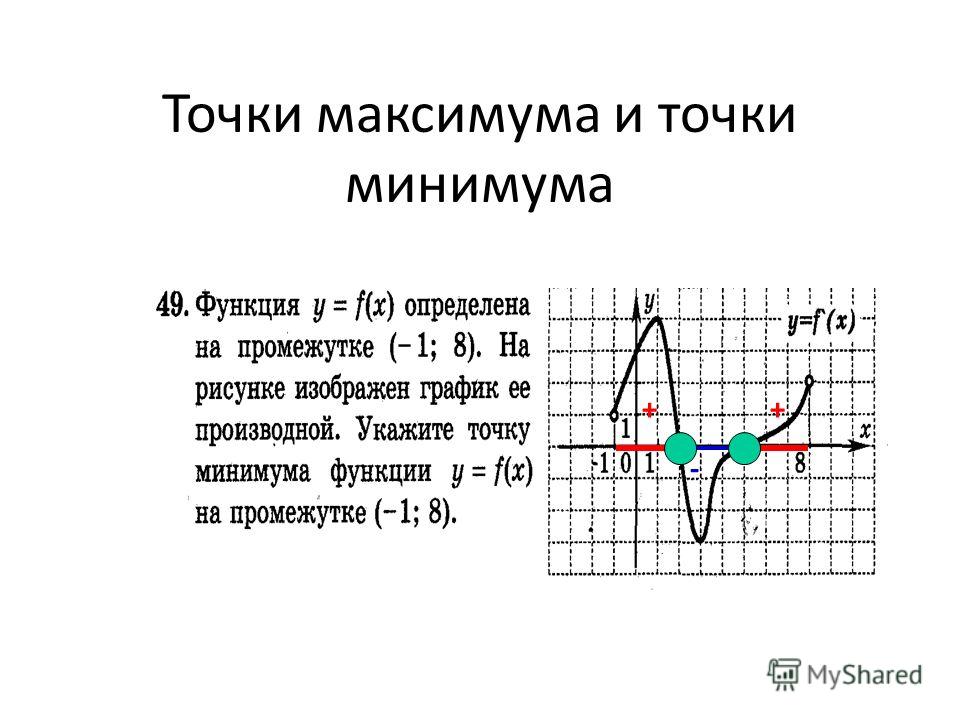
Поскольку критические точки — это точки, в которых функция меняет направление с возрастания на убывание или с убывания на возрастание, следующим шагом является исследование поведения между критическими точками.
Если производная положительна, функция возрастает. Функция — это , увеличивающая , когда она движется вверх по мере нашего движения слева направо.
Если производная отрицательна, функция убывает. Функция на уменьшается на , когда она движется вниз по мере нашего движения слева направо.
Чтобы проверить знак производной, мы просто выберем значение между каждой парой критических точек и подставим это тестовое значение в производную, чтобы посмотреть, получим ли мы положительный или отрицательный результат.
 Если тестовое значение дает положительный результат, это означает, что функция возрастает на этом интервале, а если тестовое значение дает отрицательный результат, это означает, что функция на этом интервале убывает.
Если тестовое значение дает положительный результат, это означает, что функция возрастает на этом интервале, а если тестовое значение дает отрицательный результат, это означает, что функция на этом интервале убывает.Если мы найдем одну критическую точку для функции, то нам просто нужно посмотреть на знак производной слева и справа от этой одной критической точки.
Но если мы находим несколько критических точек, то нам нужно найти знак производной слева от самой левой критической точки, справа от самой правой критической точки и между каждой критической точкой.
Продолжим один из предыдущих примеров, взглянув на знак производной между каждой критической точкой.
Пример
Критические точки функции: ???x=\pm2???. Где функция возрастает, а где убывает?
???f(x)=x+\frac{4}{x}???
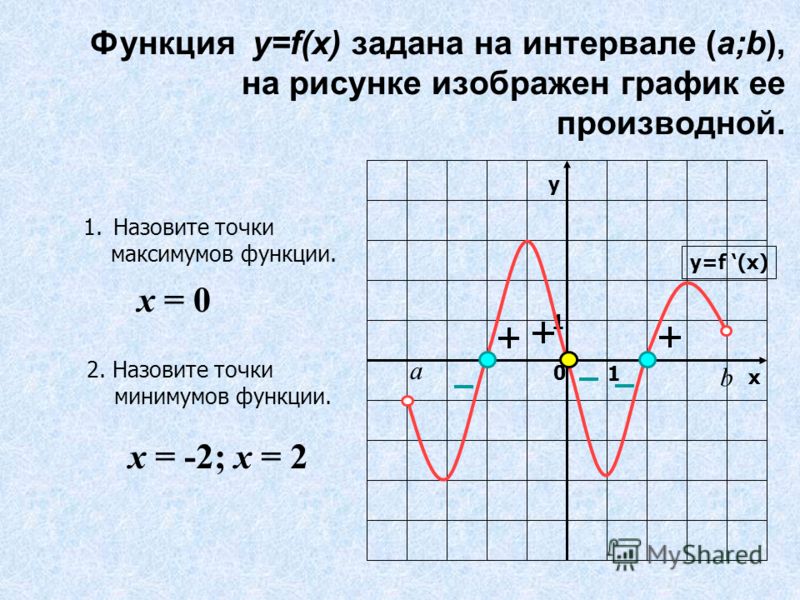
Ранее мы использовали производную, чтобы найти, что функция имеет критические точки в ???x=\pm2???. Когда у нас есть критические точки, полезно нанести их на числовую линию от наименьшего к наибольшему, слева направо.

Из этой диаграммы видно, что нам нужно протестировать три интервала. 92}???
???f'(3)=1-\frac{4}{9}???
???f'(3)=\frac{9}{9}-\frac{4}{9}???
???f'(3)=\frac{5}{9}>0???
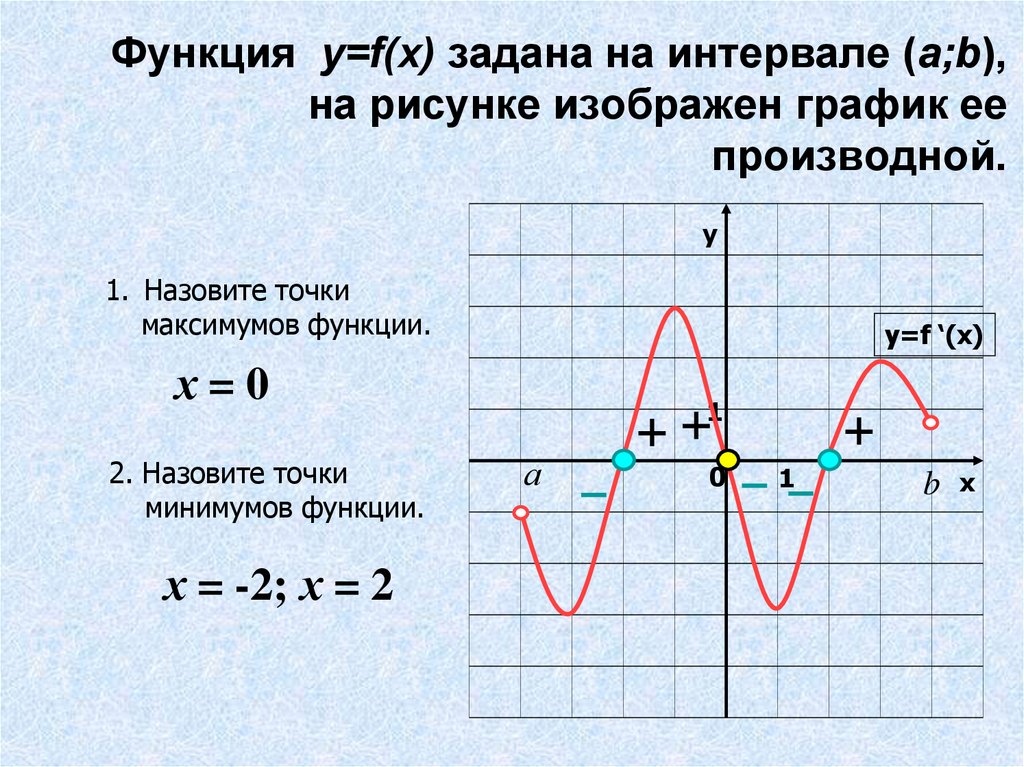
Производная была положительной на первом интервале, отрицательной на втором интервале и положительной на третьем интервале. Нанесите эти знаки на диаграмму критических точек, которую мы нарисовали ранее.
Помните, что исходная функция ???f(x)??? увеличивается там, где мы нашли положительный результат, и уменьшается там, где мы нашли отрицательный результат. Так что можно сказать
???f(x)??? увеличивается на ???-\infty
???f(x)??? убывает на ???-2
???f(x)??? увеличивается на ???2
Проверка первой производной
После того, как мы нашли интервалы, на которых функция возрастает и убывает, мы фактически уже завершили проверку первой производной, за исключением того, что прямо заявили выводы о максимальном и минимальном значениях функции.
 .
.Потому что тест первой производной — это просто тест для нахождения максимума и минимума функции.
Другими словами, если у нас есть диаграмма критических точек, заполненная знаками производной,
критерий первой производной позволяет сделать следующие выводы:
Если слева от критической точки производная отрицательна, а справа от нее положительна, то график имеет в этой точке локальный минимум (возможно, это местный минимум может быть глобальным минимумом).
Если производная положительна слева от критической точки и отрицательна справа от нее, график имеет локальный максимум в этой точке (и, возможно, этот локальный максимум может быть глобальным максимумом).
Итак, для предыдущего примера проверка первой производной позволяет сделать вывод, что функция имеет локальный максимум в точке ???x=-2??? и локальный минимум при ???x=2???.

Получить доступ к полному курсу исчисления 1
Начать
Изучайте математикуКриста Кинг математика, учитесь онлайн, онлайн-курс, онлайн-математика, исчисление 1, исчисление i, исчисление 1, исчисление i, приложения производных, приложения дифференцирования, производные приложения, рисование графиков, рисование кривых, зарисовка кривых, зарисовка графиков, критические точки, поиск критических точек, тест первой производной, локальный максимум, локальные максимумы, локальные экстремумы, локальный экстремум, локальный минимум, локальные минимумы, глобальные экстремумы, глобальные максимумы, глобальный максимум, глобальные минимумы, глобальный минимум, относительный экстремум, относительный экстремум, относительный максимум, относительный максимум, относительный минимум, относительный минимум, абсолютный экстремум, абсолютный экстремум, абсолютный максимум, абсолютный максимум, абсолютный минимум, абсолютный минимум, оптимизация
0 лайковПервый производный тест
Первый производный тест
Первый производный тест (Мотивация и теорема)
Если f — функция, то f имеет относительный максимум при x = c, если для всех точек a вблизи c, f(c) > f(a), и f имеет относительный минимум при x = c, если для всех точек a вблизи c, f(c) < f(a).

Рассмотрим относительный максимум, он у нас слева, функция возрастает а справа функция убывающая. Так же и для родственника минимум, справа функция убывающая, а слева функция растет.
Теперь мы можем сформулировать первый критерий производной:
Первый производный тест
Позволять ф быть дифференцируемой функцией с ф ‘(с) = 0 тогда
Если ф'(х) изменяется с положительного на отрицательное, а затем ф есть родственник максимум при в.
Если ф ‘(x) меняется с отрицательного на положительное, тогда у f есть родственник минимум в с.
Пример
Найдите и классифицируйте относительные экстремумы
f(x) = x(1 — x) 2/5
Решение
Сначала установите первую производную равной нулю, чтобы найти критические точки.

f ‘(x) = (1 — x) 2/5 — 2/5 х (1 — х) -3/5 = 0
Теперь умножьте на (1 — х) 3/5
(1 — х) — 2/5 х = 0, 1–7/5 x = 0, x = 5/7 @ 0,714Так что есть критическая точка на 5/7. Уведомление также, что существует критическая точка при x = 1, так как первый производная там не определена (обратите внимание на отрицательный показатель степени -3/5). Чтобы определить, является ли критическим точка является относительным максимумом, минимумом или ни тем, ни другим, выберите число чуть выше и просто ниже критического значения.
х 0,7 0,8 2 ф'(х) 0,04 -0,3 1,8 Результат Увеличение По убыванию Увеличение
Мы видим, что f возрастает слева от критического числа и убывает справа от критического числа. Следовательно, 5/7 — это
относительный максимум.
Следовательно, 5/7 — это
относительный максимум. Фактический график показан ниже
Упражнение
Классифицировать относительные экстремумы
е (х) = х + 1 / х
Ответ (Наведите указатель мыши на желтый прямоугольник)
Глобальный экстремум
Определение глобального экстремума
Мы говорим, что функция f имеет глобальный максимум (минимум) на [бита с если для всех х в [а, б],
f(c) > x (f(c) < x)
Для определения глобального максимума и минимума поступим следующим образом:
1) Найдите все критические точки f и запишите значения y в таблицу.

2) Найдите f(a) и f(b) и добавить их в таблицу.
3) Наибольшее число в таблице будет глобальным максимумом, и наименьшее число в таблице будет глобальным минимумом.
Пример
Найдите глобальный максимум и минимум
е(х) = 2х 3 +3x 2 — 36x + 2
на интервале [-10,3]
Решение
Мы вычисляем
f'(x) = 6x 2 + 6x — 36 = 6(x - 2)(x + 3)
Следовательно, есть критические точки при 2 и -3.
Мы вычисляем f(2) = -42, f(-3) = 83, f(-10) = -1942, f(3) = -25
с ф(к) -10 -1338 -3 83 2 -42 3 -25 Следовательно, на [-10,3] f имеет глобальный минимум -1338 при x = -10 и глобальный максимум 83 при x = -3.

Ниже представлен график.
Упражнение:
Найдите абсолютные экстремумы
х 3 — 12х на отрезке [0,4].
Ответ (Наведите указатель мыши на желтый прямоугольник)
Заявка
Стоимость в центах поставки x гамбургеров составляет
С = .5x 2 + 100 0 < х < 200
Определить количество гамбургеров, при котором средняя стоимость будет минимальной.
Решение
Средняя стоимость определяется путем деления стоимости на количество единиц. Мы имеют
пр. = С/х = 0,5 х + 200/х
Возьмите производную, чтобы найти критические точки
авеню = 0,5 — 200/x 2 = 0 Умножить по х 2
0,5 x 2 — 200 = 0
х 2 + 400 = 0
x = 20
Теперь используйте таблицу, чтобы определить, минимум происходит в критической точке или конечной точке.


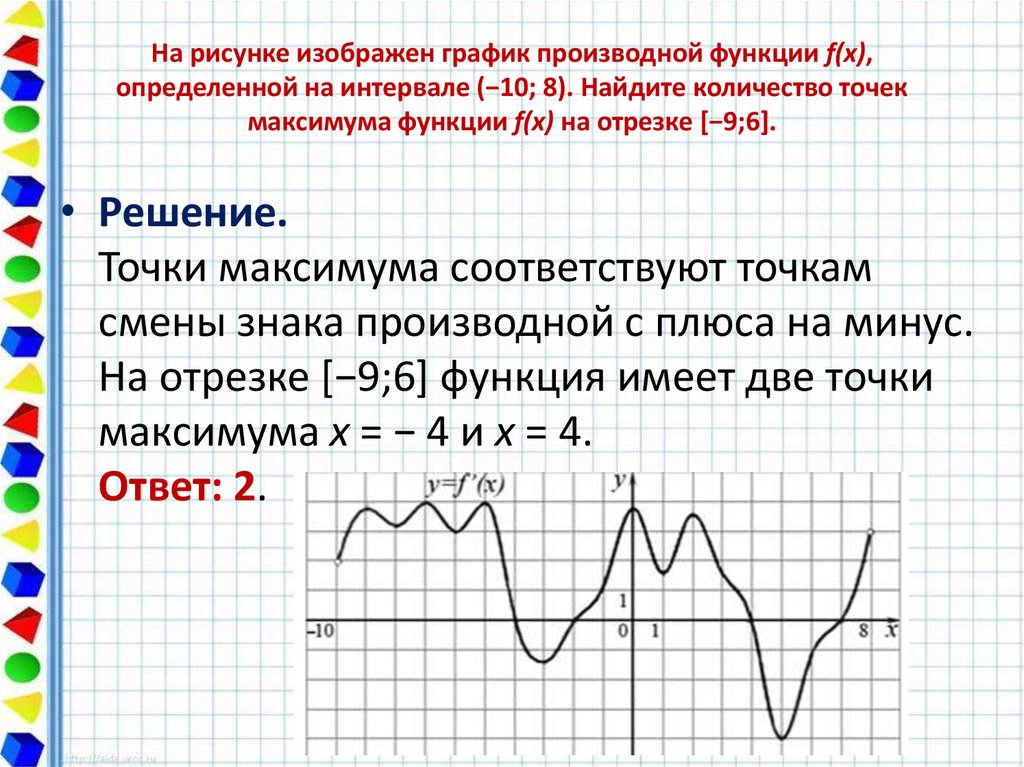 Поэтому f(x) — f(x 0 ) f(x) f(x 0 ) .
Поэтому f(x) — f(x 0 ) f(x) f(x 0 ) .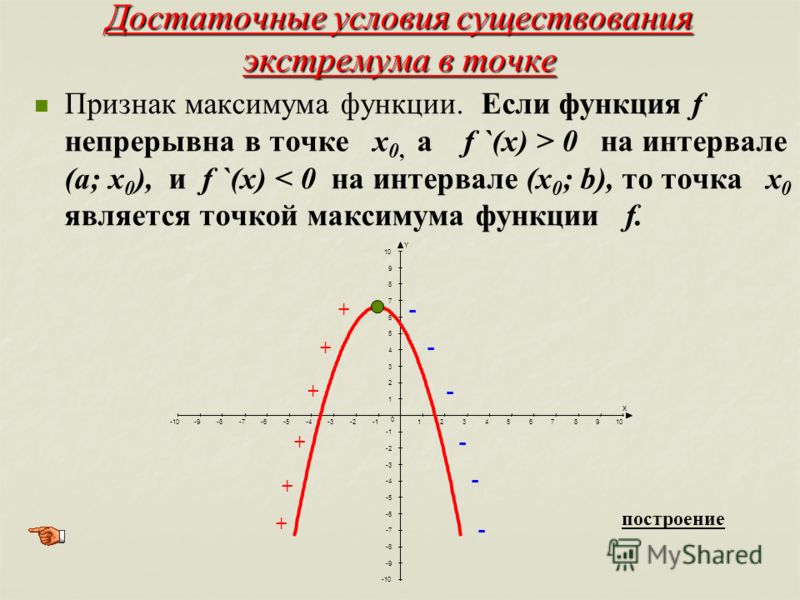
 У функции может быть бесконечно много локальных/относительных минимумов, но у нее будет только один (или ни одного) глобальный/абсолютный минимум. 92???, которая представляет собой параболу с вершиной в начале координат, которая раскрывается. Эта парабола имеет только один локальный минимум при ???x=0???, этот локальный минимум также является глобальным минимумом, но парабола не имеет ни локального максимума, ни глобального максимума.
У функции может быть бесконечно много локальных/относительных минимумов, но у нее будет только один (или ни одного) глобальный/абсолютный минимум. 92???, которая представляет собой параболу с вершиной в начале координат, которая раскрывается. Эта парабола имеет только один локальный минимум при ???x=0???, этот локальный минимум также является глобальным минимумом, но парабола не имеет ни локального максимума, ни глобального максимума.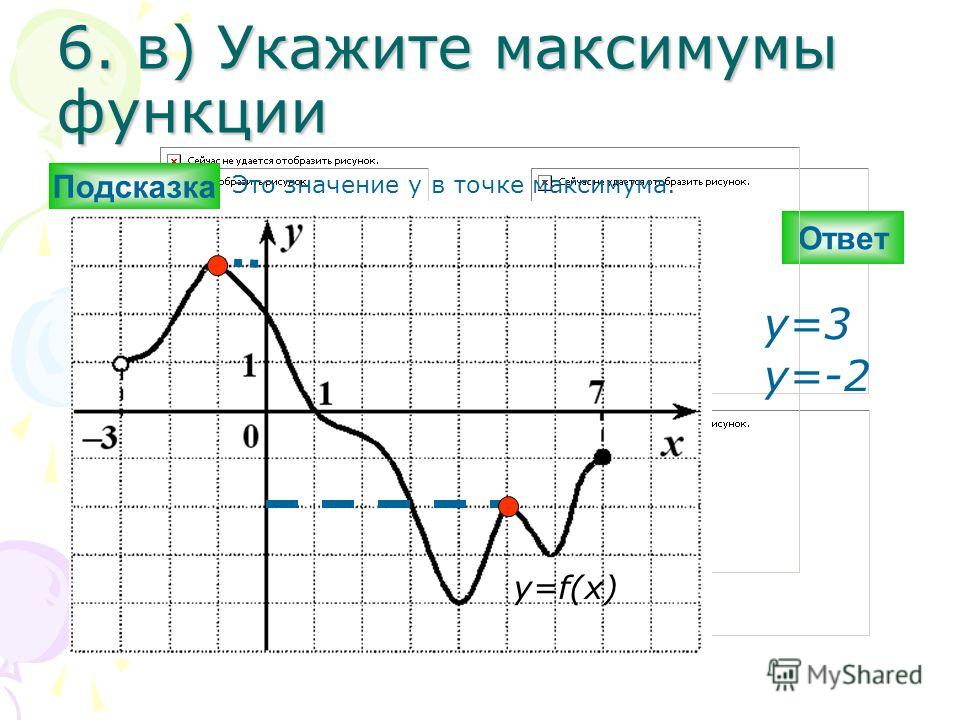

 Если тестовое значение дает положительный результат, это означает, что функция возрастает на этом интервале, а если тестовое значение дает отрицательный результат, это означает, что функция на этом интервале убывает.
Если тестовое значение дает положительный результат, это означает, что функция возрастает на этом интервале, а если тестовое значение дает отрицательный результат, это означает, что функция на этом интервале убывает.
 .
.
 Следовательно, 5/7 — это
относительный максимум.
Следовательно, 5/7 — это
относительный максимум.