Какие из следующих учреждений верны? 1) Диагонали тра… -reshimne.ru
Новые вопросы
Ответы
Похожие вопросы
Основания равнобокой трапеции равны 10 и 20 см. а диагональ является биссектрисой её тупого угла Найдите площадь этой трапеции…
Пожалуйста решите задачу, через 2 часа надо сдать!!!Найти:NP…
При пересечении двух прямых получилось 4 угла. Величина одного из углов в градусах на 136 больше другого. Найти сумму двух самых больших углов…
Найдите все углы треугольника MNK, если они пропорциональны следующим числам 3;4;5.
..
В прямоугольном треугольнике всk угол в=90, угол с =60, вс=12 см.
Найдите гипотенузу….
Математика
Литература
Алгебра
Русский язык
ГеометрияАнглийский язык
Химия
Физика
Биология
Другие предметы
История
Обществознание
Окружающий мир
География
Українська мова
Українська література
Қазақ тiлi
Беларуская мова
Информатика
ЭкономикаМузыка
Право
Французский язык
Немецкий язык
МХК
ОБЖ
| Утверждение | Верно? |
| Биссектриса равнобедренного треугольника, проведённая из вершины, противолежащей основанию, делит основание на две равные части. | Да |
| Внешний угол треугольника больше каждого не смежного с ним внутреннего угла. | Да |
| В прямоугольном треугольнике катет больше гипотенузы. | Нет |
| В треугольнике АВС, для которого АВ = 4, ВС = 5, АС = 6, угол B — наибольший. | Да |
| Диагонали параллелограмма пересекаются под прямым углом и в точке пересечения делятся пополам. | Нет |
| Биссектриса равнобедренного треугольника, проведённая из вершины перпендикулярна основанию. | Да |
| Биссектриса треугольника делит пополам сторону, к которой проведена? | Нет |
| Биссектриса угла делит угол пополам. | Да |
Биссектриса угла любого параллелограмма является его диагональю. | Нет |
| Биссектриса угла треугольника делит противоположную сторону на отрезки, пропорциональные двум другим сторонам. | Да |
| Биссектрисы смежных углов взаимно перпендикулярны. | Да |
| Биссектрисы треугольника не могут пересекаться в одной точке | Нет |
| Биссектрисы треугольника пересекаются в одной точке, которая является центром окружности, описанной около этого треугольника. | Нет |
| Биссектрисы треугольника пересекаются в центре его вписанной окружности. | Да |
| Биссектрисы углов параллелограмма прилежащих к одной стороне, пересекаются под прямым углом. | |
| Вертикальные углы равны. | Да |
| В каждом треугольнике углы при основании равны. | Нет |
| В квадрате диагонали пересекаются под прямым углом. | Да |
В любой выпуклый семиугольник можно вписать окружность. | Нет |
| В любой прямоугольник можно вписать окружность. | Нет |
| В любой прямоугольный треугольник можно вписать окружность. | Да |
| В любой ромб можно вписать окружность. | Да |
| В любой трапеции диагонали перпендикулярны. | Нет |
| В любой трапеции диагонали равны. | Нет |
| В любой треугольник можно вписать окружность. | Да |
| В любой четырёхугольник можно вписать не более одной окружности. | Да |
| В любой четырёхугольник можно вписать окружность. | Нет |
| В любом выпуклом четырёхугольнике все углы острые. | Нет |
| В любом выпуклом четырёхугольнике все углы прямые. | Нет |
| В любом выпуклом четырёхугольнике все углы тупые. | Нет |
В любом описанном около окружности четырехугольнике суммы противоположных сторон равны. | Да |
| В любом описанном четырёхугольнике сумма противоположных углов равна 180°. | Да |
| В любом параллелограмме диагонали равны. | Нет |
| В любом параллелограмме диагонали точкой пересечения делятся пополам. | Да |
| В любом прямоугольнике все стороны равны. | Нет |
| В любом прямоугольнике диагонали взаимно перпендикулярны. | Нет |
| В любом прямоугольнике диагонали равны. | Да |
| В любом равнобедренном треугольнике медиана, проведённая из вершины основания, является биссектрисой и высотой. | Да |
| В любом ромбе диагонали перпендикулярны. | Да |
| В любом треугольнике выполняется теорема Пифагора. | Нет |
| В любом треугольнике против большего угла лежит большая сторона. | Да |
В любом треугольнике против большей стороны лежит меньший угол. | Нет |
| В любом треугольнике сумма двух сторон больше третьей стороны. | Да |
| В любом треугольнике сумма двух сторон меньше третьей стороны. | Нет |
| В любом тупоугольном треугольнике есть острый угол. | Да |
| В любую окружность можно вписать два подобных, но неравных треугольника. | Нет |
| В любую окружность можно вписать прямоугольник. | Да |
| В любую равнобедренную трапецию можно вписать окружность. | Нет |
| Внешний угол треугольника больше каждого внутреннего угла. | Нет |
| Внешний угол треугольника больше не смежного с ним внутреннего угла. | Да |
| Внешний угол треугольника всегда тупой. | Нет |
| Внешний угол треугольника равен сумме двух внутренних углов, не смежных с ним. | Да |
Внешний угол треугольника равен сумме его внутренних углов. | Нет |
| Внутренние накрест лежащие углы, образованные двумя параллельными прямыми и секущей, равны. | Да |
| Во всякий четырёхугольник можно вписать окружность. | Нет |
| Во всяком треугольнике биссектриса угла равна его медиане. | Нет |
| Во всяком треугольнике высота проведённая к основанию, совпадает с медианой. | Нет |
| Вокруг любого выпуклого восьмиугольника можно описать окружность. | Нет |
| Вокруг любого параллелограмма можно описать окружность. | Нет |
| Вокруг любого треугольника можно описать окружность. | Да |
| Вокруг любого четырёхугольника можно описать окружность. | Нет |
| Вокруг параллелограмма всегда можно описать окружность. | Нет |
| Вокруг равнобедренной трапеции можно описать окружность. | Да |
Вокруг тупоугольного треугольника нельзя описать окружность. | Нет |
| В окружности на диаметр опирается прямой угол. | Да |
| В окружности радиуса 2 можно провести хорду длиной 3. | Да |
| В окружность можно вписать угол, равный 200° | Нет |
| В параллелограмме все стороны равны. | Нет |
| В параллелограмме диагонали точкой пересечения делятся пополам. | Да |
| В параллелограмме есть два равных угла. | Да |
| В параллелограмме противоположные углы равны. | Да |
| Вписанные углы окружности равны. | Нет |
| Вписанные углы, опирающиеся на одну и ту же дугу, равны. | Да |
| Вписанные углы, опирающиеся на одну и ту же хорду окружности, равны. | Нет |
| Вписанный угол измеряется дугой, на которую он опирается. | Нет |
Вписанный угол измеряется половиной дуги, на которую он опирается. | Да |
| Вписанный угол, опирающийся на диаметр окружности, прямой. | Да |
| Вписанный угол, опирающийся на диаметр окружности, равен 90°. | Да |
| Вписанный угол, опирающийся на полуокружность — развёрнутый. | Нет |
| Вписанный угол равен половине угловой величины дуги, на которую он опирается. | Да |
| Вписанный угол равен половине центрального, опирающегося на туже дугу. | Да |
| В плоскости все точки, равноудалённые от заданной точки, лежат на одной окружности. | Да |
| В плоскости для точки, лежащей вне круга, расстояние до центра круга больше его радиуса. | Да |
| В подобных треугольниках соответствующие стороны равны. | Нет |
| В подобных треугольниках сходственные стороны пропорциональны. | Да |
| В правильном многоугольнике все стороны равны. | Да |
В правильном многоугольнике все углы равны. | Да |
| В правильном треугольнике все углы прямые. | Нет |
| В прямоугольнике диагонали являются биссектрисами. | Нет |
| В прямоугольнике диагонали являются биссектрисами его углов. | Нет |
| В прямоугольной трапеции основания параллельны. | Да |
| В прямоугольном треугольнике гипотенуза больше катета. | Да |
| В прямоугольном треугольнике гипотенуза меньше катета. | Нет |
| В прямоугольном треугольнике гипотенуза в два раза больше каждого из катетов. | Нет |
| В прямоугольном треугольнике гипотенуза всегда меньше суммы его катетов. | Да |
| В прямоугольном треугольнике гипотенуза равна сумме катетов. | Нет |
| В прямоугольном треугольнике катет больше гипотенузы. | Нет |
В прямоугольном треугольнике катет, лежащий против угла к 30° равен половине гипотенузы. | Да |
| В прямоугольном треугольнике квадрат гипотенузы равен разности квадратов катетов. | Нет |
| В прямоугольном треугольнике квадрат гипотенузы равен сумме катетов. | Нет |
| В прямоугольном треугольнике любой катет меньше гипотенузы. | Да |
| В прямоугольном треугольнике синус одного из углов равен 0. | Нет |
| В прямоугольном треугольнике тангенсом острого угла а называется отношение sin a / cos a. | Да |
| В равнобедренной трапеции диагонали равны. | Да |
| В равнобедренной трапеции углы при основании равны. | Да |
| В равнобедренном прямоугольном треугольнике все стороны равны. | Нет |
| В равнобедренном прямоугольном треугольнике каждый острый угол равен 45°. | Да |
| В равнобедренном треугольнике все стороны равны. | Нет |
В равнобедренном треугольнике все углы равны. | Нет |
| В равнобедренном треугольнике имеется не более двух равных углов. | Нет |
| В равнобедренном треугольнике медиана, проведённая к основанию, является одновременно и биссектрисой. | Да |
| В равнобедренном треугольнике медиана, проведённая к основанию, является одновременно и высотой. | Да |
| В равнобедренном треугольнике углы при основании равны. | Да |
| В равностороннем треугольнике АВС медиана AK равна высоте CH. | Да |
| В равностороннем треугольнике все углы острые. | Да |
| В равностороннем треугольнике все углы равны. | Да |
| В равностороннем треугольнике каждый угол равен 45°. | Нет |
| В равностороннем треугольнике медианы пересекаются в одной точке. | Да |
| В ромбе все углы прямые. | Нет |
В ромбе диагонали пересекаются под прямым углом. | Да |
| В ромбе противоположные углы равны. | Да |
| В ромб нельзя вписать окружность. | Нет |
| Все вписанные углы окружности равны. | Нет |
| Все высоты равностороннего треугольника равны. | Да |
| Все диаметры окружности равны между собой. | Да |
| Все квадраты имеют равные площади. | Нет |
| Все прямоугольные треугольники подобны. | Нет |
| Все прямоугольные треугольники подобны друг другу. | Нет |
| Все равнобедренные треугольники подобны. | Нет |
| Все равнобедренные треугольники равны. | Нет |
| Все точки каждой из двух параллельных прямых равноудалены от другой прямой. | Да |
| Все углы квадрата прямые. | Да |
| Все углы правильного пятиугольника равны 112°. | Нет |
Все углы правильного шестиугольника равны 135°. | Нет |
| Все углы пятиугольника равны. | Да |
| Все углы ромба равны. | Нет |
| Все хорды одной окружности равны между собой. | Нет |
| Всякий равнобедренный треугольник является остроугольным. | Нет |
| Всякий равносторонний треугольник является остроугольным. | Да |
| Всякий равносторонний треугольник является равнобедренным. | Да |
| В трапеции боковые стороны параллельны. | Нет |
| В трапеции сумма длин боковых сторон всегда меньше суммы оснований. | Нет |
| В трапецию АВCD с основаниями ВС = 7, AD = 10, и боковыми сторонами AB = CD = 8 можно вписать окружность. | Нет |
| В трапецию с основаниями 6 и 3 и боковыми сторонами 4 и 4 можно вписать окружность. | Нет |
В треугольнике ABC, для которого AB = 3, BC = 4, АС = 5, угол С наименьший. | Да |
| В треугольнике АВС, для которого АВ = 4, BC = 5, AC = 6, угол A наибольший. | Нет |
| В треугольнике АВС, для которого АВ = 4, ВС = 5, АС = 6, угол B — наибольший | Да |
| В треугольнике АВС, для которого АВ = 6, BC = 8, АС = 11, угол при вершине С — наименьший. | Да |
| В треугольнике АВС, для которого ∠A = 40°, ∠B = 60°, ∠C = 80°, сторона AC — наибольшая. | Нет |
| В треугольнике АВС, для которого ∠A = 40°, ∠B = 55°, ∠C = 85° сторона AC — наименьшая. | Нет |
| В треугольнике АВС, для которого ∠A = 44°, ∠B = 55°, ∠C = 81° сторона BC — наибольшая. | Нет |
| В треугольнике АВС, для которого ∠A = 45°, ∠B = 55°, ∠C = 80° сторона AC — наименьшая | Нет |
| В треугольнике АВС, для которого ∠A = 47°, ∠B — 64°, сторона АВ — наибольшая. | Да |
| В треугольнике АВС, для которого ∠A = 50°, ∠B = 60°, ∠C = 70° сторона AB — наибольшая | Да |
В треугольнике АВС, для которого ∠A = 50°, ∠B = 60°, ∠C = 70° сторона BC — наименьшая. | Да |
| В треугольнике любая сторона меньше суммы двух других сторон. | Да |
| В треугольнике может быть только один тупой угол. | Да |
| В треугольнике против большего угла лежит большая сторона. | Да |
| В треугольнике против большего угла лежит меньшая сторона. | Нет |
| В треугольнике против большей стороны лежит больший угол. | Да |
| В треугольнике против большей стороны лежит меньший угол. | Нет |
| В треугольнике против меньшего угла лежит меньшая сторона. | Да |
| В треугольнике против меньшего угла лежит большая сторона. | Нет |
| В треугольнике против меньшей стороны лежит больший угол. | Нет |
| В треугольнике против меньшей стороны лежит меньший угол. | Да |
| В треугольнике сумма двух сторон больше третьей стороны. | Да |
В тупоугольном треугольнике все углы тупые. | Нет |
| В тупоугольном треугольнике сумма углов больше 180 градусов. | Нет |
| Высота прямоугольного треугольника, опущенная на гипотенузу, делит его на два подобных треугольника. | Да |
| Высота прямоугольного треугольника, проведённая из вершины прямого угла, есть среднее пропорциональное для отрезков, на которые делится гипотенуза этой высотой. | Да |
| Высота равнобедренного треугольника проведённая к основанию, является медианой и биссектрисой. | Да |
| Гипотенуза длиннее катета. | Да |
| Гипотенуза прямоугольного треугольника, вписанного в окружность, в два раза больше её радиуса. | Да |
| Гипотенуза равна сумме квадратов катетов. | Нет |
| Гипотенуза — самая длинная сторона в прямоугольном треугольнике. | Да |
| Два угла с общей стороной называются смежными. | Нет |
Две окружности пересекаются, если радиус одной окружности больше радиуса другой окружности. | Нет |
| Две прямые всегда пересекаются. | Нет |
| Две прямые, параллельные третьей прямой, перпендикулярны друг другу. | Нет |
| Две прямые, перпендикулярные к третьей, не пересекаются. | Да |
| Две прямые, перпендикулярные одной и той же прямой, не пересекаются. | Да |
| Две прямые, перпендикулярные третьей прямой, параллельны друг другу. | Да |
| Две прямые, перпендикулярные третьей прямой, перпендикулярны друг другу. | Нет |
| Диагонали квадрата взаимно перпендикулярны. | Да |
| Диагонали квадрата делят его углы пополам. | Да |
| Диагонали квадрата пересекаются под прямым углом. | Да |
| Диагонали квадрата равны. | Да |
| Диагонали квадрата точкой пересечения делятся пополам. | Да |
Диагонали любого прямоугольника делят его на 4 равных треугольника. | Нет |
| Диагонали любого прямоугольника равны. | Да |
| Диагонали параллелограмма делят его углы пополам. | Нет |
| Диагонали параллелограмма пересекаются под прямым углом и в точке пересечения делятся пополам. | Нет |
| Диагонали параллелограмма перпендикулярны. | Нет |
| Диагонали параллелограмма равны. | Нет |
| Диагонали прямоугольника взаимно перпендикулярны. | Нет |
| Диагонали прямоугольника пересекаются под прямым углом и точкой пересечения делятся пополам. | Нет |
| Диагонали прямоугольника равны. | Да |
| Диагонали прямоугольника точкой пересечения делятся пополам. | Да |
| Диагонали прямоугольной трапеции равны. | Нет |
| Диагонали равнобедренной трапеции равны. | Да |
Диагонали ромба взаимно перпендикулярны. | Да |
| Диагонали ромба в точке пересечения делятся пополам. | Да |
| Диагонали ромба пересекаются под прямым углом. | Да |
| Диагонали ромба пересекаются под углом 60°. | Нет |
| Диагонали ромба перпендикулярны. | Да |
| Диагонали ромба равны. | Нет |
| Диагонали ромба точкой пересечения делятся пополам. | Да |
| Диагонали трапеции пересекаются и делятся точкой пересечения пополам. | Нет |
| Диагонали трапеции пересекаются под прямым углом. | Нет |
| Диагонали трапеции равны. | Нет |
| Диагонали трапеции точкой пересечения делятся пополам. | Нет |
| Диагональ квадрата равна его стороне. | Нет |
| Диагональ параллелограмма делит его на два равных треугольника | Да |
Диагональ параллелограмма делит его углы пополам. | Нет |
| Диагональ равнобедренной трапеции делит её на два равных треугольника. | Нет |
| Диагональ трапеции делит её на два равных треугольника. | Нет |
| Диагональ трапеции равна квадратному корню из суммы квадратов её оснований. | Нет |
| Диаметр делит окружность на две равные дуги. | Да |
| Диаметр окружности в два раза больше её радиуса. | Да |
| Диаметр окружности в два раза меньше его радиуса. | Нет |
| Длина вектора равна квадратному корню из суммы его координат. | Да |
| Длина вектора, равного сумме двух векторов, не превосходит сумму длин этих векторов. | Нет |
| Длина гипотенузы прямоугольного треугольника больше суммы длин его катетов. | Нет |
| Длина гипотенузы прямоугольного треугольника меньше суммы длин его катетов. | Да |
Длина катета прямоугольного треугольника равна длине гипотенузы, умноженной на косинус угла, образованного этим катетом и гипотенузой. | Да |
| Длина окружности вычисляется по формуле С = 2πR. | Да |
| Длина окружности равна её удвоенному радиусу. | Нет |
| Длина окружности равна πR. | Нет |
| Длина окружности радиуса R равна 2πR. | Да |
| Длина суммы двух векторов равна сумме их длин. | Нет |
| Для любого четырёхугольника, вписанного в окружность, сумма углов, прилежащих к одной стороне, равна 180° | Нет |
Для любого числа к и любых векторов а, b справедливо равенство | Да |
| Для точки, лежащей на окружности, расстояние до центра окружности равно радиусу. | Да |
| Для точки, лежащей внутри круга, расстояние до центра круга меньше его радиуса. | Да |
| Если в выпуклом четырёхугольнике диагонали перпендикулярны, то этот четырёхугольник — ромб. | Нет |
Если в параллелограмме две высоты равны, то этот параллелограмм — ромб. | Да |
| Если в параллелограмме две смежные стороны равны, то такой параллелограмм является ромбом. | Да |
| Если в параллелограмме две соседние стороны равны, то такой параллелограмм является ромбом. | Да |
ОГЭ по математике — РазноеКак высчитать окружность зная диаметр калькулятор. Составление системы уравнений
§ 117. Длина окружности и площадь круга.
1. Длина окружности. Окружностью называется замкнутая плоская кривая линия, все точки которой находятся на равном расстоянии от одной точки (О), называемой центром окружности (рис. 27).
Окружность вычерчивается с помощью циркуля. Для этого острую ножку циркуля ставят в центр, а другую (с карандашом) вращают вокруг первой до тех пор, пока конец карандаша не вычертит полной окружности. Расстояние от центра до любой точки окружности называется её радиусом. Из определения следует, что все радиусы одной окружности равны между собой.
Отрезок прямой линии (АВ), соединяющий две любые точки окружности и проходящий через её центр, называется диаметром . Все диаметры одной окружности равны между собой; диаметр равен двум радиусам.
Как найти длину окружности? Практически в некоторых случаях длину окружности можно найти путём непосредственного измерения. Это можно сделать, например, при измерении окружности сравнительно небольших предметов (ведро, стакан и т. п.). Для этого можно воспользоваться рулеткой, тесьмой или шнуром.
В математике применяется приём косвенного определения длины окружности. Он состоит в вычислении по готовой формуле, которую мы сейчас выведем.
Если мы возьмём несколько больших и малых круглых предметов (монета, стакан, ведро, бочка и т. д.) и измерим у каждого из них длину окружности и длину диаметра, то получим для каждого предмета два числа (одно, измеряющее длину окружности, и другое — длину диаметра). Естественно, что для малых предметов эти числа будут небольшими, а для крупных — большими.
Однако если мы в каждом из этих случаев возьмём отношение полученных двух чисел (длины окружности и диаметра), то при тщательном выполнении измерения найдём почти одно и то же число. Обозначим длину окружности буквой С , длину диаметра буквой D , тогда отношение их будет иметь вид С: D . Фактические измерения всегда сопровождаются неизбежными неточностями. Но, выполнив указанный опыт и произведя необходимые вычисления, мы получим для отношения С: D примерно следующие числа: 3,13; 3,14; 3,15. Эти числа очень мало отличаются одно от другого.
В математике путём теоретических соображений установлено, что искомое отношение С: D никогда не меняется и оно равно бесконечной непериодической дроби, приближённое значение которой с точностью до десятитысячных долей равно 3,1416 . Это значит, что всякая окружность длиннее своего диаметра в одно и то же число раз. Это число принято обозначать греческой буквой π (пи). Тогда отношение длины окружности к диаметру запишется так: С: D = π .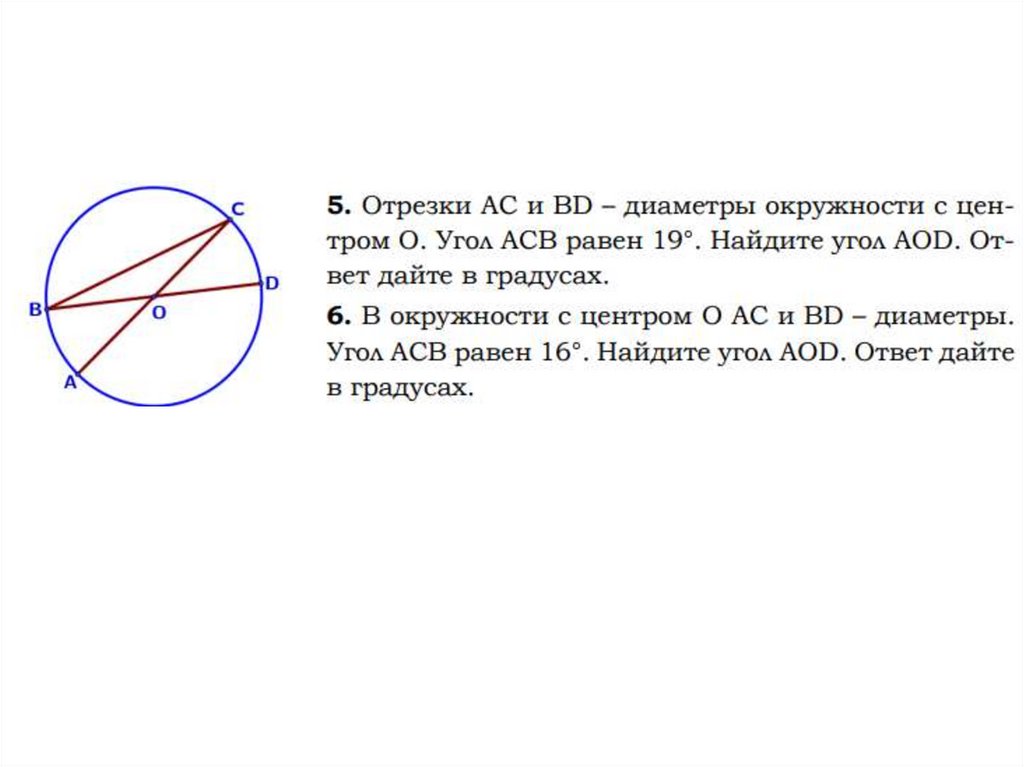
Мы будем ограничивать это число только сотыми долями, т. е. брать π = 3,14.
Напишем формулу для определения длины окружности.
Так как С: D = π , то
C = πD
т. е. длина окружности равна произведению числа π на диаметр.
Задача 1. Найти длину окружности (С ) круглой комнаты, если диаметр её D = 5,5 м.
Принимая во внимание изложенное выше, мы должны для решения этой задачи увеличить диаметр в 3,14 раза:
5,5 3,14 = 17,27 {м).
Задача 2. Найти радиус колеса, у которого длина окружности 125,6 см.
Эта задача обратна предыдущей. Найдём диаметр колеса:
125,6: 3,14 = 40 (см).
Найдём теперь радиус колеса:
40: 2 = 20 (см).
2. Площадь круга. Чтобы определить площадь круга, можно было бы начертить на бумаге круг данного радиуса, покрыть его прозрачной клетчатой бумагой и потом сосчитать клетки, находящиеся внутри окружности (рис. 28).
Но такой способ неудобен по многим причинам.
Во-первых, вблизи контура круга получается ряд неполных клеток, о величине которых судить трудно. Во-вторых, нельзя покрыть листом бумаги большой предмет (круглую клумбу, бассейн, фонтан и др.). В-третьих, подсчитав клетки, мы всё-таки не получаем никакого правила, позволяющего нам решать другую подобную задачу. В силу этого поступим иначе. Сравним круг с какой-нибудь знакомой нам фигурой и сделаем это следующим образом: вырежем круг из бумаги, разрежем его сначала по диаметру пополам, затем каждую половину разрежем ещё пополам, каждую четверть — ещё пополам и т. д., пока не разрежем круг, например, на 32 части, имеющие форму зубцов (рис. 29).
Затем сложим их так, как показано на рисунке 30, т. е. сначала расположим 16 зубцов в виде пилы, а затем в образовавшиеся отверстия вложим 15 зубцов и, наконец, последний оставшийся зубец разрежем по радиусу пополам и приложим одну часть слева, другую — справа. Тогда получится фигура, напоминающая прямоугольник.
Длина этой фигуры (основание) равна приблизительно длине полуокружности, а высота — приблизительно радиусу.
Тогда площадь такой фигуры можно найти путём умножения чисел, выражающих длину полуокружности и длину радиуса. Если обозначим площадь круга буквой S , длину окружности буквой С , радиус буквой r , то можем записать формулу для определения площади круга:
которая читается так: площадь круга равна длине полуокружности, умноженной на радиус.
Задача. Найти площадь круга, радиус которого равен 4 см. Найдём сначала длину окружности, потом длину полуокружности, а затем умножим её на радиус.
1) Длина окружности С = π D = 3,14 8 = 25,12 (см).
2) Длина половины окружности C / 2 = 25,12: 2= 12,56 (см).
3) Площадь круга S = C / 2 r = 12,56 4 = 50,24 (кв. см).
§ 118. Поверхность и объём цилиндра.
Задача 1. Найти полную поверхность цилиндра, у которого диаметр основания 20,6 см и высота 30,5 см.
Форму цилиндра (рис. 31) имеют: ведро, стакан (не гранёный), кастрюля и множество других предметов.
Полная поверхность цилиндра (как и полная поверхность прямоугольного параллелепипеда) состоит из боковой поверхности и площадей двух оснований (рис. 32).
Чтобы наглядно представить себе, о чём идёт речь, необходимо аккуратно сделать модель цилиндра из бумаги. Если мы от этой модели отнимем два основания, т. е. два круга, а боковую поверхность разрежем вдоль и развернём, то будет совершенно ясно, как нужно вычислять полную поверхность цилиндра. Боковая поверхность развернётся в прямоугольник, основание которого равно длине окружности. Поэтому решение задачи будет иметь вид:
1) Длина окружности: 20,6 3,14 = 64,684 (см).
2) Площадь боковой поверхности: 64,684 30,5= 1972,862(кв.см).
3) Площадь одного основания: 32,342 10,3 = 333,1226 (кв.см).
4) Полная поверхность цилиндра:
1972,862 + 333,1226 + 333,1226 = 2639,1072 (кв. см) ≈ 2639 (кв. см).
Задача 2. Найти объём железной бочки, имеющей форму цилиндра с размерами: диаметр основания 60 см и высота 110 см.
Чтобы вычислить объём цилиндра, нужно припомнить, как мы вычисляли объём прямоугольного параллелепипеда (полезно прочитать § 61).
Единицей измерения объёма у нас будет кубический сантиметр. Сначала надо узнать, сколько кубических сантиметров можно расположить на площади основания, а затем найденное число умножить на высоту.
Чтобы узнать, сколько кубических сантиметров можно уложить на площади основания, надо вычислить площадь основания цилиндра. Так как основанием служит круг, то нужно найти площадь круга. Затем для определения объёма умножить её на высоту. Решение задачи имеет вид:
1) Длина окружности: 60 3,14 = 188,4 (см).
2) Площадь круга: 94,2 30 = 2826 (кв. см).
3) Объём цилиндра: 2826 110 = 310 860 (куб. см).
Ответ. Объём бочки 310,86 куб. дм.
Если обозначим объём цилиндра буквой V , площадь основания S , высоту цилиндра H , то можно написать формулу для определения объёма цилиндра:
V = S H
которая читается так: объём цилиндра равен площади основания, умноженной на высоту.
§ 119. Таблицы для вычисления длины окружности по диаметру.
При решении различных производственных задач часто приходится вычислять длину окружности. Представим себе рабочего, который изготовляет круглые детали по указанным ему диаметрам. Он должен всякий раз, зная диаметр, вычислить длину окружности. Чтобы сэкономить время и застраховать себя от ошибок, он обращается к готовым таблицам, в которых указаны диаметры и соответствующие им длины окружностей.
Приведём небольшую часть таких таблиц и расскажем, как ими пользоваться.
Пусть известно, что диаметр окружности равен 5 м. Ищем в таблице в вертикальном столбце под буквой D число 5. Это длина диаметра. Рядом с этим числом (вправо, в столбце под названием «Длина окружности») увидим число 15,708 (м). Совершенно так же найдём, что если D = 10 см, то длина окружности равна 31,416 см.
По этим же таблицам можно производить и обратные вычисления. Если известна длина окружности, то можно найти в таблице соответствующий ей диаметр.
Пусть длина окружности равна приблизительно 34,56 см. Найдём в таблице число, наиболее близкое к данному. Таковым будет 34,558 (разница 0,002). Соответствующий такой длине окружности диаметр равен приблизительно 11 см.
Таблицы, о которых здесь сказано, имеются в различных справочниках. В частности, их можно найти в книжке «Четырёхзначные математические таблицы» В. М. Брадиса. и в задачнике по арифметике С. А. Пономарёва и Н. И. Сырнева.
Окружностью называется ряд равноудалённых точек от одной точки, которая, в свою очередь, является центром этой окружности. Окружность имеет также свой радиус, равный расстоянию этих точек от центра.
Отношение длины, какой либо окружности к её диаметру, для всех окружностей одинаково. Это отношение есть число, являющееся математической константой, которое обозначается греческой буквой π .
Определение длины окружности
Произвести расчёт окружности можно по следующей формуле:
L = π D = 2 π r
r — радиус окружности
D — диаметр окружности
L — длина окружности
π — 3.
14
Задача:
Вычислить длину окружности , имеющей радиус 10 сантиметров.
Решение:
Формула для вычисления дины окружности имеет вид:
L = π D = 2 π r
где L – длина окружности, π – 3,14 , r – радиус окружности, D – диаметр окружности.
Таким образом, длина окружности, имеющей радиус 10 сантиметров равна:
L = 2 × 3,14 × 10 = 62,8 сантиметра
Окружность представляет собой геометрическую фигуру, являющуюся совокупностью всех точек на плоскости, удаленных от заданной точки, которая называется ее центром, на некоторое расстояние, не равное нулю и именуемое радиусом. Определять ее длину с различной степенью точности ученые умели уже в глубокой древности: историки науки считают, что первая формула для вычисления длины окружности была составлена примерно в 1900 году до нашей эры в древнем Вавилоне.
С такими геометрическими фигурами, как окружности, мы сталкиваемся ежедневно и повсеместно.
Именно ее форму имеет внешняя поверхность колес, которыми оснащаются различные транспортные средства. Эта деталь, несмотря на свою внешнюю простоту и незатейливость, считаются одним из величайших изобретений человечества, причем интересно, что аборигены Австралии и американские индейцы вплоть до прихода европейцев совершенно не имели понятия о том, что это такое.
По всей вероятности, самые первые колеса представляли собой отрезки бревен, которые насаживались на ось. Постепенно конструкция колеса совершенствовалась, их конструкция становилась все более и более сложной, а для их изготовления требовалось использовать массу различных инструментов. Сначала появились колеса, состоящие из деревянного обода и спиц, а затем, для того, чтобы уменьшить износ их внешней поверхности, ее стали обивать металлическими полосами. Для того чтобы определить длины этих элементов, и требуется использовать формулу расчета длины окружности (хотя на практике, вероятнее всего, мастера это делали «на глаз» или просто опоясывая колесо полосой и отрезая требуемый ее участок).
Следует заметить, что колесо используется отнюдь не только в транспортных средствах. Например, его форму имеет гончарный круг, а также элементы шестеренок зубчатых передач, широко применяемых в технике. Издавна колеса использовались в конструкциях водяных мельниц (самые древние из известных ученым сооружений такого рода строились в Месопотамии), а также прялок, применявшихся для изготовления нитей из шерсти животных и растительных волокон.
Окружности нередко можно встретить и в строительстве. Их форму имеют достаточно широко распространенные круглые окна, очень характерные для романского архитектурного стиля. Изготовление этих конструкций – дело весьма непростое и требует высокого мастерства, а также наличия специального инструмента. Одной из разновидностей круглых окон являются иллюминаторы, устанавливаемые в морских и воздушных судах.
Таким образом, решать задачу определения длины окружности часто приходится инженерам-конструкторам, разрабатывающим различные машины, механизмы и агрегаты, а также архитекторам и проектировщикам.
Поскольку число π , необходимое для этого, является бесконечным, то с абсолютной точностью определить этот параметр не представляется возможным, и поэтому при вычислениях учитывается та ее степень, которая в том или ином конкретном случае является необходимой и достаточной.
Одной линейкой здесь не обойтись, необходимо знать специальные формулы. Единственное, что от нас потребуется — это определить диаметр или радиус круга. В некоторых задачах эти величины обозначены. Но что делать, если у нас нет ничего, кроме рисунка? Не беда. Диаметр и радиус можно вычислить с помощью обычной линейки. Теперь приступим к самому основному.
Формулы, которые должен знать каждый
Еще в почти 4 000 лет назад, учёные выявили удивительное соотношение: если длину окружности разделить на ее диаметр, то получается одно и то же число, которое равно примерно 3,14. Это значение назвали именно с этой буквы в древнегреческом языке начиналось слово «периметр» и «окружность». На основании того открытия, которое совершили древние ученые, можно рассчитать длину любой окружности:
Где P означает длину (периметр) окружности,
D — диаметр, П — число «Пи».
Длина окружности круга может также быть посчитана через ее радиус (r), который равен половине длины диаметра. Вот и вторая формула, которую нужно запомнить:
Как узнать диаметр окружности?
Представляет собой хорду, которая проходит через центр фигуры. При этом она соединяет две наиболее удалённые точки в круге. Исходя из этого, можно самостоятельно прочертить диаметр (радиус) и измерить его длину с помощью линейки.
Способ 1: вписываем прямоугольный треугольник в круг
Рассчитать длину окружности будет несложно, если мы найдем ее диаметр. Необходимо начертить в круге где гипотенуза будет равна диаметру окружности. Для этого необходимо иметь под рукой линейку и угольник, иначе ничего не получится.
Способ 2: вписываем любой треугольник
На стороне круга отмечаем три любые точки, соединяем их — получаем треугольник. Важно, чтобы центр окружности лежал в области треугольника, это можно сделать на глаз. Проводим к каждой стороне треугольника медианы, точка их пересечения совпадёт с центром окружности.
А когда нам известен центр, можно с помощью линейки легко провести диаметр.
Данный способ очень похож на первый, но может применяться при отсутствии угольника или в тех случаях, когда нет возможности чертить на фигуре, например на тарелке. Необходимо взять лист бумаги с прямыми углами. Прикладываем лист к кругу так, чтобы одна вершина его угла соприкасалась с краем круга. Далее отмечаем точками места, где стороны бумаги пересекаются с линией окружности. Соединяем эти точки с помощью карандаша и линейки. Если под рукой ничего нет, просто согните бумагу. Эта линия и будет равна длине диаметра.
Пример задачи
- Ищем диаметр с помощью угольника, линейки и карандаша по способу № 1. Предположим, получилось 5 см.
- Зная диаметр, мы легко можем его вставить в нашу формулу: P = d П = 5*3,14 = 15,7В нашем случае получилось около 15,7. Теперь вы без особых проблем сможете объяснить, как рассчитать длину окружности.
- если известен диаметр окружности, то формула выглядит так L = ПD
- если известен радиус окружности, то формула имеет следующий вид L = 2Пr.
Формула длины окружности
Если воспользоваться Яндексом, то длину окружности можно посчитать в самом поисковом интерфейсе.
Введите в Яндексе формула длины окружности , он вам выдаст формулу расчета и окошко для ввода значения. Дальше нужно будет нажать кнопку quot;Посчитатьquot;.Окружность это такая геометрическая фигура, которая является совокупностью всех своих точек на плоскости, равноудаленных от ее центра, на расстояние, называемое радиусом.
Для того, чтобы вычислить длину окружности, обозначаемую обычно как L, надо радиус, обозначаемый как R, умножить на 2 и на число Пи. L=2ПиR. Пи — величина постоянная и равна 3,14.
Или можно взять удвоенный радиус, то есть диаметр (D) и тогда формула будет выглядеть так: L=ПиD.
Можно найти длину окружности не зная радиуса. Для этого нужно знать площадь круга.
Формула для расчета длины окружности по известной площади круга выглядит так:
L=2*корень квадратный пи*S
где S площадь круга.
Длина окружности
Можете скопировать себе на компьютер нижеприведенную табличку с основными формулами окружности и круга.
Она вас, при решении геометрических задач, еще не раз выручит.Здесь же присутствует формула длины окружности. Она имеет вид: L=2ПR
На сайте quot;Сборник формулquot;, можно посчитать длину окружности, введя имеющиеся у вас данные. Там же,
Решение уравнений:
Геометрическая прогрессия:
Комбинаторика:
Решить химическое уравнение
Известно, что независимо от длины окружности, ее отношение к диаметру является постоянным числом.
Если известен диаметр окружности, то нужно эту величину умножить на число Пи (3,14).
Формула выглядит так:
Если известен радиус, то чтобы найти диаметр, умножаем его на два, а для нахождения длины окружности опять же на число Пи.
Окружностью в геометрии называют фигуру на плоскости, все точки, лежащие на окружности круга, удалены на равном расстоянии от центра окружности
Радиусом окружности называют в геометрии величину расстояния, отрезок от центра окружности до ее любой точки на окружности.
Длину окружности с радиусом вычисляют по формуле
Длина окружности L равно 2pi умножить на R.
Или выглядит формула так. Чтобы не путаться, запомните, что длина окружности это есть периметр круга.
r — это радиус
D — диаметр
Приблизительно 3,14
Но окружность — это не круг
Смотрите картинку, на которой видна разница между кругом и окружностью
Окружность это кривая, ограничивающая круг. Все ее точки находятся на равном от центра расстоянии.
В формуле вычисления длины окружности используются значения радиуса или двойная величина радиуса — диаметр и число, всегда имеющее значение 3,14.
Формула, таким образом, выглядит так: L=d или L=2R , где L — значение длины окружности, получаемое умножением числа (3,14) на величину радиуса окружности или двойного диаметра.
Еще из средней школьной программы отчетливо помню формулу измерения длины окружности. Эта формула выглядит так- 2Пr, где r- это радиус окружности, которая равна половине диаметра, а число П неизменна и равна 3.14.
Формула длины окружности равна Пи умноженное на Диаметр или Пи умноженное на Радиус умноженный на 2.
Длину окружности можно найти одним из представленных способов:
Введите в Яндексе формула длины окружности , он вам выдаст формулу расчета и окошко для ввода значения. Дальше нужно будет нажать кнопку quot;Посчитатьquot;.
Она вас, при решении геометрических задач, еще не раз выручит.Очень часто при решении школьных заданий по или физике возникает вопрос — как найти длину окружности, зная диаметр? На самом деле никаких сложностей в решении этой проблемы нет, нужно только чётко представлять себе, какие формулы , понятия и определения требуются для этого.
Вконтакте
Основные понятия и определения
- Радиус — это линия, соединяющая центр окружности и её произвольную точку . Он обозначается латинской буквой r.
- Хордой называется линия, соединяющая две произвольные точки лежащие на окружности .
- Диаметр — это линия, соединяющая два пункта окружности и проходящая через её центр . Он обозначается латинской буквой d.
- — это линия, состоящая из всех точек, находящихся на равном расстоянии от одной избранной точки, именуемой её центром. Её длину будем обозначать латинской буквой l.
Он обозначается латинской буквой d.Площадь круга — это вся территория, заключённая внутри окружности . Она измеряется в квадратных единицах и обозначается латинской буквой s.
Пользуясь нашими определениями, приходим к выводу, что диаметр круга равен его самой большой хорде.
Внимание! Из определения, что такое радиус круга можно узнать, что такое диаметр круга. Это два радиуса отложенные в противоположных направлениях!
Диаметр окружности.
Нахождение длины окружности и её площади
Если нам дан радиус окружности, то диаметр окружности описывает формула d = 2*r . Таким образом, для ответа на вопрос, как найти диаметр круга, зная его радиус, достаточно последний умножить на два .
Формула длины окружности, выраженная через её радиус, имеет вид l = 2*П*r . 2 = 4*s/П . Для определения самого диаметра потребуется извлечь корень квадратный из правой части . Получится d = 2*sqrt(s/П).
Решение типовых заданий
- Узнаем, как найти диаметр, если дана длина окружности. Пусть она равняется 778,72 километра. Требуется найти d. d = 778,72/3,14 = 248 километров. Вспомним, что такое диаметр и сразу определим радиус, для этого определённое выше значение d разделим пополам. Получится r = 248/2 = 124 километра.
- Рассмотрим, как найти длину данной окружности, зная её радиус. Пусть r имеет значение 8 дм 7 см. Переведём это все в сантиметры, тогда r будет равняться 87 сантиметров. Воспользуемся формулой, как найти неизвестную длину круга. Тогда наше искомое будет равняться l = 2*3,14*87 = 546,36 см . Переведём наше полученное значение в целые числа метрических величин l = 546,36 см = 5 м 4 дм 6 см 3,6 мм.
- Пусть нам требуется определить площадь данной окружности по формуле через её известный диаметр. 2/(4П) = 2209/12,56 = 175,87 кв. м.
Длина окружности
Каковы части круга
by Veerendra
До сих пор мы обсуждали треугольник и четырехугольник, которые имеют линейные границы. Окружность – это замкнутая фигура, имеющая криволинейную границу.
Когда мы думаем о кругах, самое первое, что приходит на ум, это их круглая форма, например, браслеты, монеты, кольца, тарелки, чапати, пицца, компакт-диски и т. д. Колеса автомобиля, автобуса, велосипеда, грузовика, поезд и самолет также имеют круглую форму. Если мы возьмем камень, привяжем его к одному концу веревки и раскачаем в воздухе, держась за другой конец веревки, путь, прочерченный камнем, будет круговым путем, и он образует круг.
Подробнее:
- Периметр круга
- Обычный хорд двух пересекающих кругов
- Строительство круга
- Область круга
- из кругов
- СЕРИОН Площадь сегмента окружности
- Площадь сектора окружности
- Классификация треугольников
- Окружность: постоянное расстояние от заданной фиксированной точки на плоскости.
- Центр: Окружность — это замкнутая фигура, состоящая из точек на плоскости, находящихся на одинаковом расстоянии от фиксированной точки, называемой центром окружности. На рисунке О — это центр.
- Радиус: Постоянное расстояние от его центра называется радиусом окружности. На рисунке радиус OA равен
- Хорда: Отрезок, соединяющий две точки на окружности, называется хордой окружности. На рисунке АВ — хорда окружности. Если хорда проходит через центр, то это самая длинная хорда. PQ, PR и ST — хорды окружности. Хорда ST проходит через центр, следовательно, это диаметр.
- Диаметр: Хорда, проходящая через центр окружности, называется диаметром окружности. Круг имеет бесконечное число диаметров. CD — это диаметр окружности, как показано на рисунке. Если d — диаметр окружности, то d = 2r. где r — радиус. или самая длинная хорда называется диаметром.
На рисунке AB — диаметр, а дуги CD и DC — полуокружности. - Дуга: Непрерывная часть круга называется дугой. Пусть A,B,C,D,E,F будут точками на окружности. Круг разделен на разные части. Тогда все части AB, BC, CD, DE, EF и т. д. являются дугами окружности.
Пусть P,Q — две точки на окружности. Эти P, Q делят круг на две части. Каждая часть представляет собой дугу. Эти дуги обозначены в направлении против часовой стрелки - Окружность круга: Периметр круга называется его окружностью. Длина окружности радиуса r равна 2πr.
- Полукруг: Диаметр круга делит круг на две равные части. Каждая часть называется полукругом. Мы также можем сказать, что половина круга называется полукругом. На рисунке AXB и AYB представляют собой два полукруга.
- Отрезок: Пусть AB будет хордой окружности. Затем AB делит область, заключенную в окружность (т. е. круговой диск), на две части. Каждая из частей называется сегментом окружности. Отрезок, содержащий малую дугу, называется малым отрезком, а отрезок, содержащий большую дугу, называется большим отрезком, а отрезок окружности — это область между дугой и хордой окружности.
- Центральные углы: Рассмотрим круг. Угол, образуемый дугой в центре О, называется центральным углом. Вершина центрального угла всегда находится в центре O.
- Градусная мера дуги: Градусная мера малой дуги — это мера центрального угла, образуемого дугой.
Градусная мера длины окружности всегда равна 360°. - Окружность внутри и снаружи
Окружность делит плоскость, на которой лежит, на три части.
(i) Внутри круга. который называется внутренней частью круга
(ii) Круг
(iii) Вне круга, который называется внешним видом круга.
Круг и его внутренняя часть составляют круглую область. - Сектор:
Сектор – это область круглого диска, расположенная между дугой и двумя радиусами, соединяющими концы дуги и центр. OAB представляет собой сектор, как показано на рисунке.
Квадрант: Одна четвертая круглого диска называется квадрантом. - Положение точки:
Точка внутри круга: Говорят, что точка P, такая что OP < r, лежит внутри круга.
Точка внутри круга также называется внутренней точкой . (Пример: центр окружности)
Точка вне круга: Говорят, что точка Q, такая что OQ > r, лежит вне круга C (O, r) = {X, OX = r}
Точка вне круга окружность также называется внешней точкой .
Точка на окружности: Точка S, такая, что OS = r, лежит на окружности C(O, r) = {X ,OX = r}.
Круглый диск: Определяется как набор внутренних точек и точек на окружности. В системе обозначений это записывается как: C(O, r) = {X : P OX ≤ r} - Концентрические окружности:
Окружности с одинаковым центром и разным радиусом называются концентрическими окружностями.
Примечание. Слово «радиус» используется для отрезка, соединяющего центр с любой точкой на окружности, а также для его длины. - Конгруэнтность окружностей и дуг
Конгруэнтность окружностей: Две окружности называются конгруэнтными тогда и только тогда, когда одна из них может быть наложена на другую так, чтобы она точно покрывала ее. Это означает, что две окружности конгруэнтны тогда и только тогда, когда их радиусы равны. т. е. C (O, r) и C (O’ , r) конгруэнтны тогда и только тогда, когда r = s.
Конгруэнтные дуги: Две дуги окружности конгруэнтны, если одну из них можно наложить на другую так, чтобы она точно покрывала ее. Это возможно только в том случае, если градусная мера двух дуг одинакова.
Пример 1: Возьмем две точки А и В на плоском листе. Нарисуйте круг с центром А, радиусом АС и внешней стороной В.
Решение: Отметьте на бумаге две точки A и B.
A • • B
Поскольку точка B должна находиться снаружи круга, возьмите A в качестве центра и радиус (r) меньше, чем AB, чтобы нарисовать круг.
Пример 2 : Найдите диаметр круга радиусом 6 см.
Решение: Мы знаем,
Диаметр = 2 × радиус
∴ Диаметр = 2 × 6 см = 12 см Диаметр, внутренний и внешний вид круга, части круга, сектор, сегмент, полукруг
геометрия — Откуда мы знаем, что соотношение между длиной окружности и диаметром одинаково для всех кругов?
Спросил
Изменено 7 месяцев назад
Просмотрено 16 тысяч раз
$\begingroup$
Число $\pi$ определяется как отношение длины окружности к ее диаметру. Откуда мы знаем, что значение $\pi$ верно для каждого круга? Откуда мы действительно знаем, что значение одинаково для каждого круга?
Откуда мы знаем, что $\pi = {C\over d}$ для любой окружности? Существует ли доказательство, утверждающее следующее: для любого круга мы знаем, что $\pi = {C\over d}$. Разве такое утверждение не требует доказательства, учитывая, что $\pi$ так широко используется в задачах, связанных с кругами, сферами и т. д. Откуда мы действительно знаем, что значение $\pi$ верно для всех кругов?
- геометрия
- пи
$\endgroup$
8
$\begingroup$
Это не очень строгое доказательство, но именно так меня научили тому факту, что длина окружности пропорциональна ее радиусу.
Рассмотрим две концентрические окружности, как на рисунке выше. Радиус меньшей из них равен $r$, а большей — $R$; их окружности равны $c$ и $C$ соответственно.
Мы проводим две линии через центр, чтобы они пересекались с каждым кругом, образуя два треугольника, как показано на рисунке. Отношение их сторон $r/R = r/R$, и они имеют общий угол $\alpha$, значит, они подобны. Таким образом, $k/K = r/R$. Также обратите внимание, что если $\beta$ обозначает полный (360 градусов) угол окружности, то $\beta/\alpha \cdot k \приблизительно c$ и $\beta/\alpha \cdot K \приблизительно C$.
Можно сказать, что $\frac{c}{C} \ приблизительно \frac{\beta/\alpha \cdot k}{\beta/\alpha \cdot K} = \frac{r}{R}$. По мере того, как угол $\alpha$ становится все меньше и меньше (стремясь к нулю, чтобы сделать ограничивающий аргумент), аппроксимации $\beta/\alpha \cdot k \ приблизительно c$ и $\beta/\alpha \cdot K \ приблизительно C $ растут точнее. В предельном случае — и именно здесь «доказательство» несколько нестрогое — мы получаем, что $\frac{c}{C} = \frac{r}{R}$.
Таким образом, $c/r = C/R$ или эквивалентно $c/(2r) = C/(2R)$: длина окружности, деленная на диаметр, всегда является константой для любых двух окружностей, поскольку любые две окружности можно сделать концентрическими. банальным переводом. Мы называем эту магическую константу $\pi$.
$\endgroup$
$\begingroup$
Вот строгое доказательство.
Во-первых, нам нужно определить расстояние между двумя точками на участке кривой. Это называется длиной дуги и определяется как предел суммы отрезков линии кривой. 92} } \text{ и }\phi(x) = rx$$
$\endgroup$
3
$\begingroup$
Чтобы показать, что $\pi$ постоянна, мы должны показать, что для двух окружностей диаметров $d_1$ и $d_2$ и окружностей $c_1$ и $c_2$ соответственно $\frac{c_1}{d_1}= \frac{c_2}{d_2}$.
Если $d_1=d_2$, то две окружности конгруэнтны, потому что одну можно положить на другую, и они выстроятся в линию. Без ограничения общности можно считать $d_1\lt d_2$. Нарисуйте круги концентрически. Тогда $d_2=kd_1$ для некоторого $k$. Если мы сможем показать, что $c_1=kc_2$, тогда $\frac{c_2}{d_2}=\frac{kc_1}{kd_1}=\frac{c_1}{d_1}$, и все будет готово.
Обозначьте общий центр двух окружностей $O$. Постройте два луча, исходящие из $O$ наружу, которые делят каждую из окружностей окружностей на $n$ равных частей, где $n\gt 2$. Обозначьте точки, в которых два луча пересекают внутреннюю окружность $A$ и $B$, и точки, в которых они пересекают внешнюю окружность, $A’$ и $B’$. Выберите $A’$ так, чтобы он лежал на том же луче, что и $A$.
Теперь рассмотрим треугольники $AOB$ и $A’OB’$. Эти два треугольника подобны, и, кроме того, соотношение $\frac{\overline {A’B’}}{\overline{AB}}=\frac{A’}{A}=\frac{\frac{d_2}{ 2}}{\frac{d_1}{2}}=\frac{d_2}{d_1}=\frac{kd_1}{d_1}=k$. Следовательно, $\overline{A’B’}=k\overline{AB}$.
Периметр правильного $n$-угольника, вписанного во внутреннюю окружность, равен $n$ копий $\overline{AB}$, а периметр правильного $n$-угольника, вписанного во внешнюю окружность, равен $ в n$ раз больше длины $\overline{A’B’}$.
Следовательно, периметр внутреннего $n$-угольника равен $n|\overline{AB}|$, а периметр внешнего $n$-угольника равен $n|\overline{A’B’} |=kn|\overline{AB}|$. Отношение двух периметров равно $k$ и не зависит от $n$.
Взятие $n$ произвольно большим дает, что отношение двух окружностей также равно $k$, и результат доказан.
$\endgroup$
$\begingroup$
Очень интересный вопрос. Я полагаю, что любой ответ будет иметь отношение к тому, как вообще определяется периметр. Если принять его за предел n-глонов, то нетрудно увидеть, что отношение периметров многоугольников (не менее $2n$-полигонов) к их диаметру постоянно. Таким образом, и в пределе соотношение останется постоянным.
Примечание. Ранние греческие математики представляли круги (и многие другие искривленные объекты) как границы многоугольников.
$\endgroup$
1
$\begingroup$
Я не знаю, почему вы, плоскоземельцы, считаете, что отношение длины окружности к диаметру равно числу пи. Это только предельный случай для очень маленьких кругов. Я проверил свой глобус и обнаружил, что, например, круг диаметром 12 000 миль имеет длину окружности примерно 24 000 миль. Это отношение 2, а не пи.
Конечно, возможны и более крупные круги, диаметр которых превышает половину земного шара, и предельным случаем является диаметр 24 000 миль для крошечного круга, который охватывает всю землю, за исключением крошечной области вокруг южного полюса с окружностью. близко к нулю. Таким образом, соотношение может быть настолько маленьким, насколько вам нравится.
$\endgroup$
2
$\begingroup$
Так я всегда представлял себе этот вопрос.
Подумайте о равностороннем треугольнике, отношение его периметра к расстоянию от угла до центра постоянно, независимо от длины стороны равностороннего треугольника.
Теперь замените его квадратом. Отношение его периметра к расстоянию от угла до центра также постоянно, независимо от длины стороны квадрата.
К настоящему времени вы, вероятно, догадываетесь, что будет дальше. Да, это пятиугольник. Тот же результат.
Шестиугольник, семиугольник, восьмиугольник, нонагон, десятиугольник и т. д.
Да, опять тот же результат.
Окружность — это просто многоугольник с равными бесконечными сторонами бесконечно малой длины. И, естественно, отношение его периметра (окружности) к расстоянию от его угла до центра (радиуса) также является константой независимо от того, насколько велик круг. Таким образом, это отношение было определено как 2π.
Надеюсь это поможет!
$\endgroup$
$\begingroup$
Более строгий и полный ответ дан мной и соавтором в недавней статье под названием «Почему отношение длины окружности любого круга к его диаметру является константой?», которая будет опубликована в следующем номере журнала. «College Mathematics Journal» (апрель 2022 г.), см. Веб-сайт Тейлора и Фрэнсиса. Я опубликую ссылку, как только она будет опубликована в Интернете.
$\endgroup$
1
Твой ответ
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Обязательно, но не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.6.2: Идентификация компонентов круга — K12 LibreTexts
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 2179
Компоненты, длина окружности и площадь окружности.
Части окружностей
Окружности
Окружность — это множество всех точек плоскости, находящихся на одинаковом расстоянии от определенной точки, называемой центр . Центр окружности внизу — точка A. Мы называем эту окружность «окружностью A» и обозначаем \(\bigodot A\).
Рисунок \(\PageIndex{1}\)Важные части круга
Радиус : Расстояние от центра круга до его внешнего края.
Хорда : Отрезок, концы которого лежат на окружности.
Диаметр : Хорда, проходящая через центр окружности. Длина диаметра в два раза больше длины радиуса.
Секущая : Линия, пересекающая окружность в двух точках.
Касательная : Линия, пересекающая окружность ровно в одной точке.
Точка касания : Точка, в которой касательная касается окружности.
Рисунок \(\PageIndex{2}\)Касательный луч \(\overrightarrow{TP}\) и касательный сегмент \(\overline{TP}\) также называются касательными.
Касательные окружности : Две или более окружностей, пересекающихся в одной точке.
Концентрические окружности : Две или более окружностей с одинаковым центром, но разными радиусами.
Конгруэнтные окружности : Две или более окружностей с одинаковым радиусом, но разными центрами
Рисунок \(\PageIndex{3}\)Что, если вы проведете линию через окружность от одной стороны к другой, которая не проходит через центр? Что, если вы нарисуете линию вне круга, которая касается круга в одной точке? Как бы вы назвали эти линии, которые вы нарисовали?
Пример \(\PageIndex{1}\)
Найдите части \(\bigodot A\), которые лучше всего соответствуют каждому описанию.
Рисунок \(\PageIndex{4}\)- Радиус A
- Хорда
- Касательная
- Точка касания
- Диаметр А
- секанс А
Решение
- \overline{HA}\) или \overline{AF}\)
- \(\overline{CD}\), \(\overline{HF}\) или \overline{DG}\)
- \(\overleftrightarrow{BJ}\)
- \(Точка Н\)
- \(\overline{HF}\)
- \(\overleftrightarrow{BD}\)
Пример \(\PageIndex{2}\)
Нарисуйте пример того, как две окружности могут пересекаться без, с одной и с двумя точками пересечения. Вы сделаете три отдельных рисунка.
Решение
Рисунок \(\PageIndex{5}\)Пример \(\PageIndex{3}\)
Определите, конгруэнтны ли какие-либо из следующих окружностей.
Решение
От каждого центра считайте единицы до внешнего края круга. Легче всего считать по вертикали или по горизонтали. Делая это, мы имеем:
\(\begin{aligned} \text{Радиус } \bigodot A&=3\text{единица измерения} \\ \text{Радиус } \bigodot B&=4\text{единица измерения}\ \ \text{Радиус } \bigodot C&=3\text{ unit }\end{aligned} \)
Из этих измерений мы видим, что \(\bigodot A\cong \bigodot C\).
Обратите внимание, что круги конгруэнтны. Длины радиусов равны.
Пример \(\PageIndex{4}\)
Возможна ли прямая, которая трижды пересекает окружность? Если да, нарисуйте один. Если нет, объясните.
Решение
Невозможно. По определению все линии прямые . Максимальное количество раз, когда линия может пересекать окружность, равно двум.
Пример \(\PageIndex{5}\)
Все ли окружности одинаковы?
Решение
Да. Все круги одинаковой формы, но не обязательно одинакового размера, поэтому они похожи.
Обзор
Определите, какой термин лучше всего описывает каждую из следующих частей \(\bigodot P\).
Рисунок \(\PageIndex{7}\)- \(\overline{KG}\)
- \(\overleftrightarrow{FH}\)
- \(\overline{FH}\)
- \(Е\)
- \(\overleftrightarrow{BK}\)
- \(\overleftrightarrow{CF}\)
- \(А\)
- \(\overline{JG}\)
- Какая самая длинная хорда в любом круге?
Используйте приведенный ниже график, чтобы ответить на следующие вопросы.
- Найдите радиус каждого круга.
- Есть ли конгруэнтные окружности? Откуда вы знаете?
- Найдите все общие касательные для \(\bigodot B\) и \(\bigodot C\).
- \(\bigodot C\) и \(\bigodot E\) внешне касаются. Что такое \(СЕ\)?
- Найдите уравнение \(\overline{CE}\).
Ресурсы
Словарь
| Срок | Определение |
|---|---|
| хорда | Отрезок, концы которого лежат на окружности. |
| Круг | Окружность — это набор всех точек на определенном расстоянии от данной точки в двух измерениях. |
| концентрические окружности | Два или более круга с одним центром, но разными радиусами. |
| конгруэнтные окружности | Два или более круга с одинаковым радиусом, но разными центрами. |
| Диаметр | Диаметр — это мера расстояния через центр окружности. Диаметр равен удвоенной мере радиуса. |
| точка касания | Точка, в которой касательная касается окружности. |
| Радиус | Радиус круга — это расстояние от центра круга до края круга. |
| Окружность | Окружность круга — это мера расстояния вокруг внешнего края круга. |
| Секущая | Секанс угла прямоугольного треугольника — это значение, которое находится путем деления длины гипотенузы на длину стороны, примыкающей к данному углу. Отношение секущей обратно пропорционально отношению косинуса. |
| Тангенс | Тангенс угла прямоугольного треугольника — это величина, которая находится путем деления длины стороны, противолежащей данному углу, на длину стороны, примыкающей к данному углу. |