Точка максимума функции онлайн калькулятор: Экстремумы функции онлайн

Содержание

Калькулятор цен | Microsoft Azure

Избранные

Ознакомьтесь с наиболее популярными продуктами Azure

ИИ + машинное обучение

Создавайте приложения нового поколения, используя возможности искусственного интеллекта для любых разработчиков и любых сценариев.

Аналитика

Получите такие преимущества, как сбор, хранение, обработка, анализ и визуализация данных любого типа и объема и с любой скоростью.

Вычислительная среда

Воспользуйтесь возможностями облачных вычислений и масштабирования по требованию. При этом вы платите только за те ресурсы, которые используете.

Контейнеры

Разрабатывайте и администрируйте контейнерные приложения быстрее благодаря встроенным средствам

Базы данных

Продолжайте быстро развиваться и оперативно внедряйте инновации благодаря безопасным полностью управляемым службам баз данных корпоративного уровня.

DevOps

Быстрое внедрение инноваций с помощью простых и надежных средств для непрерывной поставки

Средства для разработчиков

Создавайте и непрерывно доставляйте облачные приложения, а также управляйте ими, используя любую платформу и любой язык

Гибридная и многооблачная среда

Получайте новинки Azure в любом месте — добавьте гибкость и инновации облачных вычислений в свои локальные рабочие нагрузки

Удостоверение

Управление удостоверениями и доступом пользователей для защиты устройств, данных, приложений и инфраструктуры от сложных угроз

Интеграция

Без проблем интегрируйте локальные и облачные приложения, данные и процессы в масштабах всего предприятия.

Интернет вещей

Подключайте ресурсы или среды, находите аналитику и применяйте продуманные действия по преобразованию организации

Управление

Упрощайте, автоматизируйте и оптимизируйте управление облачными ресурсами и обеспечение их соответствия требованиям

Мультимедиа

Доставка видео высокого качества в любую точку, в любое время и на любое устройство

Миграция

Упрощение и ускорение миграции в облако с помощью наших руководств, инструментов и ресурсов

Смешанная реальность

Объедините реальный и цифровой мир в решениях с эффектом присутствия и возможностями взаимодействия

Мобильные приложения

Сборка и развертывание кроссплатформенных и нативных приложений для любых мобильных устройств

Работа в сети

Объедините облачные и локальные службы и инфраструктуру, чтобы обеспечить максимальное удобство работы своим клиентам и пользователям.

Безопасность

Защита предприятия от сложных угроз для гибридных облачных нагрузок

Хранилище

Получите безопасное облачное хранилище с высоким уровнем масштабируемости для данных, приложений и рабочих нагрузок.

Интернет

Быстрая и эффективная сборка, развертывание и масштабирование мощных веб-приложений

Виртуальный рабочий стол Windows

Лучший интерфейс виртуального рабочего стола, поставляемый Azure

Как найти диапазон функции — MathCracker.com

Алгебра Учебники

Изучение того, как найти диапазон функции, может оказаться очень важным в алгебре и исчислении, потому что это дает вам возможность оценить, какие значения достигаются функцией. Или, другими словами, позволяет найти набор всех изображений с помощью функции

Задача поиска точек, которые могут быть достигнуты функцией, очень полезна. Например, у вас может быть производственная функция $q(x)$, которая дает вам объем вывода, полученный для $x$ единиц ввода.

Мы хотели бы знать, сколько единиц ввода необходимо для производства $b$ единиц вывода. Другими словами, нам нужно найти $x$, чтобы $q(x) = b$, что является еще одним способом узнать, находится ли $b$ в диапазоне функции $q(x)$.

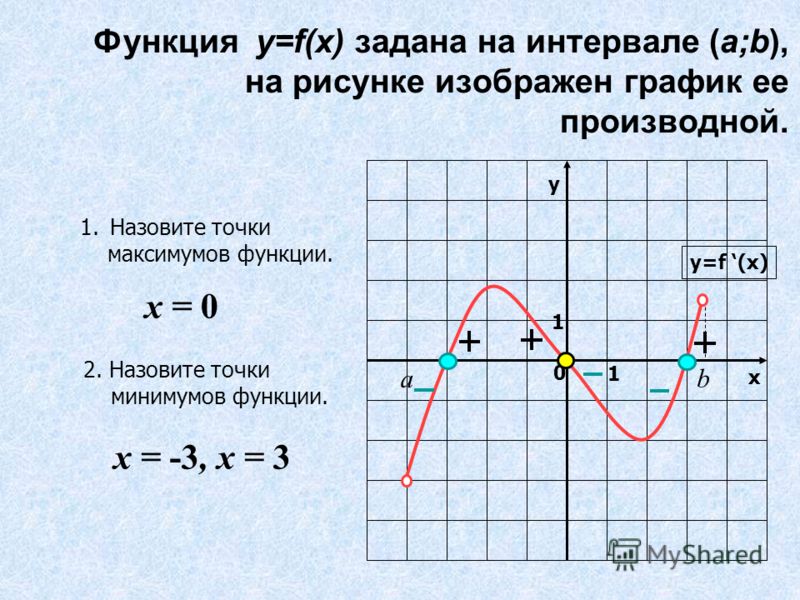
В этом уроке мы больше сконцентрируемся на механике нахождения диапазона. Для более концептуального подхода к домену и диапазону вы можете проверьте этот учебник .

Алгебраический способ определения диапазона функции

Так же, как когда мы узнали, как вычислить домен, не существует единого рецепта для нахождения диапазона, это действительно зависит от структуры функции $f(x)$.

Тем не менее, всегда будет использоваться один алгебраический прием. ТАКИМ способом вы найдете диапазон. Обращать внимание:

Скажем, нам нужно получить диапазон заданной функции $f(x)$. Затем мы рассмотрим типичное действительное число $y$ и попытаемся решить для $x$ следующее уравнение:

\[f(x) = y\]

Нам нужно определить, для каких значений $y$ приведенное выше уравнение может быть решено для $x$.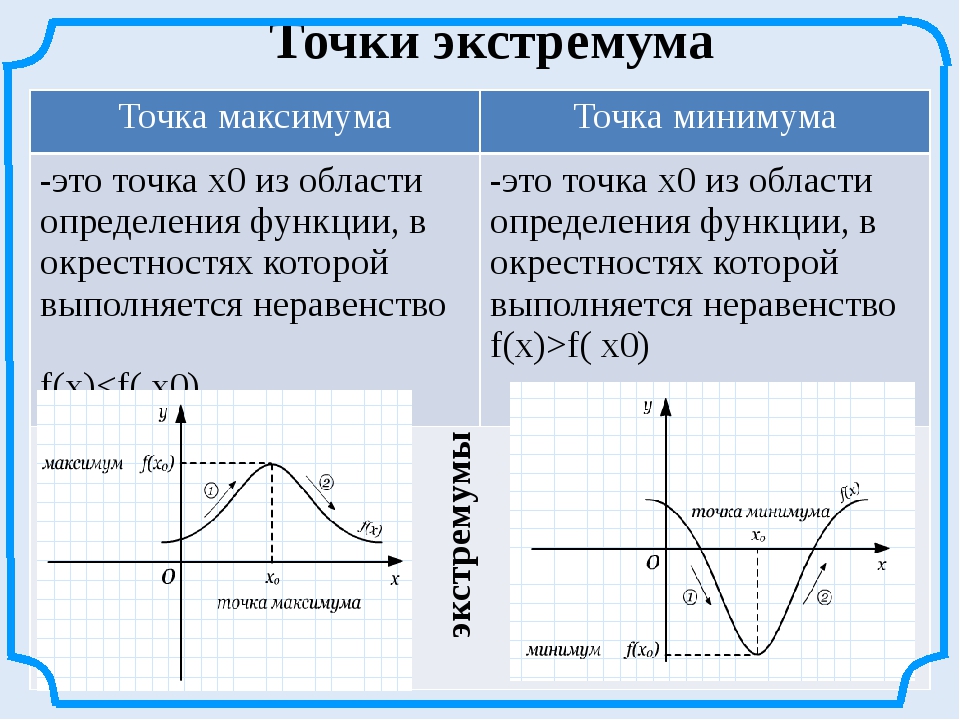

Вот и все. Конечно, это может быть сложно сделать, в зависимости от структуры функции $f(x)$, но это то, что вам нужно сделать.

Итак, это алгебраический способ, способ найти диапазон функции без построения графиков.

ПРИМЕР 1

Найдите диапазон функции $\displaystyle f(x) = \frac{x+1}{x-3}$:

ОТВЕЧАТЬ:

Мы продолжаем использовать алгебраический способ: пусть $y$ будет числом, и мы решим для $x$ в следующем уравнении: $f(x) = y$. Значение $y$ находится в диапазоне, если $f(x) = y$ может быть решено для $x$.

В этом случае мы имеем:

\[\large f(x) = y \Leftrightarrow \frac{x+1}{x-3} = y\] \[\Rightarrow \,\,\,x+1 = y\left( x-3 \right)\] \[\Rightarrow \,\,\,x+1 = yx-3y\] \[\Rightarrow \,\,\,x-yx=-1-3y\] \[\Rightarrow \,\,\,x\left( 1-y \right)=-1-3y\] \[\Rightarrow \,\,\,x=\frac{3y+1}{y-1}\]

Следовательно, когда будет четко определено $x$? Почти для всех $y$, кроме случая $y = 1$, потому что в этом случае у нас есть деление на $0$. Следовательно, диапазон $f$ в этом случае — это вся вещественная линия, кроме 1.

Если мы используем обозначение интервалов, мы можем написать $Range(f) = (-\infty, 1) \cup (1, +\infty)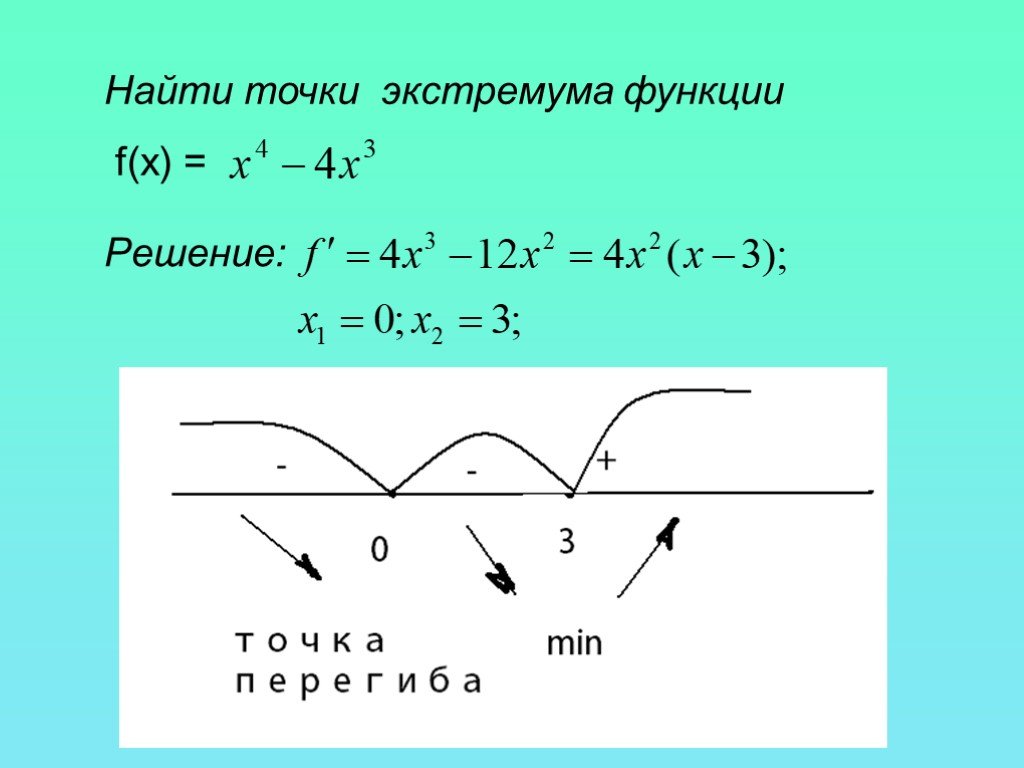$. 2 — 4(1)(3-y)}}{2(1)}\] \[\Rightarrow \displaystyle \,\,\, x = \frac{4 \pm \sqrt{16 — 4(3-y)}}{2}\] \[\Rightarrow \displaystyle \,\,\, x = \frac{4 \pm \sqrt{16 — 12 + 4y}}{2}\] \[\Rightarrow \displaystyle \,\,\, x = \frac{4 \pm \sqrt{4 + 4y}}{2}\] \[\Rightarrow \displaystyle \,\,\, x = 2 \pm \sqrt{1+y}\]

Теперь, видя это последнее выражение, когда будет хорошо определено $x$? Нам нужно, чтобы аргумент квадратного корня был неотрицательным, поэтому нам нужно:

\[1+y \ge 0\]

что означает, что $y \ge -1$. Если мы используем обозначение интервалов, мы можем написать $Range(f) = [-1, +\infty)$.

В этом примере мы могли бы решить эту проблему, используя тот факт, что $f(x) = x^2 — 4x + 3$ является квадратичной функцией, а ее график представляет собой параболу, которая открывается вверх. 2 — 4x + 3\) делает это еще более понятным:

Мы можем видеть, что на основе графика минимум достигается в $x = 2$, что в точности соответствует координате x вершины.

Риск использования графика для определения диапазона заключается в том, что вы потенциально можете неправильно прочитать критические точки на графике и дать неточную оценку того, где функция достигает своего максимума или минимума.

Другие стратегии поиска диапазона функции

Как мы видели в предыдущем примере, иногда мы можем найти диапазон функции, просто взглянув на ее график.

Например, вы хотите найти диапазон функции $f(x) = x + 3$. График показан ниже:

На графике выше не показаны минимальные или максимальные точки. Более того, когда $x$ большое и положительное значение, значение функции также большое и положительное. И аналогично, когда $x$ очень отрицательно, значение функции также очень отрицательное.

Интуиция подсказывает, что функция может принимать любые отрицательные и положительные значения, выбирая достаточно большие (положительные или отрицательные) значения $x$. И тогда можно сделать вывод, что диапазон — это вся реальная линия, которая равна $(-\infty, +\infty)$ с использованием обозначения интервала.

Такой анализ верен с точки зрения результата, но ненадежен с точки зрения аргументации. У «графического метода» поиска диапазона есть та же проблема: он привлекателен с интуитивной точки зрения, но довольно скуден с точки зрения содержания.

Обычно, если возможно, мы должны предпочесть аналитический / алгебраический путь. В этом примере нам нужно найти $x$:

\[x + 3 = y\] \[\Rightarrow \,\, x = y — 3\]

Итак, есть ли какие-либо ограничения на $y$ для правильного определения $x$? Вовсе нет, поэтому нет никаких ограничений на $y$, и можно сделать вывод, что диапазон — это вся реальная линия.

Вы можете проверить эту статью, если хотите знать, как найти домен функции вместо.

Есть много веских алгебраических причин для нахождения диапазона, одна из них состоит в том, что он является частью процессов для найти обратную функцию .

Учебник по алгебре Как найти диапазон Примеры расчета дальности

Калькулятор критических точек, экстремумов и седловых точек

Калькулятор попытается найти критические (стационарные) точки, относительные (локальные) максимумы и минимумы, а также седловые точки многомерной функции с показанными шагами.

Связанный калькулятор: Калькулятор множителей Лагранжа

Функция $$$f{\left(x,y\right)}$$$: 9{2} + 2 \ вправо) | _ {\ влево (\ влево (х, у \ вправо) = \ влево (0, \ гидроразрыва {4} {3} \ вправо) \ вправо)} = \ гидроразрыва {4} {3}$$$ больше, чем $$$0$$$, можно утверждать, что $$$\left(0, \frac{4}{3}\right)$$$ является относительным минимумом.

Так как $$$D{\left(- \frac{\sqrt{2}}{2},1 \right)} = -8$$$ меньше, чем $$$0$$$, можно утверждать что $$$\left(- \frac{\sqrt{2}}{2}, 1\right)$$$ является седловой точкой.

Поскольку $$$D{\left(\frac{\sqrt{2}}{2},1 \right)} = -8$$$ меньше, чем $$$0$$$, можно утверждать, что $$$\left(\frac{\sqrt{2}}{2}, 1\right)$$$ — седловая точка.

Ответ

Относительный максимум

$$$\left(x, y\right) = \left(0, 0\right)$$$A, $$$f{\left(0 ,0 \right)} = 2$$$A

Относительный минимум

$$$\left(x, y\right) = \left(0, \frac{4}{3}\right )\приблизительно \влево(0, 1,333333333333333\вправо)$$$A, $$$f{\left(0,\frac{4}{3} \right)} = \frac{22}{27}\приблизительно 0,814814814814815$$$A

Седловые точки

$$$\left(x, y\right) = \left(- \frac{\sqrt{2}}{2}, 1\right)\ приблизительно \left(-0,707106781186548, 1\right)$$$A, $$$f{\left(- \frac{\sqrt{2}}{2},1 \right)} = 1$$$A

$$$\влево(x, y\вправо) = \влево(\frac{\sqrt{2}}{2}, 1\вправо)\приблизительно \влево(0,707106781186548, 1\вправо)$$ $A, $$$f{\left(\frac{\sqrt{2}}{2},1 \right)} = 1$$$A

Калькулятор экстремумов — поиск экстремумов и седловых точек

Введение to Калькулятор экстремумов

Калькулятор экстремумов — это онлайн-инструмент, который вычисляет экстремум функции. Это лучший онлайн-инструмент, который предоставляет вам экстремальные и минимальные точки заданной функции без выполнения длительных вычислений. Он берет значение функции от пользователя и выдает экстремумы в течение минуты. Вы также можете рассчитать глобальные максимумы и минимумы с помощью этого инструмента.

В исчислении экстремумы и минимумы являются двумя важными понятиями, которые помогают решать задачи оптимизации, такие как максимизация прибыли, минимизация количества материала, необходимого для строительства, и нахождение максимальной высоты горы. Здесь мы познакомим вас с инструментом многомерного калькулятора точек экстремума, который поможет вам найти экстремальные точки функции.

Как найти крайнюю точку?

Экстремальная точка функции находится там, где она принимает экстремальное значение. Это может быть очень маленькое или очень большое значение по сравнению с окружающими значениями. Например, вершина холма — это максимум, а дно долины — это минимум. Максимумы указывают на наивысшее значение функции, а минимумы указывают на наименьшее значение.

Например, минимальное значение fx=x2+1 равно y=1, что получается, когда мы берем минимальное значение x, равное нулю. Итак,

$$ f(0) \;=\; 0 \;+\;1 \;=\; 1 $$

Формула, используемая Калькулятором экстремальных точек с шагами

Этот инструмент предназначен для вычисления экстремальных точек любой заданной функции. Для нахождения экстремальных значений используются следующие шаги:

Преобразует заданную функцию в виде,
$$ f'(x) \;=\; 0 $$
Это делается путем вычисления производной данной функции и записи ее равной нулю.
На этом шаге вычисляется значение x.
Значение x подставляется в заданную функцию, которая дает экстремальное значение.

Как использовать калькулятор экстремумов функций с шагами?

С помощью этого инструмента легко найти крайние точки любой функции. Есть несколько простых шагов к его использованию. Это:

После нажатия кнопки расчета вы получите решение в течение нескольких секунд.

На первом этапе необходимо ввести значение функции.
Или вы можете использовать опцию загрузки примеров.
Просмотрите функцию, показанную ниже.
Нажмите кнопку расчета.

Зачем использовать калькулятор максимумов и минимумов?

В математике часто нужно найти точки максимума и минимума функции. Он также имеет множество приложений в реальных задачах. Но расчет крайних точек может быть сложным. Многие студенты связывают экстремальное значение с абсолютным значением, что неверно. Поэтому вам нужно использовать этот инструмент.

Калькулятор экстремумов с несколькими переменными обеспечивает простой и быстрый способ вычисления экстремальных значений. Вам не нужно путать абсолютные значения и экстремальные значения. Мы можем найти производную в любой точке от максимума до минимума с помощью калькулятора производной в точке.

Преимущества использования Калькулятора критических точек и экстремумов

Вы можете получить много преимуществ при использовании нашего инструмента. Вот некоторые из его замечательных преимуществ:

Калькулятор максимальных и минимальных значений прост в использовании, поскольку позволяет вычислять экстремумы любой функции одним щелчком мыши.
Это бесплатное использование, и вам не нужно платить никаких сборов.
— более эффективный инструмент, чем другие инструменты премиум-класса.
Вы также можете получить значение экстремума заданной функции и ее трехмерный график. Итак, вы можете понять разброс крайних точек.

Часто задаваемые вопросы

Что такое крайняя точка в исчислении?

В исчислении экстремальная точка функции — это точка, в которой функция принимает самые высокие или самые низкие значения по сравнению с ближайшими значениями. Минимальная и максимальная точки являются крайними точками данной функции.