Кривые второго порядка построение графика – Кривые второго порядка

3.2 Кривые второго порядка

Задачи по теме «Кривые второго порядка»

Задача 1. Привести уравнение кривой к каноническому виду и построить ее.

Решение.

2

а). Выделим полные квадраты пои по:или- каноническое уравнение окружности с центром в точкеи радиусом.

б).

.

— окружность,,

.

Задача 2. а) Найти точки пересечения прямойи окружности.

Решение. Чтобы найти точки пересечения двух линий, нужно решить систему их уравненийи. Для этого подставимв уравнение окружности:, осталось найти;.

Ответ:,.

б) Показать, что прямая и окружностьне пересекаются.

Решение. Для этого достаточно показать, что система уравненийирешений не имеет. Подставимв уравнение окружности:, дискриминант уравнения. Решений у системы нетточек пересечения у линий нет.

Задача 3. Окружность касается осей координат и проходит через точку. Составить уравнение этой окружности.

Решение.Так как окружность касается осей координат, тов уравнении, т.е.

и (почему?). Таким образом, каноническое уравнение окружности. Чтобы найти, подставим в это уравнение координаты точки, через которую проходит окружность:

,,.

Ответ: ;.

Задача 4. Вычислить кратчайшее расстояние от точкидо окружности.

Решение.– кратчайшее расстояние от точкидо окружности. Очевидно,.– центр окружности,- ее радиус. Приведем уравнение окружности к каноническому видуили,. Вычислим длину отрезка.

Ответ:.

Задача 5. Составить уравнение окружности, диаметром которой является отрезок прямой, заключенный между осями координат.

Решение.Преобразуем уравнение прямойк виду «уравнение прямой в отрезках на осях»:, откуда видно, что-и точки пересечения прямой с

осями координат, — диаметр окружности по условию задачи. Следовательно, центр

окружности — точка– середина, т.е. координаты центра окружности,

ведь ,, а радиус окружности

2

. Уравнение окружности по :

.

Ответ:.

Задача 6.Окружность задана уравнением. Составить уравнение ее диаметра, перпендикулярного хорде.

Решение. Диаметрпроходит через центр окружности.

П

2

риведем уравнение окружности к каноническому виду

или , откуда. По условию задачи диаметр

перпендикулярен данной прямой , значит, по условию перпендикулярности

двух прямых , получим, т.к. угловой коэффициент данной

прямой . Итак, прямая:, или, или.

Ответ:.

Задача 7. Написать каноническое уравнение эллипса, у которого расстояние от одного из фокусов до концов большой оси равно 5 и 1.

Решение.Общий вид канонического уравнения эллипса :, где– большая полуось эллипса, а- малая полуось эллипса. Найдем их. По

условию задачи ,, следовательно,или

,,– фокусное расстояние эллипса,

откуда – полуфокусное расстояние. Зависимость

между параметрами ,,у эллипса:

. Таким образом, каноническое

уравнение эллипса: .

Ответ:.

Задача 8. Найти полуоси, координаты вершин, фокусов, эксцентриситет эллипса. Построить его.

Решение. Приведем уравнение эллипса к каноническому видуили, откуда;, т.к. для эллипса, то. Таким образом:;;;;;. Эксцентриситет эллипса.

Ответ: .

Задача 9.Привести уравнение кривой к каноническому виду:. Построить эту кривую, найти ее эксцентриситет.

Решение. Выделим в уравнении кривой полные квадраты по

и:или. Из уравнения

видно, что центр симметрии эллипса (данной кривой) находится в точке;

— малая и– большая полуоси эллипса,;.

Ответ:.

Задача 10.Дана гипербола. Найти координаты ее вершин, фокусов, эксцентриситет и уравнения асимптот этой гиперболы.

Решение.Каноническое уравнение гиперболы, следовательно, для данной гиперболы,. Зависимость между параметрами гиперболы:

,. Значит,;;

;;;;; асимптоты:

или. (Ответ)

Задача 11. Привести уравнение кривой к каноническому виду и построить ее:.

Р

4

ешение.Приведем уравнение к каноническому виду, выделив полные квадраты пои:или, из уравнения

следует, что центр симметрии кривой ,- действительная,

4

— мнимая полуоси гиперболы;-

полуфокусное расстояние гиперболы .

Задача 12. Привести уравнение кривойк каноническому виду, построить кривую.

Решение. Преобразуем данное уравнение. Выделив пополный квадрат:

или- это каноническое уравнение параболы

5

. Из этого уравнения видно, что вершина параболы -, ось

симметрии параллельна оси .

Задача 13.Камень, брошенный под острым углом к горизонту, описал дугу параболы и упал на расстоянии 16 м от начального положения. Определить параметр параболической траектории, зная, что наибольшая высота, достигнутая камнем, равна 12 м.

Решение. Выберем систему таким образом, чтобы можно было задать параболу

5

каноническим уравнением вида. Из условий задачи видно, что в этой

системе координат координаты точек ,, т.к.,.

Подставим координаты одной из них в уравнение параболы: ,

отсюда .

Ответ: .

Задача 14. Струя воды, выбрасываемая фонтаном, принимает форму параболы, параметр которого равен. Определить высоту струи, если известно, что она падает в бассейн на расстоянии 2 м от места выхода.

Решение. Решая эту задачу, можно воспользоваться рисунком предыдущей задачи и уравнением параболы. По условию задачи известно, чтом,, следовательно,,,. Подставим в уравнение параболы данный параметр и координаты точки, через которую проходит парабола, например:, откуда. Это ордината точеки, а также и высота параболы, следовательно,.

Ответ:

studfiles.net

Определить вид кривой 2-го порядка онлайн · Как пользоваться Контрольная Работа РУ

Приведём примеры кривых второго порядка, для которых можно определить канонический вид онлайн:

Кривая

Уравнение	Канонический вид	Тип	Измерение
9x^2+12xy+4y^2-24x-16y+3=0	x^2=1	Две параллельные прямые	Кривая
x^2-2xy+y^2-10x-6y+25=0	y^2=4*sqrt(2)*x	Парабола	Линия
5x^2+4xy+y^2-6x-2y+2=0	x^2/(1/sqrt(2*sqrt(2)+3))^2 + y^2/(1/sqrt(-2*sqrt(2)+3))^2=0	Вырожденный эллипс	Линия
5*x^2+ 4*x*y+8*y^2+8*x+14*y+5=0	x^2/(3/4)^2+y^2/(1/2)^2=1	Эллипс

Ислледование на определение вида кривой будет выглядеть примерно так:

Имеется два способа: Прямой метод и метод инвариантов:

Дано ур-ние кривой 2-порядка: $$5 x^{2} + 4 x y + 8 x + 8 y^{2} + 14 y + 5 = 0$$ Это уравнение имеет вид: $$a_{11} x^{2} + 2 a_{12} x y + 2 a_{13} x + a_{22} y^{2} + 2 a_{23} y + a_{33} = 0$$ где $$a_{11} = 5$$ $$a_{12} = 2$$ $$a_{13} = 4$$ $$a_{22} = 8$$ $$a_{23} = 7$$ $$a_{33} = 5$$ Вычислим определитель $$\Delta = \left|\begin{matrix}a_{11} & a_{12}\\a_{12} & a_{22}\end{matrix}\right|$$ или, подставляем $$\Delta = \left|\begin{matrix}5 & 2\\2 & 8\end{matrix}\right|$$ $$\Delta = 36$$ Т.к. $$\Delta$$ не равен 0, то находим центр канонической системы координат. Для решаем систему уравнений $$a_{11} x_{0} + a_{12} y_{0} + a_{13} = 0$$ $$a_{12} x_{0} + a_{22} y_{0} + a_{23} = 0$$ подставляем коэффициенты $$5 x_{0} + 2 y_{0} + 4 = 0$$ $$2 x_{0} + 8 y_{0} + 7 = 0$$ тогда $$x_{0} = — \frac{1}{2}$$ $$y_{0} = — \frac{3}{4}$$ Тем самым мы перешли к уравнению в системе координат O’x’y’ $$a’_{33} + a_{11} x’^{2} + 2 a_{12} x’ y’ + a_{22} y’^{2} = 0$$ где $$a’_{33} = a_{13} x_{0} + a_{23} y_{0} + a_{33}$$ или $$a’_{33} = 4 x_{0} + 7 y_{0} + 5$$ $$a’_{33} = — \frac{9}{4}$$ тогда ур-ние превратится в $$5 x’^{2} + 4 x’ y’ + 8 y’^{2} — \frac{9}{4} = 0$$ Делаем поворот системы полученной координат на угол φ $$x’ = \tilde x \cos{\left (\phi \right )} — \tilde y \sin{\left (\phi \right )}$$ $$y’ = \tilde x \sin{\left (\phi \right )} + \tilde y \cos{\left (\phi \right )}$$ φ — определяется из формулы $$\cot{\left (2 \phi \right )} = \frac{a_{11} — a_{22}}{2 a_{12}}$$ подставляем коэффициенты $$\cot{\left (2 \phi \right )} = — \frac{3}{4}$$ тогда $$\phi = — \frac{1}{2} \operatorname{acot}{\left (\frac{3}{4} \right )}$$ $$\sin{\left (2 \phi \right )} = — \frac{4}{5}$$ $$\cos{\left (2 \phi \right )} = \frac{3}{5}$$ $$\cos{\left (\phi \right )} = \sqrt{\frac{1}{2} \cos{\left (2 \phi \right )} + \frac{1}{2}}$$ $$\sin{\left (\phi \right )} = \sqrt{- \cos^{2}{\left (\phi \right )} + 1}$$ $$\cos{\left (\phi \right )} = \frac{2 \sqrt{5}}{5}$$ $$\sin{\left (\phi \right )} = — \frac{\sqrt{5}}{5}$$ подставляем коэффициенты $$x’ = \frac{2 \sqrt{5}}{5} \tilde x + \frac{\tilde y}{5} \sqrt{5}$$ $$y’ = — \frac{\tilde x}{5} \sqrt{5} + \frac{2 \sqrt{5}}{5} \tilde y$$ тогда ур-ние превратится из $$5 x’^{2} + 4 x’ y’ + 8 y’^{2} — \frac{9}{4} = 0$$ в $$8 \left(- \frac{\tilde x}{5} \sqrt{5} + \frac{2 \sqrt{5}}{5} \tilde y\right)^{2} + 4 \left(- \frac{\tilde x}{5} \sqrt{5} + \frac{2 \sqrt{5}}{5} \tilde y\right) \left(\frac{2 \sqrt{5}}{5} \tilde x + \frac{\tilde y}{5} \sqrt{5}\right) + 5 \left(\frac{2 \sqrt{5}}{5} \tilde x + \frac{\tilde y}{5} \sqrt{5}\right)^{2} — \frac{9}{4} = 0$$ упрощаем $$4 \tilde x^{2} + 9 \tilde y^{2} — \frac{9}{4} = 0$$ Данное уравнение является эллипсом $$\frac{\tilde x^{2}}{\left(\frac{3}{4}\right)^{2}} + \frac{\tilde y^{2}}{\left(\frac{1}{2}\right)^{2}} = 1$$ — приведено к каноническому виду.
Центр канонической системы координат в точке O:

(-1/2, -3/4)

Базис канонической системы координат $$\vec e_1 = \left ( \frac{2 \sqrt{5}}{5}, \quad — \frac{\sqrt{5}}{5}\right )$$ $$\vec e_2 = \left ( \frac{\sqrt{5}}{5}, \quad \frac{2 \sqrt{5}}{5}\right )$$

Метод инвариантов

Дано ур-ние линии 2-порядка: $$5 x^{2} + 4 x y + 8 x + 8 y^{2} + 14 y + 5 = 0$$ Это уравнение имеет вид: $$a_{11} x^{2} + 2 a_{12} x y + 2 a_{13} x + a_{22} y^{2} + 2 a_{23} y + a_{33} = 0$$ где $$a_{11} = 5$$ $$a_{12} = 2$$ $$a_{13} = 4$$ $$a_{22} = 8$$ $$a_{23} = 7$$ $$a_{33} = 5$$ Инвариантами данного уравнения при преобразовании координат являются определители: $$I_{1} = a_{11} + a_{22}$$

     |a11  a12|
I2 = |        |
     |a12  a22|

$$I_{3} = \left|\begin{matrix}a_{11} & a_{12} & a_{13}\\a_{12} & a_{22} & a_{23}\\a_{13} & a_{23} & a_{33}\end{matrix}\right|$$ $$I{\left (\lambda \right )} = \left|\begin{matrix}a_{11} — \lambda & a_{12}\\a_{12} & a_{22} — \lambda\end{matrix}\right|$$

     |a11  a13|   |a22  a23|
K2 = |        | + |        |
     |a13  a33|   |a23  a33|

подставляем коэффициенты $$I_{1} = 13$$

     |5  2|
I2 = |    |
     |2  8|

$$I_{3} = \left|\begin{matrix}5 & 2 & 4\\2 & 8 & 7\\4 & 7 & 5\end{matrix}\right|$$ $$I{\left (\lambda \right )} = \left|\begin{matrix}- \lambda + 5 & 2\\2 & — \lambda + 8\end{matrix}\right|$$

     |5  4|   |8  7|
K2 = |    | + |    |
     |4  5|   |7  5|

$$I_{1} = 13$$ $$I_{2} = 36$$ $$I_{3} = -81$$ $$I{\left (\lambda \right )} = \lambda^{2} — 13 \lambda + 36$$ $$K_{2} = 0$$ Т.к. $$I_{2} > 0 \wedge I_{1} I_{3} < 0$$ то по признаку типов линий:
данное уравнение имеет тип : эллипс.
Составляем характеристическое уравнение для нашей линии: $$- I_{1} \lambda + I_{2} + \lambda^{2} = 0$$ или $$\lambda^{2} — 13 \lambda + 36 = 0$$ $$\lambda_{1} = 9$$ $$\lambda_{2} = 4$$ тогда канонический вид уравнения будет $$\tilde x^{2} \lambda_{1} + \tilde y^{2} \lambda_{2} + \frac{I_{3}}{I_{2}} = 0$$ или $$9 \tilde x^{2} + 4 \tilde y^{2} — \frac{9}{4} = 0$$ $$\frac{\tilde x^{2}}{\left(\frac{1}{2}\right)^{2}} + \frac{\tilde y^{2}}{\left(\frac{3}{4}\right)^{2}} = 1$$ — приведено к каноническому виду.

www.kontrolnaya-rabota.ru

Кривые и поверхности второго порядка

3. Построение графиков

Подтвердим результаты проведённого исследования данного уравнения кривой (3.1) второго порядка, построив соответствующие графики кривых при разных a.

При a = 3 уравнение (3.1) принимает вид:

2x² + 4xy + 3y² + 8x – 6y +5 = 0

Графиком данного уравнения является парабола:

При a = 6 уравнение (3.1) принимает вид:

x² + 4xy + 3y² + 8y² – 6y +5 = 0

Графиком данного уравнения является гипербола:

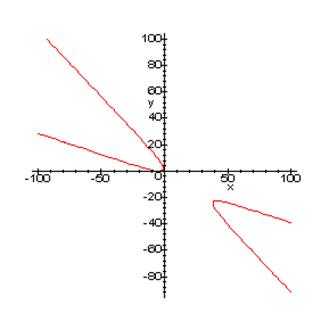
При a = 0 уравнение (3.1) принимает вид

5x² + 4xy + 3y² + 8y² – 6y +5 = 0

Графиком данного уравнения является эллипс. Изобразим в данной системе также график канонического уравнения эллипса (3.6):

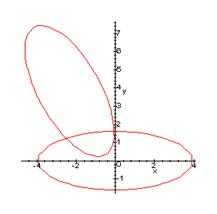
4. Вывод

Исследовав данное общее уравнение кривой второго порядка, мы установили, что при значении параметра a = 0 уравнение задаёт эллипс . Привели уравнение к каноническому виду, применяя преобразования параллельного переноса и поворота. При параллельном переносе коэффициенты при первых степенях стали равны нулю, при повороте координатных осей коэффициенты при смешанном произведении стали равны нулю. Построили графики для всех фигур, которое может задавать данное уравнение, построили график эллипса в общей и канонической системе координат.

1. Определение типа поверхности

Для данного уравнения поверхности второго порядка:

4x² — z² + 12xz + 6y — 8z + 5 = 0 (4.1)

Определить тип поверхности с помощью инвариантов.

4 + 0 -1 = 3 = — 4 – 36 = — 40

Определим характер расположения центра: Данная поверхность не имеет центра , так как выполняется условие I ₃ = 0, I ₄ ¹ 0. При этом инвариант I ₄ = 360 > 0, следовательно, графиком уравнения (4.1) является гиперболический параболоид .

2. Приведение к каноническому виду

Совершим параллельный перенос начала координат в некоторую точку O ‘( x ₀ , y ₀ , z ₀ ) . При этом координаты x , y , z произвольной точки пространства в системе координат Oxyz и координаты x ‘, y ‘, z ‘ этой же точки в новой системе координат в системе координат O ‘ x ‘ y ‘ z ‘ связаны соотношением:

(4.2)

Подставляя уравнения (4.2) в уравнение (4.1) получим уравнение поверхности S в новой системе координат O ‘ x ‘ y ‘ z ‘ :

4(x’+x₀ )² — (z’+z₀ )² + 12(x’+x₀ )(z’+z₀ ) + 6y’ — 8(z’+z₀ ) + 5 = 0

4x’² + 8x’x₀ + 4x₀² — z’² — 2z’z₀ — z₀² + 12x’z’ + 12z’z₀ + 12x₀ z’ + 12x₀ z₀ + 6y’ — 8z’ — 8z₀ + 5 = 0

4x’² — z’² + 12x’z’ + 6y’ + (12x₀ — 2z₀ — 8)z’ + (8x₀ + 12z₀ )x’ + (4x₀² — z₀² + 12x₀ z₀ — 8z₀ +5)=0 (4.3)

Для того, чтобы новое начало координат O'(x₀ , y₀ , z₀ ) было центром поверхности (4.1) необходимо и достаточно, чтобы в уравнении (4.3) отсутствовал член с x’ и z’ в первой степени:

Решая данную систему, находим x₀ =

и y₀ = . Подставим полученные значения в уравнение (4.2):

4x’² — z’² + 12x’z’ + 6y’ + (

)z’ + ()x’ + () = 0

4x’² — z’² + 12x’z’ + 6y’ +

=0 (4.4)

Поскольку коэффициент при x’z’ не равен нулю, то продолжим дальнейшее преобразование, совершив поворот осей координат на угол a. Координаты произвольной точки поверхности будут связаны следующими соотношениями:

(4.5)

Подставив выражения из (4.5) в уравнение (4.4), получим следующее:

4(Xcosa — Zsina)² – (Xsina + Zcosa)² + 12(Xcosa — Zsina)(Xsina + Zcosa) + 6Y +

= 0

4X² cos² a — 8XZcosasina + 4Z2sin² a — X2sin² a — 2XZsin² a — 2XZcosasina -Z² cos² a + 12X² cosasina + 12XZcos² a — 12XZsin² a — 12Z² sinacosa + 6Y +

= 0

(4cos² a-sin² a+12cosasina)X² +(4sin² a-cos² a-12sinacosa)+(-8cosasina-2cosasina+12cos² a-12sin² a)XZ+6Y+

=0 (4.6)

Найдём угол a такой, что коэффициент при XZ будет равен нулю:

-8cosasina-2cosasina+12cos² a-12sin² a=0

6tg² a+5tga-6=0

D = 25+144 = 169 = 13²

Откуда следует, что tga =

или tga = . Возьмём tga = . Тогда найдём cosa==, sina=. Подставим найдённые значения в уравнение (4.6):

(

)X² +()Z² +()XZ+6Y+=0 (4.7)

— это каноническое уравнение поверхности (4.1). Оно имеет сдвиг по оси O’Y на (-

).

3. Исследование формы поверхности методом сечений

Проведём исследование графика уравнения (4.7) методом сечения плоскостями.

Рассмотрим линии

, полученные в сечениях гиперболического параболоида плоскостями Y=h. Эти линии определяются системой уравнений:

Следовательно, уравнения проекций линий

на плоскость ZO ‘ X имеют вид: :

Рассмотрим три случая:

Если h +

>0, h >, запишем полученное уравнение в виде: (4.8)

Уравнение (4.8) задаёт гиперболы с центрами в точках (0, h ,0).

Полуоси гипербол:

a =

— действительная полуось, b = — мнимая полуось, увеличиваются с увеличением h . При различных значениях h получим семейство соответствующих гипербол:

h = 1 a=

; b=;

h=2 a=

; b=;

h=3 a=

; b=;

Изобразим данные гиперболы на рисунке:

Если h +

=0, h =, запишем полученное уравнение в виде: или

mirznanii.com

Расчет кривой второго порядка на плоскости по точкам

Полученная формула

Коэффициенты через пробел

Калькулятор предназначен для расчета и создания уравнения кривых второго порядка на декартовой плоскости по нескольким точкам, от двух до пяти.

Не является секретом то, что уравнение кривой второго порядка может быть представлена формулой

Мы будем использовать чуть измененную формулу, разделив все коэффициенты на a6

отсюда видно, что кривую второго порядка  можно однозначно определить по пяти точкам.

Кривая второго порядка при различных коэффициентах может превращатся в следующие «типы»:

— Эллипс

— Окружность

— Парабола

— Гипербола

— пара пересекающихся прямых

— пара паралельных несовпадающих прямых

— пары совпадающих прямых

— линии, вырождающиеся в точку

— «нулевые линии», то есть «линии», вовсе не имеющие точек

Если Вам интересны формулы при которых получаются все эти типы, то пожалуйста

  — окружность

 — «нулевая» окружность

 — эллипс

  —  точка

  —  равносторонняя гипербола

  — пара пересекающихся прямых

 — формула параболы

 — пара параллельных прямых

 — нулевая линия

 — пара совпадающих прямых

Этот сервис позволяет Вам по заданным точкам определить, какую же кривую второго порядка провести через эти точки. Кроме этого, Вы увидите все основные параметры полученной кривой второго порядка. 

От Вас лишь понадобится предоставить боту от двух до пяти декартовых координат, что бы бот мог решить эту задачу.

Инварианты и сводная таблица

Любая кривая второго порядка  характеризуется  тремя инвариантами, имеющими вид

 

И одним семиинвариантом

 

если Вам интересно, откуда они появились, то рекомендуем  прочитать книгу «Аналитическая геометрия — Делоне»

Характеристическое уравнение кривой второго порядка:

Таким образом сводная таблица имеет вид

 

 

Анализируя написанные онлайн калькуляторы по этой теме, нашел интересную «особенность». Попробовав рассчитать по трем точкам  кривую второго порядка, зная что эти точки принадлежат окружности, я с завидным постоянством получал ответ, что графиком(формой)полученного уравнения кривой является эллипс.

Нет формально, конечно стоит признать что окружность является частным примером эллипса, но ведь можно пойти дальше и признать что и эллипс и гипербола и парабола, являются лишь частным примером кривой второго порядка общего вида,  и в ответах таких калькуляторов выдавать ответ  пользователю «вы получили уравнение второго порядка» и всё…  не соврали же…

Такое сверхлегкое трактование и смешение определений геометрических фигур, никак не способствует пониманию  и сути решаемых задач. Это как в анекдоте «А теперь нарисуем квадрат со сторонами 3 на 4»(с)  И не поймешь то ли рисовать квадрат, то ли прямоугольник….

Синтаксис 

Jabber:  kp2 <строка>

Строкой является список чисел  разделенное пробелами. 

А каждое «число» представляет собой абсциссу  и ординату точки  разделенные двоеточием.

Координат или их «замен» должно быть ровно шесть

То есть если мы знаем пять координат то 6 элементом у нас будет единица.

В вкладке Пример Вы сможете увидеть решения некоторые.

Если в строке  есть числа не имеющие : то это означает  что это неизменяемый соответствующий коэффициент кривой второго порядка.

Например если в строке стоит ноль на первой позиции строки   то это означает что A1=0

Бот вычисляет численные параметры кривой. Если же Вам надо нарисовать кривую второго порядка на плоскости, просьба использовать программу GeoGebra и материал Построить график функции c помощью GeoGebra

Примеры

Пример:

Начнем сразу с проверочного примера

Вообще, убедимся правильно ли считает бот?

Итак, есть у нас функция x*x+3x-11=y

определим значения при x=1,2,3,4,5

значения получились такие y=-7,-1,7,17,29

и зададим эти точки в качестве исходных

пишем kp2 1:-7 2:-1 3:7 4:17 5:29

в результате получаем следующее:

На первый взгляд получилось далеко не то, что должно получится.

Но если мы уберем нулевые коэффициенты, и разделим все на  0.09091 то результат будет такой 

{tex}-x^2-3*x+y+11=0{tex}

то есть

Что и требовалось доказать  в качестве правильности расчетов  нашего бота.

---

Теперь пусть у нас есть всего лишь три точки

С координатами x=1,2,3 и y=-7,-1,7

Логично, что это тоже самое уравнение параболы  что мы разбирали в первом примере. НО! при трех точках такое решение не единственное.

Давайте попробуем задать боту  всего три координаты и скажем ему какого вида уравнение мы хотим получить.

Например:

Это частное уравнение кривой второго порядка в котором коэффициенты а1 и а5 равны нулю

Скажем об этом боту

kp2 0 1:-7 2:-1 3:7 0 1

где 0- показывает какие коэффициенты нам НЕ надо  учитывать, а 1 — это постоянный коэффициент, то есть его находить нет необходимости. Он известен.

Видим что не учитываем 1 и 5 коэффициент.

получим

Кривая второго порядка a1*x*x+a2*y*y+a3*x*y+a4*x+a5*y+a6 = 0

Коэффициент a2 при y*y равен -0.00621100

Коэффициент a3 при x*y равен 0.03312600

Коэффициент a4 при x равен -0.46376800

Коэффициент a6 равен 1

 

То есть есть еще одна кривая которая проходит через заданные три точки

это

 

Кто желает может проверить. Но уверяю что все правильно.

 

 

• Расчет параметров прямой линии по заданным параметрам >>

abakbot.ru

Глава V кривые второго порядка Парабола

Определение: Параболой называется геометрическое место точек плоскости, равноудаленных от некоторой точки,называемой фокусом параболы и некоторой прямой, называемой директрисой параболы.

Уравнение параболы принятo записывать в следующем виде:

y² = 2px , p>0 (1)

Свойства параболы непосредственно следуют из

свойств уравнения:

1.Абсцисса любой точки параболы неотрицательна.

2.Парабола проходит через начало координат.

3.Парабола симметрична относительно оси абсцисс.

4.При неограниченном возрастании абсциссы x ордината у возрастает по абсолютной величине.

Точка F(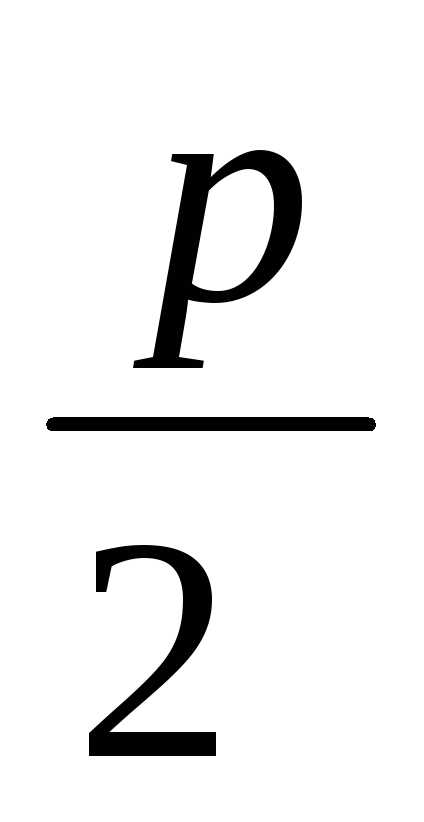;0) называетсяфокусом параболы, прямая —директрисой.

Величина р называется фокальным параметром или просто параметром параболы.

Эллипс

Определение. Эллипсом называется множество точек плоскости, сумма расстояний от каждой из которых до двух данных точек F₁ и F₂ этой плоскости, называемых фокусами эллипса, есть величина постоянная, равная 2а (а>0), большая, чем расстояние между фокусами.

Д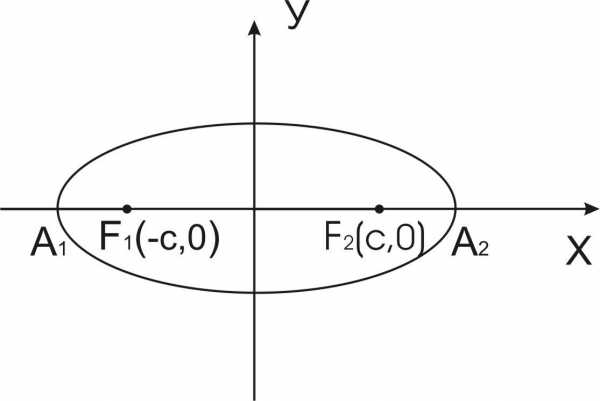ля составления уравнениэллипса выберем прямоугольную декартову систему координат так, чтобы ось ОХ проходила через фокусы F₁ и F₂, а начало координат — точка О находилась в середине отрезка F₁F₂.

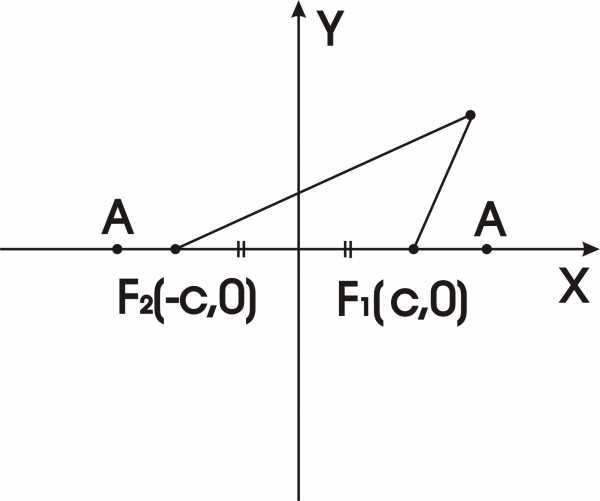Обозначим F₁F₂ = 2с. Тогда F₁(-с,0), F₂(c,0). Пусть М(х,у)— произвольная точка эллипса. Тогда MF₁+ MF₂= 2а, а>с.

Так как , и уравнение принимает вид:

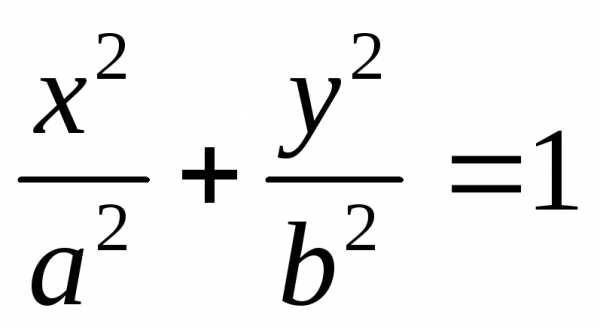. (2)

Пусть координаты точки М₁(х₁,у₁)удовлетворяют уравнению (2).

Обозначим r₁ = F₁M₁, r₂ = F₂M₂ — фокальные радиусы точек М1 М₂. Тогда , , 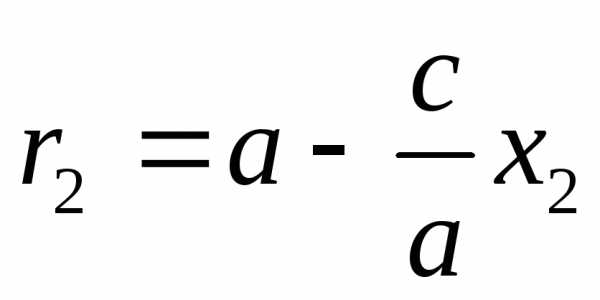значит, r₁+r₂=2a.

Теперь по свойствам уравнения (2) исследуем геометрические свойства эллипса.

1. Оси ОХ и ОУ являются осями симметрии эллипса. Следовательно, эллипс достаточно исследовать только в первой координатной четверти.

2. Эллипс пересекает координатные оси в точках А₁(-а,0), А₂(а,0), В₁(0,b), В₂(0,-b), называемых вершинами эллипса.

3. Эллипс расположен в прямоугольнике, ограниченном прямыми х=а, у =b.

4. Из уравнений следует, что при возрастании х от 0 до а в первой координатной четверти, у убывает от b до 0.

По полученным свойствам строим эллипс Отрезок А₁А₂ и его длина 2а называются большой осью эллипса, а отрезок B₁B₂ и его длина 2b называются малой осью эллипса. Отрезок ОА₁ с длиной а и отрезок ОВ₁ с длиной b называются соответственно большой и малой полуосями эллипса. Длина отрезка F₁F₂=2с называется фокусным расстоянием, начало координат— центр эллипса.

Если а=b, то получаем каноническое уравнение окружности

Уравнения х = acost, у = bsint —

Параметрические уравнения эллипса.

Определение. Эксцентриситетом эллипса называется число

Так как с<а, то 0<c<1. Заметим, что у окружности оба фокуса

совпадают, поэтому с = 0 и ε = 0.

.

Следовательно, эксцентриситет характеризует форму эллипса.

Используя понятия эксцентриситета, можно выразить фокальные радиусы произвольной точки M(x,у) эллипса:

r₁=а+εх, r₂=а—εх

studfiles.net

8.5. Исследование кривых второго порядка

Исследование кривых второго порядка.

Общее уравнение кривой второго порядка можно представить уравнением

Чтобы определить тип кривой, нужно вычислить дискриминант старших членов

и дискриминант уравнения

Если то кривая центральная, еслито кривая нецентральная.

В зависимости от значений общее уравнение кривой определяет следующий геометрический образ,

Таблица 1

	эллипс	точка
	гипербола	пара пересекающихся прямых
	парабола	пара параллельных прямых

Преобразование центральной кривой.

1. Найдем координаты центра кривой, для чего составим и решим систему

Решение системы будет точка – центр кривой.

Необходимо выполнить параллельный перенос начала координат системы в центр кривой – точкуПосле преобразования параллельного переноса общее уравнениекривой второго порядка не будет содержать членов с первыми степенями переменных иа группа старших членов останется неизменной.

Уравнение примет вид

2. Найдем угол поворота системы по формуле

Вычислим

Знак выбирается в соответствии с тем, в какой четверти выбран угол

Если при этом вычисление окажется затруднительным, то следует, знаянайтииз таблиц.

Подставить значение в формулы поворота осей координат

Формулы поворота подставим в уравнение

При этом преобразовании в уравнении кривой коэффициент при произведении обратится в нуль, свободный членостанется неизменным.

Уравнение примет вид

Это уравнение, которое приводится к каноническому.

Преобразование нецентральной кривой

Преобразование кривой параболического типа следует начать с поворота системы координат на угол который находится по формуле

Вычислим по формулам

Подставим значения в формулы поворота осей координат

Формулы поворота подставим в заданное уравнение. При этом преобразовании в уравнении кривой коэффициенты при иили приобратятся в нуль, а свободный член остается неизменным.

Уравнение кривой примет вид

или

В полученном уравнении выделим квадрат двучлена, т.е. приведем к виду

или

т.е.

Выполнить преобразование параллельного переноса начала координат в вершину параболы, обозначив

где точка вершина параболы, начало координат системы

Уравнение кривой при этом примет вид

— это каноническое уравнение параболы.

Преобразование нецентральной кривой

Если то уравнение кривой можно представить в виде

Решив это квадратное уравнение относительно двучлена получим пару параллельных прямых

где корни квадратного уравнения относительно двучлена

Рассмотрим пример. Преобразовать к каноническому виду и построить кривую

Вычислим дискриминант старших членов

Вычислим дискриминант уравнения

Вывод: следовательно, кривая центральная-эллипс.

Выполним преобразование параллельного переноса начала координат в центр кривой, координаты которого найдем из системы

Центр кривой – точка

Уравнение примет вид

данное уравнение не содержит членов с первыми степенями группа старших членов остается неизменной.

Выполним преобразование поворота осей координат, на угол которой найдем по формуле

Формулы поворота осей координат примут вид

Подставим их в уравнение кривой, получим

каноническое уравнение эллипса, где

Найдем точки пересечения кривой с осью для чего решим систему

Точки пересечения

Выполним построение

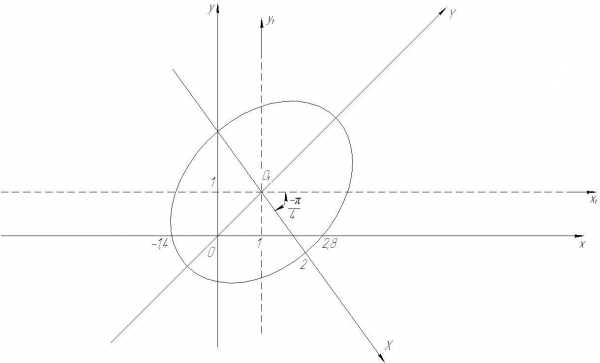
Рис. 20

Контрольные вопросы

1. Записать каноническое уравнение окружности и ее основные характеристики.

2. Записать каноническое уравнение эллипса и перечислить его характеристики.

3. Записать каноническое уравнение гиперболы и назвать ее характеристики.

4. Записать каноническое уравнение параболы.

5. Знать схему исследования кривых второго порядка.

Лекция №9. Плоскость

9.1. Плоскость и ее уравнения.

9.2. Общее уравнение плоскости и его частные виды.

9.3. Угол между плоскостями. Условие параллельности и перпендикулярности двух плоскостей.

9.4. Нормальное уравнение плоскости. Уравнение плоскости в отрезках.

studfiles.net

III Международный конкурс научно-исследовательских и творческих работ учащихся Старт в науке

ПОСТРОЕНИЕ НЕКОТОРЫХ КРИВЫХ ВТОРОГО ПОРЯДКА В ПОЛЯРНОЙ СИСТЕМЕ КООРДИНАТ, ЗАВИСИМОСТЬ КРИВЫХ ОТ КОЭФФИЦИЕНТОВ

Веретенникова А.Л. 1

---

1

Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке «Файлы работы» в формате PDF

Введение

Конечно же, каждый из нас слышал о таких понятиях как график функции, система координат, гипербола и т.п. Всё это является составляющими темы «Функции», с которой знакомимся мы в школе ещё в среднем звене.

Функция — в математике соответствие между элементами двух множеств, установленное по такому правилу, что каждому элементу одного множества ставится в соответствие некоторый элемент из другого множества. Этот закон определяется уравнением , и на основе него строится график в плоской системе координат, задаваемой двумя осями X и Y. Двигаясь от 6 до 10 класса, мы усложняли уравнения и графики, вводили новые понятия, но никогда не выходили за рамки основного определения функции и принципа построения графиков. То есть нами не рассматривалась возможность построения, например, такой кривой как трехлепестковая полярная роза. Единственным, наверное, примером кривой (не функции) была окружность, которая встречалась нам как тригонометрии, так и при решении задания №18 с параметром в ЕГЭ. В 10-м классе на уроке информатики в рамках работы в табличном процессоре я столкнулся с построением графиков функций, и чтобы расширить область преподаваемого нам материала, заглянул за рамки заданных ограничений. В этом и заключается одна из целей, поставленных в данной работе — расширить знания по теме графики, попрактиковаться в области их построения. Таким образом, объектом моего исследования стали кривые II порядка — графики, в уравнениях которых нет такой строгой зависимости Y от X, как в функциях. Другим предметом моего исследования являются системы координат прямоугольная и полярная, а именно связь между декартовыми и полярными координатами.

Вот главная цель работы: построить графики кривых II порядка в полярной системе координат, а также выяснить, как различаются их графики в зависимости от варьирования коэффициентов и параметров функций. Для достижения целей работы было поставлено несколько задач:

• пополнить знания о стандартных (невырожденных) кривых II порядка: эллипс, параболу, гиперболу;

• рассмотреть нестандартные кривые II порядка;

• познакомиться с полярной системой координат и сопоставить с декартовой, уже изучавшейся в школе.

Процесс решения каждой из задач был разбит на 2 этапа:

• изучение и разбор теоретического материала, знакомство с новыми понятиями;

• применение полученных знаний на практике, построение графиков.

1.Исследование кривых второго порядка 1.1. Стандартные кривые II порядка

Историческая справка: впервые кривые второго порядка изучались одним из учеников Платона. Его работа заключалась в следующем: если взять две пересекающиеся прямые и вращать их вокруг биссектрисы угла, ими образованного, то получится конусная поверхность. Если же пересечь эту поверхность плоскостью, то в сечении получаются различные геометрические фигуры, а именно эллипс, окружность, парабола, гипербола и несколько вырожденных фигур. Однако эти научные знания нашли применение лишь в XVII, когда стало известно, что планеты движутся по эллиптическим траекториям, а пушечный снаряд летит по параболической. Ещё позже стало известно, что если придать телу первую космическую скорость, то оно будет двигаться по окружности вокруг Земли, при увеличении этой скорости — по эллипсу, а при достижении второй космической скорости тело по параболе покинет поле притяжения Земли.

Алгебраической кривой второго порядка называется кривая , уравнение которой в декартовой системе координат имеет вид , где не все коэффициенты А, В и С равны одновременно нулю (иначе — прямая, т.е. алгебраическая кривая первого порядка). Кривые второго порядка делятся на вырожденные и невырожденные. Вырожденные кривые второго порядка это прямые и точки, которые задаются уравнением второй степени. Если уравнению второго порядка не удовлетворяет ни одна точка плоскости, то тоже говорят, что уравнение определяет вырожденную кривую (мнимую кривую второго порядка). Если же кривая невырожденная, то для неё найдётся такая декартова прямоугольная система координат, в которой уравнение этой кривой имеет один из следующих трёх видов:

Эллипс, гипербола, парабола

Эллипсом называется геометрическое место точек, для которых сумма расстояний до двух фиксированных точек плоскости, называемых фокусами, есть постоянная величина, большая, чем расстояние между фокусами. Постоянную сумму расстояний произвольной точки эллипса до фокусов принято обозначать через . Фокусы эллипса обозначают буквами и , расстояние между ними — через . По определению эллипса .

Гиперболой называется геометрическое место точек на плоскости, для каждой из которых абсолютное значение разности расстояний до двух данных точек, называемых фокусам, одинаково и равно

Параболой называется множество точек на плоскости, расстояния от которых до данной точки, называемой фокусом, и до данной прямой, называемой директрисой, равны. С гиперболой мы часто сталкиваемся в повседневной жизни. По параболистической траектории летит брошенный вверх камень, отскакивает мяч от пола, движутся планеты вокруг Солнца.

1.2. Системы координат

Система координат — комплекс определений, реализующий метод координат, то есть способ определять положение точки или тела с помощью чисел или других символов. Совокупность чисел, определяющих положение конкретной точки, называется координатами этой точки. Знания обычного человека в большинстве случаев ограничиваются одной-двумя системами координат. На самом же деле их существует великое множество: прямоугольная, полярная, аффинная, сферическая, цилиндрическая и т.д. На одном из уроков алгебры мы затрагивали кое-какие из них, а в этом исследовании я решил сопоставить две: прямоугольную (ёще называющуюся декартовой) и полярную (как хорошо знакомую и в корне отличающуюся).

1.2.1. Декартова система координат

Прямоугольная, или Декартова, система координат — прямолинейная система координат на плоскости или в пространстве, обычно с взаимно перпендикулярными осями и одинаковыми масштабами по осям. Названа по имени Р Декарта. Это наиболее простая и поэтому часто используемая система координат как на плоскости, так и в пространстве.

Историческая справка: Декарт впервые ввел координатную систему в своей работе «Рассуждение о методе» в 1637 году. Она существенно отличалась от общепринятой в наши дни. Он использовал косоугольную систему координат на плоскости, рассматривая кривую относительно некоторой прямой с фиксированной системой отсчета. Положение точек кривой задавалось с помощью системы параллельных отрезков, наклонных или перпендикулярных к исходной прямой. Декарт не вводил второй координатной оси, не фиксировал направления отсчета от начала координат. Только в 18 в. сформировалось современное понимание координатной системы, получившее имя Декарта.

Данная система координат на плоскости образуется двумя взаимно перпендикулярными осями координат OX и OY. Эти оси пересекаются в точке O, которая называется началом координат, на каждой оси выбрано положительное направление, указанное стрелками, и единица измерения отрезков на осях. Единицы измерения одинаковы для обеих осей. Положительное направление осей (в правосторонней системе координат) выбирают так, чтобы при повороте оси OX против часовой стрелки на 90° её положительное направление совпало с положительным направлением оси OY. Четыре угла — четверти (I, II, III, IV) — образованные осями координат OX и OY, называются координатными углами.

1.2.2. Полярная система координат

Полярная система координат — двумерная система координат, в которой каждая точка на плоскости определяется двумя числами — полярным углом и полярным радиусом. Полярная система координат особенно полезна в случаях, когда отношения между точками проще изобразить в виде радиусов и углов; в более распространённой, декартовой или прямоугольной системе координат, такие отношения можно установить только путём применения тригонометрических уравнений.

Полярная система координат задаётся лучом, который называют нулевым или полярной осью. Точка, из которой выходит этот луч, называется началом координат или полюсом. Любая точка на плоскости определяется двумя полярными координатами: радиальной и угловой. Радиальная координата (обычно обозначается r) соответствует расстоянию от точки до начала координат. Угловая координата, также называется полярным углом или азимутом и обозначается , равна углу, на который нужно повернуть против часовой стрелки полярную ось для того, чтобы попасть в эту точку.

Определённая таким образом радиальная координата может принимать значения от нуля до бесконечности, а угловая координата изменяется в пределах от 0° до 360°. Однако, для удобства область значений полярной координаты можно расширить за пределы полного угла, а также разрешить ей принимать отрицательные значения, что отвечает повороту полярной оси по часовой стрелке.

1.2.3. Связь между декартовыми и полярными координатами

Пару полярных координат и можно перевести в Декартовы координаты x и y путём применения тригонометрических функций синуса и косинуса:

в то время как две декартовы координаты x и y могут быть переведены в полярную координату :

(по теореме Пифагора).

1.3. Нестандартные кривые второго порядка

Просмотрев этот раздел, неосведомлённый человек может подумать, что часть нестандартных кривых второго порядка можно спокойно отнести к стандартным, другая же часть не имеет с ними ничего общего. Некоторые из них действительно представляют собой красивые витиеватые узоры, но некоторые выглядят как-то слишком просто, без изысков. Конечно, такое мнение имеет место существовать. Но ведь дело в степени и области применения кривых: одни встречаются постоянно, другие — только в узких специализированных целях — и в сложности уравнения. Хотелось бы в этом разделе рассмотреть наиболее интересные кривые: спираль Архимеда, улитка Паскаля, Розы Гранди. В разделе «Кривые II порядка в полярной системе координат» я перевел графики в другую полярную систему координат и построил их с помощью табличного процессора.

Кривые второго порядка в полярной системе координат

Эта часть является самой главной в моей работе, так как в ней описывается построение графиков в полярной системе координат в табличном процессоре MSExcel 2007. Выполняя построения мы старались акцентировать внимание на красоте математики, на том насколько все гениальное просто, ведь математика это предметная область, в которой все для жизни.

Полярная роза (Розы Гранди)

Полярная роза — известная математическая кривая, похожая на цветок с лепестками. Она может быть определена простым уравнением в полярных координатах: ,

для произвольной постоянной (включая 0). Если — целое число, то это уравнение будет определять розу с лепестками для нечётных, либо с лепестками для чётных . Если — рациональное, но не целое, график, заданный уравнением, образует фигуру, подобную розе, но лепестки будут перекрываться. Розы с 2, 6, 10, 14 и т. д. лепестками этим уравнением определить невозможно. Переменная определяет длину лепестков.

Если считать, что радиус не может быть отрицательным, то при любом натуральном мы будем иметь — лепестковую розу. Таким образом, уравнение будет определять розу с двумя лепестками. С геометрической точки зрения радиус — это расстояние от полюса до точки и он не может быть отрицательным.

— трехлепестковая роза	— клевер
— космея		Два графика в одной системе

Улитка Паскаля

Улитка Паскаля ― плоская алгебраическая кривая 4-го порядка. Названа по имени Этьена Паскаля (отца Блеза Паскаля), впервые рассмотревшего её.

Уравнение в полярных координатах:

Здесь — диаметр исходной окружности, а — расстояние, на которое смещается точка вдоль радиус-вектора.

В зависимости от диапазона получаются следующие графики

Спираль Архимеда

Архимедова спираль названа в честь её изобретателя, древнегреческого математика Архимеда. Эту спираль можно определить с помощью простого полярного уравнения:

Изменения параметра приводят к повороту спирали, а параметра — расстояния между витками, которое является константой для конкретной спирали. Спираль Архимеда имеет две ветви, одну для >0, а другую для

Просмотров работы: 505

school-science.ru