Точка максимума функции как найти: Как найти экстремум (точки минимума и максимума) функции

Содержание

Значения функции и точки максимума и минимума

Назад к списку

Значения функции и точки максимума и минимума

Наибольшее значение функции

Наменьшее значение функции

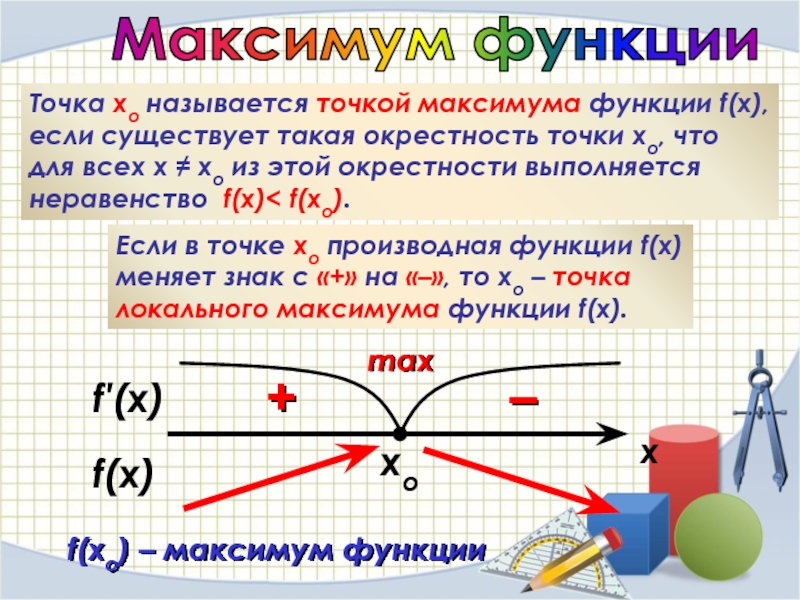
Точки max

Точки min

Как говорил крестный отец: «Ничего личного». Только производные!

Статью Как посчитать производные? надеюсь, ты изучил, без этого дальше будет проблематично.

12 задание по статистике считается достаточно трудным, а все потому, что ребята не прочитали эту статью (joke). В большинстве случаев виной всему невнимательность.

12 задание бывает двух видов:

Найти точку максимума / минимума (просят найти значения «x»).
Найти наибольшее / наименьшее значение функции (просят найти значения «y»).

Как же действовать в этих случаях?

Найти точку максимума / минимума

Взять производную от предложенной функции.
Приравнять ее к нулю.
Найденный или найденные «х» и будут являться точками минимума или максимума.
Определить с помощью метода интервалов знаки и выбрать, какая точка нужна в задании.

Задания с ЕГЭ:

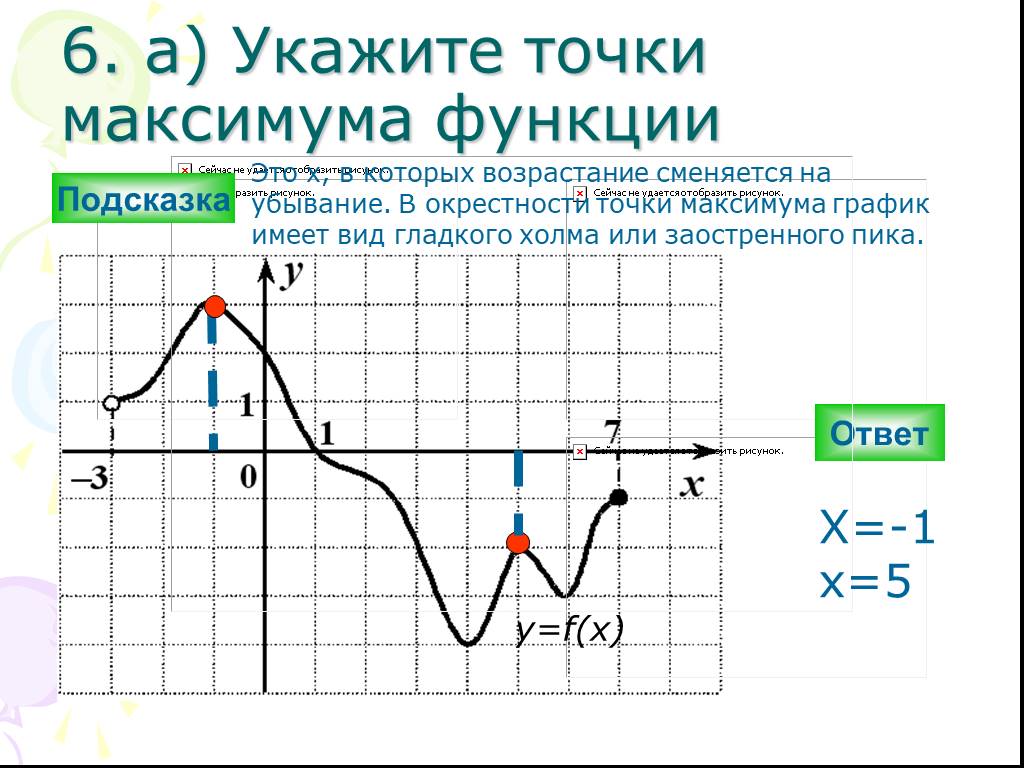
Найдите точку максимума функции

Берем производную:

Приравняем ее к нулю:
Получили одно значение икса, для нахождения знаков подставим −20 слева от корня и 0 справа от корня в преобразованную производную (последняя строчка с преобразованием):

Все верно, сначала функция возрастает, затем убывает — это точка максимума!
Ответ: −15

Найдите точку минимума функции

Преобразуем и возьмем производную:

Получается один корень «−2», однако не стоит забывать о «−3», она тоже будет влиять на изменение знака.

Отлично! Сначала функция убывает, затем возрасает — это точка минимума!

Ответ: −2

Найти наибольшее / наименьшее значение функции

Взять производную от предложенной функции.
Приравнять ее к нулю.
Найденный «х» и будет являться точкой минимума или максимума.
Определить с помощью метода интервала знаки и выбрать, какая точка нужна в задании.
В таких заданиях всегда задается промежуток: иксы, найденные в пункте 3, должны входить в данный промежуток.
Подставить в первоначальное уравнение полученную точку максимума или минимума, получаем наибольшее или наименьшее значение функции.

Задания с ЕГЭ:

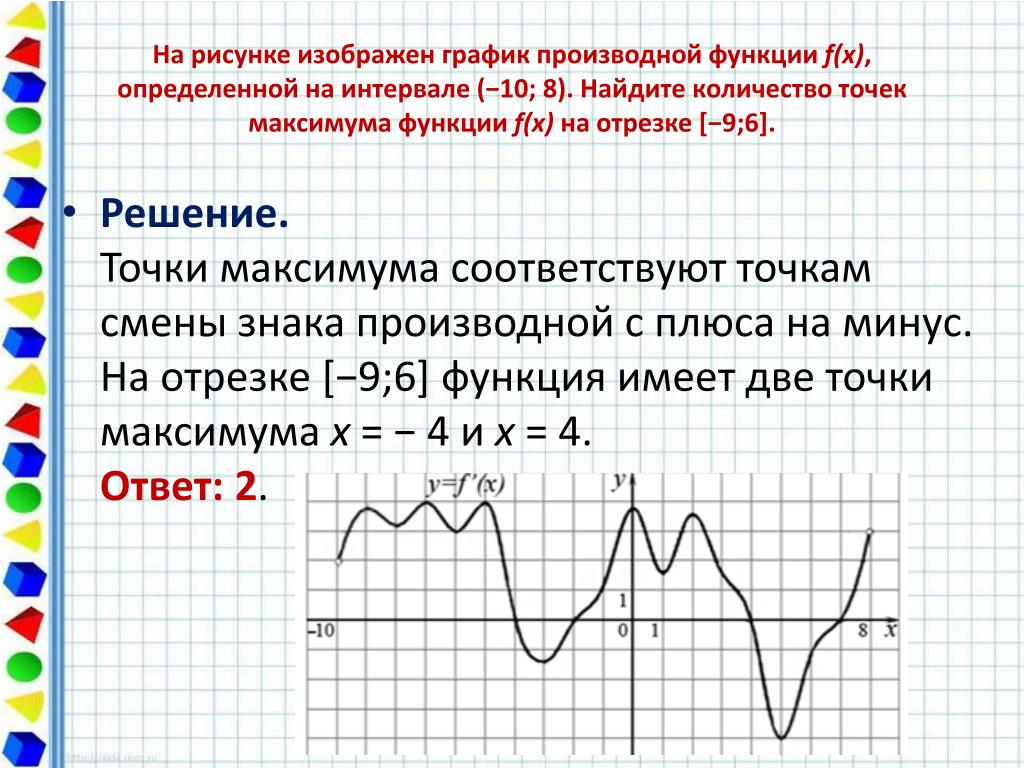
Найдите наибольшее значение функции на отрезке [−4; −1]

Преобразуем и возьмем производную:
«3» не вдходит в промежуток [−4; −1]. Значит, остается проверить «−3» — это точка максимума?

Подходит, сначала функция возрастает, затем убывает — это точка максимума, и в ней будет наибольшее значение функции. Остается только подставить в первоначальную функцию:

Ответ: −6

Найдите наибольшее значение функции на отрезке [0; 1,5π]

Берем производную:
Находим, чему равняется sin(x):
Но такое невозможно! Sin(x). ..
Получается, что уравнение не имеет решения, и в таких ситуациях нужно подставлять крайние значения промежутка в первоначальное уравнение:

Наибольшее значение функции равно «11» при точке максимума (на этом отрезке) «0».

Ответ: 11

Выводы:

70% ошибок заключается в том, что ребята не запоминают, что в ответ на наибольшее/наименьшее значение функции нужно написать «y», а на точку максимума/минимума написать «х».
Нет решения у производной при нахождении значений функции? Не беда, подставляй крайние точки промежутка!
Ответ всегда может быть записан в виде числа или десятичной дроби. Нет? Тогда перерешивай пример.
В большинстве заданий будет получаться одна точка и наша лень проверять максимум или минимум будет оправдана. Получили одну точку — можно смело писать в ответ.
А вот с поиском значения функции так поступать не стоит! Проверяйте, что это нужная точка, иначе крайние значения промежутка могут оказаться больше или меньше.

Будь в курсе новых статеек, видео и легкого математического юмора.

Как найти точки минимума и максимума функции, анализируя функцию, её производную и область определения

Поиск точки максимума и минимума функции — довольно распространенная задача в математическом анализе. Иногда требуется экстремум. Многие думают, что под словом «экстремум» подразумевают наибольшее или наименьшее значение функции. Это не совсем верно. Значение может быть наибольшим или минимальным, но не являться экстремумом.

Содержание:

Глобальный и локальный максимум
Исследование
- Область допустимых аргументов
- Асимптоты
- Производная и экстремумы
- Концы интервала и сравнение результатов
Видео

Глобальный и локальный максимум

Максимум бывает локальным или глобальным. Точка локального максимума — это аргумент, который при подстановке в f(x) даёт значение не меньше, чем в других точках из области около этого аргумента. Для глобального максимума эта область расширяется до всей области допустимых аргументов. Для минимума всё наоборот. Экстремум — это локальное экстремальное — минимальное или максимальное — значение.

Как правило, если математиков интересует глобально самое большое значение f(x), то в интервале, не на всей оси аргументов. Подобные задачи обычно сформулированы фразой «найдите точку максимума функции на отрезке». Здесь подразумевается, что надо выявить аргумент, при котором она не меньше, чем на всём остальном указанном отрезке. Поиск локального экстремума является одним из шагов решения такой задачи.

Дано y = f(x). Требуется определить пик функции на указанном отрезке. f(x) может достигать его в точке:

экстремума, если она попадает в указанный отрезок,
разрыва,
ограничивающей заданный отрезок.

Исследование

Пик f(x) на отрезке или в интервале находится путём исследования данной функции. План исследования для нахождения максимума на отрезке (или интервале):

Найти область допустимых аргументов и пересечения этой области с областью исследования.

2 определена на всей оси аргументов. А y = 1/x определена для всех аргументов, кроме x = 0.

Найти пересечение области допустимых аргументов и исследуемого отрезка (интервала) требуется для того, чтобы исключить из рассмотрения ту часть интервала, где функция не определена. Например, требуется найти минимум y = 1/x на отрезке от -2 до 2. На самом деле требуется исследовать два полуинтервала от -2 до 0 и от 0 до 2, так как уравнение у = 1/0 не имеет решения.

Асимптоты

Асимптота — это такая прямая, к которой функция тянется, но не дотягивается. Если f(x) существует на всей числовой прямой и неразрывна на ней, то вертикальной асимптоты у неё нет. Если же она разрывна, то точка разрыва является вертикальной асимптотой. Для y = 1/x асимптота задаётся уравнением x = 0. Эта функция тянется к нулю по оси аргументов, но дотянется до него, только устремившись в бесконечность.

Если на исследуемом отрезке имеется вертикальная асимптота, около которой функция стремится в бесконечность с плюсом, то пик f(x) на здесь не определяется. 3. У неё не может быть экстремумов, она убывает на всей оси аргументов.

2) Достаточно, чтобы при пересечении точки экстремума у производной менялся знак. То есть, до максимума f(x) растёт, а после максимума она убывает — производная была положительной, а стала отрицательной.

После того как аргументы для локального максимума были найдены их надо подставить в исходное уравнение и получить максимальное значение f(x).

Концы интервала и сравнение результатов

При поиске максимума на отрезке необходимо проверить значение на концах отрезка. Например, для y = 1/x на отрезке [1; 7] максимум будет в точке x = 1. Даже если внутри отрезка есть локальный максимум, нет никакой гарантии, что значение на одном из концов отрезка не будет больше этого максимума.

Теперь необходимо сравнить значения в точках разрыва (если f(x) здесь не стремится в бесконечность), на концах исследуемого интервала и экстремум функции. Наибольшее из этих значений и будет максимумом функции на заданном участке прямой.

Для задачи с формулировкой «Найдите точку минимума функции» необходимо выбрать наименьшее из локальных минимумов и значений на концах интервала и в точках разрыва.

Видео

Максимальные и минимальные значения — Подход к исчислению

Подход

C A L C U L U S

Содержание | Дом

МЫ ГОВОРИМ, ЧТО ФУНКЦИЯ f ( x ) имеет относительное максимальное значение при x = a ,
, если f ( a ) равно 90 017 больше , чем любое значение, непосредственно предшествующее или следующее за ним.

Мы называем это «относительным» максимумом, потому что другие значения функции на самом деле могут быть больше.

Мы говорим, что функция f ( x ) имеет относительное минимальное значение при x = b ,
, если f ( b ) на меньше 90 018, чем любое значение, непосредственно предшествующее или следующее за ним.

Опять же, другие значения функции на самом деле могут быть меньше. При таком понимании мы отбросим термин «относительный».
Значение функции, значение y , максимальное или минимальное, называется экстремальным значением.
Теперь, что характеризует график при экстремальном значении?
Касательная к кривой горизонтальна . Мы видим это в точках A и B . Наклон каждой касательной линии — производная при оценке a или b — это 0,
f ‘ ( x ) = 0,
Более того, в точках непосредственно от слева от максимума — в точке C — наклон касательной положителен: f ‘ ( x ) > 0. справа — в точке D — наклон отрицательный: f ‘ (
x )
Другими словами, максимум f ‘ ( x ) меняет знак с + на — .
Как минимум, f ‘ ( x ) меняет знак с − на + . Мы видим, что в точках E и F  .
Также можно заметить, что в максимуме при A график вогнут вниз. (Тема 14 Precalculus.) Хотя, как минимум, на B он вогнут вверх.
Значение x , при котором функция имеет либо максимум, либо минимум, называется критическим значением. На рисунке —
— критические значения x = a и x = b .
Критические значения определяют точки поворота, в которых касательная параллельна оси x . Критические значения — если они есть — будут решений от до f ‘ ( x ) = 0,
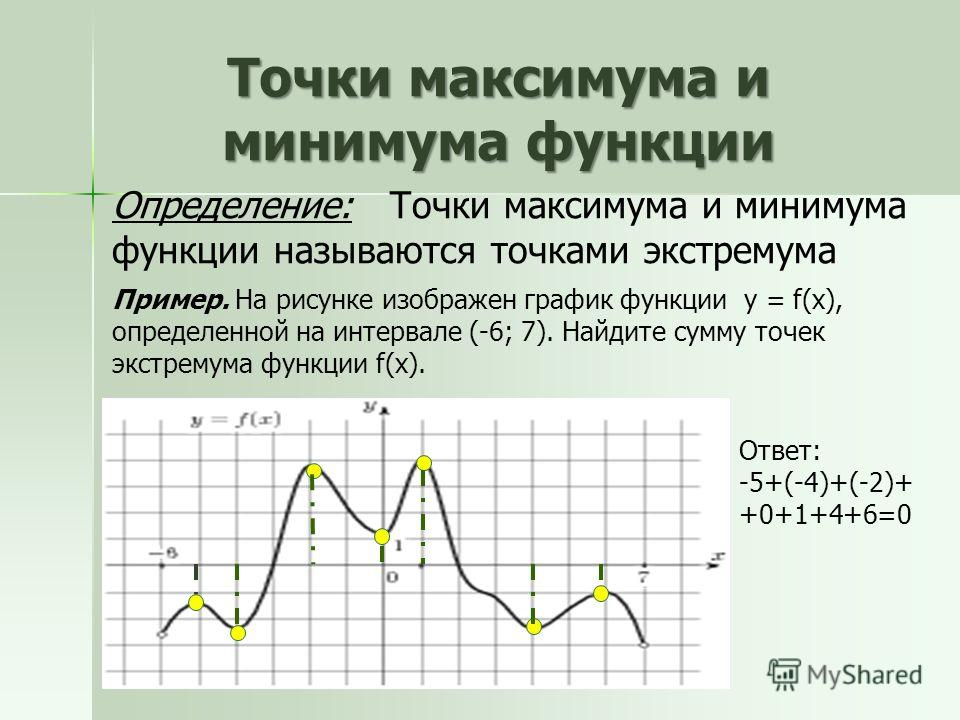
Пример 1.   Пусть f ( x ) =
x ² − 6 х + 5.
Есть ли критические значения — поворотные точки? Если да, то определяют ли они максимум или минимум? И каковы координаты на графике этого максимума или минимума?
Решение . f ‘ ( x ) = 2 x − 6 = 0 означает x = 3. (Урок 9 алгебры.)
x = 3 — единственное критическое значение. Это х -координата точки поворота. Чтобы определить координату y , оцените f при этом критическом значении — оцените f (3):

ф ( х ) = x ² − 6 x + 5

f (3) = 3 ² − 6 · 3 + 5

= −4.
Крайнее значение равно −4. Чтобы увидеть, является ли это максимумом или минимумом, в этом случае мы можем просто посмотреть на график.
f ( x ) — это парабола, и мы видим, что точка поворота является минимумом.
Найдя значение x , где производная равна 0, то мы обнаружили, что вершина параболы находится в точке (3, −4).
Но не всегда мы сможем посмотреть на график. Алгебраическое условие минимума состоит в том, что f ‘ ( x ) меняет знак с − на + . Это мы видим в точках E , B , F  выше. Значение наклона увеличивается.
Теперь сказать, что наклон увеличивается, значит сказать, что при критическом значении вторая производная (Урок 9) — скорость изменения наклона —
плюс .
Опять же, вот f ( x ):
ф ( х ) = x ² − 6 x + 5.

f ‘ ( x ) = 2 х − 6,

f » ( x ) = 2.
f » оценивается при критическом значении 3 — f» (3) = 2 — положительный. Это говорит нам алгебраически, что критическое значение 3 определяет минимум.
Достаточные условия
Теперь мы можем сформулировать эти достаточные условия для экстремальных значений функции при критическом значении и :
Функция имеет минимальное значение при

x = a if f ‘ ( a ) = 0
и f » ( a ) = a положительное число.
Функция имеет максимальное значение при x = a if f ‘ ( a ) = 0
и f » ( a ) = a отрицательное число.
В случае максимума наклон касательной равен уменьшается — идет от положительного к отрицательному. Мы видим, что в точках C , A , D .
Пример 2. Пусть f ( х ) = 2 х ³ — 9 х ² + 12 х — 3.
Есть ли экстремальные значения? Во-первых, существуют ли какие-либо критические значения — решения для f ‘ ( x ) = 0 — и определяют ли они максимум или минимум? И каковы координаты на графике этого максимума или минимума? Где поворотные моменты?
   Решение .
f’ ( х ) = 6 х ² — 18 х + 12 = 6( х ² − 3 х + 2)

= 6( х — 1)( х — 2)

= 0
подразумевает:
x = 1 или x = 2.
(Урок 37 Алгебры.)
Это критические значения. Каждый из них определяет максимум или он определяет минимум? Чтобы ответить, мы должны оценить вторую производную при каждом значении.
ф’ ( х ) = 6 x ² − 18 x + 12.

f » ( x ) = 12 x − 18.

ж» (1) = 12 — 18 = -6.
Вторая производная отрицательна. Таким образом, функция имеет максимум при разрешении x = 1,
.
Чтобы найти y -координату — экстремальное значение — в этом максимуме мы оцениваем f (1):
ф ( х ) = 2 x ³ − 9 x ² + 12 x − 3

f (1) = 2 − 9 + 12 − 3

= 2.
Максимум приходится на точку (1, 2).
Далее, определяет ли x = 2 максимум или минимум?
ф» ( х ) = 12 x − 18.

ф» (2) = 24 — 18 = 6.
Вторая производная положительна. Таким образом, функция имеет минимум при x = 2,
.
Чтобы найти y -координату — экстремальное значение — при этом минимуме, мы оцениваем ф (2):
ф ( х ) = 2 x ³ − 9 x ² + 12 x − 3.

f (2) = 16 − 36 + 24 − 3

= 1.
Минимум приходится на точку (2, 1).
Вот собственно график f ( x ):
Решения f » ( x ) = 0 указывают точку перегиба в этих решениях, а не максимум или минимум. Пример: y = x ³ . г» = 6 x = 0 подразумевает x = 0. Но x = 0 является точкой перегиба на графике y = x ³ , а не максимумом или минимумом.
Другой пример: y = sin x . Решения y » = 0 — это произведения π, которые являются точками перегиба.
Задача 1.   Найти координаты вершины параболы
г = х ² — 8 х + 1.
Чтобы увидеть ответ, наведите указатель мыши на цветную область.
Чтобы снова закрыть ответ, нажмите «Обновить» («Reload»).
Сначала решай задачу сам!
у’ = 2 х — 8 = 0,
Отсюда следует, что x = 4. Это x -координата вершины. Чтобы найти координату y , оцените г в х = 4:
y = 4 ² − 8 · 4 + 1 = −15.
Вершина находится в точке (4, −15).
Задача 2.   Исследуйте каждую функцию на наличие максимумов и минимумов.
а) y = x ³ − 3 x ² + 2,
у’ = 3 х ² — 6 x = 3 x ( x — 2) = 0 подразумевает
x = 0 или x = 2.
у» ( х ) = 6 х — 6,
г» (0) = -6.
Вторая производная отрицательна. Это означает, что максимальное значение составляет x = 0. Это максимальное значение равно
.
г (0) = 2.
Далее,
г» (2) = 12 — 6 = 6.
Вторая производная положительна. Это означает, что минимальное значение составляет x = 2. Это минимальное значение равно
.
y (2) = 2 ³ − 3 · 2 ² + 2 = 8 − 12 + 2 = −2.
б) y = −2 x ³ − 3 х ² + 12 х + 10.
При x = 1 максимум y = 17.
При x = -2 есть минимум y = -10.
c) y = 2 x ³ + 3 x ² + 12 x − 4,
Так как f ‘ ( х ) = 0 не имеет действительных решений, экстремальных значений нет.
d) y = 3 x ⁴ − 4 x ³ − 12 x ² + 2, 9 0003
При x = 0 максимум y = 2.
При x = -1 есть минимум y = -3.
При x = 2 минимум г = -30.
Следующий урок: Применение максимальных и минимальных значений
Содержание | Дом
Пожалуйста, сделайте пожертвование, чтобы TheMathPage оставался онлайн.
Даже 1 доллар поможет.
Copyright © 2021 Лоуренс Спектор
Вопросы или комментарии?
Электронная почта: teacher@themathpage. com

исчисление — Чтобы найти максимальное значение функции
Поскольку мы имеем дело с абсолютным значением функции, мы можем интерпретировать абсолютное значение как расстояние от функции до оси $x$ независимо от направления. Другими словами, мы просто хотим найти точку, наиболее удаленную от оси $x$, независимо от того, находится ли она выше или ниже оси, поскольку расстояние (абсолютное значение) — это все, что нам нужно максимизировать. Имея это в виду, становится ясно, что максимум $\lvert f(x) \rvert$ должен быть либо максимумом, либо минимумом $f(x)$. 92 + 16 х + 6 $$ К сожалению, это последнее выражение больше нельзя разложить на множители, и, поскольку не существует формулы пятой степени для нахождения корней, лучшее, что мы можем сделать, — это найти корни с помощью численных методов. Сделав это, вы обнаружите, что действительные корни даются \начать{выравнивать} x_1 &\приблизительно -0,24569\\ x_2 & \приблизительно 0,687122\\ x_3 & \приблизительно 3,44225 \end{выравнивание} Однако, если мы на самом деле подставим $x_2$ в уравнение $(1)$, мы увидим, что мы не получаем $0$ (на самом деле это приблизительно равно $-3,18$).
No related posts.