Четырехугольники. Решение задач — презентация онлайн
1. ГЕОМЕТРИЯ 8 КЛАСС
«Четырехугольники»2. Математику нельзя изучать, наблюдая, как это делает сосед! А. Нивен
3. Цели урока:
Закрепить, обобщитьтеоретический материал по
теме «Четырехугольники»
Совершенствовать навыки
решения задач по теме
4. Правила работы в группе
№Выбрать капитана.
Капитаны по ходу урока заполняют оценочные листы
для своей группы.
В конце урока капитаны подсчитывают баллы,
набранные каждым участником и всей командой в
целом.
Ф.И.
задания
Защита
Домаш
него
задани
я
Таб
лиц
а
Тест
1
2
5
7
итог
Решени
е задач
(обосно
ванност
ь)
Провер
очная
работа
(тест)
Баллы за
ответы и
дополнен
ия
3
4
5
6
3
5
5
Примеч
ание
баллы
оц
ен
ка
25-30
18-22
13-17
5
4
3
1
2
3
4
Максимальный балл
Общее количество
5.
 СодержаниеЦели урока
СодержаниеЦели урокаПравила работы в
группе
Разминка
Кроссворд
Ответы к кроссворду
Защита презентаций
(творческое домашнее
задание)
Параллелограмм
Трапеция
Прямоугольник
Ромб
Квадрат
Схема
Теоретическая самостоятельная
работа (таблица)
Теоретический тест
Задачи на готовых чертежах
Минутка отдыха (+гимнастика
для глаз)
№1; №2;
№3
Решение задач
Проверочная работа (тест)
Основные результаты работы
Контрольные вопросы
Домашнее задание
6. Разминка!
7. Определить номера клеток , в которых находятся четырехугольники ?
Определить номера клеток , вкоторых находятся четырехугольники
1
2
3
4
5
6
7
8
9
?
8. Четырехугольники
12
3
4
5
6
7
8
9
9. КРОССВОРД
По горизонтали:5
6
7
1
2
1. Четырехугольник, у
которого противоположные
стороны параллельны
2.
 Четырехугольник, у
Четырехугольник, укоторого только две
стороны параллельны
3. Параллелограмм, у которого
все углы прямые
4. Точки из которых выходят
стороны четырехугольника
По вертикали:
8
3
4
1. Сумма длин всех сторон
5. Отрезок, соединяющий
противолежащие вершины
6. Прямоугольник, у которого
все стороны равны
7. Параллелограмм , у
которого все стороны равны
8. Отрезок, соединяющий
соседние вершины
10. Ответы к кроссворду
По горизонтали:1. Четырехугольник, у
которого противоположные
стороны параллельны
2. Четырехугольник, у
которого только две
стороны параллельны
3. Параллелограмм, у которого
все углы прямые
4. Точки из которых выходят
стороны четырехугольника
По вертикали:
1. Сумма длин всех сторон
5. Отрезок, соединяющий
противолежащие вершины
6. Прямоугольник, у которого
все стороны равны
7. Параллелограмм , у
которого все стороны равны
8.
 Отрезок, соединяющий
Отрезок, соединяющийсоседние вершины
11. Четырехугольники:
параллелограммромб
трапеция
квадрат
прямоугольник
другие четырехугольники
Защита
презентаций
Трапеция
Параллелограмм
Прямоугольник
Ромб
Квадрат
14. Установите взаимосвязь по свойствам между данными четырехугольниками:
Другие?
?
15. Проверка теоретических знаний заполните таблицу
1.Противолежащие стороныпараллельны и равны.
2. Все стороны равны.
3. Противолежащие углы равны,
сумма соседних углов равна 180.
4. Все углы прямые.
5. Диагонали пересекаются и точкой
пересечения делятся пополам.
6. Диагонали равны.
7. Диагонали взаимно
перпендикулярны и являются
биссектрисами углов.
16. ПРАВИЛЬНЫЕ ОТВЕТЫ
1.Противолежащие стороныпараллельны и равны.
+
+
+
+
2. Все стороны равны.
—
—
+
+
3. Противолежащие углы равны,
сумма соседних углов равна 180.
+
+
+
+
4. Все углы прямые.
—
+
—
+
5. Диагонали пересекаются и точкой +
пересечения делятся пополам.
+
+
+
6. Диагонали равны.
—
+
—
+
7. Диагонали взаимно
перпендикулярны и являются
биссектрисами углов.
—
—
+
+
17. Проверочный тест
1 вариант2 вариант
1. Любой прямоугольник является:
а) ромбом;
б) квадратом;
в) параллелограммом;
г) нет правильного ответа.
1. Любой ромб является:
а) квадратом;
б) прямоугольником;
в) параллелограммом;
г) нет правильного ответа.
2. Если в четырехугольнике диагонали
перпендикулярны, то этот
четырехугольника) ромб;
б) квадрат;
в) прямоугольник;
г) нет правильного ответа.
2. Если в параллелограмме диагонали
перпендикулярны, то этот параллелограмм:
а) ромб;
б) квадрат;
в) прямоугольник;
г) нет правильного ответа.
Ромб – это четырехугольник, в котором…
а) диагонали точкой пересечения делятся
пополам и равны;
б) диагонали взаимно перпендикулярны и
точкой пересечения делятся пополам;
в) противолежащие углы равны, а
противолежащие стороны параллельны;
г) нет правильного ответа.
Прямоугольник – это четырехугольник, в
котором:
а) противолежащие стороны параллельны, а
диагонали равны;
б) диагонали точкой пересечения делятся
пополам и являются биссектрисами углов;
в) два угла прямые и две стороны равны;
г) нет правильного ответа.
18. ПРАВИЛЬНЫЕ ОТВЕТЫ
ПРАВИЛЬНЫЕ1 вариант
ОТВЕТЫ
2 вариант
1. Любой прямоугольник является:
а) ромбом;
б) квадратом;
в) параллелограммом;
г) нет правильного ответа.
1. Любой ромб является:
а) квадратом;
б) прямоугольником;
в) параллелограммом;
г) нет правильного ответа.
2. Если в четырехугольнике диагонали
перпендикулярны, то этот
четырехугольника) ромб;
б) квадрат;
в) прямоугольник;
г) нет правильного ответа.
2. Если в параллелограмме диагонали
перпендикулярны, то этот параллелограмм:
а) ромб;
б) квадрат;
в) прямоугольник;
г) нет правильного ответа.
Ромб – это четырехугольник, в котором…
а) диагонали точкой пересечения делятся
пополам и равны;
б) диагонали взаимно перпендикулярны и
точкой пересечения делятся пополам;
в) противолежащие углы равны, а
противолежащие стороны параллельны;
г) нет правильного ответа.

Прямоугольник – это четырехугольник, в
котором:
а) противолежащие стороны параллельны, а
диагонали равны;
б) диагонали точкой пересечения делятся
пополам и являются биссектрисами углов;
в) два угла прямые и две стороны равны;
г) нет правильного ответа.
19. Решение задач на готовых чертежах
АВСД- параллелограмм, АВ= 4 см.,КДВС- ромб. ДВ=ДС
АД= 7 см. Найти < В, <С, <Д , ВС, СД Найти < КСВ — ?
-?
7 см
В
Д
С
60° 60°
55°
125°
60°
К
60°
125°
55°
А
60° 60°
С
Д
7 см
АВСМ- р/б трапеция,ВС= 5
см.,АМ=7 см, ВК АМ . Найти: СМ-?
5 см В С
В
С
В
30°
А
АС=АР
1 см
45°
Д
5 см
К
<С= <Р
<СДВ= 90 -45 = 45 ,
СВ=ВД=АМ=1см
45°
Д
1 см
М
В
ВДМА- квадрат, ВС= МР= 1 см
Найти: АМ-?
45°
60°
<КСВ= 120
А
М
Р
20. Решение задач на готовых чертежах
АВСД- прямоугольник,<АОВ=60°,ВО = 8 см.
 Найти < АВО,<ОВС, СД- ?
Найти < АВО,<ОВС, СД- ?С
60°
60°
60°
60°
8
О
Р
Д
А
А
КДВМ- параллелограмм. < К= 30°,
СВ= 8 см., СА =3см. Найти МВ, КМ-?
8 см
М
В
А
М
СВ=КМ=8см
В
Р= 56 см
О
50°
А
К
30°
АМОТ– трапеция,< А= 40°, МО=ОТ,
АМ МТ. Найти < О — ?
3 см
С
14
7
30°
7
8
Д
О
В
АВСД- ромб. АД= 14 см., <ОДВ = 60
Найти Р-периметр ромба.
80°
50°
40°
МО // АТ
Т
<АМО=180º- 40º=140º
< ТМО=140º-90º=50º
22. Решение задач
В ромбе ABCDбиссектриса угла
ВAC пересекает
сторону ВС и
диагональ BD
соответственно в
точках М и N.
Найдите угол
АNВ, если
АМС = 120 .
B
М
?
120
N
A
О
D
C
23. Решение:
В ромбе противолежащие углы равны идиагонали являются биссектрисами его углов,
т.е. <ВАС = <ВАD : 2 =<ВСD : 2 = <ВСА.

В
Т.к. АМ – биссектриса <ВАС, а <ВАС = <ВСА,
то <МАС = <МСА : 2.
В треугольнике АМС
М
<МАС + <МСА = 180º — <АМС
?
<МАС + <МСА =180º -120º
N
120º
<МАС + <МСА = 60º.
<МАС = <МСА : 2, тогда
А
О
<МАС = 20º,
<ВАС = 40º.
В ромбе диагонали
взаимно перпендикулярны,
треугольник АОВ – прямоугольный,
<АВО = 90º — <ВАО = 50º.
Д
В треугольнике АВN <BAN = <МАС = 20º, <ABN = 50º, тогда
<ANB = 180º – (20º + 50º) = 110º.
Ответ: < ANB = 110º.
С
24. Проверочная работа (19 минут)
Ф.И.№
Решите тест, ответы запишите
в таблицу
вариант №
Ответ
1
2
3
4
5
6
7
8
9
10
Верно
25. Таблица верных ответов
№1 вариант
2 вариант
1
2
24 см
6 см
30 см
9 см
3
4
В
А
Г
Д
5
6
140º, 40º,140º
90º, 45º,45º
126º, 126º,54º
60º, 120º, 60º, 120º
7
∆АВС=∆ДСВ, ∆АСД=∆ДВА,
∆АВО=∆ДСО
∆АВС=∆СДА, ∆АВД=∆СДВ,
∆ВОС=∆ДОА, ∆АОВ=∆СОД
8
В, В
В, Б
9
21 см
9 см
10
6 см, 2 см
12 см,3 см, 10 см, 3 см
27.
 Самостоятельная работа. (разноуровневая ) (20 минут)Выбери уровень работы
Самостоятельная работа. (разноуровневая ) (20 минут)Выбери уровень работы(А,Б, В,).
28. итог урока ОСНОВНЫЕ РЕЗУЛЬТАТЫ
Мы повторилиТеоретический материал по теме
«Четырехугольники»
Совершенствовали
Навыки решения задач
Проверили
свои знания и умения по теме
29. Контрольные вопросы
В параллелограмме:-противоположные стороны …
-противоположные углы…
-сумма углов, прилежащих к одной
стороне….
-диагонали…
В прямоугольнике:
— диагонали
В ромбе:
— диагонали
В равнобедренной трапеции:
— углы, при основании…
— диагонали …
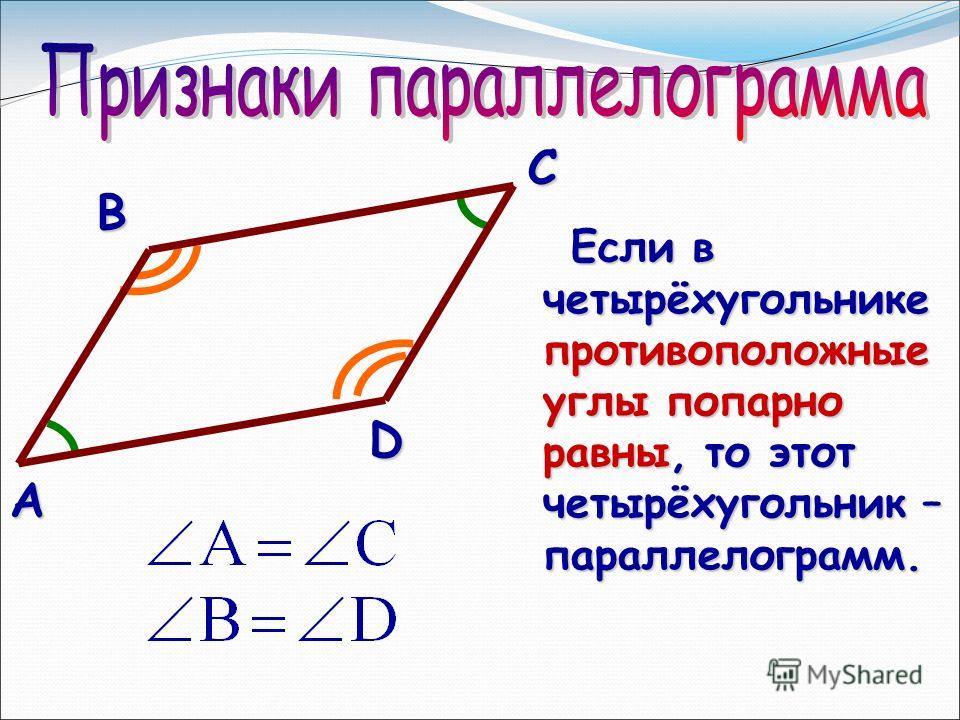
Признаки параллелограмма:
— если в четырехугольнике …, то этот
четырехугольник- параллелограмм.
30. Домашнее задание
Подготовка к контрольнойработе
-повторить теоретический материал,
-решить задачи (индивидуальные карточки)
Как начертить четырехугольник
Четырёхугольники
Четырёхугольник — это выпуклый многоугольник с четырьмя углами и четырьмя сторонами. Четырёхугольник образуется замкнутой ломаной линией, состоящей из четырёх звеньев, и той частью плоскости, которая находится внутри ломаной.
Четырёхугольник образуется замкнутой ломаной линией, состоящей из четырёх звеньев, и той частью плоскости, которая находится внутри ломаной.
Обозначение четырёхугольника составляют из букв, стоящих при его вершинах, называя их по порядку. Например, говорят или пишут: четырёхугольник ABCD :
В четырёхугольнике ABCD точки A, B, C и D — это вершины четырёхугольника, отрезки AB, BC, CD и DA — стороны.
Вершины, принадлежащие одной стороне, называются соседними, вершины, не являющиеся соседними, называются противолежащими:
В четырёхугольнике ABCD вершины A и B, B и C, C и D, D и A — соседние, а вершины A и C, B и D — противолежащие. Углы, лежащие при соседних вершинах, также называются соседними, а при противолежащих вершинах — противолежащими.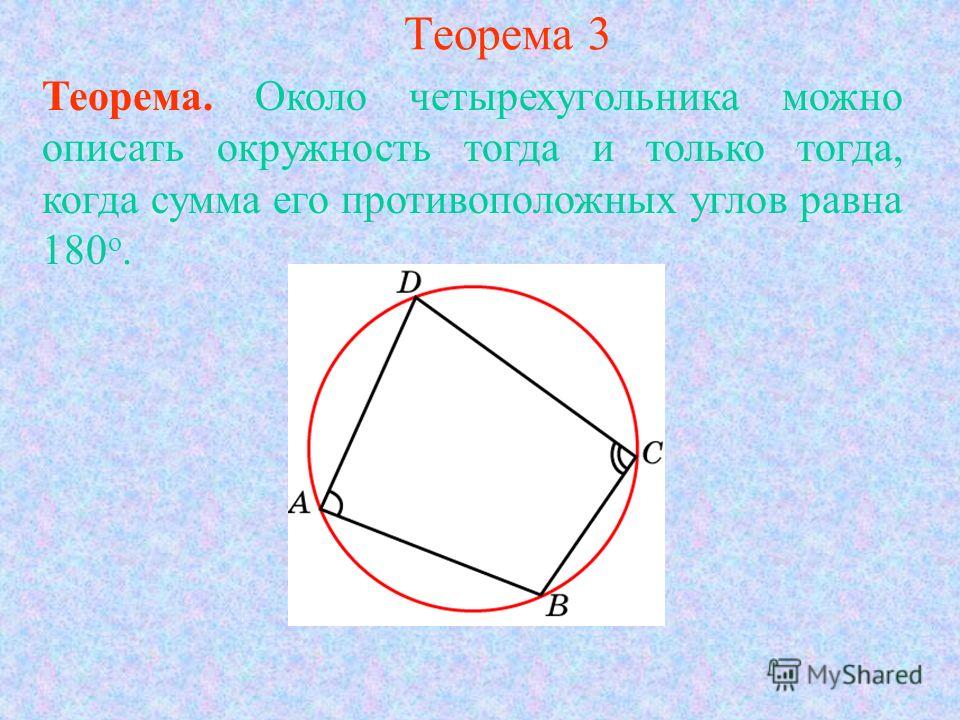
Стороны четырёхугольника также можно попарно разделить на соседние и противолежащие: стороны, имеющие общую вершину, называются соседними (или смежными), стороны, не имеющие общих вершин — противолежащими:
Стороны AB и BC, BC и CD, CD и DA, DA и AB — смежные, а стороны AB и DC, AD и BC — противолежащие.
Если противолежащие вершины соединить отрезком, то такой отрезок будет называться диагональю четырёхугольника. Учитывая, что в четырёхугольнике есть всего две пары противолежащих вершин, то и диагоналей может быть всего две:
Отрезки AC и BD — диагонали.
Виды четырёхугольников
Рассмотрим основные виды выпуклых четырёхугольников:
- Трапеция — четырёхугольник, у которого одна пара противоположных сторон, параллельны друг другу, а другая пара не параллельны.

- Равнобедренная трапеция — трапеция, у которой боковые стороны равны.
- Прямоугольная трапеция — трапеция, у которой один из углов прямой.
- Прямоугольник — параллелограмм, у которого все углы равны.
- Ромб — параллелограмм, у которого все стороны равны.
- Квадрат — параллелограмм, у которого равны и стороны и углы. И прямоугольник и ромб могут быть квадратом.
Свойства углов выпуклых четырёхугольников
У всех выпуклых четырёхугольников углы обладают следующими двумя свойствами:
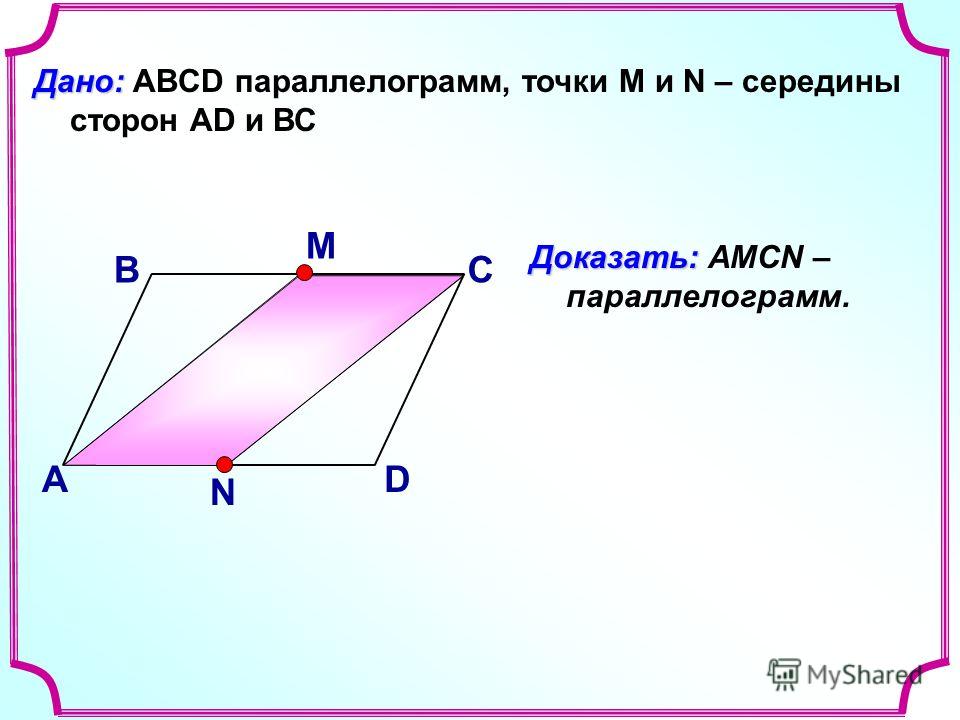
Четырехугольником ABCD называется фигура, которая состоит из четырех точек А, В, С, D по три, не лежащих на одной прямой, и четырех отрезков AB, BC, CD и AD, соединяющих эти точки.
На рисунках изображены четырехугольники.
Точки А, В, С и D называются вершинами четырехугольника, а отрезки AB, BC, CD и AD — сторонами.
 Вершины А и С, В и D называются противолежащими вершинами. Стороны AB и CD, BC и AD называются противолежащими сторонами.
Вершины А и С, В и D называются противолежащими вершинами. Стороны AB и CD, BC и AD называются противолежащими сторонами.Четырехугольники бывают выпуклые (на рисунке — левый) и невыпуклые (на рисунке — правый).
Каждая диагональ выпуклого четырехугольника разделяет его на два треугольника (диагональ АС разделяет ABCD на два треугольника ABC и ACD; диагональ BD — на BCD и BAD). У невыпуклого четырехугольника только одна из диагоналей разделяет его на два треугольника (диагональ AC разделяет ABCD на два треугольника ABC и ACD; диагональ BD — не разделяет).
Рассмотрим основные виды четырехугольников, их свойства, формулы площади:
Параллелограмм
Параллелограммом называется четырехугольник, у которого противоположные стороны попарно параллельны.
ABCD-параллелограмм: AB||DC, AD||BC Свойства:
- В параллелограмме противоположные стороны равны и противоположные углы равны.

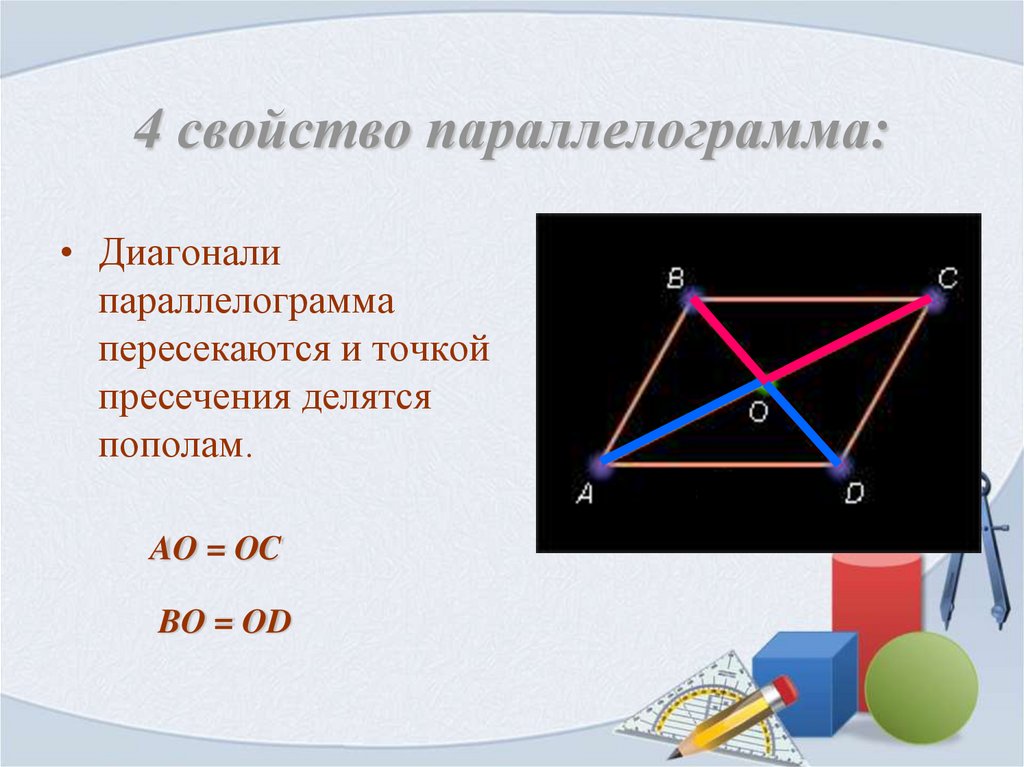
- Диагонали параллелограмма точкой пересечения делятся пополам.
Признаки параллелограмма:
1. Если в четырехугольнике две стороны равны и параллельны, то этот четырехугольник — параллелограмм.
2. Если в четырехугольнике противоположные стороны попарно равны, то этот четырехугольник – параллелограмм.
3. Если в четырехугольнике диагонали пересекаются и точкой пересечения делятся пополам, то этот четырехугольник – параллелограмм.Площадь параллелограмма:
Трапеция
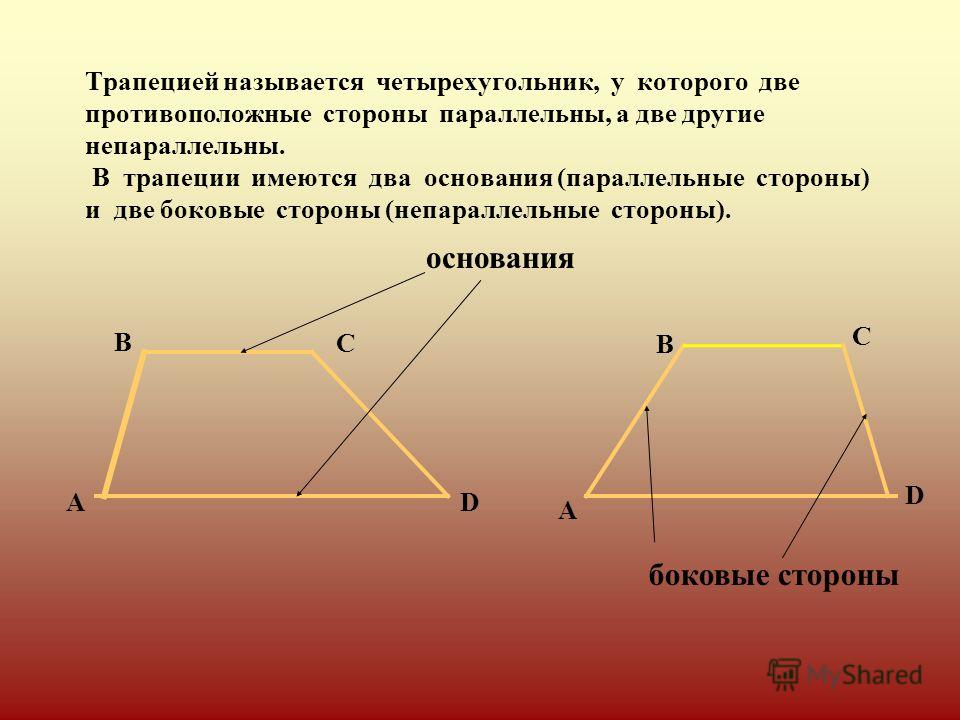
Трапецией называется четырехугольник, у которого две стороны параллельны, а две другие стороны не параллельны.
Основаниями называются параллельные стороны, а две другие стороны — боковыми сторонами.
Трапеция называется равнобедренной, если ее боковые стороны равны. Трапеция, один из углов которой прямой, называется прямоугольной. 
Средней линией трапеции называется отрезок, соединяющий середины ее боковых сторон.
ТЕОРЕМА.
Средняя линия трапеции параллельна основаниям и равна их полусумме.
Площадь трапеции:
Ромбом называется параллелограмм, у которого все стороны равны.
Свойства:
- Ромб обладает всеми свойствами параллелограмма.
- Диагонали ромба взаимно перпендикулярны и делят его углы пополам.
Площадь ромба:
Прямоугольник
Прямоугольником называется параллелограмм, у которого все углы равны.
Свойства:
- Прямоугольник обладает всеми свойствами параллелограмма.
- Диагонали прямоугольника равны.
Признак прямоугольника:
Если в параллелограмме диагонали равны, то этот параллелограмм – прямоугольник.

Площадь прямоугольника:
Квадрат
Квадратом называется прямоугольник, у которого все стороны равны.
Свойства:
Квадрат обладает всеми свойствами прямоугольника и ромба (прямоугольник является параллелограммом, поэтому и квадрат является параллелограммом, у которого все стороны равны, т.е. ромбом).
- Все углы квадрата прямые.
- Диагонали квадрата равны, взаимно перпендикулярны точкой пересечения делятся пополам и делят углы квадрата пополам.
Площадь квадрата:
- отправить денежный перевод с карты на карту мгновенно и без комиссий по ссылке . Ссылка на перевод . В поле «Добавьте комментарий» необходимо указать «в дар» или «подарок».
- оставить комментарий ниже.
Автор: Аникина Марина
Комментарии к этой заметке:
Очень понравилась эта статья ) Все интересно и понятно) Очень помогло! Спасибо)
Геометрия.
 Урок 4. Четырехугольники
Урок 4. ЧетырехугольникиСмотрите бесплатные видео-уроки на канале Ёжику Понятно.
Видео-уроки на канале Ёжику Понятно. Подпишись!
Содержание страницы:
- Определение четырехугольника
- Выпуклые четырехугольники
- Параллелограмм
- Робм
- Прямоугольник
- Квадрат
- Трапеция
- Примеры решений заданий из ОГЭ
Определение четырехугольника
Четырехугольником называется фигура, которая состоит из четырех точек (вершин) и четырех отрезков (сторон), которые последовательно соединяют вершины. При этом никакие три из данных точек не должны лежать на одной прямой, а соединяющие их отрезки не должны пересекаться.
Четырехугольники бывают выпуклые ( A B C D ) и невыпуклые ( A 1 B 1 C 1 D 1 ) .

Выпуклые четырехугольники
В задачах ОГЭ встречаются выпуклые четырехугольники, поэтому подробно изучим их.
Смежные стороны – соседние стороны, которые выходят из одной вершины. Пары смежных сторон: A B и A D , A B и B C , B C и C D , C D и A D .
Противолежащие стороны – несмежные стороны (соединяют разные вершины). Пары противолежащих сторон: A B и C D , B C и A D .
Противолежащие вершины – вершины, не являющиеся соседними (лежат друг напротив друга). Пары противолежащих вершин: A и C , B и D .
Диагонали четырехугольника – отрезки, соединяющие противолежащие вершины. A C и B D – диагонали четырехугольника A B C D .
Диагонали выпуклого четырехугольника пересекаются в одной точке.
Площадь произвольного выпуклого четырехугольника можно найти по формуле:
S = 1 2 d 1 d 2 ⋅ sin φ
где d 1 и d 2 – диагонали четырехугольника, φ – угол между диагоналями (острый или тупой – не важно).

Рассмотрим более подробно некоторые виды выпуклых четырехугольников.
Класс параллелограммов : параллелограмм, ромб, прямоугольник, квадрат.
Класс трапеций : произвольная трапеция, прямоугольная трапеция, равнобокая (равнобедренная) трапеция.
Параллелограмм
Параллелограмм – четырехугольник, у которого противолежащие стороны попарно параллельны.
Свойства параллелограмма:
- Противолежащие стороны равны.
- Противоположные углы равны.
- Диагонали точкой пересечения делятся пополам.
- Сумма углов, прилежащих к одной стороне, равна 180 ° .
- Сумма квадратов диагоналей равна сумме квадратов сторон. d 1 2 + d 2 2 = 2 ( a 2 + b 2 )
Площадь параллелограмма можно найти по трём формулам.
Как произведение стороны и высоты, проведенной к ней.
Поскольку стороны имеют разные длины, то высоты, которые к ним проведены, тоже будут иметь разные длины.

Как произведение двух смежных (соседних) сторон на синус угла между ними.
Как полупроизведение диагоналей на синус угла между ними.
Ромб – параллелограмм, у которого все стороны равны.
Свойства ромба:
- Диагонали пересекаются под прямым углом.
- Диагонали являются биссектрисами углов, из которых выходят.
- Сохраняются все свойства параллелограмма.
Площадь ромба можно найти по трём формулам.
Как произведение стороны ромба на высоту ромба.
Как квадрат стороны ромба на синус угла между двумя сторонами.
Как полупроизведение диагоналей ромба.
Прямоугольник
Прямоугольник – это параллелограмм, у которого все углы равны 90 ° .
Свойства прямоугольника:
- Диагонали прямоугольника равны.
- Сохраняются все свойства параллелограмма.
Площадь прямоугольника можно найти по двум формулам:
Как произведение двух смежных (соседних) сторон прямоугольника.

Как полупроизведение диагоналей (так как они обе равны, обозначим их буквой d ) на синус угла между ними.
Квадрат
Квадрат – прямоугольник, у которого все стороны равны.
Свойства квадрата:
- Сохраняет свойства ромба.
- Сохраняет свойства прямоугольника.
Площадь квадрата можно вычислить по двум формулам:
Как квадрат стороны.
Как полупроизведение квадратов диагоналей (диагонали в квадрате равны).
ТрапецияТрапеция – это четырехугольник, у которого две стороны параллельны, а две другие нет.
Стороны, которые параллельны друг другу называются основаниями , другие две стороны называются боковыми сторонами .
B C и A D – основания, A B и C D – боковые стороны трапеции A B C D .
Свойства трапеции:
сумма углов, прилежащих к боковой стороне, равна 180 ° .

Средняя линия трапеции – отрезок, соединяющий середины боковых сторон.
Средняя линия параллельна основаниям. Её длина находится по формуле: m = a + b 2
Площадь трапеции можно найти по двум формулам:
Как полусумму оснований на высоту. Поскольку полусумма оснований есть средняя линия трапеции, можно найти площадь трапеции как произведение средней линии на высоту.
Как полупроизведение диагоналей на синус угла между ними.
Виды трапеций
Прямоугольная трапеция – трапеция, у которой два угла прямые.
Равнобокая (равнобедренная) трапеция – трапеция, у которой боковые стороны равны.
Презентация к уроку : Решение задач по теме: Четырехугольники доклад, проект
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экономика
Презентация на тему Презентация к уроку : Решение задач по теме: Четырехугольники, предмет презентации: Геометрия. Этот материал в формате pptx (PowerPoint) содержит 19 слайдов, для просмотра воспользуйтесь проигрывателем. Презентацию на заданную тему можно скачать внизу страницы, поделившись ссылкой в социальных сетях! Презентации взяты из открытого доступа или загружены их авторами, администрация сайта не отвечает за достоверность информации в них, все права принадлежат авторам презентаций и могут быть удалены по их требованию.
Этот материал в формате pptx (PowerPoint) содержит 19 слайдов, для просмотра воспользуйтесь проигрывателем. Презентацию на заданную тему можно скачать внизу страницы, поделившись ссылкой в социальных сетях! Презентации взяты из открытого доступа или загружены их авторами, администрация сайта не отвечает за достоверность информации в них, все права принадлежат авторам презентаций и могут быть удалены по их требованию.
Решение задач по теме:
« Четырехугольники».
МАОУСОШ №22
Г. Таганрог
Учитель математики: Шилова Г.В.
Ответы к кроссворду
По горизонтали:
1. Четырехугольник, у которого противоположные стороны параллельны
2. Четырехугольник, у которого только две стороны параллельны
3. Параллелограмм, у которого все углы прямые
4. Точки из которых выходят стороны четырехугольника
По вертикали:
1. Сумма длин всех сторон
Сумма длин всех сторон
5. Отрезок, соединяющий противолежащие вершины
6. Прямоугольник, у которого все стороны равны
7. Параллелограмм , у которого все стороны равны
8. Отрезок, соединяющий соседние вершины
Математический диктант:
1
2
3
4
5
ОТВЕТЫ:
1) 1,2,3,4
2)1,2,3,4
3)5
4)2,4
5)1,2,3,4
6)2,4
7)2,4
8)3,4
9)3,4
10)4
Применение
В физике применяют параллелограмм при изучении сил, при нахождении равнодействующей силы.
В жизни параллелограмм – это рамы велосипедов, мотоциклов, где для жёсткости проведена диагональ.
— Применение
Прямоугольник несёт красоту, чёткость, стройность.
Оглянитесь вокруг: стены, пол, потолок, поверхность стола, футбольное поле, грани карандашей, даже записная книжка – все это прямоугольники.
Попробуйте построить дом или сделать раму для картины, не зная свойств прямоугольника.
— Применение?
В основании мраморных колонн лежит квадрат.
Ваши товарищи, играя в шахматы, фигуры
по квадратам передвигают.
В хирургическом отделении для пересадки кожи применяют специальную машинку, которая вырезает кожу в виде квадратов.
Их располагают на обожжённом участке
в шахматном порядке.
Любят меня рисовать на тканях художники, используют в узорах ковровщицы.
Плиточники укладывают плитки
в виде ромба,– из них получаются красивые узоры.
Реечный домкрат для легковых автомобилей также имеет форму ромба.
Применение.
№ 1
А
В
Е
С
D
32
o
ABCD – параллелограмм.
Найти : С, D.
32◦
32◦
64◦
116◦
№ 2
60
0
2 см
10 см
N
K
E
P
M
MNKP – параллелограмм.
Найти: MP, PK.
10 см
4 см
4 см
30◦
№ 3
В
Е
С
А
D
ABCD – параллелограмм.
Найти: Р , AЕD.
ABCD
5
5
5
10
Р=30см
5
90◦
№ 4
А
В
С
D
ABCD – прямоугольник, ОЕ = 2 см.
Найти: АС, АВ.
2 см
60◦
60◦
60◦
30◦
4 см
АС=8см, АВ=4см
№ 5
6 см
60
о
А
В
С
D
M
N
ABCD – ромб.
Найти: MD + DN
30◦
3см
3см
3 см
=3см+3см=6см
60◦
30◦
6см
№ 6
55
о
А
В
С
D
ABCD – ромб.
Найти BAD.
55◦
70◦
70◦
55◦
55◦
№ 7
D
А
В
С
ABCD – ромб., ∟В=120◦ , диагональ BD=8см,
Найти периметр ромба.
60◦
8см
60◦
60◦
8см
Р=4∙8см=32см
Самостоятельная работа:
Мы побывали в семействе четырехугольников и вспомнили, что:
1. Противолежащие стороны равны
Противолежащие стороны равны
у ромба, квадрата, прямоугольника, параллелограмма.
2. Противолежащие углы равны
у ромба, квадрата, прямоугольника, параллелограмма.
3. Диагонали равны
у прямоугольника, квадрата.
4. Диагонали взаимно перпендикулярны
у ромба, квадрата.
5. Диагонали являются биссектрисами углов
у ромба, квадрата.
6. Диагонали равны и являются биссектрисами
у квадрата.
Д/з.
Скачать презентацию
Это сайт презентаций, где можно хранить и обмениваться своими презентациями, докладами, проектами, шаблонами в формате PowerPoint с другими пользователями. Мы помогаем школьникам, студентам, учителям, преподавателям хранить и обмениваться учебными материалами.
Для правообладателей
Обратная связь
Email: Нажмите что бы посмотреть
Четырехугольник Форма, типы, свойства, определение
Четырехугольник в геометрии — это замкнутая форма, образованная соединением четырех точек, среди которых любые три точки не лежат на одной прямой.
| 1. | Четырехугольник Определение |
| 2. | Типы четырехугольников |
| 3. | Свойства четырехугольника |
| 4. | Часто задаваемые вопросы о четырехугольниках |
Четырехугольник Определение
Четырехугольник — это многоугольник с четырьмя сторонами, четырьмя углами и четырьмя вершинами. Всякий раз, когда мы называем четырехугольник, мы должны помнить о порядке вершин. Например, следующий четырехугольник следует назвать ABCD, BCDA, ADCB или DCBA. Его нельзя назвать ACBD или DBAC, так как они меняют порядок вершин, в которых образован четырехугольник.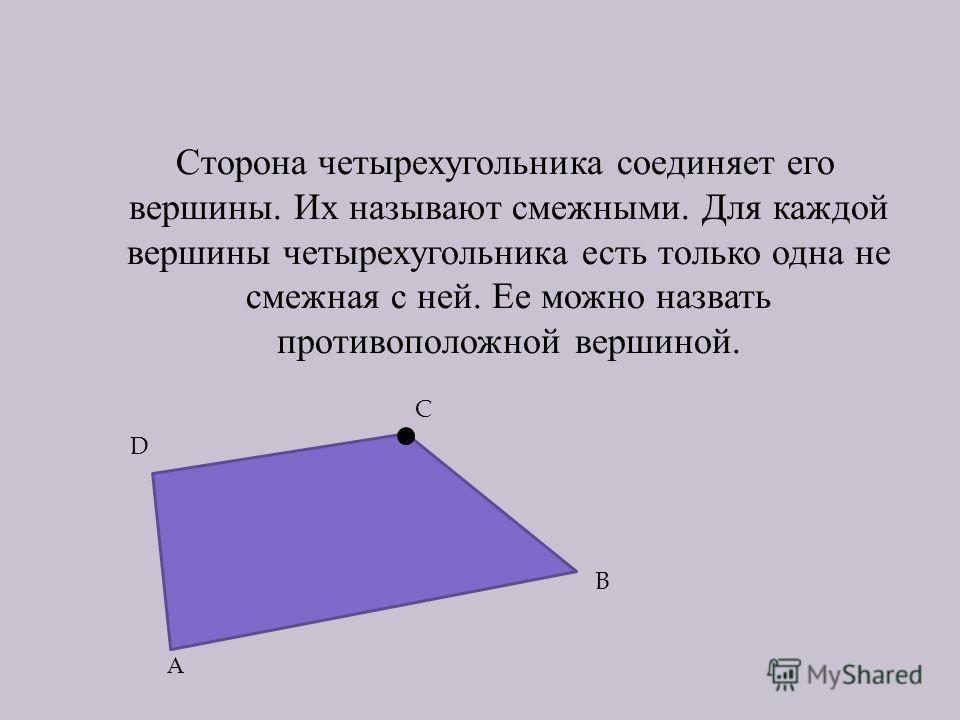
Типы четырехугольников
Хотя четырехугольник всегда имеет четыре стороны, четыре угла и четыре вершины, размеры сторон и углов различаются. Следует отметить, что сумма внутренних углов четырехугольника всегда равна 360°. В следующей таблице перечислены различные типы четырехугольников.
Свойства четырехугольника
Каждый из рассмотренных выше четырехугольников имеет свои свойства. Однако есть некоторые свойства, общие для всех четырехугольников. Они следующие.
- У них четыре стороны.
- У них четыре вершины.
- У них две диагонали.
- Сумма всех внутренних углов равна 360°.
Мы подробно изучим другие свойства различных четырехугольников. Мы можем идентифицировать четырехугольник, используя следующие свойства четырехугольников.
Квадрат
Квадрат – это четырехугольник с четырьмя равными сторонами и четырьмя прямыми углами.
Квадрат имеет:
- Четыре равные стороны
АВ = ВС = CD = DA - Четыре прямых угла
∠ А= ∠В = ∠С = ∠D = 90° - Две пары параллельных сторон
AB ∥ DC и AD ∥ BC - Две равные диагонали
АС = BD - Диагонали, перпендикулярные друг другу
АС ⊥ БД - Диагонали, которые делят друг друга пополам.
Прямоугольник
Прямоугольник – это четырехугольник с двумя парами равных и параллельных противоположных сторон и четырьмя прямыми углами.
Прямоугольник имеет:
- Две пары параллельных сторон
AB ∥ DC и AD ∥ BC - Четыре прямых угла
∠А = ∠В = ∠С = ∠D = 90° - Противоположные стороны равной длины
AB = DC и AD = BC - Две равные диагонали
- Диагонали, которые делят друг друга пополам.
Параллелограмм
Параллелограмм – это четырехугольник, у которого обе пары противоположных сторон параллельны.
Параллелограмм имеет:
- Две пары параллельных сторон
PQ ∥ RT и PR ∥ QT - Противоположные стороны равной длины
PQ = RT и PR = QT - Противоположные углы равны
∠P = ∠T и ∠Q = ∠R - Две диагонали, которые делят друг друга пополам.
Трапеция
Трапеция – это четырехугольник, у которого одна пара противоположных сторон параллельна.
- Стороны, параллельные друг другу, называются основаниями .
На приведенном выше рисунке основаниями являются EF и GH. - Стороны, не параллельные друг другу, называются ножками .
На приведенном выше рисунке EG и FH являются ветвями.
В сторонах, углах и диагоналях трапеции нет ничего особенного. Но если две непараллельные противоположные стороны имеют одинаковую длину, то это называется Равнобедренная трапеция. Следующий четырехугольник XYZW является равнобедренной трапецией, у которой катеты равны, т. е. WX = ZY, и диагонали тоже равны, т. е. XZ = WY.
е. WX = ZY, и диагонали тоже равны, т. е. XZ = WY.
Ромб
Ромб – четырехугольник с четырьмя равными сторонами.
Ромб имеет:
- Две пары параллельных сторон
EH ∥ FG и EF ∥ HG - Четыре равные стороны
EH = HG = GF = FE - Противолежащие углы равны
∠E = ∠G и ∠H = ∠F - Диагонали, перпендикулярные друг другу
ЭГ ⊥ ВЧ - Диагонали, которые делят друг друга пополам.
Воздушный змей
Воздушный змей — четырехугольник, у которого две пары смежных сторон равны.
Обратите внимание на следующие свойства воздушного змея. Воздушный змей имеет:
- Две пары равных смежных сторон
AB = BC и CD = DA - Одна пара противоположных углов (тупых), равных
∠А = ∠С - Диагонали, перпендикулярные друг другу
АС ⊥ БД - Более длинная диагональ делит меньшую диагональ пополам.
Think Tank
- Можно ли назвать воздушного змея параллелограммом?
- Какие элементы трапеции надо изменить, чтобы она стала параллелограммом?
Площадь четырехугольника
Площадь четырехугольника — это количество единичных квадратов, которые могут быть в него вписаны. В следующей таблице перечислены формулы для нахождения площади четырехугольника.
В следующей таблице перечислены формулы для нахождения площади четырехугольника.
☛Темы, связанные с четырехугольниками
Ознакомьтесь с некоторыми интересными статьями, посвященными четырехугольникам.
- Геометрические фигуры
- Треугольники
- Евклидова геометрия
- Твердые формы
- Уголки
- Параллелограммы
- Свойство суммы углов в четырехугольниках
Четырехугольник Примеры
Пример 1: Найдите значение угла x° на следующем рисунке.
Решение:
Мы знаем, что сумма углов четырехугольника равна 360°.
Это можно записать как: x + 67 + 77 + 101 = 360°
х + 245 = 360°
Следовательно, х = 115°Пример 2: Какова площадь четырехугольного воздушного змея, диагонали которого имеют длину 10 единиц и 20 единиц?
Решение:
Диагонали данного воздушного змея: \(d_{1}\) = 10 и \(d_{2}\) = 20
Площадь воздушного змея вычисляется по формуле:
Площадь = (½) × \(d_{1}\) × \(d_{2}\)
А = (½) × 10 × 20
= 100
Следовательно, площадь воздушного змея = 100 квадратных единиц.
Пример 3: Какова площадь следующего четырехугольника (равнобедренной трапеции)?
Решение:
Площадь равнобедренной трапеции вычисляется по формуле: Площадь равнобедренной трапеции равна (1/2) × (a + b) × h, где «a» и «b» — основания h — высота равнобедренной трапеции. В этом примере заданы размеры:
a = 16, b = 40 и h = 15
Площадь = (1/2) × (a + b) × h
= (1/2) × (16 + 40) × 15
= (1/2) × 56 × 15
= 420 квадратных единиц.
перейти к слайдуперейти к слайдуперейти к слайду
Есть вопросы по основным математическим понятиям?
Станьте чемпионом по решению проблем, используя логику, а не правила. Узнайте, почему математика стоит за нашими сертифицированными экспертами Cuemath.
Записаться на бесплатный пробный урок
Практические вопросы по четырехугольнику
перейти к слайдуперейти к слайду
Часто задаваемые вопросы о четырехугольнике
Что такое четырехугольник?
Четырехугольник — это замкнутая двумерная фигура, имеющая 4 стороны, 4 угла и 4 вершины. Несколько примеров четырехугольников: квадрат, прямоугольник и трапеция.
Несколько примеров четырехугольников: квадрат, прямоугольник и трапеция.
Какие существуют типы четырехугольников?
Существуют различные типы четырехугольников, которые идентифицируются на основе их уникальных свойств. Например, квадрат, прямоугольник, параллелограмм, ромб, воздушный змей, трапеция, равнобедренная трапеция относятся к категории четырехугольников.
Чему равна сумма внутренних углов четырехугольника?
В любом четырехугольнике сумма внутренних углов всегда равна 360°. Например, прямоугольник — это четырехугольник, каждый из внутренних углов которого равен 9.0°, что делает его (90 × 4) = 360°.
Какие общие свойства есть у четырехугольников?
Хотя существуют разные типы четырехугольников, у них есть несколько общих свойств. Они перечислены следующим образом:
- У них четыре стороны.
- У них четыре вершины.
- У них две диагонали.
- Сумма всех внутренних углов равна 360°.
Как найти площадь четырехугольника?
Площадь — это пространство, занимаемое любой фигурой.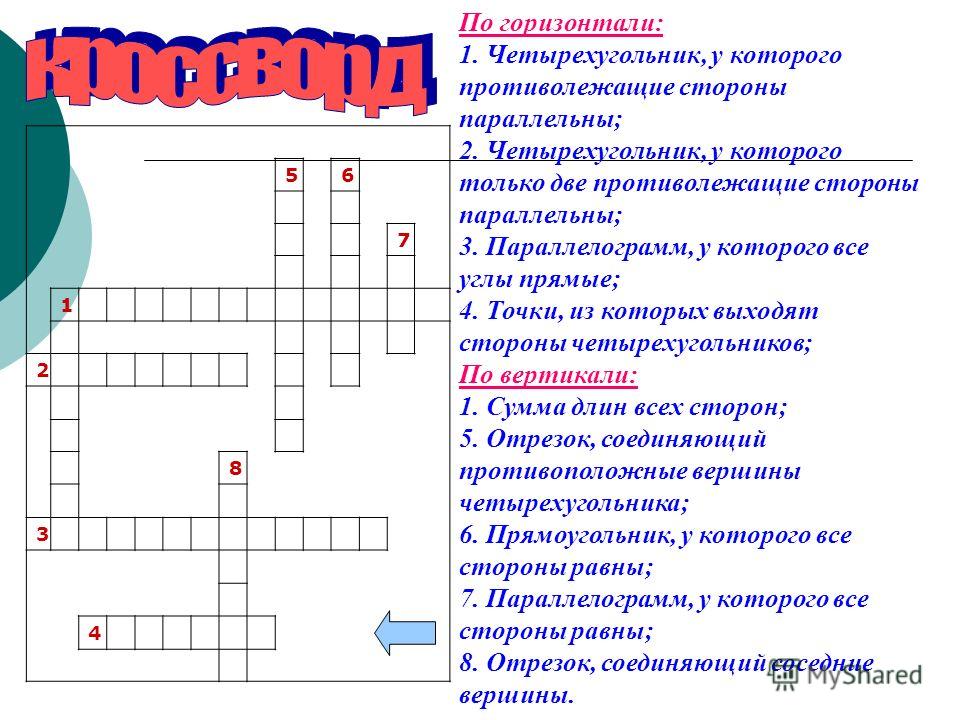 Четырехугольник – это фигура, имеющая 4 стороны, а пространство, занимаемое четырехугольником, называется его площадью. Несколько примеров четырехугольников квадрат и прямоугольник. Площадь квадрата со стороной «а» вычисляется по формуле: Площадь = «а × а» или 2 , а площадь прямоугольника, длина которого равна «l», а ширина равна «w», вычисляется по формуле формула: Площадь = ‘l × b’. Площадь четырехугольника всегда выражается в квадратных единицах.
Четырехугольник – это фигура, имеющая 4 стороны, а пространство, занимаемое четырехугольником, называется его площадью. Несколько примеров четырехугольников квадрат и прямоугольник. Площадь квадрата со стороной «а» вычисляется по формуле: Площадь = «а × а» или 2 , а площадь прямоугольника, длина которого равна «l», а ширина равна «w», вычисляется по формуле формула: Площадь = ‘l × b’. Площадь четырехугольника всегда выражается в квадратных единицах.
Как найти периметр четырехугольника?
Периметр — это длина границы любой формы. Поскольку мы знаем, что у четырехугольника 4 стороны, периметр четырехугольника можно найти, сложив все стороны четырехугольника. Например, если прямоугольник имеет длину 6 единиц и ширину 4 единицы, мы используем формулу для периметра прямоугольника: 2 (длина + ширина). Подставляя значения в формулу: 2 (6 + 4) = 20 единиц.
Скачать БЕСПЛАТНЫЕ учебные материалы
Скачать бесплатно рабочие листы для 5 класса
Скачать бесплатные рабочие листы для 6 класса
Скачать бесплатные рабочие листы для 9 класса
Четырехугольники с заданиями
Какая фигура получается при соединении середины любого четырехугольника?
Геометрия происходит от греческого слова, означающего «Измерение Земли». Это раздел математики, занимающийся свойствами пространства, т. е. визуальным изучением форм, положения фигур, узоров, размеров и т. д. Геометрия является предметом бесчисленных разработок, поэтому существует много типов. Это евклидова геометрия, неевклидова геометрия, алгебраическая геометрия, риманова геометрия и симплектическая геометрия.
Это раздел математики, занимающийся свойствами пространства, т. е. визуальным изучением форм, положения фигур, узоров, размеров и т. д. Геометрия является предметом бесчисленных разработок, поэтому существует много типов. Это евклидова геометрия, неевклидова геометрия, алгебраическая геометрия, риманова геометрия и симплектическая геометрия.
Четырехугольник
Четырехугольник можно разделить на два слова: Четырехугольник означает четыре, а боковой означает сторону. Итак, четырехугольник — это замкнутая фигура с четырьмя сторонами. У него было четыре вершины. Стороны четырехугольника равны/не равны/параллельны/неправильны, что приводит к различным геометрическим фигурам. Пример: Квадрат, Прямоугольник, Ромб, Параллелограмм, Трапеция и т.д.
Середина стороны делит сторону любой фигуры на две равные части (по длине). В четырехугольнике будет середина каждой стороны, то есть четыре середины.
Есть несколько факторов, которые определяют форму, образованную путем соединения середины четырехугольника. Этими факторами являются тип четырехугольника, диагональные свойства и т. д. Эти факторы влияют на форму, образованную путем соединения средних точек в данном четырехугольнике. Давайте рассмотрим различные сценарии, чтобы лучше понять.
Этими факторами являются тип четырехугольника, диагональные свойства и т. д. Эти факторы влияют на форму, образованную путем соединения средних точек в данном четырехугольнике. Давайте рассмотрим различные сценарии, чтобы лучше понять.
Какая фигура получится, если соединить середины любого четырехугольника?
Решение:
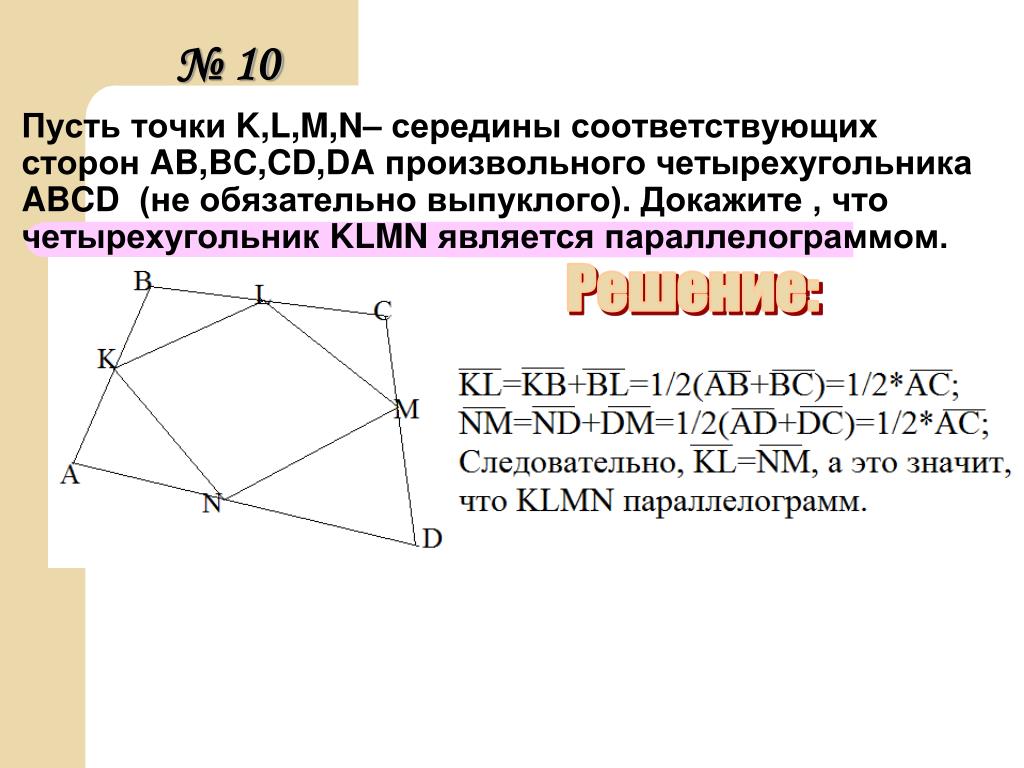
Рассмотрим четырехугольник ABCD. Найдите форму фигуры, образованной соединением средних точек.
Здесь A, B, C, D — вершины четырехугольника
P, Q, R, S — середины сторон AB, AC, BD и CD соответственно.
Поскольку середина делит сторону на равные части, AP = PB, и то же самое будет применяться ко всем сторонам.
BC — диагональ четырехугольника, образующего два треугольника ABC и BCD.
Рассмотрим треугольник BCD
CB параллелен SR (CB || SR)
Согласно теореме о средней точке
SR = CB/2
Итак, CB||SR и SR = CB/2 ⇢ (1)
То же, что и в треугольнике ABC
QP||CB и QP = CB/2 ⇢ (2)
Из (1) и (2)
SR||QP и SR = QP
Поскольку одна пара противоположных сторон равна по длине и параллельна друг другу, Результирующая фигура, соединяющая середины четырехугольника, становится параллелограммом .
Примеры вопросов
Вопрос 1: Рассмотрим ромб ABCD, который также является разновидностью четырехугольника. Найдите форму фигуры, образованной соединением середин.
Решение:
Пусть ABCD — ромб, а P, Q, R, S — середины сторон AB, BC, CD, DA соответственно.
В треугольнике ABD имеем:
PS || BD & PS = BD/2 ….(1)
(согласно теореме о средней точке.)
теорема о средней точке.)
Из уравнений (1) и (2) получаем,
PS || QR
Значит, PQRS является параллелограммом
Поскольку диагонали ромба делят друг друга пополам под углом 90° (Прямые углы)
Диагонали перпендикулярны друг другу
AC ⊥ BD
Поскольку PS || QR & PQ || SR & AC⊥ BD
PQ также перпендикулярно QR.
PQ ⊥ QR (∠PQR = 90°)
Следовательно, PQRS — прямоугольник.
Итак, фигура, образованная совмещением середин ромба, образует прямоугольник .
Вопрос 2: Если фигура, образованная соединением середины четырехугольника, является квадратной, только если, объясните условие.
Решение:
Пусть ABCD — ромб, а P, Q, R, S — середины сторон AB, BC, CD, DA соответственно.
Данный PQRS является квадратом.
Такой, что PQ = QR = RS = SP ….(1)
Также диагонали в квадрате имеют одинаковую длину, т. е. PR = SQ
Но PR = BC & SQ = AB
Следовательно, AB = BC (поскольку PR = SQ)
Итак, все стороны четырехугольника равны.
Данный четырехугольник должен быть квадратом или ромбом.
В треугольнике ADC имеем
RS||AC & RS = AC/2 ….(2)
(Согласно теореме о средней точке.)
В треугольнике BDC имеем
QR |900| BD & QR = BD/2 …..(3)
(Согласно теореме о средней точке. 0
Из уравнения (1),
RS = QR
Значит, AC/2 = BD/2
AC = BD
Таким образом, длины диагоналей четырехугольника равны, Значит, ABCD представляет собой квадрат с диагоналями, перпендикулярными друг другу.
Вопрос 3: Какая фигура образована соединением середин параллелограмма.
Решение:
Данная фигура представляет собой параллелограмм ABCD с серединами P, Q, R, S для сторон AB, BD, CD, AC соответственно.
В треугольнике ABC имеем
PS || BC & PS = BC/2 ….(1)
(Согласно теореме о средней точке.)
В треугольнике BDC имеем:
QR || BC & QR = BC/2 ….(2)
(Согласно теореме о средней точке.)
Из уравнения (1) и (2) получаем,
PS || QR
Итак, PQRS — параллелограмм.
Вопрос 4. Какая фигура получится, если соединить середины четырехугольника, диагонали которого равны?
Ответ:
Ромб, представляющий собой замкнутую двумерную плоскую фигуру. Он считается своеобразным параллелограммом и имеет свою идентичность четырехугольника из-за своих уникальных особенностей.
Поскольку все его стороны имеют одинаковую длину, ромб также известен как равносторонний четырехугольник. Название «ромб» происходит от древнегреческого слова «rhombos», что буквально означает «вращаться».
Вопрос 5. Какая фигура получится, если соединить середины четырехугольника, диагонали которого перпендикулярны, но не имеют одинаковой длины?
Ответ:
Прямоугольник, представляющий собой четырехугольник с равными углами со всех сторон и равными и параллельными противоположными сторонами. В нашей среде есть множество прямоугольных элементов. Каждая форма прямоугольника имеет два различных измерения: длину и ширину. Длина и ширина прямоугольника определяются как длинная и меньшая сторона соответственно.
Калькулятор периметра четырехугольника
Вам нужен калькулятор периметра четырехугольника , чтобы помочь вам решить эти математические задачи? Вы знаете координаты фигуры с четырьмя сторонами, но понятия не имеете 😕 как вычислить периметр и вам нужна помощь❓ У нас есть именно тот инструмент, который вам нужен. Наш калькулятор как найти периметр четырехугольника разработан, чтобы помочь вам найти периметр любой фигуры с четырьмя сторонами и четырьмя вершинами.
Наш калькулятор как найти периметр четырехугольника разработан, чтобы помочь вам найти периметр любой фигуры с четырьмя сторонами и четырьмя вершинами.
В этой статье вы узнаете больше о:
- Что такое четырехугольник;
- Что такое вогнутый четырехугольник;
- Как найти периметр четырехугольника по четырем сторонам;
- Как вычислить периметр четырехугольника по координатам; и
- Как использовать наш калькулятор периметра четырехугольника.
Итак, каков периметр четырехугольника?
Периметр четырехугольника — это расстояние вокруг четырехугольника. Итак, чтобы найти периметр четырехугольника 🟧, нам нужно складываем все стороны . Однако реальная трудность заключается в том, что мы не всегда знаем, каковы эти измерения в математике или в реальной жизни. Здесь на помощь приходит наш калькулятор.
Продолжайте читать, чтобы узнать, как найти периметр четырехугольника, когда известны все стороны , а также когда известны только координаты вершин.
Что такое четырехугольник?
Четырехугольник представляет собой замкнутую форму с четырьмя прямыми сторонами, углами и вершинами. Некоторые примеры четырехугольников: квадрат , воздушный змей, ромб, трапеция и параллелограмм.
Что такое вогнутый четырехугольник?
Вогнутый четырехугольник представляет собой четырехстороннюю фигуру, у которой один внутренний угол больше 180 градусов. Кроме того, вогнутый четырехугольник имеет одну диагональ, лежащую в области фактической формы.
Как найти периметр четырехугольника по его сторонам
Нахождение периметра четырехугольника по известным сторонам — довольно простая задача. Складываем все стороны вместе. Конечно, иногда мы можем знать только две стороны. С большинством четырехугольников это все еще довольно просто.
Например, если четырехугольник является квадратом, прямоугольником, параллелограммом или любой другой формой с двумя равными противоположными сторонами и углами, обычное решение состоит в том, чтобы умножить длину на два и ширину на два, а затем сложить ответы вместе, чтобы доехать до периметра.
Однако мы не можем сделать это для более неправильных форм, таких как трапеция, если у нас нет дополнительной информации. 92}D=(x2−x1)2+(y2−y1)2
- Подставьте соответствующие xxx и yyy координаты всех сторон и вычислите длины.
- После завершения шага 2 вам нужно сложить все ответы вместе.
- Результат — периметр.
Пример:
Даны координаты четырехугольника DEFG как ( 5, 7 ), ( 8, 7 ), ( 1, 3 ) и ( 8 , 3 3 9 , 9, соответственно) найти периметр.
Пусть значения D , ( 5 и 7 ) BE X₁, Y₁ Значения E , ( 8, 7 ), x₂, y₂ . ( 1, 3 ) равны x₃, y₃ , а значения G , ( 9, 3 ) равны x₄, y₄ .
Теперь постройте график, чтобы вы могли четко видеть, какие точки соединяются, образуя ваш четырехугольник.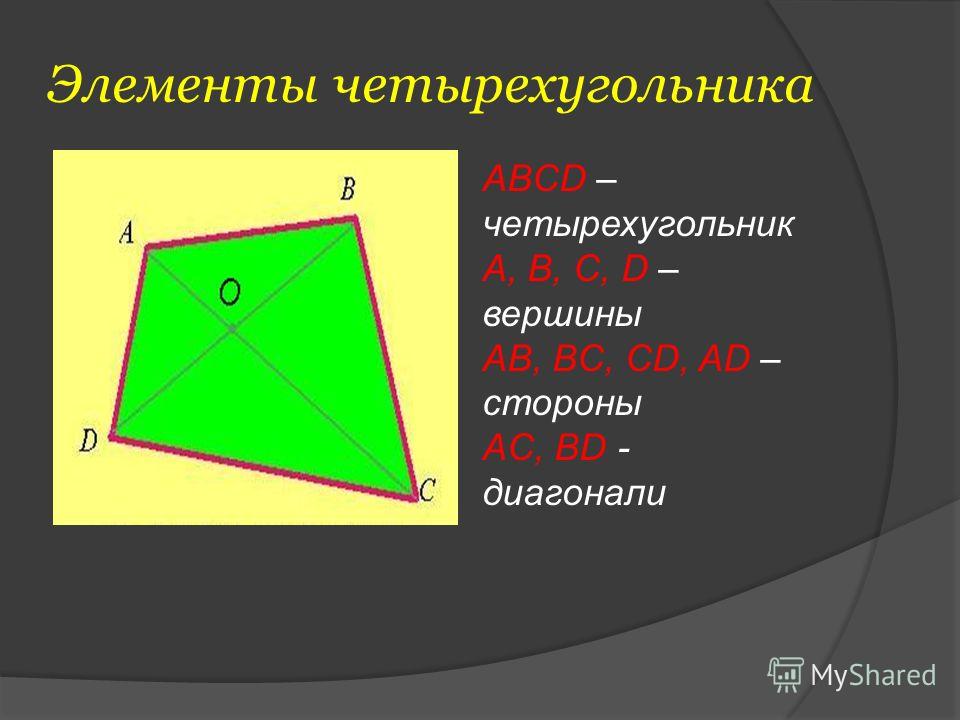
Используя формулу расстояния, найдем линию DE 92}\\[.5em]
&= \sqrt{16 + 16}\\[.5em]
&= \sqrt{32}\\[.5em]
&= 5,7
\end{align*}FD=(5−1)2+(7−3)2
=(4)2+(4)2
=16+16
=32
=5,7
Как только вы нашли длины всех сторон, остается только сложить все длины вместе. Итак, периметр четырехугольника равен:
DEFG=3+8+4.1+5.7=20.8\small \начать{выравнивать*} DEFG &= 3 + 8 + 4,1+ 5,7\\[0,5em] &= 20,8 \end{align*}DEFG=3+8+4.1+5.7=20.8
Как пользоваться нашим калькулятором периметра четырехугольника
Периметр четырехугольника — это два калькулятора в одном. Это позволяет нам вычислить расстояние вокруг любой четырехсторонней формы, используя либо известную длину всех сторон, либо координаты всех вершин. Итак, вот шаги, которые вы должны выполнить, чтобы использовать наш калькулятор:
- Чтобы выбрать, какой из этих калькуляторов вы хотите использовать, выберите один из вариантов, доступных в поле с пометкой 9.
 0145 Дано .
0145 Дано . - Если вы выберете опцию 4 стороны , теперь вы должны ввести значения четырех сторон.
- После выполнения шага 2 калькулятор отобразит ваш ответ в поле с периметром.
- Если вы выберете четыре вершины в поле Учитывая , вы увидите второй калькулятор, где вам нужно будет ввести координаты x и y фигуры, периметр которой вы хотите вычислить.
- После того, как вы введете координаты, наш калькулятор возвращает как длину каждой стороны, так и периметр фигуры.
Другие калькуляторы четырехугольников
Вот некоторые похожие калькуляторы, которые могут вас заинтересовать:
- Калькулятор четырехугольников;
- Калькулятор площади трапеции;
- Калькулятор площади прямоугольника;
- Калькулятор площади квадрата;
- Калькулятор периметра квадрата;
- Калькулятор периметра прямоугольника;
- Калькулятор периметра трапеции;
- Периметр прямоугольника с заданной площадью; и
- Калькулятор длины и ширины прямоугольника с заданным периметром.


 Вершины А и С, В и D называются противолежащими вершинами. Стороны AB и CD, BC и AD называются противолежащими сторонами.
Вершины А и С, В и D называются противолежащими вершинами. Стороны AB и CD, BC и AD называются противолежащими сторонами.
 Урок 4. Четырехугольники
Урок 4. Четырехугольники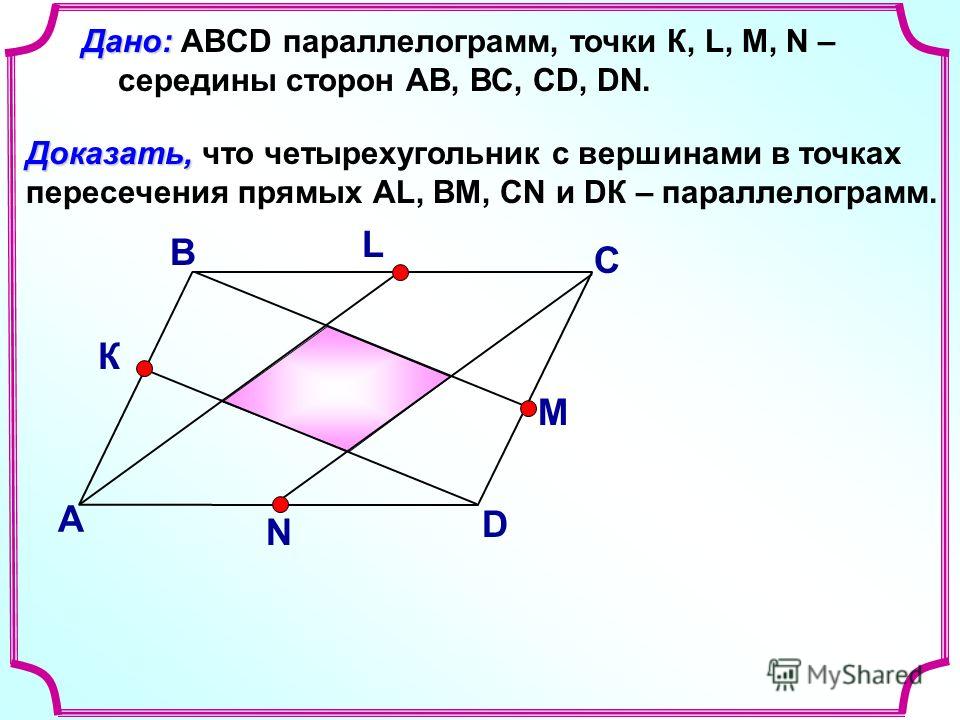




 Поскольку все его стороны имеют одинаковую длину, ромб также известен как равносторонний четырехугольник. Название «ромб» происходит от древнегреческого слова «rhombos», что буквально означает «вращаться».
Поскольку все его стороны имеют одинаковую длину, ромб также известен как равносторонний четырехугольник. Название «ромб» происходит от древнегреческого слова «rhombos», что буквально означает «вращаться».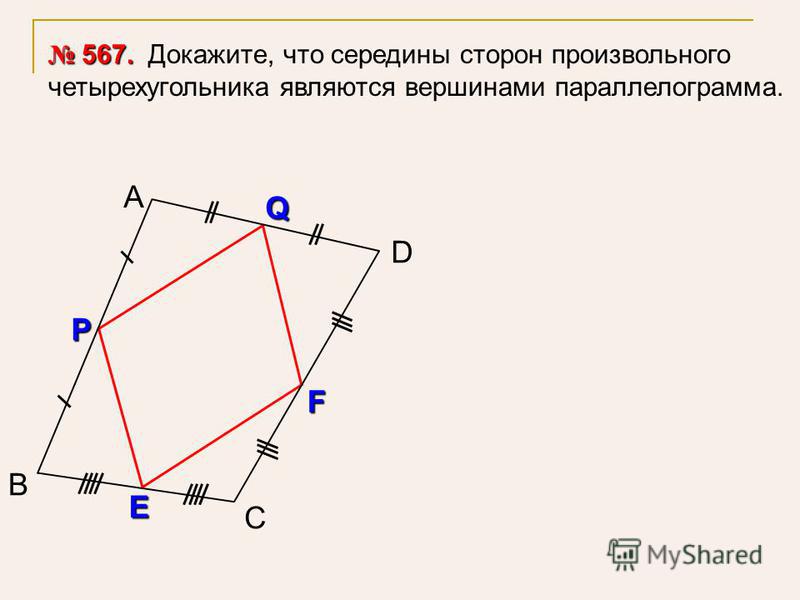 0145 Дано .
0145 Дано .