Точки из которых выходят стороны четырехугольника – Зачетный урок по геометрии в 8-м классе по теме «Четырехугольники»

Четырёхугольники

• «Четырехугольники»

• Работу выполнила
• учениц а 9 класса
• Боярко Яна
• учитель: Лата С.В.

КРОССВОРД

По горизонтали:

1. Четырехугольник, у которого противоположные стороны параллельны

2. Четырехугольник, у которого только две стороны параллельны

3. Параллелограмм, у которого все углы прямые

4. Точки из которых выходят стороны четырехугольника

По вертикали:

1. Сумма длин всех сторон

5. Отрезок, соединяющий противолежащие вершины

6. Прямоугольник, у которого все стороны равны

7. Параллелограмм , у которого все стороны равны

8. Отрезок, соединяющий соседние вершины

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

 

 

 

 

 

 

 

 

 

 

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

5

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

3

 

 

6

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

7

 

 

 

 

8

 

 

 

 

4

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Ответы к кроссворду

По горизонтали:

1. Четырехугольник, у которого противоположные стороны параллельны

2. Четырехугольник, у которого только две стороны параллельны

3. Параллелограмм, у которого все углы прямые

4. Точки из которых выходят стороны четырехугольника

По вертикали:

1. Сумма длин всех сторон

5. Отрезок, соединяющий противолежащие вершины

6. Прямоугольник, у которого все стороны равны

7. Параллелограмм , у которого все стороны равны

8. Отрезок, соединяющий соседние вершины

Четырехугольники:

параллелограмм

трапеция

ромб

прямоугольник

квадрат

другие четырехугольники

Параллелограмм

• Параллелограммом называется четырёхугольник, у которого противоположные стороны попарно параллельны.

Ромб

• Ромбом называется параллелограмм, у которого все стороны равны.

Трапеция

• Трапецией называется четырёхугольник, у которого две стороны параллельны, а две другие не параллельны.

Квадрат

• Квадратом называется прямоугольник, у которого все стороны равны.

Прямоугольник

• Прямоугольником называется параллелограмм, у которого все углы прямые.

Задача

B

В ромбе ABCD биссектриса угла В AC пересекает сторону ВС и диагональ BD соответственно в точках М и N. Найдите угол АNВ , если

АМС = 120 .

М

?

120

N

C

A

О

D

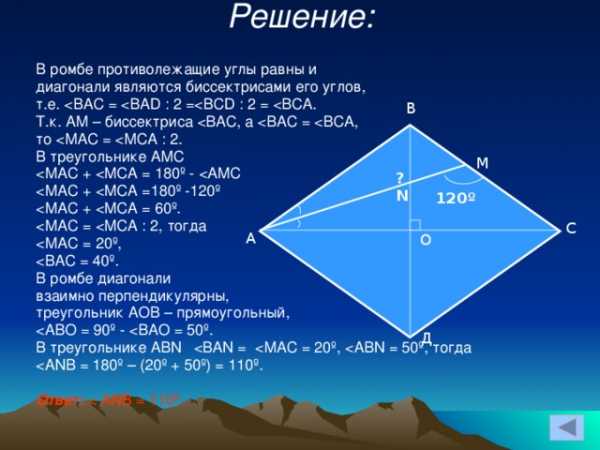
Решение:

В ромбе противолежащие углы равны и

диагонали являются биссектрисами его углов,

т.е.

Т.к. АМ – биссектриса

то

В треугольнике АМС

В ромбе диагонали

взаимно перпендикулярны,

треугольник АОВ – прямоугольный,

В треугольнике АВN

Ответ:

В

М

?

N

120 º

С

А

О

Д

спасибо

всем за внимание

videouroki.net

Разработка урока «Площади четырехугольников»

Разделы: Математика

Класс:

---

Цели урока:

• Проверка и систематизация знаний учащихся по данной теме.
• Развитие мыслительной деятельности при выполнении практической работы.
• Развитие творческих способностей, логического мышления учащихся.

Оборудование: мультимедийный проектор, магнитная доска, раздаточный материал, демонстрационный материал для творческой работы № 1.

ХОД УРОКА

I. Организационный момент.

Приветствие учащихся.

II. Объявление темы и цели урока.

III. Проверка знаний.

Для проверки теоретических знаний учащихся проводится математический диктант (каждому ученику раздается сетка кроссвордов).

По горизонтали:

1. Четырехугольник, у которого противолежащие стороны параллельны;
2. Четырехугольник, у которого только две противолежащие стороны параллельны;
3. Параллелограмм, у которого все углы прямые;
4. Точки, из которых выходят стороны четырехугольников;

По вертикали:

1. Сумма длин всех сторон;
2. Отрезок, соединяющий противолежащие стороны четырехугольника;
3. Прямоугольник, у которого все стороны равны;
4. Параллелограмм, у которого все стороны равны;
5. Отрезок, соединяющий соседние вершины.

Проверка выполняется c помощью мультимедийного проектора.

IV. Самостоятельная работа по карточкам.

Для закрепления формул площади выполнить задания, подготовленные на карточках:

Ко всем четырехугольникам подберите формулы для вычисления их площади:

Четырехугольники	Формулы для вычисления площади
Квадрат Прямоугольник Ромб Параллелограмм Трапеция

а)
б) S = aІ
в)
г) S = ab sin?
д) S = ah
е)
ж)
з)
и)
к) S=(ср.л.)h

Для выполнения проверки учащиеся обмениваются карточками. В это время на экране высвечивается таблица правильных ответов, по числу которых и выставляется оценка.

Карточки сдаются учителю.

V. Творческая работа.

Для отработки практических навыков использования формул проводится творческая работа № 1.

На парту раскладывается набор равнобедренных прямоугольных треугольников, которые равны между собой. Боковая сторона равнобедренного треугольника равна 4 см (30 треугольников).

Задание. Из этих треугольников составить: квадрат с площадью 16 кв.см, ромб – с площадью 32 кв.см, прямоугольник – с площадью 32 кв.см, квадрат – с площадью 64 кв.см, параллелограмм – с площадью 48 кв.см, трапецию – с площадью 48 кв.см.

На развороте магнитной доски ученики по очереди выполняют пункты творческого задания, используя демонстрационный материал. Учитель проверяет правильность задания и демонстрирует его учащимся.

1) Квадрат

 

Рисунок 2

S = aІ
S = 4І = 16(см²)

2) Ромб

Рисунок 3

а) или , где

б)

3) Прямоугольник

 Рисунок 4

S = 4 х 8 = 32(см²)

4) Квадрат

Рисунок 5

S = 8 х 8 = 64(см²)

5) Трапеция

Рисунок 6

6) Параллелограмм

 Рисунок 7

S = ah
S = 4 х 12 = 48(см²)

Учащиеся могут предложить другие варианты решения творческого задания.

VI. Итог урока.

25.02.2005

Поделиться страницей:

urok.1sept.ru

Повторение по теме»Четырехугольники и их площади»

Тема «Повторение по теме «Четырехугольники и их площади»

(математический кроссворд и карточки по теме)

Автор: Осипова М.В.

г.Ковров, Владимирская обл., МБОУ СОШ №9

-1-

Математический

кроссворд по теме «Четырехугольники» 8кл.

По горизонтали:

1. Четырехугольник, у которого противолежащие стороны параллельны.

2. Четырехугольник, у которого только две противолежащие стороны параллельны.

3. Параллелограмм, у которого все углы прямые.

4. Точки, из которых выходят стороны четырехугольника.

По вертикали:

1. Сумма длин всех сторон.

5. Отрезок, соединяющий противолежащие стороны четырехугольника.

6. Прямоугольник, у которого все стороны равны.

7. Параллелограмм, у которого все стороны равны.

8. Отрезок, соединяющий соседние вершины.

-2-

Ко всем четырехугольникам подбери формулы для вычисления их площади:

Четырехугольники

Формулы для вычисления площади

Квадрат

Прямоугольник

Параллелограмм

Трапеция

Треугольник

а) S=ah г) S=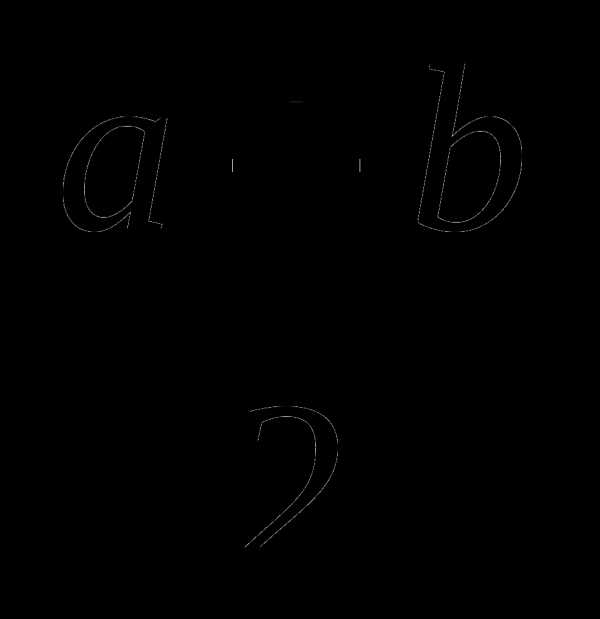h ж) S= a²

б) S= ah д) S= 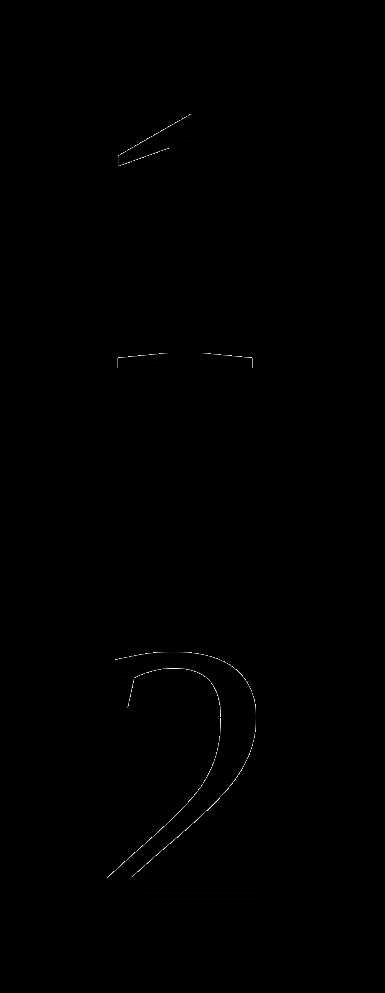ab

в) S= ab е) S= ab

Ко всем четырехугольникам подбери формулы для вычисления их площади:

Четырехугольники

Формулы для вычисления площади

Квадрат

Прямоугольник

Параллелограмм

Трапеция

Треугольник

а) S=ah г) S=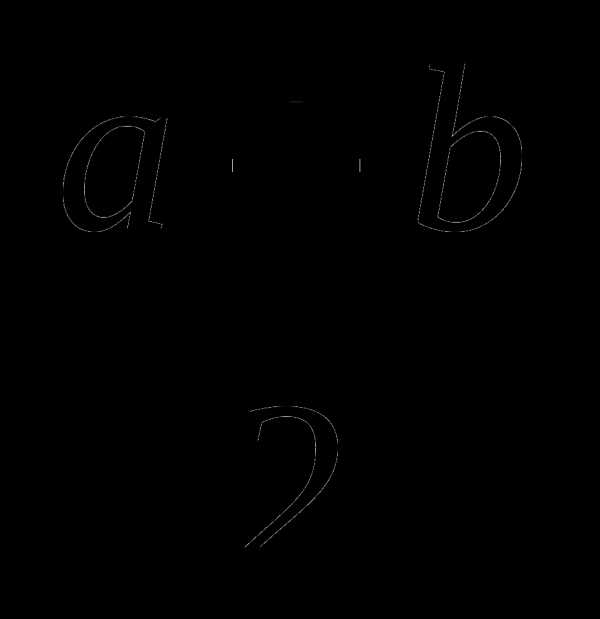h ж) S= a²

б) S= ah д) S= ab

в) S= ab е) S= ab

infourok.ru

План-конспект урока по геометрии (8 класс) по теме: Четырехугольники

Открытый урок по геометрии в 8-м классе.

 Урок-зачет по теме: «Четырехугольники»

Учитель.

Тема нашего урока: урок-зачёт по теме «Четырёхугольники», который пройдёт в форме соревнования между двумя командами. В ходе урока мы систематизируем наши знания, вспомним определения, свойства, признаки, будем решать задачи, отгадывать кроссворды. Этот материал урока послужит многим в развитии интереса к геометрии.

I. Представление команд

Команда «РИТМ».

Девиз: «Решай, Ищи, Твори, Мысли»

Команда «Геометр».

Девиз:

Готовы бой принять мы смело
И свой девиз мы дарим вам:
Искать, решать, считать умело,
Ну, а победа – только нам!

II Разминка команд

Каждой команде предлагается кроссворд, в ходе отгадывания которого вспомните определения четырёхугольников, элементы четырёхугольников. Успех будет зависеть от каждого члена команды. (Рисунок1)

По горизонтали:

1. Четырёхугольник, у которого противоположные стороны параллельны.

2. Четырёхугольник, у которого только две противоположные стороны параллельны.

3. Параллелограмм, у которого все углы прямые.

4. Точки, из которых выходят стороны четырёхугольников.

По вертикали

:

5. Отрезок, соединяющий противолежащие вершины четырёхугольника.

6. Прямоугольник, у которого все стороны равны.

7. Параллелограмм, у которого все стороны равны.

8. Отрезок, соединяющий соседние вершины четырёхугольника.

1. Прослушайте сказку, которая закончится вопросами. Кто первым и правильно ответит на них?

… Собрались все четырёхугольники на лесной поляне и стали обсуждать вопрос о выборе своего короля. Долго спорили и не могли прийти к единому мнению. И вот один старый параллелограмм сказал: «Давайте все отправимся в царство четырёхугольников. Кто первым придёт, тот и будет королём!» Все согласились. Рано утром все отправились в далёкое путешествие. На пути фигур встретилась река, которая сказала: «Переплывут меня только те, у кого диагонали пересекаются, и точкой пересечения делятся пополам». Часть четырёхугольников остались на берегу, а остальные благополучно переплыли и пошли дальше.

На пути им встретилась высокая гора, которая сказала, что даст пройти только тем, у кого диагонали равны.

Несколько путешественников остались у горы, остальные пошли дальше. Дошли до большого обрыва, где был узкий мост. Мост сказал, что пропустит тех, у кого диагонали пересекаются под прямым углом. По мосту прошёл только один четырёхугольник, который первым добрался до царства и был провозглашён королём.

Вопросы:

Кто стал королём? (квадрат)

Кто был основным его соперником? (прямоугольник)

Кто первым вышел из соревнования? (трапеция)

2. Из каждой команды по одному «архитектору». Каждый получает набор равнобедренных прямоугольных треугольников. Кто быстрее составит все возможные четырёхугольники.

3. Остальные по плакатам в парах решают задачи.

Угол ВАС равен 40°, угол САД равен 20°. Найти все остальные углы АВСД.

Плакат 1.

Угол BAD равен 10°. Найти все неизвестные углы.

Плакат 2.

Угол ВАС равен углу ACD, угол CAD равен АСВ. Доказать, что ABCD – параллелограмм

.

Плакат 3.

Найти стороны параллелограмма ABCD, если его периметр равен 24 см,

АВ:ВС= 2:1.

Плакат 4.

ЕРКМ – ромб. ЕК=5см, угол КЕМ равен 60°. Найти периметр ромба.

Плакат 5.

Найти стороны параллелограмма АВСД, если периметр равен 24 см, АВ=АД

.

Плакат 6.

АВСД – трапеция, ВС=ЕД. Доказать, что ВСДЕ –параллелограмм.

Плакат 7.

III. Домашнее задание.

Сейчас вы услышите рассказы, почему четырёхугольники так называются (учащиеся представляют заранее подготовленные сообщения)

1 ученик

:

Термин «параллелограмм» греческого происхождения и согласно Проклу, был введён Евклидом.

Понятие параллелограмма и некоторые его свойства были известны ещё пифагорейцам. В «Началах» Евклида доказывается следующая теорема:

в параллелограмме противоположные стороны равны и противоположные углы равны, а диагональ разделяет его пополам.

Евклид не упоминает о том, что точка пересечения диагоналей параллелограмма делит их пополам. Он не рассматривает ни прямоугольника, ни ромба. Полная теория параллелограмма была разработана к концу средних веков и появилась в учебниках лишь в XVII веке. Все теоремы о параллелограммах основываются непосредственно или косвенно на аксиоме параллельности Евклида.

Параллелограмм даёт определения прямоугольнику, ромбу; в жизни параллелограмм –это рамы велосипедов, мотоциклов, где для жёсткости проведена диагональ. В физике параллелограмм применяется при изучении разложения сил, при нахождении равнодействующих сил.

2 ученик:

Слово «ромб» тоже греческого происхождения, оно означало в древности вращающееся тело, веретено, юлу. Ромб связывали первоначально с сечением, проведённым в обмотанном веретене. В «Началах» Евклида термин «ромб» встречается только один раз, свойства ромба вообще не изучаются.

Реечный домкрат для легковых автомобилей имеет форму ромба. Плиточники укладывают плитку в виде ромба, квадрата – из них получаются красивые узоры.

3 ученик:

Термин «квадрат» происходит от латинского слова – сделать четырёхугольным.

«Первый четырёхугольник, с которым познакомилась геометрия, был квадрат» писал Д.

Д. Мордухай-Болтовский.

Трапеция –

слово греческое, означавшее в древности «столик». Сравните трапеза, трапезная. В «Началах» термин «трапеция» применяется не в современном, а в другом смысле: любой четырёхугольник (не параллелограмм). «Трапеция» в нашем смысле встречается впервые у древнегреческого математика Посидония.

IV. Конкурс капитанов.

1. За одну минуту нарисовать человека, используя разные виды четырёхугольников.

2. Задание 1-ому капитану:

Каждую сторону ромба разделить на три равные части и через точки деления провести прямые, параллельные сторонам. Сколько ромбов получилось? (ответ – 14)

Задание 2-ому капитану:

Дан параллелограмм. Середины каждой пары его противолежащих сторон соединены отрезками. Сколько параллелограммов получилось? (ответ – 9)

V. Конкурс.

Тёмная лошадка.

Знаете ли вы меня- , хочу проверить.

Любую площадь я могу измерить.

Ведь у меня четыре стороны

И все они между собой равны.

И у меня равны все диагонали,

Углы мне они делят пополам и ими

На части равные разбит я сам. (Квадрат)

VI Вопросы команд друг другу

Чем отличается квадрат от ромба?

Чем отличается квадрат от прямоугольника?

VII Подведение итогов, награждение.

nsportal.ru

главная

Разработка урока «Площади четырехугольников»

Цели урока:

Проверка и систематизация знаний учащихся по данной теме.

Развитие мыслительной деятельности при выполнении практической работы.

Развитие творческих способностей, логического мышления учащихся.

Оборудование: мультимедийный проектор, раздаточный материал, демонстрационный материал для творческой работы № 1.

ХОД УРОКА

I. Организационный момент.

Приветствие учащихся.

II. Объявление темы и цели урока.

III. Проверка знаний.

Для проверки теоретических знаний учащихся проводится математический диктант (каждому ученику раздается сетка кроссвордов).

По горизонтали:

Четырехугольник, у которого противолежащие стороны параллельны;

Четырехугольник, у которого только две противолежащие стороны параллельны;

Параллелограмм, у которого все углы прямые;

Точки, из которых выходят стороны четырехугольников;

По вертикали:

Сумма длин всех сторон;

Отрезок, соединяющий противолежащие стороны четырехугольника;

Прямоугольник, у которого все стороны равны;

Параллелограмм, у которого все стороны равны;

Отрезок, соединяющий соседние вершины.

Проверка выполняется c помощью мультимедийного проектора.

IV. Самостоятельная работа по карточкам.

Для закрепления формул площади выполнить задания, подготовленные на карточках:

Ко всем четырехугольникам подберите формулы для вычисления их площади:

Четырехугольники	Формулы для вычисления площади
Квадрат Прямоугольник Ромб Параллелограмм Трапеция

Для выполнения проверки учащиеся обмениваются карточками. В это время на экране высвечивается таблица правильных ответов, по числу которых и выставляется оценка.

Карточки сдаются учителю.

V. Творческая работа.

Для отработки практических навыков использования формул проводится творческая 

работа № 1.

На парту раскладывается набор равнобедренных прямоугольных треугольников, которые равны между собой. Боковая сторона равнобедренного треугольника равна 4 см (30 треугольников).

Задание. Из этих треугольников составить: квадрат с площадью 16 кв.см, ромб – с площадью 
32 кв.см, прямоугольник – с площадью 32 кв.см, квадрат – с площадью 64 кв.см, параллелограмм – с площадью 48 кв.см, трапецию – с площадью 48 кв.см.

На развороте магнитной доски ученики по очереди выполняют пункты творческого задания, используя демонстрационный материал. Учитель проверяет правильность задания и демонстрирует его учащимся.

VI. Итог урока.

www.ppschool13.narod.ru

Ответы@Mail.Ru: что такое четырёхугольник?

Четырёхугольник — это геометрическая фигура (многоугольник), состоящая из четырёх точек (вершин), три из которых не лежат на одной прямой, и четырёх отрезков (сторон), последовательно соединяющих эти точки. Различают выпуклые и не выпуклые четырёхугольники, не выпуклый четырёхугольник может быть самопересекающимся Виды четырёхугольников: Параллелограмм — четырёхугольник, у которого все противоположные стороны попарно равны и параллельны; Прямоугольник — четырёхугольник, у которого все углы прямые; Ромб — четырёхугольник, у которого все стороны равны; Квадрат — четырёхугольник, у которого все углы прямые и все стороны равны; Трапеция — четырёхугольник, у которого две противоположные стороны параллельны; Дельтоид — четырёхугольник, у которого две пары смежных сторон равны. Антипараллелограмм, или контрпараллелограмм — четырёхугольник, в котором каждые две противоположные стороны равны между собою, но не параллельны, в отличие от параллелограмма, а антипараллельны.

это либо квадратный унитаз либо геометрическая фигура содержащая четыре стороны и четыре угла

четыре угла по 90 градусов

То, что имеет 4 угла ) Любая фигура с 4мя углами.

touch.otvet.mail.ru

Математику нельзя изучать, наблюдая, как это делает сосед

microbik.ru

1 ГЕОМЕТРИЯ 8 КЛАСС «Четырехугольники» (Урок обобщения, систематизации и контроля знаний и умений) Цели урока: Закрепить, обобщить теоретический материал по теме «Четырехугольники» Совершенствовать навыки решения задач по теме Правила работы в группе Выбрать капитана. Капитаны по ходу урока заполняют оценочные листы для своей группы. В конце урока капитаны подсчитывают баллы, набранные каждым участником и всей командой в целом. Содержание Цели урока Правила работы в группе Разминка Кроссворд Ответы к кроссворду Защита презентаций (творческое домашнее задание) Параллелограмм Трапеция Прямоугольник Ромб Квадрат Схема Определить номера клеток , в которых находятся четырехугольники ? Четырехугольники КРОССВОРД По горизонтали: 1. Четырехугольник, у которого противоположные стороны параллельны 2. Четырехугольник, у которого только две стороны параллельны 3. Параллелограмм, у которого все углы прямые 4. Точки из которых выходят стороны четырехугольника По вертикали: 1. Сумма длин всех сторон 5. Отрезок, соединяющий противолежащие вершины 6. Прямоугольник, у которого все стороны равны 7. Параллелограмм , у которого все стороны равны 8. Отрезок, соединяющий соседние вершины Ответы к кроссворду По горизонтали: 1. Четырехугольник, у которого противоположные стороны параллельны 2. Четырехугольник, у которого только две стороны параллельны 3. Параллелограмм, у которого все углы прямые 4. Точки из которых выходят стороны четырехугольника По вертикали: 1. Сумма длин всех сторон 5. Отрезок, соединяющий противолежащие вершины 6. Прямоугольник, у которого все стороны равны 7. Параллелограмм , у которого все стороны равны 8. Отрезок, соединяющий соседние вершины Четырехугольники: Установите взаимосвязь по свойствам между данными четырехугольниками: Проверка теоретических знаний заполните таблицу ^ Проверочный тест ^ Решение задач на готовых чертежах Решение задач В ромбе ABCD биссектриса угла ВAC пересекает сторону ВС и диагональ BD соответственно в точках М и N. Найдите угол АNВ, если АМС = 120 . Решение: В ромбе противолежащие углы равны и т.е. Т.к. АМ – биссектриса то В треугольнике АМС В ромбе диагонали взаимно перпендикулярны, треугольник АОВ – прямоугольный, В треугольнике АВN Ответ: Проверочная работа (19 минут) Решите тест, ответы запишите в таблицу Таблица верных ответов итог урока ОСНОВНЫЕ РЕЗУЛЬТАТЫ Мы повторили Теоретический материал по теме «Четырехугольники» Совершенствовали Навыки решения задач Проверили свои знания и умения по теме Контрольные вопросы В параллелограмме: -противоположные стороны … -противоположные углы… стороне…. -диагонали… В прямоугольнике: — диагонали В ромбе: — диагонали В равнобедренной трапеции: — углы, при основании… — диагонали … Признаки параллелограмма: — если в четырехугольнике …, то этот четырехугольник- параллелограмм. Домашнее задание Подготовка к контрольной работе -решить задачи (индивидуальные карточки)

microbik.ru